Лекция 3 динамика вращательного движения
44
В природе и технике
мы постоянно сталкиваемся с вращательным
движением. При изучении динамики
поступательного движения твердого тела
использовались такие понятия как масса m,
сила 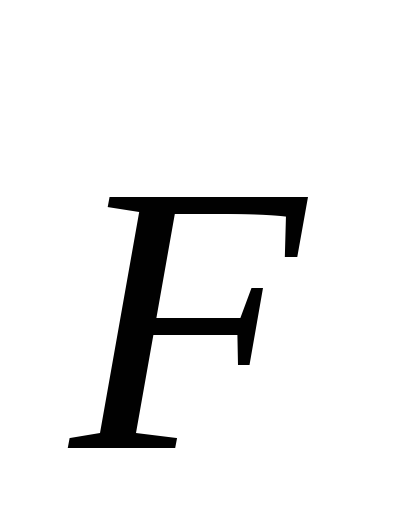 ,
импульс тела
,
импульс тела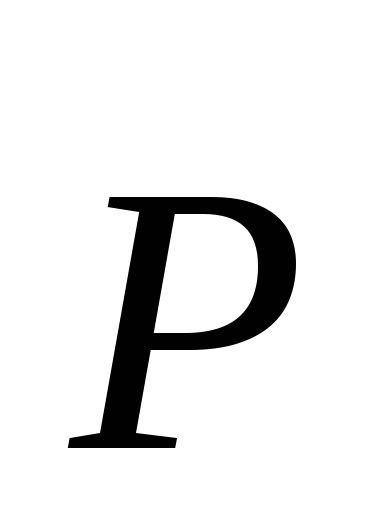 .
Однако для вращательного движения этих
понятий недостаточно. Для вращательного
движения необходимы новые понятия:
момент силы
.
Однако для вращательного движения этих
понятий недостаточно. Для вращательного
движения необходимы новые понятия:
момент силы 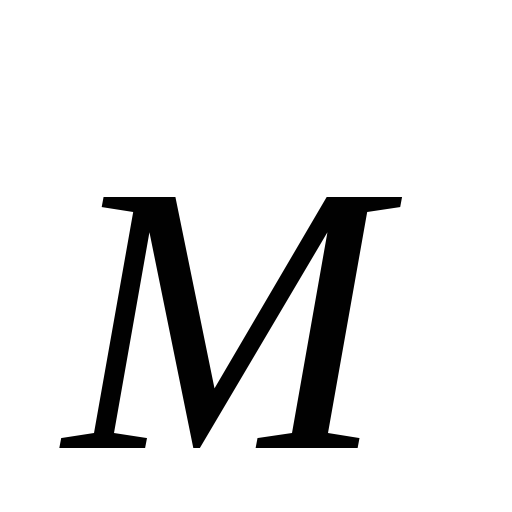 ,
момент импульса
,
момент импульса 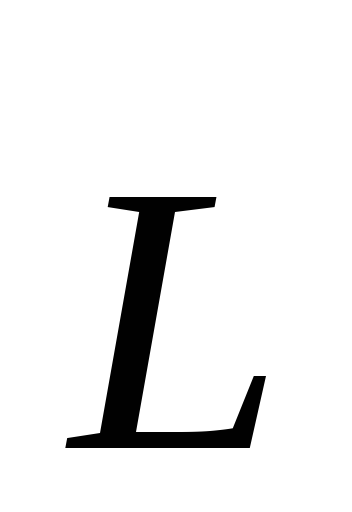 ,
момент инерцииI.
,
момент инерцииI.
3.1. Основной закон динамики вращательного движения материальной точки
Пусть материальная точка движется по окружности радиусом
 .
Положение точки будем характеризовать
радиус-вектором
.
Положение точки будем характеризовать
радиус-вектором ,
проведенным из центра окружности. Под
действием касательной силы
,
проведенным из центра окружности. Под
действием касательной силы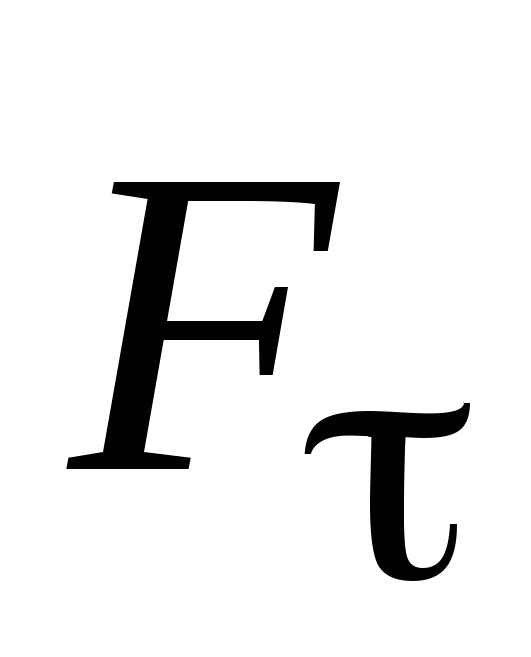 ,
материальная точка приобретает
касательное ускорение
,
материальная точка приобретает
касательное ускорение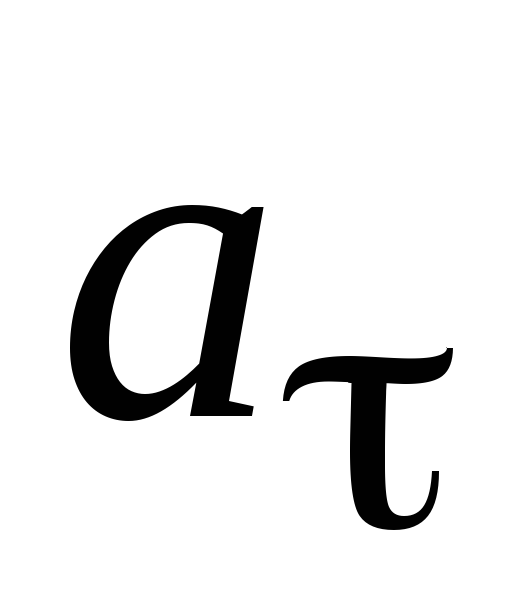 (рис. 3.1).
(рис. 3.1). 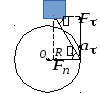
Рис. 3.1
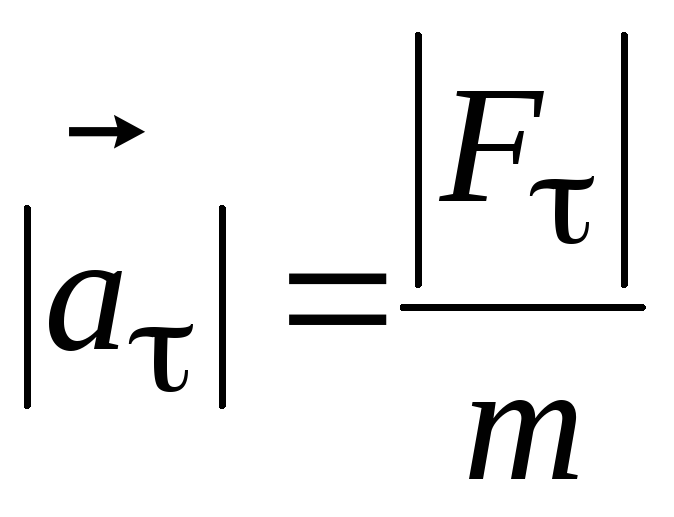 .
.
Выразим 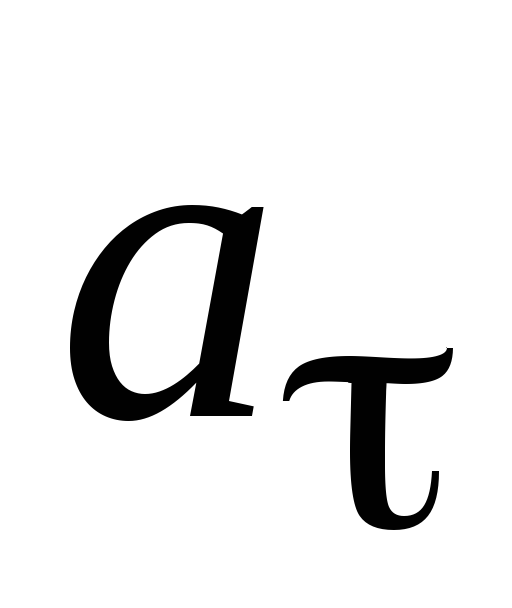 через угловое ускорение:
через угловое ускорение: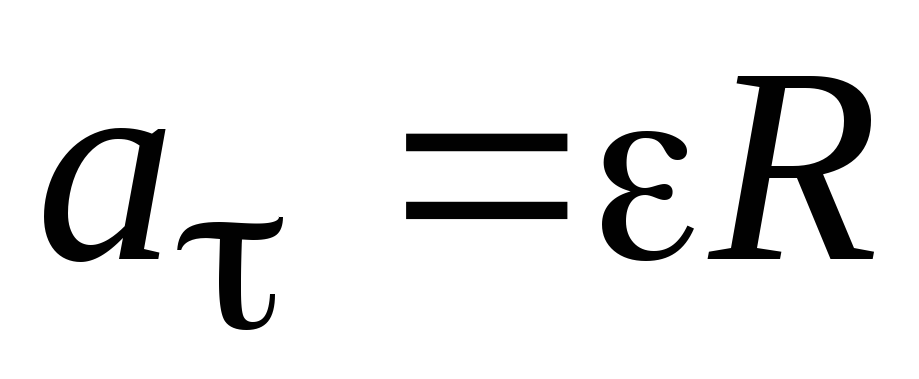 .
С учетом этого, умножая и деля наR, получим:
.
С учетом этого, умножая и деля наR, получим:
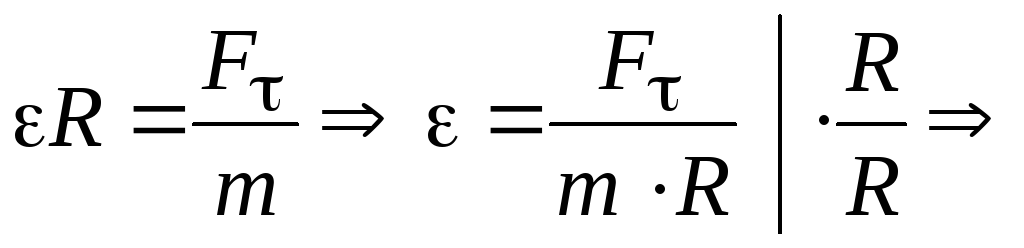
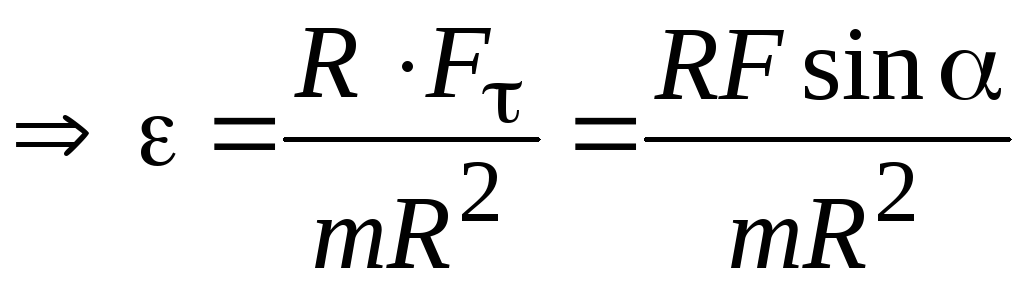 (3.1)
(3.1)
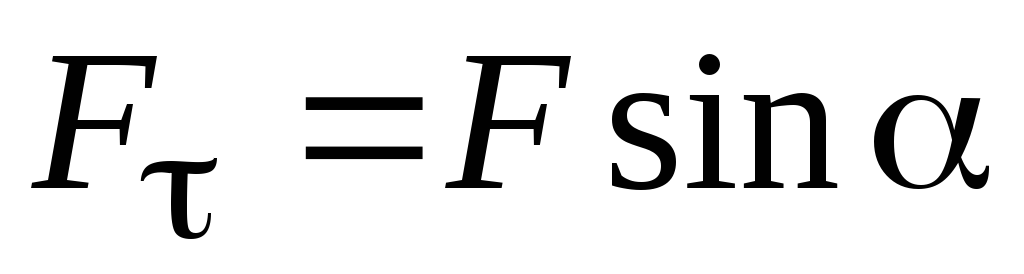 ,
где
угол между векторами
,
где
угол между векторами  и
и ).
). Введем обозначения:  момент силы материальной точки;
момент силы материальной точки; 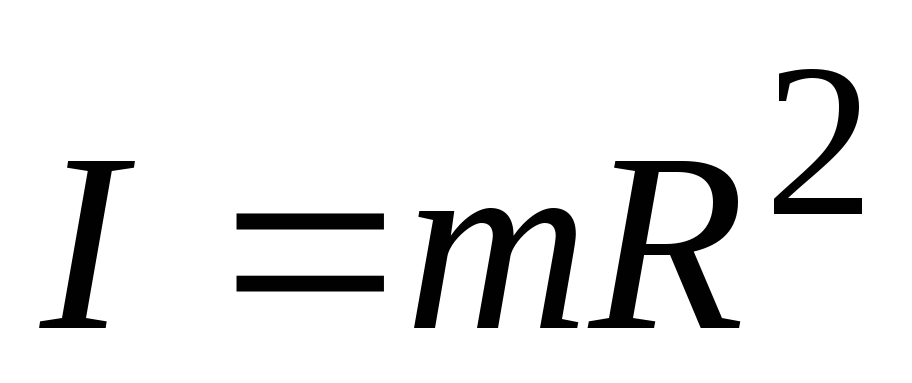 момент инерции материальной точки.
момент инерции материальной точки.
Тогда уравнение (3.1) примет вид:
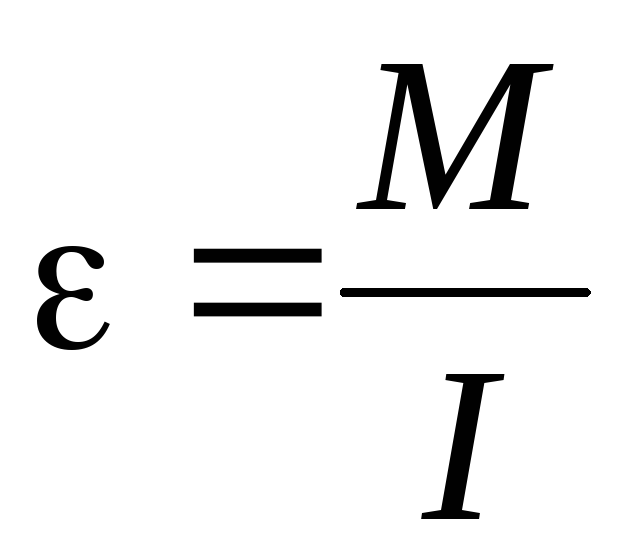 .
(3.2)
.
(3.2)
Угловое ускорение  является вектором, а
является вектором, а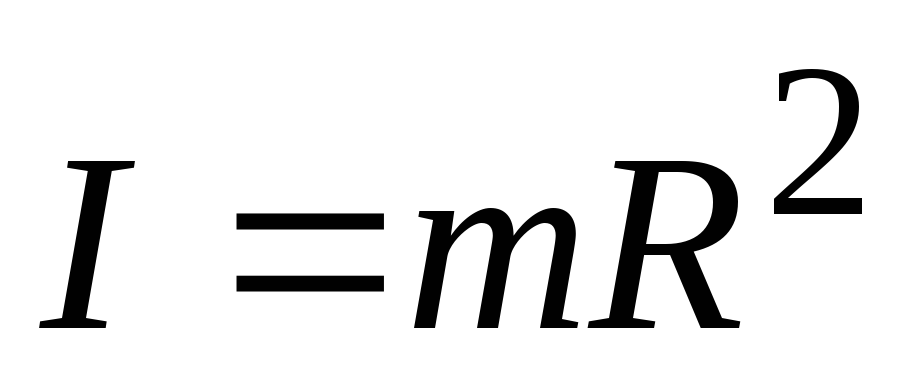
скаляр, поэтому
скаляр, поэтому 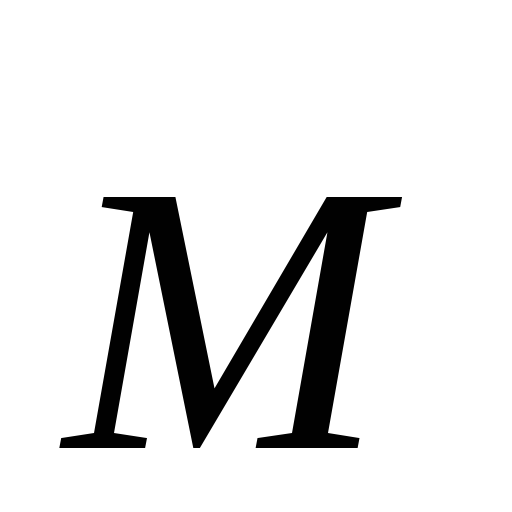 – тоже вектор, направление которого
совпадает с направлением
– тоже вектор, направление которого
совпадает с направлением .
В силу этого формулу (3.2) запишем в
векторном виде:
.
В силу этого формулу (3.2) запишем в
векторном виде: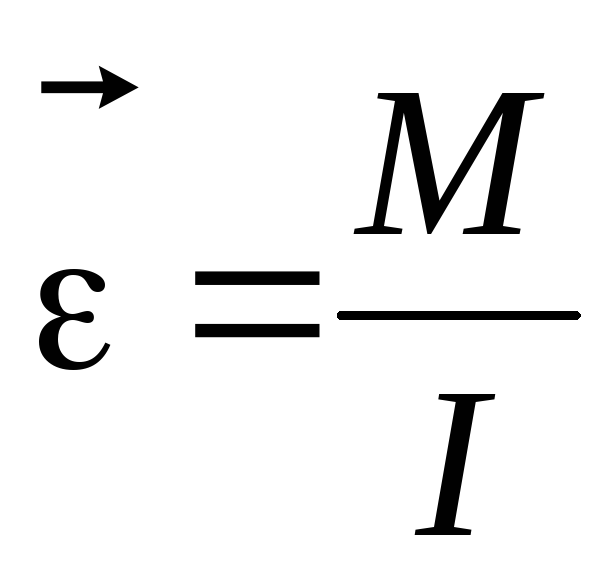
3.2. Момент силы относительно оси и точки
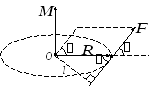
Рис.3.2
Согласно формуле
(3.2), момент силы 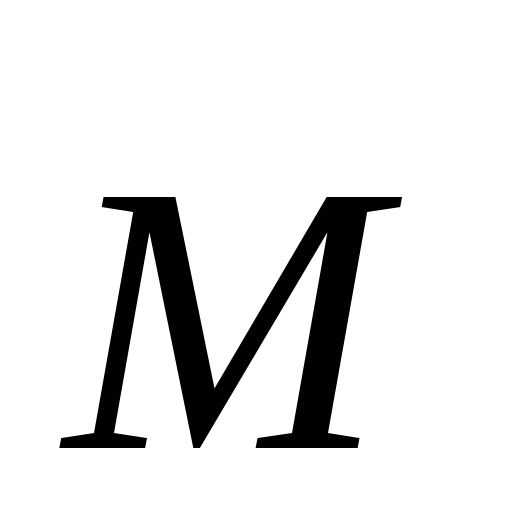 обуславливает угловое ускорение тела.
Следовательно,момент
силы
обуславливает угловое ускорение тела.
Следовательно,момент
силы
Моментом силы 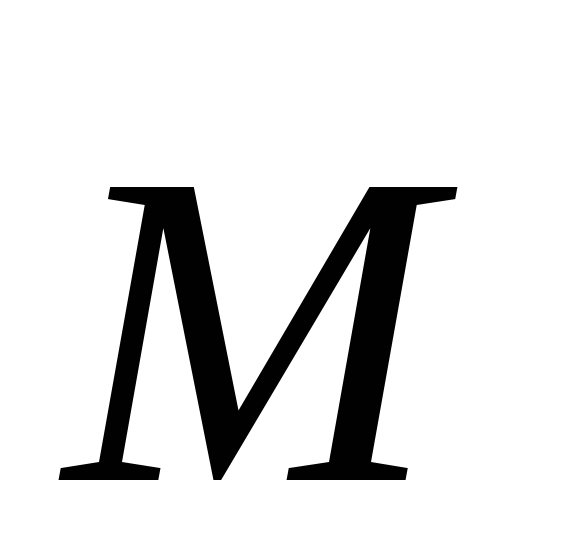 относительно точкиО называется векторное произведение
радиус-вектора
относительно точкиО называется векторное произведение
радиус-вектора  ,
проведенного из этой точки в точку
приложения силы, на силу
,
проведенного из этой точки в точку
приложения силы, на силу ,
т.е.
,
т.е.
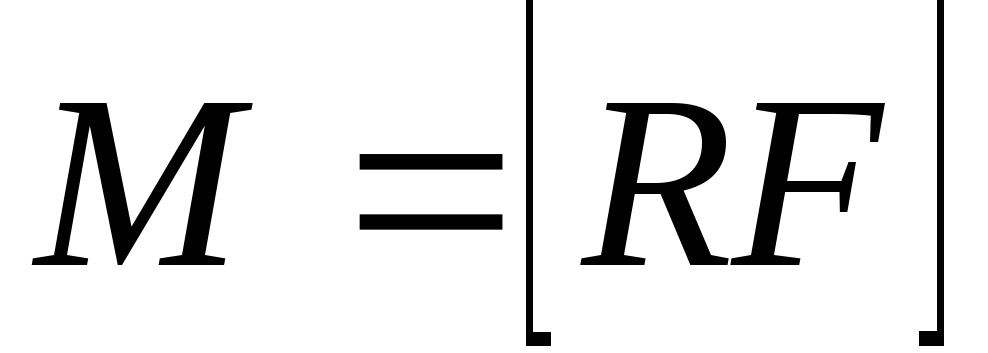 .
(3.3)
.
(3.3)
Вектор 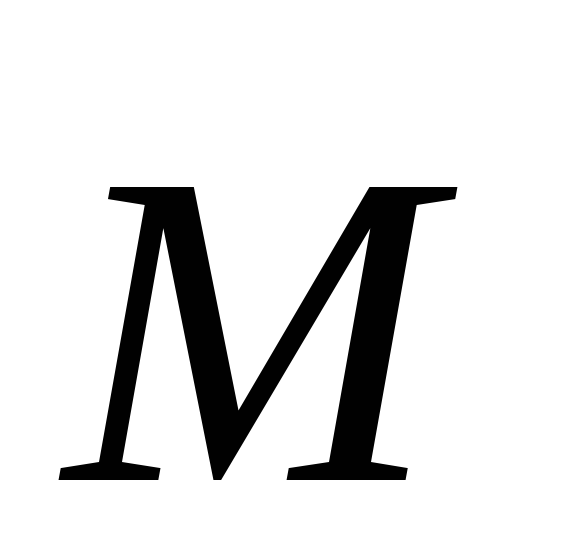
 и
и .
Его направление совпадает с поступательным
движением правого винта при его вращении
от
.
Его направление совпадает с поступательным
движением правого винта при его вращении
от к
к (рис.3.2).
(рис.3.2).Модуль момента силы можно записать как
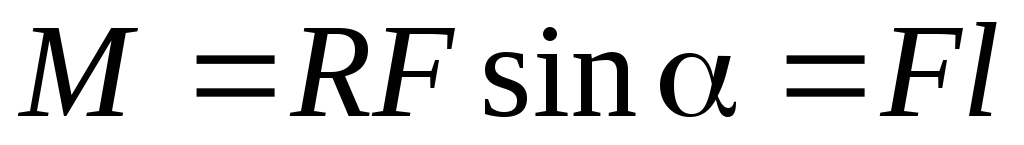
где 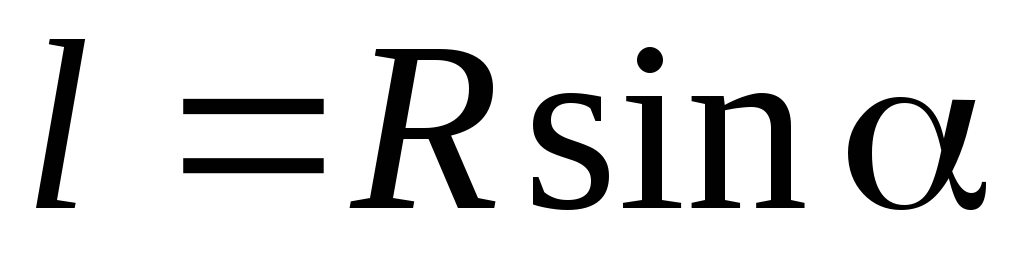
плечо силы
плечо силы  — кратчайшее расстояние от точкиО до линии действия силы.
— кратчайшее расстояние от точкиО до линии действия силы.
Момент силы относительно неподвижной оси z.

Моментом силы, относительно неподвижной оси
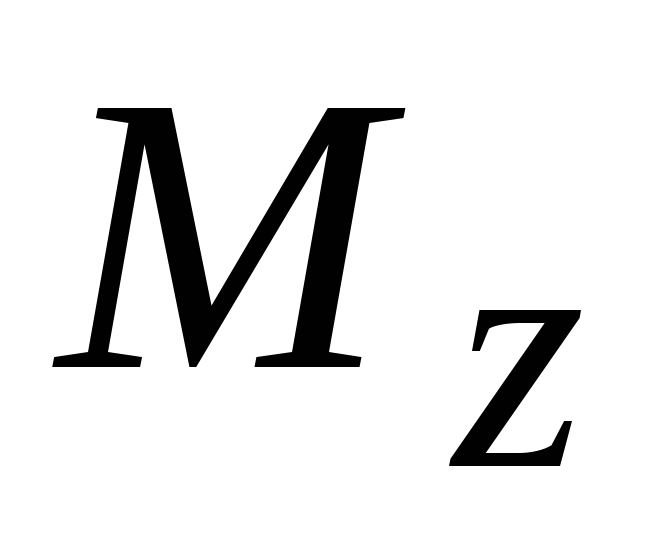 ,
равная проекции на эту ось вектора
момента силы
,
равная проекции на эту ось вектора
момента силы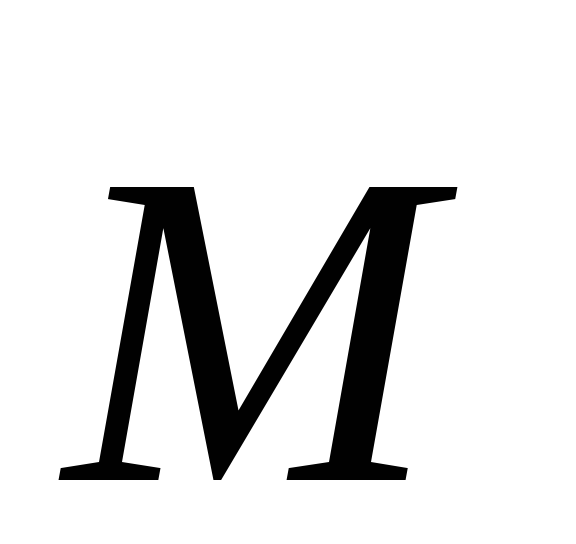 ,
определенного относительно произвольной
точки данной осиz
,
определенного относительно произвольной
точки данной осиz 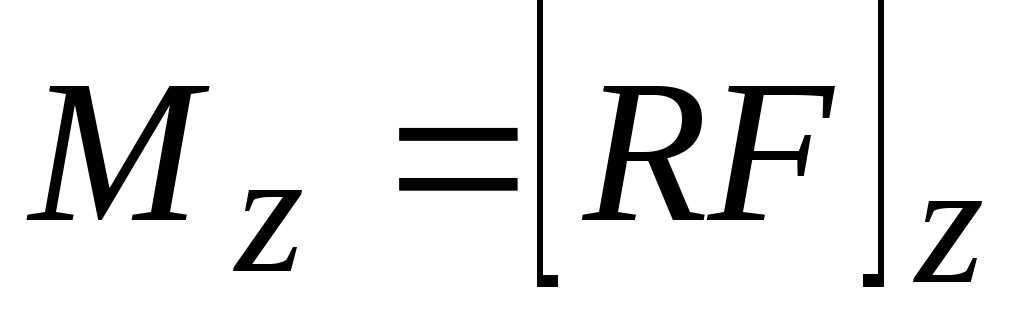 .
(3.5)
.
(3.5)
3.3. Момент инерции относительно неподвижной оси
Моментом инерции
тела относительно неподвижной оси называется физическая величина, равная
сумме произведений элементарных масс
на квадраты их расстояний до рассматриваемой
оси. Суммирование производится по всем
элементарным массам 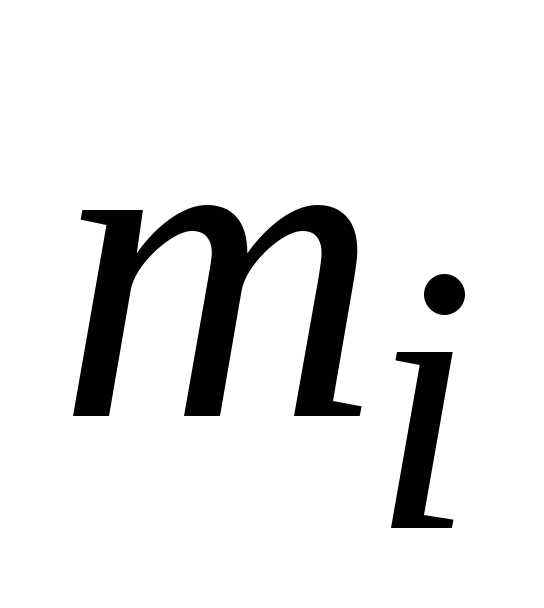
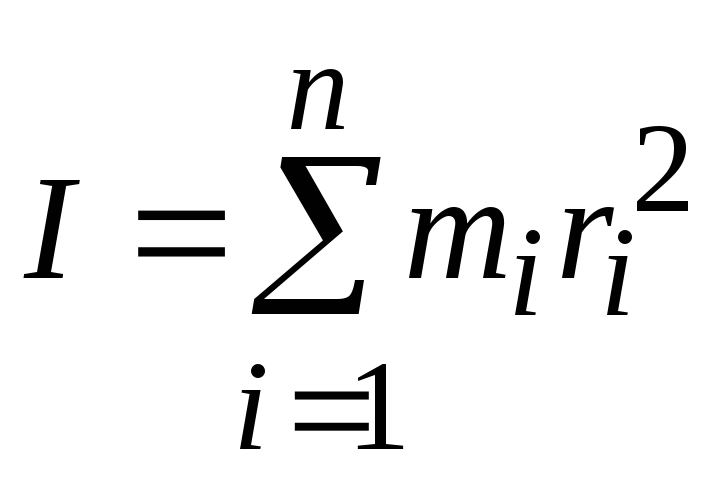 (3.6)
(3.6)
Момент инерции I – величина аддитивная: момент инерции тела равен сумме моментов инерций его частей.
В случае непрерывного распределения масс момент инерции определяется как
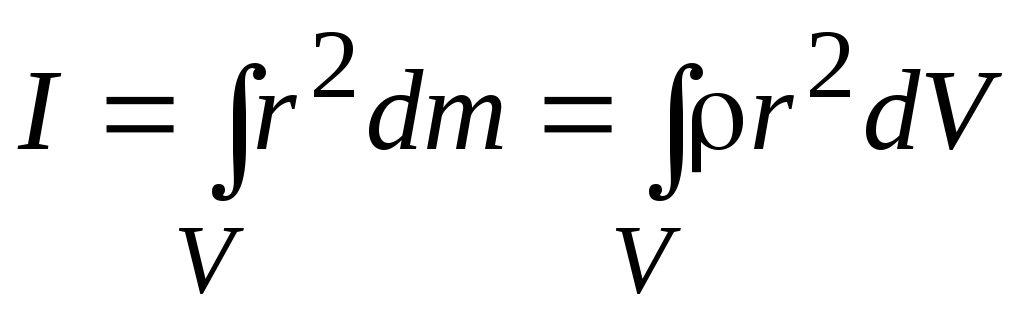 ,
(3.7)
,
(3.7)
где плотность тела в данной точке.
Физический смысл
момента инерции I.
Из опытов следует, что вращающиеся тела
обладают способностью противодействовать
изменению угловой скорости, которой
они обладают, т.е. противодействуют
приобретению углового ускорения.
Например, автомобильное колесо труднее
раскрутить, чем велосипедное. Это
свойство тел было названо инертностью
тела при вращательном движении. Из
соотношения 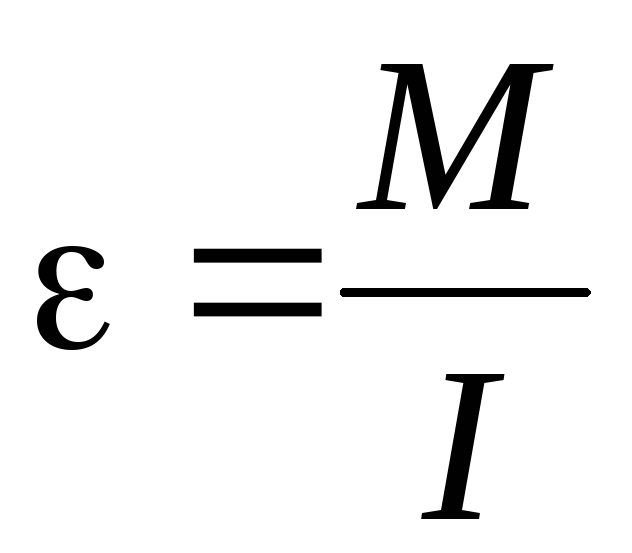 вытекает, что чем больше момент инерцииI,
тем меньше угловое ускорение ,
т.е. тем больше тело противодействует
изменению его угловой скорости.
Следовательно, величина
вытекает, что чем больше момент инерцииI,
тем меньше угловое ускорение ,
т.е. тем больше тело противодействует
изменению его угловой скорости.
Следовательно, величина 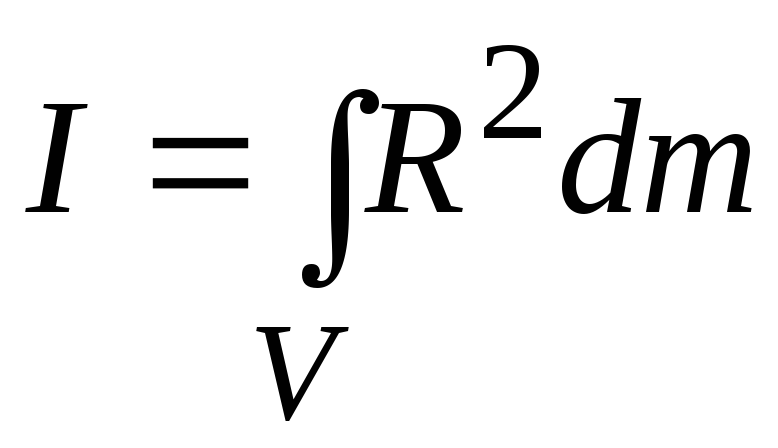
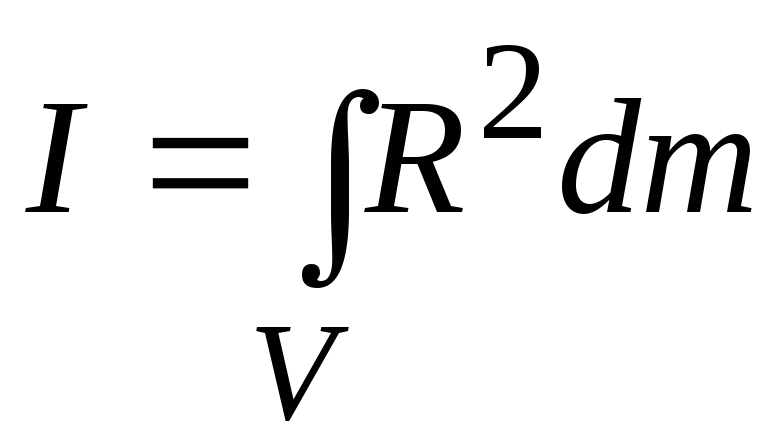 можно провести лишь для тел правильной
формы — цилиндра, шара и др.
можно провести лишь для тел правильной
формы — цилиндра, шара и др.Пример 1. Вычислим момент инерции тонкостенного обруча массой т и радиуса R относительно оси, проходящей через его центр перпендикулярно к его плоскости (рис.3.3).
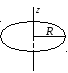
Рис.3.3
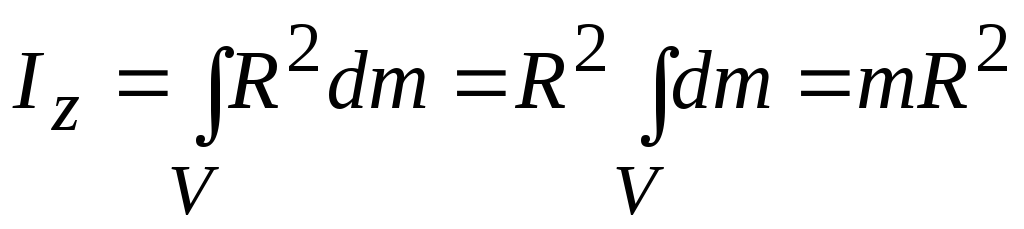 .
(3.8)
.
(3.8)
Пример 2. Вычислим момент инерции однородного сплошного цилиндра, радиуса R относительно его геометрической оси (рис.3.4).
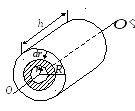
Рис.3.4
Разобьем цилиндр
на отдельные полые концентрические
цилиндры бесконечно малой толщины dr с внутренним радиусом r и внешним радиусом r + dr.
Момент инерции каждого полого цилиндра: 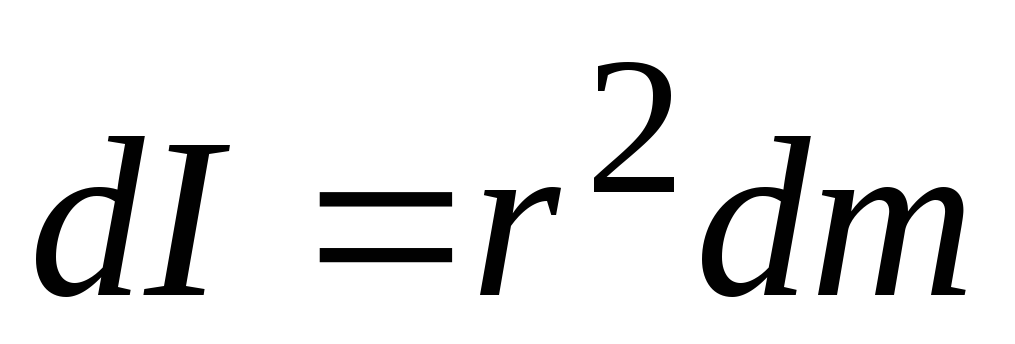 ;
объем элементарного цилиндра:
;
объем элементарного цилиндра: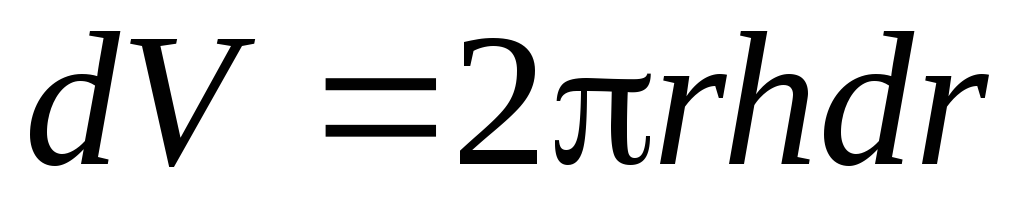 ;
его масса:
;
его масса: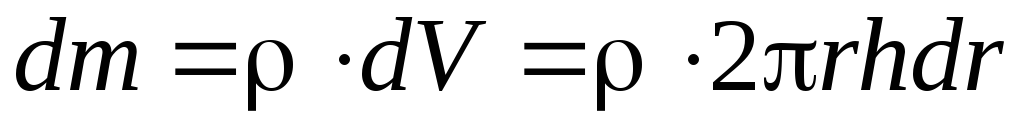 .
С учетом этого элементарный момент
инерции равен:
.
С учетом этого элементарный момент
инерции равен: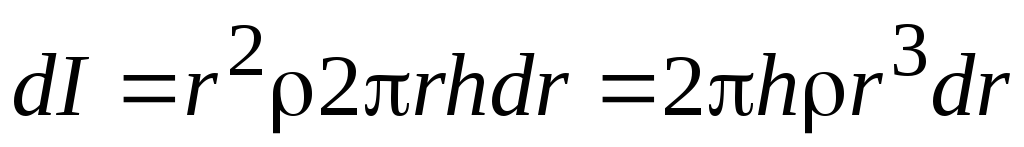 .
.
Момент инерции сплошного цилиндра:
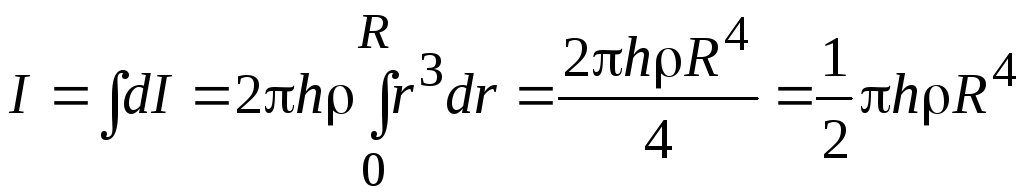 .
.
Поскольку объем
цилиндра V=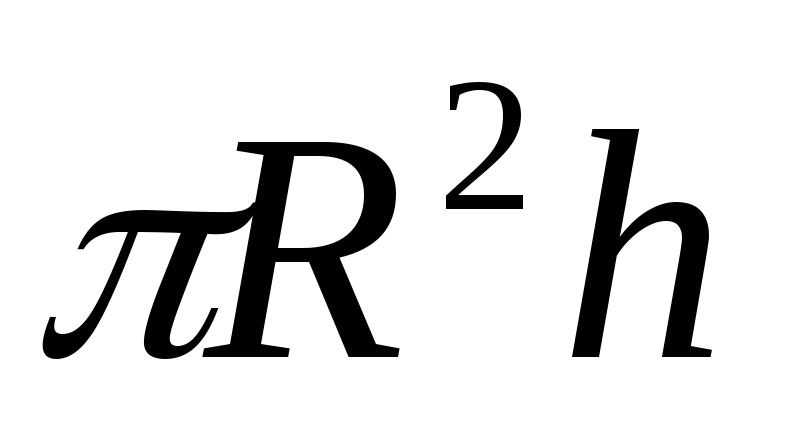 ,
его масса
,
его масса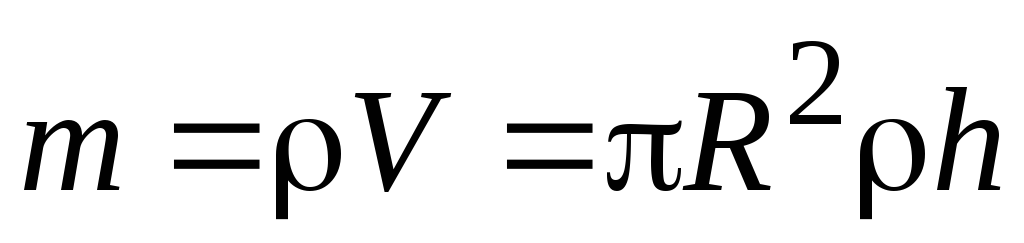 ,
то
момент инерции сплошного цилиндра
,
то
момент инерции сплошного цилиндра
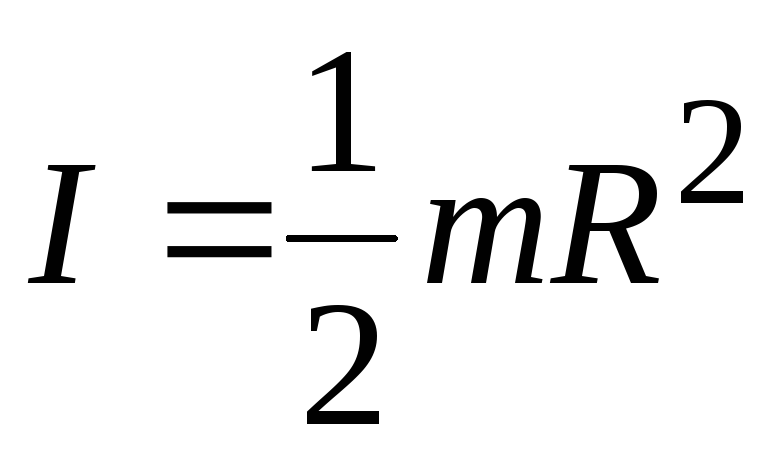 (3.9)
(3.9)
В таблице 3.1 приведены моменты инерции однородных тел
Таблица 3.1
Тело | Положение оси вращения | Момент инерции |
Полый тонкостенный цилиндр | Ось симметрии | |
Сплошной цилиндр или диск | Ось симметрии | |
Шар, радиуса R | Ось проходит через центр шара | |
Прямой тонкий стержень длиной l | 1. Ось перпендикулярна стержню и проходит через его середину | |
Прямой тонкий стержень длиной l | 2. Ось проходит через конец стержня | |
Теорема Штейнера. Если известны
моменты инерции тела относительно осей,
проходящих через центр масс С,
то момент инерции относительно
произвольной оси z находят, используя теорему Штейнера: момент инерции
тела I относительно произвольной оси вращения
равен моменту его инерции 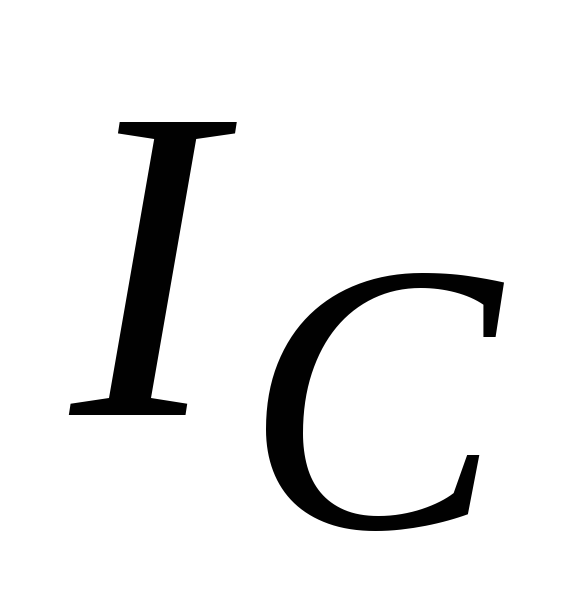 относительно параллельной оси, проходящей
через центр масс тела, сложенному с
произведением массы т тела на квадрат
расстояния а между ними:
относительно параллельной оси, проходящей
через центр масс тела, сложенному с
произведением массы т тела на квадрат
расстояния а между ними:
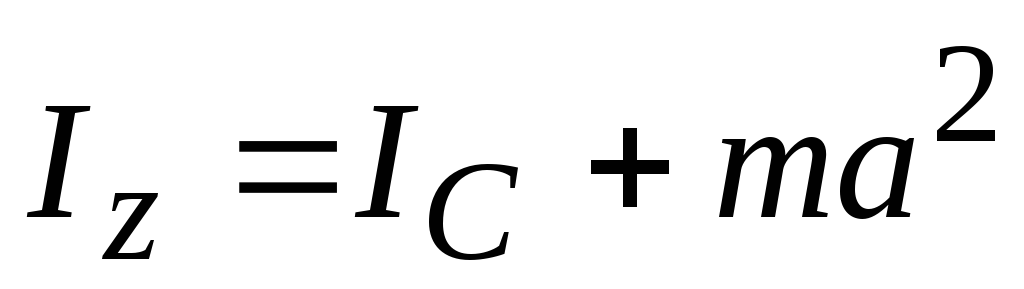 .
(3.10)
.
(3.10)
Пример: Момент инерции тонкого стержня длины l относительно оси, проходящей через его конец (рис.3.5)
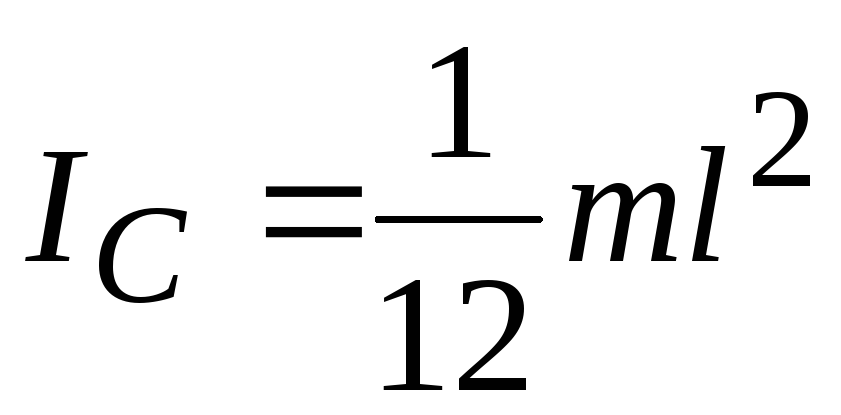 .
.
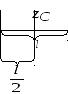
Рис.3.5
По теореме Штейнера
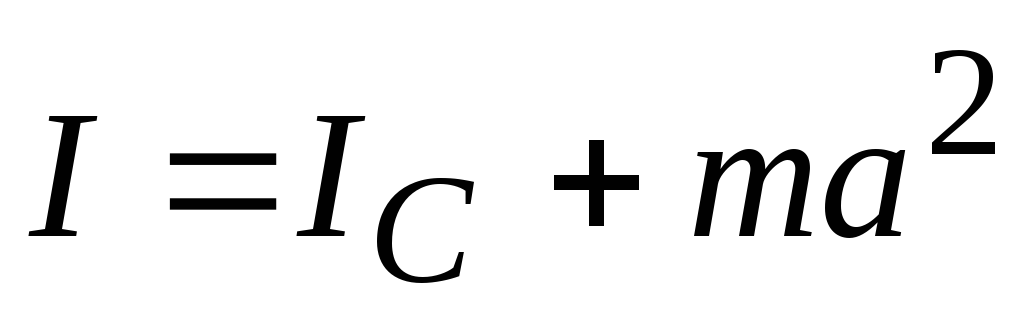
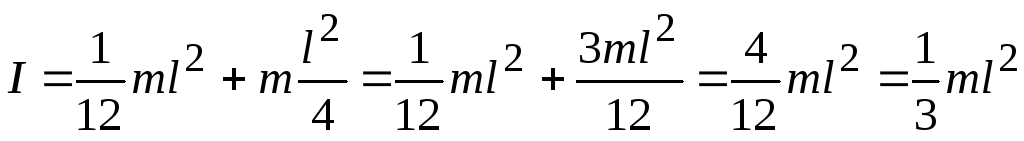 .
.
9. Основное уравнение динамики вращательного движения твердого тела вокруг оси. Момент инерции.
Основное уравнение динамики вращательного движения твёрдого тела вокруг неподвижной оси имеет вид:
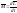
где  —
суммарный момент внешних сил, действующих
на тело, относительно оси вращения;
—
суммарный момент внешних сил, действующих
на тело, относительно оси вращения;
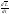 —
производная от момента количества
движения;
—
производная от момента количества
движения;
 —
момент количества движения твёрдого
тела относительно оси вращения,
—
момент количества движения твёрдого
тела относительно оси вращения,  —
угловая скорость вращения тела,
—
угловая скорость вращения тела,
 —
момент инерции тела относительно данной
оси вращения, равный сумме моментов
инерции материальных точек
—
момент инерции тела относительно данной
оси вращения, равный сумме моментов
инерции материальных точек  ,
находящихся на кратчайшем расстоянии
,
находящихся на кратчайшем расстоянии относительно
этой оси.
относительно
этой оси.
Момент
инерции тела  относительно произвольной оси,
параллельной оси, проходящей через
центр масс, определяется по теореме
Гюйгенса-Штейнера:
относительно произвольной оси,
параллельной оси, проходящей через
центр масс, определяется по теореме
Гюйгенса-Штейнера:
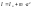
где  — момент инерции тела относительно оси
вращения, проходящей через центр его
масс,
— момент инерции тела относительно оси
вращения, проходящей через центр его
масс, —
масса тела,
—
масса тела, —
кратчайшее расстояние между осями.
—
кратчайшее расстояние между осями.
Если
за время движения момент инерции не
измениться (что реализуется в данной
установке), т.е.  ,
то уравнение (1) принимает вид:
,
то уравнение (1) принимает вид:
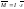 (3)
(3)
где 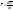 —
угловое ускорение тела, связанное с
тангенциальным ускорением
—
угловое ускорение тела, связанное с
тангенциальным ускорением любой точки тела равенством:
любой точки тела равенством:
10. Энергия, как единая мера различных форм движения материи. Работа. Вычисление работы переменной силы. Мощность.
Энергия – это скалярная физическая величина, являющаяся единой мерой различных форм движения материи и мерой перехода движения материи из одних форм в другие
Энергия в природе не возникает из ничего и не исчезает; она только может переходить из одной формы в другую.
Механическая
работа —
это физическая величина, являющаяся
скалярной количественной мерой действия
силы или сил на тело или систему,
зависящая от численной величины,
направления силы (сил) и от перемещения
точки (точек) тела или системы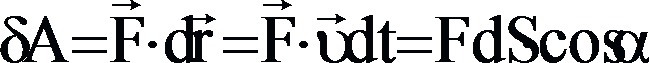
Работа
силы на участке траектории от точки 1 до точки 2 равна алгебраической сумме элементарных
работ на отдельных бесконечно малых
участках пути. Эта сумма приводится к
интегралу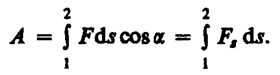 Единица
работы —джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н
на пути 1 м (1 Дж=1 Н•м). Чтобы
охарактеризовать скорость совершения
работы, вводят понятие мощности:
Единица
работы —джоуль (Дж): 1 Дж — работа, совершаемая силой 1 Н
на пути 1 м (1 Дж=1 Н•м). Чтобы
охарактеризовать скорость совершения
работы, вводят понятие мощности: 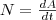 За
время dt силаF совершает работу Fdr,
и мощность, развиваемая этой силой, в
данный момент времени
За
время dt силаF совершает работу Fdr,
и мощность, развиваемая этой силой, в
данный момент времени 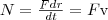 т.
е. равна скалярному произведению вектора
силы на вектор скорости, с которой
движется точка приложения этой силы;
N — величина скалярная. Единица
мощности —ватт (Вт): 1 Вт — мощность, при которой за время
1 с совершается работа 1 Дж (1 Вт = 1 Дж/с).
т.
е. равна скалярному произведению вектора
силы на вектор скорости, с которой
движется точка приложения этой силы;
N — величина скалярная. Единица
мощности —ватт (Вт): 1 Вт — мощность, при которой за время
1 с совершается работа 1 Дж (1 Вт = 1 Дж/с).
Работа переменной силы. Если сила или равнодействующая сил изменяет свою величину или направление (движение по криволинейной траектории, причем угол α ≠ 900), то работа ∆А, совершаемая переменной силой F (или Fрез) на конечном участке траектории вычисляется следующим образом.
Работа
А, совершаемая силой F, равна
алгебраической сумме работ, совершаемых
каждой из сил F i на своем малом участке А = ∆А1 + ∆А2 +….+ ∆А N = ( F1∙∆ r1)
+ (F 2∙∆ r2)
+ …+( F N∙∆ rN)
=  (Fi∙∆ ri),
(Fi∙∆ ri),
,где i = 1,2…… N — номер элементарного участка траектории.
Динамика вращательного движения
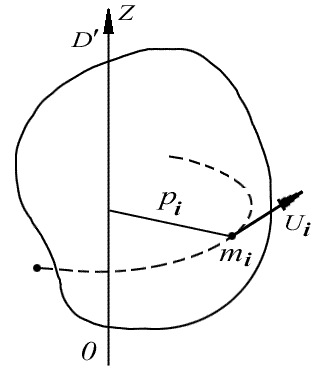
Установим взаимосвязь между кинематическими и динамическими параметрами вращательного движения. Пусть твердое тело вращается вокруг неподвижной осиZZ′. Т.к. все точки тела движутся по окружностям, плоскость которых перпендикулярна оси вращения, то это означает, что равнодействующие сил приложенных к каждой точке лежат в плоскости траекторий. Разложим равнодействующую сил, приложенную к элементу массыmiна две составляющие:– вдоль радиусаи– касательную к троектории. Нормальная составляющая сил, линия действия которой лежит в плоскости траектории, проходит черезZZ′и обеспечивает центростремительное ускорение элемента массыmi и не влияет на величину углового ускорения. Составляющаявызывает тангенциальное ускорение. По второму закону Ньютона
. (20)
С учетом (16)
Fi,=miri. (21)
Умножив (21) на ri, получим:
, (22)
, (23)
где – момент силыотносительно осиZZ′.
Моментом силы называется вектор, модуль которого равен произведению модуля силы на длину плеча. Направление вектора перпендикулярно к плоскости, в которой лежит вектор силы, и определяется по правилу буравчика.
Плечом силы называется кратчайшее расстояние от оси вращения до линии действия силы.
Скалярная величина называется момент инерции материальной точки относительно осивращенияZZ′.
Просуммируем (23) по всем элементам массы тела: . Получим:
или в векторном виде(24)
Здесь — результирующий момент силы, действующий на тело;- момент инерции тела.
Равенство (24) называется основным уравнением динамики вращательного движения. Т.к. скалярная величина Jвсегда положительная, то векторные величиныивсегда направлены в одну сторону вдоль оси вращения тела.
Основное уравнение динамики вращательного движения по форме сходно с математическим выражением второго закона Ньютона:
↔
Из сопоставления вытекает, что при вращательном движении роль силы играет момент силы (вращательный момент), а инертные свойства тела выражаются моментом инерции тела – J.
Момент импульса. Закон сохранения момента импульса
Моментом импульса материальной точки относительно оси вращения называют векторную величину, модуль которой
.(25)
Тогда момент импульса абсолютно твердого тела относительно неподвижной оси вращения
или в векторной форме, (26)
т.е. лежит на оси вращения и совпадает по направлению с(на-
правление определяется так же как и для– по правилу буравчика).
Запишем для нашего тела основное уравнение динамики вращательного движения в виде:
(27)
Если М = 0, то dL/dt= 0 т.е.
L=J=const. (28)
Момент импульса тела остается неизменным, если суммарный момент всех внешних сил действующих на тело равен нулю – это закон сохранения момента импульса.
Для системы из Nтел, которые вращаются вокруг общей оси, закон сохранения импульса записывается в виде:
. (29)
Момент инерции твёрдых тел разной формы теорема штейнера
Из определения момента инерции тел в общем виде:
(30)
следует, что эта величина является аддитивной. Это означает, что моменты инерции тел в некоторых случаях можно найти интегрированием исходя из геометрических соображений.
В качестве примера найдём момент инерцииJтонкого стержня длинойl, массойmи диаметромd<<lотносительно осипроходящей через его центр масс перпендикулярно к стержню (Рис. 4). Выделим на расстояниихот оси вращения элемент стержня бесконечно малой толщиныdx.
Масса этого элемента dm=Sdx, где– плотность материала,S– площадь поперечного сечения. Момент инерции элемента массыdm:
() Учитывая, что элементы массы dm попарно симметричны относитель-
но оси вращения 00‘, проинтегрируем левую часть () в пределах от 0 доJ, а правую в пределах от 0 доl/2. Получим:
()
Т.к. – масса стержня, то окончательно для тонкого стержня
(33)
Определим момент инерции диск или цилиндра радиусомR, высотойhи массойmотносительно его геометрической оси, параллельной образующей. Выделим цилиндрический слой бесконечно малой толщиныdrи радиусомr. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя
.
Т.к. rизменяется в пределах отr= 0 доr=R, то интегрируя получим:
но ,
(36)
Без выводов запишем:
а) шар радиусом R и массой m, относительно оси, проходящей через его центр –(31)
б) полый тонкостенный цилиндр радиусом Rи массойm, относительно его геометрической оси, параллельной образующей –
(32)
Согласно теореме Штейнера момент инерции тела – Jотносительно любой оси, параллельной оси проходящей через центр масс этого тела –
, (33)
где J0– момент инерции тела относительно оси, проходящей через центр масс,d– расстояние между осями. Например, если ось вращения проходит через конец стержня,
то (34)
В качестве примера Определим момент инерции Jтонкого стержня длинойl, массойmи диаметромd<<l. Относительно осик перпендикулярной
а) тонкий однородный стержень.
к стержню и проходящей через его центр масс.
Выделим на расстоянии хот оси вращения элемент стержня бесконечно малой толщиныdx.
Масса этого элемента dm=Sdx, где-плотность материала,
S-площадь поперечного сечения. Момент инерции элемента массыdm
Интегрируем левую и правую части в пределах от 0 до Jи правую от 0 доl/2. Учитывая, что элементы попарно симметричны, получим:
Т.к. , то окончательно(33)
б) диск или цилиндр радиусом R, высотойhи массойm.
Определим момент инерции цилиндра относительно его геометрической оси, параллельной образующей.
Выделим цилиндрический слой бесконечно малой толщиныdrи радиусомr. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя
.
Т.к. rизменяется в пределах отr= 0 доr=R, то интегрируя получим:
но ,
(36)
Без выводов запишем:
а) тонкий однородный стержень –
(31)
б) диск или цилиндр радиусом R, высотойhи массойm-
(32)
Согласно теореме Штейнера момент инерции тела — Jотносительно любой оси, параллельной оси проходящей через центр масс этого тела
, (33)
где J0– момент инерции тела относительно оси через центр масс,d- расстояние между осями. Например, если ось вращения проходит через конец стержня,
то (34)
В качестве примера найдём момент инерции Jтонкого стержня длинойl, массойmи диаметромd<<l. Относительно осик перпендикулярной
а) тонкий однородный стержень.
к стержню и проходящей через его центр масс.
Выделим на расстоянии хот оси вращения элемент стержня бесконечно малой толщиныdx.
Масса этого элемента dm=Sdx, где-плотность материала,
S-площадь поперечного сечения. Момент инерции элемента массыdm
Интегрируем левую и правую части в пределах от 0 до Jи правую от 0 доl/2. Учитывая, что элементы попарно симметричны, получим:
Т.к. , то окончательно(33)
б) диск или цилиндр радиусомR, высотойhи массойm.
Определим момент инерции цилиндра относительно его геометрической оси, параллельной образующей.
Выделим цилиндрический слой бесконечно малой толщины drи радиусомr. Очевидно, что все элементы этого слоя будут иметь одинаковые моменты инерции. Это, значит, что момент инерции слоя
.
Т.к. rизменяется в пределах отr= 0 доr=R, то интегрируя получим:
но ,
(36)
Без выводов запишем:
а) тонкий однородный стержень –
(31)
б) диск или цилиндр радиусом R, высотойhи массойm-
(32)
Согласно теореме Штейнера момент инерции тела — Jотносительно любой оси, параллельной оси проходящей через центр масс этого тела
, (33)
где J0– момент инерции тела относительно оси через центр масс,d- расстояние между осями. Например, если ось вращения проходит через конец стержня,
то (34)
Без выводов запишем:
а) тонкий однородный стержень – ДОПОЛНИТЬ ВЫВОДОМ
(31)
б) диск или цилиндр радиусом R, высотойhи массойm-
(32)
Согласно теореме Штейнера момент инерции тела — J относительно любой оси, параллельной оси проходящей через центр масс этого тела
,(33)
гдеJ0– момент инерции тела относительно оси через центр масс,d- расстояние между осями. Например, для стержня, если ось вращения проходит через его конец (рис.1):
(34)
Динамика вращательного движения.
Основные понятия.
Момент
силы относительно
оси вращения 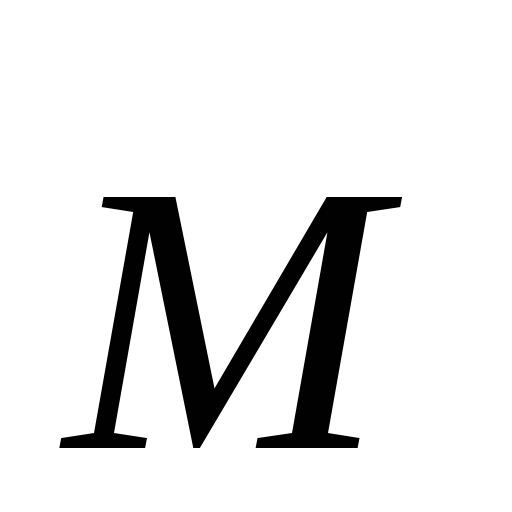 – это векторное призведение радиус-вектора
на силу.
– это векторное призведение радиус-вектора
на силу.
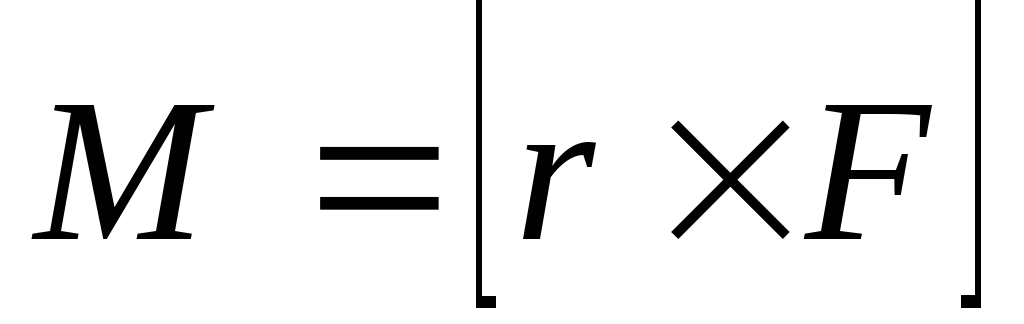 (1.14)
(1.14)
Момент силы – это вектор, направление которого определяется по правилу буравчика (правого винта) в зависимости от направления силы, действующей на тело. Момент силы направлен вдоль оси вращения и не имеет конкретной точки приложения.
Численное значение данного вектора определяется по формуле:
M=rFsin (1.15),
где — угол между радиус-вектором и направлением действия силы.
Если =0 или , момент силы М=0, т.е. сила, проходящяя через ось вращения или совпадающяя с ней, вращения не вызывает.
Наибольший по модулю вращающий момент создается, если сила действует под углом =/2 (М 0) или =3/2 (М 0).
Используя понятие плеча силы (плечо силы d – это перпендикуляр, опущенный из центра вращения на линию действия силы), формула момента силы принимает вид:
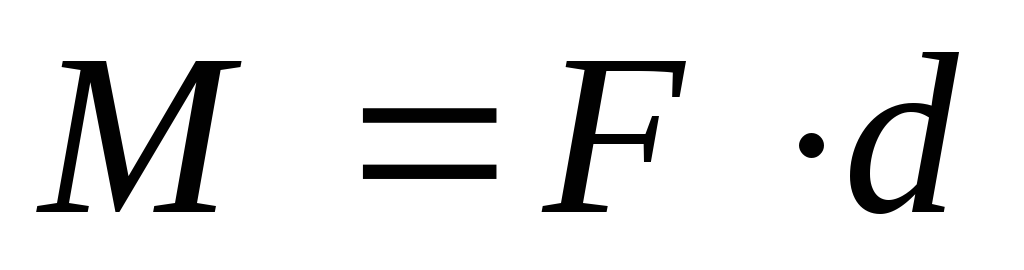 ,
где
,
где 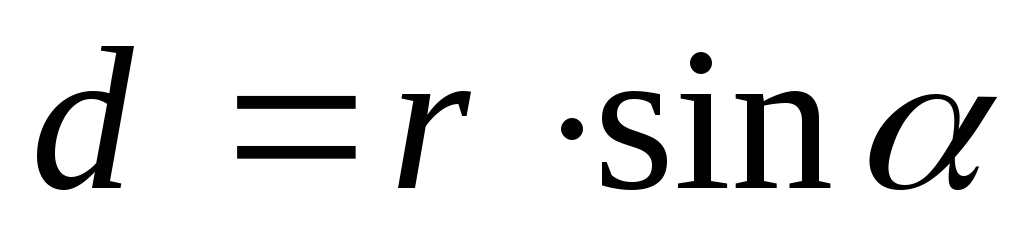 (1.16)
(1.16)
Правило моментов сил (условие равновесия тела, имеющего неподвижную ось вращения):
Для того, чтобы тело, имеющее неподвижную ось вращения, находилось в равновесии, необходимо, чтобы алгебраическая сумма моментов сил, действующих на данное тело, равнялась нулю.
Мi =0 (1.17)
Единицей измерения момента силы в системе СИ является [Нм]
При вращательном движении инертность тела зависит не только от его массы, но и от распределения ее в пространстве относительно оси вращения.
Инертность при вращении характеризуется моментом инерции тела относительно оси вращения J.
Момент инерции материальной точки относительно оси вращения – это величина, равная произведению массы точки на квадрат ее расстояния от оси вращения:
J=m r2 (1.18)
Моментом инерции тела относительно оси называется сумма моментов инерции материальных точек, из которых состоит тело:
J= m r2 (1.19)
Момент инерции тела зависит от его массы и формы, а также от выбора оси вращения. Для определения момента инерции тела относительно некоторой оси используется теорема Штейнера-Гюйгенса:
J=J0+m d2 (1.20),
где J0 – момент инерции относительно параллельной оси, проходящей через цент масс тела, d – расстояние между двумя параллельными осями. Момент инерции в СИ измеряется в [кгм2]
Момент инерции при вращательном движении туловища человека определяют опытным путем и рассчитывают приблизительно по формулам для цилиндра, круглого стержня или шара.
Момент инерции человека относительно вертикальной оси вращения, которая проходит через центр масс (центр масс тела человека находится в сагиттальной плоскости немного впереди второго крестцового позвонка), в зависимости от положения человека, имеет следующие значения: при стойке “смирно” – 1,2 кгм2; при позе «арабеск» – 8 кгм2; в горизонтальном положении – 17 кгм2.
Работа во вращательном движении совершается при вращении тела под действием внешних сил.
Элементарная работа силы во вращательном движении равна произведению момента силы на элементарный угол поворота тела:
dA=M d (1.21)
Если на тело действует несколько сил, то элементарная работа равнодействующей всех приложенных сил определяется по формуле:
dA=M d (1.22),
где М – суммарный момент всех внешних сил, действующих на тело.
Кинетическая энергия вращающегося тела Wк зависит от момента инерции тела и угловой скорости его вращения:
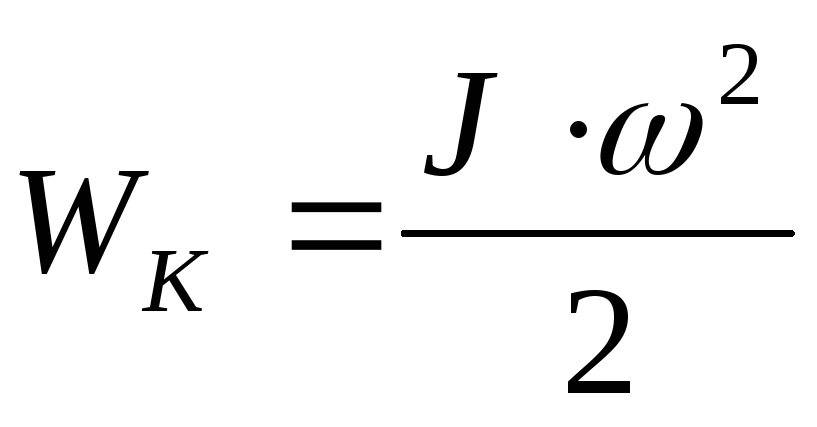 (1.23)
(1.23)
Момент
импульса (момент количества движения) 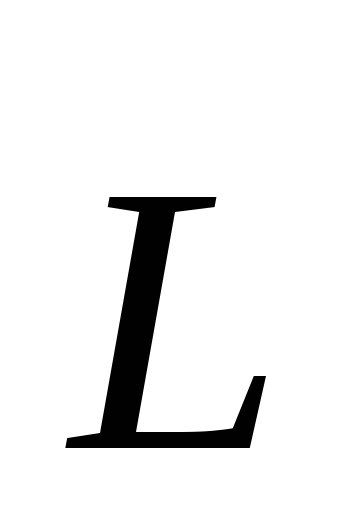 – величина,
численно равная произведению импульса
тела на радиус вращения.
– величина,
численно равная произведению импульса
тела на радиус вращения.
L=p r=m V r (1.24).
После соответствующих преобразований можно записать формулу для определения момента импульса в виде:
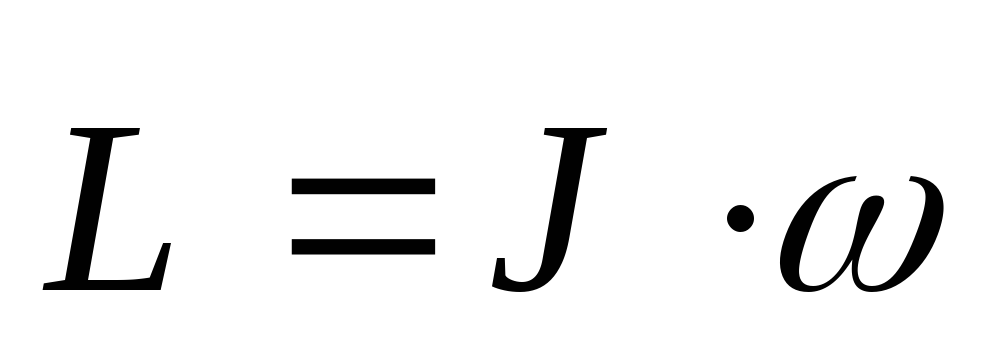 (1.25).
(1.25).
Момент
импульса 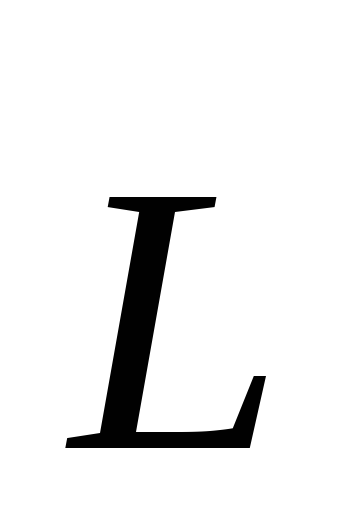 – вектор, направление которого
определяется по правилу правого винта.
Единицей измерения момента импульса в
СИ являетсякгм2/с
– вектор, направление которого
определяется по правилу правого винта.
Единицей измерения момента импульса в
СИ являетсякгм2/с
Основные законы динамики вращательного движения.
Основное уравнение динамики вращательного движения:
Угловое ускорение тела, совершающего вращательное движение, прямо пропорционально суммарному моменту всех внешних сил и обратно пропорционально моменту инерции тела.
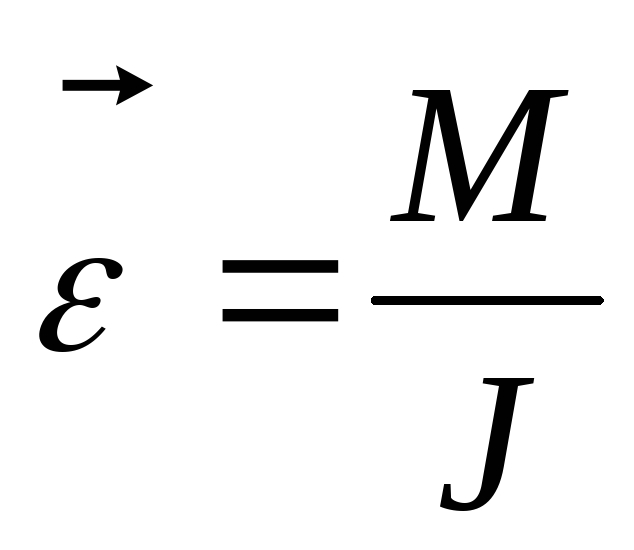 (1.26).
(1.26).
Данное уравнение играет ту же роль при описании вращательного движения, что и второй закон Ньютона для поступательного движения. Из уравнения видно, что при действии внешних сил угловое ускорение тем больше, чем меньше момент инерции тела.
Второй закон Ньютона для динамики вращательного движения можно записать в ином виде:
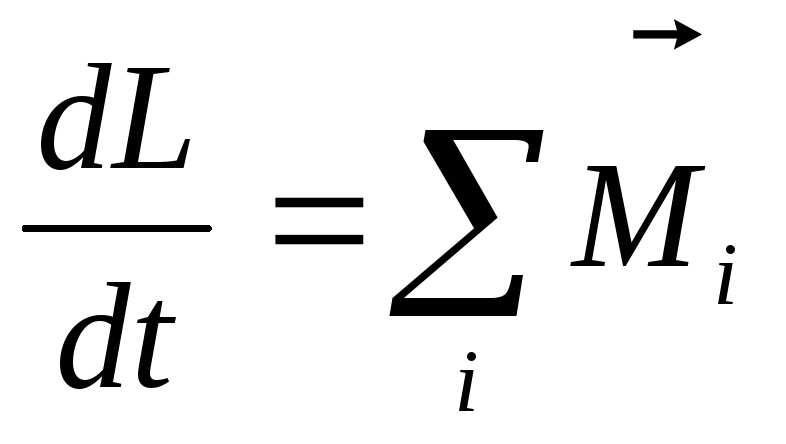 (1.27),
(1.27),
т.е. первая производная от момента импульса тела по времени равна суммарному моменту всех внешних сил, действующих на данное тело.
Закон сохранения момента импульса тела:
Если суммарный момент всех внешних сил, действующих на тело, равен нулю, т.е.
M =0, тогда dL/dt=0 (1.28).
Из
этого следует 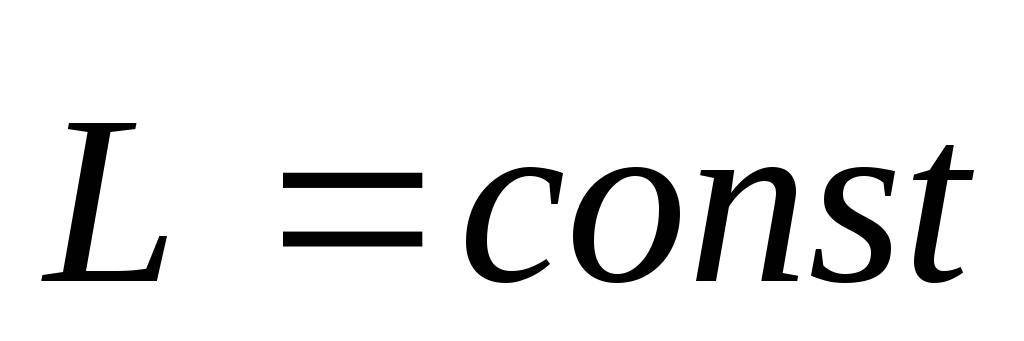 или
или 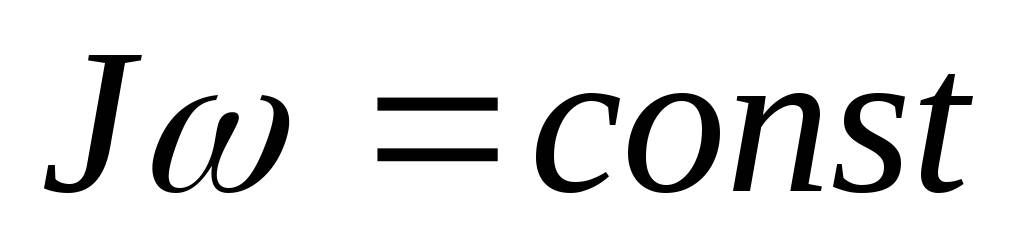 (1.29).
(1.29).
Это утверждение составляет сущность закона сохранения момента импульса тела, который формулируется следующим образом:
Момент импульса тела остается постоянным, если суммарный момент внешних сил, действующих на вращающееся тело, равен нулю.
Этот закон является справедливым не только для абсолютно твердого тела. Примером является фигурист, который выполняет вращение вокруг вертикальной оси. Прижимая руки, фигурист уменьшает момент инерции и увеличивает угловую скорость. Чтобы затормозить вращения, он, наоборот, широко разводит руки; в результате момент инерции увеличивается, и угловая скорость вращения уменьшается.
В заключение приведем сравнительную таблицу основных величин и законов, характеризующих динамику поступательного и вращательного движений.
Таблица 1.4.
Поступательное движение | Вращательное движение | ||
Физическая величина | Формула | Физическая величина | Формула |
Масса | m | Момент инерции | J=mr2 |
Сила | F | Момент силы | M=Fr, если |
Импульс тела (количество движения) | p=mV | Момент импульса тела | L=mVr; L=J |
Кинетическая энергия |
| Кинетическая энергия |
|
Механическая работа | dA=FdS | Механическая работа | dA=Md |
Основное уравнение динамики поступательного движения |
| Основное уравнение динамики вращательного движения |
|
Закон сохранения импульса тела |
| Закон сохранения момента импульса тела |
если |
§ 3. Динамика вращательного движения твердого тела вокруг неподвижной оси Основные формулы
• Момент силы F, действующей на тело, относительно оси вращения
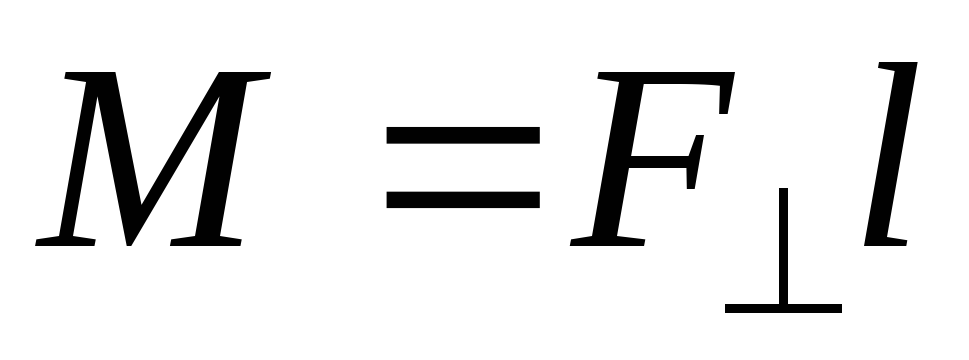 ,
,
где 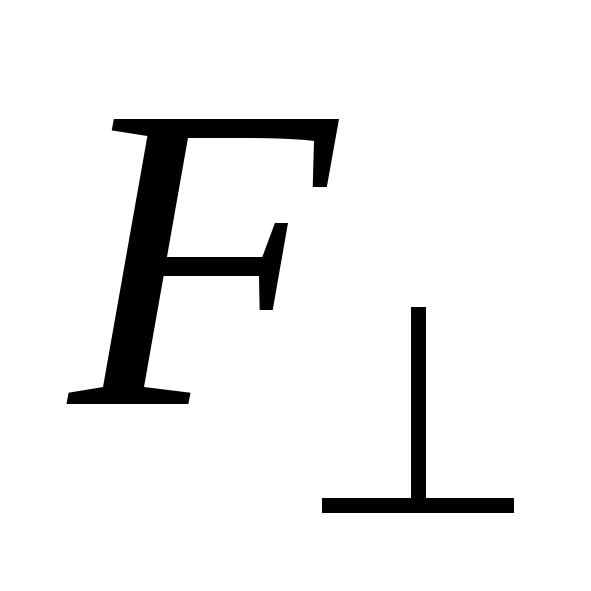 — проекция
силы F на плоскость, перпендикулярную оси
вращения; l
— плечо
силы F (кратчайшее
расстояние от оси вращения до линии
действия силы).
— проекция
силы F на плоскость, перпендикулярную оси
вращения; l
— плечо
силы F (кратчайшее
расстояние от оси вращения до линии
действия силы).
• Момент инерции относительно оси вращения:
а) материальной точки
J=mr2,
где т — масса точки; r — расстояние ее от оси вращения;
б) дискретного твердого тела
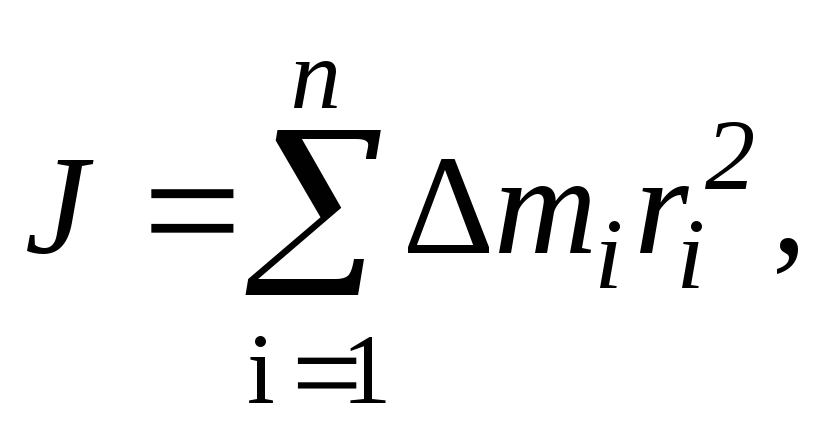
где 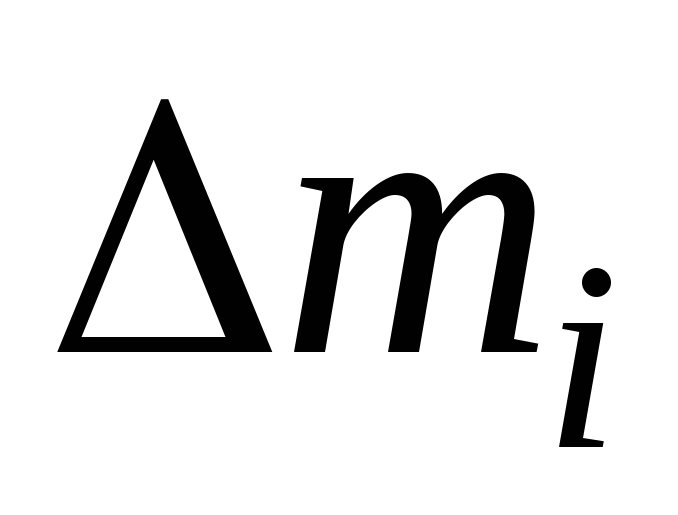 — масса i-го элемента тела; ri — расстояние
этого элемента от оси вращения; п — число
элементов тела;
— масса i-го элемента тела; ri — расстояние
этого элемента от оси вращения; п — число
элементов тела;
в) сплошного твердого тела
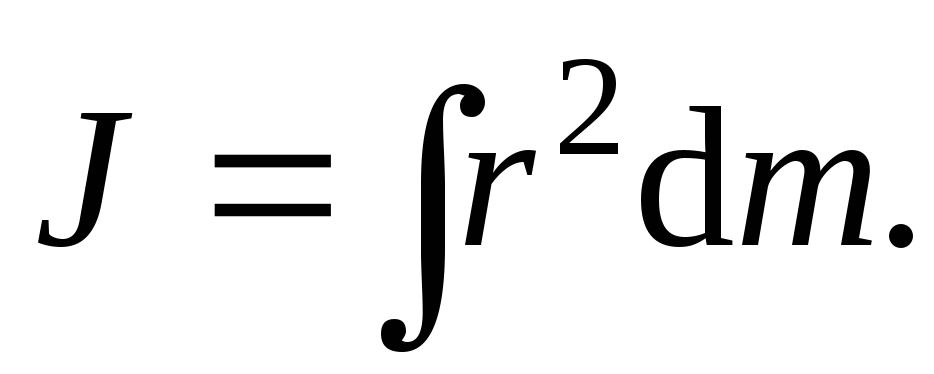
Если тело однородно,
т. е. его плотность  одинакова по всему объему, то
одинакова по всему объему, то
dm= dV и
dV и 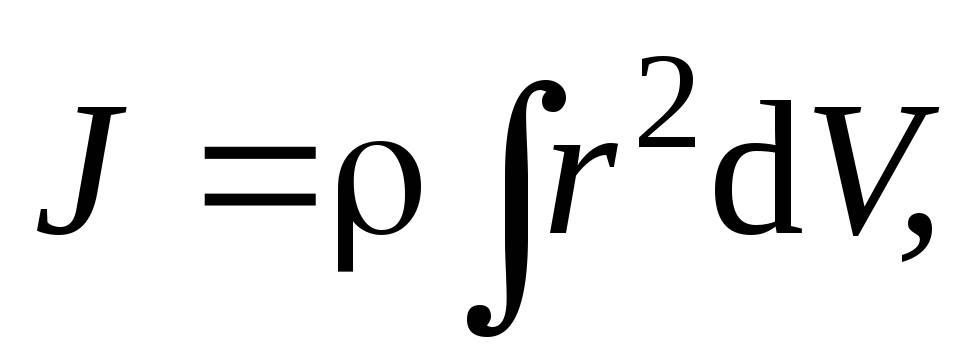
где V — объем тела.
• Моменты инерции некоторых тел правильной геометрической формы:
Тело | Ось, относительно которой определяется момент инерции | Формула момента инерции |
Однородный тонкий стержень массой т и длиной l Тонкое кольцо, обруч, труба радиусом R и массой т, маховик радиусом R и массой т, распределенной по ободу Круглый однородный диск (цилиндр) радиусом R и массой т Однородный шар массой т и радиусом R | Проходит через центр тяжести стержня перпендикулярно стержню Проходит через конец стержня перпендикулярно стержню Проходит через центр перпендикулярно плоскости основания Проходит через центр диска перпендикулярно плоскости основания Проходит через центр шара | 1/12ml2 1/3ml2 mR2 1/2mR2 2/5mR2 |
• Теорема Штейнера. Момент инерции тела относительно произвольной оси
J=J0+ma2,
где J0 — момент инерции этого тела относительно оси, проходящей через центр тяжести тела параллельно заданной оси; а — расстояние между осями; m — масса тела.
• Момент импульса вращающегося тела относительно оси
L=J .
.
• Закон сохранения момента импульса
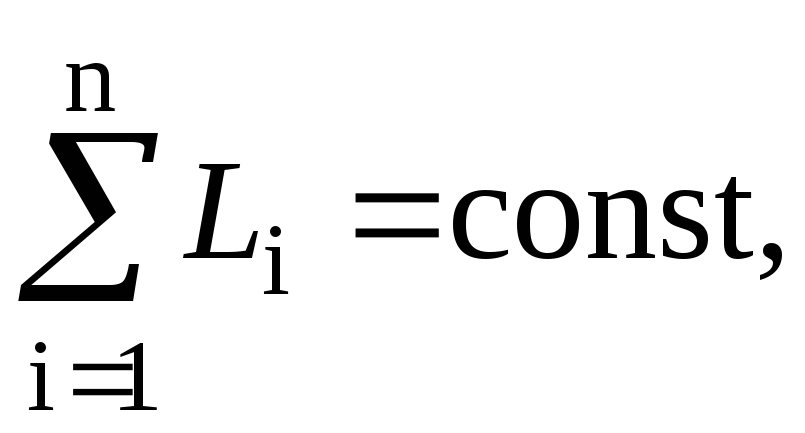
где Li — момент импульса i-го тела, входящего в состав системы. Закон сохранения момента импульса для двух взаимодействующих тел
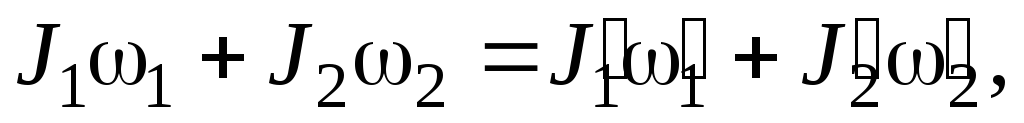
где 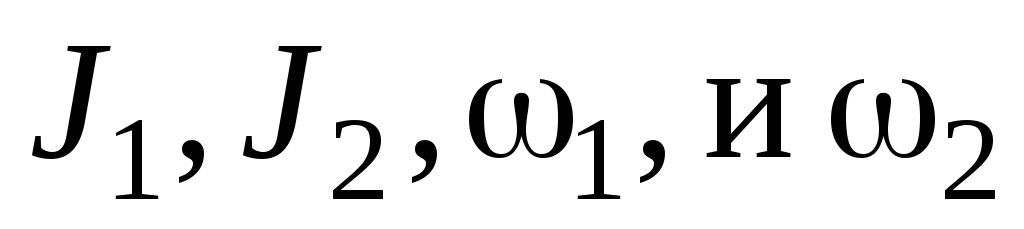 —
моменты инерции и угловые скорости тел
до взаимодействия:
—
моменты инерции и угловые скорости тел
до взаимодействия: 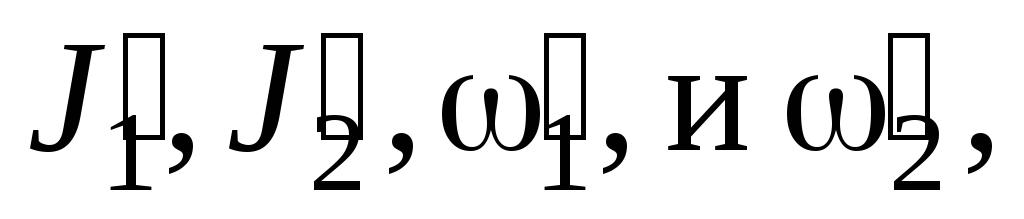 —
те же величины после взаимодействия.
—
те же величины после взаимодействия.
Закон сохранения момента импульса для одного тела, момент инерции которого меняется,
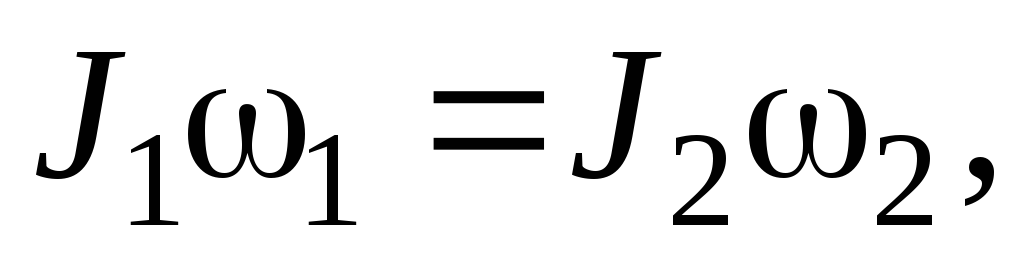
где 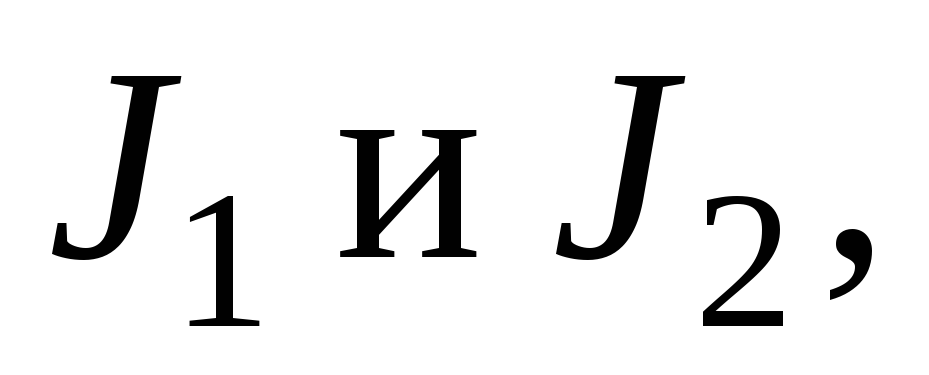 —
начальный и конечный моменты инерции;
—
начальный и конечный моменты инерции; 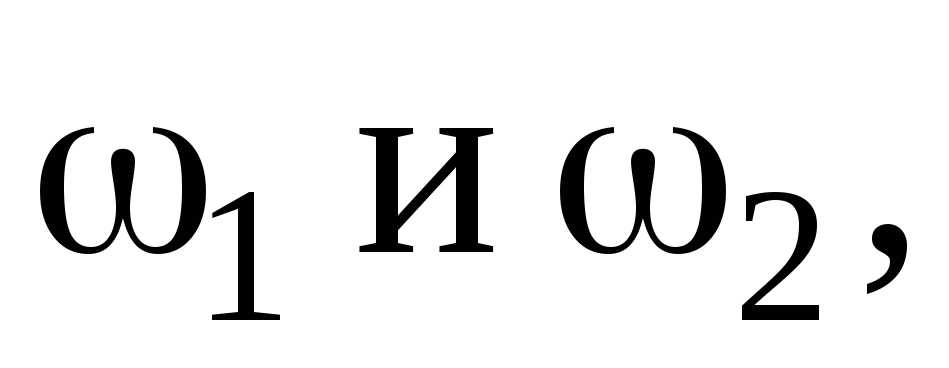 —• начальная
и конечная угловые скорости тела.
—• начальная
и конечная угловые скорости тела.
• Основное уравнение динамики вращательного движения твердого тела относительно неподвижной оси
Mdt=d(J ),
где М — момент
силы, действующей на тело в течение
времени dt;
),
где М — момент
силы, действующей на тело в течение
времени dt;
J — момент
инерции тела;  — угловая
скорость; J
— угловая
скорость; J — момент импульса.
— момент импульса.
Если момент силы и момент инерции постоянны, то это уравнение записывается в виде
М t=J
t=J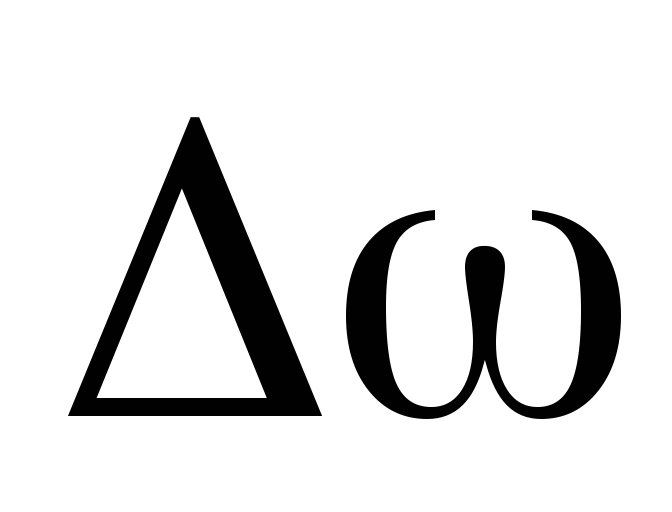 .
.
В случае постоянного момента инерции основное уравнение динамики вращательного движения принимает вид
M=J ,
где
,
где  — угловое
ускорение.
— угловое
ускорение.
• Работа постоянного момента силы М, действующего на вращающееся тело,
A=M,
где — угол поворота тела.
• Мгновенная мощность, развиваемая при вращении тела,
N=M .
.
• Кинетическая энергия вращающегося тела
T=1/2J.
• Кинетическая энергия тела, катящегося по плоскости без скольжения,
T==1/2mv2+l/2J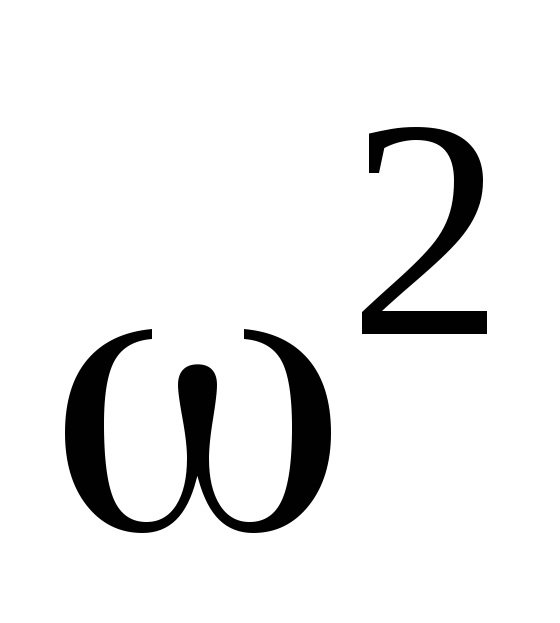 ,
,
где l/2mv2 — кинетическая энергия поступательного
движения тела; v — скорость
центра инерции тела; l/2J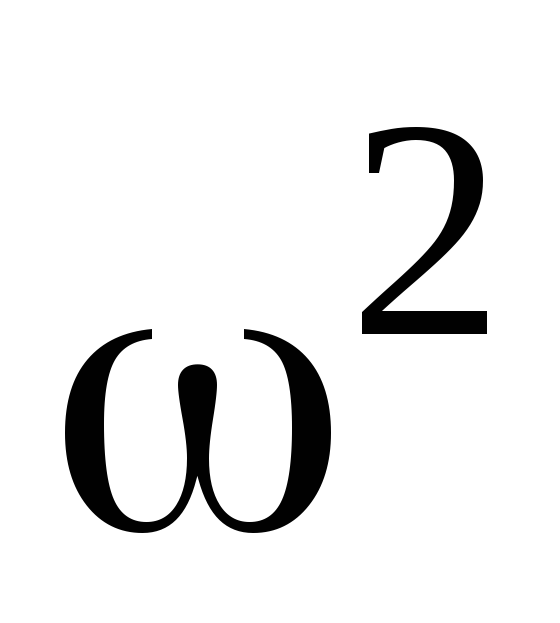 ,—
кинетическая энергия вращательного
движения тела вокруг оси, проходящей
через центр инерции.
,—
кинетическая энергия вращательного
движения тела вокруг оси, проходящей
через центр инерции.
• Работа, совершаемая при вращении тела, и изменение кинетической энергии его связаны соотношением
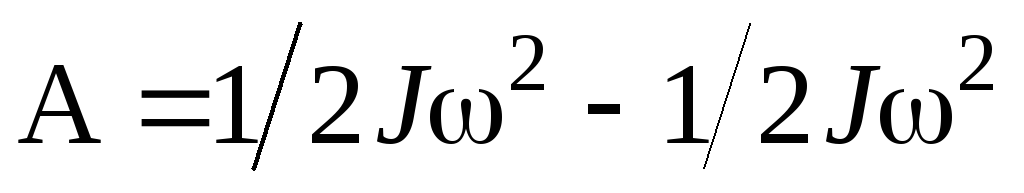 .
.
• Величины, характеризующие динамику вращательного движения, и формулы, описывающие это движение, аналогичны соответствующим величинам и формулам поступательного движения.
Эта аналогия раскрывается следующей таблицей:
П
 оступательное
движение Вращательное движение
оступательное
движение Вращательное движение

Основной закон динамики
F t=mv2—mv1; M
t=mv2—mv1; M t=J
t=J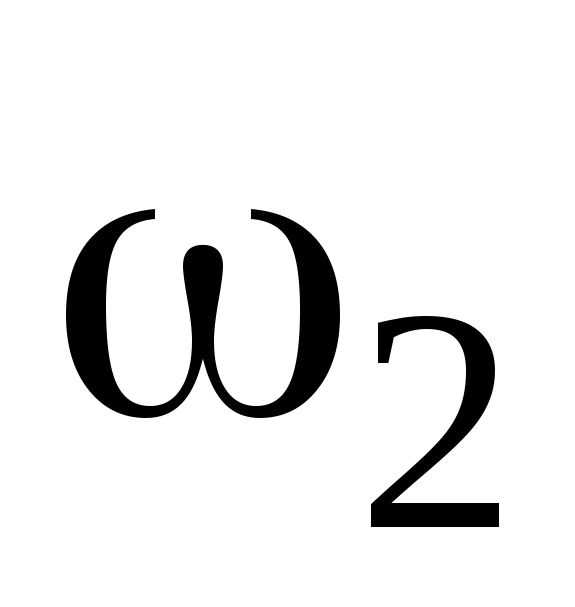 —J
—J ;
;
F
=
та
М = .J
Закон сохранения
импульса момента импульса
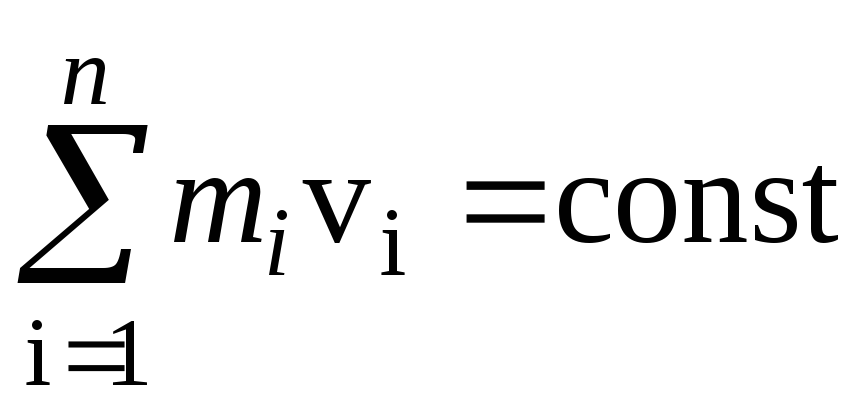
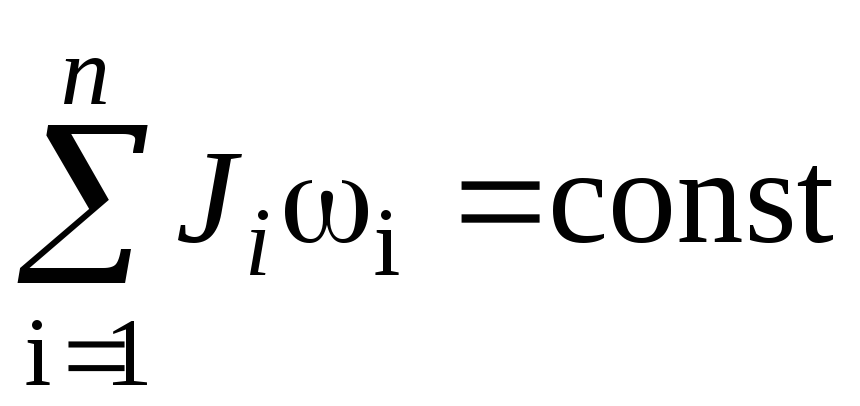
Работа и мощность
A=Fs;
А=М ,
,
N=Fv
N=M
Кинетическая энергия
Т =1/2 mv2 T=1/2J
=1/2 mv2 T=1/2J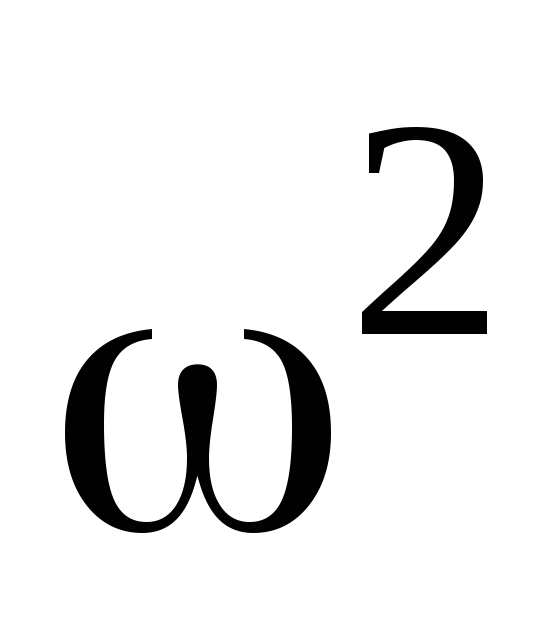
Энергия вращательного движения — Википедия
Материал из Википедии — свободной энциклопедии
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 октября 2015; проверки требуют 4 правки. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 октября 2015; проверки требуют 4 правки.Кинетическая энергия вращательного движения — энергия тела, связанная с его вращением.
Основные кинематические характеристики вращательного движения тела — его угловая скорость (ω{\displaystyle \omega }) и угловое ускорение.
Основные динамические характеристики вращательного движения — момент импульса L{\displaystyle L} относительно оси вращения z{\displaystyle z}, а именно:
- Lz=Izω{\displaystyle L_{z}=I_{z}\omega }
и кинетическая энергия
- Ek=Izω22{\displaystyle E_{k}={\frac {I_{z}\omega ^{2}}{2}}}
где Iz{\displaystyle I_{z}} — момент инерции тела относительно оси вращения.
Похожий пример можно найти при рассмотрении вращающейся молекулы с главными осями инерции I1, I2 и I3. Вращательная энергия такой молекулы задана выражением
- Hrot=12(I1ω12+I2ω22+I3ω32),{\displaystyle H^{\mathrm {rot} }={\tfrac {1}{2}}(I_{1}\omega _{1}^{2}+I_{2}\omega _{2}^{2}+I_{3}\omega _{3}^{2}),}
где ω1, ω2, и ω3 — главные компоненты угловой скорости.
В общем случае, энергия при вращении с угловой скоростью ω→{\displaystyle {\vec {\omega }}} находится по формуле:
- T=12ω→⋅I⋅ω→{\displaystyle T={\frac {1}{2}}{\vec {\omega }}\cdot I\cdot {\vec {\omega }}}, где I{\displaystyle I} — тензор инерции.
Точно по тем же самым рассуждениям, как и в случае поступательного движения, равнораспределение подразумевает, что при тепловом равновесии средняя вращательная энергия каждой частицы одноатомного газа: (3/2)kBT. Аналогично, теорема о равнораспределении позволяет вычислить среднеквадратичную угловую скорость молекул.
1.10
1.10. УРАВНЕНИЕ ДИНАМИКИ ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ
Твердое тело как система материальных точек. Движение центра инерции твердого тела. Кинетическая энергия вращающегося тела. Понятие момента инерции относительно неподвижной оси. Теорема Штейнера. Моменты инерции некоторых простейших тел. Уравнение динамики вращательного движения относительно неподвижной оси.
Движение твердого тела в общем случае определяется двумя векторными уравнениями. Одно из них — уравнение движения центра масс (4.11), другое-уравнение моментов в С-системе (6.24):
| (10.1) |
Зная
законы действующих внешних сил, точки
их приложения и начальные условия, можно
с помощью этих уравнений найти как
скорость, так и положение каждой точки
твердого тела в любой момент времени,
т. е. полностью решить задачу о движении
тела. Однако, несмотря на кажущуюся
простоту уравнений (10.1),
решение их в общем случае представляет
собой весьма трудную задачу. Это прежде
всего обусловлено тем обстоятельством,
что связь между собственным моментом
импульса 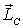 и
скоростями отдельных точек твердого
тела в С-системе
оказывается сложной, за исключением
немногих частных случаев. Мы не будем
рассматривать эту задачу в общем виде
(она решается в курсе теоретической
механики) и ограничимся в дальнейшем
только отдельными частными случаями.
и
скоростями отдельных точек твердого
тела в С-системе
оказывается сложной, за исключением
немногих частных случаев. Мы не будем
рассматривать эту задачу в общем виде
(она решается в курсе теоретической
механики) и ограничимся в дальнейшем
только отдельными частными случаями.
Если
перенести силы вдоль направления их
действия, то ясно, что не изменятся ни
их результирующая 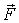 ,
ни их суммарный момент
,
ни их суммарный момент 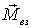 .
При этом уравнения (10.1)
тоже не изменятся, а следовательно не
изменится и движение твердого тела.
Поэтому точки приложения внешних сил
можно переносить вдоль направления
действия сил — удобный прием решения
задач, которым постоянно пользуются.
.
При этом уравнения (10.1)
тоже не изменятся, а следовательно не
изменится и движение твердого тела.
Поэтому точки приложения внешних сил
можно переносить вдоль направления
действия сил — удобный прием решения
задач, которым постоянно пользуются.
Рассмотрим
теперь понятие равнодействующей силы.
В тех случаях, когда суммарный момент
всех внешних сил оказывается
перпендикулярным результирующей силе,
т. е. 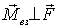 ,
все внешние силы могут быть сведены к одной силе
,
все внешние силы могут быть сведены к одной силе 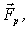 ,
действующей вдоль определенной прямой.
В самом деле, если относительно некоторой
точки О суммарный момент
,
действующей вдоль определенной прямой.
В самом деле, если относительно некоторой
точки О суммарный момент 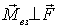 ,
то всегда можно найти такой вектор
,
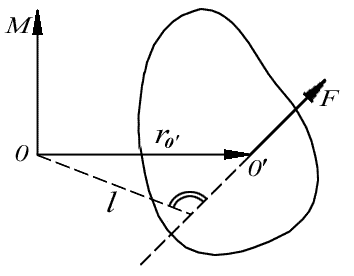
то всегда можно найти такой вектор  (рис.
10.1), что при заданных
(рис.
10.1), что при заданных 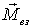 и
и 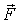
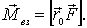
При
этом выбор 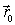 неоднозначен:
прибавление к нему любого вектора
неоднозначен:
прибавление к нему любого вектора 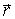 ,
,
|
Рис. 10.1. Введение понятия равнодействующей силы |
параллельного 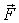 ,
не изменит последнего равенства. А это
означает, что данное равенство определяет
не точку «приложения» силы
,
не изменит последнего равенства. А это
означает, что данное равенство определяет
не точку «приложения» силы 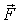 ,
а линию ее действия. Зная модули M и F соответствующих
векторов, можно найти плечо l силы
,
а линию ее действия. Зная модули M и F соответствующих
векторов, можно найти плечо l силы 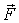 (рис.6.14):
(рис.6.14): 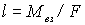 .
.
Таким
образом, если 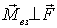 ,
систему сил, действующих на отдельные
точки твердого тела, можно заменить
одной равнодействующей
силой — силой, которая равна результирующей
,
систему сил, действующих на отдельные
точки твердого тела, можно заменить
одной равнодействующей
силой — силой, которая равна результирующей 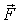 и
создает момент, равный суммарному
моменту
и
создает момент, равный суммарному
моменту 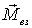 всех
внешних сил.
всех
внешних сил.
Таким
случаем является действие однородного
силового поля, например поля тяжести,
в котором действующая на каждую частицу
сила имеет вид 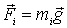 .
В этом случае суммарный момент сил
тяжести относительно любой точки О равен
.
В этом случае суммарный момент сил
тяжести относительно любой точки О равен
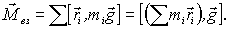
Стоящая
в круглых скобках сумма, равна 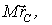 где
где 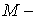 масса
тела
масса
тела 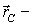 радиус-вектор
его центра масс относительно точки O.
Поэтому
радиус-вектор
его центра масс относительно точки O.
Поэтому
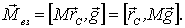
Это
означает, что равнодействующая 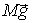 сил
тяжести проходит через центр масс тела.
Обычно говорят, что равнодействующая
сил тяжести приложена к центру масс
тела или к его центру тяжести. Момент
этой силы относительно центра масс тела
равен нулю.
сил
тяжести проходит через центр масс тела.
Обычно говорят, что равнодействующая
сил тяжести приложена к центру масс
тела или к его центру тяжести. Момент
этой силы относительно центра масс тела
равен нулю.
Теперь перейдем к рассмотрению частных случаев движения твердого тела.
Вращение вокруг неподвижной оси.
Рассмотрим вращение твердого тела вокруг неподвижной оси. Найдем выражение для момента импульса твердого тела относительно оси 00′ (рис. 6.15). Момент импульса частицы можно записать в виде
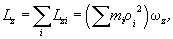
где 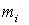 и
и 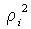 —
масса и расстояние от оси вращения
—
масса и расстояние от оси вращения 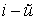 частицы
твердого тела,
частицы
твердого тела, 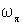 —
его угловая скорость. Обозначив величину,
стоящую в круглых скобках, через I,
получим
—
его угловая скорость. Обозначив величину,
стоящую в круглых скобках, через I,
получим
| (10.2) |
Моментом инерции материальной точки относительно оси вращения называется произведение массы этой точки на квадрат кратчайшего расстояния от оси.
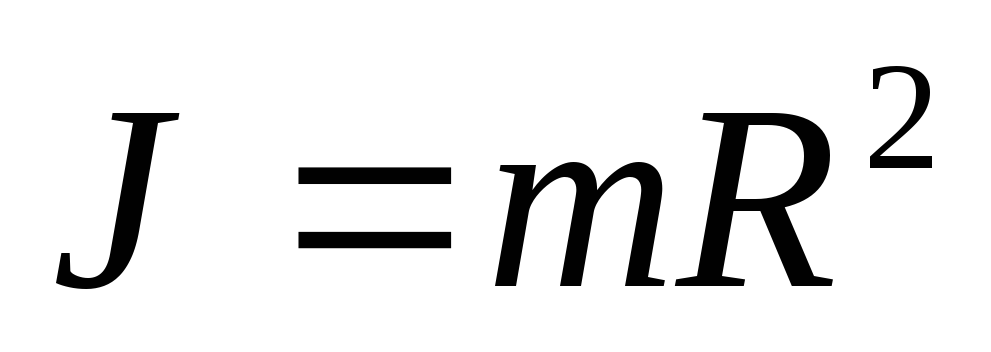
Моментом инерции системы (тела) относительно оси вращения называется физическая величина, равная сумме произведений масс n материальных точек системы на квадраты их расстояний до рассматриваемой оси.
| (10.3) | |
| ||
Рис. 10.2. Вращение твердого тела вокруг оси | ||
Момент инерции твердого тела зависит от распределения масс относительно интересующей нас оси и является величиной аддитивной. Вычисление момента инерции тела проводится по формуле
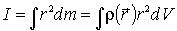
где dm
и dV
— масса и объем элемента тела, находящегося
на расстоянии 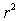 от
интересующей нас оси z,
от
интересующей нас оси z, 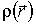 —
плотность тела в данной точке.
—
плотность тела в данной точке.
Моменты инерции некоторых однородных твердых тел относительно оси, проходящей через центр масс тела, приведены в следующей таблице (здесь т — масса тела):
Вид твердого тела | Положение оси | Момент
инерции |
Тонкий стержень длины L | Перпендикулярно стержню |
|
Сплошной цилиндр радиуса R | Совпадает с осью цилиндра |
|
Тонкий диск радиуса R | Совпадает с диаметром диска |
|
Шар радиуса R | Проходит через центр шара |
|
Вычисление момента инерции твердого тела произвольной формы относительно той или иной оси представляет собой, вообще говоря, довольно кропотливую в математическом отношении задачу. Однако в некоторых случаях нахождение момента инерции значительно упрощается, если воспользоваться теоремой Штейнера: момент инерции I относительно произвольной оси z равен моменту инерции относительно оси параллельной данной и проходящей через центр масс С тела, плюс произведение массы т тела нa квадрат расстояния а между осями:
| (10.4) |
Таким
образом, если известен момент инерции 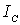 то
нахождение момента инерции I элементарно.
то
нахождение момента инерции I элементарно. Например, момент инерции тонкого стержня
(массы т и длины l)
относительно оси, перпендикулярной
стержню и проходящей через его конец,
равен
Например, момент инерции тонкого стержня
(массы т и длины l)
относительно оси, перпендикулярной
стержню и проходящей через его конец,
равен
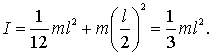
Кинетическая
энергия вращательного
движения — энергия тела,
связанная с его вращением. Получим
выражение для кинетической энергии
вращающегося твердого тела с неподвижной
осью вращения. Учитывая связь скорости 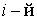 частицы
вращающегося твердого тела с угловой
скоростью
частицы
вращающегося твердого тела с угловой
скоростью 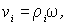 запишем
запишем
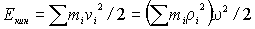 ,
,
или, более
коротко 
| (10.5) |
где I
— момент инерции тела относительно оси
вращения, 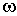 —
его угловая скорость.
—
его угловая скорость.
Запишем выражение для кинетической энергии твердого тела при плоском движении, когда тело участвует как во вращетельном, так и в поступательном движении. В этом случае
| (10.6) |
где 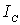 —
момент инерции тела относительно оси
вращения, проходящей через его центр
масс,
—
момент инерции тела относительно оси
вращения, проходящей через его центр
масс, 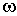 -угловая
скорость тела, т — его масса,
-угловая
скорость тела, т — его масса, 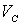 —
скорость центра инерции тела в K-системе
отсчета. Таким
образом, кинетическая
энергия твердого тела при плоском
движении складывается из энергии
вращения в С-системе и энергии, связанной
с движением центра масс.
—
скорость центра инерции тела в K-системе
отсчета. Таким
образом, кинетическая
энергия твердого тела при плоском
движении складывается из энергии
вращения в С-системе и энергии, связанной
с движением центра масс.
Запишем основное уравнение динамики вращения твердого тела с неподвижной осью вращения. Это уравнение легко получить, как следствие как следствие уравнения моментов для материальной точки, если продифференцировать (10.2) по времени, тогда
| (10.7) |
где 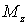 —
суммарный момент всех внешних сил
относительно оси вращения,
—
суммарный момент всех внешних сил
относительно оси вращения, 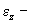 проекция
углового ускорения на ось вращения. Из
этого уравнения, в частности, видно, что
момент инерции I определяет инерционные свойства твердого
тела при вращении: при одном и том же
значении момента сил
проекция
углового ускорения на ось вращения. Из
этого уравнения, в частности, видно, что
момент инерции I определяет инерционные свойства твердого
тела при вращении: при одном и том же
значении момента сил 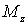 тело
с большим моментом инерции приобретает
меньшее угловое ускорение. Моменты сил
относительно оси — величины алгебраические:
их знаки зависят как от выбора
положительного направления оси z,
совпадающей с осью вращения, так и от
направления
тело
с большим моментом инерции приобретает
меньшее угловое ускорение. Моменты сил
относительно оси — величины алгебраические:
их знаки зависят как от выбора
положительного направления оси z,
совпадающей с осью вращения, так и от
направления
|
Рис. 10.3. Выбор положительного направления вращения (правый винт) |
«вращения»
соответствующего момента силы. Например,
выбрав положительное направление оси z,
как показано на рис. 10.3, мы тем самым
задаем и положительное направление
отсчета угла — оба эти направления
связаны правилом правого винта. Полагают,
что если некоторый момент «вращает»
в положительном направлении угла, то
он считается положительным, и наоборот.
А знак суммарного момента 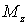 в
свою очередь определяет знак
в
свою очередь определяет знак 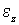 —
проекции вектора углового ускорения
на ось z.
—
проекции вектора углового ускорения
на ось z.
Интегрирование
уравнения (10.7)
с учетом начальных условий -значений
угловой скорости и угла 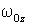 и
и 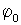 начальный
момент времени — позволяет полностью
решить задачу о вращении твердого тела
вокруг неподвижной оси, т. е. найти
зависимость от времени угловой скорости
начальный
момент времени — позволяет полностью
решить задачу о вращении твердого тела
вокруг неподвижной оси, т. е. найти
зависимость от времени угловой скорости 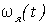 и
угла поворота
и
угла поворота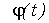 .
.
Заметим,
что уравнение (10.7)
справедливо в любой системе
отсчета, жестко связанной с осью вращения.
Однако если система отсчета неинерциальная,
то необходимо помнить, что момент сил 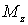 включает
в себя не только моменты сил взаимодействия
с другими телами, но и моменты сил
инерции.
включает
в себя не только моменты сил взаимодействия
с другими телами, но и моменты сил
инерции.
6



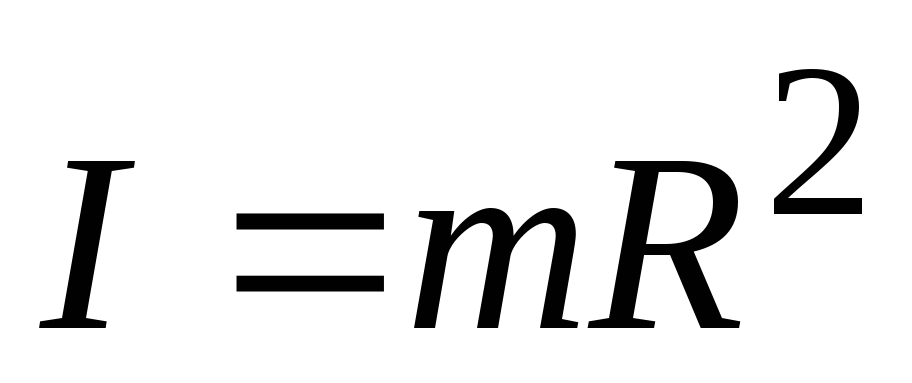


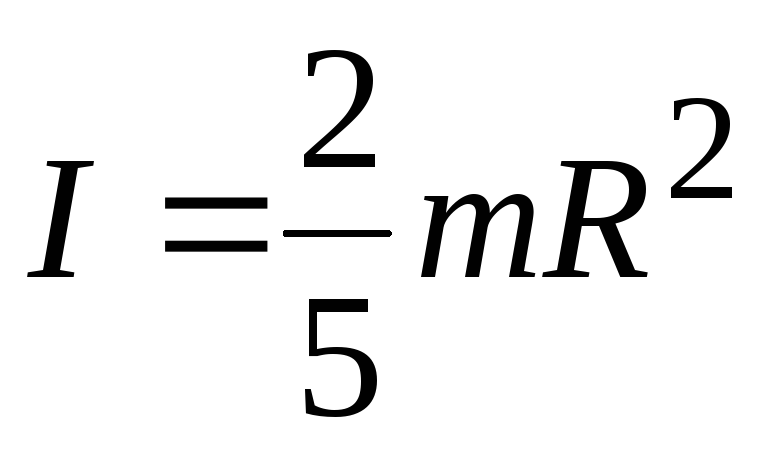

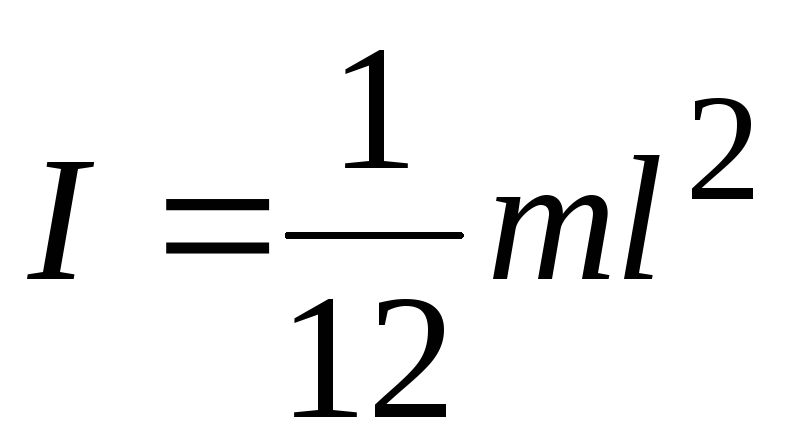
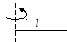
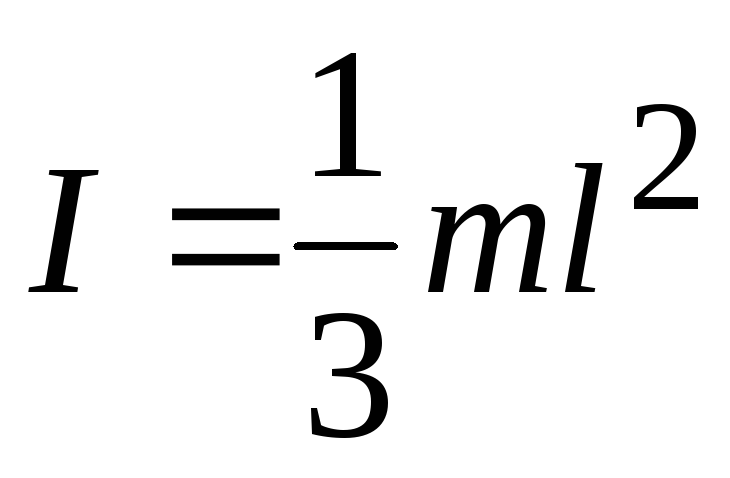
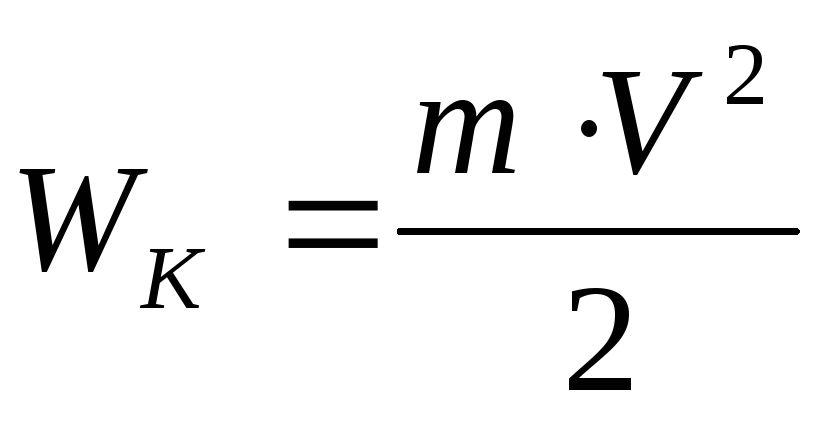
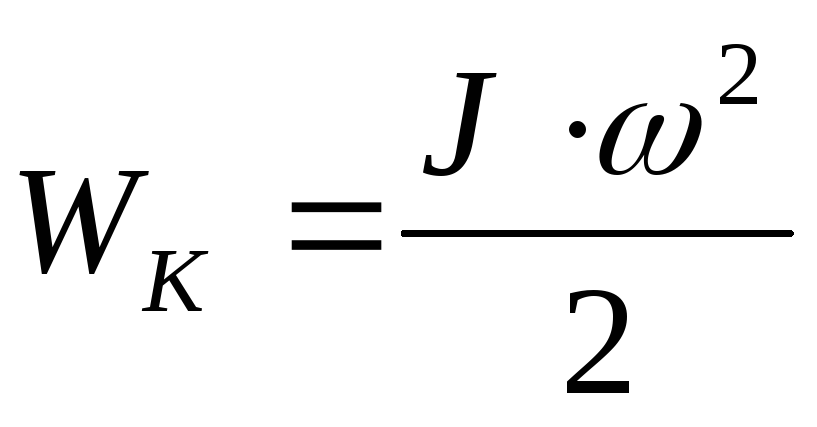
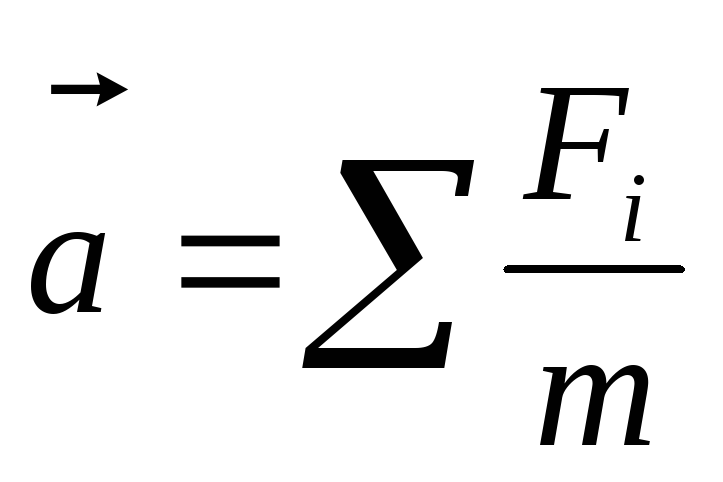
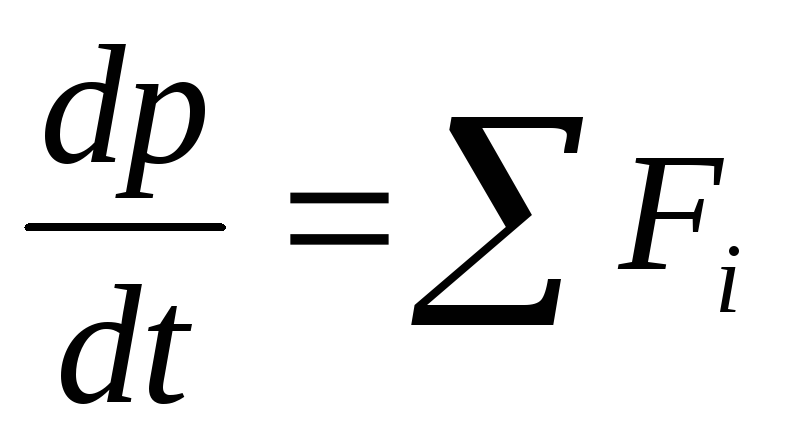
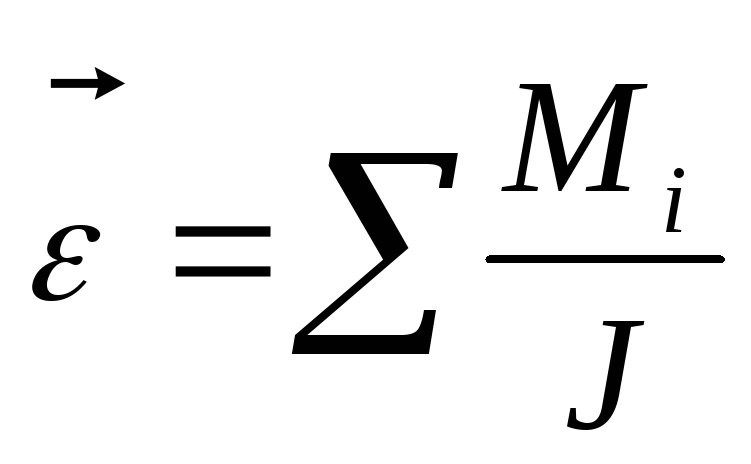
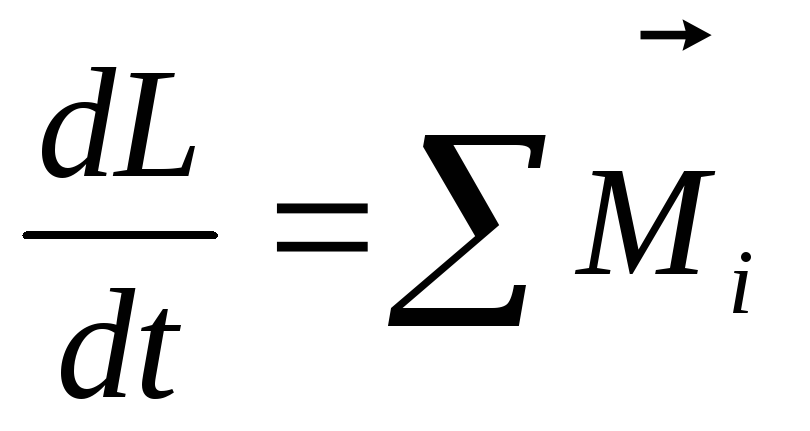 ,
,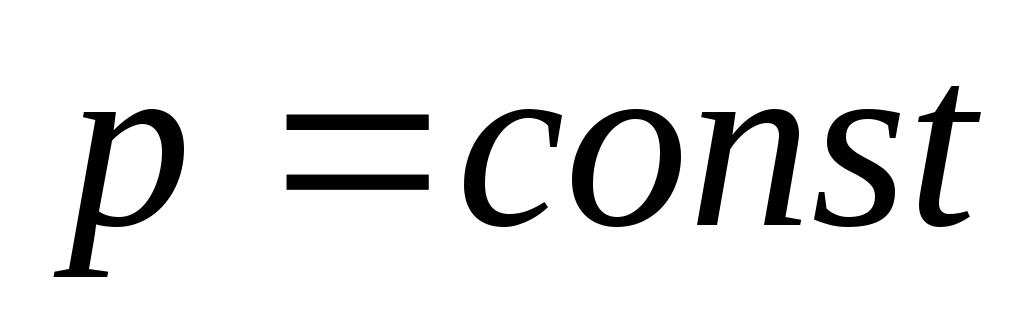 или
или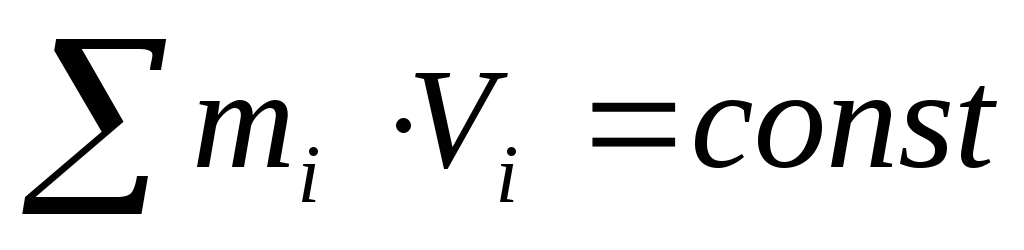 если
если 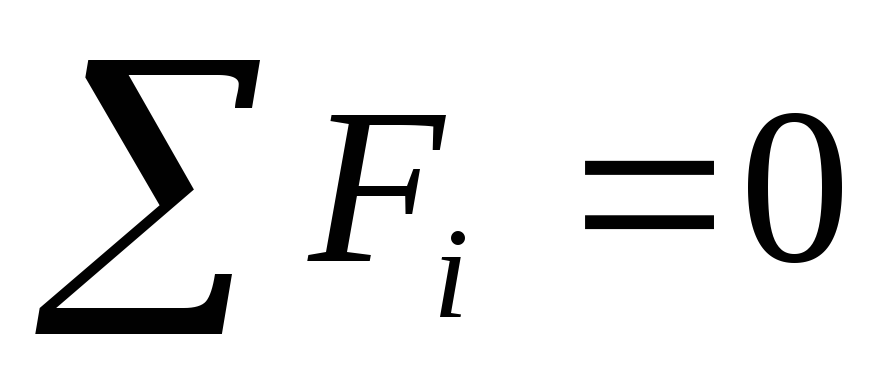
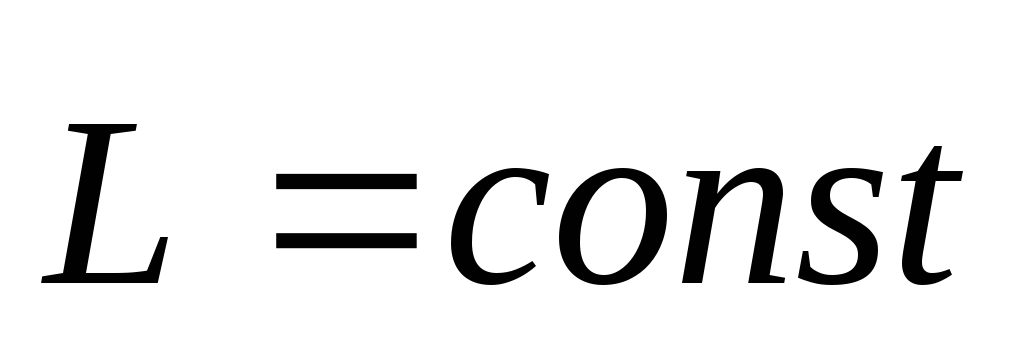 или J=const,
или J=const,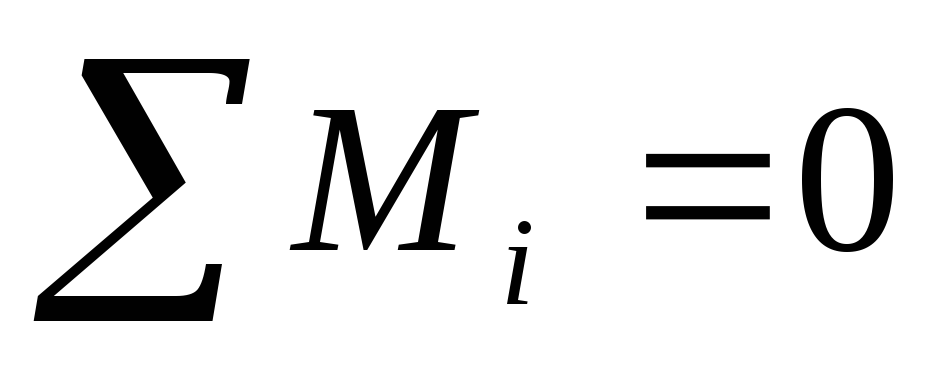
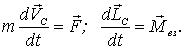
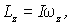
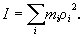
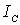
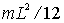
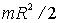
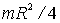
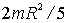
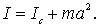
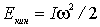 ,
,