Момент инерции прямоугольного сечения
Определение и общие понятия о моменте инерции
Осевым (экваториальным) моментом инерции сечения по отношению к некоторой оси называют взятую по всей его площади S сумму произведений элементарных площадок на квадраты их расстояний от этой оси:
Полярным моментом инерции сечения относительно точки (полюса) называют сумму произведений элементарных площадок на квадраты расстоянии от них до полюса, при этом сумма берется по всей площади S:
где (рис.1)
Если оси, по отношению к которым известны моменты инерции взаимно перпендикулярны, то легко найти полярный момент инерции относительно точки пересечения этих осей, как сумму осевых моментов инерции.
Центробежным моментом инерции сечения по отношению к некоторым взаимно перпендикулярным осям называют сумму произведений элементарных площадок на их расстояния от этих осей, взятых по всей площади сечения S:
Осевой момент инерции прямоугольного сечения
Найдем осевой момент инерции прямоугольника, который имеет высоту h и ширину относительно оси X, которая проходит через основание прямоугольника (рис.2).
Выделим из нашего прямоугольника элементарную площадку dS (рис.2). Основания этой площадки параллельны осям X и Y. Высота полоски составляет dy, ширина b. Площадь данной полоски равна:
Расстояние от полоски до оси X равно y. Используя второе выражение из (1), для момента инерции сечения относительно оси X имеем:
Для получения момента инерции прямоугольного сечения относительно оси Y элементарную полоску выделяют параллельно оси Y. Проводят аналогичную последовательность действий, при этом получают:
Центробежный момент инерции прямоугольного сечения
Центробежный момент инерции прямоугольного сечения относительно осей XY(рис. 2) () равен:
Если оси X и Y провести через центр тяжести прямоугольного сечения, то центробежный момент инерции равен нулю, так ка эти оси совпадают с осями симметрии.
Примеры решения задач
понятие, расчет для двух положений осей — OneKu
Содержание статьи:Математика и физика являются, пожалуй, двумя научными дисциплинами, которые ближе всего связаны друг с другом. Так, результаты одной из них используются для развития другой. Одним из ярких примеров, отражающих их взаимодействие, является расчет момента инерции прямоугольника относительно оси.
О моменте инерции в математике и физике
Многие люди, знакомые с физикой или математикой, наверняка, слышали об этом понятии. Тем не менее, стоит разобраться в нем подробнее, чтобы не возникало путаницы.
Вам будет интересно:Астрология — это наука о чем? Доводы за и против, объект изучения
В физике под моментом инерции понимают характеристику вращающейся системы, которая описывает инерционные свойства тела. Например, для точки с массой m, которая совершает круговые движения вокруг оси, находящейся от нее на расстоянии r, эта величина выражается формулой:
I = m*r2.
Откуда видно, что описывается она килограммами на квадратный метр.
В математике момент инерции — это совершенно иная вещь, которая вычисляется не относительно трехмерного объекта, а относительно плоского тела или сечения. В общем случае можно говорить о моменте инерции n-го порядка. В данной же статье, при вычислении момента инерции прямоугольника, речь пойдет о величине второго порядка.
Момент инерции 2-го порядка для сечения
Стоит перейти к математической формулировке рассматриваемой величины. Итак, в математике она появляется в виде следующего определения:
Io = ∫∫A(r2*dA).
Здесь Io — момент инерции второго порядка, вычисляемый относительно оси O; A — площадь сектора, для которого определяется величина Io; dA — элемент площади сектора, который находится от оси O на расстоянии r.
Эта формула показывает, что размерностью Io является единица расстояния в четвертой степени (м4), что отличает его от момента инерции для тела в физике (см. пункт выше).
Зачем вычисляют величину Io? Конечно же, это не чистая математическая задача, которая не имеет прикладного характера. Момент инерции Io для сечений различной формы необходим при расчетах сгибающих напряжений в инженерных конструкциях, например, для балок.
Далее приведены расчеты для осевого момента инерции прямоугольника при различном положении оси вращения O относительно объекта.
Ось проходит через центр фигуры параллельно одной из сторон
Пусть дан прямоугольник с размерами сторон a и b. Допустим, что ось O делит фигуру на две равные половины и параллельна стороне a. Эта ситуация изображена на рисунке ниже.
Двойной интеграл для такой ситуации можно посчитать достаточно просто, поскольку расстояние r любого элемента с площадью dA будет равно x. При этом интегрирование проводится от -b/2 до +b/2 (ось O пересекает начало координат по оси x). Что касается пределов интегрирования по y, то их можно выбрать, как от -a/2 до +a/2 (начало координат в центре фигуры), так и от 0 до a (начало координат лежит на середине одной из сторон длиной b). Для определенности стоит выбрать второй вариант. Тогда общая формула для момента инерции второго порядка запишется в виде:
Io = ∫0a∫-b/2+b/2(x2*dx*dy).
Вычисляем двойной интеграл по порядку, подставляем известные пределы, получается:
Io = x3/3|-b/2+b/2*y|0a = b3*a/12.
Таким образом, получена формула момента инерции прямоугольника для оси, проходящей через его середину параллельно сторонам с длиной a.
Очевидно, что если ось будет проходить параллельно сторонам b, то ничего не изменится в расчете, за исключением того, что обозначения сторон поменяются местами. То есть получится формула:
Io = a3*b/12.
Ось проходит через сторону прямоугольника
В этом случае ситуация полностью аналогична предыдущей, только теперь ось O1 сдвинута к одному из краев фигуры. Для расчета такого момента инерции необходимо лишь поменять пределы интегрирования по соответствующей стороне.
Пусть ось O1 будет проходить через сторону a, тогда пределы интегрирования по x будут от 0 до b. Если подставить их в формулу, получится:
Io1 = x3/3|0b*y|0a = b3*a/3.
Соответственно, если ось O1 проходит через b, тогда получится:
Io1 = a3*b/3.
Как видно, смещение оси к краю фигуры приводит к увеличению ее момента инерции в 4 раза.
Стоит отметить, что формулы для случая, рассмотренного в данном пункте, можно было получить с использованием теоремы Штейнера, которая имеет аналогичный вид, что и в случае расчета момента инерции тела в физике:
Io1 = Io + d2*A.
Здесь d — расстояние между осями O и O1. Если обе оси параллельны сторонам a фигуры, тогда d = b/2 (половина длины стороны b прямоугольника). Поскольку площадь прямоугольника равна a*b, то получится:
Io1 = b3*a/3 + (b/2)2*a*b = b3*a/12 + b3*a/4 = b3*a/3.
Таким же образом применяется эта теорема для оси O1, параллельной стороне b, только d в этом случае будет равен уже a/2.
Источник
Вопрос 7

Осевой момент
инерции сечения относительно оси 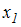 равен …
равен …
Ответ 7

Для круглого сечения диаметром 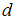
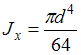 .
Ось
.
Ось расположена
параллельно центральной. Воспользуемся
формулой для определения осевого момента
инерции сечения при переходе от
центральной оси к нецентральной,
расположенной параллельно центральной.
расположена
параллельно центральной. Воспользуемся
формулой для определения осевого момента
инерции сечения при переходе от
центральной оси к нецентральной,
расположенной параллельно центральной.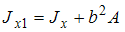 ,
где
,
где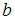
 их,А– площадь поперечного
сечения. Тогда
их,А– площадь поперечного
сечения. Тогда .
.Вопрос 8

При переходе от
центральной оси  к
осиx осевой момент инерции круга …
к
осиx осевой момент инерции круга …
Ответ 8

Связь между осевыми моментами инерции
относительно параллельных осей, одна
из которых центральная, записывается
в виде формулы  гдеа− межосевое расстояние,А– площадь фигуры. При переходе от оси
гдеа− межосевое расстояние,А– площадь фигуры. При переходе от оси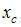 к
осиxосевой момент инерции круга
увеличивается на величину
к
осиxосевой момент инерции круга
увеличивается на величину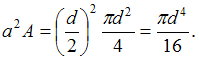
Задание 19
Вопрос 1

Из указанных центральных осей сечения равнобокого уголка главной центральной является……
Ответ 1
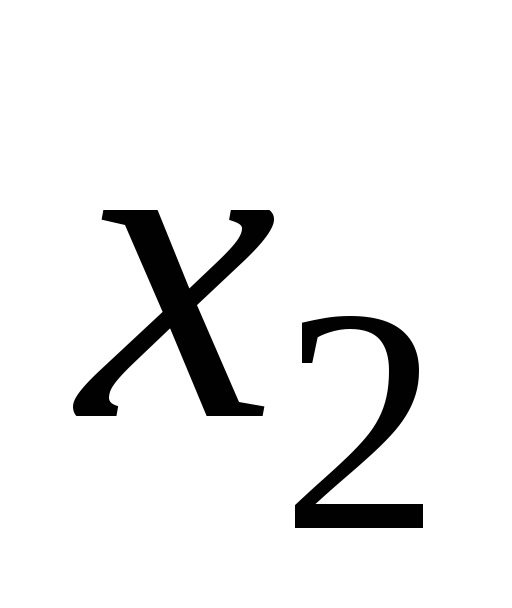
Вопрос 2
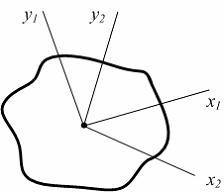
Для сечения известны
осевые моменты инерции относительно
осей  :
: см4,
см4, 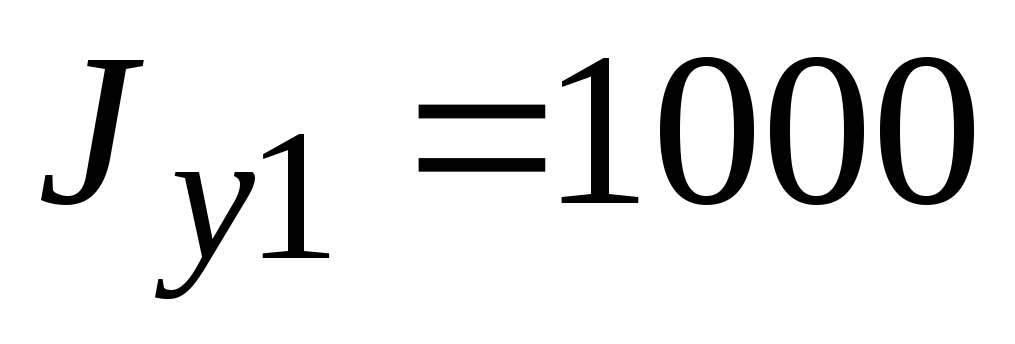 см4,
см4,  см4.
Осевой моментинерции относительно оси
см4.
Осевой моментинерции относительно оси  равен ___ см4.
равен ___ см4.
Ответ 2
2500
(т.к.  откуда
откуда )
)
Вопрос 3

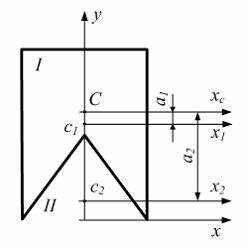
Фигура состоит из двух кругов одинакового диаметра. Главные центральные моменты инерции фигуры равны….
Ответ 3

(Фигура имеет две оси симметрии, которые являются главными центральными осямию

Моменты инерции относительно этих осей:

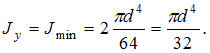
Вопрос 4
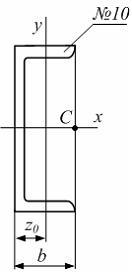
На рисунке показано
поперечное сечение швеллера №10. Параметры
сечения: 
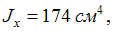

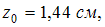
 Главные
моменты инерции относительно главных
осей, проходящих через точкуС,
равны___
Главные
моменты инерции относительно главных
осей, проходящих через точкуС,
равны___  и ___
и ___
Ответ 4
174 и 129,2
 Для
точкиСглавными осями являются осиxи(см.
рисунок).
Для
точкиСглавными осями являются осиxи(см.
рисунок). и
и − главные
моменты инерции.
− главные
моменты инерции.

Вопрос 5

Момент инерции
сечения относительно главной центральной
оси 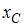 равен …
равен …
Ответ 5
37а4
 Для
вычисления
Для
вычисления сечения
используем формулу
сечения
используем формулу
 .
.
Задание 20
Вопрос 1

Осевой момент
инерции прямоугольника относительно
оси  определяется по формуле……
определяется по формуле……
Ответ 1

Вопрос 2
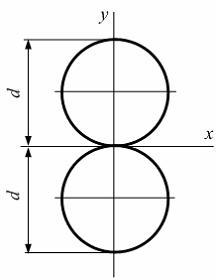
Момент инерции
площади фигуры, состоящей из двух кругов,
относительно оси  равен….
равен….
Ответ 2
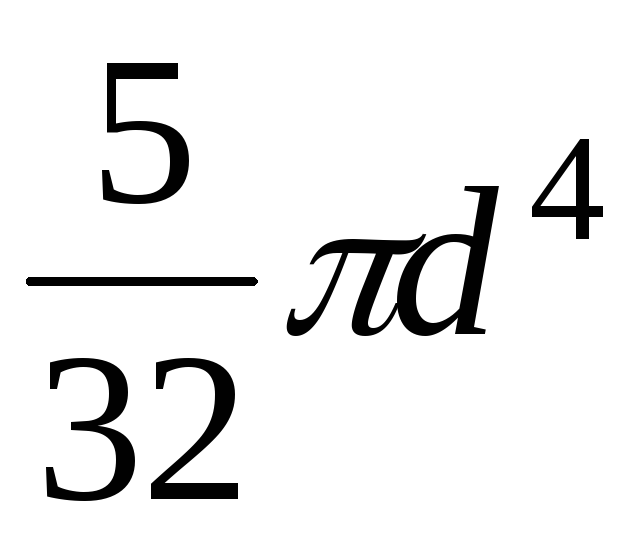
Вопрос 3
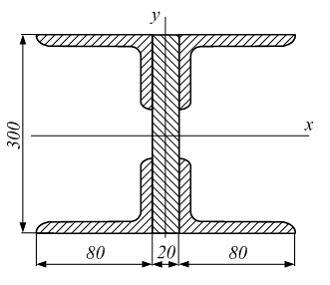
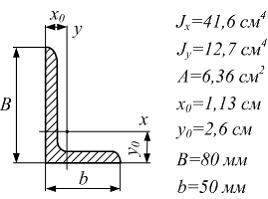
Поперечное сечение
балки составлено из вертикального листа
и четырех неравнобоких уголков  .
Характеристики уголка заданы. Размеры
уголка заданы вмм.
Моменты инерции сечения
и
.
Характеристики уголка заданы. Размеры
уголка заданы вмм.
Моменты инерции сечения
и соответственно равны ___ и ___ см4.
соответственно равны ___ и ___ см4.
Ответ 3
9445 и 516
(т.к. 

где
, )
)
Вопрос 4

Осевой момент инерции сечения в форме кольца относительно оси С – С равен….
Ответ 4
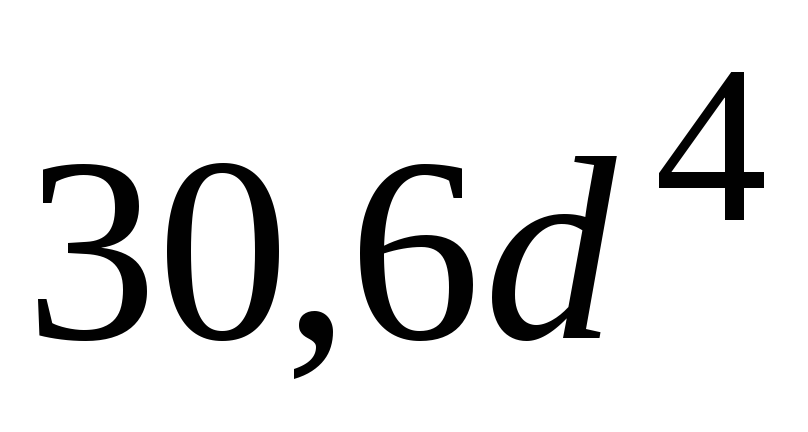
(Выделим в сечении два круга:

круг Iдиаметром и кругIIдиаметром
и кругIIдиаметром .
При решении задачи используем формулу,
связывающую моменты инерции двух
параллельных осей, одна из которыхС
– С, а другаяV – V. Осевой момент
инерции кольца
.
При решении задачи используем формулу,
связывающую моменты инерции двух
параллельных осей, одна из которыхС
– С, а другаяV – V. Осевой момент
инерции кольца где
где

 Таким
образом
Таким
образом

Вопрос 5

Осевой момент
инерции сечения в форме кольца относительно
оси 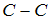 ,
проходящей через его центр тяжести,
равен.…
,
проходящей через его центр тяжести,
равен.…
Ответ 5

Сечение разобьем на две фигуры: круг I
диаметром 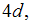 круг II диаметром
круг II диаметром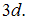 Момент инерции кольца
Момент инерции кольца
Вопрос 6

Осевой момент инерции фигуры (см. рисунок) относительно главной центральной оси x равен …
Ответ 6
59,05а4
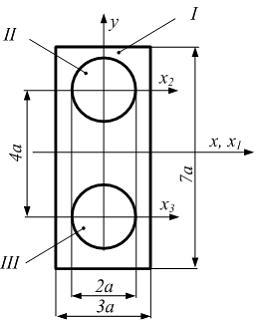 Осьx– центральная, она проходит через
центр тяжести поперечного сечения.
Разбиваем сложную фигуру на простейшие
(прямоугольник и два круга). Осевой
момент инерции сечения
Осьx– центральная, она проходит через
центр тяжести поперечного сечения.
Разбиваем сложную фигуру на простейшие
(прямоугольник и два круга). Осевой
момент инерции сечения
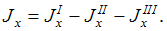
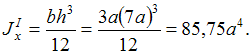
Для определения осевого момента инерции
круга относительно оси xиспользуем
формулу, связывающую моменты инерции
относительно двух параллельных осей,
одна из которых центральная. Таким
образом,
Таким
образом,
Вопрос 6
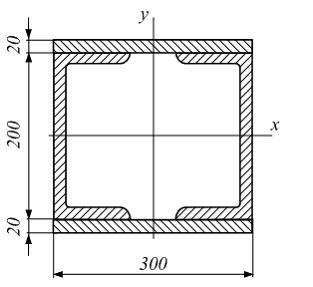
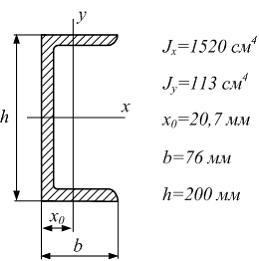
Поперечное сечение балки составлено из двух швеллеров №20 и листов, прикрепленных с помощью сварки. Характеристики швеллера приведены. Размеры на рисунке даны в мм. Осевой момент инерции сечения относительно главной центральной оси x равен ___ см4.
Ответ 6
17600 см3
Разбиваем сложное сечение на ряд простых фигур: два швеллера и два прямоугольника, которые обозначены индексами 1 и 2 соответственно (см. рис.).
 Осьxявляется главной центральной осью
сечения. Осевые моменты инерции простых
фигур относительно своих главных
центральных осей, расположенных
параллельно осиx, равны
Осьxявляется главной центральной осью
сечения. Осевые моменты инерции простых
фигур относительно своих главных
центральных осей, расположенных
параллельно осиx, равны
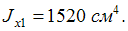 Ось x1совпадает с осьюx.
Осьx2удалена от осиxна расстоянии
Ось x1совпадает с осьюx.
Осьx2удалена от осиxна расстоянии Поэтому
при определении момента инерции второй
фигуры относительно осиxнадо
воспользоваться формулой перехода к
параллельным осям. Окончательно имеем
Поэтому
при определении момента инерции второй
фигуры относительно осиxнадо
воспользоваться формулой перехода к
параллельным осям. Окончательно имеем .
.
2. Моменты инерции плоских фигур.
Осевыми моментами инерции площади фигуры называют выражения
 ;
;  .
.
Полярным
моментом инерции площади фигуры относительно
полюса  называют
называют
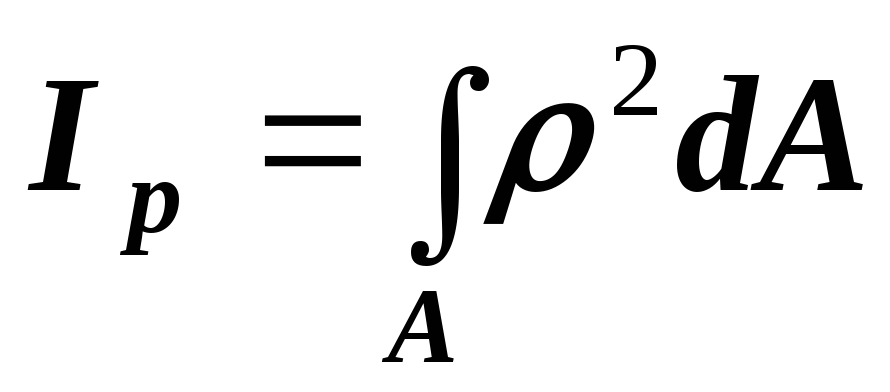 .
.
Е сли
через полюс проведена система взаимно
перпендикулярных осей
сли
через полюс проведена система взаимно
перпендикулярных осей и
и (рис. 10), то(как гипотенуза
(рис. 10), то(как гипотенуза ).
).
Тогда
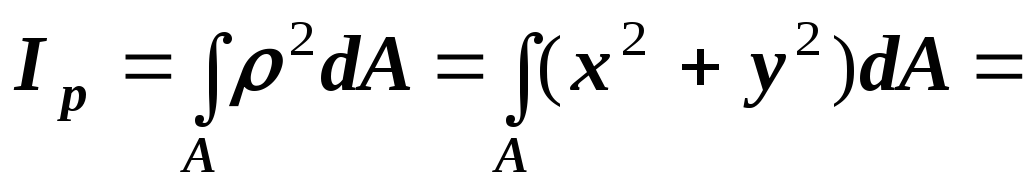
 ,
,
то
есть полярный момент инерции
относительно полюса  равен сумме осевых моментов инерции
относительно осей, проходящих через
полюс.
равен сумме осевых моментов инерции
относительно осей, проходящих через
полюс.
Отметим, что величины осевых и полярных моментов инерции положительны.
Центробежным
моментом инерции называют  .
Единицы измерения осевых, полярных
и центробежных моментов инерции —
.
Единицы измерения осевых, полярных
и центробежных моментов инерции — .
.
Центробежный момент инерции может быть положительным, отрицательным и равным нулю.
Оси, относительно которых центробежный момент инерции равен нулю, называют главными осями. Две взаимно перпендикулярные оси, одна из которых является осью симметрии фигуры, называются главными осями. Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями.
В ычислим
моменты инерции прямоугольника
относительно центральных осей,
параллельных его сторонам (рис. 11).
ычислим
моменты инерции прямоугольника
относительно центральных осей,
параллельных его сторонам (рис. 11).
Выделим
элементарную площадку  в виде узкого прямоугольника,
параллельного оси
в виде узкого прямоугольника,
параллельного оси .
Площадь элемента
.
Площадь элемента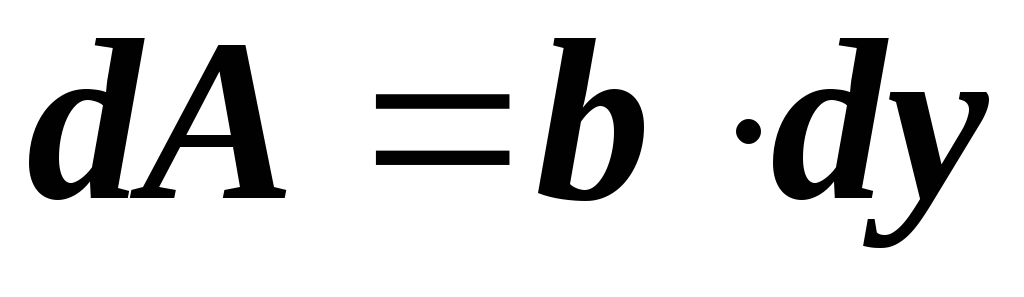 .
.
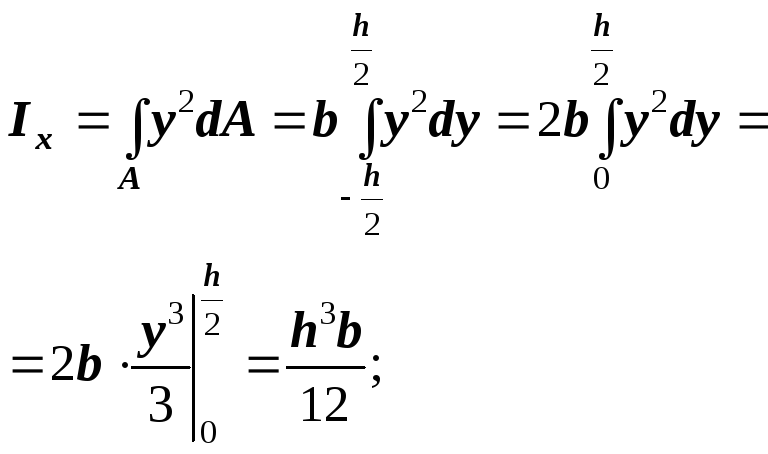
Аналогично,
если выделить элементарную вертикальную
полоску шириной  ,
получим:
,
получим: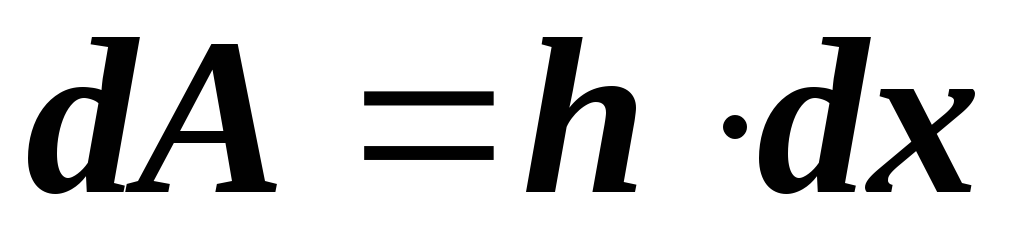 и
и
 .
.
В ычислим
полярный момент инерции круга
относительно его центра, а также
момент инерции относительно центральной
оси.
ычислим
полярный момент инерции круга
относительно его центра, а также
момент инерции относительно центральной
оси.
При
вычислении полярного момента инерции
выделим элементарную полоску в виде
тонкого кольца толщиной  (рис. 12). Площадь такого элемента
равна
(рис. 12). Площадь такого элемента
равна


Ввиду
малости слагаемым  пренебрегаем.
пренебрегаем.
Полярный момент инерции

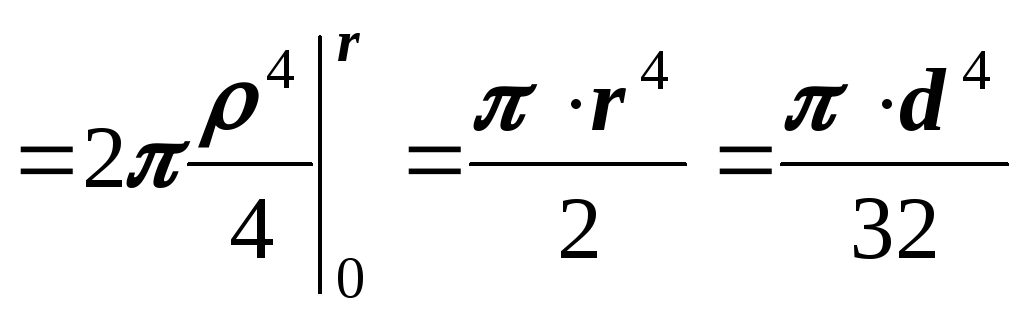 .
.
В
силу симметрии фигуры  .
Используя свойство осевых и полярных
моментов инерции
.
Используя свойство осевых и полярных
моментов инерции
 ,
получим:
,
получим: 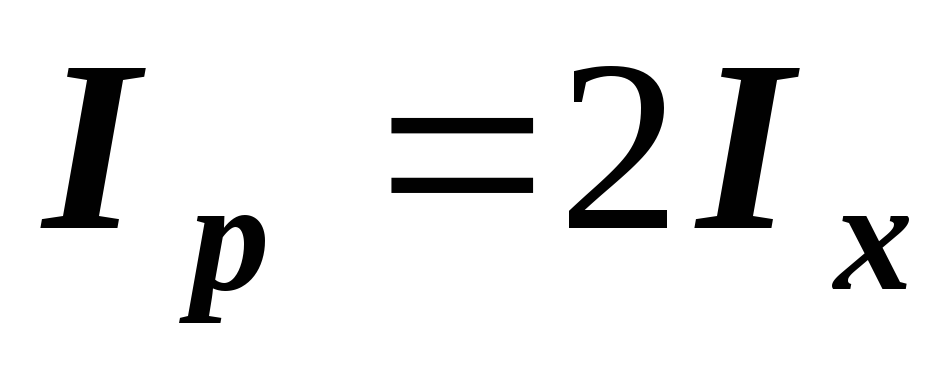 .
Отсюда
.
Отсюда
 .
.
3. Моменты инерции сложных сечений.
В расчетной практике часто приходится вычислять моменты инерции сложных сечений. Для прокатных профилей (рис. 13) геометрические характеристики сведены в таблицы, которые называются сортаментом прокатной стали.
Рис. 13. | двутавр | | швеллер | | Равнобокий уголок | | неравнобокий уголок |
Пусть
требуется определить моменты инерции
сложной фигуры относительно осей 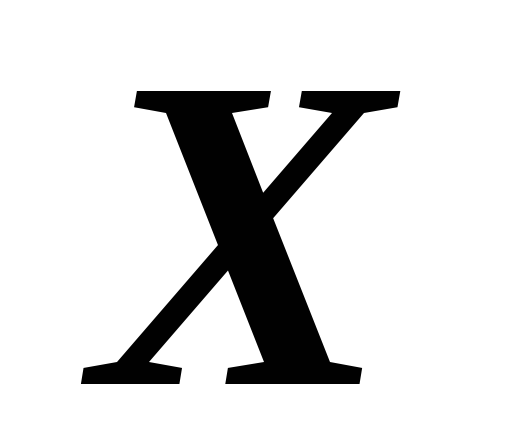 ,
, (рис. 14). При вычислении моментов
инерции сложных сечений их нужно
разбить на простые части, моменты
инерции которых известны.
(рис. 14). При вычислении моментов
инерции сложных сечений их нужно
разбить на простые части, моменты
инерции которых известны.
 Из
основного свойства интеграла суммы
следует, что момент инерции сложной
фигуры равен сумме моментов инерции
составных ее частей.
Из
основного свойства интеграла суммы
следует, что момент инерции сложной
фигуры равен сумме моментов инерции
составных ее частей.
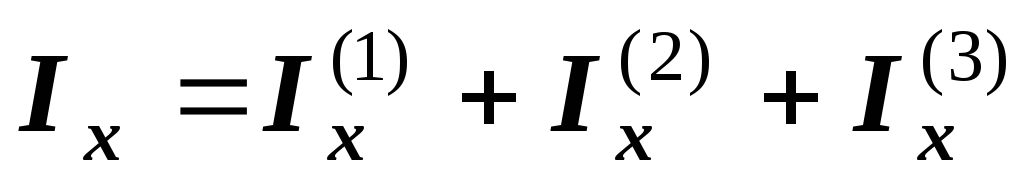 ;
;
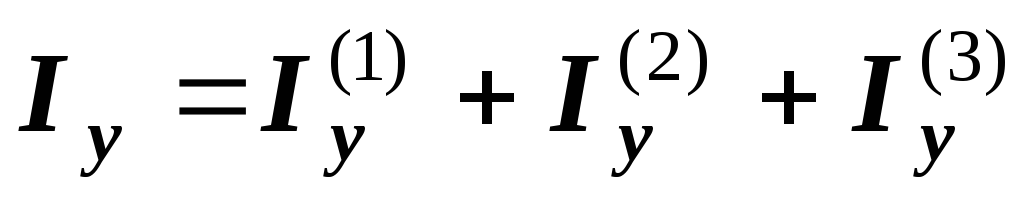 .
.
Если в сечении имеется отверстие (рис. 15), то его удобно считать фигурой с отрицательной площадью.

 ;
;
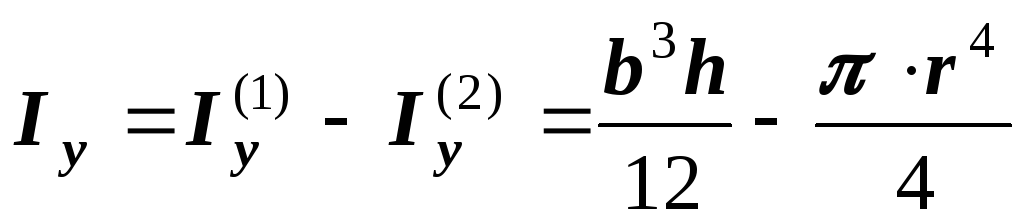 .
.
5 вопрос
5
Моменты инерции однородных тел правильной формы.
Момент
инерции материальной точки определяется
произведением массы материальной точки
на квадрат расстояния от оси вращения
до рассматриваемой точки.Моменты инерции
однородных тел правильной формы
относительно оси проходящей через их
центр масс рассчитываются достаточно
просто исходя из формул объемов тел, и
определения плотности в виде  .
Поясним это на примере однородного
цилиндра. Мысленно разобьем цилиндр на
концентрические слои толщиной
.
Поясним это на примере однородного
цилиндра. Мысленно разобьем цилиндр на
концентрические слои толщиной  ,
тогда масса цилиндра радиуса —
,
тогда масса цилиндра радиуса — очевидно,
будет равна
очевидно,
будет равна  ,
здесь
,
здесь  —
высота цилиндра. Момент инерции
рассматриваемого слоя
—
высота цилиндра. Момент инерции
рассматриваемого слоя  .Прямое
интегрирование последнего выражения
позволяет получить полный момент
цилиндра
.Прямое
интегрирование последнего выражения
позволяет получить полный момент
цилиндра
 .Учитывая,
что масса равна
.Учитывая,
что масса равна  ,
окончательно получим
,
окончательно получим  .
.
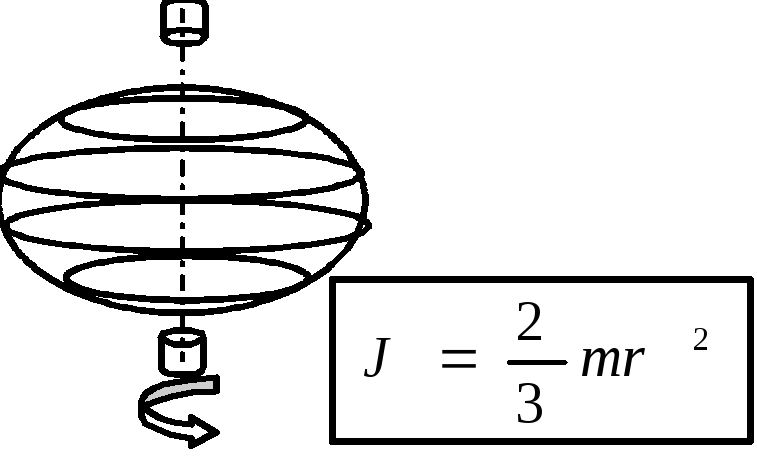
Аналогично рассуждая, можно получить формулы для расчета моментов инерций и для других тел вращения правильной формы, для случая, когда ось вращения проходит через центр масс рассматриваемого тела
| (закрепленный посередине)
| (закрепленный см. рис.)
|
|
|
|
 Теорема
ШТЕЙНЕРА.
Теорема
ШТЕЙНЕРА.
Момент инерции данного тела относительно, какой либо данной оси зависит не только от массы, формы и размеров тела, но также от положения тела по отношению к этой оси.
Согласно теореме Гюйгенса — Штейнера — момент инерции тела J относительно произвольной оси (рис. 6.4) равен сумме:
1)момента инерции этого тела J0, относительно оси, проходящий через центр масс этого тела, и параллельной рассматриваемой оси,
2)
произведения массы тела на квадрат
расстояния между осями. 
Лекция №13-механика
Лекция №13
Тема: «Геометрические характеристики сечения»
Вопросы:
1. Статические моменты сечения
2. Моменты инерции сечения
3. Моменты инерции прямоугольника, круга и кольца
4. Изменение моментов инерции с поворотом осей. Главные оси и главные моменты инерции
1. Статические моменты сечения
Статическим моментом сечения относительно оси X (см. рис. 1) называется выражение:
 (1)
(1)
и относительно оси Y:
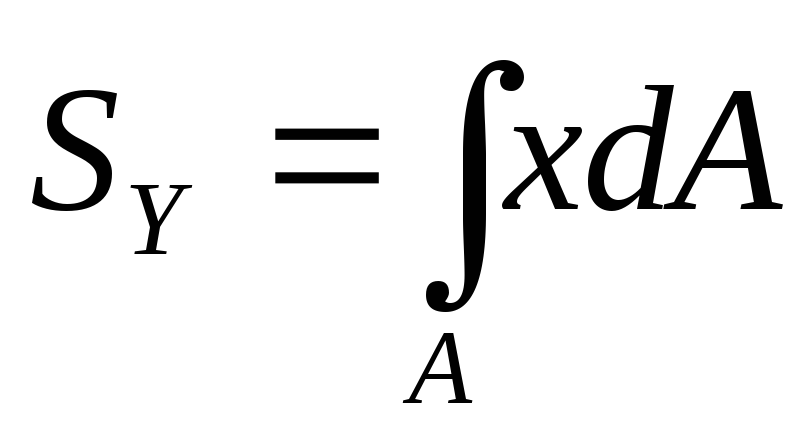 (2)
(2)

Рис. 1
Статический момент имеет размерность см3 или м3, может быть положительным, отрицательным или равным нулю. Если статический момент ранен нулю, то ось проходит через центр тяжести сечения и называется центральной осью. Поэтому оси симметрии фигур вceгда являются центральными.
Определим как
изменяется статический момент фигуры
с параллельным переносом оси. Пусть ось
Хо является центральной (см. рис. 2), а
ось X
смещена на расстояние а.
Из рисунка видно, что:  .
.

Рис. 2
Статический момент фигуры относительно оси X равен:
 .
.
Интеграл 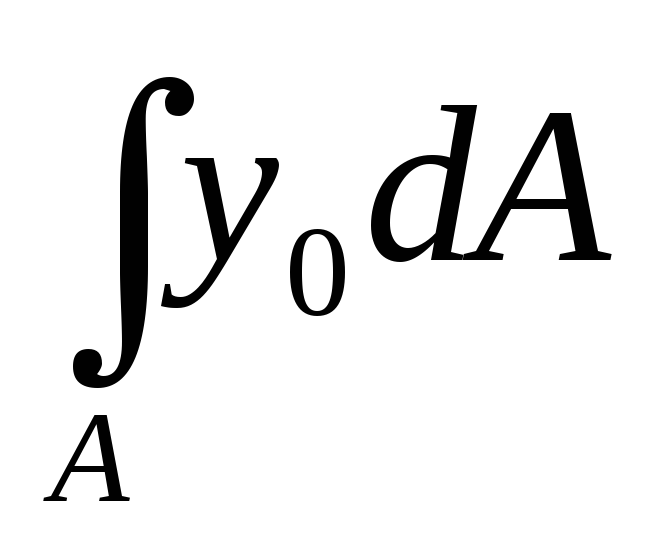 представляет собой статический момент
относительно оси Хо,
т.е. центральной оси. Мы уже отмечали,
что статические моменты относительно
центральных осей равны нулю.
представляет собой статический момент
относительно оси Хо,
т.е. центральной оси. Мы уже отмечали,
что статические моменты относительно
центральных осей равны нулю.
 ;
;
В результате получим:

или
 .
.
Если заменить 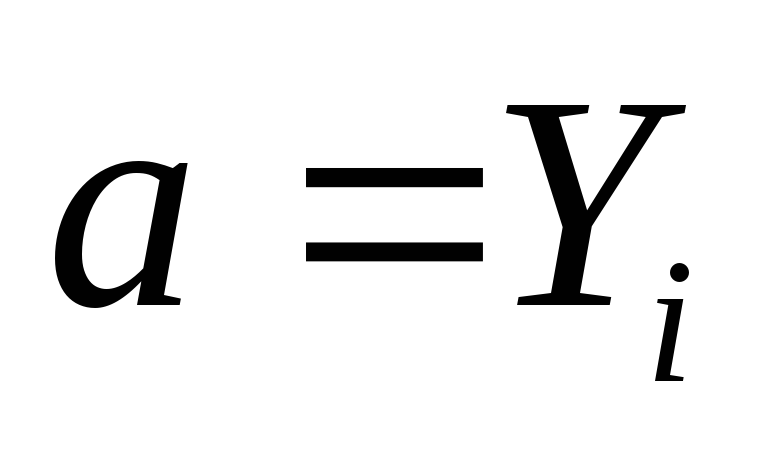 – ординату центра тяжести фигуры, то
получим:
– ординату центра тяжести фигуры, то
получим:
 и
и  (2)
(2)
По формулам (2) можно определить координаты центра тяжести фигуры. Если фигура имеет сложные очертания, то ее разбивают на несколько простых (прямоугольники, треугольники, секторы, сегменты и т.д.) и статический момент находят как сумму статических моментов простых фигур. Статический момент простых фигур определяют, преобразовав формулу (2):
 и
и  (3)
(3)
Пример: Определить центр тяжести фигуры (рис. 3). Размеры даны в см.

Рис.3
Решение: Разбиваем фигуру на два прямоугольника (на рисунке пронумерованы 1 и 2). Оси X и Y проводим чeрез центр тяжести одной из фигур (прямоугольника 1), что значительно облегчает подсчеты, так как:
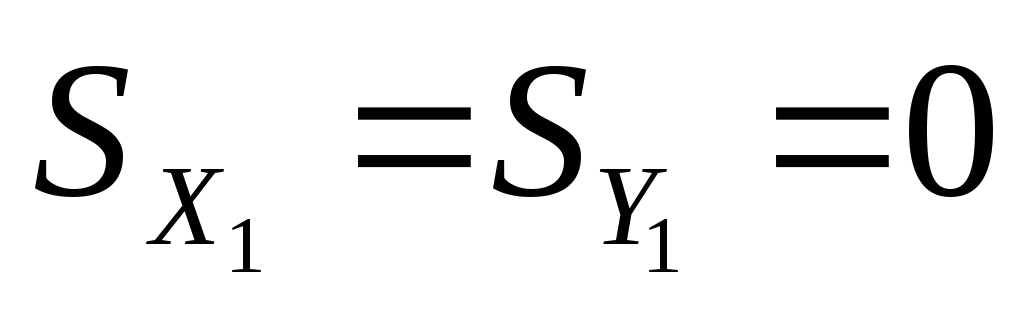 .
.
По формуле (3) находим:
 ,
,
 .
.
Общая площадь фигуры равна:
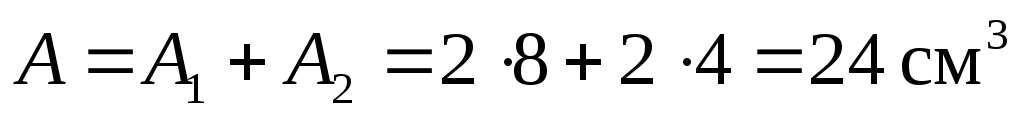 .
.
Координаты центра тяжести определим по формуле (2):
 ;
;
 .
.
Проверка: Если фигура вычерчена в масштабе, то центр тяжести находится па прямой, соединяющей центры тяжести простых фигур.
2. Моменты инерции сечения
Осевым моментом инерции относительно оси X называется выражение:

относительно оси Y: (4)
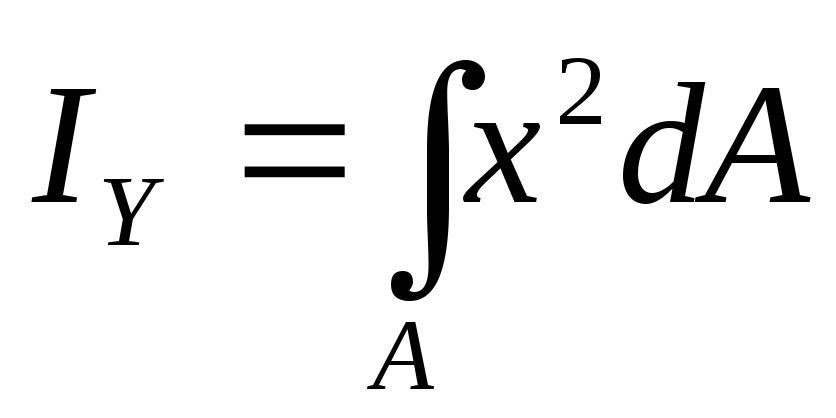
Полярным моментом инерции является выражение (см. рис. 4):
 (5)
(5)
Осевые и полярный моменты инерции всегда положительны и имеют размерность см4 или м4. Из рисунка 4 видно, что:
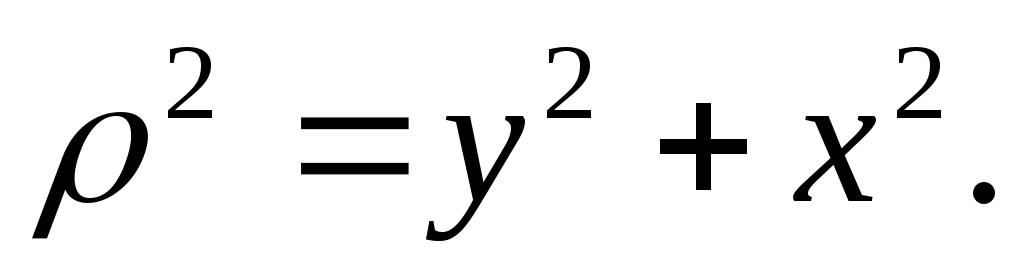
поэтому:


Рис. 4
или
 (6)
(6)
Полярный момент инерции равен сумме осевых.
Помимо осевых и полярного момента инерции в ряде случаев определяют центробежный момент:
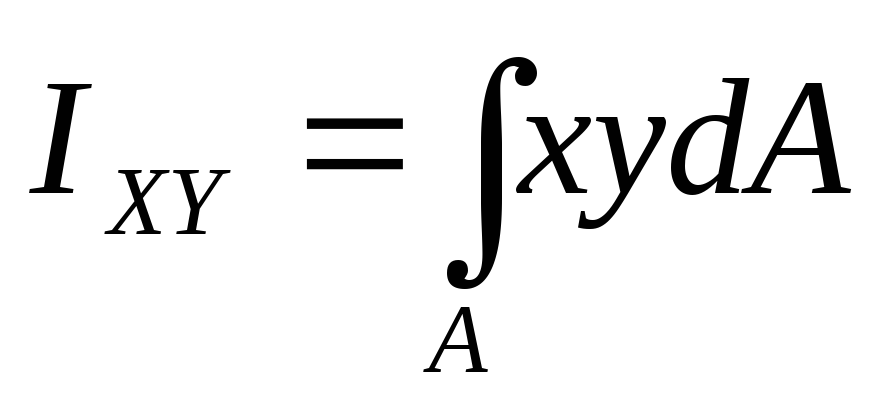 . (7)
. (7)
Центробежный момент инерции может быть положительным, отрицательным и равным нулю. Размерность та же, что и осевых и полярных моментов – см4 или м4.
Определим, как изменяется осевой момент инерции с параллельным переносом оси. Пусть ось Хо – центральная (см. рис. 2). Из рисунка видно, что:
 ,
,
Тогда:

Интеграл  – это момент инерции относительно
центральной оси Хо,
т.е.
– это момент инерции относительно
центральной оси Хо,
т.е.  интеграл
интеграл  – это статический момент относительно
центральной оси, а он всегда равен нулю.
– это статический момент относительно
центральной оси, а он всегда равен нулю.
В результате получим:
 (8)
(8)
Из формулы (8) видно, что осевой момент минимальный при а=0, т.е. центральный осевой момент имеет наименьшее значение.
Рассмотрим изменение центробежного момента инерции с параллельным переносом осей (см. рис. 5). Оси Xо и Yо – центральные.

Рис.5
Из рисунка 5 видно, что:
 ,
,  .
.
Центробежный момент равен:

Интеграл  представляет собой центробежный момент
инерции, интегралы
представляет собой центробежный момент
инерции, интегралы 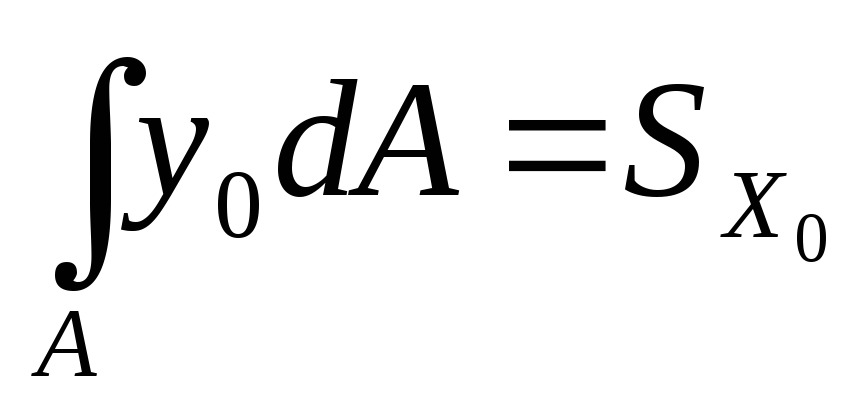 и
и  – статические моменты относительно
центральных осей Xо и Yо.
Как известно, центральные статические
моменты равны нулю. Поэтому:
– статические моменты относительно
центральных осей Xо и Yо.
Как известно, центральные статические
моменты равны нулю. Поэтому:
 (9)
(9)
Если одна из
центральных осей являйся осью симметрии
фигуры, то  и формула (9) упростится:
и формула (9) упростится:
 (10)
(10)
3. Моменты инерции прямоугольника, круга и кольца
3.1. Осевой момент прямоугольника
Определим центральный осевой момент прямоугольника. Возьмем бесконечно тонкую полоску толщиной dy на расстоянии y от оси X (рис. 6). Тогда:

 (11)
(11)

Рис. 6
3.2. Моменты инерции круга и кольца
Определим полярный
момент инерции круга. Возьмем бесконечно
тонкое кольцо толщиной  на
расстоянии
на
расстоянии  от
центра круга (рис.7). Площадь кольца можно
определить, развернув прямоугольник.
от
центра круга (рис.7). Площадь кольца можно
определить, развернув прямоугольник.
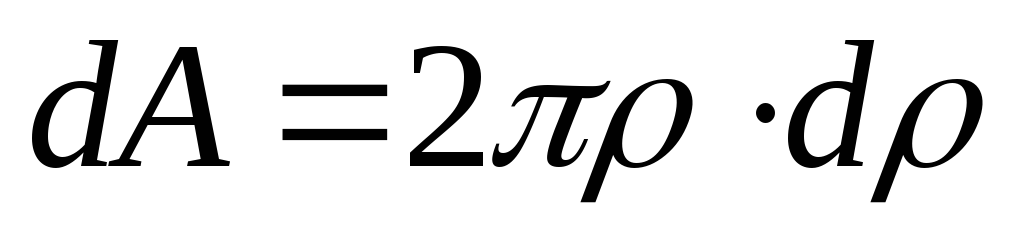 .
.
Полярный момент равен:

Обычно при подсчетах пользуются не радиусом, а диаметром:
 и
и  ,
,
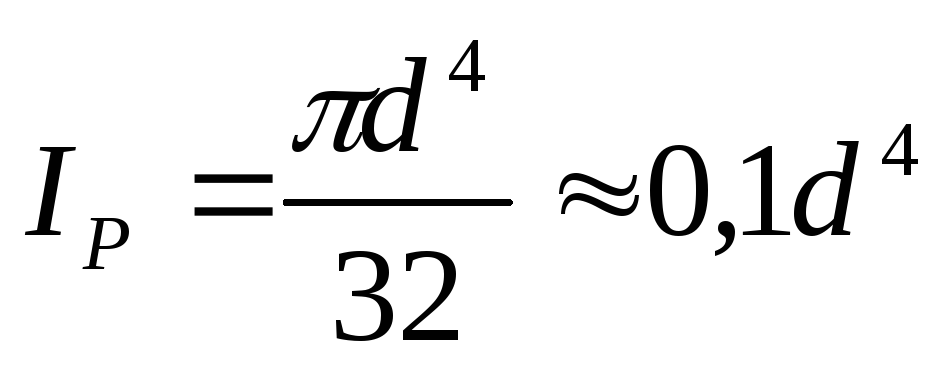 (12)
(12)
Полярный момент инерции фигуры равен сумме осевых моментов:
 ,
,
но для круга  ,
поэтому:
,
поэтому:
 (13)
(13)
Моменты инерции кольца можно определить как разность моментов инерции большого и малого кругов (рис. 8).

Рис.7 Рис.8

или
 (14)
(14)
где  ;
;
 (15)
(15)
4. Изменение моментов инерции с поворотом осей. Главные оси и главные моменты инерции
Определим, как
изменяются осевые моменты инерции с
поворотом осей. Пусть оси X
и Y
проходят под углом  к осям X1 и Y1 (см. рис. 9)
к осям X1 и Y1 (см. рис. 9)
С поворотом осей значение осевых и центробежных моментов инерции меняются. Для практических целей весьма важно определить положение осей, когда осевой момент максимальный и минимальный. При максимальном моменте сопротивление изгибу наибольшее, при минимальном – наименьшее. Оси, относительно которых осевые моменты имеют экстремальные значения, называют главными осями.
Положение осей,
когда центробежный момент инерции равен
нулю, также соответствует главным осям,
т.е. если  ,
то X
и Y
– главные оси.
,
то X
и Y
– главные оси.
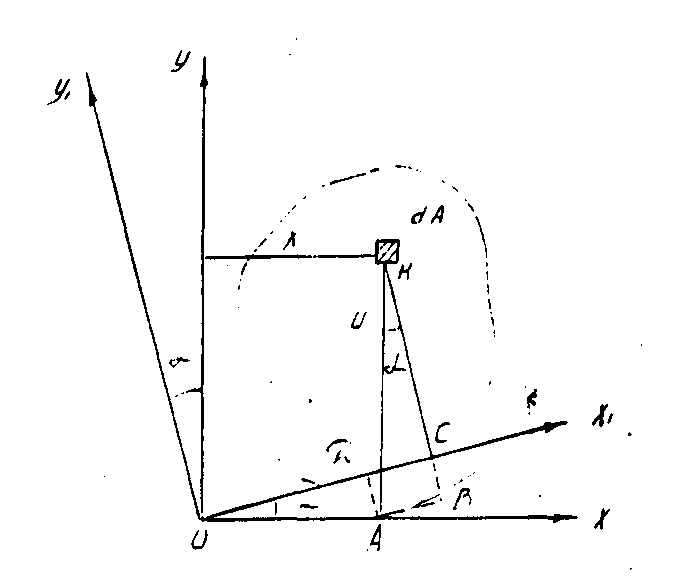
Рис. 9
Формула для определения положения двух осей, относительно одной из которых осевой момент инерции максимален, а относительно другой – минимален имеет следующий вид:
 (16)
(16)
Моменты инерции относительно главных осей называются главными моментами инерции. Главные моменты инерции имеют максимум и минимум. Они определяются по формуле:
 (17)
(17)
Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями.
Во многих случаях удается сразу определить положение главных центральных осей. Если фигура имеет ось симметрии, то она является одной из главных центральных осей, вторая проходит через центр тяжести сечения перпендикулярно первой. Сказанное следует из того, что относительно оси симметрии и любой оси, ей перпендикулярной, центробежный момент инерции равен нулю.
В случае если два главных центральных момента инерции сечения равны между собой, то у этого сечения любая центральная ось является главной, и все главные центральные моменты инерции одинаковы (круг, квадрат, шестиугольник, равносторонний треугольник).
4.2. Основные теоремы о моментах инерции

Осевыми моментами инерции сечения называются интегралы
Jx = ∫ y2dA J y = ∫ x2dA | (4.1) | ||
A | , | A |
|
Центробежным моментом инерции называется интеграл |
| ||
Jxy | = ∫ xydA | (4.2) | |
| A |
|
|
Полярным моментом инерции называется интеграл |
| ||
Jρ | = ∫ ρ 2dA | (4.3) | |
| A |
|
|
Так как ρ 2 = x2 + y2 , то |
|
|
|
Jρ | = Jx | + J y , |
|
т.е. полярный момент инерции сечения относительно заданной точки равен сумме осевых моментов инерции относительно двух взаимно перпендикулярных осей, проходящих через эту точку.
4.1.4. Радиусы инерции
Величины, определяемые по формулам:
ix = | J | x | ; iy = | J y | , – называются радиусами инерции относительно осей x и y |
| A | ||||
| A |
|
| ||
соответственно
4.2.1. Теорема о моментах инерции относительно осей, параллельных центральным
Осевой момент инерции сечения относительно произвольной оси равен моменту инерции относительно центральной оси параллельной данной плюс произведение квадрата расстояния между осями на площадь сечения.
Центробежный момент инерции сечения относительно произвольных осей координат равен центробежному моменту инерции относительно центральных осей параллельных данным плюс произведение площади сечения на расстояния между осями.
Рассмотрим сечение произвольной формы площадью A. Пусть оси x и y являются центральными (т.е. проходящими через центр тяжести сечения), и известны моменты инерции
Jx, Jy, Jxy. Требуется определить моменты инерции Jx1 , J y1 , Jx1y1 относительно осей x1 и y1, смещенных параллельно центральным осям на расстояния a и b соответственно.
44

Координаты элементарной площадки dA в системе координат (x1, y1): x1=x+b; y1=y+a.
По определению осевого момента инерции (4.1)
Jx1 = ∫( y + a)2 dA = Jx + 2a∫ ydA + a2 A ,
A A
где ∫ ydA = Sx = 0 .
A
Таким образом,
J | x1 | = J | x | + a2 A | (4.4) |
|
|
|
|
Рассуждая аналогичным образом, можно получить
J | y1 | = J | y | + b2 A | (4.5) |
|
|
|
|
По определению центробежного момента инерции (4.2):
Jx y | = ∫ x1 y1dA = ∫( y + a)(x + b)dA = Jxy + abA. | ||
1 | 1 | A | |
|
| A | |
4.2.2. Вычисление моментов инерций простейших фигур
Прямоугольник.
Сначала определим моменты инерции прямоугольника относительно осей x1 и y1.
Выделим на расстоянии y1 от оси x1 элементарную площадку dA высотой dy1 и шириной, равной ширине прямоугольника:
По определению осевого момента инерции (4.1)
Jx1 = ∫ y12dA.
A
Заменим интеграл по площади интегралом по высоте
h |
| 3 |
| h |
| 3 | |
|
|
| |||||
Jx1 = ∫ y12bdy1 | = b | y1 |
|
|
| = bh | . |
| |||||||
0 | 3 |
| 0 | 3 |
| ||
|
|
| |||||
Аналогично
45

Jy1 = hb33 .
Моменты инерции относительно центральных осей x и y определим, пользуясь теоремой о моментах инерции относительно осей, параллельных центральным (4.4):
Jx = Jx1 − | h 2 | bh = | bh4 | bh4 | bh4 | ||||
| 2 | 3 | − | 4 = | 12 . | ||||
Аналогично |
|
|
|
|
|
|
|
|
|
|
| J |
| = | hb3 | . |
|
| |
|
| y | 12 |
|
| ||||
|
|
|
|
|
|
| |||
|
|
|
|
|
|
|
| ||
Круг.
Определим полярный момент инерции круга. Выделим на расстоянии ρ от центра круга элементарный слой dA толщиной dρ .
По определению полярного момента инерции (4.3)
Jρ | = ∫ ρ 2dA . |
|
|
|
|
|
|
| A |
|
|
|
|
|
|
Заменим интеграл по площади интегралом по радиусу |
|
|
|
|
|
| |
Jρ = d∫/ 2 ρ 2 2πρdρ = 2π d∫/ 2 ρ 3dρ = 2π | ρ 4 |
| d / 2 | = | πd 4 . | ||
| |||||||
4 |
|
|
| ||||
0 | 0 |
|
| 0 |
| 32 | |
|
|
|
| ||||
Так как Jp=Jx+Jy и для круга Jx=Jy, то осевой момент инерции
J |
| = | J | ρ | = | πd 4 | . | |
x | 2 | 64 | ||||||
|
|
|
| |||||
|
|
|
|
| ||||
Прямоугольный треугольник.
Определим момент инерции треугольника относительно оси x1, совпадающей с его нижней стороной.
Выделим на расстоянии y1 от оси x1 элементарную площадку dA высотой dy1. Ширина площадки из подобия треугольников:
|
|
|
| by |
| = b | h − y1 | . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
|
|
|
|
| 1 |
|
|
| h |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
Момент инерции |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| h | b(h − y | ) |
|
|
|
|
| y3 |
| h |
|
|
| b y4 |
| h | bh4 |
| bh4 |
| bh4 | |||||||||
|
|
|
|
|
|
|
|
|
|
|
| ||||||||||||||||||||
J x1 = ∫ y12dA = ∫ y12 |
| 1 |
| dy1 = b | 1 |
|
|
|
| − |
|
|
|
|
| 1 |
|
| = |
| − |
| = |
| . | ||||||
h |
|
| 3 |
|
| h 4 | 3 | 4 | 12 | ||||||||||||||||||||||
A | 0 |
|
|
|
|
|
|
|
| 0 |
|
|
|
| 0 |
|
|
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||
Относительно центральной оси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
| Jx | = Jx | h 2 | bh | = | bh4 | − | bh4 | = |
| bh4 |
|
|
|
|
|
| ||||||||||||||
| − |
| 2 | 12 |
|
| 18 | 36 | . |
|
|
|
|
| |||||||||||||||||
|
| 1 |
| 3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
| |||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
Аналогично для второй оси |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
| J y |
| = | hb3 | ; J y = | hb3 | . |
|
|
|
|
|
|
|
|
|
|
| |||||||||||
|
|
|
| 12 | 36 |
|
|
|
|
|
|
|
|
|
|
| |||||||||||||||
|
|
| 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
4.2.3. Теорема о моментах инерции при повороте осей координат
Рассмотрим сечение произвольной формы площадью A. Пусть известны моменты инерции относительно осей x и y: Jx, Jy, Jxy. Требуется определить моменты инерции Jx1 , J y1 , Jx1y1
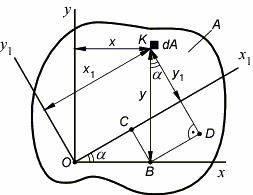
относительно осей x1 и y1, повернутых по отношению к осям x и y на угол α. Выделим в окрестности точки K с координатами x и y элементарную площадку dA.
Координаты площадки dA в повернутой системе координат:
x1 = OC + BD = x cosα + y sinα , y1 = KD − CB = y cosα − x sinα .
Осевые моменты инерции:
J x1 = ∫ y12dA = ∫( y cosα − x sinα )2 dA = Jx cos2 α + J y sin2 α − Jxy sin 2α ,
| A | A |
J y1 | = ∫ x12dA = ∫(x cosα + y sinα )2 dA = J ycos2 α + Jx sin2 α + Jxy sin 2α . | |
| A | A |
Сложив попарно левые и правые части полученных уравнений, найдем:
J x1 + J y1 = J x + J y .
Таким образом, сумма моментов инерции относительно осей прямоугольной системы координат не изменяется при их повороте. Как было показано выше, эта сумма равна полярному моменту инерции относительно начала координат.