Момент инерции определение: определение, законы, формулы для чайников – Список моментов инерции — Википедия — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Определение момента инерции тела и положения центра масс

Space Electronics KSR — самые точные инструменты в мире для определения момента инерции (МИ) и положения центра масс (ЦМ).
Данная линейка инструментов настоятельно рекомендуется для определения масс-инерционных характеристик ракет, спутников и баллистических объектов.
Оборудование может быть использовано для полезной нагрузки массой от 100 грамм до 10 тонн и тяжелее.

Концепция измерения
Сферический подшипник поддерживает поворотный стол и выступает в роли шарнира для измерения дисбаланса, возникающего от смещения центра масс испытуемого объекта относительно оси подшипника.

Определение момента инерции тела происходит при помощи торсиона, зажатого снизу и прикрепленного сверху к газовому подшипнику, образуя, таким образом, перевернутый крутильный маятник.

Ключевые особенности
Наилучшая достигаемая точность — измерение ЦМ с точностью до 25 микрон и МИ с точностью до 0.1% Один инструмент может измерять полезную нагрузку, вес которой составляет всего 4% от максимального веса, на который рассчитан инструмент.

Полная автоматизация процесса — выберите определение момента инерции или центра масс на экране компьютера и процесс измерения запуститься автоматически.
Использование газовых подшипников значит полную совместимость с чистыми комнатами. Нет риска загрязнения, нет высокого давления, нет опасности взрыва.

Огромная устойчивость от опрокидывающих моментов. Инструмент не опрокидывается даже при высоком расположении ЦМ.
Полностью программная поддержка метрических и дюймовых единиц. Система координат определяется пользователем — значения ЦМ и МИ сообщаются непосредственно в системе координат полезной нагрузки.

Оборудование для калибровки согласно стандартам НИСТ входит в комплект поставки каждого инструмента.

Дисбаланс от центра масс измеряется непосредственно;
Изменение положения ЦМ можно наблюдать в живую;
Автоматическое устранение ошибоквыравнивания.

Опциональная весоизмерительная платформа и манипулятор для определения координат позволяет напрямую собирать данные о весе и системе координат испытуемого объекта непосредственно на инструменте.

Общая спецификация линейки (для конкретной модели значения необходимо уточнять)
Измерения за один установ: 2 координаты центра масс и 1 значение момента инерции;
Диапазон масс нагрузок: От 100 грамм до 10 тонн;

Точность определения ЦМ: 0.1% от измеренного значения дисбаланса;
Точность определения МИ: 0.1% от измеренного значения;
Требования к электросети: 115 ВAC, 60 Hz или 220 ВAC, 50 Hz, одна фаза;
Требования к сетия сжатого воздуха: Источник чистого сухого воздуха или азота, 7 бар, 60 л/мин;
Требования к полу: Бетонный пол, 15 см. толщиной.

Момент инерции — с русского на все языки

Момент инерции — Размерность L2M Единицы измерения СИ кг·м² СГС … Википедия

МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z наз. величина, определяемая… … Физическая энциклопедия

МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, механическая величина, играющая при вращательном движении ту же роль, что масса при движении поступательном. Например ускорение при поступательном движении обратно пропорционально массе, ускорение вращательного движения (угловое… … Большая медицинская энциклопедия

МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Современная энциклопедия

МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Большой Энциклопедический словарь

Момент инерции — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Иллюстрированный энциклопедический словарь

МОМЕНТ ИНЕРЦИИ — (обозначение I), для вращающегося тела сумма произведений, полученных путем умножения масс точек вращающегося тела на квадраты их расстояний от оси вращения. Нахождение этого распределения массы важно при определении силы, необходимой, чтобы… … Научно-технический энциклопедический словарь

Момент инерции — – величина, характеризующая распределение масс в теле и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении. [Полякова, Т.Ю. Автодорожные мосты: учебный англо русский и русско английский терминологический… … Энциклопедия терминов, определений и пояснений строительных материалов

момент инерции — 3.24 момент инерции (moment of inertia): Интегральная сумма произведений массы отдельных частей тела на квадраты расстояний (радиусов) их центров тяжести от заданной оси. Источник: ГОСТ Р 52776 2007: Машины электрические вращающиеся. Номинальные… … Словарь-справочник терминов нормативно-технической документации

Момент инерции — (Moment d inertie, Trägheitsmoment, Moment of inertia) понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же рода, не давая ему особого названия: один из путей, приводящий к его определению, следующий.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона

момент инерции

— величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Энциклопедический словарь

момент инерции — с английского на русский

См. также в других словарях:

Момент инерции — Размерность L2M Единицы измерения СИ кг·м² СГС … Википедия
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. В механике различают М. и. осевые и центробежные. Осевым М. и. тела относительно оси z наз. величина, определяемая… … Физическая энциклопедия
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, механическая величина, играющая при вращательном движении ту же роль, что масса при движении поступательном. Например ускорение при поступательном движении обратно пропорционально массе, ускорение вращательного движения (угловое… … Большая медицинская энциклопедия
МОМЕНТ ИНЕРЦИИ — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Современная энциклопедия
МОМЕНТ ИНЕРЦИИ — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступат. движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Большой Энциклопедический словарь
Момент инерции — МОМЕНТ ИНЕРЦИИ, мера инертности твердых тел при вращательном движении (подобно тому как масса является мерой инертности при поступательном движении). При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела,… … Иллюстрированный энциклопедический словарь
МОМЕНТ ИНЕРЦИИ — (обозначение I), для вращающегося тела сумма произведений, полученных путем умножения масс точек вращающегося тела на квадраты их расстояний от оси вращения. Нахождение этого распределения массы важно при определении силы, необходимой, чтобы… … Научно-технический энциклопедический словарь
Момент инерции — – величина, характеризующая распределение масс в теле и являющаяся, наряду с массой, мерой инертности тела при непоступательном движении. [Полякова, Т.Ю. Автодорожные мосты: учебный англо русский и русско английский терминологический… … Энциклопедия терминов, определений и пояснений строительных материалов
момент инерции — 3.24 момент инерции (moment of inertia): Интегральная сумма произведений массы отдельных частей тела на квадраты расстояний (радиусов) их центров тяжести от заданной оси. Источник: ГОСТ Р 52776 2007: Машины электрические вращающиеся. Номинальные… … Словарь-справочник терминов нормативно-технической документации
Момент инерции — (Moment d inertie, Trägheitsmoment, Moment of inertia) понятие это введено в науку Эйлером, хотя уже Гюйгенс раньше пользовался выражением того же рода, не давая ему особого названия: один из путей, приводящий к его определению, следующий.… … Энциклопедический словарь Ф.А. Брокгауза и И.А. Ефрона
момент инерции — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Энциклопедический словарь

Книги

Механика и молекулярная физика. Учебное пособие, Ландау Лев Давидович, Ахиезер Александр Ильич, Лифшиц Евгений Михайлович. Трудно писать о книге Л. Д. Ландау, А. И. Ахиезера, Е. М. Лифшица, потому что это как раз тот случай, когда ни книга, ни, тем более, её авторы, как принято говорить,`в рекламене нуждаются`.… Подробнее Купить за 1849 грн (только Украина)
Физика. Механика. Молекулярная физика и термодинамика. Лабораторный практикум. Часть 2, Сергей Валянский. Лабораторный практикум по разделам «Механика» и «Молекулярная физика и термодинамика» состоит из двух частей. Во второй части приведены описания восьми лабораторных работ, поставленных на… Подробнее Купить за 484 руб электронная книга
Физика. Механика. Молекулярная физика и термодинамика. Лабораторный практикум. Часть 2, Сергей Валянский. Лабораторный практикум по разделам «Механика» и «Молекулярная физика и термодинамика» состоит из двух частей. Во второй части приведены описания восьми лабораторных работ, поставленных на… Подробнее Купить за 484 руб электронная книга

Другие книги по запросу «момент инерции» >>

Определение момента инерции тел

Цель работы: определить с помощью крутильного маятника зависимость момента инерции тела от расстояния до оси вращения, проверить выполнение теоремы Штейнера.

Оборудование: крутильный маятник, секундомер, составной цилиндр.

Теоретическое введение

Момент инерции – это физическая величина, являющаяся мерой инертности тела при его вращательном движении. В этом смысле он подобен массе, являющейся мерой инертности тела при поступательном движении. Величина момента инерции, по определению, равна сумме произведений масс частиц тела на квадраты их расстояний r до оси вращения:

J = S m_ir_i²или J = ò r²dm. (1)

В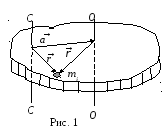еличина момента инерции тела зависит не только от массы тела, но и от расположения частей тела относительно оси вращения. Чем дальше от оси находятся части тела, тем больше момент инерции.

Теоретический расчет момента инерции тел упрощается при применении теоремы Штейнера. Получим уравнение теоремы. Пусть точка О – центр масс тела, через которую проходит ось О – О, а параллельно ей на некотором расстоянии а ось С− С (рис. 1). Установим связь между моментами инерции тела относительно этих осей.

Представим вектор от оси С – С до некоторого элемента массы m_iкак сумму векторов 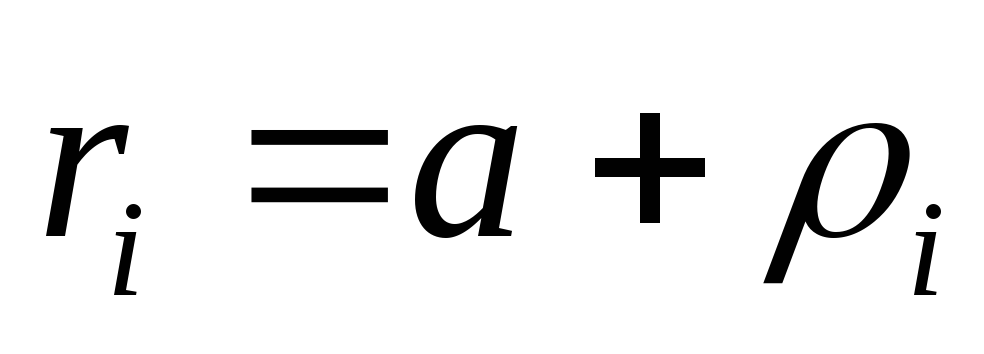(рис. 1). Подставив в определяющую формулу момента инерции (1) радиус—вектор r и возведя сумму в квадрат, получим

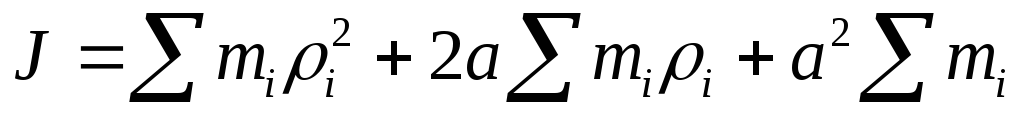. (2)

Первый член этого уравнения J₀– момент инерции тела относительно оси О – О, проходящей через центр масс. Во втором члене сумма определяет положение центра масс тела относительно оси О – О, и так как ось проходит через центр масс, то эта сумма равна нулю. Третий член – это произведение суммы масс частиц, то есть массы тела на квадрат расстояния между осями. Итак,

J= J₀+ m a² . (3)

Это уравнение теоремы Штейнера: момент инерции тела относительно произвольной оси равен сумме момента инерции тела относительно оси, проходящей через центр масс и параллельной данной оси, и произведению массы тела на квадрат расстояния между осями. В тех случаях, когда момент инерции относительно оси, проходящей через центр масс J₀, можно сравнительно легко рассчитать, теорема Штейнера позволяет определить момент инерции относительно произвольной оси J_с, избежав весьма трудоемких расчетов.

Теорему Штейнера можно экспериментально подтвердить, если измерить момент инерции тела при разных расстояниях а от оси вращения до центра масс тела. Если зависимость J(a ²) будет линейной с угловым коэффициентом, равным массе тела, то теорема верна.

Одним из методов измерения момента инерции тел является метод крутильного маятника. Крутильный маятник – это тело, произвольной формы, подвешенное на упругих струнах. В лабораторной установке – это рамка (рис.1). Если рамку отклонить от положения равновесия и отпустить, то она под действием момента упругих сил струны (M =−kα) возвращается к положению равновесия, но по инерции проходит положение равновесия, закручивая струну в противоположном направлении. Возникают вращательные колебания. Применим основной закон динамики вращательного движения: произведение момента инерции рамки на угловое ускорение равно моменту упругих сил подвеса:

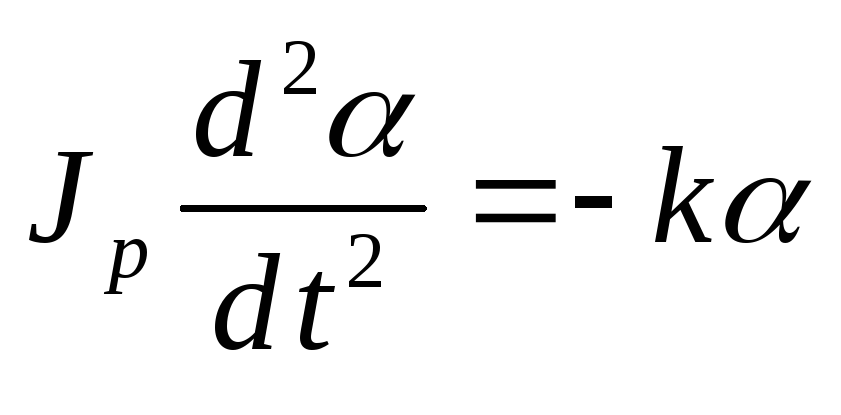. (4)

Это дифференциальное уравнение второго порядка. Его решением должна быть функция, обращающая его в тождество. В данном случае это уравнение гармонических колебаний 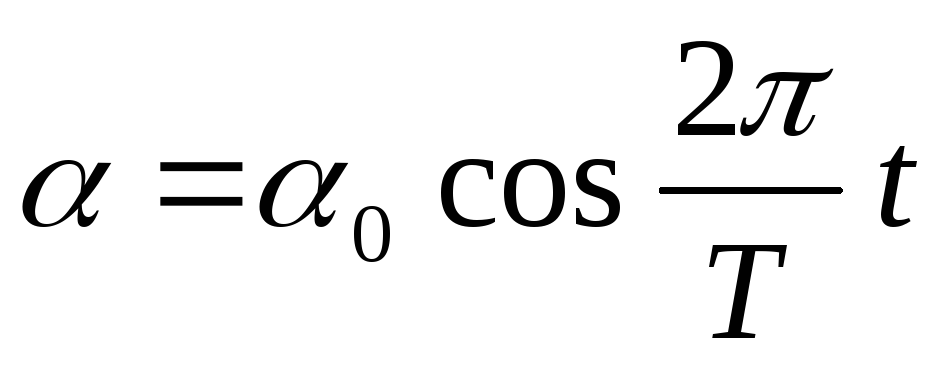, гдеТ – период колебаний. Подставив функцию в уравнение (4), получим, что она будет решением, если период колебаний маятника равен

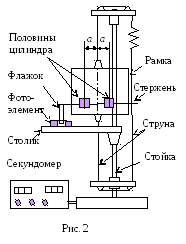
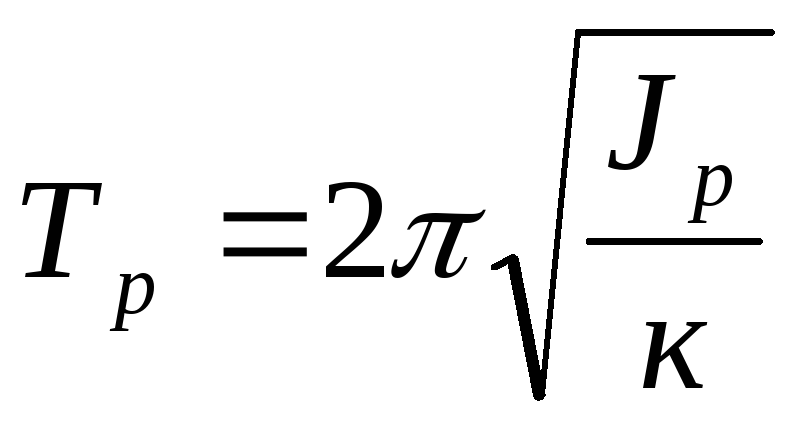_. (5)

Исследуемое тело представляет собой составной цилиндр из двух половин, полуцилиндров. Наденем их на стержень на одинаковом расстоянии а (рис. 2). Момент инерции маятника изменится и будет равен сумме момента инерции рамки и искомого момента инерции цилиндра. Период тоже изменится и станет равным

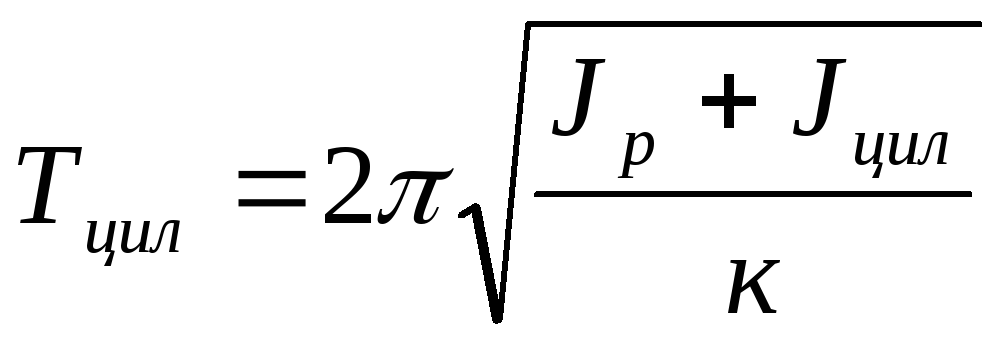. (6)

Решая совместно уравнения (5) и (6), исключая коэффициент упругости к, получим формулу для экспериментального определения момента инерции цилиндра по известному моменту инерции рамки

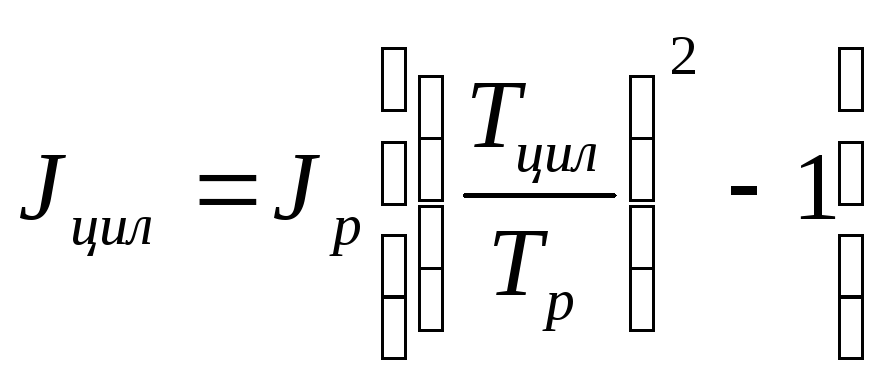. (7)

Содержание

1. Цель работы……………………………………………………………4

2. Теоретическая часть………………………………………………..….4

3. Экспериментальная часть……………………………………………..7

3.1. Описание установки…………………………………………………7

3.2. Порядок выполнения работы……………………………………….8

3.2.1. Определение моментов инерции математического и

физического маятников……………………………………………8

3.2.2. Определение момента инерции физического маятника

в зависимости от распределения массы…………………………10

4. Контрольные вопросы……………………………………………….11

Список литературы………………………………………………….11 Лабораторная работа № 5 Определение моментов инерции тел произвольной формы

1. Цель работы

Определение момента инерции математического и физического маятника, а также изучение зависимости момента инерции физического маятника от распределения массы.

2. Теоретическая часть

Основное уравнение динамики вращательного движения тела вокруг неподвижной оси имеет вид:

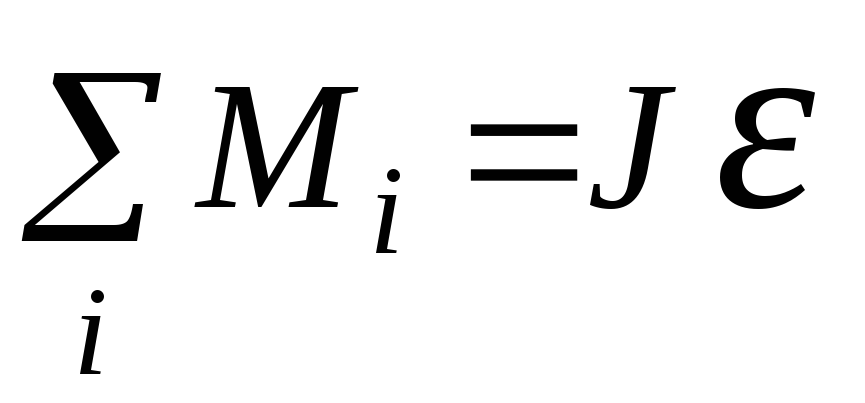, (1)

где 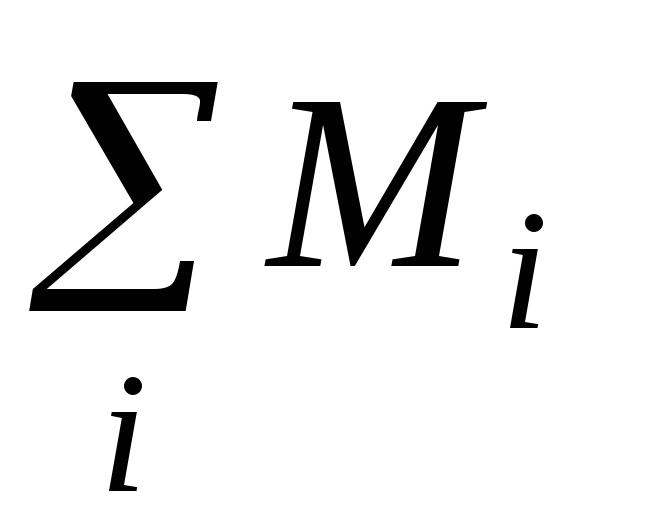– векторная сумма моментов всех сил относительно оси вращения, 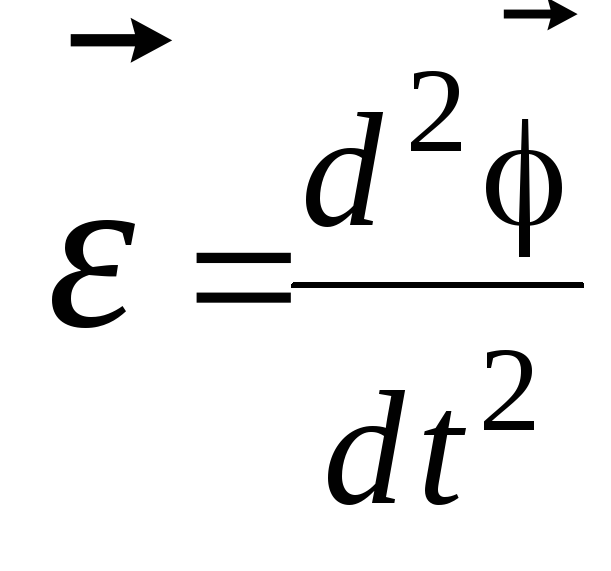– угловое ускорение тела, т.е. вторая производная по времени от угла поворота φ тела. Соотношение (1) аналогично 2 – му закону Ньютона в динамике поступательного движения и в таком виде записывается в тех случаях, когда момент инерции тела при вращении не изменяется.

Моментом инерции материальной точки относительно некоторой оси называется величина, равная произведению массы точки на квадрат ее расстояния от оси вращения

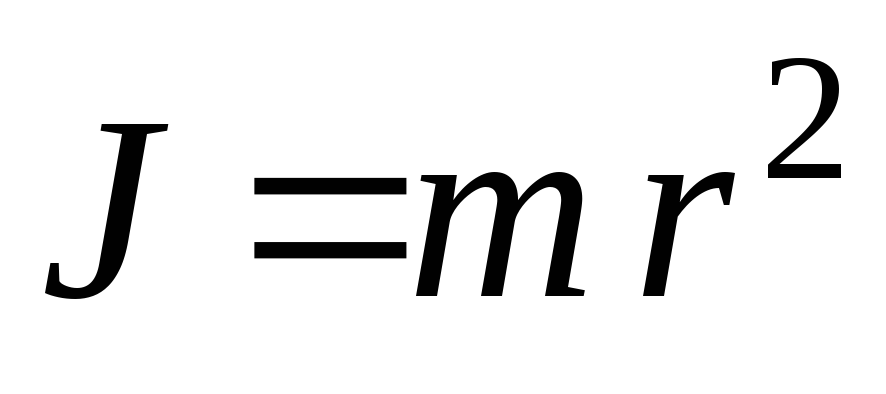. (2)

Для протяженных тел момент инерции определяется как сумма моментов инерции элементарных масс 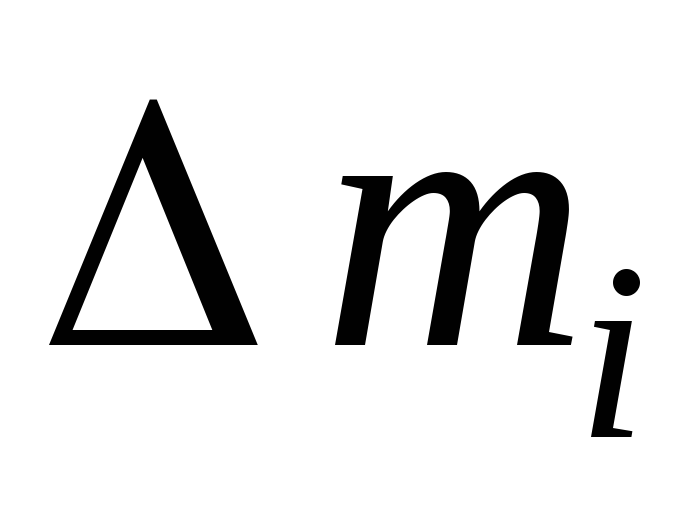(материальных точек), на которые можно разбить тело:

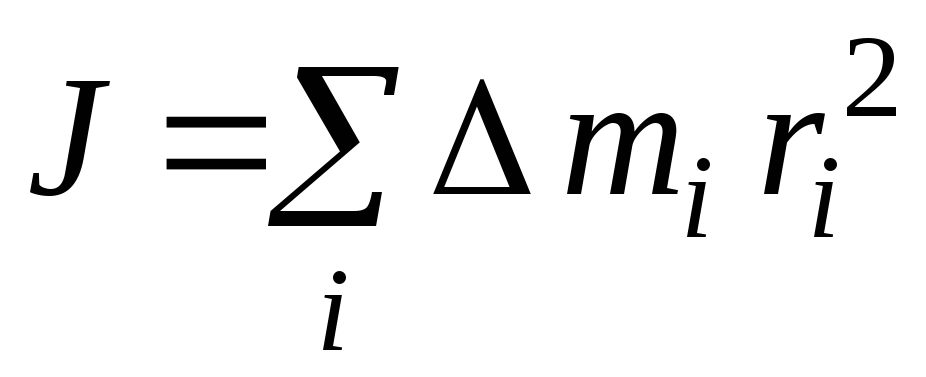. (3)

Имеются различные методы экспериментального определения моментов инерции. В настоящей работе определение моментов инерции тел произвольной формы производится методом колебаний. Для этих целей измеряется период колебаний Т математического и физического маятников.

Математическим маятником называется материальная точка массой m₀, подвешенная на невесомой, нерастяжимой нити и совершающая колебания под действием силы тяжести.

Момент инерции математического маятника

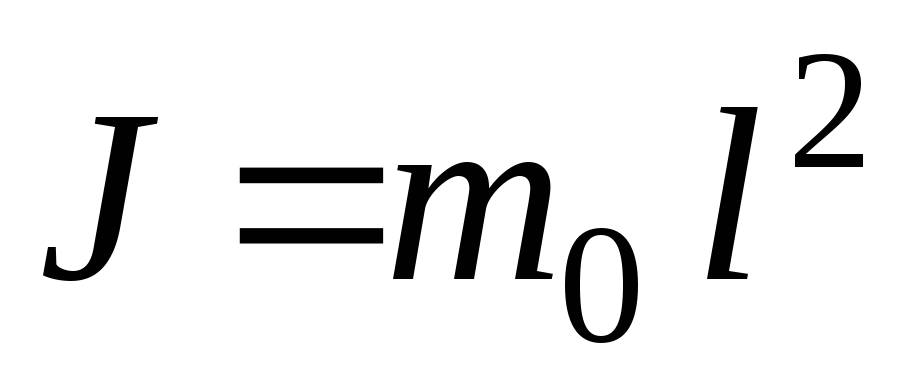, (4)

где l – длина маятника.

Период колебаний математического маятника определяется по формуле

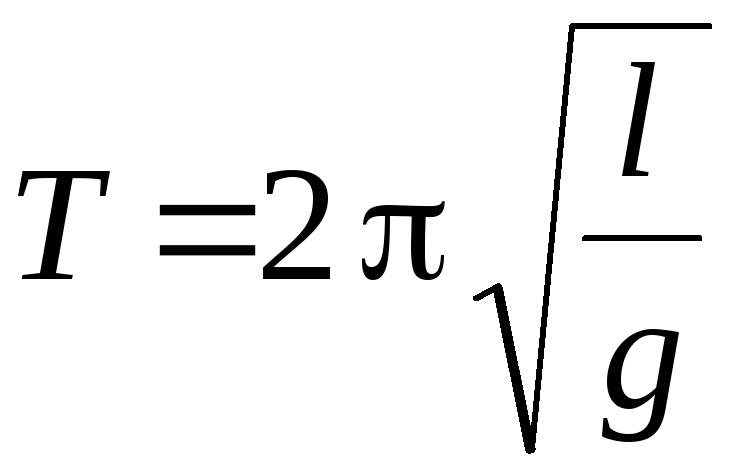. (5)

Физическим маятником называется твердое тело, совершающее колебания вокруг неподвижной горизонтальной оси, не совпадающей с его центром инерции, под действием силы тяжести.

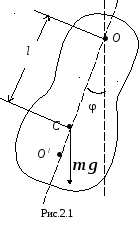
Если отклонить маятник от положения равновесия на угол φ (рис. 1), то момент силы, стремящийся вернуть маятник в положение равновесия равен

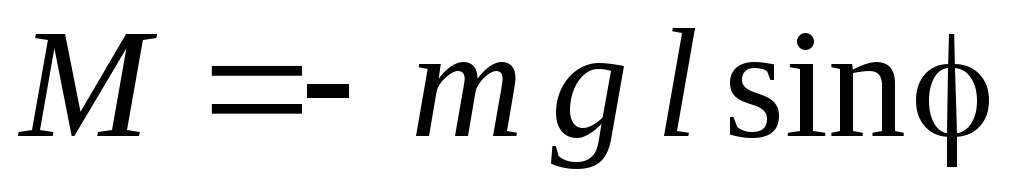. (6)

В (6) l – расстояние между точкой подвеса и центром инерции маятника С, m – масса маятника, 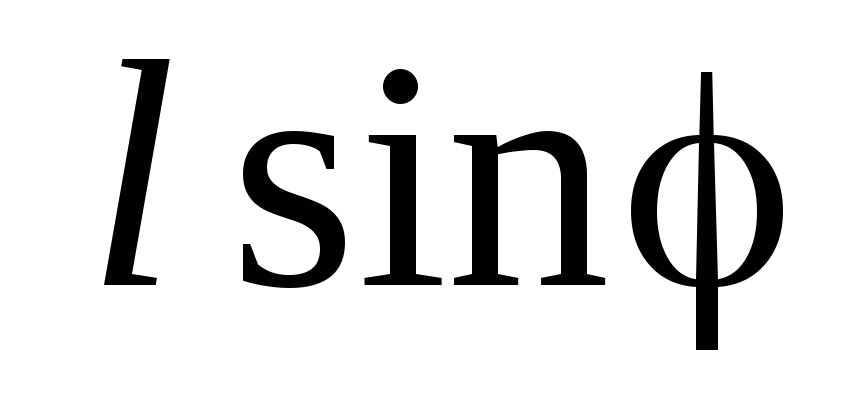– плечо силы тяжести. Основное уравнение динамики вращательного движения (1) с учетом (6) можно записать в виде

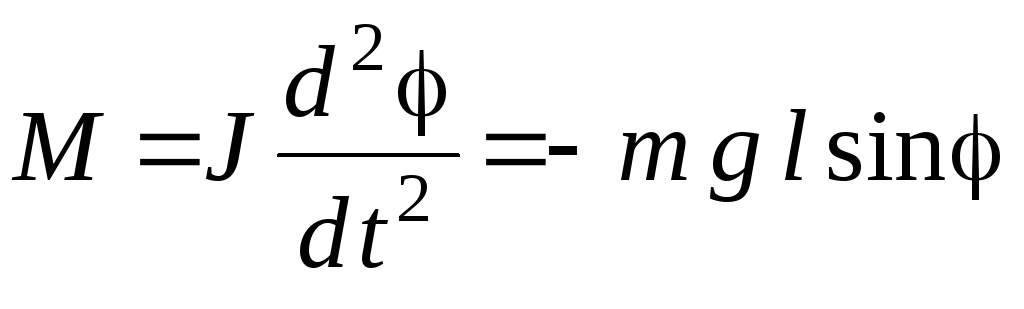При малых углах отклонения 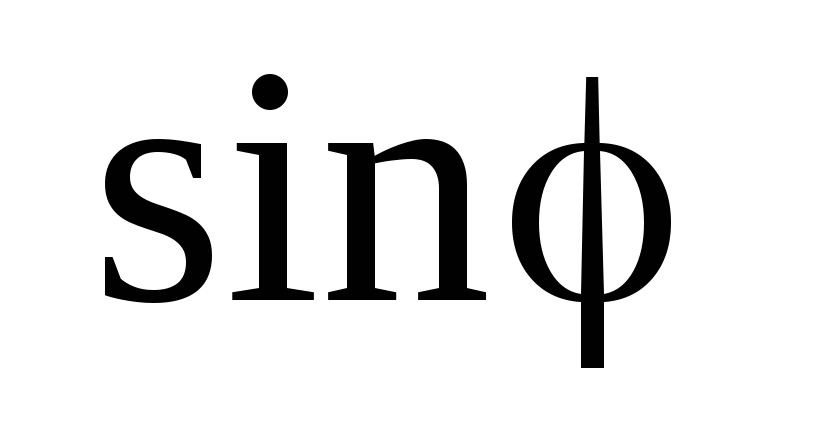~ φ, тогда

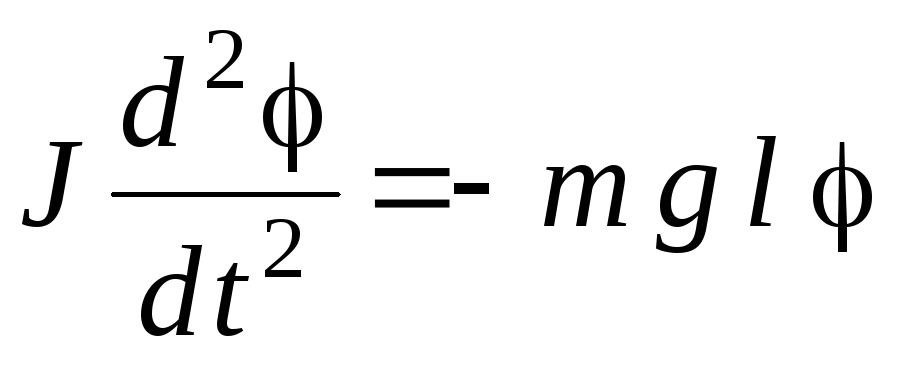. (7)

Уравнение (7) можно переписать в виде

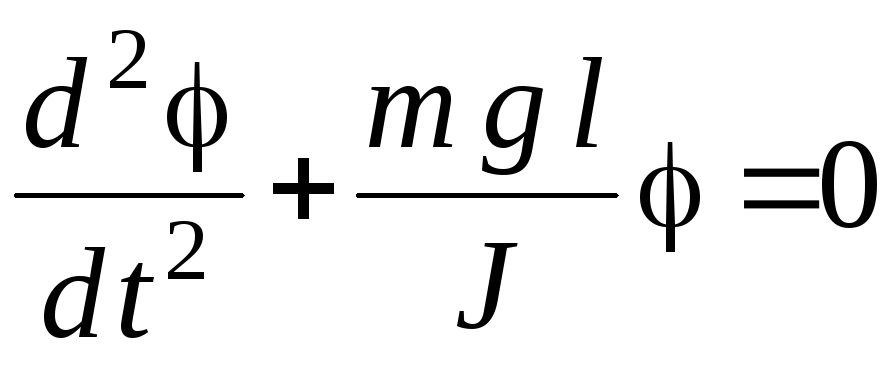(8)

или

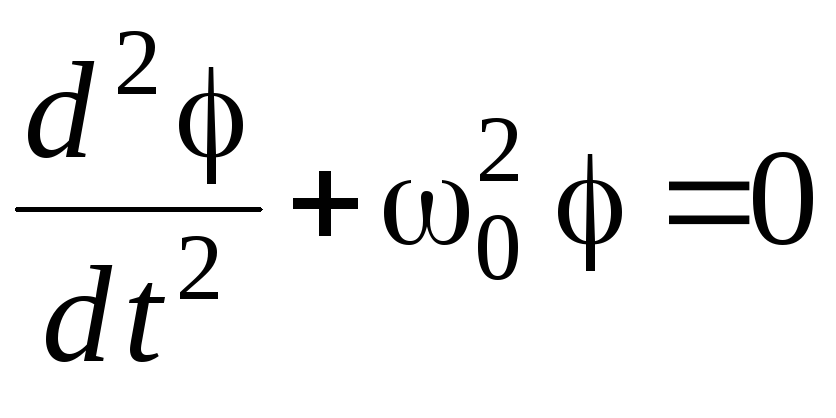. (9)

Решение этого уравнения имеет вид

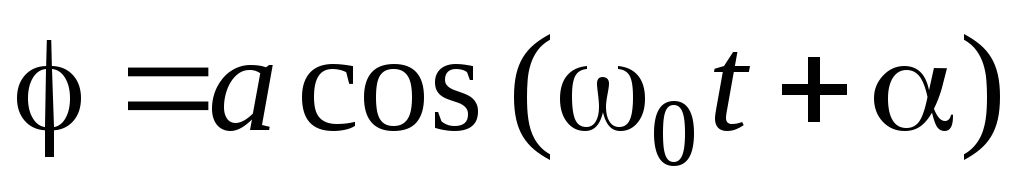, (10)

где а и α – произвольные постоянные. Через ω₀² обозначена величина

ω₀²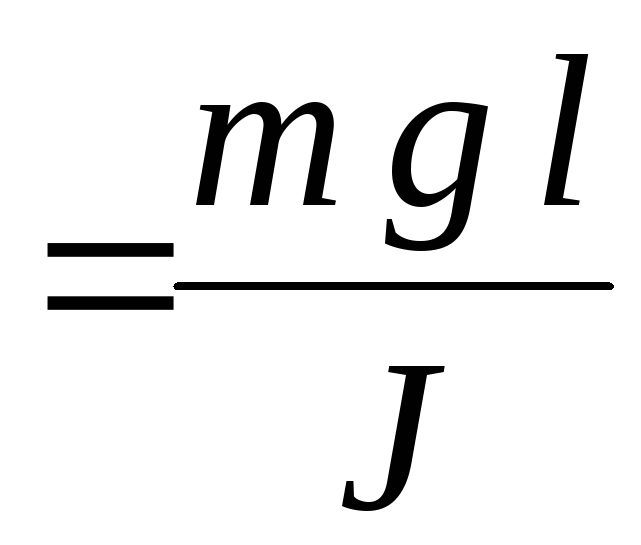. (11)

Из уравнений (9) и (10) следует, что при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания, частота которых зависит от массы маятника, момента инерции маятника относительно оси вращения и расстояния между осью вращения и центром инерции маятника. Зная ω₀, можно рассчитать период колебания Т физического маятника:

ω₀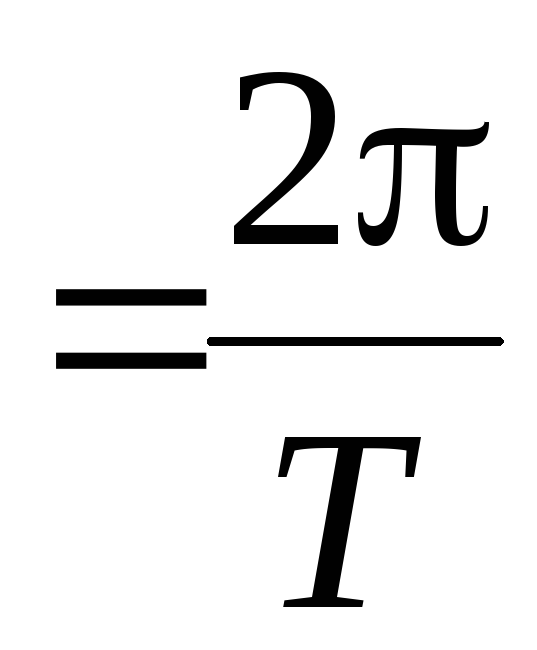, 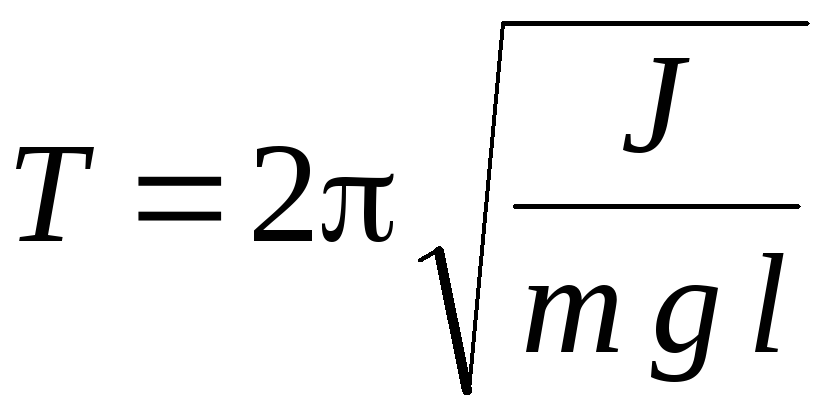. (12)

Из сопоставления формул (5) и (12) следует, что математический маятник длиной

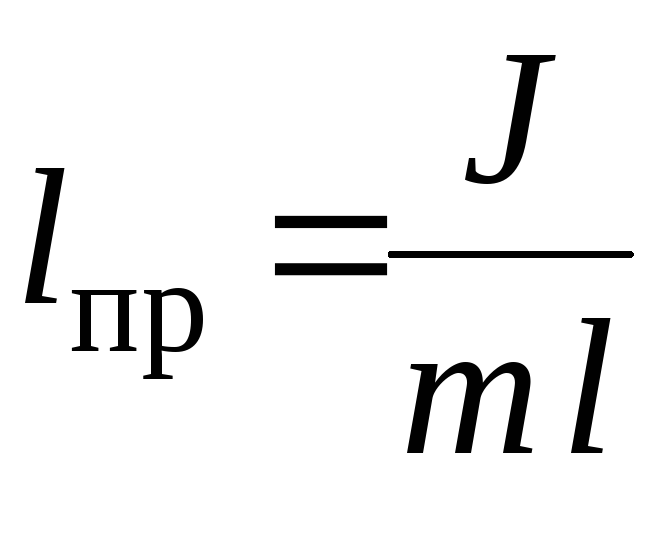(13)

будет иметь такой же период колебаний, что и данный физический маятник. Величину 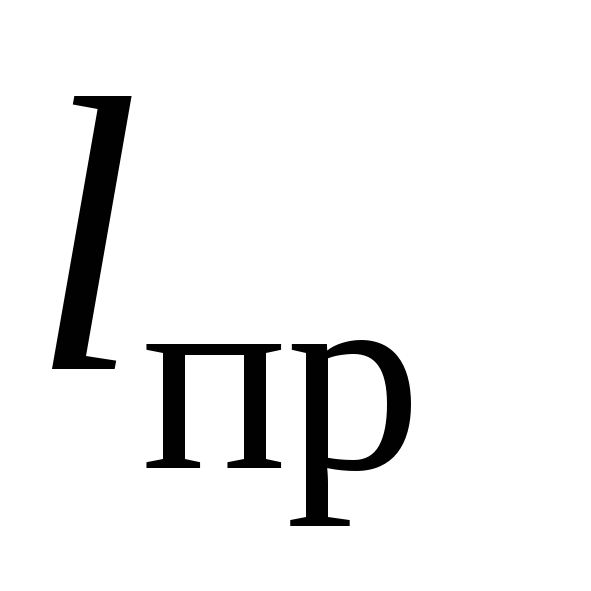называют приведенной длиной физического маятника.

Точка на прямой, соединяющей точку подвеса с центром инерции, лежащая на расстоянии приведенной длины от оси вращения О, называется центром качания физического маятника О^/.

По теореме Штейнера момент инерции тела относительно любой оси

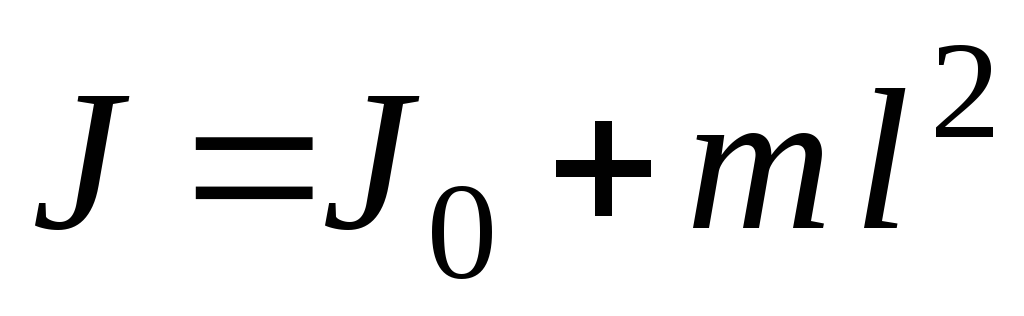, (14)

где 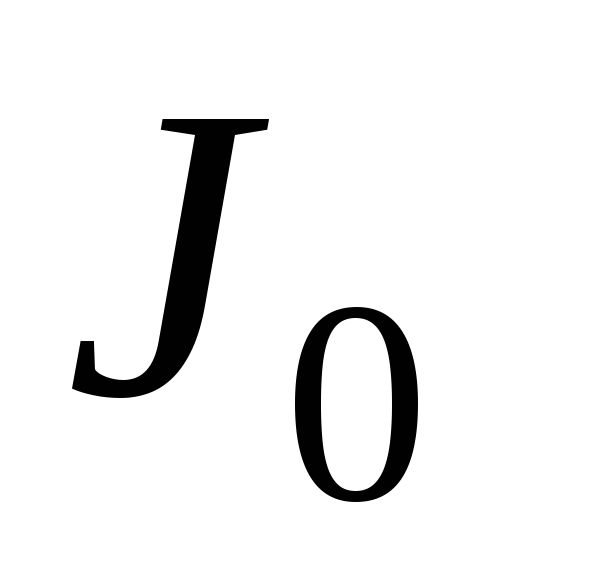– момент инерции тела относительно оси, проходящей через центр тяжести, l – расстояние между осями.

Подставим в уравнение (13) момент инерции, определяемый выражением (14):

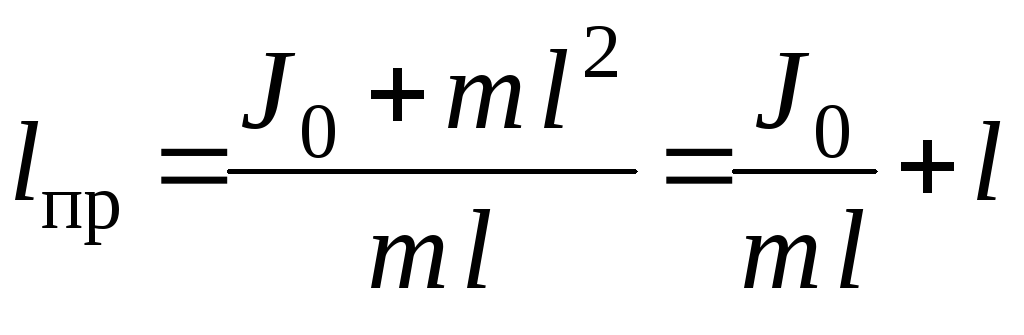. (15)

Из уравнения (15) видно, что приведенная длина всегда больше l, так что точка подвеса О и центр качания О^/ лежат по разные стороны от центра инерции С. Зная период колебания Т, массу маятника m и приведенную длину, можно рассчитать момент инерции J физического маятника:

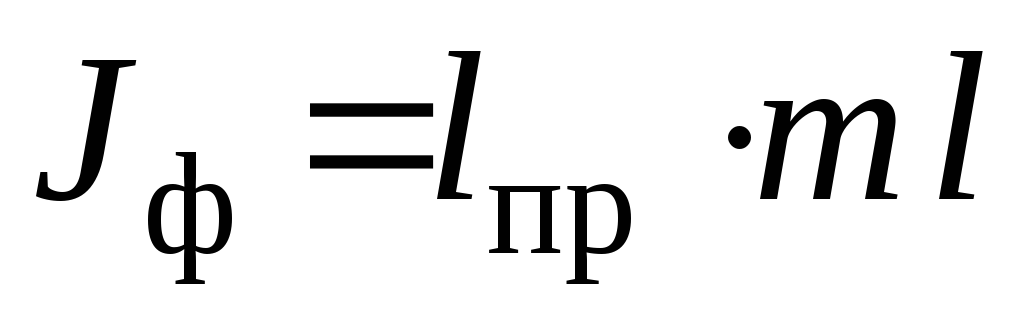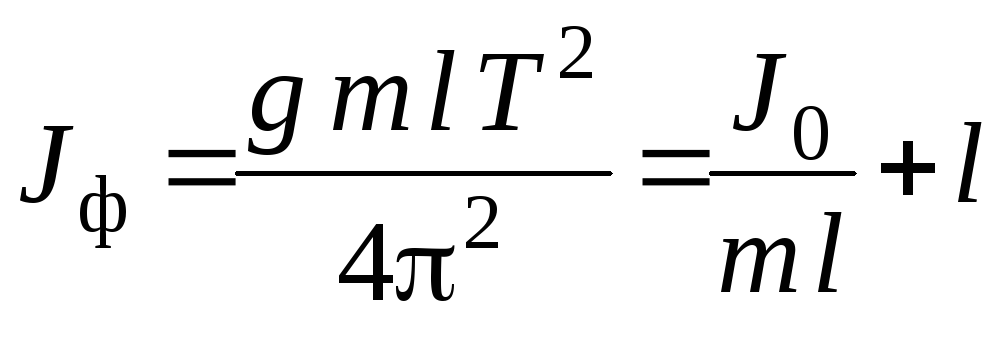или . (16)

№03определение момента инерции тел

Лабораторная работа № 3

определение момента инерции тел и

проверка основного зАкона динамики

вращательного движения

Цель работы: определить момент инерции маятника Обербека, изучить зависимости углового ускорения от момента инерции при неизменном моменте силы.

Приборы и принадлежности: маятник Обербека, двухметровая линейка, секундомер, штангенциркуль, шнур длиной 2,5 м, грузы массой 100 г и 200 г.

Теория работы

Момент инерции I_i материальной точки с массой Δm_i , находящейся на расстоянии r_i от оси вращения, численно равен произведению массы математической точки на квадрат расстояния её от оси, т.е. I_i = Δm_ir_i² (рис.1).

Тело можно представить состоящим из n таких элементарных масс. Тогда момент инерции тела:

I = .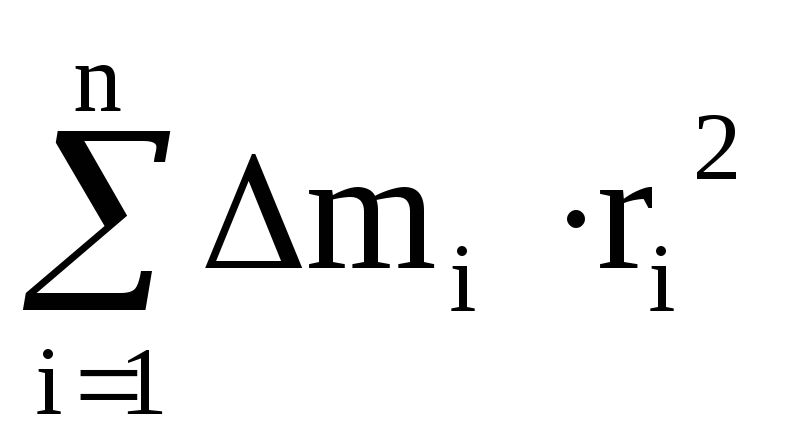

Единица измерения момента инерции в СИ: [I] = кг·м². Вращение тела вокруг оси вызывается вращающим моментом или просто моментом силы. Моментом М силы относительно оси вращения называют векторную величину, численно равную произведению силы F на длину d перпендикуляра, опущенного из центра вращения на направление действия силы, называемого плечом силы:

М = F·d.

Под действием момента силы закрепленное на оси твердое тело приобретает угловое ускорение β:

β = ,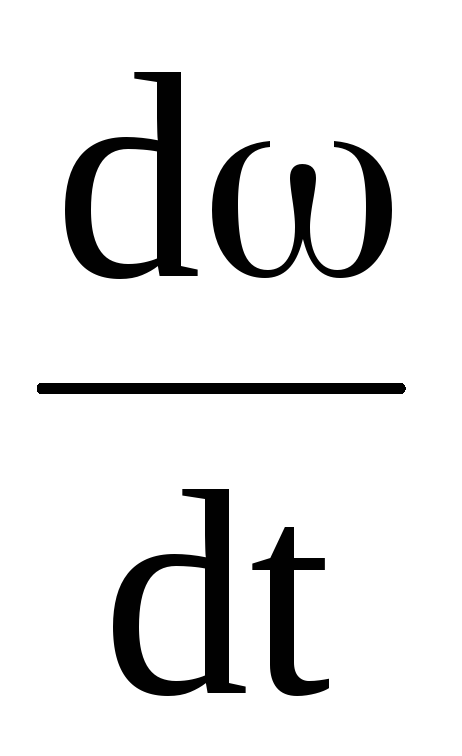

где ω – угловая скорость.

Зависимость углового ускорения β вращающегося тела от момента М действующей на тело силы и момента инерции I тела относительно оси, вокруг которой происходит вращение, определяется основным уравнением (законом) динамики вращательного движения:

М = I β = I.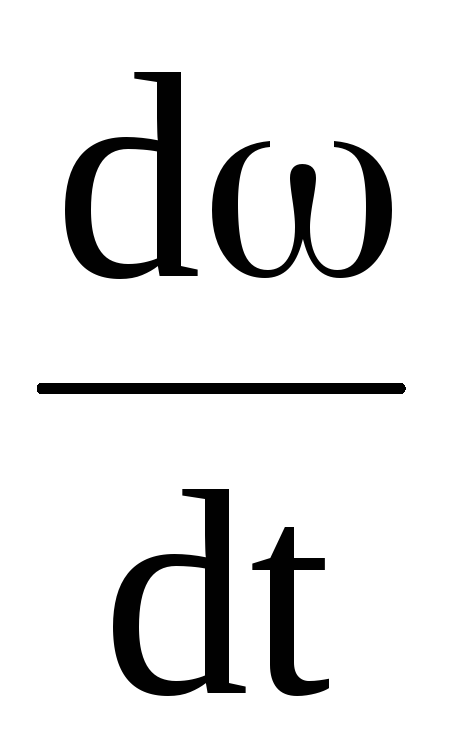

Формула закона для вращательного движения аналогична формуле закона Ньютона для поступательного движения:

F = ma.

Силе F соответствует момент силы М; ускорению а – угловое ускорение β; массе m – момент инерции I. Подобно тому, как масса m характеризует инерционные свойства тела при поступательном движении, момент инерции I характеризует инерционные свойства тел при вращательном движении.

Знание момента инерции тел, а также основного закона динамики вращательного движения необходимо во многих областях науки и технике. В некоторых разделах космической и спортивной медицины, ортопедии, бионики возникает необходимость измерения момента инерции тела человека и отдельных его частей. Момент инерции при вращательном движении туловища человека или его конечностей вычисляют приблизительно по формулам момента инерции цилиндра и круглого стержня или определяют из опыта. В молекулярной биологии определяют моменты инерции сложных молекул. По их значениям классифицируют молекулы многих исследуемых веществ. Знание моментов инерции молекул необходимо также при определении вращательной энергии молекул в квантовой механике.

Описание установки

Момент инерции тела может быть определен из закона динамики вращательного движения: I = 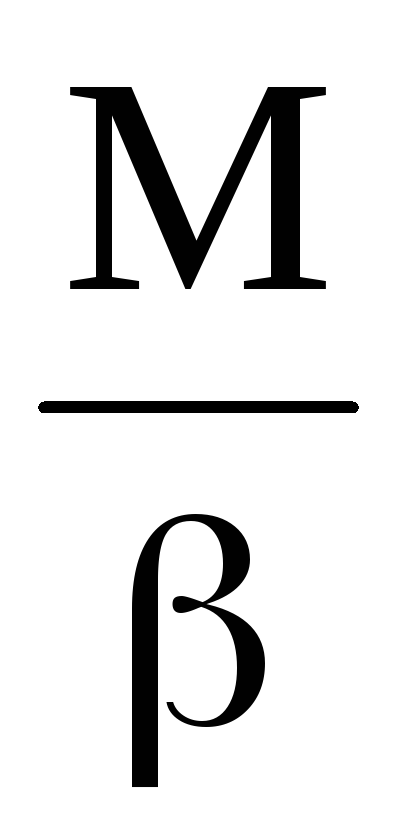. (1)

Для измерения действующего на тело момента силы и сообщенного этому телу углового ускорения применяют крестообразный маятник Обербека (рис.2).

Прибор состоит из шкива L радиусом r, закреплённого на оси O; четырёх стержней, расположенных под углом 90º друг к другу и четырёх одинаковых цилиндрических грузов m₀, которые можно перемещать вдоль стержней и закреплять на определённых расстояниях.

Грузы закрепляются симметрично, т.е. так, чтобы центр тяжести маятника находился на оси вращения.

Прибор приводится во вращательное движение грузом, масса которого m. Груз прикрепляется к концу шнура, намотанного на шкив.

Если груз, подвешенный на нити, падает с высоты h за время t, то h = 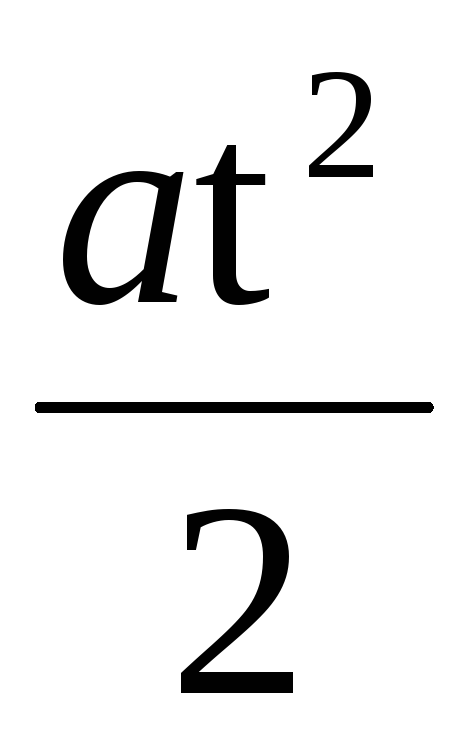, где а – линейное ускорение на ободе шкива. Тогда:

а = 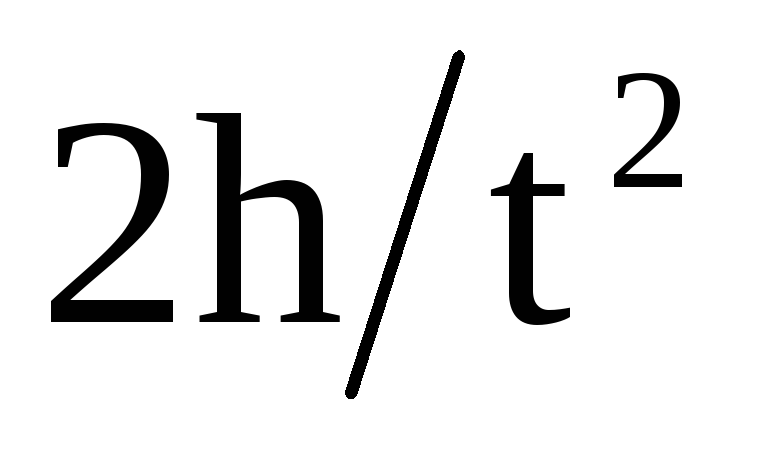. (2)

При этом шкив со стержнями и расположенными на нём грузами будет вращаться с угловым ускорением β:

β = 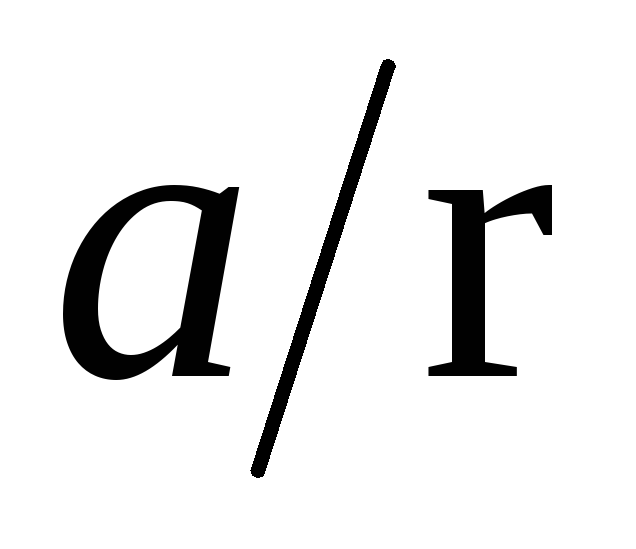. (3)

Из (2) и (3) следует, что:

β = 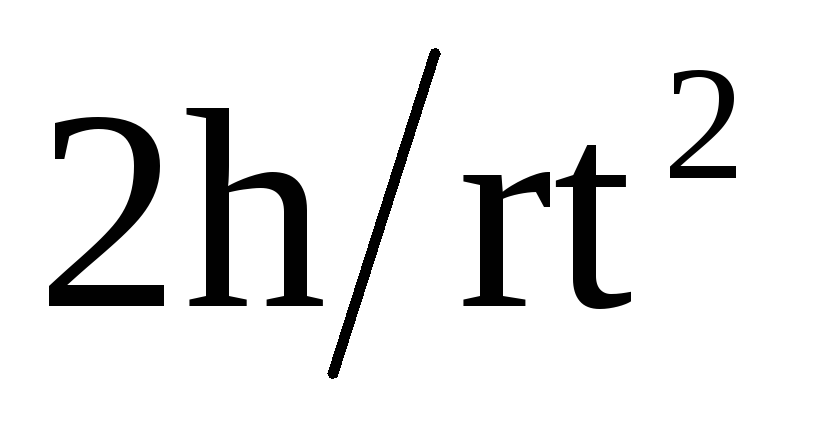. (4)

Вращающий момент найдем по формуле: М = Т·r, где Т – сила натяжения нити, r – плечо этой силы.

Силу натяжения нити найдем из II закона Ньютона для груза массой m:

ma = 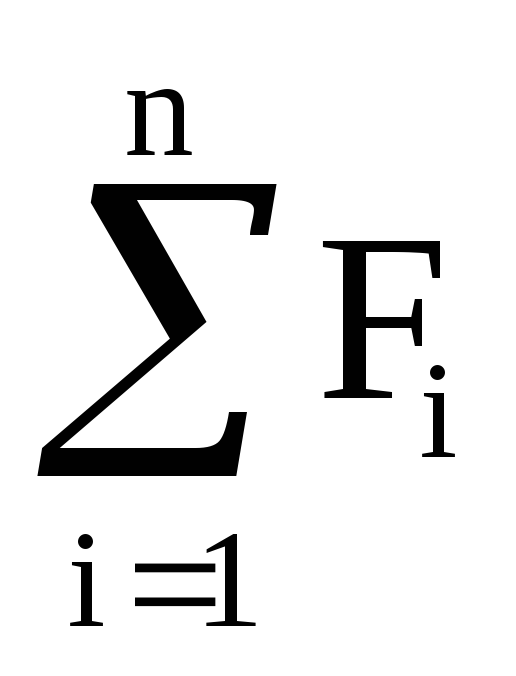, но ma = mg – T, откуда Т = mg – ma.

Тогда: М = (mg – ma) · r = m (g — 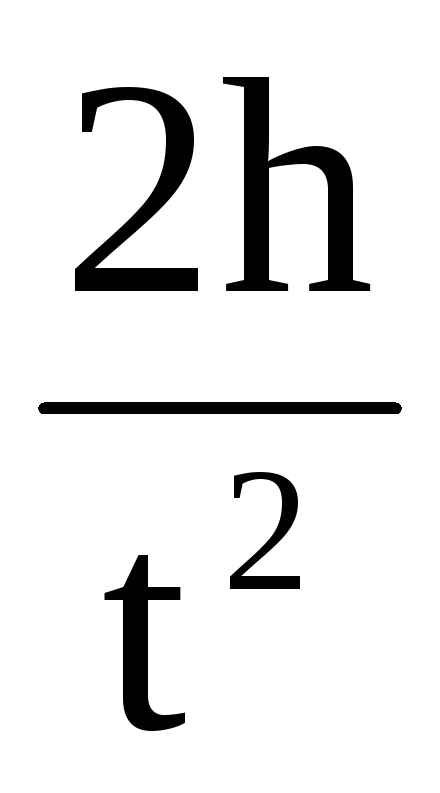) · r. (5)

Подставив в формулу (1), формулы (4) и (5) получим:

I = 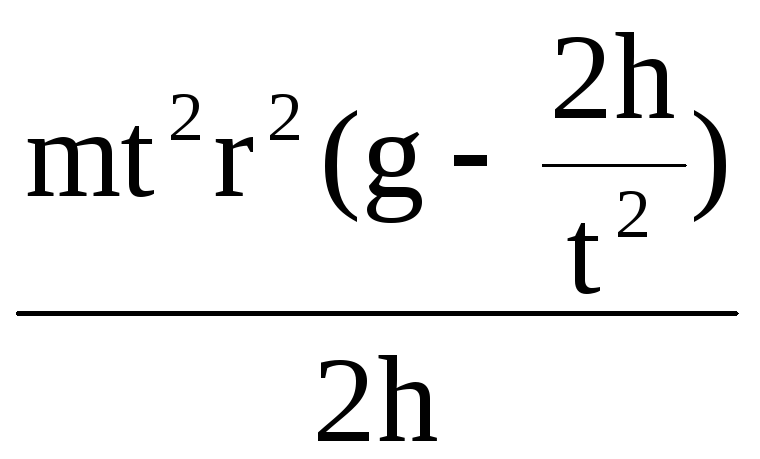. (6)

Для определения момента инерции I необходимо определить опытным путём все величины, стоящие в правой части формулы (6).

Порядок выполнения работы

1. Определение момента инерции маятника.

Переместить грузы к концам стержней и закрепить их винтами на последних делениях, нанесенных на стержнях. При этом маятник не должен поворачиваться, если систем правильно сбалансирована.
К концу нити прикрепить груз. Намотать равномерно нить на шкив.
На линейке нанести две метки на расстоянии, соответствующем высоте падения h.
С помощью штангенциркуля определить радиус шкива.
Предоставив возможность грузу m падать, по секундомеру определить время падения. Секундомер включить в момент начала падения груза от верхней метки на линейке и остановить в момент прохождения нижней метки.
Опыт повторить для двух разных грузов (например, 100 и 200 г). Данные опытов занести в таблицу 1.

Таблица 1

№ п/п

кг

t_,

кг·м²

<I>,

кг·м²

Определить дважды моменты инерции маятника по формуле (6) и найти его среднее значение.

2. Исследование законов вращательного движения.

Последовательно закрепить грузы симметрично на размеченных на стержнях делениях и описанным в первом опыте способом найти время t для различных положений грузов.
Маятник приводить в движение с помощью одного и того же груза, т.е. m = const.
Полученные данные занести в таблицу 2.

Таблица 2

№ п/п

h, м

t, c

M, Н·м

β , c^-2

I, кг·м²

Приложение

m =

r =

3. По формулам (5), (4) и (1) определить: момент силы, угловое ускорение и момент инерции маятника для каждого случая.

Контрольные вопросы

Что называется моментом инерции материальной точки тела? Какие свойства тел он характеризует?
В каких единицах в системе СИ изменяется момент инерции?
Что называется моментом силы? В каких единицах он измеряется?
В каких областях медицины необходимо знание моментов инерции тел?
Сформулировать и записать уравнение динамики вращательного движения. Сравнить его со II законом Ньютона для поступательного движения.
Вывести расчетную формулу для определения момента инерции маятника Обербека.
Какая зависимость между угловым ускорением и моментом инерции маятника при постоянном значении момента силы?

момент инерции — с русского на английский

Момент инерции — Размерность L2M Единицы измерения СИ кг·м² СГС … Википедия

момент инерции — величина, характеризующая распределение масс в теле и являющаяся наряду с массой мерой инертности тела при непоступательном движении. Различают осевые и центробежные моменты инерции. Осевой момент инерции равен сумме произведений масс mi всех… … Энциклопедический словарь

Определение момента инерции тела и положения центра масс

Момент инерции — с русского на все языки

момент инерции — с английского на русский

См. также в других словарях:

Книги

Определение момента инерции тел

Теоретическое введение

Содержание

Список литературы………………………………………………….11 Лабораторная работа № 5 Определение моментов инерции тел произвольной формы

1. Цель работы

2. Теоретическая часть

Если отклонить маятник от положения равновесия на угол φ (рис. 1), то момент силы, стремящийся вернуть маятник в положение равновесия равен

№03определение момента инерции тел

Теория работы

момент инерции — с русского на английский

alexxlab

Добавить комментарий Отменить ответ

Рубрики