Физические основы механики
1Сформулируйте теорему Штейнера.
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния от центра инерции тела до выбранной оси.
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно параллельной оси, проходящей через центр тела, и произведения массы тела на квадрат расстояния от центра тела до выбранной оси.
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно параллельной оси, проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния от центра инерции тела до выбранной оси.
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно параллельной оси, проходящей через центр инерции тела, и произведения массы тела на расстояние от центра инерции тела до выбранной оси.
Момент инерции тела относительно произвольной оси равен сумме момента инерции относительно оси, проходящей через центр тела, и произведения массы тела на расстояние от центра тела до выбранной оси.
1Сформулируйте теорему о моментах инерции плоских фигур.
Если через произвольную точку плоской фигуры приведена некоторая ось, то момент инерции относительно этой оси равен сумме моментов инерции относительно двух взаимно перпендикулярных осей, проходящих через эту же точку.
Если через произвольную точку плоской фигуры приведена ортогональная к фигуре ось, то момент инерции относительно этой оси равен сумме моментов инерции относительно двух осей, лежащих в плоскости фигуры и проходящих через эту же точку.
Если через произвольную точку тела приведена некоторая ось, то момент инерции относительно этой оси равен сумме моментов инерции относительно двух взаимно перпендикулярных осей, проходящих через эту же точку.
Если через произвольную точку плоской фигуры приведена ортогональная к фигуре ось, то момент инерции относительно этой оси равен сумме моментов инерции относительно двух взаимно перпендикулярных осей, лежащих в плоскости фигуры и проходящих через эту же точку.
Если через произвольную точку плоской фигуры приведена ортогональная к фигуре ось, то момент инерции относительно этой оси равен сумме моментов инерции относительно двух взаимно перпендикулярных осей, лежащих в плоскости фигуры.
Ответ неверный!
16. Момент инерции. Вычисление моментов инерции ноторых тел относительно оси симметрии (тонкий стержень, обруч, диск). Теорема Штейнера.
Момент инерции — скалярная физическая величина, характеризующая распределение масс в теле, равная сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).
Единица измерения СИ: кг·м².
Обозначение: I или J.
 Для
расчета моментов
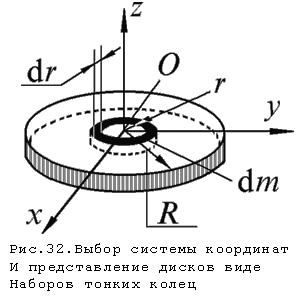
инерции тонкого диска массы m и радиуса R выберем систему координат так, чтобы
ее оси совпадали с главными центральными
осями (рис.32). Определим момент инерции
тонкого однородного диска относительно
оси
Для
расчета моментов
инерции тонкого диска массы m и радиуса R выберем систему координат так, чтобы
ее оси совпадали с главными центральными
осями (рис.32). Определим момент инерции
тонкого однородного диска относительно
оси
радиусом r и наружным r+dr.
Площадь такого кольца ds=2r
$\pi$ dr, а его
масса 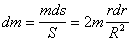 ,
гдеS= $\pi$ R2 — площадь всего диска. Момент инерции
тонкого кольца найдется по формуле dJ=dmr2.
Момент инерции всего диска определяется
интегралом
,
гдеS= $\pi$ R2 — площадь всего диска. Момент инерции
тонкого кольца найдется по формуле dJ=dmr2.
Момент инерции всего диска определяется
интегралом
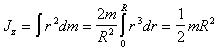
Вычисление
Пусть
тонкий стержень имеет длину l и массу m.
Разделим его на малые элементы длины dx (рис.27), масса которых 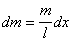 .
Если выбранный элемент находится на
расстоянии x от оси, то его момент инерции
.
Если выбранный элемент находится на
расстоянии x от оси, то его момент инерции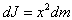 ,
т.е.
,
т.е.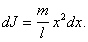 Интегрируя
последнее соотношение в пределах от 0 до l/2 и удваивая полученное выражение (для
учета левой половины стержня), получим
Интегрируя
последнее соотношение в пределах от 0 до l/2 и удваивая полученное выражение (для
учета левой половины стержня), получим 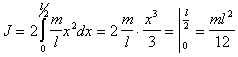
Момент
инеpции обручаотносительно оси,
пpоходящей чеpез центp кольца пеpпендикуляpно
к его плоскости. В этом случае все
элементаpные массы обруча удалены от
оси на одинаковое pасстояние, поэтому
в сумме (3.18) r2 можно вынести за знак
суммы, т. е.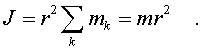
Теорема Штейнера:
В общем случае вращения тела произвольной формы вокруг произвольной оси, вычисление момента инерции может быть произведено с помощью теоремы Штейнера: момент инерции относительно произвольной оси равен сумме момента инерции J0 относительно оси, параллельной данной и проходящей через центр инерции тела, и произведения массы тела на квадрат расстояния между осями: J=J0+ma^2.
Например,
момент инерции диска относительно оси
О’ в соответствии с теоремой Штейнера: 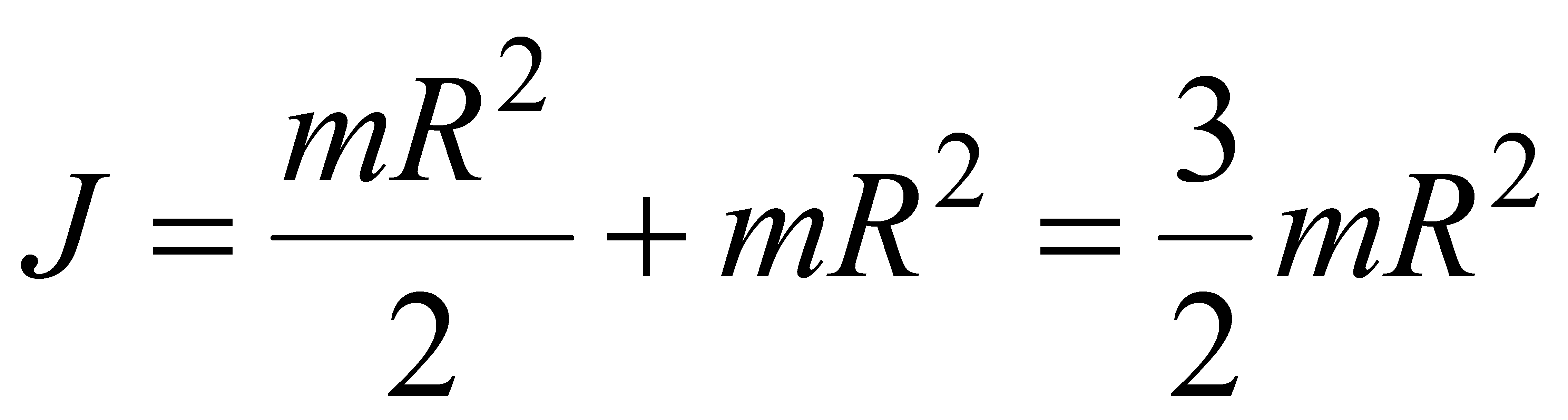
17. Момент инерции однородного тела вращения. Моменты инерции конуса, шара.
Линия 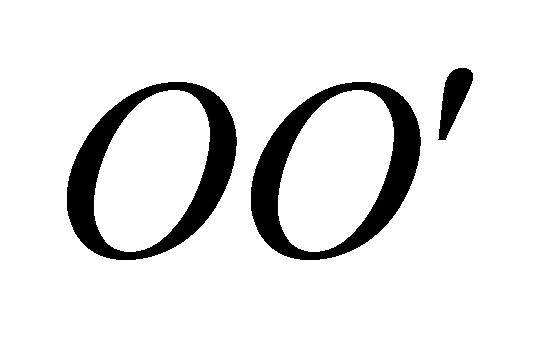 — ось вращения.
— ось вращения.
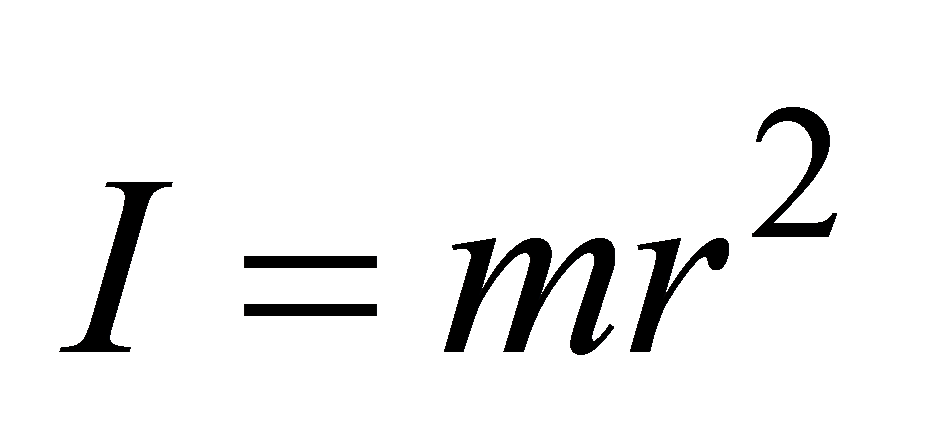 — масса на квадрат радиуса окружности,
по которой движется материальная точка.
— масса на квадрат радиуса окружности,
по которой движется материальная точка.
Все
тело мысленно разбиваем на маленькие
объемы. Масса этого кусочка 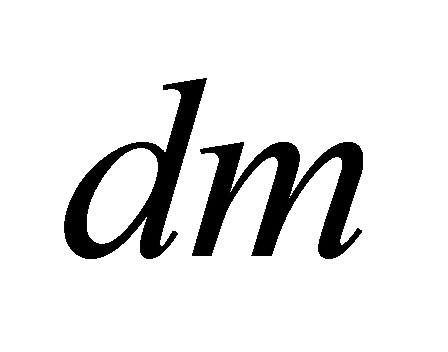 .
.
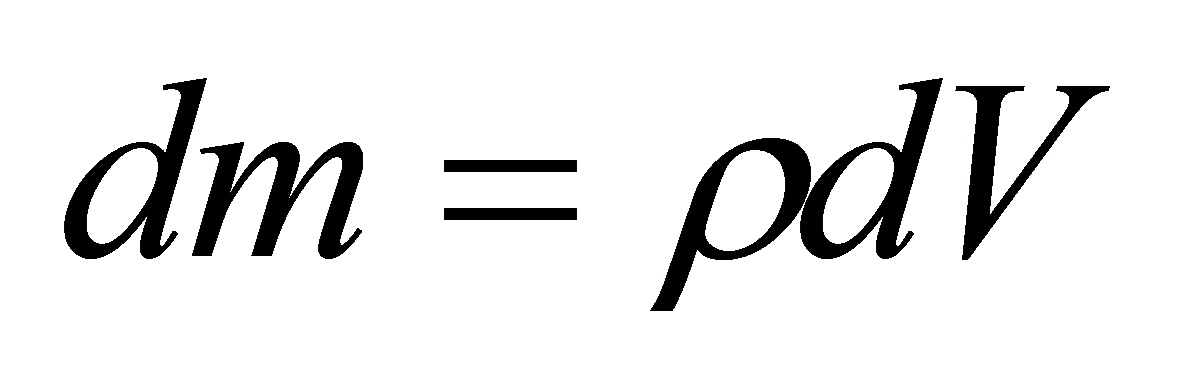
Твердое тело представляется как совокупность системы точечных масс.
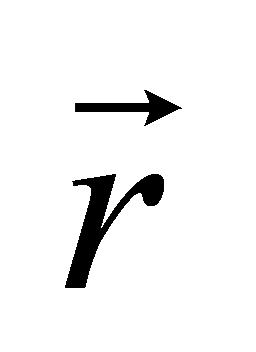 — расстояние, на котором находится точка
от оси вращения.
— расстояние, на котором находится точка
от оси вращения.
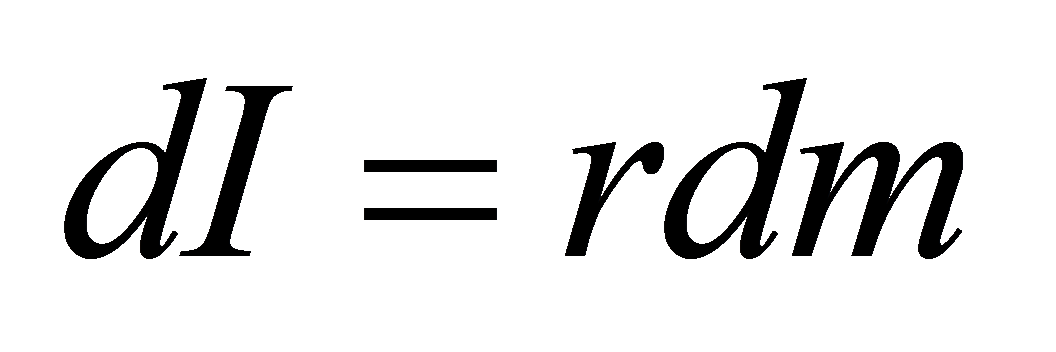
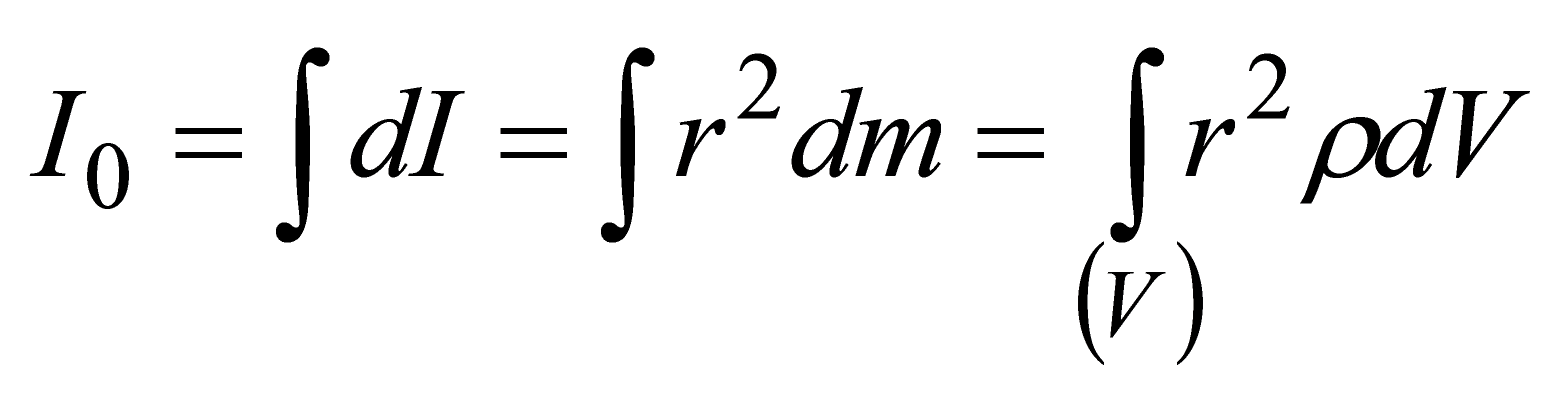 — общий алгоритм определения собственного
момента инерции твердого тела, относительно
оси проходящей через центр инерции
данного тела.
— общий алгоритм определения собственного
момента инерции твердого тела, относительно
оси проходящей через центр инерции
данного тела.
Момент инерции шара.
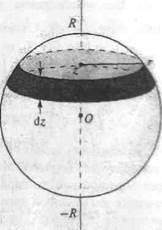
Сплошной шар массы m и радиуса R можно рассматривать как совокупность бесконечно тонких сферических слоев с массами dm , радиусом r, толщиной dr (рис.35).

Рассмотрим
малый элемент сферического слоя $\delta$
m с координатами x, y, z.
Его моменты инерции относительно осей
проходящих через центр слоя — $\delta$
Jx, $\delta$ Jy, $\delta$ Jz,
равны Т.
е. можно записать 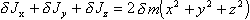 (п.26)
(п.26)
Так как для
элементов сферического слоя x2+y2+z2=r2 то 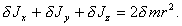 После
интегрирования по всему объему слоя
получим
После
интегрирования по всему объему слоя
получим 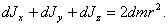 (п.27)
(п.27)
Так как, в силу
симметрии для сферического слоя dJx=dJy=dJz=dJ , а 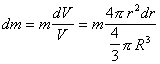 ,
то
,
то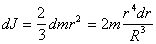 Интегрируя по всему объему шара,
получаем
Интегрируя по всему объему шара,
получаем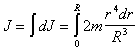 Окончательно
(после интегрирования) получим, что
момент инерции шара относительно оси,
проходящей через его центр равен
Окончательно
(после интегрирования) получим, что
момент инерции шара относительно оси,
проходящей через его центр равен 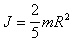
Разобьём КОНУС на цилиндрические слои ось толщиной dr. Масса такого слоя dm = r2dr,
где ρ – плотность материала, из которого изготовлен конус. Момент инерции этого слоя dI = dm.r2.
Момент инерции всего конуса складывается из моментов инерции всех слоёв:
I = 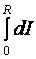 =
= 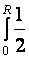 ρπ r 4dr =
ρπ r 4dr = 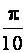 ρR5.
ρR5.
Остаётся выразить
его через массу всего цилиндра: m = 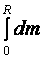 =
=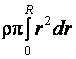 =
= 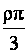 R3,
R3,
отсюда ρ
= 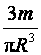 , I =
, I = 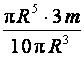 =
= 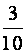 mR2.
mR2.
Физические основы механики
Движение материальной точки характеризуется перемещением, скоростью, ускорением. Но при вращении твердого тела все его элементы имеют разные перемещения, различные скорости. Удобно найти переменные, одинаковые для всех элементов твердого тела. Мы их, собственно, уже знаем — угол поворота, угловая скорость, угловое ускорение. Соответственно, изучая динамику вращения, вместо импульса и силы мы будем оперировать их угловыми аналогами — моментом импульса и моментом силы.
Уравнение движения. В теме 4.8 было выведено уравнение движения системы материальных точек в виде
где моменты импульса и силы определялись как
Внутренние силы между телами системы, напомним, выпали из уравнений движения. Абсолютно твердое тело можно рассматривать как систему частиц (материальных точек) с неизменными расстояниями между ними. Поэтому выписанные уравнения применимы для твердого тела, а неизменность расстояний между его точками позволяет характеризовать вращение тела вокруг неподвижной оси единственной координатой — углом поворота. Поэтому мы можем упростить приведенное выше уравнение движения. Прежде всего, нас не интересуют в данный момент напряжения, возникающие в оси. Кроме того, для описания вращения достаточно рассмотреть проекции векторов моментов импульса и силы на ось вращения.
Рис. 7.1. Момент импульса L двух шаров массы m, соединенных стержнем. Вся система вращается вокруг оси z c угловой скоростью ω
Направим ось z вдоль оси вращения и выделим в твердом теле элемент массой , положение которого характеризуется радиус-вектором (рис. 7.2).
Рис. 7.2 Вращение твердого тела вокруг неподвижной оси 0z
Момент импульса этого элемента есть
Рис. 7.3. Момент импульса системы направлен вдоль оси вращения.
Радиус-вектор можно представить как сумму его проекций на ось z и плоскость ху :
где вектор лежит в плоскости вращения и направлен от оси к выделенному элементу (см. рис. 7.1). Имеем:
Первое слагаемое — вектор, направленный противоположно Поэтому оно не дает вклада в z-компоненту момента импульса. Второе слагаемое — вектор, направленный вдоль оси z. Так как
и
можем написать:
Суммируя по всем элементам тела, получаем
где
Величина называется моментом инерции тела.
Говоря о моменте инерции, всегда указывают, относительно какой именно оси вращения он определен (в данном случае — это ось z). Момент инерции того же тела относительно какой-то другой оси примет иное значение. Сохраняется только общее правило его вычисления: берется сумма по элементам массы, составляющим тело, умноженным на квадраты расстояний этих элементов массы до оси вращения.
В случае непрерывного распределения масс с плотностью сумма заменится на интеграл по всему объему тела:
Если тело однородно, то его плотность во всех точках постоянна и можно вынести из-под знака интеграла.
Записываем теперь уравнение движения в проекции на ось z :
Если момент инерции не зависит от времени, то дифференцировать нужно только угловую скорость, в результате получаем основное уравнение динамики вращательного движения твердого тела в виде
Производная угловой скорости по времени — это угловое ускорение
Видео 7.1. Основное уравнение динамики вращательного движения. Демонстрация, вытекающей из него связи между угловым ускорением, моментом силы и моментом инерции
Рассмотрим теперь момент внешних сил. Разложим силу на вектор в направлении оси
Используя снова аналогичное разложение радиус-вектора
получаем для момента внешних сил :
Первое слагаемое равно нулю. Два следующих содержат единичный орт — вектор k, направленный вдоль оси 0z и, следовательно, не дают вклада в проекцию . Оба вектора
лежат в плоскости xy и, следовательно, последнее слагаемое направлено параллельно оси 0z. Если — угол между этими векторами, то
где — плечо силы (см. тему. 4.8). Силу
надо здесь понимать в алгебраическом смысле: она входит со знаком минус, если сила тормозит вращение.
Момент инерции. Найдем моменты инерции для простейших (геометрически правильных) форм твердого тела, масса которого равномерно распределена по объему.
Рис. 7.4. Моменты инерции различных тел
1. Момент инерции обруча относительно оси, перпендикулярной к его плоскости и проходящей через его центр.
Обруч считается бесконечно тонким, то есть толщиной обода можно пренебречь по сравнению с радиусом . Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, можно вынести из-под знака интеграла:
где — полная масса обруча.
2. Момент инерции диска
Диск считается бесконечно тонким, если его толщина много меньше радиуса . Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие обручи радиусом и шириной (рис. 7.5).
Рис. 7.5 Вычисление момента инерции диска относительно оси z, перпендикулярной его плоскости и проходящей через центр
Площадь поверхности обруча равна произведению его длины окружности на ширину: . Поскольку масса m диска распределена равномерно, масса единицы площади равна , так что масса обруча равна
Момент инерции обруча мы уже знаем:
Осталось просуммировать моменты инерции всех таких обручей:
Такой же результат получится и для момента инерции цилиндра конечной длины относительно его продольной оси.
3. Момент инерции шара относительно его диаметра.
Поступим аналогичным образом: «нарежем» шар на бесконечно тонкие диски толщиной , находящиеся на расстоянии z от центра (рис. 7.6).
Рис. 7.6. Момент инерции шара относительно его диаметра
Радиус такого диска
Объем диска равен его площади, умноженной на толщину:
Массу диска находим, разделив массу шара на его объем и умножив на объем диска:
Момент инерции диска был найден выше. В применении к данному случаю он равен
Момент инерции шара находится интегрированием по всем таким дискам:
4. Момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню.
Пусть стержень имеет длину . Направим ось x вдоль стержня. Начало координат по условию находится в центре стержня (рис. 7.7).
Рис. 7.7. Момент инерции тонкого стержня относительно оси, проходящей через его середину перпендикулярно стержню
Возьмем элемент стержня длиной , находящийся на расстоянии x от оси вращения. Его масса равна
а момент инерции
Отсюда находим момент инерции стержня:
Теорема Штейнера. В приведенных примерах оси проходят через центр масс (центр инерции) тела. Момент инерции относительно других осей вращения определяется в соответствии с теоремой Штейнера:
Рис. 7.8. К выводу теоремы Штейнера
Момент инерции тела относительно произвольной оси равен сумме момента инерции JC относительно параллельной оси, проходящей через центр инерции тела, и величины ma2 — произведения массы тела на квадрат расстояния от центра инерции тела до выбранной оси, то есть
Продемонстрируем сначала применение теоремы Штейнера. Вычислим момент инерции тонкого стержня относительно оси, проходящей через его край перпендикулярно стержню. Прямое вычисление сводится к тому же интегралу, возникшему при вычислении момента инерции стержня относительно оси, проходящей через его середину, но взятому в других пределах:
Расстояние до оси, проходящей через центр масс, равно a = l/2. По теореме Штейнера получаем тот же результат:
Вывод теоремы Штейнера иллюстрируется рис. 7.8, 7.9
Рис. 7.9. К выводу теоремы Штейнера
Пусть одна ось проходит в направлении единичного вектора n через центр масс С твердого тела (системы тел), а другая — параллельно ей через некоторую точку 0. Из центра масс в направлении второй оси проводим ортогональный осям вектор a, который определяет положение точки 0. Радиус-векторы некоторого элемента системы массой относительно точек С и 0 обозначаем и , соответственно. Момент инерции этого элемента относительно оси С есть
где — расстояние элемента от оси. По теореме Пифагора (см. рис. 7.9).
Катет равен проекции векторов и на ось вращения, то есть
Используя эти выражения и суммируя по всем элементам системы, находим момент инерции относительно оси, проходящей через точку С, и, аналогичным образом, момент инерции относительно параллельной оси, проходящей через точку 0 :
Здесь выражение для получено из простой заменой на .
Как видно из рис. 7.9, векторы и связаны между собой:
причем
так как векторы n и а ортогональны и их скалярное произведение
Тогда мы можем преобразовать выражение для :
Первое слагаемое в правой части — момент инерции относительно оси, проходящей через точку C. Третье слагаемое равно , где
— полная масса системы.
Второе слагаемое равно нулю, так как оно пропорционально радиус-вектору центра инерции относительно самого центра инерции. Окончательно:
что и требовалось доказать.
Теорема Штейнера связывает моменты инерции относительно параллельных осей. Иногда оказывается полезной другая теорема, связывающая моменты инерции относительно трех взаимно перпендикулярных осей. Однако эта теорема относится только к плоским фигурам, толщиной которых можно пренебречь по сравнению с размерами в двух других направлениях. Итак, теорема о моментах инерции плоских фигур:
Если через произвольную точку 0 плоской фигуры приведена ортогональная к фигуре ось, то момент инерции относительно этой оси равен сумме моментов инерции относительно двух взаимно перпендикулярных осей, лежащих в плоскости фигуры и проходящих через эту же точку 0.
Иными словами, берем на фигуре произвольную точку 0 и проводим координатные оси так, чтобы 0x и 0y лежали в плоскости фигуры. Тогда, согласно теореме, момент инерции относительно оси 0z равен сумме моментов инерции относительно осей 0x и 0y:
При этом расположение осей 0x, 0y может быть произвольным; главное, чтобы они лежали в плоскости фигуры (рис. 7.10).
Рис. 7.10. Моменты инерции плоской фигуры относительно взаимно перпендикулярных осей
Из рисунка видно, что
что и требовалось доказать.
Найдем, например, момент инерции диска относительно его диаметра. Два ортогональных диаметра диска равноправны, поэтому
Согласно теореме о плоской фигуре
откуда
Теперь можно применить теорему Штейнера, чтобы найти, например, момент инерции относительно оси , параллельной диаметру и проходящей через край диска (см. рис. 7.10):
| Обратная связь | Нахождение момента инерции – вычислительная задача. Найдем моменты инерции для простейших геометрически правильных форм твердого тела, масса которого равномерно распределена по объему. Момент инерции обруча относительно оси перпендикулярно его плоскости и проходящей через его центр. Обруч будем считать бесконечно тонким, т. е. толщиной обода можно пренебречь по сравнению с радиусом R. Поскольку в этой системе все массы находятся на одинаковом расстоянии от оси вращения, R2 можно вынести из-под знака интеграла:
где
Момент инерции диска относительно оси, перпендикулярной его плоскости и проходящей через центр. Диск будем считать бесконечно тонким, т. е. его толщина много меньше радиуса R. Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие кольца радиусом г и шириной dr.
Площадь выделенного кольца равна произведению его длины окружности на ширину кольца: 2πrdr. Поскольку масса m диска распределена равномерно, то масса единицы площади диска равна m/(πR2). Масса кольца: dm = 2πrdr(m/πR2) = (2m/πR2)rdr. Момент инерции кольца: dI = drm2 = (2m/πR2)r3dr. Просуммируем моменты инерций всех таких колец:
Момент инерции шара относительно его диаметра.
Объем диска dVz равен его площади, умноженной на толщину: dVz = πr2dz. Массу выделенного диска dm находим, разделив массу шара т на его объем 4πR3/3 и умножив на объем диска:
Момент инерции диска в данном случае:
Момент инерции шара находится интегрирование по всем таким дискам:
Момент инерции тонкого стержня относительно оси вращения, проходящей через его середину перпендикулярно стержню. Пусть стержень имеет длину l. Направим ось х вдоль стержня. Начало координат пусть находится на середине стержня. Возьмем элемент стержня длиной dx, находящийся на расстоянии х от оси вращения. Его масса равна dm = (m/l)dx, а момент инерции стержня – dI = dmx2 = (m/l)x2dx Отсюда находим момент инерции стержня:
Маятник Максвелла Для определения момента инерции тел с вращательной симметрией используется маятник Максвелла. В нем исследуемое тело совершает сложное плоско-параллельное движение. Небольшой диск (маховичок), насаженный туго на ось, опускается под действием силы тяжести на двух нитях, предварительно намотанных на ось маховичка. Нити во время движения разматываются до полной длины, раскрутившийся маховичок продолжает вращательное движение в том же направлении и наматывает нити на ось, вследствие чего он поднимается вверх, замедляя при этом вращение. Дойдя до верхней точки, диск опять опускается вниз и т. д. Маховичок будет совершать колебания вверх и вниз, поэтому устройство называют маятником. Движение маятника Максвелла можно рассматривать как сложное, состоящее из поступательного движения вниз и вращательного вокруг своей оси симметрии. Поступательное движение описывается соответствующим уравнением динамики, которое мы запишем в проекциях на вертикальную ось, совпадающей по направлению с вектором g, где g – ускорение свободного падения: mа = mg — 2Т. Уравнение динамики для вращательной составляющей этого движения имеет следующий вид в проекциях на горизонтальную ось, совпадающей по направлению с вектором М: Iε = M, где m – масса маятника, 2T – суммарное натяжение нитей подвеса, I – момент инерции маятника относительно горизонтальной оси, ε – угловое ускорение, М – момент натяжения нитей, равный 2TR, где R – радиус оси подвеса маятника. Взаимосвязь между поступательным и вращательным движениями: а =εR, а=2h/t2, где h – путь, проходимый маятником от верхней точки до нижней, t – время движения маятника при прохождении пути h. Из написанных выше уравнений получаем следующее: I = mR2*(gt2/2h – 1) = md2/4*(gt2/2h – 1) Эта формула выражает момент инерции маятника Максвелла, который состоит из оси, диска и кольца. Таким образом, момент инерции маятника Максвелла можно записать в виде: I = Iо + Iд + Iк, где I – момент инерции маятника Максвелла, Iо – момент инерции оси подвеса, Iд – момент инерции диска, Iк – момент инерции накладного кольца. Аналогично можно записать и массу маятника Максвелла: m = mо + mд + mк, где m – масса маятника Максвелла, mо – масса оси подвеса, mд – масса диска, mк – масса съемного кольца. Выразим момент инерции кольца: Iк = I — Iо — Iд. Для исключения неизвестных величин проведем эксперимент с кольцами разной массы. Запишем для каждого кольца выражение Iк1 = I1 — Iо — Iд, Iк2 = I2 — Iо — Iд Так как внешние и внутренние радиусы колец одинаковы, то:
Решив систему уравнений, получим:
Для третьего кольца момент инерции будет равен:
Таблица 1Формулы расчета момента инерции
где
Экспериментальная часть Для определения момента инерции тел вращения будем использовать специальную установку – маятник Максвелла.
1 – основание, 2 – стойка, 3 – неподвижный верхний кронштейн, 4 – подвижный кронштейн, 5 – электромагнит, 6 – вороток с фиксатором, 7 – фотодатчик, 8 – ось с закрепленным на ней диском, 9 – бифилярный подвес, 10 – сменное металлическое кольцо, 11 – миллисекундомер.
Упражнение 1. Определение момента инерции маятника Максвелла. 1. Включаем в сеть шнур питания миллисекундомера и нажимаем на кнопку «сеть», расположенную на лицевой панели секундомера. При этом загораются лампочки фотодатчика и цифровые индикаторы миллисекундомера. 2. Устанавливаем на диске маятника кольцо с массой mк1.
3. По шкале на стойке 2 определяем ход маятника h от верхней точки до нижней. h = 23,2 см = 0,232 м 4. Вращая маятник, зафиксируем его в верхнем положении при помощи электромагнита, следя за тем, чтобы нить наматывалась на ось виток к витку. Нажимаем на кнопку «сброс» и убеждаемся, что индикатор секундомера обнулился. 5. Плавно нажимаем кнопку «пуск» на милисекундомере и измеряем время хода маятника t. Измерения повторяем 10 раз. Находим среднее значение хода маятника tср. 6. Проделываем пп. 2-5 с кольцами массой mк2 и mк3. 7. Измеряем штангенциркулем радиус оси Ro, радиус диска Rд, внешний Rвнеш и внутренний Rвн радиусы трех колец с разной массой. Измеряем длину оси λ, толщину диска bд и толщину накладных колец bк. Масса диска с осью равна 120г. Измерения выполнены с учетом поправки на 9,9 мм. 8. Результаты всех измерений оформляем в виде таблицы.
9. По формулам рассчитаем экспериментальные значение момента инерции маятника Максвелла с первым, вторым и третьим кольцом. I = mR2*(gt2/2h – 1)
10. Вычислим доверительный интервал в определении момента инерции маятника и относительную ошибку согласно теории погрешности для всех трех случаев.
11. Запишем конечные результаты для моментов инерции маятника Максвелла с первым, вторым и третьим кольцом с учетом доверительного интервала и относительной погрешности.
12. По формулам рассчитаем теоретические значения момента инерции маятника Максвелла с первым, вторым и третьим кольцом.
13. Вычислим относительную ошибку измерения: Е = ∆ х / хист. * 100%
Упражнение 2. Определение момента инерции накладных колец. 1. Включаем в сеть шнур питания миллисекундомера и нажимаем на кнопку «сеть», расположенную на лицевой панели секундомера. При этом загораются лампочки фотодатчика и цифровые индикаторы миллисекундомера. 2. Устанавливаем на диске маятника кольцо с массой mк1. 3. По шкале на стойке 2 определяем ход маятника h от верхней точки до нижней. h = 23,2 см = 0,232 м 4. Вращая маятник, зафиксируем его в верхнем положении при помощи электромагнита, следя за тем, чтобы нить наматывалась на ось виток к витку. Нажимаем на кнопку «сброс» и убеждаемся, что индикатор секундомера обнулился. 5. Плавно нажимаем кнопку «пуск» на милисекундомере и измеряем время хода маятника t. Измерения повторяем 10 раз. Находим среднее значение хода маятника tср. 6. Проделываем пп. 2-5 с кольцами массой mк2 и mк3. 7. Измеряем штангенциркулем радиус оси Ro, радиус диска Rд, внешний Rвнеш и внутренний Rвн радиусы трех колец с разной массой. Измерения выполнены с учетом поправки на 9,9 мм. 8. Результаты всех измерений оформляем в виде таблицы.
9. По формулам рассчитаем экспериментальные значения момента инерции маятника Максвелла с первым, вторым и третьим кольцом.
10. Вычислим доверительный интервал в определении момента инерции маятника и относительную ошибку согласно теории погрешности для всех трех случаев.
11. Запишем конечные результаты для моментов инерции маятника Максвелла с первым, вторым и третьим кольцом с учетом доверительного интервала и относительной погрешности.
12. По формуле рассчитаем теоретические значения момента инерции первого, второго и третьего кольца:
13. Вычислим относительную ошибку измерения: Е = ∆ х / хист. * 100%
Вывод: | |
Лекция 3. Динамика вращательного движения твердого тела
6
[1] гл.4
План лекции
Момент инерции.
Момент силы. Основное уравнение динамики вращательного движения.
Момент импульса. Закон сохранения момента импульса.
Работа и кинетическая энергия при вращательном движении.
Момент инерции.
При рассмотрении вращательного движения необходимо ввести новые физические понятия: момент инерции, момент силы, момент импульса.
Момент инерции является мерой инертности тела при вращательном движении тела.
М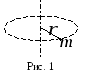 омент
инерции материальной точки относительно
неподвижной оси вращения равен
произведению её массы на квадрат
расстояния до рассматриваемой оси
вращения (рис.1):
омент
инерции материальной точки относительно
неподвижной оси вращения равен
произведению её массы на квадрат
расстояния до рассматриваемой оси
вращения (рис.1):
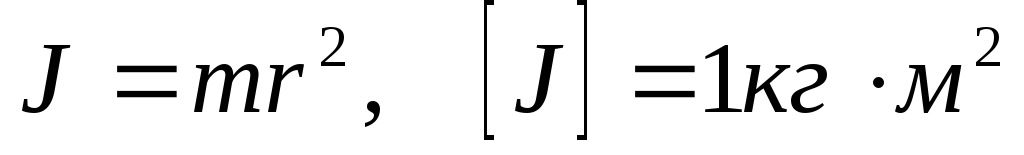 .
.
 зависит
только от массы материальной точки и
её положения относительно оси вращения
и не зависит от наличия самого вращения.
зависит
только от массы материальной точки и
её положения относительно оси вращения
и не зависит от наличия самого вращения.
Момент инерции — скалярная и аддитивная величина, поэтому момент инерции тела равен сумме моментов инерции всех его точек:
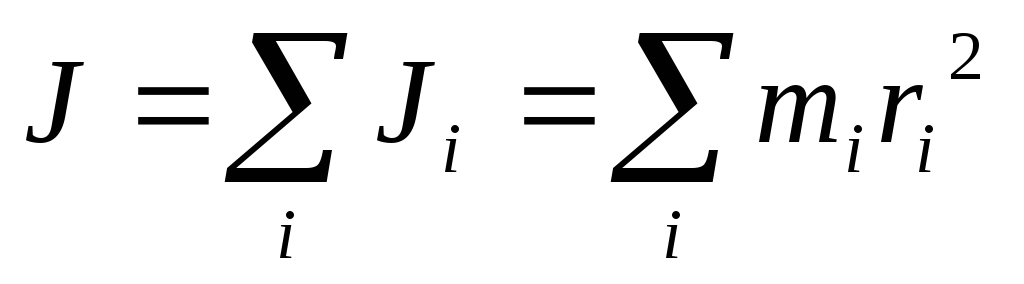 .
.
В случае непрерывного распределения массы эта сумма сводится к интегралу:

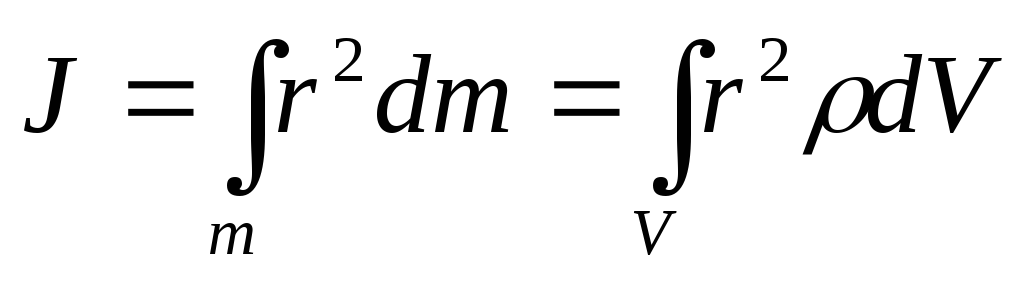 ,
,
где 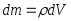 —
масса
малого объема тела
—
масса
малого объема тела 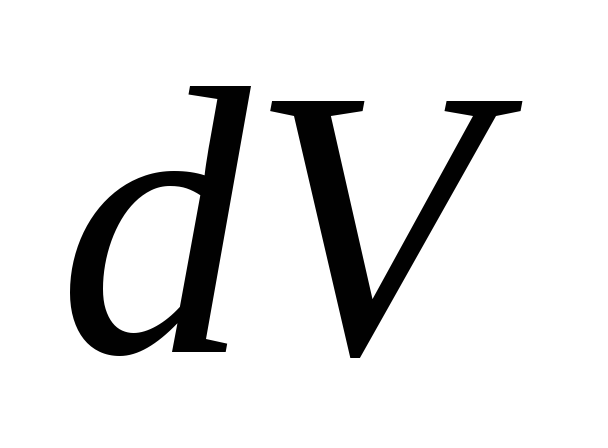 ,
, 
плотность тела,
плотность тела, 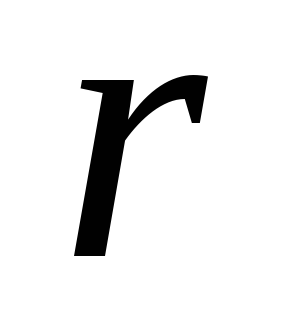 — расстояние от элемента
— расстояние от элемента 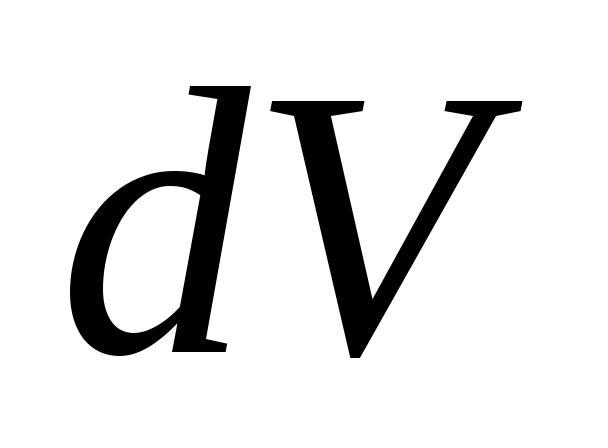 до оси вращения.
до оси вращения.
Момент инерции является аналогом массы при вращательном движении. Чем больше момент инерции тела, тем труднее изменить угловую скорость вращаемого тела. Момент инерции имеет смысл только при заданном положении оси вращения. Бессмысленно говорить просто о “моменте инерции”. Он зависит :
1)от положения оси вращения;
2)от распределения массы тела относительно оси вращения, т.е. от формы тела и его размеров.
Экспериментальным доказательством этого является опыт со скатывающимися цилиндрами.
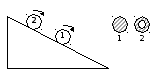
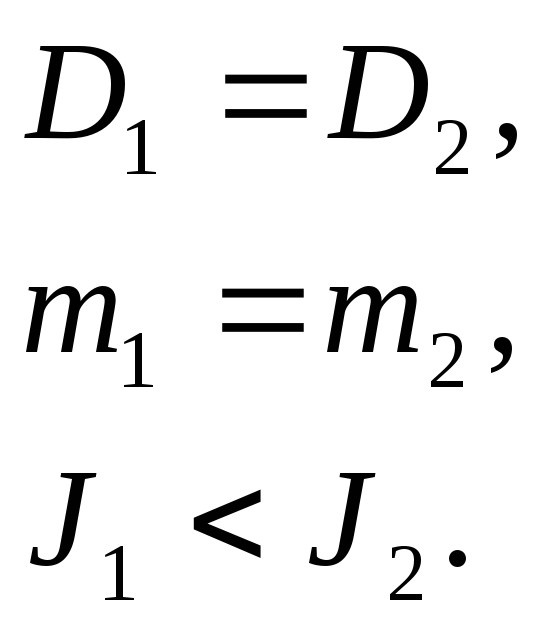
Произведя интегрирование для некоторых однородных тел, можно получить следующие формулы (ось вращения проходит через центр масс тела).
Момент инерции обруча (толщиной стенок пренебрегаем) или полого цилиндра:
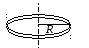
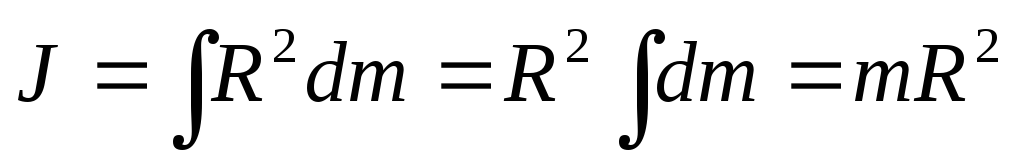 .
.
Момент инерции диска или сплошного цилиндра радиуса R:
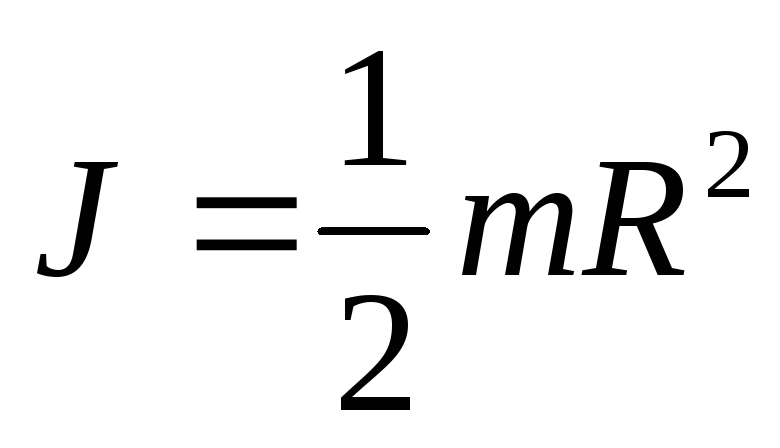 .
.
Момент инерции шара

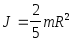 .
.
Момент инерции стержня
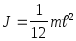 .
.
Е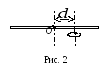 сли
для тела известен момент инерции
относительно оси, проходящей через
центр масс, то момент инерции относительно
любой оси, параллельной первой, находится
по теореме
Штейнера:
момент инерции тела относительно
произвольной оси равен моменту инерции
J0 относительно
оси, параллельной данной и проходящей
через центр масс тела, сложенному с
произведением массы тела на квадрат
расстояния между осями.
сли
для тела известен момент инерции
относительно оси, проходящей через
центр масс, то момент инерции относительно
любой оси, параллельной первой, находится
по теореме
Штейнера:
момент инерции тела относительно
произвольной оси равен моменту инерции
J0 относительно
оси, параллельной данной и проходящей
через центр масс тела, сложенному с
произведением массы тела на квадрат
расстояния между осями.
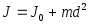 ,
,
где d расстояние от центра масс О до оси вращения (рис.2).
Центр масс — воображаемая точка, положение которой характеризует распределение массы данного тела. Центр масс тела движется так же, как двигалась бы материальная точка той же массы под действием всех внешних сил, действующих на данное тело.
Понятие момента инерции было введено в механику отечественным ученым Л. Эйлером в середине XVIII века, и с тех пор широко используется при решении многих задач динамики твердого тела. Значение момента инерции необходимо знать на практике при расчете различных вращающихся узлов и систем (маховиков, турбин, роторов электродвигателей, гироскопов). Момент инерции входит в уравнения движения тела (корабля, самолета, снаряда, и т.п.). Его определяют, когда хотят узнать параметры вращательного движения летательного аппарата вокруг центра масс при действии внешнего возмущения (порыва ветра и т.п.).
§21.Момент инерции.
Определение: Моментом
инерции материальной точки относительно
неподвижной оси называется скалярная
физическая величина, являющаяся мерой
инертности этой точки при вращательном
движении и, равная произведению её массы
на квадрат расстояния до оси, т.е. 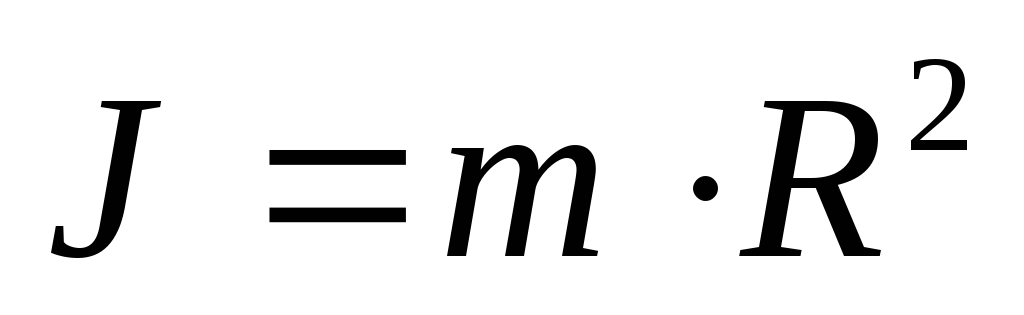 ,
а также
,
а также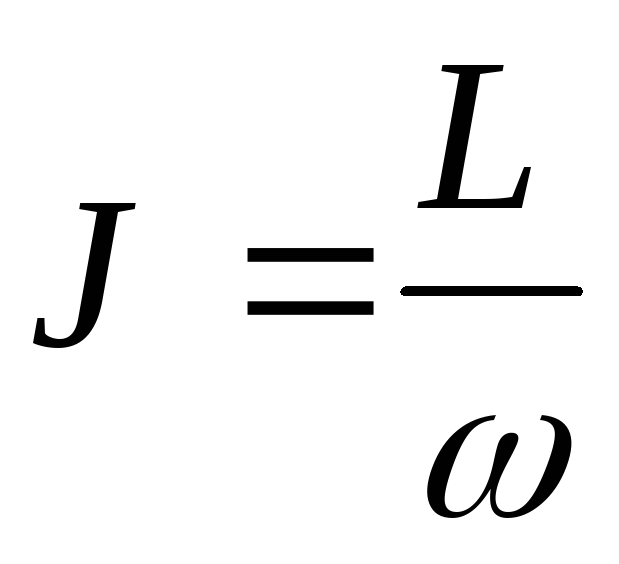 ,
где
,
где —
угловая скорость тела относительно
данной оси.
—
угловая скорость тела относительно
данной оси.
Определение: Моментом
инерции системы материальных точек
относительно неподвижной оси называется
скалярная физическая величина, являющаяся
мерой инертности этой системы при
вращательном движении и, равная
алгебраической сумме произведений масс
всех материальных точек системы на
квадрат их расстояний до оси, т.е. 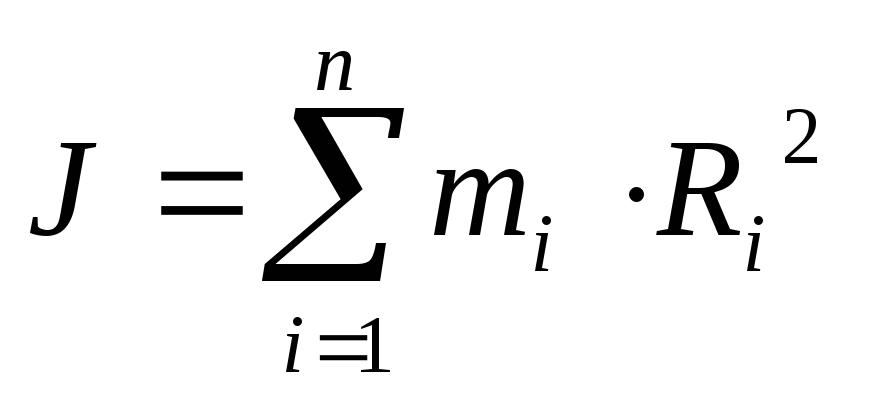 .
.
Момент инерции определен только относительно оси.
В случае непрерывного распределения
масс с плотностью сумма заменится
на интеграл по всему объему тела: 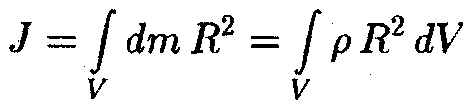 (Интегрирование производится по всему
объёму; пределы интегрирования
устанавливаются исходя из конфигурации
тела и его размеров). Если тело однородно,
то его плотность во всех точках постоянна
и можно вынести из-под знака интеграла.
(Интегрирование производится по всему
объёму; пределы интегрирования
устанавливаются исходя из конфигурации
тела и его размеров). Если тело однородно,
то его плотность во всех точках постоянна
и можно вынести из-под знака интеграла.
Найдем моменты инерции для простейших
(геометрически правильных) форм твердого
тела, масса которого равномерно
распределена по объему, т.е. 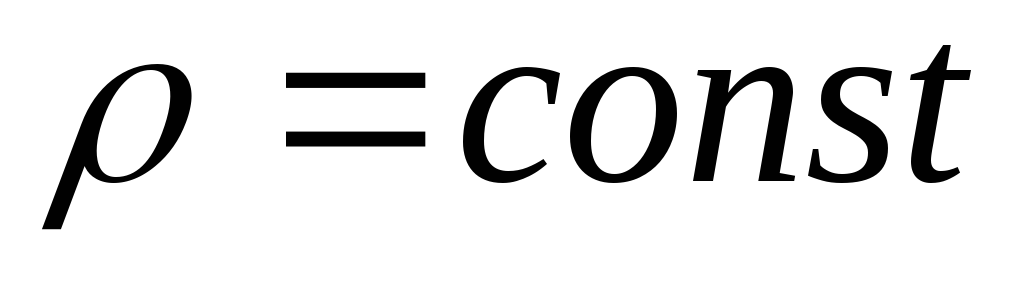 .
.
1. Момент инерции обручаотносительно оси, перпендикулярной к его плоскости и проходящей через его центр.
Обруч считается бесконечно тонким, т.е.
толщиной обода можно пренебречь по
сравнению с радиусом R..
Поскольку в этой системе все массы
находятся на одинаковом расстоянии от
оси вращения, R2можно вынести из-под знака интеграла: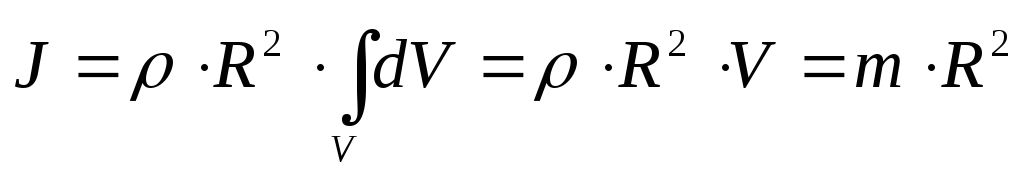 ,
гдеm— полная масса обруча.
,
гдеm— полная масса обруча.
2. Момент инерции дискаотносительно оси, перпендикулярной его плоскости и проходящей через центр. Диск считается бесконечно тонким, т.е. его толщина много меньше радиуса R.Момент инерции, согласно определению, величина аддитивная: момент инерции целого тела равен сумме моментов инерции его частей. Разобьем диск на бесконечно тонкие обручи радиусомsи толщинойds (См.рис.).
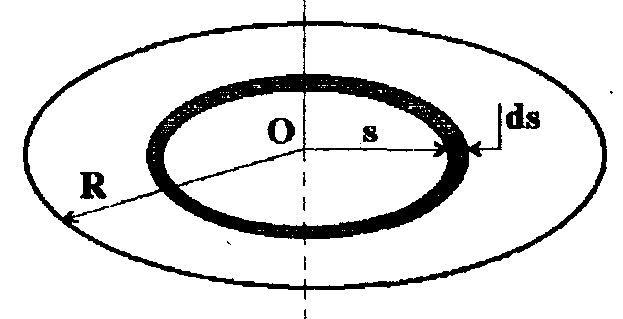
Момент инерции диска относительно перпендикулярной оси, проходящей через центр.
Площадь поверхности обруча равна произведению его длины на толщину: 2 s ds.Поскольку массатдиска распределена равномерна, масса обручаdmпропорциональна площади его поверхности:
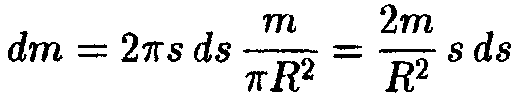 .
.
Момент инерции обруча мы уже знаем: 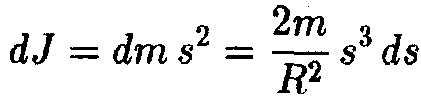 . Осталось просуммировать моменты
инерции всех таких обручей:
. Осталось просуммировать моменты
инерции всех таких обручей: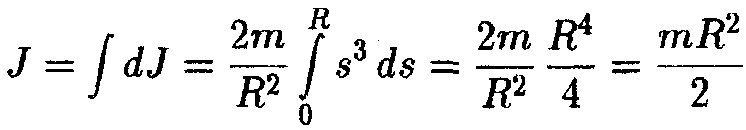 .
.
Такой же результат получится и для момента инерции цилиндра конечной длины относительно его продольной оси.
3. Момент инерции шараотносительно его диаметра. Поступим аналогичным образом: «нарежем» шар на бесконечно тонкие диски толщинойdz.находящиеся на расстоянииzот центра (См.рис.).
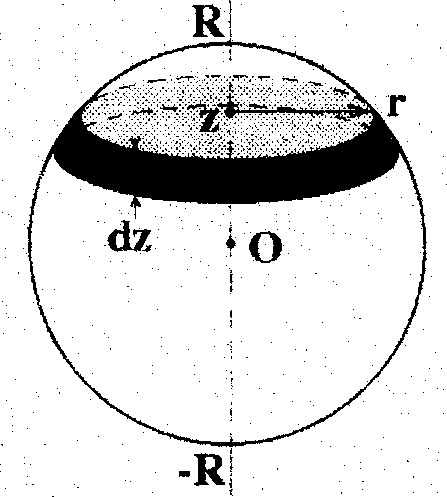
Момент инерции шара относительно диаметра.
Радиус такого диска равен 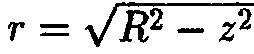 . Объем дискаdVz равен произведению его площади
на толщину:
. Объем дискаdVz равен произведению его площади
на толщину:
 . Массу дискаdmнаходим, разделив массу шаратна его объем
. Массу дискаdmнаходим, разделив массу шаратна его объем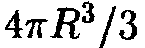 , умножив на объем диска:
, умножив на объем диска:
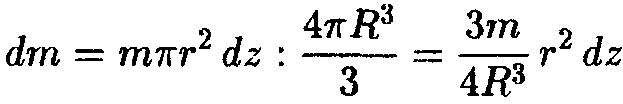 .
.
Момент инерции диска был найден выше. В применении к данному случаю, он равен:
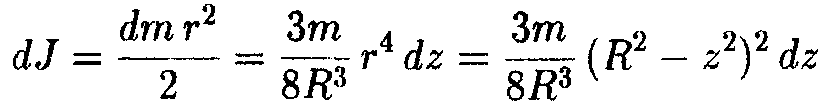 .
.
Момент инерции шара находится интегрированием по всем таким дискам:
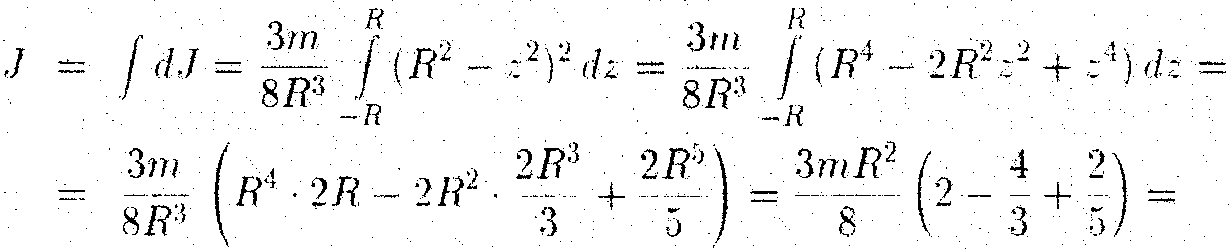
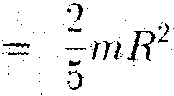
4.Момент инерции тонкого стержняотносительно оси, проходящей через его середину перпендикулярно стержню.
Пусть стержень имеет длину ℓ.Направим осьxвдоль стержня. Начало координат по условию находится в центре стрежня. Возьмем элемент стержня длинойdx.находящийся на расстоянииxот оси вращения. Его масса равна
dm = (m/ℓ) dx,а момент инерцииdJ=(m/ℓ) x2 dx. Отсюда находим момент инерции стрежня:
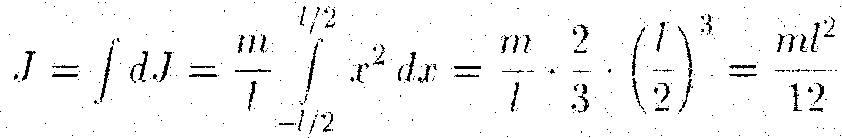 (*).
(*).
Момент инерции величина аддитивная,
т.е. суммарный момент инерции системы
тел относительно какой-либо оси, равен
сумме моментов инерции каждого из тел
данной системы относительно той же оси: 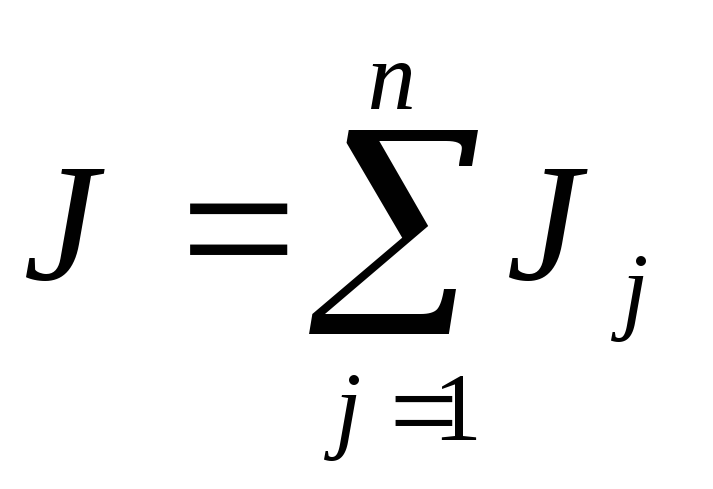
Физический смысл момента инерции:Инерционные свойства при поступательном движении характеризуются только массой тела, т.е. зависит только от массы. Инерционные свойства при вращательном движении характеризуются моментом инерции, т.е. зависят от его массы, расстояния до оси вращения и расположению теда по отношению к этой оси. Последнее означает, что относительно двух разных осей инерционные свойства вращательного движения одного и того же движения тела будут разными. Пример.
Формула момента инерции диска, J
Момент инерции тела, которое можно представить в виде совокупности дискретных частиц, относительно оси вращения равен:
где – масса i-ой материальной точки тела; – расстояние от материальной точки i до оси вращения. При рассмотрении твердого тела как сплошной среды с непрерывным распределением массы определение момента инерции заменяют следующим:
где – элемент массы тела; – плотность тела; – элементарный объем.
Момент инерции однородного диска
Рассмотрим, как находится момент инерции однородного диска, если его радиус равен R, а масса m. Ось вращения пусть проходит через центр инерции данного диска (точку О) и будет перпендикулярна его плоскости (рис.1).
Диск можно заменить совокупностью бесконечно тонких колец, радиусы которых изменяются от нуля до R. На рис.1 выделено одно из таких колец. Рассмотрим это кольцо. Радиус его обозначим как Момент инерции данного кольца (обозначим его равен (см. формулу момента инерции тонкого кольца):
Массу данного кольца (а точнее цилиндра) можно представить как:
где – высота цилиндра. Подставим выражение для в формулу (3) и проведем интегрирование:
где – масса диска.
Если диск можно считать абсолютно тонким или он является частью цилиндра, то формула для вычисления момента инерции диска относительно оси, проходящей через его центр масс, и перпендикулярной плоскости диска, имеет вид:
В случае плоского распределения масс выполняется равенство:
где оси вращения совпадают с осями декартово системы координат. И если мы будем считать, что ось Z проходит через центр инерции диска и перпендикулярна его плоскости, то моменты инерции относительно осе X и Y будут равны:
Иногда величины моментов инерции называют моментами инерции диска относительно его диаметров.


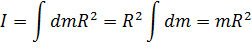
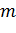 – полная масса обруча.
– полная масса обруча.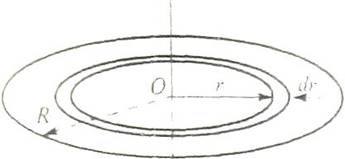
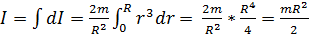 .
.
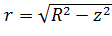 .
.
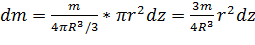 .
.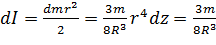 .
.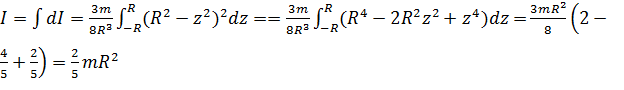 .
.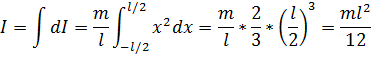
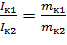 .
.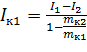 ,
,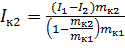 .
.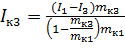 .
.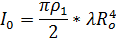
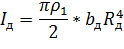
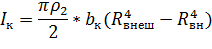
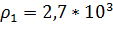 кг/м3 – плотность материала, из которого изготовлена ось и диск;
кг/м3 – плотность материала, из которого изготовлена ось и диск; 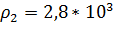 кг/м3 – плотность материала кольца; Ro – радиус оси; Rд – радиус диска; Rвнеш и Rвн – внешний и внутренний радиусы кольца; λ – длина оси; bд – толщина диска; bк – толщина накладного кольца.
кг/м3 – плотность материала кольца; Ro – радиус оси; Rд – радиус диска; Rвнеш и Rвн – внешний и внутренний радиусы кольца; λ – длина оси; bд – толщина диска; bк – толщина накладного кольца.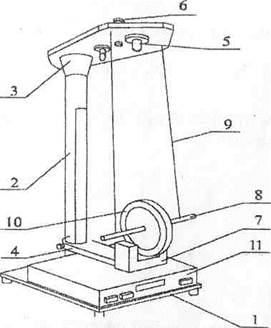
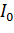 , кг*м2
, кг*м2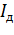 , кг*м2
, кг*м2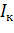 , кг*м2
, кг*м2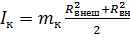 .
.