Главные оси инерции и главные моменты инерции (Лекция №18)

   Как уже известно, зная для данной фигуры центральные моменты инерции , и , можно вычислить момент инерции и относительно любой другой оси.

   При этом можно за основную систему осей принять такую систему, при которой формулы существенно упрощаются. Именно, можно найти систему координатных осей, для которых центробежный момент инерции равен.нулю. В самом деле, моменты инерции и всегда положительны, как суммы положительных слагаемых, центробежный же момент

может быть и положительным и отрицательным, так как слагаемые zydF могут быть разного знака в зависимости от знаков z и у для той или иной площадки. Значит, он может быть равен нулю.

   Оси, относительно которых центробежный момент инерции обращается в нуль, называются главными осями инерции. Если начало такой системы помещено в центре тяжести фигуры, то это будут главные центральные оси. Эти оси мы будем обозначать и ; для них

Найдем, под каким углом наклонены к центральным осям у и z (фиг. 198) главные оси.

Рис.1. Расчетная модель для определения положения главных осей инерции.

 

   В известном выражении для перехода от осей yz к осям , для центробежного момента инерции дадим углу значение ; тогда оси и , совпадут c главными, и центробежный момент инерции будет равен нулю:

или

откуда:

(1)

   Этому уравнению удовлетворяют два значения , отличающиеся на 180°, или два значения , отличающиеся на 90°. Таким образом, это уравнение дает нам положение

двух осей, составляющих между собой прямой угол. Это и будут главные центральные оси и , для которых .

   Пользуясь этой формулой, можно по известным , и получить формулы для главных моментов инерции и . Для этого опять воспользуемся выражениями для осевых моментов инерции общего положения. Они определяют значения и если вместо подставить

(2)

   Полученными соотношениями можно пользоваться при решении задач. Одним из главных моментов инерции является , другим .

   Формулы (2) можно преобразовать к виду, свободному от значения . Выражая и через и подставляя их значения в первую формулу (2), получим, делая одновременно замену из формулы (1):

Заменяя здесь из формулы (1) дробь на

получаем

(3)

   К этому же выражению можно прийти, делая подобное же преобразование второй формулы (3).

   За основную систему центральных осей, от которых можно переходить к любой другой, можно взять не Оу и Oz, а главные оси и ; тогда в формулах не будет фигурировать центробежный момент инерции (). Обозначим угол, составленный осью , (Рис.2) с главной осью , через . Для вычисления , и , переходя от осей и нужно в ранее найденных выражениях для , и , заменить угол через , а , и — через , и . В результате получаем:

   По своему виду эти формулы совершенно аналогичны формулам для нормальных и касательных напряжений по двум взаимно-перпендикулярным площадкам в элементе, подвергающемся растяжению в двух направлениях. Укажем лишь формулу, позволяющую из двух значений угла выделить то, которое соответствует отклонению первой главной оси (дающей max J) от начального положения оси у:

   Теперь можно окончательно формулировать, что надо сделать, чтобы получить возможность простейшим образом вычислять момент инерции фигуры относительно любой оси. Необходимо через центр тяжести фигуры провести оси Оу и Oz так, чтобы, разбивая фигуру на простейшие части, мы могли легко вычислить моменты , и после этого следует найти по формуле (14.17) величину угла и вычислить главные центральные моменты инерции и по формулам (14.18).

Рис.2. Расчетная модель нахождения положения главных осей.

 

   Далее, можно найти момент инерции относительно любой центральной оси (Рис.2), наклоненной к под углом :

   Зная же центральный момент инерции , можно сейчас же найти момент инерции относительно любой параллельной ей оси , проходящей на расстоянии (рис.2) от центра тяжести:

   Во многих случаях удается сразу провести главные оси фигуры; если фигура имеет ось симметрии, то это и будет одна из главных осей. В самом деле, при выводе формулы мы уже имели дело с интегралом, представляющим собой центробежный момент инерции сечения относительно осей у и z; было доказано, что если ось Oz является осью симметрии, этот интеграл обращается в нуль.

   Стало быть, в данном случае оси Оу и Oz являются главными центральными осями инерции сечения. Таким образом,

ось симметрии — всегда главная центральная ось; вторая главная центральная ось проходит через центр тяжести перпендикулярно к оси симметрии.

   Пример. Найти моменты инерции прямоугольника (Рис.3) относительно осей и и центробежный момент его относительно тех же осей.

Рис.3. Пример расчета моментов инерции.

 

   Центральные оси у и z как оси симметрии будут главными осями; моменты инерции сечения относительно этих осей равны:

Центральные моменты относительно повернутых осей и равны:

Центробежный момент инерции относительно осей и равен:

Координаты центра тяжести прямоугольника относительно осей и равны:

Моменты инерции относительно осей и равны:

Центробежный момент инерции равен:

 

Наибольшее и наименьшее значения центральных моментов инерции.

   Как известно, центральные моменты инерции являются наименьшими из всех моментов относительно ряда параллельных осей.

   Найдем теперь крайние значения (максимум и минимум) для центральных моментов инерции. Возьмем ось , и начнем ее вращать, т. е. менять угол ; при этом будет изменяться величина

Наибольшее и наименьшее значения этого момента инерции соответствуют углу , при котором производная обращается в нуль. Эта производная равна:

Подставляя в написанное выражение и приравнивая его нулю, получаем:

отсюда

   Таким образом, осями с наибольшим и наименьшим центральными моментами инерции будут главные центральные оси. Так как при повороте центральных осей сумма соответствующих моментов инерции не меняется, то

Когда один из центральных моментов инерции достигает наибольшего значения, другой оказывается минимальным, т, е. если

то

   Следовательно, главные центральные оси инерции — это такие взаимно перпендикулярные оси, проходящие через центр тяжести сечения, относительно которых центробежный момент инерции обращается в нуль, а осевые моменты инерции имеют наибольшее и наименьшее значения.

Дальше…

6.6. Главные оси инерции и главные моменты инерции

6.6. ГЛАВНЫЕ ОСИ ИНЕРЦИИ И ГЛАВНЫЕ МОМЕНТЫ ИНЕРЦИИ

При изменении угла α значения Iz1, Iy1, Iz1y1 (6.13) изменяются, и при некотором значении угла α0 они принимают экстремальные значения. Взяв первую производную по углу α от формул (6.13) и приравняв ее нулю, получим: Эта формула определяет положение двух осей, относительно одной из которых осевой момент максимален, а относительно другой – минимален. Такие оси называют главными. Моменты инерции относительно главных осей называют главными моментами инерции. Их вычисляют следующим образом: Главные оси обладают следующими свойствами: центробежный момент инерции относительно них равен нулю; моменты инерции относительно главных осей экстремальны; для симметричных сечений оси симметрии являются главными. Главные оси, проходящие через центр тяжести фигуры, называют главными центральными осями инерции. Пример 6.4. Определить, каким образом изменяется момент инерции квадратного сечения при его повороте. Решение. Момент инерции относительно повернутой оси: Поскольку оси z, y квадрата являются осями симметрии, то есть главными, то центробежный момент инерции относительно них Izy = 0: Выводы. 1. Моменты инерции квадратного сечения с изменением положения центральных осей остаются постоянными. 2. В квадрате и других правильных многоугольниках (треугольниках, пятиугольниках) любая центральная ось является и главной. Такие фигуры называют фигурами равного сопротивления. Пример 6.5. Для фигуры, представленной в примере 6.1, определить главные центральные моменты инерции. Решение. Расстояния между центральной осью составной фигуры и собственными центральными осями элементов Моменты инерции относительно центральных осей, параллельных основанию и высоте a1= y1 – yC = 5 – 3,5 = 1,5 см; a2= y2 – yC = 1 – 3,5 = –2,5 см; b1= z1 – zC = 1 – 2,5 = –1,5 см; b2= z2 – zC = 5 – 2,5 = 2,5 см. Центробежный момент инерции Направления главных осей инерции Угол α0 (положительный) откладываем против хода часовой стрелки от оси с большим моментом инерции, то есть zC . Величины главных центральных моментов инерции

8.Главные оси инерции и главный момент инерции.

Главные оси инерции и главные моменты инерции.

При изменении угла 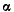величины Ix1, Iy1 и Ix1y1 изменяются. Найдем значение угла, при котором Ix1 и Iy1имеют экстремальные значения; для этого возьмем от Ix1 или Iy1 первую производную по 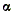и преравняем ее нулю: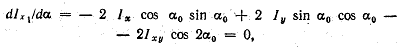или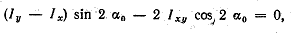откуда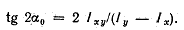(1.28)

Эта формула определяет положение двух осей, относительно одной из которых осевой момент инерции максимален, а относительно другой — минемален.

Такие оси называют главными. Моменты инерции относительно главных осей называются главными моментами инерции.

Значения главных моментов инерции найдем из формул (1.23) и (1.24), подставив в них 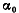из формулы (1.28), при этом используем известные формулы тригонометрии для функций двойных углов.

После преобразований получим следующую формулу для определения главных моментов инерции: 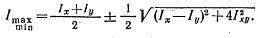 (1.29)

Исследуя вторую производную 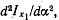можно установить, что для данного случая (Ix < Iy) максимальный момент инерции Imax имеет место относительно главной оси, повернутой на угол 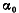по отношению к оси х, а минимальный момент инерции — относительно другой, перпендикулярной оси. В большинстве случаев в этом исследовании нет надобности, так как по конфигурации сечений видно, какая из главных осей соответствует максимуму момента инерции.

Главные оси, проходящие через центр тяжести сечения, называются главными центральными осями.

Во многих случаях удается сразу определить положение главных центральных осей. Если фигура имеет ось симметрии, то она является одной из главных центральных осей, вторая проходит через центр тяжести сечения перпендикулярно первой. Сказанное следует из того обстоятельства, что относительно оси симметрии и любой оси, ей перпендикулярной, центробежный момент инерции равен нулю.

В случае если два главных центральных момента инерции сечения равны между собой, то у этого сечения любая центральная ось является главной, и все главные центральные моменты инерции одинаковы (круг, квадрат, шестиугольник, равносторонний шестиугольник).

9.Основные геометрические характеристики сечений

Здесь: C — центр тяжести плоских сечений;

A — площадь сечения;

I_x , I_y — осевые моменты инерции сечения относительно главных осей;

I_xI , I_yI — осевые моменты инерции относительно вспомогательных осей;

I_p — полярный момент инерции сечения;

W_x , W_y — осевые моменты сопротивления;

W_p — полярный момент сопротивления

Прямоугольное сечение

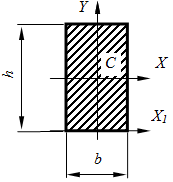
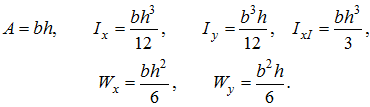
Сечение равнобедренный треугольник

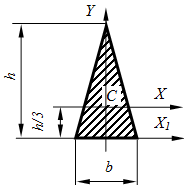
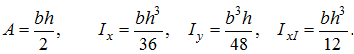
10.Основные виды сил, действующие на тело. Момент силы относительно центра. Свойства момента сил.

При рас­смот­ре­нии ме­ха­ни­че­ских задач боль­шин­ство сил, дей­ству­ю­щих на тела, можно от­не­сти к трем ос­нов­ным раз­но­вид­но­стям:

— сила все­мир­но­го тя­го­те­ния;

— сила тре­ния;

— сила упру­го­сти.

Все окру­жа­ю­щие нас тела при­тя­ги­ва­ют­ся к Земле, это обу­слов­ле­но дей­стви­ем сил все­мир­но­го тя­го­те­ния. Если мы будем пре­не­бре­гать со­про­тив­ле­ни­ем воз­ду­ха, то мы уже знаем, что все тела па­да­ют на Землю с оди­на­ко­вым уско­ре­ни­ем – уско­ре­ни­ем сво­бод­но­го па­де­ния.

Как и вся­кий пред­мет, тело, под­ве­шен­ное на пру­жине, стре­мит­ся упасть вниз из-за при­тя­же­ния Земли, но, когда пру­жи­на рас­тя­нет­ся до неко­то­рой длины, тело оста­нав­ли­ва­ет­ся, то есть при­хо­дит в со­сто­я­ние ме­ха­ни­че­ско­го рав­но­ве­сия. Мы уже знаем, что ме­ха­ни­че­ское рав­но­ве­сие на­сту­па­ет, когда сумма сил, дей­ству­ю­щих на тело, равна нулю. Это озна­ча­ет, что сила тя­же­сти, дей­ству­ю­щая на груз, долж­на урав­но­ве­сить­ся с неко­то­рой силой, дей­ству­ю­щей со сто­ро­ны пру­жи­ны. Эта сила, на­прав­лен­ная про­тив силы тя­же­сти и дей­ству­ю­щая со сто­ро­ны пру­жи­ны, на­зы­ва­ет­ся силой упру­го­сти.

Прой­дя неко­то­рое рас­сто­я­ние, тело оста­нав­ли­ва­ет­ся, ско­рость тела умень­ша­ет­ся от на­чаль­но­го зна­че­ния до нуля, то есть уско­ре­ние тела – ве­ли­чи­на от­ри­ца­тель­ная. Сле­до­ва­тель­но, на тело со сто­ро­ны по­верх­но­сти дей­ству­ет сила, ко­то­рая стре­мит­ся оста­но­вить это тело, то есть дей­ству­ет про­тив его ско­ро­сти. Эта сила на­зы­ва­ет­ся силой тре­ния.  

Момент силы относительно центра (точки).

    Моментом силы F относительно центра (точки) О называется вектор m_o(F) равный векторному произведению радиуса вектора r,  проведенного из центра О в точку А приложения силы, на вектор силы F: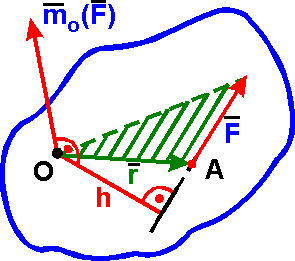

    Вектор m_o(F) приложен в точке О и направлен  плоскости, проходящей через центр О и силу F, в ту сторону, откуда сила видна стремящейся повернуть тело вокруг центра О против хода часовой стрелки.

    Модуль m_o(F) равен произведению модуля силы F на плечо h:

где плечо h  перпендикуляр, опущенный из центра О на линию действия силы F.

    Момент m_o(F) характеризует вращательный эффект силы F относительно центра (точки) О.

    Свойства момента силы:

    1. Момент силы относительно центра не изменяется при переносе силы вдоль линии ее действия в любую точку;

    2. Если линия действия силы проходит через центр О (h = 0), то момент силы относительно центра О равен нулю.

Главный момент инерции Википедия

Моме́нт ине́рции — скалярная физическая величина, мера инертности во вращательном движении вокруг оси, подобно тому, как масса тела является мерой его инертности в поступательном движении. Характеризуется распределением масс в теле: момент инерции равен сумме произведений элементарных масс на квадрат их расстояний до базового множества (точки, прямой или плоскости).

Единица измерения в Международной системе единиц (СИ): кг·м².

Обозначение: I или J.

Различают несколько моментов инерции — в зависимости от типа базового множества до которого отсчитываются расстояния от элементарных масс.

Осевой момент инерции[ | ]

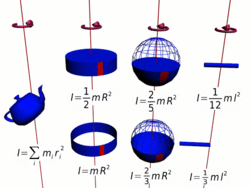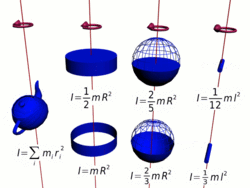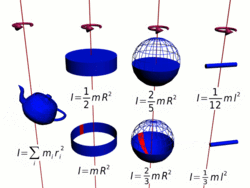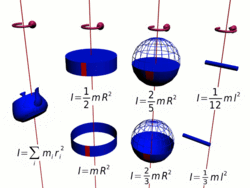Осевые моменты инерции некоторых тел

Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси^[1]:

Ja=∑i=1nmiri2,{\displaystyle J_{a}=\sum _{i=1}^{n}m_{i}r_{i}^{2},}

где:

• m_i — масса i-й точки,
• r_i — расстояние от i-й точки до оси.

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении.

J

4.3. Понятие о главных осях. Главные моменты инерции

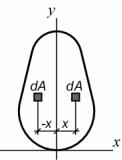
Центробежный момент инерции:

J x1y1 = ∫ x1 y1dA = ∫(x cosα + y sinα )( y cosα − xsinα )dA =

A		A
= J xy cos2 α − J y		sin 2α		+ J x	sin 2α	− J xy sin 2 α =
		2			2
= J xy cos 2α +	J x − J y		sin 2α
		2

Главными осями называются такие оси координат, относительно которых центробежный момент инерции равен нулю.

Пользуясь теоремой о моментах инерции при повороте осей координат, найдем положение главных осей:

J x y = J xy cos 2α +					Jx − J y						sin 2α = 0.
1	1							2
Разделим каждое из слагаемых на cos 2α :
	J		+ tg2α	J x			− J y		= 0 ,
		xy					2
откуда
		tg2α = −					2Jxy				.
						J	x	− J
									y

Полученный угол α откладывается против часовой стрелки относительно исходной системы координатных осей.

Моменты инерции в главных осях координат принимают экстремальные значения. Для

доказательства возьмем первую производную от J x по α и приравняем ее к нулю:

1

dJ x1

= − J

2sinα cosα + 2J cosα sinα − J

2 cos 2α =

dα

x

y

xy

= 2(J y cosα sinα − J x sinα cosα − J xy cos 2α ) = 0

Или:

J y − J x

sin 2α − J

cos 2α = 0 , откуда tg2α = −

2Jxy

,

2

xy

Jx − J y

то есть среди множества осей, которые можно провести через заданную точку именно относительно главных осей осевые моменты инерции принимают экстремальные значения.

Взаимно перпендикулярные оси, из которых хотя бы одна совпадает с осью симметрии, являются главными осями.

Очевидно, что каждой элементарной площадке, расположенной по одну сторону от оси симметрии, соответствует точно такая же по другую сторону, для которой произведение координат отличается только знаком. Таким образом, центробежный момент инерции

J xy = ∫ xydA = 0.

A

Главные оси можно провести через любую точку сечения, однако наибольший интерес представляют главные оси, проходящие через центр тяжести (главные центральные оси).

Интересно, что, если два главных центральных момента инерции сечения равны между собой (Jx = Jy, Jxy = 0), то, согласно теореме о моментах инерции при повороте осей координат, у этого сечения любая центральная ось является главной и все главные центральные моменты инерции одинаковы. В некоторых случаях такие фигуры легко указать: они имеют более двух осей симметрии (равносторонний треугольник, квадрат, другие правильные многоугольники, круг, кольцо).

Лекция № 2

Центробежный момент инерции относительно осей координат – сумма произведений элементарных площадей dA на их расстояния до этих осей, взятая по всей площади сечения А.

Если хотя бы одна из осей y или z является осью симметрии сечения, центробежный момент инерции такого сечения относительно этих осей равен нулю (так как в этом случае каждой положительной величине z·y·dA можем поставить в соответствие точно такую же, но отрицательную, по другую сторону от оси симметрии сечения, см. рисунок).

Рассмотрим дополнительные геометрические характеристики, которые могут быть получены из перечисленных основных и также часто используются в расчетах на прочность и жесткость.

Полярный момент инерции

Полярным моментом инерции Jp называют характеристику

J p = Jz + J y .

С другой стороны,

J p = Jz + J y = ∫y2 dA +∫z2 dA = ∫(y2 + z2 ) dA = ∫ρ2 dA.

A A A A

Полярный момент инерции (относительно данной точки) – сумма произведений элементарных площадей dA на квадраты их расстояний (ρ2 = y2 + z2 ) до этой точки, взятая по всей площади сечения А.

Размерность моментов инерции – м4 в СИ.

Момент сопротивления Момент сопротивления относительно некоторой оси – величина равная мо-

менту инерции относительно той же оси отнесенному к расстоянию (ymax или zmax) до наиболее удаленной от этой оси точки

W =	J	z	; W	=	J y	.
z	ymax		y		zmax

Размерность моментов сопротивления – м3 в СИ.

Радиус инерции Радиусом инерции сечения относительно некоторой оси, называется величи-

на, определяемая из соотношения:

	iz =	J	z	,	iy =	J y	.
		A				A

Радиусы инерции выражаются в м в системе СИ.

Замечание: сечения элементов современных конструкций часто представляют собой некоторую композицию из материалов с разным сопротивлением упругим деформациям, характеризуемым, как известно из курса физики, модулем Юнга E. В самом общем случае неоднородного сечения модуль Юнга является непрерывной функцией координат точек сечения, т. е. E=E(z, y). Поэтому жесткость неоднородного по упругим свойствам сечения

1. Вывод формул для моментов инерции простейших фигур (прямоугольник, треугольник, круг)

Прямоугольное сечение.

Прямоугольное сечение имеет две оси симметрии, а главные центральные оси Сx и Cy проходят через середины параллельных сторон.

Главный центральный момент инерции относительно оси x

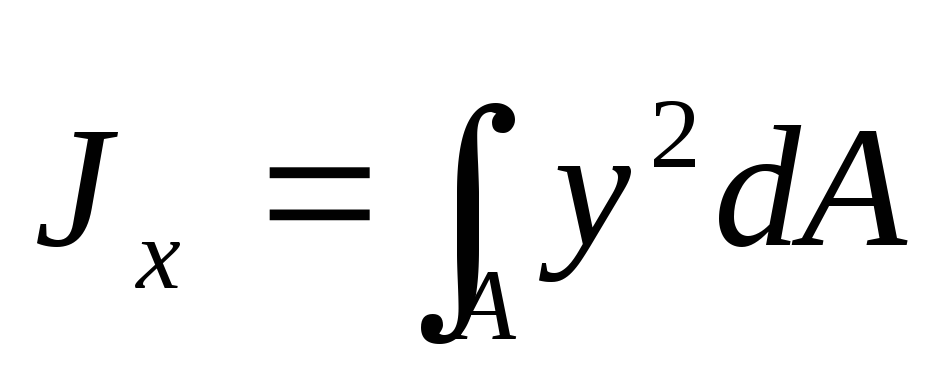
Элементарную площадку dA в этом случае можно представить в виде полоски во всю ширину сечения и толщиной dy, значит dA=b*dy. Подставим под знак интеграла значение dA и проинтегрировав по всей площади, т.е. в пределах изменения ординаты y от –h/2 до +h/2, получим

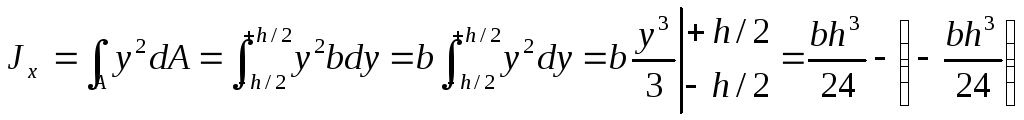
Окончательно

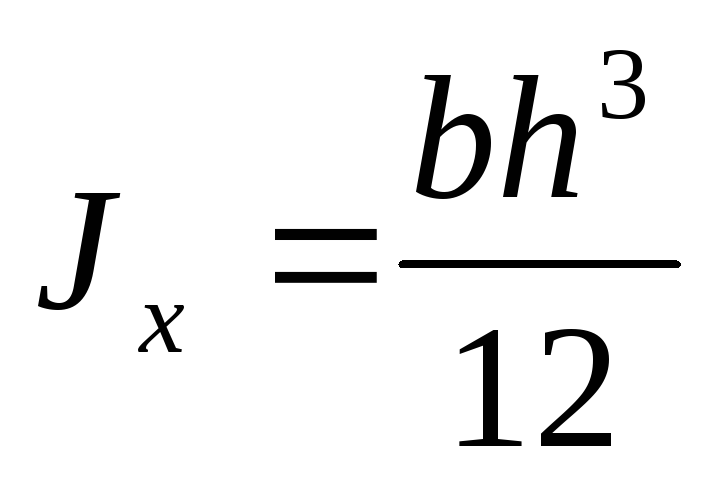
Аналогично получим формулу главного центрального момента инерции прямоугольника относительно оси y:

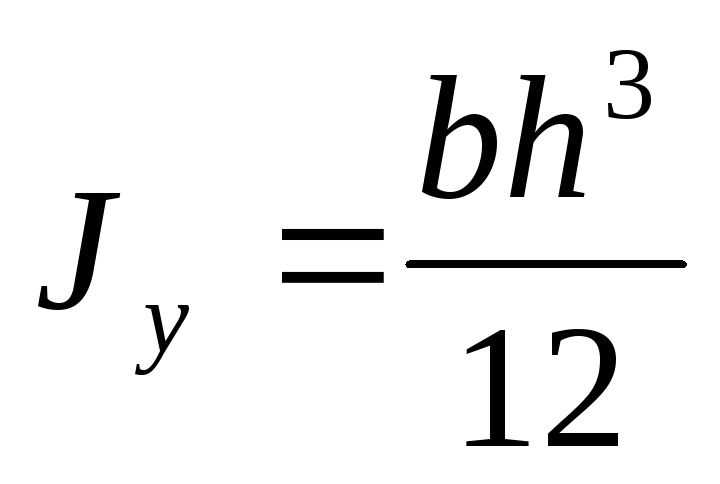
Круглое сечение

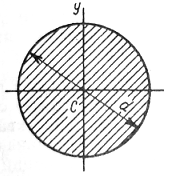
Для круга главные центральные моменты инерции относительно осей x и y равны между собой.

Поэтому из равенства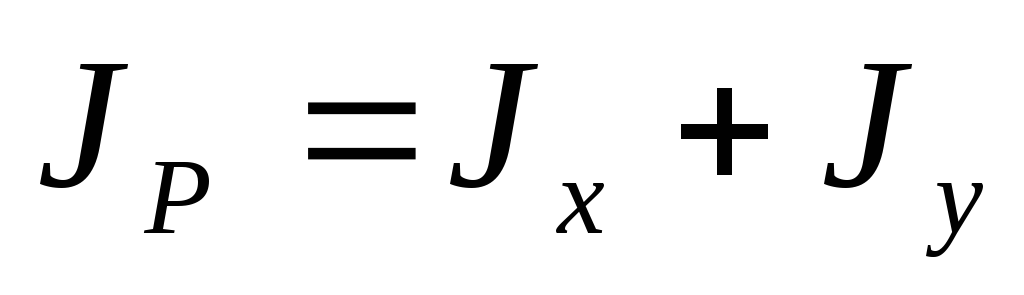

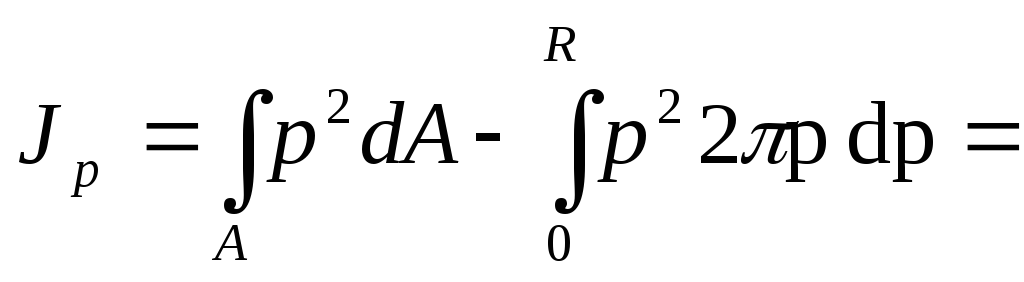
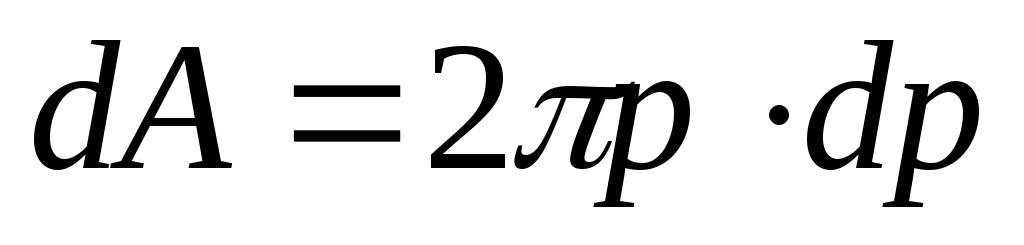
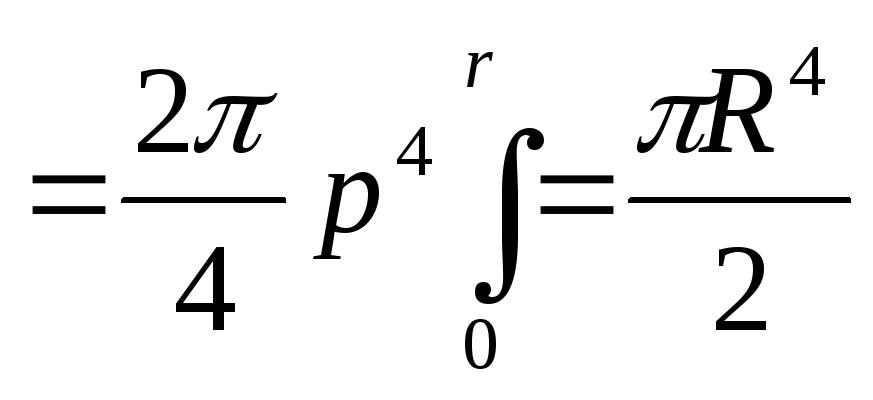
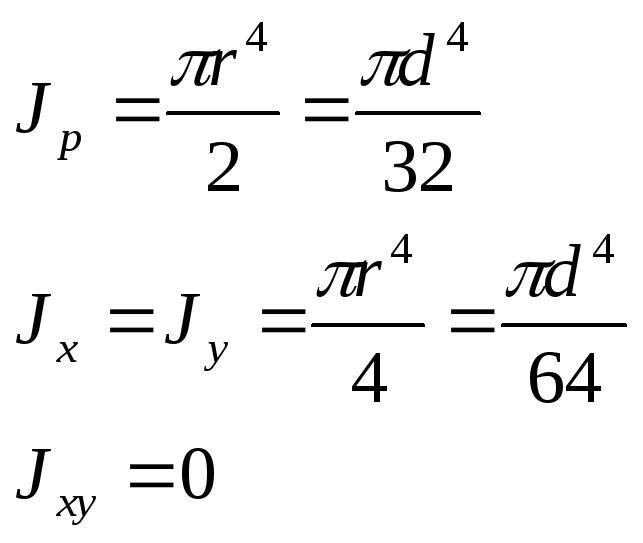
Треугольник

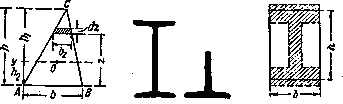
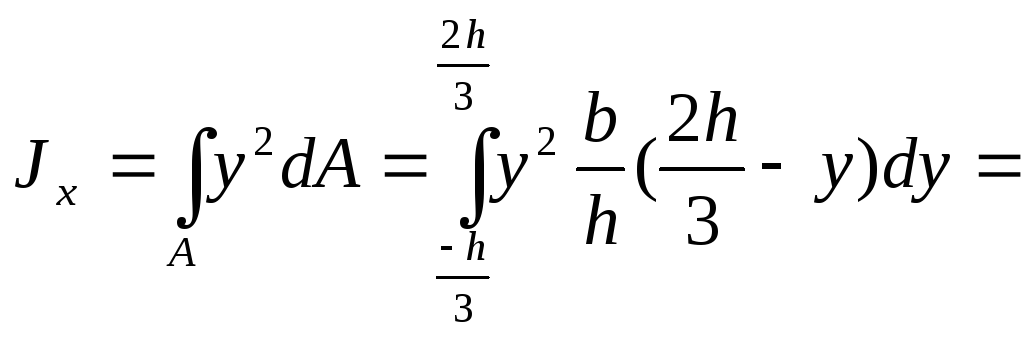
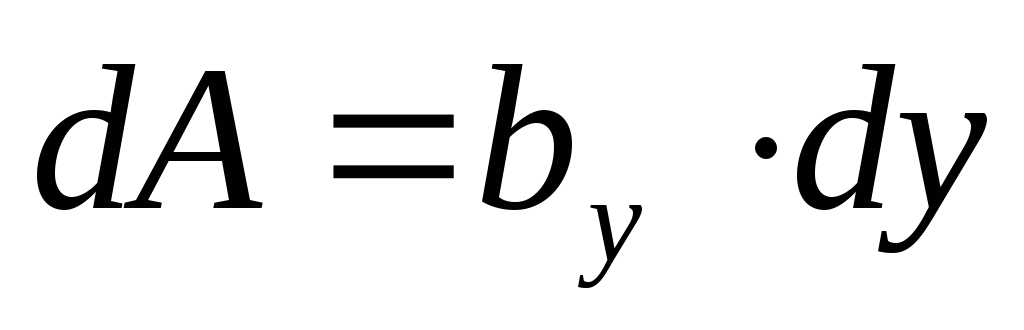
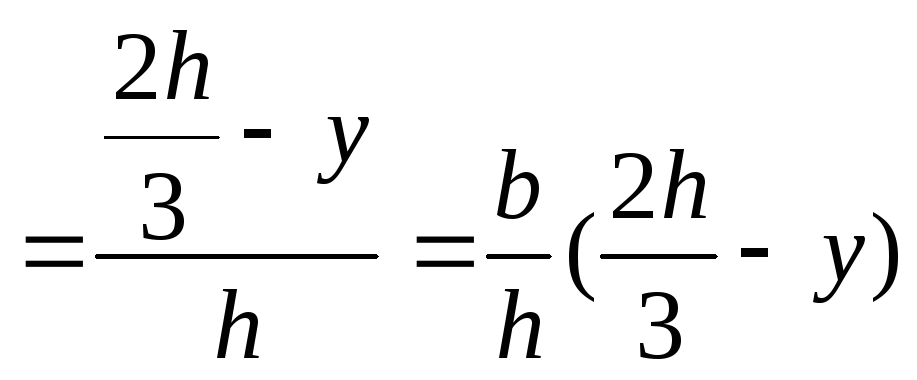
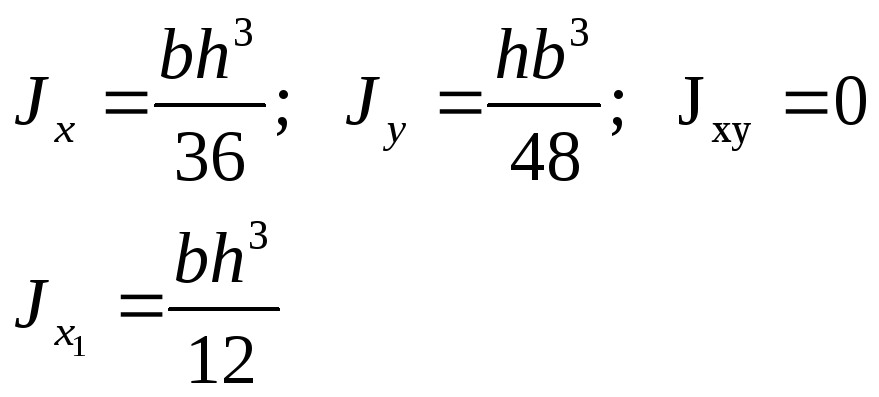
2.Изменение моментов инерции при переходе от центральных осей к параллельным:

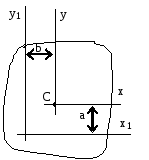
J_x1=J_x + a²А;

J_y1=J_y + b²А;

момент инерции относительно любой оси равен моменту инерции относительно центральной оси, параллельной данной, плюс произведение площади фигуры на квадрат расстояния между осями. J_y1x1=J_yx + abF; («a» и «b» подставляют в формулу с учетом их знака).

3.Изменение моментов инерции при повороте осей

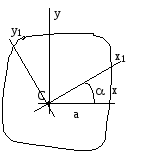
J_x1=J_xcos² + J_ysin² — J_xysin2; J_y1=J_ycos² + J_xsin² + J_xysin2;

J_x1y1=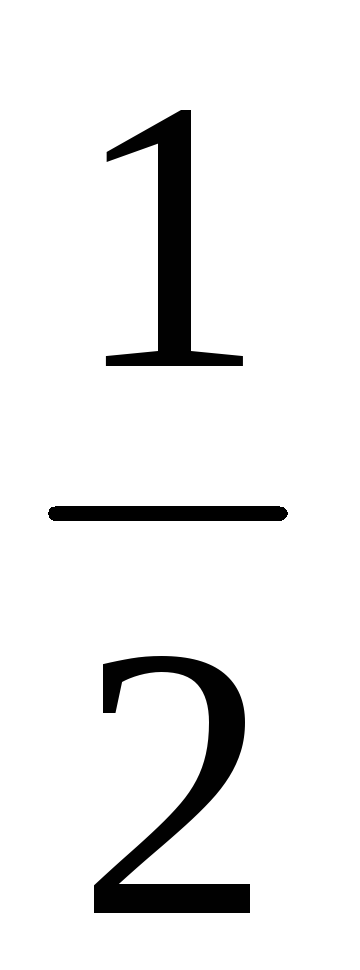(J_x — J_y)sin2 + J_xycos2 ;

Угол >0, если переход от старой системы координат к новой происходит против час.стр. J_y1 + J_x1= J_y + J_x

Экстремальные (максимальное и минимальное) значения моментов инерции называются главными моментами инерции. Оси, относительно которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси инерции взаимно перпендикулярны. Центробежные моменты инерции относительно главных осей = 0, т.е. главные оси инерции — оси, относительно которых центробежный момент инерции = 0. Если одна из осей совпадает или обе совпадают с осью симметрии, то они главные. Угол, определяющий положение главных осе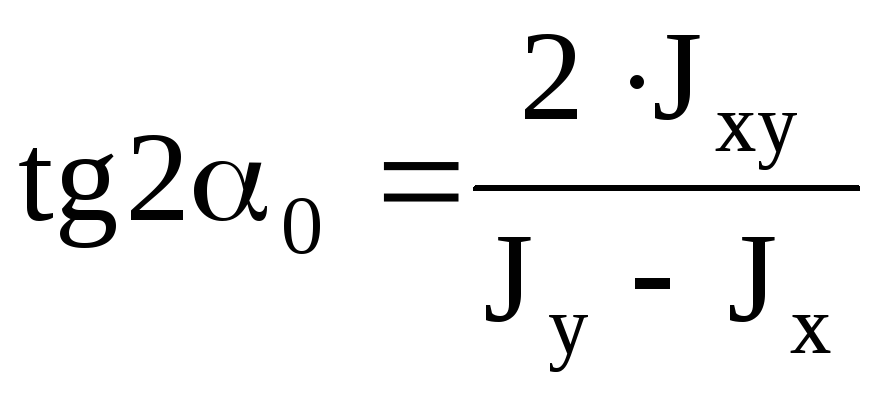й: , если

₀>0  оси поворачиваются против час.стр. Ось максимума всегда составляет меньший угол с той из осей, относительно которой момент инерции имеет большее значение. Главные оси, проходящие через центр тяжести, называются главными центральными осями инерции. Моменты инерции относительно этих осей: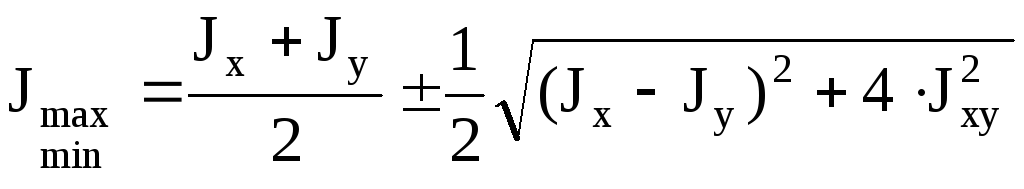

J_max + J_min= J_x + J_y. Центробежный момент инерции относительно главных центральных осей инерции равен 0. Если известны главные моменты инерции, то формулы перехода к повернутым осям:

J_x1=J_maxcos² + J_minsin²; J_y1=J_maxcos² + J_minsin²; J_x1y1=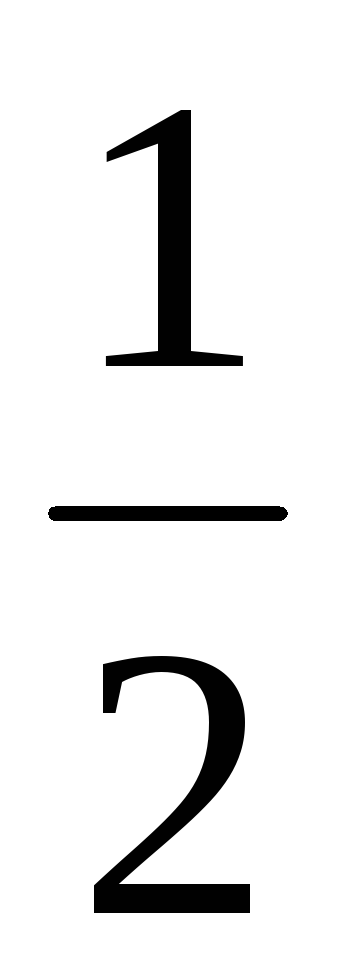(J_max — J_min)sin2;

4.Классификация элементов конструкций

Стержнем наз. Геом тела у которых один из размеров много больше других.

Пластины или оболочки – это геом тела у которых один из размеров << других

Массивные тела— все размеры одного порядка

5.Основные допущения о свойствах материала

Однородные – в люб. точке материалы имеют одинак. физико-химич. св-ва;

Сплошная среда – кристаллич. строение и микроскопич. дефекты не учитываются;

Изотропны – механич. св-ва не зависят от направления нагружения;

Идеальная упругость – полностью восстанавливают форму и размеры после снятия нагрузки.

6.Типы опор

а) Шарнирно – неподвижная (двухсвязная) опора: Воспринимает как вертикальные, так и горизонтальные усилия (усилия под углом).

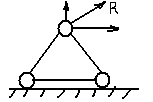
б) Шарнирно – подвижная опора – воспринимает только вертикальные нагрузки. Реакция опоры всегда направлена вдоль опорного стержня, перпендикулярно опорной поверхности

в) Жесткая заделка (трехсвязная)

Реакции в опорах определяют из условия равновесия (уравнение статики).

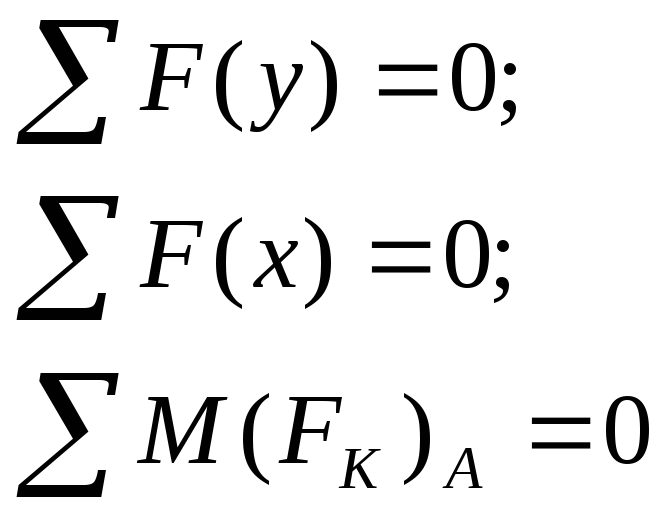
7.Классификация нагрузок

1. По месту действия

Поверхностные и объемные

а) сосредоточенная сила

б) распределенная сила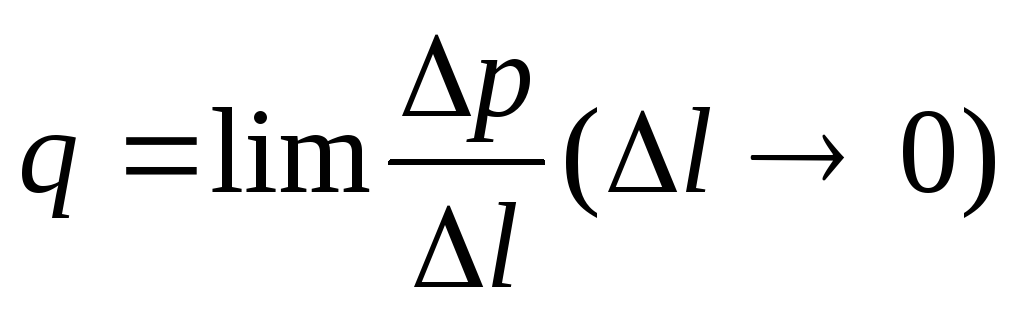

прямоугольная Rq= qa

треугольная Rq= ½ qa

в) сосредоточенный момент

изгибающий

скручивающий

г) распределенный момент

Rmz= mz a –равнодейств распр мом

2. По времени действия

Постоянные и временные

3. По характеру действия

Статические и динамические

4. По характеру возникновения

Активная(известны) и реактивная (неизвестны)

8.Основные принципы изучаемого курса

При расчете сложного сопротивления используется принцип независимости действия сил. Сложный вид нагружения представляется как система простых видов нагружения действующих независимо друг от друга. Решение при сложном сопротивлении получается в результате сложения решений полученных при простых видах нагружения.

принцип Сен-Венана

на достаточном удалении от места приложения нагрузки характер её воздействия не зависит от способа её приложения, а зависит от величины равнодействующей.

9.Внутренние усилия. Метод сечений (Метод РОЗУ)

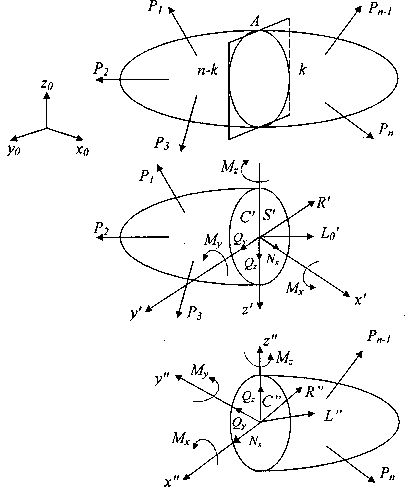
Nz=∑z (pi) нормальная с

Qx=∑x (pi) поперечная с

Qy=∑y (pi)

Mz=∑mz (pi) крутящий момент

Mx=∑mx (pi) изгибающий

My=∑my (pi)

Разрезаем мысл тело плоск

Отбрасываем одну из г внутр усил

Заменяем внутр усилиями

Уравновешив внутр ус внеш нагр

10.Правило знаков внутренних усилий

Правило знаков поперечных сил при изгибе:

Крутящий момент

Против ЧС при взгляде со стороны сеч то +

Правило знаков изгибающих моментов:

Правило проверки правильности построения эпюр нагружения:

В сечениях балки, где приложены внешние сосредоточенные нагрузки на эпюре д.б. скачёк на величину этой нагрузки.

11.Эпюры внутренних усилий

ПРИ РАСТЯЖЕНИИ-СЖАТИИ

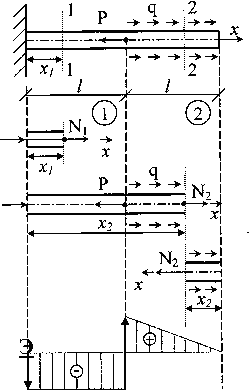
ПРИ КРУЧЕНИИ

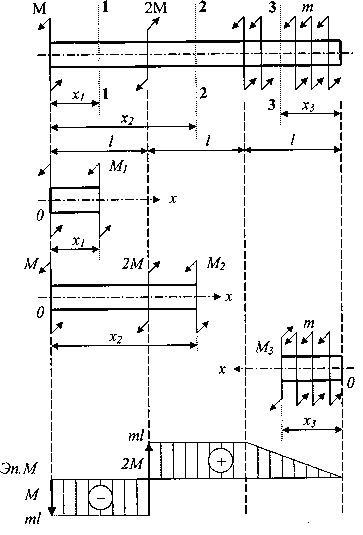
при прямом изгибе

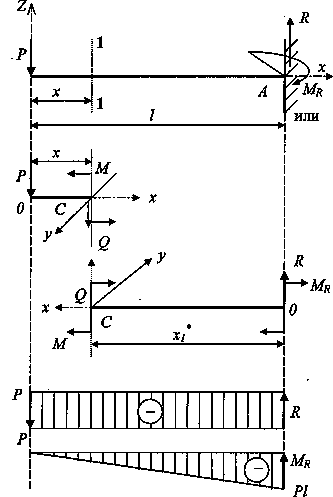
12.Дифференциальные зависимости при изгибе

; ;

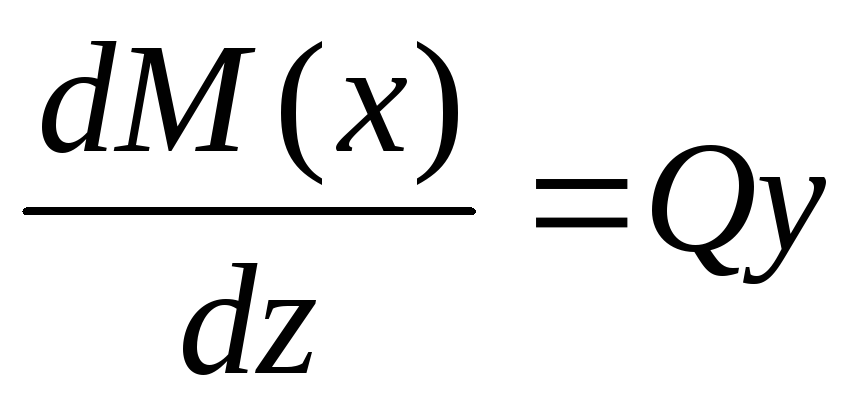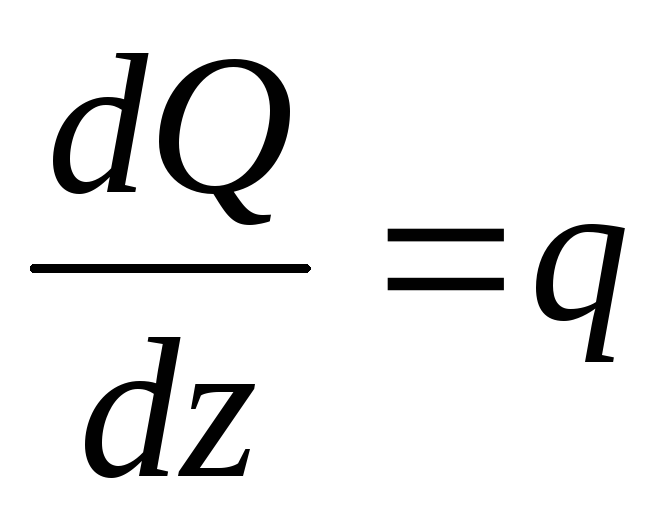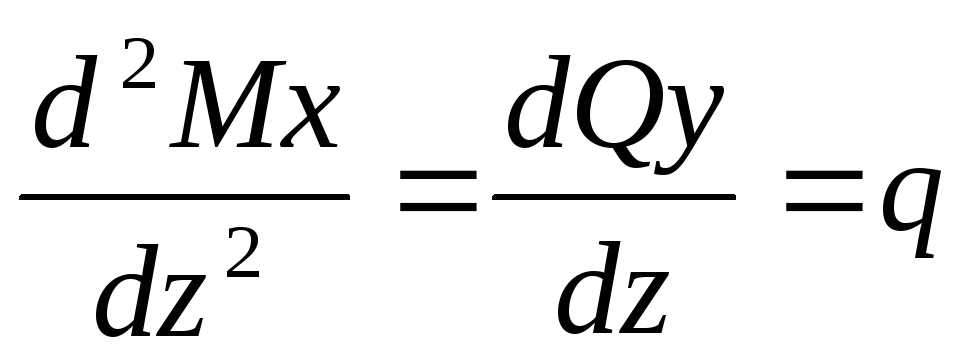
13.Следствия из дифференциальных зависимостей

1. Если на участке нет распр нагр (q=0) то поперечная сила на этом участке имеет пост вел., а эпюры изгиб мом меняются по лин закону

2. На уч на котором присутст распр нагр пост интенсивн. Поперечная сила меняется по лин зак , а эпюры по закону квадр параболы. Причем эпюра мх всегда напр навстречу распр нагрузке. Где Qy равно 0 эпюра мх имеет экстремум. Если Qy равно 0 на всем участке, то мх постоян величину

4. На участке где Qy>0 эпюра мх возрастает слева направо

5. В том сеч. где приложена сосред сила эпюра Qy имеет скачок на вел этой силы. В сеч где сосред момент эпюра мх имеет скачок на величену этого момента