Расчёт моментов инерции некоторых тел
Момент инерции тела относительно оси и относительно точки. Момент инерции материальной точки относительно оси равен произведению массы точки на квадрат расстояния точки до оси. Чтобы найти момент инерции тела (с непрерывным распределением вещества) относительно оси, надо мысленно разбить его на такие малые элементы, чтобы каждый из них можно было считать материальной точкой бесконечно малой массыdm = dV. Тогда момент инерции тела относительно оси равен интегралу по объёму тела:
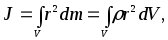(1)
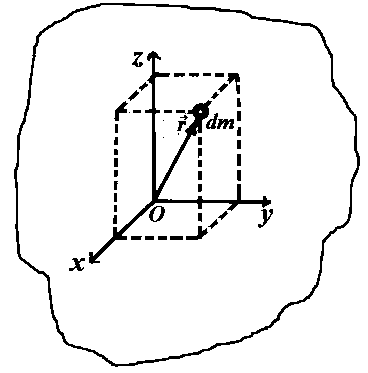
Рис. 1
Вычисление момента инерции тела относительно оси часто упрощается, если предварительно вычислить его момент инерции относительно точки .Он вычисляется по формуле, аналогичной (1):
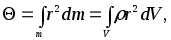(2)
где r– расстояние элементаdmдо выбранной точки (относительно которой вычисляется). Пусть эта точка является началом системы координатX, Y, Z(рис. 1). Квадраты расстояний элементаdmдо координатных осейX, Y, Z
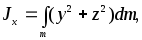
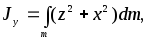
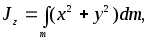
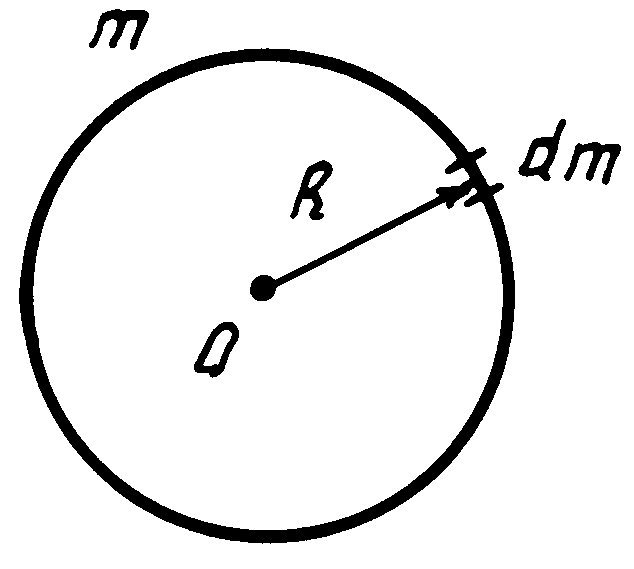
Рис. 2
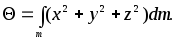
Из этих соотношений следует, что
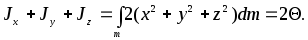(3)
Таким образом, сумма моментов инерции тела относительно трёх любых взаимно перпендикулярных осей , проходящих через одну точку, равна удвоенному моменту инерции тела относительно этой точки.
Момент инерции тонкого кольца.Все элементы кольцаdm(рис. 2) находятся на одинаковом расстоянии, равном радиусу кольцаR,от его оси симметрии (осьY) и от его центра. Момент инерции кольца относительно осиY
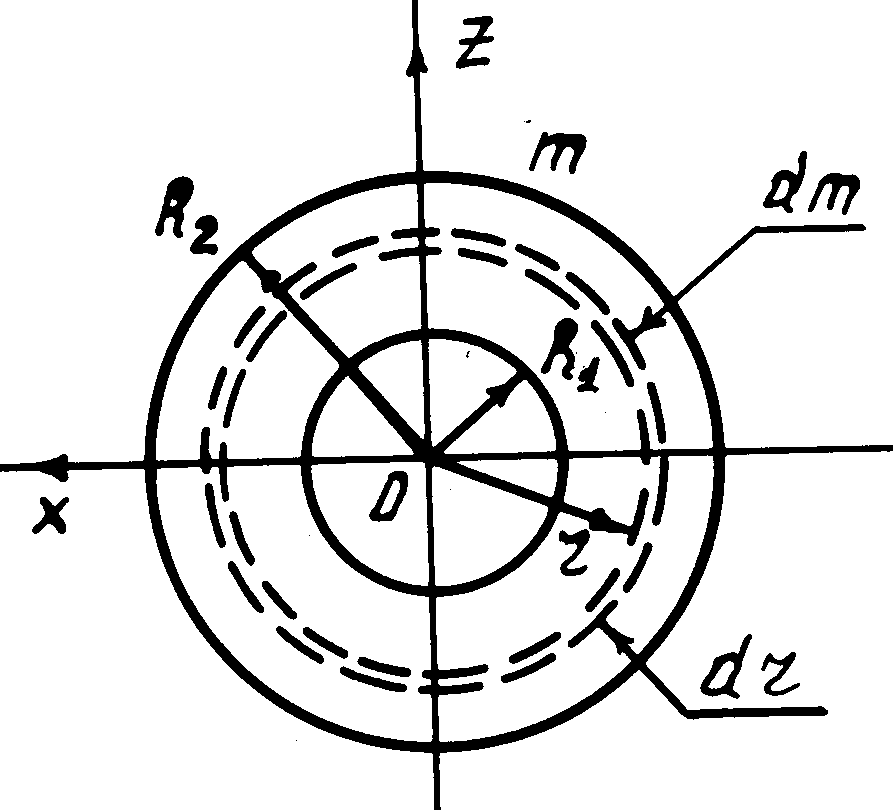
Рис. 3
(4)Момент инерции тонкого диска.Пусть тонкий однородный диск массыmс концентрическим отверстием (рис. 3) имеет внутренний и внешний радиусыR1
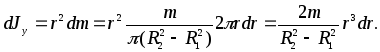(5)
Момент инерции
диска:
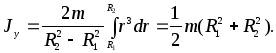(6)
В частности, полагая в (6) R1 = 0, R2
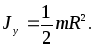(7)
Момент инерции диска относительно его оси симметрии не зависит от толщины диска. Поэтому по формулам (6) и (7) можно вычислять моменты инерции соответствующих цилиндров относительно их осей симметрии.
Момент инерции тонкого диска относительно его центра также вычисляется по формуле (6), = Jy,а моменты инерции относительно осейXиZравны между собой,J
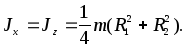(8)
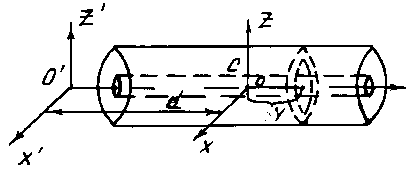
Рис. 4
Момент инерции цилиндра.Пусть имеется полый симметричный цилиндр массыm, длины h, внутренний и внешний радиусы которого равны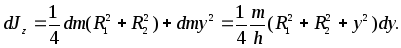 
(9)
Момент инерции всего цилиндра
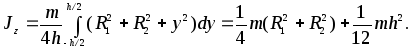(10)
Момент инерции цилиндра относительно оси Z(оси вращения маятника) найдём по теореме Гюйгенса – Штейнера
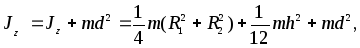
где d– расстояние от центра масс цилиндра до осиZ. В работе 16 этот момент инерции обозначен какJц
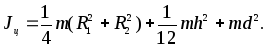
МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Нанесение экспериментальных точек и проведение по ним графика «на глаз», а также определение по графику абсцисс и ординат точек, не отличаются высокой точностью. Её можно повысить, если использовать аналитический метод. Математическое правило построения графика заключается в подборе таких значений параметров «а» и «в» в линейной зависимости вида у = ах + b, чтобы сумма квадратов отклонений уi (рис. 5) всех экспериментальных точек от линии графика была наименьшей (метод «наименьших квадратов»), т.е. чтобы величина
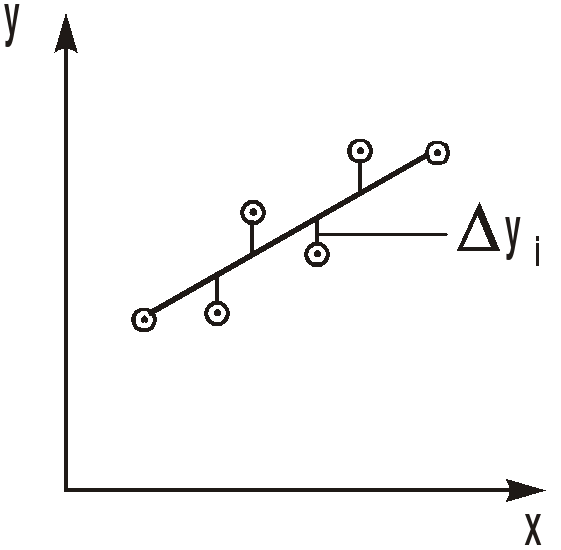
Рис. 5
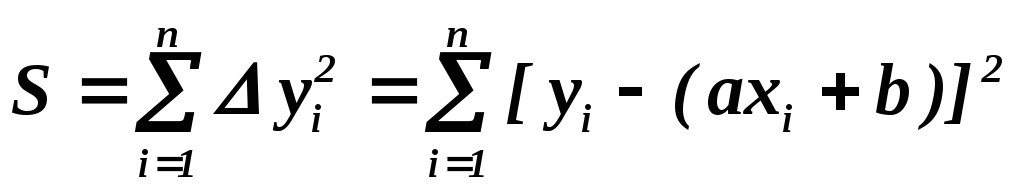(1)
имела минимум. Здесь xi и yi значения величин х и у в i-том измерении, n количество измерений. Величина S будет минимальной, если её частные производные по параметрам а и b будут равны нулю:
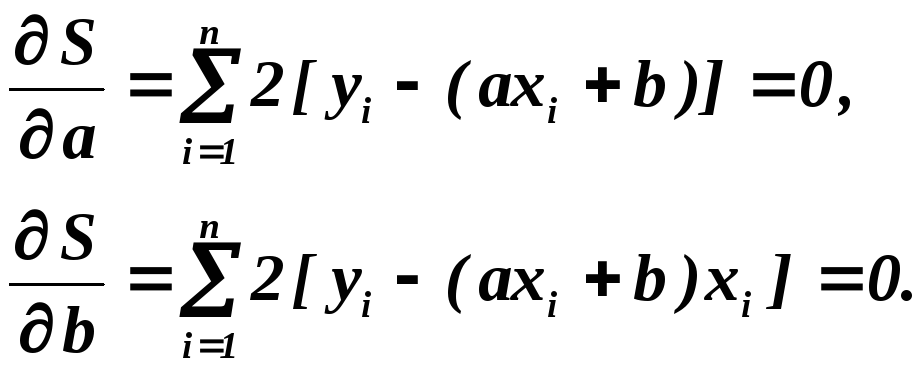
(2)Отсюда наилучшие значения параметров «а» и «b» равны:
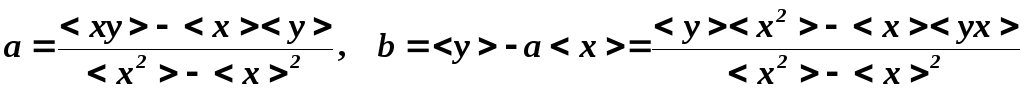(3)
где средние
значения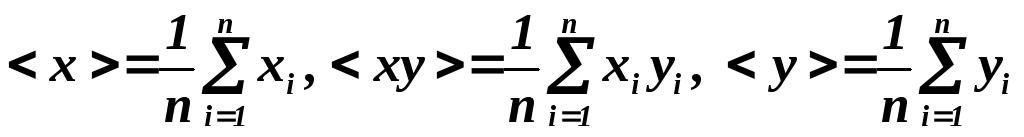 
,
.
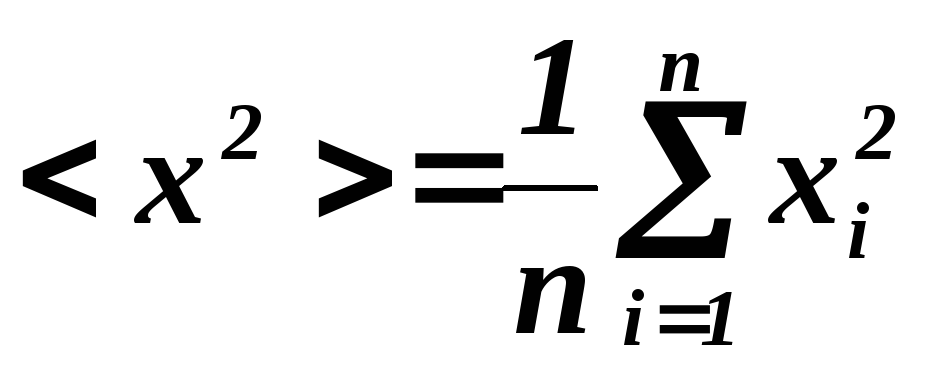Введем обозначения
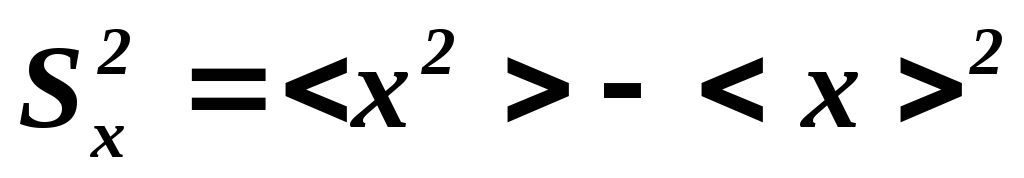
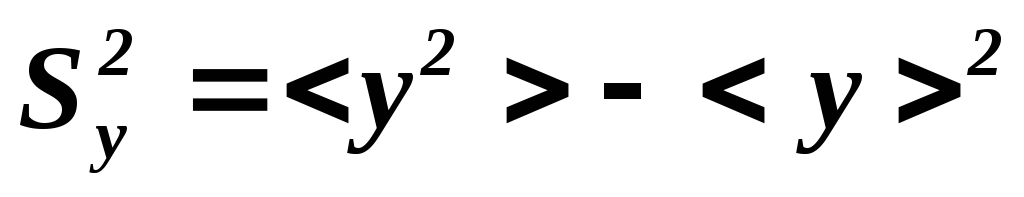(4)Абсолютные случайные погрешности асл и bсл определяются по формулам:
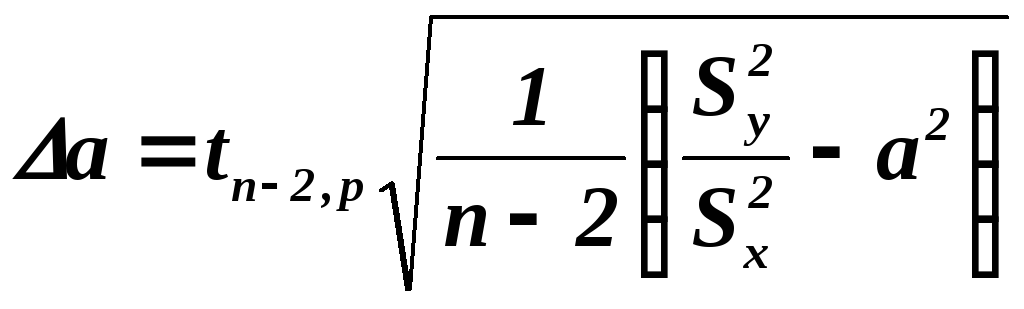и 
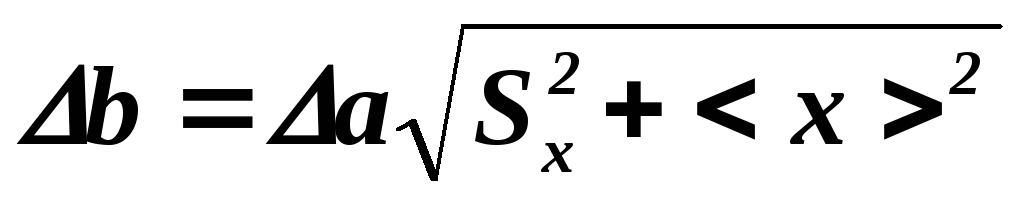(5)
где tp,n-2 коэффициент Стьюдента для доверительной вероятности P и (n-2) измерений. При P = 0,95 и n 12-15 коэффициент tp,n-2 = 2,25, а при P = 0,997 и тех же значениях n коэффициент tp,n-2 = 3,25.
16
V. Вывод формулы для определения момента инерции.
Пусть при вращении диск поднялся, на высоту h =h1 — h2 (рис. 1). Тогда приращение потенциальной энергии равно
.
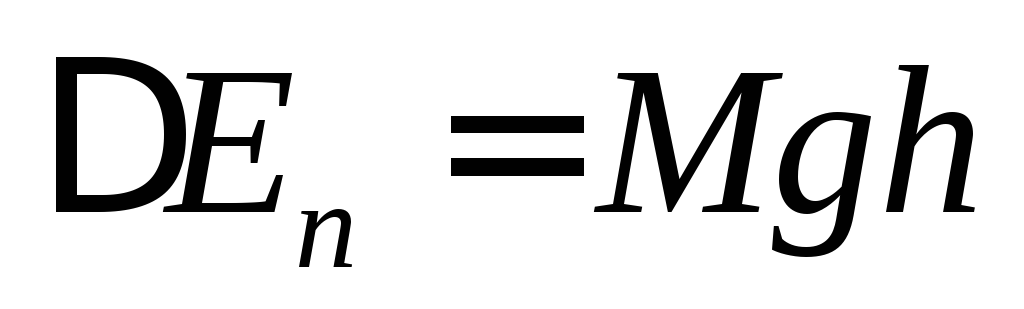При опускании нижнего диска потенциальная энергия переходит в кинетическую энергию вращательного движения
,
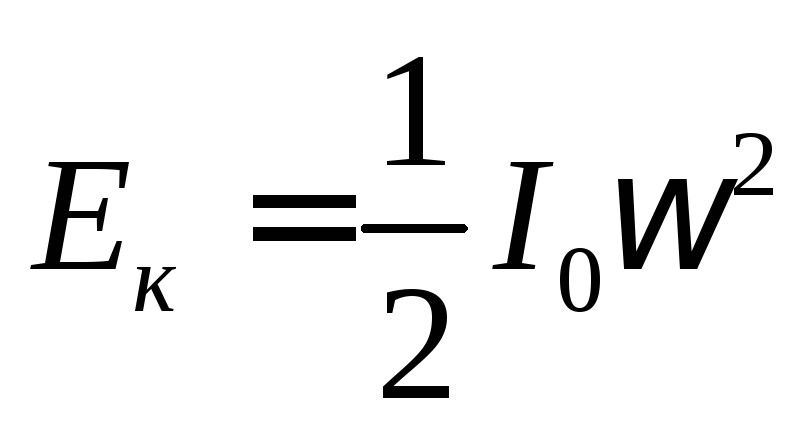где I0 — момент инерции нижнего диска, — угловая скорость диска.
В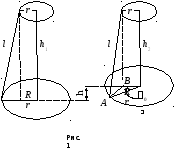
момент прохождения диском положения
равновесия угловая скорость,
а, следовательно, и кинетическая энергия,
принимает максимальное значение, т.е. = 0.
Если пренебречь трением, то на основании закона сохранения энергии для колеблющегося диска можно записать:
.
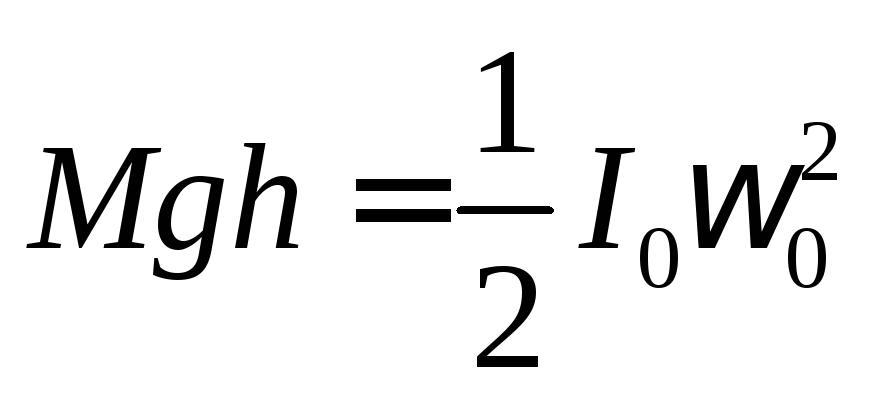(2)
Угловая скорость , являющаяся первой производной от смещения по времени, может быть записана
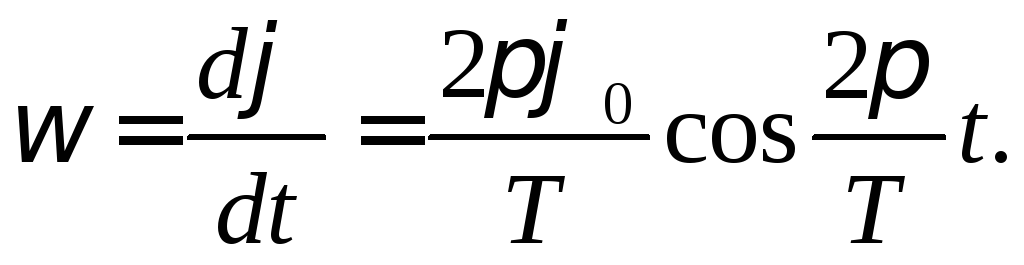
Максимальное значение угловой скорости равно:
.
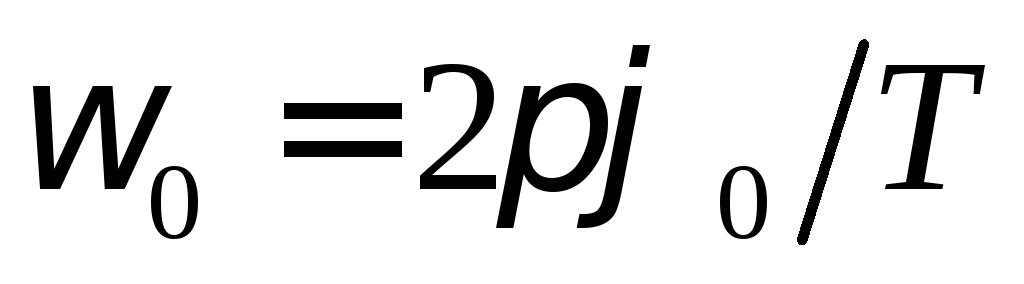(3)
На основании выражений (2) и (3) имеем:
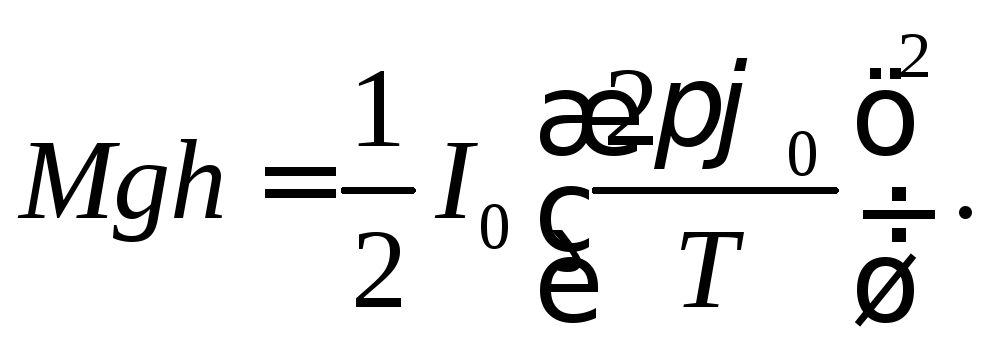(4)
Найдем величину h при повороте диска на малый угол 0, считая, что h1 + h2 2l:
.
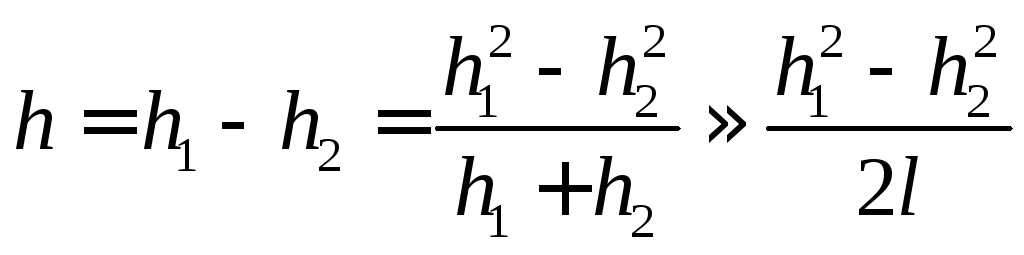(5)
Из рис.1 ясно, что
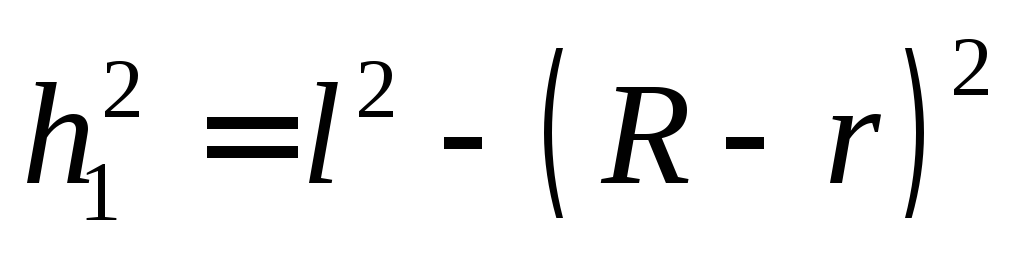и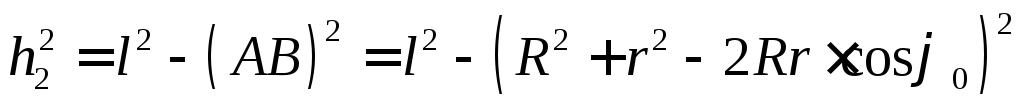 
.
Подставляя
значение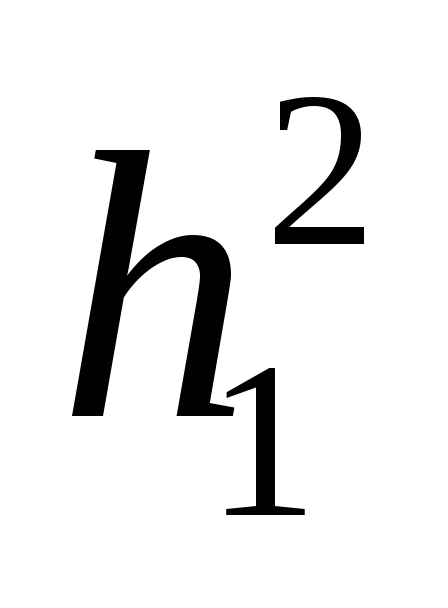 
и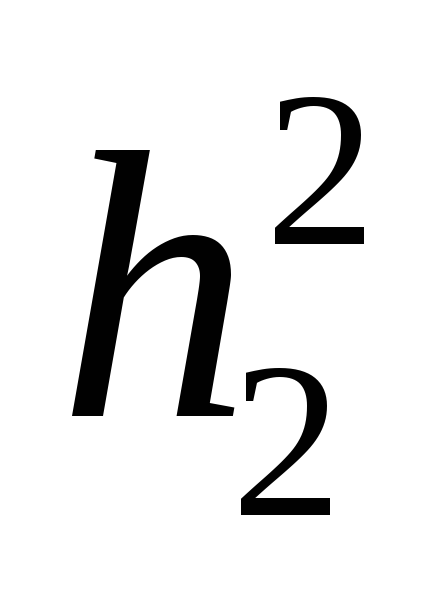 
в (5), получим:
.
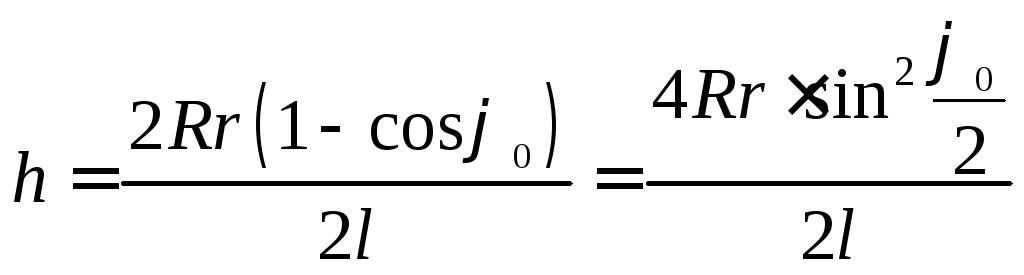Вследствие малости угла 0 синус можно заменить аргументом:
.
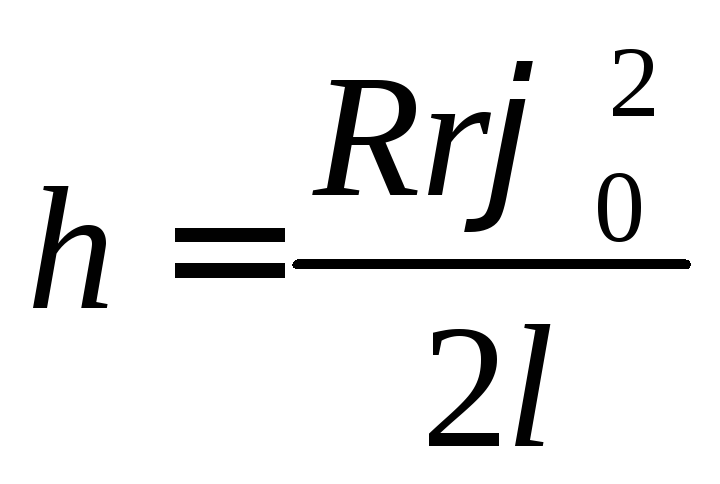(6)
Подставив выражения (3) и (6) в формулу (2), получим:
,
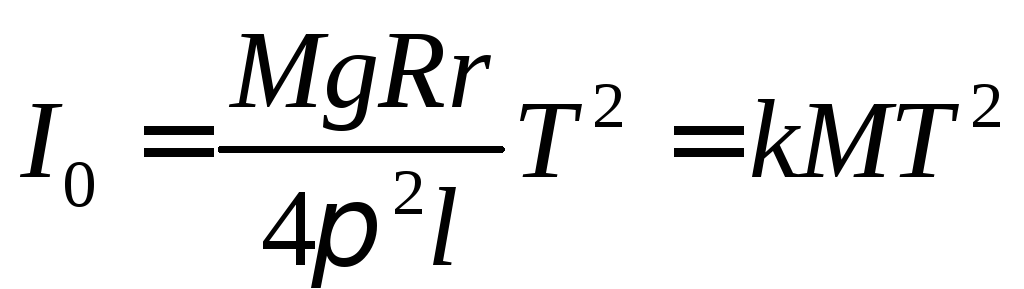или
,
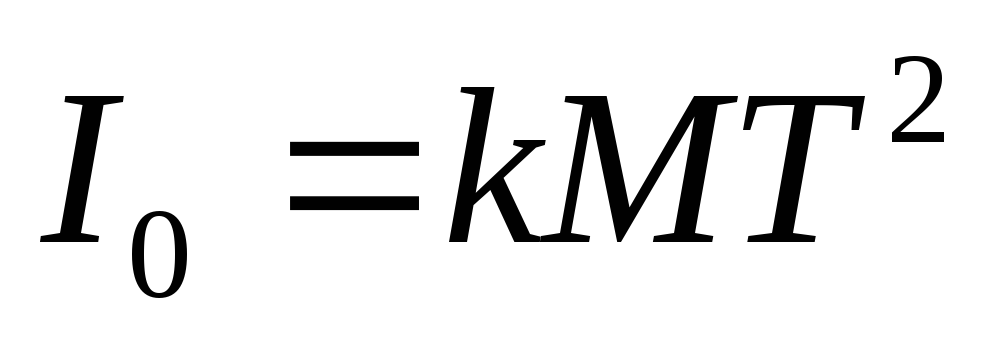(7)
где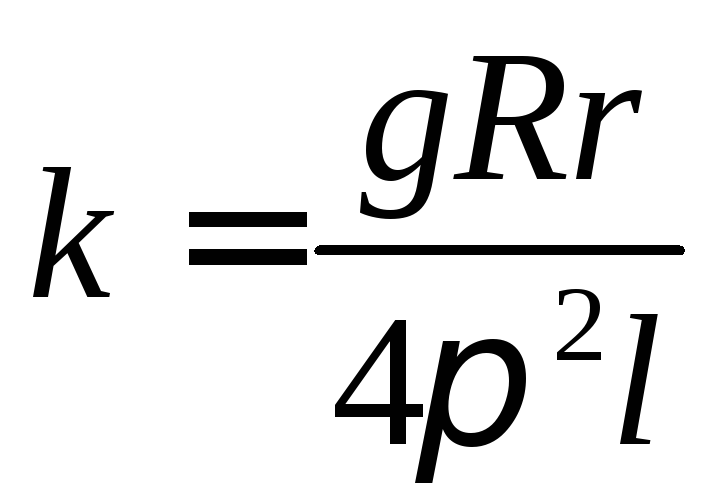 
— постоянная установки.
IV. Порядок выполнения лабораторной работы
1. Определение момента инерции i0 диска без нагрузки.
а) Заставить диск совершать крутильные колебания с малой амплитудой (10 15 градусов). Секундомером измерить времяtсовершенияnполных колебаний (n– задаётся преподавателем). Все измерения провести несколько раз. Все значения занести в табл.1.
б) Провести статистическую обработку времени t по методу Стьюдента.
в) Определить период колебаний диска Т = t /n, занести данные в таблицу 1.
г) Занести в табл.2 массу диска М и постоянную установкиk.
д) По формуле (7) рассчитать значение момента инерции диска I0, результат занести в таблицу 2.
е) Вычислить относительные и абсолютные погрешности по формулам (8) – (9) и занести результаты в таблицу 3.
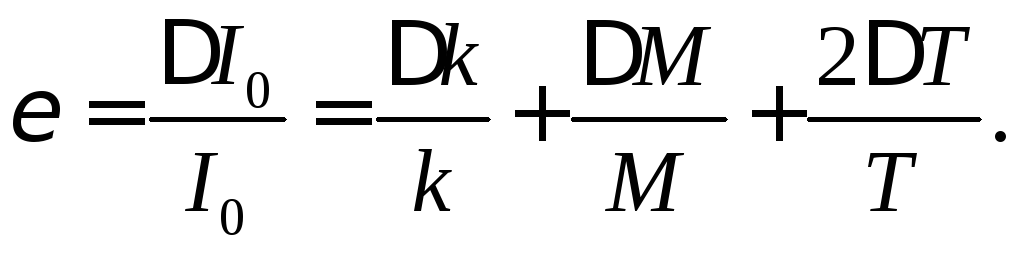(8)
.
(9)
Абсолютная погрешность периода колебаний определяется следующим образом
.
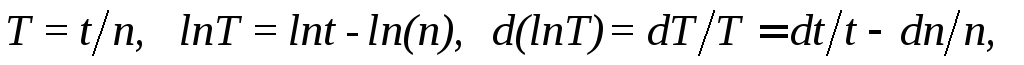
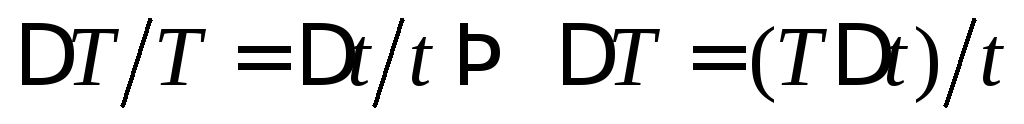Таблица 1
№/№ п/п | t | t | t2 | Sn | t(,n) | tсл | tпр | t | n | T | T |
с | с | с2 | с | – | с | c | с | – | с | с | |
1 | |||||||||||
2 | |||||||||||
3 | |||||||||||
… | |||||||||||
cреднее |
Таблица 2
k | M | m | d | I0 | I1 | I2 | I3 | |
м2с–2 | кг | кг | м | кгм2 | кгм2 | кгм2 | кгм2 | |
Среднее значение | ||||||||
Абсолютная погрешность | 510-4 | |||||||
Относительная погрешность |
Осевые моменты инерции некоторых тел
Осевые моменты инерции некоторых тел
Моменты инерции однородных тел простейшей формы относительно некоторых осей вращения | |||
Тело | Описание | Положение оси a | Момент инерции Ja |
Материальная точка массы m | На расстоянии r от точки, неподвижная | ||
Полый тонкостенный цилиндр или кольцо радиуса r и массы m | Ось цилиндра | ||
Сплошной цилиндр или диск радиуса r и массы m | Ось цилиндра | ||
Полый толстостенный цилиндр массы m с внешним радиусом r2 и внутренним радиусом r1 | Ось цилиндра | ||
Сплошной цилиндр длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | ||
Полый тонкостенный цилиндр (кольцо) длины l, радиуса r и массы m | Ось перпендикулярна к цилиндру и проходит через его центр масс | ||
Прямой тонкий стержень длины l и массы m | Ось перпендикулярна к стержню и проходит через его центр масс | ||
Тонкостенная сфера радиуса r и массы m | Ось проходит через центр сферы | ||
Шар радиуса r и массы m | Ось проходит через центр шара | ||
Конус радиуса r и массы m | Ось конуса | ||
Равнобедренный треугольник с высотой h, основанием a и массой m | Ось перпендикулярна плоскости треугольника и проходит через вершину | ||
Правильный треугольник со стороной a и массой m | Ось перпендикулярна плоскости треугольника и проходит через центр масс | ||
Квадрат со стороной a и массой m | Ось перпендикулярна плоскости квадрата и проходит через центр масс | ||
Вывод формул
Тонкостенный цилиндр (кольцо, обруч)
Момент инерции тела равен сумме моментов инерции составляющих его частей. Разобъём тонкостенный цилиндр на элементы с массой dm и моментами инерции dJi. Тогда
Поскольку все элементы тонкостенного цилиндра находятся на одинаковом расстоянии от оси вращения, формула (1) преобразуется к виду
Толстостенный цилиндр (кольцо, обруч)
Пусть имеется однородное кольцо с внешним радиусом R, внутренним радиусом R1, толщиной h и плотностью ρ. Разобьём его на тонкие кольца толщиной dr. Масса и момент инерции тонкого кольца радиуса r составит
Момент инерции толстого кольца найдём как интеграл
Поскольку объём и масса кольца равны
получаем окончательную формулу для момента инерции кольца
Однородный диск (сплошной цилиндр)
Рассматривая цилиндр (диск) как кольцо с нулевым внутренним радиусом (R1 = 0), получим формулу для момента инерции цилиндра (диска):
Сплошной конус
Разобьём конус на тонкие диски толщиной dh, перепендикулярные оси конуса. Радиус такого диска равен
где R – радиус основания конуса, H – высота конуса, h – расстояние от вершины конуса до диска. Масса и момент инерции такого диска составят
Интегрируя, получим
Сплошной однородный шар
Разобъём шар на тонкие диски толщиной dh, перпендикулярные оси вращения. Радиус такого диска, расположенного на высоте h от центра сферы, найдём по формуле
Масса и момент инерции такого диска составят
Момент инерции сферы найдём интегрированием:
Тонкостенная сфера
Для вывода воспользуемся формулой момента инерции однородного шара радиуса R:
Вычислим, насколько изменится момент инерции шара, если при неизменной плотности ρ его радиус увеличится на бесконечно малую величину dR.
Тонкий стержень (ось проходит через центр)
Разобъём стержень на малые фрагменты длиной dr. Масса и момент инерции такого фрагмента равна
Интегрируя, получим
Тонкий стержень (ось проходит через конец)
При перемещении оси вращения из середины стержня на его конец, центр тяжести стержня перемещается относительно оси на расстояние l/2. По теореме Штейнера новый момент инерции будет равен
V. Вывод формулы для определения момента инерции.
Пусть при вращении диск поднялся, на высоту h =h1 — h2 (рис. 1). Тогда приращение потенциальной энергии равно
.
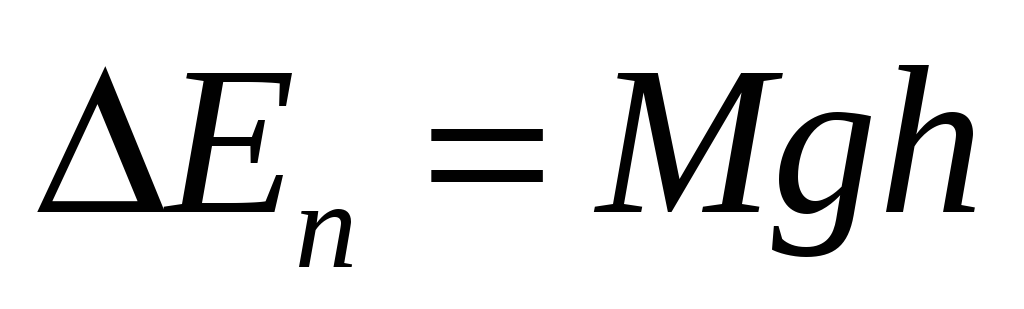При опускании нижнего диска потенциальная энергия переходит в кинетическую энергию вращательного движения
,
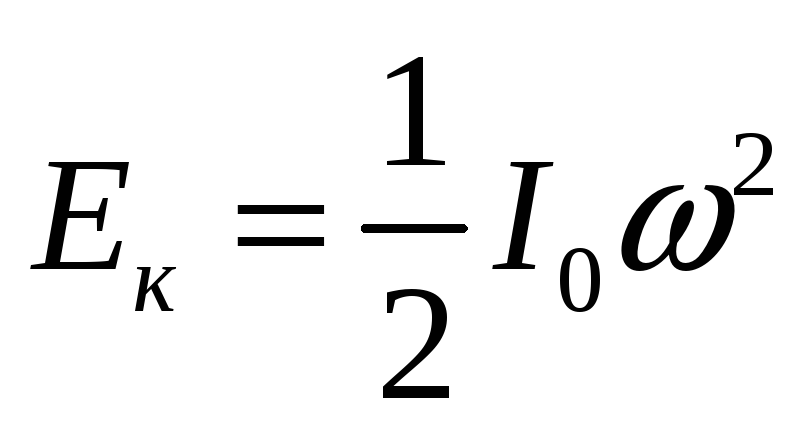где I0 — момент инерции нижнего диска, — угловая скорость диска.
В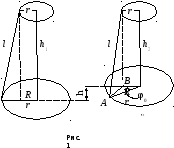
момент прохождения диском положения
равновесия угловая скорость ,
а, следовательно, и кинетическая энергия,
принимает максимальное значение, т.е. = 0.
Если пренебречь трением, то на основании закона сохранения энергии для колеблющегося диска можно записать:
.
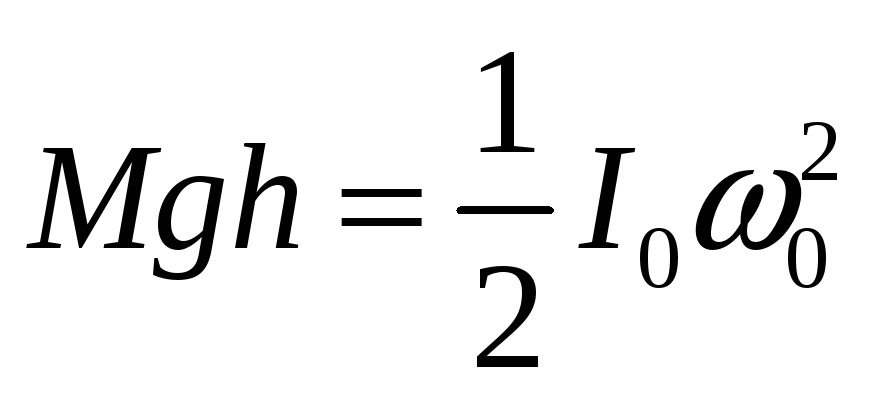(2)
Угловая скорость , являющаяся первой производной от смещения по времени, может быть записана
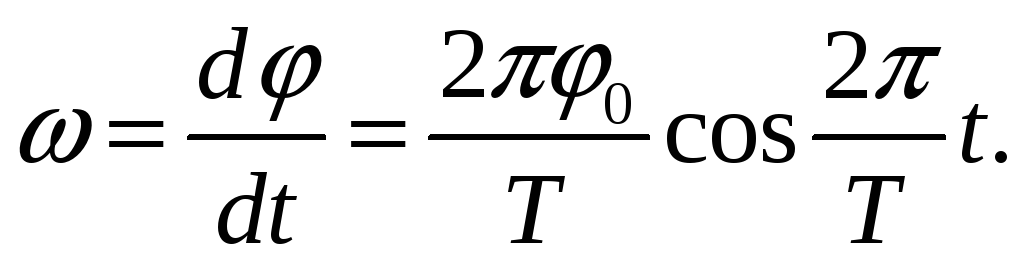
Максимальное значение угловой скорости равно:
.
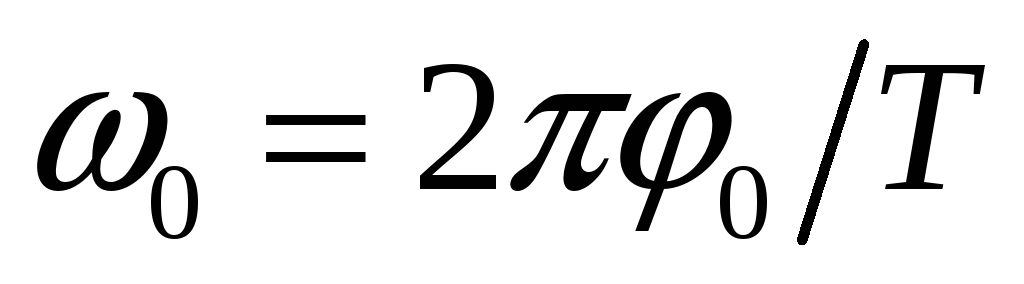(3)
На основании выражений (2) и (3) имеем:
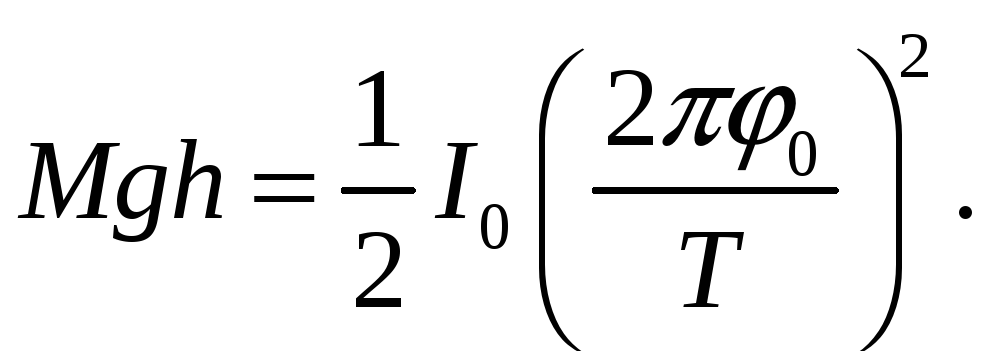(4)
Найдем величину h при повороте диска на малый угол 0, считая, что h1 + h2 2l:
.
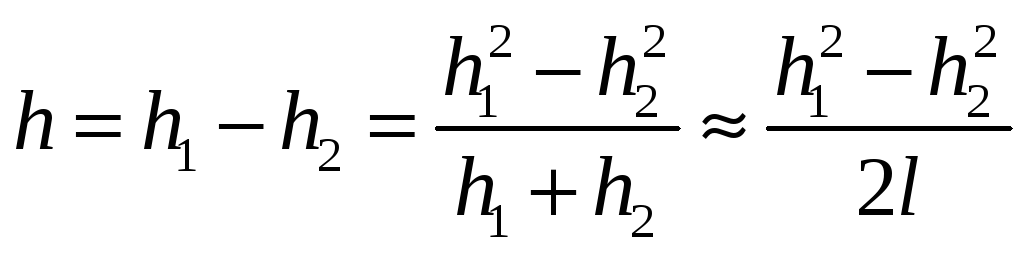(5)
Из рис.1 ясно, что
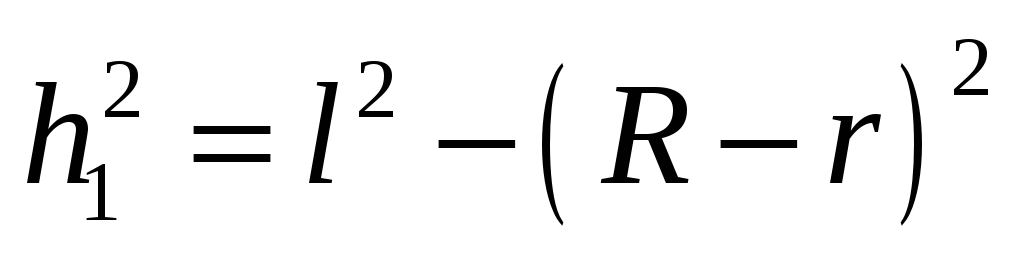и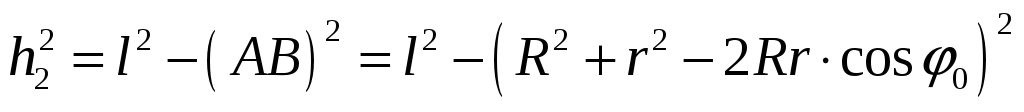 
.
Подставляя
значение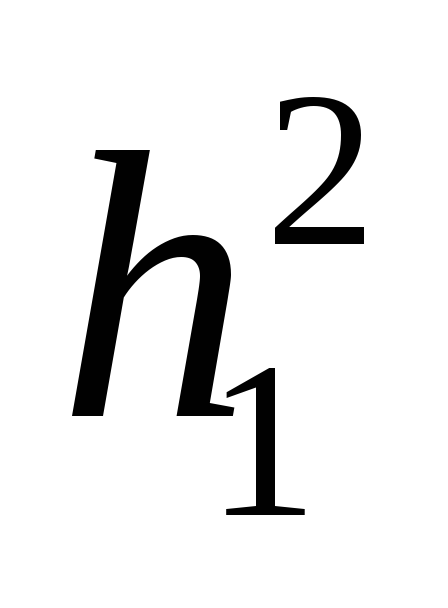 
и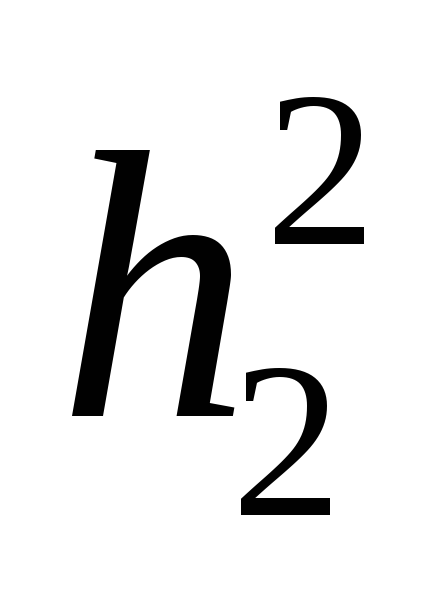 
в (5), получим:
.
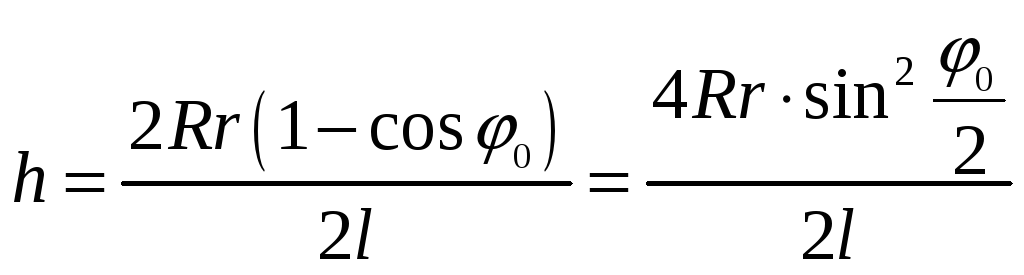Вследствие малости угла 0 синус можно заменить аргументом:
.
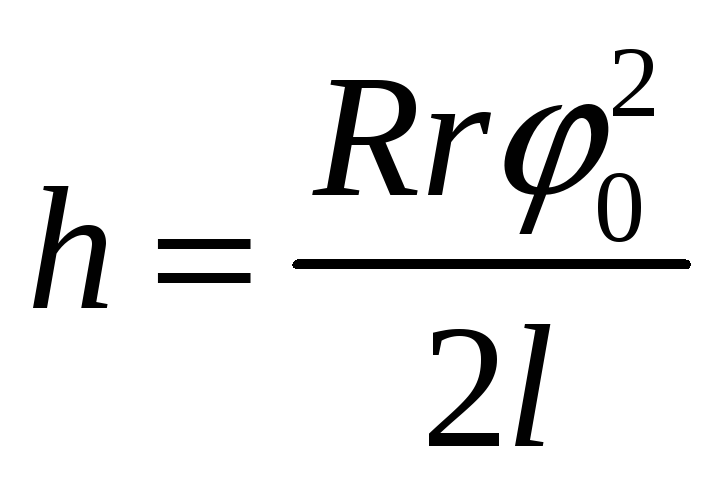(6)
Подставив выражения (3) и (6) в формулу (2), получим:
,
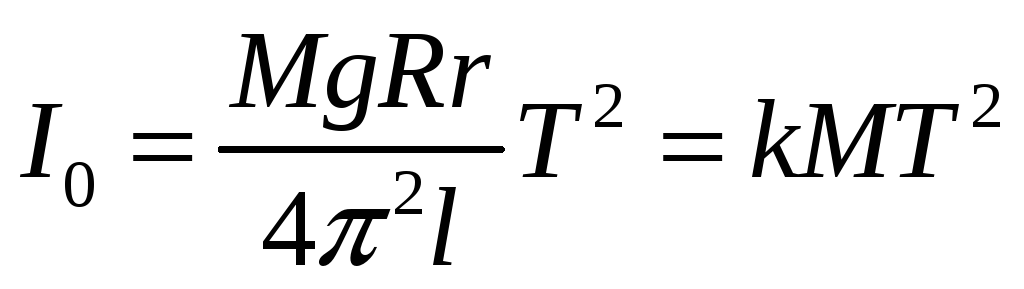или
,
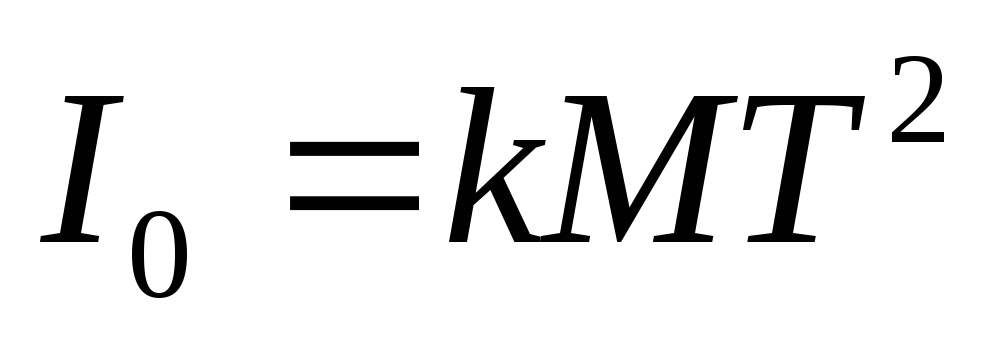(7)
где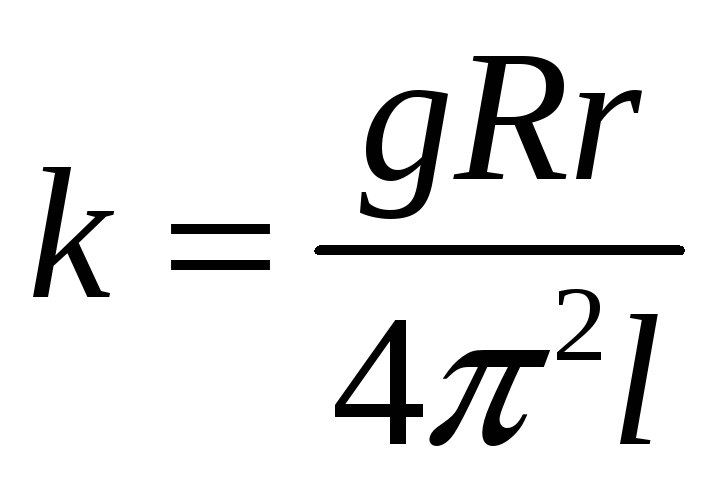 
— постоянная установки.
IV. Порядок выполнения лабораторной работы
1. Определение момента инерции i0 диска без нагрузки.
а) Заставить диск совершать крутильные колебания с малой амплитудой (10 15 градусов). Секундомером измерить время t совершения n полных колебаний (n – задаётся преподавателем). Все измерения провести несколько раз. Все значения занести в табл.1.
б) Провести статистическую обработку времени t по методу Стьюдента.
в) Определить период колебаний диска Т = t /n, занести данные в таблицу 1.
г) Занести в табл.2 массу диска М и постоянную установки k.
д) По формуле (7) рассчитать значение момента инерции диска I0, результат занести в таблицу 2.
е) Вычислить относительные и абсолютные погрешности по формулам (8) – (9) и занести результаты в таблицу 3.
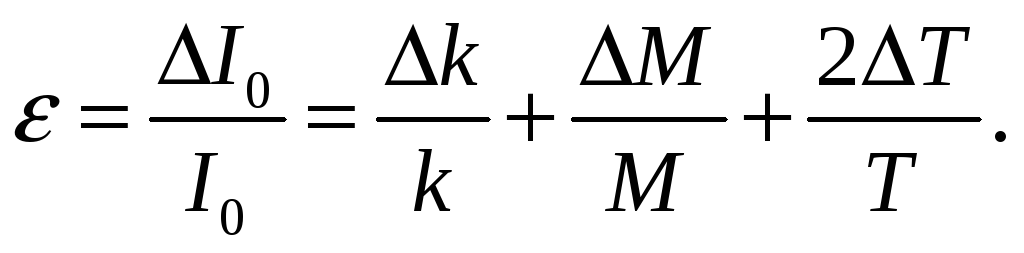(8)
.
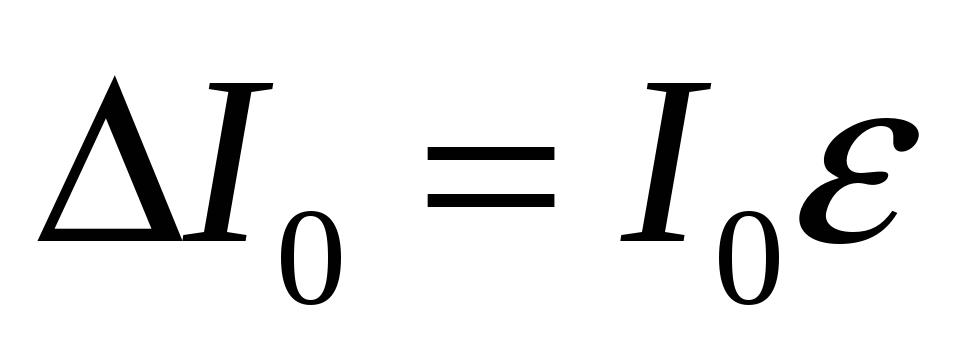(9)
Абсолютная погрешность периода колебаний определяется следующим образом
.
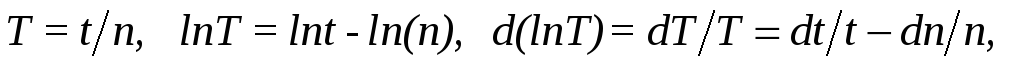
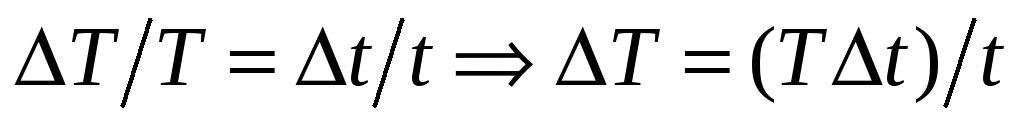Таблица 1
№/№ п/п | t | t | t2 | Sn | t(,n) | tсл | tпр | t | n | T | T |
с | с | с2 | с | – | с | c | с | – | с | с | |
1 | |||||||||||
2 | |||||||||||
3 | |||||||||||
… | |||||||||||
cреднее |
Таблица 2
k | M | m | d | I0 | I1 | I2 | I3 | |
м2с–2 | кг | кг | м | кгм2 | кгм2 | кгм2 | кгм2 | |
Среднее значение | ||||||||
Абсолютная погрешность | 510-4 | |||||||
Относительная погрешность |
Момент инерции цилиндра, теория и примеры
Это скалярная (в общем случае тензорная) величина. Для непрерывного однородного тела, вращающегося около оси, момент инерции определяют как:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.
Для получения формулы расчета момента инерции однородного цилиндра, мы его представим как совокупность бесконечно тонких дисков, а диск, в свою очередь – совокупность бесконечно тонких колец. Поэтому мы сначала получим выражение для момента инерции кольца, затем диска и только в самом окончании цилиндра.
Момент инерции тонкого кольца
Пусть кольцо имеем радиус R. Его называют бесконечно тонким, если его ширина и толщина много меньше радиуса. Пусть кольцо вращается относительно оси Z, перпендикулярной плоскости кольца и проходит через центр кольца (рис.1).
Выделим на кольце элементарную массу (), – плотность кольца; – элементарный объем кольца. Для нахождения момента инерции кольца нам следует найти интеграл (1). Все элементарные массы находятся на одном расстоянии от оси, то есть распределение массы кольца имеет цилиндрическую (осевую) симметрию.
Момент инерции бесконечно тонкого однородного диска
Пусть диск имеет радиус R. Он вращается относительно оси, которая проходит через его центр инерции, перпендикулярно его плоскости. Диск представим как систему бесконечно тонких колец, радиусы которых изменяются от нуля до R. Одно из таких колец изображено на рис.2.
Так как момент инерции тонкого кольца мы уже нашли, то его возьмем за элементарный:
где – масса выделенного кольца, равная:
Найдем момент инерции бесконечно тонкого диска, учитывая: :
массу бесконечно тонкого диска можно считать равной:
тогда момент инерции диска равен:
Момент инерции цилиндра
Для того, чтобы найти момент инерции однородного цилиндра, вращающегося относительно своей оси, представим его как совокупность дисков, толщиной . Формула (7) справедлива для диска имеющего толщину, поэтому в качестве элементарной массы мы возьмем диск. Тогда имеем:
где – высота цилиндра. Тогда момент инерции цилиндра относительно его собственной оси равен:
где масса цилиндра равна:
Примеры решения задач
V. Вывод формулы для определения момента инерции.
Пусть при вращении диск поднялся, на высоту h =h1 — h2 (рис. 1). Тогда приращение потенциальной энергии равно
.
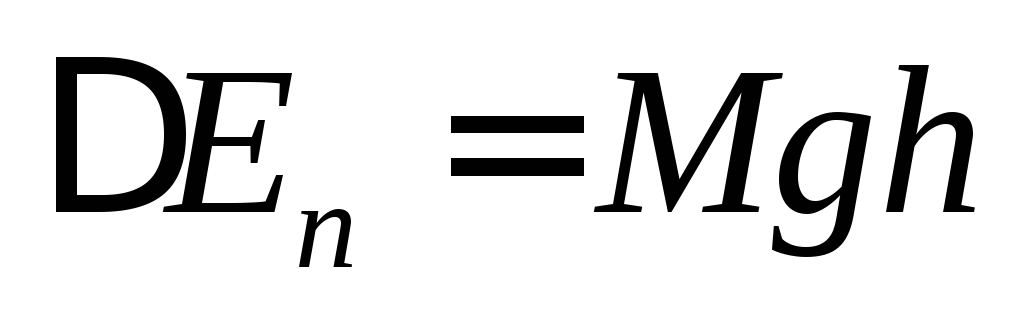При опускании нижнего диска потенциальная энергия переходит в кинетическую энергию вращательного движения
,
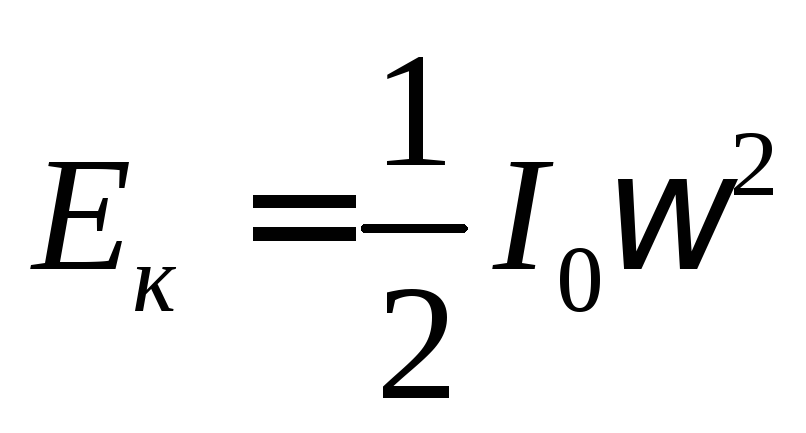где I0 — момент инерции нижнего диска, — угловая скорость диска.
В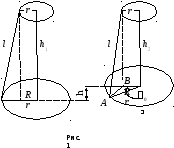
момент прохождения диском положения
равновесия угловая скорость,
а, следовательно, и кинетическая энергия,
принимает максимальное значение, т.е. = 0.
Если пренебречь трением, то на основании закона сохранения энергии для колеблющегося диска можно записать:
.
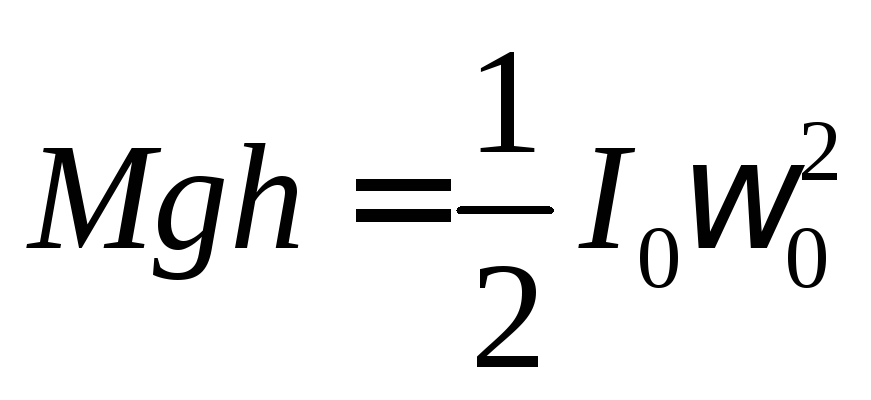(2)
Угловая скорость , являющаяся первой производной от смещения по времени, может быть записана
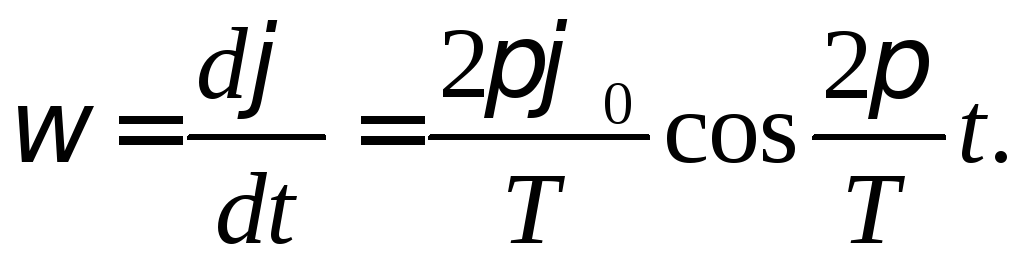
Максимальное значение угловой скорости равно:
.
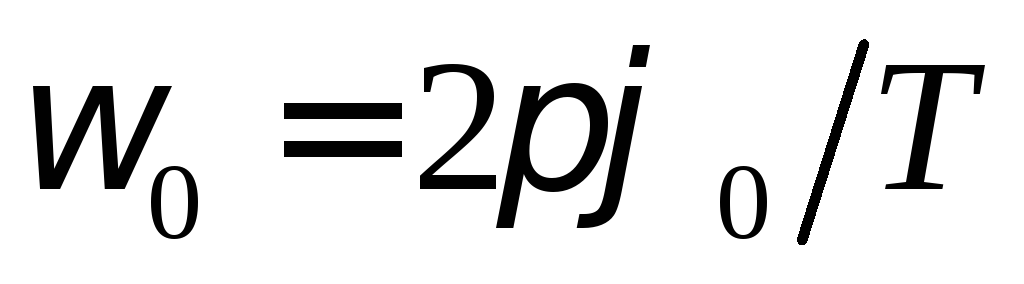(3)
На основании выражений (2) и (3) имеем:
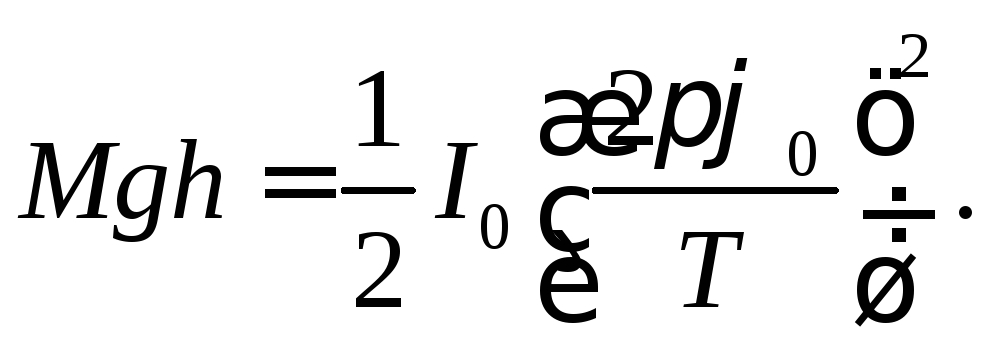(4)
Найдем величину h при повороте диска на малый угол 0, считая, что h1 + h2 2l:
.
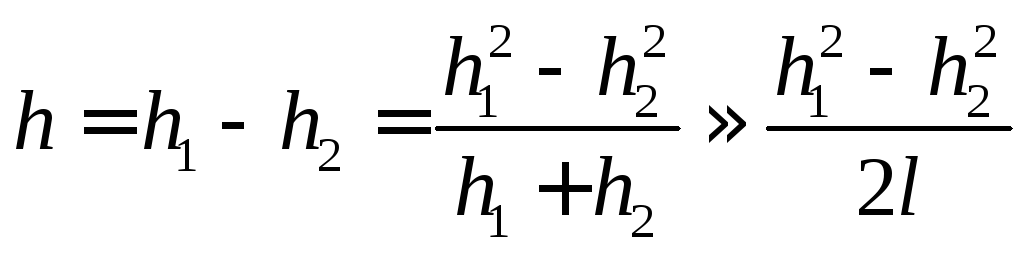(5)
Из рис.1 ясно, что
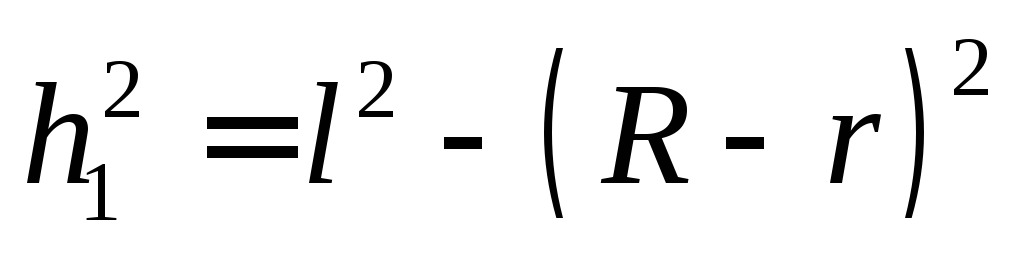и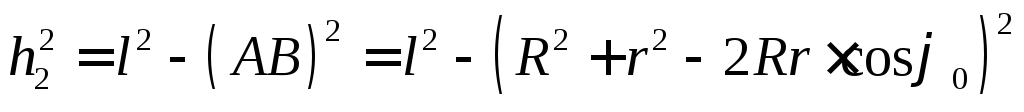 
.
Подставляя
значение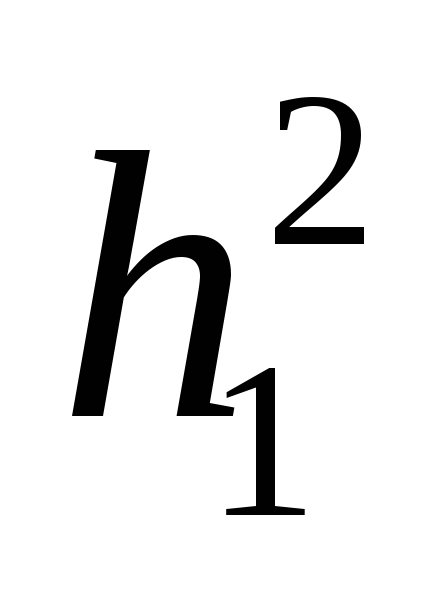 
и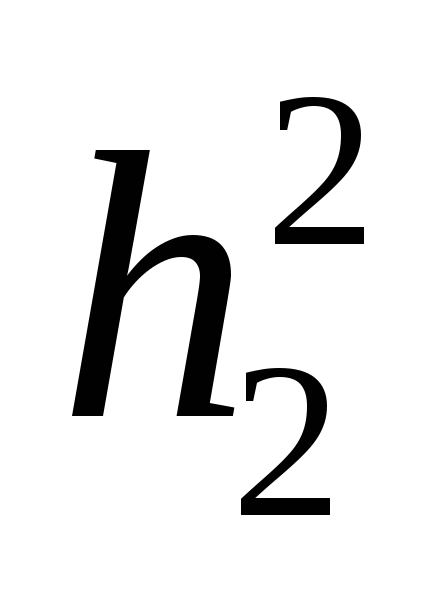 
в (5), получим:
.
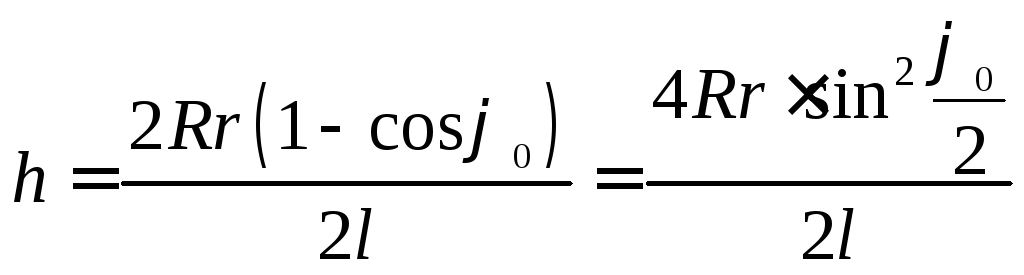Вследствие малости угла 0 синус можно заменить аргументом:
.
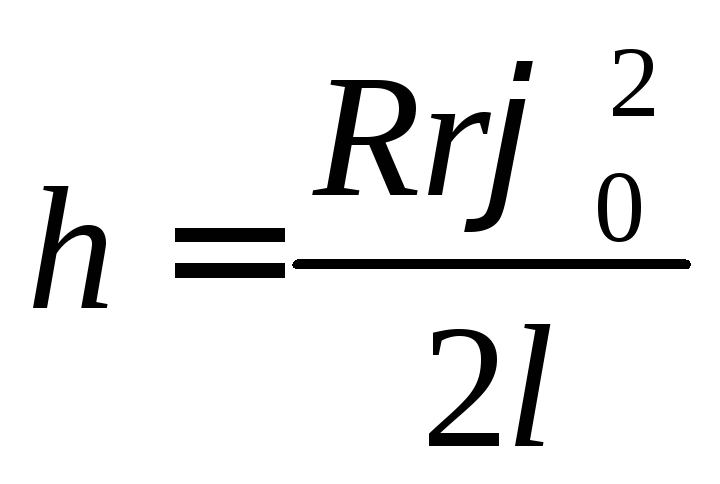(6)
Подставив выражения (3) и (6) в формулу (2), получим:
,
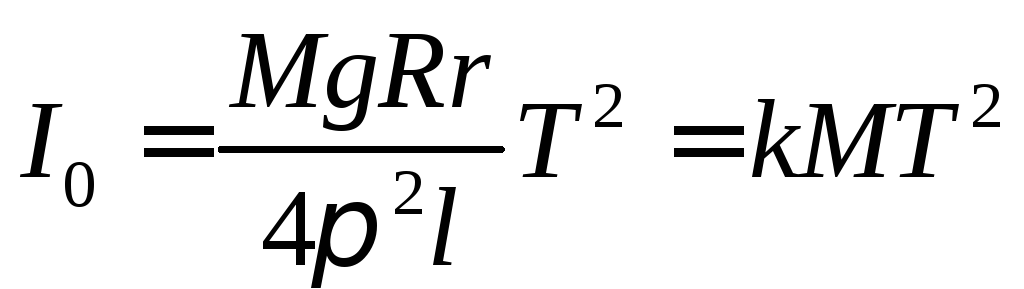или
,
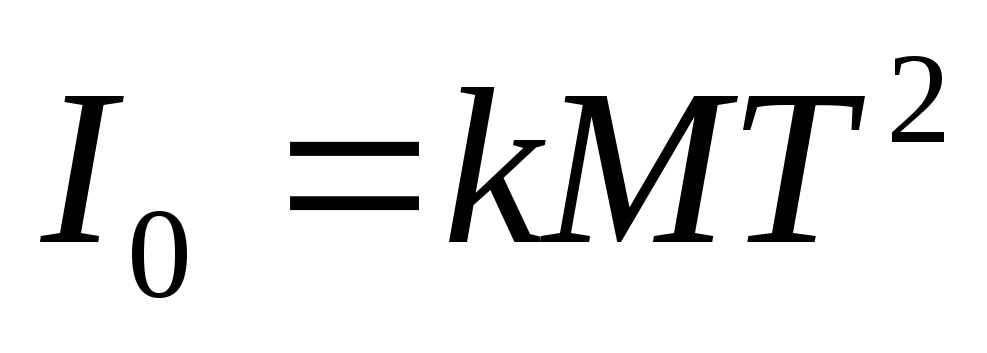(7)
где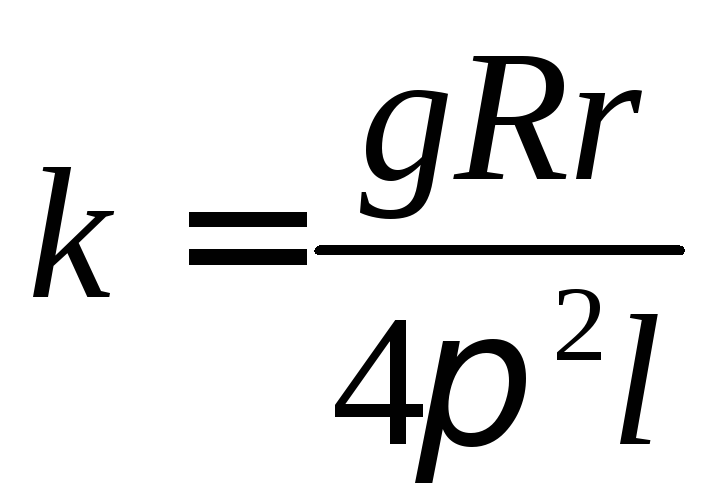 
— постоянная установки.
IV. Порядок выполнения лабораторной работы
1. Определение момента инерции i0 диска без нагрузки.
а) Заставить диск совершать крутильные колебания с малой амплитудой (10 15 градусов). Секундомером измерить времяtсовершенияnполных колебаний (n– задаётся преподавателем). Все измерения провести несколько раз. Все значения занести в табл.1.
б) Провести статистическую обработку времени t по методу Стьюдента.
в) Определить период колебаний диска Т = t /n, занести данные в таблицу 1.
г) Занести в табл.2 массу диска М и постоянную установкиk.
д) По формуле (7) рассчитать значение момента инерции диска I0, результат занести в таблицу 2.
е) Вычислить относительные и абсолютные погрешности по формулам (8) – (9) и занести результаты в таблицу 3.
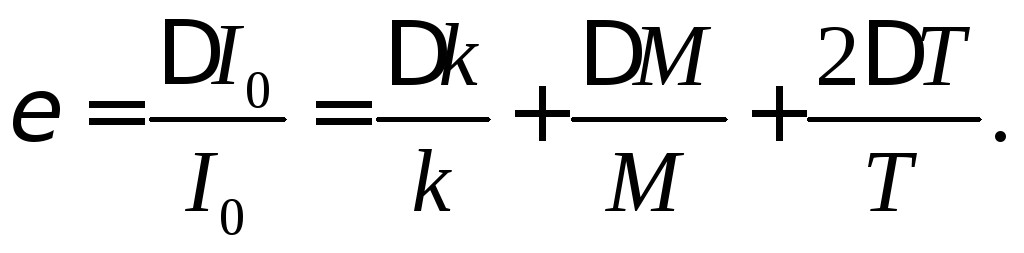(8)
.
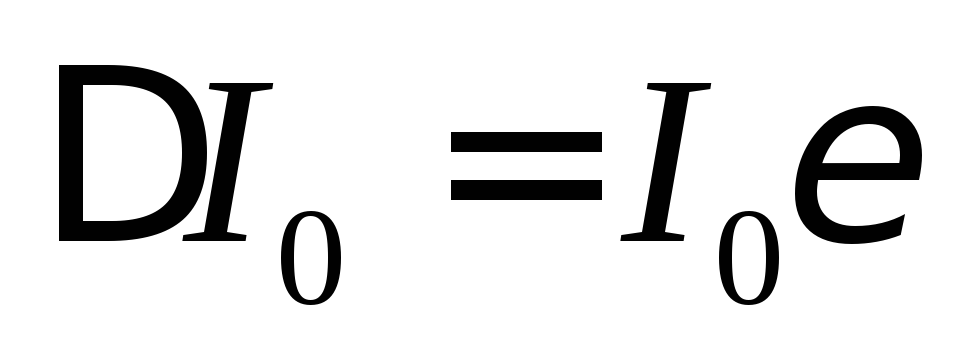(9)
Абсолютная погрешность периода колебаний определяется следующим образом
.
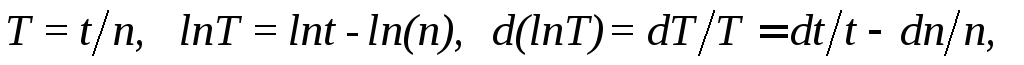
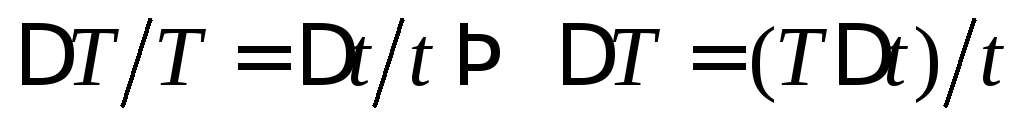Таблица 1
№/№ п/п | t | t | t2 | Sn | t(,n) | tсл | tпр | t | n | T | T |
с | с | с2 | с | – | с | c | с | – | с | с | |
1 | |||||||||||
2 | |||||||||||
3 | |||||||||||
… | |||||||||||
cреднее |
Таблица 2
k | M | m | d | I0 | I1 | I2 | I3 | |
м2с–2 | кг | кг | м | кгм2 | кгм2 | кгм2 | кгм2 | |
Среднее значение | ||||||||
Абсолютная погрешность | 510-4 | |||||||
Относительная погрешность |
Момент инерции шара, теория и примеры
Это скалярная (в общем случае тензорная) величина. Для непрерывного однородного тела, вращающегося около оси, момент инерции определяют как:
где r – функция положения материальной точки в пространстве; – плотность тела; –объем элемента тела.
Момент инерции однородного шара
Однородный по объем шар можно представить как систему сферических слоев (или тонких дисков), обладающих массами ().
По условию шар является однородным, плотность его можно представить как:
где – объем всего шара; m – масса всего шара.
В качестве элементарной массы выберем сферический слой радиуса r (указанный на рис.1). Его массу можно представить как:
При этом объем рассматриваемого сферического слоя равен:
Момент инерции тонкого диска (толщина диска ) равен:
Выделенный нами диск находится на расстоянии h от центра шара. Радиус рассматриваемого нами диска связан с расстоянием h выражением:
Тогда формулу (4) преобразуем к виду:
Просуммируем моменты инерции всех дисков:
Получили, что момент инерции однородного шара, относительно его диаметра равен:
Момент инерции полого шара (сферы)
Момент инерции сферы удобно находить, используя полярный момент инерции. Это момент инерции тела относительно некоторой точки, назовем ее O. Он равен произведению всех масс точек тела на квадраты расстояний от них до точки О. Если через полюс О провести прямоугольные оси, то полярный момент () равен:
Полярный момент инерции равен половине суммы моментов инерции тела относительно трех прямоугольных осей, которые проходят через полюс:
В центре тяжести тела полярный момент инерции имеет минимальной значение.
Рассмотрим сферу радиуса R. Для нее удобно сначала найти полярный момент инерции относительно ее центра ():
Согласно формуле (10) и зная, что для сферы , имеем:
Получаем, что момент инерции сферы (полого шара) равен:
