Закон всемирного тяготения.

Задача 8.1.1. При увеличении в 3 раза расстояния между точечными телами сила их гравитационного притяжения

Увеличивается в 3 раза	Уменьшается в 3 раза
Увеличивается 9 раз	Уменьшается в 9 раз

Задача 8.1.2. Как изменится сила взаимодействия двух точечных тел, если при неизменном расстоянии между ними массу одного увеличить в 2 раза, массу второго увеличить в 3 раза?

Увеличится в 3 раза	Увеличится в 2 раза
Увеличится в 6 раз	Увеличится в 3/2 раза

Задача 8. 1.3. Как изменится сила взаимодействия двух точечных тел, если массу одного тела увеличить в два раза, второго — в четыре раза, а расстояние между телами — в восемь раз?

Уменьшается в 2 раза	Уменьшается в 4 раза
Уменьшается в 8 раз	Уменьшается в 16 раз

Задача 8.1.4. На каком расстоянии от центра Земли ускорение свободного падения составляет половину ускорения свободного падения на ее поверхности? Радиус Земли .

Задача 8.1.5. Определить ускорение свободного падения на поверхности Марса, если масса Марса приблизительно в 10 раз меньше массы Земли, а радиус приблизительно в 2 раза меньше радиуса Земли.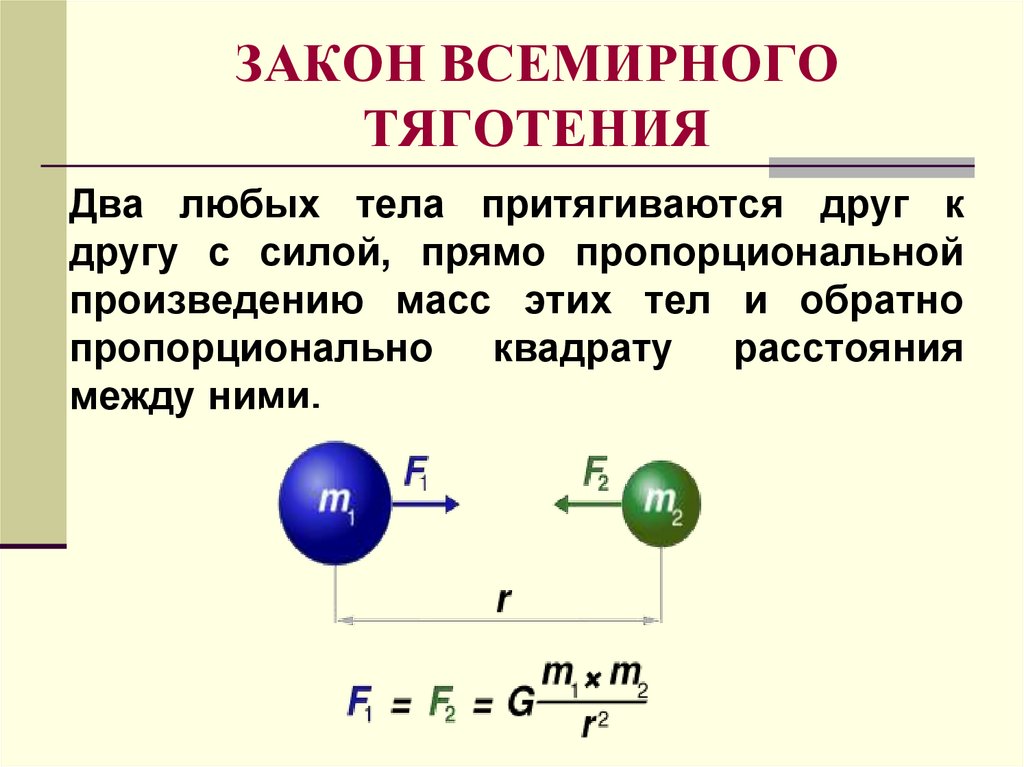

Считать, что ускорение свободного падения на поверхности Земли = м/с².

Задача 8.1.6. Два точечных тела с массами и удерживают на некотором расстоянии друг от друга. Тела одновременно отпускают. Сравнить ускорения тел. Тела взаимодействуют по закону всемирного тяготения.

Задача 8.1.7. Известно, что масса Меркурия составляет 1/18 массы Земли, а расстояние от Меркурия до Солнца в 2,5 раза меньше расстояния от Земли до Солнца. Во сколько раз сила притяжения Земли к Солнцу больше силы притяжения Меркурия к Солнцу?

В 2,2 раза	В 2,9 раза
В 6,25 раза	В 18 раз

Задача 8.1.8. Ракета удаляется от земли. На каком расстоянии от поверхности земли сила гравитационного притяжения ракеты к земле уменьшается в 4 раза по сравнению с силой притяжения на поверхности?

Задача 8.1.9. Три точечных тела с массами , и расположены на одной прямой на одинаковых расстояниях друг от друга (см. рисунок). Чему равна сила, действующая на центральное тело?

Задача 8.1.10. Три точечных тела массой каждое расположены в вершинах равнобедренного прямоугольного треугольника с катетами, равными (см. рисунок). Чему равна сила, действующая на тело, находящееся в вершине прямого угла?

Разработка урока по физике «Закон всемирного тяготения» (9класс)

Тема урока: Силы в механике. Силы всемирного тяготения. Закон всемирного тяготения.

Цель: Познакомить учащихся с формулировкой и математической записью закона всемирного тяготения. Научить решать задачи на расчет силы тяготения.

Задачи урока:

Образовательная:  изучить закон всемирного тяготения, добиться понимания этого закона, умения применить его для решения задач;

Развивающие — умение делать выводы, совершенствование интеллектуальных способностей и развитие речи учащихся, стимулирование интереса к предмету путём привлечения дополнительного материала. Совершенствовать навыки учащихся и расширять их границы при выполнении качественных, расчетных  задач.

Воспитательные: продолжить работу по формированию у учащихся добросовестного отношения к учебному труду, гуманности, эстетического восприятия мира; воспитать стремление к познанию.

Тип урока: изучение нового материала

Методы: наглядный, частично-поисковый, беседа
Оборудование: мультимедийный комплекс, презентация, тесты.

Ход урока

1.      Психологический настрой. Физминутка.

2.      Проверка дом. задания

1.Упр 11. Заслушивание информации о выполнении домашней работы (консультанты). Некоторые задачи, которые вызвали затруднения у учащихся выполнить у доски.

          2.Тестирование по законам Ньютона

1.      Как формулируется III закон Ньютона? 

 1.Тело движется равномерно и прямолинейно (или покоится), если на него не действуют другие тела (или действие других тел скомпенсировано)

2. Сила упругости, возникающая при деформации тела, прямо пропорциональна величине абсолютного удлинения
3. Действие равно противодействию
4.Тела действуют друг на друга силами равными по абсолютному значению, направленными вдоль одной прямой и противоположными по направлению

2. III закон Ньютона математически можно записать так:

1.F = ma2.F = μN3.F₁₂ = −F₂₁4.Fx = −kx5.затрудняюсь ответить

3. Как формулируется II закон Ньютона?

 1.Тело движется равномерно в инерциальной системе, если воздействие других тел не скомпенсировано
2.Ускорение, приобретаемое телом, прямо пропорционально равнодействующей всех сил, действующих на тело, и обратнопропорционально его массе
3.Направление ускорения тела совпадает с направлением равнодействующей всех сил, действующих на тело
4.Модуль ускорения тела прямо пропорционален модулю равнодействующей всех сил и обратно пропорционален массе тела
5. затрудняюсь ответить

4.Векторная величина, являющаяся мерой взаимодействия тела с другими телами, в результате чего тело приобретает ускорение,- это…

А. — вес тела

Б. Сила реакции опоры

в. Равнодействующая сила

г. Сила упругости

5.Пружина динамометра растягивается под действием приложенных двух сил по 3 Н. Каково показание динамометра?

А. 0Н

Б. 3 Н

В.6 Н

Г. 9 Н.

6. В каких системах отсчета выполняются законы Ньютона?
А. неинерциальных
Б.инерциальных
В. В любых
Г. подвижных
7. Два мальчика тянут за концы динамометра в противоположные направления с силой 5 Н. Каковы показания динамометров?
А. 10 Н и 10 Н.
Б. 5 Н. и 0 Н
В. 5 Н и 5Н
Г. 3 Н и 7 Н

8. Тела действуют друг на друга при их взаимодействии силами:
А. равными по величине и совпадающими по направлению
Б. Равными по величине и направленными в противоположные стороны
В. разными по величине и направленными в одну сторону
Г. силами разной природы

 

3.  Объяснение новой темы в сочетании с беседой.

Из истории физики…

Датский астроном Тихо Браге (1546-1601), долгие годы наблюдавший за движением планет, накопил огромное количество интересных данных, но не сумел их обработать.

Иоганн Кеплер (1571-1630) используя идею Коперника о гелиоцентрической системе и результаты наблюдений Тихо Браге, установил законы движения планет вокруг Солнца, однако и он не смог объяснить динамику этого движения

.

Исаак Ньютон открыл этот закон в возрасте 23 лет, но целых 9 лет не публиковал его, так как имевшиеся тогда неверные данные о расстоянии между Землей и Луной не подтверждали его идею. Лишь в 1667 году, после уточнения этого расстояния, закон всемирного тяготения был наконец отдан в печать.

Ньютон предположил, что ряд явлений, казалось бы не имеющих ничего общего (падение тел на Землю, обращение планет вокруг Солнца, движение Луны вокруг Земли, приливы и отливы и т.

д.), вызваны одной причиной.

Окинув единым мысленным взором “земное” и “небесное”, Ньютон предположил, что существует единый закон всемирного тяготения, которому подвластны все тела во Вселенной — от яблок до планет!

В 1667 г. Ньютон высказал предположение, что между всеми телами действуют силы взаимного притяжения, которые он назвал силами всемирного тяготения.

Исаак Ньютон — английский физик и математик, создатель теоретических основ механики и астрономии. Он открыл закон всемирного тяготения, разработал дифференциальное и интегральное исчисления, изобрел зеркальный телескоп и был автором важнейших экспериментальных работ по оптике. Ньютона по праву считают создателем «классической физики».

Закон всемирного тяготения

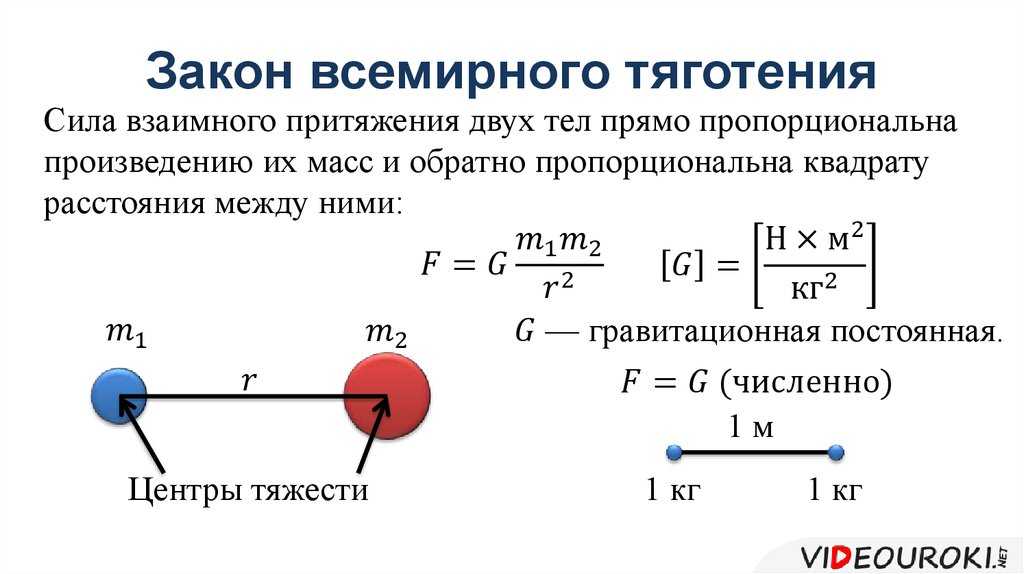
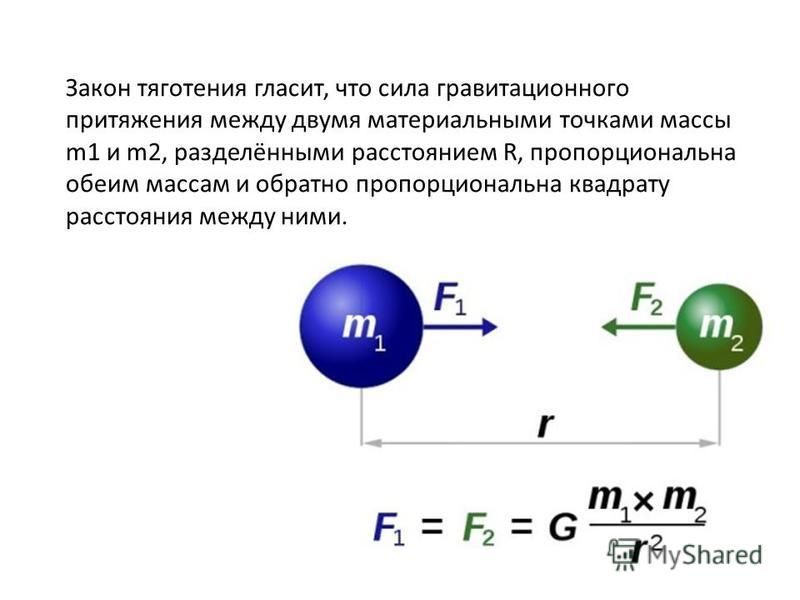
В 1687 г. Ньютон установил один из фундаментальных законов механики, получивший название закона всемирного тяготения: “Два любых тела притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними”

.

где m₁ и m₂ – массы взаимодействующих тел, r – расстояние между телами, G – коэффициент пропорциональности, одинаковый для всех тел в природе и называемый постоянной всемирного тяготения или гравитационной постоянной.

Запомнить

·         Гравитационное взаимодействие – это взаимодействие, свойственное всем телам Вселенной и проявляющееся в их взаимном притяжении друг к другу.

·         Гравитационное поле – особый вид материи, осуществляющее гравитационное взаимодействие.

Механизм гравитационного взаимодействия

В настоящее время механизм гравитационного взаимодействия представляется следующим образом: Каждое тело массой М создает вокруг себя поле, которое называют гравитационным. Если в некоторую точку этого поля поместить пробное тело массой т, то гравитационное поле действует на данное тело с силой F, зависящей от свойств поля в этой точке и от величины массы пробного тела.

Эксперимент Генри Кавендиша по определению гравитационной постоянной.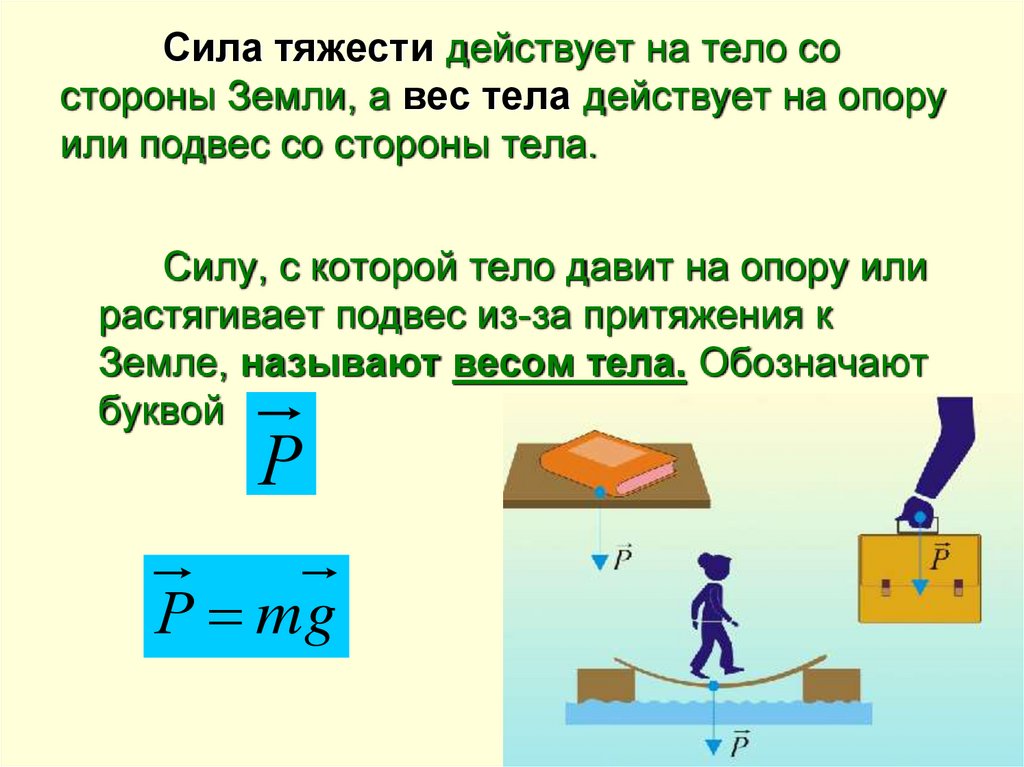

Английский физик Генри Кавендиш определил, насколько велика сила притяжения между двумя объектами. В результате была достаточно точно определена гравитационная постоянная, что позволило Кавендишу впервые определить и массу Земли.

Гравитационная постоянная

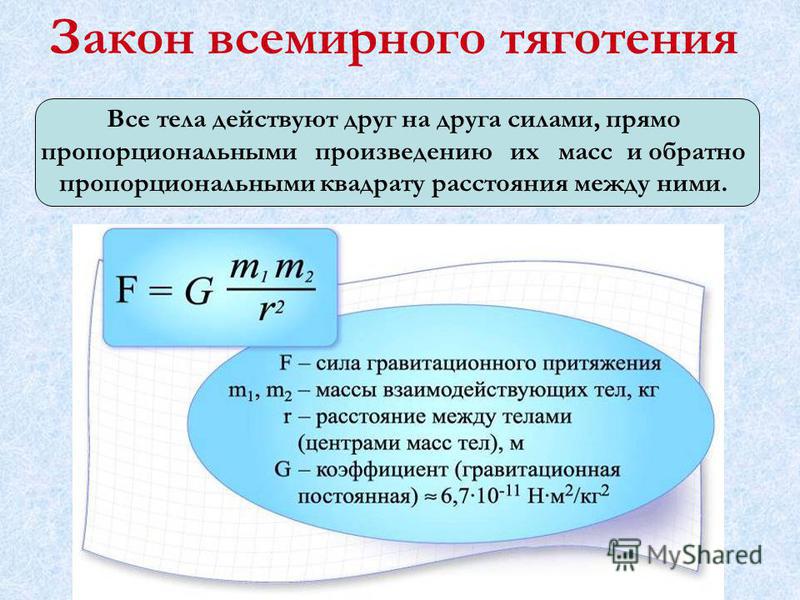
G — гравитационная постоянная, она численно равна силе гравитационного притяжения двух тел, массой по 1 кг. Каждое, находящихся на расстоянии 1 м одно от другого.

G — универсальная гравитационная постоянная

G=6,67 * 10 ^-11 Н м² /кг ²

Гравитационная постоянная показывает, с какой силой взаимодействуют тела единичной массы на единичном расстоянии друг от друга: .

Сила взаимодействия между двумя точечными телами прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между ними: .

— сила тяжести всем телам независимо от их массы сообщает одинаковое ускорение.

 

Сила взаимного притяжения всегда направлена вдоль прямой, соединяющей тела.

Границы применимости закона

Закон всемирного тяготения имеет определенные границы применимости; он применим для:

1) материальных точек;

2) тел, имеющих форму шара;

3) шара большого радиуса, взаимодействующего с телами, размеры которых много меньше размеров шара.

Закон неприменим, например, для взаимодействия бесконечного стержня и шара.

Сила тяготения очень мала и становится заметной только тогда, когда хотя бы одно из взаимодействующих тел имеет очень большую массу (планета, звезда).

3.      Закрепление. Решение задач

1.      Почему мы не замечаем гравитационного притяжения между окружающими нас телами?

2.      Два корабля массой 50000 т каждый стоят на рейде на расстоянии 1 км друг от друга. Какова сила притяжения между ними?

Д А Н О:

F — ?

Решение:

Ответ: F = 0,17 Н

3.       Известно, что период обращения Луны вокруг Земли составляет 27,3 суток, среднее расстояние между центрами Луны и Земли равно 384000 километров. Вычислить ускорение Луны и найти во сколько раз оно отличается от ускорения свободного падения камня вблизи поверхности Земли, то есть на расстоянии равном радиусу Земли (6400 км).

выведение закона

С другой стороны, отношение расстояний от Луны и камня до центра Земли равно:

Нетрудно заметить, что

5.Прямо прямо пропорцианальная зависимость

Из второго закона Ньютона следует, что между силой и ускорением, которое она вызывает, существует прямо пропорциональная зависимость:

Следовательно, сила тяготения так же, как и ускорение, обратно пропорциональна квадрату расстояния между телом и центром Земли:

 

Галилео Галилей экспериментально доказал, что все тела падают на Землю с одним и тем же ускорением, называемым ускорением свободного падения (опыт с падением разных тел в трубке с откачанным воздухом)

Почему это ускорение одинаково для всех тел?

Это возможно только в том случае, если сила тяготения пропорциональна массе тела: F ~ m . Действительно, тогда, например, увеличение или уменьшение массы в два раза вызовет соответствующее изменение силы тяготения в два раза, но ускорение по второму закону Ньютона останется прежним

С другой стороны, во взаимодействии всегда участвуют два тела, на каждое из которых по третьему закону Ньютона действуют одинаковые по модулю силы:

Следовательно, сила тяготения должна быть пропорциональна массе обоих тел.

Так Ньютон пришёл к выводу, что сила тяготения между телом и Землёй прямо пропорциональна произведению их масс:

6.Итоги урока

Обобщая всё выше изложенное относительно силы тяготения плане-ты Земля и любого тела, приходим к следующему утверждению : сила тяготения между телом и Землёй прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между их центрами, что можно записать в виде

Выполняется ли этот закон только для Земли или является всеобщим?

Чтобы ответить на этот вопрос, Ньютон использовал кинематические законы движения планет Солнечной системы, сформулированные немецким учёным Иоганном Кеплером на основании многолетних астрономических наблюдений датскогоучёного Тихо Браге.

7. Подумай и ответь

1.      Почему Луна не падает на Землю?

2.      Почему мы замечаем силу притяжения всех тел к Земле, но не замечаем взаимного притяжения между самими этими телами?

3.      Как двигались бы планеты, если бы сила притяжения Солнца внезапно исчезла?

4.      Как двигалась бы Луна, если бы она остановилась на орбите?

5.      Притягивает ли Землю стоящий на ее поверхности человеке? Летящий самолет? Космонавт, находящийся на орбитальной станции?
— новый слайд-
Некоторые тела (воздушные шары, дым, самолеты, птицы) поднимаются вверх, несмотря на тяготение. Как вы думаете, почему? Нет ли здесь нарушения закона всемирного тяготения?

6.      Что нужно сделать, чтобы увеличить силу тяготения между двумя телами?

7.      Какая сила вызывает приливы и отливы в морях и океанах Земли?

8.      Почему мы не замечаем гравитационного притяжения между окружающими нас телами?

8.Вопрос-ответ

Составьте вопросы и затем дайте ответ к рисункам 1-4.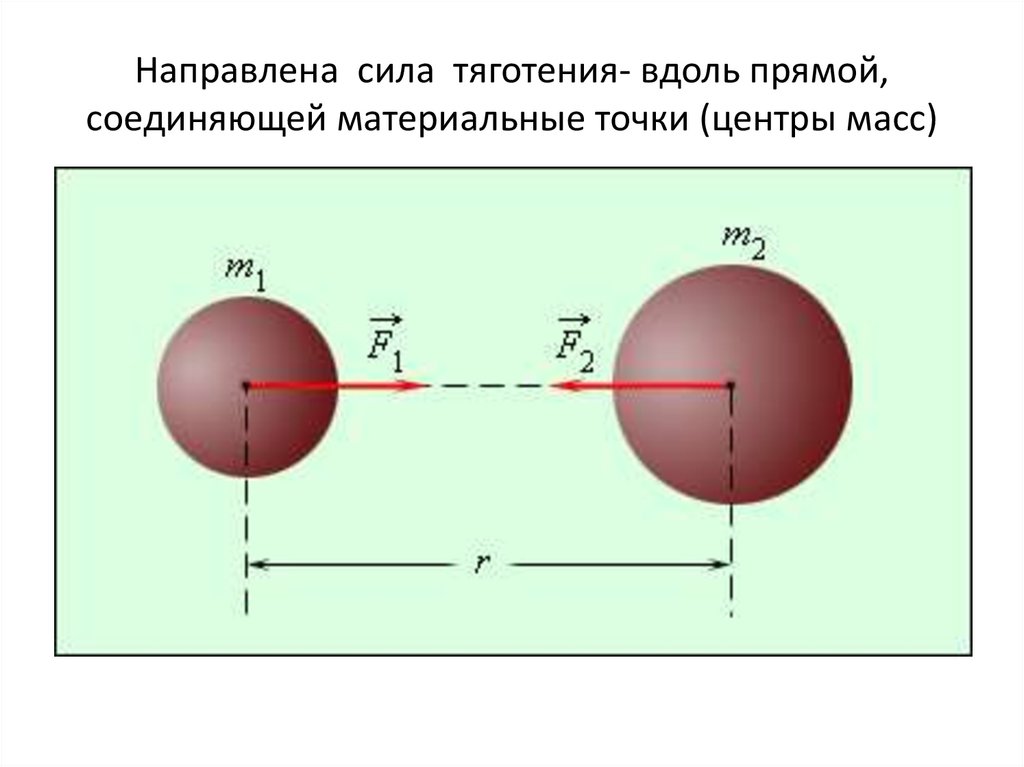

9. Домашнее задание:  §15 Упр 12(3,4)
7. Итоги урока (Выставление оценок и их комментарий).

8. Рефлексия

Работа с сигнальными карточками.

Зеленая карточка. Я удовлетворен уроком. Урок был полезен для меня. Я с пользой и хорошо работал на уроке. Я понимал все, о чем говорилось и что делалось на уроке.

Желтая карточка. Урок был интересен. Я принимал в нем участие. Урок был в определенной степени полезен для меня. Я отвечал с места, выполнил ряд заданий. Мне было на уроке достаточно комфортно.

Красная карточка. Пользы от урока я получил мало. Я не очень понимал, о чем идет речь. Мне это не нужно. К ответу на уроке я был не готов.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Цель урока:

·         создавать условия для формирования познавательного интереса, активности учащихся;

·         вывести закон всемирного тяготения;

·         способствовать развитию конвергентного мышления;

·         способствовать эстетическому воспитанию учащихся;

·         формирование коммуникационного общения;

Из истории физики. ..

Датский астроном Тихо Браге (1546-1601), долгие годы наблюдавший за движением планет, накопил огромное количество интересных данных, но не сумел их обработать.

Иоганн Кеплер (1571-1630) используя идею Коперника о гелиоцентрической системе и результаты наблюдений Тихо Браге, установил законы движения планет вокруг Солнца, однако и он не смог объяснить динамику этого движения.

Исаак Ньютон открыл этот закон в возрасте 23 лет, но целых 9 лет не публиковал его, так как имевшиеся тогда неверные данные о расстоянии между Землей и Луной не подтверждали его идею. Лишь в 1667 году, после уточнения этого расстояния, закон всемирного тяготения был наконец отдан в печать.

Ньютон предположил, что ряд явлений, казалось бы не имеющих ничего общего (падение тел на Землю, обращение планет вокруг Солнца, движение Луны вокруг Земли, приливы и отливы и т.д.), вызваны одной причиной.

Окинув единым мысленным взором “земное” и “небесное”, Ньютон предположил, что существует единый закон всемирного тяготения, которому подвластны все тела во Вселенной — от яблок до планет!

В 1667 г. Ньютон высказал предположение, что между всеми телами действуют силы взаимного притяжения, которые он назвал силами всемирного тяготения.

Исаак Ньютон — английский физик и математик, создатель теоретических основ механики и астрономии. Он открыл закон всемирного тяготения, разработал дифференциальное и интегральное исчисления, изобрел зеркальный телескоп и был автором важнейших экспериментальных работ по оптике. Ньютона по праву считают создателем «классической физики».

Закон всемирного тяготения

В 1687 г. Ньютон установил один из фундаментальных законов механики, получивший название закона всемирного тяготения: “Два любых тела притягиваются друг к другу с силой, модуль которой прямо пропорционален произведению их масс и обратно пропорционален квадрату расстояния между ними”

.

где m₁ и m₂ – массы взаимодействующих тел, r – расстояние между телами, G – коэффициент пропорциональности, одинаковый для всех тел в природе и называемый постоянной всемирного тяготения или гравитационной постоянной.

Запомнить

·         Гравитационное взаимодействие – это взаимодействие, свойственное всем телам Вселенной и проявляющееся в их взаимном притяжении друг к другу.

·         Гравитационное поле – особый вид материи, осуществляющее гравитационное взаимодействие.

Механизм гравитационного взаимодействия

В настоящее время механизм гравитационного взаимодействия представляется следующим образом: Каждое тело массой М создает вокруг себя поле, которое называют гравитационным. Если в некоторую точку этого поля поместить пробное тело массой т, то гравитационное поле действует на данное тело с силой F, зависящей от свойств поля в этой точке и от величины массы пробного тела.

Эксперимент Генри Кавендиша по определению гравитационной постоянной.

Английский физик Генри Кавендиш определил, насколько велика сила притяжения между двумя объектами. В результате была достаточно точно определена гравитационная постоянная, что позволило Кавендишу впервые определить и массу Земли.

Гравитационная постоянная

G — гравитационная постоянная, она численно равна силе гравитационного притяжения двух тел, массой по 1 кг. Каждое, находящихся на расстоянии 1 м одно от другого.

G — универсальная гравитационная постоянная

G=6,67 * 10 ^-11 Н м² /кг ²

Сила взаимного притяжения всегда направлена вдоль прямой, соединяющей тела.

Границы применимости закона

Закон всемирного тяготения имеет определенные границы применимости; он применим для:

1) материальных точек;

2) тел, имеющих форму шара;

3) шара большого радиуса, взаимодействующего с телами, размеры которых много меньше размеров шара.

Закон неприменим, например, для взаимодействия бесконечного стержня и шара.

Сила тяготения очень мала и становится заметной только тогда, когда хотя бы одно из взаимодействующих тел имеет очень большую массу (планета, звезда).

 

Почему мы не замечаем гравитационного притяжения между окружающими нас телами?

Воспользуемся законом всемирного тяготения и сделаем некоторые расчёты:

Два корабля массой 50000 т каждый стоят на рейде на расстоянии 1 км друг от друга. Какова сила притяжения между ними?

Д А Н О:

F — ?

Решение:

Ответ: F = 0,17 Н

задача

Известно, что период обращения Луны вокруг Земли составляет 27,3 суток, среднее расстояние между центрами Луны и Земли равно 384000 километров. Вычислить ускорение Луны и найти во сколько раз оно отличается от ускорения свободного падения камня вблизи поверхности Земли, то есть на расстоянии равном радиусу Земли ( 6400 километров ).

выведение закона

С другой стороны, отношение расстояний от Луны и камня до центра Земли равно:

Нетрудно заметить, что

Прямо пропорцианальная зависимость

Из второго закона Ньютона следует, что между силой и ускорением, которое она вызывает, существует прямо пропорциональная зависимость:

Следовательно, сила тяготения так же, как и ускорение, обратно пропорциональна квадрату расстояния между телом и центром Земли:

 

Галилео Галилей экспериментально доказал, что все тела падают на Землю с одним и тем же ускорением, называемым ускорением свободного падения (опыт с падением разных тел в трубке с откачанным воздухом)

Почему это ускорение одинаково для всех тел?

Это возможно только в том случае, если сила тяготения пропорциональна массе тела: F ~ m . Действительно, тогда, например, увеличение или уменьшение массы в два раза вызовет соответствующее изменение силы тяготения в два раза, но ускорение по второму закону Ньютона останется прежним

С другой стороны, во взаимодействии всегда участвуют два тела, на каждое из которых по третьему закону Ньютона действуют одинаковые по модулю силы:

Следовательно, сила тяготения должна быть пропорциональна массе обоих тел.

Так Ньютон пришёл к выводу, что сила тяготения между телом и Землёй прямо пропорциональна произведению их масс:

итоги урока

Обобщая всё выше изложенное относительно силы тяготения плане-ты Земля и любого тела, приходим к следующему утверждению : сила тяготения между телом и Землёй прямо пропорциональна произведению их масс и обратно пропорциональна квадрату расстояния между их центрами, что можно записать в виде

Выполняется ли этот закон только для Земли или является всеобщим?

Чтобы ответить на этот вопрос, Ньютон использовал кинематические законы движения планет Солнечной системы, сформулированные немецким учёным Иоганном Кеплером на основании многолетних астрономических наблюдений датскогоучёного Тихо Браге.

Подумай и ответь

9.      Почему Луна не падает на Землю?

10.  Почему мы замечаем силу притяжения всех тел к Земле, но не замечаем взаимного притяжения между самими этими телами?

11.  Как двигались бы планеты, если бы сила притяжения Солнца внезапно исчезла?

12.  Как двигалась бы Луна, если бы она остановилась на орбите?

13.  Притягивает ли Землю стоящий на ее поверхности человеке? Летящий самолет? Космонавт, находящийся на орбитальной станции?
— новый слайд-
Некоторые тела (воздушные шары, дым, самолеты, птицы) поднимаются вверх, несмотря на тяготение. Как вы думаете, почему? Нет ли здесь нарушения закона всемирного тяготения?

14.  Что нужно сделать, чтобы увеличить силу тяготения между двумя телами?

15.  Какая сила вызывает приливы и отливы в морях и океанах Земли?

16.  Почему мы не замечаем гравитационного притяжения между окружающими нас телами?

Вопрос-ответ

Составьте вопросы и затем дайте ответ к рисункам 1-4.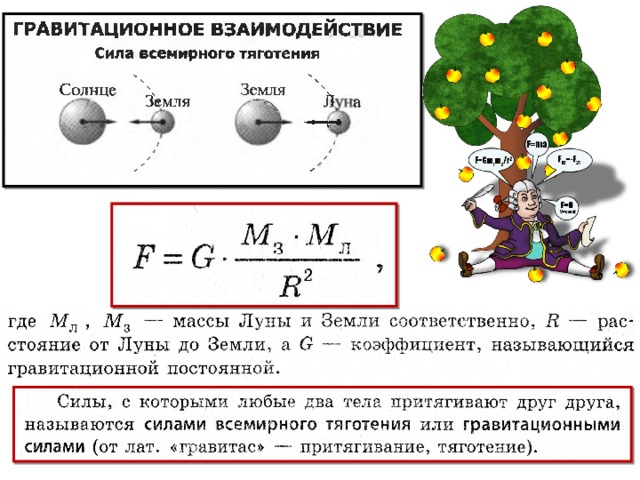 2}$? Я сбит с толку тем, как сила может быть промежуточной, будь то на теле А, или на теле Б, или на обоих.

Предположим, что тело A действует с силой $F$ на тело B, поэтому, согласно 3-му закону Ньютона, B также должно действовать на A.

Рассмотрим этот случай для гравитационной силы между двумя телами. Если тело A действует с силой $g$ на тело B, то тело B также должно действовать с силой $g$ на A, но B также действует с силой тяжести $X$ на A, следовательно, A также будет действовать с силой $X$ на тело B. Б. Итак, как действуют две силы? Я дал представление на этой диаграмме.

• ньютоновская механика
• силы
• ньютоновская гравитация

$\endgroup$

6

$\begingroup$

Третий закон Ньютона говорит нам, что сила, действующая на А со стороны В, равна (по величине, с противоположным направлением) силе, действующей на В со стороны А. 2}$, чтобы описать гравитационное взаимодействие между парой масс. 92}$. B испытывает ту же силу по отношению к A. Это 2 силы в этом сценарии.

Где Х появляется на картинке. Другой силы X нет.

На вашей диаграмме « сила реакции G » и X не являются двумя различными силами. Это одно и то же.
Аналогично, на вашей диаграмме « сила реакции X » и G — одно и то же

$\endgroup$

7

$\begingroup$

Один из способов взглянуть на это так: силы всегда приходят парами. Например, вы начинаете со вселенной, в которой есть только один объект, затем вы добавляете еще один объект, и природа тут же создаст пару сил. Не то чтобы Луна чувствовала, что Земля тянет ее, и в ответ тянула саму Землю.

Нельзя взять такую ​​пару сил и обозначить одну как действие, а другую как противодействие, или одну как причину, а другую как следствие.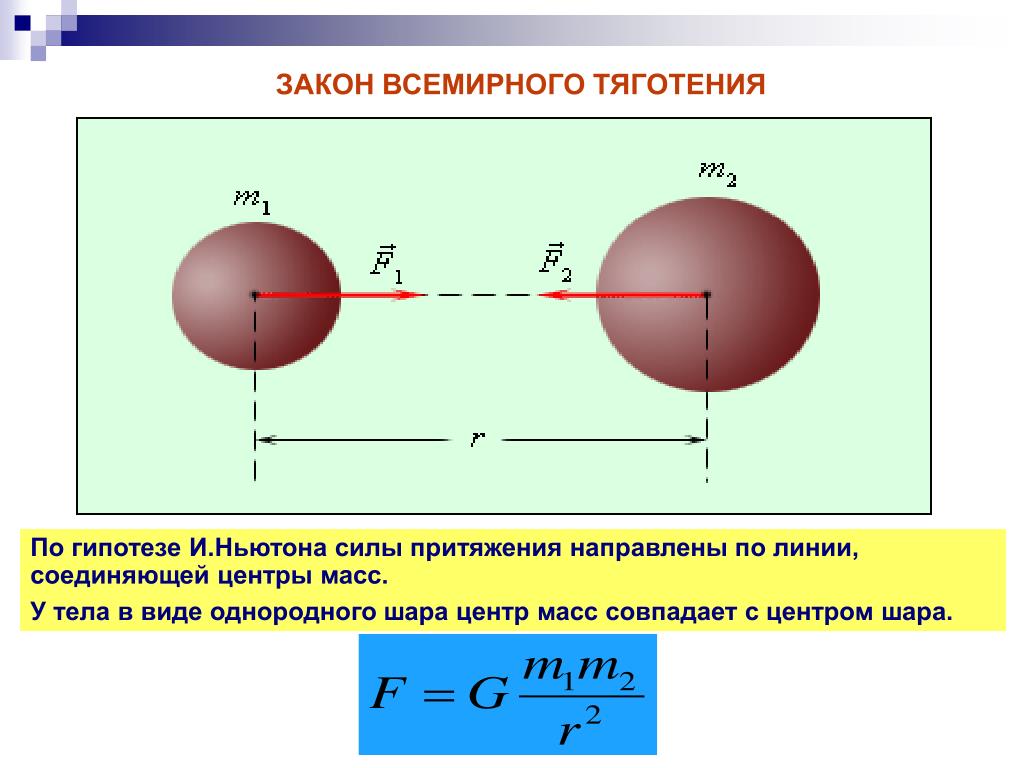 Скорее и являются проявлениями внутренней работы природы, и, насколько нам известно, эти действия лучше всего не описываются с точки зрения силы, а скорее как «если бы вещи двигались как в этот раньше, они будут двигаться как , потом ».

Несмотря на то, что силы не являются фундаментальными, они являются очень полезными математическими объектами, и симметрия, которую они проявляют в третьем законе Ньютона, является лишь одной из многих симметрий, которыми обладает Вселенная.

$\endgroup$

1

$\begingroup$

Значение слова «между» в данном случае такое же, как значение между в предложении:

Любовь двух людей

Понятно, что любви в воздухе не бывает. Один человек любит другого. У воздуха нет мозга, а значит, нет ни эмоций, ни чувств.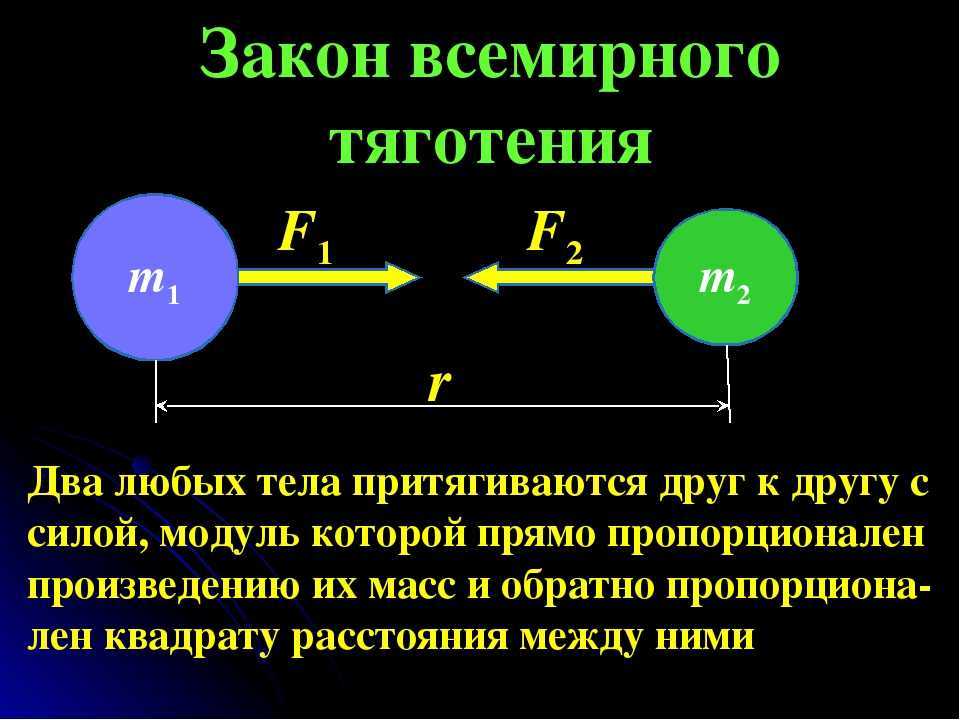

Слово между в приведенном выше предложении означает, что человек А любит человека Б, а человек Б любит человека А.

Таким образом, фраза: «сила между двумя телами» означает, что тело А действует с силой на тело В (эта сила равна на тело В), а тело В воздействует на тело А (эта сила равна на тело В). тело А).

$\endgroup$

3

$\begingroup$

Это не индивидуальная сила, которая существует в пространстве между ними, а скорее между ними в том случае, когда оба тела действуют друг на друга с силой, которая постепенно притягивает их к точке между ними по мере того, как они притягиваются друг к другу , в конечном счете они просто являются двойниками друг друга, равными и противоположными реакциями.

$\endgroup$

1

$\begingroup$

Сила (нефиктивная) — это описание взаимодействия между двумя объектами. Так что, конечно, взаимодействие действует на оба объекта с одинаковой величиной (третий закон Ньютона). $A$ действует на $B$ с той же силой, что и $B$ на $A$. Гравитация такая же. Это взаимодействие между $A$ и $B$. Вы можете разделить его на 2 части: форсировать $B$ на $A$ и форсировать $A$ на $B$. Но на самом деле это 1 взаимодействие.

Побочное примечание: Гравитация как взаимодействие между $A$ и $B$ допустима только в самых основных положениях ньютоновской механики. Позже это описывается как другие вещи, но я не хочу смущать вас.

$\endgroup$

2

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но никогда не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

домашнее задание и упражнения — Почему гравитация действует в центре масс?

спросил 5 лет, 11 месяцев назад

Изменено 5 лет, 11 месяцев назад

Просмотрено 12 тысяч раз

$\begingroup$

Извините за тривиальный вопрос.

Почему гравитация действует в центре масс?

Если у нас есть сплошное $E$, не должна ли гравитация действовать на все точки $(x,y,z)$ в $E$? Почему же тогда, когда мы решаем задачи, мы учитываем только силу веса от центра масс?

• домашние задания и упражнения
• ньютоновская механика 9{n}м_и} \end{уравнение}$$ Поскольку тело $E$ имеет постоянную массу, вы можете получить приведенное выше определение центра масс путем простого интегрирования.

  $\endgroup$

  3

  $\begingroup$

  Это верно только в однородном поле, и вот почему: центр масс — это средневзвешенное по массе положение протяженного объекта. Между тем, полная гравитационная сила есть сумма по всем частям объекта, взвешенная по массе: взвешенные по массе интегралы для среднего и суммы одинаковы. В действительности центр тяжести отличается от центра масс, поскольку переменное гравитационное поле меняет последнюю сумму по частям. Если вы мне не верите, посмотрите на данные НАСА SRTM, в которых радарная антенна на 200-футовой штанге космического корабля «Шаттл» сделала радиолокационную карту Земли — поскольку поле Земли неоднородно, центр тяжести был ниже. чем центр масс, и штука продолжала катиться (представьте себе гантель под углом 45 градусов) — поправки на тягу заставляли стрелу колебаться, и это можно увидеть как рябь на высоте карты.

  $\endgroup$

  $\begingroup$

  Рассмотрим две ситуации, показанные ниже.
  Одна (левая диаграмма), где две массы находятся в неоднородном гравитационном поле, и другая (правая диаграмма), где две массы находятся в однородном гравитационном поле.

  В обоих случаях центр масс находится посередине между двумя массами $M$.
  В неоднородном гравитационном поле гравитационное притяжение массы, ближайшей к большой массе $W$, больше, чем гравитационное притяжение другой массы $w$, поэтому центр тяжести двух масс находится в положении $G$ который не находится посередине между двумя массами.
  В однородном гравитационном поле гравитационное притяжение двух масс $W$ одинаково, поскольку центр тяжести двух масс находится посередине между ними $G$, что совпадает с положением центра масс.

  Чтобы быть уверенным, что центр масс и центр тяжести находятся в одной и той же точке, массы должны находиться в однородном гравитационном поле.

  $\endgroup$

  $\begingroup$

  Единственный раз, когда нам нужно знать, где действует сила, это когда мы вычисляем крутящий момент. Для контактных сил ясно, что сила действует в точке контакта. Но для такой силы, как гравитация, которая действует на расстоянии, все менее ясно.

  В действительности твердый объект состоит из множества частиц, и на каждую из них действуют небольшая гравитационная сила и крутящий момент. Когда нас интересует только ускорение, нам нужна только сумма всех этих сил, которая равна $\vec{F}_{tot} = \sum_i m_i \vec{g}= M\vec{g}$. Но как насчет крутящих моментов?

  Мы хотели бы представить, что эта полная гравитационная сила действует в одной точке для расчета крутящего момента. Существует ли точка $\vec{x}_{cg}$ такая, что $\vec{x}_{cg}\times \vec{F}_{tot}$ дает такой же общий крутящий момент, как суммирование всех малых крутящие моменты?

  Если мы суммируем все крутящие моменты, то получим $\vec{\tau}_{tot} = \sum_i \vec{x}_i\times (m_i\vec{g}) = \left(\frac{1 }{M}\sum_i m_i \vec{x}_i\right) \times (M\vec{g})$. Это говорит нам называть $\vec{x}_{cg} = \frac{1}{M}\sum_i m_i \vec{x}_i$ центром тяжести, и если мы предположим, что полная сила тяжести действует в этот момент он всегда даст нам правильный ответ для гравитационного момента. Наконец, мы замечаем, что оно имеет ту же форму, что и определение центра масс!

  Однако! Если вы проведете вычисления самостоятельно, то заметите, что если $\vec{g}$ варьируется от частицы к частице, то этот вывод не работает. В этом случае центр тяжести фактически не определен. Не может быть $\vec{x}_{cg}$, который делает то, что мы хотим, и даже если он есть, он не уникален, за исключением нескольких особых случаев.

  $\endgroup$

  $\begingroup$

  В действительности гравитация действует на все части массы независимо. Для твердого тела или жидкости части действуют друг на друга. И если размер массы мал по сравнению с нелинейностью гравитационного поля, «массовый эффект» является средним значением всех независимых эффектов, поэтому вы можете смоделировать его как происходящий «в центре тяжести».

  С другой стороны, если размер объекта велик по сравнению с нелинейностью гравитационного поля, необходимо выполнить интеграл массы по полю, чтобы принять во внимание так называемые «приливные эффекты». «. Очень длинный объект, падающий в черную дыру, будет разорван на части из-за взаимодействия различных сил, воздействующих на объект. Это легче понять, если представить себе длинный объект как поток воды (очень малая прочность на растяжение)

  $\endgroup$

  $\begingroup$

  Гравитация заставляет притягивать каждую частицу объекта.

  Если удерживать объект в одной случайной точке, то гравитация притягивает частицы слева и справа от этой точки. Он создает крутящий момент на каждой из этих частиц. Если суммарный крутящий момент с левой стороны больше, чем с правой, то объект вращается против часовой стрелки.

  Выберите другую точку, и крутящие моменты распределятся по-другому.