Момент силы и правило моментов

Определение

Статика — раздел механики, изучающий условия равновесия тел.

Виды равновесия

Устойчивое равновесие
	Если тело вывести из устойчивого равновесия, то появляется сила, возвращающая его в положение равновесия. Устойчивому равновесию соответствует минимальное значение потенциальной энергии (Ep min).
Неустойчивое равновесие
	Если тело вывести из неустойчивого равновесия, то возникает сила, удаляющая тело от положения равновесия. Неустойчивому равновесию соответствует максимальное значение потенциальной энергии (Ep max).
Безразличное равновесие
	При выведении тела из положения безразличного равновесия дополнительных сил не возникает.

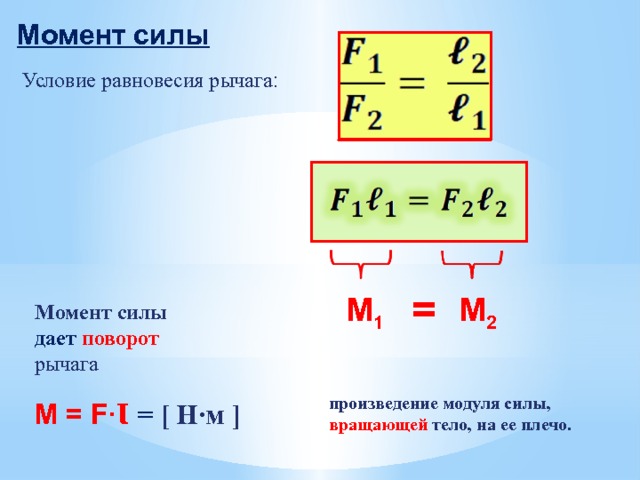
Момент силы

Определение

Момент силы — векторная физическая величина, модуль которой равен произведению модуля силы на плечо силы:

M = Fd

M — момент силы. Единица измерения — Ньютон на метр (Н∙м). Направление вектора момента силы всегда совпадает с направлением вектора силы. d — плечо силы. Единица измерения — метр (м).

Плечо силы — кратчайшее расстояние между осью вращения и линией действия силы.

Пример №1. Стальной шар массой 2 кг колеблется на нити длиной 1 м. Чему равен момент силы тяжести относительно оси, проходящей через точку О перпендикулярно плоскости чертежа, в состоянии, представленном на рисунке?

Плечом силы тяжести, или кратчайшим путем от прямой, проходящей через точку О перпендикулярно плоскости чертежа, до линии действия силы тяжести, будет отрезок, равный максимальному отклонению шара от положения равновесия. Следовательно:

M = Fd = mgd = 2∙10∙0,5 = 10 (Н∙м)

Момент силы может быть положительным и отрицательным.

Если сила вызывает вращение тела по часовой стрелке, то такой момент считают положительным:

M₁ = F₁d₁

Если сила вызывает вращение тела против часовой стрелки, то такой момент считают отрицательным:

M₂ = F₂d₂

Правило моментов

Тело, имеющее неподвижную ось вращения, находится в равновесии, если алгебраическая сумма моментов всех приложенных к телу сил относительно этой оси равна нулю:

∑Mi=0

Иначе правило моментов можно сформулировать так:

Сумма моментов сил, вызывающих вращение тела по часовой стрелке, равна сумме моментов сил, вызывающих вращение тела против часовой стрелки.

∑Mпо час. стр.=∑Mпр. час. стр.

Условия равновесия тел

Тело не участвует в поступательном движении:	∑→Fi=0; →vo=0
Тело не участвует во вращательном движении:	∑Mi=0; ω0=0
Тело находится в состоянии равновесия (не участвует ни в поступательном, ни во вращательном движении)	∑→Fi=0; →vo=0 и ∑→Fi=0; →vo=0

Простые механизмы

Определение

Простые механизмы — приспособления, служащие для преобразования силы. К ним относится рычаг, наклонная плоскость, блоки, клин и ворот.

Наклонная плоскость
	Дает выигрыш в силе. Чтобы поднять груз на высоту h, нужно приложить силу, равную силе тяжести этого груза. Но, используя наклонную плоскость, можно приложить силу, равную произведению силы тяжести на синус угла уклона плоскости: mgsin. θ<mg
Рычаг
	Дает выигрыш в силе, равный отношению плеча второй силы к плечу первой: F1F2..=d2d1..
Неподвижный блок
	Изменяет направление действия силы. Модули и плечи сил при этом равны: F1 = F2 M1 = M2
Подвижный блок
	Дает выигрыш в силе в 2 раза: d1 = R d2 = 2R F1 = 2F2
Клин
	Делит силу на две равные части, направление которых зависит от формы клина: →F=→F1+→F2

Золотое правило механики

При использовании простых механизмов мы выигрываем в силе, но проигрываем в расстоянии.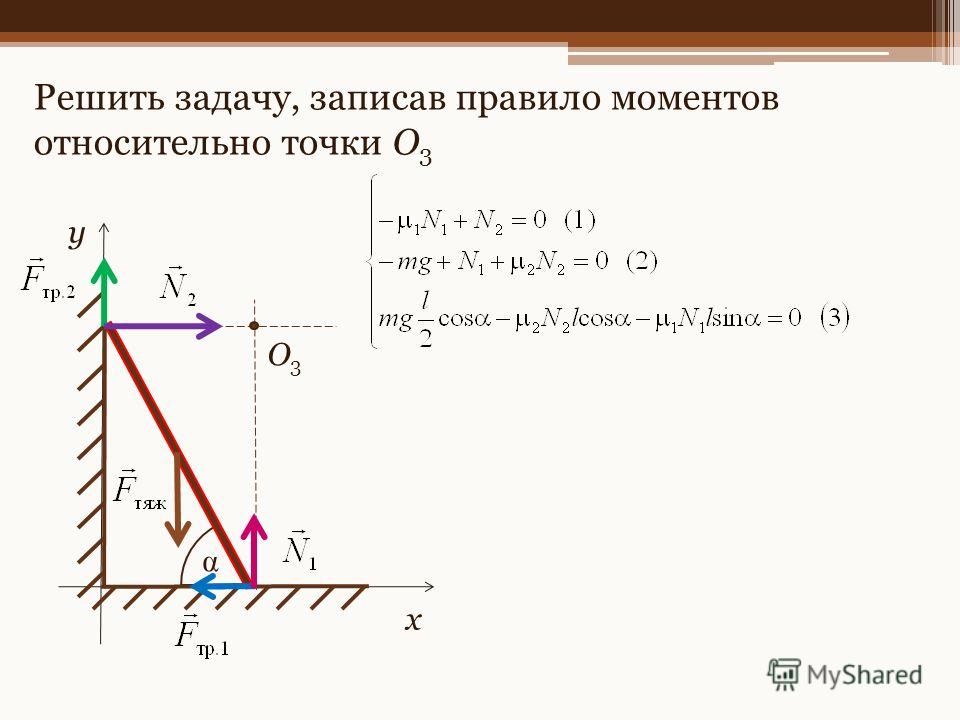 Поэтому выигрыша в работе простые механизмы не дают.

Задание EF22660 Мальчик взвесил рыбу на самодельных весах с коромыслом из лёгкой рейки (см. рисунок). В качестве гири он использовал батон хлеба массой 0,8 кг. Определите массу рыбы.

---

Алгоритм решения

1.Записать исходные данные.

2.Записать правило моментов и выполнить решение в общем виде.

3.Подставить известные данные и вычислить искомую величину.

Решение

Известна лишь масса батона: m₁ = 0,8 кг. Но мы также можем выразить плечи для силы тяжести батона и хлеба. Для этого длину линейки примем за один. Так как линейка поделена на 10 секций, можем считать, что длина каждой равна 0,1. Тогда плечи сил тяжести батона и рыба соответственно равны:

d₁ = 0,3

d₂ = 0,4

Запишем правило моментов:

F₁ d₁ = F₂ d₂

Сила тяжести равна произведению массы на ускорение свободного падения.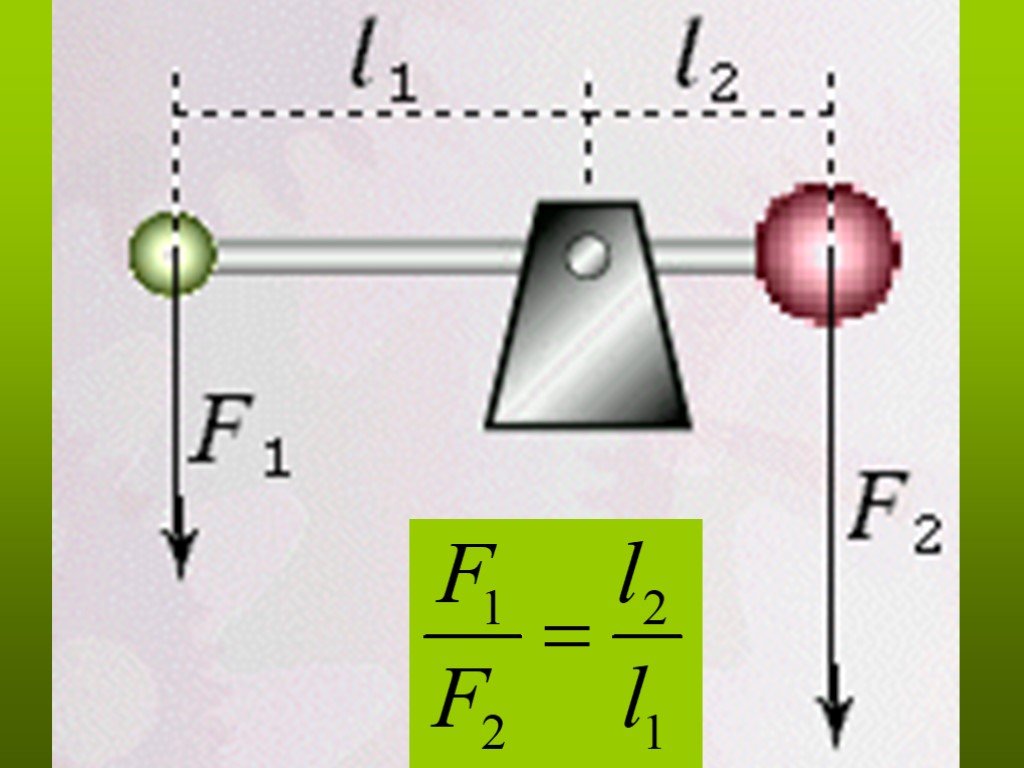 Поэтому:

m₁gd₁ = m₂gd₂

m₁d₁ = m₂d₂

Отсюда масса рыбы равна:

m2=m1d1d2..=0,8·0,30,4..=0,6 (кг)

.

Ответ: 0,6

pазбирался: Алиса Никитина | обсудить разбор | оценить

Задание EF18706

Однородный куб опирается одним ребром на пол, другим на вертикальную стену (см. рисунок). Плечо силы трения F

тр относительно оси, проходящей через точку О₃ перпендикулярно плоскости чертежа, равно…

Ответ:

а) 0

б) О₂О₃

в) О₂В

г) О₃В

---

Алгоритм решения

1. Сформулировать определение плеча силы.
2. Найти плечо силы трения и аргументировать ответ.

Решение

Плечом силы трения называют кратчайшее расстояние от оси вращения до линии, вдоль которой действует сила.

Чтобы найти такое расстояние, нужно провести из точки равновесия перпендикуляр к линии действия силы трения. Отрезок, заключенный между этой точкой и линией, будет являться плечом силы трения. На рисунке этому отрезку соответствует отрезок О₃В.

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор | оценить

Алиса Никитина | Просмотров: 9.1k

Физика. 8 класс

Физика. 8 класс

Кикоин И.К., Кикоин А.К. Физика. 8 класс. Учебное пособие. — 4-е изд., перераб. — М.: Просвещение, 1973. — 256 с. Советская фундаментальная наука, и физика в частности, была одной из сильнейших в мире. А по каким учебникам учились в школе и готовились к экзаменам будущие лучшие в мире ученые? Вашему вниманию предлагается учебник по физике для советских восьмиклассников. Охватывает разделы «Кинематика», «Динамика, «Равновесие тел» и «Законы сохранения в механике». Оглавление Глава 1. Общие сведения о движении § 1. ПОСТУПАТЕЛЬНОЕ ДВИЖЕНИЕ ТЕЛ. МАТЕРИАЛЬНАЯ ТОЧКА § 2. ПОЛОЖЕНИЕ ТОЧКИ (ТЕЛА) В ПРОСТРАНСТВЕ § 3. ПЕРЕМЕЩЕНИЕ § 4. ПОНЯТИЕ О ВЕКТОРАХ. ВЕКТОР ПЕРЕМЕЩЕНИЯ. КООРДИНАТЫ ТЕЛА § 5. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: СЛОЖЕНИЕ ВЕКТОРОВ § 6. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: ВЫЧИТАНИЕ ВЕКТОРОВ § 7. ДЕЙСТВИЯ НАД ВЕКТОРАМИ: УМНОЖЕНИЕ ВЕКТОРА НА СКАЛЯР § 8. ПРЯМОЛИНЕЙНОЕ РАВНОМЕРНОЕ ДВИЖЕНИЕ § 9. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ДВИЖЕНИЯ § 10. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ § 11. ОТНОСИТЕЛЬНОСТЬ ДВИЖЕНИЯ (ПРОДОЛЖЕНИЕ) § 12. ЕДИНИЦЫ ИЗМЕРЕНИЙ ДЛИНЫ И ВРЕМЕНИ Глава 2. Прямолинейное неравномерное движение § 13. СРЕДНЯЯ СКОРОСТЬ § 14. МГНОВЕННАЯ СКОРОСТЬ § 15. УСКОРЕНИЕ. РАВНОУСКОРЕННОЕ ДВИЖЕНИЕ § 16. НАПРАВЛЕНИЕ УСКОРЕНИЯ § 17. ПЕРЕМЕЩЕНИЕ ПРИ РАВНОУСКОРЕННОМ ДВИЖЕНИИ § 18. СРЕДНЯЯ СКОРОСТЬ ПРИ ПРЯМОЛИНЕЙНОМ РАВНОУСКОРЕННОМ ДВИЖЕНИИ. СВЯЗЬ МЕЖДУ ПЕРЕМЕЩЕНИЕМ И СКОРОСТЬЮ § 19. ИЗМЕРЕНИЕ УСКОРЕНИЯ § 20. СВОБОДНОЕ ПАДЕНИЕ ТЕЛ § 21. ДВИЖЕНИЕ ТЕЛА, БРОШЕННОГО ВЕРТИКАЛЬНО ВВЕРХ Глава 3. Криволинейное движение § 22. ПЕРЕМЕЩЕНИЕ И СКОРОСТЬ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 23. УСКОРЕНИЕ ПРИ КРИВОЛИНЕЙНОМ ДВИЖЕНИИ § 24. ДВИЖЕНИЕ ПО ОКРУЖНОСТИ. УГОЛ ПОВОРОТА И УГЛОВАЯ СКОРОСТЬ § 25. УСКОРЕНИЕ ПРИ РАВНОМЕРНОМ ДВИЖЕНИИ ТЕЛА ПО ОКРУЖНОСТИ § 26. ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА § 27. ОБ ОТНОСИТЕЛЬНОСТИ ДВИЖЕНИЯ ТЕЛА ПРИ ВРАЩЕНИИ СИСТЕМЫ ОТСЧЕТА Динамика Глава 4. Законы движения § 28. ТЕЛА И ИХ ОКРУЖЕНИЕ. ПЕРВЫЙ ЗАКОН НЬЮТОНА § 29. ПОЧЕМУ ВОЗНИКАЮТ УСКОРЕНИЯ § 30. ВЗАИМОДЕЙСТВИЕ TEЛ. УСКОРЕНИЯ ТЕЛ ПРИ ИХ ВЗАИМОДЕЙСТВИИ § 31. ИНЕРТНОСТЬ ТЕЛ § 32. МАССА ТЕЛ § 33. МАССА ЛУНЫ § 34. СИЛА § 35. ВТОРОЙ ЗАКОН НЬЮТОНА § 36. ВТОРОЙ ЗАКОН НЬЮТОНА (продолжение) § 37. ИЗМЕРЕНИЕ СИЛ. ДИНАМОМЕТР § 38. ТРЕТИЙ ЗАКОН НЬЮТОНА § 39. ЗНАЧЕНИЕ ЗАКОНОВ НЬЮТОНА Глава 5. Силы природы § 40. ЭЛЕКТРОМАГНИТНЫЕ СИЛЫ § 41. СИЛА УПРУГОСТИ § 42. СИЛА ВСЕМИРНОГО ТЯГОТЕНИЯ § 43. ПОСТОЯННАЯ ВСЕМИРНОГО ТЯГОТЕНИЯ § 44. СИЛА ТЯЖЕСТИ § 45. ВЕС ТЕЛ § 46. ИЗМЕРЕНИЕ МАССЫ ТЕЛ ВЗВЕШИВАНИЕМ § 47. МАССА ЗЕМЛИ § 48. СИЛА ТРЕНИЯ. ТРЕНИЕ ПОКОЯ § 49. СИЛА ТРЕНИЯ СКОЛЬЖЕНИЯ § 50. СИЛА СОПРОТИВЛЕНИЯ, ВОЗНИКАЮЩАЯ ПРИ ДВИЖЕНИИ ТЕЛА В ЖИДКОСТИ ИЛИ В ГАЗЕ Глава 6. Применение законов движения § 51. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ УПРУГОСТИ § 52. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: НАЧАЛЬНАЯ СКОРОСТЬ ТЕЛА РАВНА НУЛЮ ИЛИ ПАРАЛЛЕЛЬНА СИЛЕ ТЯЖЕСТИ § 53. ВЕС ТЕЛА, ДВИЖУЩЕГОСЯ С УСКОРЕНИЕМ § 54. НЕВЕСОМОСТЬ § 55. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ПОД УГЛОМ К ГОРИЗОНТУ § 56. ДВИЖЕНИЕ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ: ТЕЛО БРОШЕНО ГОРИЗОНТАЛЬНО § 57. ИСКУССТВЕННЫЕ СПУТНИКИ ЗЕМЛИ. ПЕРВАЯ КОСМИЧЕСКАЯ СКОРОСТЬ § 58. ДВИЖЕНИЕ ПЛАНЕТ § 59. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ СИЛЫ ТРЕНИЯ § 60. ДВИЖЕНИЕ ТЕЛА ПОД ДЕЙСТВИЕМ НЕСКОЛЬКИХ СИЛ § 61. ПАДЕНИЕ ТЕЛА В ГАЗЕ ИЛИ В ЖИДКОСТИ § 62. НАКЛОН ТЕЛ ПРИ ДВИЖЕНИИ НА ПОВОРОТАХ § 63. ПРИ КАКИХ УСЛОВИЯХ ТЕЛА ДВИЖУТСЯ ПОСТУПАТЕЛЬНО? ЦЕНТР МАСС И ЦЕНТР ТЯЖЕСТИ § 64. ВСЕГДА ЛИ ВЕРНЫ ЗАКОНЫ МЕХАНИКИ НЬЮТОНА Равновесие тел Глава 7. Элементы статики § 65. РАВНОВЕСИЕ ТЕЛ ПРИ ОТСУТСТВИИ ВРАЩЕНИЯ § 66. РАВНОВЕСИЕ ТЕЛА С ЗАКРЕПЛЕННОЙ ОСЬЮ. МОМЕНТ СИЛЫ § 67. ПРАВИЛО МОМЕНТОВ § 68. УСТОЙЧИВОСТЬ РАВНОВЕСИЯ ТЕЛ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 69. РАВНОВЕСИЕ ТЕЛ НА ОПОРАХ Законы сохранения в механике Глава 8. Закон сохранения импульса § 70. СИЛА И ИМПУЛЬС § 71. ЗАКОН СОХРАНЕНИЯ ИМПУЛЬСА § 72. РЕАКТИВНОЕ ДВИЖЕНИЕ Глава 9. Механическая работа и мощность § 74. ПОЧЕМУ РАБОТА ОПРЕДЕЛЯЕТСЯ КАК ПРОИЗВЕДЕНИЕ § 75. БОЛЕЕ ОБЩЕЕ ОПРЕДЕЛЕНИЕ РАБОТЫ § 76. РАБОТА, СОВЕРШАЕМАЯ СИЛАМИ, РАВНОДЕЙСТВУЮЩАЯ КОТОРЫХ НЕ РАВНА НУЛЮ. ТЕОРЕМА О КИНЕТИЧЕСКОЙ ЭНЕРГИИ § 77. РАБОТА СИЛЫ ТЯЖЕСТИ § 78. РАБОТА СИЛЫ УПРУГОСТИ § 79. РАБОТА СИЛЫ ТРЕНИЯ § 80. МОЩНОСТЬ Глава 10. Закон сохранения энергии § 82. РАБОТА ТЕЛА И ИЗМЕНЕНИЕ ЕГО СОСТОЯНИЯ. ПОНЯТИЕ ОБ ЭНЕРГИИ § 83. ПОТЕНЦИАЛЬНАЯ И КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 84. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ УПРУГО ДЕФОРМИРОВАННОГО ТЕЛА § 85. ПОТЕНЦИАЛЬНАЯ ЭНЕРГИЯ ТЕЛА, НАХОДЯЩЕГОСЯ ПОД ДЕЙСТВИЕМ СИЛЫ ТЯЖЕСТИ § 36. КИНЕТИЧЕСКАЯ ЭНЕРГИЯ § 87. ЗАКОН СОХРАНЕНИЯ ЭНЕРГИИ § 88. МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И СИЛА ТРЕНИЯ § 89. ПРЕВРАЩЕНИЕ ЭНЕРГИИ И ИСПОЛЬЗОВАНИЕ МАШИН § 90. КОЭФФИЦИЕНТ ПОЛЕЗНОГО ДЕЙСТВИЯ § 91. СТОЛКНОВЕНИЕ ТЕЛ § 92. ДВИЖЕНИЕ ЖИДКОСТИ ПО ТРУБАМ. ЗАКОН БЕРНУЛЛИ § 93. О ЗНАЧЕНИИ ЗАКОНОВ СОХРАНЕНИЯ Заключение Лабораторные работы 1. Определение ускорения тела при равноускоренном движении 2. Определение коэффициента трения скольжения 3. Изучение движения тела по параболе 4. Выяснение условия равновесия рычага 5. Определение центра тяжести плоской пластины Ответы к упражнениям

Коэффициенты корреляции

Коэффициенты корреляции Вернуться к оглавлению

Обзор урока

• Корреляция
• Момент продукта Pearson (r)
• Копьеносец Ро
• Факторы, влияющие на размер r
• Домашнее задание

Корреляция

Обычное использование слова корреляция относится к отношения между двумя или более объектами (идеями, переменными. ..). В статистике слово корреляция относится к отношениям между двумя переменными. Мы хотим иметь возможность определить количественно это отношение, измерить его силы, разработать уравнение для прогнозирования результатов и, в конечном счете, сделать проверяемый вывод о родительской популяции. Этот урок посвящен измерению его силы, с уравнением, которое будет на следующем уроке, а выводы по тестированию намного позже.

Примеры: одна переменная может быть числом охотники в регионе, а другой переменной может быть популяция оленей. Возможно, по мере увеличения числа охотников популяция оленей уменьшается. это пример отрицательная корреляция : как одна переменная увеличивается, другой уменьшается. Положительная корреляция — это то место, где две переменные реагируют одинаково, увеличиваясь или уменьшаясь вместе. Температура в градусах Цельсия и Фаренгейта имеет положительную корреляцию.

Момент продукта Pearson

Как определить, есть ли корреляция? Наблюдая за графиками, человек может сказать, есть ли корреляция по тому, как близко данные напоминают линию. Если точки разбросаны, то может быть нет корреляции . Если точки будут точно соответствовать квадратное или показательное уравнение, и т. д. , тогда у них есть нелинейная корреляция . В этом курсе мы ограничимся линейными корреляциями и, следовательно, линейная регрессия. Поскольку данные почти линейны, данные могут быть заключены в эллипс. Большая ось (длина) эллипса относительно малой оси (ширины) эллипса, являются показателем степени корреляции.

Как можно определить путем осмотра тип корреляции?
Если график переменных представляет собой линию с положительным наклоном, то существует положительная корреляция ( x увеличивается по мере увеличения y ). Если наклон линии отрицательный, то существует отрицательная корреляция (при увеличении x y уменьшении).

Важным аспектом корреляции является то, насколько она сильна . Сила корреляции измеряется корреляция коэффициент r .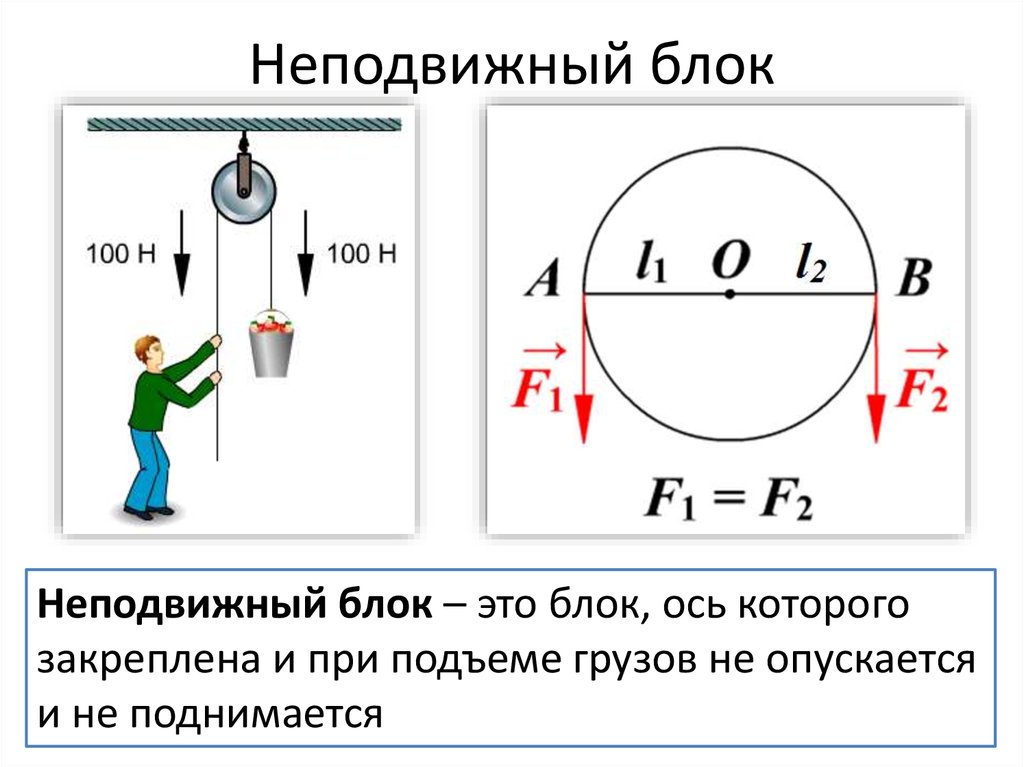 Другое название для r — корреляция моментов продукта Пирсона. коэффициент в честь Карла Пирсона, разработавшего его около 1900 года. Обычно используются как минимум три различные формулы чтобы вычислить это число и эти разные формулы представляют несколько разные подходы к проблеме. Однако такое же значение для r получается любой из различных процедур. Сначала мы даем 9Формула исходной оценки 0020. n имеет обычное значение количества упорядоченных пар есть в нашем образце. Также важно признать разница между суммой квадратов и квадраты сумм!

г = п ху — ( х )( г ) sqrt[ n ( x 2 ) — ( x ) 2 ] · sqrt[ n ( y 2 ) — ( г ) 2 ]

Далее мы представляем формулу оценки отклонения . Эта формула ближе к истории развития поскольку он дает среднее перекрестное произведение стандартные оценки двух переменных, но в вычислительно более простой формат.

г =         ху sqrt( x 2 y 2 )

Нам нужно сделать несколько замечаний относительно обозначений, поскольку x и y переменных в формуле выше были преобразованы из исходных переменных путем вычитания их средств.

Наконец, мы представляем формулу ковариации , что является еще одним подходом. Ковариации обычно дано между двумя переменными, и это одна из причин, почему. (Следует отметить, что размер ковариации зависит в единицах измерения, используемых для каждой переменной. Однако коэффициент корреляции — нет.)

r =    с ху    с x с г

r часто обозначается как r _xy чтобы подчеркнуть две рассматриваемые переменные.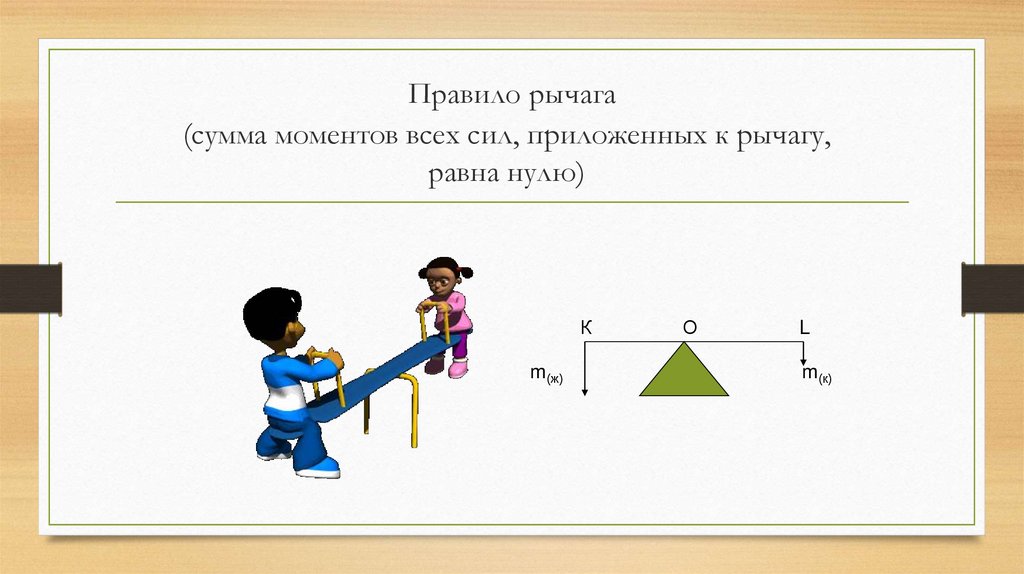 Для выборок коэффициент корреляции представлен как r а коэффициент корреляции для популяций обозначается греческой буквой ро (которая может выглядеть как стр. ). Имейте в виду, что коэффициент корреляции ро Спирмена также использует греческую букву ро, но обычно применяется к образцам и данным ранжирования (порядковые данные).

Чем ближе r к +1, тем сильнее положительная корреляция. Чем ближе r к -1, тем сильнее отрицательная корреляция. Если | г | = 1 точно, две переменные идеально коррелированы ! Температура в градусах Цельсия и Фаренгейта идеально коррелирует.

Формальная проверка гипотезы может быть применена к r определить, насколько значим результат. Это предмет Хинкля, глава 17 и этот урок 12. Дистрибутив Student t с n -2 степени свободы.

Помните, корреляция не подразумевает причинно-следственной связи.

Нулевое значение для r не означает, что корреляции нет, может быть нелинейная корреляция. Также могут быть задействованы смешанные переменные . Предположим, вы обнаружить, что майнеры имеют более высокий, чем в среднем, уровень рак легких. У вас может возникнуть соблазн немедленно заключить что их занятие является причиной, тогда как, возможно, регион имеет обильные утечки радиоактивного газа радона из подземных областей, и все люди в этой области затронуты. Или, может быть, они заядлые курильщики….

r ² часто используется и называется коэффициент детерминации . Это доля изменения значений и . это объясняется регрессией по методу наименьших квадратов y на x . Это будет обсуждаться далее в уроке 6 после введения метода наименьших квадратов.

Коэффициенты корреляции, величина которых находится в диапазоне от 0,9 до 1,0. указывают переменные, которые можно считать очень сильно коррелированными. Коэффициенты корреляции, величина которых находится в диапазоне от 0,7 до 0,9.указывают переменные, которые можно считать сильно коррелированными. Коэффициенты корреляции, величина которых находится в диапазоне от 0,5 до 0,7. указывают переменные, которые можно считать умеренно коррелированными. Коэффициенты корреляции, величина которых находится в диапазоне от 0,3 до 0,5. указывают переменные, которые имеют низкую корреляцию . Коэффициенты корреляции, величина которых меньше 0,3 имеют небольшую, если вообще имеют (линейную) корреляцию. Мы можем легко видеть, что 0,9< |r| < 1,0 соответствует 0,81 < r ² < 1,00; 0,7 < |r| < 0,9 соответствует 0,49 < r ² < 0,81; 0,5 < |r| < 0,7 соответствует 0,25 < r ² < 0,49; 0,3 < |r| < 0,5 соответствует 0,09 < г ² < 0,25; и 0,0 < |r| < 0,3 соответствует 0,0 < r ² < 0,09.

Копейщик Ро для рейтинговых/порядковых данных

Часто бывает так, что данные, которые мы хотим измерить корреляцию ибо не является интервалом или отношением уровня измерения. Был разработан коэффициент корреляции Ро Спирмена. чтобы справиться с этой ситуацией. Это досадное исключение из общего правила, Греческие буквы — параметры населения! Есть и другие.

Формула расчета ро Спирмена коэффициент корреляции следующий.

ро (р) = 1 —   6 d 2 н ( н 2 -1)

n – количество парных рангов и d – разница между парными разрядами. Если равных результатов нет, коэффициент корреляции Спирмена ро будет еще ближе к коэффициенту корреляции моментов произведений Пирсона. Также обратите внимание, что эту формулу легко понять, если Вы понимаете, что сумма квадратов от 1 до п можно выразить как n ( n + 1)(2 n + 1)/6.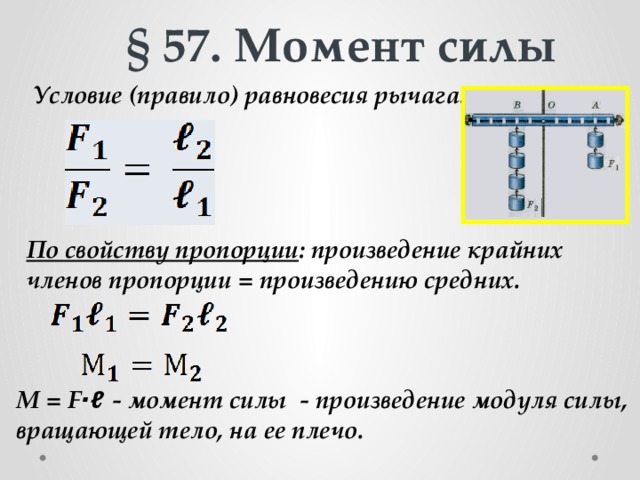 Отсюда вы можете получить наименьшую сумму d ² равен нулю, а наибольшая сумма d ² равна удвоенная сумма квадратов нечетных целых чисел до n /2, и тогда такая сумма масштабируется между -1 и +1.

Пример: Предположим, у нас есть результаты тестов из 110, 107, 100, 96, 89, 78, 67, 66 и 49. Они соответствуют рангам с 1 по 9. Если бы были дубликаты, то нам пришлось бы найти средний рейтинг для дубликатов и подставьте это значение для наших рангов. Соответствующие общие баллы на первой странице были следующими: 29, 32, 27, 29, 25, 25, 21, 26, 22. Таким образом, эти ранги следующие: 2,5, 1, 4, 2,5, 6,5, 6,5, 9, 5, 8. (Обратите внимание, что если бы мы изменили порядок, назначив ранги от низкого к высокому, а не от высокого к низкому, в результате Коэффициент корреляции Ро Спирмена изменил бы знак.)

Мы построили таблицу ниже из информации выше. Мы добавили дополнительные столбцы d и d ² для простоты расчета ро Спирмена.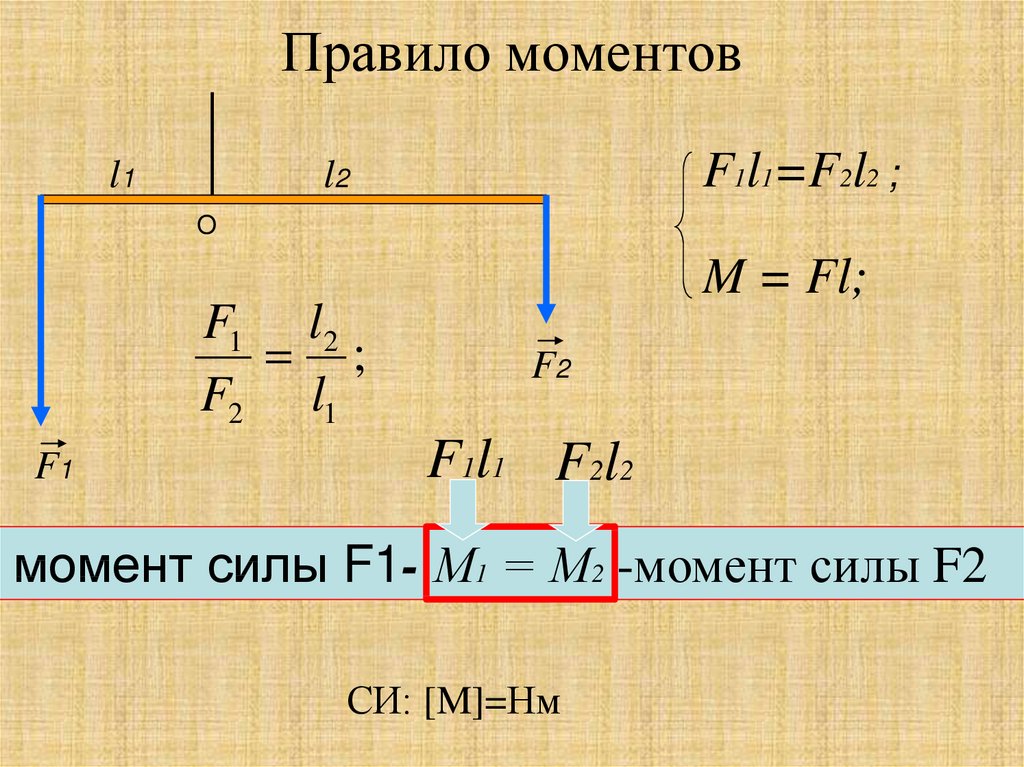 Используя формулу Ро Спирмена, мы получаем 1-6(24)/(9(80)) = 0,80.

409363 40163 4 6 308

Total ( x )	page 1 ( y )	x rank	y rank	d	d 2	xy	x 2	y 2
110	29	1	2.5	-1.5	2.25	3190	12100	841
107	32	2	1	1	1	3424	11449	1024
100	27	3	4	-1	1	2700	10000	763 2700	1000000	729979363 2700	1000000	729979793 2700	1000000	7963
96	29	4	2. 5	1.5	2.25	2784	9216	841
89	25	5	6,5	-1,5	2,25	2225	7921	625
78	25	6	6.5	-0.5	0.25	1950	6084	625
67	21	7	9	-2	4	1407
66	26	8	5	3	9	1716	4356	8 66
49	22	9	8	1	1	1078	4
—	—			——	—-	——	——	—-
762	236	:суммы:		0	24	20474	6 236363 981086

Мы добавили дополнительные столбцы xy , x ² , и y ² для облегчения расчета коэффициент корреляции моментов произведений Пирсона. Использование формулы сырой оценки для момента продукта Пирсона коэффициент корреляции получаем (9×20474-762×236)/кв.кв.((9×68016-762 ² )(9×6286-236 ² ) = 0,843. г ² = 0,71 что означает 71% вариации и объясняется изменением x . Также верно и, возможно, полезнее знать, что та же корреляция коэффициент получается при обмене x и y . Однако получится другое уравнение. Возможно, имеет смысл использовать результаты первой страницы чтобы предсказать окончательный результат теста, а не наоборот!

Факторы, влияющие на размер

r Мы рассмотрели, как вычислить r , что означают различные значения, но также важно понять, какие факторы на это влияют. Во-первых, помните, имеет смысл только вычислять коэффициент корреляции, если данные парных наблюдений измеренных на интервале или шкала отношений. Далее, поскольку нас здесь интересуют только линейные корреляция, момент произведения Пирсона коэффициент корреляции будет недооценивать отношения, если есть криволинейные отношения. Рекомендуется создать диаграмму рассеяния перед расчет любых коэффициентов корреляции, а затем действовать только в том случае, если корреляция достаточно сильна.

По мере увеличения однородности группы дисперсия уменьшается, а величина коэффициент корреляции стремится к нулю. Таким образом, исследователь должен убедиться, достаточной неоднородности (изменчивости), чтобы отношения могут проявляться. В общем случае коэффициент корреляции не зависит от размера группы.

ЗАДНЯЯ ЧАСТЬ	ДОМАШНЕЕ ЗАДАНИЕ	ДЕЯТЕЛЬНОСТЬ	ПРОДОЛЖИТЬ

---

• электронная почта: [email protected]
• голос/почта: 269 471-6629/ BCM&S Smith Hall 106; Университет Эндрюса; Берриен Спрингс,
• аудитория: 269 471-6646; Smith Hall 100/ ФАКС: 269 471-3713; МИ, 49104-0140
• домашний: 269 473-2572; 610 Н. Главная улица; Берриен Спрингс, Мичиган 49103-1013
• URL-адрес: http://www.andrews.edu/~calkins/math/edrm611/edrm05.htm
• Copyright © 1998-2005, Кит Г. Калкинс. Пересмотрено 18 июля 2005 г. или позднее.

Рука с моментом

— формула, определение, примеры Момент силы или просто момент — это термин, используемый в физике для описания стремления силы заставить тело вращаться вокруг заданной точки или оси. Это отличается от тенденции тела переводить или двигаться в направлении действия силы.

В этой концепции большое значение имеет плечо момента или расстояние от оси вращения. Изменяя плечо момента, простые механизмы, такие как рычаг, шкив, шестерня и большинство других, создают механическое преимущество. Ньютон-метр (кгм²/с²) на данный момент является единицей СИ. Давайте углубимся в концепции плеча момента и крутящего момента.

Скачать формулы для машиностроения GATE — Сопротивление материалов

Содержание

• 1. Что такое рычаг момента?
• 2. Как векторы силы связаны с моментами?
• 3. Пример рычага момента
• 4. Проблемы с рычагом момента

Прочитать статью полностью

Что такое рычаг момента?

Плечо момента шарнира — это расстояние между его осью и линией силы, действующей на него. В действии используется плечо момента для каждого сустава. Чем больше длина плеча момента, тем большая нагрузка будет передаваться на ось сустава посредством рычага.

Определение рычага момента

«Способность объекта вращаться вокруг оси определяется действием силы, которая определяется плечом момента».

Загрузить формулы для машиностроения GATE — проектирование машин

Формула рычага момента

В качестве примера рассмотрим попытку разделения гайки и болта. Предположим, что маленькое плечо момента не позволяет вам выполнить задачу вручную. В этом случае вы можете использовать полумесяц, который дает вам значительно большее плечо момента и позволяет вам прикладывать гораздо меньшее усилие для создания гораздо большего крутящего момента (силы вращения) на гайке. По следующим причинам крутящий момент на оси:

Крутящий момент = Сила x Момент плеча

Следовательно, формула плеча момента будет:

Момент плеча = Крутящий момент / Сила

Что такое крутящий момент?

Крутящий момент — вращательный эквивалент силы в физике и механике. Он также известен как момент, момент силы, сила вращения или эффект поворота, в зависимости от области исследования. Это пример того, как сила может изменить вращательное движение тела. Идея возникла благодаря изучению Архимедом рычагов, как показала его известная цитата: «Дайте мне рычаг и точку опоры, и я сдвину Землю».

Как векторы силы связаны с моментами?

Вектор силы представляет направление силы. С точки зрения инженерной механики, мы знаем об основах линии силы тяжести. Когда мы поднимаем объект, действуют несколько векторов силы. У нас есть такие силы, как гравитация, трение об объект, реакция земли, мышечные силы (возникающие вдоль линии между началом и местом прикрепления мышцы), импульсные силы и многое другое. Сумма всех векторов и соответствующих им сил определяет, каким будет движение.

Пример моментного рычага

Например, если бы я ударил боксерскую грушу, то работали бы следующие силы и векторы.

• Я генерировал силу от своих ног, чтобы начать удар силами реакции земли.
• Внутренние силы от каждой задействованной мышцы, в том числе в стопе, ногах, туловище и руке.
• Сила за моей рукой.
• Импульс мешка.

Загрузить формулы для машиностроения GATE — Технология производства и материалы

Проблемы с моментом Рычаг

Вопрос [1] — Сила 16 Н создает момент 64 Нм. Плечо момента _____.

Ответ — 4 м

Вопрос [2] — Однородная балка длиной 1 м и массой 2 кг поднимается вертикально вверх силой F на отметке 100 см. Какая минимальная сила необходима для этого?

Ответ — 10 N

Часто задаваемые вопросы о Moment Arm

• Что означает «Moment Arm»?

  Расстояние, измеренное перпендикулярно между линией действия силы и центром моментов, известно как плечо момента или плечо рычага.

• Что такое плечо момента и крутящий момент?

  Результатом вращения линейной силы является крутящий момент, также известный как момент или момент силы. Крутящий момент рассчитывается как произведение силы и плеча момента, которое представляет собой угол между линией действия силы и ее осью вращения.

• Почему важно плечо момента?

  Влияние силы, вызывающей (или предотвращающей) вращение предмета вдоль оси, определяется плечом момента. Это кратчайшее возможное перпендикулярное расстояние между осью сустава и линией силы, прилагаемой для сопротивления.

• Почему крутящий момент называется моментом?

  Момент — это фраза, используемая для описания стремления объекта вращаться вокруг оси при приложении одной или нескольких сил, но не обязательно при изменении углового момента объекта (это понятие в физике называется крутящим моментом).

• Что такое плечо момента мышцы?

  Расстояние между линией действия мышцы и осью сустава называется плечом мышечного момента.