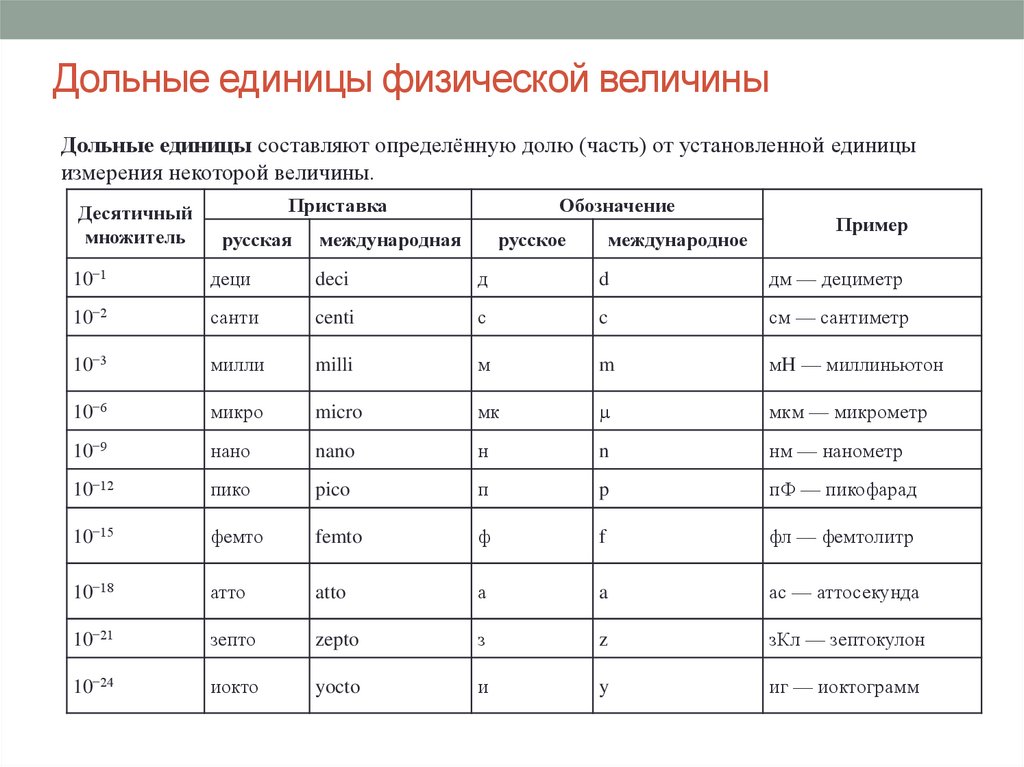
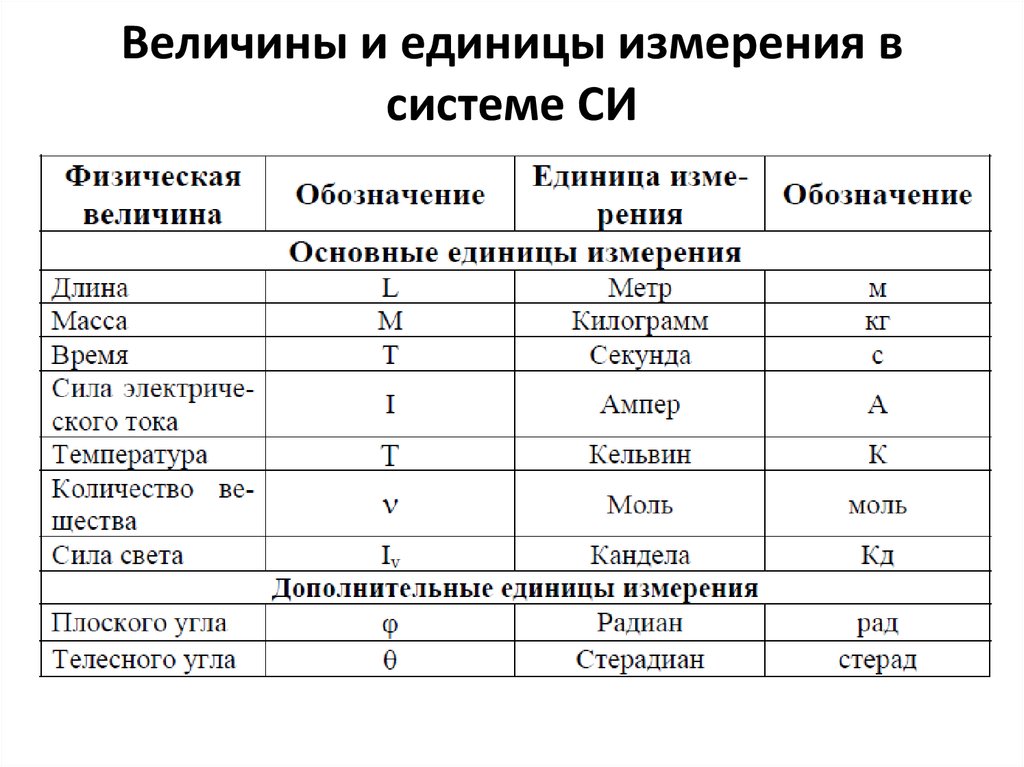
Единицы измерения физических величин. Международная система единиц (СИ)
Чтобы решить, как можно быстрее приехать к бабушке: на автобусе, трамвае или такси, мы сравниваем скорости их движения. В данном примере скорость движения — физическая величина. Она количественно описывает физическое явление — движение. Если скорость легкового автомобиля 90 км/ч, а трактора — 30 км/ч, то мы понимаем, что автомобиль движется в 3 раза быстрее трактора.
Для количественного описания физического явления нагревания служит физическая величина — температура. Если температура воды в чайнике 80 °C, а в стакане 20 °C, то это значит, что вода в чайнике нагрета в 4 раза сильнее, чем в стакане.
В физике используется множество разных физических величин: длина, сила, давление, громкость, напряжение, сопротивление и др.
Каждая физическая величина имеет символическое обозначение, числовое значение и единицу измерения. Например, длина бруска l = 0,2 м. Здесь l — символическое обозначение длины, 0,2 — числовое значение, м — сокращенное обозначение единицы длины (метра). Символами физических величин, как правило, являются буквы латинского и греческого алфавитов.
Здесь l — символическое обозначение длины, 0,2 — числовое значение, м — сокращенное обозначение единицы длины (метра). Символами физических величин, как правило, являются буквы латинского и греческого алфавитов.
Еще пример: масса арбуза m = 5 кг. Масса — физическая величина, m — ее символическое обозначение, 5 — числовое значение, кг — сокращенное обозначение единицы массы (килограмма).
Исторически сложилось так, что у разных народов и государств единицы измерения одних и тех же физических величин различались. Чаще всего это были единицы, соответствующие размерам отдельных частей тела человека, массе семени бобов и т. д. Пользоваться такими единицами было неудобно, особенно в торговле между разными государствами. Например, в Англии в качестве одной из единиц измерения длины использовался фут (1 фут = 30,5 см), а на Руси — аршин (1 аршин = 71,1 см). Необходимо было упорядочить систему единиц, сделать ее удобной в использовании всеми странами.
В 1960 г. была введена единая Международная система единиц (сокращенно СИ — Система Интернациональная). Ею пользуется большинство стран.
была введена единая Международная система единиц (сокращенно СИ — Система Интернациональная). Ею пользуется большинство стран.
Основными единицами в СИ являются: 1 метр (м) — для длины, 1 килограмм (кг) — для массы, 1 секунда (с) — для промежутка времени, 1 Кельвин (К) — для температуры. О других единицах вы узнаете позже.
Но всегда ли удобно, например, измерять промежуток времени в секундах, а длину — в метрах?
Действительно, промежуток времени движения поезда из Минска в Москву измеряют в часах (ч), а путь — в километрах (км). Единицы 1 ч и 1 км — это неосновные единицы. Между основными и неосновными единицами существует связь. Например, 1 км = 1000 м, 1 ч = 3600 с.
Основные единицы измерения имеют свои эталоны. Эталоны хранятся в г. Севре (Франция) в Международном бюро мер и весов.К примеру, там есть эталон килограмма. Это цилиндр из платино-иридиевого сплава. По эталону изготавливаются копии, которыми пользуются различные страны. По мере изучения физики вы познакомитесь с эталонами других единиц измерения.
Примеры решения задач
1. В одной из книг немецкого путешественника XVII в. есть такие строки: «Шелковая материя, привозимая с востока, называется русскими «китайкой», и каждый кусок содержит ни больше ни меньше как восемь с четвертью аршина». Сколько метров было в куске материи?
Решение. Так как 1 аршин = 71,1 см, то восемь с четвертью аршина будут равны:
8¼ аршина = 8,25 ⋅ 71,1 см ≈ 586,6 см ≈ 5,9 м.
Ответ: в куске было примерно 5,9 м ткани.
2. В известной книге английского писателя Джонатана Свифта «Путешествие Гулливера» можно прочитать: «На расстоянии четырех ярдов от меня напротив моего правого уха я услышал стук, продолжавшийся больше часа, точно возводилась какая-то постройка. Повернув голову, насколько позволяли державшие ее веревочки и колышки, я увидел деревянный помост, возвышавшийся над землей на полтора фута». Выразите расстояние четыре ярда и высоту полтора фута в сантиметрах (см) и метрах (м).
Решение. Известно, что 1 ярд = 91,4 см, 1 фут = 30,5 см. Тогда
4 ярда = 4 ⋅ 91,4 см = 365,6 см = 3,7 м;
1,5 фута = 1,5 ⋅ 30,5 см = 45,75 см = 0,46 м.
Ответ: 4 ярда = 3,7 м; 1,5 фута = 0,46 м.
Читать далее
| ← Роль измерений в физике. Прямые и косвенные измерения | Действия над физическими величинами → |
Единицы измерения с древности до наших дней
Наука начинается с тех пор как начинают измерять.
Д.И. Менделеев
С давних пор люди сталкивались с необходимостью определять расстояния, длины предметов, время, площади, объемы и т. д.
Измерения нужны были и в строительстве, и в торговле, и в астрономии, фактически в любой сфере жизни. Очень большая точность измерений нужна была при строительстве египетских пирамид.
Рис. 0
Значение измерений возрастало по мере развития общества и, в частности, по
мере развития науки.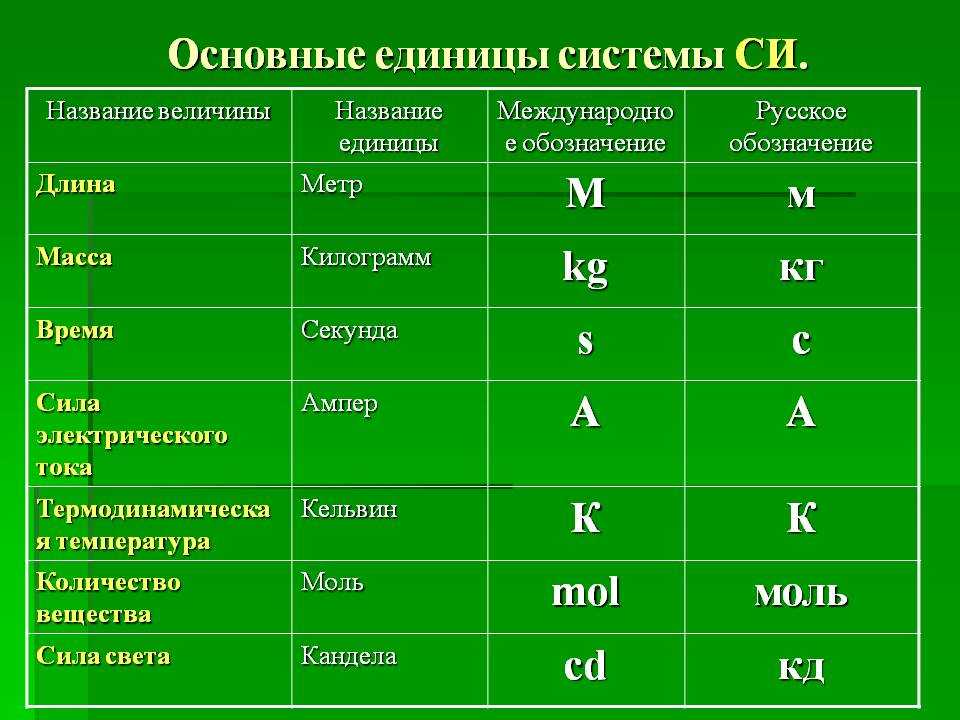 А чтобы измерять, необходимо было придумать единицы
различных физических величин. Вспомним, как написано в учебнике: “Измерить
какую-нибудь величину – это значит сравнить ее с однородной величиной, принятой
за единицу этой величины”.
А чтобы измерять, необходимо было придумать единицы
различных физических величин. Вспомним, как написано в учебнике: “Измерить
какую-нибудь величину – это значит сравнить ее с однородной величиной, принятой
за единицу этой величины”.
Целью моей работы было выяснить: какие существовали и существуют сейчас единицы длины и массы, каково их происхождение?
Вершок, локоть и другие единицы…
Измеряй все доступное измерению и делай не доступное измерению доступным”.
Г.Галилей
Самыми древними единицами были субъективные единицы. Так, например, моряки измеряли путь трубками, т. е. расстоянием, которое проходит судно за время, пока моряк выкурит трубку. В Испании похожей единицей была сигара, в Японии – лошадиный башмак, т. е. путь, который проходила лошадь, пока не износится привязанная к ее копытам соломенная подошва, заменявшая подкову.
В программе Олимпийских игр Древней Эллады был бег на стадию. Установлено,
что греческая стадия (или стадий) это длина стадиона в Олимпии – 192,27 м.
Стадий равняется расстоянию, которое проходит человек спокойным шагом за время
от появления первого луча солнца, при его восходе, до момента, когда диск солнца
целиком окажется над горизонтом. Это время приблизительно равно двум минутам …
Установлено,
что греческая стадия (или стадий) это длина стадиона в Олимпии – 192,27 м.
Стадий равняется расстоянию, которое проходит человек спокойным шагом за время
от появления первого луча солнца, при его восходе, до момента, когда диск солнца
целиком окажется над горизонтом. Это время приблизительно равно двум минутам …
Стадий, как единица измерения расстояний, был и у римлян (185 см), и у вавилонян (около 195 см), и у египтян (195 см).
В Сибири в стародавние времена употреблялась мера расстояний – бука. Это расстояние, на котором человек перестает видеть раздельно рога быка.
У многих народов для определения расстояния использовалась единица длины стрела – дальность полета стрелы. Наши выражения “не подпускать на ружейный выстрел”, позднее “на пушечный выстрел” – напоминают о подобных единицах длины.
Древние римляне расстояния измеряли шагами или двойными шагами (шаг левой
ногой, шаг правой). Тысяча двойных шагов составляла милю (лат.
Длину веревки или ткани неудобно измерять шагами или стадиями. Для этого оказались пригодными встречающиеся у многих народов единицы, отождествляемые с названиями частей человеческого тела. Локоть – расстояние от конца пальцев до локтевого сустава.
Рис. 1 Рис. 2
Мерой длины для тканей, веревок и т.п. наматывающихся материалов у многих народов был двойной локоть. Этой мерой мы и сейчас пользуемся для приблизительной оценки длины…
На Руси долгое время в качестве единицы длины использовали аршин (примерно 71 см). Эта мера возникла при торговле с восточными странами (перс, “арш” – локоть). Многочисленные выражения: “Словно аршин проглотил”, “Мерить на свой аршин” и другие – свидетельствуют о ее распространении.
Для измерения меньших длин применяли пядь – расстояние между концами
расставленных большого и указательного пальцев.
Рис. 3
Пядь или, как ее еще называли, четверть (18 см) составляла 1 / 4 аршина, а 1/ 16 аршина равнялся вершок (4,4 см).
Очень распространенной единицей длины была сажень. Впервые упоминание о ней встречается в XI в. С 1554 г. сажень устанавливают равной 3 аршинам (2,13 м) и она получает название царской (или орленой, печатной) в отличие от произвольных – маховой и косой. Маховая сажень – размах рук – равна примерно 2,5 аршинам. Рыбак, который показывает, какую большую рыбу он упустил, демонстрирует нам маховую.
Рис. 4
Косая сажень – расстояние от конца вытянутой вверх правой руки до носка левой ноги, она примерно равна 3,25 аршинам.
Рис. 5
Вспомним, как в сказках о великанах: “Косая сажень в плечах”. Удивительно
совпадение древнеримской меры длины — «архитектурной трости» и древнерусской
косой сажени: 248 см.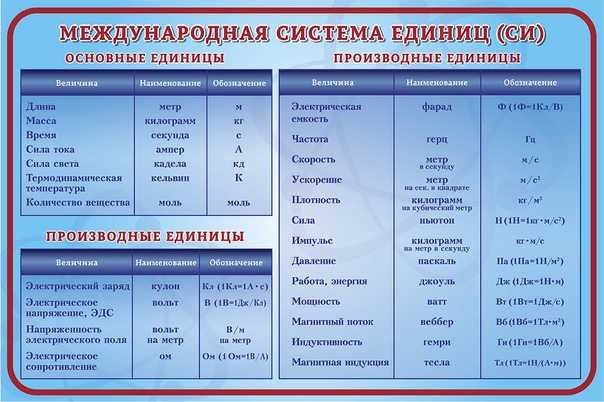
При сложении упомянутой выше косой сажени вчетверо получаем «литовский локоть» (62 см).
В странах Западной Европы издавна применяли в качестве единиц дюйм (2,54 см) –длина сустава большого пальца (от голл. “дюйм” – большой палец) и фут (30 см) – средняя длина ступни человека (от англ. “фут” – ступня).
Рис. 6 Рис. 7
Локоть, вершок, пядь, сажень, дюйм, фут и т. д. очень удобны при измерениях,
так как они всегда “под руками”. Но единицы длины, соответствующие частям
человеческого тела, обладают большим недостатком: у различных людей пальцы,
ступни и т. д. имеют разную длину. Чтобы избавиться от произвола, в XIV в.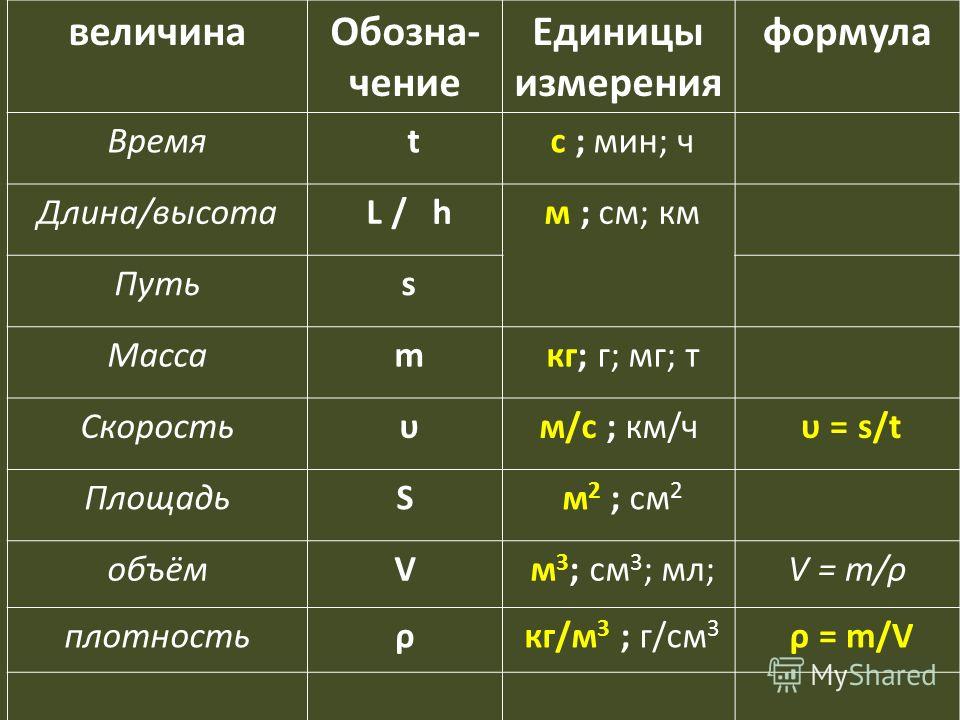 субъективные единицы начинают заменять набором объективных единиц. Так,
например, в 1324 г. в Англии был установлен законный дюйм, равный длине трех
приставленных друг к другу ячменных зерен, вытянутых из средней части колоса .
Фут определили как среднюю длину ступни шестнадцати человек, выходящих из
церкви, т. е. обмером случайных людей стремились получить более постоянное
значение единицы – среднюю длину ступни.
субъективные единицы начинают заменять набором объективных единиц. Так,
например, в 1324 г. в Англии был установлен законный дюйм, равный длине трех
приставленных друг к другу ячменных зерен, вытянутых из средней части колоса .
Фут определили как среднюю длину ступни шестнадцати человек, выходящих из
церкви, т. е. обмером случайных людей стремились получить более постоянное
значение единицы – среднюю длину ступни.
Рис. 8
Какую величину мы определяем, взвешивая тело на рычажных весах?
Какой народ и когда изобрел рычажные весы – неизвестно. Возможно, что это было сделано многими народами независимо друг от друга, а простота использования послужила причиной их широкого распространения.
Рис. 9
При взвешивании на рычажных весах на одну чашку кладут взвешиваемое тело, на
другую – гири. Гири подбирают так, чтобы установить равновесие.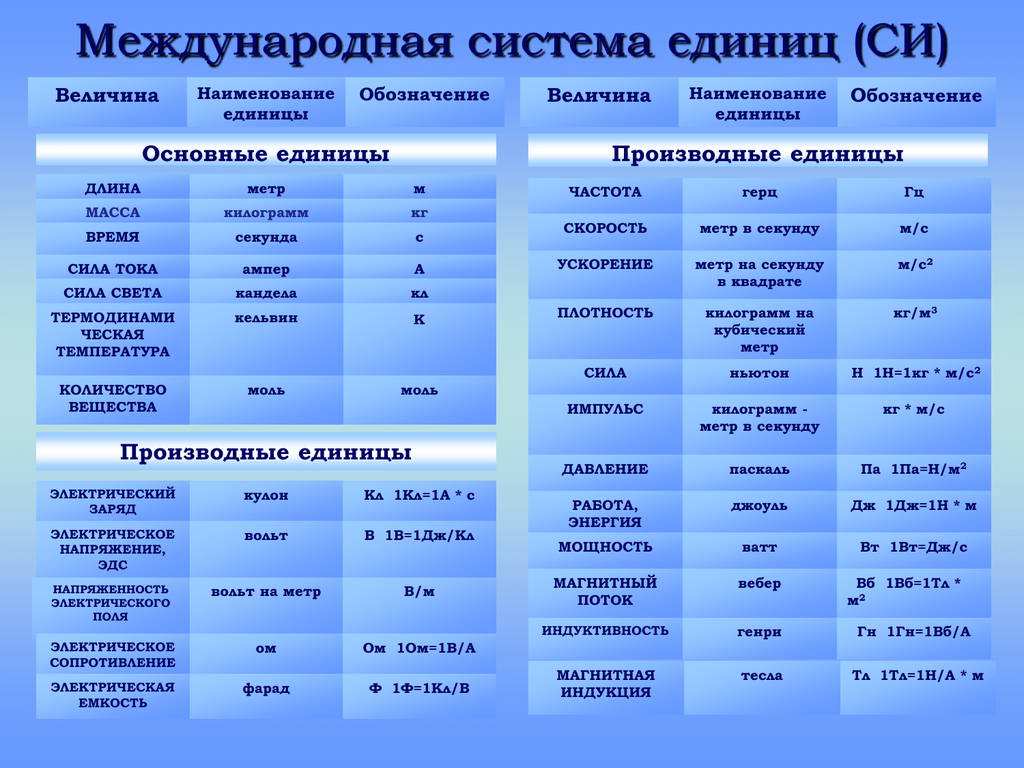 При этом
уравновешиваются массы взвешиваемого тела и гирь. Если уравновешенные весы
перенести, например, на Луну, где вес тела меньше, чем на Земле, в 6 раз,
равновесие не нарушится, так как вес и тела, и гирь на Луне уменьшился в
одинаковое число раз, а масса осталась прежней.
При этом
уравновешиваются массы взвешиваемого тела и гирь. Если уравновешенные весы
перенести, например, на Луну, где вес тела меньше, чем на Земле, в 6 раз,
равновесие не нарушится, так как вес и тела, и гирь на Луне уменьшился в
одинаковое число раз, а масса осталась прежней.
Следовательно, взвешивая тело на рычажных весах, мы определяем его массу, а не вес.
Единицы массы, как и единицы длины, сначала устанавливались по природным образцам. Чаще всего по массе какого-нибудь семени. Так, например, массу драгоценных камней определяли и до сих пор определяют в каратах (0,2 г) – это масса семени одного из видов бобов.
Рис. 10
Позднее за единицу массы стали принимать массу воды, наполняющей сосуд
определенной вместимости. Например, в Древнем Вавилоне за единицу массы
принимали талант – массу воды, наполняющей такой сосуд, из которого вода
равномерно вытекает через отверстие определенного размера в течение одного часа.
По массе зерен или воды изготовляли металлические гири разной массы. Ими пользовались при взвешивании.
Гири, служившие эталоном (образцом), хранились в храмах или правительственных учреждениях.
На Руси древнейшей единицей массы была гривна (409,5 г). Существует предположение, что эта единица ввезена к нам с Востока. Впоследствии она получила название фунта. Для определения больших масс использовался пуд (16,38 кг), а малых – золотник (12,8 г).
В 1791 г. во Франции было принято решение создать десятичную метрическую систему мер. Основными величинами в этой системе были выбраны длина и масса.
Комиссия, в которую входили крупнейшие французские ученые, предложила принять
за единицу длины 1/40000000 часть длины земного меридиана, проходящего через
Париж. Измерить длину
меридиана было поручено астрономам Мешену и Деламберу. Работа продолжалась шесть
лет. Ученые измерили часть длины меридиана, расположенную между городами
Дюнкерком и Барселоной, а затем вычислили полную длину четверти меридиана от
полюса до экватора.
Рис. 11
На основании их данных из платины был изготовлен эталон новой единицы. Эту единицу назвали метром – от греческого слова “метрон”, что значит “мера”.
Рис. 12
За единицу массы была принята масса одного кубического дециметра дистиллированной воды при температуре ее наибольшей плотности 4°С, определяемая взвешиванием в вакууме. Был изготовлен эталон этой единицы, названной килограммом, в виде платинового цилиндра
В 1869 г. Петербургская академия наук обратилась к научным учреждениям всего
мира с призывом сделать предложенную французскими учеными десятичную метрическую
систему мер международной. В этом обращении говорилось и о том, что “достижения
науки привели к необходимости отказаться от прежнего определения метра как
1/40000000 доли четверти длины парижского меридиана, так как позднейшие более
точные измерения меридиана давали другие результаты”. Кроме того, стало
известно, что длина меридиана со временем меняется. Но так как немыслимо было
после каждого измерения меридиана менять длину метра, то Петербургская академия
наук предложила принять метр, хранившийся во французском архиве (архивный метр),
за прототип – первый образец и изготовить с него возможно точные и устойчивые
копии для разных стран, сделав этим метрическую систему мер международной.
Кроме того, стало
известно, что длина меридиана со временем меняется. Но так как немыслимо было
после каждого измерения меридиана менять длину метра, то Петербургская академия
наук предложила принять метр, хранившийся во французском архиве (архивный метр),
за прототип – первый образец и изготовить с него возможно точные и устойчивые
копии для разных стран, сделав этим метрическую систему мер международной.
Когда же была введена метрическая система мер в нашей стране? Передовые
русские ученые, много сделавшие для того, чтобы метрическая система мер стала
международной, не смогли преодолеть сопротивления царского правительства
введению метрической системы мер в нашей стране. Удалось добиться только того,
что в 1899 г. был принят закон, подготовленный Д. И. Менделеевым, по которому
наравне с российскими мерами “дозволялось применять в России международный метр
и килограмм”, а также кратные им единицы – грамм, сантиметр и др.
Вопрос об использовании метрической системы мер в России был окончательно решен после Великой Октябрьской социалистической революции. 14 сентября 1918 г. Советом Народных Комиссаров РСФСР было издано постановление, в котором говорилось: “Положить в основу всех измерений международную метрическую систему мер и весов с десятичными подразделениями и производными”.
Заключение
По подсчету академика Б. С. Якоби (сторонника превращения метрической системы в международную), от замены прежней системы мер на метрическую преподавание арифметики в школе выиграло третью часть времени, отводившегося на этот предмет. Соответственно значительно упростились расчеты в промышленности и торговле.
Вывод: такую длинную историю прошли длина и масса , пока не стали измеряться в метрах и килограммах соответственно.
Что имеем сейчас:
Единицы СИ
Размерности основных величин в СИ
Базовые единицы СИ
Физические величины
Единица СИ
Символ
Длина
метр
м
Масса
килограмм
кг
Время
секунда
с
Сила тока
ампер
А
Температура
кельвин
К
Количество вещества
моль
моль
Сила света
кандела
кд
Определения базовых единиц
- Метр равен расстоянию, которое проходит плоская электромагнитная
волна в вакууме за 1/299792458 долю секунды.

- Килограмм равен массе международного прототипа килограмма.
- Секунда равна 9 192 631 770 периодам излучения, соответствующего переходу между двумя сверхтонкими уровнями основного состояния атома цезия 133Cs.
- Ампер равен силе постоянного тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м друг от друга, вызвал бы на каждом участке проводника длиной 1 м силу взаимодействия, равную 2·10–7 Н.
- Кельвин равен 1/273,16 части термодинамической температуры тройной точки воды.
- Моль равен количеству вещества системы, содержащей столько же структурных элементов, сколько содержится атомов в углероде 12C массой 0,012 кг.
- Кандела равна силе света в заданном направлении от источника,
испускающего монохроматическое излучение частотой 540·1012 Гц,
энергетическая сила света которого в этом направлении составляет 1/683
Вт/ср.

Использованная литература:
- С.А.Шабалин. Измерения для всех.
- Энциклопедия Кирилла и Мефодия.
- А.Г.Чертов. Физические величины.
- И.Г.Кириллова. Книга для чтения по физике.
Предсказание многих свойств квантовой системы по очень небольшому числу измерений
- Статья
- Опубликовано:
- Синь-Юань Хуан ORCID: orcid.org/0000-0001-5317-2613 1,2 ,
- Ричард Куенг 1,2,3 и
- Джон Прескилл 1,2,4
4
19 тыс.
 обращений
обращений210 цитирований
88 Альтметрический
Сведения о показателях
Предметы
- Теория информации и вычисления
- Математика и вычисления
- Квантовая информация
- Квантовая физика
- Теоретическая физика
Abstract
Предсказание свойств сложных крупномасштабных квантовых систем имеет важное значение для разработки квантовых технологий. Мы представляем эффективный метод построения приближенного классического описания квантового состояния с использованием очень небольшого количества измерений состояния. Это описание, называемое «классической тенью», можно использовать для предсказания множества различных свойств; порядка \({\mathrm{log}}\,(M)\) измерений достаточно, чтобы точно предсказать M различные функции государства с высокой вероятностью успеха. Количество измерений не зависит от размера системы и насыщает теоретико-информационные нижние границы. Кроме того, целевые свойства для прогнозирования могут быть выбраны после завершения измерений. Мы подкрепляем наши теоретические выводы обширными численными экспериментами. Мы применяем классические тени для предсказания квантовой точности, энтропии запутанности, двухточечных корреляционных функций, средних значений локальных наблюдаемых и энергетической дисперсии локальных гамильтонианов многих тел. Численные результаты подчеркивают преимущества классических теней по сравнению с ранее известными методами.
Это описание, называемое «классической тенью», можно использовать для предсказания множества различных свойств; порядка \({\mathrm{log}}\,(M)\) измерений достаточно, чтобы точно предсказать M различные функции государства с высокой вероятностью успеха. Количество измерений не зависит от размера системы и насыщает теоретико-информационные нижние границы. Кроме того, целевые свойства для прогнозирования могут быть выбраны после завершения измерений. Мы подкрепляем наши теоретические выводы обширными численными экспериментами. Мы применяем классические тени для предсказания квантовой точности, энтропии запутанности, двухточечных корреляционных функций, средних значений локальных наблюдаемых и энергетической дисперсии локальных гамильтонианов многих тел. Численные результаты подчеркивают преимущества классических теней по сравнению с ранее известными методами.
Это предварительный просмотр содержимого подписки, доступ через ваше учреждение
Соответствующие статьи
Статьи открытого доступа со ссылками на эту статью.
Интеллектуальная сертификация квантовых симуляторов с помощью машинного обучения
- Тайлун Сяо
- , Цзинчжэн Хуан
- … Гуйхуа Цзэн
npj Квантовая информация Открытый доступ 28 ноября 2022 г.
Байесовская оптимизация стохастической градиентной линии для эффективной шумоустойчивой оптимизации параметризованных квантовых схем
- Сиро Тамия
- и Хаята Ямасаки
npj Квантовая информация Открытый доступ 27 июля 2022 г.

Байесовская томография высокоразмерных бифотонных частотных гребенок на кристалле с рандомизированными измерениями
- Сюань-Хао Лу
- , Картик В. Миилсвами
- … Джозеф М. Люкенс
Связь с природой Открытый доступ 27 июля 2022 г.
Варианты доступа
Подписаться на журнал
Получить полный доступ к журналу на 1 год
99,00 €
всего 8,25 € за выпуск
Подписаться
Расчет налогов будет завершен во время оформления заказа.
Купить статью
Получите ограниченный по времени или полный доступ к статье на ReadCube.
32,00 $
Купить
Все цены указаны без учета стоимости.
Рис. 1: Иллюстрация построения классического представления, классической тени, квантовой системы из рандомизированных измерений. Рис. 2: Прогнозирование квантовой точности с использованием классических теней (измерения Клиффорда) и NNQST. Рис. 3: Прогнозирование двухточечных корреляционных функций с использованием классических теней (измерения Паули) и NNQST. Рис. 4: Прогнозирование энтропии Реньи запутанности с использованием классических теней (измерения Паули) и Brydges et al. протокол. Рис. 5: Применение классических теней (измерения Паули) к вариационному квантовому моделированию решеточной модели Швингера.
Доступность данных
Исходные данные доступны для этой статьи. Все другие данные, подтверждающие графики в этой статье и другие результаты этого исследования, можно получить у соответствующего автора по обоснованному запросу.
Доступность кода
Исходный код для эффективной реализации предложенной процедуры доступен по адресу https://github.com/momohuang/predicting-quantum-properties.
Ссылки
Preskill, J. Квантовые вычисления в эпоху NISQ и позже. Quantum 2 , 79 (2018).
Артикул Google Scholar
Cramer, M. et al. Эффективная томография квантового состояния. Нац. коммун. 1 , 149 (2010).
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Карраскилья Дж., Торлай Г., Мелко Р.
 Г. и Аолита Л. Реконструкция квантовых состояний с помощью генеративных моделей. Нац. Мах. Интел. 1 , 155–161 (2019).
Г. и Аолита Л. Реконструкция квантовых состояний с помощью генеративных моделей. Нац. Мах. Интел. 1 , 155–161 (2019).Артикул Google Scholar
Torlai, G. et al. Нейросетевая томография квантового состояния. Нац. физ. 14 , 447–450 (2018).
Артикул Google Scholar
Ааронсон С. Теневая томография квантовых состояний. В Proceedings of the 50th Annual ACM SIGACT Symposium on Theory of Computing ( STOC 2018 ) 325–338 (ACM, 2018)
Ааронсон, С. и Ротблюм, Г. Н. Нежное измерение квантовых состояний конфиденциальности. In Proceedings of 51st Annual ACM SIGACT Symposium on Theory of Computing ( СТОК 2019 ) 322–333 (ACM, 2019).
Гута М., Кан Дж., Куенг Р. Дж. и Тропп Дж. А. Томография быстрого состояния с оптимальными границами ошибок.
 J. Phys. А 53 , 204001 (2020).
J. Phys. А 53 , 204001 (2020).Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar
Готтесман, Д. Коды стабилизаторов и квантовая коррекция ошибок Кандидатская диссертация, Калифорнийский технологический институт (1997).
Фано, Р. М. Передача информации : Статистическая теория коммуникаций (MIT Press, 1961).
Джеррум, М. Р., Валиант, Л. Г. и Вазирани, В. В. Случайное создание комбинаторных структур из равномерного распределения. Теор. вычисл. науч. 43 , 169–188 (1986).
Артикул MathSciNet Google Scholar
Немировский А. С., Юдин Д. Б. Сложность задач и эффективность методов оптимизации (Wiley-Interscience, 1983).
Гринбергер, Д.
 М., Хорн, М. А. и Цайлингер, А. в Теорема Белла, квантовая теория и концепции Вселенной. Фундаментальные теории физики Vol. 37 (изд. Кафатос, М.) 69–72 (Спрингер, 1989).
М., Хорн, М. А. и Цайлингер, А. в Теорема Белла, квантовая теория и концепции Вселенной. Фундаментальные теории физики Vol. 37 (изд. Кафатос, М.) 69–72 (Спрингер, 1989).Деннис Э., Китаев А., Ландаль А. и Прескилл Дж. Топологическая квантовая память. Дж. Матем. физ. 43 , 4452–4505 (2002).
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar
Фламмиа, С. Т. и Лю, Ю.-К. Прямая оценка точности по нескольким измерениям Паули. Физ. Преподобный Летт. 106 , 230501 (2011).
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Гюн О. и Тот Г. Обнаружение запутывания. Физ. Респ. 474 , 1–75 (2009).
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar
Вейленманн, М.
 , Дайв, Б., Трилло, Д., Агилар, Э. А. и Наваскуэс, М. Обнаружение запутанности помимо измерения точности. Физ. Преподобный Летт. 124 , 200502 (2020).
, Дайв, Б., Трилло, Д., Агилар, Э. А. и Наваскуэс, М. Обнаружение запутанности помимо измерения точности. Физ. Преподобный Летт. 124 , 200502 (2020).Артикул ОБЪЯВЛЕНИЯ Google Scholar
Кандала, А. и др. Аппаратно-эффективный вариационный квантовый решатель для малых молекул и квантовых магнитов. Природа 549 , 242–246 (2017).
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Кокаил, К. и др. Самопроверяющееся вариационное квантовое моделирование решетчатых моделей. Природа 569 , 355–360 (2019).
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Хёффдинг В. в «Прорывы в статистике» 308–334 (Springer, 1992).
Бриджес, Т. и др. Исследование энтропии запутанности Реньи с помощью рандомизированных измерений.
 Наука 364 , 260–263 (2019).
Наука 364 , 260–263 (2019).Артикул ОБЪЯВЛЕНИЯ Google Scholar
Ренес Дж. М., Блюм-Кохаут Р., Скотт А. Дж. и Кейвс К. М. Симметричные информационно полные квантовые измерения. Дж. Матем. физ. 45 , 2171–2180 (2004).
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar
Нандкишор Р. и Хьюз Д. А. Локализация многих тел и термализация в квантовой статистической механике. год. Преподобный Конденс. Материя физ. 6 , 15–38 (2015).
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Dasgupta, C. & Ma, S.-k Низкотемпературные свойства случайной антиферромагнитной цепи Гейзенберга. Физ. B 22 , 1305 (1980).
Артикул ОБЪЯВЛЕНИЯ Google Scholar
«>
Ма, С.-к, Дасгупта, К. и Ху, К.-к Случайная антиферромагнитная цепочка. Физ. Преподобный Летт. 43 , 1434 (1979).
Артикул ОБЪЯВЛЕНИЯ Google Scholar
Бонет-Монройг, X., Баббуш, Р. и О’Брайен, Т. Е. Почти оптимальное планирование измерений для частичной томографии квантовых состояний. Препринт на https://arxiv.org/pdf/1908.05628.pdf (2019).
Рагхаван П. Вероятностное построение детерминированных алгоритмов: аппроксимация целочисленных программ упаковки. Дж. Вычисл. Сист. науч. 37 , 130–143 (1988).
Артикул MathSciNet Google Scholar
Спенсер Дж. Десять лекций по вероятностному методу. В серии региональных конференций CBMS-NSF по прикладной математике , 2-е изд., том. 64 (СИАМ, 1994).
Карлео Г. и Тройер М. Решение квантовой задачи многих тел с помощью искусственных нейронных сетей. Наука 355 , 602–606 (2017).
и Тройер М. Решение квантовой задачи многих тел с помощью искусственных нейронных сетей. Наука 355 , 602–606 (2017).
Артикул ОБЪЯВЛЕНИЯ MathSciNet Google Scholar
Карраскилья, Дж. и Мелко, Р. Г. Фазы машинного обучения материи. Нац. Физ . 13 , 431–434 (2017).
Артикул Google Scholar
Пайни, М. и Калев, А. Приближенное описание квантовых состояний. Препринт на https://arxiv.org/pdf/1910.10543.pdf (2019).
Скачать ссылки
Благодарности
Мы благодарим В. Альберта, Ф. Брандао, М. Эндреса, И. Рота, Дж. Троппа, Т. Видика, М. Вайленманна и Дж. Райта за ценный вклад и вдохновляющие обсуждения. . Л. Аолита и Г. Карлео дали полезные советы по презентации. Мы особенно благодарны Дж. Айверсону, который помог нам в разработке стратегии численной выборки для основных состояний торического кода. Мы также благодарим М. Пайни и А. Калева за информацию об их связанной работе 30 , где обсуждались краткие классические «моментальные снимки» квантовых состояний, полученные из случайных локальных измерений. Х.-Ю.Х. поддерживается программой Kortschak Scholars Program. Р.К. признает финансирование, предоставленное Управлением военно-морских исследований (награда № N00014-17-1-2146) и Управлением армейских исследований (награда № W911NF121054). JP признает финансирование от ARO-LPS, NSF и DOE. Институт квантовой информации и материи является Центром физических границ NSF.
Мы также благодарим М. Пайни и А. Калева за информацию об их связанной работе 30 , где обсуждались краткие классические «моментальные снимки» квантовых состояний, полученные из случайных локальных измерений. Х.-Ю.Х. поддерживается программой Kortschak Scholars Program. Р.К. признает финансирование, предоставленное Управлением военно-морских исследований (награда № N00014-17-1-2146) и Управлением армейских исследований (награда № W911NF121054). JP признает финансирование от ARO-LPS, NSF и DOE. Институт квантовой информации и материи является Центром физических границ NSF.
Информация об авторе
Авторы и филиалы
Институт квантовой информации и материи, Калифорнийский технологический институт, Пасадена, Калифорния, США
Хсин-Юань Хуанг, Ричард Куэн и Джон Прескилл
Департамент вычислительных и математических наук Калифорнии Технологический институт, Пасадена, Калифорния, США
Хсин-Юань Хуанг, Ричард Куенг и Джон Прескилл
Институт интегральных схем, Университет Иоганна Кеплера, Линц, Линц, Австрия
Richard Kueng
Walter Burke Institute for Theoretical Physics, California Institute of Technology, Pasadena, CA, USA
John Preskill
Authors
- Hsin-Yuan Huang
View author publications
You can also поищите этого автора в PubMed Google Scholar
- Richard Kueng
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- John Preskill
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
Contributions
H. -Y.H. и Р.К. разработал теоретические аспекты этой работы. Х.-Ю.Х. провел численные эксперименты и написал открытый код. Дж. П. задумал применение классических теней. Х.-Ю.Х., Р.К. и JP написали рукопись.
-Y.H. и Р.К. разработал теоретические аспекты этой работы. Х.-Ю.Х. провел численные эксперименты и написал открытый код. Дж. П. задумал применение классических теней. Х.-Ю.Х., Р.К. и JP написали рукопись.
Автор, ответственный за переписку
Переписка с Синь-Юань Хуан.
Заявление об этике
Конкурирующие интересы
Авторы не заявляют об отсутствии конкурирующих интересов.
Дополнительная информация
Информация о рецензировании Nature Physics благодарит Yi-Kai Liu и других анонимных рецензентов за их вклад в рецензирование этой работы.
Примечание издателя Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Дополнительная информация
Дополнительная информацияДополнительная информация Рис. 1–4.
Права и разрешения
Перепечатка и разрешения
Об этой статье
Эта статья цитируется
Изучение квантовых систем
- Валентин Гебхарт
- Раффаэле Сантагати
- Кристиан Бонато
Nature Reviews Physics (2023)
Подготовка случайных состояний и бенчмаркинг с квантовым хаосом многих тел
- Джунхи Чой
- Адам Л.
 Шоу
Шоу - Мануэль Эндрес
Природа (2023)
Реконструкция квантового состояния на основе машинного обучения с адаптацией к размеру
- Санджая Лохани
- Сангита Регми
- Брайан Т. Кирби
Квантовый машинный интеллект (2023)
Квантовое федеративное обучение без IID со сложностью одноразовой связи
- Хаймэн Чжао
Квантовый машинный интеллект (2023)
Интеллектуальная сертификация квантовых симуляторов с помощью машинного обучения
- Тайлун Сяо
- Цзинчжэн Хуан
- Гуйхуа Цзэн
npj Квантовая информация (2022)
Измерения и неопределенности – IB Physics
См. руководство по этой теме.
руководство по этой теме.
Основные единицы СИ
| Количество | Единица СИ | Символ |
| Масса | Килограмм | кг |
| Расстояние | Счетчик | м |
| Время | Второй | с |
| Электрический ток | Ампер | А |
| Количество вещества 9-15 |
Значащие цифры
Для определенного значения все цифры являются значащими, кроме:
- Ведущие нули
- Нули в конце, если это значение не имеет десятичной точки, например:
- 12300 имеет 3 значащих цифры. Два завершающих нуля не имеют значения.
- 012300 имеет 5 значащих цифр. Два ведущих нуля не имеют значения. Два завершающих нуля являются значащими.
 26 90
26 900 Оценка
Оценки обычно делаются с точностью до степени 10. Некоторые примеры приведены в таблицах в разделе порядков величин.
1.2 – Неопределенности и ошибкиСлучайная ошибка Систематическая ошибка Вызвано колебаниями в измерениях вокруг истинного значения (разброс). Можно уменьшить путем усреднения по повторным измерениям.
Не обусловлено предвзятостью.
Вызвано фиксированными отклонениями измерений от истинного значения. Нельзя уменьшить путем усреднения по повторным измерениям. Вызвано предвзятостью.
Примеры: Колебания комнатной температуры
Шумы в цепях
Человеческая ошибка
Примеры: Ошибка калибровки оборудования, например, ошибка смещения нуля
Неправильный метод измерения
Физические измерения иногда выражаются в виде x±Δx.
 Например, 10±1 будет означать диапазон измерения от 9 до 11.
Например, 10±1 будет означать диапазон измерения от 9 до 11.Абсолютная неопределенность Δx Дробная неопределенность Δх/х Неопределенность в процентах Δx/x*100% 9п Δy/y=|n|Δa/a (|n|, умноженное на дробную неопределенность) Планки ошибок
Столбики погрешностей — это столбцы на графиках, которые указывают на неопределенность. Они могут быть горизонтальными или вертикальными с общей длиной двух абсолютных неопределенностей.
Линия наилучшего соответствия : Прямая линия, проведенная на графике таким образом, чтобы среднее расстояние между точками данных и линией было минимальным.
Максимальная/минимальная строка: Две линии с максимально возможным наклоном и минимально возможным наклоном при условии, что они обе проходят через все планки погрешностей.

Неопределенность точек пересечения прямой линии графика: Разница между точками пересечения линии наилучшего соответствия и линии максимума/минимума.
Неопределенность градиента: Разница между градиентами линии наилучшего соответствия и линии максимума/минимума.
1.3 – Векторы и скалярыСкаляр Вектор Величина, которая определяется только своей величиной. Количество, которое определяется как величиной, так и направлением. Примеры: Расстояние
Скорость
Время
Энергия
Примеры: Рабочий объем
Скорость
Ускорение
Сила
Сложение и вычитание векторов можно выполнять методом параллелограмма или методом головы к хвосту.





 обращений
обращений
 Г. и Аолита Л. Реконструкция квантовых состояний с помощью генеративных моделей. Нац. Мах. Интел. 1 , 155–161 (2019).
Г. и Аолита Л. Реконструкция квантовых состояний с помощью генеративных моделей. Нац. Мах. Интел. 1 , 155–161 (2019). J. Phys. А 53 , 204001 (2020).
J. Phys. А 53 , 204001 (2020). М., Хорн, М. А. и Цайлингер, А. в Теорема Белла, квантовая теория и концепции Вселенной. Фундаментальные теории физики Vol. 37 (изд. Кафатос, М.) 69–72 (Спрингер, 1989).
М., Хорн, М. А. и Цайлингер, А. в Теорема Белла, квантовая теория и концепции Вселенной. Фундаментальные теории физики Vol. 37 (изд. Кафатос, М.) 69–72 (Спрингер, 1989). , Дайв, Б., Трилло, Д., Агилар, Э. А. и Наваскуэс, М. Обнаружение запутанности помимо измерения точности. Физ. Преподобный Летт. 124 , 200502 (2020).
, Дайв, Б., Трилло, Д., Агилар, Э. А. и Наваскуэс, М. Обнаружение запутанности помимо измерения точности. Физ. Преподобный Летт. 124 , 200502 (2020).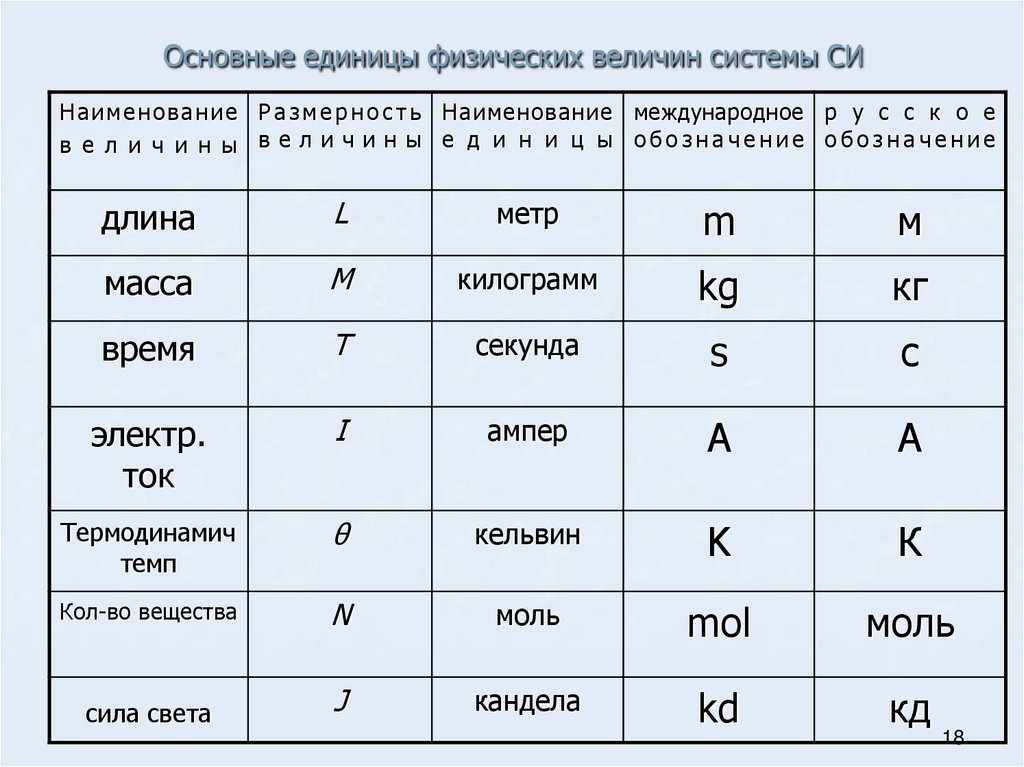 Наука 364 , 260–263 (2019).
Наука 364 , 260–263 (2019). Шоу
Шоу 26 90
26 90 Например, 10±1 будет означать диапазон измерения от 9 до 11.
Например, 10±1 будет означать диапазон измерения от 9 до 11.