лабораторная работа 32

Лабораторная работа № 32   ИЗУЧЕНИЕ ЗАВИСИМОСТИ СОПРОТИВЛЕНИЯ МЕТАЛЛОВ ОТ ТЕМПЕРАТУРЫ   Цель работы — определение температурного коэффициента сопротивления меди. Приборы и принадлежности: исследуемый медный проводник, измерительный мост или омметр, термометр.   Элементарная теория проводимости металлов   Величина электрического сопротивления R конкретного металлического проводника зависит как от геометрической формы (т.е. размеров), так и от физических свойств материалов. Для однородного изотропного проводника правильной геометрической формы длиной l и площадью сечения S величина сопротивления R равна  R = ,                                            (1)   где r — удельное сопротивление материала, Ом×м. Обратная величина , т.е. , называется удельной проводимостью. Единица измерения  —  (См – сименс).   Величины  и  зависят от химических примесей, дефектов кристаллической решетки, магнитного состояния вещества, температуры, давления и других факторов. При постоянном давлении для неферромагнитных несверхпроводящих и изотропных проводников вблизи комнатной температуры и выше (до температуры плавления) удельное сопротивление пропорционально Т. При низких температурах вблизи абсолютного нуля наблюдается нелинейная зависимость (~ Т) удельного сопротивления  (кривая 1 на рис. 1). Величина остаточного сопротивления  при Т= 0 К зависит от примесей химических элементов, дефектов кристаллической решетки. У абсолютно чистого проводника с идеальной кристаллической решеткой при Т = 0 К удельное сопротивление r равно нулю (кривая 2 на рис. 1).

Рис. 1

Далее рассматриваем неферромагнитные и изотропные металлические проводники. Температурную зависимость удельного сопротивления ρ изотропных проводников объясняет квантовая теория металлов. Электроны проводимости (валентные)  движутся беспорядочно и в отсутствии внешнего электрического поля они находятся в поле кристаллической решетки в равновесном состоянии. Как в классической,  так в квантовой теории электрическое сопротивление объясняется взаимодействием электронов — проводимости с дефектами (примеси, искажение решетки, вакансии  и т. д.) кристаллической решетки, т.е. рассеянием электронов на дефектах. В отсутствие внешнего электрического поля (Е=0) из-за беспорядочного движения, электроны испытывают столкновение (рассеяние) с колеблющимися в узлах  решетки,  ионами, примесями и другими. В результате чего изменяются  их направление и величина скорости движения. Поэтому, в среднем число электронов, движущихся в одном направлении равно числу электронов, движущихся в противоположном направлении.  Соответственно, отсутствует преимущественное направление движения электронов, скорость упорядоченного движения равна нулю, ток – отсутствует. В грубом приближение,  траекторию движения электронов проводимости при Е=0, можно представить в следующем виде:

Рис. 2

где <υ> — средняя скорость теплового движения электрона. Это мгновенная фотография беспорядочного движения электрона. Стрелками обозначены положения вектора скорости теплового движения. Под действием внешнего электрического поля  электроны-проводимости будут совершать упорядоченное движение (см. рис. 3), т.к. на них будет действовать  электрическая сила Fе = еЕ. Электроны будут приобретать дополнительную кинетическую энергию, которую отдают дефектам. Сразу после столкновения приобретенная электроном  кинетическая энергия равна нулю, соответственно начальная скорость упорядоченного движения, также равна нулю. Затем, под действием поля  , электроны опять будут приобретать дополнительную кинетическую энергию, которую также отдает дефектам и т. д.. Следовательно, при взаимодействии электронов с дефектами  происходит передача энергии и импульса.

Рис. 3

Рассмотрим классическую теорию. Под действием внешнего электрического поля  электроны  будут совершать упорядоченное движение (см. рис. 3), т.к. на них  действует  электрическая сила Fе = еЕ , кроме того, на электрон со стороны поля кристаллической решетки  действует сила сопротивления F с = -. Поэтому общая сила, действующая на электрон, равна F = еЕ –.                                       (2)   По второму закону Ньютона mа = еЕ –.                                    (3)   Дрейфовая скорость  будет увеличиваться до тех пор, пока Fе = Fс, а = 0, т.е. еЕ = , отсюда u =.                                            (4).   Величина, равная b = , называется подвижностью электрона.   Смысл коэффициента следующий. Пусть Е = 0, тогда (3) запишется в виде mа = –.Так как ускорение электрона определяется по формуле:    , то     ,      или      .             (5)   Из (5) следует, что u=. Если , то t = τ и  это время, за ко- торое электрон  уменьшает дрейфовую скорость в  раз. За это время он пробегает расстояние, которое называется транспортным: L = ,                                           (6) где γ – число столкновений (рассеяния) электронов с дефектами; – средняя длина свободного пробега электрона между двумя последовательными столкновениями. За  время τ электрон испытывает γ число столкновений с дефектами кристаллической решетки и пробегает транспортное расстояние L. С другой стороны, транспортное расстояние равно L=, так как электрон движется со средней скоростью. С  учетом (6) получим  или .                          (7)   Подставляя (7) в (4), найдем u = .                                       (8)   Плотность тока равна j = nеu,                                                          (9)   где n – концентрация электронов. Подставляя (8) в (9), получим j =.                                    (10)   Закон Ома в дифференциальной форме j =.                                                (11)   Тогда с учетом (10) и (11) имеем  и .                    (12)   Полученная, с точки зрения квантовой теории, формула удельного сопротивления  ρ имеет такой же вид, что и формулы (12). Но вместо  m, , , рассмотренные в классической теории, в квантовой теории вводятся: эффективная масса , фермиевская скорость   и длина свободного пробега . Учитывая эти изменения, формула (12) приобретет следующий вид (13): .                                     (13)   Квантово-механические расчеты показывают, что при низких температурах число столкновений , а . Тогда удельное сопротивление ρ пропорционально и сопротивление металлов обусловлено рассеянием электронов проводимости на дефектах и ионах кристаллической решетки. При высоких температурах сопротивление в основном обусловлено рассеянием электронов на тепловых ионах кристаллической решетки (фононах), а сопротивление, обусловленное рассеянием электронов на дефектах, пренебрежимо мало. Поэтому при высоких температурах  не зависит от Т, а . Тогда . Расчет показывает, что при высоких температурах удельное сопротивление зависит от температуры:  ,                                              (14) где α – температурный коэффициент сопротивления;  – удельное сопротивление при температуре 0 °С; t – температура по шкале Цельсия. Температурный коэффициент α равен относительному изменению удельного сопротивления при изменении температуры проводника на 1 градус: , .   Для металлических изотропных проводников коэффициент  почти не зависит от температуры и примерно равен . Так как сопротивление металлических проводников зависит от  [см. формулу (1)], т.е. R~, то с учетом (14) сопротивление можно представить в виде R = R0(1+).                                     (15)   Откуда можно найти :   ,                                      (16)   где R­0 – сопротивление проводника при t = 0°С.   Для металлических проводников , т.е. с увеличением температуры сопротивление увеличивается. Поэтому эти проводники называются проводниками I рода. 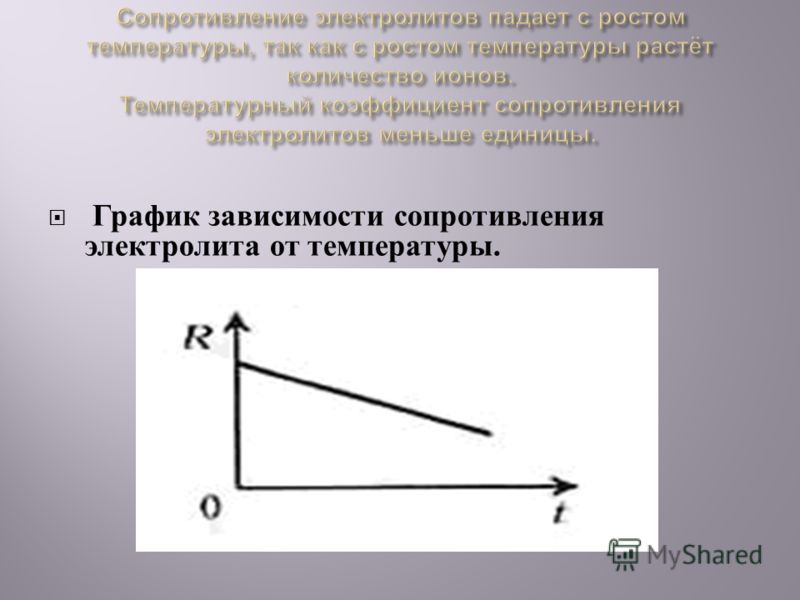Для электролитов, графита и других , т.е. с увеличением температуры сопротивление проводника уменьшается. Они называются проводниками II рода.   Ход работы   Схема установки приведена на рис. 4. Исследуемый проводник помещается в колбу, заполненную непроводящей жидкостью (масло, глицерин, дистиллированная вода). Температура измеряется термометром. Для равномерного нагревания жидкость перемешивается мешалкой. Исследуемый проводник R подключается в качестве неизвестного сопротивления к клеммам измерительного моста. Измеряют сопротивление исследуемого проводника при комнатной температуре. Включают нагреватель и непрерывно перемешивают жидкость мешалкой.

Рис. 4

При нагревании через каждые 5-10 °С измеряют сопротивление проводника. Измерения проводят до температуры 80-90 °С. Полученные результаты заносят в таблицу.

Таблица

t, °C   R, Ом

Строят зависимость R= ƒ(t), откладывая по оси абсцисс значения температуры, а по оси ординат значения R. Значения R0 и  определяют следующим образом: продолжают полученную прямую до пересечения с осью R (рис. 5). Точка пересечения дает значение R0. Значение  вычисляют по формуле .   Точка а – точка, выбранная вами на полученной прямой между двумя последними экспериментальными точками.

Рис. 5

Вопросы для допуска к работе   1. Какова цель работы? 2. Почему сопротивление металлов увеличивается с возрастанием температуры? 3. Что называется температурным коэффициентом сопротивления? Выведите размерность температурного коэффициента сопротивления.   Вопросы для защиты работы   1. Объясните механизм проводимости в металлах. 2. В чем существенные отличия объяснения электрического сопротивления в классической теории металлов от квантовой? 3. Вывести формулу температурной зависимости удельного сопротивления. 4. Какие проводники называются проводниками I и II рода?

IV. Зависимость сопротивления проводника от температуры

Если пропустить ток от аккумулятора через стальную спираль, а за тем начать нагревать ее в пламени горелки, то амперметр покажет уменьшение силы тока. Это означает, что с изменением температуры сопротивление проводника меняется.

Если при температуре, равной  , сопротивление проводника равно  , а при температуре   оно равно  , то относительное изменение сопротивления, как показывает опыт, прямо пропорционально изменению температуры:  .

Коэффициент пропорциональности   называют температурным коэффициентом сопротивления. Он характеризует зависимость сопротивления вещества от температуры. Температурный коэффициент сопротивления численно равен относительному изменению сопротивления проводника при нагревании на 1 К. Для всех металлических проводников   и незначительно меняется с изменением температуры. Если интервал изменения температуры не велик, то температурный коэффициент можно считать постоянным и равным его среднему значению на этом интервале температур. У чистых металлов  .

При нагревании проводника его геометрические размеры меняются не значительно. Сопротивление проводника меняется в основном за счет изменения его удельного сопротивления. Можно найти зависимость этого удельного сопротивления от температуры:  .

Так как   мало меняется при изменении температуры проводника, то можно считать, что удельное сопротивление проводника линейно зависит от температуры (рис. 1).

Рис. 1

Х отя коэффициент   довольно мал, учет зависимости сопротивления от температуры при расчете нагревательных приборов просто необходим. Так, сопротивление вольфрамовой нити лампы накаливания увеличивается при прохождении по ней тока более чем в 10 раз.

У некоторых сплавов, на пример у сплава меди с никелем, температурный коэффициент сопротивления очень мал:

; удельное сопротивление константа не велико:  . Такие сплавы используют для изготовления эталонных сопротивлений и добавочных сопротивлений к измерительным приборам, т.е. в тех случаях, когда требуется, чтобы сопротивление заметно не менялось при колебаниях температуры.

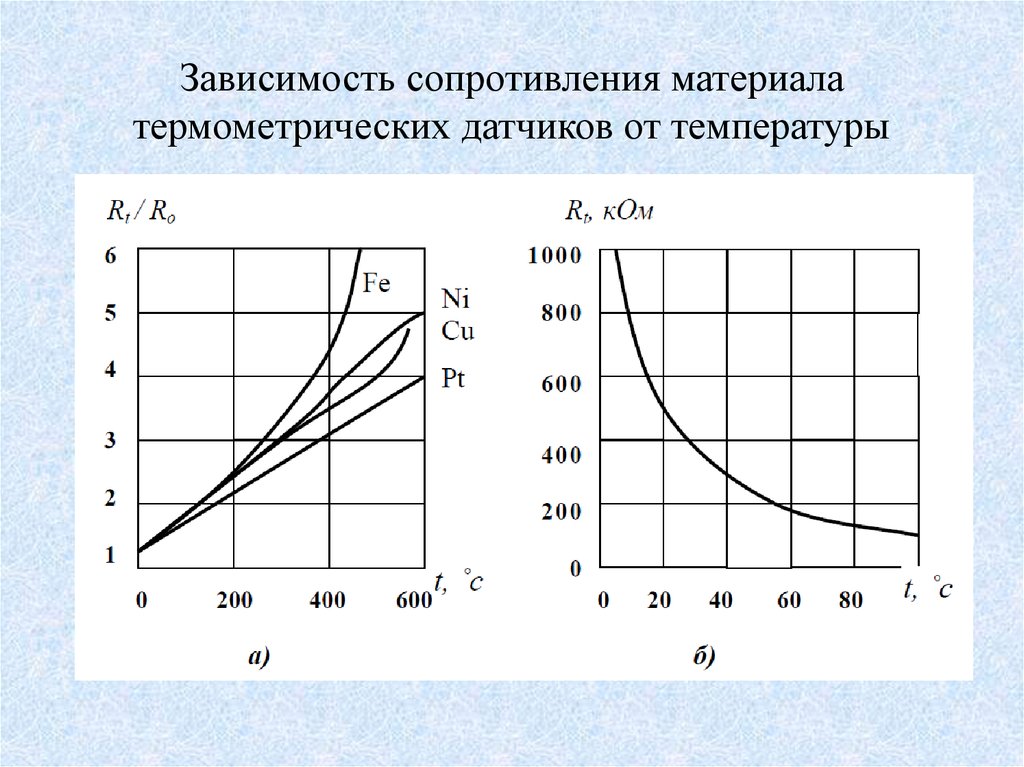
Зависимость сопротивления металлов от температуры используют в термометрах сопротивления. Обычно в качестве основного рабочего элемента такого термометра берут платиновую проволоку, зависимость сопротивления которой от температуры хорошо известна. Об изменениях температуры судят по изменению сопротивления проволоки, которое можно измерить.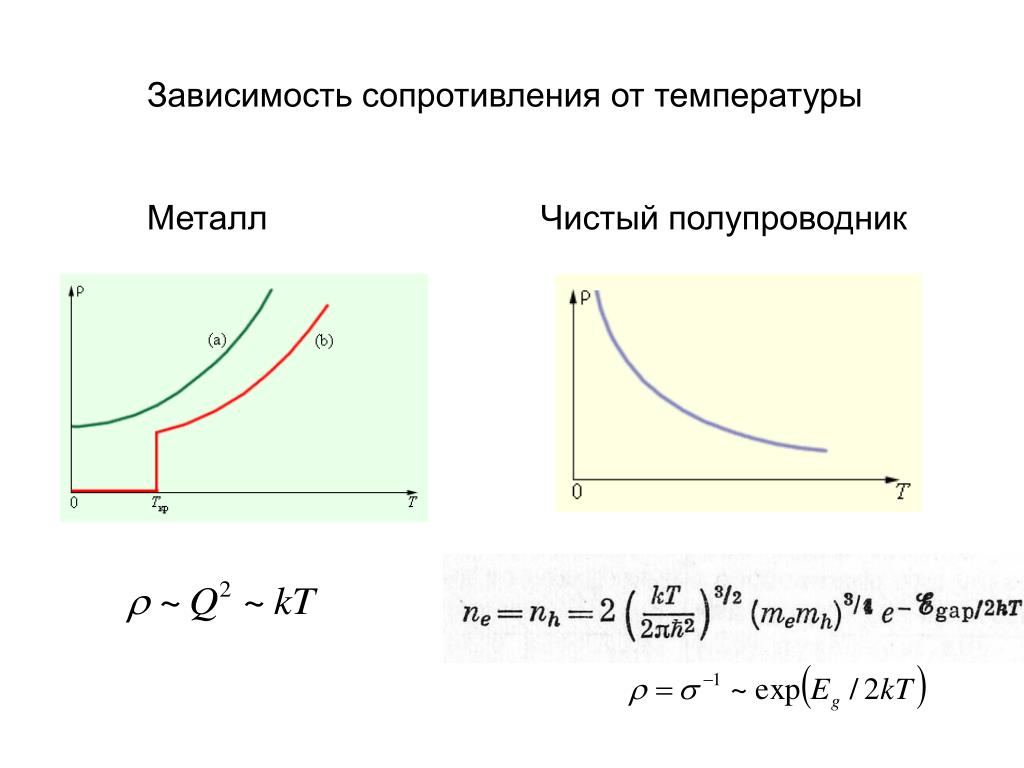 Такие термометры позволяют измерять очень низкие и очень высокие температуры, когда обычные жидкостные термометры не пригодны.

Удельное сопротивление металлов растет линейно с увеличением температуры. У растворов электролитов оно уменьшается при увеличении температуры.

Р ис. 2

В 1911 г. Голландский физик Камерлинг-Оннес открыл замечательное явление–сверхпроводимость. Он обнаружил, что при охлаждении ртути в жидком гелии еесопротивление сначала меняется постепенно, а за тем при температуре   очень резко падает до нуля (рис. 2). Это явление было названо сверх проводимостью. Позже было открыто много других сверхпроводников. Сверхпроводимость наблюдается при очень низких температурах–около  .

Если в кольцевом проводнике, находящемся в сверхпроводящем состоянии, создать ток, а за тем устранить источник электрического тока, то сила этого тока не меняется сколь угодно долго. В обычном же не сверхпроводящем проводнике электрический ток прекращается.

Сверхпроводники находят широкое применение. Так, сооружают мощные электромагниты со сверхпроводящей обмоткой, которые создают магнитное поле на протяжении длительных интервалов времени без затрат энергии. Ведь выделения теплоты в сверхпроводящей обмотке не происходит.

Однако получить сколь угодно сильное магнитное поле с помощью сверхпроводящего магнита нельзя. Очень сильное магнитное поле разрушает сверхпроводящее состояние. Такое поле может быть создано током в самом сверхпроводнике. Поэтому для каждого проводника в сверхпроводящем состоянии существует критическое значение силы тока, превзойти которое, не нарушая этого состояния, нельзя.

Если бы удалось создать сверх проводящие материалы при температурах, близких к комнатным, то была бы решена проблема передачи энергии по проводам без потерь.В настоящее время физики работают над ее решением.

Многие металлы и сплавы при температурах ниже   полностью теряют сопротивление, т. е. становятся сверхпроводниками. Недавно была открыта высокотемпературная сверхпроводимость.

Краткое примечание о том, как удельное сопротивление зависит от температуры

Удельное электрическое сопротивление, также известное как удельное электрическое сопротивление, представляет собой способность материала противодействовать или сопротивляться потоку заряда или тока. Это зависит от поведения материала и температуры. Не имеет значения, какова форма и размер конкретного вещества. Омметр — это единица СИ для измерения удельного сопротивления конкретного объекта.

Удельное сопротивление углеродных резисторов находится в обратной зависимости от температуры. При повышении температуры удельное сопротивление материала уменьшается и наоборот. Символ ро (⍴) обозначает удельное сопротивление. Удельное сопротивление также обратно связано с проводимостью материала. Если вы знаете значение проводимости материала, вам просто нужно сделать это взаимно, чтобы узнать правильное значение удельного сопротивления.

Зависимость удельного сопротивления от температуры

Существует три вида материалов: металлы или проводники, полупроводники и изоляторы. Материалы, которые позволяют электричеству течь через них, являются проводниками. Полупроводники — это тип материала, который находится между металлами и изоляторами. Они обладают большей проводимостью, чем изоляторы, и меньшей, чем проводящие материалы. Изоляторы – это материалы, препятствующие протеканию тока.

Металлы или проводники имеют низкое удельное сопротивление и положительный температурный коэффициент. Поэтому при повышении температуры удельное сопротивление металла увеличивается. Полупроводники – материалы с отрицательным температурным коэффициентом. С повышением температуры значение удельного сопротивления в полупроводниках уменьшается. Полупроводники ведут себя как проводники при высоких температурах, критических температурах или пиках и дают положительный температурный коэффициент. Температурная зависимость полупроводников от удельного сопротивления сильно влияет на их использование в электронике.

Температура влияет на удельное сопротивление вещества. Для проводников, полупроводников и изоляторов температурная зависимость удельного сопротивления меняется в зависимости от природы вещества. Прежде чем мы перейдем к полупроводникам, давайте поговорим о том, как изменяется сопротивление в проводниках и изоляторах.

Как удельное сопротивление металлов или проводников зависит от температуры

При нагревании проводника его температура повышается, и его атомы начинают сильно вибрировать. Это приводит к хаотическому движению свободных и других электронов и их столкновению. Свободные электроны, ответственные за протекание тока, теряют энергию из-за этих столкновений.

При нормальных условиях проводники имеют низкое удельное сопротивление. Удельное сопротивление проводников, особенно металлов, увеличивается, когда подвижность или скорость дрейфа уменьшается из-за истощения энергии. Удельное сопротивление металла увеличивается с повышением температуры, что дает ему положительный температурный коэффициент сопротивления. С повышением температуры сопротивление проводника увеличивается, а его проводимость уменьшается.

Как удельное сопротивление изоляторов зависит от температуры

Изоляторы не имеют свободных электронов в обычных условиях. У них есть электроны, которые плотно упакованы с ядром. При повышении температуры электроны разрывают эти связи и получают возможность свободно двигаться, поэтому изоляторы мигрируют в зону проводимости.

Повышение температуры уменьшает разницу энергий между валентной зоной и зоной проводимости. Таким образом, проводимость изолятора увеличивается, поскольку сопротивление изолятора уменьшается с температурой. Изоляторы имеют отрицательный температурный коэффициент удельного сопротивления.

Как удельное сопротивление полупроводников зависит от температуры

Энергетическая щель между зоной проводимости и валентной зоной сокращается при повышении температуры в полупроводниках. При высоких температурах валентные электроны в полупроводниковом материале накапливают достаточно энергии, чтобы разорвать ковалентную связь и перейти в зону проводимости.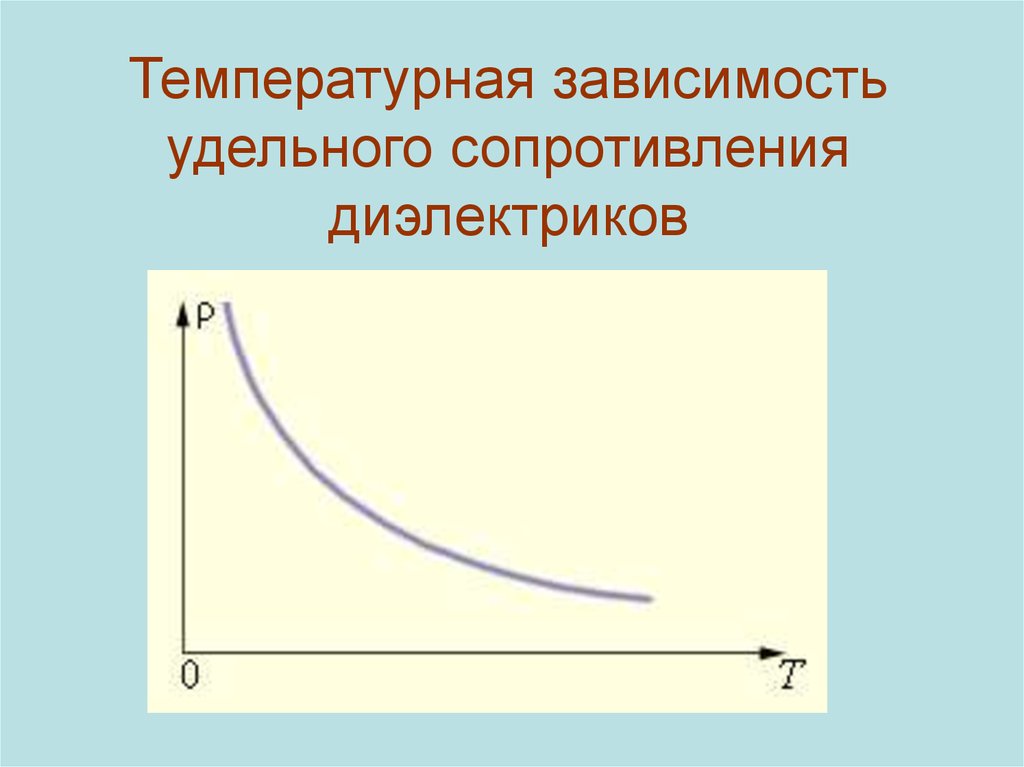

При высоких температурах это приводит к увеличению количества носителей заряда в полупроводнике. Удельное сопротивление полупроводника уменьшается по мере увеличения концентрации носителей заряда. При повышении температуры удельное сопротивление полупроводника уменьшается, что делает его более проводящим. При высоких температурах полупроводник обладает отличной проводимостью.

Полупроводники имеют отрицательный температурный коэффициент сопротивления. Эта функция используется для использования полупроводников в электронных приложениях. Температура полупроводникового кристалла повышается при приложении внешнего напряжения, увеличивая в нем плотность термически созданных носителей. Образуется больше электронно-дырочных пар, что облегчает прохождение тока через полупроводник.

Легирование полупроводника донорными или акцепторными примесями улучшает его характеристики. Такие полупроводники называются внешними полупроводниками. Внешние полупроводники имеют более высокое удельное сопротивление, чем собственные (нелегированные или чистые) полупроводники.

Температурная зависимость удельного сопротивления полупроводников очень выгодна. Современные полупроводниковые приборы возможны только из-за отрицательного температурного коэффициента сопротивления.

Заключение

Удельное сопротивление указывает на свойство электрической цепи. Проводники с низким удельным сопротивлением, такие как золото и серебро, обеспечивают эффективный поток электричества. Изоляторы, такие как резина и стекло, обладают высоким сопротивлением и создают опасность для прохождения электричества. Полупроводники сохраняют свойства, существующие между этими двумя материалами.

С повышением температуры удельное сопротивление проводников увеличивается, тогда как удельное сопротивление полупроводников и изоляторов уменьшается.

15.3 Сопротивление и удельное сопротивление – Физика Колледжа Дугласа 1104 Индивидуальный учебник – зима и лето 2020

Глава 15 Электрический ток, сопротивление и закон Ома

Резюме

• Объясните понятие удельного сопротивления.
• Используйте удельное сопротивление для расчета сопротивления определенных конфигураций материала.
• Используйте термический коэффициент удельного сопротивления для расчета изменения сопротивления в зависимости от температуры.

Сопротивление объекта зависит от его формы и материала, из которого он состоит. Цилиндрический резистор на рис. 1 легко анализировать, и таким образом мы можем получить представление о сопротивлении более сложных форм. Как и следовало ожидать, электрическое сопротивление цилиндра [латекс]\boldsymbol{R}[/латекс] прямо пропорционально его длине [латекс]\жирный символ{L}[/латекс], аналогично сопротивлению трубы потоку жидкости. . Чем длиннее цилиндр, тем больше столкновений зарядов с его атомами произойдет. Чем больше диаметр цилиндра, тем больший ток он может пропускать (опять же аналогично потоку жидкости по трубе). На самом деле, [латекс]\boldsymbol{R}[/латекс] обратно пропорциональна площади поперечного сечения цилиндра [латекс]\жирный символ{А}[/латекс].

Рисунок 1. Однородный цилиндр длиной L и площадью поперечного сечения A . Его сопротивление потоку тока аналогично сопротивлению трубы потоку жидкости. Чем длиннее цилиндр, тем больше его сопротивление. Чем больше его площадь поперечного сечения A , тем меньше его сопротивление.

Для данной формы сопротивление зависит от материала, из которого состоит объект. Различные материалы оказывают различное сопротивление потоку заряда. Мы определяем удельное сопротивление  [латекс]\boldsymbol{\rho}[/латекс] вещества, так что сопротивление  [латекс]\жирныйсимвол{R}[/латекс] объекта прямо пропорционально [латекс]\жирныйсимвол{ \ро}[/латекс]. Удельное сопротивление [латекс]\boldsymbol{\rho}[/латекс] — это внутреннее свойство материала, не зависящее от его формы или размера. Сопротивление [латекс]\boldsymbol{R}[/латекс] однородного цилиндра длиной [латекс]\boldsymbol{L}[/латекс], площадью поперечного сечения [латекс]\boldsymbol{A}[/латекс] , и изготовлен из материала с удельным сопротивлением [латекс]\boldsymbol{\rho}[/латекс], составляет

[латекс]\boldsymbol{R =}[/латекс] [латекс]\boldsymbol{\frac{\rho L}{A}}[/латекс].

В таблице 1 приведены репрезентативные значения [латекс]\жирныйсимвол{\ро}[/латекс]. Материалы, перечисленные в таблице, разделены на категории проводников, полупроводников и изоляторов на основе широких групп удельного сопротивления. Проводники имеют наименьшее удельное сопротивление, а изоляторы — наибольшее; полупроводники имеют промежуточное сопротивление. Проводники имеют разную, но большую плотность свободного заряда, в то время как большинство зарядов в изоляторах связаны с атомами и не могут свободно перемещаться. Полупроводники занимают промежуточное положение, имея гораздо меньше свободных зарядов, чем проводники, но обладая свойствами, из-за которых количество свободных зарядов сильно зависит от типа и количества примесей в полупроводнике. Эти уникальные свойства полупроводников используются в современной электронике, что будет рассмотрено в последующих главах. 9{11}}[/латекс] Таблица 1. Удельное сопротивление [латекс]\boldsymbol{\rho}[/латекс] различных материалов при 20ºC

Пример 1.

Расчет диаметра резистора: нить накала фары

Нить накала автомобильной фары изготовлена ​​из вольфрама и имеет морозостойкость [латекс]\boldsymbol{0,350 \;\Omega}[/латекс]. Если нить представляет собой цилиндр длиной 4,00 см (можно свернуть в спираль для экономии места), то каков ее диаметр?

Стратегия

Мы можем преобразовать уравнение [латекс]\boldsymbol{R = \frac{\rho L}{A}}[/latex], чтобы найти площадь поперечного сечения [латекс]\boldsymbol{A}[/latex] нить из предоставленной информации. Тогда его диаметр можно найти, предполагая, что он имеет круглое поперечное сечение.

Решение

Площадь поперечного сечения, полученная перестановкой выражения сопротивления цилиндра, приведенного в [латекс]\жирный символ{R = \frac{\rho L}{A}}[/latex],

[латекс]\boldsymbol{A =}[/латекс] [латекс]\boldsymbol{\frac{\rho L}{R}}[/латекс] 9{-5} \;\textbf{m}} \end{array}.[/latex]

Обсуждение

Диаметр чуть меньше одной десятой миллиметра. Он заключен в кавычки только до двух цифр, потому что [латекс]\жирныйсимвол{\ро}[/латекс] известен только до двух цифр.

Удельное сопротивление всех материалов зависит от температуры. Некоторые даже становятся сверхпроводниками (нулевое сопротивление) при очень низких температурах. (См. рис. 2.) И наоборот, удельное сопротивление проводников увеличивается с повышением температуры. Поскольку атомы вибрируют быстрее и преодолевают большие расстояния при более высоких температурах, электроны, движущиеся через металл, совершают больше столкновений, что фактически увеличивает удельное сопротивление. При относительно небольших изменениях температуры (около 100ºC или меньше) удельное сопротивление [латекс]\boldsymbol{\rho}[/латекс] зависит от изменения температуры [латекс]\жирныйсимвол{\Delta T}[/латекс], как это выражается в следующем уравнении

[латекс]\boldsymbol{ \rho = \rho_{0} (1 + \alpha \Delta T)},[/latex]

, где [latex]\boldsymbol{\rho_0}[/latex] — исходное удельное сопротивление, а [latex]\boldsymbol{\alpha}[/latex] — температурный коэффициент удельного сопротивления . (См. значения [латекс]\жирныйсимвол{\альфа}[/латекс] в таблице 2 ниже.) Для больших изменений температуры [латекс]\жирныйсимвол{\альфа}[/латекс] может меняться, или нелинейное уравнение может быть нужно найти [латекс]\boldsymbol{\rho}[/латекс]. Обратите внимание, что [латекс]\жирныйсимвол{\альфа}[/латекс] положителен для металлов, что означает, что их удельное сопротивление увеличивается с температурой. Некоторые сплавы были разработаны специально, чтобы иметь небольшую температурную зависимость. Манганин (состоящий из меди, марганца и никеля), например, имеет [латекс]\boldsymbol{\alpha}[/латекс]  близок к нулю (до трех цифр по шкале в таблице 2), поэтому его удельное сопротивление лишь незначительно меняется в зависимости от температуры. Это полезно, например, для создания эталона сопротивления, не зависящего от температуры.

Рис. 2. Сопротивление образца ртути равно нулю при очень низких температурах — это сверхпроводник примерно до 4,2 К. Выше этой критической температуры его сопротивление делает резкий скачок, а затем увеличивается почти линейно с температурой. 9{-3}}[/латекс]

Таблица 2: Температурные коэффициенты удельного сопротивления [латекс]\boldsymbol{\alpha}[/латекс]

Отметим также, что [латекс]\жирныйсимвол{\альфа}[/латекс] имеет отрицательное значение для полупроводников, перечисленных в таблице 2, что означает, что их удельное сопротивление уменьшается с повышением температуры. Они становятся лучшими проводниками при более высокой температуре, потому что повышенное тепловое возбуждение увеличивает количество свободных зарядов, доступных для переноса тока. Это свойство уменьшения [латекса] \boldsymbol{\rho}[/латекса] с температурой также связано с типом и количеством примесей, присутствующих в полупроводниках.

Сопротивление объекта также зависит от температуры, так как [латекс]\boldsymbol{R_0}[/латекс] прямо пропорционально [латекс]\жирныйсимвол{\ро}[/латекс]. Для цилиндра мы знаем [латекс]\boldsymbol{R = \rho L/A}[/latex], и поэтому, если [латекс]\boldsymbol{L}[/латекс] и [латекс]\boldsymbol{A}[ /латекс] не сильно меняются с температурой, [латекс]\boldsymbol{R}[/латекс] будет иметь ту же температурную зависимость, что и [латекс]\жирныйсимвол{\rho}[/латекс].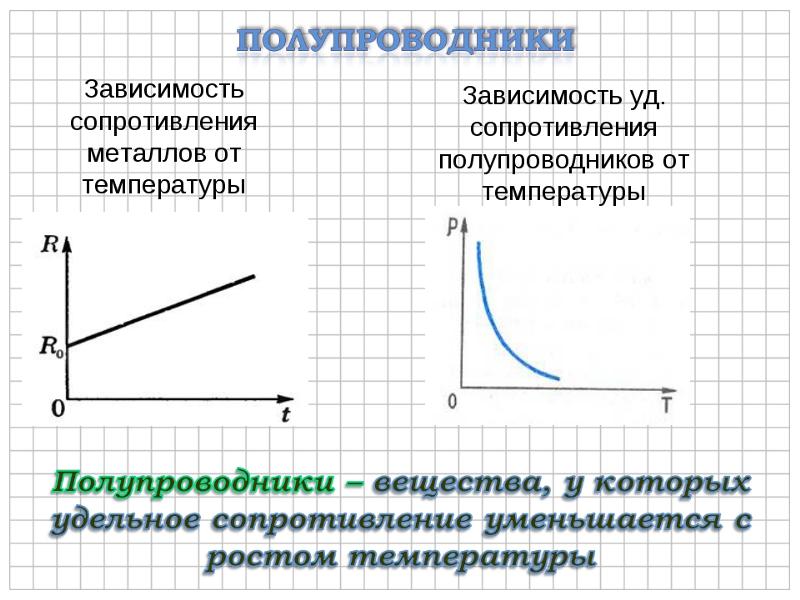 (Изучение коэффициентов линейного расширения показывает, что они примерно на два порядка меньше типичных температурных коэффициентов удельного сопротивления, поэтому влияние температуры на [латекс]\boldsymbol{L}[/латекс] и [латекс]\boldsymbol {A}[/latex] примерно на два порядка меньше, чем на [latex]\boldsymbol{\rho}[/latex].) Таким образом,

[латекс]\boldsymbol{R = R_0(1 + \alpha \Delta T)}[/latex]

— зависимость сопротивления объекта от температуры, где [latex]\boldsymbol{R_0}[/latex] — исходное сопротивление, а [latex]\boldsymbol{R}[/latex] — сопротивление после изменения температуры [ латекс]\boldsymbol{\Delta T}[/латекс]. Многие термометры основаны на влиянии температуры на сопротивление. (См. рис. 3.) Одним из наиболее распространенных является термистор, полупроводниковый кристалл с сильной температурной зависимостью, сопротивление которого измеряется для получения его температуры. Устройство маленькое, поэтому быстро приходит в тепловое равновесие с той частью человека, к которой прикасается.

Рисунок 3. Эти известные термометры основаны на автоматизированном измерении сопротивления термистора в зависимости от температуры. (кредит: Biol, Wikimedia Commons)

Пример 2: Расчет сопротивления: сопротивление горячей нити

Хотя следует соблюдать осторожность при применении [латекс]\boldsymbol{ \rho = \rho_0(1 + \alpha \Delta T)}[ /latex] и [latex]\boldsymbol{R = R_0(1 + \alpha \Delta T)}[/latex] для изменений температуры более 100ºC, для вольфрама уравнения работают достаточно хорошо при очень больших изменениях температуры. Каково же тогда сопротивление вольфрамовой нити в предыдущем примере, если ее температуру повысить с комнатной (20°С) до типичной рабочей температуры 2850°С? 9{\circ}C)]} \\[1em] & \boldsymbol{4.8 \;\Omega} \end{array}.[/latex]

Обсуждение

Это значение согласуется с примером сопротивления фары в Пример 1 Глава 20.2 Закон Ома: сопротивление и простые цепи.

Исследования PhET: сопротивление в проводе

Узнайте о физике сопротивления в проводе. Измените его удельное сопротивление, длину и площадь, чтобы увидеть, как они влияют на сопротивление провода. Размеры символов в уравнении меняются вместе со схемой провода.

Рис. 4. Сопротивление в проводе

• Сопротивление [латекс]\boldsymbol{R}[/латекс] цилиндра длиной [латекс]\boldsymbol{L}[/латекс] и площадью поперечного сечения [латекс]\boldsymbol{A}[/латекс] [латекс]\boldsymbol{R = \frac{\rho L}{A}}[/latex], где [латекс]\boldsymbol{\rho}[/латекс] — удельное сопротивление материала.
• Значения [латекс]\жирныйсимвол{\rho}[/латекс] в таблице 1 показывают, что материалы делятся на три группы: проводники, полупроводники и изоляторы .
• Температура влияет на удельное сопротивление; для относительно небольших изменений температуры [латекс]\boldsymbol{\Delta T}[/latex], удельное сопротивление равно [латекс]\boldsymbol{\rho = \rho_0(1 + \alpha \Delta T)}[/latex], где [ латекс]\boldsymbol{\rho_0}[/латекс] — исходное удельное сопротивление, а αα — температурный коэффициент удельного сопротивления.
• В таблице 2 приведены значения [латекс]\жирныйсимвол{\альфа}[/латекс], температурный коэффициент удельного сопротивления.
• Сопротивление [латекс]\boldsymbol{R}[/латекс] объекта также зависит от температуры: [латекс]\boldsymbol{R = R_0(1 + \alpha \Delta T)}[/латекс], где [латекс ]\boldsymbol{R_0}[/latex] — исходное сопротивление, а [latex]\boldsymbol{R}[/latex] — сопротивление после изменения температуры.

Задачи и упражнения

1: Чему равно сопротивление отрезка медной проволоки 12-го калибра диаметром 2,053 мм длиной 20,0 м?

2: Диаметр медной проволоки 0-го калибра 8,252 мм. Найти сопротивление такого провода длиной 1,00 км, по которому осуществляется передача электроэнергии.

3: Если вольфрамовая нить диаметром 0,100 мм в лампочке должна иметь сопротивление [латекс]\boldsymbol{0,200 \;\Омега}[/латекс] при 20,0ºC, какой длины она должна быть? 93 \;\textbf{V}}[/latex] применяется к нему? (Такой стержень можно использовать, например, для изготовления детекторов ядерных частиц).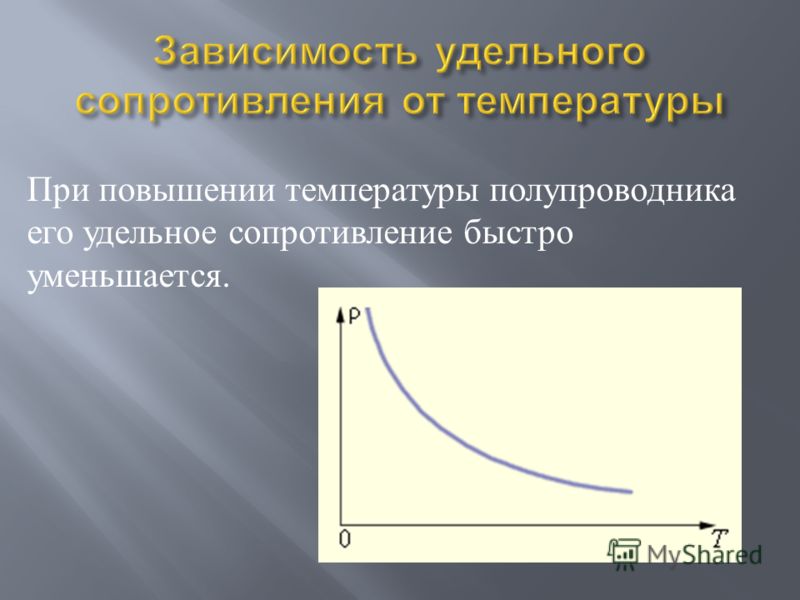 в габаритах? (б) Происходит ли это в бытовой электропроводке при обычных обстоятельствах?

7: Резистор из нихромовой проволоки используется в тех случаях, когда его сопротивление не может измениться более чем на 1,00% от его значения при 20,0ºC. В каком диапазоне температур его можно использовать?

8: Из какого материала изготовлен резистор, если его сопротивление при 100°С на 40,0% больше, чем при 20,0°С?

9: Электронное устройство, предназначенное для работы при любой температуре в диапазоне от –10,0ºC до 55,0ºC, содержит чисто углеродные резисторы. Во сколько раз увеличивается их сопротивление в этом диапазоне?

10: (а) Из какого материала изготовлен провод, если он имеет длину 25,0 м, диаметр 0,100 мм и сопротивление [латекс]\boldsymbol{77,7 \;\Omega}[/latex] при 20,0ºС? б) Каково его сопротивление при 150°С?

11: При постоянном температурном коэффициенте удельного сопротивления, каково максимальное уменьшение сопротивления константановой проволоки в процентах, начиная с 20,0ºC?

12: Проволоку протягивают через матрицу, растягивая ее в четыре раза по сравнению с первоначальной длиной.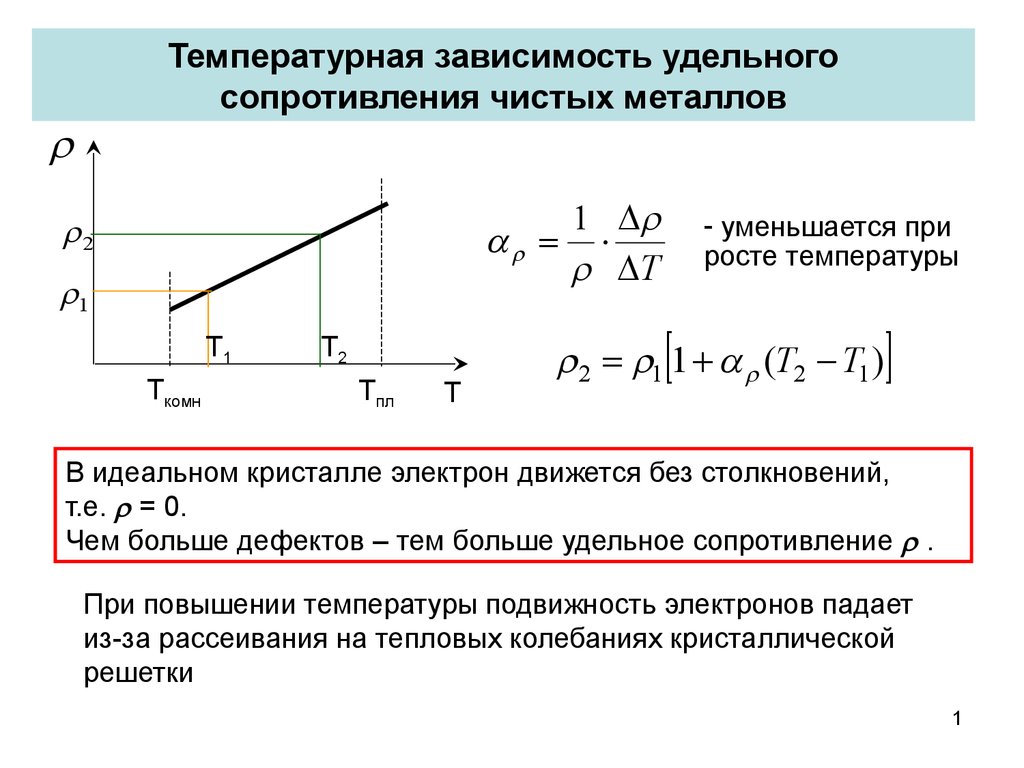 Во сколько раз увеличивается его сопротивление?

13: Медная проволока имеет сопротивление [латекс]\boldsymbol{0,500 \;\Омега}[/латекс] при 20,0ºC, а железная проволока имеет сопротивление [латекс]\boldsymbol{0,525 \; \Omega}[/latex] при той же температуре. При какой температуре их сопротивления равны? 9{\circ} \textbf{C}}[/latex]), когда он имеет ту же температуру, что и пациент. Какова температура тела пациента, если сопротивление термистора при этой температуре составляет 82,0% от его значения при 37,0°С (нормальная температура тела)? (b) Отрицательное значение для [латекс]\boldsymbol{\alpha}[/латекс] может не поддерживаться при очень низких температурах. Обсудите, почему и так ли это, здесь. (Подсказка: сопротивление не может стать отрицательным.)

15: Комплексные концепции

(a) Повторите упражнение 2 с учетом теплового расширения вольфрамовой нити. Вы можете принять коэффициент теплового расширения [латекс]\boldsymbol{12 \times 10^{-6}/^{\circ} \textbf{C}}[/латекс].