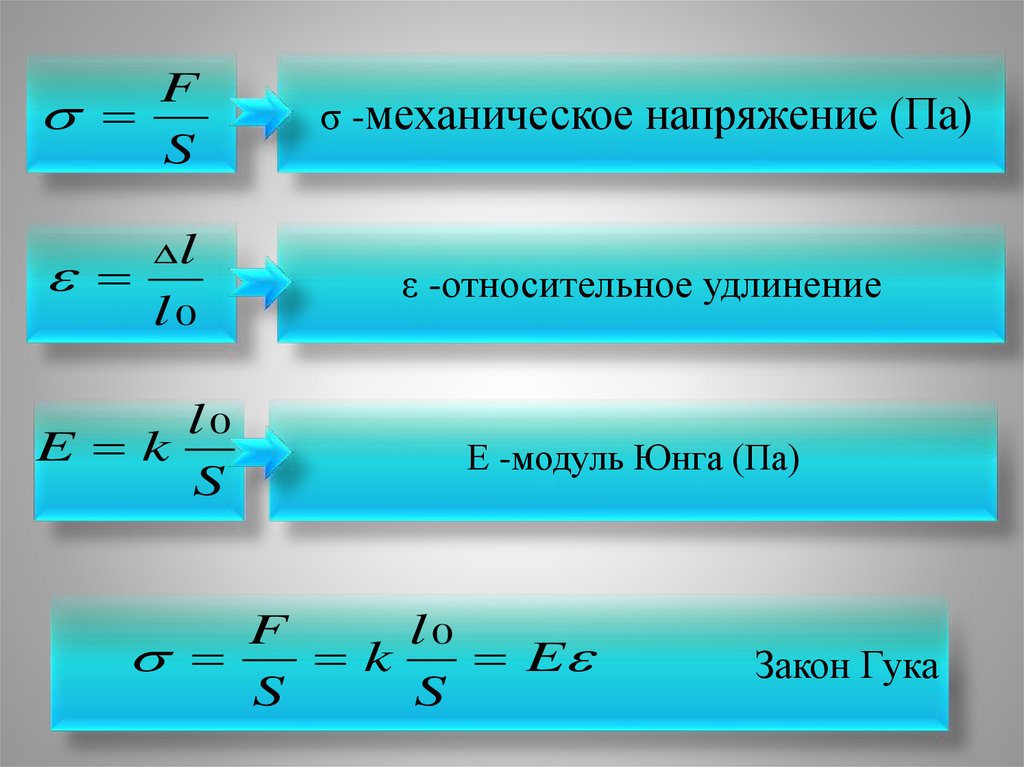
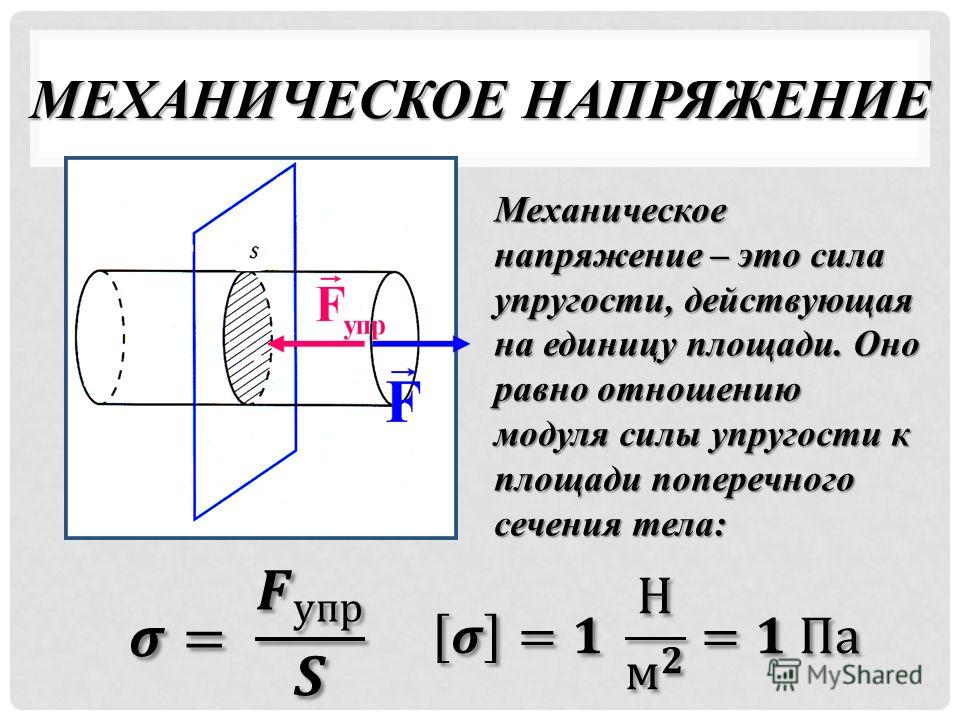
Механическое напряжение тел — определение и формула, свойства твердых тел

При взаимодействии твердых тел с различными факторами окружающей среды могут возникать изменения — как внутренние, так и внешние. Одним из примеров является механическое напряжение, появляющееся в недрах тела. Оно определяет степень возможных изменений при повреждении.

Основные понятия в физике

Механическое напряжение – мера внутренних сил объекта, которая возникает под влиянием различных факторов. Например, при появлении деформации, во время которой внешние силы стараются изменить взаимное расположение частиц, а внутренние — препятствуют этому процессу, ограничивая его каким-то определенным значением. Таким образом, можно сказать, что механическое напряжение — это прямое следствие нагрузки на тело.

Можно выделить два основных вида механического напряжения:

1. Нормальное – приложено на единичную площадку сечения по нормали к нему.
2. Касательное – приложено на площадку сечения по касательной к нему.

Совокупность этих напряжений, действующих в одной точке, называют напряженным состоянием в этой точке.

Измеряемое в паскалях (Па) механическое напряжение: формула расчета представлена ниже

Q=F/S,

Где Q –механическое напряжение (Па), F — сила, возникающая внутри тела при деформации (Н), S – площадь (мм).

Свойства твердых тел

Твердые тела, как и все прочие, состоят из атомов, однако у них очень прочная структура, которая практически не подвергается деформации, т.е. объем и форма остаются постоянными. Такие объекты обладают рядом уникальных свойств, которые можно разделить на две большие группы:

1. Физические.
2. Химические.

К физическим можно отнести следующие:

1. Механические – изучают их при помощи соответствующего воздействия на тело. К этим свойствам можно отнести упругость, хрупкость, прочность, т.е. все, что связано со способностью сопротивляться деформации, вызванной внешними факторами.
2. Тепловые – изучают влиянием разных температур на объект. К ним можно отнести расширение при нагревании, теплопроводность, теплоемкость.
3. Электрические – эти свойства связаны с движением электронов внутри тела и их способностью собираться в упорядоченный поток при воздействии внешних факторов. Пример — электрическая проводимость.
4. Оптические – изучаются с помощью световых потоков. К этим свойствам относятся светоотражение, поглощение света, дифракция.
5. Магнитные – определяются наличием магнитных моментов у составляющих твердого тела. За них, так же, как и за электрические, отвечают отрицательно заряженные частицы благодаря своему строению и определенному движению.

К химическим свойствам относится все, что связано с реакцией на воздействие соответствующими веществами и процессами, происходящими при этом. Пример — окисление, разложение. Строение кристаллической решетки также относится к этим свойствам объекта.

Также можно выделить небольшую группу физико-химических свойств. К ней относятся те из них, что проявляются как при механическом, так и при химическом воздействии. Пример — горение, во время которого происходят изменения по двум вышеуказанным характеристикам.

Механические свойства твердых тел – кратко закон Гука, формулы (10 класс)

4.4

Средняя оценка: 4.4

Всего получено оценок: 217.

4.4

Средняя оценка: 4.4

Всего получено оценок: 217.

Любые конструкции, используемые в технике, должны выдерживать заданные нагрузки. Для правильного расчета конструкций необходимо знать механические свойства твердых тел и законы, которые описывают их поведение. Кратко рассмотрим эту тему.

Механическое напряжение

В кристалле твердого тела между ядрами атомов существуют ковалентные связи, в которых электроны являются общими для соседних атомов.

Рис. 1. Ковалентная связь.

При небольшом увеличении расстояния между атомами (деформации), возникнут силы, препятствующие дальнейшему удалению. Для макроскопического кристалла эти силы зависят от свойств вещества и от количества связей, к которым приложено усилие разрыва. Пока структура кристалла не нарушена, снятие нагрузки возвращает кристалл в исходное состояние. Такая деформация назвается упругой.

Поскольку количество связей пропорционально площади сечения разрываемого образца, появляется возможность ввести специальный параметр, характеризующие эти силы – «механическое напряжение» (или просто «напряжение»).

Механическое напряжение равно отношению силы разрыва, приложенной к образцу, к поперечной площади разрываемого образца:

$$\sigma ={F\over S}$$

Из данной формулы можно получить размерность механического напряжения. Поскольку сила измеряется в ньютонах, а площадь в квадратных метрах, единица напряжения получается равной ньютону на квадратный метр или паскалю.

Заметим, что деформация может быть не только разрывной, но с сжимающей, формула и размерность напряжения останутся прежними.

Закон Гука

Итак, при упругой деформации кристалла, возникают силы, стремящиеся вернуть кристалл в ненапряженное состояние. Опыты показывают, что силы эти тем больше, чем больше деформация. То есть, механическое напряжение $\sigma$ кристалла пропорционально его относительному удлинению:

$$\sigma =E{|Δl|\over l_0}$$

Данный закон был установлен в 1660 Р.Гуком, и носит его имя.

Рис. 2. Роберт Гук.

Модуль Юнга и жесткость

Коэффициент пропорциональности $E$ в формуле называется модулем Юнга, его физический смысл в том, что это напряжение, возникающие в кристалле при единичном относительном удлинении (или при удвоении абсолютного линейного размера кристалла). Единица его измерения такая же, как и у напряжения – паскаль.

Часто для характеристики упругих элементов удобнее использовать не модуль Юнга, а такой параметр, как жесткость, равную силе, возникающей при растяжении на единичную длину.

Связь между модулем Юнга и жесткостью легко вывести из закона Гука. Подставим в формулу Закона Гука выражение для механического напряжения, приведенное выше:

$${F\over S} =E{|Δl|\over l_0}$$

Откуда:

$$F ={ES\over l_0}|Δl|=k|Δl|$$

Таким образом, жесткость пружины прямо пропорциональна модулю Юнга:

$$k ={ES\over l_0}$$

Пределы пропорциональности и упругости.

Закон Гука хорошо выполняется для небольших деформаций, пока ковалентные связи в кристалле не нарушены. Максимальное напряжение, при котором закон Гука полностью выполняется, называется пределом пропорциональности.

Если кристалл продолжать деформировать дальше – изменение напряжения становится нелинейным, а затем, связи начинают разрываться, в результате кристалл уже не возвращается к своему прежнему состоянию, и некоторые остаточные деформации в нем остаются и после снятия.

Максимальное напряжение, при котором в кристалле после снятия усилия не остается заметных остаточных деформаций, называется пределом упругости. Как правило, пределы пропорциональности и упругости для большинства веществ отличаются менее, чем на 1%, при решении задач по физике в 10 классе школы их можно считать равными.

Рис. 3. Условная диаграмма растяжения.

Что мы узнали?

При деформации в кристалле возникают силы, сопротивляющиеся деформации. Закон, связывающий механическое напряжение с удлинением кристалла, называется законом Гука. Этот закон действует до некоторого максимального значения (предела пропорциональности). Коэффициент пропорциональности в законе Гука называется модулем Юнга. Модуль Юнга прямо пропорционален жесткости кристалла.

Тест по теме

Доска почёта

Чтобы попасть сюда — пройдите тест.

Пока никого нет. Будьте первым!

Оценка доклада

4.4

Средняя оценка: 4.4

Всего получено оценок: 217.

---

А какая ваша оценка?

Калькулятор напряжения

Создано Bogna Szyk

Отзыв Стивена Вудинга

Последнее обновление: 21 декабря 2022 г.

Содержание:

• Как рассчитать деформацию и напряжение расчетов
• Модуль упругости единиц
• Часто задаваемые вопросы

Этот калькулятор напряжения поможет вам решить задачи в механике, связанные с напряжением, деформацией и модулем Юнга. За несколько простых шагов вы узнаете зависимость между напряжением и деформацией для любого материала, который остается эластичным. Мы также научим вас, как рассчитать деформацию и как применять уравнение напряжения.

🔎 Этот калькулятор рассчитан на осевое напряжение. Если вы изучаете поперечный сдвиг, вам следует воспользоваться нашим калькулятором напряжения сдвига.

Как рассчитать деформацию и напряжение

Деформация определяется как мера деформации — пропорция между изменением длины и первоначальной длиной объекта. Например, если взять резинку и растянуть ее так, чтобы она стала в два раза длиннее первоначальной, то деформация будет равна 1 (100%).

Формула деформации:

ε=ΔLL1=L2−L1L1\varepsilon = \frac{\Delta L}{L_1} = \frac{L_2 — L_1}{L_1}ε=L1​ΔL​=L1​L2​−L1​

L₁ обозначает начальную длину, L₂ – конечную длину, а ΔL – изменение длины. Обратите внимание, что деформация безразмерна.

Напряжение, с другой стороны, является мерой давления, которое частицы материала оказывают друг на друга. Она определяется как сила, действующая на объект на единицу площади. Однако это отличается от давления; при расчете напряжения рассматриваемая площадь должна быть настолько малой, чтобы анализируемые частицы считались однородными. Если принять во внимание большую площадь, расчетное напряжение обычно является средним значением.

Уравнение напряжения:

σ=FA\sigma = \frac{F}{A}σ=AF​

F обозначает силу, действующую на тело, а A обозначает площадь. Единицы напряжения такие же, как и единицы давления — паскали (обозначение: Па) или ньютоны на квадратный метр.

Положительное напряжение означает, что объект находится в состоянии растяжения — он «хочет» удлиниться (Калькулятор удлинения). Отрицательное напряжение означает, что находится в сжатии и «хочет» стать короче.

Вы знаете?
Деформация бывает двух видов — инженерная и истинная. Узнайте больше в нашем калькуляторе истинной деформации

Модуль Юнга (напряжение в зависимости от деформации)

Если материал линейно-упругий , то напряжение и деформация напрямую связаны следующей формулой:

E=σεE = \frac{ \sigma}{\varepsilon}E=εσ​

E — модуль упругости или модуль Юнга . Это материальная константа, разная для каждого вещества.

Что такое линейно-упругое поведение материала? Если мы прикладываем напряжение к материалу, деформация увеличивается пропорционально. Это может быть верно только для некоторого диапазона напряжений — после того, как мы достигнем определенного значения, материал может сломаться или поддаться. Уступчивость – это увеличение деформации в постоянно напряженном состоянии.

Пример расчета

Предположим, мы хотим найти модуль Юнга стали. Для этого мы подготовили стальной стержень, который тянули с большим усилием.

1. Решаем, что сила, приложенная к тяге, будет равна 30 кН ( 30*10³ Н ).
2. Определяем размеры стержня. Допустим длина 2 м (2000 мм) и площадь поперечного сечения 1 см² ( 1*10⁻⁴ м² ).
3. Мы заметили, что стержень удлинился на 3 мм.
4. Рассчитываем деформацию стержня по формуле:
   ε = ΔL/L₁ = 3/2000 = 0,0015 .
5. Рассчитываем напряжение по формуле напряжения: σ = F/A = 30*10³ / (1*10⁻⁴) = 300*10⁶ = 300 МПа .
6. Наконец, мы делим напряжение на деформацию, чтобы найти модуль Юнга стали: E = σ/ε = 300*10⁶ / 0,0015 = 200*10⁹ = 200 ГПа .

Единицы модуля упругости

Единицы модуля Юнга такие же, как единицы давления и напряжения: паскали или ньютоны на квадратный метр. В единицах СИ:

1 Па = 1 Н / 1 м² = 1 кг·м / с² / м² = 1 кг / (м·с²)

Если вас интересует механика, воспользуйтесь калькулятором крутящего момента. Или изучите калькулятор круга Мора, чтобы понять различные типы напряжений.

Часто задаваемые вопросы

Что означает высокий модуль Юнга?

Чем выше модуль упругости или модуль Юнга, тем жестче материал. Это означает, что он может выдерживать большее количество нагрузок.

Какой тип напряжения действует на конкретное поперечное сечение стойки из-за сегмента над ней?

Напряжение в поперечном сечении колонны отрицательное или сжимающее напряжение из-за веса сегмента над указанным поперечным сечением.

Как оценить напряжение в определенном поперечном сечении стойки?

Для оценки напряжения в определенном поперечном сечении стойки:

1. Найдите вес сегмента над ней.
2. Подставьте значение веса вместо силы в формулу для напряжения, σ = F/A , где F — сила, а A — площадь поперечного сечения.
3. Ура! Вы только что узнали напряжение, действующее на поперечное сечение!

В чем разница между текучестью и пределом прочности при растяжении?

Предел текучести твердого материала равен максимальному растягивающему напряжению, которое он может выдержать до того, как произойдет остаточная деформация. Предел прочности равен максимальному напряжению, которое он может выдержать до разрушения .

Bogna Szyk

Площадь (A)

Сила (F)

Назначение (σ)

Расчет деформации

Начальная длина (L₁)

Конечная длина (L₂)

изменение длины (ΔL)

Деформация (ε)

Модуль Юнга (E)

Ознакомьтесь с 33 подобными материалами и механикой сплошных сред 🧱

Угол скручивания Допуск на изгиб Число твердости по Бринеллю… Еще 30

Что такое механическое напряжение: Прочность материала

Размер и форма твердого тела. Из-за механического воздействия или внешних сил тело меняет свою форму. Мы можем выразить это изменение формы тела напряжением в механике. Это явление механического напряжения и деформации можно лучше всего понять, поняв кривую напряжения-деформации.

Содержание

• Что такое механическое напряжение?
• Пример напряжения, действующего на тело
• Типы механического напряжения ?

Что такое механическое напряжение?

Механическое напряжение — мера внутреннего сопротивления, проявляемого телом или материалом при приложении к нему внешней силы. это обозначается сигмой (σ).

Предел упругости материала – это предел, при котором сила сопротивления становится равной приложенным силам. В пределе упругости внешние силы, действующие на тело, равны внутренним силам.

Формула механического напряжения

Математически механическое напряжение равно внутренней силе сопротивления, действующей на тело на единицу площади.

Напряжение – это свойство площади или поверхности. Его значение в любой точке можно определить, рассматривая A→0

Единица напряжения

Единицей механического напряжения в системе СИ является Н/м². Но в паспорте материала это написано как МПа.

Преобразование единиц измерения
1 МПа = 1 Н / мм²
1 тыс. Кв. бар = 0,1 Н/мм²

Пример напряжения, действующего на тело

Рассмотрим случай, когда вы кладете на стол резиновую ленту и осторожно поднимаете ее. Какое механическое напряжение возникнет внутри резиновой ленты?

Резиновая лента на столеЧеловек, тянущий резиновую ленту

Удерживая резиновую ленту, механическое  Напряжение не будет возникать внутри резиновой ленты  , поскольку внешнее усилие не будет оказывать никакого сопротивления в резиновой ленте. Это явление известно как Движение твердого тела .

При движении твердого тела объект перемещается из своего исходного положения без какой-либо физической деформации.

Но если мы потянем резинку в противоположном направлении, чтобы произвести прогиб. Механическое напряжение будет производиться внутри резиновой ленты. Следовательно, мы можем сделать вывод, что механическое напряжение не будет возникать без прогиба или внутреннего сопротивления.

Виды механического напряжения ?

Механическое напряжение действует на площадь поперечного сечения тела. Мы можем классифицировать инженерное напряжение на следующие типы в зависимости от положения и направления приложенной внешней силы.

Виды механического напряжения

1) Одноосное нормальное напряжение

Напряжение, действующее на тело перпендикулярно площади его поперечного сечения, известно как одноосное нормальное напряжение. Это приводит либо к сжатию, либо к удлинению твердого тела. Мы можем классифицировать одноосное нормальное напряжение на два типа:

1. Напряжение растяжения
2. Напряжение сжатия

Напряжение растяжения

Напряжение, действующее на тело из-за двух равных и противоположных внешних тяговых сил, известно как Напряжение растяжения 8. Напряжение растяжения  приводит к общему увеличению длины и уменьшению площади поперечного сечения тела.

Напряжение сжатия

Механическое напряжение, действующее на тело из-за двух равных и противоположных толкающих сил, известно как напряжение сжатия. Напряжение сжатия  приводит к увеличению площади поперечного сечения и уменьшению длины корпуса.

2) Напряжение сдвига

Напряжение сдвига

Напряжение, действующее на тело из-за двух равных и противоположных сил, действующих по разным линиям действия, называется напряжением сдвига. Касательное напряжение действует по касательной к площади тела и приводит к угловой деформации. Мы измеряем касательное напряжение как угол.

Формула напряжения сдвига

Напряжение сдвига (γ) = θ

Таким образом, механическое напряжение — это внутреннее сопротивление, проявляемое телом при приложении к нему внешней силы.