Преобразования Лоренца

Преобразования Лоренца

_{Lorentz Transformations}

    Преобразования Лоренца − преобразования координат и времени какого-либо события при переходе от одной инерциальной системы отсчёта к другой. Инерциальная система отсчёта – система отсчёта, движущаяся прямолинейно с постоянной скоростью v. Преобразования Лоренца отражают равноправие всех инерциальных систем отсчёта в описании законов природы. Если инерциальная система отсчёта K’ движется относительно инерциальной системы отсчёта K с постоянной скоростью v вдоль оси x, то преобразования Лоренца имеют вид

y = y’, z = z’,

(1)

c — скорость света в вакууме, β = v/c. Формулы, выражающие x’, y’, z’, t’ через x, y, z, t получаются из соотношения (1) заменой v на -v.

Рис. Система координат K’ движется относительно неподвижной системы координат K со скоростью v вдоль оси x.

    При v << c преобразования Лоренца переходят в преобразования Галилея

x = x’ + vt, y = y’, z = z’, t = t’.

Из преобразований Лоренца следует, что промежутки времени Δt и отрезки длины Δl зависят от движения системы отсчёта. Если в системе K’ два события, происходящие в одном и том же месте, разделены интервалом времени Δt’, то в системе K эти же происходящие в разных местах события разделены промежутком времени Δt

Если отрезок, покоящийся в системе K’, имеет длину Δl’, то его длина Δl в системе K, т.е. расстояние между двумя одновременными в K событиями регистрации положения концов отрезка, принимает значение

Поперечные размеры тел при этом не изменяются.
    Формулы преобразования скорости:

Электрическое поле E и магнитное поле H при преобразовании Лоренца преобразуются следующим образом:

Координаты 4-мерного вектора энергии-импульса с компонентами (ε/c, p_x, p_y, p_z) при преобразовании Лоренца преобразуются следующим образом:

Энергия частицы

Импульс частицы

    Преобразования Лоренца, указывающие на относительность промежутков времени и отрезков длины между двумя событиями, оставляют инвариант­ной, т.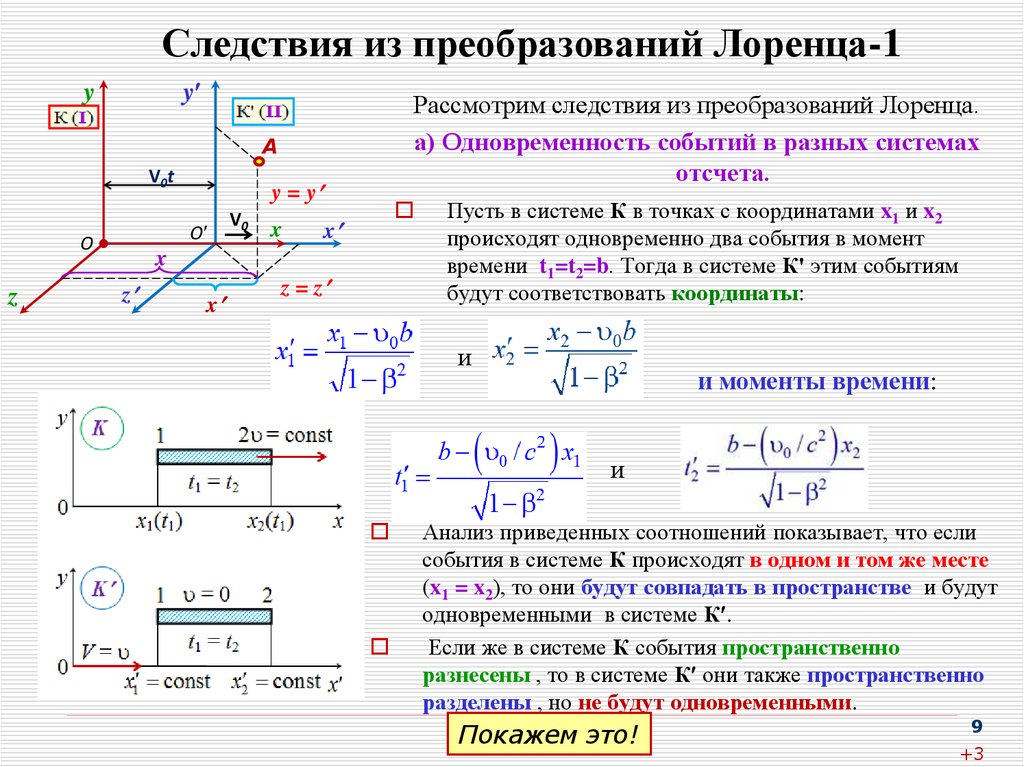

е. не зависящей от выбора системы отсчёта, их комбинацию, называемую интервалом.

Инвариантом при преобразовании Лоренца является также квадрат 4-вектора энергии-импульса

---

См. также

• Мир атомных ядер
• Фундаментальные частицы и взаимодействия
• Основные соотношения релятивистской физики
• Методы анализа процессов взаимодействия
• Фундаментальные частицы и их взаимодействия
• Лекции по основам кинематики элементарных процессов
• Новая физика XX века
• Преобразования систем координат
• Кинематика реакций
• Для любознательных

Преобразование Лоренца | это… Что такое Преобразование Лоренца?

Преобразованиями Лоренца в физике, в частности в специальной теории относительности (СТО), называются преобразования, которым подвергаются пространственно-временные координаты (x,y,z,t) каждого события при переходе от одной инерциальной системы отсчета (ИСО) к другой.

Аналогично преобразованиям Лоренца при таком переходе подвергаются координаты любого 4-вектора.

Чтобы явно различить преобразования Лоренца со сдвигами начала отсчёта и без сдвигов, когда это необходимо, говорят о неоднородных и однородных преобразованиях Лоренца.

Преобразования Лоренца без сдвигов начала отсчёта образуют группу Лоренца, со сдвигами — группу Пуанкаре, иначе называемую неоднородной группой Лоренца.

С математической точки зрения преобразования Лоренца — это преобразования, сохраняющие неизменной метрику Минковского, то есть, в частности, последняя сохраняет при них простейший вид при переходе от одной инерциальной системы отсчёта к другой (другими словами преобразования Лоренца — это аналог для метрики Минковского ортогональных преобразований, осуществляющих переход от одного ортонормированного базиса к другому, то есть аналог поворота координатных осей для пространства-времени). В математике или теоретической физике преобразования Лоренца могут относиться к любой размерности пространства.

Именно преобразования Лоренца, смешивающие — в отличие от преобразований Галилея — пространственные координаты и время, исторически стали основой для формирования концепции единого пространства-времени.

• Следует заметить, что лоренц-ковариантны не только фундаментальные уравнения (такие, как уравнения Максвелла, описывающее электромагнитное поле, уравнение Дирака, описывающее электрон и другие фермионы), но и такие макроскопические уравнения, как волновое уравнение, описывающее (приближенно) звук, колебания струн и мембран, и некоторые другие (только тогда уже в формулах преобразований Лоренца под
  c следует иметь в виду не скорость света, а какую-то другую константу, например скорость звука). Поэтому преобразования Лоренца могут быть плодотворно использованы и в связи с такими уравнениями (хотя и в довольно формальном смысле, впрочем, мало отличающемся — в своих рамках — от их применения в фундаментальной физике).

Содержание 1 Вид преобразований при коллинеарных (параллельных) пространственных осях 2 Вывод преобразований 2. 1 Алгебраический вывод 2.2 Группа симметрий уравнений Максвелла 2.3 Наглядный вывод преобразований Лоренца 2.3.1 Преобразование для поперечных осей (п.1) 2.3.2 Замедление времени (п.2) 2.3.3 Относительность одновременности (п.3) 2.3.4 Лоренцевское сокращение длины (п.4) 3 Разные формы записи преобразований 3.1 Вид преобразований при произвольной ориентации осей 3.2 Преобразования Лоренца в матричном виде 4 Свойства преобразований Лоренца 5 Связанные определения 6 История 7 Примечания 8 Литература 9 См. также

Вид преобразований при коллинеарных (параллельных) пространственных осях

Если ИСО K‘ движется относительно ИСО K с постоянной скоростью V вдоль оси x, а начала пространственных координат совпадают в начальный момент времени в обеих системах, то преобразования Лоренца (прямые) имеют вид:

где c — скорость света в вакууме, величины со штрихами измерены в системе

K‘, без штрихов — в K.

Эта форма преобразования (то есть при выборе коллинеарных осей), называемое иногда бустом (англ. boost) или лоренцевским бустом (особенно в англоязычной литературе), несмотря на свою простоту включает, по сути, всё специфическое физическое содержание преобразований Лоренца, так как пространственные оси всегда можно выбрать таким образом, а при желании добавить пространственные повороты не представляет трудности (см. это в явном развёрнутом виде ниже), хотя и делает формулы более громоздкими.

• Формулы, выражающие обратное преобразование, то есть выражающие x‘,y‘,z‘,t‘ через x,y,z,tможно получить просто заменой V на − V (абсолютная величина относительной скорости движения систем отсчёта | V | одинакова при измерении её в обеих системах отсчёта, поэтому можно при желании снабдить V штрихом, только при этом надо внимательно следить за тем, чтобы знак и определение соответствовали друг другу) и взаимной заменой штрихованных x и t с нештрихованными. Или решая систему уравнений (1) относительно x’, y’, z’, t’.
• Надо иметь ввиду, что в литературе преобразования Лоренца часто записывается для упрощения в системе единиц, где
  c = 1, что действительно делает их вид более изящным.
• Видно, что при преобразованиях Лоренца события, одновременные в одной системе отсчёта, не являются одновременными в другой (относительность одновременности), кроме того у движущегося тела сокращается продольный размер по сравнению с тем, какой оно имеет в сопутствующей ему системе отсчёта (лоренцево сокращение), а ход движущихся часов замедляется, если наблюдать их из «неподвижной» системы отсчёта (релятивистское замедление времени).

Вывод преобразований

Преобразования Лоренца могут быть получены абстрактно, из групповых соображений (в этом случае они получаются с неопределённым

c), как обобщение преобразований Галилея (что было проделано Пуанкаре — см. ниже). Однако впервые были получены как преобразования, относительно которых ковариантны уравнения Максвелла (то есть по сути — которые не меняют законов электродинамики и оптики). Могут также быть получены из предположения линейности преобразований и постулата одинаковости скорости света во всех системах отсчёта (являющегося упрощённой формулировкой требования ковариантности электродинамики относительно искомых преобразований, и распространением принципа равноправия инерциальных систем отсчёта — принципа относительности — на электродинамику), как это делается в специальной теории относительности (СТО) (при этом c в преобразованиях Лоренца получается определённым и совпадает со скоростью света).

Надо заметить, что если не ограничивать класс преобразований координат линейными, то первый закон Ньютона выполняется не только для преобразований Лоренца, а для более широкого класса дробно-линейных преобразований (однако этот более широкий класс преобразований — за исключением, конечно, частного случая преобразований Лоренца — не сохраняет метрику постоянной).

Алгебраический вывод

На основании нескольких естественных предположений (основным из которых является предположение о существовании принципиально максимальной скорости распространения взаимодействий) можно показать, что при смене ИСО должна сохраняться величина

ds² = c²dt² − dx² − dy² − dz²,

называемая интервалом. Из этой теоремы напрямую следует общий вид преобразований Лоренца (см. ниже). Здесь рассмотрим лишь частный случай. Для наглядности при переходе в ИСО K‘, движущуюся со скоростью v, выберем в исходной системе K ось X сонаправленной с v, а оси Y и Z расположим перпендикулярно оси X. Оси ИСО K‘ выберем сонаправленными с осями ИСО K. При таком преобразовании

Мы будем искать линейные преобразования Лоренца, так как при бесконечно малых преобразованиях координат дифференциалы новых координат линейно зависят от дифференциалов старых координат, а в силу однородности пространства и времени коэффициенты не могут зависеть от координат, только от взаимной ориентации и скорости ИСО.

То, что поперечные координаты не могут меняться, ясно из соображений изотропности пространства. Действительно, величина y‘ не может изменяться и при этом не зависеть от x (кроме как при вращении вокруг v, которое мы исключаем из рассмотрения), в чём легко убедиться подстановкой таких линейных преобразований в выражение для интервала. Но если она зависит от x, то точка с координатой (0,x,0,0) будет иметь ненулевую координату y‘, что противоречит наличию симметрии вращения системы относительно v и изотропии пространства. Аналогично для z‘.

Наиболее общий вид таких преобразований:

где α — некоторый параметр, называемый быстротой. Обратные преобразования имеют вид

Ясно, что точка, покоящаяся в ИСО K, должна будет двигаться в ИСО K‘ со скоростью − v. С другой стороны, если точка покоится, то

Учитывая, что при смене ИСО не должна меняться ориентация пространства, получим что

Следовательно, уравнение для быстроты однозначно разрешимо:

а преобразования Лоренца имеют вид

Параметр γ называется лоренц-фактором.

Группа симметрий уравнений Максвелла

Наглядный вывод преобразований Лоренца

Примем постулаты СТО, сводящиеся к расширенному принципу относительности, утверждающему, что все физические процессы протекают в точности одинаково во всех инерциальных системах отсчета (уточняющий его принцип постоянства скорости света в СТО означает расширение принципа относительности на электродинамику вместе с уточняющим утверждением о том, что нет никакой фундаментальной физической среды (эфира), которая выделяла бы одну из систем отсчета на опыте — то есть если даже эфир и есть, то его наличие не должно никак нарушать принципа относительности на практике). Кроме того, полезно явно подчеркнуть, что принцип постоянства скорости света означает наличие именно конечной скорости (скорости света), заложенной в фундаментальные законы (уравнения), одной и той же для всех инерциальных систем отсчета, причём и в каждой системе отсчета величина скорости света одинакова для любых направлений его распространения (это используется ниже).

Преобразование для поперечных осей (п.1)

Пусть есть две бесконечные плоскости, перпендикулярные оси y. Расстояние между этими плоскостями очевидно не должно зависеть от скорости движения плоскостей вдоль самих себя (то есть переходя в себя же), а значит — не зависит от выбора системы отсчета среди движущихся вдоль оси x. (Чтобы быть совсем уверенным в этом, можно провести мысленный эксперимент, заключающийся в измерении времени, требующегося лучу света, движущемуся вдоль y в каждой такой системе отсчета, для того, чтобы, стартовав на одной плоскости, достичь второй, и увидеть, что такое время очевидно будет одинаковым, если верны постулаты СТО).

То же самое, конечно, верно и для оси z. Поэтому, исключив для простоты физически неинтересный случай поворота координат второй системы относительно первой на постоянный (независящий от времени) угол, получаем:

y = y‘,z = z‘

Замедление времени (п.2)

Показать, что любые процессы (например ход часов) выглядит медленнее из системы отсчета где носитель этого процесса (например часы) движется, чем в его собственной системе отсчета (в которой он неподвижен), и найти количественно фактор такого замедления, можно, рассмотрев мысленный эксперимент со «световыми часами», представляющими собой источник и приемник света, удаленные друг от друга на известное фиксированное расстояние L, и отмеряющие, таким образом, интервал времени L/c, соответствующий времени прохождения света от источника до приемника (это можно непрерывно повторять). Все другие часы, из принципу относительности, должны идти точно так же.

Для более прямого соответствия формы полученного результата формуле прямого преобразования Лоренца, будем считать, что наши световые часы покоятся в нештрихованой системе отсчета K, штрихованая же система отсчета K’ пусть движется для определенности вправо вдоль оси x со скоростью V. Источник и приемник расположим вдоль оси y при x=0. Это частный случай, который позволит нам получить сперва отдельно частное и более простое преобразование для времени.

Поместим источник в начальный момент времени в начало координат, обозначив его A (см. рисунок, там он изображен красной точкой), а приемник обозначим B (синяя точка). В нештрихованой системе отсчета (на рисунке слева) импульс света летит точно по оси y (B, как и A в этой системе неподвижны). Таким образом, от излучения до поглощения света в этой системе проходит время .

В штрихованой же системе отсчета точки A и B движутся влево со скоростью V. Особенно нас интересует движение точки B, обозначенное на рисунке пунктиром. Из-за этого ее смещения, равного , свету в этой системе отсчета приходится пройти не расстояние L, а большее (на рисунке путь света от A к B изображен зеленой линией). Это расстояние нетрудно выразить с помощью теоремы Пифагора, и оно же равно ct’, откуда:

(ct‘)² = L² + (Vt‘)²,

а учитывая упомянутые чуть выше L = ct и выражая t’ через t, имеем:

,

что и является преобразованием Лоренца для времени для условия x = 0.

(по сути же это есть замедление времени при наблюдении часов — или любого другого процесса с локальным носителем — из системы отсчета, движущейся относительно него: мы видим, что t’ > t).

Относительность одновременности (п.3)

Кроме замедления времени в движущейся системе отсчета (замедления хода всех часов движущейся лаборатории при наблюдении их из неподвижной), оказывается, что начало отсчета времени в движущейся системе отсчета также не совпадает с таковым в неподвижной, причем сдвиг этого начала отсчета — разный в разных точках — зависит от x (часы, выглядящие синхронными в своей собственной системе отсчета, выглядят идущими с разным опережением-отставанием, зависящим от их пространственного расположения, если на них смотреть из другой системы отсчета, такой, в которой их собственная система отсчета движется).

Чтобы стало понятным само существо проблемы, придется так или иначе обдумать вопрос, а что значит, что часы в разных удаленных друг от друга точках пространства (например, в разных городах) идут одинаково (синхронно), как в этом можно убедиться, или как (с помощью какой процедуры) можно синхронизировать часы в разных местах, если изначально они не были синхронны.

Уже простейший способ синхронизации, заключающийся в том, что все часы синхронизируют в одном месте, а затем переносят в разные точки, позволяет качественно убедиться в том, что часы, синхронизированные в одной системе отсчета, будут выглядеть показывающими разное время из другой системы отсчета. Дело в том, что для часов, которые мы переносим вправо по оси x и влево по оси x, — время будет замедляться по-разному, так как их скорость будет обязательно различной в этой другой системе отсчета.

Это можно было бы аккуратно рассмотреть количественно, получив так искомый здесь результат. Но более просто этого достичь позволяет рассмотрение синхронизации с помощью световых сигналов (а принцип относительности говорит, что любой корректный способ синхронизации должен дать один и тот же результат, в чём, впрочем, при желании можно убедиться и явно).

Итак, рассмотрим синхронизацию с помощью световых сигналов. Этот процесс может заключаться, например, в обмене световыми сигналами между двумя удаленными хронометрами: если сигналы испущены в одно и то же время, то до получения сигнала по каждым часам пройдет одно и то же время. Но еще проще несколько другой (эквивалентный этому) способ: можно точно в середине отрезка, соединяющего хронометры, произвести вспышку света, и утверждать, что свет придет к обоим хронометрам одновременно.

В собственной системе отсчета (в которой хронометры неподвижны) картина симметрична. Однако в любой другой системе отсчета оба хронометра движутся (для определенности будем считать, что вправо), и тогда свету от середины отрезка, соединяющего их в начальный момент, потребуется меньше времени, чтобы дойти до левого хронометра (движущегося навстречу свету), чем до правого (который импульс света должен догонять).

Таким образом, хронометры, синхронные в своей собственной системе отсчета, по часам другой системы отсчета выглядят несинхронными. А это и означает, что события, одновременные в одной системе отсчета, неодновременны в другой. Это и называется относительностью одновременности.

Несложные геометрические выкладки позволяют (изобразив движение световых импульсов и хронометров на плоскости xt), получить выражение для сдвига начала отсчета времени:

− Vx / c²

• (для упрощения мы здесь рассматривали только часы, разнесенные вдоль оси x, но, конечно, всё может быть рассчитано и для общего случая).

Таким образом, сводя вместе результаты пунктов 1 и 2, получаем для преобразования времени

.

Лоренцевское сокращение длины (п.4)

Рассмотрев движение светового импульса вдоль оси x (а не вдоль y, как было в п.1), и потребовав (на основании постулата одинаковости скорости света во всех инерциальных системах отсчёта), чтобы расстояние между двумя точками было всегда равно времени, за которое свет идёт от одной точки до другой, делённому на (константу) скорость света, можно получить фактор сокращения расстояний вдоль оси x, а учитывая, что смещение начала отсчёта − Vt очевидно, можно получить и преобразование для x:

.

Однако ещё проще теперь понять, что x‘ выражается именно таким образом, заметив, что в плоскости x − ct график движения^[1] импульса света должен быть прямой, наклонённой под 45° (из-за того, что скорость света — всегда c), а значит и масштаб по x и по ct должен быть одинаковым, а выражения в системе единиц c = 1 — симметричными.

• Таким образом достаточно наглядно получаются преобразования Лоренца при коллинеарных пространственных осях. Конечно, возможен и обратный порядок рассуждений: можно сначала получить преобразования Лоренца каким-то более абстрактным способом, например — одним из упомянутых в статье выше, а потом получить все эффекты, разобранные в этапах данного наглядного доказательства, в качестве простого формального следствия преобразований Лоренца.

Разные формы записи преобразований

Вид преобразований при произвольной ориентации осей

В силу произвольности введения осей координат, многие задачи можно свести к указанному случаю. Если же задача требует иного расположения осей, то можно воспользоваться формулами преобразований в более общем случае. Для этого радиус-вектор точки

,

где  — орты, надо разбить на составляющую параллельную скорости и составляющую ей перпендикулярную

.

Тогда преобразования получат вид

,

где  — абсолютная величина скорости,  — абсолютная величина продольной составляющей радиус-вектора.

Эти формулы для случая параллельных осей, но с произвольно направленной скоростью, можно преобразовать к виду, впервые полученному Герглоцем:

.

Обратите внимание, что самый общий случай, когда начала координат не совпадают в нулевой момент времени, здесь не приведён с целью экономии места. Его можно получить, добавив к преобразованиям Лоренца трансляцию (смещение начала координат).

Преобразования Лоренца в матричном виде

Для случая коллинеарных осей преобразования Лоренца записываются в виде

,

где .

При произвольной ориентации осей, в форме 4-векторов это преобразование записывается как:

где E — единичная матрица 33,  — тензорное умножение трехмерных векторов.

Надо иметь ввиду, что в литературе матрица преобразований Лоренца часто записывается для упрощения в системе единиц, где c = 1.

Произвольное однородное преобразование Лоренца можно представить как некоторую композицию вращений пространства и элементарных преобразований Лоренца, затрагивающих только время и одну из координат. Это следует из алгебраической теоремы о разложении произвольного вращения на простые.

Свойства преобразований Лоренца

• Можно заметить, что в случае, когда , преобразования Лоренца переходят в преобразования Галилея. То же самое происходит в случае, когда . Это говорит о том, что специальная теория относительности совпадает с механикой Ньютона либо в мире с бесконечной скоростью света, либо при скоростях, малых по сравнению со скоростью света. Последее объясняет, каким образом сочетаются эти две теории — первая является обобщением и уточнением второй, а вторая — предельным случаем первой, оставаясь в этом качестве верной приближенно (с некоторой точностью, на практике часто очень и очень большой) при достаточно малых (по сравнению со скоростью света) скоростях движений.

• Преобразования Лоренца сохраняют инвариантным интервал для любой пары событий (точек пространства-времени) — то есть любой пары точек пространства — времени:

(убедиться в этом нетрудно, например, убедившись явно в том, что матрица преобразования Лоренца L — ортогональна в смысле метрики, определяемой таким выражением, то есть если , что проще всего проверить для буста, для трехмерных же вращений это очевидно, следовательно, верно и для любых их композиций; как только мы узнали, что преобразования ортогональны, значит расстояние, вычисленное в такой метрике, неизменно в любой системе координат — по свойству ортогональных преобразований).

• В частности, инвариантность интервала имеет место и для случая s = 0, а значит — гиперповерхность в пространстве-времени, которая определяется равенством нулю интервала до заданной точки — световой конус — является неподвижной при преобразованиях Лоренца (что является проявлением инвариантности скорости света). Внутреность двух полостей конуса соответствует времениподобным — вещественным — интервалам от их точек до вершины, внешняя область — пространственноподобным — чисто мнимым (в принятой в этой статье сигнатуре интервала).
• Другие инвариантные гиперповерхности однородных преобразований Лоренца (аналоги сферы для пространства Минковского) — гиперболоиды: двуполостный гиперболоид для времениподобных интервалов относительно начала координат, и однополостный — для пространственноподобных интервалов.

• Матрицу преобразования Лоренца при коллинеарных пространственных осях (в системе единиц c=1) можно представить как:

где . В этом легко убедиться, учитывая и проверив выполнение соответствущего тождества для матрицы преобразования Лоренца в обычном виде.

• Если принять введенные Минковским обозначения , то преобразование лоренца для такого пространства сводится к повороту на мнимый угол в плоскости, включающей ось (для случая движения вдоль оси — в плоскости x₀x₁). Это очевидно исходя из подстановки в матрицу, приведенную чуть выше -и немного изменив ее, чтобы учесть вводимую мнимость временной координаты — и сравнении ее с обычной матрицей вращения.

Связанные определения

Лоренц-инвариантность — свойство физических законов записываться одинаково во всех инерциальных системах отсчета(с учетом преобразований Лоренца). Принято считать, что этим свойством должны обладать все физические законы, и экспериментальных отклонений от него не обнаружено. Однако некоторые теории пока не удаётся построить так, чтобы выполнялась Лоренц-инвариантность.

История

Преобразования названы в честь их первооткрывателя — Х. А. Лоренца, который впервые ввел их (вместо преобразований Галилея) в качестве преобразований, связывающих геометрические величины (длины, углы), измеренных в разных инерциальных системах отсчета, чтобы устранить противоречия между электродинамикой и механикой, которые имелись в ньютоновской формулировке, включающей преобразования Галилея, что в конечном итоге привело к успеху при существенной модификации механики.

Сначала было обнаружено, что уравнения Максвелла инвариантны относительно этих преобразований (В. Фогтом в 1887 г.). Это же было повторено Лармором в 1900 г..

В 1892 г. Лоренц ввёл теорию сокращения, предполагающую сокращение длин всех твёрдых тел в направлении движения, количественно совпадающее с тем, что понимается сейчас под лоренцевым сокращением.

Преобразования Лоренца были впервые опубликованы в 1904 г. но в то время их форма была несовершенна. К современному, полностью самосогласованному виду их привёл французский математик А. Пуанкаре. Только в 1905 г. Пуанкаре и затем Эйнштейн в своей теории относительности пришёл к широко популярной впоследствии формально-аксиоматической трактовке этих преобразований. Пуанкаре же ввел термины «преобразования Лоренца» и «группа Лоренца», показал, исходя из эфирной модели, невозможность обнаружить движение относительно абсолютной системы отсчета (системы, в который эфир неподвижен), модифицировав таким образом принцип относительности Галилея. Ему же принадлежит групповой вывод явного вида преобразований Лоренца (с неопределенным c) без независимого постулата инвариантности скорости света.

Примечания

1. ↑ Минковский назвал такой график движения мировой линией; однако в этом параграфе мы не будем углубляться в связь преобразований Лоренца с понятием пространства Минковского в полном его объёме, прежде всего — чтобы не усложнять и не прерывать элементарный вывод, который удобнее считать независимым от каких-либо дополнительных специальных понятий, ограничившись только элементарными геометрическими и алгебраическими понятиями лишь настолько, насколько они необходимы. По сути, речь идёт именно о преобразовании координат в пространстве Минковского, причём в данном параграфе, исходя из постулата постоянства скорости света, как раз и выясняются определённые свойства этого пространства, как и преобразований Лоренца — в качестве удобных преобразований координат в нём. Но ещё раз для ясности подчеркнем, что для самого вывода не нужно знать ничего кроме того, что явно сказано в основном тексте параграфа.

Литература

• Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7
• Физическая энциклопедия, т.2 — М.:Большая Российская Энциклопедия стр.608 и стр.609.
• Ф. И. Фёдоров Группа Лоренца. — М.: Наука, 1979. 384 с.
• Гельфанд И. М., Минлос Р. А., Шапиро З. Я. Представление группы вращений и группы Лоренца. М., 1958.

См. также

• Сложное движение (формула преобразования скорости, согласованная с преобразованиями Лоренца)

13.

2: Матрица преобразования Лоренца и метрический тензор

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

17446

• Тимон Идема
• Делфтский технологический университет через TU Delft Open

В этом разделе мы объединили пространство и время в один четырехвектор и определили новый скалярный продукт на пространстве этих четырех векторов. В главе 11 мы определили преобразования Лоренца пространственных и временных координат, которые являются линейными преобразованиями. Линейные преобразования, конечно, могут быть представлены матрицами, и для наших четырехвекторов мы можем записать соответствующую матрицу преобразования Лоренца, переписав уравнение (11. {\prime}=L \overline{\boldsymbol{x}}\label{13.2.1}\]

Здесь \(L\) — матрица \(4 \times 4\):

\[L=\left( \begin{array}{cccc}{\gamma(u)} & {-\gamma(u) \frac{u}{c}} & {0} & {0} \\ {-\gamma(u) \frac{u}{c}} & {\gamma(u)} & {0} & {0} \\ {0} & {0} & {1} & {0} \ \ {0} & {0} & {0} & {1}\end{массив}\right)\label{13.2.2}\]

Как и в случае четырехвекторов, мы начинаем маркировать строки и столбцы \(L\) с индекса 0. Чтобы указать разницу с матрицами в регулярном пространстве, принято обозначать индексы векторов регулярного пространства и матриц латинскими буквами. (например, \(\boldsymbol{v}_{i}\) для \(i\)-й компоненты вектора \(v\) и \(A_{i j}\) для \(i\)-й строки , \(j\)-й столбец матрицы \(A\)), а также векторов пространства Минковского и матриц с греческими буквами, поэтому мы пишем \(x_{\mu}\) для \(\mu\) й компонент четырехмерного вектора \(\overline{\boldsymbol{x}}\), где \(\mu\) может принимать значения 0, 1, 2 или 3,

Мы также можем записать уравнение \ref{13. 1} в индексной форме:

---

Эта страница под названием 13.2: Матрица преобразования Лоренца и метрический тензор распространяется в соответствии с лицензией CC BY-NC-SA 4.0 и была создана, изменена и/или курирована Тимоном Идема (TU Delft Open) через исходный контент, который был отредактирован для стиль и стандарты платформы LibreTexts; подробная история редактирования доступна по запросу.

1. Наверх

• Была ли эта статья полезной?

1. Тип изделия

   Раздел или Страница

   Автор

   Тимон Идема

   Лицензия

   CC BY-NC-SA

   Версия лицензии

   4,0

   Показать оглавление

   нет

2. Теги

   1. Матрица преобразования Лоренца
   2. источник@https://textbooks. open.tudelft.nl/textbooks/catalog/book/14

специальная теория относительности — Преобразование общей матрицы Лоренца

Из рисунка 01:

Преобразование Лоренца из $\:\mathrm{S}\equiv \{xy\eta, \eta=ct\}\:$ в $\ :\mathrm{S_{1}}\equiv \{x_{1}y_{1}\eta_{1}, \eta_{1}=ct_{1}\}\:$ \begin{уравнение} \begin{bmatrix} х_{1}\\ у_{1}\\ \эта_{1} \end{bmatrix} знак равно \begin{bmatrix} \hphantom{-}\cosh\zeta & 0 & -\sinh\zeta \\ 0 и 1 и 0 \\ -\sinh\zeta & 0 & \hphantom{-}\cosh\zeta \\ \end{bmatrix} \begin{bmatrix} Икс\\ у\\ \эта \end{bmatrix} \, \quad \tanh\zeta=\dfrac{u}{c} \тег{01} \end{уравнение} или же \begin{уравнение} \mathbf{X_{1}}=\mathrm{L_{1}}\mathbf{X}\, \qquad \mathrm{L_{1}}= \begin{bматрица} \hphantom{-}\cosh\zeta & 0 & -\sinh\zeta \\ 0 и 1 и 0 \\ -\sinh\zeta & 0 & \hphantom{-}\cosh\zeta \\ \end{bmatrix} \тег{01″} \end{уравнение}

Из рисунка 02:

Преобразование Лоренца из $\:\mathrm{S_{1}}\equiv \{x_{1}y_{1}\eta_{1}, \eta_{1}=ct_{ 1}\}\:$ в $\:\mathrm{S_{2}}\equiv \{x_{2}y_{2}\eta_{2}, \eta_{2}=ct_{2}\}\ :$ \begin{уравнение} \begin{bматрица} х_{2}\\ у_{2}\\ \эта_{2} \end{bmatrix} знак равно \begin{bматрица} 1 и 0 и 0 \\ 0 &\hphantom{-}\cosh\xi & -\sinh\xi \\ 0 & -\sinh\xi & \hphantom{-}\cosh\xi \\ \end{bmatrix} \begin{bматрица} х_{1}\\ у_{1}\\ \эта_{1} \end{bmatrix} \, \quad \tanh\xi=\dfrac{w}{c} \тег{02} \end{уравнение} или же \begin{уравнение} \mathbf{X_{2}}=\mathrm{L_{2}}\mathbf{X_{1}}\, \qquad \mathrm{L_{2}}= \begin{bматрица} 1 и 0 и 0 \\ 0 &\hphantom{-}\cosh\xi & -\sinh\xi \\ 0 & -\sinh\xi & \hphantom{-}\cosh\xi \\ \end{bmatrix} \тег{02″} \end{уравнение} Обратите внимание, что из-за стандартных конфигураций матрицы $\:\mathrm{L_{1}}, \mathrm{L_{2}}\:$ являются вещественно-симметричными.

Из уравнений (01) и (02) имеем \begin{уравнение} \mathbf{X_{2}}=\mathrm{L_{2}}\mathbf{X_{1}}=\mathrm{L_{2}}\mathrm{L_{1}}\mathbf{ X}\Longrightarrow\mathbf{X_{2}}=\Lambda\mathbf{X} \тег{03} \end{уравнение} где $\:\Lambda\:$ композиция двух преобразований Лоренца $\:\mathrm{L_{1}}, \mathrm{L_{2}}\:$ \begin{уравнение} \Lambda=\mathrm{L_{2}}\mathrm{L_{1}}= \begin{bматрица} 1 и 0 и 0 \\ 0 &\hphantom{-}\cosh\xi & -\sinh\xi \\ 0 & -\sinh\xi & \hphantom{-}\cosh\xi \\ \end{bmatrix} \begin{bматрица} \hphantom{-}\cosh\zeta & 0 & -\sinh\zeta \\ 0 и 1 и 0 \\ -\sinh\zeta & 0 & \hphantom{-}\cosh\zeta \\ \end{bmatrix} \тег{04} \end{уравнение} то есть \begin{уравнение} \лямбда= \begin{bматрица} \hphantom{-}\cosh\zeta & 0 & -\sinh\zeta \\ \hphantom{-}\sinh\zeta\sinh\xi &\hphantom{-}\cosh\xi & -\cosh\zeta\sinh\xi \\ -\sinh\zeta\cosh\xi & -\sinh\xi & \hphantom{-}\cosh\zeta\cosh\xi \\ \end{bmatrix} \тег{04″} \end{уравнение}

Матрица преобразования Лоренца $\:\Lambda\:$ несимметрична, поэтому системы $\:\mathrm{S},\mathrm{S_{2}}\:$ не входят в стандартную конфигурацию. Но можно было бы написать так \begin{уравнение} \Lambda=\mathrm{R}\cdot\mathrm{L} \тег{05} \end{уравнение} где $\:\mathrm{L}\:$ — симметричная матрица преобразования Лоренца от $\:\mathrm{S}\:$ до промежуточной системы $\:\mathrm{S’_{2}}\:$ в стандартной конфигурации к нему и перемещается вместе с $\:\mathrm{S_{2}}\:$, а $\:\mathrm{R}\:$ является чисто пространственным преобразованием из $\:\mathrm{S ‘_{2}}\:$ в $\:\mathrm{S_{2}}$.

Теперь вам нужно сначала найти матрицу преобразования Лоренца $\:\mathrm{L}\:$, а затем доказать, что $\:\mathrm{R}\:$ \begin{уравнение} \ в коробке {\ цвет {синий} {\: \: \ mathrm {R} = \begin{bматрица} \cos\phi & -\sin\phi & 0 \\ \sin\phi &\hphantom{-}\cos\phi & 0 \\ 0 и 0 и 1 \\ \end{bmatrix} \, \:\text{где}\: \tan\phi =\dfrac{\sin\zeta\sinh\xi} {\cosh\zeta+\cosh\xi}\, \: \phi\in\left (-\dfrac{\pi}{2},+\dfrac{\pi}{2}\right)}\:\:\vphantom{\begin{matrix}1\\1\\1\\1\\ 1\конец{матрица}}} \тег{06} \end{уравнение} представляющий поворот плоскости от $\:\mathrm{S’_{2}}\:$ до $\:\mathrm{S_{2}}\:$, см. {2} \! \ xi} {1 \! + \! \ cosh \! \ zeta \ cosh \! \ xi} & \ sinh \! \ xi \ vphantom {\ dfrac {\ dfrac {} {}}{\tfrac{}{}}}\\ \sin\!\zeta \cosh\!\xi & \sinh\!\xi & \cosh\!\zeta\cosh\!\xi \vphantom{\dfrac{\dfrac{}{}}{\tfrac{} {}}} \end{bmatrix} \тег{17} \end{уравнение} Вышеупомянутое матричное умножение заканчивается следующим выражением \begin{уравнение} \mathrm{R}= \begin{bматрица} \dfrac{\cosh\!\zeta\!+\!\cosh\!\xi}{1\!+\!\cosh\!\zeta\cosh\!\xi} &\!- \dfrac{\sinh \!\zeta\sinh\!\xi}{1\!+\!\cosh\!\zeta\cosh\!\xi} & \hphantom{-} 0 \vphantom{\dfrac{\dfrac{}{} }{\tfrac{}{}}}\\ \dfrac{\sin\!\zeta\sinh\!\xi}{1\!+\!\cosh\!\zeta\cosh\!\xi} & \hphantom{\!-} \dfrac{\cosh\ !\zeta\!+\!\cosh\!\xi}{1\!+\!\cosh\!\zeta\cosh\!\xi} & \hphantom{-} 0 \vphantom{\dfrac{\dfrac {}{}}{\tfrac{}{}}}\\ 0 & 0 & \hphantom{-} 1 \vphantom{\dfrac{\dfrac{}{}}{\tfrac{}{}}} \end{bmatrix} \тег{18} \end{уравнение} Но \begin{уравнение} \left(\dfrac{\cosh\!\zeta\!+\!\cosh\!\xi}{1\!+\!\cosh\!\zeta\cosh\!\xi}\right)^{2 }+\left(\dfrac{\sin\!\zeta\sinh\!\xi}{1\!+\!\cosh\!\zeta\cosh\!\xi}\right)^{2}=1 \тег{19} \end{уравнение} поэтому мы можем определить \begin{уравнение} \cos\phi\stackrel{def}{\equiv}\dfrac{\cosh\!\zeta\!+\!\cosh\!\xi}{1\!+\!\cosh\!\zeta\cosh\ !\xi}\, \qquad \sin\phi =\dfrac{\sin\!\zeta\sinh\!\xi}{1\!+\!\cosh\!\zeta\cosh\!\xi} \, \qquad \phi \in \left(-\tfrac{\pi}{2},+\tfrac{\pi}{2}\right) \тег{20} \end{уравнение} и наконец \begin{уравнение} \mathrm{R}= \begin{bматрица} \cos\phi & -\sin\phi & 0 \\ \sin\phi &\hphantom{-}\cos\phi & 0 \\ 0 и 0 и 1 \\ \end{bmatrix} \тег{21} \end{уравнение} доказательство того, что $\:\mathrm{R}\:$ является вращением, см.