Векторная масса или масса двумерна?

У нас масса двумерна??? Я вам предлогаю самим задуматься. Масса Планка (максима, планковская масса) — единица массы в планковской системе единиц. Частица с такой массой имеет гравитационный радиус в разы меньше комптоновской длины волны ≈ 1,2209·1019 ГэВ/c² = 2,176·10−8 кг.

Мне кажется, что тут что-то не так. Как деформировать планковскую величину? В трехмерном мире? Остается главным вопросом …. Если всё же из трехмерного мира можно создать двумерный, то каким образом его увидят в трехмерном??? Одна из пространственных координат 0, существование плоскости равно 0. Духмерный мир 0. Если одно из измерений стремиться к 0. Побудим в этот момент наблюдающими и от третьего лица, мысленно остановим время, все процессы, чтоб разобрать все по полочкам. А время имеет планковскую величину, так как существуют путешественники во времени, не так ли? Значит можно зафиксироваться на планковской величине времени, то есть остановить его. Остановили??? Мы пришли к первому. Одно из измерений 0 и существование плоскости 0.

Ни капли рождения вселенной из логики, а логический вывод с собственной точки зрения, глядя на происходящее. Между тем я лишь брал все из интернета и вставил свои ”умозаключения”, кто из вас умнее и поможет объяснить мою неправоту??? Взаимодействие = взаимоотношение, у кого голова есть, поймет. У меня есть гипотеза… Но, возможно там будет не совсем понятно почему именно в форме шара получаются звезды. Я её после подправлю…

Почему в невесомости капли воды принимают шарообразную форму? Если взять давление элементарных частиц, то сил движений окажется меньше между молекулами, чем вне них. А первое, что получается в космосе после волчка, это плазменный шар с магнитным полем. А по моей гипотезе это частицы темной материи, которые при столкновении получают вращательное движение, а значит волновое колебание квинтэссенции, то есть их объём для взаимодействий увеличился, а значит для них темная материя становится потоком более мелких частиц.

Кому интересно есть еще на стене в вк…. Ссылка на контакт: https://m.vk.com/ogarkov86

Submitted by Сережа ОСА

Два вида физических величин: скалярные величины и векторные величины | LAMPA

«Что-то я не помню такой темы в физике» — первое, что, наверное, пришло вам в голову. Да, вы правы — тема незаметная, но в некоторых учебниках она присутствует. «А нужна она мне для ЕГЭ?» Нужна. Точно нужна. Очень нужна. Постоянно нужна.

Давайте приступим. Надо запомнить, что в физике (школьной) есть два типа физических величин:

• скалярная величина;
• векторная величина.

Скалярная величина — это просто число. Ну, например, масса тела MMM — это скалярная величина. Пусть, например, M=3M = 3M=3 кг. Время ttt — скалярная величина. Например, время может быть такое: t=7t = 7t=7 сек. 

Векторная величина. Что это такое? Давайте вспомним (а для тех, кто не знал — узнаем), что

вектор — это направленный отрезок.

Стрелка — по-простому. У стрелки (вектора) есть длина (длина стрелки) и направление. Вектор — это нечто, что обладает длиной и направлением.

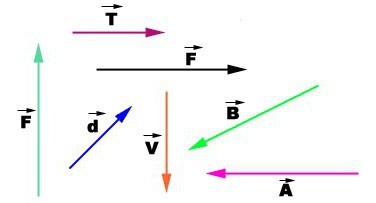
Примеры векторных величин: сила F⃗\vec {F}F⃗, скорость V⃗\vec{V}V⃗.

Длина вектора обозначается специальным символом — символом модуля | | — это две параллельные палочки. Например, ∣F⃗∣|\vec{F}|∣F⃗∣ — модуль силы;  ∣V⃗∣|\vec{V}|∣V⃗∣ — модуль скорости. Модуль вектора — это уже число. Например, может быть так, что модуль силы ∣F⃗∣=8|\vec{F}|=8∣F⃗∣=8 H, модуль скорости ∣V⃗∣=8|\vec{V}|=8∣V⃗∣=8 м/с.

Направление вектора изображается на картинке. Куда показывает вектор — туда он и направлен. Например, бывает так, что вектор направлен вверх, вниз и т.д. Вектор может быть направлен вдоль какой-то плоскости. Примеры можете видеть на картинках.

Может возникнуть вопрос: а как отличить векторную величину от скалярной? Или так: как я узнаю, что передо мной вектор, а не скаляр?

Ну, самое простое — это опыт. Решая задачи, читая теоретический материал, вы со временем запомните, какие величины векторные, а какие скалярные. Физических величин не так много, как может показаться.

А способ чуть посложнее — это представить эти величины и решить для себя: могут они иметь направление? Если да — то это вектор, если нет — скаляр.

Например: заряд конденсатора. Если заряд имеет направление, то куда он направлен? Непонятно — поэтому, скорее всего, заряд — это скалярная величина.

Другой пример: длина отрезка. Если эта физическая величина имеет направление, то откуда куда она направлена: от точки 1 до точки 2? Или от точки 2 до точки 1? Трудно выбрать — поэтому, скорее всего, длина отрезка — это скаляр.

Вес — Википедия

Вес — сила, с которой тело действует на опору (или подвес, или другой вид крепления), препятствующую падению, возникающая в поле сил тяжести

[1]^[2]. Единица измерения веса в Международной системе единиц (СИ) — ньютон, иногда используется единица СГС — дина.

Вес P{\displaystyle \mathbf {P} } тела, покоящегося в инерциальной системе отсчёта, равен силе тяжести, действующей на тело, и пропорционален массе m{\displaystyle m} и ускорению свободного падения g{\displaystyle \mathbf {g} } в данной точке:

P=mg.{\displaystyle \mathbf {P} =m\mathbf {g} .}

Широтное уменьшение силы тяжести mg

Ускорение свободного падения зависит от высоты над земной поверхностью и — ввиду несферичности Земли, а также ввиду её вращения — от географических координат точки измерения. В результате суточного вращения Земли существует широтное уменьшение веса: на экваторе вес примерно на 0,3 % меньше, чем на полюсах. Другим фактором, влияющим на значение g{\displaystyle \mathbf {g} } и, соответственно, вес тела, являются гравитационные аномалии, обусловленные особенностями строения земной поверхности и недр в окрестностях точки измерения. Если тело находится вблизи другой планеты, а не Земли, то ускорение свободного падения будет определяться массой и размерами этой планеты, наряду с расстоянием между её поверхностью и телом.

При движении системы «тело» — «опора или подвес» относительно инерциальной системы отсчёта с ускорением w{\displaystyle \mathbf {w} } вес перестаёт совпадать с силой тяжести:

P=m(g−w).{\displaystyle \mathbf {P} =m(\mathbf {g} -\mathbf {w} ).}

Например, если ускорение (независимо от скорости) лифта направлено вверх, то вес находящегося в нём груза увеличивается, а если вниз, то уменьшается. Ускорение за счёт вращения Земли не входит в w{\displaystyle \mathbf {w} }, оно уже учтено в g{\displaystyle \mathbf {g} }. Состояние отсутствия веса (невесомость) наступает вдали от притягивающего объекта, либо когда тело находится в свободном падении, то есть при g−w=0{\displaystyle \mathbf {g} -\mathbf {w} =0}.

Тело массой m{\displaystyle m}, вес которого анализируется, может стать субъектом приложения дополнительных сил, косвенно обусловленных присутствием гравитационного поля, в том числе силы Архимеда и трения. При этом воздействие изучаемого тела на опоры и подвесы будет опосредовано наличием указанных привходящих факторов.^{[прояснить]}

В официальном определении, приведённом в преамбуле, отсутствует конкретизация, должны ли учитываться подобные факторы. Не оговорено также, обязательно ли роль опоры-подвеса должно играть упругое твёрдое тело и что если опор несколько. Кроме того, в публикациях встречаются и неэквивалентные дефиниции веса^[3][4]

[5]. Отсюда, несмотря на ясность природы фигурирующих сил, возникают терминологические неопределённости.^{[источник не указан 670 дней]}

Так, при учёте только вклада силы тяжести покоящемуся на наклонной поверхности телу приписывается направленный по нормали к опоре вес mgcos⁡α{\displaystyle mg\cos \alpha }, где α{\displaystyle \alpha } — угол наклона^[4]. Но если учесть ещё и силу трения покоя (а она, по третьему закону Ньютона, приложена и к телу, и к опоре), то вектор веса станет равным mg{\displaystyle m\mathbf {g} }^[3]. Аналогично с силой Архимеда: в жидкости или газе с плотностью ρ{\displaystyle \rho } на тело действует подъёмная сила FA=−ρgV{\displaystyle \mathbf {F} _{A}=-\rho \mathbf {g} V} (где V{\displaystyle V} — объём тела), из-за которой, скажем, воздействие тела на неровное

[6] дно водоёма ослабляется. Трактуя эту ситуацию, можно либо заявить, что вес тела снижается на вес вытесненного объёма воды, либо считать, что вес по-прежнему составляет mg{\displaystyle m\mathbf {g} } и есть ещё подлежащая отдельному анализу архимедова сила.^{[источник не указан 670 дней]}В целом, в литературе доминирует подход^{[1][7][нет в источнике]}, при котором вес тела в покое вблизи Земли всегда приравнивается mg{\displaystyle m\mathbf {g} }. Этот подход означает, что вес тела с точностью до знака равен векторной сумме всех сил (кроме силы тяжести), действующих на тело, включая силы Архимеда («жидкая опора» ^[3]) и трения, при учёте всех имеющихся опор-подвесов совместно.

Для многих задач описанные неопределённости несущественны, так как чаще всего рассматривается неподвижное тело на сухой горизонтальной поверхности.^{[источник не указан 670 дней]}

Понятие «вес» в физике не является необходимым^[8]. В принципе, можно вообще отменить этот термин и говорить либо о «массе», либо о «силе»^[9] такой-то природы. Использование понятия «вес» во многом связано просто с привычкой^[8] и языковыми традициями.

Очевидно более содержательной величиной является

суммарная сила воздействия на опору, в нерусскоязычных изданиях иногда именуемая «кажущимся весом» (англ. apparent weight, фр. poids apparent). Знание этой величины, например, может помочь оценить способность конструкции удержать изучаемое тело в данных условиях. В ряде случаев — скажем, в ситуации привязанного на улице шарика, наполненного гелием, — кажущийся вес может оказаться направленным против вектора g{\displaystyle \mathbf {g} } ввиду влияния FA{\displaystyle \mathbf {F} _{A}}.

Вес можно измерять с помощью пружинных весов, которые могут служить и для косвенного измерения массы, если их соответствующим образом проградуировать; рычажные весы в такой градуировке не нуждаются, так как в этом случае сравниваются массы, на которые действует одинаковое ускорение свободного падения или сумма ускорений в неинерциальных системах отсчёта. При взвешивании с помощью технических пружинных весов вариациями ускорения свободного падения обычно пренебрегают, так как влияние этих вариаций обычно меньше практически необходимой точности взвешивания.

На результате измерений может в некоторой степени сказаться сила Архимеда, если при взвешивании с помощью рычажных весов сравниваются тела с различной плотностью.

В физике вес и масса — разные понятия. Вес — векторная величина, сила, с которой тело действует на горизонтальную опору или вертикальный подвес. Масса — скалярная величина, мера инертности тела (инертная масса) либо заряд гравитационного поля (гравитационная масса). У этих величин отличаются и единицы измерения (в системе СИ масса измеряется в килограммах, а вес — в ньютонах). Возможны ситуации с нулевым весом и ненулевой массой одного и того же тела, например, в условиях невесомости у всех тел вес равен нулю, а масса у каждого тела своя. И если в состоянии покоя тела показания весов будут нулевыми, то при ударе по весам тел с одинаковыми скоростями воздействие будет разным (см. закон сохранения импульса, закон сохранения энергии).

Вместе с тем строгое различение понятий веса и массы принято в основном в науке и технике, а во многих повседневных ситуациях слово «вес» продолжает использоваться, когда фактически речь идёт о «массе». Например, мы говорим, что какой-то объект «весит один килограмм», несмотря на то, что килограмм представляет собой единицу массы

[10]. Кроме того, термин «вес» в значении «масса» традиционно использовался в цикле наук о человеке — в словосочетании «вес тела человека», вместо современного «масса тела человека»^[11]. В связи с этим метрологические организации отмечают, что неправильное использование термина «вес» вместо термина «масса» должно прекращаться и во всех тех случаях, когда имеется в виду масса, должен использоваться термин «масса»^[12][13].

III Генеральная конференция по мерам и весам, проведённая в 1901 году, подчеркнула, что термин «вес» обозначает величину той же природы, что термин «сила». Конференция определила вес тела как произведение массы тела на ускорение, обусловленное гравитационным притяжением. Стандартный вес тела конференцией был определён как произведение массы тела на стандартное ускорение, обусловленное гравитационным притяжением. В свою очередь для стандартного ускорения было принято значение 980,665 см/с^2[14].

1. ↑ ^{1 2} Рудой Ю. Г. Вес // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1988. — Т. 1: Ааронова — Бома эффект — Длинные линии. — С. 262. — 707 с. — 100 000 экз.
2. ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2005. — Т. I. Механика. — С. 373. — 560 с. — ISBN 5-9221-0225-7.
3. ↑ ^{1 2 3} И. Е. Каган «Вес тела» (IX класс) // Фізiка: праблемы выкладання. – 2001. – № 3. – С. 58-74.
4. ↑ ^{1 2} С. В. Задорожная «Вес тела» // Сайт педаг. сообщ. «Урок.рф» (2016).
5. ↑ Во многих иноязычных публикациях вес (см., например, начало немецкой версии статьи) синонимизируется с силой тяжести, что в российской педагогике считается ошибкой.
6. ↑ Неровность нужна для подтекания воды под опору, см. Л. Г. Асламазов: Гидростатика // Квант. – 1972. – № 12. (с. 57, рис. 9ав).
7. ↑ Allen L. King. Weight and weightlessness (англ.) // American Journal of Physics (англ.)русск. : journal. — 1963. — Vol. 30. — P. 387. — DOI:10.1119/1.1942032. — Bibcode: 1962AmJPh..30..387K.
8. ↑ ^{1 2} В. Г. Зубов. Механика. М.: Наука, 1978. — 352 с. // см. § 71, с. 176: «В механике понятие веса является совершенно лишним. Но так как это слово простое, привычное, то им часто пользуются».
9. ↑ The National Standard of Canada, CAN/CSA-Z234.1-89 Canadian Metric Practice Guide, January 1989: 5.7.3. Considerable confusion exists in the use of the term «weight». <…> In scientific and technical work, the term «weight» should be replaced by the term «mass» or «force», depending on the application.
10. ↑ Ранее в технике широко использовалась единица силы килограмм-сила — одна из основных единиц системы МКГСС.
11. ↑ Медицинская энциклопедия на Академике.
12. ↑ ISO 80000-4:2006, Quantities and units — Part 4: Mechanics.
13. ↑ SI Units: Mass (англ.). Weights and Measures. NIST. Дата обращения 7 декабря 2016.
14. ↑ Declaration on the unit of mass and on the definition of weight; conventional value of g (англ.). Resolution of the 3rd CGPM (1901). BIPM. Дата обращения 1 ноября 2015.

Видеоурок: вес тела

Масса векторная величина. Векторная величина

Все величины, с которыми нам приходится встречаться в физике и, в частности, в одном из ее разделов механики, можно разделить на два типа:

а) скалярные, которые определяются одним действительным положительным или отрицательным числом. Примером таких величин могут служить время, температура;

б) векторные, которые определяются направленным пространственным отрезком прямой (или тремя скалярными величинами) и обладают свойствами, приведенными ниже.

Примером векторных величин служат сила, скорость, ускорение.

Декартова система координат

Когда речь идет о направленных отрезках, то следует указать объект, по отношению к которому это направление определяется. В качестве такого объекта принимается декартова система координат, составляющими которой являются оси.

Осью называется прямая, на которой указано направление. Три взаимно перпендикулярные оси, пересекающиеся в точке О, названные соответственно образуют прямоугольную декартову систему координат. Декартова система координат может быть правой (рис. 1) или левой (рис. 2). Эти системы являются зеркальным изображением друг друга и не могут быть совмещены каким-либо перемещением.

Во всем дальнейшем изложении всюду принимается правая система координат. В правой системе координат положительное направление отсчета всех углов принимается против часовой стрелки.

Это соответствует направлению совмещения осей х с у, если глядеть с положительного направления оси

Свободные векторы

Вектор, характеризуемый только длиной и направлением в заданной системе координат, носит название свободного. Свободный вектор изображается отрезком заданной длины и направления, начало которого расположено в любой точке пространства. На чертеже вектор изображается стрелкой (рис. 3).

Векторы обозначаются одной жирной буквой или двумя буквами, соответствующими началу и концу стрелки с черточкой над ними или

Величину вектора называют его модулем и обозначают одним из указанных способов

Равенство векторов

Так как основными характеристиками вектора считаются его длина и направление, то векторы называются равными, если их направления и величины совпадают. В частном случае равные векторы могут быть направлены вдоль одной прямой. Равенство векторов, например а и b (рис. 4), записывается в виде:

Если векторы (а и b) равны по модулю, но диаметрально противо положны по направлению (рис. 5), то это записывается в виде:

Векторы, имеющие одинаковое или диаметрально противоположное направление, называются коллинеарными.

Умножение вектора на скаляр

Произведение вектора а на скаляр К называется вектор по модулю, равный совпадающий по направлению с вектором а, если К положительно, и диаметрально ему противоположный, если К отрицательно.

Единичный вектор

Вектор, у которого модуль равен единице и направление совпадает с заданным вектором а, называется единичным вектором данного вектора или его ортом. Орт обозначается . Всякий вектор через его орт можно представить в виде

Единичные векторы, расположенные вдоль положительных направлений координатных осей, обозначаются соответственно (рис. 6).

Сложение векторов

Правило сложения векторов постулируется (оправданием для этого постулата служат наблюдения над реальными объектами векторной природы). Этот постулат заключается в том, что два вектора

Переносят в какую-либо точку пространства так, чтобы начала их совпадали (рис. 7). Направленная диагональ параллелограмма, построенного на этих векторах (рис. 7), называется суммой векторов сложение векторов записывается в виде

и носит название сложения по правилу параллелограмма.

Указанное правило сложения векторов можно осуществить еще и следующим образом: в любой точке пространства откладывается вектор далее, от конца вектора откладывается вектор (рис. 8). Вектор а, начало которого совпадает с началом вектора а конец — с концом вектора будет суммой векторов

Последнее правило сложения векторов удобно, если нужно сложить более чем два вектора. Действительно, если нужно сложить несколько векторов, то, используя указанное правило, следует построить ломаную, сторонами которой являются заданные векторы, причем начало какого-либо вектора совпадает с концом предыдущего вектора. Суммой этих векторов будет вектор, начало которого совпадает с началом первого вектора, а конец совпадает с концом последнего вектора (рис. 9). Если заданные векторы образуют замкнутый многоугольник, то говорят, что сумма векторов равна нулю.

Из правила построения суммы векторов следует, что сумма их не зависит от порядка, в котор

Векторная величина в физике. Примеры векторных величин

Физика и математика не обходятся без понятия «векторная величина». Ее необходимо знать и узнавать, а также уметь с нею оперировать. Этому обязательно стоит научиться, чтобы не путаться и не допускать глупых ошибок.

Как отличить скалярную величину от векторной?

Первая всегда имеет только одну характеристику. Это ее числовое значение. Большинство скалярных величин могут принимать как положительные, так и отрицательные значения. Их примерами может служить электрический заряд, работа или температура. Но есть такие скаляры, которые не могут быть отрицательными, например, длина и масса.

Векторная величина, кроме числовой величины, которая всегда берется по модулю, характеризуется еще и направлением. Поэтому она может быть изображена графически, то есть в виде стрелки, длина которой равна модулю величины, направленной в определенную сторону.

При письме каждая векторная величина обозначается знаком стрелки на буквой. Если идет речь о числовом значении, то стрелка не пишется или ее берут по модулю.

Какие действия чаще всего выполняются с векторами?

Сначала — сравнение. Они могут быть равными или нет. В первом случае их модули одинаковые. Но это не единственное условие. У них должны быть еще одинаковые или противоположные направления. В первом случае их следует называть равными векторами. Во втором они оказываются противоположными. Если не выполняется хотя бы одно из указанных условий, то векторы не равны.

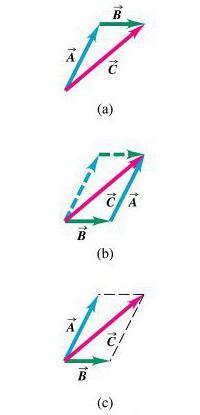
Потом идет сложение. Его можно сделать по двум правилам: треугольника или параллелограмма. Первое предписывает откладывать сначала один вектор, потом от его конца второй. Результатом сложения будет тот, который нужно провести от начала первого к концу второго.

Правило параллелограмма можно использовать, когда нужно сложить векторные величины в физике. В отличие от первого правила, здесь их следует откладывать от одной точки. Потом достроить их до параллелограмма. Результатом действия следует считать диагональ параллелограмма, проведенную из той же точки.

Если векторная величина вычитается из другой, то они снова откладываются из одной точки. Только результатом будет вектор, который совпадает с тем, что отложен от конца второго к концу первого.

Какие векторы изучают в физике?

Их так же много, как скаляров. Можно просто запомнить то, какие векторные величины в физике существуют. Или знать признаки, по которым их можно вычислить. Тем, кто предпочитает первый вариант, пригодится такая таблица. В ней приведены основные векторные физические величины.

Обозначение в формуле	Наименование
v	скорость
r	перемещение
а	ускорение
F	сила
р	импульс
Е	напряженность электрического поля
В	магнитная индукция
М	момент силы

Теперь немного подробнее о некоторых из этих величин.

Первая величина — скорость

С нее стоит начать приводить примеры векторных величин. Это обусловлено тем, что ее изучают в числе первых.

Скорость определяется как характеристика движения тела в пространстве. Ею задается числовое значение и направление. Поэтому скорость является векторной величиной. К тому же ее принято разделять на виды. Первый является линейной скоростью. Ее вводят при рассмотрении прямолинейного равномерного движения. При этом она оказывается равной отношению пути, пройденного телом, ко времени движения.

Эту же формулу допустимо использовать при неравномерном движении. Только тогда она будет являться средней. Причем интервал времени, который необходимо выбирать, обязательно должен быть как можно меньше. При стремлении промежутка времени к нулю значение скорости уже является мгновенным.

Если рассматривается произвольное движение, то здесь всегда скорость — векторная величина. Ведь ее приходится раскладывать на составляющие, направленные вдоль каждого вектора, направляющего координатные прямые. К тому же определяется он как производная радиус-вектора, взятая по времени.

Вторая величина — сила

Она определяет меру интенсивности воздействия, которое оказывается на тело со стороны других тел или полей. Поскольку сила — векторная величина, то она обязательно имеет свое значение по модулю и направление. Так как она действует на тело, то важным является еще и точка, к которой приложена сила. Чтобы получить наглядное представление о векторах сил, можно обратиться к следующей таблице.

Сила	Точка приложения	Направление
тяжести	центр тела	к центру Земли
всемирного тяготения	центр тела	к центру другого тела
упругости	место соприкосновения взаимодействующих тел	против внешнего воздействия
трения	между соприкасающимися поверхностями	в сторону, противоположную движению

Также еще векторной величиной является равнодействующая сила. Она определяется как сумма всех действующих на тело механических сил. Для ее определения необходимо выполнить сложение по принципу правила треугольника. Только откладывать векторы нужно по очереди от конца предыдущего. Результатом окажется тот, который соединяет начало первого с концом последнего.

Третья величина — перемещение

Во время движения тело описывает некоторую линию. Она называется траекторией. Эта линия может быть совершенно разной. Важнее оказывается не ее внешний вид, а точки начала и конца движения. Они соединяются отрезком, который называется перемещением. Это тоже векторная величина. Причем оно всегда направлено от начала перемещения к точке, где движение было прекращено. Обозначать его принято латинской буквой r.

Здесь может появиться такой вопрос: «Путь — векторная величина?». В общем случае это утверждение не является верным. Путь равен длине траектории и не имеет определенного направления. Исключением считается ситуация, когда рассматривается прямолинейное движение в одном направлении. Тогда модуль вектора перемещения совпадает по значению с путем, и направление у них оказывается одинаковым. Поэтому при рассмотрении движения вдоль прямой без изменения направления перемещения путь можно включить в примеры векторных величин.

Четвертая величина — ускорение

Оно является характеристикой быстроты изменения скорости. Причем ускорение может иметь как положительное, так и отрицательное значение. При прямолинейном движении оно направлено в сторону большей скорости. Если перемещение происходит по криволинейной траектории, то вектор его ускорения раскладывается на две составляющие, одна из которых направлена к центру кривизны по радиусу.

Выделяют среднее и мгновенное значение ускорения. Первое следует рассчитывать как отношение изменения скорости за некоторый промежуток времени к этому времени. При стремлении рассматриваемого интервала времени к нулю говорят о мгновенном ускорении.

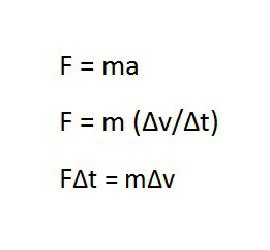
Пятая величина — импульс

По-другому его еще называют количеством движения. Импульс векторной величиной является из-за того, что напрямую связан со скоростью и силой, приложенной к телу. Обе они имеют направление и задают его импульсу.

По определению последний равен произведению массы тела на скорость. Используя понятие импульса тела, можно по-другому записать известный закон Ньютона. Получается, что изменение импульса равно произведению силы на промежуток времени.

В физике важную роль имеет закон сохранения импульса, который утверждает, что в замкнутой системе тел ее суммарный импульс является постоянным.

Мы очень кратко перечислили, какие величины (векторные) изучаются в курсе физики.

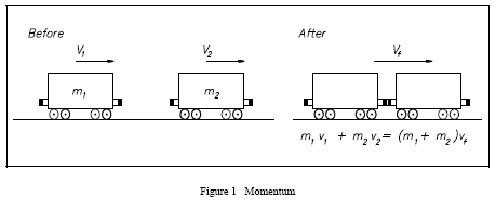
Задача о неупругом ударе

Условие. На рельсах стоит неподвижная платформа. К ней приближается вагон со скоростью 4 м/с. Массы платформы и вагона — 10 и 40 тонн соответственно. Вагон ударяется о платформу, происходит автосцеп. Необходимо вычислить скорость системы «вагон-платформа» после удара.

Решение. Сначала требуется ввести обозначения: скорость вагона до удара — v₁, вагона с платформой после сцепки — v, масса вагона m₁, платформы — m₂. По условию задачи необходимо узнать значение скорости v.

Правила решения подобных заданий требуют схематичного изображения системы до и после взаимодействия. Ось OX разумно направить вдоль рельсов в ту сторону, куда движется вагон.

В данных условиях систему вагонов можно считать замкнутой. Это определяется тем, что внешними силами можно пренебречь. Сила тяжести и реакция опоры уравновешены, а трение о рельсы не учитывается.

Согласно закону сохранения импульса, их векторная сумма до взаимодействия вагона и платформы равна общему для сцепки после удара. Сначала платформа не двигалась, поэтому ее импульс был равен нулю. Перемещался только вагон, его импульс — произведение m₁ и v₁.

Так как удар был неупругий, то есть вагон сцепился с платформой, и дальше он стали катиться вместе в ту же сторону, то импульс системы не изменил направления. Но его значение стало другим. А именно произведением суммы массы вагона с платформой и искомой скорости.

Можно записать такое равенство: m₁ * v₁ = (m₁ + m₂) * v. Оно будет верно для проекции векторов импульсов на выбранную ось. Из него легко вывести равенство, которое потребуется для вычисления искомой скорости: v = m₁ * v₁ / (m₁ + m₂).

По правилам следует перевести значения для массы из тонн в килограммы. Поэтому при подстановке их в формулу следует сначала умножить известные величины на тысячу. Простые расчеты дают число 0,75 м/с.

Ответ. Скорость вагона с платформой равна 0,75 м/с.

Задача с разделением тела на части

Условие. Скорость летящей гранаты 20 м/с. Она разрывается на два осколка. Масса первого 1,8 кг. Он продолжает двигаться в направлении, в котором летела граната, со скоростью 50 м/с. Второй осколок имеет массу 1,2 кг. Какова его скорость?

Решение. Пусть массы осколков обозначены буквами m₁ и m₂. Их скорости соответственно будут v₁ и v₂. Начальная скорость гранаты — v. В задаче нужно вычислить значение v₂.

Для того чтобы больший осколок продолжал двигаться в том же направлении, что и вся граната, второй должен полететь в обратную сторону. Если выбрать за направление оси то, которое было у начального импульса, то после разрыва большой осколок летит по оси, а маленький — против оси.

В этой задаче разрешено пользоваться законом сохранения импульса из-за того, что разрыв гранаты происходит мгновенно. Поэтому, несмотря на то что на гранату и ее части действует сила тяжести, она не успевает подействовать и изменить направление вектора импульса с его значением по модулю.

Сумма векторных величин импульса после разрыва гранаты равна тому, который был до него. Если записать закон сохранения импульса тела в проекции на ось OX, то он будет выглядеть так: (m₁ + m₂) * v = m₁ * v₁ — m₂ * v₂. Из него просто выразить искомую скорость. Она определится по формуле: v₂ = ((m₁ + m₂) * v — m₁ * v₁) / m₂. После подстановки числовых значений и расчетов получается 25 м/с.

Ответ. Скорость маленького осколка равна 25 м/с.

Задача про выстрел под углом

Условие. На платформе массой M установлено орудие. Из него производится выстрел снарядом массой m. Он вылетает под углом α к горизонту со скоростью v (данной относительно земли). Требуется узнать значение скорости платформы после выстрела.

Решение. В этой задаче можно использовать закон сохранения импульса в проекции на ось OX. Но только в том случае, когда проекции внешних равнодействующих сил равна нулю.

За направление оси OX нужно выбрать ту сторону, куда полетит снаряд, и параллельно горизонтальной линии. В этом случае проекции сил тяжести и реакции опоры на OX будут равны нулю.

Задача будет решена в общем виде, так как нет конкретных данных для известных величин. Ответом в ней является формула.

Импульс системы до выстрела был равен нулю, поскольку платформа и снаряд были неподвижны. Пусть искомая скорость платформы будет обозначена латинской буквой u. Тогда ее импульс после выстрела определится как произведение массы на проекцию скорости. Так как платформа откатится назад (против направления оси OX), то значение импульса будет со знаком минус.

Импульс снаряда — произведение его массы на проекцию скорости на ось OX. Из-за того, что скорость направлена под углом к горизонту, ее проекция равна скорости, умноженной на косинус угла. В буквенном равенстве это будет выглядеть так: 0 = — Mu + mv * cos α. Из нее путем несложных преобразований получается формула-ответ: u = (mv * cos α) / M.

Ответ. Скорость платформы определяется по формуле u = (mv * cos α) / M.

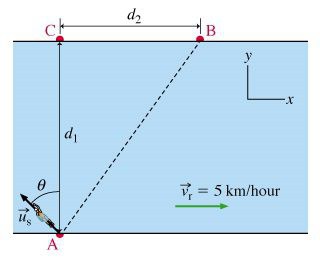
Задача о переправе через реку

Условие. Ширина реки по всей ее длине одинакова и равна l, ее берега параллельны. Известна скорость течения воды в реке v₁ и собственная скорость катера v₂. 1). При переправе нос катера направлен строго к противоположному берегу. На какое расстояние s его снесет вниз по течению? 2). Под каким углом α нужно направить нос катера, чтобы он достиг противоположного берега строго перпендикулярно к точке отправления? Сколько времени t потребуется на такую переправу?

Решение. 1). Полная скорость катера является векторной суммой двух величин. Первая из них течение реки, которое направлено вдоль берегов. Вторая — собственная скорость катера, перпендикулярная берегам. На чертеже получается два подобных треугольника. Первый образован шириной реки и расстоянием, на которое сносит катер. Второй — векторами скоростей.

Из них следует такая запись: s / l = v₁ / v₂. После преобразования получается формула для искомой величины: s = l * (v₁ / v₂).

2). В этом варианте задачи вектор полной скорости перпендикулярен берегам. Он равен векторной сумме v₁ и v₂. Синус угла, на который должен отклоняться вектор собственной скорости, равен отношению модулей v₁ и v₂. Для расчета времени движения потребуется разделить ширину реки на сосчитанную полную скорость. Значение последней вычисляется по теореме Пифагора.

v = √(v₂² – v₁²), тогда t = l / (√(v₂² – v₁²)).

Ответ. 1). s = l * (v₁ / v₂), 2). sin α = v₁ / v₂, t = l / (√(v₂² – v₁²)).

Вес — это скаляр или вектор?

Мы можем изменить определение вещей, когда это будет полезно. Определения служат нам. Если определение бесполезно, отдельные лица и сообщества изменяют его, иногда на лету, иногда в контексте, иногда явно, иногда неявно.

В повседневной жизни вес — это скаляр. Вы не записываете направление веса бананов, которые вы покупаете. Настаивать, что это вектор, бесполезно в этом контексте, и существуют определения, чтобы прояснить коммуникацию и решить проблемы.

Помогает ли добавление направления к весу банана решить какие-либо проблемы? Или это шум? Является ли скалярный вес банана проблемой коммуникации в этом случае?

Будут другие контексты, в которых вы хотите, чтобы вес был вектором; возможно при расчете орбитальной механики вашего банана. Даже там, вес не может быть полезной концепцией, потому что есть гораздо лучшие способы решить орбитальную механику, чем говорить о направленном весе вещей (скажем, потенциалы поля).

В формальной математике очень специфические и точные определения используются для того, чтобы абстракции, которые не соответствуют какой-либо физической ситуации, обсуждались и разбирались единообразно. Формальная математика часто грабится физикой, но физика не формальная математика.

Физики и инженеры уйдут и расскажут о дельта-функциях Дирака, значение которых равно 0 везде, кроме 0, и чей интеграл от любого отрицательного значения до положительного равен 1, а затем свернут его с другой функцией.

Теперь есть способы формализовать это, но по большей части физики и инженеры не беспокоятся . «Дельта Дирака не является функцией» полезна при ее формализации, но не так полезна при работе с ней . Знание формализации может быть полезно, чтобы избежать возможных ловушек, но обычно не полезно при попытке использовать его в качестве инструмента для прогнозирования поведения какой-либо системы.

Физика — это игра с использованием математики (или любого другого полезного инструмента) для предсказания (и иногда объяснения) поведения физических систем. Часто существует множество разных математических игр, и вы будете использовать разные для разных систем. Ньютоновская динамика — это игра, которая работает в своей области, и в ней скорость является аддитивной. Относительность — игра, которая слишком сложна для некоторых областей, но покрывает некоторую территорию, которую не охватывает динамика Ньютона; в относительности скорость не аддитивна. В ньютоновской динамике скорость представляет собой простой вектор в евклидовом пространстве. В рамках теории относительности это не простой вектор в евклидовом пространстве.

Вес — это скаляр в некоторых играх физики. В других это не может быть. Почти в любой разумной ситуации, которую вы столкнетесь, Weight будет скалярным, потому что почти в каждой игре по физике, где важно направление веса, использование веса на основе вектора не будет лучшим инструментом, который у вас есть.

axsvl77

Это лучший ответ. Физика предоставляет модели для понимания мира. Когда работает одна модель, хорошо. Когда это не так, используйте другой. Лучше не увязнуть в обозначениях.

---

Wtrmute

Обычно, когда вы имеете дело с наклонной плоскостью, ваш вес должен быть векторным. Если вы моделируете маятник, вы можете использовать лапласиан, но обычно проще использовать векторы. Я согласен, что, возможно, большую часть времени вы не будете иметь дело с весом как с силой (скорее, вы имеете дело со скалярной массой ), но мы не можем сказать, что «почти в каждой игре по физике, где важно направление веса, используя «Весовой вектор» не будет лучшим инструментом, который у вас есть ».

---

Джепп Стиг Нильсен

Вы: Существуют другие контексты, в которых вы хотите, чтобы вес был вектором; возможно при расчете орбитальной механики вашего банана. Теперь, когда бананы находятся на орбите, они явно невесомые , поэтому теперь мы подходим к другому философскому вопросу, а именно, равен ли нулевой вектор скалярному нулю (и имеет ли величина нулевого размера даже размерность (единицу), такую ​​как ньютонов)? (Я просто пытаюсь быть юмористическим).

---

Yakk

@jeppe они невесомы в некоторых системах отсчета. Решение орбитальной механики в системах отсчета, где они невесомы, кажется неоптимальным.

Векторные величины

 

Векторные величины и скаляры

 

В курсе физике часто встречаются такие величины, для описания которых достаточно знать только числовые значения. Например, масса, время, длина.

 

Величины, которые характеризуются только числовым значением, называются скалярными или скалярами.

Кроме скалярных величин, используются величины, которые имеют и числовое значение и направление. Например, скорость, ускорение, сила.

 

Величины, которые характеризуются числовым значением и направлением, называются векторными или векторами.

 

Обозначаются векторные величины соответствующими буквами со стрелкой наверху или выделяются жирным шрифтом. Например, вектор силы обозначается  или F. Числовое значение векторной величины называется модулем или длиной вектора. Значение вектора силы обозначают F или .

 

Изображение вектора

Векторы изображают направленными отрезками. Началом вектора называют ту точку, откуда начинается направленный отрезок (точка А на рис. 1), концом вектора – точку, в которой заканчивается стрелка (точка B на рис. 1).

рис. 1

 

Два вектора называются равными, если они имеют одинаковую длину и направлены в одну сторону. Такие вектора изображают направленными отрезками, имеющими одинаковые длины и направления. Например, на рис. 2 изображены векторы .

рис. 2

 

При изображении на одном рисунке двух и более векторов, отрезки строят в заранее выбранном масштабе. Например, на рис. 3 изображены вектора, длины которых υ1 = 2 м/c, υ2 = 3 м/c.

рис. 3

Способ задания вектора

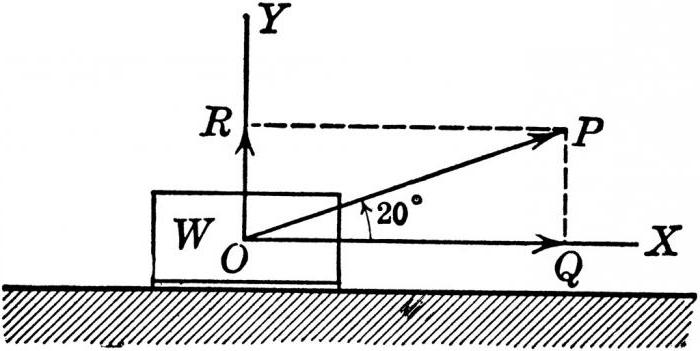
На плоскости вектор можно задавать несколькими способами:

1. Указать координаты начала и конца вектора. Например, вектор  на рис. 4 задан координатами начала вектора – (2, 4) (м), конца – (6, 8) (м). рис. 4

 

2. Указать модуль вектора (его значение) и угол между направлением вектора и некоторым заранее выбранным направлением на плоскости. Часто за такое направление в положительную сторону оси 0Х. Углы, измеренные от этого направления против часовой стрелки, считаются положительными. На рис. 5  вектор  задан двумя числами b и α , указывающими длину и направление вектора. рис. 5