Как измерять крутящий момент? | Dewesoft
Автор: Грант Малой Смит (Grant Maloy Smith), специалист по сбору данных
Данная статья об измерении крутящего момента поможет вам:
- Понять, что такое крутящий момент
- Узнать, как измерять крутящий момент
- Ознакомиться со спецификой измерения крутящего момента при сборе данных
Что такое крутящий момент?
Если вы не пропускали уроки физики в школе, то помните, что сила — это воздействие, приводящее тело в движение в течение времени. Например, простое линейное усилие может толкнуть (или притянуть) массу в состоянии покоя и изменить её скорость путём ускорения. Крутящий момент — сила, которая вызывает вращение тела по своей оси вращения. Так, крутящий момент — это крутящее усилие, которое называют вращающей силой.
Наиболее очевидный пример крутящего момента — приводной вал автомобиля. Вызываемый двигателем крутящий момент вала приводит автомобиль в движение. Крутящий момент — это вектор: это означает, что он имеет направление.
Вызываемый двигателем крутящий момент вала приводит автомобиль в движение. Крутящий момент — это вектор: это означает, что он имеет направление.
Крутящий момент — усилие, вращающее или поворачивающее приводной вал, винт или колесо.
Вращающее усилие
Также крутящий момент называют моментом или моментом силы. Как правило, крутящий момент обозначают символом $τ$ (греческой буквой «т»). Единица измерения крутящего момента по системе СИ — $N\cdot m$ (Н·м).
В США для его выражения используют футо-фунты ($ft/lbs$). Для перевода $N\cdot m$ в $ft/lbs$ достаточно разделить $N\cdot m$ на 1,356.
Старшина второй статьи Джеймс Р. Эванс (James R. Evans) осматривает приводной вал хвостового винта вертолёта ВМС США. Снимок из открытого доступа, Wikimedia Commons
Для чего измеряют крутящий момент?
Измерение механического крутящего момента торсионных валов — важнейший этап проектирования и сбора различных машин, а также устранения их неисправностей.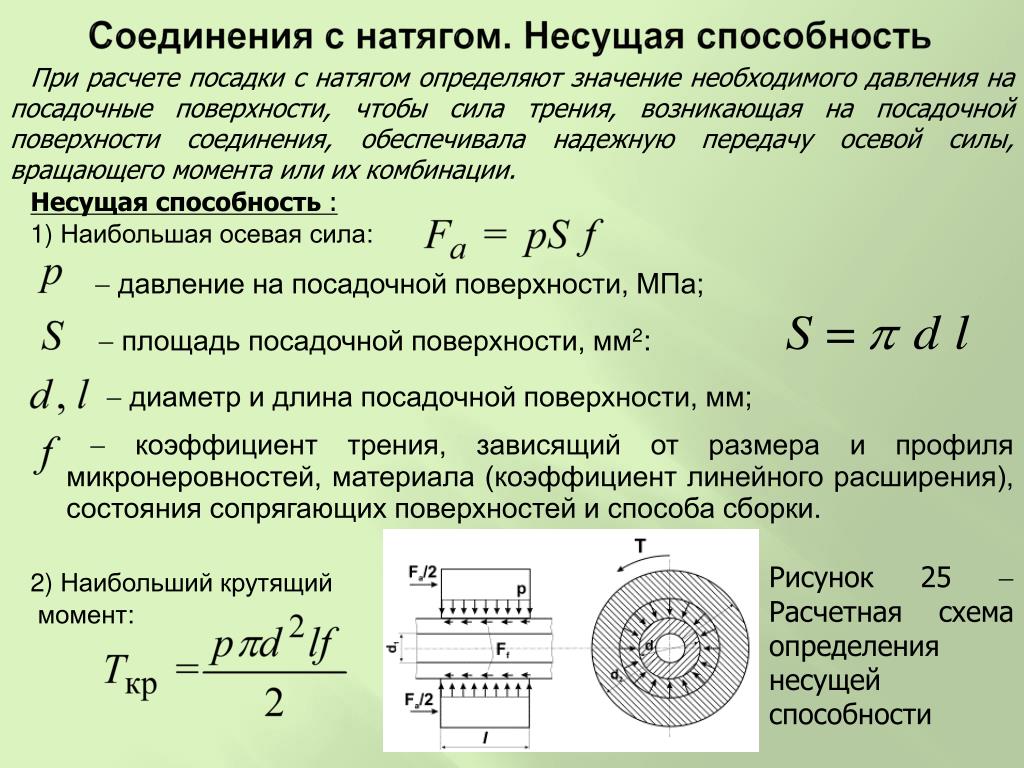 Истинное значение механического крутящего момента вала, пропеллера или другого вращающегося компонента — единственный способ понять, отвечает ли он требованиям.
Истинное значение механического крутящего момента вала, пропеллера или другого вращающегося компонента — единственный способ понять, отвечает ли он требованиям.
В некоторых случаях крутящий момент необходимо отслеживать постоянно: например, чтобы предотвратить потенциально опасный чрезмерный крутящий момент, который может привести к выходу системы из строя. Также измерения крутящего момента играют важную роль при диагностическом техническом обслуживании.
Какие виды крутящего момента существуют?
Крутящий момент делится на два вида: вращающий и реактивный:
- вращающий — то есть вращающий или динамический крутящий момент;
- реактивный — то есть стационарный или статичный крутящий момент.
Вращающий момент
Тела, которые многократно (или постоянно) вращаются вокруг своей оси (например, валы, турбины, колёса), имеют вращающий момент.
Реактивный момент
Воздействующая на тело статичная сила называется реактивным крутящим моментом. Например, при попытке закрутить болт ключом на болт воздействует реактивная сила. Такая сила воздействует даже тогда, когда болт не крутится. В таких случаях крутящий момент измеряют не за полный оборот.
Например, при попытке закрутить болт ключом на болт воздействует реактивная сила. Такая сила воздействует даже тогда, когда болт не крутится. В таких случаях крутящий момент измеряют не за полный оборот.
Как измеряется крутящий момент?
Крутящий момент можно измерить косвенно или напрямую. Если известны КПД двигателя и скорость вала, с помощью измерителя мощности можно вычислить крутящий момент. Такое измерение называют косвенным.
Более точным методом является прямое измерение крутящего момента с помощью датчиков крутящего момента или роторных моментомеров. Чем они отличаются?
Датчики реактивного (статичного) крутящего момента
Датчик Torquemaster. CC BY-SA 3.0, Wikimedia Commons
Датчик реактивного крутящего момента измеряет статический крутящий момент.
Пример датчика крутящего момента — динамометрический ключ. С помощью таких ключей можно точно измерить крутящий момент, прилагаемый к болту, гайке или другому креплению. В основании ключа можно задать нужный крутящий момент, после чего при затягивании крепления оператором до нужного момента раздастся щелчок. Как правило, такие ключи называют щелчковыми. На них можно задать несколько значений момента.
В основании ключа можно задать нужный крутящий момент, после чего при затягивании крепления оператором до нужного момента раздастся щелчок. Как правило, такие ключи называют щелчковыми. На них можно задать несколько значений момента.
Цифровые динамометрические ключи оснащены иглой или цифровым дисплеем, на котором отображается прилагаемое усилие. Ряд электронных моделей (в частотности промышленных) имеют память, в которой хранится каждое измерение значение (для ведения документации или контроля качества).
Принцип работы щелчкового динамометрического ключа продемонстрирован в следующем видео:
В основе датчика реактивного крутящего момента лежит кварцевый пьезоэлектрический датчик или тензодатчик. Сегодня на рынке представлены различные виды и конфигурации динамометрических ключей и отвёрток.
Датчики крутящего момента
Датчик крутящего момента — это преобразователь, который преобразовывает вращающий момент в сигнал, который можно измерить, проанализировать, отобразить и сохранить. Преобразователи крутящего момента применяются для испытаний крутящего момента двигателя, испытаний ДВС, испытаний электродвигателей, валов, турбин, генераторов и т.д.
Преобразователи крутящего момента применяются для испытаний крутящего момента двигателя, испытаний ДВС, испытаний электродвигателей, валов, турбин, генераторов и т.д.
Измерить крутящий момент можно как напрямую, так и косвенно.
Косвенное измерение крутящего момента — более экономичный и удобный метод измерения, точность которого уступает методу прямого измерения. Он подходит для случаев, когда известен КПД двигателя и имеется возможность измерить скорость вала и расход тока.
Прямое измерение — более точный способ. Для прямого измерения на вале закрепляют тензодатчик, который измеряет крутящее усилие на вале.
На вале закрепляют тензодатчик. Вращательное усилие заставляет вал вращаться.
При повороте вала двигателем вращательное усилие будет незначительным. Из-за жёсткости стали увидеть вращение нельзя, однако его можно считать с помощью закреплённых на вале тензодатчиков. Четыре датчика образуют мост Уитстона, выход которого балансируется и нормируется системой измерения крутящего момента.
Выход тензодатчика можно передать по проводу (если возможно) или дистанционно на систему измерения крутящего момента или систему сбора данных.
Стандартная система измерения крутящего момента
Внутри датчика крутящего момента выходы закреплённых на вале тензодатчиков передаются на электронные компоненты по контактному кольцу (на тензодатчики должно подаваться питание). Также можно подключить бесщёточный или индуктивный датчик: он повышает скорость и меньше изнашивается, а значит требует меньшего технического обслуживания. Бесконтактным способом можно измерить угол и частоту вращения.
Системы сбора данных Dewesoft — идеальные решения для измерения любых физических параметров, в том числе крутящего момента. В них встроены изолированные блоки преобразования сигналов, которые сокращают количество шумов и гарантируют высокую точность данных. Также они имеют входы счётчика, частоты вращения и энкодера, а значит подходят для одновременного измерения скорости, угла и положения вала. В системах сбора данных данные с аналоговых и цифровых счётчиков полностью синхронизированы между собой, и этот фактор играет важную роль при решении любых задач, особенно при испытании вибрации кручения и вращения. Подробнее об этом — в следующем разделе.
В системах сбора данных данные с аналоговых и цифровых счётчиков полностью синхронизированы между собой, и этот фактор играет важную роль при решении любых задач, особенно при испытании вибрации кручения и вращения. Подробнее об этом — в следующем разделе.
Испытание вибрации кручения и вращения в ПО Dewesoft X
Стационарные системы измерения крутящего момента
В представленной выше системе датчик крутящего момента закреплён между двигателем и тормозом с помощью соединений с каждой стороны. Проходящий через вал датчик оснащен тензодатчиком, который измеряет крутящее усилие вала. После преобразования выход сигнала отправляется на систему сбора данных, цифровой дисплей или аварийную систему (при мониторинге, а не записи данных).
При необходимости датчики крутящего момента можно оснастить энкодером, который точно выводит скорость и угол вала. Такие выводы применяют для анализа вибрации кручения и вращения. Выводы скорости и угла крайне важны при использовании динамометров для вычисления выходной мощности (выраженной в $HP$ или $Kw$) и КПД двигателя.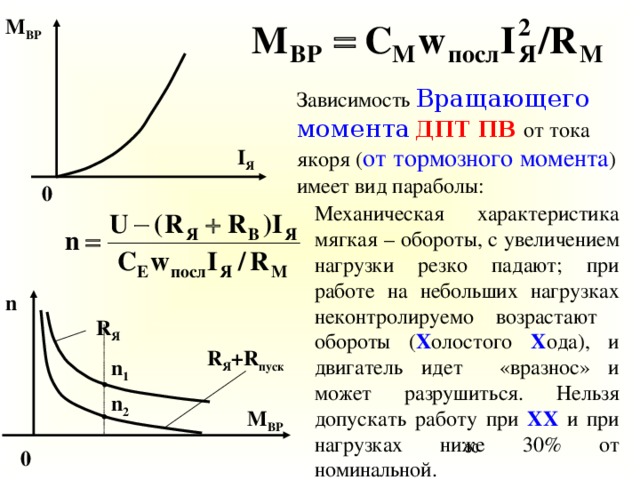
Портативные системы измерения крутящего момента
Для временных измерений крутящего момента тензодатчики можно закрепить на приводном вале. Компактный интерфейс с питанием от аккумулятора питает датчики и дистанционно передаёт данные на ближайший блок преобразования, в котором с помощью системы сбора данных их можно записать, отобразить или проанализировать.
Беспроводной датчик крутящего момента. Изображение предоставлено компанией Parker-LORD MicroStrain Sensing
Беспроводные датчики Parker-Lord совместимы с ПО Dewesoft X: их можно объединить с системами сбора данных и использовать на неограниченном количестве каналов.
Области применения порядкового анализа
Вибрации кручения могут стать причиной выхода торсионных валов из строя. Анализ вибрации вращения и кручения — важный способ устранения неисправностей валов, коленчатых валов и зубчатых передач в автомобилестроении, промышленности и в производстве электроэнергии.
Что такое вибрация кручения?
Вибрации кручения — угловые вибрации тела (как правило, вала по оси вращения). Данные механических вибраций вызваны изменениями крутящего момента с течением времени, наложенными на постоянную скорость торсионного вала. В автомобилестроении основной причиной вибраций кручения становятся колебания полезной мощности двигателя.
Данные механических вибраций вызваны изменениями крутящего момента с течением времени, наложенными на постоянную скорость торсионного вала. В автомобилестроении основной причиной вибраций кручения становятся колебания полезной мощности двигателя.
Вибрации кручения оценивают как изменение скорости вращения в цикле вращения. Изменения частоты вращения обусловлены нестабильным крутящим моментом или переменной нагрузкой.
Что такое вибрация вращения?
Вибрация вращения — динамическая составляющая скорости вращения. При точном измерении вибрации вращения вала в некоторых участках разгона можно увидеть сильное отклонение скорости вращения. Отклонение возникает в результате угловой вибрации, пересекающей собственную угловую частоту вала. Угловая вибрация вычисляется путём отсечения постоянной составляющей скорости или угла вращения;
Вибрация кручения зависит от ряда параметров: свойств материала и условий эксплуатации (температуры, нагрузки, частоты вращения и т.д.).
Как измерять вибрацию вращения и кручения
В этом коротком видео показаны способы измерения вибрации и вращения, а также описана базовая теория и практические преимущества таких измерений.
Модуль вибрации кручения Dewesoft X автоматически вычисляет следующие параметры:
- угол поворота: фильтрованное значение угла вибрации;
- скорость вращения: фильтрованное значение скорости вибрации;
- угол кручения: динамический угол кручения, который представляет собой разность углов, полученных от датчика 1 и датчика 2;
- скорость кручения: разница угловых скоростей, полученных от датчика 1 и датчика 2;
- опорный угол по оси X: опорный угол, который всегда составляет от 0 до 360° и может быть использован в качестве опорного на графике XY;
- частота: об/мин.
Вычисления можно провести в ходе измерения, а также на этапе обработки (по необработанным данным).
Итог
Датчики крутящего момента применяются для решения сотен задач во всех отраслях. Датчики реактивного крутящего момента применяются в динамометрических ключах и других инструментах.

Крутящий момент — важный параметр в множестве отраслей. К счастью, его можно измерить с помощью датчиков и преобразователей, и отобразить, записать и проанализировать с помощью систем сбора данных.
Поделиться статьёй:
Что такое крутящий момент, и почему он важен?
Добавлено 28 июля 2019 в 14:30
Узнайте о крутящем моменте, его применении к двигателям, и почему значения крутящего момента так важны для ваших проектов.
В базовой физике вы, вероятно, привыкли думать о линейных силах, например, о силе тяжести, притягивающей предметы вниз, или о силе, которую вы прикладываете к тележке для покупок, толкая ее. Крутящий момент аналогичен линейным силам, но в то время как линейные силы заставляют объект двигаться по прямой линии, крутящий момент заставляет объекты вращаться.
Крутящий момент аналогичен линейным силам, но в то время как линейные силы заставляют объект двигаться по прямой линии, крутящий момент заставляет объекты вращаться.
Если вы когда-либо открывали дверь, у вас должно быть интуитивное понимание крутящего момента. Когда вы открываете дверь, вы прикладываете силу на той стороне двери, которая находится дальше всего от петель. Поскольку дверь твердая, ваша сила, действующая на расстоянии от центра вращения двери (петли), заставляет дверь вращаться и открываться. Вы можете открыть дверь, нажав на сторону двери, ближайшую к петлям, однако, как вы знаете, для открытия двери в этом случае потребуется гораздо больше усилий. Это потому, что, уменьшая расстояние между вами и центром вращения двери, вы создаете меньший крутящий момент.
Крутящий момент рассчитывается путем умножения линейной силы на расстояние, на котором эта сила действует от центра вращения. Классическим примером крутящего момента является гаечный ключ при откручивании гайки.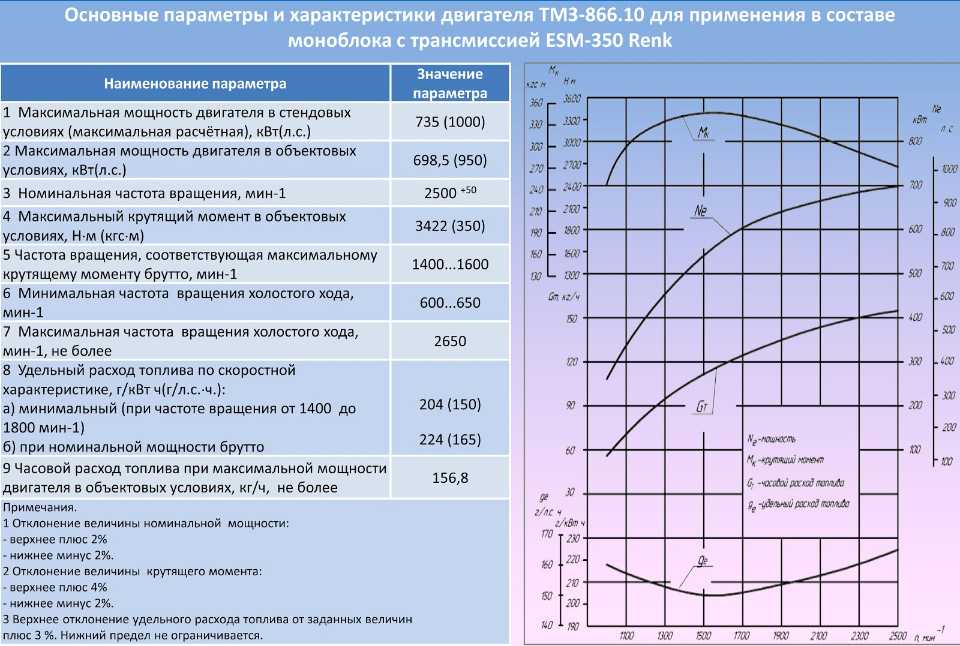 Если у вас есть гаечный ключ длиной 20 см, и вы нажимаете на ключ с силой 2 кг, крутящий момент на гайке составит (20 см x 2 кг =) 40 кг·см.
Если у вас есть гаечный ключ длиной 20 см, и вы нажимаете на ключ с силой 2 кг, крутящий момент на гайке составит (20 см x 2 кг =) 40 кг·см.
Когда мы смотрим на двигатели, расчет крутящего момента аналогичен – сила, умноженная на расстояние.
Единственное отличие состоит в том, что в отличие от гаечного ключа, где сила прикладывается к рычагу, в случае с двигателем крутящий момент прикладывается непосредственно в центре вращения, создавая линейную силу на конце рычага. Размышляя о крутящем моменте двигателя, вы можете представить себе двигатель, использующий руку для поднятия веса. Максимальный вес, который может поднять двигатель, будет соответствовать максимальному крутящему моменту.
Рисунок 2 – В двигателях крутящий момент прикладывается в центре вращения для создания линейной силы.Двигатели, предназначенные для обеспечения большего крутящего момента, способны оказывать большее воздействие на другие объекты.
Почему крутящий момент важен?
Крутящий момент, в особенности при разработке систем с двигателями, которые обеспечивают правильную величину крутящего момента, невероятно важен в широком диапазоне различных применений.
Допустим, вы строите робота. Если вы хотите построить более крупного робота или робота, способного поднимать тяжелые предметы, вам понадобятся более мощные двигатели, способные создавать больший крутящий момент, чтобы заставить робота двигаться.
Для летательных аппаратов крутящий момент, создаваемый двигателями, напрямую определяет максимальную подъемную силу, которую могут создавать пропеллеры.
Рисунок 3 – Создание подъемной силы крутящим моментом.Если вы строите автомобиль и хотите, чтобы он ускорялся быстрее, вам потребуется от двигателей больший крутящий момент – в автомобиле сила, движущая его вперед, равна (примерно) крутящему моменту двигателя, деленному на радиус колес.
Электромобили, такие как Tesla Model S, известны своим быстрым ускорением, потому что их электродвигатели генерируют огромную величину крутящего момента.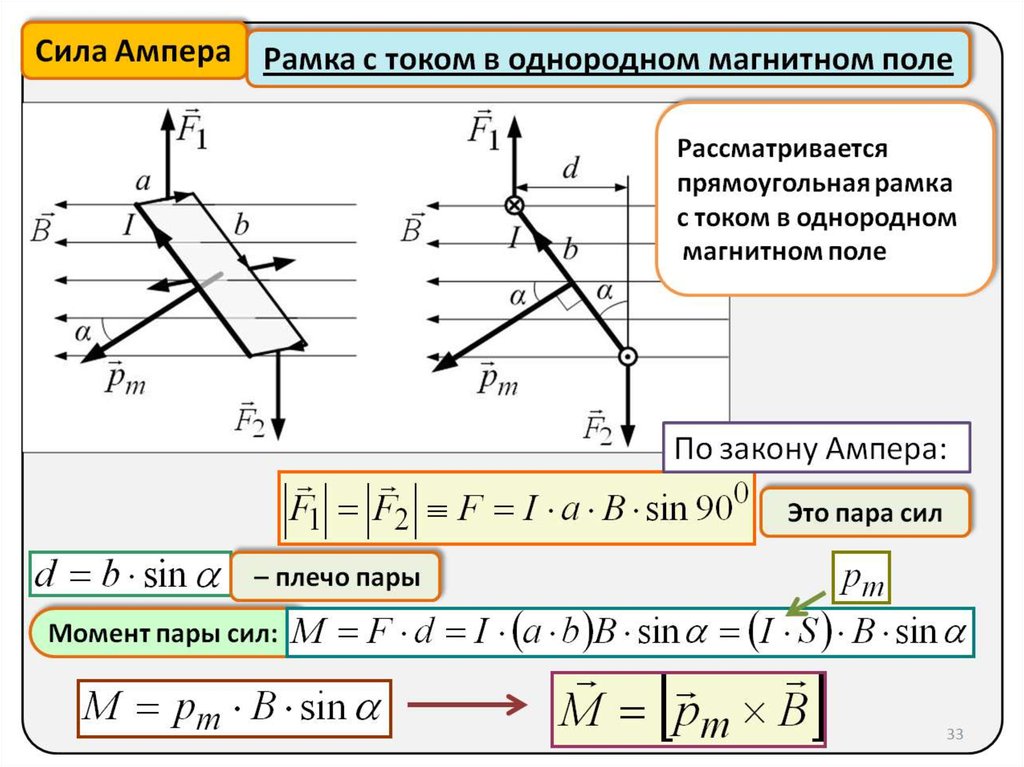 Этот крутящий момент непосредственно передается в большую силу, применяемую колесами к поверхности дороги. Как учат основы физики, воздействие на объект большей силы заставит его ускоряться быстрее.
Этот крутящий момент непосредственно передается в большую силу, применяемую колесами к поверхности дороги. Как учат основы физики, воздействие на объект большей силы заставит его ускоряться быстрее.
Какие факторы влияют на крутящий момент двигателя
Когда речь идет о максимальном значении крутящего момента двигателя, существует три разных, но взаимосвязанных ограничивающих фактора.
Механические свойства материалов
Во-первых, это механические свойства материалов. Хорошим примером такого подхода к проектированию являются разные серводвигатели.
Более дешевые сервоприводы с более низким крутящим моментом используют пластиковые шестерни, обычно сделанные из нейлона. Производство пластиковых шестеренок недорогое, что делает сервоприводы с нейлоновыми шестеренками более дешевыми в производстве, и, следовательно, их можно дешевле купить. Нейлоновые шестерни также более легкие, по сравнению с металлическими, что является важным фактором для робототехники и летательных аппаратов. Однако если на эти нейлоновые шестерни будет приложен слишком большой крутящий момент, они сломаются.
Однако если на эти нейлоновые шестерни будет приложен слишком большой крутящий момент, они сломаются.
Сервоприводы с более высоким крутящим моментом содержат металлические шестерни, поэтому они могут выдавать более высокий крутящий момент без поломок.
Материалы, используемые в конструкции двигателя, играют огромную роль в определении того, какой крутящий момент двигатель будет способен создать.
Рисунок 4 – Двигатели изготавливаются из различных материалов, но, как правило, те, что изготовлены из металла, имеют более высокий крутящий момент, чем те, что изготовлены из нейлона или другого пластика.Максимальное напряжение двигателя
Вторым фактором, влияющим на максимальный крутящий момент двигателя, является максимальное напряжение, на которое рассчитан двигатель. Если вы посмотрите на страницу характеристик любого сервопривода, вы найдете разные значения крутящего момента для разных напряжений. Более высокие напряжения дают двигателю большую мощность для обеспечения более высокого крутящего момента.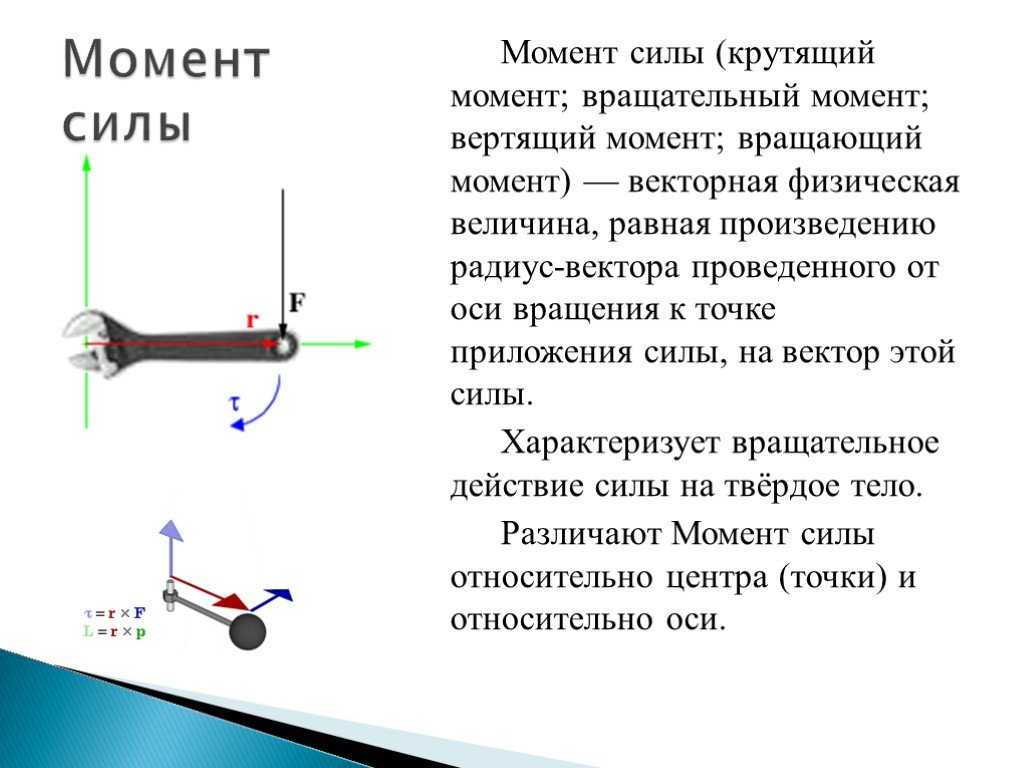 Тем не менее, двигатель и его схема управления могут принимать ограниченное напряжение из-за возможности перегрева и сгорания. Максимальное напряжение, которое двигатель может принять без сбоев, влияет на величину его максимального крутящего момента.
Тем не менее, двигатель и его схема управления могут принимать ограниченное напряжение из-за возможности перегрева и сгорания. Максимальное напряжение, которое двигатель может принять без сбоев, влияет на величину его максимального крутящего момента.
Тепловыделение двигателя
Это подводит нас к последнему фактору, ограничивающему максимальный крутящий момент двигателя. Поскольку двигатели работают, они генерируют ненужное тепло. Чем тяжелее работает двигатель, тем больше тепла он выделяет.
Для большинства двигателей, используемых в любительских проектах, от двигателей постоянного тока до сервоприводов и шаговых двигателей, создаваемое тепло просто излучается в воздух. У них нет активного охлаждения, как, например, в электромобиле. Следовательно, двигатель ограничен тем, какой крутящий момент (а также скорость) он может генерировать без риска сбоя по температуре.
Измерьте крутящий момент двигателя сами
Мы рассмотрели, почему так важно оставаться в пределах максимального крутящего момента двигателя. Так что же делать, если вы думаете, что ваш двигатель не соответствует требованиям? Не бойтесь! У нас есть проект, который может показать вам, как измерить крутящий момент серводвигателя (в следующей статье).
Дважды проверьте крутящий момент вашего серводвигателя перед тем, как добавить его в свой проект. Это поможет вам избавиться от разочарований от сборки и от повторного переделывания.
Оригинал статьи:
- Scott Hatfield. What is Torque and Why Does it Matter?
Теги
ДвигательКрутящий моментТепловыделениеЭлектродвигательКак рассчитать крутящий момент электродвигателя
- Полезное
- Справочная информация
- Крутящий момент электродвигателя – расчет, формула, таблица
Крутящий момент электродвигателя – это сила вращения его вала. Именно момент вращения определяет мощность Вашего двигателя. Измеряется в ньютонах на метр Н*м или в килограмм-силах на метр кгс*м.
Именно момент вращения определяет мощность Вашего двигателя. Измеряется в ньютонах на метр Н*м или в килограмм-силах на метр кгс*м.
Виды крутящих моментов:
- Номинальный – значение момента при стандартном режиме работы и стандартной номинальной нагрузке на двигатель.
- Максимальный – предельное значение, по достижении которого нагрузка уравновесит двигатель и остановит его.
В данной таблице собраны крутящие моменты наиболее распространенных в Украине электродвигателей АИР, а также требуемый при пуске – пусковой, максимально допустимый для данного типа электродвигателя – максимальный крутящий момент и момент инерции двигателей АИР (усилие важное при подборе электромагнитного тормоза, например)
Мощности асинхронных электродвигателей:
| Двигатель | кВт/об | Мном, Нм | Мпуск, Нм | Ммакс, Нм | Минн, Нм |
| АИР56А2 | 0,18/2730 | 0,630 | 1,385 | 1,385 | 1,133 |
| АИР56В2 | 0,25/2700 | 0,884 | 1,945 | 1,945 | 1,592 |
| АИР56А4 | 0,12/1350 | 0,849 | 1,868 | 1,868 | |
| АИР56В4 | 0,18/1350 | 1,273 | 2,801 | 2,801 | 2,292 |
| АИР63А2 | 0,37/2730 | 1,294 | 2,848 | 2,848 | 2,330 |
| АИР63В2 | 0,55/2730 | 1,924 | 4,233 | 4,233 | 3,463 |
| АИР63А4 | 0,25/1320 | 1,809 | 3,979 | 3,979 | 3,256 |
| АИР63В4 | 0,37/1320 | 2,677 | 5,889 | 5,889 | 4,818 |
| АИР63А6 | 0,18/860 | 1,999 | 4,397 | 4,397 | 3,198 |
| АИР63В6 | 0,25/860 | 2,776 | 6,108 | 6,108 | 4,442 |
| АИР71А2 | 0,75/2820 | 2,540 | 6,604 | 6,858 | 4,064 |
| АИР71В2 | 1,1/2800 | 3,752 | 8,254 | 9,004 | 6,003 |
| АИР71А4 | 0,55/1360 | 3,862 | 8,883 | 9,269 | 6,952 |
| АИР71В4 | 0,75/1350 | 5,306 | 13,264 | 13,794 | 12,733 |
| АИР71А6 | 0,37/900 | 3,926 | 8,245 | 8,637 | 6,282 |
| АИР71В6 | 0,55/920 | 5,709 | 10,848 | 12,560 | 9,135 |
| АИР71В8 | 0,25/680 | 3,511 | 5,618 | 6,671 | 4,915 |
| АИР80А2 | 1,5/2880 | 4,974 | 10,943 | 12,932 | 8,953 |
| АИР80В2 | 2,2/2860 | 7,346 | 15,427 | 19,100 | 13,223 |
| АИР80А4 | 1,1/1420 | 7,398 | 16,275 | 17,755 | 12,576 |
| АИР80В4 | 1,5/1410 | 10,160 | 22,351 | 24,383 | 17,271 |
| АИР80А6 | 0,75/920 | 7,785 | 16,349 | 17,128 | 12,457 |
| АИР80В6 | 1,1/920 | 11,418 | 25,121 | 26,263 | 20,553 |
| АИР80А8 | 0,37/680 | 5,196 | 10,393 | 11,952 | 7,275 |
| АИР80В8 | 0,55/680 | 7,724 | 15,449 | 16,221 | 10,814 |
| АИР90L2 | 3/2860 | 10,017 | 23,040 | 26,045 | 17,030 |
| АИР90L4 | 2,2/1430 | 14,692 | 29,385 | 35,262 | 29,385 |
| АИР90L6 | 1,5/940 | 15,239 | 30,479 | 35,051 | 28,955 |
| АИР90LА8 | 0,75/700 | 10,232 | 15,348 | 20,464 | 15,348 |
| АИР90LВ8 | 1,1/710 | 14,796 | 22,194 | 32,551 | 22,194 |
| АИР100S2 | 4/2850 | 13,404 | 26,807 | 32,168 | 21,446 |
| АИР100L2 | 5,5/2850 | 18,430 | 38,703 | 44,232 | 29,488 |
| АИР100S4 | 3/1410 | 20,319 | 40,638 | 44,702 | 32,511 |
| АИР100L4 | 4/1410 | 27,092 | 56,894 | 65,021 | 43,348 |
| АИР100L6 | 2,2/940 | 22,351 | 42,467 | 35,762 | |
| АИР100L8 | 1,5/710 | 20,176 | 32,282 | 40,352 | 30,264 |
| АИР112М2 | 7,5/2900 | 24,698 | 49,397 | 54,336 | 39,517 |
| АИР112М4 | 5,5/1430 | 36,731 | 73,462 | 91,827 | 58,769 |
| АИР112МА6 | 3/950 | 30,158 | 60,316 | 66,347 | 48,253 |
| АИР112МВ6 | 4/950 | 40,211 | 80,421 | 88,463 | 64,337 |
| АИР112МА8 | 2,2/700 | 30,014 | 54,026 | 66,031 | 42,020 |
| АИР112МВ8 | 3/700 | 40,929 | 73,671 | 90,043 | 57,300 |
| АИР132М2 | 11/2910 | 36,100 | 57,759 | 79,419 | 43,320 |
| АИР132S4 | 7,5/1440 | 49,740 | 99,479 | 124,349 | 79,583 |
| АИР132М4 | 11/1450 | 72,448 | 173,876 | 210,100 | 159,386 |
| АИР132S6 | 5,5/960 | 54,714 | 109,427 | 120,370 | 87,542 |
| АИР132М6 | 7,5/950 | 75,395 | 150,789 | 165,868 | 120,632 |
| АИР132S8 | 4/700 | 54,571 | 98,229 | 120,057 | 76,400 |
| АИР132М8 | 5,5/700 | 75,036 | 135,064 | 165,079 | 105,050 |
| АИР160S2 | 15/2940 | 48,724 | 97,449 | 155,918 | 2,046 |
| АИР160М2 | 18,5/2940 | 60,094 | 120,187 | 192,299 | 2,884 |
| АИР180S2 | 22/2940 | 71,463 | 150,071 | 250,119 | 4,288 |
| АИР180М2 | 30/2940 | 97,449 | 214,388 | 341,071 | 6,821 |
| АИР200М2 | 37/2950 | 119,780 | 275,493 | 383,295 | 16,769 |
| АИР200L2 | 45/2940 | 146,173 | 380,051 | 584,694 | 19,003 |
| АИР225М2 | 55/2955 | 177,750 | 408,824 | 710,998 | 35,550 |
| АИР250S2 | 75/2965 | 241,568 | 628,078 | 966,273 | 84,549 |
| АИР250М2 | 90/2960 | 290,372 | 784,003 | 1161,486 | 116,149 |
| АИР280S2 | 110/2960 | 354,899 | 887,247 | 1171,166 | 212,939 |
| АИР280М2 | 132/2964 | 425,304 | 1233,381 | 1488,563 | 297,713 |
| АИР315S2 | 160/2977 | 513,268 | 1231,844 | 1693,786 | 590,259 |
| АИР315М2 | 200/2978 | 641,370 | 1603,425 | 2116,521 | 962,055 |
| АИР355SMA2 | 250/2980 | 801,174 | 1281,879 | 2403,523 | 2163,171 |
| АИР160S4 | 15/1460 | 98,116 | 186,421 | 284,538 | 7,457 |
| АИР160М4 | 18,5/1460 | 121,010 | 229,920 | 350,930 | 11,375 |
| АИР180S4 | 22/1460 | 143,904 | 302,199 | 402,932 | 15,110 |
| АИР180М2 | 30/1460 | 196,233 | 470,959 | 588,699 | 27,276 |
| АИР200М4 | 37/1460 | 242,021 | 532,445 | 847,072 | 46,952 |
| АИР200L4 | 45/1460 | 294,349 | 647,568 | 941,918 | 66,229 |
| АИР225М4 | 55/1475 | 356,102 | 997,085 | 1317,576 | 145,289 |
| АИР250S4 | 75/1470 | 487,245 | 1218,112 | 1559,184 | 301,605 |
| АИР250М4 | 90/1470 | 584,694 | 1461,735 | 1871,020 | 467,755 |
| АИР280S4 | 110/1470 | 714,626 | 2072,415 | 2429,728 | 578,847 |
| АИР280М4 | 132/1485 | 848,889 | 1697,778 | 2886,222 | 1612,889 |
| АИР315S4 | 160/1487 | 1027,572 | 2568,931 | 3802,017 | 2363,416 |
| АИР315М4 | 200/1484 | 1287,062 | 3217,655 | 4247,305 | 3603,774 |
| АИР355SMA4 | 250/1488 | 1604,503 | 3690,356 | 4492,608 | 8985,215 |
| АИР355SMВ4 | 315/1488 | 2021,673 | 5054,183 | 5862,853 | 12534,375 |
| АИР355SMС4 | 355/1488 | 2278,394 | 5012,466 | 6151,663 | 15493,078 |
| АИР160S6 | 11/970 | 108,299 | 205,768 | 314,067 | 12,021 |
| АИР160М6 | 15/970 | 147,680 | 339,665 | 443,041 | 20,675 |
| АИР180М6 | 18,5/970 | 182,139 | 400,706 | 546,418 | 29,324 |
| АИР200М6 | 22/975 | 215,487 | 517,169 | 711,108 | 50,209 |
| АИР200L6 | 30/975 | 293,846 | 617,077 | 881,538 | 102,846 |
| АИР225М6 | 37/980 | 360,561 | 721,122 | 1081,684 | 186,050 |
| АИР250S6 | 45/986 | 435,852 | 784,533 | 1307,556 | 440,210 |
| АИР250М6 | 55/986 | 532,708 | 1012,145 | 1811,207 | 633,922 |
| АИР280S6 | 75/985 | 727,157 | 1454,315 | 2326,904 | 1090,736 |
| АИР280М6 | 90/985 | 872,589 | 1745,178 | 2792,284 | 1657,919 |
| АИР315S6 | 110/987 | 1064,336 | 1809,372 | 2873,708 | 4044,478 |
| АИР315М6 | 132/989 | 1274,621 | 2166,855 | 3696,400 | 5735,794 |
| АИР355МА6 | 160/993 | 1538,771 | 2923,666 | 3539,174 | 11848,540 |
| АИР355МВ6 | 200/993 | 1923,464 | 3654,582 | 4423,968 | 17118,832 |
| АИР355MLA6 | 250/993 | 2404,330 | 4568,228 | 5529,960 | 25485,901 |
| AИР355MLB6 | 315/992 | 3032,510 | 6065,020 | 7278,024 | 40029,133 |
| АИР160S8 | 7,5/730 | 98,116 | 156,986 | 235,479 | 13,246 |
| АИР160М8 | 11/730 | 1007,329 | 1712,459 | 2417,589 | 181,319 |
| АИР180М8 | 15/730 | 196,233 | 333,596 | 529,829 | 41,994 |
| АИР200М8 | 18,5/728 | 242,685 | 509,639 | 606,714 | 67,952 |
| АИР200L8 | 22/725 | 289,793 | 579,586 | 724,483 | 88,966 |
| АИР225М8 | 30/735 | 389,796 | 701,633 | 1052,449 | 214,388 |
| АИР250S8 | 37/738 | 478,794 | 861,829 | 1196,985 | 481,188 |
| АИР250М8 | 45/735 | 584,694 | 1052,449 | 1520,204 | 695,786 |
| АИР280S8 | 55/735 | 714,626 | 1357,789 | 2143,878 | 1071,939 |
| АИР280М8 | 75/735 | 974,490 | 1754,082 | 2728,571 | 1851,531 |
| АИР315S8 | 90/740 | 1161,486 | 1509,932 | 2671,419 | 4413,649 |
| АИР315М8 | 110/742 | 1415,768 | 2265,229 | 3964,151 | 6370,957 |
| АИР355SMA8 | 132/743 | 1696,635 | 2714,616 | 3902,261 | 12215,774 |
| AИР355SMB8 | 160/743 | 2056,528 | 3496,097 | 4935,666 | 18097,443 |
| AИР355MLA8 | 200/743 | 2570,659 | 4627,187 | 6940,781 | 26991,925 |
| AИР355MLB8 | 250/743 | 4498,654 | 7647,712 | 10796,770 | 58032,638 |
Расчет крутящего момента – формула
Габариты электродвигателей АИР:
Примечание: при расчете стоит учесть коэффициент проскальзывания асинхронного двигателя. Номинальное количество оборотов двигателя не совпадает с реальным. Точное количество оборотов вы сможете найти, зная маркировку, в таблице выше.
Номинальное количество оборотов двигателя не совпадает с реальным. Точное количество оборотов вы сможете найти, зная маркировку, в таблице выше.
Где, Р — мощность электродвигателя в киловаттах (кВт). N — количество оборотов вала в минуту.
71828 28.01.2019
Вернуться к списку новостей
домашнее задание и упражнения — Максимальная угловая скорость для остановки за один оборот при известном крутящем моменте
Вопрос задан
Изменено 9 лет, 4 месяца назад
Просмотрено 5к раз
$\begingroup$
У меня есть объект, который я могу вращать с заданным крутящим моментом. Я хотел бы прекратить применение крутящего момента, как только я достигну определенной максимальной скорости вращения. Максимальная скорость вращения должна быть определена таким образом, чтобы приложение максимального крутящего момента останавливало вращение объекта за один оборот. Если я знаю свой крутящий момент и момент инерции, как я могу найти максимальную скорость вращения, чтобы позволить мне остановить объект за один оборот?
Максимальная скорость вращения должна быть определена таким образом, чтобы приложение максимального крутящего момента останавливало вращение объекта за один оборот. Если я знаю свой крутящий момент и момент инерции, как я могу найти максимальную скорость вращения, чтобы позволить мне остановить объект за один оборот?
Время — это то, что нужно.
Я пытался найти угловое ускорение, необходимое для остановки объекта, но остался с переменной времени. Из уравнений, которые я пробовал, у меня осталась переменная времени, а также максимальная угловая скорость.
- домашние задания и упражнения
- вращательная динамика
- крутящий момент
- вращение
$\endgroup$
3
$\begingroup$
92 = \tau_\text{max} \Delta\theta$$ $$ \omega_\text{max} = \sqrt{\frac{2\tau_\text{max}\Delta\theta}{I}}$$Вы рассматриваете $\Delta\theta$ как $2 \pi$, за один полный оборот, следовательно:
$$\omega_\text{max} = \sqrt{\frac{4\pi\tau_\text{max}}{I}}$$
Где $ I$ — это момент инерции вашего объекта.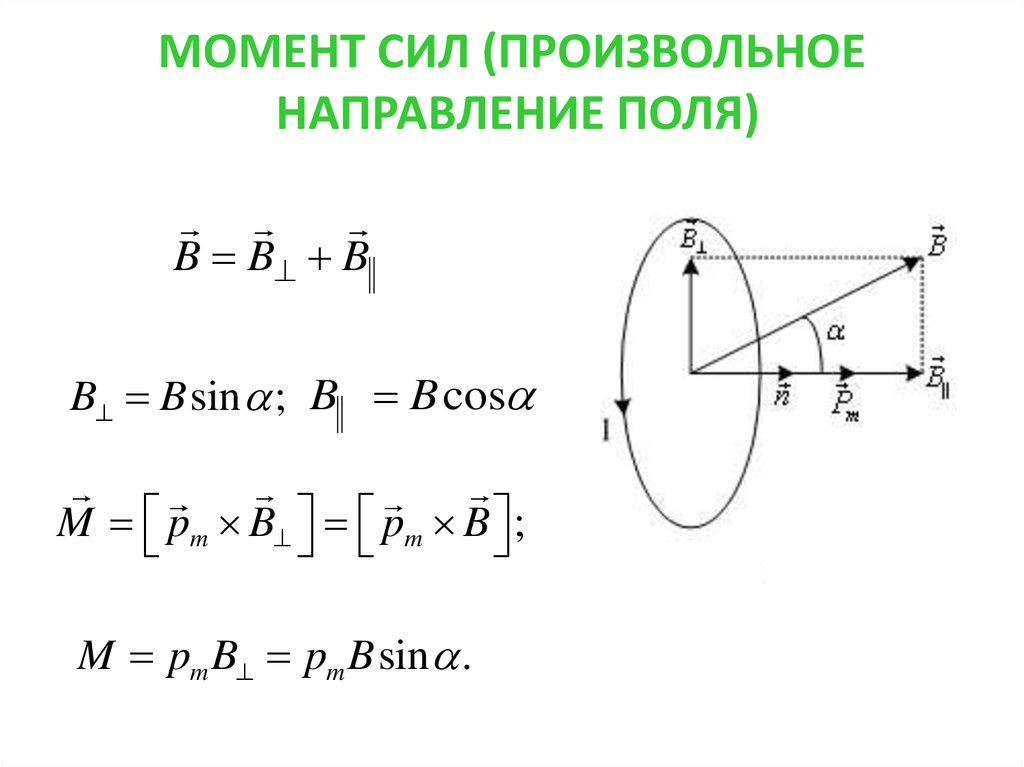 2+2a\Delta x$). 92=2\альфа\cdot2\pi$$
(опять же, игнорируйте знаки)
$$\omega_{max}=\sqrt{4\alpha\pi}$$
что то же самое, что и выше, поскольку $\alpha=\frac \tau I$
2+2a\Delta x$). 92=2\альфа\cdot2\pi$$
(опять же, игнорируйте знаки)
$$\omega_{max}=\sqrt{4\alpha\pi}$$
что то же самое, что и выше, поскольку $\alpha=\frac \tau I$
$\endgroup$
0
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
2.
 17: Вращение твердого тела и тензор инерции
17: Вращение твердого тела и тензор инерции- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 8367
- Джереми Татум
- Университет Виктории
Предполагается, что эта глава должна быть ограничена расчетом моментов инерции тел различной формы, а не огромной темой вращательной динамики твердых тел, которая требует отдельной главы. В этом разделе я просто для интереса упомяну две небольшие темы, связанные с главными осями, и третью тему, по мере необходимости немного более подробно, прежде чем перейти к разделу 2.18. 92 /(2I ) \), где \( I \) — момент инерции. Если изолированное тело (например, астероид) вращается вокруг неглавной оси, оно будет подвержено внутренним напряжениям. Если тело нежесткое, это приведет к искажениям (напряжениям), которые могут вызвать вибрацию тела. Если к тому же тело неупругое, то колебания быстро затухнут (если затухание больше критического, то тело даже не будет вибрировать). Энергия, которая изначально была кинетической энергией вращения, будет преобразована в тепло (которое будет излучаться). Тело теряет кинетическую энергию вращения. Однако в отсутствие внешних моментов \(L\) остается постоянным. Следовательно, в то время как \(E\) уменьшается, \(I\) увеличивается. Тело регулирует свое вращение до тех пор, пока оно не будет вращаться вокруг своей оси с максимальным моментом инерции, при этом дальнейшие напряжения исчезнут, и ситуация останется стабильной.
Если тело нежесткое, это приведет к искажениям (напряжениям), которые могут вызвать вибрацию тела. Если к тому же тело неупругое, то колебания быстро затухнут (если затухание больше критического, то тело даже не будет вибрировать). Энергия, которая изначально была кинетической энергией вращения, будет преобразована в тепло (которое будет излучаться). Тело теряет кинетическую энергию вращения. Однако в отсутствие внешних моментов \(L\) остается постоянным. Следовательно, в то время как \(E\) уменьшается, \(I\) увеличивается. Тело регулирует свое вращение до тех пор, пока оно не будет вращаться вокруг своей оси с максимальным моментом инерции, при этом дальнейшие напряжения исчезнут, и ситуация останется стабильной.
В общем случае вращательное движение твердого тела, эллипс моментов которого является трехосным, довольно сложное и хаотичное, причем тело кувыркается снова и снова, по-видимому, случайным образом. Однако если тело нежесткое и неупругое (какими на практике являются все реальные тела), оно в конце концов начнет вращаться вокруг своей оси с максимальным моментом инерции. Время, необходимое телу, первоначально хаотично кувыркающемуся снова и снова, пока оно не достигнет своего конечного блаженного состояния вращения вокруг своей оси с максимальным моментом инерции, зависит от того, насколько быстро оно вращается. Для большинства небольших астероидов неправильной формы затраченное время сравнимо с возрастом образования Солнечной системы или превышает его, поэтому неудивительно обнаружить некоторые астероиды с вращением не вокруг главной оси (NPA). Однако было обнаружено несколько быстро вращающихся астероидов NPA, и для быстрых вращателей можно было бы ожидать, что вращение PA было достигнуто давным-давно. Считается, что что-то (например, столкновение) должно было произойти с этими быстро вращающимися астероидами NPA относительно недавно в истории Солнечной системы.
Время, необходимое телу, первоначально хаотично кувыркающемуся снова и снова, пока оно не достигнет своего конечного блаженного состояния вращения вокруг своей оси с максимальным моментом инерции, зависит от того, насколько быстро оно вращается. Для большинства небольших астероидов неправильной формы затраченное время сравнимо с возрастом образования Солнечной системы или превышает его, поэтому неудивительно обнаружить некоторые астероиды с вращением не вокруг главной оси (NPA). Однако было обнаружено несколько быстро вращающихся астероидов NPA, и для быстрых вращателей можно было бы ожидать, что вращение PA было достигнуто давным-давно. Считается, что что-то (например, столкновение) должно было произойти с этими быстро вращающимися астероидами NPA относительно недавно в истории Солнечной системы.
Другой интересной темой является устойчивость жесткого ротатора, вращающегося вокруг главной оси, к малым возмущениям от его вращательного состояния. Хотя я этого здесь не доказываю (доказательство можно провести либо математически, либо с помощью качественных аргументов), вращение вокруг любой из осей максимального или минимального момента инерции устойчиво, тогда как вращение вокруг промежуточной оси неустойчиво. Читатель может убедиться в этом сам. Найдите что-нибудь трехосное, например, небольшой деревянный брусок в форме прямоугольного параллелепипеда с неравными сторонами. Определите оси наибольшего, наименьшего и промежуточного моментов инерции. Подбрасывайте тело в воздух, одновременно заставляя его вращаться вокруг той или иной из этих осей, и вы сможете сами убедиться, что в двух случаях вращение устойчиво, а в третьем неустойчиво.
Читатель может убедиться в этом сам. Найдите что-нибудь трехосное, например, небольшой деревянный брусок в форме прямоугольного параллелепипеда с неравными сторонами. Определите оси наибольшего, наименьшего и промежуточного моментов инерции. Подбрасывайте тело в воздух, одновременно заставляя его вращаться вокруг той или иной из этих осей, и вы сможете сами убедиться, что в двух случаях вращение устойчиво, а в третьем неустойчиво.
Теперь я более подробно рассмотрю третью тему, а именно соотношение между угловым моментом \(\bf L\) и угловой скоростью \(\boldsymbol{\omega} \). Из элементарной (и двумерной) механики читатель знаком с соотношением \(L = I \omega \). Что мы собираемся найти в случае трехмерного твердого тела, так это соотношение \(\bf{L} = \mathbb{I}\boldsymbol{\omega} \). Здесь \( \bf L \) и \( \boldsymbol{\omega} \) — это, конечно, векторы, но они не обязательно параллельны друг другу. Они параллельны, только если тело вращается вокруг главной оси вращения. Величина \( \mathbb{I} \) является тензором, известным как тензор инерции . Читатели знакомы с уравнением \({\bf F}= m {\bf a}\). Здесь два вектора имеют одинаковое направление, а m — скалярная величина, которая не меняет направление вектора, на который она умножается. Обычно тензор (если его матричное представление не равно диагонали ) изменяет направление, а также величину вектора, на который он умножает. Читатель может подумать о других примерах тензоров в физике. Есть несколько. На ум приходит диэлектрическая проницаемость анизотропного кристалла; в уравнении \( {\bf D= \boldsymbol{\epsilon} E}\) и \( \bf E \) не параллельны, если они оба не направлены вдоль одной из кристаллографических осей.
Величина \( \mathbb{I} \) является тензором, известным как тензор инерции . Читатели знакомы с уравнением \({\bf F}= m {\bf a}\). Здесь два вектора имеют одинаковое направление, а m — скалярная величина, которая не меняет направление вектора, на который она умножается. Обычно тензор (если его матричное представление не равно диагонали ) изменяет направление, а также величину вектора, на который он умножает. Читатель может подумать о других примерах тензоров в физике. Есть несколько. На ум приходит диэлектрическая проницаемость анизотропного кристалла; в уравнении \( {\bf D= \boldsymbol{\epsilon} E}\) и \( \bf E \) не параллельны, если они оба не направлены вдоль одной из кристаллографических осей.
Если на тело не действуют внешние крутящие моменты, \( \bf L \) постоянна как по величине, так и по направлению. Однако мгновенный вектор угловой скорости не фиксирован ни в пространстве, ни по отношению к телу, если только тело не вращается вокруг главной оси и тензор инерции диагональен.
Так много для предварительного просмотра и качественного описания. Теперь приступайте к работе.
Я должен предположить, что знаком с уравнением для компонентов векторного произведения двух векторов:
\[ {\bf A \times B } = (A_{y}B_{z}-A_{z } B_ {y}) {\ bf \ шляпа {x}} + (A_ {z} B_ {x} — A_ {z} B_ {z} {\ bf) \ шляпа {y}} + (A_ {x} B_{y}-A_{y}B_{z}){\bf \hat{z}} \label{eq:2.17.1} \]
Я также собираюсь предположить, что читатель знает, что угловой момент частицы массы \( m \) на векторе положения \( \bf r \) (компоненты (\( x,y,z \)) ) ) и движущейся со скоростью \(\bf v \) (компоненты ( \( \dot{x} , \dot{y} , \dot{z} \))) есть \( m { \bf r \times v} \). Для набора частиц (или протяженного твердого тела, которое, как мне сказали, состоит из набора частиц, называемых атомами), угловой момент равен
\[\begin{align} {\bf L } &= \sum m {\bf r \times v} \\ &= \sum [m(y \dot{z} — z \dot{y}) { \bf \hat{x} } + m(z \dot{x} — x \dot{z}) { \bf \hat{y} } + m(x \dot{y} — y \dot{x }) { \bf \hat{z} } ] \end{align} \nonumber \]
Я также предполагаю, что связь между линейной скоростью \( \bf v \)( \( \dot{x} , \dot {y} , \dot{z} \)) и угловая скорость \( \boldsymbol{\omega} \) \( ( ( \omega_{x} , \omega_{y} , \omega_{z} ) \) понимается быть \( \bf v = \boldsymbol{\omega} \times r \), так что , например, \( \dot{z} = \omega_{x} y — \omega_{y}x.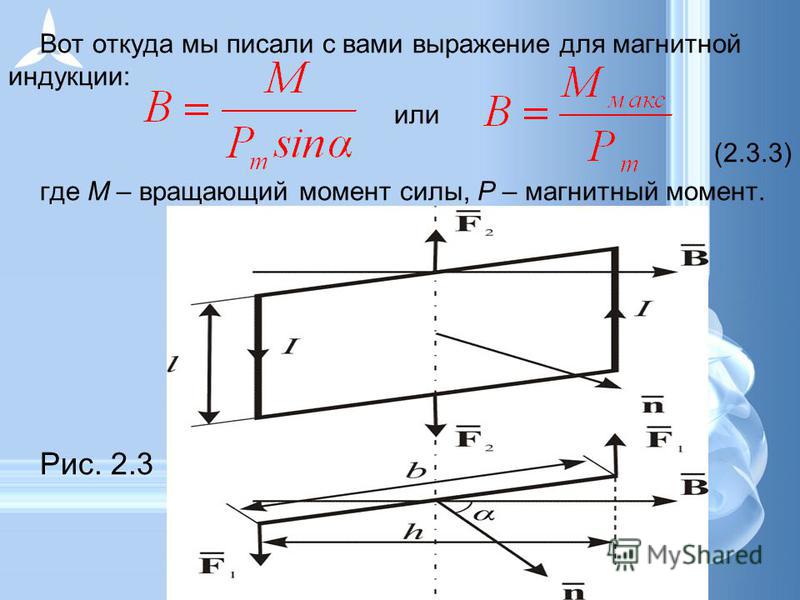 \) тогда 92) {\bf \шляпа{х}} + {\текст и т.д.} \\ &= (А\омега_{х} — Н\омега_у — G\омега_z) {\бф \шляпа{х}} + () { \bf \шляпа{y}} + (){ \bf \шляпа{z}}. \end{align} \nonumber \]
\) тогда 92) {\bf \шляпа{х}} + {\текст и т.д.} \\ &= (А\омега_{х} — Н\омега_у — G\омега_z) {\бф \шляпа{х}} + () { \bf \шляпа{y}} + (){ \bf \шляпа{z}}. \end{align} \nonumber \]
Наконец, мы получаем
\[ { \bf L } = \left(\begin{array}{c}L_x\\ L_y \\ L_z \end{array}\right) = \left(\begin{array}{c}A \ -H \ -G\\ -H \quad B \ -F \\ -G \ -F \quad C\end{массив}\right) \left( \begin{array}{c}\omega_x\\ \omega_y \\ \omega_z \end{array}\right) \label{eq:2.17.2} \]
Это уравнение \( \bf L =\ mathbb{I} \boldsymbol{\omega} \), упомянутые выше. Тензор инерции иногда записывают в виде
\[\mathbb{I} I = \left( \begin{array}{c}I_{xx} \ I _{xy} \ I _{xz} \\ I_{xy} \ I _{yy} \ I _{yz} \\ I_{xz} \ I _{yz} \ I _{zz} \end{array} \right) \nonumber \]
так что, например, \( I_{xy} = — Н \). Это симметричная матрица (но не ортогональная матрица).
Эта страница под названием 2.17: Вращение твердого тела и тензор инерции распространяется под лицензией CC BY-NC 4. 0 и была создана, изменена и/или курирована Джереми Татумом посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
0 и была создана, изменена и/или курирована Джереми Татумом посредством исходного контента, который был отредактирован в соответствии со стилем и стандартами Платформа LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Джереми Татум
- Лицензия
- СС BY-NC
- Версия лицензии
- 4,0
- Показать оглавление
- нет
- Метки
- тензор инерции
- источник@http://orca.
 phys.uvic.ca/~tatum/classmechs.html
phys.uvic.ca/~tatum/classmechs.html
Модель постоянной мощности при вращении руки — новый подход к уравнению Хилла
Всемирный журнал механики Том 04 № 06 (2014 г.), идентификатор статьи: 47446, 12 страниц
10.4236/wjm.2014.46018
Модель постоянной мощности при вращении руки — новый подход к уравнению Хилла
Ахти Рахикайнен, Микко Вирмавирта
Центр нервно-мышечных исследований, кафедра биологии физической активности, Университет Ювяскюля, Ювяскюля, Финляндия
Электронная почта: ahrahik.zz@ kolumbus.fi
Copyright © 2014, авторы и издательство Scientific Research Publishing Inc.
Эта работа находится под лицензией Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/
Поступила в редакцию 19 марта 2014 г.; пересмотрено 18 апреля 2014 г.; принято 16 мая 2014 г.
АННОТАЦИЯ
Целью данного исследования было дальнейшее развитие модели постоянной мощности предыдущего исследования и предоставление окончательного решения уравнения силы-скорости Хилла. Вращения предплечья и всей руки трех разных испытуемых выполнялись вниз (разгибание локтя и плеча) и вверх (сгибание локтя и плеча) с максимальной скоростью. Эти вращения рук регистрировались с помощью специальной системы камер, и теоретически полученная модель постоянной максимальной мощности была адаптирована к экспериментально измеренным данным. Момент инерции секторов руки рассчитывали с помощью иммерсионной методики определения точных значений коэффициентов трения локтевого вращения и вращения всей руки. Эксперименты настоящего исследования подтвердили выводы предыдущего исследования, в котором теоретически полученное уравнение с постоянной максимальной мощностью согласовывалось с экспериментально измеренными результатами. Результаты настоящего исследования были сопоставлены с механикой модели Хилла, и было получено дальнейшее развитие зависимости силы от скорости Хилла: модель Хилла была преобразована в модель постоянной максимальной мощности, состоящую из трех различных компонентов мощности.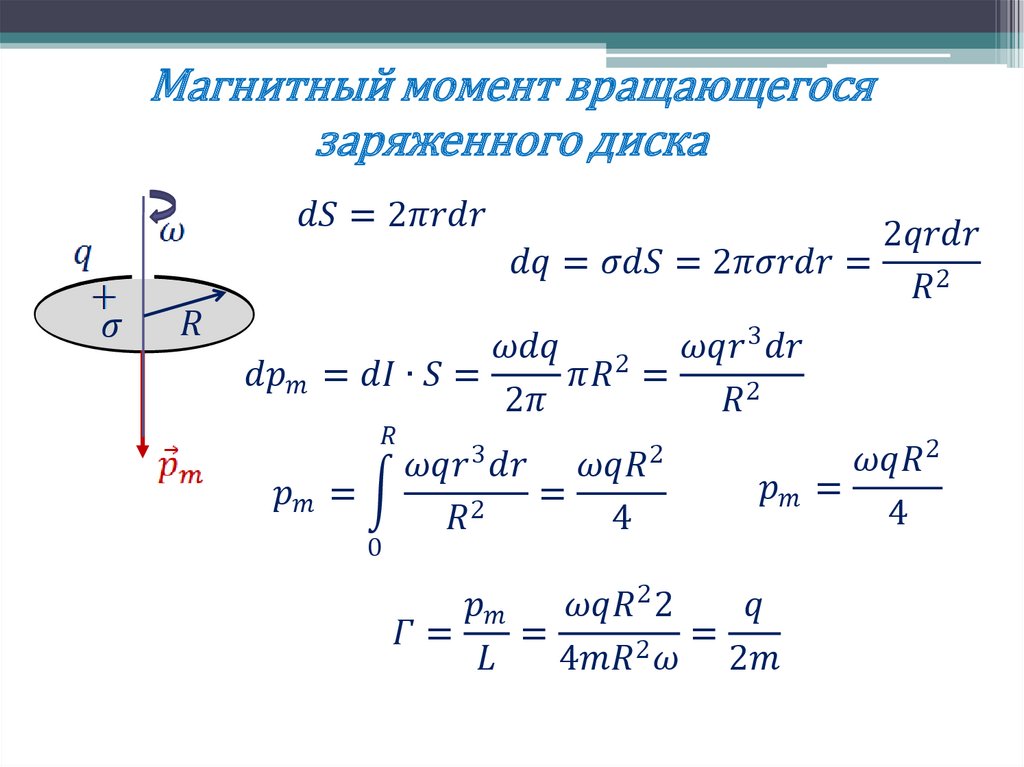 Был сделан вывод, что существуют три различных состояния движения: 1) состояние малой скорости, максимального ускорения без внешней нагрузки, что соответствует гипотезе о постоянном моменте; 2) состояние высокой скорости, максимальной мощности без внешней нагрузки, которое относится к гипотезе постоянной мощности и 3) состояние максимальной мощности с внешней нагрузкой, которое относится к уравнению Хилла. Это новый подход к уравнению Хилла.
Был сделан вывод, что существуют три различных состояния движения: 1) состояние малой скорости, максимального ускорения без внешней нагрузки, что соответствует гипотезе о постоянном моменте; 2) состояние высокой скорости, максимальной мощности без внешней нагрузки, которое относится к гипотезе постоянной мощности и 3) состояние максимальной мощности с внешней нагрузкой, которое относится к уравнению Хилла. Это новый подход к уравнению Хилла.
Ключевые слова:
Движения рук, соотношение сила-скорость, мышечная сила, уравнение Хилла
1. Введение из наиболее существенных уравнений уравнения
0285 0 — максимально возможная скорость, a и b — постоянная сила и постоянная скорость. Максимальная мощность P 0 обычно составляет около 30 % от v 0 [4]. При вращательном движении момент М соответствует силе F, а угловая скорость соответствует скорости v в уравнении Хилла.
мышечная механика, и он был объектом биомеханических исследований в течение многих лет (например, [3] — [6]). В механике мышц это соотношение часто представляется уравнением Хилла, где F — текущая мышечная сила при текущей скорости сокращения, a — постоянная сила, b — постоянная скорость, F 0 — максимальная изометрическая мышечная сила, т. е. максимальная сила, которую может развить мышца при заданной постоянной длине, а v — скорость [1] [2] . Для сравнения различных мышц b лучше всего выражается через b/l 0 , где l 0 — стандартная длина мышцы. Это уравнение было основано на лабораторных измерениях с помощью эргометра Левина-Ваймана, в котором активированная мышца расслаблялась с подходящей скоростью в состоянии изолированной мышцы. Затем полученная постоянная скорость была нанесена на график в зависимости от наблюдаемого натяжения. Сила, измеряемая скелетной мышцей при максимальном напряжении, зависит от нескольких внутренних и внешних факторов, которые были тщательно изучены (например, [3] [7] [8]). Мацумото [9] упомянул, что, поскольку почти все изотонические данные были ограничены одной длиной мышцы l 0 , максимальная длина практически без напряжения покоя и измеренные скорости являются теми начальными значениями, когда груз начинает двигаться.
В механике мышц это соотношение часто представляется уравнением Хилла, где F — текущая мышечная сила при текущей скорости сокращения, a — постоянная сила, b — постоянная скорость, F 0 — максимальная изометрическая мышечная сила, т. е. максимальная сила, которую может развить мышца при заданной постоянной длине, а v — скорость [1] [2] . Для сравнения различных мышц b лучше всего выражается через b/l 0 , где l 0 — стандартная длина мышцы. Это уравнение было основано на лабораторных измерениях с помощью эргометра Левина-Ваймана, в котором активированная мышца расслаблялась с подходящей скоростью в состоянии изолированной мышцы. Затем полученная постоянная скорость была нанесена на график в зависимости от наблюдаемого натяжения. Сила, измеряемая скелетной мышцей при максимальном напряжении, зависит от нескольких внутренних и внешних факторов, которые были тщательно изучены (например, [3] [7] [8]). Мацумото [9] упомянул, что, поскольку почти все изотонические данные были ограничены одной длиной мышцы l 0 , максимальная длина практически без напряжения покоя и измеренные скорости являются теми начальными значениями, когда груз начинает двигаться. Исследуя область длин l £ l 0 для изотонически сокращающейся мышцы, Мацумото [9] обнаружил, что константы a/F 0 и b/l 0 остаются постоянными во всем диапазоне длин, в котором происходит укорочение. происходит. В отличие от изолированных мышечных препаратов Хилла, сила (F) задействованных мышц при вращательном движении создает момент (M = r ´ F) относительно сустава. Длина плеча момента мышцы (r) изменяется по мере того, как вращательное движение происходит вокруг оси сустава. Это вращательное движение является совместным действием сил нескольких различных мышц. Однако трудно определить вклад каждой мышцы в производство силы из-за множества различных факторов, а также определить крутящий момент относительно сустава. Райкова [10] использовала несколько мышц-разгибателей и мышц-сгибателей в своей модели сгибательно-разгибательного движения в локтевом суставе. Кроме того, сила скелетной мышцы представляет собой совокупность сил, генерируемых активными двигательными единицами, принадлежащими этой мышце [11].
Исследуя область длин l £ l 0 для изотонически сокращающейся мышцы, Мацумото [9] обнаружил, что константы a/F 0 и b/l 0 остаются постоянными во всем диапазоне длин, в котором происходит укорочение. происходит. В отличие от изолированных мышечных препаратов Хилла, сила (F) задействованных мышц при вращательном движении создает момент (M = r ´ F) относительно сустава. Длина плеча момента мышцы (r) изменяется по мере того, как вращательное движение происходит вокруг оси сустава. Это вращательное движение является совместным действием сил нескольких различных мышц. Однако трудно определить вклад каждой мышцы в производство силы из-за множества различных факторов, а также определить крутящий момент относительно сустава. Райкова [10] использовала несколько мышц-разгибателей и мышц-сгибателей в своей модели сгибательно-разгибательного движения в локтевом суставе. Кроме того, сила скелетной мышцы представляет собой совокупность сил, генерируемых активными двигательными единицами, принадлежащими этой мышце [11]. Райкова и др. [12] упомянули, что доступ к каждой двигательной единице (ДЕ) невозможен, и свойства рекрутирования и развития силы всех отдельных ДЕ не могут быть известны. В данной работе [12] моделировался процесс обучения быстрому сгибанию локтевого сустава в горизонтальной плоскости и результат сравнивался с экспериментально измеренными данными.
Райкова и др. [12] упомянули, что доступ к каждой двигательной единице (ДЕ) невозможен, и свойства рекрутирования и развития силы всех отдельных ДЕ не могут быть известны. В данной работе [12] моделировался процесс обучения быстрому сгибанию локтевого сустава в горизонтальной плоскости и результат сравнивался с экспериментально измеренными данными.
Предыдущие эксперименты Rahikainen et al. [13] основывались на теории вращения руки, включающей четыре фазы: 1) начало движения; 2) фаза постоянного максимального вращательного момента; 3) фаза постоянной максимальной мышечной силы; 4) остановка движения. Предполагалось, что мышечная система способна передавать только определенное количество химической энергии за время сокращения, и поэтому вращение руки должно иметь максимальную мощность, которую нельзя превышать. Предполагалось также, что максимальная мощность действует в определенном диапазоне скоростей, которые считались постоянной максимальной мощностью, а это возможно только при достаточно высокой скорости. Скорость движения увеличивается до точки, где возникает максимальная мощность, а действующий вращающий момент меньше максимального момента. Следовательно, мощность остается постоянной при увеличении угловой скорости и уменьшении момента.
Скорость движения увеличивается до точки, где возникает максимальная мощность, а действующий вращающий момент меньше максимального момента. Следовательно, мощность остается постоянной при увеличении угловой скорости и уменьшении момента.
Настоящее исследование продолжает эксперименты Rahikainen et al. [13] и далее развивает свою теорию механики. В предыдущем исследовании была представлена модель постоянной мощности, и была оценена ее достоверность и точность результатов. В настоящем исследовании новые эксперименты по вращению рук трех испытуемых были зафиксированы с помощью двух разных систем записи. Использовались более точные расчеты моментов инерции и новое, более эффективное определение согласованного диапазона измеренных и теоретических кривых угловой скорости. Также был представлен новый подход к уравнению Хилла. В левой части уравнения Хилла постоянная a имеет размерность силы, а b размерность скорости, иначе сложение невозможно. Следовательно, (F + a) — это сила, а (v + b) — скорость, а сила, умноженная на скорость, — это мощность, как показано на рисунке 1. Член (F + a) (v + b) — это общая мощность мышц. в том числе Fv, которая представляет собой мощность перемещения внешней нагрузки. Правая часть уравнения, b (F 0 + а), включает только константы, в связи с этим уравнение можно рассматривать как модель постоянной мощности. Однако постоянная мощность уравнения Хилла, представленная в данной статье, является не упомянутой выше мощностью исходной кривой Хилла, как ее обычно считают в биомеханике, а суммой трех различных составляющих мощности (см. Обсуждение и выводы). Модель постоянной мощности в этом исследовании действует во время высокоскоростных движений без внешней нагрузки, где уравнение Хилла, кажется, не очень хорошо соответствует экспериментальным точкам ([2], стр. 32, рис. 3). В качестве объяснения этого несоответствия Хилл упомянул, что «резкий подъем в конце кривой в области очень низкого натяжения был обусловлен наличием ограниченного числа волокон с высокой собственной скоростью, и никакое такое уравнение не могло соответствовать наблюдаемым точкам ниже.
Член (F + a) (v + b) — это общая мощность мышц. в том числе Fv, которая представляет собой мощность перемещения внешней нагрузки. Правая часть уравнения, b (F 0 + а), включает только константы, в связи с этим уравнение можно рассматривать как модель постоянной мощности. Однако постоянная мощность уравнения Хилла, представленная в данной статье, является не упомянутой выше мощностью исходной кривой Хилла, как ее обычно считают в биомеханике, а суммой трех различных составляющих мощности (см. Обсуждение и выводы). Модель постоянной мощности в этом исследовании действует во время высокоскоростных движений без внешней нагрузки, где уравнение Хилла, кажется, не очень хорошо соответствует экспериментальным точкам ([2], стр. 32, рис. 3). В качестве объяснения этого несоответствия Хилл упомянул, что «резкий подъем в конце кривой в области очень низкого натяжения был обусловлен наличием ограниченного числа волокон с высокой собственной скоростью, и никакое такое уравнение не могло соответствовать наблюдаемым точкам ниже. П/П 0 = 0,05”. Настоящая модель основана на способности мышечной системы передавать химическую энергию, поэтому нет необходимости знать вклад отдельных вовлеченных мышц.
П/П 0 = 0,05”. Настоящая модель основана на способности мышечной системы передавать химическую энергию, поэтому нет необходимости знать вклад отдельных вовлеченных мышц.
Цель настоящего исследования состояла в том, чтобы изучить, как теоретическая модель постоянной мощности, которая была сначала использована в линейном движении [14], а затем применена к вращательному движению [13], согласуется с измеренными кривыми угловой скорости в экспериментах по вращению руки. Дальнейшая цель исследования состояла в том, чтобы определить, как уравнение Хилла функционирует как модель с постоянной мощностью, и сравнить уравнение Хилла с моделью настоящего исследования.
2. Материалы и методы
В настоящем исследовании измерения вращения руки (субъекты S1 и S2) были записаны с помощью специальной системы камер [15] [16]. На рис. 2 показан принцип работы системы, в которой угловая скорость вычислялась по формуле:
(1)
, где R — длина плеча, ΔS — расстояние между двумя последовательными точками измерения, а ∆T — приращение времени. Дополнительное сгибание и разгибание в локтевом суставе были выполнены для одного субъекта S3 с использованием системы анализа движения Vicon с 8 камерами. Эта система позволила использовать более высокую частоту кадров (300 Гц). Испытуемыми были нормальные здоровые люди разного возраста и уровня физической активности (S1: 62 года, 1,80 м, 82 кг; S2: 35 лет, 1,69).м, 73 кг, занятия айкидо, поднятие тяжестей и S3: 25 лет, 1,83 м, 70 кг, прыжки в высоту).
Дополнительное сгибание и разгибание в локтевом суставе были выполнены для одного субъекта S3 с использованием системы анализа движения Vicon с 8 камерами. Эта система позволила использовать более высокую частоту кадров (300 Гц). Испытуемыми были нормальные здоровые люди разного возраста и уровня физической активности (S1: 62 года, 1,80 м, 82 кг; S2: 35 лет, 1,69).м, 73 кг, занятия айкидо, поднятие тяжестей и S3: 25 лет, 1,83 м, 70 кг, прыжки в высоту).
Точность специальной системы камер описана в ссылках [13] [15] — [17] . Кривые зависимости угловой скорости от времени были нарисованы (с толщиной линии 0,5 мм) на бумаге в клетку, где 1 мм соответствовал угловой скорости 0,1 рад/с и времени 1 мс, что давало точность кривых скорости. Теоретическая и измеренная кривые угловой скорости совпадали в пределах расстояний 35 — 70 мм, что было достаточно для проверки модели постоянной мощности в экспериментах по вращению руки. Небольшие колебания в начале движения в фазе постоянной мощности отсутствовали, поэтому проверка модели постоянной мощности была возможна во всех экспериментах. Точность записывающего устройства Vicon, подтвержденная расчетом среднеквадратичной ошибки для каждой камеры, во время калибровки колебалась от 0,06 до 0,17 мм.
Точность записывающего устройства Vicon, подтвержденная расчетом среднеквадратичной ошибки для каждой камеры, во время калибровки колебалась от 0,06 до 0,17 мм.
2.1. Модель вращения руки
Модель, используемая в настоящем исследовании, построена в соответствии со II законом Ньютона и впервые была использована для линейного движения [14], а затем применена к вращательному движению [13] Rahikainen et al. Теория вращения руки такова: в начале движения угловая скорость, естественно, равна нулю, и для создания силы требуется некоторое время. В этой ранней фазе движения на движение влияют упругие свойства мышечно-сухожильного комплекса, но в состоянии полного напряжения эти упругие элементы не оказывают дальнейшего динамического влияния. После этого может быть
Рисунок 2. Пример сгибания локтя. Углы поворота между двумя изображениями рук (0-200 мс) даны с шагом 20 мс в соответствии со световыми метками. Примечательно, что сила момента мышц, участвующих в сгибании локтя, меняется в процессе движения, а, следовательно, меняется и вклад мышц в мощность.
предполагали, что действует максимальная мышечная сила, а при вращательном движении действует и максимальный вращательный момент. На этой фазе движения действует постоянная величина трения скольжения. Поскольку мышечная система способна передавать только определенное количество химической энергии во время сокращения, должна существовать постоянная максимальная мощность, которую мышца способна генерировать в определенном диапазоне скоростей. По мере увеличения скорости движение достигает точки, в которой действует максимальная мощность, а действующий вращающий момент меньше максимального момента. Таким образом, мощность остается постоянной при увеличении угловой скорости и уменьшении момента. Теперь действует жидкостное трение, прямо пропорциональное скорости. Постоянное трение скольжения уменьшается по мере уменьшения усилий в суставе и становится незначительным. Во время фазы постоянной мощности вращательный момент модели представляет собой момент инерции, умноженный на угловое ускорение, которое равно моменту, создаваемому мышечной силой, за вычетом момента, создаваемого внутренним трением мышцы. После этого добавляется эффект гравитационной силы (см. пункт 2.3). Модель вращения руки представляет собой уравнение движения:
После этого добавляется эффект гравитационной силы (см. пункт 2.3). Модель вращения руки представляет собой уравнение движения:
(2)
где
Момент инерции при вращении руки I
Угловая скорость
Мощность, создаваемая мышцами руки P
Время T
Момент, создаваемый мышечной силой
Момент, создаваемый мышечной силой
Коэффициент трения C
Внутреннее трение мышц – это жидкостное трение внутри мышцы, которое прямо пропорционально скорости. Такое же жидкостное трение использовалось в исследовании Rahikainen et al. [17], который был первоначально заимствован у Алонсо и Финна [18]. Предполагалось, что первоначально движение происходит при постоянном максимальном моменте, а затем момент, создаваемый мышечной силой (в уравнении 2), является постоянным. Также предполагалось, что по мере увеличения скорости движение происходит с постоянной максимальной мощностью в определенном диапазоне скоростей, и тогда мощность P в уравнении 2 постоянна. Чтобы определить справедливость этой гипотезы, уравнение 2 было решено для функции угловая скорость-время, и это уравнение было использовано для определения достоверности.
Чтобы определить справедливость этой гипотезы, уравнение 2 было решено для функции угловая скорость-время, и это уравнение было использовано для определения достоверности.
Решение уравнения 2 из предыдущего исследования [13] :
(3)
2.2. Расчет момента инерции
Массовое распределение секторов рук испытуемого отличалось от средних значений массовых таблиц в литературе. Поэтому массовое распределение секторов рук определялось погружением секторов рук в воду. Массы секторов рукава рассчитывались путем умножения объема перетекшей воды на плотность соответствующего сектора рукава. Измерялась длина всей руки испытуемого со сжатым кулаком, а также измерялись длины секторов руки (кисть, предплечье и плечо). По Винтеру [6] плотность секторов рук (кг/л) была следующей: кисть 1,16, предплечье 1,13, плечо 1,07.
Определение момента инерции:
(4)
где dm — вращающаяся масса, r — расстояние вращающейся массы от оси вращения. Вычисление момента инерции относительно конца сектора плеча при условии равномерного распределения масс:
(5)
где m — масса вращающегося плеча, а L — длина вращающегося плеча. Вычисление момента инерции относительно центра сектора плеча при условии равномерного распределения масс:
Вычисление момента инерции относительно центра сектора плеча при условии равномерного распределения масс:
(6)
Поскольку распределение массы в секторе плеча неравномерно, момент инерции дополнительной массы рассчитывался по формуле :
(7)
где m — дополнительная масса сектора руки, r — расчетное расстояние центра тяжести дополнительной массы от оси вращения. Расстояния, длины и массы секторов рук испытуемых представлены в таблице 1. Затем эти значения подставляются в вышеупомянутые уравнения 4-7 для расчета конечных моментов инерции вращения предплечья и всей руки вокруг локтевого и плечевого суставов (пример для S1 обобщены в таблице 2).
Момент инерции вращения предплечья
Предплечье
Момент инерции основной массы предплечья относительно локтевого сустава (m = 1,0 кг, L = 0,28 м):
Момент инерции дополнительной массы предплечья относительно локтевого сустава (m = 0,24 кг, r = 0,07 м):
Рука
Момент инерции сектора руки относительно центра масс (m = 0,58 кг, L = 0,11 м):
Момент инерции сектора руки относительно локтя соединение (m = 0,58 кг, r = 0,34 м):
Таблица 1. Расчетное массовое распределение секторов рук. Дополнительная масса предплечья обусловлена перераспределением массы мышцы на другой конец сектора руки.
Расчетное массовое распределение секторов рук. Дополнительная масса предплечья обусловлена перераспределением массы мышцы на другой конец сектора руки.
Таблица 2. Сводная информация для расчета момента инерции вращения предплечья (верхняя часть) и вращения всей руки (нижняя часть) для одного испытуемого. Момент инерции рассчитывается относительно локтевого сустава, центра масс (ЦМ) и плечевого сустава.
Аккумулятор для светового маркера
Момент инерции батареи относительно локтевого сустава (m = 0,26 кг, r = 0,37 м):
Суммарный момент инерции вращения предплечья относительно локтевого сустава
Момент инерции вращения всей руки
Плечо
Момент инерции относительно плечевого сустава (m = 2,14 кг, L = 0,30 м):
Предплечье
Момент инерции большой массы предплечья относительно центра масс (m = 1,0 кг, L = 0,28 м):
Момент инерции относительно плечевого сустава (m = 1,0 кг, r = 0,44 м):
Момент инерции дополнительной массы относительно плечевого сустава (m = 0,24 кг, r = 0,37 м):
Кисть
Момент инерции сектора кисти относительно центра масс (m = 0,58, L = 0,11 м):
Момент инерции сектора кисти относительно плечевого сустава (m = 0,58 кг, r = 0,64 м):
Батарея светового маркера
Момент инерции батареи относительно плечевого сустава (m = 0,26 кг, r = 0,67 м):
Суммарный момент инерции при вращении всей руки вокруг плечевого сустава
Согласно приведенным выше расчетам соответствующие моменты инерции вращения предплечья и вращения всей руки для S2 составили 0,110 и 0,551 кг×м 2 , соответственно. Поскольку общая длина предплечья и кисти у испытуемых S1 и S3 была одинакова, предполагалось, что моменты инерции этих сегментов также были одинаковыми и, следовательно, момент инерции вращения предплечья вокруг локтевого сустава для S3 был 0,131 кг×м 2 . Измерения с системой камер Vicon для S3 проводились с отражающими маркерами, и соответствующий момент инерции без батареи составлял 0,095 кг×м 2 .
Поскольку общая длина предплечья и кисти у испытуемых S1 и S3 была одинакова, предполагалось, что моменты инерции этих сегментов также были одинаковыми и, следовательно, момент инерции вращения предплечья вокруг локтевого сустава для S3 был 0,131 кг×м 2 . Измерения с системой камер Vicon для S3 проводились с отражающими маркерами, и соответствующий момент инерции без батареи составлял 0,095 кг×м 2 .
2.3. Влияние гравитационной силы на движение
При вращении предплечья влияние гравитационной силы незначительно по сравнению с максимальными мышечными усилиями, а момент, вызванный гравитацией, был исключен из модели движения (уравнение 2). При полном вращении плеча этот момент добавляется к механике движения следующим образом: Мощность, создаваемая этим гравитационным моментом, равна, где mg — сила тяжести сегментов плеча, r — расстояние центра тяжести сегментов от оси вращения. и угловая скорость вращения руки. Теоретическая угловая скорость (уравнение 3) и измеренная угловая скорость совпадают в очень узком диапазоне скоростей, и мощность, вызванная силой тяжести, может быть рассчитана как постоянный коэффициент. Он входит в мощность P согласно предыдущему исследованию [13] .
Он входит в мощность P согласно предыдущему исследованию [13] .
2.4. Определение согласованного диапазона измеренных и теоретических кривых угловой скорости
На рисунке 3 показана методика, которая использовалась для определения согласованного диапазона измеренных и теоретических угловых скоростей
Б) измеренной и теоретической угловой скорости. Нулевая точка времени для теоретической угловой скорости находится на пересечении оси времени и ломаной кривой (дополнительную информацию см. В тексте). Теоретическая кривая угловой скорости (пунктирная линия) совпадает с измеренной кривой (сплошная линия) между A и B.
кривые скорости. Значения коэффициента трения (C) и мощности (P) были получены путем подгонки теоретических кривых угловой скорости к измеренным. Эти две кривые совпадают только в том случае, если в процессе подбора используются определенные значения C и P. Измеренные значения угловой скорости показаны точками на кривой скорости, а теоретическая угловая скорость (уравнение 3) показана пунктирной линией. Согласованный диапазон был найден с использованием следующей итерационной процедуры: на основе предыдущих экспериментов были выбраны рандомизированные начальные значения (см. рис. 3) в пределах согласованного диапазона для угловой скорости в точке 1. Нулевая точка на оси времени для теоретического углового скорость была выбрана за 0,050 с до точки 1, что соответствует 0,060 с на временной оси рисунка. После этого наблюдалось направление процесса итерации, и после некоторой итерации конечная теоретическая угловая скорость была построена в соответствии с уравнением 3, чтобы соответствовать измеренной кривой скорости. Правильная теоретическая угловая скорость была получена с нулевой точкой на 0,073 с по оси времени. Соотношение мощности и коэффициента трения на рисунке 3 равно 9.0005
Согласованный диапазон был найден с использованием следующей итерационной процедуры: на основе предыдущих экспериментов были выбраны рандомизированные начальные значения (см. рис. 3) в пределах согласованного диапазона для угловой скорости в точке 1. Нулевая точка на оси времени для теоретического углового скорость была выбрана за 0,050 с до точки 1, что соответствует 0,060 с на временной оси рисунка. После этого наблюдалось направление процесса итерации, и после некоторой итерации конечная теоретическая угловая скорость была построена в соответствии с уравнением 3, чтобы соответствовать измеренной кривой скорости. Правильная теоретическая угловая скорость была получена с нулевой точкой на 0,073 с по оси времени. Соотношение мощности и коэффициента трения на рисунке 3 равно 9.0005
(8)
Конечная теоретическая угловая скорость получена с моментом инерции I = 0,135 кг×м 2 , значением коэффициента трения C = 2,92 кг×м 2 /с и соотношением мощности и коэффициента трения P /C = 354 1/с 2 .
3. Результаты
Эксперименты по вращению руки, зарегистрированные системой камер Рахикайнена [16], представлены на рисунках 4-7, а эксперименты с системой анализа движения Vicon на рисунке 8. Кривые теоретической угловой скорости отмечены на рисунках 4-8. пунктирными линиями и они совпадают с кривыми измеренных угловых скоростей (сплошные линии) между точками А — В, где движение происходит с постоянной мощностью. Вначале движение происходит с постоянным ускорением, затем начинает оказывать влияние жидкостное трение и непосредственно перед участком А — В (постоянная мощность) ускорение уменьшается, после чего движение, наконец, останавливается. В общем случае участки A — B имеют достаточную длину, чтобы проверить существование модели постоянной мощности. Измерения на Рисунке 8 с Испытуемым S3, выполненные системой анализа движения Vicon, не имели четкого участка постоянного ускорения в начале движения. Высокие колебания в этом сечении сделали его неопределенным. В разгибании локтя колебание слабое и в начале движения можно выделить обычный участок постоянного ускорения. Также кажется, что участок с постоянным ускорением на рис. 6 имеет такие же колебания, как и на рис. 8.
Также кажется, что участок с постоянным ускорением на рис. 6 имеет такие же колебания, как и на рис. 8.
Измеренные данные на рисунках 4-8 были сглажены путем подбора полиномиальной кривой 6 -го порядка . Используемые значения коэффициента трения варьировались от 2,8 до 3,1 кг×м 2 /с при вращении предплечья и от 3,6 до 3,8 кг×м 2 /с при
. Рисунок 4. Два разгибания локтя (субъект S1). Теоретическая кривая угловой скорости (пунктирная линия) совпадает с измеренной кривой (сплошная линия) между A и B.
Рисунок 5. Разгибание локтя (закрашенные кружки) и сгибание в локтевом суставе (незаштрихованные кружки) субъекта S1. Теоретическая кривая угловой скорости (пунктирная линия) совпадает с измеренной кривой (сплошная линия) между A и B.
Рисунок 6. Разгибание плеча (закрашенные кружки) и сгибание плеча (незаштрихованные кружки) субъекта S1. Теоретическая кривая угловой скорости (пунктирная линия) совпадает с измеренной кривой (сплошная линия) между A и B.
Рисунок 7. Разгибание плеча (закрашенные кружки) и сгибание плеча (незакрашенные кружки) субъекта S2. Теоретическая кривая угловой скорости (пунктирная линия) совпадает с измеренной кривой (сплошная линия) между A и B.
Рис. 8. Разгибание локтя (заштрихованные кружки) и сгибание в локтевом суставе (светлые кружки) субъекта S3. Теоретическая кривая угловой скорости (пунктирная линия) совпадает с измеренной кривой (сплошная линия) между А и В. Углы локтевого сустава для максимальной угловой скорости составляли 123° (разгибание) и 81° (сгибание).
полных оборота руки. Максимальные угловые скорости составляли от 13,7 рад/с (сгибание плеча) до 24,8 рад/с (разгибание локтя). Влияние соотношения мощности и коэффициента трения P/C на изменение угловой скорости ясно видно на рисунках 4-8. На рисунке 4 показаны типичные вариации последовательных испытаний одного и того же субъекта. Эффект гравитации можно увидеть на рисунках 6 и 7, поскольку разгибание плеча имеет большую угловую скорость вращения, чем сгибание плеча.
4. Обсуждение и выводы
Настоящее исследование подтвердило существование модели постоянной мощности при вращении руки с максимальной скоростью. Теоретическая и измеренная кривые угловой скорости показали небольшой диапазон совпадения, поскольку повороты руки были выполнены с максимальной скоростью, но диапазон был достаточно большим для проверки модели. Если бы существовала постоянная сила, противодействующая вращению руки, скорость движения была бы медленнее, а кривая зависимости скорости от времени вращения руки соответствовала бы теоретической кривой постоянной мощности (пунктирная линия, рис. 4-8), выравниваясь по горизонтали с течением времени. Таким образом, постоянная сила при вращении руки соответствует постоянной скорости точно так же, как сила соответствует скорости в уравнении Хилла.
После начала вращения руки движение продолжается в состоянии низкой скорости, высокого ускорения без внешней нагрузки. В этой фазе движения предполагается (гипотеза), что движение происходит при постоянном максимальном мышечном моменте. Измерения вращательных движений показывают, что движение происходит с постоянным угловым ускорением. Следовательно, мы можем заключить, что крутящий момент, ускоряющий движение, или правая часть уравнения 2, является постоянным.
Измерения вращательных движений показывают, что движение происходит с постоянным угловым ускорением. Следовательно, мы можем заключить, что крутящий момент, ускоряющий движение, или правая часть уравнения 2, является постоянным.
Крутящий момент, создаваемый максимальным мышечным моментом, является и согласно гипотезе постоянным. Момент, создаваемый силой трения, непостоянен (из-за члена скорости), и, следовательно, эта гипотеза не выполняется. Однако вывод «движение происходит с постоянным ускорением» интересен и требует более пристального изучения. В уравнении 2 предполагалось, что кинетическое трение прямо пропорционально скорости в начале движения. Это новая гипотеза, которая не обязательно верна. Возможно, что кинетическое трение при малых скоростях постоянно, а при больших прямо пропорционально скорости. Это приводит к постоянному крутящему моменту, ускоряющему движение в начале движения.
После фазы постоянного углового ускорения движение продолжается с большой скоростью и малым ускорением без внешней нагрузки. Предполагается, что в этой фазе движение происходит с постоянной максимальной мышечной силой. Эта гипотеза кажется верной между A и B на рисунках 4-8. Это самый интересный вывод настоящего исследования, и дальнейшее развитие уравнения Хилла дало еще один тип модели постоянной мощности.
Предполагается, что в этой фазе движение происходит с постоянной максимальной мышечной силой. Эта гипотеза кажется верной между A и B на рисунках 4-8. Это самый интересный вывод настоящего исследования, и дальнейшее развитие уравнения Хилла дало еще один тип модели постоянной мощности.
Окончательное решение уравнения силы-скорости Хилла
Эксперименты настоящего исследования подтвердили выводы предыдущего исследования [13], в котором теоретически полученное уравнение с постоянной максимальной мощностью согласовывалось с экспериментально измеренными результатами. Поскольку уравнение Хилла также является моделью с постоянной мощностью, в этом отношении его можно рассматривать так же, как и модель данного исследования. Соотношение сила-скорость Хилла было получено в ходе экспериментов, в которых скорость мышечного сокращения измерялась относительно некоторой постоянной силы. Эксперименты с уравнением Хилла, естественно, начинались с нулевой скорости и продолжались так же, как и эксперименты настоящего исследования, на всех этапах. Из-за внешней нагрузки опыты по уравнению Хилла имели меньшие скорости и, следовательно, можно было достичь максимальной скорости в пределах точности измерения. Измерения настоящего исследования проводились без внешней нагрузки, и ни одно из них не достигло максимальной теоретической скорости уравнения 3.
Из-за внешней нагрузки опыты по уравнению Хилла имели меньшие скорости и, следовательно, можно было достичь максимальной скорости в пределах точности измерения. Измерения настоящего исследования проводились без внешней нагрузки, и ни одно из них не достигло максимальной теоретической скорости уравнения 3.
Результаты экспериментов Хилла могут быть преобразованы в уравнение гиперболы, описывающее зависимость движения от силы и скорости. На рис. 9 представлено дальнейшее развитие зависимости Хилла «сила-скорость».
Рисунок 9. Зависимость Хилла сила-скорость представлена асимптотами (пунктирные линии). В традиционном представлении гиперболы a и b отрицательны, но здесь они относятся к положительным постоянным членам уравнения Хилла. Уравнение Хилла (F + a) (v + b) = константа означает, что площадь прямоугольника A + B + C постоянна.
Оси сила-скорость показаны, а асимптоты нарисованы ломаными линиями. Уравнение Хилла (F + a) (v + b) = константа подразумевает, что площадь прямоугольника (F + a) (v + b) постоянна. Общая мощность мышцы состоит из трех различных компонентов, представленных прямоугольниками A, B и C. Площадь прямоугольника A = F v представляет собой мощность, необходимую мышце для противодействия внешней нагрузке (см. кривую мощности на рисунке 1). При отсутствии внешней нагрузки эта мощность расходуется на ускорение. Площадь прямоугольника B = (F + a) b представляет собой мощность внутренней потери энергии мышцей. Эта мощность создает противодействие внешней нагрузке. Так как скорость равна нулю, эта мощность В является наибольшей и, следовательно, не связана с внешним движением. Затем, по мере увеличения скорости, эта мощность сначала быстро уменьшается, а затем медленно при более высоких скоростях. Площадь прямоугольника C = va представляет мощность трения из-за движения системы мышечной нагрузки. Поскольку мощность — это сила, умноженная на скорость, сила трения равна а. Это не сила, прямо пропорциональная скорости, обычно известная как жидкостное трение (которое используется в настоящем исследовании), а постоянная сила трения, известная как трение скольжения.
Общая мощность мышцы состоит из трех различных компонентов, представленных прямоугольниками A, B и C. Площадь прямоугольника A = F v представляет собой мощность, необходимую мышце для противодействия внешней нагрузке (см. кривую мощности на рисунке 1). При отсутствии внешней нагрузки эта мощность расходуется на ускорение. Площадь прямоугольника B = (F + a) b представляет собой мощность внутренней потери энергии мышцей. Эта мощность создает противодействие внешней нагрузке. Так как скорость равна нулю, эта мощность В является наибольшей и, следовательно, не связана с внешним движением. Затем, по мере увеличения скорости, эта мощность сначала быстро уменьшается, а затем медленно при более высоких скоростях. Площадь прямоугольника C = va представляет мощность трения из-за движения системы мышечной нагрузки. Поскольку мощность — это сила, умноженная на скорость, сила трения равна а. Это не сила, прямо пропорциональная скорости, обычно известная как жидкостное трение (которое используется в настоящем исследовании), а постоянная сила трения, известная как трение скольжения. Теперь мы можем видеть, что существуют три различных состояния движения: 1) в начале движения характеризуется состоянием малой скорости с максимальным ускорением без внешней нагрузки; затем 2) по мере продолжения движения состояние высокой скорости, максимальной мощности без внешней нагрузки и 3) состояние максимальной мощности с внешней нагрузкой, что соответствует уравнению Хилла. Максимальная мощность обусловлена тем, что передача энергии внутри мышечной системы должна иметь максимальную скорость и, следовательно, выработка мышечной силы также должна иметь определенную максимальную скорость. В уравнении Хилла максимальная мощность обусловлена способностью поднимать грузы, а в экспериментах настоящего исследования — высокой скоростью движения.
Теперь мы можем видеть, что существуют три различных состояния движения: 1) в начале движения характеризуется состоянием малой скорости с максимальным ускорением без внешней нагрузки; затем 2) по мере продолжения движения состояние высокой скорости, максимальной мощности без внешней нагрузки и 3) состояние максимальной мощности с внешней нагрузкой, что соответствует уравнению Хилла. Максимальная мощность обусловлена тем, что передача энергии внутри мышечной системы должна иметь максимальную скорость и, следовательно, выработка мышечной силы также должна иметь определенную максимальную скорость. В уравнении Хилла максимальная мощность обусловлена способностью поднимать грузы, а в экспериментах настоящего исследования — высокой скоростью движения.
Мышечная механика настоящего исследования основана на экспериментах, которые проводились с максимальной скоростью, поэтому фаза постоянной мощности стала короткой. Если есть постоянная сила, противодействующая движению, движение становится медленнее, и можно сделать вывод, что кривая времени-скорости выравнивается по горизонтали со скоростью, указанной в уравнении Хилла. Другой тип механики применяется, если используется меньше мышечной силы, и традиционное уравнение Хилла применяется к движениям, которым сопротивляется внешняя сила. Из результатов настоящего исследования видно, как эти состояния движения соотносятся друг с другом, и полученные данные позволяют развивать мышечную механику в этой области современной науки. Расчетные методы данного исследования могут быть применены в научных областях спорта и медицины.
Другой тип механики применяется, если используется меньше мышечной силы, и традиционное уравнение Хилла применяется к движениям, которым сопротивляется внешняя сила. Из результатов настоящего исследования видно, как эти состояния движения соотносятся друг с другом, и полученные данные позволяют развивать мышечную механику в этой области современной науки. Расчетные методы данного исследования могут быть применены в научных областях спорта и медицины.
Ссылки
- Хилл, А.В. (1938) Тепло укорочения и динамические константы мышц. Труды Королевского общества B, Лондон, 126, 136–195.
- Хилл, А.В. (1970) Первые и последние эксперименты по мышечной механике. Издательство Кембриджского университета, Кембридж.
- Герцог, В. (1999) Связь сила-скорость. В: Нигг, Б.М. и Herzog, W., Eds., Biomechanics of the Musculo-Skeletal System, John Wiley & Sons Ltd., Chichester, 173-180.
- Херцог В. (2000) Механические свойства и характеристики скелетных мышц. В: Под ред.
 Зациорского В., Биомеханика в спорте, Blackwell Science, University Press, Cambridge, 21-32.
Зациорского В., Биомеханика в спорте, Blackwell Science, University Press, Cambridge, 21-32. - Макинтош, Б.Р. и Холаш, Р.Дж. (2000) Выходная мощность и скоростные характеристики мышц. В: Нигг, Б.М., Макинтош, Б.Р. и Местер, Дж., ред., Биомеханика и биология движения. Кинетика человека, Кинетика человека, Шампейн, 193-210.
- Винтер, Д.А. (2004) Биомеханика и двигательный контроль движений человека, 3-е издание, John Wiley & Sons Inc., Hoboken, 215-222.
- Чаллис, Дж.Х. (2000) Мышечно-сухожильная архитектура и спортивные результаты. В: Под ред. Зациорского В., Биомеханика в спорте, Blackwell Science, University Press, Cambridge, 33-55.
- Рассье, Д.Э., Макинтош, Б.Р. и Herzog, W. (1999) Зависимость от длины производства активной силы в скелетных мышцах. Журнал прикладной физиологии, 86, 1445-1457.
- Matsumoto, J. (1967) Обоснованность соотношения сила-скорость для мышечного сокращения в области длины, l ≤ l 0 . Журнал общей физиологии, 50, 1125-1137.
 http://dx.doi.org/10.1085/jgp.50.5.1125
http://dx.doi.org/10.1085/jgp.50.5.1125 - Райкова Р.Т. (1996) Модель сгибательно-разгибательного движения в локтевом суставе — некоторые проблемы моделирования и расчета мышечных сил. Журнал биомеханики, 29, 763-772. http://dx.doi.org/10.1016/0021-9290(95)00072-0
- Райкова Р., Аладжов Х., Целиховски Дж. и Крутки П. (2013) Подход к моделированию Моделирование мышечной силы путем суммирования сил сокращения двигательных единиц. Вычислительно-математические методы в медицине, 2013, ID статьи: 625427.
- Райкова Р.Т., Габриэль Д.А. и Аладжов, Х.Ц. (2005) Сравнение двух моделей мышц в динамических условиях. Компьютеры в биологии и медицине, 35, 373-387.
- Рахикайнен, А., Авела, Дж. и Вирмавирта, М. (2012) Моделирование соотношения сила-скорость при движении рук. Всемирный журнал механики, 2, 90-97. http://dx.doi.org/10.4236/wjm.2012.22011
- Рахикайнен, А. и Лухтанен, П. (2004) Исследование влияния вращения тела на толчок рук в толкании ядра. Российский журнал биомеханики, 8, 78-93.



 phys.uvic.ca/~tatum/classmechs.html
phys.uvic.ca/~tatum/classmechs.html Зациорского В., Биомеханика в спорте, Blackwell Science, University Press, Cambridge, 21-32.
Зациорского В., Биомеханика в спорте, Blackwell Science, University Press, Cambridge, 21-32. http://dx.doi.org/10.1085/jgp.50.5.1125
http://dx.doi.org/10.1085/jgp.50.5.1125