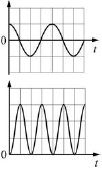
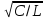Максимальная сила тока протекающая через катушку формула |

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:

где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
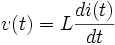
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
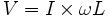
где ω является угловой частотой резонансной частоты F:
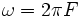
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
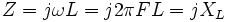
Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей
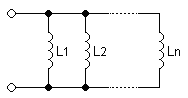
Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
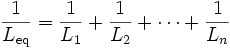
Последовательное соединение индуктивностей

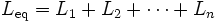
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
Добротность катушки индуктивности
На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.
Добротность катушки индуктивности может быть найдена через следующую формулу:
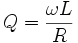
где R является собственным сопротивлением обмотки.
Катушка индуктивности. Формула индуктивности
Базовая формула индуктивности катушки:

- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
- l = длина катушки в метрах (м)
Индуктивность прямого проводника:
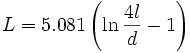
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
Индуктивность катушки с воздушным сердечником:
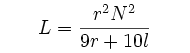
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
Индуктивность многослойной катушки с воздушным сердечником:

- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
Индуктивность плоской катушки:

- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.

Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
в Справочник 0 1,137 Просмотров
Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Индуктивность (измеряется в Генри) — это эффект возникновения магнитного поля вокруг проводника с током. Ток, протекающий через катушку индуктивности, создает магнитное поле, которое имеет связь с электродвижущей силой (ЭДС) оказывающее противодействие приложенному напряжению.

Возникающая противодействующая сила (ЭДС) противостоит изменению переменного напряжения и силе тока в катушке индуктивности. Это свойство индуктивной катушки называется индуктивным сопротивлением. Следует отметить, что индуктивное сопротивление находится в противофазе к емкостному реактивному сопротивлению конденсатора в цепи переменного тока. Путем увеличения числа витков можно повысить индуктивность самой катушки.
Накопленная энергия в индуктивности
Как известно магнитное поле обладает энергией. Аналогично тому, как в полностью заряженном конденсаторе существует запас электрической энергии, в индуктивной катушке, по обмотке которой течет ток, тоже существует запас — только уже магнитной энергии.
Энергия, запасенная в катушке индуктивности равна затраченной энергии необходимой для обеспечения протекания тока I в противодействии ЭДС. Величина запасенной энергии в индуктивности можно рассчитать по следующей формуле:

где L — индуктивность, I — ток, протекающий через катушку индуктивности.
Гидравлическая модель
Работу катушки индуктивности можно сравнить с работой гидротурбины в потоке воды. Поток воды, направленный сквозь еще не раскрученную турбину, будет ощущать сопротивление до того момента, пока турбина полностью не раскрутится.
Далее турбина, имеющая определенную степень инерции, вращаясь в равномерном потоке, практически не оказывая влияния на скорость течения воды. В случае же если данный поток резко остановить, то турбина по инерции все еще будет вращаться, создавая движение воды. И чем выше инерция данной турбины, тем больше она будет оказывать сопротивление изменению потока.
Также и индуктивная катушка сопротивляется изменению электрического тока протекающего через неё.
Индуктивность в электрических цепях
В то время как конденсатор оказывает сопротивление изменению переменного напряжения, индуктивность же сопротивляется переменному тока. Идеальная индуктивность не будет оказывать сопротивление постоянному току, однако, в реальности все индуктивные катушки сами по себе обладают определенным сопротивлением.
В целом, отношение между изменяющимися во времени напряжением V(t) проходящим через катушку с индуктивностью L и изменяющимся во времени током I(t), проходящим через нее можно представить в виде дифференциального уравнения следующего вида:
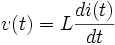
Когда переменный синусоидальной ток (АС) протекает через катушку индуктивности, возникает синусоидальное переменное напряжение (ЭДС). Амплитуда ЭДС зависит от амплитуды тока и частоте синусоиды, которую можно выразить следующим уравнением:
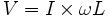
где ω является угловой частотой резонансной частоты F:
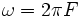
Причем, фаза тока отстает от напряжения на 90 градусов. В конденсаторе же все наоборот, там ток опережает напряжение на 90 градусов. Когда индуктивная катушка соединена с конденсатором (последовательно либо параллельно), то образуется LC цепь, работающая на определенной резонансной частоте.
Индуктивное сопротивление ХL определяется по формуле:

где ХL — индуктивное сопротивление, ω — угловая частота, F — частота в герцах, и L индуктивность в генри.
Индуктивное сопротивление — это положительная составляющая импеданса. Оно измеряется в омах. Импеданс катушки индуктивности (индуктивное сопротивление) вычисляется по формуле:
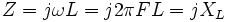
Схемы соединения катушек индуктивностей
Параллельное соединение индуктивностей

Напряжение на каждой из катушек индуктивностей, соединенных параллельно, одинаково. Эквивалентную (общую) индуктивность параллельно соединенных катушек можно определить по формуле:
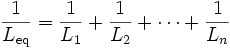
Последовательное соединение индуктивностей

Ток, протекающий через катушки индуктивности соединенных последовательно, одинаков, но напряжение на каждой катушке индуктивности отличается. Сумма разностей потенциалов (напряжений) равна общему напряжению. Общая индуктивность последовательно соединенных катушек можно высчитать по формуле:
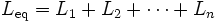
Эти уравнения справедливы при условии, что магнитное поле каждой из катушек не оказывает влияние на соседние катушки.
Добротность катушки индуктивности
На практике катушка индуктивности имеет последовательное сопротивление, созданное медной обмоткой самой катушки. Это последовательное сопротивление преобразует протекающий через катушку электрический ток в тепло, что приводит к потере качества индукции, то есть добротности. Добротность является отношением индуктивности к сопротивлению.
Добротность катушки индуктивности может быть найдена через следующую формулу:
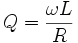
где R является собственным сопротивлением обмотки.
Катушка индуктивности. Формула индуктивности
Базовая формула индуктивности катушки:

- L = индуктивность в генри
- μ 0 = проницаемость свободного пространства = 4π × 10 -7 Гн / м
- μ г = относительная проницаемость материала сердечника
- N = число витков
- A = Площадь поперечного сечения катушки в квадратных метрах (м 2 )
- l = длина катушки в метрах (м)
Индуктивность прямого проводника:
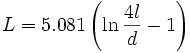
- L = индуктивность в нГн
- l = длина проводника
- d = диаметр проводника в тех же единицах, что и l
Индуктивность катушки с воздушным сердечником:
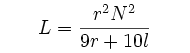
- L = индуктивность в мкГн
- r = внешний радиус катушки
- l = длина катушки
- N = число витков
Индуктивность многослойной катушки с воздушным сердечником:

- L = индуктивность в мкГн
- r = средний радиус катушки
- l = длина катушки
- N = число витков
- d = глубина катушки
Индуктивность плоской катушки:

- L = индуктивность в мкГн
- r = средний радиус катушки
- N = число витков
- d = глубина катушки
Конструкция катушки индуктивности
Катушка индуктивности представляет собой обмотку из проводящего материала, как правило, медной проволоки, намотанной вокруг либо железосодержащего сердечника, либо вообще без сердечника.
Применение в качестве сердечника материалов с высокой магнитной проницаемостью, более высокой чем воздух, способствует удержанию магнитного поля вблизи катушки, тем самым увеличивая ее индуктивность. Индуктивные катушки бывают разных форм и размеров.
Большинство изготавливаются путем намотки эмалированного медного провода поверх ферритового сердечника.

Некоторые индуктивные катушки имеют регулируемый сердечник, при помощи которого обеспечивается изменение индуктивности.
Миниатюрные катушки могут быть вытравлены непосредственно на печатной плате в виде спирали. Индуктивности с малым значением могут быть расположены в микросхемах с использованием тех же технологических процессов, которые используются при создании транзисторов.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.

По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
«>
Максимальная сила тока протекающего через катушку формула |
Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
2018-04-07
В электрической цепи, схема которой показана на рисунке, все резисторы одинаковые, и сопротивление каждого из них равно $R$. Цепь очень давно подключена к источнику переменного напряжения $U(t) = U_ <0>cos omega t$. ?мкость $C$ конденсатора и индуктивность $L$ катушки подобраны таким образом, что выполняется соотношение: $omega L = 1/( omega C)$.
1) Найдите максимальное напряжение на конденсаторе.
2) Найдите максимальную силу тока, протекающего через катушку.
3) Ключ К замыкают в момент, когда ток через катушку не течёт. Найдите количество теплоты, которое выделится в каждом из резисторов, расположенных на рисунке справа от ключа К, после его замыкания.
4) Как изменятся ответы для количеств теплоты, выделившихся в тех же резисторах, если ключ размыкают в момент, когда ток через катушку максимален?
5) Как изменятся ответы на вопросы 1), 2), 3) и 4), если катушка и конденсатор будут подключены к тем же точкам А и В не параллельно друг другу, а последовательно друг за другом?
Поскольку в условии сказано, что цепь была подключена к источнику переменного напряжения давно, то это означает, что все переходные процессы в такой цепи давно прекратились. Для переменного тока параллельно соединенные конденсатор и катушка с выбранными значениями параметров $C$ и $L$ представляют собой бесконечно большое сопротивление (в любой момент времени сумма сил токов, текущих через конденсатор и катушку равна нулю, поскольку импедансы этих элементов цепи одинаковы, а токи через них текут в протифофазе). Поэтому до замыкания ключа ток во всех семи резисторах одинаковый и равен $I(t) = U_ <0>cos( omega t)/(7R)$. Напряжение на конденсаторе и на катушке в любой момент времени также одинаковое, оно равно $4U_ <0>cos( omega t)/7$. Амплитуда этого переменного напряжения и есть максимальное напряжение на конденсаторе, то есть $U_ = 4U_<0>/7$. Амплитуда тока, текущего через катушку, равна
Как уже говорилось, равные по модулю токи текут через конденсатор и через катушку в противофазе, в результате чего ток, протекающий по проводникам, соединяющим $L-C$ контур с узлами А и В, равен нулю. В колебательном контуре запасена электрическая энергия, равная $CU^<2>_/2$, или $LI_^<2>/2$, или $8C(U_<0>)^<2>/49$, которая после замыкания ключа превратится в теплоту, выделившуюся в резисторах, расположенных справа от ключа.
Она распределится между пятью резисторами, которые находятся правее ключа. Из этой энергии 4/5 доли выделится в резисторе, расположенном между ключом и конденсатором, то есть $W_ <1>= 32CU_<0>^<2>/245$. В каждом из четырех оставшихся резисторов выделится четвертая часть от 1/5 доли энергии конденсатора, то есть 1/20 часть от упомянутой энергии: $W_ <2>= 2CU_<0>^ <2>/ 245$.
От момента замыкания ключа теплота, выделившаяся в каждом из пяти резисторов, никак не зависит.
Если конденсатор и катушка будут подключены не параллельно, а последовательно друг за другом, то в этом случае для переменного тока такой колебательный контур представляет собой «короткое замыкание», то есть сопротивление на участке А — В равно нулю. В этом случае максимальный ток через катушку (и через конденсатор тоже) равен $U_<0>/(3R)$. Максимальная амплитуда напряжения на конденсаторе равна
В колебательном контуре до замыкания ключа была запасена энергия: $LU_<0>^<2>/(18R^<2>)$.
Эта энергия после замыкания ключа превратится в теплоту, которая выделится в тех же пяти резисторах, расположенных на рисунке справа от ключа, в такой же пропорции, как и для параллельного соединения конденсатора и катушки. То есть в резисторе, расположенном на рисунке между ключом и колебательным контуром, выделится 4/5 от запасенной в контуре энергии, то есть: $2LU_<0>^<2>/(45R^<2>)$, а в каждом из оставшихся четырех резисторов выделится по 1/20 от запаса энергии в контуре, то есть по $LU_<0>^<2>/(360R^<2>)$.
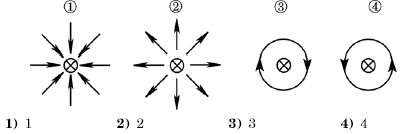
1. На каком из рисунков правильно изображены линии магнитной индукции для тонкого очень длинного прямого провода, по которому течет постоянный ток, направленный перпендикулярно плоскости рисунка «от нас» ?
Ответ__________ |
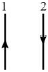
2. На рисунке изображены два длинных тонких прямых провода, по которым течет постоянный электрический ток. Направление протекания тока показано стрелками. Как направлена сила Ампера, действующая на проводник 2? ( вправо, влево, к наблюдателю, от наблюдателя) Ответ_________________ |
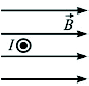
3. Прямой проводник с током I с силой находится в однородном магнитном поле с индукцией B (см. рисунок). Каково направление силы Ампера, действующей на этот проводник? (вправо, влево, вверх вниз) Ответ____________________
|
4.Прямолинейный проводник длиной L, по которому течет ток I, помещен в однородное магнитное поле перпендикулярно линиям индукции Ответ______________________________ |
Ответ_________________________ |
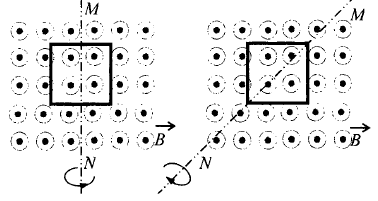
6. На рисунке показаны два способа вращения проволочной рамки в однородном магнитном поле, линии индукции которого перпендикулярны плоскости чертежа. Вращение происходит вокруг оси МN.Ток в рамке 1)существует в обоих случаях 2)не существует ни в одном из случаев 3)существует только в первом случае 4)существует только во втором случае. Ответ__________ |
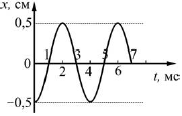
7. На рисунке изображен график зависимости координаты x тела, совершающего гармонические колебания, от времени t. Определите частоту этих колебаний. Ответ _____________ Гц. |
8.В колебательном контуре зависимость силы тока I в катушке индуктивности от времени t имеет вид I=0,01Cos(106 π t), где все величины выражены в СИ. Период колебаний силы тока в этом колебательном контуре равен Ответ ________мк с. |
9.Сила тока, протекающего через катушку индуктивностью 0,08 Гн, равномерно убывает на 0,4 А за каждую секунду. Чему равна по модулю ЭДС самоиндукции, возникающая в катушке? Ответ _________________ В. |
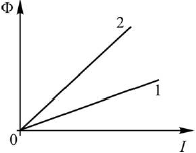
10. На графике показаны зависимости магнитного потока Ф, пронизывающего катушку, от силы тока I для катушек 1 и 2. У какой из катушек больше индуктивность? 1) У катушки 1 2) У катушки 2 3) Индуктивности катушек одинаковы 4) Однозначно ответить нельзя Ответ__________ |
11. Какие из перечисленных колебательных процессов нельзя отнести к электромагнитным колебаниям? 1) Колебания заряда конденсатора в контуре, состоящем из конденсатора и катушки индуктивности. 2) Колебания силы тока в контуре, состоящем из конденсатора и катушки индуктивности. 3) Колебания груза на пружине в постоянном магнитном поле. 4) Ни один из описанных выше колебательных процессов. Ответ__________ |
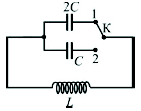
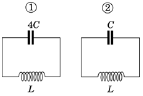
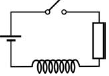
12. Как и во сколько раз изменится частота собственных электромагнитных колебаний в изображенном на рисунке контуре, если перевести ключ из положения 1 в положение 2? Ответ_____________________ |
13.На рисунке изображены схемы двух электрических колебательных контуров. Отношение частоты собственных колебаний в первом контуре к частоте собственных колебаний во втором контуре равно Ответ______________ |
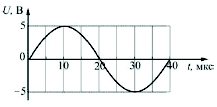
14. Напряжение U между обкладками конденсатора в колебательном контуре изменяется со временем t согласно зависимости, изображенной на рисунке. Сила тока (по модулю) в этом контуре увеличивается от нулевого до максимального значения в интервале времени 1) от 10 мкс до 30 мкс 2) от 10 мкс до 20 мкс и от 30 мкс до 40 мкс 3) от 20 мкс до 40 мкс 4) от 0 мкс до 10 мкс и от 20 мкс до 30 мкс Ответ__________ |
15. При вращении проводящей рамки в магнитном поле в ней 1) протекает переменный электрический ток 2) протекает постоянный электрический ток 3) происходит разделение электрических зарядов и возникает постоянное электрическое поле 4) ничего не происходит Ответ__________ |
16.
А Б Ответ |
17. В электрической цепи, схема которой изображена на рисунке, замыкают ключ. Как изменяются после замыкания ключа следующие физические величины: сила тока в цепи, энергия магнитного поля катушки, модуль действующей в катушке ЭДС самоиндукции? Для каждой величины определите соответствующий характер изменения: Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться. Физические величины . Их изменение. А) Сила тока в цепи 1)увеличивается Б) Энергия магнитного поля катушки. 2)уменьшается В)Выделяющаяся на резисторе тепловая мощность. 3)не изменяется. А Б В Ответ |
18. Колебательный контур состоит из конденсатора емкостью C и катушки индуктивностью L. При электромагнитных колебаниях, происходящих в этом контуре, максимальное напряжение на конденсаторе равно U. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами. ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ ФОРМУЛЫ А) энергия, запасенная в колебательном контуре 1) CU 2/2 2) U 2/2L Б) максимальная сила тока, протекающего через 3) UL/ C катушку 4) U Ответ: А Б
|
19.Груз пружинного маятника отклоняют на небольшое расстояние вертикально вниз от положения равновесия и отпускают. Принимая за начало колебаний (t = 0) момент времени, в который груз отпускают, установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами. ГРАФИКИ ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
А) 1) координата груза 2) скорость груза 3) кинетическая энергия груза 4) потенциальная энергия пружины Б) Ответ: А Б
|
20. В однородном горизонтальном магнитном поле с индукцией 0,01 Тл находится прямолинейный проводник, расположенный в горизонтальной плоскости перпендикулярно линиям индукции поля. Какой ток следует пропустить по проводнику, чтобы сила Ампера уравновесила силу тяжести? Масса единицы длины проводника 0,01 кг/м. Ответ ______________ А. |
Подготовка к ЕГЭ по физике (№18)
№1. По участку цепи постоянного тока с сопротивлением R течёт ток I. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) мощность тока, выделяющаяся на резисторе
Б) напряжение на резисторе
ФОРМУЛЫ
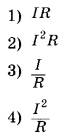
№2. К выводам резистора с сопротивлением R приложено напряжение U. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) сила тока, протекающего через резистор
Б) мощность тока, выделяющаяся на резисторе
ФОРМУЛЫ
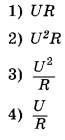
№3. Установите соответствие между формулами для расчёта физических величин в цепях постоянного тока и названиями этих величин. В формулах использованы обозначения: R — сопротивление резистора; I — сила тока; U — напряжение на резисторе. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ФОРМУЛЫ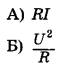
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) напряжение на резисторе
2) сила тока
3) мощность электрического тока
4) работа электрического тока
№4. Установите соответствие между формулами для расчёта физических величин в цепях постоянного тока и названиями этих величин. В формулах использованы обозначения: R — сопротивление резистора; I — сила тока; U — напряжение на резисторе.
ФОРМУЛЫ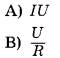
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) напряжение на резисторе
2) сила тока
3) мощность электрического тока
4) работа электрического тока
№5. Конденсатор колебательного контура длительное время подключён к источнику постоянного напряжения (см. рисунок). В момент времени t = 0 переключатель К переводят из положения 1 в положение 2. Приведённые ниже графики А и Б представляют изменения физических величин, характеризующих колебания в контуре после этого (Т — период электромагнитных колебаний в контуре).
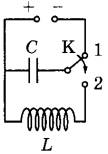
Установите соответствие между графиками и физическими величинами, зависимости которых от времени эти графики могут представлять.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ГРАФИКИ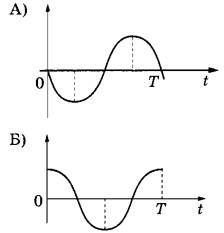
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) сила тока в катушке
2) энергия магнитного поля катушки
3) энергия электрического поля конденсатора
4) заряд на левой обкладке конденсатора
№6. От точечного источника света S, находящегося на главной оптической оси тонкой собирающей линзы с фокусным расстоянием F на расстоянии 1,5.F от неё, распространяются два луча: a и b, как показано на рисунке.
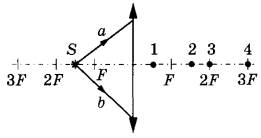
В какой точке: 1, 2, 3 или 4 — пересекутся эти лучи после преломления линзой?
№7. Заряженная частица массой m, несущая положительный заряд q, движется перпендикулярно линиям индукции однородного магнитного поля B по окружности со скоростью v. Действием силы тяжести пренебречь.
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) модуль силы Лоренца, действующей на частицу
Б) период обращения частицы по окружности
ФОРМУЛЫ
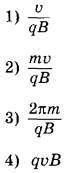
№8. Заряженная частица массой m, несущая положительный заряд q, движется со скоростью v по окружности радиусом R перпендикулярно линиям индукции однородного магнитного поля. Действием силы тяжести пренебречь. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) модуль силы Лоренца, действующей на частицу
Б) индукция магнитного поля
ФОРМУЛЫ
№9. На неподвижном проводящем уединённом шарике радиусом R находится заряд Q. Точка О — центр шарика, OA = 3R/4, ОВ = 3R, ОС = 3R/2. Модуль напряжённости электростатического поля заряда Q в точке С равен Ес. Чему равен модуль напряжённости электростатического поля заряда Q в точке А и точке В?
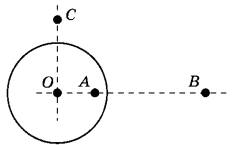
Установите соответствие между физическими величинами и их значениями.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) модуль напряжённости электростатического поля шарика в точке А
Б) модуль напряжённости электростатического поля шарика в точке В
ИХ ЗНАЧЕНИЯ
№10. На неподвижном проводящем уединённом конусе высотой Н и радиусом основания R = H/2 находится заряд Q. Точка О — центр основания конуса, OA = ОС = 2R, OB = R, угол АОС прямой, отрезки OA и ОС лежат в плоскости основания конуса. Модуль напряжённости электростатического поля заряда Q в точке С равен Ес. Чему равен модуль напряжённости электростатического поля заряда Q в точке А и точке В?
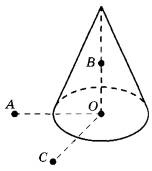
Установите соответствие между физическими величинами и их значениями.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) модуль напряжённости электростатического поля конуса в точке А
Б) модуль напряжённости электростатического поля конуса в точке В
ИХ ЗНАЧЕНИЯ
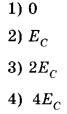
№11. В первой экспериментальной установке отрицательно заряженная частица влетает в однородное магнитное поле так, что вектор скорости v0 перпендикулярен индукции магнитного поля (рис. 1). Во второй экспериментальной установке вектор скорости v0 такой же частицы параллелен напряжённости электрического поля (рис. 2). Установите соответствие между экспериментальными установками и траекториями движения частиц в них.
А) в первой установке
Б) во второй установке
ТРАЕКТОРИЯ
1) прямая линия
2) окружность
3) спираль
4) парабола
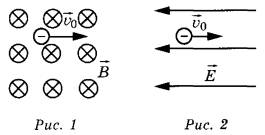
№12. В первой экспериментальной установке положительно заряженная частица влетает в однородное магнитное поле так, что вектор v0 перпендикулярен индукции магнитного поля (рис. 1). Во второй экспериментальной установке вектор v0 той же частицы параллелен напряжённости электрического поля (рис. 2).
Установите соответствие между экспериментальной установкой и траекторией движения частицы в ней.
ДВИЖЕНИЕ ЧАСТИЦЫА) в первой установке
Б) во второй установке
ТРАЕКТОРИЯ
1) спираль
2) прямая линия
3) окружность
4) парабола
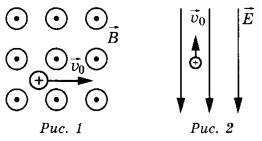
№13. Пучок монохроматического света переходит из воды в воздух. Частота световой волны — v, длина световой волны в воде — λ, показатель преломления воды относительно воздуха — n.
Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) скорость света в воздухе
Б) длина световой волны в воздухе
ФОРМУЛЫ
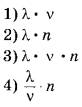
№14. Пучок монохроматического света переходит из воздуха в воду. Скорость света в воздухе c, длина световой волны в воздухе — λ, показатель преломления воды относительно воздуха — n. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) длина световой волны в воде
Б) частота световой волны в воде
ФОРМУЛЫ
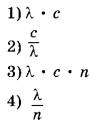
№15. Колебательный контур состоит из конденсатора ёмкостью C и катушки индуктивностью L. При свободных электромагнитных колебаниях, происходящих в этом контуре, максимальный заряд пластины конденсатора равен q. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами. Сопротивлением контура пренебречь.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) максимальная энергия электрического поля конденсатора
Б) максимальная сила тока, протекающего через катушку
ФОРМУЛЫ
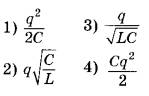
№16. Установите соответствие между формулами для вычисления физических величин в схемах постоянного тока и названиями этих величин. В формулах использованы обозначения: I — сила тока; U — напряжение; R — сопротивление резистора.
ФОРМУЛЫА) 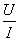
Б) 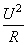
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) заряд, протёкший через резистор
2) сила тока через резистор
3) мощность тока, выделяющаяся на резисторе
4) сопротивление резистора
№17. В опыте нить накала лампочки расположена вблизи главной оптической оси тонкой линзы с фокусным расстоянием F перпендикулярно этой оси. Расстояние 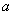 от линзы до спирали равно 2F. Сначала в опыте использовали рассеивающую линзу, а затем — собирающую. Установите соответствие между видом линзы, использовавшейся в опыте, и свойствами изображения. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
от линзы до спирали равно 2F. Сначала в опыте использовали рассеивающую линзу, а затем — собирающую. Установите соответствие между видом линзы, использовавшейся в опыте, и свойствами изображения. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
А) линза рассеивающая
Б) линза собирающая
СВОЙСТВА ИЗОБРАЖЕНИЯ
1) действительное, перевёрнутое, равное по размерам
2) мнимое, прямое, уменьшенное
3) действительное, увеличенное, перевёрнутое
4) мнимое, увеличенное, перевёрнутое
№18. В опыте нить накала лампочки расположена вблизи главной оптической оси тонкой линзы с фокусным расстоянием F перпендикулярно этой оси. Расстояние a от линзы до спирали равно 3F. Сначала в опыте использовали собирающую линзу, а затем — рассеивающую. Установите соответствие между видом линзы, использовавшейся в опыте, и свойствами изображения. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ВИД ЛИНЗЫА) линза собирающая
Б) линза рассеивающая
СВОЙСТВА ИЗОБРАЖЕНИЯ
1) действительное, увеличенное, перевёрнутое
2) мнимое, прямое, уменьшенное
3) действительное, уменьшенное, перевёрнутое
4) мнимое, увеличенное, перевёрнутое
№19. На рисунке показана цепь постоянного тока. Сопротивления обоих резисторов одинаковы и равны R. Внутренним сопротивлением источника тока можно пренебречь. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать (E — ЭДС источника тока). К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
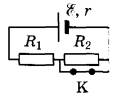
А) тепловая мощность на резисторе R1 при замкнутом ключе К
Б) тепловая мощность на резисторе R1 при разомкнутом ключе К
ФОРМУЛЫ
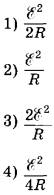
№20. Колебательный контур состоит из конденсатора ёмкостью C и катушки индуктивностью L. При свободных электромагнитных колебаниях, происходящих в этом контуре, максимальная сила тока, протекающего через катушку индуктивности, равна I. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами. Сопротивлением контура пренебречь.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) максимальная энергия магнитного поля катушки индуктивности
Б) максимальный заряд конденсатора
ФОРМУЛЫ
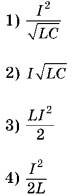
№21.Установите соответствие между физическими величинами и их единицами измерения в системе СИ.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) Ёмкость конденсатора
Б) Сопротивление резистора
ЕДИНИЦЫ ИЗМЕРЕНИЯ
1) 1 Ф
2) 1 Ом
3) 1 Гн
4) 1 Тл
№22. Установите соответствие между физическими величинами и их единицами измерения в системе СИ.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) Магнитный поток
Б) Потенциал электростатического поля
ЕДИНИЦЫ ИЗМЕРЕНИЯ
1) 1 Тл
2) 1 В
3) 1 В/м
4) 1 Вб
№23.Зависимость силы тока от времени в идеальном колебательном контуре описывается выражением 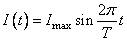 , где Т — период колебаний. В момент
, где Т — период колебаний. В момент 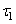 энергия катушки с током равна энергии конденсатора:
энергия катушки с током равна энергии конденсатора: 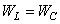 , — а напряжение на конденсаторе равно U. Каковы напряжение на конденсаторе в момент
, — а напряжение на конденсаторе равно U. Каковы напряжение на конденсаторе в момент 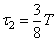 и амплитуда напряжения на конденсаторе?
и амплитуда напряжения на конденсаторе?
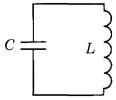
А) напряжение на конденсаторе в момент 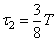
Б) амплитуда напряжения на конденсаторе
ФОРМУЛЫ ДЛЯ ИХ ВЫЧИСЛЕНИЯ
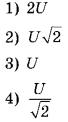
№24. Зависимость силы тока от времени в идеальном колебательном контуре описывается выражением 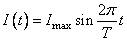 , где Т — период колебаний. В момент
, где Т — период колебаний. В момент 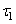 энергия катушки с током равна энергии конденсатора:
энергия катушки с током равна энергии конденсатора: 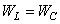 , — а сила тока в контуре равна I. Каковы заряд конденсатора в момент
, — а сила тока в контуре равна I. Каковы заряд конденсатора в момент 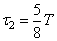 и амплитуда заряда конденсатора?
и амплитуда заряда конденсатора?

А) заряд конденсатора в момент 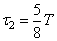
Б) амплитуда заряда конденсатора
ФОРМУЛЫ ДЛЯ ИХ ВЫЧИСЛЕНИЯ
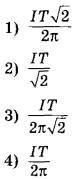
№25. При подключении проводника к полюсам гальванического элемента на поверхности проводника появляются заряды: положительные вблизи положительного полюса, отрицательные вблизи отрицательного полюса — и возникает электрический ток. Заряды на поверхности проводника создают в пространстве электрическое поле, а ток — магнитное поле. Проводник, подключённый к гальваническому элементу, проходит через отверстие в доске. На рисунках 1-4 при помощи линий поля изображены электрическое и магнитное поля, создаваемые проводником в плоскости доски (вид сверху). Установите соответствие между видами поля и рисунками, изображающими линии поля.
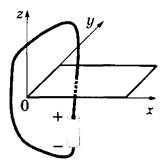
А) электрическое поле
Б) магнитное поле
ИЗОБРАЖЕНИЯ ЛИНИЙ ПОЛЯ
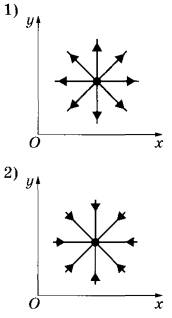
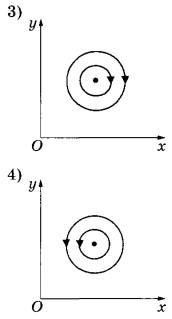
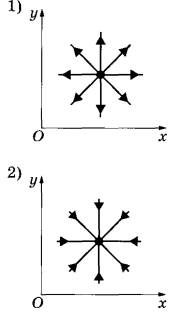
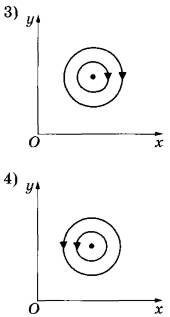
№26. При подключении проводника к полюсам гальванического элемента на поверхности проводника появляются заряды: положительные вблизи положительного полюса, отрицательные вблизи отрицательного полюса — и возникает электрический ток. Заряды на поверхности проводника создают в пространстве электрическое поле, а ток — магнитное поле. Проводник, подключённый к гальваническому элементу, проходит через отверстие в доске. На рисунках 1-4 при помощи линий поля изображены электрическое и магнитное поля, создаваемые проводником в плоскости доски (вид сверху). Установите соответствие между видами поля и рисунками, изображающими линии поля.
А) электрическое поле
Б) магнитное поле
ИЗОБРАЖЕНИЯ ЛИНИЙ ПОЛЯ
№27. На рисунке показан ход луча света через стеклянную призму, находящуюся в воздухе. Точка О — центр окружности.
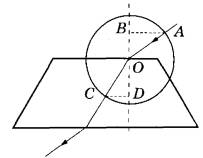
Установите соответствие между физическими величинами и формулами, выражающими их в рассматриваемой задаче.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) показатель преломления стекла n
Б) синус угла преломления в точке О
ФОРМУЛЫ

№28 . На рисунке показан ход луча света через стеклянную призму, находящуюся в воздухе. Точка О — центр окружности.
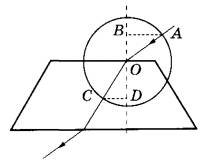
Установите соответствие между формулами и физическими величинами, которые они выражают в рассматриваемой задаче.
ФОРМУЛЫ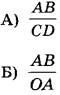
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
1) синус угла падения в точке О
2) синус угла преломления в точке О
3) показатель преломления воздуха
4) показатель преломления стекла
№29 Колебательный контур состоит из катушки индуктивностью L и конденсатора ёмкостью С. В процессе свободных электромагнитных колебаний, происходящих в этом контуре, максимальный заряд пластины конденсатора равен q. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) максимальная энергия электрического поля конденсатора
Б) максимальная сила тока, протекающего через катушку
ФОРМУЛЫ
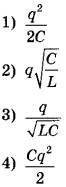
№30. Колебательный контур состоит из катушки индуктивностью L и конденсатора ёмкостью С. В процессе свободных электромагнитных колебаний, происходящих в этом контуре, максимальная сила тока в катушке индуктивности равна I. Установите соответствие между физическими величинами и формулами, по которым их можно рассчитать.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫА) максимальная энергия магнитного поля катушки индуктивности
Б) максимальный заряд на обкладке конденсатора
ФОРМУЛЫ
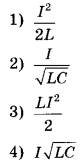
Катушка индуктивности
Катушка индуктивности, как показано на рис. 4.11, представляет собой простомоток провода. Условное обозначение катушки индуктивности показано на рис. 4.12. В отличие от конденсатора, который препятствует изменению приложенного к нему напряжения, катушка индуктивности препятствует изменению протекающего через нее тока. Иными словами,

Рис. 4.12. Условное обозначение катушки индуктивности. Рис. 4.13
если ток, подаваемый в схему, которая содержит катушку, резко увеличить, то ток в схеме будет нарастать плавно до достижения своего максимального значения.
Способность катушки индуктивности препятствовать изменению силы тока, протекающего через нее, носит название индуктивности этой катушки. Индуктивность обозначается буквой L, единицей ее измерения является генри (Гн).
Постоянная времени RС-цепи
На рис. 4.13 последовательная цепочка из конденсатора и резистора соединяется через ключ с источником питания. Когда ключ находится в положении 1, конденсатор постепенно заряжается через сопротивление, пока напряжение на нем не достигнет уровня Е т. е. ЭДС или напряжения источника питания.
Процесс заряда конденсатора показан на рис. 4.14(а) экспоненциальной кривой. Время, за которое напряжение на конденсаторе достигает значения 0,63 от максимума, т. е. в данном случае 0,63Е, называется постоянной времени контура или цепи.
Вернемся к рис. 4.13. Если ключ установить в положение 2, конденсатор будет сохранять запасенную энергию. При переведении ключа в положение3 конденсатор начинает разряжаться на землю через резистор R, и напряжение на нем постепенно падает до нуля. Процесс разряда конденсаторапоказан на рис. 4.14(б). В этом случае постоянной времени цепи называется время, за которое напряжение на конденсаторе уменьшается 0,63 от своего максимального значения.

Рис. 4.14. Кривые заряда (а) и разряда (б) конденсатора, где t — постоянная времени.
Как для случая заряда, так и для случая разряда конденсатора через резистор R постоянная времени цепи выражается формулой
где t — постоянная времени в секундах, С — емкость в фарадах, R — сопротивление, выраженное в омах.
Например, для случая С = 10мкФ и R= 10 кОм постоянная времени цепи равна
На рис. 4.15 изображены графики процессов заряда для цепей с малой и с большой постоянной времени.

Рис. 4.15. Процессы заряда для цепей с малой и с большой постоянной времени.
Постоянная времени RL-цепи
Рассмотрим схему, изображенную на рис. 4.16. Катушка индуктивности L соединена последовательно с резистором R, имеющим сопротивление 1 кОм. В момент замыкания ключа S ток в цепи равен нулю, хотя под действиемЭДС источника он, казалось бы, должен резко увеличиться. Однако катушка индуктивности, как известно, препятствует всякому изменению силы тока, протекающего через нее, поэтому ток в цепи будет возрастать по экспоненциальному закону, как показано на рис. 4.17. Ток будет возрастать до тех пор, пока не достигнет своего максимального значения. После этого увеличение тока прекратится, а падение напряжения на резисторе R станет равным приложенному напряжению Е. Установившееся значение тока равно
E/R = 20 В/1 кОм = 20 мА.
Скорость изменения тока в цепи зависит от конкретных значений R и L. Время, необходимое для того, чтобы сила тока достигла значения, равного 0,63 от его максимальной величины, носит название постоянной времени цепи. Постоянная времени вычисляется по формуле L/R где L выражается в генри, а R — в омах. В этом случае постоянная времени получается в секундах. Используя значения L и R, указанные на рисунке, получаем
Следует заметить, что, чем больше R, тем меньше L/R и тем быстрее изменяется ток в цепи.

Рис. 4.16.

Рис. 4.17. Экспоненциальное увеличение тока, протекающего через катушку индуктивности.
Сопротивление по постоянному току
Катушка индуктивности, включенная в цепь, не препятствует протеканию постоянного тока, если, конечно, но принимать во внимание очень малое сопротивление провода, из которого она сделана. Следовательно, катушка индуктивности имеет нулевое или очень малое сопротивление и может рассматриваться в цепи постоянного тока как цепь короткого замыкания. Конденсатор же в связи с наличием в нем изолирующего диэлектрика имеет бесконечное или очень большое сопротивление и может рассматриваться в цепи постоянного тока как разрыв.
Векторное представление
Сигнал синусоидальной формы может быть представлен в виде вектора ОА, вращающегося против часовой стрелки с угловой скоростью ω= 2πf, где f – частота сигнала (рис. 4.18). По мере того как поворачивается вектор, ордината его конца характеризует показанный на рисунке синусоидальный сигнал. Один полный оборот вектора (360°, или 2π) соответствует одному полному периоду. Половина оборота (180°, или π) соответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода).
Теперь рассмотрим два синусоидальных сигнала, представленных на рис. 4.19(а) векторами ОА и ОВ соответственно. Если оба сигнала имеют одинаковые частоты, то векторы ОА и ОВ будут вращаться с одинаковой угловой скоростью ω= 2πf. Это означает, что угол между этими векторами

Рис. 4.18. Векторное представление синусоидального сигнала.

Рис. 4.19. Разность фаз. Вектор ОА опережает вектор ОВ
(или вектор ОВ отстает от вектора ОА) на угол θ.
изменяться не будет. Говорят, что вектор ОА опережает вектор ОВ на угол θ, а вектор ОВ отстает от вектора ОА на угол в. На рис. 4.19(б) эти сигналы развернуты во времени.
Если оба этих синусоидальных сигнала сложить, то в результате получим другой синусоидальный сигнал, имеющий ту же частоту f, но другую амплитуду. Результирующий сигнал может быть представлен вектором ОТ, который, как показано на рис. 4.19(в), является векторной суммой векторов ОА и ОВ. Вектор ОТ опережает вектор ОВ на угол α и отстает от вектора ОА на угол γ. Дальше вы увидите, что векторное представление является весьма удобным приемом при анализе и расчете цепей переменного тока.
В этом видео рассказывается о катушке индуктивности:


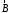 . Как изменится сила Ампера, действующая на проводник, если его длина будет в 2 раза больше, индукция магнитного поля уменьшится в 4 раза, а сила тока в проводнике останется прежней?
. Как изменится сила Ампера, действующая на проводник, если его длина будет в 2 раза больше, индукция магнитного поля уменьшится в 4 раза, а сила тока в проводнике останется прежней? 5.Электрон е, влетевший в зазор между полюсами электромагнита, имеет скорость
5.Электрон е, влетевший в зазор между полюсами электромагнита, имеет скорость 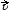 , перпендикулярную вектору индукции
, перпендикулярную вектору индукции 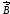 магнитного поля, направленному вертикально (см. рисунок). Куда направлена действующая на электрон сила Лоренца
магнитного поля, направленному вертикально (см. рисунок). Куда направлена действующая на электрон сила Лоренца 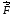 ? (вправо, влево, к наблюдателю, от наблюдателя)
? (вправо, влево, к наблюдателю, от наблюдателя)