Магнитное поле — что это, определение и ответ

Электрические и магнитные явления связаны, так как имеют общую природу ― электромагнитное поле. Движение электрических зарядов всегда создает магнитное поле, а магнитное поле, в свою очередь, всегда вызывает перемещение электрических зарядов.

Так как ток ― это направленное перемещение электрических зарядов, то протекание тока в проводнике всегда создает магнитное поле вокруг проводника.

Линии магнитного поля, которое создается проводниками с электрическим током.

Для изображения магнитных полей используют магнитные силовые линии ― линии, на которых модуль вектора магнитной индукции одинаков и равен В, а сам вектор магнитной индукции \(\overrightarrow{B}\) направлен по касательной к линии. Линии магнитной индукции всегда замкнуты.

Для обозначения направлений движения тока и направлений магнитных силовых линий, помимо стрелок «вправо» → и «влево» ←, используются знаки «от нас» ― ⊗ или ⊕ (как торец оперения стрелы, летящей от нас), и «к нам» • или ⊙ (как острие летящей на нас стрелы).

Чтобы определить направление вектора магнитной индукции \(\overrightarrow{B}\), которое создает ток, протекающий в прямом проводнике, используется правило правого винта: если представить, что вкручиваешь винт по направлению тока ― то направление вращения винта покажет направление вектора магнитной индукции.

Магнитное поле, которое создает ток в прямом проводнике, представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. При этом, некоторая область магнитного поля всегда направлена на нас, а другая ― от нас.

Чтобы определить направление вектора магнитной индукции \(\overrightarrow{B}\), которое создает ток, в круговом проводнике или витках катушки, используется правило правого винта: если ток вращается по часовой стрелке, то магнитное поле будет направленно «от нас». Если ток течет против часовой стрелки, то ток будет направлен «на нас».

Сила Ампера ― сила, действующая на проводник с током со стороны магнитного поля.

Сила ампера равна

F_A = IBLsinα, где

F_A ― сила Ампера [Н];

I ― сила тока в проводнике [A];

B ― магнитная индукция [Тл];

L ― длина проводника [м];

sinα ― синус угла между проводником и вектором магнитной индукции.

Сила Ампера максимальна, если между проводником и вектором магнитной индукции угол равен α = 90°, так как sinα = sin90° = 1 и F_A = IBLsin90° = IBL.

Если проводник расположен параллельно вектору магнитной индукции, т. е. α = 0° ― сила Ампера отсутствует, так как sinα = sin0° = 0 и F_A = IBLsin0° = 0.

Направление силы Ампера определяется по правилу левой руки: если ладонь расположить так, чтобы линии магнитного поля входили в ладонь, а четыре пальца указывали направление тока ― то противопоставленный большой палец укажет направление силы Ампера.

Взаимодействие проводников с током

Ток, протекающий в проводнике, создает магнитное поле. Если рядом расположен еще один проводник, в котором протекает ток ― то второй проводник оказывается в магнитном поле, которое создает первый. На проводник в магнитном поле действует сила Ампера, в результате чего проводники с током или притягиваются, или отталкиваются друг от друга.

Пусть в проводниках 1 и 2 токи текут в одном направлении. Тогда первый проводник создает магнитное поле, направленное против часовой стрелки. В области, близлежащей к проводнику 2 это поле направлено перпендикулярно проводнику и от него. Согласно правилу левой руки, сила Ампера, которая действует со стороны магнитного поля, создаваемого проводником 1 на проводник с током 2, F_1-2 направлено в сторону проводника 1.

Проводник 2 действует на проводник 1 аналогично, и сила ампера, с которой магнитное поле проводника 2 действует на проводник 1 F_2-1 направлена в сторону проводника 2.

Таким образом, силы Ампера, с которым действуют проводники друг на друга ― F_1-2 и F_2-1 направлены навстречу друг другу и проводники притягиваются.

Пусть теперь ток в проводнике 2 течет в том же направлении, а ток в проводнике 1 ― в противоположном. Магнитное поле, которое создает проводник 1, будет направлено по часовой стрелке, а в ближайшей к проводнику 2 области ― на нас. Согласно правилу левой руки, такое магнитное поле создает силу Ампера, направленную от проводника 1.

Магнитное поле, которое создает проводник 2, будет направлено как в первом случае, но из-за того, что ток в проводнике 1 течет в противоположную сторону, сила Ампера F_2-1 будет направлена от проводника 2.

Силы Ампера, с которым действуют проводники друг на друга ― F_1-2 и F_2-1 направлены в разные стороны и проводники отталкиваются.

Магнитное поле постоянного магнита. Магниты обладают собственным магнитным полем. Силовые линии магнита выходят из северного магнитного полюса (N) и входят в южный магнитный полюс (S).

Магнитные поля двух магнитов взаимодействуют друг с другом, переориентируя магниты так, чтобы магнитные линии выходили из северного магнитного полюса и входили в ближайший южный магнитный полюс. При этом одинаковые полюса двух магнитов, отталкиваются, а разные ― притягиваются.

2.7.9 Магнитное поле прямоугольного провода с током

Flash model

Вычислим распределение магнитного поля в пространстве, создаваемое прямоугольным проводником с плотностью тока , длиной , шириной и толщиной , и (рис. 1).

Рис. 1.  Поперечное сечение прямоугольного проводника.

Рис. 2.  Схематическое изображение бесконечно тонкой нити, по которой течёт постоянный ток .

Согласно закону Био-Савара-Лапласа [1,2], магнитное поле , создаваемое бесконечно тонкой и длиной ниткой, на расстояние от неё (рис. 2) в гауссовой системе определяется выражением

(1)

где , – скорость света, – ток, протекающий по нити, и магнитное поле сонаправлено с векторным произведением .

Разобьём поперечное сечение проводника на бесконечное число нитей сечением (рис. 1). Тогда, магнитное поле, создаваемое каждой элементарной ниткой в точке в соответствии с формулой (1) определяется выражением

(2)

где , – плотность тока, – наикратчайшее расстояние от элементарной нити до точки A, – угол между вектором и осью, , причём . В дальнейшем, магнитное поле вдоль оси Y не будет вычисляться, так как очевидно, что в произвольной точке оно равно нулю.

Суммарное магнитное поле, в точке , можно вычислить, проинтегрировав выражение (2) по всему поперечному сечению проводника

(3)

где была выполнена замена переменных . Интегралы вида

(4)

выражаются через аналитические функции следующим образом:

(5)

Производные функций и вдоль оси Z, в соответствии с (5), определяются формулами

(6)

Аналогично, вторые производные функций и , вдоль оси Z, в соответствии с (5) определяются выражениями

(7)

Таким образом, магнитное поле , заданное выражениями (3) выражается через формулы (5) следующим образом

(8)

Производные компонент магнитного поля вдоль оси Z, по аналогии с (8), в соответствии с (6) определяются выражениями

(9)

Вторые производные компонент магнитного поля вдоль оси Z, по аналогии с (8), в соответствии с (7) определяются выражениями

(10)

Зная выражения для первой и второй производных магнитного поля, можно рассчитать силу взаимодействия магнитного зонда (и ее производную) и проводника с током. Данные вычисления для случаев различной геометрии зонда приведены в приложении.

На основе теории малых колебаний зонда (см.

пункт 2.3.4) также разработана специальная Flash модель, которая теоретически вычисляет изменение амплитуды, фазы, частоты колебаний зонда в процессе второго прохода стандартного динамического МСМ режима над поверхностью образца.

 

---

Выводы.

• Получены аналитические зависимости пространственного распределения магнитного поля, его первой и второй производной над поверхностью прямоугольного проводника с током, см. формулы (8-10).
• Теоретические зависимости пространственного распределения магнитного поля, его первой и второй производной в зависимости от параметров проводника можно проанализировать в специально разработанном Flash приложении.

Литература.

1. Д.В. Сивухин. Электричество (Общий курс физики). М.: Наука 1983. — 688 c.
2. Р. Фейнман., Р. Лейтос., М. Сэндс. Фейнмановские лекции по физике. Электричество и магнетизм. М.: МИР 1977. — 299.

Магнетизм | Определение, примеры, физика и факты

магнитное поле от токовой петли

Посмотреть все СМИ

Ключевые люди:

Джон Б. Гуденаф Пьер Кюри Петр Леонидович Капица Юлиус Плюкер Питер Перегрин де Марикур

Похожие темы:

магнит ферромагнетизм магнитная цепь антиферромагнетизм магнитный полюс

Просмотреть весь соответствующий контент →

Резюме

Прочтите краткий обзор этой темы

магнетизм , явление, связанное с магнитными полями, которые возникают в результате движения электрических зарядов. Это движение может принимать различные формы. Это может быть электрический ток в проводнике или заряженные частицы, движущиеся в пространстве, или это может быть движение электрона по атомной орбите. Магнетизм также связан с элементарными частицами, такими как электрон, которые обладают свойством, называемым вращением.

Основой магнетизма являются магнитные поля и их воздействие на материю, как, например, отклонение движущихся зарядов и крутящих моментов на другие магнитные объекты. Доказательством наличия магнитного поля является магнитная сила, действующая на заряды, движущиеся в этом поле; сила направлена ​​под прямым углом как к полю, так и к скорости заряда. Эта сила отклоняет частицы, не изменяя их скорости. Отклонение можно наблюдать по крутящему моменту стрелки компаса, который выравнивает стрелку с магнитным полем Земли. Игла представляет собой намагниченный тонкий кусок железа, т. е. небольшой стержневой магнит. Один конец магнита называется северным полюсом, а другой конец – южным полюсом. Сила между северным и южным полюсами притягивает, тогда как сила между одинаковыми полюсами отталкивает. Магнитное поле иногда называют магнитной индукцией или плотностью магнитного потока; это всегда символизируется цифрой

Б . Магнитные поля измеряются в единицах тесла (Тл). (Другой единицей измерения, обычно используемой для B , является гаусс, хотя он больше не считается стандартной единицей. Один гаусс равен 10 ⁻⁴ тесла.) поток через любую замкнутую поверхность равен нулю. (Замкнутая поверхность — это та, которая полностью окружает объем.) Это выражается математически как div B = 0 и может быть понято физически с точки зрения силовых линий, представляющих Б . Эти линии всегда замкнуты сами на себя, так что если они в какой-то момент входят в какой-то объем, то должны и выйти из этого объема. В этом отношении магнитное поле сильно отличается от электрического поля. Силовые линии электрического поля могут начинаться и заканчиваться на заряде, но, несмотря на многочисленные поиски так называемых магнитных монополей, не было найдено эквивалентного магнитного заряда.

Наиболее распространенным источником магнитных полей является петля электрического тока.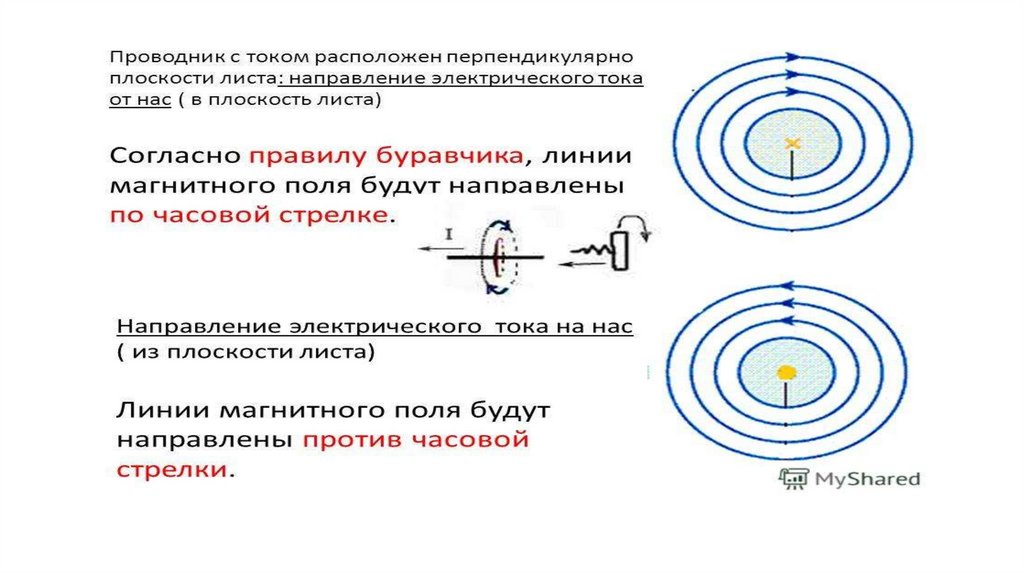

Это может быть электрический ток в круглом проводнике или движение электрона по орбите в атоме. С обоими этими типами токовых петель связан магнитный дипольный момент, значение которого равно i A , произведение тока i и площади петли A . Кроме того, электроны, протоны и нейтроны в атомах имеют магнитный дипольный момент, связанный с их собственным спином; такие магнитные дипольные моменты представляют собой еще один важный источник магнитных полей. Частицу с магнитным дипольным моментом часто называют магнитным диполем. (Магнитный диполь можно рассматривать как крошечный стержневой магнит. Он имеет то же магнитное поле, что и такой магнит, и ведет себя так же во внешних магнитных полях.) Помещенный во внешнее магнитное поле, магнитный диполь может подвергаться воздействию крутящий момент, стремящийся выровнять его с полем; если внешнее поле неоднородно, на диполь также может действовать сила.

Все вещества в той или иной степени обладают магнитными свойствами. Помещенное в неоднородное поле вещество либо притягивается, либо отталкивается в направлении градиента поля. Это свойство описывается магнитной восприимчивостью вещества и зависит от степени намагниченности вещества в поле. Намагниченность зависит от величины дипольных моментов атомов в веществе и степени, в которой дипольные моменты выровнены друг относительно друга. Некоторые материалы, такие как железо, обладают очень сильными магнитными свойствами из-за выравнивания магнитных моментов их атомов в определенных небольших областях, называемых доменами. В нормальных условиях различные домены имеют поля, которые компенсируют друг друга, но они могут быть выровнены друг с другом, создавая чрезвычайно большие магнитные поля. Различные сплавы, такие как NdFeB (сплав неодима, железа и бора), поддерживают выравнивание своих доменов и используются для изготовления постоянных магнитов. Сильное магнитное поле, создаваемое типичным трехмиллиметровым магнитом из этого материала, сравнимо с электромагнитом, состоящим из медной петли, по которой течет ток в несколько тысяч ампер.

Для сравнения, сила тока в обычной лампочке составляет 0,5 ампера. Поскольку выравнивание доменов материала создает магнит, нарушение упорядоченного выравнивания разрушает магнитные свойства материала. Термическое возбуждение, возникающее в результате нагревания магнита до высокой температуры, разрушает его магнитные свойства.

Сила магнитных полей сильно различается. Некоторые репрезентативные значения приведены в таблице.

Оформите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подписаться сейчас

Типичные магнитные поля
внутри атомных ядер	10 11 Т
в сверхпроводящих соленоидах	20 т
в циклотроне со сверхпроводящей катушкой	5 Т
возле небольшого керамического магнита	0,1 Тл
Поле Земли на экваторе	4(10 −5 ) Т
в межзвездном пространстве	2(10 −10 ) Т

магнитных полей, создаваемых токами: закон Ампера | Физика |

Цели обучения

К концу этого раздела вы сможете:

• Рассчитать ток, создающий магнитное поле.
• Используйте правило правой руки 2, чтобы определить направление тока или направление контуров магнитного поля.

Какой ток необходим для создания значительного магнитного поля, возможно, такого же сильного, как поле Земли? Геодезисты скажут вам, что воздушные линии электропередач создают магнитные поля, которые мешают показаниям их компаса. Действительно, когда в 1820 году Эрстед обнаружил, что ток в проводе влияет на стрелку компаса, он не имел дело с чрезвычайно большими токами. Как форма проводов, по которым течет ток, влияет на форму создаваемого магнитного поля? Ранее мы отмечали, что токовая петля создает магнитное поле, подобное магнитному стержню, но как насчет прямого провода или тороида (бублика)? Как направление создаваемого током поля связано с направлением тока? Ответы на эти вопросы исследуются в этом разделе вместе с кратким обсуждением закона, управляющего полями, создаваемыми токами.

Магнитное поле, создаваемое длинным прямым проводом с током: правило правой руки 2

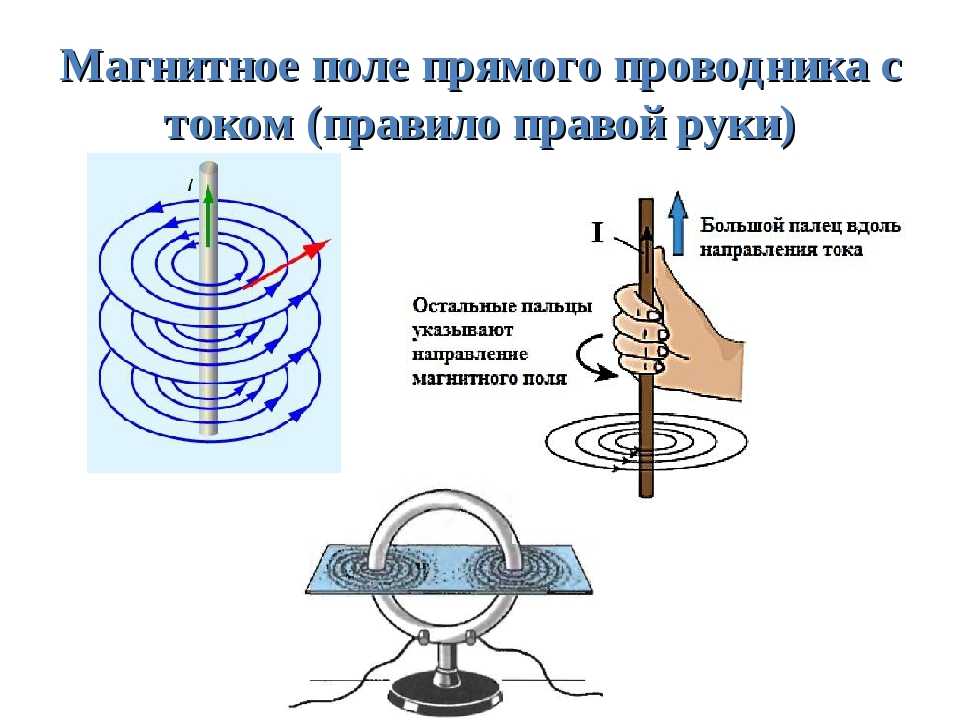
Магнитные поля имеют как направление, так и величину. Как отмечалось ранее, одним из способов определения направления магнитного поля является использование компаса, как показано для длинного прямого провода с током на рисунке 1. Датчики Холла могут определять величину поля. Обнаружено, что поле вокруг длинного прямого провода представляет собой кольцевые петли. Правило правой руки 2 (RHR-2) вытекает из этого исследования и действительно для любого текущего сегмента — большой палец указывают в направлении тока, а пальцы скручиваются в направлении создаваемых им петель магнитного поля .

Рис. 1. (a) Компасы, расположенные рядом с длинным прямым проводом с током, показывают, что силовые линии образуют круглые петли с центром на проводе. (b) Правило правой руки 2 гласит, что если большой палец правой руки указывает в направлении течения, остальные пальцы сгибаются в направлении поля. Это правило согласуется с полем, отображаемым для длинного прямого провода, и справедливо для любого текущего сегмента. 9{-7}\text{T}\cdot\text{ m/A}\\µ0​=4π×10−7T⋅ m/A

 является проницаемостью свободного пространства . ( μ ₀ — одна из основных констант в природе. Позже мы увидим, что μ ₀ связано со скоростью света.) Поскольку провод очень длинный, величина поля зависит только по расстоянию от провода r , а не по положению вдоль провода.

Пример 1. Расчет тока, создающего магнитное поле

Найти силу тока в длинном прямом проводе, который на расстоянии 5,0 см от провода создавал бы магнитное поле, вдвое превышающее земное.

Стратегия

Поле Земли составляет около 5,0 × 10 ⁻⁵ Тл, поэтому здесь B за счет проволоки принимается равным 1,0 × 10 ⁻⁴ Тл. Уравнение

B=μ0I2πrB=\frac{\mu_ {0}I}{2\pi r}\\B=2πrµ0​I​

 можно использовать для нахождения I , поскольку все остальные величины известны. 9{-7}\text{ T}\cdot\text{m/A}}\\ & =& 25\text{ A}\end{массив}\\I​==​μ0​2πrB​=4π×10 −7 T⋅m/A2π(5,0×10−2 м)(1,0×10−4 T)​25 A​

Обсуждение

Таким образом, умеренно большой ток создает значительное магнитное поле на расстоянии 5,0 см от длинного прямого провода. Обратите внимание, что ответ указан только с двумя цифрами, поскольку в этом примере поле Земли указано только с двумя цифрами.

Закон Ампера и др.

Магнитное поле длинного прямого провода имеет больше значений, чем вы можете предположить на первый взгляд. Каждый отрезок тока создает магнитное поле, подобное магнитному полю длинного прямого провода, а полное поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым отрезком. Формальная формулировка направления и величины поля, обусловленного каждым сегментом, называется законом Био-Савара . Интегральное исчисление необходимо для суммирования поля для тока произвольной формы. Это приводит к более полному закону, называемому законом Ампера , который связывает магнитное поле и ток в общем виде. Закон Ампера, в свою очередь, является частью Уравнения Максвелла , которые дают полную теорию всех электромагнитных явлений. Рассмотрение того, как уравнения Максвелла кажутся разным наблюдателям, привело к современной теории относительности и осознанию того, что электрические и магнитные поля — это разные проявления одного и того же явления. Большая часть этого выходит за рамки этого текста как на математическом уровне, требующем исчисления, так и на том количестве места, которое может быть уделено этому. Но для заинтересованных студентов, и особенно для тех, кто продолжает заниматься физикой, инженерией или подобными занятиями, дальнейшее углубление в эти вопросы откроет описания природы, которые элегантны и глубоки. В этом тексте мы будем помнить об общих особенностях, таких как RHR-2 и правила для линий магнитного поля, перечисленные в Магнитных полях и Линии магнитного поля, концентрируясь на полях, создаваемых в определенных важных ситуациях.

Установление связей: теория относительности

Слушая все, что мы делаем об Эйнштейне, иногда создается впечатление, что он изобрел теорию относительности из ничего. Напротив, одним из мотивов Эйнштейна было решить трудности, связанные с пониманием того, как разные наблюдатели видят магнитные и электрические поля.

Магнитное поле, создаваемое круговым контуром с током

Магнитное поле вблизи проволочной петли с током показано на рисунке 2. Как направление, так и величина магнитного поля, создаваемого петлей с током, являются сложными. RHR-2 можно использовать для задания направления поля вблизи контура, но для получения более подробной информации необходимо картографирование с помощью компаса и правил относительно силовых линий, приведенных в разделе «Магнитные поля и линии магнитного поля». Есть простая формула для напряженность магнитного поля в центре круглой петли . Это

B=µ0I2R(в центре петли)B=\frac{\mu_{0}I}{2R}\left(\text{в центре петли}\right)\\B=2Rµ0​I​ (в центре петли)

, где R — радиус петли. Это уравнение очень похоже на уравнение для прямого провода, но оно действительно только в центре круглой петли из проволоки. Сходство уравнений указывает на то, что аналогичная напряженность поля может быть получена в центре контура. Один из способов получить большее поле — иметь Н петли; тогда поле равно Б = Нмк ₀ I /(2 R ). Обратите внимание, что чем больше петля, тем меньше поле в ее центре, поскольку ток проходит дальше.

Рис. 2. (a) RHR-2 показывает направление магнитного поля внутри и снаружи контура с током. (b) Более детальное картографирование с помощью компаса или зонда Холла дополняет картину. Поле похоже на поле стержневого магнита.

Магнитное поле, создаваемое токоведущим соленоидом

Соленоид представляет собой длинную катушку провода (с множеством витков или петель, в отличие от плоской петли). Из-за своей формы поле внутри соленоида может быть очень однородным, а также очень сильным. Поле сразу за катушками почти равно нулю. На рис. 3 показано, как выглядит поле и как его направление задается RHR-2.

Рис. 3. (a) Из-за своей формы поле внутри соленоида длиной l удивительно однородно по величине и направлению, на что указывают прямые и равномерно расположенные силовые линии. Поле вне катушек почти равно нулю. (b) На этом разрезе показано магнитное поле, создаваемое током в соленоиде.

Магнитное поле внутри соленоида с током очень однородно по направлению и величине. Лишь ближе к концам он начинает ослабевать и менять направление. Поле снаружи имеет ту же сложность, что и плоские петли и стержневые магниты, но напряженность магнитного поля внутри соленоида равна просто

B=μ0nI(внутри соленоида)B={\mu }_{0}nI\left(\ text{внутри соленоида}\right)\\B=μ0​nI(внутри соленоида)

, где n — количество витков на единицу длины соленоида ( н = н / л , где н количество петель и л длина). Обратите внимание, что B — это напряженность поля в любом месте однородной внутренней области, а не только в центре. Как следует из примера 2, с помощью соленоидов возможны большие однородные поля, распределенные по большому объему.

Пример 2. Расчет напряженности поля внутри соленоида

Каково поле внутри соленоида длиной 2 м, имеющего 2000 витков и пропускающего ток силой 1600 А? 9{-1}\right)\left(1600\text{ A}\right)\\ & =& 2.01\text{ T}\end{массив}\\B​==​μ0​nI=(4π×10 −7 Т⋅м/А)(1000 м−1)(1600 А)2,01 Т​

Обсуждение

Это большая напряженность поля, которую можно установить на соленоиде большого диаметра, например, при медицинском использовании магнитно-резонансной томографии (МРТ). Однако очень большой ток указывает на то, что поля такой силы получить нелегко. Такой большой ток через 1000 витков, втиснутых в длину метра, произвел бы значительный нагрев. Более высокие токи могут быть достигнуты с помощью сверхпроводящих проводов, хотя это дорого.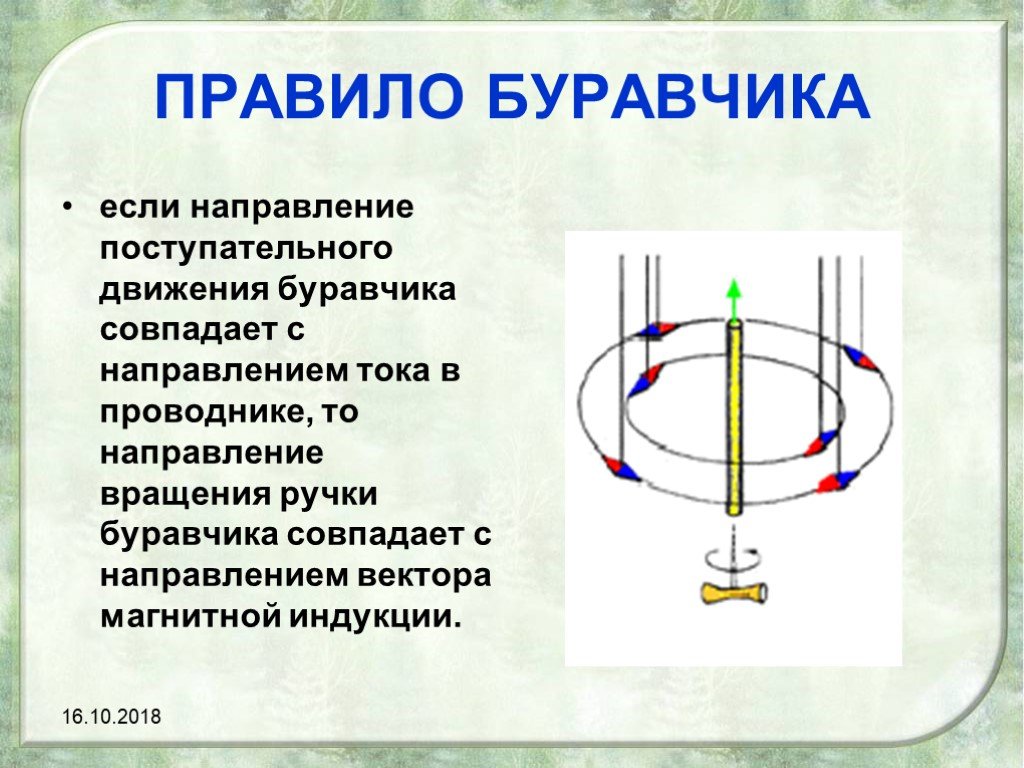 Существует верхний предел тока, поскольку сверхпроводящее состояние нарушается очень большими магнитными полями.

Есть интересные варианты плоской катушки и соленоида. Например, тороидальная катушка, используемая для удержания реактивных частиц в токамаках, очень похожа на соленоид, согнутый в окружность. Поле внутри тороида очень сильное, но круглое. Заряженные частицы движутся по кругу, следуя линиям поля, и сталкиваются друг с другом, возможно, вызывая синтез. Но заряженные частицы не пересекают силовые линии и не покидают тороид. Целый ряд форм катушек используется для создания всевозможных форм магнитного поля. Добавление ферромагнитных материалов увеличивает напряженность поля и может существенно повлиять на форму поля. Ферромагнитные материалы имеют тенденцию улавливать магнитные поля (силовые линии изгибаются в ферромагнитный материал, оставляя более слабые поля вне его) и используются в качестве экранов для устройств, на которые неблагоприятно влияют магнитные поля, в том числе магнитное поле Земли.

PhET Исследования: Генератор

Генерировать электричество с помощью стержневого магнита! Откройте для себя физику этого явления, исследуя магниты и то, как вы можете использовать их, чтобы зажечь лампочку.

Нажмите, чтобы загрузить симуляцию. Запуск с использованием Java.

Резюме раздела

• Сила магнитного поля, создаваемого током в длинном прямом проводе, определяется выражением

  B=µ0I2πr(длинный прямой провод)B=\frac{{\mu}_{0}I}{2 \pi r}\left(\text{длинный прямой провод}\right)\\B=2πrμ0​I​(длинный прямой провод) 9{-7}\text{ T}\cdot\text{ m/A}\\µ0​=4π×10−7 T⋅ m/A

   является проницаемостью свободного пространства.
• Направление магнитного поля, создаваемого длинным прямым проводом, определяется правилом правой руки 2 (RHR-2): Направьте большой палец правой руки в направлении тока, а пальцы согните в направлении магнитного поля. петли поля созданные им.
• Магнитное поле, создаваемое током, следующим по любому пути, является суммой (или интегралом) полей, создаваемых сегментами вдоль пути (величина и направление, как для прямого провода), что приводит к общей зависимости между током и полем, известной как закон Ампера. .
• Напряженность магнитного поля в центре кругового контура определяется как }\right)\\B=2Rµ0​I​(в центре цикла)
  где R — радиус петли. Это уравнение принимает вид B =     μ ₀ nI /(2 R ) для плоской катушки из N петель. РХР-2 дает направление поля вокруг петли. Длинная катушка называется соленоидом.
• Напряженность магнитного поля внутри соленоида равна

  B=µ0nI(внутри соленоида)B={\mu }_{0}\text{nI}\left(\text{внутри соленоида}\right)\\B= μ0​nI (внутри соленоида)

  где n — количество витков на единицу длины соленоида. Поле внутри очень однородно по величине и направлению.

Концептуальные вопросы

1. Нарисуйте рисунок и используйте RHR-2, чтобы найти направление магнитного поля токовой петли в двигателе (например, на рисунке 1 из книги «Крутящий момент в токовой петле»). Затем покажите, что направление крутящего момента на петле такое же, как при отталкивании одноименных полюсов и притяжении разноименных полюсов.

Глоссарий

Правило правой руки 2 (RHR-2):

правило для определения направления магнитного поля, создаваемого проводом с током: направьте большой палец правой руки в направлении тока и пальцы загибаются в направлении петель магнитного поля

напряженность магнитного поля (величина), создаваемая длинным прямым проводом с током:

определяется как

B=μ0I2πrB=\frac{\mu_{0}I} {2\pi r}\\B=2πrµ0​I​ 9{-7}T\cdot \text{м/А}\\μ0​=4π×10−7T⋅м/А

напряженность магнитного поля в центре круглой петли:

определяется как

B =μ0I2RB=\frac{{\mu }_{0}I}{2R}\\B=2Rμ0​I​

где R  радиус петли

соленоид:

тонкая проволока, намотанная в катушку, создающую магнитное поле при прохождении через нее электрического тока

напряженность магнитного поля внутри соленоида:

определяется как

B=μ0nIB={\mu }_{0}\text{nI}\\B=μ0​nI

где n  количество витков на единицу длины соленоида  n = N/l , при N число витков и l  длина)

Закон Био-Савара:

физический закон, описывающий магнитное поле, создаваемое электрическим током, с помощью специального уравнения

Ампер закон:

физический закон, утверждающий, что магнитное поле вокруг электрического тока пропорционально току; каждый отрезок тока создает магнитное поле, подобное магнитному полю длинного прямого провода, а полное поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым отрезком

Уравнения Максвелла:

набор из четырех уравнений, описывающих электромагнитные явления.