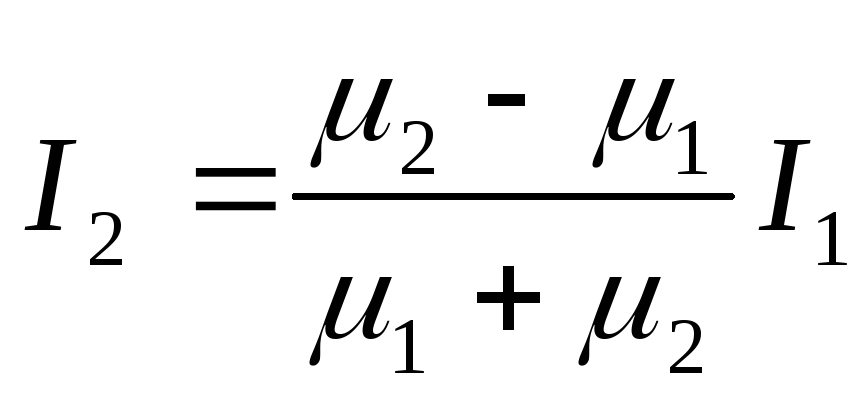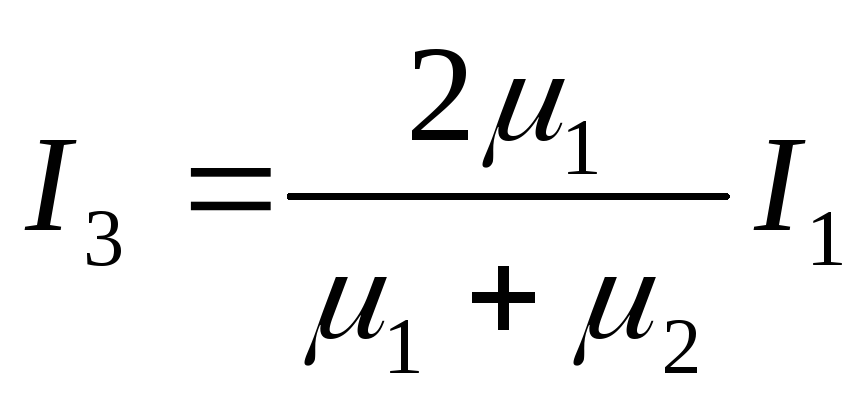Вихревой характер магнитного поля

Определение 1

Вихревой характер магнитного поля заключается в непрерывности линий индукции любого магнитного поля при отсутствии начала и конца, так как они либо замкнуты, либо уходят в бесконечность. На порождение полей не влияет характер контуров с током. Векторные поля, обладающие непрерывными силовыми линиями, называются вихревыми полями. Магнитное поле также можно считать вихревым.

Электростатические поля имеют силовые линии, начинающиеся и заканчивающиеся на электрических зарядах, причем, всегда находятся в разомкнутом состоянии. Линии магнитного поля замкнуты. Это говорит об отсутствии магнитных зарядов в природе.

Электрический ток образуется благодаря движению электрических зарядов. Так как магнитных зарядов нет, это объясняет отсутствие магнитного тока. Данное утверждение можно выразить при помощи уравнения:

Определение вихревого поля также выполнимо другим способом.

Вихревое магнитное поле

Определение 2

Векторные поля, вектор которых не равен нулю – это

вихревые магнитные поля.

Следуя из теоремы о циркуляции локального вида, которая влияет на вихревой характер магнитного поля:

rot B→=μ0j→ (2), где j→ считается объемной плотностью тока, и второй формы определения вихревого поля можно заключить, что магнитное поле будет вихревым там, где проходят токи, а безвихревым там, где их нет.

При отсутствии токов вектор магнитной индукции B→ представляется в виде градиента скалярного магнитного потенциала φm:

B→=-gradφm (3).

Если имеются токи, то данное представление невозможно.

Различие между потенциальными и вихревыми полями

Основными уравнениями магнитного поля постоянных токов считаются выражения вида:

rot B→=μ0j→div B→=0 (4).

Произведем сравнение с основными уравнениями электростатики:

rot E→=0div E→=1ε0ρ (5).

Рассматривая систему (5), видно, что электрическое поле всегда потенциально, а его источниками являются электростатические (неподвижные) заряды.

Определение 3

Основы безвихревой электродинамики Потенциальное магнитное поле (стр. 1 из 3)

При изменении симметрии действующих сил ускорение тела сменяется его деформацией, а вместо инерционного проявляется другое своё же свойство тела — его упругость.

Ньютоновская причинно-следственная связь переходит в гуковскую.

Симметрийно-физический переход в магнитостатике.

Симметрийный аспект. По аналогии с механическим примером возможен переход физических свойств магнитного поля (таблица 2) при повороте одного из двух однонаправленных токов (i2) на 180°.

Известные электромагнитные поля, с точки зрения их геометрической структуры, обладают либо замкнутыми, либо разомкнутыми силовыми линиями. Других вариантов в электромагнетизме нет.

. Поэтому безальтернативно выдвигается предположение о замене в центрально-симметричной магнитостатике исходного циркуляционного свойства магнитного поля с цилиндрообразной симметрией на потенциальное, обладающее шарообразной симметри-

Таблица 2.

ей, подобной симметрии поля электрического заряда. Новое отношение между центрально-симметричным токовым источником и его более симметричным потенциальным магнитным полем предполагается аналогичным гауссовой причинно-следственной связи для электростатики.

В природном явлении предельные симметрии причины и следствия не могут быть разными. Исскуственный перевод причины (токового источника) к более симметричному виду предположительно сопровождается аналогичным переходом в следствии (в магнитном поле).

Идея о потенциальном магнитном поле с шарообразной симметрией присутствует в гипотезе Дирака о магнитном микромонополе.

Физический аспект. Известные знания о протяжённых структурах полей получены из эмпирических фактов о результатах их локальных воздействий на электрические заряды.

Следовательно, предполагаемый переход к другой структуре магнитного поля может быть подтверждён только доказательством перехода к другой направленности локальных магнитных сил в рамках их релятивистской природы.

Для ясного понимания причины и непосредственного видения механизма такого перехода в последующем изложении приводятся в сопоставлении два одинаковых по своей сути примера, сочетающих логику и очевидность.

Суть парселловской идеи в том, что в областях сгущений силовых линий воздействие каждого токового заряда на пробный усиливается, а вобластях разряжения — уменьшается. Общая релятивистская составляющая силового воздействия при однонаправленных токах наглядно представляется ориентированной поперечно к скорости движения пробного заряда и подчиняющейся правилу левой руки.

Автором был предложен [2] аналогичный пример, основывающийся на той же парселловской идее. В нём, как и в таблице 2, всего лишь изменяется на 180° направление тока i2, сопровождаемое соответствующим поворотом диаграмм релятивистских «сплющиваний». В результате общая релятивистская составляющая силового воздействия становится ориентированной вдоль скорости движения пробного заряда (Рис.2).

Форма и количество релятивистского эффекта в поле каждого движущегося заряда,

как в однонаправленных, так и в центрально-симметричных токах, соответствуют специальной теории относительности. Разнятся лишь симметрии их наложения в области

пробного заряда, что и является истинной причиной существования поперечного и

продольного направлений магнитной силы.

i1i2

∑V

Q

Теория скалярного магнитного потенциала — Википедия

В той части пространства, где плотность тока равна нулю, магнитное поле можно рассматривать как потенциальное и напряженность магнитного поля можно представить в виде:

H=-gradUm ́

где Um — скалярный потенциал магнитного поля;

В областях не занятых током (только для этих областей имеет смысл функция Uм) при постоянном значении магнитной проницаемости (m = const) скалярный потенциал магнитного поля подчиняется уравнению Лапласа:

(V²)*Um=0

Разность магнитных потенциалов между двумя точками называют падением магнитного напряжения между этими точками.

Магнитный потенциал в отличие от электрического имеет бесконечное множество значений. Действительно, циркуляция электростатического поля по любому замкнутому контуру равна нулю. Циркуляция же магнитного поля по замкнутому контуру, охватывающему ток равна: 4π/с*I

Простейшим замкнутым контуром является круговой (с осевой однородностью за счет бесконечной длины тока) и соленоидальные векторные магнитные поля. Количество витков цилиндрической катушки (соленоида) с однонаправленной намоткой принципиального значения не имеет, гак как характер топологии поля при этом не изменяется. Ниже будет показано, что условие прямолинейности оси соленоида является важным для сохранения тина конфигурации магнитного поля.

Если же встречается электрическая система, включающая несколько таких простейших элементов, например соленоидов, то в традиционной магни­тостатике исследование её магнитного поля всегда происходит на уровне характеристик В и H. Вопрос о векторном потенциале А не ставится, и его свойства не рассматриваются. Такой подход приводит к исключению из рассмотрения потенциальной составляющей векторного потенциала, а, следовательно, и скалярного магнитного поля.

Очень важным представляется вопрос об условиях создания скалярного магнитного поля замкнутой электрической цепью, состоящей из одного или нескольких контуров. При его решении, как мы понимаем, следует опираться на свойства основной характеристики — векторного потенциала. Рассмотрим замкнутый контур в виде прямоугольника с током (рис.1). В любой точке пространства накладываются магнитные поля от четырёх токовых отрезков его образующих. В любой произвольной точке, кроме точки

О пересечения диагоналей прямоугольника, вектор А отличен от нуля. Конфигурация векторного магнитного ноля, созданного прямоугольным контуром, известна.

Не получается добавить наглядную схему (Рисунок 1)

Исследование скалярного магнитного поля прямоугольного контура с током.

Покажем, что сумма всех четырёх составляющих, вычисленных по формулеH(x,y,z)=J/4π∫0L(zdz)/r3=J/4π∗((r1−r2)/r1r2)=(J/4πr0)(sin⁡(a2)−sina1){\displaystyle H(x,y,z)=J/4\pi \int \limits _{0}^{L}(zdz)/r^{3}=J/4\pi *((r_{1}-r_{2})/r_{1}r_{2})=(J/4\pi r_{0})(\sin(a_{2})-sina_{1})} , равна нулю. Выберем произвольную точку пространства и проведем в неё радиус-векторы из всех четырёх углов, обозначив их соответственно r1,r2,r3,r4. Нетрудно увидеть, что:

H∗(x,,y,,z,)=J/4π(r1−r2r1r2+r2−r3r2r3+r3−r4r3r4+r4−r1r4r1){\displaystyle H^{*}(x^{,},y^{,},z^{,})=J/4\pi \left({\frac {r_{1}-r_{2}}{r_{1}r_{2}}}+{\frac {r_{2}-r_{3}}{r_{2}r_{3}}}+{\frac {r_{3}-r_{4}}{r_{3}r_{4}}}+{\frac {r_{4}-r_{1}}{r_{4}r_{1}}}\right)}=0

Проверим выполнения данного условия для точек, лежащих на осях симметрии контура (рис.2). В этом случае r1=r4, r2=r3, кроме того r1-r3=-(r3-r4). Следовательно, и для этих точек тоже:

H∗=(x,,y,,z,)=0{\displaystyle H^{*}=(x^{,},y^{,},z^{,})=0}

Не получается добавить наглядную схему (Рисунок 2)

Таким образом скалярное магнитное поле прямоугольным замкнутым контуром с током не создается ни в каких точках пространства

• 1.С. В. Измайлов «Курс электродинамики» для физико-математических факультетов -Москва 1962г
• 2.А. К. Томилин «Общая электродинамика» -Усть-Каменогорск 2009 г.

Магнитное поле называют вихревым, а как называют электрическое поле?

Если говорить суровым математическим языком, вихревое поле – это поле, дивергенция которого равна нулю. То есть, говоря по-простому, это поле не имеет источников, а значит его силовые линии замкнуты. Такое поле может быть задано векторным потенциалом. Примером вихревого поля является магнитное поле. Источником магнитного поля является электрический ток. Силовые линии магнитного поля прямолинейнорго тока представляют собой окружности, центром которых является проводник с током. В определённом смысле противоположностью вихревым полям являются поля потенциальные. Это поля, ротор которых равен нулю, т. е. силовые линии незамкнуты, а начинаются/кончаются либо на источниках поля, либо уходят в бесконечность. Такое поле можно задать скалярным потенциалом. Примером потенциального поля являются электростатическое и гравитационное поле. Существует всеобщее заблуждение, что магнитное поле всегда вихревое, а электрическое – потенциальное. Это не так. Например, переменное магнитное поле порождает вихревое электрическое поле, силовые линии которого замкнуты вокруг силовых линий порождающего магнитного поля. Магнитное поле чисто потенциальным быть не может, так как не существует магнитных зарядов, порождающих это поле, но при определённых условиях в ограниченной области пространства магнитное поле можно считать близким к потенциальному. Такое поле называют магнитостатическим и широко используют в технических расчётах, например в расчёте магнитопроводов электродвигателей.

Статическое электричество. Их всего два вида: вихревое и статическое. Основным действием электрического поля является силовое воздействие на неподвижные (относительно наблюдателя) электрически заряженные тела или частицы. Для того, чтобы создать электрическое поле, необходимо создать электрический заряд. Натрите какой-нибудь диэлектрик о шерсть или что-нибудь подобное, например, пластиковую ручку о собственные волосы. На ручке создастся заряд, а вокруг — электрическое поле. Заряженная ручка будет притягивать к себе мелкие обрывки бумаги. Если натирать о шерсть предмет большей ширины, например, резиновую ленту, то в темноте можно будет видеть мелкие искры, возникающие вследствие электрических разрядов. Электрическое поле часто возникает возле телевизионного экрана при включении или выключении телеприёмника. Это поле можно почувствовать по его действию на волоски на руках или лице.

только не статическое, а потенциальное. разница в другом. у вихревого поля все силовые линии замкнутые. у потенциального разомкнутые.

А нет электрического поля в Природе. И магнитное поле так же названо условно, а про вихры ее позабудьте. Все про единственное поле в нашей Вселенной есть в источнике. Это сложно.

Вихревой характер магнитного поля

Задание: Использовать понятие скалярного магнитного потенциала (${\varphi }_m$) можно только в области пространства, где $\overrightarrow{j}=0.$ Однако и в этой части пространства ${\varphi }_m$ функция не однозначная. Покажите это.

Решение:

Рассмотрим магнитное поле возле контура с током (рис.1). В соответствии с теоремой о циркуляции для любого контура выполняется равенство:

\[\oint\limits_L{\overrightarrow{B}\overrightarrow{dl}=}0\ \left(2.1\right).\]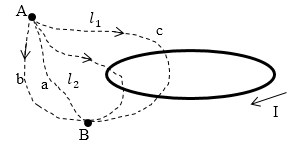

Рис. 1

Так как при отсутствии токов магнитное поле становистя потенциальным, интеграл, который берется между точками A и B не зависит от пути интегрирования, то можно записать:

\[\int\limits_{AaB}{\overrightarrow{B}\overrightarrow{dl}}=\int\limits_{AbB}{\overrightarrow{B}\overrightarrow{dl}}\ \left(2.2\right).\]

Следовательно:

\[\int\limits_{AbB}{\overrightarrow{B}\overrightarrow{dl}}=\int\limits^B_A{\overrightarrow{B}\overrightarrow{dl}}={\varphi }_{mA}-{\varphi }_{mB}\left(2.3\right).\]

Выражение (2.3) можно рассматривать как разность скалярных магнитных потенциалов в точках A и B. Если поступить, как делалось для потенциала в электростатике, то есть принять, что в какой то точке, например токе B потенциал равне нулю, то запишем:

\[\int\limits^B_A{\overrightarrow{B}\overrightarrow{dl}}={\varphi }_{mA}\left(2.4\right).\]

Однако, если выбрать контур, который будет охватывать какой-либо ток, например контур AcbB (рис.1) в таком случае линейный интеграл по замкнутому контуру от циркуляции вектора индукции по нему будет отличен от нуля:

\[\oint\limits_{AcbB}{\overrightarrow{B}\overrightarrow{dl}\ne }0\ \left(2.5\right).\]

или

\[\oint\limits_{AcBbА}{\overrightarrow{B}\overrightarrow{dl}=\int\limits_{AсB}{\overrightarrow{B}\overrightarrow{dl}}}-\int\limits_{AbB}{\overrightarrow{B}\overrightarrow{dl}}=I\ne 0\left(2.6\right).\]

В таком случае:

\[\int\limits_{AсB}{\overrightarrow{B}\overrightarrow{dl}}=\int\limits_{AbB}{\overrightarrow{B}\overrightarrow{dl}}+I=ц_{mA}-ц_{mB}+I\ \left(2.7\right).\]

Так, если мы выберем какой — то путь AnB, который охватывает ток n- раз, то получим:

\[\int\limits_{AnB}{\overrightarrow{B}\overrightarrow{dl}}={\varphi }_{mA}-{\varphi }_{mB}+nI(2.8)\]

Зададим нулевой потенциал в точке B, тогда имеем, что:

\[\int\limits_{AnB}{\overrightarrow{B}\overrightarrow{dl}}={\varphi }_{mA}+nI\left(2.9\right).\]

Уравнение (2.9) показывает, что скалярный магнитный потенциал — не однозначная величина.

Магнитное поле простыми словами

При подключении к двум параллельным проводникам электрического тока, они будут притягиваться или отталкиваться, в зависимости от направления (полярности) подключенного тока. Это объясняется явлением возникновения материи особого рода вокруг этих проводников. Эта материя называется магнитное поле (МП). Магнитной силой называется сила, с которой проводники действуют друг на друга.

Теория магнетизма возникла еще в древности, в античной цивилизации Азии. В Магнезии в горах нашли особую породу, куски которой могли притягиваться между собой. По названию места эту породу назвали «магнетиками». Стержневой магнит содержит два полюса. На полюсах особенно сильно обнаруживаются его магнитные свойства.

Магнит, висящий на нитке, своими полюсами будет показывать стороны горизонта. Его полюса будут повернуты на север и юг. На таком принципе действует устройство компаса. Разноименные полюсы двух магнитов притягиваются, а одноименные отталкиваются.

Ученые обнаружили, что намагниченная стрелка, находящаяся возле проводника, отклоняется при прохождении по нему электрического тока. Это говорит о том, что вокруг него образуется МП.

Магнитное поле оказывает влияние на:

• Перемещающиеся электрические заряды.
• Вещества, называемые ферромагнетиками: железо, чугун, их сплавы.

Постоянные магниты – тела, имеющие общий магнитный момент заряженных частиц (электронов).

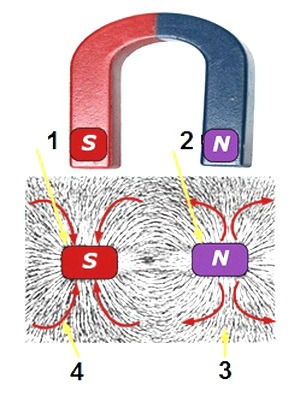
1 — Южный полюс магнита
2 — Северный полюс магнита
3 — МП на примере металлических опилок
4 — Направление магнитного поля

Силовые линии появляются при приближении постоянного магнита к бумажному листу, на который насыпан слой железных опилок. На рисунке четко видны места полюсов с ориентированными силовыми линиями.

Источники магнитного поля

• Электрическое поле, меняющееся во времени.
• Подвижные заряды.
• Постоянные магниты.

С детства нам знакомы постоянные магниты. Они использовались в качестве игрушек, которые притягивали к себе различные металлические детали. Их прикрепляли к холодильнику, они были встроены в различные игрушки.

Электрические заряды, которые находятся в движении, чаще всего имеют больше магнитной энергии, по сравнению с постоянными магнитами.

Свойства

• Главным отличительным признаком и свойством магнитного поля является относительность. Если неподвижно оставить заряженное тело в некоторой системе отсчета, а рядом расположить магнитную стрелку, то она укажет на север, и при этом не «почувствует» постороннего поля, кроме поля земли. А если заряженное тело начать двигать возле стрелки, то вокруг тела появится МП. В результате становится ясно, что МП формируется только при передвижении некоторого заряда.
• Магнитное поле способно воздействовать и влиять на электрический ток. Его можно обнаружить, если проконтролировать движение заряженных электронов. В магнитном поле частицы с зарядом отклонятся, проводники с протекающим током будут перемещаться. Рамка с подключенным питанием тока станет поворачиваться, а намагниченные материалы переместятся на некоторое расстояние. Стрелка компаса чаще всего окрашивается в синий цвет. Она является полоской намагниченной стали. Компас ориентируется всегда на север, так как у Земли есть МП. Вся планета – это как большой магнит со своими полюсами.

Магнитное поле не воспринимается человеческими органами, и может фиксироваться только особыми приборами и датчиками. Оно бывает переменного и постоянного вида. Переменное поле обычно создается специальными индукторами, которые функционируют от переменного тока. Постоянное поле формируется неизменным электрическим полем.

Основные правила

Правило буравчика

Силовая линия изображается в плоскости, которая расположена под углом 90 0 к пути движения тока таким образом, чтобы в каждой точке сила была направлена по касательной к линии.

Чтобы определить направление магнитных сил, нужно вспомнить правило буравчика с правой резьбой.

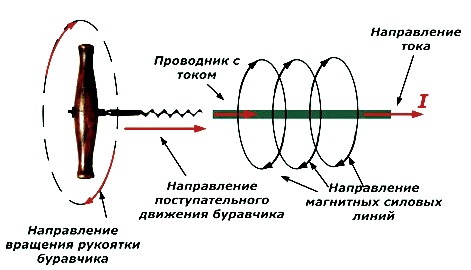
Буравчик нужно расположить по одной оси с вектором тока, рукоятку вращать таким образом, чтобы буравчик двигался в сторону его направления. В этом случае ориентация линий определится вращением рукоятки буравчика.

Правило буравчика для кольца

Поступательное перемещение буравчика в проводнике, выполненном в виде кольца, показывает, как ориентирована индукция, вращение совпадает с течением тока.

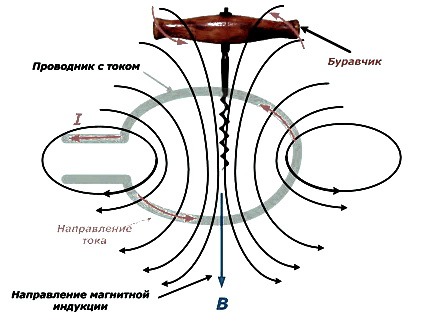
Силовые линии имеют свое продолжение внутри магнита и не могут быть разомкнутыми.

Магнитное поле разных источников суммируются между собой. При этом они создают общее поле.

Магниты с одинаковыми полюсами отталкиваются, а с разными – притягиваются. Значение силы взаимодействия зависит от удаленности между ними. При приближении полюсов сила возрастает.

Параметры магнитного поля

• Сцепление потоков (Ψ).
• Вектор магнитной индукции (В).
• Магнитный поток (Ф).

Интенсивность магнитного поля вычисляется размером вектора магнитной индукции, которая зависит от силы F, и формируется током I по проводнику, имеющему длину l: В = F / (I * l).

Магнитная индукция измеряется в Тесла (Тл), в честь ученого, изучавшего явления магнетизма и занимавшегося их методами расчета. 1 Тл равна индукции магнитного потока силой 1 Н на длине 1 м прямого проводника, находящегося под углом 90 0 к направлению поля, при протекающем токе в один ампер:

1 Тл = 1 х Н / (А х м).

Правило левой руки

Правило находит направление вектора магнитной индукции.

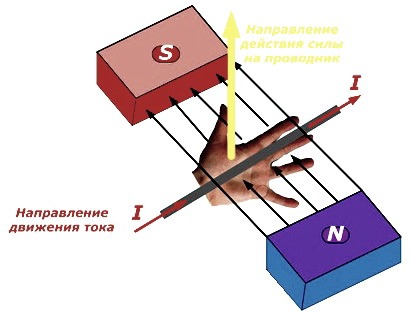
Если ладонь левой руки разместить в поле, чтобы линии магнитного поля входили в ладонь из северного полюса под 90 0 , а 4 пальца разместить по течению тока, большой палец покажет направление магнитной силы.

Если проводник находится под другим углом, то сила будет прямо зависеть от тока и проекции проводника на плоскость, находящуюся под прямым углом.

Сила не зависит от вида материала проводника и его сечения. Если проводник отсутствует, а заряды движутся в другой среде, то сила не изменится.

При направлении вектора магнитного поля в одну сторону одной величины, поле называется равномерным. Различные среды влияют на размер вектора индукции.

Магнитный поток

Магнитная индукция, проходящая по некоторой площади S и ограниченная этой площадью, является магнитным потоком.

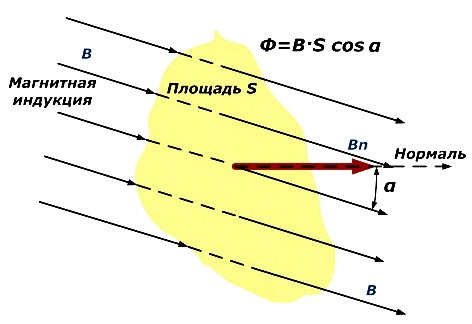
Если площадь имеет наклон на некоторый угол α к линии индукции, магнитный поток снижается на размер косинуса этого угла. Наибольшая его величина образуется при нахождении площади под прямым углом к магнитной индукции:

Ф = В * S.

Магнитный поток измеряется в такой единице, как «вебер», который равен протеканием индукции величиной

1 Тл по площади в 1 м 2 .

Потокосцепление

Такое понятие применяется для создания общего значения магнитного потока, который создан от некоторого числа проводников, находящихся между магнитными полюсами.

В случае, когда одинаковый ток I протекает по обмотке с количеством витков n, общий магнитный поток, образованный всеми витками, является потокосцеплением.

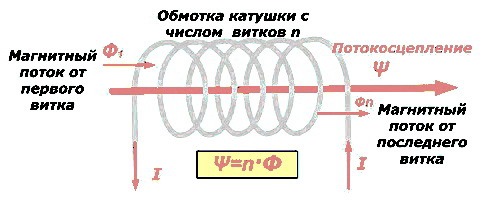
Потокосцепление Ψ измеряется в веберах, и равно: Ψ = n * Ф.

Магнитные свойства

Магнитная проницаемость определяет, насколько магнитное поле в определенной среде ниже или выше индукции поля в вакууме. Вещество называют намагниченным, если оно образует свое магнитное поле. При помещении вещества в магнитное поле у него появляется намагниченность.

Ученые определили причину, по которой тела получают магнитные свойства. Согласно гипотезе ученых внутри веществ есть электрические токи микроскопической величины. Электрон обладает своим магнитным моментом, который имеет квантовую природу, движется по некоторой орбите в атомах. Именно такими малыми токами определяются магнитные свойства.

Если токи движутся беспорядочно, то магнитные поля, вызываемые ими, самокомпенсируются. Внешнее поле делает токи упорядоченными, поэтому формируется магнитное поле. Это является намагниченностью вещества.

Различные вещества можно разделить по свойствам взаимодействия с магнитными полями. Их разделяют на группы:

• Парамагнетики – вещества, имеющие свойства намагничивания в направлении внешнего поля, обладающие низкой возможностью магнетизма. Они имеют положительную напряженность поля. К таким веществам относят хлорное железо, марганец, платину и т. д.
• Ферримагнетики – вещества с неуравновешенными по направлению и значению магнитными моментами. В них характерно наличие некомпенсированного антиферромагнетизма. Напряженность поля и температура влияет на их магнитную восприимчивость (различные оксиды).
• Ферромагнетики – вещества с повышенной положительной восприимчивостью, зависящей от напряженности и температуры (кристаллы кобальта, никеля и т. д.).
• Диамагнетики – обладают свойством намагничивания в противоположном направлении внешнего поля, то есть, отрицательное значение магнитной восприимчивости, не зависящая от напряженности. При отсутствии поля у этого вещества не будет магнитных свойств. К таким веществам относятся: серебро, висмут, азот, цинк, водород и другие вещества.
• Антиферромагнетики – обладают уравновешенным магнитным моментом, вследствие чего образуется низкая степень намагничивания вещества. У них при нагревании осуществляется фазовый переход вещества, при котором возникают парамагнитные свойства. При снижении температуры ниже определенной границы, такие свойства появляться не будут (хром, марганец).

Рассмотренные магнетики также классифицируются еще по двум категориям:

• Магнитомягкие материалы. Они обладают низкой коэрцитивной силой. При маломощных магнитных полях они могут войти в насыщение. При процессе перемагничивания у них наблюдаются незначительные потери. Вследствие этого такие материалы используются для производства сердечников электрических устройств, функционирующих на переменном напряжении (асинхронный электродвигатель, генератор, трансформатор).
• Магнитотвердые материалы. Они обладают повышенной величиной коэрцитивной силы. Чтобы их перемагнитить, потребуется сильное магнитное поле. Такие материалы используются в производстве постоянных магнитов.

Магнитные свойства различных веществ находят свое использование в технических проектах и изобретениях.

Магнитные цепи

Объединение нескольких магнитных веществ называется магнитной цепью. Они являются подобием электрических цепей и определяются аналогичными законами математики.

На базе магнитных цепей действуют электрические приборы, индуктивности, трансформаторы. У функционирующего электромагнита поток протекает по магнитопроводу, изготовленному из ферромагнитного материала и воздуху, который не является ферромагнетиком. Объединение этих компонентов является магнитной цепью. Множество электрических устройств в своей конструкции содержат магнитные цепи.

Электромагнитное поле — это такая фигня.. . Смотри, когда через кусок провода идет ток — вокруг провода появляется магнитное поле, так (есть правило буравчика, оно же правило правого винта, которое указывает отношение направления тока в проводе с направлением магнитныхь силовых линий) .

С другой стороны, если мимо проводника, по которому не течет ток, пронести магнит — в момент проноса магнита появится ток.

А теперь представь что у нас в пространстве множество проводов. Создаем в первом проводе электрическое поле, в результате чего через него начинает течь ток. Ток вызывает появление вокруг проводника магнитного поля. Это магнитное поле вызывает появление тока во 2-м проводнике, ток во 2-м проводнике вызывает появление вокруг него магнитного поля. В результате, по всем проводникам в пространстве пробегает ЭЛЕКТРОМАГНИТНАЯ ВОЛНА.

Давайте вместе разбираться в том, что такое магнитное поле. Ведь многие люди живут в этом поле всю жизнь и даже не задумываются о нем. Пора это исправить!

Магнитное поле

Магнитное поле – особый вид материи. Оно проявляется в действии на движущиеся электрические заряды и тела, которые обладают собственным магнитным моментом (постоянные магниты).

Важно: на неподвижные заряды магнитное поле не действует! Создается магнитное поле также движущимися электрическими зарядами, либо изменяющимся во времени электрическим полем, либо магнитными моментами электронов в атомах. То есть любой провод, по которому течет ток, становится также и магнитом!

Магнит

Магнит — тело, обладающее собственным магнитным полем.

У магнита есть полюса, называемые северным и южным. Обозначения «северный» и «южный» даны лишь для удобства (как «плюс» и «минус» в электричестве).

Магнитное поле изображается посредством силовых магнитных линий. Силовые линии непрерывны и замкнуты, а их направление всегда совпадает с направлением действия сил поля. Если вокруг постоянного магнита рассыпать металлическую стружку, частицы металла покажут наглядную картину силовых линий магнитного поля, выходящих из северного и входящих в южный полюс. Графическая характеристика магнитного поля — силовые линии.

Картина магнитного поля

Характеристики магнитного поля

Основными характеристиками магнитного поля являются магнитная индукция, магнитный поток и магнитная проницаемость. Но давайте обо всем по порядку.

Сразу отметим, что все единицы измерения приводятся в системе СИ.

Магнитная индукция B – векторная физическая величина, являющаяся основной силовой характеристикой магнитного поля. Обозначается буквой B. Единица измерения магнитной индукции – Тесла (Тл).

Магнитная индукция показывает, насколько сильно поле, определяя силу, с которой оно действует на заряд. Данная сила называется силой Лоренца.

Здесь q — заряд, v — его скорость в магнитном поле, B — индукция, F — сила Лоренца, с которой поле действует на заряд.

Магнитный поток Ф – физическая величина, равная произведению магнитной индукции на площадь контура и косинус между вектором индукции и нормалью к плоскости контура, через который проходит поток. Магнитный поток — скалярная характеристика магнитного поля.

Можно сказать, что магнитный поток характеризует количество линий магнитной индукции, пронизывающих единицу площади. Магнитный поток измеряется в Веберах (Вб).

Магнитный поток

Магнитная проницаемость – коэффициент, определяющий магнитные свойства среды. Одним из параметров, от которых зависит магнитная индукция поля, является магнитная проницаемость.

Магнитное поле Земли

Наша планета на протяжении нескольких миллиардов лет является огромным магнитом. Индукция магнитного поля Земли изменяется в зависимости от координат. На экваторе она равна примерно 3,1 на 10 в минус пятой степени Тесла. К тому же существуют магнитные аномалии, где значение и направление поля существенно отличаются от соседних областей. Одни из самых крупных магнитных аномалий на планете — Курская и Бразильская магнитные аномалии.

Происхождение магнитного поля Земли до сих пор остается загадкой для ученых. Предполагается, что источником поля является жидкое металлическое ядро Земли. Ядро движется, значит, движется расплавленный железо-никелевый сплав, а движение заряженных частиц – это и есть электрический ток, порождающий магнитное поле. Проблема в том, что эта теория (геодинамо) не объясняет того, как поле сохраняется устойчивым.

Магнитное поле земли

Земля – огромный магнитный диполь. Магнитные полюса не совпадают с географическими, хотя и находятся в непосредственной близости. Более того, магнитные полюса Земли движутся. Их смещение регистрируется с 1885 года. Например, за последние сто лет магнитный полюс в Южном полушарии сместился почти на 900 километров и сейчас находится в Южном океане. Полюс арктического полушария движется через Северный Ледовитый океан к Восточно-Сибирской магнитной аномалии, скорость его передвижения (по данным 2004 года) составила около 60 километров в год. Сейчас наблюдается ускорение движения полюсов — в среднем скорость растет на 3 километра в год.

Каково значение магнитного поля Земли для нас? В первую очередь магнитное поле Земли защищает планету от космических лучей и солнечного ветра. Заряженные частицы из далекого космоса не падают прямо на землю, а отклоняются гигантским магнитом и движутся вдоль его силовых линий. Таким образом, все живое оказывается защищенным от пагубной радиации.

Магнитное поле Земли

За историю Земли происходило несколько инверсий (смен) магнитных полюсов. Инверсия полюсов – это когда они меняются местами. Последний раз это явление произошло около 800 тысяч лет назад, а всего геомагнитных инверсий в истории Земли было более 400. Некоторые ученые полагают, что с учетом наблюдающегося ускорения движения магнитных полюсов следующей инверсии полюсов следует ожидать в ближайшие пару тысяч лет.

К счастью, в нашем веке смены полюсов пока не ожидается. А значит, можно думать о приятном и наслаждаться жизнью в старом добром постоянном поле Земли, рассмотрев основные свойства и характеристики магнитного поля. А чтобы Вы могли это делать, существуют наши авторы, которым можно с уверенностью в успехе поручить часть учебных хлопот! Курсовая работа международное и национальное право и другие типы работ вы можете заказать по ссылке.

Векторный потенциал магнитного поля

Векторный потенциал магнитного поля – это плавно меняющаяся от точки к точке векторная величина, ротор которой равен магнитной индукции.

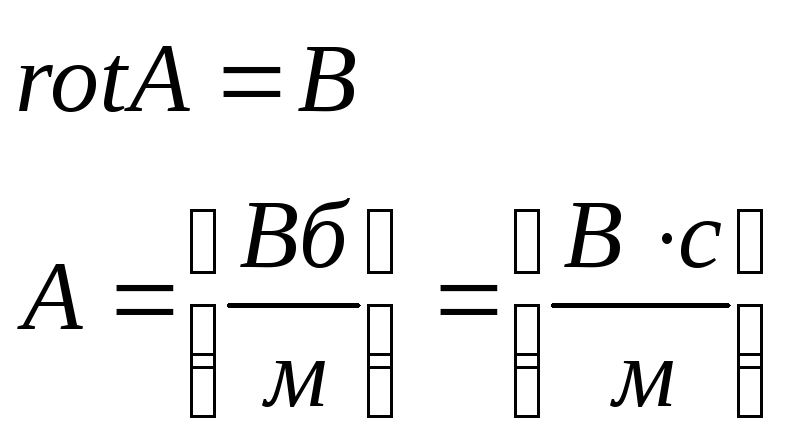
Векторный потенциал можно применять для любых областей пространства, в том числе и для областей занятых токами.

Уравнение 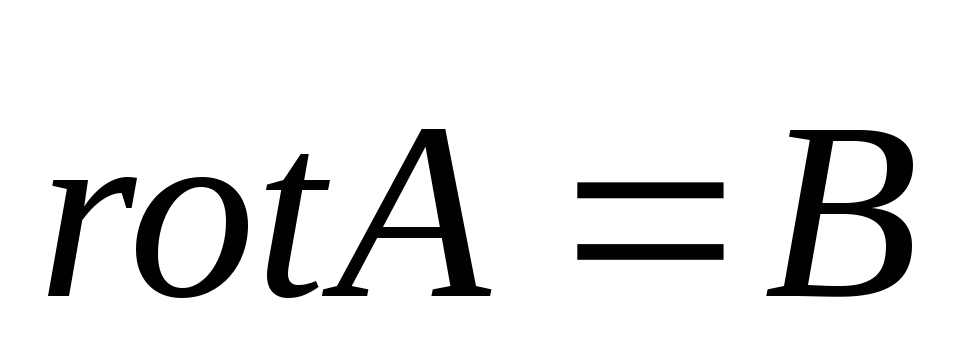возможно с учетом того, что 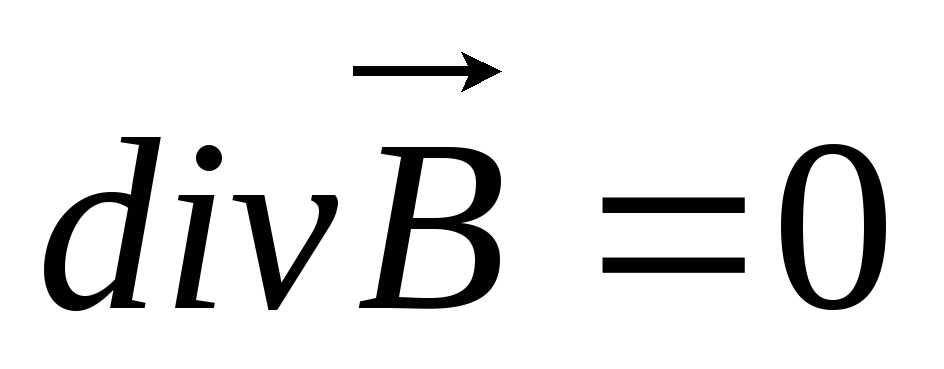(принцип непрерывности) тогда 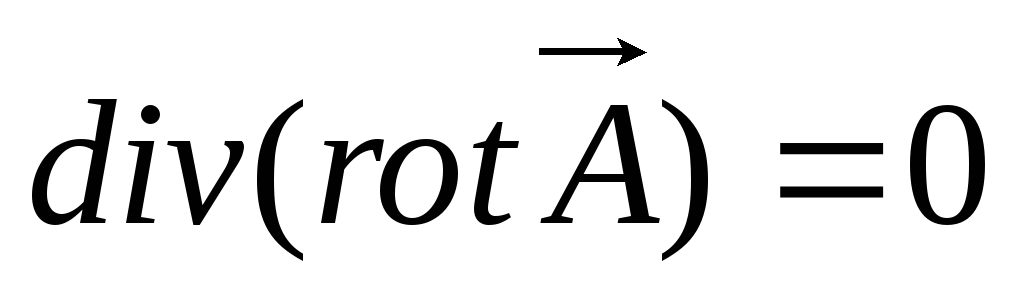, а дивергенция от любого ротора равна нулю (из математики).

Векторный потенциал магнитного поля вводится для расчета вихревых полей (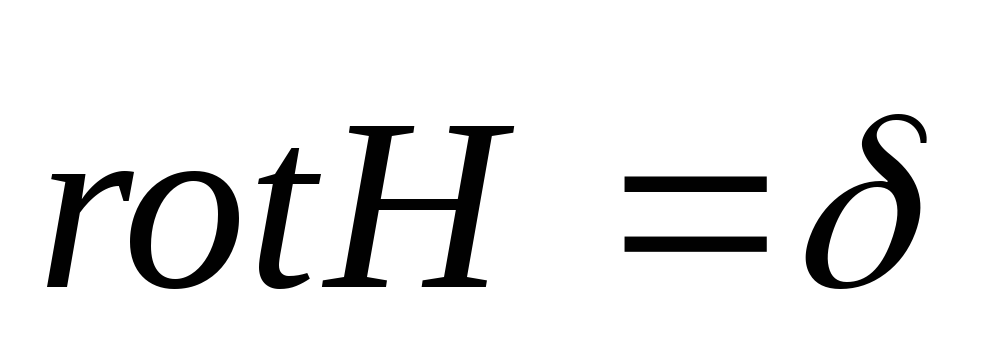). Но применим и для расчета потенциальных полей.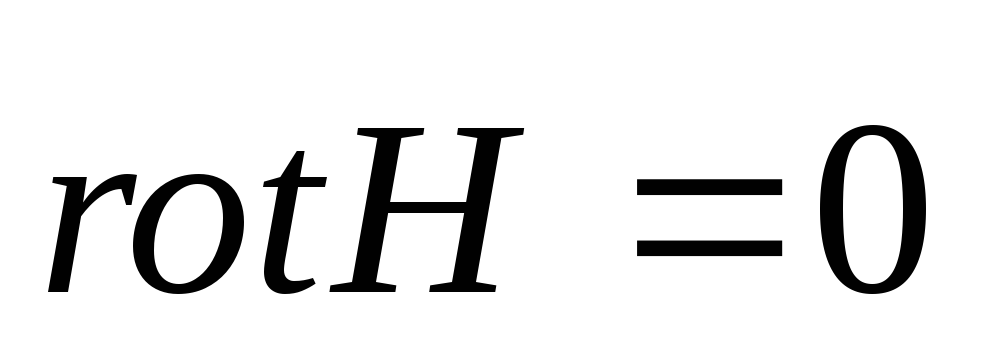

Направление векторного магнитного потенциала такое же, как и у тока в проводнике.

С помощью векторного потенциала магнитного поля решают следующие типы задач:

1) Определение магнитной индукции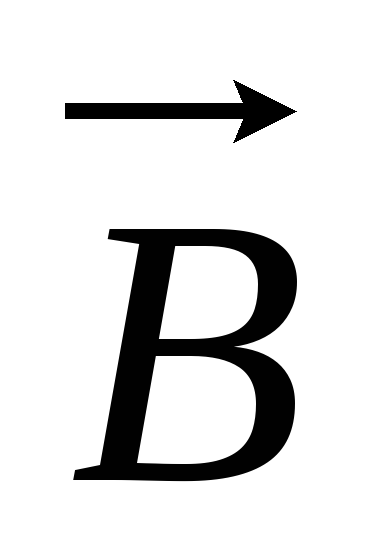

2) Определение магнитного потока, пронизывающего какой-либо контур.

Пример: Определить поток 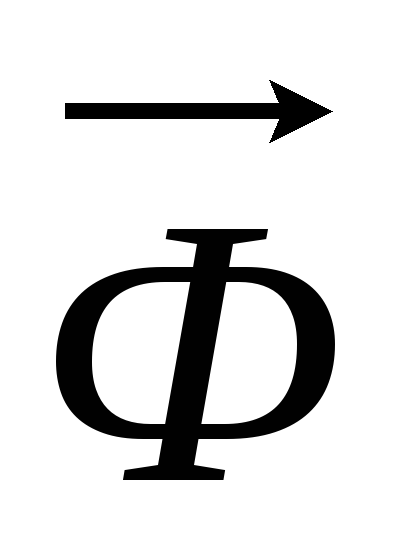, пронизывающий рамку, который создаётся проводником с током.

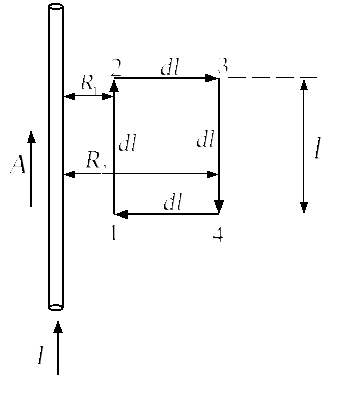
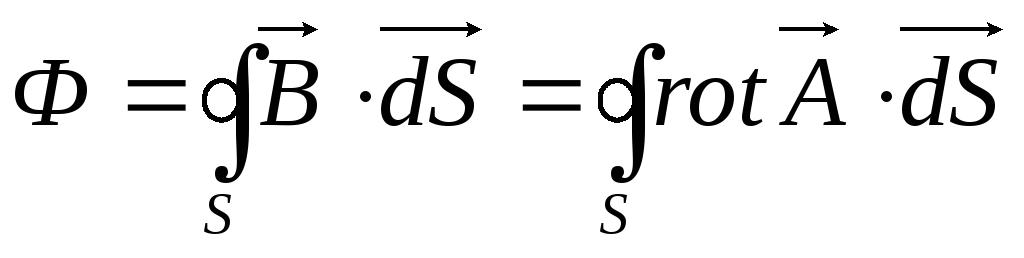
По теореме Стокса: заменим поверхностный интеграл на линейный (поток через поверхность ограниченную контуром заменим на циркуляцию по контуру):

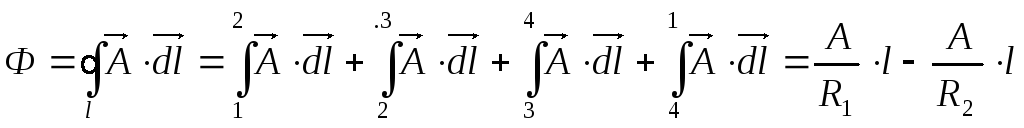
Уравнение Пуассона

Для областей занятых токами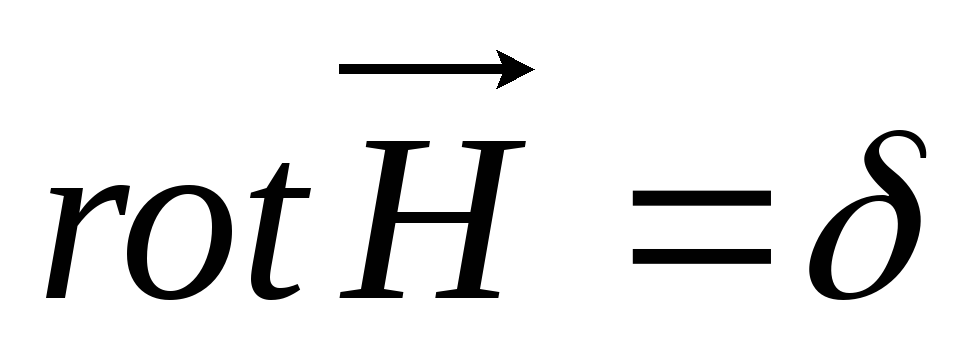

Умножим обе части уравнения на магнитную проницаемость 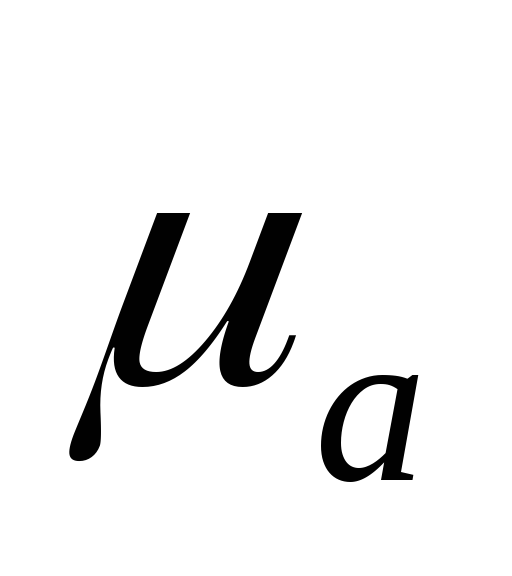=const:

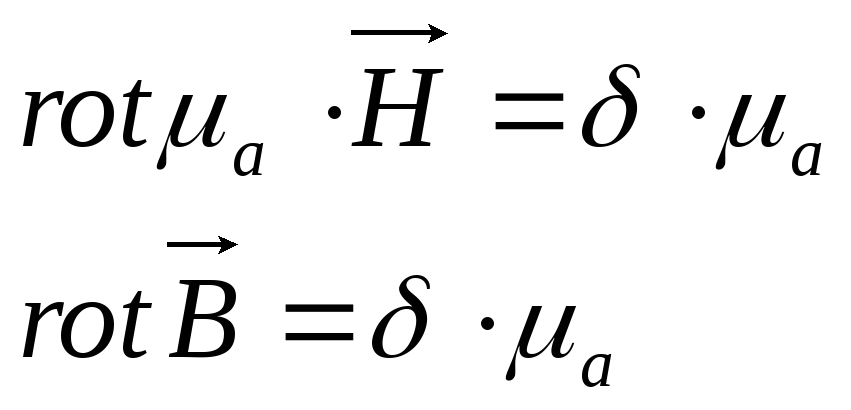
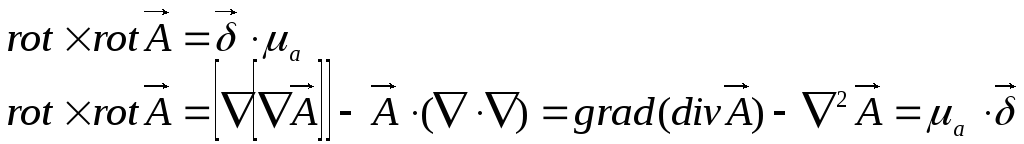
Линии векторного магнитного потенциала замкнуты на себя, то есть: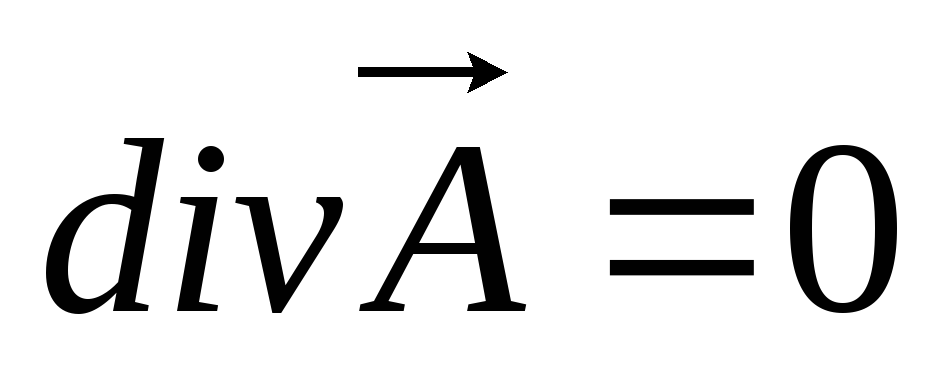

Тогда 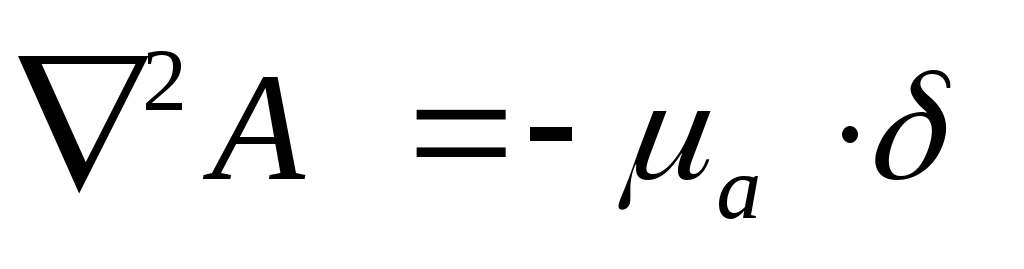-уравнение Пуассона для векторного магнитного потенциала.

Поскольку в обе части уравнения входят векторные величины, то это уравнение можно переписать для декартовой системы координат:

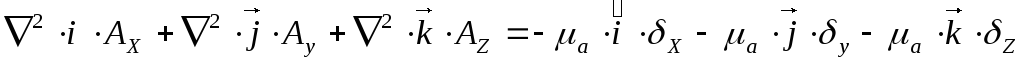
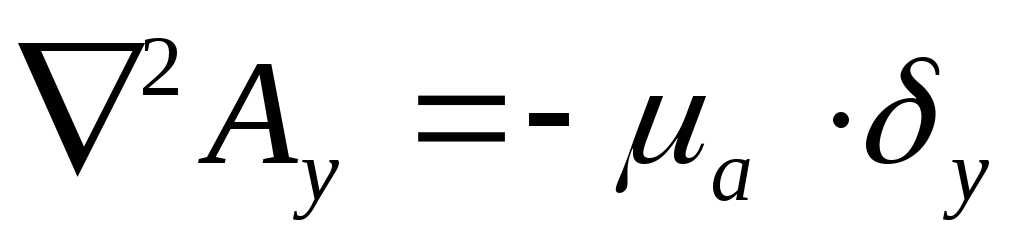
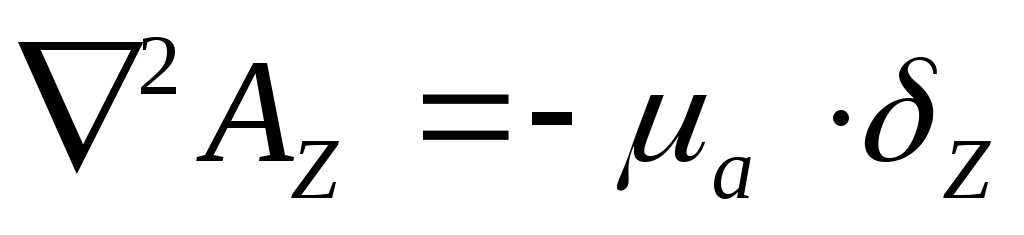
Решая это уравнение, получим проекции на оси координат:

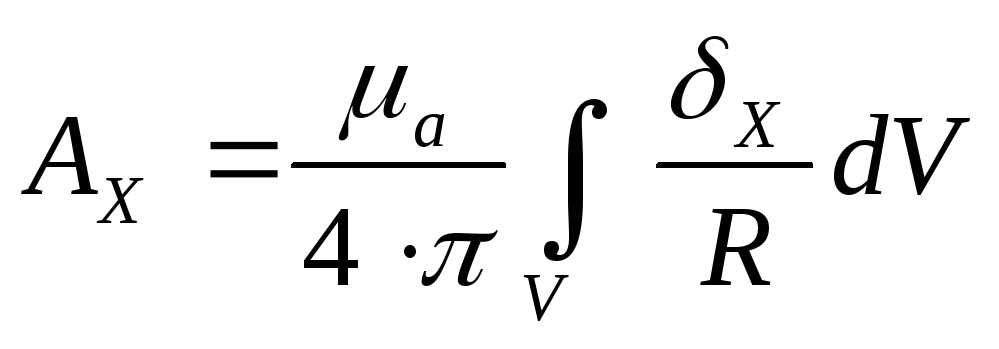
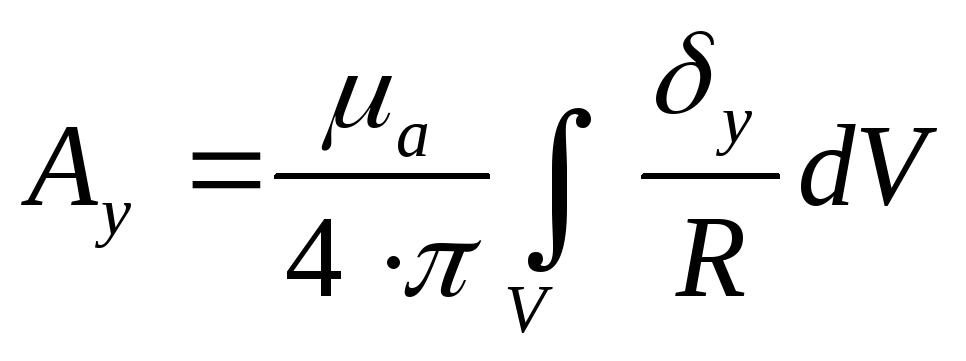
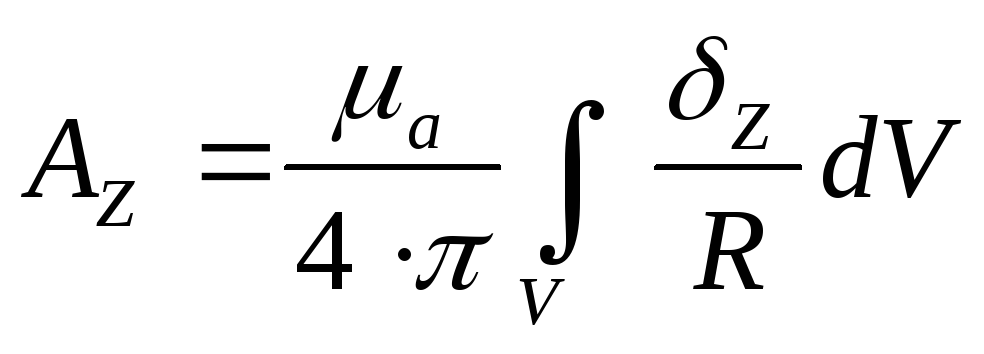
умножим на единичные орты, получим:

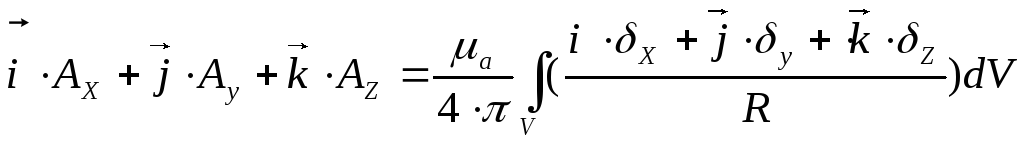
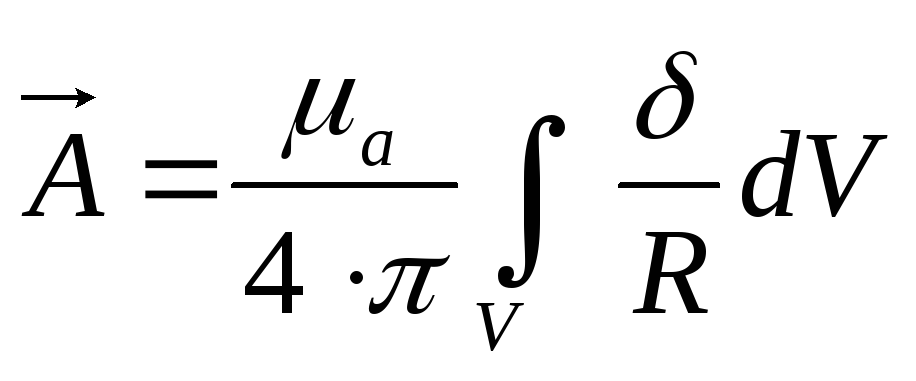— общее решение уравнения Пуассона.

С помощью этой формулы можно найти векторный потенциал в любой точке поля, для этого интеграл в правой части уравнения должен быть взят по всем областям, занятым током.

Однако, пользоваться этой формулой каждый раз нецелесообразно, так как взятие интеграла правой части формулы сопряжено обычно со значительными математическими выкладками.

Пример: В точке А необходимо определить направление

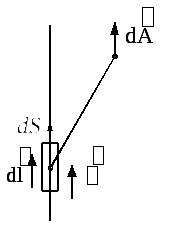
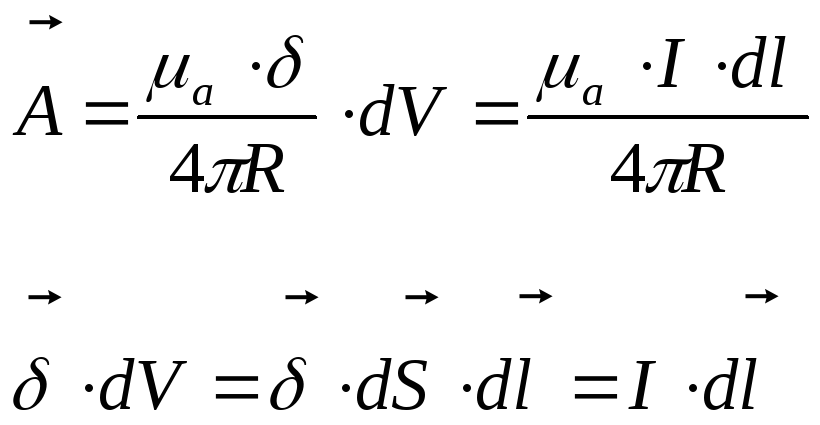
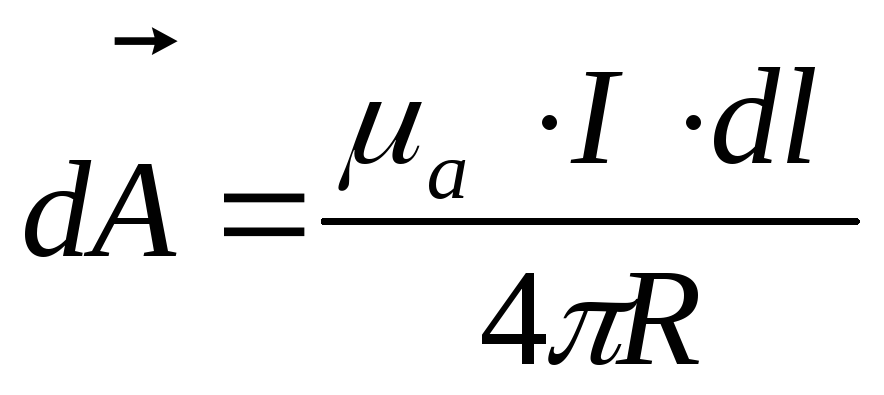
Составляющая векторного магнитного потенциала имеет такое же направление в пространстве, как и ток в элементе проводника.

Метод зеркальных изображений

В магнитном поле постоянного тока, вблизи границы раздела двух сред, для расчета поля используют метод зеркальных изображений.

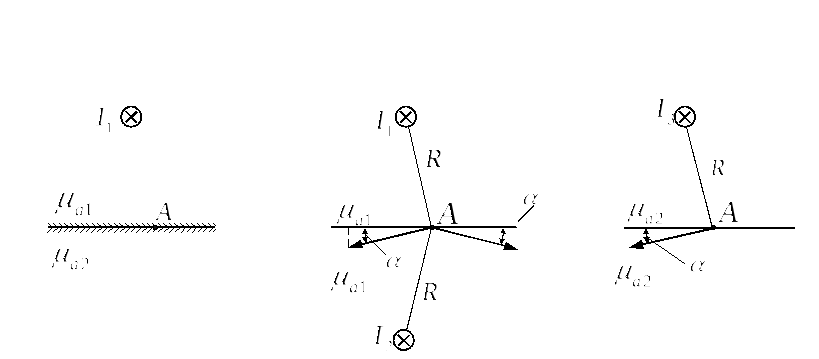
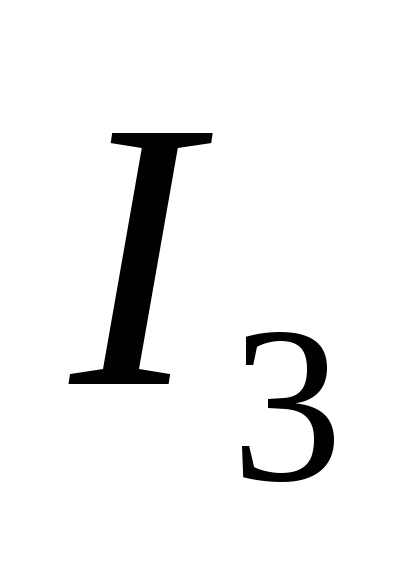Методика расчета полностью аналогична задаче расчета электростатического поля, созданного двумя заряженными осями, расположенными вблизи плоской границы раздела двух диэлектриков с различными диэлектрическими проницаемостями.. Линейная плотность заряда заменяется током (), а относительная диэлектрическая постоянная среды — относительной магнитной постоянной()

и 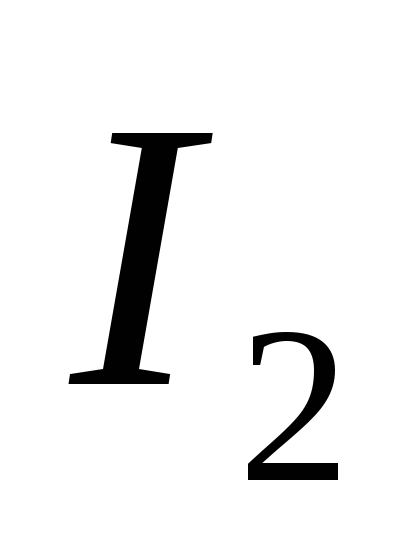— фиктивные токи

Найдем фиктивные токи, исходя из граничных условий. Для этого рассмотрим точку, лежащую на границе раздела сред; ее можно считать принадлежащей как к первой, так и ко второй среде.

Из первого граничного условия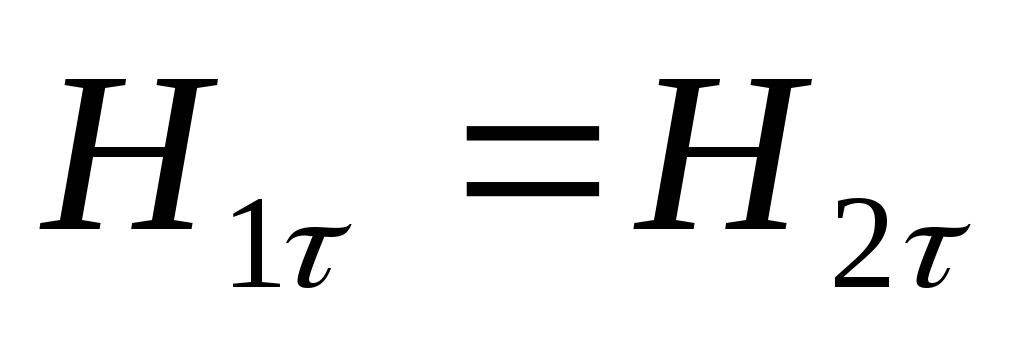

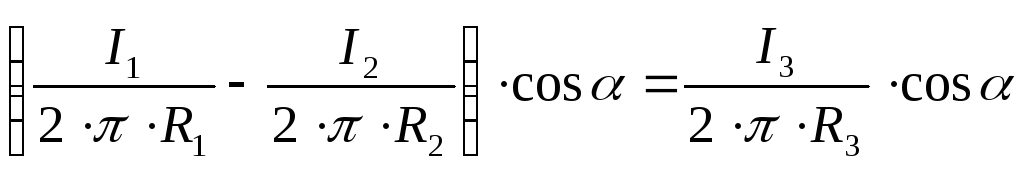
Левая часть уравнения определяет принадлежность точки первой среде.

Правая часть уравнения определяет принадлежность точки второй среде.

Сокращая одинаковые элементы в правой и левой частях уравнения, получим

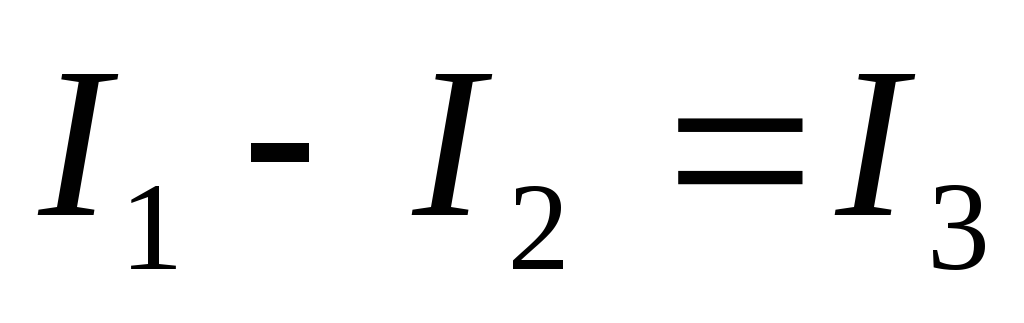
Из второго граничного условия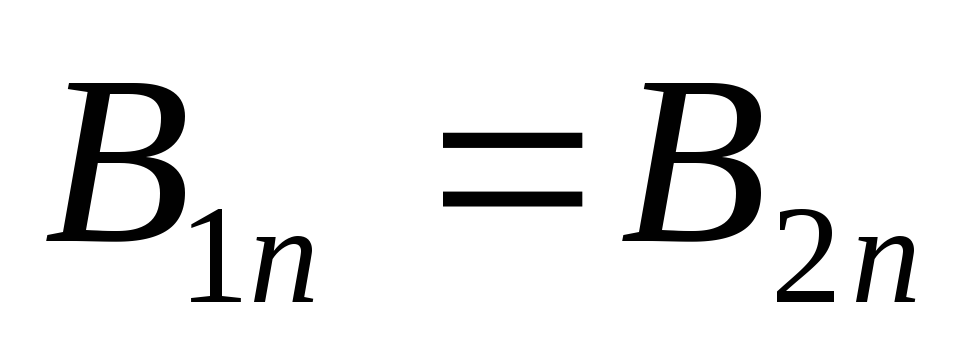

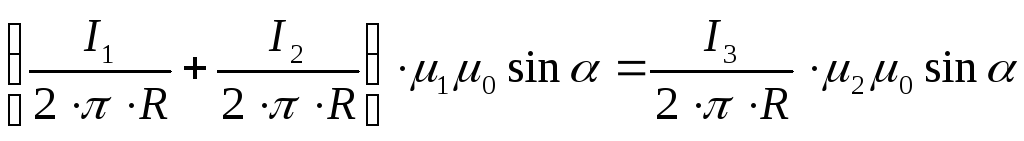
Левая часть уравнения определяет принадлежность точки к первой среде.

Правая часть уравнения определяет принадлежность точки ко второй среде.

Сокращая одинаковые элементы в правой и левой частях уравнения, получим:

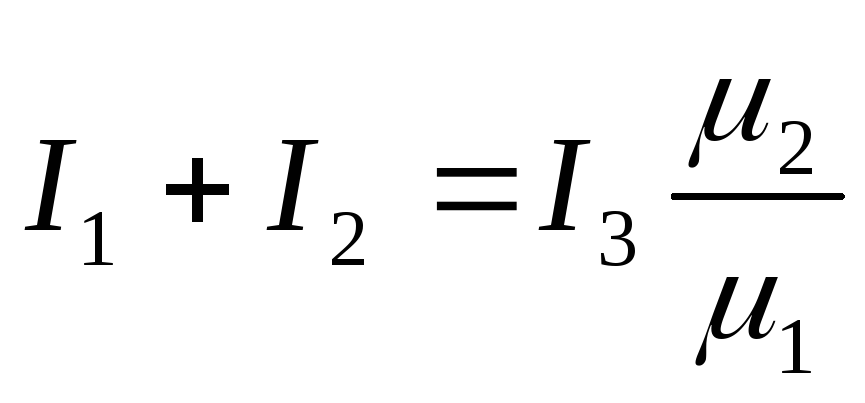
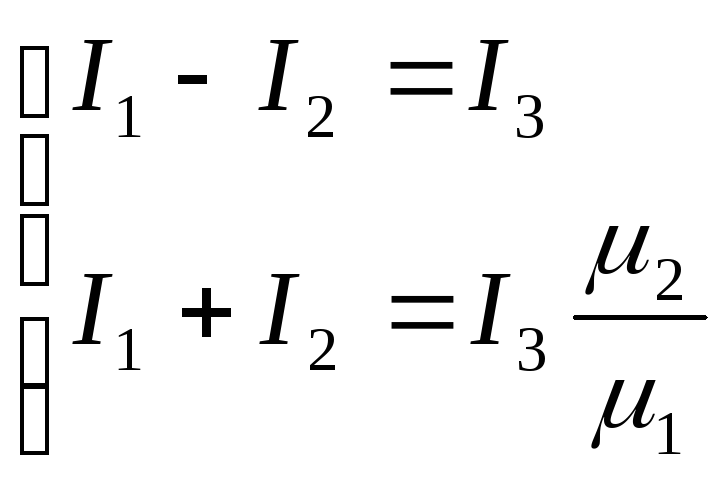
Решая систему из двух уравнений, получим значения фиктивных токов: