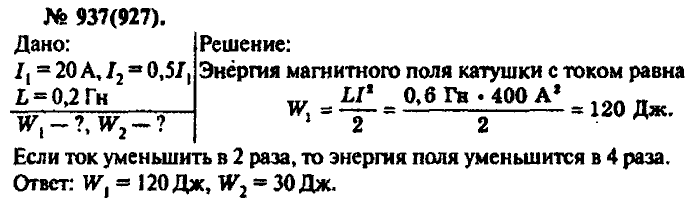42 — магнитный поток в катушке с током
Проще говоря, переменный ток превращает катушку в электрический генератор. Производимый ток направлен в сторону, противоположную внешнему току. Однако стоит отметить, что это можно сказать только с математической точки зрения, в терминах формул. На практике изменение тока в катушке подобно удару руки по воде: чем медленнее движется рука, тем меньше сопротивление воды, но чем быстрее она движется, тем больше сопротивление при ударе о жидкость. В физике это явление называется самоиндукцией. Индуктивность катушки также называется коэффициентом самоиндукции.
Содержание
42 – магнитный поток в катушке с током
Ф – магнитный поток, Вб (Вебер)
L – индуктивность катушки, Гн (Генри)
I – сила тока, A (ампер).
Индукционная катушка состоит из витков изолированного проводника. Обычно это катушки медной проволоки, покрытые краской или любой непроводящей оболочкой. Главная особенность катушки заключается в том, что при пропускании через нее электрического тока она становится электромагнитом. То есть, он начинает создавать магнитное поле. В случае постоянного тока свойства катушки невозможно переоценить – это кусок провода, который можно заменить перемычкой.
То есть, он начинает создавать магнитное поле. В случае постоянного тока свойства катушки невозможно переоценить – это кусок провода, который можно заменить перемычкой.
Когда на катушку подается переменное напряжение, начинают происходить удивительные вещи. Ток меняется, а значит, меняется напряженность магнитного поля, которое создает катушка. Магнитная индукция, создаваемая катушками, изменяется, и, следовательно, изменяется магнитный поток. А согласно закону электромагнитной индукции, изменение магнитного потока приводит к возникновению ЭДС.
Проще говоря, переменный ток превращает катушку в электрический генератор. Генерируемый ток противоположен внешнему току. Стоит отметить, однако, что говорить об этом можно только в математических терминах, в формулах. На практике изменение тока в катушке напоминает удар рукой по воде: чем медленнее движется рука, тем меньше сопротивление воды, но чем быстрее она движется, тем большее сопротивление она встречает при ударе о жидкость.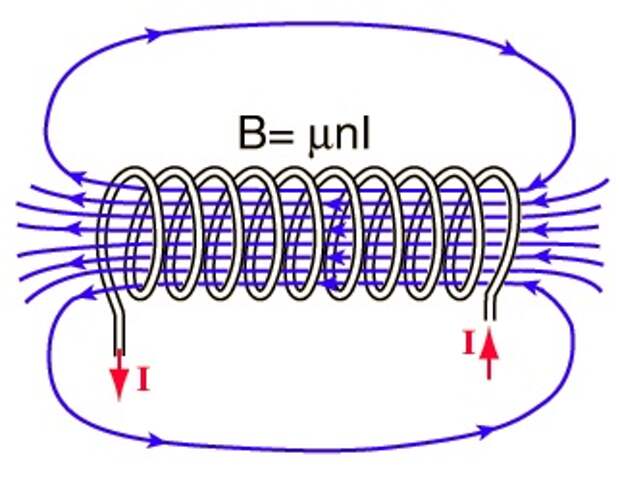 В физике это явление называется самоиндукцией. Индуктивность катушки также называется коэффициентом самоиндукции.
В физике это явление называется самоиндукцией. Индуктивность катушки также называется коэффициентом самоиндукции.
Что такое индуктивность и как она зависит от количества витков и других параметров, лучше всего понять на практике.
В этом видео все основные свойства индуктора показаны на практических примерах.
В обычной жизни люди редко сталкиваются с измерениями индуктивности и магнитного потока, поэтому эти понятия плохо запоминаются.
Простой способ узнать эти термины – понять, как работают металлоискатели и металлодетекторы. Стойки с металлоискателями можно увидеть на вокзалах и в торговых центрах. Если вы поймете, как они работают, значение таких терминов, как индуктивность и магнитный поток, станет понятным.
Проблема 42.
При силе тока 10 А в катушке возникает магнитный поток 50 мВб. Чему равна индуктивность катушки.
Дано rg = 800 кг / м³ V = 8 м³ F – ? Решение: rj = gpoj * h V = a³ a = 2m rj = 10n / kg * 800kg / m³ * 2m = 16000Pa p = F / S S = a² S = 2² = 4m² F = p * S F = 16000n / m² * 4m² = 64000n = 64Kn.
Магнитное поле катушки с индуктивностью 95 мГн имеет энергию 0,19 Дж.
Какова сила тока в катушке?
Если вы хотите узнать ответ на вопрос Каков магнитный поток катушки с индуктивностью 40 МГ при силе тока 5 А? относящиеся к уровню 5-9 классов, то вы попали на нужную страницу. В категории “Физика” вы также можете найти ответы на похожие вопросы по интересующей вас теме, используя автоматический “умный” поиск. Если после прочтения всех ответов у вас остались сомнения или представленная информация не исчерпывает тему, воспользуйтесь кнопкой в верхней части страницы, чтобы создать свой вопрос, или обсудите его с посетителями этого сайта.
A = mgh m = pV m = 7800 кг / м3 * 0, 6 м3 = 4680 кг A = 4680 кг * 5 м * 10 Н / кг = 234000 Дж = 234 кДж Ответ : 234 кДж.
Да, можно, потому что расстояние от Земли до Солнца составляет 150 000 000 км = 150 000 000 м, а скорость света – 300 000 000 м/с. Разделив первое на второе, получим 500 с, что составляет 8 минут 20 секунд.
Если мы опустим алюминиевую и серебряную ложки одинаковой массы и температуры в кипящую воду, то алюминиевая ложка получит почти в 4 раза больше тепла, чем вода, потому что
0, 8 * 20 = 16 – V 0, 8 + 0, 8 * 2 + 0, 8 * 3 + 0, 8 * 4 + 0, 8 * 5 + 0, 8 * 6 + 0, 8 * 7 + 0, 8 * 8 + 0, 8 * 9 + 0, 8 * 10 + 0, 8 * 11 + 0, 8 * 12 + 0, 8 * 13 + 0, 8 * 14 + 0, 8 * 15 + 0, 8 * 16 + 0, 8 * 17 + 0, 8 * 18 + 0, 8 * 19 + 0, 8 * 20 = 168 ..
Данные : рг = 800 кг / м³ V = 8 м³ F – ? Решение: rj = gpoj * h V = a³ a = 2m rj = 10n / kg * 800kg / m³ * 2m = 16000Pa p = F / S S = a² S = 2² = 4m² F = p * S F = 16000n / m² * 4m² = 64000n = 64Kn.
Ответ на первый вопрос – точно в.
Работы всегда больше, чем пользы. Это основной закон физики.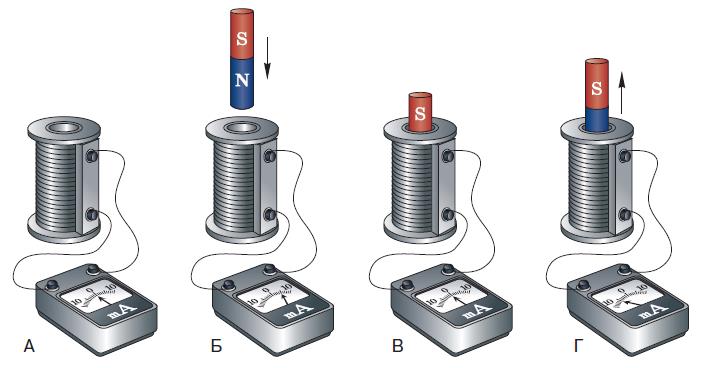 (-3)*10 = 0,2 Вб
(-3)*10 = 0,2 Вб
- 14.10.2016 15:55
- thumb_up 11
Знаете ли вы ответ? Поделитесь!
Как написать хороший ответ?
Чтобы добавить хороший ответ, вы должны:
- Правдиво отвечайте на вопросы, на которые вы знаете правильный ответ;
- Пишите подробно, чтобы ваш ответ был полным и не вызывал дополнительных вопросов;
- Пишите без грамматических, орфографических и пунктуационных ошибок.
Не стоит:
- Копирование ответов из сторонних ресурсов. Уникальные и личные объяснения высоко ценятся;
- Ответы не по существу: “Подумайте об этом”, “Расслабьтесь”, “Я не знаю” и так далее;
- Использование мата – это неуважение к пользователям;
- Запись в верхний регистр.
У вас есть какие-то сомнения?
Не можете найти правильный ответ на свой вопрос или ответа вообще нет? Используйте поисковую систему сайта, чтобы найти все ответы на похожие вопросы по физике.
Проблемы с домашним заданием? Не стесняйтесь просить о помощи – не стесняйтесь задавать вопросы!
Физика – это отрасль естествознания: естественная наука о простейших и наиболее общих законах природы, о материи, ее структуре и движении.
Проблема 2
Дано:
F = 0, 06 Vb;
t = 0,1 с.
Найти: e.
Решение:
e можно найти с помощью формулы, в которой переменные являются дельтами значений, данных нам в условии. Давайте запишем эту формулу: e = дельта F / дельта t. Важно не забывать условие, что дельта F = k*дельта t.
Давайте заменим эти значения и получим ответ.
е = 0,06 /0, 1 = 0,6.
Ответ – 0,6.
1. При силе тока 10 А в катушке индуктивностью 0,4 Гн возникает магнитный поток. Какой магнитный поток присутствует в
Проблема 1.
Дано:
L = 0,4 Гн;
I = 10 A.
Найти: F.
Решение:
Чтобы решить задачу, используйте формулу для нахождения магнитного потока. Это выглядит следующим образом: F = LI.
Давайте привяжем к нему известные нам переменные и получим ответ. F = 0,4 * 10 = 4 Вб.
Ответ: 4.
Задание 2
Дано:
Ф = 0, 06 Вб;
t = 0,1 с.
Найти: e.
Решение:
e можно найти с помощью формулы, в которой переменные являются дельтами значений, данных нам в условии. 2 /2 = 20*0,25 /2 = 5/2 = 2,5 Дж.
2 /2 = 20*0,25 /2 = 5/2 = 2,5 Дж.
Ответ: 2,5
Выберите 6 слов, связанных с темой урока.
Урок 6: Самоиндукция. Индуктивность
Поставьте фигуры в пары так, чтобы каждая пара была ответом на вопрос в заданиях.
1. какова индуктивность цепи, если ее магнитный поток составляет 0,5 мВб (ответ в Гн) при силе тока 5 А?
2. каков магнитный поток в цепи с индуктивностью 0,2 мГн, если сила тока равна 10 А (ответ в Вб)?
3. какая ЭДС самоиндукции наводится в катушке электромагнита с индуктивностью 0,4 Гн, если ток в катушке равномерно изменяется на 5 А за 0,02 с (Ответ в В)?
Физические формулы
Самоиндукция, индуктивность и энергия магнитного поля
Заполните пропуски в тексте, выбирая правильные ответы из выпадающего меню.
Длинный тонкий соленоид проводит ток $I$. Как изменятся следующие физические величины, если увеличить число витков при неизменных геометрических размерах соленоида? Поток вектора магнитной индукции через фронт соленоида, индуктивность соленоида и энергия магнитного поля.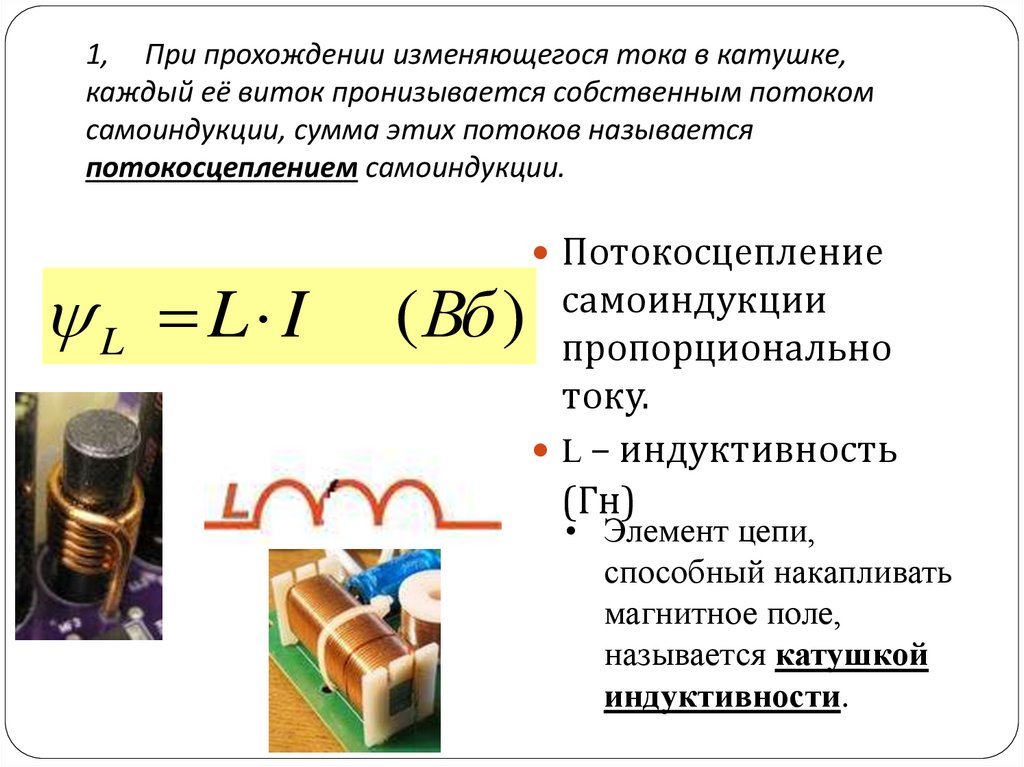
Самоиндукция
Продолжите предложение, выбрав более одного ответа.
Явление самоиндукции наблюдается, когда .
протекание постоянного тока
замыкание электрической цепи
изменение тока, протекающего в проводнике
изменение геометрии проводника
размыкание цепи
Индуктивность
Выделите мышкой 5 слов, связанных с темой урока.
1. ученый, открывший явление электромагнитной индукции.
2. единица измерения энергии магнитного поля.
3. Явление индукции ЭДС, возникающей в проводящей цепи при изменении тока, протекающего через цепь.
4. коэффициент пропорциональности, связывающий поток магнитной индукции с силой тока.
5. единица измерения индуктивности.
Электродинамика
Выделите мышкой 4 слова, относящиеся к теме урока.
1. единица электрической емкости в системе СИ.
2. единица магнитного потока в системе СИ.
3. единица тока.
4. явление, с которым сравнивается индукция ЭДС в цепи.
Индуктивность .
Разгадайте кроссворд.
Индукция ЭМП
Заполните пробел в тексте.
Индуктивная ЭДС в проводнике, движущемся в постоянном магнитном поле, вызывается силой, действующей на свободные заряды в проводнике.
Научные и физические термины
Выделите мышкой 6 слов, относящихся к теме урока.
1. единица измерения магнитной индукции.
2. единица измерения электрического заряда.
3. Явление сохранения скорости телом.
4. несколько витков изолированного проводника.
5. тело, обладающее собственным магнитным полем.
6. великий английский физик, который преобразовал магнетизм в электричество.
Магнитный поток, сила тока и индуктивность
Разложите фигуры по парам так, чтобы каждая пара была ответом на вопрос в задании.
1) Каков магнитный поток в цепи с индуктивностью 0,2 мГн при силе тока 10 А (ответ в Вб)?
2) Каким должен быть ток в обмотке дросселя с индуктивностью 0,5 Гн, чтобы энергия поля была равна 1 Дж (ответ в A)?
3. ток в катушке изменяется от 1 А до 4 А за время, равное 3 с. Это приводит к самоиндуцированной ЭДС 0,1 В. Какова индуктивность катушки (ответ в Гн)?
ток в катушке изменяется от 1 А до 4 А за время, равное 3 с. Это приводит к самоиндуцированной ЭДС 0,1 В. Какова индуктивность катушки (ответ в Гн)?
Источником магнитного поля является ток. Поэтому:
Принцип ЛенцаСуществование индукционного тока является следствием закона сохранения энергии!
Случай 1: При приближении магнита ток увеличивается, цепь замыкается: ; Магнитный поток Ф → ΔF>0 Чтобы компенсировать это изменение (увеличение) внешнего поля, необходимо магнитное поле, направленное в сторону от внешнего поля: где – так называемое индуктивное магнитное поле.
В случае 2Когда магнит удален, ток уменьшается, цепь разомкнута: . Магнитный поток Ф → ΔF<0 . Чтобы компенсировать это изменение (уменьшение), необходимо магнитное поле, сонаправленное с внешним полем: .
Источником магнитного поля является ток. Поэтому:
Поэтому:
Индукционный ток, возникающий в замкнутом контуре, имеет такое направление, что создаваемый им поток магнитной индукции в области, ограниченной контуром, стремится компенсировать изменение потока магнитной индукции, которое вызывает этот ток.
Ток в цепи имеет отрицательное направление () еслипротивоположна (т.е. ΔΦ>0). Ток в контуре имеет положительное направление (), если совпадает с (т.е. ΔΦ<0 ).
Поэтому, учитывая правило Ленца (знак), запишем выражение для закона электромагнитной индукции: .
Эта формула верна для СИ (коэффициент пропорциональности равен 1). В других системах единиц этот коэффициент отличается.
Если цепь (например, катушка) состоит из нескольких катушек, то ,
где n – количество витков. Все предыдущие формулы справедливы для линейного (равномерного) изменения магнитного потока. В произвольном случае закон пишется производной: где e – мгновенное значение ЭДС индукции.
В произвольном случае закон пишется производной: где e – мгновенное значение ЭДС индукции.
Читайте далее:
- Самоиндукция. Энергия самоиндукции, индуктивность – материал по физике PSE.
- Соленоид – это электромагнитная катушка. Что такое соленоид?.
- 1 Понятие электромагнитного поля и его различные проявления. Материальность – Работа в школе.
- Значение слова ИНДУКЦИЯ. Что такое индукция?.
- Катушка – это катушка. Что такое катушка?.
- Урок 7 Свободные и вынужденные электромагнитные колебания. колебательный контур – физика – 11 класс – Русская электронная школа.
- Магнетизм – Джеймс Трефил, энциклопедия «Двести законов Вселенной».
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ВОЛЖСКИЙ ИНСТИТУТ ЭКОНОМИКИ, ПЕДАГОГИКИ И ПРАВА» « Волжский социально-педагогический колледж» Физика в курсе «Естествознание» САМОСТОЯТЕЛЬНая РАБОТа по теме «Магнитное поле» Разработал: преподаватель физики первой квалификационной категории Бондаренко Людмила Валентиновна 2013 Билет № 1 1. А. Правило левой руки однородного магнитного поля, индукция которого 1,2 Тл, если активная длина провода 25 см, а угол, образованный им с линиями индукции, 60 °? ——————————————————————————————————————— Самостоятельная работа по теме «Магнитное поле» Билет № 2 1. Какое утверждение неправильно? Сила Ампера, действующая на проводник с током Ι в магнитном поле с индукцией В: А. Б. прямо пропорциональна Ι; В. прямо пропорциональна длине проводника; Г. равна нулю, если проводник перпендикулярен вектору индукции В. 3. Прямолинейный проводник с током длиной 5 см перпендикулярен линиям индукции однородного магнитного поля. Чему равен модуль индукции магнитного поля, если при токе в 2 А на проводник действует сила, модуль которой равен 0,01 Н? ————————————————————————————————————- Самостоятельная работа по теме «Магнитное поле» Билет № 3 1. Как взаимодействуют между собой два параллельных проводника, если по ним протекают токи в противоположных направлениях? А. Б. отталкиваются. В. Сила взаимодействия равна нулю. Г. Нет однозначного ответа. 3. Прямой провод длиной l=10 см, по которому течет ток I=20 А, находится в однородном магнитном поле с индукцией В =0,01 Тл. Найти угол а между направлениями вектора В и тока, если на провод действует сила F=10 мН. Самостоятельная работа по теме «Магнитное поле» Билет № 4 1.В опыте Эрстеда было обнаружено… А. отклонение магнитной стрелки при протекании электрического тока по проводу. Б. взаимодействие параллельных проводников с током. В. возникновение тока в замкнутой катушке при опускании в нее магнита. Г. взаимодействие двух магнитных стрелок 2. Самостоятельная работа по теме «Магнитное поле» Билет № 5 1. Сила Лоренца, действующая на движущуюся заряженную частицу в магнитном поле… А. всегда направлена параллельно скорости; Б. всегда равна нулю; В. всегда направлена параллельно магнитной индукции; Г. равна нулю или направлена перпендикулярно скорости. 3. В магнитном поле с индукцией 2 Тл движется электрон со скоростью 106 м/с, направленный перпендикулярно линиям индукции магнитного поля. Чему равен модуль силы, действующей на электрон со стороны магнитного поля? ——————————————————————————————————————- Самостоятельная работа по теме «Магнитное поле» Билет № 6 1. Сила Лоренца, действующая на движущуюся нейтральную частицу в магнитном поле, А.всегда направлена параллельно скорости Б. всегда равна нулю В. всегда направлена параллельно магнитной индукции Г. равна нулю или направлена перпендикулярно скорости 3. Электрон влетает со скоростью 105м/с в однородное магнитное поле с индукцией 2,5 Тл перпендикулярно линиям магнитной индукции. действующую на электрон (силу Лоренца). Самостоятельная работа по теме «Магнитное поле» Билет № 7 1. Что наблюдалось в опыте Эрстеда? А. взаимодействие двух проводников с током; Б. взаимодействие двух магнитных стрелок; В. поворот магнитной стрелки вблизи проводника при пропускании через него тока; Г. возникновение электрического тока в катушке при поднесении к ней магнита. ——————————————————————————————————————— Самостоятельная работа по теме «Магнитное поле» Билет № 8 1. А. Только 1. Б. Только 2. В. Только 3. Г. 1 и 2. Д. 1 и 3. Е. 2 и 3. Ж. 1,2 и 3. 2.В магнитном поле находится проводник с током. Каково направление силы Ампера. 3.Прямолинейный проводник длиной l = 0,1 м, по которому течет ток, находится в однородном магнитном поле с индукцией В = 0,4 Тл и расположен под углом 90 к вектору . Какова сила тока, если сила, действующая на проводник со стороны магнитного поля, равна 0,2 Н? Самостоятельная работа по теме «Магнитное поле» Билет № 9 1.Как можно объяснить взаимное притяжение параллельных проводников, по которым протекают постоянные электрические токи? А) взаимодействием магнитных полей электрических токов в этих проводниках; Б) взаимодействием электрических полей, существующих вокруг этих проводников; В) действием магнитного поля одного тока на второй ток и наоборот; Г) взаимодействием магнитных и электрических полей, существующих вокруг этих проводников; 2. 3.Электрон движется в вакууме со скоростью 3106 м/с в однородном магнитном поле с магнитной индукцией 0,1 Тл. Чему равна сила, действующая на электрон, если угол между направлениями скорости электрона и линиями магнитной индукции равен 90? Самостоятельная работа по теме «Магнитное поле» Билет № 10 1.Какое из приведенных ниже утверждений верно? 1) магнитное поле порождается электрическими зарядами; 2) магнитное поле порождается движущимся электрическим зарядом; 3) магнитное поле порождается электрическим током. Самостоятельная работа по теме «Магнитное поле» Билет № 11 1.Правилом правого буравчика можно воспользоваться для определения направления – 1) магнитной силовой линии; 2) тока в проводнике по известному направлению магнитной силовой линии; 2) силы Лоренца. Какое из этих продолжений фразы верно? А) только 1; Б) только 2; В) 1 и 2; Г) только 3; Д) 1 и 3. 3.Прямолинейный проводник длиной 5 см находится в однородном магнитном поле с индукцией 5 Тл и расположен под углом 30 к вектору магнитной индукции. Чему равна сила, действующая на проводник, если сила тока в проводнике 2 А? ——————————————————————————————————- Самостоятельная работа по теме «Магнитное поле» Билет № 12 1. А) взаимодействием электрических полей, существующих вокруг этих проводников; Б) взаимодействием магнитных полей электрических токов в этих проводниках; В) действием магнитного поля одного тока на второй ток и наоборот; Г) взаимодействием магнитных и электрических полей, существующих вокруг этих проводников;
Билет № 13 1. Какое из приведенных ниже утверждений верно? 1) магнитное поле порождается электрическими зарядами; 2) магнитное поле порождается движущимся электрическим зарядом; 3) магнитное поле порождается электрическим током. 2.По проводнику течет ток (направление указано стрелкой). Определите направление силы Ампера. 3. Прямолинейный проводник длиной 5 см находится в однородном магнитном поле с индукцией 5 Тл и расположен под углом 300 к вектору магнитной индукции. Чему равна сила, действующая на проводник со стороны магнитного поля, если сила тока в проводнике 2 мА? ————————————————————————————————————————— Билет № 14 1.Правилом левой руки можно воспользоваться для определения направления: 1) магнитной силовой линии; 2) силы Ампера; 3) силы тока в проводнике. Какое из этих продолжений фразы верно? А) все три; Б) только 1; В) только 2; Г) только 3; Д) 2 и 3. 3.Какая сила действует со стороны однородного магнитного поля с индукцией 30 мТл на находящийся в поле прямолинейный проводник длиной 50 см, по которому идет ток 12 А? Провод образует прямой угол с направлением вектора магнитной индукции поля. —————————————————————————————————————— Билет № 15 1.Правилом правой руки можно воспользоваться для определения направления – 1) магнитной силовой линии; 2) тока в проводнике; 3) силы Лоренца. Какое из этих продолжений фразы верно? А) только 1; Б) только 2; В) 1 и 2; Г) только 3; Д) 1 и 3.
на положительно заряженную частицу, движущуюся в магнитном поле со скоростью v? |
Расчет взаимной индуктивности и магнитной силы для катушки Биттера (блин) с нелинейным радиальным током и филаментарной круговой катушки с азимутальным током
На этой странице до 30 Тл. В данной работе мы рассчитываем взаимную индуктивность и магнитную силу между дисковой (блинной) катушкой Биттера с нелинейным радиальным током и круглой нитевидной катушкой с азимутальным током. Близкая форма, выраженная над полными эллиптическими интегралами первого и второго рода, а также лямбда-функция Хьюмана, получена для этой конфигурации либо для взаимной индуктивности, либо для магнитной силы. Результаты этого метода сравниваются с результатами, полученными усовершенствованным методом модифицированной нити для представленной конфигурации. Все результаты находятся в отличном согласии.
В данной работе мы рассчитываем взаимную индуктивность и магнитную силу между дисковой (блинной) катушкой Биттера с нелинейным радиальным током и круглой нитевидной катушкой с азимутальным током. Близкая форма, выраженная над полными эллиптическими интегралами первого и второго рода, а также лямбда-функция Хьюмана, получена для этой конфигурации либо для взаимной индуктивности, либо для магнитной силы. Результаты этого метода сравниваются с результатами, полученными усовершенствованным методом модифицированной нити для представленной конфигурации. Все результаты находятся в отличном согласии.
1. Введение
В литературе и научных работах расчеты взаимной индуктивности и магнитной силы между обычными круглыми катушками с однородными плотностями тока проводились различными методами, как аналитическими, так и численными [1–15]. Однако упоминаний о взаимной индуктивности и расчете магнитных сил между круглыми катушками, в которых плотности тока неравномерны, немного. Катушки с этой характеристикой — катушки Биттера или соленоиды Биттера.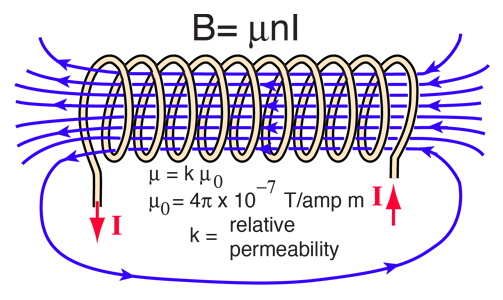 Катушки Биттера используются в приложениях с сильным магнитным полем, и они отличаются от обычных катушек тем, что имеют обратное радиальное распределение тока [16, 17]. Интересным моментом является расчет взаимной индуктивности и магнитной силы между катушками Биттера или между одной катушкой Биттера и обычной катушкой. Как правило, расчет магнитной силы между круглыми катушками тесно связан с расчетом их взаимной индуктивности. Так как их взаимная энергия равна произведению их взаимной индуктивности на токи в катушках, то составляющая магнитной силы притяжения или отталкивания в любом направлении равна произведению токов на дифференциальный коэффициент взаимной индуктивности взятые относительно этой координаты. Взаимная индуктивность и магнитная сила получены по множественным интегралам с различными функциями ядра. Таким образом, при расчете взаимной индуктивности и соответствующей магнитной силы между двумя катушками нам необходимо интегрировать их функции ядра в зависимости от конфигурации катушек.
Катушки Биттера используются в приложениях с сильным магнитным полем, и они отличаются от обычных катушек тем, что имеют обратное радиальное распределение тока [16, 17]. Интересным моментом является расчет взаимной индуктивности и магнитной силы между катушками Биттера или между одной катушкой Биттера и обычной катушкой. Как правило, расчет магнитной силы между круглыми катушками тесно связан с расчетом их взаимной индуктивности. Так как их взаимная энергия равна произведению их взаимной индуктивности на токи в катушках, то составляющая магнитной силы притяжения или отталкивания в любом направлении равна произведению токов на дифференциальный коэффициент взаимной индуктивности взятые относительно этой координаты. Взаимная индуктивность и магнитная сила получены по множественным интегралам с различными функциями ядра. Таким образом, при расчете взаимной индуктивности и соответствующей магнитной силы между двумя катушками нам необходимо интегрировать их функции ядра в зависимости от конфигурации катушек.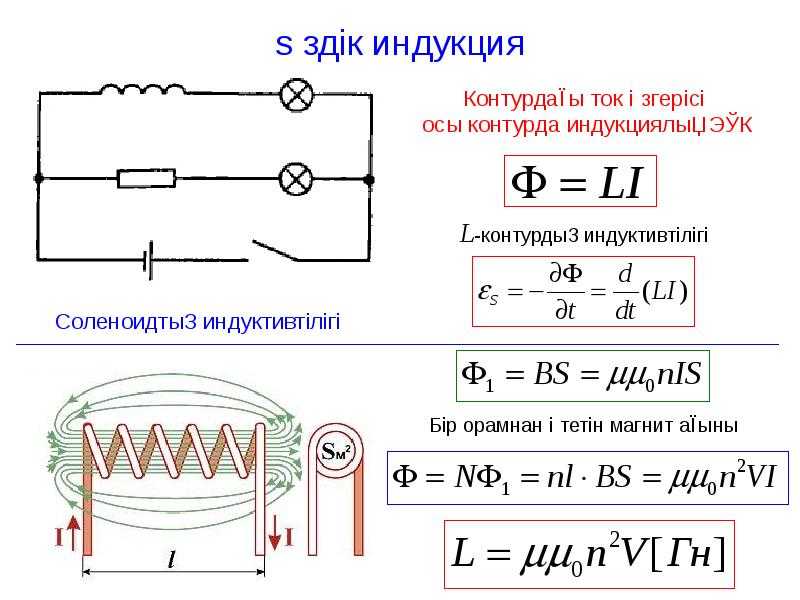 Будем надеяться, что эти функции ядра являются функциями Грина и , где «» — это расстояние между двумя катушками. Этот интегральный подход, гораздо более простой, чем дифференциальный, приводит к относительно простым выражениям, которые включаются в эти две физические величины. В данной работе мы рассчитываем взаимную индуктивность между катушкой диска Биттера с нелинейным радиальным током и круглой нитевидной катушкой с азимутальным током (обыкновенной катушкой). Катушки коаксиальные и воздушные. Либо взаимная индуктивность, либо магнитная сила получаются в замкнутом виде, выраженном через полные эллиптические интегралы первого и второго рода, а также через лямбда-функцию Хоймана [18, 19].]. Результаты этих расчетов будут сравниваться с результатами, полученными с помощью усовершенствованного метода нити для рассматриваемой конфигурации. Результаты, полученные этими двумя методами, находятся в прекрасном согласии.
Будем надеяться, что эти функции ядра являются функциями Грина и , где «» — это расстояние между двумя катушками. Этот интегральный подход, гораздо более простой, чем дифференциальный, приводит к относительно простым выражениям, которые включаются в эти две физические величины. В данной работе мы рассчитываем взаимную индуктивность между катушкой диска Биттера с нелинейным радиальным током и круглой нитевидной катушкой с азимутальным током (обыкновенной катушкой). Катушки коаксиальные и воздушные. Либо взаимная индуктивность, либо магнитная сила получаются в замкнутом виде, выраженном через полные эллиптические интегралы первого и второго рода, а также через лямбда-функцию Хоймана [18, 19].]. Результаты этих расчетов будут сравниваться с результатами, полученными с помощью усовершенствованного метода нити для рассматриваемой конфигурации. Результаты, полученные этими двумя методами, находятся в прекрасном согласии.
2. Основные выражения
Взаимная индуктивность и магнитная сила между дисковой катушкой (блинчиком) с однородной азимутальной плотностью тока и нитевидной катушкой с азимутальным током (см. рис. 1) можно рассчитать соответственно по [1, 2], где а — число витков катушки диска (блинчика).
рис. 1) можно рассчитать соответственно по [1, 2], где а — число витков катушки диска (блинчика).
Гн/м – проницаемость свободного пространства (вакуума), , , – цилиндрические координаты. Обе катушки находятся в воздухе или в немагнитной и непроводящей среде.
В [2] магнитная сила получена в близкой форме, выраженной над полным эллиптическим интегралом первого рода и лямбда-функцией Хьюмана, а магнитная сила в полуаналитической форме выражена над полным эллиптическим интегралом первого и второго рода, Хейманом Лямбда-функция плюс один простой интеграл, который должен быть оценен с помощью некоторых численных интегрирований [1].
Предположим, что дисковая катушка представляет собой катушку Биттера, в которой плотность тока неравномерна [16, 17] и определяется выражением Из (1), (2) и (4) получаем выражения взаимной индуктивности и магнитная сила между биттеровской катушкой и нитевидной катушкой выглядит следующим образом: где
3. Метод расчета
Интегрируя в (5) и (6) по и (заменяя) взаимную индуктивность и магнитную силу между биттеровским диском и нитевидной Круговой виток можно выразить соответственно в аналитическом виде следующим образом (см.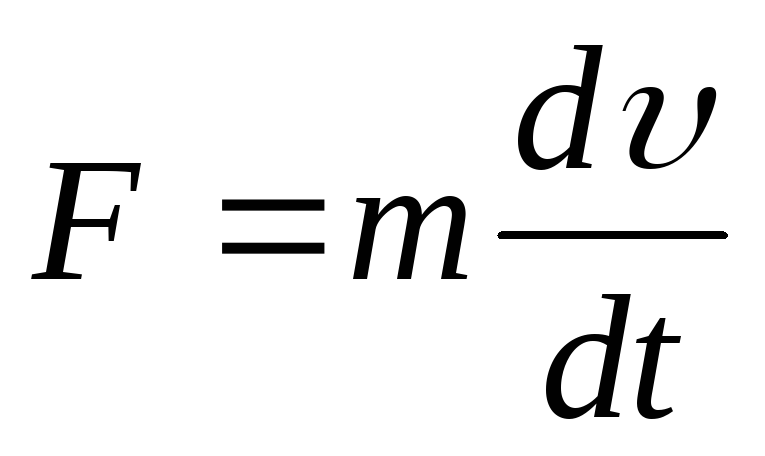 Приложения А и Б): где Таким образом, все выражения получаются в замкнутой форме, выраженной над полными эллиптическими интегралами первого и второго рода, а также лямбда-функцией Хоймана [ 18, 19].
Приложения А и Б): где Таким образом, все выражения получаются в замкнутой форме, выраженной над полными эллиптическими интегралами первого и второго рода, а также лямбда-функцией Хоймана [ 18, 19].
3.1. Особые случаи и особенности
Взаимная индуктивность . При расчете взаимной индуктивности появляются особые и особые случаи при и или = 0 и .
3.1.1. и
Этот случай является обычным случаем, охватываемым (8). В этом случае срок может быть указан в следующей упрощенной форме:
3.1.2. и
Этот случай является единственным случаем ( или ), для которого термин равен или или .
Магнитная сила . В расчете магнитной силы ее значение равно нулю, поскольку витки находятся в одной плоскости.
Обозначение выше . соответствует лямбда-функции Хьюмана, как определено в [18, 19], а функция «знак» возвращает целое число, указывающее знак числа. Функции и соответствуют полным эллиптическим интегралам первого и второго рода [18, 19].
4. Модифицированный метод накала
В [17] методом накала рассчитана взаимная индуктивность между катушкой Биттера и сверхпроводящей катушкой с однородной плотностью тока. Здесь мы приводим модифицированные формулы для взаимной индуктивности и магнитной силы для рассматриваемой конфигурации (см. рис. 2) с использованием метода накала.
Применив некоторые изменения в расчете взаимной индуктивности, приведенном в [17], мы получили взаимную индуктивность и магнитную силу между катушкой Биттера и накальной катушкой следующим образом: где выражения (13) будут использованы для подтверждения справедливости аналитических формул ( 8) и (9).
5. Примеры
Чтобы проверить справедливость новых формул, применим их к следующему набору примеров.
Пример 1. Рассчитайте взаимную индуктивность и магнитную силу между катушкой диска Биттера и нитевидной круглой катушкой со следующими размерами и числом витков. Токи в катушках единичны.
Круглая спиральная катушка . мм, мм.
мм, мм.
Катушка Bitter Disk . мм, мм, мм, .
Применяя (8) и (9) взаимную индуктивность и магнитную силу соответственно, время вычисления составляет около 0,037677 секунды.
Используя модифицированную нить (13) и (14), мы получаем число делений и время вычисления около 0,362069 секунд.
Пример 2. Рассчитайте взаимную индуктивность между диском и витой круглой катушкой со следующими размерами и числом витков.
Круглая спиральная катушка . мм, мм.
Дисковая катушка . мм, мм, мм, .
Применяя (8) и (9) взаимную индуктивность и магнитную силу соответственно, время вычисления составляет около 0,020657 секунды.
Используя модифицированную нить (13) и (14), мы получаем число делений и время вычисления около 0,030564 секунды.
Пример 3. Рассчитайте взаимную индуктивность между диском и витой круглой катушкой со следующими размерами и числом витков.
Круглая спиральная катушка . мм, мм.
Дисковая катушка . мм, мм, мм, .
Этот случай является особым случаем, потому что .
Применяя (8), (9) и (11) взаимную индуктивность и магнитную силу, соответственно, Время вычисления составляет около 0,020223 секунды.
Используя модифицированную нить (13) и (14), мы получаем число делений и время вычисления около 0,513017 секунд.
Пример 4. Рассчитайте взаимную индуктивность между диском и витой круглой катушкой со следующими размерами и числом витков.
Круглая спиральная катушка . мм, мм.
Дисковая катушка . мм, мм, мм, .
Этот случай также является особым случаем, для которого .
Применяя (8), (9) и (11) взаимную индуктивность и магнитную силу соответственно, время вычисления составляет около 0,03929 секунды.
Используя модифицированную нить (13) и (14), мы получаем число делений и время вычисления около 0,487595 секунд.
В сравнительных расчетах совпадающие значащие цифры выделены жирным шрифтом.
Таким образом, на этих примерах мы подтвердили правильность предлагаемого аналитического метода расчета взаимной индуктивности и магнитной силы между диском Биттера с нелинейным радиальным распределением тока и обычной нитевидной круглой катушкой. Все расчеты выполнены в программе Matlab.
6. Заключение
В работе получены и представлены новые точные формулы взаимной индуктивности и магнитной силы для системы диска Биттера с нелинейным радиальным током и нитевидного кругового с азимутальным в воздухе. Все выражения либо для взаимной индуктивности, либо для магнитной силы получаются в близкой форме, выраженной над полными эллиптическими интегралами первого и второго рода и лямбда-функцией Хьюмана. Также в этой статье мы привели улучшенные формулы для взаимной индуктивности и магнитной силы между обработанными катушками с использованием метода накала. Все особые случаи получаются в закрытом виде. Представленный метод может быть использован для расчета таких важных электрических величин, как взаимная индуктивность и магнитная сила, для комбинаций катушек, состоящих из катушек Биттера прямоугольного сечения и круглых катушек с равномерными плотностями тока.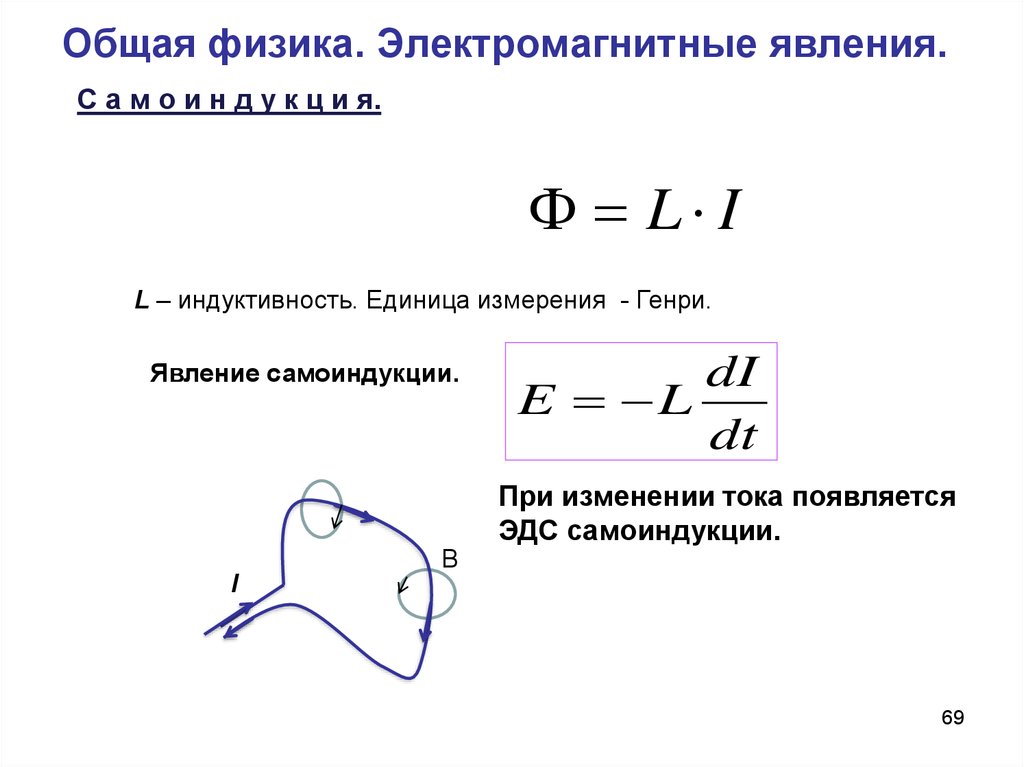
Приложение
A. Интегралы взаимной индуктивности
Первый интеграл в (5) можно решить аналитически [19]: Последний интеграл в (5) можно получить в следующем виде:где Интеграл можно получить в окончательном виде, выраженном над полными эллиптическими интегралами первого и второго рода , а также Лямбда-функцией Хоймана [18, 19]: где Заменив в выражении (5), получим (8).
B. Интегралы магнитной силы
Первый интеграл в (6) имеет аналитическое решение [19]: Последний интеграл в (6) можно представить в следующем виде: Интеграл фигурирует в Приложении А, так что подставляя в (6) получаем (9).
Конкурирующие интересы
Авторы заявляют об отсутствии конфликта интересов в отношении публикации данной статьи.
Ссылки
С. Акьель, С. И. Бабич и С. Кинчич, «Новые и быстрые процедуры расчета взаимной индуктивности коаксиальных круглых катушек (круглая катушка-дисковая катушка)», IEEE Transactions on Magnetics , vol.
 38, нет. 5, стр. 2367–2369, 2002.
38, нет. 5, стр. 2367–2369, 2002.Посмотреть по адресу:
Сайт издателя | Google Scholar
К. Акьель, С. И. Бабич, С. Кинчич и П. Дж. Лагасе, «Расчет магнитной силы между тонкими круглыми катушками и тонкой нитевидной круглой катушкой в воздухе», Журнал электромагнитных волн и приложений , том. 21, нет. 9, стр. 1273–1283, 2007.
Просмотр по адресу:
Google Scholar
С. Бабич, К. Акьель, Ю. Рен и В. Чен, «Расчет магнитной силы между круглыми катушками прямоугольного креста сечение с параллельными осями для сверхпроводящего магнита», Прогресс в исследованиях электромагнетизма B , нет. 2012. Т. 37. С. 275–288. воздух», IEEE Transactions on Magnetics , vol. 42, нет. 6, стр. 1661–1669, 2006.
Посмотреть по адресу:
Сайт издателя | Google Scholar
С.
 И. Бабич и К. Акьель, «Расчет магнитной силы между тонкими коаксиальными круглыми катушками в воздухе», IEEE Transactions on Magnetics , vol. 44, нет. 4, стр. 445–452, 2008 г.
И. Бабич и К. Акьель, «Расчет магнитной силы между тонкими коаксиальными круглыми катушками в воздухе», IEEE Transactions on Magnetics , vol. 44, нет. 4, стр. 445–452, 2008 г.Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж. Т. Конвей, «Расчеты индуктивности некоаксиальных катушек с использованием функций Бесселя», IEEE Transactions on Magnetics , vol. 43, нет. 3, стр. 1023–1034, 2007.
Посмотреть по адресу:
Сайт издателя | Google Scholar
R. Ravaud, G. Lemarquand, S. Babic, V. Lemarquand и C. Akyel, «Цилиндрические магниты и катушки: поля, силы и индуктивности», IEEE Transactions on Magnetics , vol. 46, нет. 9, стр. 3585–3590, 2010.
Посмотреть по адресу:
Сайт издателя | Google Scholar
R.
 Ravaud, G. Lemarquand, V. Lemarquand, S. Babic и C. Akyel, «Взаимная индуктивность и сила, действующая между толстыми катушками», Progress in Electro Magnetics Research , vol. 102, стр. 367–380, 2010.
Ravaud, G. Lemarquand, V. Lemarquand, S. Babic и C. Akyel, «Взаимная индуктивность и сила, действующая между толстыми катушками», Progress in Electro Magnetics Research , vol. 102, стр. 367–380, 2010.Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Шири и А. Шулайе, «Новая методология расчета магнитных сил между плоскими спиральными катушками», Прогресс в исследованиях электромагнетизма , том. 95, стр. 39–57, 2009 г.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Р. Раво, Г. Лемаркан и В. Лемаркан, «Сила и жесткость пассивных магнитных подшипников с использованием постоянных магнитов. Часть 1: осевое намагничивание», IEEE Transactions on Magnetics , vol. 45, нет. 7, стр. 2996–3002, 2009.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Р.
 Раво, Г. Лемаркан и В. Лемаркан, «Сила и жесткость пассивных магнитных подшипников с использованием постоянных магнитов. часть 2: радиальная намагниченность», IEEE Transactions on Magnetics , vol. 45, нет. 9, стр. 3334–3342, 2009.
Раво, Г. Лемаркан и В. Лемаркан, «Сила и жесткость пассивных магнитных подшипников с использованием постоянных магнитов. часть 2: радиальная намагниченность», IEEE Transactions on Magnetics , vol. 45, нет. 9, стр. 3334–3342, 2009.Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж. Кулон и Г. Менье, «Конечно-элементная реализация принципа виртуальной работы для вычисления магнитной или электрической силы и крутящего момента», IEEE Transactions on Magnetics , vol. 20, нет. 5, стр. 1894–1896, 1984.
Посмотреть по адресу:
Сайт издателя | Google Scholar
А. Бенхама, А. С. Уильямсон и А. Б. Дж. Рис, «Вычисление силы и крутящего момента на основе 2D и 3-D решений поля конечных элементов», IEE Proceedings — Electric Power Applications Journal , vol. 146, нет. 1, стр. 25–31, 1999.

Просмотр по адресу:
Google Scholar
Э. П. Фурлани, «Формула силы левитации между магнитными дисками», IEEE Transactions on Magnetics , vol. 29, нет. 6, стр. 4165–4169, 1993.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Е. П. Фурлани, «Формулы для силы и крутящего момента осевых муфт», IEEE Transactions on Magnetics , vol. 29, нет. 5, стр. 2295–2301, 1993.
Посмотреть по адресу:
Сайт издателя | Google Scholar
Дж. Т. Конвей, «Расчеты некоаксиальной силы и индуктивности для биттерных катушек и катушек с однородным радиальным распределением тока», в Трудах Международной конференции по прикладной сверхпроводимости и электромагнитным устройствам (ASEMD ’11) , стр. 61–64, Сидней, Австралия, декабрь 2011 г.

Вид:
Сайт издателя | Google Scholar
Ю. Рен, Ф. Ван, Г. Куанг и др., «Расчеты взаимной индуктивности и силы между коаксиальными битовыми катушками и сверхпроводящими катушками с прямоугольным поперечным сечением», Journal of Superconductivity and Novel Magnetism , vol. . 24, нет. 5, стр. 1687–1691, 2011.
Посмотреть по адресу:
Сайт издателя | Google Scholar
М. Абрамовиц и И. А. Стегун, Справочник по математическим функциям , Series 55, National Bureau of Standards Applied Mathematics, Washington, DC, USA, 1972.
Градштейн И.С., Рыжик И.М., Таблица интегралов, серий и произведений , Academic Press, New York, NY, USA, 1965.
Copyright
Copyright © 2016 Slobodan Babic and Cevdet Akyel. Эта статья находится в открытом доступе и распространяется в соответствии с лицензией Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.
Индукционная катушка и ее применение в практике инженера-электронщика
Несмотря на широкое использование цифровых схем, таких как процессоры, программируемые логические устройства и однокристальные схемы, которые представляют собой комбинацию этих двух, иногда разработчику электроники приходится «аналоговые» элементы, такие как: резисторы, конденсаторы или индукционные катушки. Что интересно, если резистор или конденсатор (с емкостью, исчисляемой в пикофарадах) относительно легко включить в структуру интегральной схемы, то сделать это с индукционной катушкой очень сложно. Вот почему в примечаниях по применению многих элементов до сих пор упоминается индукционная катушка в качестве внешнего компонента, добавляемого в набор. В данной статье представлены некоторые основные сведения об индукционных катушках и описание элементов их конструкции, влияющих на их параметры.
- Структура индукционной катушки
- Что такое индукционная катушка?
- Индукционная катушка – основные параметры
- Несовершенная катушка
- Заключительные замечания
Конструкция индукционной катушки
Индукционная катушка несложная. Он состоит из сердечника и намотанных на него изолированных проводов. Сердечник может быть как воздушным, так и магнитным. Важно, чтобы провода, намотанные на сердечник, были изолированы, поэтому для изготовления катушек используют изолированный провод, либо наматывают неизолированным проводом (например, так называемой серебряной сталью), но с воздушным зазором, обеспечивающим необходимое расстояние между отдельными витками провода. Если неизолированный провод намотать виток за витком, то произойдет короткое замыкание и, хотя некоторая индуктивность будет присутствовать, она обязательно будет отличаться от нужной.
Он состоит из сердечника и намотанных на него изолированных проводов. Сердечник может быть как воздушным, так и магнитным. Важно, чтобы провода, намотанные на сердечник, были изолированы, поэтому для изготовления катушек используют изолированный провод, либо наматывают неизолированным проводом (например, так называемой серебряной сталью), но с воздушным зазором, обеспечивающим необходимое расстояние между отдельными витками провода. Если неизолированный провод намотать виток за витком, то произойдет короткое замыкание и, хотя некоторая индуктивность будет присутствовать, она обязательно будет отличаться от нужной.
На практике часто встречается повреждение индукционной катушки , т.е. короткое замыкание между витками провода в результате пробоя изоляции, из-за превышения максимально допустимой температуры или напряжения. Поврежденную таким образом катушку необходимо перемотать или заменить на новую. Сетевые трансформаторы также повреждаются таким образом. Дальнейшее использование такого поврежденного трансформатора может привести к его перегреву, короткому замыканию в сети или даже возгоранию трансформатора или питаемого от него устройства.
Что такое индукционная катушка?
Индукционная катушка представляет собой элемент, который накапливает энергию в виде магнитного поля в сердечнике, поэтому он преобразует энергию электрического тока в энергию магнитного поля или наоборот. Изменение тока, протекающего по обмоткам, приводит к возникновению электродвижущей силы в направлении, противодействующем этому изменению. Точно так же переменное магнитное поле, проникающее в сердечник, вызывает индукцию напряжения. Это можно показать с помощью следующей формулы:
В этой формуле:
- e — обозначает электродвижущую силу (напряжение в вольтах), создаваемую катушкой,
- dϕ/dt — изменение магнитного потока во времени,
- di/dt — текущее изменение времени,
- L — обозначает параметр катушки, называемый индуктивностью; его единица измерения — генри.
Легко заметить упомянутую ранее особенность – ЭДС e имеет противоположное направление, чем напряжение, вызывающее протекание тока.
Индукционная катушка – основные параметры
Основными параметрами катушки являются ее индуктивность и резонансная частота. Другими словами, индуктивность — это способность катушки накапливать энергию в виде магнитного поля, вызванного протеканием тока. Индуктивность измеряется в генри и определяется как отношение временного изменения напряжения к изменению тока во времени.
Диаграммы, показывающие падение тока и напряжения на выводе индукционной катушки. Падение максимально в момент включения питания и уменьшается со временем. Падение противодействует увеличению тока, следовательно, сила тока минимальна в момент включения источника питания и увеличивается со временем. Часто говорят, что напряжение опережает ток на катушке
На рисунке выше показано, что происходит с напряжением на катушке и с током, протекающим через нее после подачи питания на ее клеммы. Сплошная красная линия иллюстрирует течение тока. Как мы можем наблюдать, ток увеличивается после подачи питания до своего пикового значения, определяемого законом Ома, т. е. отношения напряжения на клеммах к
Сплошная красная линия иллюстрирует течение тока. Как мы можем наблюдать, ток увеличивается после подачи питания до своего пикового значения, определяемого законом Ома, т. е. отношения напряжения на клеммах к
При описании параметров неидеальной катушки обсуждается резонансная частота катушки, так как она связана с паразитной емкостью.
Материал сердечника и относительная магнитная проницаемость
Очень важным элементом индукционной катушки является ее сердечник. Сердечник характеризуется типом используемого материала и связанной с ним относительной магнитной проницаемостью. Он называется относительным, потому что определяется по отношению к проницаемости вакуума. Это безразмерное число, определяемое как отношение магнитной проницаемости (абсолютное значение 90 358 мк 90 359 ) данной среды к проницаемости вакуума 90 358 мк 0 .
Это безразмерное число, определяемое как отношение магнитной проницаемости (абсолютное значение 90 358 мк 90 359 ) данной среды к проницаемости вакуума 90 358 мк 0 .
Согласно определению, магнитная проницаемость – это способность данного материала или среды изменять магнитную индукцию вместе с изменением напряженности магнитного поля. Другими словами, магнитная проницаемость — это свойство материала или среды, характеризующее его способность концентрировать линии магнитного поля.
Магнитная проницаемость, согласно данным, опубликованным в 2002 г. Комитетом по данным для науки и технологий (CODATA), представляет собой скаляр, который обозначается цифрой 9.0358 μ 0 символ и значение которого в Международной системе единиц (СИ) равно μ 0 = 4·Π·10 -7 = ок. 12,566370614·10 -7 [Гн/м = В·с/А·м] .
Индуктивность катушки выражается по следующей формуле:
Символы, используемые в формуле, означают:
- L — индуктивность в генри,
- μ 0 — магнитная проницаемость вакуума,
- μ — относительная проницаемость материала сердцевины,
- Z — количество витков провода в катушке,
- S — площадь поперечного сечения катушки,
- l — длина змеевика.

Относительная проницаемость незагрязненного воздуха мало чем отличается от проницаемости вакуума, поэтому для упрощения в инженерной практике принято, что мк = 1 и формула индуктивности воздушной катушки:
Синими линиями показаны линии силы магнитного поля, направленные в соответствии с правилом Ленца (так называемое правило правой руки).
По магнитным свойствам материалы делятся на парамагнитные материалы (материалы, которые превращаются в магниты после помещения их в магнитное поле), ферромагнитные материалы (намагничиваются в присутствии магнитного поля) и диамагнитные материалы ( ослабление магнитного поля). Тип материала сердечника сильно влияет на параметры катушки. В идеальном вакууме нет частиц, которые могли бы повлиять на корреляцию между индуктивностью и напряженностью магнитного поля. При этом в каждой материальной среде формула индуктивности будет изменяться в зависимости от проницаемости этой конкретной среды. В случае вакуума значение проницаемости равно 1. Для парамагнетиков относительная проницаемость чуть выше 1, для диамагнетиков чуть меньше 1 — различия в обоих случаях настолько малы, что в технических приложениях ими пренебрегают. а значение принимается равным 1,
В случае вакуума значение проницаемости равно 1. Для парамагнетиков относительная проницаемость чуть выше 1, для диамагнетиков чуть меньше 1 — различия в обоих случаях настолько малы, что в технических приложениях ими пренебрегают. а значение принимается равным 1,
Подытожим этот абзац, перечислив параметры катушки, оказывающие наиболее существенное влияние на ее индуктивность:
Для чего используются сердечники? Во-первых, благодаря этому можно хранить больше энергии при меньшем количестве витков, чем в случае эквивалента с воздушным сердечником. Во-вторых, это связано с механической конструкцией катушки – сердечник является опорой для витков проволоки и обеспечивает правильную установку в целевом устройстве. Третьей важной причиной является концентрация и проводимость магнитного поля. В некоторых приложениях также будет важна возможность регулировать индуктивность катушки, изменяя положение сердечника относительно витков провода, например, вставляя или выталкивая его.
Несовершенная катушка
До сих пор мы обсуждали параметры идеальной катушки. Между тем, в реальных условиях провод обмотки будет иметь некоторое сопротивление и емкость, что повлияет на фактические параметры катушки, которые мы еще не рассматривали.
Между тем, в реальных условиях провод обмотки будет иметь некоторое сопротивление и емкость, что повлияет на фактические параметры катушки, которые мы еще не рассматривали.
На рисунке показана эквивалентная схема постоянного тока реальной катушки. Резистор, представляющий сопротивление провода обмотки, был подключен последовательно к виткам катушки. При протекании тока через катушку это вызовет не только падение напряжения, но и потерю мощности в виде тепла, что может привести к перегреву катушки и изменению параметров сердечника. Как следствие, снижается и электрический КПД всего устройства.
Альтернативная принципиальная схема постоянного тока реальной катушки
В случае анализа переменного тока следует также учитывать паразитную емкость, создаваемую неизолированными слоями проводника, и поэтому эквивалентная схема, кроме резистора , включает также конденсатор, подключенный параллельно клеммам катушки. Так создается RLC-контур, а сама катушка до достижения резонансной частоты является индуктивной, а после ее достижения становится емкостной. Вот почему импеданс катушки увеличивается с резонансной частотой, достигая своего максимального значения в резонансе, и уменьшается после превышения частоты.
Вот почему импеданс катушки увеличивается с резонансной частотой, достигая своего максимального значения в резонансе, и уменьшается после превышения частоты.
Изменение реальной катушки с индуктивной на емкостную после достижения резонансной частоты. Обозначения на эквивалентной принципиальной схеме: L – индуктивность, EPC – паразитная емкость, EPR – параллельное сопротивление, обозначающее потери мощности, ESR – последовательное сопротивление, обозначающее сопротивление сердечника обмотки)
Три вида потерь мощности в индукционных катушках
При применении катушек рассматриваются три основных типа потерь мощности. Первый из них уже упоминался ранее, а именно потери, происходящие в последовательном сопротивлении, т. е. в проводе обмотки. Эту потерю мощности следует особенно учитывать, когда ток, протекающий через катушку, имеет большую силу тока. Это наиболее распространенная потеря мощности в источниках питания и силовых цепях. Это вызывает перегрев катушки и, как следствие, всего устройства. Это также наиболее распространенная причина повреждения, так как высокая температура может повредить изоляцию и вызвать короткое замыкание на катушках.
Это также наиболее распространенная причина повреждения, так как высокая температура может повредить изоляцию и вызвать короткое замыкание на катушках.
Второй тип потери мощности происходит в активной зоне. Это результат несовершенства изготовления, возникновения вихревых токов и изменения положения магнитных доменов. Такие потери являются доминирующими, когда ток, протекающий через катушку, имеет малую силу тока. Они возникают в цепях с высокой частотой, цифровых разделителях сигналов и других. Это может привести не столько к повреждению катушки, сколько к потере уровня сигнала в чувствительных цепях.
Третий вид потерь мощности возникает в результате потери магнитного потока, который может быть рассеян механическими монтажными элементами, воздушными зазорами в сердечнике или небрежным исполнением при изготовлении самой катушки.
Ознакомьтесь с нашим предложением
Заключительные замечания
Индукционная катушка является простым компонентом, и поэтому ею часто пренебрегают. Между тем, при монтаже электронной схемы, оснащенной дросселями или преобразователями, особое внимание следует уделить выбору индуктивных элементов, в том числе их резонансным частотам или параметрам материала сердечника. Используются разные ядра с текущей частотой в десятки и сотни герц и разные с частотой в сотни мегагерц и более. Иногда для высокочастотных сигналов достаточно ферритовой шайбы.
Между тем, при монтаже электронной схемы, оснащенной дросселями или преобразователями, особое внимание следует уделить выбору индуктивных элементов, в том числе их резонансным частотам или параметрам материала сердечника. Используются разные ядра с текущей частотой в десятки и сотни герц и разные с частотой в сотни мегагерц и более. Иногда для высокочастотных сигналов достаточно ферритовой шайбы.
Индукционные катушки могут изготавливаться различными способами. Обычно на сердечник наматывают от нескольких до нескольких сотен витков провода. В некоторых приложениях витки наматываются в виде дорожек на печатной плате, а иногда и замыкаются в ферритовом сердечнике. В настоящее время большинство катушек, в частности дросселей, используемых в силовых цепях, изготавливаются с целью монтажа SMT. Тем не менее, технологическая гонка идет жестко, и разрабатываются все новые магнитные материалы, способные сохранять свои характеристики и ограничивать потери, несмотря на повышение температуры и т. д.
д.
Катушка, предназначенная для работы на низкой частоте, обычно имеет железный сердечник и большое количество витков, что делает ее относительно тяжелой. Вот почему во многих приложениях, особенно уязвимых к ударам и перенапряжениям, важную роль играет способ монтажа. Обычно припаять катушку недостаточно — ее сердечник нужно правильно зафиксировать с помощью зажима, держателя или винта. При выборе катушки или преобразователя для устройства стоит учитывать этот аспект.
Применение индукционных катушек в электронике
Катушки используются для:
- блокировки протекания переменного тока в цепи,
- КЗ постоянного тока (напряжения),
- измерение времени на основе снижения текущего расхода,
- построить колебательный контур,
- построить фильтры для определенных частот,
- пара каскадов усилителя,
- уменьшить или увеличить напряжение.
Некоторые области применения катушек аналогичны применению конденсаторов.


 По какому из приведенных ниже правил можно определить направление силы Ампера?
По какому из приведенных ниже правил можно определить направление силы Ампера? по модулю прямо пропорциональна модулю В;
по модулю прямо пропорциональна модулю В; Притягиваются.
Притягиваются. Частица с отрицательным зарядом q влетела в зазор между полюсами электромагнита, имея скорость , направленную горизонтально и перпендикулярную вектору индукции магнитного поля. Куда направлена действующая на нее сила Лоренца ?
Частица с отрицательным зарядом q влетела в зазор между полюсами электромагнита, имея скорость , направленную горизонтально и перпендикулярную вектору индукции магнитного поля. Куда направлена действующая на нее сила Лоренца ? Направление тока указано стрелкой. Как направлен вектор магнитной индукции в точке С?
Направление тока указано стрелкой. Как направлен вектор магнитной индукции в точке С? Вычислить силу,
Вычислить силу, В каком случае вокруг движущегося электрона возникает магнитное поле? 1. Электрон движется равномерно и прямолинейно. 2.Электрон движется равномерно по окружности. 3.Электрон движется равноускоренно прямолинейно.
В каком случае вокруг движущегося электрона возникает магнитное поле? 1. Электрон движется равномерно и прямолинейно. 2.Электрон движется равномерно по окружности. 3.Электрон движется равноускоренно прямолинейно. В магнитном поле находится проводник с током. Каково направление силы Ампера.
В магнитном поле находится проводник с током. Каково направление силы Ампера.
 Как можно объяснить взаимное отталкивание параллельных проводников, по которым протекают постоянные электрические токи?
Как можно объяснить взаимное отталкивание параллельных проводников, по которым протекают постоянные электрические токи?
 38, нет. 5, стр. 2367–2369, 2002.
38, нет. 5, стр. 2367–2369, 2002.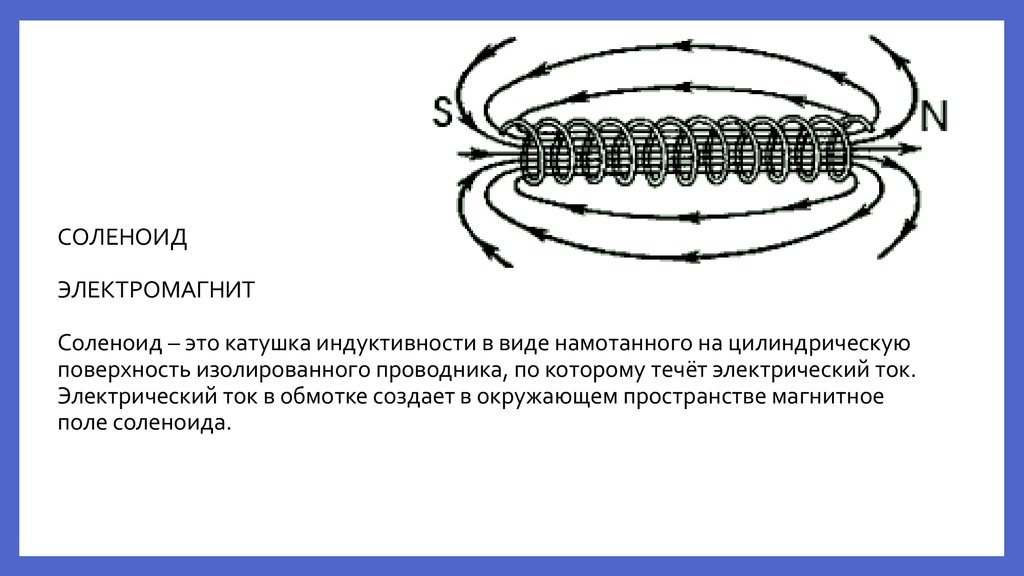 И. Бабич и К. Акьель, «Расчет магнитной силы между тонкими коаксиальными круглыми катушками в воздухе», IEEE Transactions on Magnetics , vol. 44, нет. 4, стр. 445–452, 2008 г.
И. Бабич и К. Акьель, «Расчет магнитной силы между тонкими коаксиальными круглыми катушками в воздухе», IEEE Transactions on Magnetics , vol. 44, нет. 4, стр. 445–452, 2008 г. Ravaud, G. Lemarquand, V. Lemarquand, S. Babic и C. Akyel, «Взаимная индуктивность и сила, действующая между толстыми катушками», Progress in Electro Magnetics Research , vol. 102, стр. 367–380, 2010.
Ravaud, G. Lemarquand, V. Lemarquand, S. Babic и C. Akyel, «Взаимная индуктивность и сила, действующая между толстыми катушками», Progress in Electro Magnetics Research , vol. 102, стр. 367–380, 2010. Раво, Г. Лемаркан и В. Лемаркан, «Сила и жесткость пассивных магнитных подшипников с использованием постоянных магнитов. часть 2: радиальная намагниченность», IEEE Transactions on Magnetics , vol. 45, нет. 9, стр. 3334–3342, 2009.
Раво, Г. Лемаркан и В. Лемаркан, «Сила и жесткость пассивных магнитных подшипников с использованием постоянных магнитов. часть 2: радиальная намагниченность», IEEE Transactions on Magnetics , vol. 45, нет. 9, стр. 3334–3342, 2009.