12.7. Магнитное поле соленоида

Соленоид представляет собой провод, навитый равномерно в виде спирали на общий цилиндрический каркас (см. рис. 12.14). Произведение (IN) числа витков однослойной намотки соленоида на силу тока, обтекающего витки, называется числом ампер-витков.

Рис. 12.14

Соленоиды предназначены для создания в небольшом объеме пространства достаточно сильного магнитного поля. При плотной намотке витков поле соленоида эквивалентно полю системы круговых параллельных токов с общей осью. Если диаметр d витков соленоида во много раз меньше его длины (d  l), то соленоид считается бесконечно длинным (или тонким). Магнитное поле такого соленоида практически целиком сосредоточено внутри, причем вектор магнитной индукции _внутри направлен вдоль оси соленоида и связан с направлением тока правилом правого винта.

Рис. 12.15

Рассмотрим воображаемый замкнутый контур внутри соленоида (рис. 12.15). Этот контур не охватывает токов, поэтому по теореме о циркуляции

Разобьем этот круговой интеграл на четыре интеграла (по сторонам контура) и учтем, что на отрезках (1-2) и (3-4) вектор перпендикулярен, поэтому скалярное произведение (,) здесь обращается в ноль. Индукция поля во всех точках отрезка (2-3) одинакова и равна₂₃, а на отрезке (4-1) ₄₁, причем l₂₃ = l₄₁ = l.

Таким образом, обойдя контур по часовой стрелке, получим

Так как l 0, то В₂₃ = В₄₁ = В _{внутри.}

Поскольку контур внутри соленоида был выбран произвольно, то полученный результат справедлив для любых внутренних точек соленоида, то есть поле внутри соленоида однородное:

_внутри = const.

Чтобы найти величину индукции этого поля, рассмотрим контур L₂ (а –b –c –d –а ), охватывающий N витков с током (рис. 12.15). Согласно теореме о циркуляции (и на основании предыдущих рассуждений), получим соотношение

Поле снаружи бесконечно длинного соленоида очень слабое (_{снаружи} =0), им можно пренебречь, следовательно,

(12.

35)

где n=N/l — число витков, приходящихся на единицу

длины соленоида.

Таким образом, индукция магнитного поля внутри бесконечно длинного соленоида одинакова по величине и направлению и пропорциональна числу ампер-витков, приходящихся на единицу длины соленоида.

Симметрично расположенные витки вносят одинаковый вклад в магнитную индукцию на оси соленоида, поэтому у конца полубесконечного соленоида на его оси магнитная индукция равна половине того значения, которое дает формула (12.35), т.е.

(12.36)

Практически, если (l  d), то формула (12.35) справедлива для точек в средней части соленоида, а формула (12.36) – для точек на оси вблизи его концов.

Применяя закон Био-Савара-Лапласа, можно найти магнитную индукцию поля соленоида конечной длины (рис. 12.16) в произвольной точке А на его оси:

(12. 37)

где- углы между осью соленоида и радиус- вектором, проведенным из рассматриваемой точки к концам соленоида.

Рис. 12.16

Поле такого соленоида неоднородное, величина индукции зависит от положения точки

А и длины соленоида. Для бесконечно длинного соленоида ,, и формула (12.37) переходит в формулу (12.35).

Исследование магнитного поля короткого соленоида и системы двух соленоидов (Методическое пособие по выполнению лабораторной работы)

Физика \ Общая физика

Страницы работы

5 страниц (Word-файл)

Посмотреть все страницы

Скачать файл

Фрагмент текста работы

Лабораторная работа

№6

“ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ КОРОТКОГО СОЛЕНОИДА И СИСТЕМЫ ДВУХ СОЛЕНОИДОВ”

ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ КОРОТКОГО СОЛЕНОИДА И СИСТЕМЫ ДВУХ СОЛЕНОИДОВ

Цель работы:

1. Изучить пространственное распределение магнитного поля катушки с током
2. Проверить принцип суперпозиции магнитных полей на примере двух коротких соленоидов.

Введение

Индукция магнитного поля , создаваемого элементом проводника , по которому протекает ток  в точке пространства, которая находится на расстоянии  от элемента тока , описывается законом Био-Савара-Лапласа:

                                                    (1)

Используя уравнение (1) найдем величину магнитного поля на оси витка, по которому проходит постоянный электрический ток,

                                          (2)

где  — радиус кругового витка с током,  — расстояние вдоль оси от центра круга до точки М на оси кругового тока, в которой измеряется магнитное поле. Индукция кругового тока в его центре () равна:

                                                            (3)

На рис.1 видно, что

                                            (4)

Тогда соотношение (2) может быть записано в виде

                              (5)

Совокупность близко расположенных круговых витков с током, центры которых лежат на общей оси, составляют соленоид. Магнитное поле на оси соленоида можно вычислить, как суму полей, создаваемых каждым витком с током (принцип суперпозиции).

Соленоид называется коротким, если его длина  значительно меньше радиуса обмотки соленоида , и наоборот длинным, если .

Определим индукцию в точке  (рис.2) для соленоида длиной , радиусом  и числом витков  (т.е. плотностью намотки, или числом витков на единицу длины ). Вклад участка соленоида длиной  в результирующее магнитное поле равен:

                                                 (6)

Запишем переменную  через угол . На рис. 2 видно, что , откуда . Тогда  интегрируя это выражение по углу , получим:

                                 (7)

где  и  - углы, под какими видно радиусы соленоида из точки на его оси, в которой вычисляется магнитное поле (рис. 2). Если точка на оси лежит внутри соленоида, то удобно ввести угол  (рис. 3). Тогда формула (7) с учетом формулы (3), принимает вид:

                               (8)

Магнитное поле в центре короткого соленоида равно

                                                        (9)

Принцип суперпозиции магнитных полей можно проверить экспериментально, используя два коротких соленоида (катушки Гельмгольца). Результирующее поле в точке М (рис.4) при этом определяется алгебраической суммой полей, которые создаются каждой катушкою отдельно, а распределение  вдоль оси соленоидов будет определяться суммой кривых  и , создаваемых каждой катушкой отдельно (рис. 5).

На рис.5 проиллюстрирована суперпозиция полей, создаваемых катушками Гельмгольца при протекании токов одинакового направления.

Описание экспериментальной установки

Описание установки показано на рис. 6. Катушка  неподвижна, а катушка  может перемещаться по направляющим. Расстояние между центрами катушек определяется по шкале, которая располагается на панели. Измерительный датчик D закреплен на стержне, который может перемещаться вдоль оси соленоида. Датчик позволяет измерять индукцию магнитного поля на оси системы. Переменный ток, который протекает по соленоиду, создает в пространстве переменное магнитное поле, которое возбуждает в катушке D электродвижущую силу индукции (ЭДС):

                                              (10)

где  — поток вектора индукции магнитного поля через катушку,  — площадь сечения катушки датчика,  — число витков катушки датчика. Учитывая, что

                                   (11)

получим

,                                          (12)

где линейная частота переменного тока .

Измерения  можно проводить или вольтметром, или при помощи осциллографа. В связи с тем, что входное сопротивление вольтметра очень велико, можно записать, что

.                                                               (13)

Тогда из (12) с учетом соотношения (13), можно получить амплитудное значение индукции магнитного поля

,                                                (14)

где .

При использовании осциллографа

.                                                                    (15)

Радиусы коротких соленоидов , длины намотки , число витков обмоток соленоидов .

Выполнение работы

1.  Показать, что соленоид, который используется, можно считать коротким. Для этого, используя геометрические размеры соленоида, сравнить формулы (3) и (9). При этом принять число витков одинаковыми.

2.  Собрать схему показную на рис.7, используя неподвижную катушку .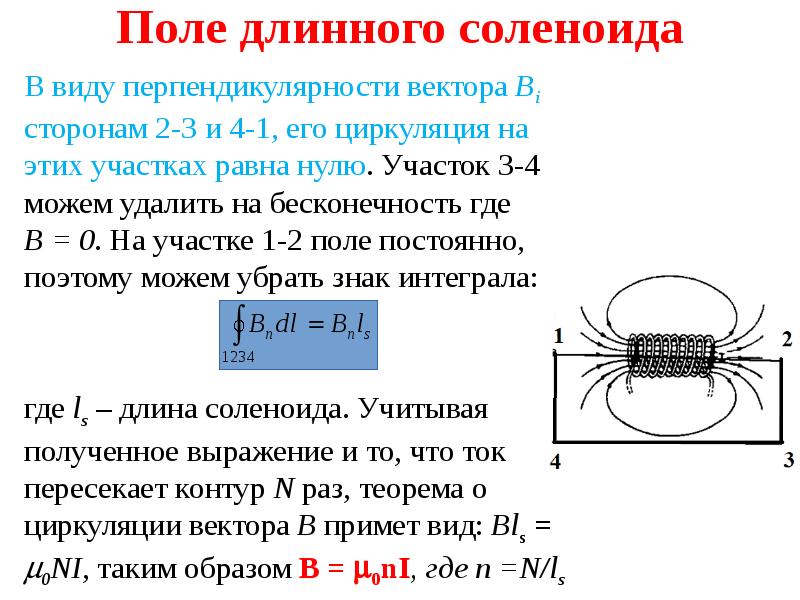 Установить ток через соленоид . С помощью измерительного датчика  найти индукцию  в центре соленоида. Перемещая зонд вдоль оси соленоида, измерять поле первой катушки

Похожие материалы

Информация о работе

Скачать файл

Магнитное поле вдоль оси короткого толстого соленоида | Учитель физики

Пропустить пункт назначения

01 февраля 2018 г.

Фрэнсис Ксавьер Харт

Учитель физики 56, 104–106 (2018)

https://doi.org/10.1119/1.5021438

• Взгляды
  • Содержание артикула
  • Рисунки и таблицы
  • Видео
  • Аудио
  • Дополнительные данные
  • Экспертная оценка
• Делиться
  • Твиттер
  • Фейсбук
  • Реддит
  • LinkedIn
• Инструменты

  • Перепечатки и разрешения

  • Иконка Цитировать Цитировать

• Поиск по сайту

Citation

Фрэнсис Ксавьер Харт; Магнитное поле вдоль оси короткого толстого соленоида.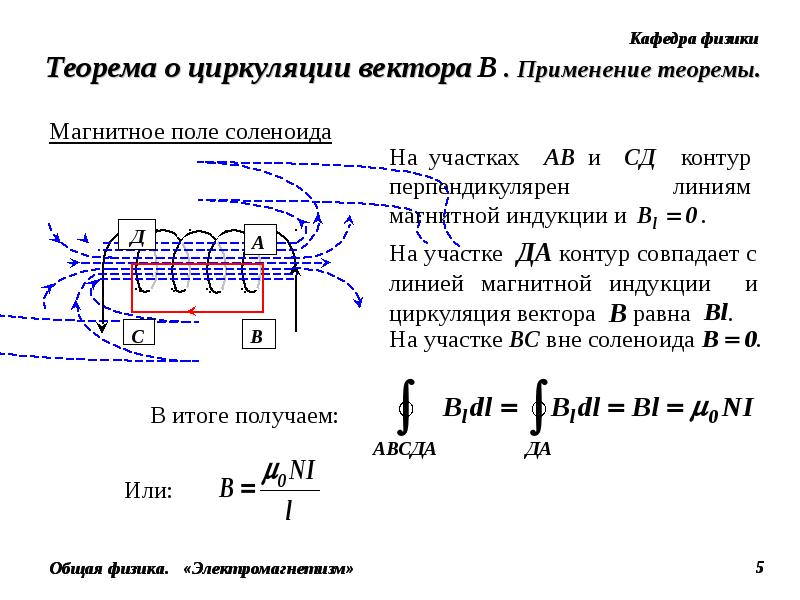 Учитель физики 1 февраля 2018 г.; 56 (2): 104–106. https://doi.org/10.1119/1.5021438

Скачать файл цитаты:

• Рис (Зотеро)
• Менеджер ссылок
• EasyBib
• Подставки для книг
• Менделей
• Бумаги
• КонецПримечание
• РефВоркс
• Бибтекс

панель инструментов поиска

Расширенный поиск |Поиск по цитированию

Обычно мы просим студентов сравнить результаты своих экспериментальных измерений с предсказаниями простой физической модели, которая хорошо понятна. Однако на практике физики должны сравнивать свои экспериментальные измерения с предсказаниями нескольких моделей, ни одна из которых не может хорошо работать во всем диапазоне измерений. Ниже описан эксперимент, который мы используем во втором семестре двухсеместрового курса, предназначенного для специалистов по химии, биохимии и биологии, в качестве примера такой ситуации. Эксперимент состоит из трех частей. В первой части студенты, работая в группах по два-три человека, калибруют поисковую катушку. Во второй части они располагают катушку на различных расстояниях от центра толстого конечного соленоида и измеряют поле в каждой позиции. В третьей части они используют три модели для предсказания магнитного поля в каждой из этих позиций. Затем учащиеся должны решить, лучше ли одна модель предсказывает результаты измерений. Если ни одна модель не может этого сделать, они должны решить, какая модель лучше всего работает в каком диапазоне.

Темы

Электрооборудование, Измерительные приборы, Магнитные поля, Термодинамические состояния и процессы, катушка Гельмгольца, электромагнитные катушки, Образование, биохимия, Физики, Государственная политика и управление

В настоящее время у вас нет доступа к этому контенту.

У вас еще нет аккаунта? регистр

Physics for Science & Engineering II

от Office of Academic Technologies на Vimeo.

Пример. Магнитное поле идеального соленоида

Ранее мы рассчитали магнитное поле, создаваемое длинным прямым проводом с током. Когда мы рассматривали бесконечно длинный провод, по которому течет ток i, этот ток создавал магнитное поле на некотором расстоянии r от провода, и магнитное поле было равно Mu нулю i на протяжении 2 Pi r. Мы видели, что геометрия силовых линий магнитного поля была такова, что они имели форму концентрических окружностей, а затем ложились вдоль плоскостей, перпендикулярных проволоке. Таким образом, в этом месте магнитное поле, создаваемое этим током, было направлено в плоскость.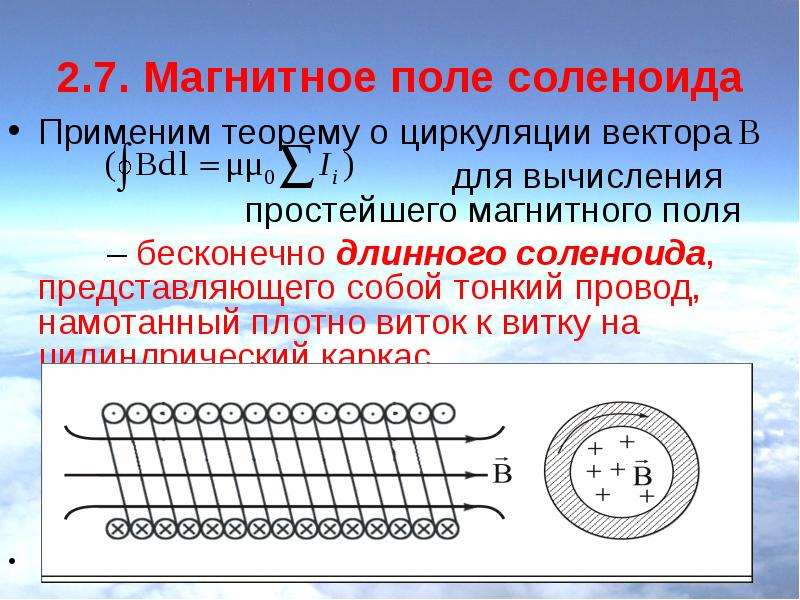 Мы нашли в результате как закона [НЕРАЗБОРЧИВО], так и закона Ампера. Когда мы смотрим на этот результат здесь, мы видим, что магнитное поле прямо пропорционально току. Другими словами, если мы увеличим ток, то получим большее магнитное поле. Поэтому, если нашей целью является создание очень сильного магнитного поля в этой точке, мы просто увеличиваем ток, протекающий по проводу.

Очевидно, чтобы иметь возможность это сделать, чтобы увеличить ток, другими словами, через провод, мы применяем все большую и большую разность потенциалов между двумя концами провода. Проблема с этой операцией в том, что мы всегда получаем верхний предел. Другими словами, если мы применяем разность потенциалов выше некоторого определенного предельного значения для данной среды, мы можем легко разрушить электрические свойства этой среды. Следовательно, увеличивая ток, мы можем увеличить магнитное поле до некоторой определенной точки, но мы не можем превысить или выйти за пределы этого предельного значения.

Тогда возникает проблема с созданием очень сильного магнитного поля с использованием того же количества тока. Можем ли мы это сделать? И ответ на этот вопрос – да. На самом деле, это можно сделать очень просто, взяв проволоку и скрутив ее в спираль. Что-то вроде этого. Как пружина. Когда ток пропускается через эту систему, как мы видим, он будет входить в плоскость в этой точке, с точки зрения поперечного сечения, и выходить из плоскости из нижней части, и он будет течь и входить в самолет здесь и выходит из самолета в этой точке, и так далее, и тому подобное.

Если мы посмотрим на эту картинку с точки зрения поперечного сечения, то получим примерно такую ​​систему. Когда мы разрежем его вертикально с точки зрения поперечного сечения, мы получим верхнюю ветвь, что-то вроде этой, и нижнюю ветвь. Если верхняя ветвь переносит ток не в плоскости, то нижняя ветвь будет переносить ток в плоскости примерно так. Так что в трехмерном смысле ток выходит из плоскости здесь и входит в плоскость там. Ниже плоскости она движется в этом направлении, выходит и входит в плоскость вот так, и так далее, и тому подобное.

Поэтому, когда мы смотрим на систему, мы можем рассматривать ее как группу токовых петель, которые генерируют определенное магнитное поле. Если мы посмотрим на каждый из этих потоков отдельно и применим правило правой руки, держа большой палец правой руки, направленный вне плоскости, мы увидим, что пальцы правой руки будут вращаться вокруг большого пальца против часовой стрелки. Следовательно, на этой плоскости этот ток будет генерировать силовые линии магнитного поля, вращающиеся против часовой стрелки. Так и следующий, а затем следующий, следующий, и так далее, и так далее.

Если провести аналогичный анализ для нижних ветвей, по которым ток идет в плоскость, то удерживая большой палец, направленный в плоскость, и обводя пальцы правой руки вокруг большого пальца, мы увидим, что в В этом случае линии магнитного файла, создаваемые этим током, будут иметь форму концентрических кругов, и они будут вращаться по часовой стрелке. Так и следующий, следующий, следующий и так далее и тому подобное.

Ну, конечно, эти витки расположены очень близко друг к другу, и в результате этого магнитное поле, создаваемое вот этим током, будет накладываться на следующее, а затем оно наложится на следующее, а затем пересекаться со следующим. В результате этого все магнитные поля, создаваемые каждым витком, будут добавляться к следующему, а затем возвращаться за пределы этой формации и замыкаться на себе. Поскольку мы знаем, что у нас не может быть открытых силовых линий магнитного поля, они всегда замыкаются сами на себя. Точно так же будет перекрываться нижняя ветвь. Магнитное поле, создаваемое каждым витком, будет добавляться к следующему и генерировать силовые линии примерно так. Таким образом, в результате этого формирования мы придем к геометрии силовых линий магнитного поля, что эти силовые линии, в конечном счете, замыкаются друг на друга вдоль этих направлений.

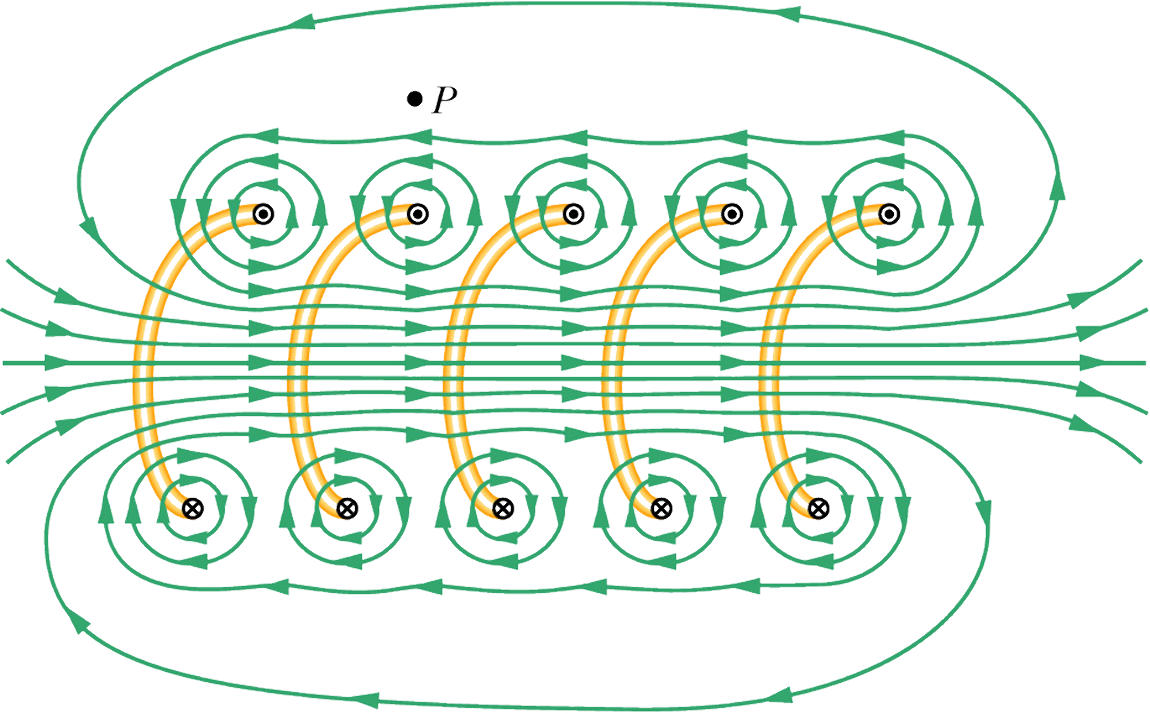
Теперь мы можем видеть, что геометрия силовых линий такой текущей геометрии будет очень похожа на случай стержневых магнитов. Если мы вспомним простой стержневой магнит с северным полюсом здесь и южным полюсом здесь, то геометрия силовых линий такого магнита была очень похожа на геометрию силовых линий, которую мы получаем, если поместить провод в спиральную форму этого магнита. тип. Как вы помните, для магнитов мы сказали, что обычное направление силовых линий магнитного поля таково, что они выходят из северного полюса и входят в южный полюс.

В этом смысле формация здесь становится такой, что этот конец соответствует северному полюсу магнита, а затем этот конец соответствует южному полюсу. На самом деле мы можем легко определить, какой конец будет северным, а какой снова южным, применяя правило правой руки. Если мы просто согнем пальцы правой руки в направлении, в котором протекает ток, то есть в данном случае он будет входить и выходить перпендикулярно плоскости экрана, а ток будет течь против часовой стрелки, и удерживая большой палец снова в открытом положении, мы увидим, что большой палец будет указывать вправо. Поэтому правый конец формации будет соответствовать северному полюсу. Тогда другая рука будет естественно соответствовать южному полюсу такого магнитного устройства.

Мы называем такие системы соленоидами. Попробуем определить магнитное поле соленоида. Что-то вроде этого. Применяя закон Ампера. Магнитное поле, скажем, идеального соленоида. Под идеальным соленоидом мы подразумеваем магнитное поле, как вы помните, касательное к силовым линиям, проходящим через интересующую точку. Таким образом, внутри соленоида у нас будет самое сильное магнитное поле, потому что количество силовых линий, проходящих через единицу площади, связано с силой магнитного поля, и мы можем легко увидеть, что оно самое сильное на концах, а также внутри соленоида, потому что эта числовая плотность будет одинаковой, пока мы находимся внутри соленоида. Как только мы покинем соленоид и уйдем от него, например, в этой области, мы увидим, что тангенс b будет примерно таким. По мере удаления от соленоида наружу напряженность магнитного поля будет уменьшаться, потому что количество линий, проходящих через единицу поверхности, будет становиться все меньше и меньше.

Если мы обозначим длину соленоида как l, а его диаметр как d, когда l намного больше, чем d, тогда b out становится очень маленьким, и мы можем рассматривать это так, как если бы оно стремилось к нулю. Если b out равно нулю, то мы называем этот тип соленоида идеальным соленоидом. Поэтому для идеального соленоида напряженность магнитного поля вне соленоида можно принять равной нулю. Для такого случая попробуем определить магнитное поле внутри этого идеального соленоида. Чтобы сделать это, мы применим закон Ампера, и, как мы помним, закон Ампера был проинтегрирован по замкнутому контуру e dot d l, равный нулю Mu, умноженному на i.

Хорошо. Скажем снова, что l представляет собой длину соленоида, а заглавная буква N представляет собой количество витков соленоида. Малый n — это число витков, и это просто общее количество витков, деленное на общую длину соленоида. Чтобы иметь возможность применить этот закон, мы должны выбрать замкнутый контур. В этом случае предположим, что наша точка интереса находится в этом месте.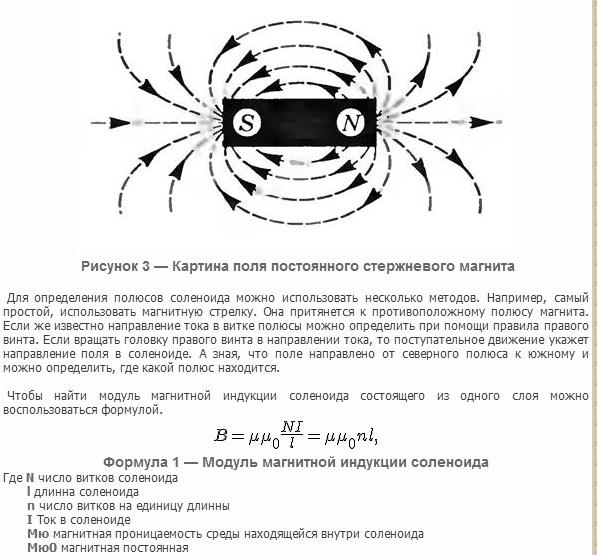 Мы хотим определить магнитное поле в этой точке p, которая находится внутри соленоида, и мы выберем замкнутый контур в виде прямоугольника, проходящего через эту точку p и совпадающего с магнитным полем линия, проходящая через эту точку.

В этот момент соответствующая линия магнитного поля будет направлена ​​слева направо, примерно так. Поэтому мы выбираем нашу петлю так, чтобы одна сторона прямоугольной петли совпадала с линией магнитного поля в точке, и здесь магнитное поле будет касаться этой линии. Следовательно, вдоль этой линии в этой точке магнитное поле будет направлено слева направо вот так. Одна сторона петли, которую мы выбираем, совпадает с магнитным полем или с линией магнитного поля, а другая сторона петли находится вне соленоида.

d l, инкрементальный вектор смещения, находится вдоль контура, поэтому на этом отрезке он будет таким. На этом отрезке будет так. Вектор приращения смещения для внешнего сегмента указывает влево, а для этого сегмента будет направлен вниз.

Хорошо. Когда мы смотрим на эту петлю, мы видим, что она состоит из четырех сегментов. А именно, это сегмент 1, сегмент 2, сегмент 3, сегмент 4. Таким образом, это интегрирование с обратной связью e точка d l. Мы можем выразить это как интегралы по путям вдоль каждого из этих сегментов и, наконец, сложить их вместе, чтобы получить интегрирование с обратной связью. Другими словами, мы можем выразить этот интеграл, левую часть, как интеграл по первому отрезку b dot d l. Запишем это в явном виде. Для первого отрезка b указывает вправо, d l также указывает вправо, поэтому угол между ними равен нулю градусов, поэтому для этого отрезка мы имеем b d l, умноженный на косинус угла между ними, и это косинус нуля. Здесь я должен избавиться от этого кругового знака, потому что этот интеграл принимает открытый путь или открытую линию по сегменту 1. Другими словами, это не интегрирование с замкнутым контуром с этой формой.

Плюс интеграл второго сегмента. Когда мы смотрим на интеграл по второму сегменту, некоторые части второго сегмента находятся внутри соленоида, тогда как некоторые части находятся снаружи соленоида. Поэтому мы можем разделить этот интеграл на два отрезка, сказав, что интеграл отсюда туда. Для этой части у нас есть магнитное поле, направленное вправо повсюду внутри соленоида, поэтому здесь оно указывает, например, вот так. d l направлен вверх, поэтому угол между ними равен 90 градусов. В то время как снаружи у нас есть нулевое магнитное поле для идеального соленоида. Следовательно, у нас есть b d l косинус 90 для части внутри соленоида, поэтому мы можем назвать его b внутри для этой области. Тогда у нас также есть отрезок вне второго пути, и для этой части у нас есть b out dot d l, но для этой области b out равно нулю, а также внутри области, поскольку косинус 90 равен нулю, будет не должно быть вклада от интеграла по второму отрезку.

Двигаемся дальше, для интеграла по третьему сегменту, и это снова вне области соленоида, и для идеального соленоида магнитное поле в этой области равно нулю. Таким образом, мы обозначили b out точками вектора приращения смещения d l , и, поскольку b out равно нулю, интегрирование третьего сегмента также не даст никакого вклада.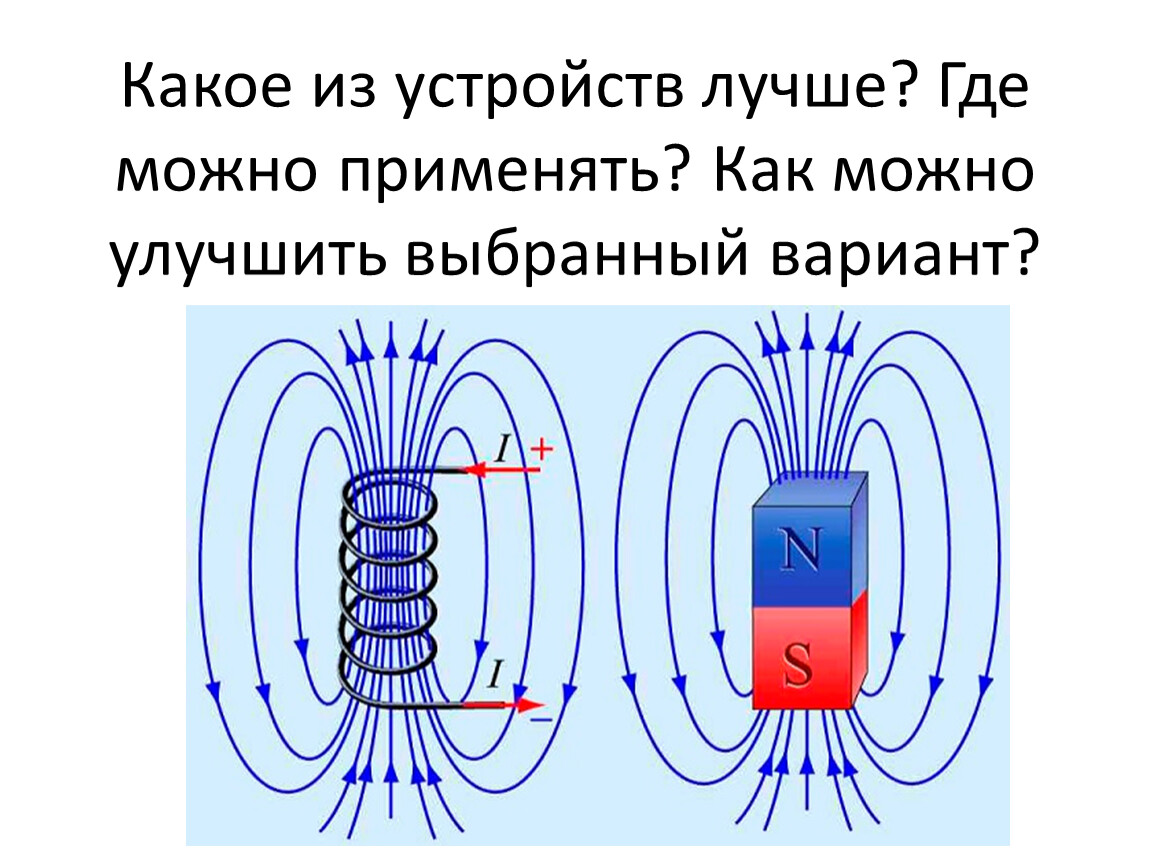

Идем дальше, плюс интеграл по четвертому сегменту, и четвертый сегмент очень похож на второй сегмент. Часть его находится снаружи соленоида, а часть внутри соленоида. Внутри соленоида угол между вектором магнитного поля и d l составляет 90 градусов. Косинус 90 от скалярного произведения даст нам ноль. С внешней части этого сегмента магнитное поле равно нулю. Поэтому для этой области, опять же, для внутренней части, мы имеем d d l косинус 90, а косинус 90 равен нулю, плюс для того же сегмента вне соленоида, поскольку магнитное поле равно нулю, никакого вклада в магнитное поле снова не будет.

Теперь, если мы сложим эти интегралы по открытым путям по первому, второму, третьему и четвертому сегментам, то все эти интегралы по путям в сумме дадут интеграл по замкнутому контуру по этому прямоугольному контуру, и все они должны в сумме давать Mu ноль раз i прилагается. Если мы посмотрим на эти интегралы, выживет только первый. Косинус нуля равен 1 и пока мы находимся на этом первом отрезке, так как он совпадает с силовой линией магнитного поля, поэтому напряженность магнитного поля будет везде вдоль этой линии одинакова. Следовательно, величина магнитного поля для этой части постоянна, тогда мы можем вынести ее за пределы интеграла. В итоге мы получим, что интеграл от d l по первому сегменту, умноженный на b, равен Mu, умноженному на ноль, умноженному на i.

Теперь интеграл от d l по первому отрезку даст нам длину этого отрезка. Другими словами, если мы сложим все эти dl вместе, то есть интегрируем по этой длине, мы в конечном итоге придем к тому, какой будет эта длина. Поскольку это петля, которую мы выбираем, мы можем придать ей любые размеры, какие захотим, и назовем ее длину, например. В этом случае мы получаем b, умноженное на a, равно Mu, умноженное на i, умноженное на i. Итак, левая часть закона Ампера выполнена, теперь мы попытаемся вычислить правую часть, которую я приложил.

Теперь, чтобы сделать это, вернемся к нашей диаграмме. То, что мы подразумеваем под i вложенным, — это чистый ток, протекающий через область, окруженную этой петлей, которая является этой областью. Мы хотим выяснить, какой ток протекает через эту область. Чистый ток, протекающий через область, окруженную этой замкнутой петлей, амперной петлей, — это то, что мы называем замкнутым. Ну, конечно, этот ток будет равен количеству витков, проходящих через эту поверхность. Если мы можем выразить количество витков, проходящих через эту поверхность, поскольку каждый виток несет ток i, то это число витков, умноженное на ток i, даст нам чистый ток, протекающий через эту поверхность.

Ну, так как мы знаем общее количество витков, а также общую длину соленоида, то общее количество витков, разделенное на общую длину, даст нам число витков, которое мы определяем как немного n. Таким образом, у нас будет такое количество витков на единицу длины. Теперь, если мы умножим эту числовую плотность витков на длину интересующей нас области, которая является этой областью, то это даст нам общее количество витков по этой длине. Таким образом, умноженное на n, мы получим общее количество витков на этой длине. Поскольку каждый виток несет ток i, это число, умноженное на ток i, даст нам вложенное i.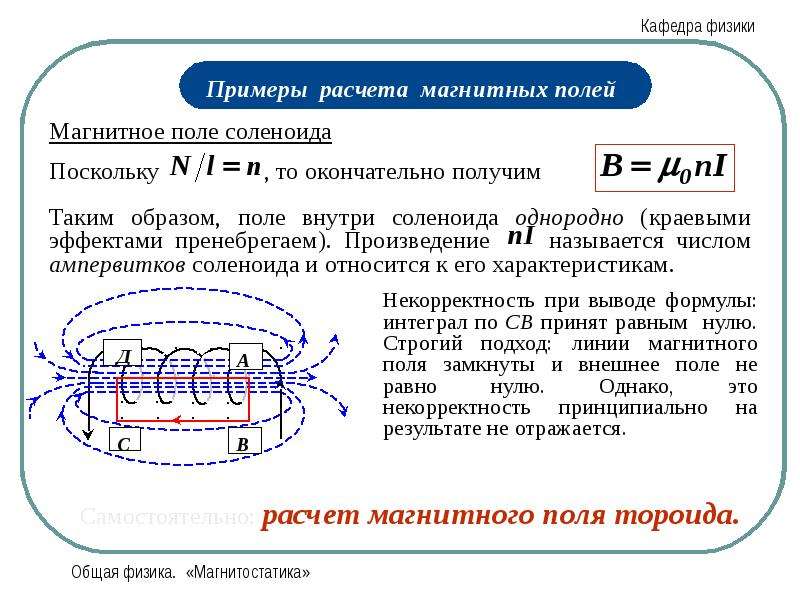 Следовательно, здесь мы имеем плотность числа витков, n, умноженную на а, что даст нам общее количество витков вдоль а. То есть в явном виде. Скажем, общее количество витков разделить на общую длину соленоида, а затем умножить на а, и все это даст нам общее количество витков по длине а.

Если мы умножим эту величину на i, то есть ток, протекающий через один виток, то мы получим общее число токов, проходящих через интересующую область. Это ток через каждый виток. Все в порядке. Таким образом, заключенное i равно n, умноженному на i. Таким образом, левая часть была равна d a, а правая часть у нас будет Mu ноль раз, поскольку i заключено, мы имеем n раз a, умноженное на i. Как видите, длина петли, которую мы выбираем, будет сокращаться с обеих сторон, поэтому не имеет значения, насколько короткой или длинной мы выбираем длину этой петли. В конце концов они нейтрализуются, и магнитное поле идеального соленоида будет равно Mu, умноженному на нуль, умноженному на числовую плотность соленоида, умноженную на ток, протекающий через соленоид.