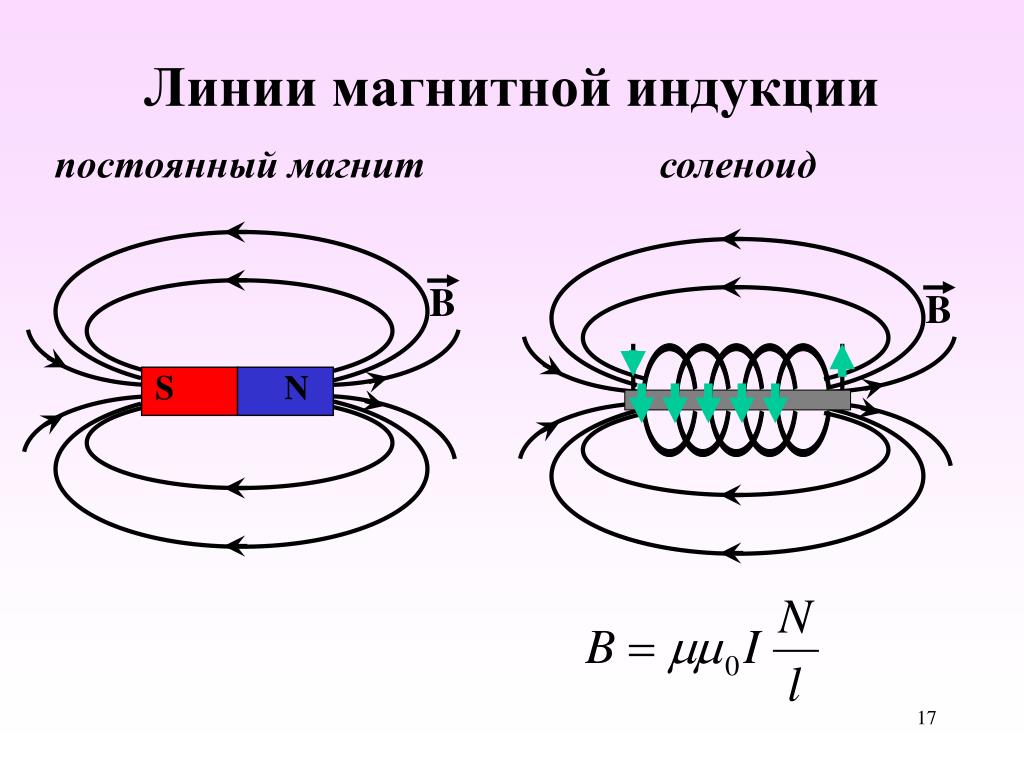
Магнитное поле соленоида. Формула, суть явления

• admin
• 13.08.2022
• 0 comments

Магнитное поле соленоида представляет собой суперпозицию отдельных полей, которые создаются каждым витком в отдельности. Через все витки протекает один и тот же ток. Оси всех витков лежат на одной лини. Соленоид представляет собой катушку индуктивности, имеющую цилиндрическую форму. Эта катушка намотана из проводящей проволоки. При этом витки уложены плотно друг к другу и имеют одном направление. При этом считается, что длинна катушки значительно превышает диаметр витков.

Давайте рассмотрим магнитную индукцию, создаваемую каждым витком. Видно, что индукция внутри каждого витка направлена в одну и ту же сторону. Если смотреть в центр витка, то индукция от его краев будет складываться. При этом индукция магнитного поля между двух соседних витков направлена встречно. Так как она создана одним и тем же током то она компенсируется.

Рисунок 1 — Поле создаваемое отдельными витками соленоида

 

Если витки соленоида намотаны достаточно плотно, то между всеми витками встречное поле будет компенсировано, а внутри витков произойдет сложение отдельных поле в одно общее. Линии этого поля будут проходить внутри соленоида, и охватывать его снаружи.

Если исследовать магнитное поле внутри соленоида любыми способами, например, с помощью железных опилок то можно сделать вывод, что оно однородно. Лини магнитного поля в этой области представляют собой параллельные прямые. Мало того что они параллельны сами себе но они еще параллельны оси соленоида. Выходя за приделы соленоида, они искривляются и замыкаются снаружи катушки.

Рисунок 2 — Поле создаваемое соленоидом

Из рисунка видно, что поле создаваемое соленоидом похоже на поле, которое создает постоянный стержневой магнит. На одном конце силовые линии выходят из соленоида и этот конец аналогичен северному полюсу постоянного магнита. А в другой они входят, и этот конец соответствует южному полюсу. Отличие же заключается в том, что поле присутствует и внутри соленоида. И если провести опыт с железными опилками, то они втянутся в пространство между витками.

Но если внутрь соленоида вставить деревянный сердечник либо сердечник из любого другого немагнитного материала, то при проведении опыта с железной стружкой картина поля постоянного магнита и соленоида будет идентична.

Так как деревянный сердечник не исказит силовые лини, но при этом не даст проникнуть опилкам внутрь катушки.

 Рисунок 3 — Картина поля постоянного стержневого магнита

Для определения полюсов соленоида можно использовать несколько методов. Например, самый простой, использовать магнитную стрелку. Она притянется к противоположному полюсу магнита. Если же известно направление тока в витке полюсы можно определить при помощи правила правого винта. Если вращать головку правого винта в направлении тока, то поступательное движение укажет направление поля в соленоиде. А зная, что поле направлено от северного полюса к южному и можно определить, где какой полюс находится.

Чтобы найти модуль магнитной индукции соленоида состоящего из одного слоя можно воспользоваться формулой.

Формула 1 — Модуль магнитной индукции соленоида

Где N число витков соленоида

 l длинна соленоида

  n число витков на единицу длинны

 I Ток в соленоиде

      Мю магнитная проницаемость среды находящейся внутри соленоида

      Мю0 магнитная постоянная

Магнитное поле соленоида

Соленоидом называется совокупность N одинаковых витков изолированного проводящего провода, равномерно намотанных на общий каркас или сердечник.

По виткам проходит одинаковый ток. Магнитные поля, созданные каждым витком в отдельности, складываются по принципу суперпозиции. Индукция магнитного поля внутри соленоида велика, а вне его — мала. Для бесконечно длинного соленоида индукция магнитного поля вне соленоида стремится к нулю. Если длина соленоида во много раз больше диаметра его витков, то соленоид можно практически считать бесконечно длинным. Магнитное поле такого соленоида целиком сосредоточено внутри него и является однородным (рис.6).

Величину индукции магнитного поля внутри бесконечно длинного соленоида можно определить, используя теорему о циркуляции вектора :циркуляция вектора по произвольному замкнутому контуру равна алгебраической сумме токов, охватываемых контуром, умноженной на магнитную постоянную μ_о:

, (20)

где μ₀ = 4π 10^-7 Гн/м.

Рис. 6. Магнитное поле соленоида

Для определения величины магнитной индукции В внутри соленоида выберем замкнутый контур ABCD прямоугольной формы, где — элемент длины контура, задающий направление обхода (рис.6). При этом длиныAB и CD будем считать бесконечно малыми.

Тогда циркуляция вектора по замкнутому контуруABCD, охватывающему N витков, равна:

(21)

На участках AB и CD произведение , так как вектораивзаимно перпендикулярны. Поэтому

. (22)

На участке DA вне соленоида интеграл, так как магнитное поле вне контура равно нулю.

Тогда формула (21) примет вид:

, (23)

где l – длина участка BC. Сумма токов, охватываемых контуром, равна

, (24)

где I_c – сила тока соленоида; N – число витков, охватываемых контуром ABCD.

Подставив (23) и (24) в (20), получим:

. (25)

Из (25) получим выражение для индукции магнитного поля бесконечно длинного соленоида:

. (26)

Так как число витков на единицу длину соленоида n равно:

(27)

то окончательно получим:

. (28)

Если внутрь соленоида помещен сердечник, то формула (28) для В примет вид:

. (29),

где  — магнитная проницаемость материала сердечника.

Таким образом, индукция В магнитного поля соленоида определяется током соленоида I_c, числом витком n на единицу длины соленоида и магнитной проницаемостью материала сердечника.

Магнетроном называется двухэлектродная электронная лампа (диод), содержащая накаливаемый катод и холодный анод и помещенная во внешнее магнитное поле.

Анод диода имеет форму цилиндра радиусом . Катод представляет собой полый цилиндр радиусом, вдоль оси которого расположена нить накала, как правило, изготавливаемая из вольфрама (рис.7).

Раскалённый катод в результате явления термоэлектронной эмиссии испускает термоэлектроны, которые образуют вокруг катода электронное облако. При подаче анодного напряжения (рис.8), электроны начинают перемещаться от катода к аноду вдоль радиусов, что приводит к возникновению анодного тока. Анодный ток регистрируется миллиамперметром.

Рис.7. Схема диода

Рис.8. Электрическая схема цепи

Величина анодного напряжения регулируется потенциометром R_A. Чем больше анодное напряжение, тем большее количество электронов за единицу времени достигает анода, следовательно, тем больше анодный ток.

Напряжённость электрического поля Е между катодом и анодом такая же, как и в цилиндрическом конденсаторе:

, (30)

где r – расстояние от оси катода до данной точки пространства между катодом и анодом.

Из формулы (30) следует, что напряжённость поля Е обратно пропорциональна расстоянию r до оси катода. Следовательно, напряженность поля максимальна у катода.

Так как

r_к <<r_a, (31)

то значение логарифма ln стремится к большой величине. Тогда с увеличением расстояния r напряженность электрического поля между катодом и анодом снижается до нуля. Поэтому, можно считать, что электроны приобретают скорость под действием поля только вблизи катода, и дальнейшее их движение к аноду происходит с постоянной по величине скоростью.

Внешнее магнитное поле, в которое помещён диод, создаётся соленоидом (рис.8). Длина соленоида l много больше диаметра его витков, поэтому поле внутри соленоида можно считать однородным. Ток в цепи соленоида изменяется с помощью потенциометра R

C (рис.8) и регистрируется амперметром.

Характер движения электронов в зависимости от величины поля соленоида показан на рис. 9. Если ток в цепи соленоида отсутствует, то индукция магнитного поля В = 0. Тогда электроны движутся от катода к аноду практически по радиусам.

Увеличение тока в цепи соленоида приводит к возрастанию величины В. При этом, траектории движения электронов начинают искривляться, однако все электроны достигают анода. В анодной цепи будет течь ток такой же, как и в отсутствии магнитного поля.

Рис.9. Зависимость анодного тока I_A от величины тока соленоида I_c в идеальном (1) и реальном (2) случаях, а также характер движения электронов в зависимости от величины поля соленоида.

При некотором значении тока в соленоиде радиус окружности, по которой движется электрон, становится равным половине расстояния между катодом и анодом:

.. (32)

Электроны в этом случае касаются анода и уходят к катоду (рис.9). Такой режим работы диода называется критическим. При этом по соленоиду течёт критический ток I_кр, которому соответствует критическое значение индукции магнитного поля В = В_кр.

При В = В_кр анодный ток в идеальном случае должен скачком уменьшиться до нуля. При В > В_кр электроны не попадают на анод (рис.9), и анодный ток также будет равен нулю (рис.9, кривая 1).

Однако на практике, вследствие некоторого разброса скоростей электронов и нарушения соосности катода и соленоида, анодный ток уменьшается не скачком, а плавно (рис.9, кривая 2). При этом значение силы тока соленоида, соответствующее точке перегиба на кривой 2, считается критическим I_кр. Критическому значению тока соленоида соответствует анодный ток, равный:

, (33)

где – максимальное значение анодного тока при В = 0.

Зависимость анодного тока I_A от величины индукции магнитного поля В (или от тока в соленоиде) при постоянном анодном напряжении и постоянном накале называется сбросовой характеристикой магнетрона.

Магнитное поле соленоида

Магнитное поле соленоида
Next: Происхождение постоянного магнетизма Вверх: Магнетизм Предыдущий: Закон Ампера о круговых движениях Соленоид представляет собой плотно намотанную спиральную катушку проволоки, диаметр которой мал по сравнению с к его длине. Магнитное поле, создаваемое в центре или сердечнике , соленоида с током по существу равномерна и направлена ​​вдоль оси соленоида. Вне соленоида магнитное поле намного слабее. На рис. 27 показано (довольно схематично) магнитное поле, создаваемое типичным соленоидом. Соленоид намотан из одного спирального провода, по которому течет ток. Обмотка достаточно тугая, чтобы каждый виток соленоида хорошо приблизительно как круглая проволочная петля, лежащая в плоскости, перпендикулярной оси соленоид, по которому течет ток. Предположим, что там таких витков на единицу осевой длины соленоида. Что величина магнитного поля в сердечнике соленоида?

Рисунок 27: Соленоид.

Чтобы ответить на этот вопрос, применим схему Ампера. закон к прямоугольной петле. Сначала нужно найти линейный интеграл магнитного поля вокруг. Вдоль и магнитное поле практически перпендикулярна петле, поэтому вклада в линейный интеграл от этих участков контура. Вдоль магнитного поля примерно однородно, величины , скажем, и направлена ​​параллельно петле. Таким образом вклад в линейный интеграл от этого участка контура , где длина . Вдоль магнитного поля напряженность практически незначительна, поэтому этот участок цикла не влияет на линию интеграл. Отсюда следует, что линейный интеграл магнитное поле вокруг просто

(178)

По круговому закону Ампера этот линейный интеграл равен умножить на алгебраическую сумму токи, протекающие по контуру. Так как длина петля по оси соленоида , петля пересекает витков соленоида, через каждый из которых протекает ток. Таким образом, общая ток, протекающий по контуру, равен . Этот ток считается положительный ток, так как если мы посмотрим против направления токи текут в каждом витке ( т. е. на страницу на рисунке), цикл циркулирует эти токи против часовой стрелки. Контурный закон Ампера дает

(179)

что сводится к

(180)

Таким образом, магнитное поле в сердечнике соленоида прямо пропорциональна произведению ток, протекающий вокруг соленоида, и число витков на единицу длины соленоида. Это, результат точно в предел, при котором длина соленоида намного превышает его диаметр.

---

Next: Происхождение постоянного магнетизма Вверх: Магнетизм Предыдущий: Закон Ампера о круговых движениях

Ричард Фицпатрик 2007-07-14

Магнитное поле в формуле соленоида

Соленоид представляет собой длинный провод, скрученный в форме спирали, который помогает создавать однородное магнитное поле. Его можно интерпретировать как круговую петлю, если расстояние между витками меньше. Однородность внутреннего магнитного поля соленоида возрастает с увеличением его длины. Полное магнитное поле соленоида равно сумме магнитных полей, создаваемых на каждом его витке. Идеальный соленоид имеет нулевое внешнее поле и однородное внутреннее поле, так как его длина намного больше радиуса витков.

 

Формула магнитного поля в соленоиде

Магнитное поле в соленоиде максимально, когда длина соленоида больше радиуса его контуров. Это зависит от различных факторов, таких как количество витков на единицу длины, сила тока в катушке и проницаемость материала, используемого в соленоиде. Магнитное поле соленоида находится по формуле:

B = μ _o IN/L

где,

μ _o — постоянная проницаемости со значением 1,26 × 10 ⁻⁶ Тл/м,

Н — число витков в соленоиде,

I — ток, проходящий через катушку,

L — длина катушки.

Вывод

Формула для магнитного поля внутри соленоида может быть получена с помощью Закона Ампера.

Рассмотрим соленоид длины n, через каждый виток которого проходит ток I.

Мы знаем, что интеграл по замкнутому амперианскому пути прямоугольной формы определяется выражением

  …… (1)

Теперь полный ток, проходящий через соленоид, определяется выражением

I _T = число витков в соленоиде × Ток, проходящий через каждый виток

I _T = (nh) (I)               …… (2)

Используя закон Ампера, мы можем заключить, что

Из (1) и (2) мы есть

Bh = μ _o I _T

Bh = μ _o I (nh)

B = μ _o nI

Полагая n = N/L, поскольку n — количество единиц на единицу длины, получаем

900 31 В = мк _o IN/L

Отсюда выводится формула для магнитного поля внутри соленоида.

Примеры задач

Задача 1. Найти величину магнитного поля внутри соленоида длиной 2 м и 100 витками на единицу длины, если через него проходит ток силой 5 А.

Решение:

Имеем,

n = 200, L = 2, I = 5

Найдите количество витков по формуле n = N/L.

N = nl

= 200 (2)

= 400 витков

Используя формулу для магнитного поля, получаем 4π × 10 ^–7 × (400/2) × 5

= 4π × 10 ^–7 × 200 × 5

= 12,56 × 10 ^-4 T

Задача 2. Найти величину магнитного поля внутри соленоида длиной 5 м и 500 витков на единицу длины, если через него проходит ток силой 10 А.

Решение:

Имеем,

n = 500, L = 5, I = 10

Найдите количество витков по формуле n = N/L.

N = nl

= 500 (5)

= 2500 витков

Используя формулу для магнитного поля, имеем

B = μ _o IN/L

= 4π × 10 ^–7 × (2500/5) × 10

= 4π × 10 ^–7 × 500 × 10

= 6,3 × 10 ^-2 T

9003 1 Задача 3. Найти значение магнитного поле внутри соленоида 2 м и 200 витков, если через него проходит ток 3 А.

Решение:

Имеем,

N = 200, L = 2, I = 3 00 или В/Л

= 4π × 10 ^–7 × (200/2) × 3

= 4π × 10 ^–7 × 100 × 3

= 3,78 × 10 ^-5 T

Задача 4. Найти значение числа витков для соленоида длиной 4 м, если через него проходит ток 2 А и поле равно 1,25 × 10 ^-4 Тл.

× 10 ^-4 , L = 4, I = 2

Используя формулу для магнитного поля имеем,

B = μ _o IN/L

=> 1,25 × 10 ^-4 = 4π × 10 ^–7 × (N/4) × 2

=> N = (1,25 × 10 90 109 -4 )/(0,5 × 1,26 × 10 ⁻⁶ )

=> N = 100

Задача 5. Найти значение числа витков для соленоида длиной 8 м, если через него проходит ток 6 А. а поле равно 1,88 × 10 ^-4 T.