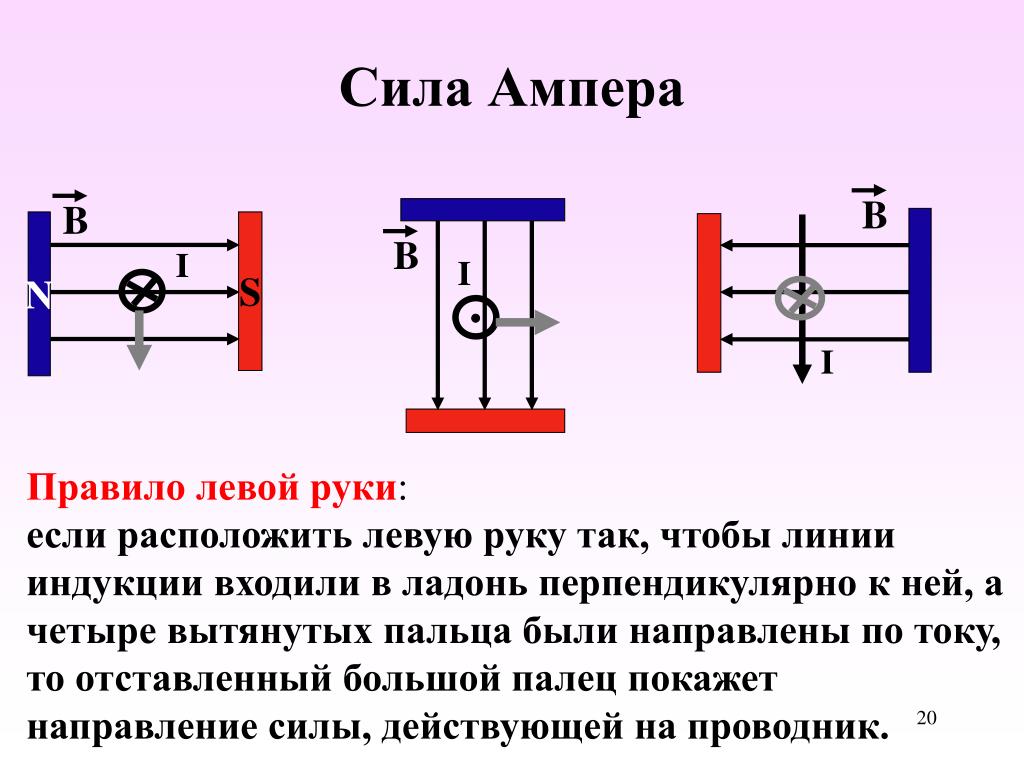
Правило левой руки для силы Ампера – примеры и формулировка определения кратко
4
Средняя оценка: 4
Всего получено оценок: 81.
4
Средняя оценка: 4
Всего получено оценок: 81.
Из курса физики известно, что на проводник с током, помещенный в магнитное поле, действует сила Ампера. Для определения направления этой силы используется специальное правило, называемое правилом левой руки. Поговорим кратко об этом правиле.
Сила и закон Ампера
На заряд, движущийся в магнитном поле, действует со стороны этого поля сила, называемая силой Лоренца.
Рис. 1. Сила Лоренца.Если в магнитное поле помещен проводник с током, то силы Лоренца, действующие на движущиеся носители заряда в этом проводнике, складываются в силу, называемую силой Ампера.
Модуль силы Ампера рассчитывается по закону Ампера:
$$F= I |\overrightarrow B| Δl sin \alpha,$$
где:
- $F$ — модуль силы Ампера;
- $I$ — величина тока в проводнике;
- $B$ — индукция магнитного поля;
- $Δl$ — длина проводника;
- $\alpha$ — угол между линиями магнитного поля и направлением тока в проводнике.
Направление силы Ампера
Обычно действие сил совпадает с направлением движения тел или с направлением на источник силы. В случае с силой Ампера ситуация иная.
Направление действия силы Ампера не совпадает ни с направлением движения тока, ни с направлением вектора магнитной индукции. Сила Ампера направлена перпендикулярно обоим этим направлениям. То есть, если линии магнитного поля направлены по вертикали, а проводник расположен горизонтально слева направо, то сила Ампера будет направлена вдоль линии «вперед-назад». Причем ее направление также будет зависеть от направлений магнитной индукции и электрического тока в проводнике. «Просто запомнить» все направления невозможно. Поэтому для силы Ампера установили специальное мнемоническое правило левой руки.
Правило левой руки
Формулировка правила левой руки для силы ампера звучит так:
Если расположить левую руку так, чтобы четыре пальца были направлены по направлению движения тока в проводнике, а перпендикулярная составляющая индукции $B_{\perp}$ входила в ладонь, то отставленный большой палец покажет направление силы Ампера.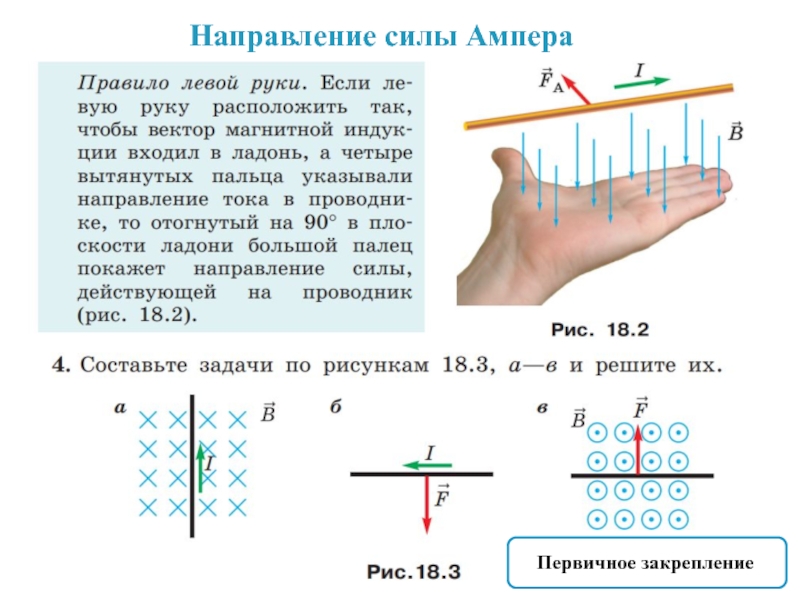
Как пользоваться этим правилом? Разберем примеры.
- Допустим, проводник расположен горизонтально, и ток по нему идет вперед. Следовательно, четыре пальца левой руки надо вытянуть вперед по этому направлению.
- Теперь допустим, что линии магнитного поля направлены сверху вниз (сверху «север» подковообразного магнита, снизу — «юг»). Следовательно, левую руку надо повернуть ладонью вверх, чтобы линии магнитного поля входили в ладонь и «прокалывали» ее (четыре пальца по-прежнему должны быть вытянуты вперед).
- Отставленный большой палец левой руки будет направлен влево. Это и есть направление силы Ампера для данной ситуации.
Другой пример.
- Пусть проводник расположен вертикально. А магнитное поле направлено справа налево (справа «север» магнита, слева — «юг»).
- Располагаем левую руку четырьмя пальцами вверх. Ладонь открытой стороной должна «смотреть вправо», чтобы магнитные линии входили и «прокалывали» ее.
- Отставленный большой палец покажет назад. Именно так и будет направлена сила Ампера в данном случае.
Обратите внимание, что силу Ампера порождает только перпендикулярная составляющая магнитного поля. А значит, руку надо располагать так, чтобы линии магнитного поля всегда входили в нее под углом, максимально близким к прямому.
Особым случаем является ситуация, когда направление тока и магнитной индукции совпадает. В этом случае руку невозможно расположить так, чтобы линии магнитной индукции входили в нее. Следовательно, силы Ампера здесь не возникнет. В самом деле, если линии магнитной индукции параллельны направлению тока, то перпендикулярная составляющая этих линий равна нулю, и значение силы Ампера в вышеприведенной формуле также равно нулю.
Что мы узнали?
Для определения направления силы Ампера используется специальное мнемоническое правило левой руки. С помощью этого правила можно не только определить направление силы Ампера, но и обнаружить случай, когда сила Ампера равна нулю.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4
Средняя оценка: 4
Всего получено оценок: 81.
А какая ваша оценка?
Правило левой руки – формула, определение, примеры, кратко о применении
4.2
Средняя оценка: 4.2
Всего получено оценок: 128.
4.2
Средняя оценка: 4.2
Всего получено оценок: 128.
Из курса физики известно, что действие магнитного поля на движущиеся заряды и на проводник с током заключается в появлении силы Лоренца или Ампера. В отличие от большинства других сил, направление действия этих сил не совпадает с направлением действия поля, породившего их. Поэтому было сформулировано специальное мнемоническое правило — правило левой руки. Кратко рассмотрим порядок применения этого правила, разберём характерные примеры.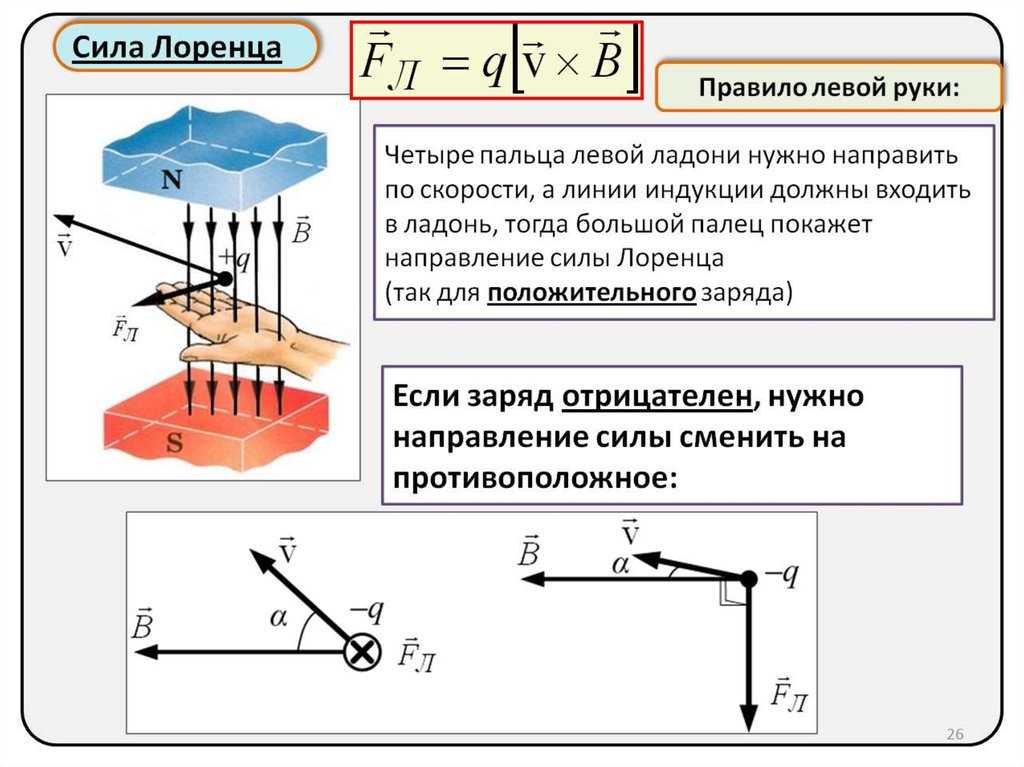
Силы Лоренца и Ампера
Магнитное поле порождается движущимися электрическими зарядами. И в свою очередь электрические заряды, движущиеся в магнитном поле, испытывают силовое воздействие с его стороны.
Сила, действующая на движущийся заряд, называется силой Лоренца.
Рис. 1. Сила Лоренца.
Модуль силы Лоренца равен:
$$F_L = qvB sin \alpha$$
где:
- $F_L$ — величина силы Лоренца;
- $q$ — величина движущегося заряда;
- $v$ — скорость движения заряда;
- $B$ — индукция магнитного поля;
- $\alpha$ — угол между векторами скорости и индукции.
Поскольку электрический ток представляет собой упорядоченное движение электрических зарядов, то в случае, когда он протекает через магнитное поле, силы Лоренца, действующие на отдельные носители, складываются в одну общую силу, которая называется силой Ампера.
Рис. 2. Сила Ампера.
Модуль силы Ампера определяется с помощью формулы, похожей на формулу силы Лоренца:
$$F_A= I Δl B sin \alpha$$
где:
- $F_ A$ — величина силы Ампера;
- $I$ — сила тока в проводнике;
- $Δl$ — длина проводника;
- $B$ — индукция магнитного поля;
- $\alpha$ — угол между векторами тока и индукции.
Схожесть формул объясняется тем, что сила Ампера является макроскопическим проявлением силы Лоренца. Направление действия этих сил совпадает.
Определение и формула
Экспериментальным путём Ампер установил, что между двумя параллельными проводниками, подключенными к постоянному току, действует притяжение (однонаправленные токи) либо отталкивание (если направления противоположные). Эти силы взаимодействия определяются параметрами токов (прямо пропорциональная зависимость), и расстоянием между проводниками (обратно пропорциональная зависимость).
Расчёт амперовой силы на единицу длины проводника осуществляется по формуле:
где F – сила, I1, I2 – величина тока в проводниках, а μ – магнитная проницаемость среды, окружающей проводники (см. рис. 1).
Природой взаимодействия является магнитное поле, образованное перемещаемыми по проводникам электрическими зарядами. Под влиянием магнитного поля на электрические заряды возникает сила магнитной индукции, которую обозначают символом B.
Линии, в каждой точке которых касательные к ним совпадают с направлением соответствующих векторов магнитной индукции, получили название линий электромагнитной индукции. Применяя мнемоническое правило буравчика, можно определить ориентацию в пространстве линий магнитной индукции. То есть, при ввинчивании буравчика в сторону, куда направлен вектор электрического тока, движение концов его рукоятки укажет направление векторов индукции.
Из сказанного выше следует, что в проводниках, с одинаково ориентированными токами, направления векторов магнитной индукции совпадают, а значит, векторы сил направлены навстречу друг к другу, что и вызывает притяжение.
Рис. 1. Взаимодействие параллельных проводников
Подобным образом проводники взаимодействуют не только между собой, но и с магнитными полями любой природы. Если такой проводник окажется в магнитном поле, то на элемент, расположенный в зоне действия магнита, будет действовать сила, которую именуют Амперовой:
Для вычисления модуля этой силы пользуются формулой: dF = IBlsinα , где α — угол, образованный векторами индукции и ориентацией тока.
Рассмотренную нами зависимость описывает закон Ампера, формулировка которого понятна из рисунка 2.
Рис. 2. Формулировка закона Ампера
Не трудно сообразить, что когда α = 900, то sinα = 1. В этом случае величина F приобретает максимальное значение: F = B*L*I, где L– длина проводника, оказавшегося под действием магнитного поля.
Таким образом, из закона Ампера вытекает:
- проводник с током реагирует на магнитные поля.
- действующая сила находится в прямо пропорциональной зависимости от параметров тока, величины магнитной индукции и размеров проводника.
Обратите внимание, что на данном рисунке 3 проводник расположен под углом 90º к линиям магнитной индукции, что вызывает максимальное действие магнитных сил.
Рис. 3. Проводник в магнитном поле
Направление сил Лоренца и Ампера
Заметим, что в обоих случаях сила возникает только тогда, когда вектор скорости движения зарядов и вектор магнитной индукции не параллельны.
{-7} \) Ньютона.
Закон взаимодействия токов – два находящихся в вакууме параллельных проводника, диаметры которых много меньше расстояний между ними, взаимодействуют с силой прямо пропорциональной произведению токов в этих проводниках и обратно пропорциональной расстоянию между ними.
ЗаконыФормулы Физика Теория Электричество Закон
Источник
Правило левой руки
Правило левой руки звучит так.
Если расположить левую руку так, чтобы четыре пальца были направлены по направлению движения положительного заряда (или по направлению тока), а линии магнитной индукции входили в ладонь, «прокалывая» её, то большой палец покажет направление силы Лоренца (или силы Ампера).
Как пользоваться этим правилом? Разберём примеры.
Допустим, ток по проводнику течёт слева направо. А линии магнитной индукции направлены вверх.
Направляем левую руку четырьмя пальцами вправо. Ладонь должна «смотреть» вниз, так, чтобы линии магнитной индукции входили в ладонь и «прокалывали» её.
Отставленный большой палец покажет направление назад.
Это и будет направление силы Ампера в данном случае. Действительно, плоскость, образованная векторами тока и магнитной индукции, — вертикальна, и сила Ампера перпендикулярна ей.
Другой пример. Электрон движется назад, «на наблюдателя», между полюсами магнита, причём северный находится справа.
Линии магнитной индукции направлены справа налево, следовательно, ладонь левой руки должна быть направлена вправо. Электрон заряжен отрицательно, то есть четыре пальца руки должны быть направлены против его движения — вперёд. Отставленный большой палец будет направлен вверх. Это и будет направление силы Лоренца в данном случае.
Рис. 3. Правило левой руки.
Правило Буравчика
Этоправило на практике достаточно удобно для определения такого значения магнитного поля, как направленность напряжённости. Использовать это правило возможно при условии, что к проводнику с током будет прямолинейно расположено магнитное поле._images/prezentaciya_(1)_4.jpg)
С его помощью можно без наличия специализированных приборов определить различные физические величины (момент сил, импульса, вектор магнитной индукции).
Это правило:
- поясняет особенность электромагнетизма;
- объясняет физику движения магнитных полей, сопутствующих ему.
Формулировка правила буравчика состоит в следующем: если буравчик с правой нарезкой вкручивается вдоль линии тока, то направление магнитного поля совпадает с направлением рукоятки этого буравчика.
Основным принципом, используемым в правиле винта, является выбор направленности для базисов и векторов. Зачастую на практике определено использовать правый базис. Левые базисы используются крайне редко, в случае когда использование правого неудобно или в целом нецелесообразно. Этот принцип также применим и на соленоиде.
Соленоидом называется катушка со вплотную привязанными витками. Главным требованием является протяжённость катушки, которая должна быть существенно больше, нежели её диаметр.
Кольца соленоида напоминают поле непрерывного магнита. Магнитная стрелка, находясь в свободном вращении и находясь рядом с проводником тока, будет образовывать поле и устремиться занимать вертикальную позицию, проходящую вдоль проводника.
В этом случае оно звучит так: если охватить соленоид таким образом, чтобы пальцы показывали на направленность тока в винтах, то выпяченный заглавный палец правой руки покажет направленность рядов магнитной индукции.
Различные толкования правила буравчика говорят о том, что все его описания приспосабливаются к различным случаям их применения.
Правило правой руки говорит о следующем: охватив элемент, который исследуется таким образом, чтобы пальцы сжатого кулака показывали вектор магнитных линий, при поступательном движении вдоль магнитных линий, заглавный отогнутый на 90 градусов сравнительно ладошки палец покажет направленность движения тока.
В случае когда дан движущийся проводник, принцип будет иметь следующую формулировку: разместить руку так, чтобы силовые линии поля вертикально вступали в ладонь; заглавный палец руки, выставленный вертикально, будет ориентировать направленность перемещения этого проводника, в этом случае четыре остальных выставленных пальца, будут иметь такую же направленность, как и индукционный ток.
Его применение присуще при расчёте катушек, в которых образуется влияние на ток, что влечёт за собой формирование при потребности противотока.
В реальной жизни также применимо следствие этого принципа: если размесить ладошку правой руки так, чтобы линии магнитного силового поля входили в эту ладошку, а пальцы навести на линию перемещения заряженных частиц по оттопыренному заглавному пальцу, то возможно обозначить, куда будет направляться линия данной силы, оказывающая смещающее влияние на проводник. Иными словами, силы, дающей возможность вращать момент силы на валу любого двигателя, работающего с помощью электрического тока.
Видео
И в завершение небольшой видео урок о силе Ампера.
Автор: Павел Чайка, главный редактор журнала Познавайка
При написании статьи старался сделать ее максимально интересной, полезной и качественной. Буду благодарен за любую обратную связь и конструктивную критику в виде комментариев к статье. Также Ваше пожелание/вопрос/предложение можете написать на мою почту [email protected] или в Фейсбук, с уважением автор.
Страница про автора
Литература
- Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 321-322, 324-327.
- Жилко, В. В. Физика: учеб. пособие для 11-го кл. общеобразоват. учреждений с рус. яз. обучения с 12-летним сроком обучения (базовый и повышенный уровни) /В. В. Жилко, Л. Г. Маркович. — 2-е изд., исправленное. — Минск: Нар. асвета, 2008. — С. 157-164.
Закон Ампера – Колледж физики
Глава 22 Магнетизм
Резюме
- Рассчитайте ток, создающий магнитное поле.
- Используйте правило правой руки 2, чтобы определить направление тока или направление контуров магнитного поля.
Какой ток необходим для создания значительного магнитного поля, возможно, такого же сильного, как поле Земли? Геодезисты скажут вам, что воздушные линии электропередач создают магнитные поля, которые мешают показаниям их компаса.
Действительно, когда в 1820 году Эрстед обнаружил, что ток в проводе влияет на стрелку компаса, он не имел дело с чрезвычайно большими токами. Как форма проводов, по которым течет ток, влияет на форму создаваемого магнитного поля? Ранее мы отмечали, что токовая петля создает магнитное поле, подобное магнитному стержню, но как насчет прямого провода или тороида (бублика)? Как направление создаваемого током поля связано с направлением тока? Ответы на эти вопросы исследуются в этом разделе вместе с кратким обсуждением закона, управляющего полями, создаваемыми токами.
Магнитные поля имеют как направление, так и величину. Как отмечалось ранее, одним из способов определения направления магнитного поля является использование компаса, как показано для длинного прямого провода с током на рисунке 1. Датчики Холла могут определять величину поля. Обнаружено, что поле вокруг длинного прямого провода представляет собой кольцевые петли. Из этого исследования вытекает правило правой руки 2 (RHR-2), которое справедливо для любого сегмента тока: направьте большой палец в направлении тока, а остальные пальцы согните в направлении петель магнитного поля , созданный им.
Напряженность (величина) магнитного поля , создаваемая длинным прямым проводом с током 9{-7} \;\textbf{T} \cdot \text{m/A}}[/latex] — проницаемость свободного пространства. ([латекс]{\mu _0}[/латекс] — одна из основных констант в природе. Позже мы увидим, что [латекс]{\му _0}[/латекс] связано со скоростью света.) Поскольку провод очень длинный, величина поля зависит только от расстояния от провода [латекс]{r}[/латекс], а не от положения вдоль провода.
Пример 1. Расчет тока, создающего магнитное поле
Найдите силу тока в длинном прямом проводе, который на расстоянии 5,0 см от провода создает магнитное поле, вдвое превышающее магнитное поле Земли.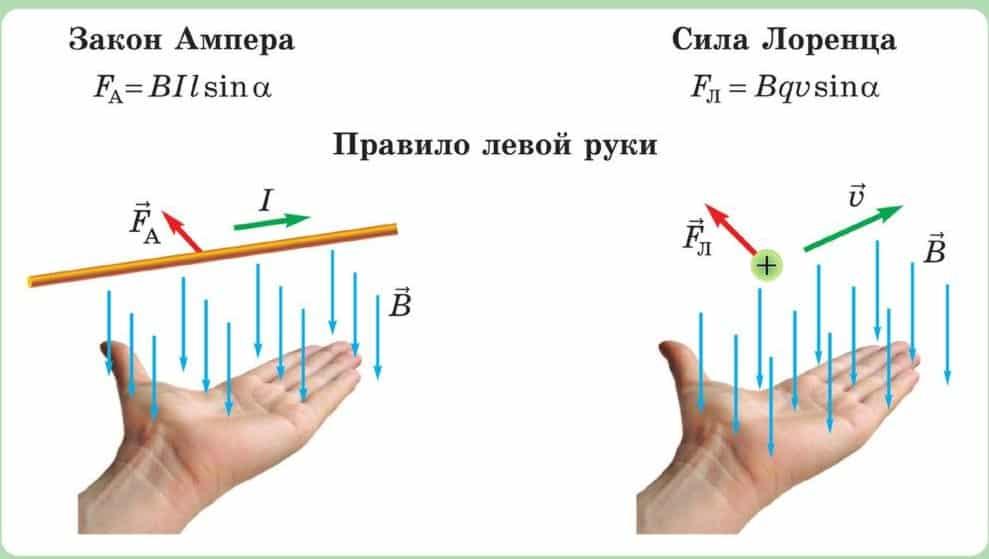
9{-7} \; \textbf{T} \cdot \text{m/A}}} \\[1em] & {25 \;\textbf{A}} \end{array}[/latex]
Обсуждение
Итак, умеренно большой ток создает значительное магнитное поле на расстоянии 5,0 см от длинного прямого провода. Обратите внимание, что ответ указан только с двумя цифрами, поскольку в этом примере поле Земли указано только с двумя цифрами.
Магнитное поле длинного прямого провода имеет больше значений, чем вы можете предположить на первый взгляд. Каждый сегмент тока создает магнитное поле, как у длинного прямого провода, а полное поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым сегментом. Формальная формулировка направления и величины поля, обусловленного каждым сегментом, называется законом Био-Савара . Интегральное исчисление необходимо для суммирования поля для тока произвольной формы. Это приводит к более полному закону, называемому законом Ампера , который связывает магнитное поле и ток в общем виде.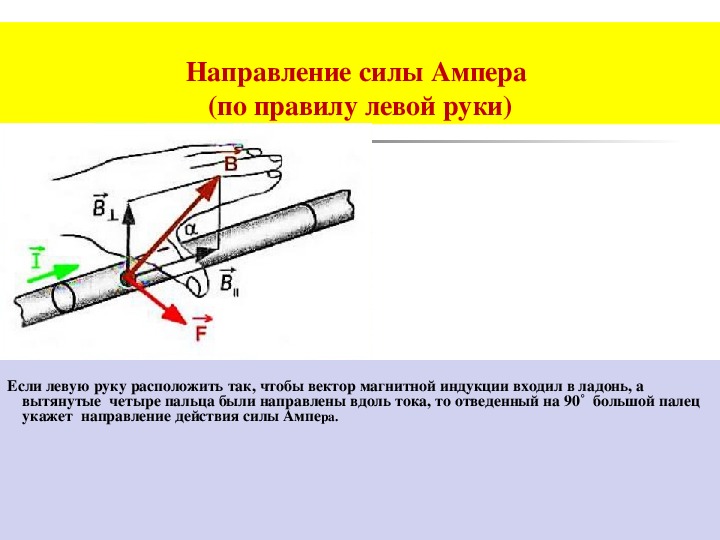
Закон Ампера, в свою очередь, является частью Уравнения Максвелла , которые дают полную теорию всех электромагнитных явлений. Рассмотрение того, как уравнения Максвелла кажутся разным наблюдателям, привело к современной теории относительности и осознанию того, что электрические и магнитные поля — это разные проявления одного и того же явления. Большая часть этого выходит за рамки этого текста как на математическом уровне, требующем исчисления, так и на том количестве места, которое может быть уделено этому. Но для заинтересованных студентов, и особенно для тех, кто продолжает заниматься физикой, инженерией или подобными занятиями, дальнейшее углубление в эти вопросы откроет описания природы, которые элегантны и глубоки. В этом тексте мы будем помнить об общих особенностях, таких как RHR-2 и правила для линий магнитного поля, перечисленные в Главе 22.3 Магнитные поля и силовые линии магнитного поля, концентрируясь на полях, создаваемых в некоторых важных ситуациях.
Установление связей: относительность
Слушая все, что мы делаем об Эйнштейне, у нас иногда создается впечатление, что он изобрел теорию относительности из ничего.
Напротив, одним из побуждений Эйнштейна было решить трудности, связанные с пониманием того, как разные наблюдатели видят магнитные и электрические поля.
Магнитное поле вблизи проволочной петли с током показано на рисунке 2. Как направление, так и величина магнитного поля, создаваемого петлей с током, являются сложными. RHR-2 можно использовать для определения направления поля вблизи контура, но для получения более подробной информации необходимо картографирование с помощью компаса и правил относительно силовых линий, приведенных в главе 22.3 «Магнитные поля и силовые линии магнитного поля». Есть простая формула для напряженность магнитного поля в центре круглой петли. Это
[латекс] {B =} [/латекс] [латекс] {\ гидроразрыва {\ mu _0I} {2R}} [/ латекс] [латекс] \ textbf {(в центре петли)} [/латекс]
, где [латекс]{R}[/латекс] — радиус петли. Это уравнение очень похоже на уравнение для прямого провода, но оно действительно только в центре круглой петли из проволоки.
Сходство уравнений указывает на то, что аналогичная напряженность поля может быть получена в центре контура. Один из способов увеличить поле — использовать [latex]{N}[/latex] петель; тогда поле будет [латекс]{B = N \mu _0I/(2R)}[/латекс]. Обратите внимание, что чем больше петля, тем меньше поле в ее центре, поскольку ток проходит дальше.
Соленоид представляет собой длинную катушку провода (с множеством витков или петель, в отличие от плоской петли). Из-за своей формы поле внутри соленоида может быть очень однородным, а также очень сильным. Поле сразу за катушками почти равно нулю. На рис. 3 показано, как выглядит поле и как его направление задается RHR-2.
Рис. 3. (a) Из-за своей формы поле внутри соленоида длиной l удивительно однородно по величине и направлению, на что указывают прямые и равномерно расположенные силовые линии.
Поле вне катушек почти равно нулю. (b) На этом разрезе показано магнитное поле, создаваемое током в соленоиде.Магнитное поле внутри соленоида с током очень однородно по направлению и величине. Лишь ближе к концам он начинает ослабевать и менять направление. Поле снаружи имеет такую же сложность, как и плоские петли и стержневые магниты, но напряженность магнитного поля внутри соленоида просто
[латекс] {B = \mu _0nI \; (\text{внутри соленоида})},[/latex]
, где [латекс]{n}[/латекс] — количество петель на единицу длины соленоида ([латекс]{n = N/l}[/латекс], с [латекс]{N}[/латекс] количество петель и [латекс]{л}[/латекс] длина). Обратите внимание, что [латекс]{B}[/латекс] — это напряженность поля в любом месте внутри однородной области, а не только в центре. Большие однородные поля, распределенные по большому объему, возможны с соленоидами, как следует из примера 2.
Пример 2: Расчет напряженности поля внутри соленоида
Каково поле внутри соленоида длиной 2,00 м, который имеет 2000 витков и пропускает ток силой 1600 А?
Стратегия
Чтобы найти напряженность поля внутри соленоида, мы используем [латекс]{B = \mu _0nI}[/латекс].
{-1}}.[/латекс] 9{-1}) \; (1600 \;\textbf{A})} \\[1em] & {2.01 \;\textbf{T}}. \end{array}[/latex]
Обсуждение
Это большая напряженность поля, которая может быть установлена на соленоиде большого диаметра, например, при медицинском использовании магнитно-резонансной томографии (МРТ). Однако очень большой ток указывает на то, что поля такой силы получить нелегко. Такой большой ток через 1000 витков, втиснутых в длину метра, произвел бы значительный нагрев. Более высокие токи могут быть достигнуты с помощью сверхпроводящих проводов, хотя это дорого. Существует верхний предел тока, поскольку сверхпроводящее состояние нарушается очень большими магнитными полями.
Есть интересные варианты плоской катушки и соленоида. Например, тороидальная катушка, используемая для удержания реактивных частиц в токамаках, очень похожа на соленоид, согнутый в окружность. Поле внутри тороида очень сильное, но круглое. Заряженные частицы движутся по кругу, следуя линиям поля, и сталкиваются друг с другом, возможно, вызывая синтез.
Но заряженные частицы не пересекают силовые линии и не покидают тороид. Целый ряд форм катушек используется для создания всевозможных форм магнитного поля. Добавление ферромагнитных материалов увеличивает напряженность поля и может существенно повлиять на форму поля. Ферромагнитные материалы имеют тенденцию улавливать магнитные поля (силовые линии изгибаются в ферромагнитный материал, оставляя более слабые поля вне его) и используются в качестве экранов для устройств, на которые неблагоприятно влияют магнитные поля, в том числе магнитное поле Земли.
PhET Исследования: Генератор
Генерация электричества с помощью стержневого магнита! Откройте для себя физику этого явления, исследуя магниты и то, как вы можете использовать их, чтобы зажечь лампочку.
Рис. 4. Генератор- Сила магнитного поля, создаваемого током в длинном прямом проводе, равна
[латекс] {B =} [/латекс] [латекс] {\ гидроразрыва {\ mu _0I} {2 \ pi r}} [/латекс] [латекс] \ текст {(длинная прямая проволока)}, [/ латекс]
- Направление магнитного поля, создаваемого длинным прямым проводом, определяется правилом правой руки 2 (RHR-2): Направьте большой палец правой руки в направлении тока, а пальцы согните в направлении создаваемых им петель магнитного поля .
- Магнитное поле, создаваемое током, следующим по любому пути, представляет собой сумму (или интеграл) полей, создаваемых сегментами вдоль пути (величина и направление, как для прямого провода), что приводит к общей зависимости между током и полем, известной как закон Ампера. .
- Напряженность магнитного поля в центре круглой петли равна
[латекс] {B =} [/латекс] [латекс] {\ гидроразрыва {\ mu _0I} {2R}} [/ латекс] [латекс] \ textbf {(в центре петли)} [/латекс]
- где [латекс]{R}[/латекс] — радиус петли. Это уравнение принимает вид [латекс]{B = \mu _0nI/(2R)}[/латекс] для плоской катушки из [латекса]{N}[/латекс] петель. РХР-2 дает направление поля вокруг петли. Длинная катушка называется соленоидом.
- Напряженность магнитного поля внутри соленоида равна .
[латекс] {B = \mu _0nI \; (\text{внутри соленоида})},[/latex]
- где [латекс]{n}[/латекс] — количество петель на единицу длины соленоида. Поле внутри очень однородно по величине и направлению.
- Правило правой руки 2 (RHR-2)
- правило для определения направления магнитного поля, индуцируемого проводом с током: большой палец правой руки указать в направлении тока, а остальные пальцы согнуть в направлении петель магнитного поля
- напряженность магнитного поля (величина), создаваемая длинным прямым проводом с током 9{-7} \;\textbf{T} \cdot \;\text{м/А}}[/латекс]
- напряженность магнитного поля в центре круглой петли
- определяется как [латекс]{B = \frac{\mu _0I}{2R}}[/латекс], где [латекс]{R}[/латекс] — радиус петли
- соленоид
- тонкая проволока, свернутая в катушку, создающую магнитное поле при пропускании через нее электрического тока
- напряженность магнитного поля внутри соленоида
- определяется как [латекс]{B = \mu _0nI}[/латекс], где nn — количество петель на единицу длины соленоида ([латекс]{n = N/l}[/латекс], с [латекс] {N}[/latex] количество петель и [latex]{l}[/latex] длина)
- Закон Био-Савара
- физический закон, описывающий магнитное поле, создаваемое электрическим током, с помощью специального уравнения
- Закон Ампера
- физический закон, утверждающий, что магнитное поле вокруг электрического тока пропорционально току; каждый отрезок тока создает магнитное поле, подобное магнитному полю длинного прямого провода, а полное поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым отрезком
- Уравнения Максвелла
- набор из четырех уравнений, описывающих электромагнитные явления
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Это еще не все, что нужно знать о равномерном круговом движении. Это подготовка к уроку. Более подробные примечания и примеры приведены в конспектах занятий, презентациях и демонстрациях. См. ссылки ниже.
Это означает, что положительные заряды должны использоваться для описания направления тока, потому что положительные заряды отталкиваются от положительной клеммы.
Эта фраза использовалась в одних из первых публикаций о токе. Ток определяется тем, как быстро течет заряд. Заряд обозначается буквой «Q», а время — «t». Ток математически моделируется
Когда мы делаем это, закон Ампера становится чем-то, с чем большинству из нас очень легко работать…
