App Store: Математическая головоломка
Описание
Головоломка с числами в стиле классических японских математических головоломок
«Если люди отказываются верить в простоту математики, то это только потому, что они не понимают всю сложность жизни» — Джон фон Нейман
Любишь головоломки с числами в стиле классических японских математических головоломок? Тогда эта интеллектуальная игра именно для тебя)
ПРАВИЛА
Подставь числа так, чтобы результат во всех направлениях сошёлся. Помни: каждое действие в этой логической головоломке рассматривается отдельно, поэтому порядок выполнения слева направо, а не как в законах математики) Если нужен совет — воспользуйся подсказками)
Приятный бонус — игра без интернета)
ЯРКИЕ МОМЕНТЫ
Красочные фоны открывающиеся по мере прохождения игры заставят твое чувство прекрасного трепетать от счастья, а различные варианты оформления цифр придутся по вкусу даже образцовому аскету.
Надеемся Вам понравится играть в наши игры, мы их делали с любовью к загадкам и головоломкам) Спасибо, что выбираете их)
Версия 6.1
— небольшие исправления
Спасибо, что Вы с нами)
Оценки и отзывы
Оценок: 23
Мозги таки кипят
Очень хотелось поставить 5, правда, но не могу — бесят периодические вылеты, которые случаются даже на iPhone 6s. В остальном, занимательная игрушка, рекомендую всем, кто хочет держать мозги в тонусе)
Системные ошибки
Есть уровни которые не возможно пройти из-за нелепых ошибок
Плохо
Всё время вылетает.
Невозможно играть.
Невозможно играть.Разработчик Stanislav Hatnyuk указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.
Данные, используемые для отслеживания информации
Следующие данные могут использоваться для отслеживания информации о пользователе в приложениях и на сайтах, принадлежащих другим компаниям:
Не связанные с пользователем данные
Может вестись сбор следующих данных, которые не связаны с личностью пользователя:
Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее
Информация
- Провайдер
- Stanislav Hatnyuk
- Размер
- 11,4 МБ
- Категория
- Игры
- Возраст
- 4+
- Copyright
- © «2021 SH»
- Цена
- Бесплатно
- Поддержка приложения
- Политика конфиденциальности
Другие приложения этого разработчика
Вам может понравиться
Алгебра, теория чисел, математическая логика: профессии после окончания программы
Войдите или зарегистрируйтесь, чтобы открыть доступ к новым функциям
- Регистрация
- Вход
Восстановить пароль
Напомнить логин
*В логине разрешены латинские буквы/цифры/точка/@
Выберите город, в который хотите поступатьАбаканАлатырьАлександровАлексеевкаАльметьевскАмурский институт железнодорожного транспортаАнапаАнгарскАнжеро-СудженскАпатитыАргунАрзамасАрмавирАрмянскАрхангельскАстанаАстраханьАчинскБакуБалаковоБалашихаБалашовБарнаулБатайскБелгородБелогорскБелорецкБелоярскийБердскБерезникиБийскБиробиджанБлаговещенскБогородскБодайбоБокситогорскБратскБрянскБугульмаБугурусланБуденновскВалдайВеликие ЛукиВеликий НовгородВеликий УстюгВельскВладивостокВладикавказВладимирВолгоградВолгодонскВолжскийВологдаВолосовоВоркутаВоронежВоткинскВыборгВышний ВолочекВязникиВятские ПоляныГеленджикГлазовГорно-АлтайскГородецГородовиковскГрозныйГрязиГрязовецГусь-ХрустальныйДальнегорскДербентДзержинскДивногорскДимитровградДмитровДомодедовоДонскойДубнаДудинкаДушанбеЕкатеринбургЕлабугаЕлецЕлизовоЕреванЕссентукиЖелезногорскЖирновскЗаречныйЗеленокумскЗимаЗлатоустИвановоИжевскИрбитИркутскИшимЙошкар-ОлаКазаньКалининградКалугаКаменск-УральскКамызякКанашКанскКарачаевскКарачевКаспийскКемеровоКерчьКизлярКиржачКировКирово-ЧепецкКисловодскКовровКольчугиноКомсомольск-на-АмуреКонаковоКондопогаКопейскКоркиноКоряжмаКостромаКотласКотовскКрасноборскКраснодарКраснокаменскКраснокамскКраснослободскКрасноярскКудымкарКуйбышевКулебакиКумертауКунгурКурганКурскКызылЛаганьЛениногорскЛеснойЛесозаводскЛесосибирскЛивныЛикино-ДулёвоЛипецкЛугаЛысьваЛюберцыМагаданМагасМагнитогорскМайкопМахачкалаМегионМиассМинскМинусинскМихайловскМичуринскМончегорскМоршанскМоскваМурманскМуромМценскНабережные ЧелныНальчикНаро-фоминскНаходкаНевинномысскНерчинскНефтекамскНефтекумскНефтеюганскНижневартовскНижнекамскНижнеудинскНижний НовгородНижний ТагилНиколаевск-на-АмуреНикологорыНовозыбковНовокузнецкНовомосковскНовороссийскНовосибирскНовочебоксарскНовый УренгойНорильскНоябрьскОбнинскОдинцовоОзерскОмскОмутнинскОрелОренбургОрловОрскОсаОчёрПензаПермьПетрозаводскПетропавловск-КамчатскийПетушкиПечораПодольскПриозерскПрокопьевскПрохладныйПсковПущиноПятигорскРайчихинскРаменскоеРжевРостовРостов-на-ДонуРубцовскРыбинскРязаньс.
Регистрируясь через данную форму, я соглашаюсь с политикой конфиденциальности и согласен на обработку персональных данных.
Хочу, что вы отправляли мне индивидуальные подборки и лучшие предложения от вузов по нужным мне критериям.
Вводите только ваши реальные данные или вы не сможете пользоваться сервисом в полной мере
Системы счисления | Цифровые схемы 1: двоичные, булевы и логические
Системы счисления
Сохранить Подписаться
Пожалуйста, войдите, чтобы подписаться на это руководство.
После входа в систему вы будете перенаправлены обратно к этому руководству и сможете подписаться на него.
Десятичный: основание 10
У нас 10 пальцев, поэтому число 10 для нас естественно. Мы считаем и делаем математику, используя десятичные числа. Другой термин для этого — base-10. На самом деле это означает, что мы используем 10 уникальных цифр, и когда мы складываем эти цифры вместе, чтобы получить большее число, каждое место, смещающееся влево, стоит в десять раз больше, чем место справа от него.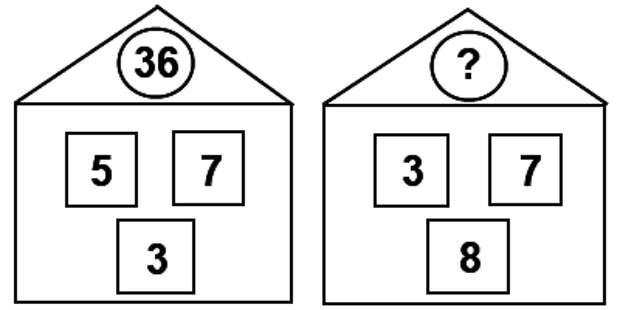
Это намного подробнее. Так почему же это используется в компьютерах? Оказывается, глубоко внутри компьютеры состоят из очень простых схем. Настолько просто, что все в терминах включено или выключено. Это напрямую соответствует 1 и 0. Следовательно, двоичный код напрямую соответствует тому, как компьютеры хранят информацию.
Потенциальная проблема заключается в том, что последовательность единиц и нулей легко может быть десятичным числом. Обычно мы ставим перед двоичными числами префикс 0b , чтобы было понятно, особенно в исходном коде. В этом случае номер примера будет записан как
Octal
Двоичная система довольно многословна и утомительна для работы, поэтому были приняты другие, более компактные системы счисления.
В восьмеричной системе (также известной как основание 8) мы используем цифры от 0 до 7 (т.е. 8 уникальных цифр, и у нас есть те, что лежат в основе 10, так почему бы не использовать их повторно).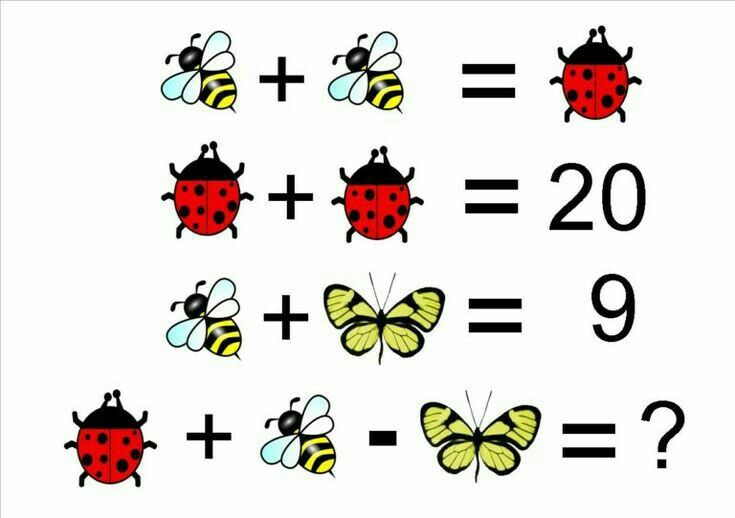
Кроме того, каждое место представляет собой степень 8: 1, 8, 64 и т. д.
Восьмеричное число было распространено на заре вычислительной техники, когда компьютеры обычно имели 12-, 24- или 36-битные слова вместо 8, 16, 32, или 64 бита, которые были распространены с тех пор. Для представления одной восьмеричной цифры в двоичном формате требуется ровно 3 цифры. Учитывая, что те ранние длины слов были кратны трем, восьмеричное число было естественным выбором. Наш предыдущий пример (3571, он же 110111110011) в восьмеричном формате будет 6763. 93
Вы можете ясно увидеть этот перевод, если разделите двоичное число на группы из 3 цифр, начиная справа: 110 111 110 011.
Поскольку восьмеричные числа очень похожи на десятичные, мы обычно ставим перед ними префикс . 0о . Таким образом, наш пример обычно записывается как 0o6763 . Опять же, это стандарт в исходном коде.
Шестнадцатеричный
Также известный как шестнадцатеричный, шестнадцатеричный с основанием 16.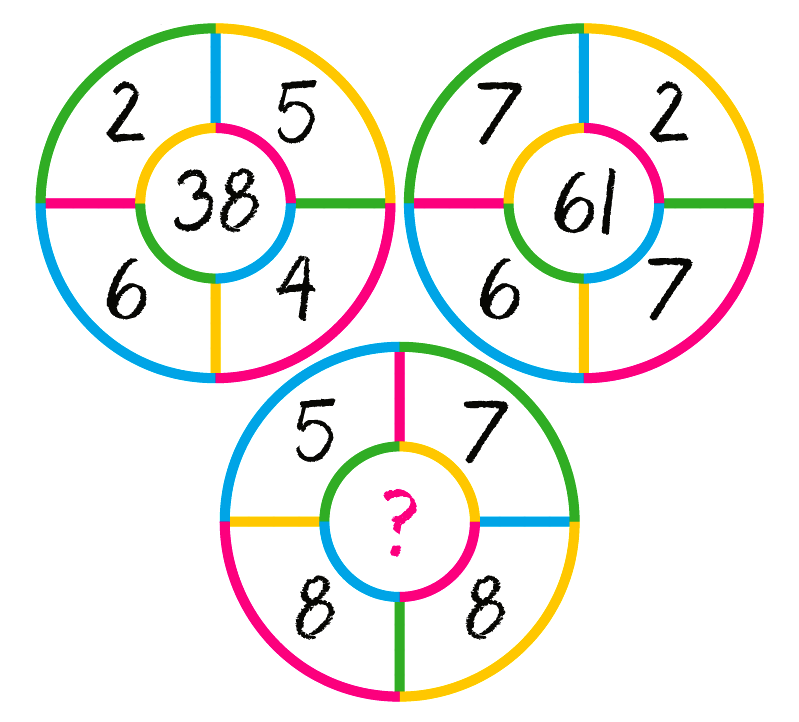
То есть каждая цифра соответствует степени 16.
В отличие от восьмеричного, где у нас было много цифр из десятичного, чтобы использовать, нам нужно 16 уникальных цифр для шестнадцатеричного. У нас есть много буквенных символов, так что мы можем позаимствовать несколько. На самом деле для шестнадцатеричного числа мы используем цифры 0 — 9 плюс буквы A — F (или так же часто: a — f ).
0-9 имеют свои обычные значения, но буквы имеют следующие десятичные значения:
-
A - 10 -
Б - 11 -
С - 12 -
Д - 13 -
Е - 14 -
Ф-15
Подобно восьмеричной, шестнадцатеричная цифра представляет ровно 4 двоичных цифры. Если мы возьмем двоичное число и разделим его на группы по 4 цифры (начиная справа), каждая группа будет соответствовать шестнадцатеричной цифре.
-
0 - 0000 -
1 - 0001 -
2 - 0010 -
3 - 0011 -
4 - 0100 -
5 - 0101 -
6 - 0110 -
7 - 0111 -
8 - 1000 -
9 - 1001 -
А - 1010 -
Б - 1011 -
С - 1100 -
Д - 1101 -
Э - 1110 -
Ф-1111
Как и прежде, мы используем префикс для обозначения шестнадцатеричного числа. Нет, не 0h почему-то. Вместо этого мы используем 0x .
Поскольку современные компьютеры используют длину слова, кратную 8, шестнадцатеричный формат является довольно стандартным. На самом деле часто бывают ситуации, когда значением является байт (8 бит), например значения красного, зеленого и синего цветов в спецификации цвета.
В подобных случаях стандартно использовать шестнадцатеричные числа. Вместо (192, 255, 128) обычно пишут (0xC0, 0xFF, 0x80) . То же самое обычно делается с 16- и 32-битными числами. Это делает очевидным, что значение должно соответствовать определенному количеству битов и не может быть чем угодно.
Почему?
Итак, если десятичная система счисления используется нами повсеместно на протяжении всей жизни, то почему такое увлечение двоичной и подобной системой (например, шестнадцатеричной)? Это сводится к тому факту (упомянутому ранее), что компьютеры внутри работают в двоичном формате. Если мы собираемся изучать внутреннюю структуру компьютеров, в данном случае цифровую логику, гораздо проще использовать двоичную (или аналогичную) систему, потому что это основа всего в этом мире.
Введение Булева логика
Это руководство было впервые опубликовано 22 марта 2018 года. обновлено 22 марта 2018 г.
Эта страница (Системы счисления) последний раз обновлялась 05 марта 2018 г.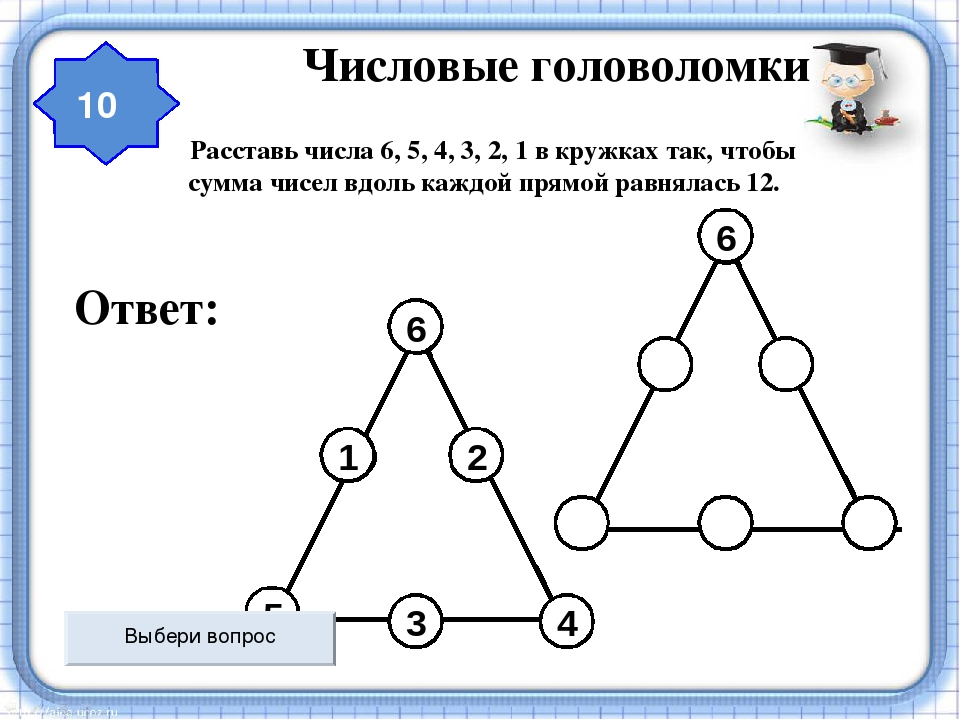
Текстовый редактор на базе tinymce.
Числовые логические головоломки — Griddlers.net
Судоку
Судоку — это логическая головоломка с размещением чисел. Цель состоит в том, чтобы заполнить сетку цифрами так, чтобы каждый столбец и каждая строка содержали цифры только один раз.
Нет блоков (латинский квадрат)
Латинский квадрат представляет собой массив n x n, заполненный n различными цифрами, каждая из которых встречается ровно один раз в каждой строке и ровно один раз в каждом столбце. Правило латинских квадратов:
|
Прямоугольные блоки
Наиболее распространенным пределом являются прямоугольные блоки. А 9Сетка x9 состоит из 9 блоков, как показано на рисунке. Прямоугольные блоки Правила:
|
Неправильные блоки (головоломки)
В головоломку играют так же, как в судоку, за исключением того, что в сетке есть неправильные блоки, также известные как клетки. Правила неправильных блоков:
|
Диагональные варианты
Обычно добавляются ограничения на размещение цифр помимо обычных строк и столбцов. Одним из ограничений является диагональный вариант. Диагональные варианты Правило:
|
Комбинированные варианты
Варианты можно комбинировать. Прямоугольные блоки и диагональные варианты Правила:
|
Например: сетка может иметь как прямоугольные блоки, так и диагональные линии. Также может быть более 2 диагональных линий.Перекрывающиеся варианты
Перекрывающиеся варианты состоят из нескольких головоломок. Общие блоки выделяются другим цветом. Here are some examples of overlapping Sudokus:
Double-Doku
Sensei
Gattai Near-2
Wing-3
Gattai-3
Sohei
Butterfly
Flower-4
Самурай
Гаттай-8
Киллер
Сетка судоку Киллер покрыта клетками (группами ячеек), отмеченными пунктирными контурами. Killer Sudoku Rules:
|
Каждая клетка заключает в себе 2 или более ячеек. Верхняя левая ячейка помечена суммой клеток, которая представляет собой сумму всех цифр решения для ячеек внутри клетки.Больше/Меньше
Больше (или меньше) Судоку не содержит подсказок (цифр). Вместо этого есть «Больше, чем» (>) или «Меньше, чем» ( Правила «больше / меньше чем»:
|
Какуро
Какуро играется на сетке из заполненных и зачеркнутых ячеек, «черных» и «белых» соответственно. Правило Какуро:
|
Сетка разделена на «входы» (линии белых ячеек) черными ячейками. Черные ячейки содержат косую черту от левого верхнего угла к правому нижнему и число в одной или обеих половинах. Эти числа называются «подсказками».Kalkuldoku
Сетка разделена на сильно очерченные клетки (группы ячеек). Числа в ячейках каждой клетки должны давать определенное «целевое» число при объединении с использованием указанной математической операции (сложения, вычитания, умножения или деления). Kalkuldoku Правила:
|
Футошики
Футошики играют на сетке, которая может показывать некоторые цифры в начале. Кроме того, есть «Больше, чем» (>) или «Меньше, чем» ( Правила Футошики:
|
Стриты
Стриты разыгрываются на сетке, которая частично разделена черными ячейками на отсеки. Отсеки должны содержать стрит — набор последовательных цифр — но в любом порядке (например: 2-1-3-4). В черных ячейках также могут быть белые подсказки. Правила стрита:
|
Небоскреб
В головоломке «Небоскреб» числа расположены вдоль края сетки. Эти числа обозначают количество зданий , которые вы бы увидели с этого направления, если бы существовал ряд небоскребов с высотой, равной элементам в этой строке или столбце. Например: если в строке 4 ячейки и если первое число в ячейке равно 4, вы увидите только один небоскреб, потому что 4-этажный небоскреб скрывает 1-этажный, 2-этажный и 3-этажный небоскребы. Небоскребы Правила:
|
Небоскребы с парками
В головоломке Небоскребы может быть парков (пустые ячейки). Небоскребы с парками Правила:
|
Суммарные небоскребы
Цифры вдоль края сетки суммарных небоскребов указывают сумму высот видимых зданий. Sum Skyscrapers Правила:
|
