В прошлом задании мы говорили о представлении чисел в компьютере, и знаем, что каждое число представляется в виде определённой последовательности значений битов. В каждом бите может храниться ноль или единица. То есть, по сути, представление чисел (в будущем мы увидим, что не только чисел, а вообще любых данных) в компьютере является дискретной структурой. Поэтому, изучение дискретных структур – важная часть информатики. В этом задании мы будем изучать наиболее простую дискретную структуру, которая называется высказыванием.
Например, предложение: «Я – твой друг» является высказыванием, а предложение: «Положи это сюда!» высказыванием не является, поскольку не является повествовательным предложением.
Истинность или ложность каждого высказывания зависит от трактовки его содержания. Например, высказывание: «Город Москва – столица России» является истинным, а высказывание: «Город Санкт-Петербург стоит на реке Лене» является ложным.
Высказывание: «Эта шляпа – красная» является простым, в то время как высказывание: «Если прямая пересекает одну из двух параллельных прямых, то она пересекает и вторую» является примером сложного высказывания, которое, по сути, состоит из трёх простых: «две прямые параллельны», «прямая пересекает одну из двух прямых», «прямая пересекает другую прямую». В сложном высказывании простые высказывания соединяются при помощи логических связок. В рассмотренном выше примере логической связкой является союз «если то».
Алгебра логики изучает структуру сложных логических высказываний и способы установления их истинности при помощи алгебраических методов. Причём, конкретное содержание высказываний предметом изучения алгебры логики не является, и, соответственно, интересовать нас в дальнейшем не будет.
Причём, конкретное содержание высказываний предметом изучения алгебры логики не является, и, соответственно, интересовать нас в дальнейшем не будет.
В прошлом задании при изучении основ программирования мы столкнулись с понятиями констант и переменных. Константа – это некоторое конкретное значение, а переменная – это объект, который может менять свои значения и которому можно присваивать различные значения. Этими же понятиями пользуется и алгебра логики, чтобы абстрагироваться от конкретных содержаний высказываний. Будем считать, что любое простое высказывание – это есть константа. И введём понятие переменной в алгебре логики.
В отличие от языков программирования в алгебре логики нет ограничений при именовании переменных. Переменные могут иметь абсолютно любые имена, но чаще всего их обозначают заглавными или строчными латинскими буквами (`A, B, C, x, y, z, s`), либо последовательностью, состоящей из заглавной или строчной латинской буквы и целого числа (`A1, A2, A4, A10000000`).
В процессе формализации нужно сделать следующие действия: выделить из сложного высказывания простые и превратить их в логические переменные. Затем каждая логическая связка превращается в логическую операцию. В описанных действиях остаётся два непонятных момента. Первый – что такое логическая операция, и второй – каким образом логические связки превращаются в логические операции. Будем последовательно отвечать на эти вопросы.
Для того чтобы определить операцию, необходимо указать количество операндов (объектов, над которыми выполняется операция) их тип и результат выполнения операции. Логические операции чаще всего имеют два операнда, как и математические. Однако мы также будем изучать операции, которые имеют всего один операнд. Независимо от количества операнды должны быть логического типа, то есть иметь значение
Независимо от количества операнды должны быть логического типа, то есть иметь значение
Очевидно, что если у операции два операнда, и значением каждого является `0` или `1`, то существует всего четыре набора значений операндов `(00, 01, 10, 11)`. Для каждого из наборов необходимо определить значение логической операции. Удобно это представлять в виде таблицы. Таблицы соответствия значений логических операций набору значений операндов называются
Алгебра логики — Умскул Учебник
На этой странице вы узнаете- Что такое алгебра логики и зачем здесь котики?
- Как вычислить истинность логического выражения?
- Для чего нужны законы логики?
Как часто поведение котов вам кажется странным? А если кот в галстуке или вооружен? Сейчас будем разбираться в логике с помощью этих пушистых созданий.
Обратите внимание на этого персонажа:
Я скажу про него две вещи:
- Этот кот в галстуке.
- Этот кот белого цвета.
Очевидно, что с первым высказыванием и поспорить нельзя, а вот второе — наглая ложь. А если я захочу вас запутать: «Этот кот в галстуке или он белого цвета, из чего следует, что он белого цвета и в галстуке или не белый». Что это в итоге — правда или ложь?
Чтобы это определить, в математике есть отдельный раздел.
Алгебра логики — это раздел математики, который занимается логическими операциями над высказываниями.
Любое высказывание может быть либо истинным, либо ложным. Цель алгебры логики — определять истинность логических выражений на основании отдельных высказываний. Алгебра логики действительно может, например, складывать и умножать высказывания друг с другом, и чтобы в записи это выглядело адекватно, истину принято обозначать как 1, а ложь — как 0.
| Что такое алгебра логики и зачем здесь котики? В примере с котиком высказывание А было истинно, а высказывание В — ложно. |
Как вычислить истинность логического выражения?
Термин высказывание, мы теперь знаем. Но что такое логическое выражение? Выражение — это уравнение из высказываний, как математическое уравнение из чисел.
«Этот кот вооружен и его глаза зеленого цвета», — в одном выражении мы использовали два высказывания.
Истинность выражения определяется истинностью логических высказываний, а также логическими операторами, которые стоят между ними.
Например, я скажу про того же самого кота: «Этот кот вооружен и его глаза голубые». Это будет наглая ложь, так как я употребил союз И, то есть подразумеваю, что оба высказывания истинны — что неправда. Но если бы я сказал: «Этот кот вооружен или его глаза голубые», союз ИЛИ защитил бы меня от клейма лжеца. Я делаю акцент на истинности только одного высказывания из двух.
Но если бы я сказал: «Этот кот вооружен или его глаза голубые», союз ИЛИ защитил бы меня от клейма лжеца. Я делаю акцент на истинности только одного высказывания из двух.
Так и работают логические операторы — в зависимости от них все выражение и принимает значение истины или лжи.
Основные логические операторы алгебры логики:
- Конъюнкция: логическое умножение или логическое И. В записи обозначается как ∧. А ∧ В дает истину только в том случае, если оба высказывания А и В истинны.
Называется логическим умножением, потому что имеет схожий принцип работы: если хоть один из множителей будет равен 0, все выражение будет равно 0.
В примере про кота выше выражение «Этот кот вооружен ∧ его глаза голубые» будет ложным. Он вооружен, но глаза у него не голубые. Одно из высказываний не выполнилось, так что конъюнкция равна 0.
- Дизъюнкция: логическое сложение или логическое ИЛИ.
 В записи обозначается как ∨. А ∨ В дает истину в том случае, если хотя бы одно из высказываний истинно.
В записи обозначается как ∨. А ∨ В дает истину в том случае, если хотя бы одно из высказываний истинно.Называется логическим сложением за схожесть: если складывать только 0 и 1, чем мы и занимаемся, то достаточно одному слагаемому быть 1, чтобы все выражение не было равно 0.
Важно сразу понять — если применить логическое сложение к двум единицам (1 ∨ 1), мы получим не 2, а все еще 1. Все-таки единица здесь означает не число, а истину, и сложив две, мы не получим одну сверх-истину.
Тогда выражение «Этот кот вооружен ∨ его глаза голубые» будет уже истинным: глаза его не голубые, но он все-таки вооружен. Дизъюнкция вернет нам 1.
- Инверсия: логическое отрицание или логическое НЕ. Превращает истину в ложь и наоборот.
Ложное высказывание «Его глаза голубые» можно легко превратить в истину, если сказать «Его глаза НЕ голубые». В записи обозначается чертой над выражением или знаком ¬, например, ¬А.

- Эквиваленция, если проще — равенство. Если оба высказывания равны (оба 0 или оба 1), то получим истину, иначе — ложь. Обозначается как ≡.
Истинным будет выражение «У кота нет оружия так же, как его глаза голубые». И то, и другое — ложь, но мы их сравнили, сказав, что они одинаковы по истинности, что уже правда.
- Импликация, иначе говоря, следование. Обозначается стрелочкой, например А ⇒ В. Если из истины следует ложь, то это автоматически ложь, все остальное — истина.
Например, вас никто не просил кормить кота. Если вы этого не сделаете, ничего плохого и не случится. А если сделаете — тоже хорошо, кот будет рад. А вот если вас попросили покормить кота, надо обязательно это сделать. Не сделаете — будет плохо.
Приоритет этих операторов:
- инверсия;
- конъюнкция;
- дизъюнкция;
- импликация;
- эквиваленция.
Как и везде в математике, приоритет можно менять с помощью скобок — что в них, то выполняется в первую очередь.
В логических уравнениях высказывания используются в виде переменных, а главная проблема, которую рассматривает алгебра логики — когда точно неизвестна истинность каждого высказывания. Назовем эту ситуацию “кот в мешке”. Сказать про кота можно что угодно, но будет ли это правдой — мы не узнаем, пока не заглянем в мешок. В таких ситуациях нам может помочь таблица истинности.
Таблица истинности — это таблица, которая показывает истинность всего логического уравнения в зависимости от истинности отдельных переменных.
В этой таблице содержатся все возможные наборы переменных. Количество наборов N зависит от количества различных переменных i как N = 2i.
Чтобы удобно записать наборы, нумеруем их по порядку начиная с 0, переводим их номер в двоичную систему счисления (2сс) и записываем набор цифр.
Давайте запишем таблицы истинности для известных нам логических операторов:
- инверсия берет только 1 переменную и сразу меняет ее значение:
- конъюнкция берет две переменные и возвращает 1 только в том случае, если обе равны 1:
- дизъюнкция вернет 1, если хотя бы одна из переменных равна 1:
- эквиваленция вернет 1, если переменные равны, и 0 в противном случае:
- импликация вернет 0, если из истины будет следовать ложь, и 1 во всех остальных случаях:
| Импликацию можно выразить через дизъюнкцию: А ⇒ В = ¬А ∨ В |
Зная таблицы истинности отдельных операторов, давайте попробуем составить таблицу истинности для полного выражения.
Например, для выражения: А ∧ (В ∨ С) ≡ В ⇒ ¬А.
Важно правильно расставить порядок операций. Как и всегда, в первую очередь выполняется действие в скобках, а дальше — в порядке приоритета.
Здесь порядок операций будет следующим:
Создадим таблицу, в которой сразу пропишем все наборы 0 и 1 для переменных А и В и добавим столбцы для каждого шага вычисления.
Чтобы удобно записать наборы, пронумеруем их по порядку начиная с 0. Переведем их номер в 2сс и запишем набор цифр. У нас 3 различные переменные, поэтому должно быть 8 наборов.
- Первое действие — сложение В и С. Для каждого набора запишем результат сложения в соответствующий столбец.
- Второе действие — инверсия переменной А.
- Третье действие — умножение значения А на результат первого действия:
- Четвертое — импликация значения В и результата второго действия:
- И последнее действие — эквиваленция результатов 3 и 4 действий:
Последний столбец — и есть результат таблицы истинности. По нему можно сказать, что при А = 1, В = 0 и С = 1 все исходное выражение равно 1, а во всех остальных случаях — 0.
По нему можно сказать, что при А = 1, В = 0 и С = 1 все исходное выражение равно 1, а во всех остальных случаях — 0.
| Для чего нужны законы логики? Законы логики позволяют упрощать логические уравнения, делая их не такими большими и более решаемыми. |
Их не так уж и мало: от самых простых и очевидных до достаточно хитрых; от тех, которые встречаются очень часто до довольно редких.
Не обязательно знать все наизусть — часть из них действительно проста и похожа на правила математики начальной школы. Про остальные стоит помнить: если увидите очень большое логическое уравнение, высока вероятность того, что эти законы помогут его сократить.
Попробуем упростить исходное выражение ¬(¬А ∧ ¬В) ∨ В ∧ С:
- Первым можно увидеть закон де Моргана, где у нас идет отрицание целой скобки:
¬(¬А ∧ ¬В) ∨ В ∧ С = ¬(¬А) ∨ ¬(¬В) ∨ В ∧ С
- Здесь же появляются переменные А и В, к которым можно применить закон двойного отрицания:
¬(¬А) ∨ ¬(¬В) ∨ В ∧ С = А ∨ В ∨ В ∧ С
- Можно заметить закон поглощения — В складывается с умножением В на С:
А ∨ В ∨ В ∧ С = А ∨ В
Итого, уравнение с 3 переменными и множеством отрицаний мы смогли превратить в максимально простую запись, где осталось всего 2 переменные:
¬(¬А ∧ ¬В) ∨ В ∧ С = А ∨ В
Фактчек- Алгебра логики — это математика, которая пользуется не числами, а высказываниями, являющимися истинными или ложными.
 Истина обозначается как 1, а ложь — как 0.
Истина обозначается как 1, а ложь — как 0. - Основными логическими операторами являются инверсия, конъюнкция, дизъюнкция, импликация и эквиваленция.
- Для расчета истинности логического уравнения используется таблица истинности.
- Законы логики помогают сокращать логические уравнения.
Задание 1.
Выберите правильный порядок приоритета логических операторов:
- Импликация, эквиваленция, конъюнкция, дизъюнкция, инверсия.
- Инверсия, конъюнкция, дизъюнкция, импликация, эквиваленция.
- Инверсия, конъюнкция, дизъюнкция, эквиваленция, импликация.
- Инверсия, дизъюнкция, конъюнкция, эквиваленция, импликация.
Задание 2.
Сопоставьте название логического оператора с упрощенным:
| Инверсия | А. Умножение |
| Эквиваленция | Б. Отрицание |
| Импликация | В. Следование Следование |
| Дизъюнкция | Г. Равенство |
| Конъюнкция | Д. Сложение |
Задание 3.
Чему будет равен последний столбец таблицы истинности для уравнения: А ∨ В ⇒ ¬С?
- 11101010
- 11101111
- 11111110
- 11000100
Задание 4.
Сократите логическое выражение: ¬(А ∨ В) ∧ (¬А ∨ С)
- ¬(А ∧ В)
- ¬А ∨ ¬В ∨ С
- ¬А ∧ ¬В ∧ С
- ¬А ∧ ¬В
Ответы: 1. — 2; 2. — 1Б, 2Г, 3В, 4Д, 5А; 3. — 1; 4. — 4.
Логика как алгебра
В классической логике высказываний доказательства часто делаются с использованием правил вывода или с использованием методов таблиц и разрешений. Однако есть и другой способ построения доказательств: тот, который рассматривает логику как алгебру.
Метод алгебраический рассматривает логику как школьную алгебру, где значения ограничены вместо , а операторы являются булевыми операторами. Построение доказательства сводится к решению системы уравнений.
Построение доказательства сводится к решению системы уравнений.
Начнем с примера. Учитывая набор предпосылок, мы построим доказательство без использования каких-либо традиционных методов доказательства теорем. Вместо этого мы построим доказательство алгебраически .
Пример 1. Учитывая посылки , и , можем ли мы вывести ?
Сначала выразим посылки алгебраически:
| 1. | Помещение | |
|---|---|---|
| 2. | Помещение | |
| 3. | | Помещение |
Здесь мы используем строчные буквы для обозначения переменных:
Если — пропозициональная переменная, то — это соответствующая алгебраическая переменная , и
если — пропозициональное утверждение, то — соответствующее алгебраическое уравнение .
Посылки дают нам систему уравнений, которую мы можем решить путем замены и упрощения:
| 1. | Premise | |
|---|---|---|
| Simplification | ||
| 2. | Premise | |
| Substitution | ||
| Simplification | ||
| 3. | Помещение | |
| Замена | ||
| Упрощение |
Отсюда мы видим, что , и . Так что есть одно решение:
Можем ли мы вывести из предпосылок?
Каждое решение удовлетворяет , поэтому да , мы можем вывести .
Это доказывает . Но это дает нам нечто гораздо более ценное: полный набор решений системы уравнений. С помощью этой информации мы можем тривиально доказать или опровергнуть любое утверждение о , и . Например:
Можем ли мы вывести из предпосылок? Существует решение
Можем ли мы вывести из предпосылок?
Каждое решение удовлетворяет , поэтому да , мы можем вывести .
Разветвление
До сих пор мы могли решать уравнения только с помощью подстановки и упрощения. Но в нашем наборе инструментов есть еще один инструмент: ответвление .
Пример 2. Учитывая посылки и , можем ли мы вывести ?
| 1. | Предметка | |
|---|---|---|
| 2. | Предметка |
На этот раз, уравнения уже находятся в их простостреле, и мы не сможем выполнить. Чтобы добиться прогресса, мы рассмотрим первую предпосылку ( ) в два небольших шага: мы будем разветвлять в альтернативные реальности, одну где , а другую где . Вместе они представляют полную предпосылку, , но по отдельности мы можем справиться с ними.
А. 1. 1. | Premise | |
|---|---|---|
| 2. | Premise | |
| Substitution | ||
| Simplification |
| Б.1. | Premise | |
|---|---|---|
| 2. | Premise | |
| Substitution | ||
| Simplification |
В филиале А есть два решения:
.
В отделении B есть одно решение:
.
Все эти решения удовлетворяют исходной системе уравнений, поэтому полный набор решений: .
Можем ли мы вывести из предпосылок? Существует решение , для которого , поэтому нет , мы не можем вывести .
В этом примере одна из посылок была дизъюнктивной ( ), что позволило нам разветвиться. Но что, если ни одна из посылок не является дизъюнктивной? В этом случае мы либо преобразуем посылку в дизъюнктивную форму (например, становится ), либо вместо этого разветвляемся на тавтологию (например, ).
Частный случай: тавтология
Пример 3. Если нет предпосылок, можем ли мы вывести ?
Это вырожденный случай, когда нечего решать.
Мы просто начинаем с и переходим к последнему этапу проверки:
Каждое решение удовлетворяет , поэтому да , мы можем вывести .
Частный случай: парадокс
Пример 4. Учитывая посылки и , можем ли мы вывести ?
Здесь может представлять абсолютно любое утверждение , поэтому мы, конечно, надеемся, что это не действительный аргумент.
Начнем с перечисления помещений:
| 1. | Предметка | |
|---|---|---|
| 2. | Предметка |
и мы сразу достигнем контрада:
| 1. | Помещение | |
|---|---|---|
| 2. | Помещение | |
| Замена |
Итак, решений нет:
Можем ли мы вывести из предпосылок?
Не существует решения, для которого , поэтому нет , мы не должны выводить .
Можем ли мы вывести из предпосылок? Не существует решения, для которого , поэтому нет , мы не должны выводить .
У нас просто нет оснований делать вывод о .
Автор Спенсер Мортенсен (spencer.spencermortensen.com) .Copyright © 2020. Все права защищены.
Связь между логикой и алгеброй.
спросил
Изменено 10 лет, 2 месяца назад
Просмотрено 6к раз
$\begingroup$
Какая связь между логикой и алгеброй?
Можно ли рассматривать одно как частный случай другого?
- абстрактная алгебра
- логика
$\endgroup$
2
$\begingroup$
Логика и алгебра связаны, но не являются частным случаем другого. В то время как некоторые аспекты каждой области могут быть плодотворно отражены с использованием языка другой области, не существует глобальной теории одной области с точки зрения другой области.
В то время как некоторые аспекты каждой области могут быть плодотворно отражены с использованием языка другой области, не существует глобальной теории одной области с точки зрения другой области.
Например, теория моделей, являющаяся частью логики, не имеет, насколько мне известно, прямого аналога в алгебре, тогда как теория Галуа, являющаяся частью (абстрактной) алгебры, не имеет аналога в логике.
$\endgroup$
9
$\begingroup$
Если вы имеете в виду булеву логику, то это разновидность алгебры.
Это будут утверждения типа:
$\lnot (P\land Q) \equiv \lnot P \lor \lnot Q$ (Demorgan)
и
$P\land (Q \lor R) \equiv (P\land Q) \lor (P\land R)$ (Какой-то дистрибутив)
Я читал, что когда-то они были одержим решением многочленов в замкнутой форме. Но как только была продемонстрирована неразрешимость многочлена Квинтика (степень 5), основное внимание алгебры стало уделяться общим правилам алгебры, и стали важными такие вещи, как: и операции стали более общими, чем +, -, × и ÷ элементарной алгебры.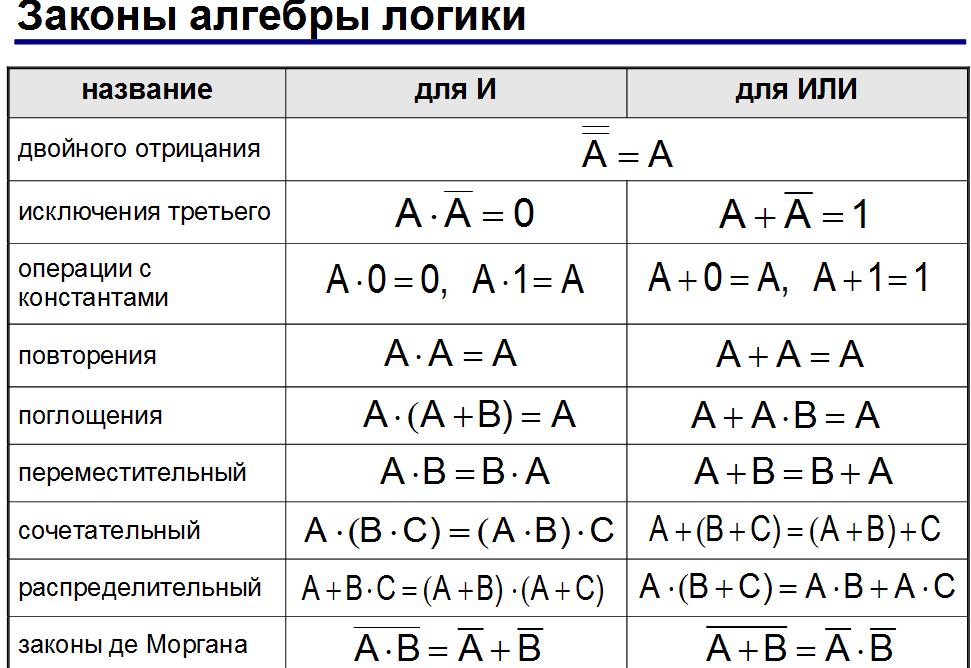
Таким образом, у вас есть вещи, подобные приведенным выше, где у вас есть такие операторы, как $\lor$ и $\land$.
Изучение общих алгебраических систем и их свойств известно сегодня как абстрактная или современная алгебра.
Более того, булева логика лежит в основе теории множеств, которая очень важна в математике, и почти идентична ей. Однажды кто-то сказал мне, что они были разработаны вместе.
$\endgroup$
$\begingroup$
Большинство математиков понимает термин логика как математическую логику. Существуют учебники по математической логике, посвященные логике предикатов, логике первого порядка, модальной логике и другим темам. Однако логика — гораздо более широкое понятие. Логика охватила бы все разумные рассуждения и, следовательно, включала бы алгебру. Связанный с этим вопрос может звучать так: является ли всякое обоснованное рассуждение подмножеством формального рассуждения? Является ли все формальное рассуждение математикой? Это очень сложные вопросы, которые обычно находятся за пределами области математики и являются частью философии, поэтому математики назвали их подмножество математической логикой. Этими вопросами занимается большая часть философии 20-го века, аналитической философии. Фреге, Рассел, Витгенштейн, Куайн, Патнэм и другие могут многое сказать об отношениях между логикой и математикой (алгеброй).
Этими вопросами занимается большая часть философии 20-го века, аналитической философии. Фреге, Рассел, Витгенштейн, Куайн, Патнэм и другие могут многое сказать об отношениях между логикой и математикой (алгеброй).
$\endgroup$
$\begingroup$
Рассмотрим алгебру натуральных чисел. Алгебра натуральных чисел — это просто арифметика натуральных чисел. Аксиомы арифметики натуральных чисел (например, аксиомы Пеано для натуральных чисел) могут быть выражены на языке (нотации) логики и теории множеств. Аксиомы теории множеств, в свою очередь, могут быть выражены на языке логики. Чтобы вывести теоремы арифметики натуральных чисел (алгебры), мы применяем аксиомы логики и теории множеств к аксиомам арифметики натуральных чисел.
Другие формы алгебры начинаются с другого набора аксиом (также выраженного на языке логики и теории множеств). Чтобы вывести теоремы этой алгебры, мы также применяем аксиомы логики и теории множеств к аксиомам этой алгебры.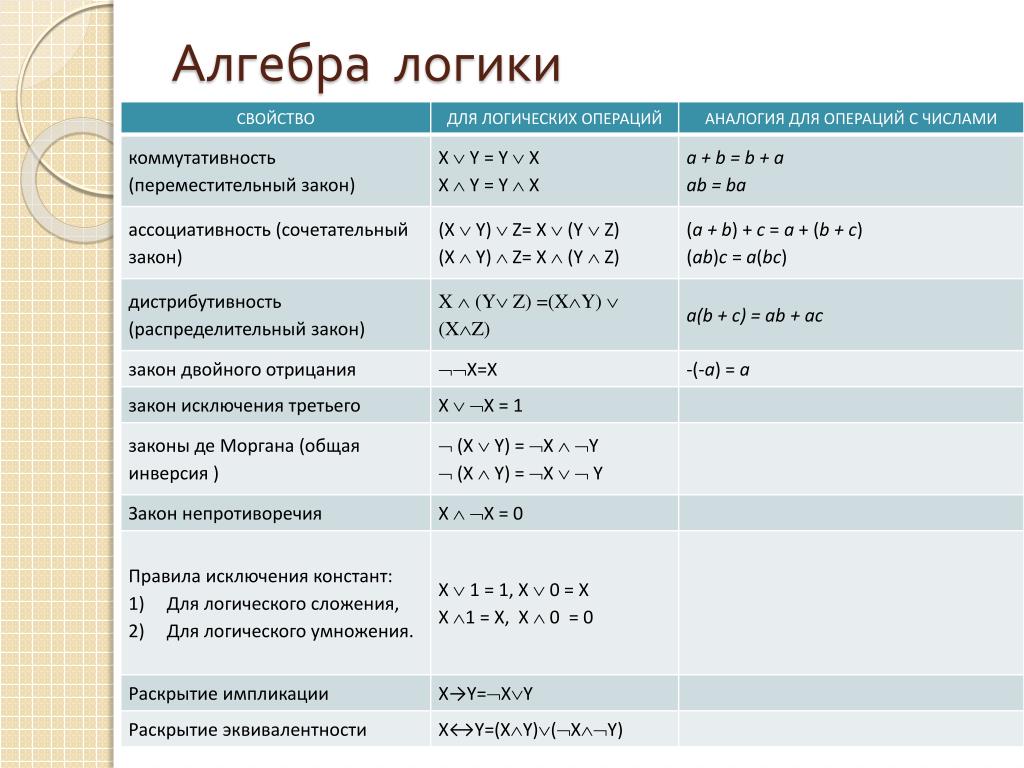


 В записи обозначается как ∨. А ∨ В дает истину в том случае, если хотя бы одно из высказываний истинно.
В записи обозначается как ∨. А ∨ В дает истину в том случае, если хотя бы одно из высказываний истинно.
 Истина обозначается как 1, а ложь — как 0.
Истина обозначается как 1, а ложь — как 0.