4
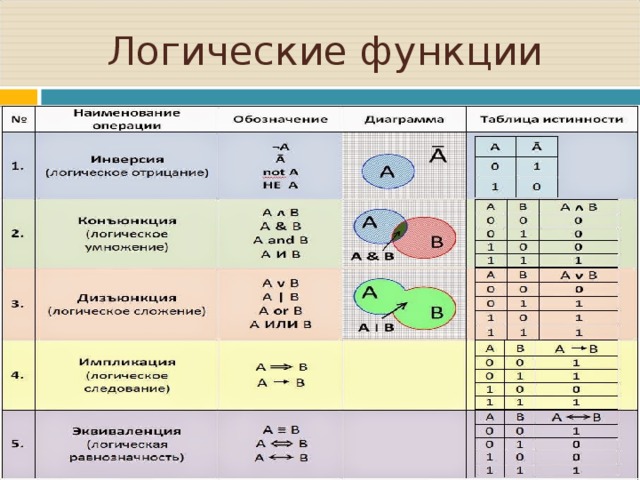
Рассмотрим более подробно некоторые логические связки, позволяющие конструировать из простых высказываний сложные. В математической логике такие связки называются логическими операциями.
2.3.1. Операция отрицания
Самой простой логической операцией, применяемой только к одному высказыванию, является операция отрицания, которая в русском языке соответствует частице «не». Отрицание высказывания А обозначается ØА или . Символ читается «не А» или «не верно, что А». Например, если высказывание А – «подсудимый виновен», то — «подсудимый не виновен».
По смыслу,
отрицание высказывания – высказывание, противоположное данному. То есть, если
высказывание А – истинное, то
высказывание — ложное, и наоборот,
если А – ложное, то — истинное. Запишем в виде таблицы значения нового, сложного
высказывания 
|
А |
|
|
1 0 |
0 1 |
Подобная таблица называется таблицей истинности[1]. Именно эту таблицу берут за определение операции отрицания. Высказывание называется
2.3.2. Дизъюнкция высказываний
Операция дизъюнкция применяется к
двум высказываниям А и В и соответствует соединению их с
помощью союза «или». Дизъюнкция обозначается с помощью знака Ú, который
ставится между высказываниями: АÚВ, что читается «А или В» или «или А, или В».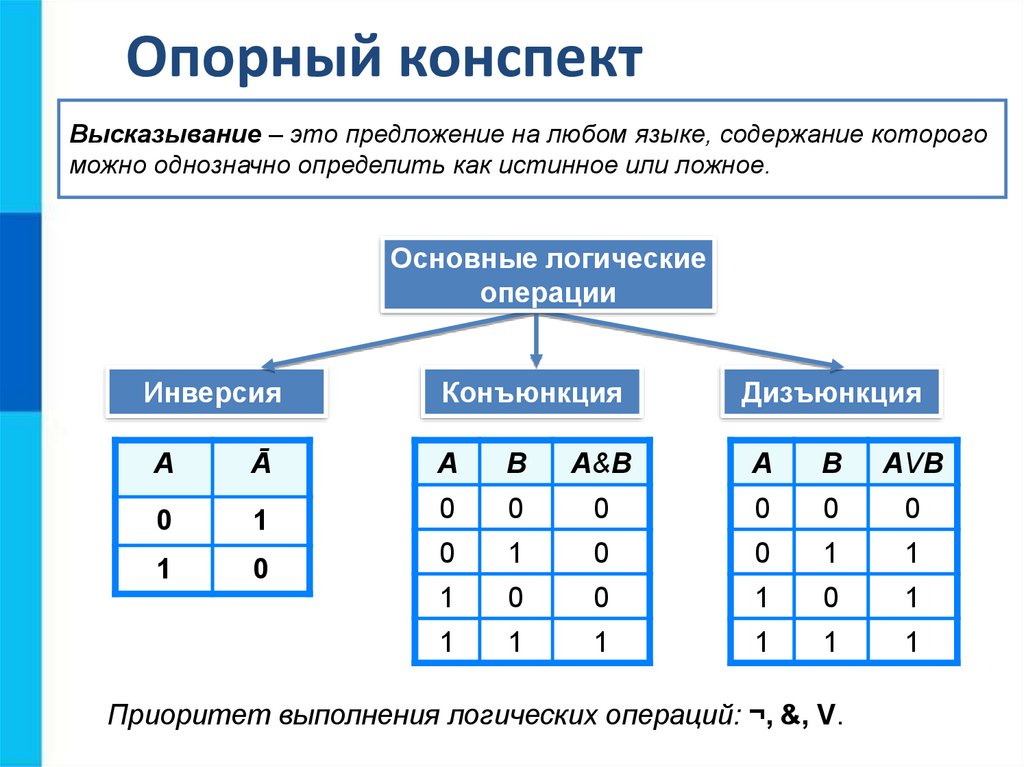 Например, «Грабеж может быть совершен с применением физического или психического насилия», «Договор
может быть заключен в устной
Например, «Грабеж может быть совершен с применением физического или психического насилия», «Договор
может быть заключен в устной
Рассмотрим
значение составленного сложного высказывания АÚВ. Если одно из высказываний истинно, а
другое ложно, то дизъюнкция
будет истинной. Если оба простых высказывания А и В ложны, то и
дизъюнкция будет ложной. А вот если оба высказывания А и В истинны, то
существует два случая. Это связано с тем, что в русском языке союз «или» имеет два значения. Одно из них неисключающее
«или», а другое – исключающее. Например, высказывание «Или я выучу этот
материал, или получу двойку» при истинных его составляющих будет ложно. Здесь
«или» понимается в исключающем смысле. А высказывание «Сейчас идет снег или
дождь» – истинно, если оба высказывания «Сейчас идет снег», «сейчас идет дождь»
– истинны и в этом случае союз «или» – неисключающий.
В логике высказываний дизъюнкция соответствует неисключающему «или». Можно дать следующее определение этой логической операции. Дизъюнкция АÚВ – сложное высказывание, которое ложно тогда и только тогда, когда оба высказывания А и В одновременно ложны. Таблица истинности операции дизъюнкция будет следующей:
|
А |
В |
AÚB |
|
1 |
1 |
1 |
|
1 |
0 |
|
|
0 |
1 |
1 |
|
0 |
0 |
0 |
Значения операции АÚВ (кроме первой строчки), как видно из таблицы, получаются
простым алгебраическим сложением значений А
и В.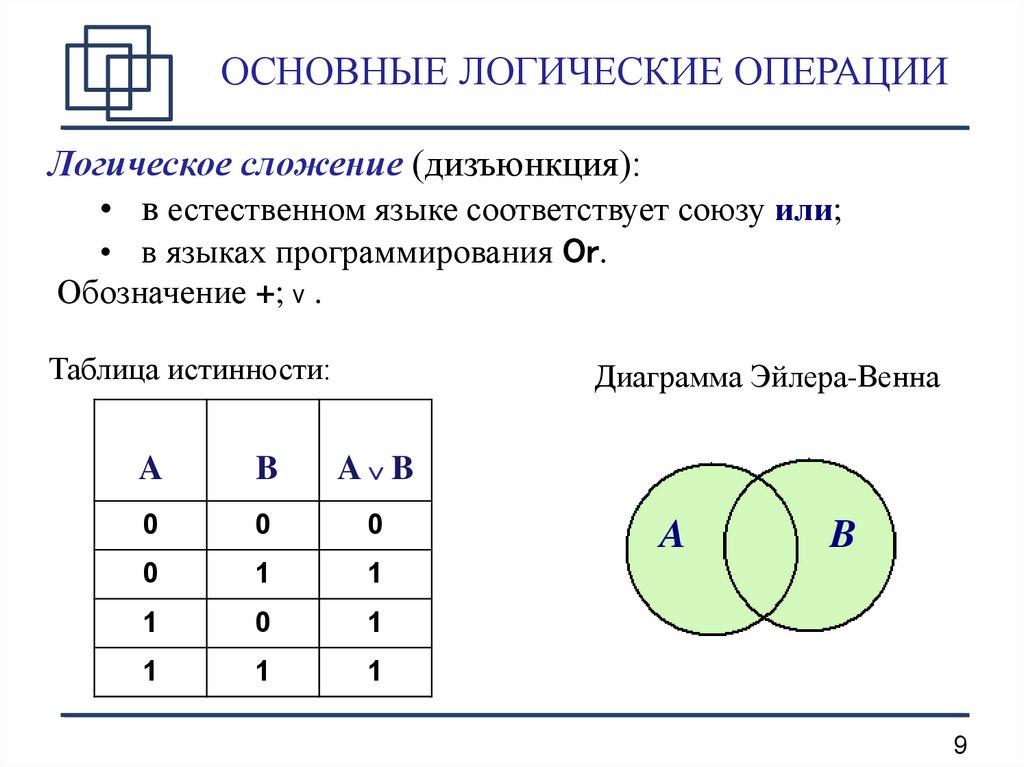
2.3.3. Конъюнкция высказываний
Операция конъюнкция применяется также к двум высказываниям А и В и соответствует соединению их с помощью союза «и». Она обозначается с помощью знака Ù или &, который ставится между высказываниями: АÙВ, что читается «А и В» или «и А, и В». Например, «Юрист должен знать и теорию государства и права, и
Рассмотрим
значение конъюнкции, исходя из смысла союза «и». Если оба высказывания А и В
будут истинными, то и конъюнкция АÙВ будет истинной.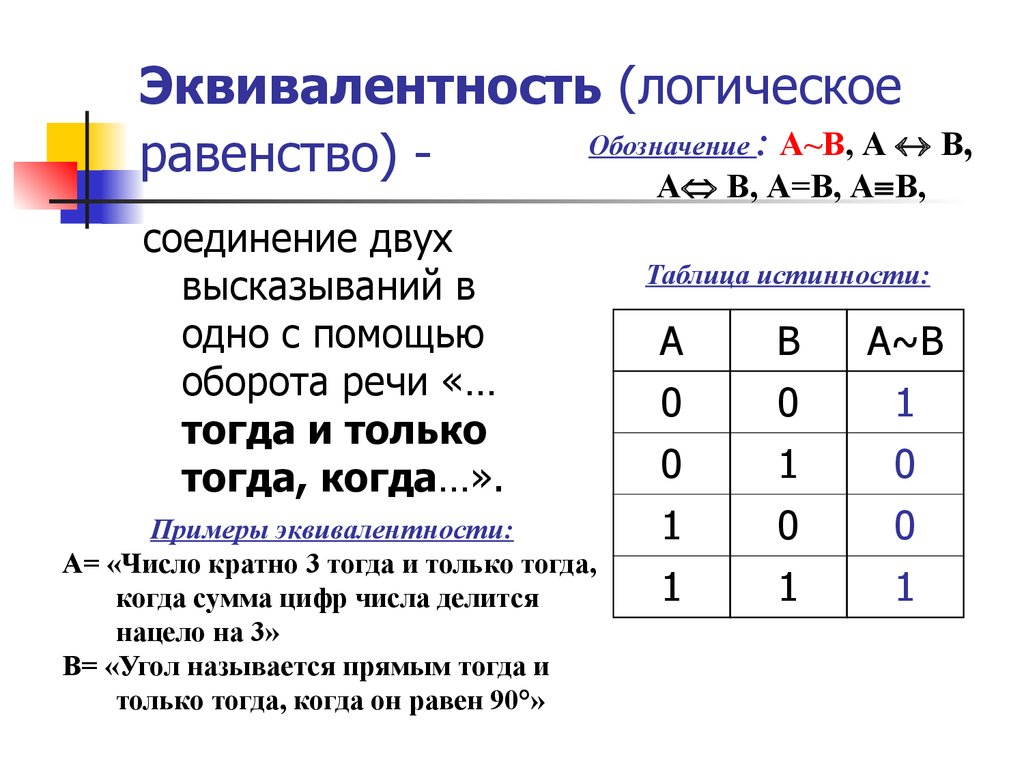 Если же хотя бы одно из
них (или оба) будут ложными, то и конъюнкция также будет ложной. Например,
высказывание «3 – нечетное число и 3
делится на 2» будет ложным. Исходя из этого, можно дать следующее определение
операции конъюнкция.
Если же хотя бы одно из
них (или оба) будут ложными, то и конъюнкция также будет ложной. Например,
высказывание «3 – нечетное число и 3
делится на 2» будет ложным. Исходя из этого, можно дать следующее определение
операции конъюнкция.
Конъюнкция АÙВ – сложное высказывание, которое истинно тогда и только тогда, когда оба высказывания А и В одновременно истинны. Таблица истинности операции конъюнкция такова:
|
А |
В |
АÙВ |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
|
Проанализировав приведенную таблицу,
можно заметить, что значения операции АÙВ получаются простым алгебраическим
умножением значений А и В.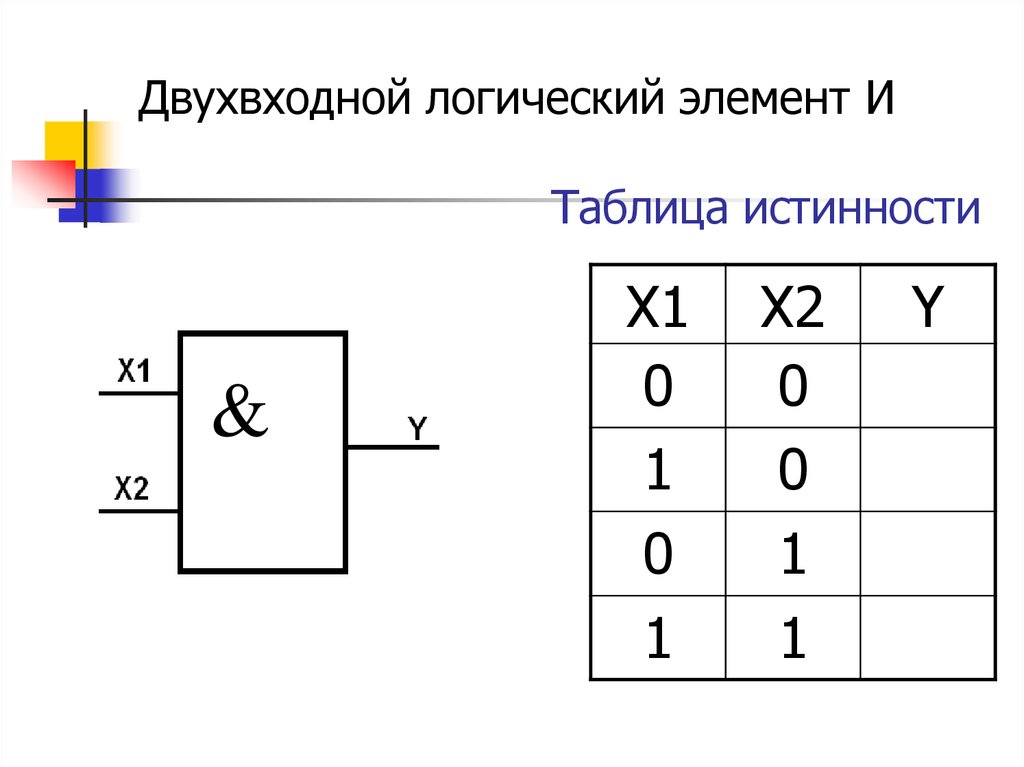 Поэтому конъюнкцию также называют
логическим умножением и обозначают, также как и в алгебре, знаком «×», который, также как и в алгебре, может опускаться.
Поэтому конъюнкцию также называют
логическим умножением и обозначают, также как и в алгебре, знаком «×», который, также как и в алгебре, может опускаться.
Рассмотренные операции отрицания, дизъюнкции и конъюнкции называют булевыми операциями. Они играют важную роль в применениях математической логики в электронике, автоматике, теории вычислительных устройств.
2.3.4. Импликация высказываний
Одной из важнейших логических
операций является операция импликация. Она соответствует объединению двух
высказываний с помощью союза «если …, то
…». Импликация обозначается с
помощью знака ®, ставящегося
между высказываниями: А®В,
что читается «А имплицирует В» или «если А, то В». В научной литературе по
логике высказываний также приводятся другие варианты прочтения этой операции: «А влечет
В», «из А следует В», «В только
если А».
Примеры. Гражданский кодекс РФ: «Если банк отказывает в принятии документов …, то он обязан незамедлительно проинформировать об этом получателя средств». «Если новый уголовный закон смягчает наказание за деяние, которое отбывается лицом, то это наказание подлежит сокращению в пределах, предусмотренных новым уголовным законом. Статья 10 УК РФ». «Если осужденный после отбытия наказания вел себя безупречно, то по его ходатайству суд может снять с него судимость до истечения срока погашения судимости. Статья 86 УК РФ». «Если 2*2=4, то 3+2=6».
Операция импликации определяется следующим образом.
Импликация высказываний А и В (А®В) – сложное высказывание, которое истинно всегда, кроме случая когда А – истинно, а В – ложно. Таким образом, таблица истинности импликации такова:
|
А |
В |
A ® B |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
Проанализируем соответствие
определения импликации с общепринятым значением сложноподчиненного предложения
с использованием союза «если .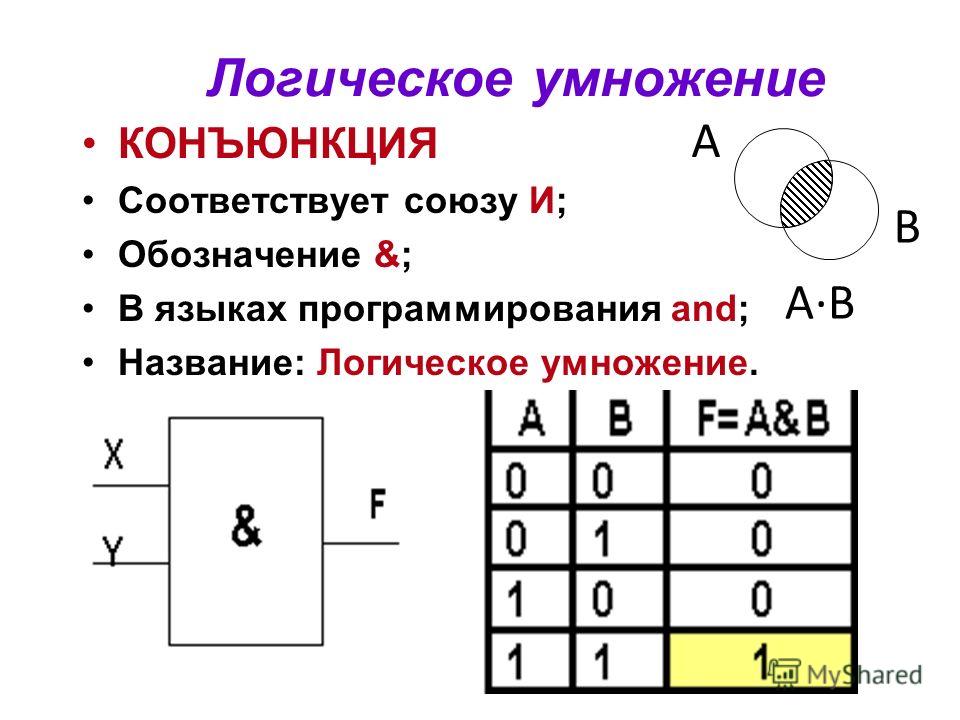 .., то …». Рассмотрим
следующее сложное высказывание: «Если
гражданин Иванов совершил кражу, то
он может быть наказан лишением свободы на срок до двух лет». Если оба
простые высказывания «гражданин Иванов совершил кражу» и «он
может быть наказан лишением свободы на срок до двух лет» истинны, то
истинность сложного высказывания не вызывает сомнения. При истинности
совершения кражи невозможность применения наказания в виде лишения свободы на
срок до двух лет должно быть оценено нами как ложное высказывание, так как такое
наказание предусмотрено статьей 158 Уголовного кодекса РФ. При ложном первом
высказывании «гражданин Иванов совершил кражу» применение данного
вида наказания к Иванову все же может быть осуществимо, если он, например,
обвиняется по статье 127 УК РФ («Незаконное лишение свободы») или по
статье 139 часть 2 УК РФ («Нарушение неприкосновенности жилища»).
Поэтому оценивание сложного высказывания как истинного соответствует истинности
импликации при данных значениях простых высказываниях в этих конкретных условиях.
.., то …». Рассмотрим
следующее сложное высказывание: «Если
гражданин Иванов совершил кражу, то
он может быть наказан лишением свободы на срок до двух лет». Если оба
простые высказывания «гражданин Иванов совершил кражу» и «он
может быть наказан лишением свободы на срок до двух лет» истинны, то
истинность сложного высказывания не вызывает сомнения. При истинности
совершения кражи невозможность применения наказания в виде лишения свободы на
срок до двух лет должно быть оценено нами как ложное высказывание, так как такое
наказание предусмотрено статьей 158 Уголовного кодекса РФ. При ложном первом
высказывании «гражданин Иванов совершил кражу» применение данного
вида наказания к Иванову все же может быть осуществимо, если он, например,
обвиняется по статье 127 УК РФ («Незаконное лишение свободы») или по
статье 139 часть 2 УК РФ («Нарушение неприкосновенности жилища»).
Поэтому оценивание сложного высказывания как истинного соответствует истинности
импликации при данных значениях простых высказываниях в этих конкретных условиях.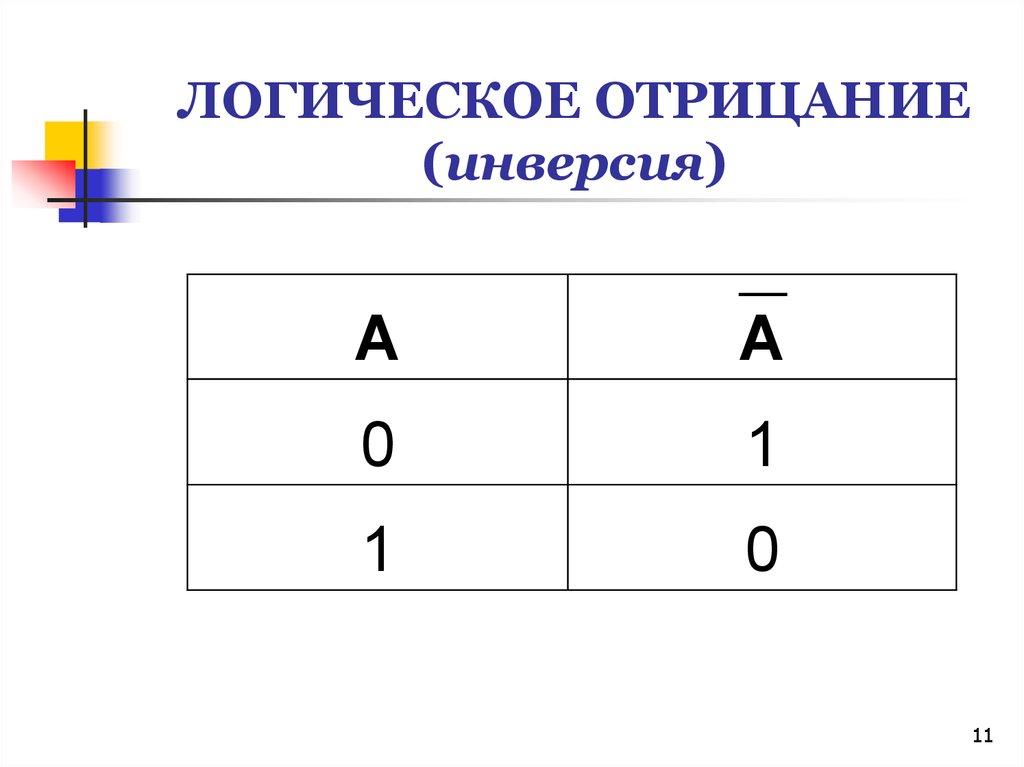 И, наконец, при ложности простых высказываний, т.е. истинности противоположных:
«гражданин Иванов не совершил кражу» и «он не может быть наказан
лишением свободы на срок до двух лет», рассмотренная причинно-следственная
связь является истинной.
И, наконец, при ложности простых высказываний, т.е. истинности противоположных:
«гражданин Иванов не совершил кражу» и «он не может быть наказан
лишением свободы на срок до двух лет», рассмотренная причинно-следственная
связь является истинной.
Рассмотрим следующие высказывания:
· «Волга впадает в Каспийское море» — истинное высказывание;
· «Дон впадает в Каспийское море» — ложное высказывание;
· «Дважды два – четыре» — истинное высказывание;
· «Дважды два – пять » — ложное высказывание.
Составим из этих простых высказываний сложные с помощью союза «если …, то …» и, интерпретируя использованный союз как импликацию, оценим значения полученных высказываний.
· «Если Волга впадает в Каспийское море, то дважды два – четыре» — истинное высказывание;
· «Если Волга впадает в Каспийское море, то дважды два – пять» — ложное высказывание;
· «Если Дон впадает в Каспийское море, то дважды два – четыре» — истинное высказывание;
·
«Если Дон впадает в Каспийское море, то дважды
два – пять» — истинное высказывание.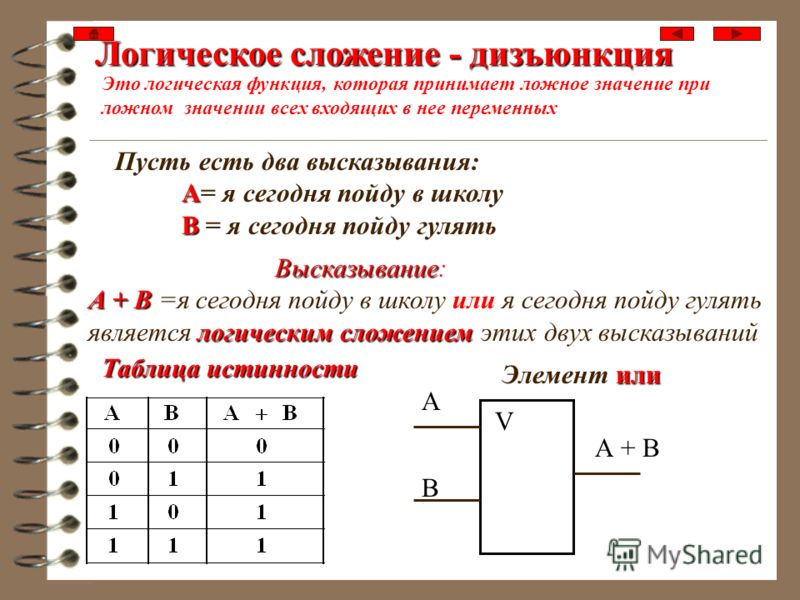
Эти утверждения не соответствуют привычному для естественного языка употреблению союза «если …, то …». Поэтому импликация лишь до некоторой степени соответствует этому союзу. И математически корректнее операцию А®В читать не «если А, то В», а «А имплицирует В». Операция импликации А®В хорошо описывается союзом «если …, то …» в случаях:
· описания причинно-следственной связи между А и В. Например, «Если долго мучиться, то что-нибудь получится»;
· выражения логического следования В из А. Например, «Если все люди смертны и Сократ – человек, то Сократ смертен».
В этих
высказываниях существует связь между содержанием высказываний А и В,
объединенных союзом. В логике высказываний рассматриваются только значения
истинности высказываний, а не их содержание. Тем самым логические операции не
выражают связь между содержанием высказываний. Логические операции, образующие
из простых высказываний сложные, определяют только соотношения между значениями
истинности этих высказываний.
Тем самым логические операции не
выражают связь между содержанием высказываний. Логические операции, образующие
из простых высказываний сложные, определяют только соотношения между значениями
истинности этих высказываний.
2.3.5. Эквивалентность высказываний
Последней введем операцию эквивалентности. Эта операция обозначается символом «, либо ~. Сложное высказывание А«В читается: «А эквивалентно В«, либо «А равносильно В«, либо «А тогда и только тогда, когда В«, либо «В, если и только если А«. Эквивалентность примерно соответствует употреблению выражения «тогда и только тогда, когда», хотя, как и в случае с импликацией, такое соответствие далеко не полное.
Приведем примеры использования операции
эквивалентности. «Два треугольника равны
тогда и только тогда, когда
три стороны одного треугольника равны соответствующим сторонам другого
треугольника». «Деяние кража равносильно тайному
хищению чужого имущества». «Распространение заведомо ложных сведений является
клеветой, если и только если эти
сведения порочат честь и достоинство другого лица или подрывают его репутацию».
«Деяние кража равносильно тайному
хищению чужого имущества». «Распространение заведомо ложных сведений является
клеветой, если и только если эти
сведения порочат честь и достоинство другого лица или подрывают его репутацию».
Эквивалентность высказываний А и В (А«В) – сложное высказывание, которое истинно, когда А и В одновременно либо истинны, либо ложны и ложно во всех других случаях. Эквивалентность определяется следующей таблицей истинности:
|
А |
В |
А«В |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
Эквивалентность соответствует двум
операциям импликации, соединенных конъюнкцией. А«В равносильно (A ® B)Ù(A ® B) , т.е. имеет
такую же таблицу истинности (рассмотрим это позднее). Поэтому эквивалентность
также называют двойной импликацией.
А«В равносильно (A ® B)Ù(A ® B) , т.е. имеет
такую же таблицу истинности (рассмотрим это позднее). Поэтому эквивалентность
также называют двойной импликацией.
§1. Логический тип переменных. Логические выражения — ЗФТШ, МФТИ
В прошлом задании мы работали с числовыми типами переменных и учили арифметику, теперь познакомимся с логическим типом переменных, который называется Boolean. Переменные этого типа имеют всего два значения — true и false (соответственно, «истина» и «ложь»). Подобно числовым переменным им можно присваивать значения при помощи оператора присваивания. При этом необходимо строго соблюдать правило совместимости типов. То есть, логическим переменным нельзя присваивать числовые значения, а числовым — логические. Так же можно выводить значения логических переменных на экран, а вот вводить их с клавиатуры нельзя!
В языке Pascal определены `6` операций сравнения, результатом которых является логическое значение:
1) «больше» (>)
2) «больше или равно» (>=)
3) «меньше» (<)
4) «меньше или равно» (<=)
5) «равно» (=)
6) «не равно» (<>).
Например, операция `5>2` всегда выдаст значение true, а операция `x<>3` выдаст значение true, если переменная `x` имеет любое значение, кроме `3`.
Сравнивать можно не только числа (причём как целые, так и вещественные), но и логические значения. При этом считается, что значение true больше, чем значение false.
При выполнении сравнений также необходимо соблюдать совместимость типов. То есть, можно сравнивать число с числом или логическое значение с логическим значением, но нельзя сравнивать число с логическим значением. Такое сравнение выдаст ошибку.
Помимо операций сравнения ещё существуют и логические операции:
1) and (конъюнкция, логическое умножение, операция «И»)
2) or (дизъюнкция, логическое сложение, операция «ИЛИ»)
3) not (отрицание, инверсия)
4) xor (строгая дизъюнкция, исключающее «ИЛИ», сложение по модулю `2`).
В скобках указаны возможные названия данных операций в алгебре логики.
Операнды этих операций должны быть логического типа. Результат вычислений также будет логический. При этом операции and, or, xor имеют по два операнда, а операция not — всего один, который записывается справа от названия операции. Названия логических операций являются служебными зарезервированными словами языка.
Результат вычислений также будет логический. При этом операции and, or, xor имеют по два операнда, а операция not — всего один, который записывается справа от названия операции. Названия логических операций являются служебными зарезервированными словами языка.
Приведём таблицы результатов логических операций для всех возможных значений операндов (в алгебре логики такие таблицы называются таблицами истинности):
|
X |
not x |
|
false |
true |
|
True |
false |
|
X |
y |
x and y |
x or y |
x xor y |
|
false |
false |
false |
False |
false |
|
false |
true |
false |
True |
True |
|
true |
false |
false |
True |
True |
|
true |
true |
true |
True |
False |
Логический результат даёт также стандартная функция odd(x), которая применяется к целочисленному аргументу х:
odd(x) = true, если `x` нечётно;
odd(x) = false, если `x` чётно.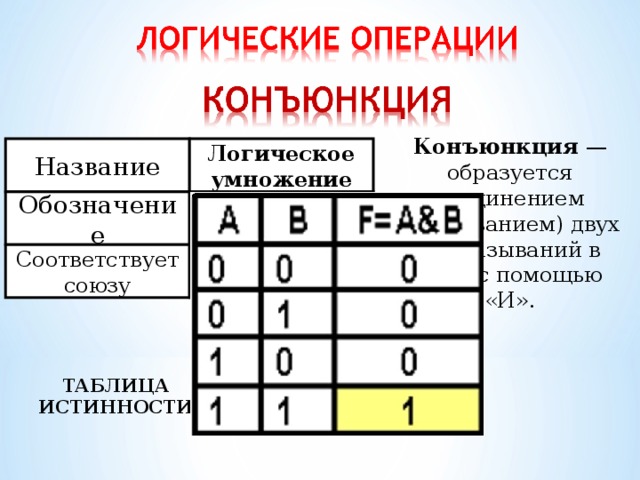
Приоритет операций в сложном выражении (содержащем в себе все виды операций, изученных нами) следующий:
1) Операция not.
2) Операции группы умножения and, *, /, div, mod
3) Операции группы сложения or, xor, +, —
4) Операции сравнения >, <, >=, <=, =, <>
Операции одного приоритета выполняются слева направо. Операции в круглых скобках имеют более высокий приоритет, чем операции вне скобок.
Рассмотрим несколько примеров на построение логических выражений. Пусть нам требуется записать логическое выражение по синтаксису языка программирования, имеющее значение true, в случае выполнения указанного условия.
Обратите внимание, что согласно таблице приоритетов, операции сравнения имеют самый низкий приоритет. Однако, как правило, в сложных выражениях нужно сначала выполнить сравнения, а потом группировать их результаты при помощи логических операций. Поэтому не нужно забывать брать операции сравнения в скобки, чтобы не получить неправильный порядок действий.
Операторы
8.1. Оператор Spread
Оператор Spread-dot ( *. ), часто сокращенно просто Оператор Spread, используется для вызова действия над всеми элементами.
агрегатного объекта. Это эквивалентно вызову действия над каждым элементом и сбору результата в список:
class Car {
Строка сделать
Струнная модель
}
деф автомобили = [
новый автомобиль(марка: "Пежо", модель: "508"),
новый автомобиль(марка: 'Renault', модель: 'Clio')] (1)
деф марки = автомобили*.марка (2)
assert makes == ['Peugeot', 'Renault'] (3) | 1 | построить список из автомобилей элементов. Список представляет собой совокупность объектов. |
| 2 | вызвать оператора спреда из списка, обратившись к свойству make каждого элемента |
| 3 | возвращает список строк, соответствующих набору make элементов |
Выражение cars*. эквивалентно  make
make cars.collect{ it.make } .
Нотация Groovy GPath позволяет сократить путь, когда указанное свойство
не является свойством содержащего списка, в этом случае он автоматически
распространение. В ранее упомянутом случае выражение тачки.марка может
можно использовать, хотя часто рекомендуется сохранять явный оператор с расставленными точками.
Оператор распространения является нулевым, что означает, что если элемент коллекции имеет значение null,
он вернет null вместо того, чтобы выдать исключение NullPointerException :
cars = [ новый автомобиль(марка: "Пежо", модель: "508"), ноль, (1) новый автомобиль(марка: 'Renault', модель: 'Clio')] assert cars*.make == ['Peugeot', null, 'Renault'] (2) утверждать null*.make == null (3)
| 1 | построить список, для которого один из элементов нулевой |
| 2 | с использованием оператора распространения вызовет , а не исключение NullPointerException |
| 3 | получатель также может быть нулевым, и в этом случае возвращаемое значение равно ноль |
Оператор распространения может использоваться в любом классе, реализующем интерфейс Iterable :
class Component {
Целочисленный идентификатор
Имя строки
}
класс CompositeObject реализует Iterable {
Компоненты защиты = [
новый компонент (id: 1, имя: «Foo»),
новый компонент (id: 2, имя: «Бар»)]
@Override
Итератор<Компонент> итератор() {
компоненты. iterator()
}
}
def составной = новый составной объект ()
утверждать составной*.id == [1,2]
утверждать составное*.имя == ['Foo','Bar']
iterator()
}
}
def составной = новый составной объект ()
утверждать составной*.id == [1,2]
утверждать составное*.имя == ['Foo','Bar'] Использовать несколько вызовов оператора растровой точки (здесь cars*.models*.name ), когда
работа с агрегатами структур данных, которые сами содержат агрегаты:
class Make {
Имя строки
Список моделей
}
@канонический
модель класса {
Имя строки
}
деф автомобили = [
новая марка (название: «Пежо»,
модели: [новая модель('408'), новая модель('508')]),
новый Марка (название: «Рено»,
модели: [новая модель('Clio'), новая модель('Captur')])
]
def makes = автомобили*.название
assert делает == ['Peugeot', 'Renault']
def модели = автомобили*.модели*.название
утверждать модели == [['408', '508'], ['Clio', 'Captur']]
assert models.sum() == ['408', '508', 'Clio', 'Captur'] // выравнивание на один уровень
assert models.flatten() == ['408', '508', 'Clio', 'Captur'] // выравниваем все уровни (в данном случае один) Рассмотрите возможность использования метода DGM collectNested вместо оператора с расставленными точками для коллекций коллекций:
class Car {
Строка сделать
Струнная модель
}
деф автомобили = [
[
новый автомобиль(марка: 'Peugeot', модель: '408'),
новый автомобиль(марка: 'Peugeot', модель: '508')
], [
новый автомобиль(марка: 'Renault', модель: 'Clio'),
новый автомобиль(марка: 'Renault', модель: 'Captur')
]
]
def models = cars. collectNested{ it.model }
утверждать модели == [['408', '508'], ['Clio', 'Captur']]
collectNested{ it.model }
утверждать модели == [['408', '508'], ['Clio', 'Captur']] 8.1.1. Распространение аргументов метода
Возможны ситуации, когда аргументы вызова метода можно найти в списке, который необходимо адаптировать к методу аргументы. В таких ситуациях вы можете использовать оператор распространения для вызова метода. Например, представьте, что у вас есть следующая подпись метода:
int function (int x, int y, int z) {
х*у+г
} , тогда, если у вас есть следующий список:
def args = [4,5,6]
, вы можете вызвать метод без определения промежуточных переменных:
assert function(*args) == 26
Можно даже смешивать обычные аргументы с расширенными:
args = [4] функция утверждения(*args,5,6) == 26
8.1.2. Элементы списка распространения
При использовании внутри литерала списка оператор расширения действует так, как если бы содержимое элемента расширения было встроено в список:
def items = [4,5] (1) список по умолчанию = [1,2,3,*элементы,6] (2) список утверждений == [1,2,3,4,5,6] (3)
| 1 | пунктов список |
| 2 | мы хотим вставить содержимое списка элементов непосредственно в список без вызова addAll |
| 3 | содержимое элементов было встроено в список |
8.
 1.3. Элементы карты распространения
1.3. Элементы карты распространенияОператор карты распространения работает аналогично оператору списка распространения, но для карт. Это позволяет вам встроить содержимое карты в другой литерал карты, как в следующем примере:
def m1 = [c:3, d:4] (1) карта защиты = [a:1, b:2, *:m1] (2) assert map == [a:1, b:2, c:3, d:4] (3)
| 1 | m1 это карта, которую мы хотим встроить |
| 2 | мы используем нотацию *:m1 для распространения содержимого m1 на карту |
| 3 | карта содержит все элементы m1 |
Должность оператора карты спреда имеет значение, как показано в следующем примере:
по умолчанию m1 = [c:3, d:4] (1) карта защиты = [a:1, b:2, *:m1, d: 8] (2) assert map == [a:1, b:2, c:3, d:8] (3)
| 1 | m1 это карта, которую мы хотим встроить |
| 2 | мы используем нотацию *:m1 для распространения содержимого m1 на карту , но переопределить ключ d после распространяя |
| 3 | карта содержит все ожидаемые ключи, но d был переопределен |
8.
 2. Оператор диапазона
2. Оператор диапазона Groovy поддерживает концепцию диапазонов и предоставляет нотацию ( .. ) для создания диапазонов объектов:
def range = 0..5 (1) утверждать (0..5).collect() == [0, 1, 2, 3, 4, 5] (2) утверждать (0..<5).collect() == [0, 1, 2, 3, 4] (3) утверждать (0<..5).collect() == [1, 2, 3, 4, 5] (4) утверждать (0<..<5).collect() == [1, 2, 3, 4] (5) утверждать (0..5) instanceof List (6) утверждать (0..5).size() == 6 (7)
| 1 | простой диапазон целых чисел, сохраненный в локальной переменной |
| 2 | и IntRange с включенными границами |
| 3 | и IntRange с исключительной верхней границей |
| 4 | и IntRange с эксклюзивной нижней границей |
| 5 | и IntRange с эксклюзивными нижними и верхними границами |
| 6 | a groovy. реализует интерфейс List |
| 7 | означает, что вы можете вызвать на нем метод размера |
Реализация диапазонов упрощена, что означает, что сохраняются только нижняя и верхняя границы. Вы можете создать диапазон
из любых Сопоставимый объект , который имеет методы next() и previous() для определения следующего/предыдущего элемента в диапазоне.
Например, вы можете создать диапазон символов следующим образом:
assert('a'..'d').collect() == ['a','b','c','d'] 8.3. Оператор космического корабля
Оператор космического корабля ( <=> ) делегирует метод compareTo :
assert (1 <=> 1) == 0
утверждать (1 <=> 2) == -1
утверждать (2 <=> 1) == 1
утверждать ('a' <=> 'z') == -1 8.4. Оператор нижнего индекса
Оператор нижнего индекса представляет собой сокращенную запись для getAt или putAt , в зависимости от того, найдете ли вы его на
левая или правая часть присваивания:
def list = [0,1,2,3,4] список утверждений[2] == 2 (1) список[2] = 4 (2) утвердить список[0..2] == [0,1,4] (3) список[0..2] = [6,6,6] (4) список утверждений == [6,6,6,3,4] (5)
| 1 | [2] можно использовать вместо getAt(2) |
| 2 | , если слева от задания, вызовет putAt |
| 3 | getAt также поддерживает диапазоны |
| 4 | так же как и putAt |
| 5 | список изменен |
Оператор нижнего индекса в сочетании с пользовательской реализацией getAt / putAt является удобным способом деструктурирования
объекты:
класс пользователя {
Длинный идентификатор
Имя строки
защита getAt(int i) { (1)
переключатель (я) {
случай 0: возвращаемый идентификатор
случай 1: вернуть имя
}
выбросить новое исключение IllegalArgumentException("Нет такого элемента $i")
}
void putAt (int i, значение по умолчанию) { (2)
переключатель (я) {
случай 0: идентификатор = значение; возвращаться
случай 1: имя = значение; возвращаться
}
выбросить новое исключение IllegalArgumentException("Нет такого элемента $i")
}
}
def user = новый пользователь (id: 1, имя: «Алекс») (3)
утвердить пользователя [0] == 1 (4)
утвердить пользователя [1] == 'Алекс' (5)
пользователь [1] = 'Боб' (6)
утверждать user. name == 'Боб' (7)
name == 'Боб' (7) | 1 | класс User определяет пользовательский getAt реализация |
| 2 | класс User определяет пользовательскую реализацию putAt |
| 3 | создать пробного пользователя |
| 4 | с помощью оператора индекса с индексом 0 позволяет получить идентификатор пользователя |
| 5 | с помощью оператора индекса с индексом 1 позволяет получить имя пользователя |
| 6 | мы можем использовать оператор нижнего индекса для записи в свойство благодаря делегированию putAt |
| 7 | и проверьте, действительно ли свойство имя было изменено |
8.
 5. Оператор безопасного индексирования
5. Оператор безопасного индексирования Groovy 3.0.0 представляет оператор безопасного индексирования, т. е. ?[] , что аналогично ?. . Например:
Строка[] массив = ['a', 'b'] assert 'b' == array?[1] // получаем с использованием индекса обычного массива array?[1] = 'c' // устанавливаем с использованием индекса обычного массива утверждать 'c' == массив? [1] массив = ноль assert null == array?[1] // возвращаем null для всех значений индекса array?[1] = 'c' // тихо игнорируем попытку установить значение утверждать массив null ==?[1] def personInfo = [имя: 'Daniel.Sun', местоположение: 'Шанхай'] assert 'Daniel.Sun' == personInfo?['name'] // используем индекс карты нормалей personInfo?['name'] = 'sunlan' // устанавливается с использованием индекса карты нормалей утверждать 'sunlan' == personInfo?['name'] информация о человеке = ноль assert null == personInfo?['name'] // возвращаем null для всех значений карты personInfo?['name'] = 'sunlan' // незаметно игнорируем попытку установить значение утверждать null == personInfo?['name']
8.
 6. Оператор принадлежности
6. Оператор принадлежности Оператор принадлежности ( в ) эквивалентен вызову метода isCase . В контексте списка это эквивалентно
для вызова содержится , как в следующем примере:
def list = ['Grace','Rob','Emmy']
утверждать («Эмми» в списке) (1)
утверждать ('Алекс' !в списке) (2) | 1 | эквивалентно вызову list.contains('Эмми') или list.isCase('Эмми') |
| 2 | отрицание членства эквивалентно вызову !list.contains('Emmy') или !list.isCase('Emmy') |
8.7. Оператор идентификации
В Groovy использование == для проверки равенства отличается от использования того же оператора в Java. В Groovy это вызов равно . Если вы хотите сравнить ссылочное равенство, вы должны использовать
Если вы хотите сравнить ссылочное равенство, вы должны использовать равно , как в следующем примере:
def list1 = ['Groovy 1.8','Groovy 2.0','Groovy 2.3'] (1) def list2 = ['Groovy 1.8','Groovy 2.0','Groovy 2.3'] (2) утверждать список1 == список2 (3) утверждать !list1.is(list2) (4) утверждать список1 !== список2 (5)
| 1 | Создать список строк |
| 2 | Создайте еще один список строк, содержащих те же элементы |
| 3 | , используя == , мы проверяем равенство объектов, что эквивалентно list1.equals(list2) в Java | .
| 4 | с использованием равно , мы можем проверить, что ссылки различны, что эквивалентно list1 == list2 в Java | .
| 5 | , используя === или !== (поддерживается и рекомендуется, начиная с Groovy 3.0.0), мы также можем проверить, являются ли ссылки различными или нет, что эквивалентно list1 == list2 и list1 != list2 на Яве |
8.8. Оператор приведения
Оператор приведения ( как ) — вариант литья. Приведение преобразует объект из одного типа в другой без их
быть совместимым для назначения. Возьмем пример:
Целое число x = 123 Строка s = (Строка) x (1)
| 1 | Целое число не может быть назначено String , поэтому оно создаст ClassCastException во время выполнения |
Это можно исправить, используя вместо этого приведение :
Целое число x = 123 Строка s = x as Строка (1)
| 1 | Целое число не может быть присвоено строке , но использование в качестве приведет к принудительному преобразованию в строку |
Когда объект принудительно преобразуется в другой, если целевой тип не совпадает с исходным типом, приведение возвращает новый объект . Правила приведения различаются в зависимости от исходного и целевого типов, и приведение может завершиться ошибкой, если не выполняется преобразование.
правила найдены. Пользовательские правила преобразования могут быть реализованы благодаря методу
Правила приведения различаются в зависимости от исходного и целевого типов, и приведение может завершиться ошибкой, если не выполняется преобразование.
правила найдены. Пользовательские правила преобразования могут быть реализованы благодаря методу asType :
класс Идентифицируемый {
Имя строки
}
класс пользователя {
Длинный идентификатор
Имя строки
def asType (Цель класса) { (1)
если (цель == Идентифицируемый) {
вернуть новый идентифицируемый (имя: имя)
}
выбросить новое исключение ClassCastException («Пользователь не может быть принужден к $ target»)
}
}
def u = новый пользователь (имя: «Ксавье») (2)
def p = u как идентифицируемый (3)
утверждать p instanceof Идентифицируемый (4)
assert !(p instanceof User) (5) | 1 | класс User определяет пользовательское правило преобразования с User на Идентифицируемый |
| 2 | мы создаем экземпляр пользователя |
| 3 | мы принуждаем экземпляр пользователя к идентифицируемому |
| 4 | цель является экземпляром Идентифицируемый |
| 5 | цель не является экземпляром Пользователь Больше |
8.
 9. Алмазный оператор
9. Алмазный оператор Алмазный оператор ( <> ) является синтаксическим сахарным оператором, добавленным для поддержки совместимости с оператором
то же имя в Java 7. Оно используется для указания того, что универсальные типы должны выводиться из объявления:
Liststrings = new LinkedList<>()
В динамическом Groovy это совершенно не используется. В Groovy со статической проверкой типов это также необязательно, так как Groovy средство проверки типов выполняет вывод типа независимо от того, присутствует этот оператор или нет.
8.10. Оператор вызова
Оператор вызова () используется для неявного вызова метода с именем call . Для любого объекта, который определяет метод вызова ,
вы можете опустить часть .call и вместо этого использовать оператор вызова:
class MyCallable {
внутренний вызов (int x) { (1)
2*х
}
}
def mc = новый MyCallable()
утверждать mc. call(2) == 4 (2)
утверждать mc(2) == 4 (3)
call(2) == 4 (2)
утверждать mc(2) == 4 (3) | 1 | MyCallable определяет метод с именем call . Обратите внимание, что нет необходимости реализовывать java.util.concurrent.Callable |
| 2 | мы можем вызвать метод, используя классический синтаксис вызова метода |
| 3 | или мы можем опустить .вызов спасибо оператору звонка |
4.2. Операторы, возвращающие логические результаты — документация python_for_ss 0.1.1
Правильное использование конструкции if-then предполагает знание
как написать строки кода, которые возвращают логические результаты
( Верно или Ложно ). Конечно, мы всегда можем
написать собственную программу (функцию) для этого.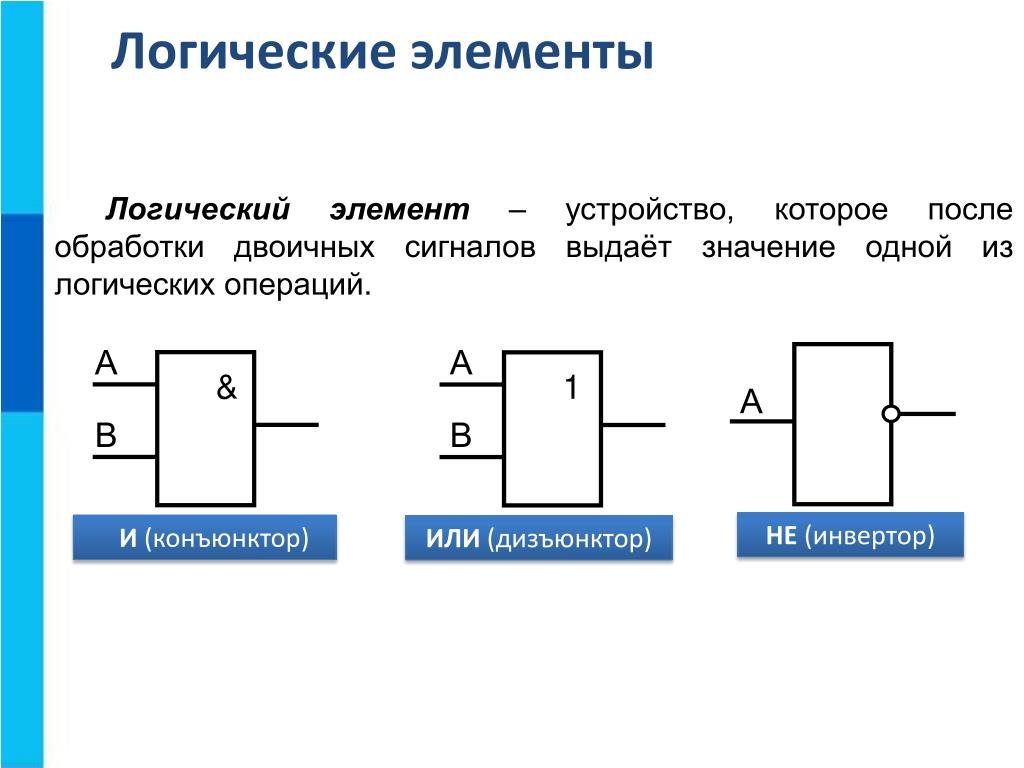 Но во многих
случаях Python предоставляет некоторые
простые способы выполнить тесты, которые вы хотите, и получить
Логические результаты или результаты, которые можно интерпретировать
как логические значения (см. ниже).
Но во многих
случаях Python предоставляет некоторые
простые способы выполнить тесты, которые вы хотите, и получить
Логические результаты или результаты, которые можно интерпретировать
как логические значения (см. ниже).
Первое, что нужно знать, это операторы, которые всегда возвращают
Булевы значения. В примерах x и y — это любой Python.
объект.
x in y: возвращаетTrue, если объект Pythonxнаходится в контейнери; в противном случае возвращаетFalse.x < y, x <= y: возвращаетTrueесли объект Pythonx«меньше чем, меньше или равно» по общим правилам сравнения объектов. В противном случае возвращаетЛожь. Обычно используется для сравнения объектов одного типа, или результаты могут быть удивительно. Работает как положено для чисел, строк (в алфавитном порядке).x > y, x >= y: возвращаетTrue, если объект Pythonx«больше, больше или равно»и. В противном случае возвращает
В противном случае возвращает False.x == y: возвращаетTrue, если объект Pythonxэквивалентноy(например, тот же номер или контейнер с тем же содержимым). В противном случае возвращаетFalse.x != y, x <> y: Синонимы; вернутьTrue, если Объект Pythonx— это , а не , эквивалентный объектуy. Если эквивалентно , возвращаетFalse.не x:x- это логическое значение или что-то в этом роде который можно интерпретировать как логическое значение.вместоИнверсия логического значения.Неправда=Ложьи наоборот., а не, может предшествовать любому допустимому тесту для изменения значения.
Наш предыдущий пример конструкции if-then в Python упустил некоторые детали:
если слово в словаре: результаты.добавить(слово)
Определение, которое мы дали конструкции «если-то», состояло в том, что
блок кода с отступом выполнялся, если результат теста был True .
Правда на самом деле немного сложнее —
и немного удобнее. Очень ограниченный набор выражений Python
типы фактически оцениваются как True и False (которые относятся к специальному
все типы данных называются Boolean ). Например,
если переменная установлена на результат этих тестов, эта переменная
будет иметь логическое значение:
>>> Х = (2 < 3) >>> Х Истинный
Но Python, как и многие другие языки программирования, позволяет
различные типы, чтобы произойти как тест в если пункт .
В большинстве случаев объекты разных типов ведут себя как Правда в тестах. Но у каждого типа Python есть некоторые
особые случаи, которые ведут себя как False . Следующее
list суммирует, какие объекты Python ведут себя как False :
Нет[Подробнее об этом особом объекте Python ниже]Ложьноль любого числового типа, например, 0, 0L, 0.
 0, 0j.
0, 0j.любая пустая последовательность, например,
'', (), [].любой пустой словарь, например,
{}.комплект([])
Так, например, следующий пункт if будет
правильно определить, является ли контейнер L пусто:
, если Л:
print('L не пусто`)
еще:
print('L пусто')
4.3.1. Особый случай
Нет Python имеет специальный объект с собственным типом данных, который называется Нет .
Вы можете думать об этом как о значении, которое означает без значения .
смысл иметь что-то подобное в том, что это позволяет
программа, предполагающая, что выражение имеет значение,
даже если это иногда не так.
Например, переменная , результат , может быть инициализирована значением None ,
с пониманием
что он получит значимое значение в какой-то момент во время вычислений,
и до этого момента имя результат по-прежнему можно будет использовать, не вызывая ИмяОшибка .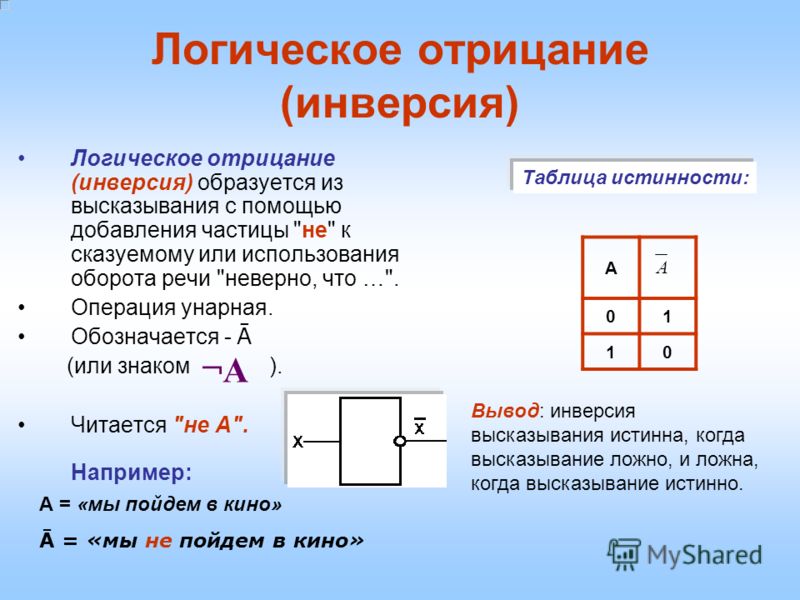 Например, в тесте он может выглядеть следующим образом:
Например, в тесте он может выглядеть следующим образом:
, если результат: вернуть результат
Это иллюстрирует свойство Нет представлен выше. В тесте он ведет себя как False .
Примечания: распечатывается как ничего.
4.3.2. Python: выражения против инструкций 91 181
В принципе выражение, следующее за , если должно
быть тестом и, следовательно, должен иметь логические значения, либо Правда или Ложь . Но, как мы только что видели, объекты Python
в целом можно интерпретировать так, как если бы они были булевыми значениями,
так на самом деле
многие различные виды выражений могут вполне разумно следовать если .
Но есть одна вещь, которая не может следовать за , если ,
простой оператор . Вот список
простых операторов Python, которые мы рассмотрели
пока (есть еще).
Тип заявления | Пример |
|---|---|
Назначение | Х = 3 |
Пропуск | пропуск |
Дел | del freq_dict['прогулка'] |
Возврат | результат возврата |
Перерыв | перерыв |
Простой оператор
инструкция Python, которая не
вернуть что-либо, по дизайну языка.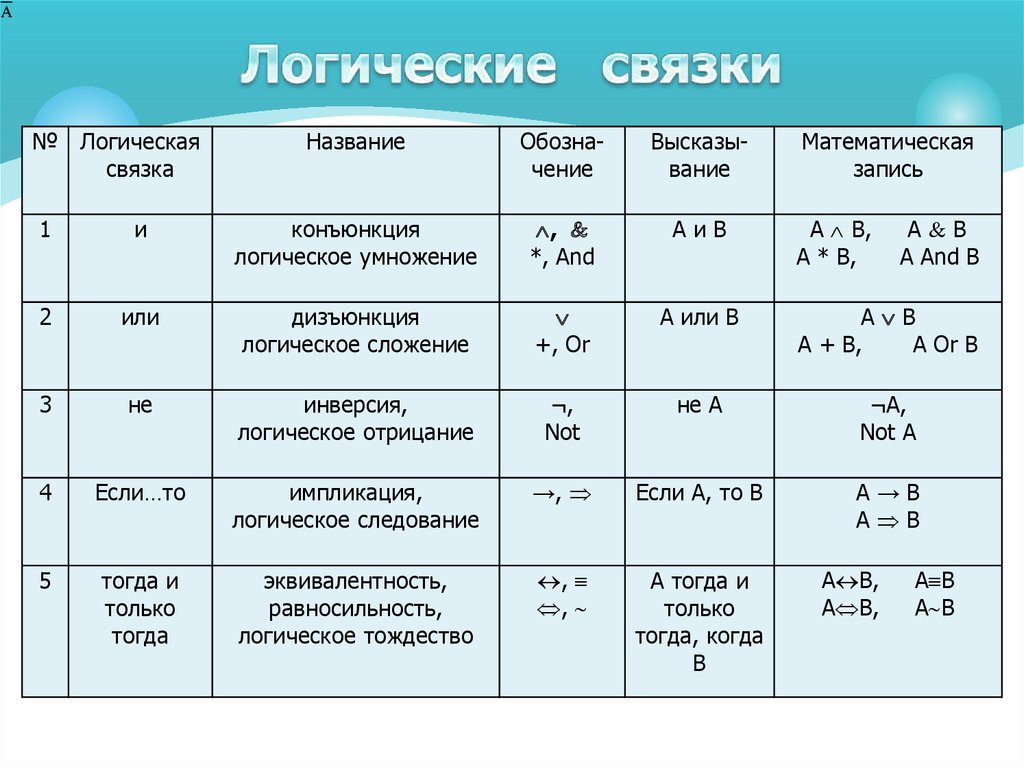 Интуитивно это
потому что каждый задуман как действие программы.
Оценка любого из них в приглашении Python
таким образом, не возвращает никакого результата, потому что для Python нет значения
сообщить:
Интуитивно это
потому что каждый задуман как действие программы.
Оценка любого из них в приглашении Python
таким образом, не возвращает никакого результата, потому что для Python нет значения
сообщить:
>>> Х = 3 >>> Х 3
Первая строка является оператором, и интерпретатор Python возвращает ничего; второй интерпретируется как просьба вернуть значение 9SyntaxError: неверный синтаксис
Конечно, имелась в виду проверка на равенство с использованием == .
Таким образом:
Х == 3
и:
означают совсем другое. Первый — это утверждение, не имеющее значения;
он просто указывает Python определить значение имени X .
быть равным 3. Второй тест возвращает True или False .
в зависимости от того, равно ли значение переменной X 3 или нет.
Первая — синтаксическая ошибка при следовании если ; второй
является действительным тестом.
4.3.3. Условные выражения
if-then или условная конструкция тесно связана с
другая конструкция Python называется условное выражение .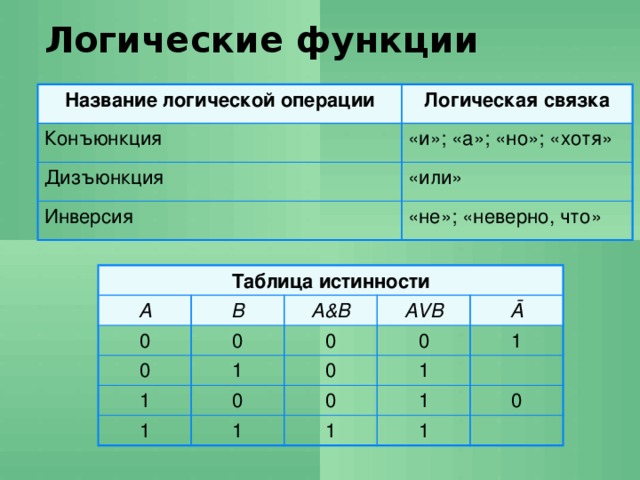
Иногда нам нужно выполнить условное присваивание; мы хотим назначить одно значение для имени при одном условии и другое значение под другим условием. Основываясь на том, что мы уже рассмотрели, задание можно сделать так:
если условие: х = истинное_значение еще: х = ложное_значение
Но этот фрагмент корректного кода Python имеет небольшую проблему с читабельностью;
похоже на любую из рассмотренных нами условных конструкций
в последних двух разделах и не дает понять, что основная задача
этого фрагмента кода состоит в том, чтобы присвоить имени значение x .
Соответственно, Python предоставляет для этого другую более удобочитаемую конструкцию:
позволяя переписать приведенный выше код следующим образом:
x = true_value, если условие еще false_value
Идиома Python справа от = — это выражение (как
это должно быть, чтобы быть законным).
Как отмечалось выше, выражение Python — это то, что имеет значение. Значение выражения выше зависит от текущего
истинность или ложность
Значение выражения выше зависит от текущего
истинность или ложность условие .
Следовательно, это условное выражение .
В документации, которая вводит это
строительство,
Гвидо ван Россум (изобретатель Python
и доброжелательный диктатор на всю жизнь) предлагает всегда использовать его с
круглые скобки, чтобы сделать границы выражения четкими:
x = (true_value, если условие еще false_value)
При обычном использовании значение else покрывает необычный
случай. Например, пусть doc будет строкой, которую нужно записать в файл.
В некоторых случаях полезно заканчивать файлы символом новой строки,
создание окончательной пустой строки, но мы не хотим этого делать, если
нет контента для записи, поэтому мы могли бы написать:
содержимое = ((doc + '\n') если doc еще '')
Таким образом, содержание имеет добавленный символ новой строки, если doc непусто. В противном случае это пустая строка.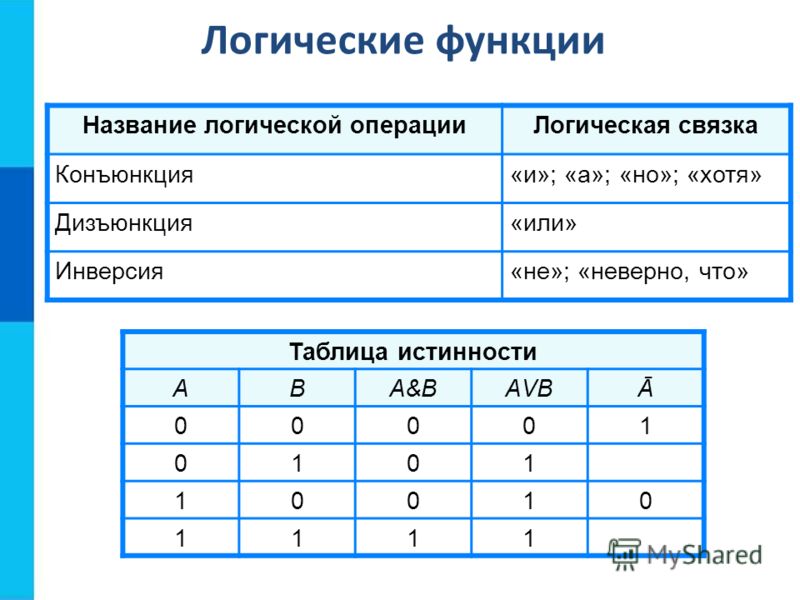


 iterator()
}
}
def составной = новый составной объект ()
утверждать составной*.id == [1,2]
утверждать составное*.имя == ['Foo','Bar']
iterator()
}
}
def составной = новый составной объект ()
утверждать составной*.id == [1,2]
утверждать составное*.имя == ['Foo','Bar'] 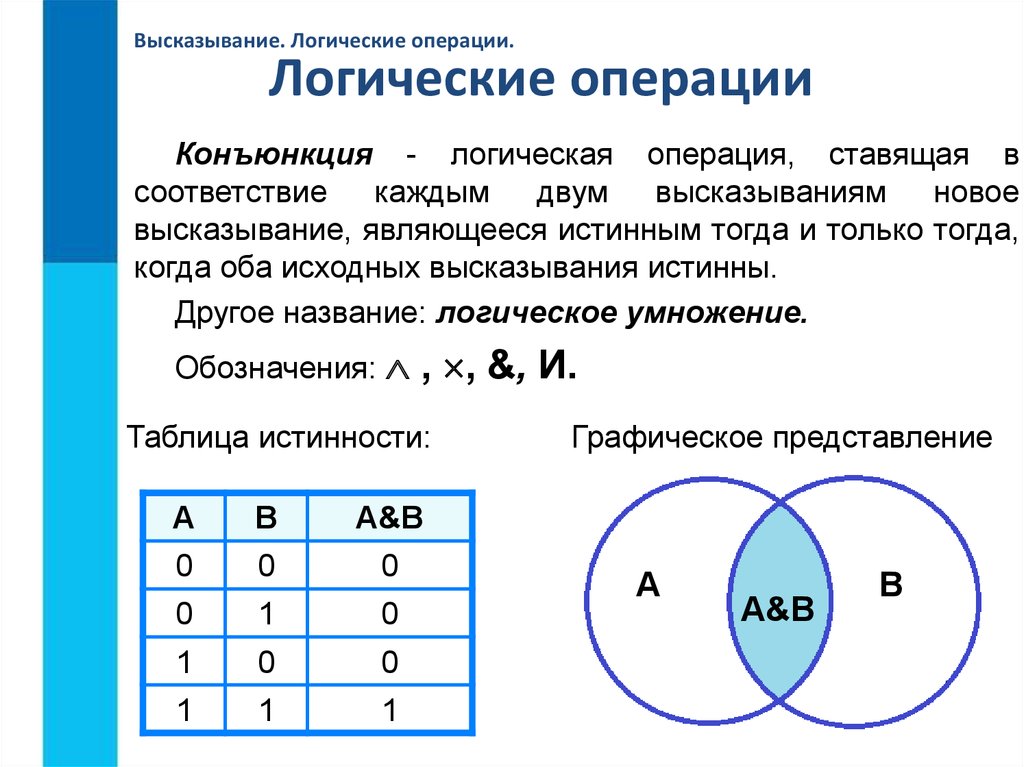 collectNested{ it.model }
утверждать модели == [['408', '508'], ['Clio', 'Captur']]
collectNested{ it.model }
утверждать модели == [['408', '508'], ['Clio', 'Captur']]  lang.Range
lang.Range  .2] == [0,1,4] (3)
список[0..2] = [6,6,6] (4)
список утверждений == [6,6,6,3,4] (5)
.2] == [0,1,4] (3)
список[0..2] = [6,6,6] (4)
список утверждений == [6,6,6,3,4] (5)  name == 'Боб' (7)
name == 'Боб' (7) 
 call(2) == 4 (2)
утверждать mc(2) == 4 (3)
call(2) == 4 (2)
утверждать mc(2) == 4 (3)  В противном случае возвращает
В противном случае возвращает 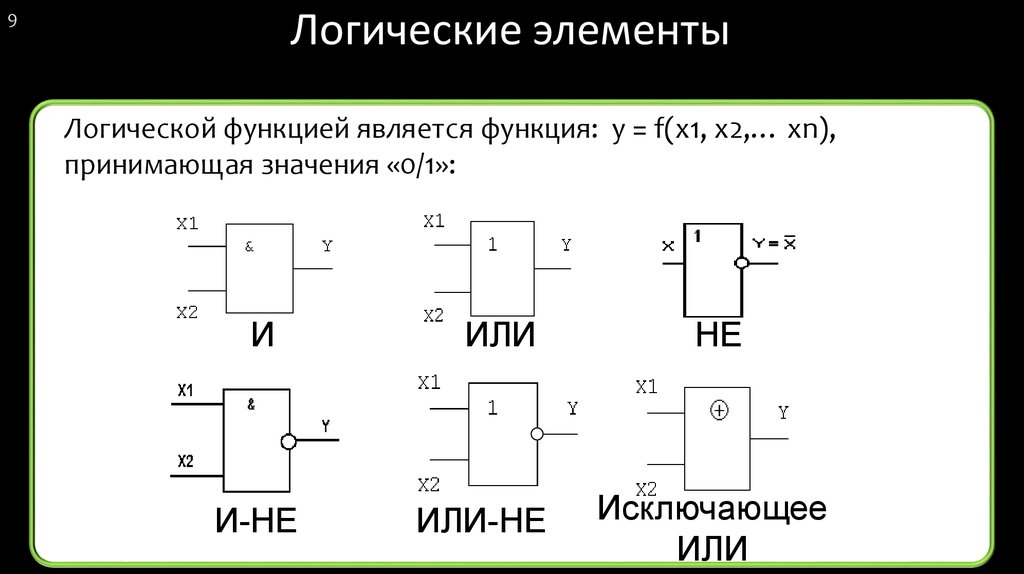 добавить(слово)
добавить(слово)
 0, 0j.
0, 0j.