Формулы и Задачи (Информатика 10) — Школа N61 г.Ульяновска
Формулы
N = 2i
N — мощность алфавита (количество знаков в алфавите)
i — информационный вес символа алфавита (количество информации в одном символе)
I — количество информации, содержащееся в выбранном сообщении (информационный объем сообщения)
K — число символов в сообщении
i — информационный вес символа (количество информации в одном символе)
Q — количество разных сообщений
N — количество символов
L — длина сообщения
Формула Хартли:
I = log2N
I — количество информации, содержащееся в выбранном сообщении
N — количество сообщений
Римская система счисления
I – 1 (палец),
V – 5 (раскрытая ладонь, 5 пальцев),
X – 10 (две ладони),
L – 50,
C – 100 (Centum),
D – 500 (Demimille),
M – 1000 (Mille)
Перевод чисел из других систем счисления в десятичную систему счисления
Развернутая запись целого числа:
a3a2a1a
Правило перевода числа из любой системы счисления в десятичную систему счисления — умножаем каждую цифру исходного числа на основание системы счисления в степени разряда, в котором находится эта цифра, а затем всё складываем.
Запись через схему Горнера:
a3a2a1a0 = ((a3 * p + a2) * p + a1) * p + a0
p — основание системы счисления в котором представлено число.
Пример:
637510 = 6 * 103
637510 = ((6 * 10 + 3) * 10 + 7) * 10 + 5
12345 = 1 * 53 + 2 * 52 + 3 * 51 + 4 * 50 = 19410
12345 = ((1 * 5 + 2) * 5 + 3) * 5 + 4 = 19410
Развернутая запись дробного числа:
0,a1a2a3a4 = a1*p-1 + a2*p-2 + a3*p-3 + a4*p-4
Запись через схему Горнера:
0,a1a2a3a4 = p-1 * (a1 + p-1
p * (0,a1a2a3a4) = a1 + p-1 * (a2 + p-1 * (a3 + p-1 * a4))
p — основание системы счисления в котором представлено число.
Пример:
0,6375 = 6 * 10-1 + 3 * 10-2 + 7 * 10-3 + 5 * 10-4
0,6375 = 10-1 * (6 + 10-1 * (3 + 10
0,12345 = 1 * 5-1 + 2 * 5-2 + 3 * 5-3 + 4 * 5-4
0,12345 = 5-1 * (1 + 5-1 * (2 + 5-1 * (3 + 5-1 * 4)))
Задачи
Алфавитный подход к измерению количества информации
Определить количество информации в 10 страницах текста (на каждой странице 32 строки по 64 символа) при использовании алфавита из 256 символов.
- информационная ёмкость символа: 256 = 28 =>> i = 8 бит = 1 байт
-
количество символов на странице:
32 * 64 = 25 -
общее количество символов:
L = 10 * 211 -
информационный объём сообщения:
I = L * i = 10 * 211 * 1 байт = 20 Кбайт
Системы счисления
X10 X16 X8 X2
0 0 0 0
1 1 1 1
2 2 2 10
3 3 3 11
4 4 4 100
5 5 5 101
6 6 6 110
7 7 7 111
8 8 10 1000
9 9 11 1001
10 A 12 1010
11 B 13 1011
12 C 14 1100
13 D 15 1101
14 E 16 1110
15 F 17 1111
16 10 20 10000
17 11 21 10001
18 12 22 10010
19 13 23 10011
20 14 24 10100
21 15 25 10101
22 16 26 10110
23 17 27 10111
24 18 30 11000
25 19 31 11001
26 1A 32 11010
27 1B 33 11011
28 1C 34 11100
29 1D 35 11101
30 1E 36 11110
31 1F 37 11111
32 20 40 100000
Логические операции
Логической операцией

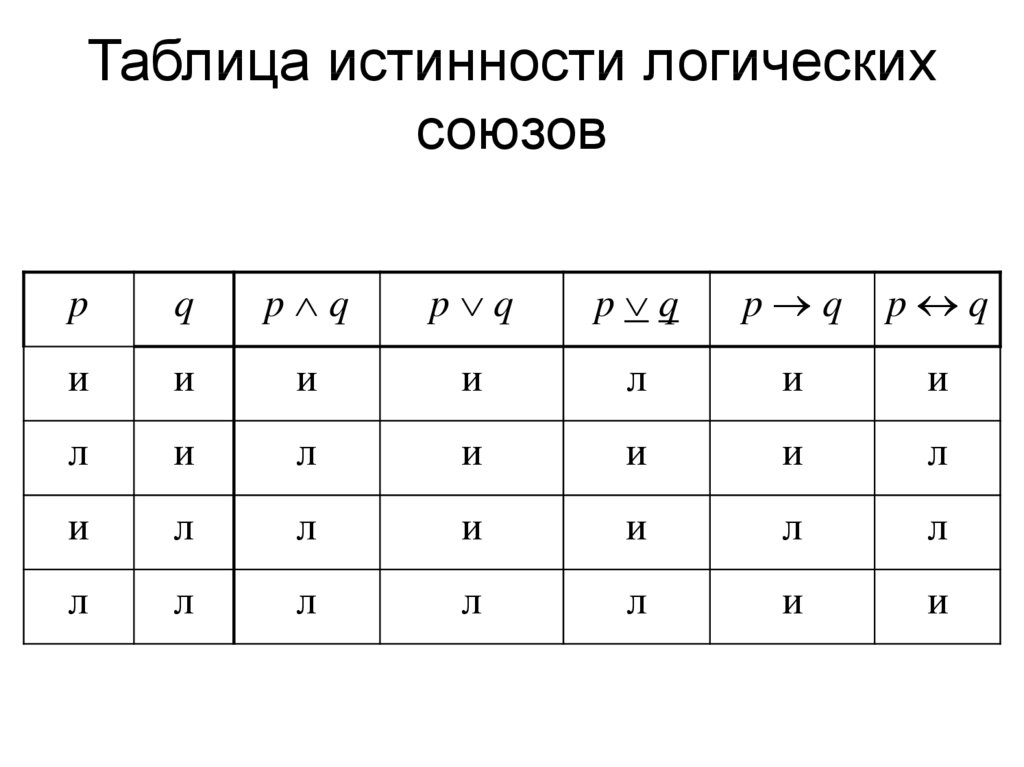
Зависимости между логическими функциями (операциями) и логическими переменными устанавливаются с помощью таблиц истинности. Используются следующие логические операции: НЕ, И, ИЛИ, исключающее ИЛИ, тождество.
Логическая операция НЕ (инверсия, операция логического отрицания). Действие, которое определяется операцией НЕ произойдет, если отсутствует фактор его определяющий.
Таблица истинности для операции НЕ имеет вид:
| A | |
| 0 | 1 |
| 1 | 0 |
Действие, связанное с операцией НЕ можно записать следующим образом:
Логическая операция И (конъюнкция, операция логического умножения). Действие, которое определяется операцией И произойдет, если выполняются все влияющие на него факторы (условия).
Логическая операция ИЛИ (дизъюнкция, операция логического сложения). Действие, которое определяется операцией ИЛИ произойдет, если выполняются хотя бы одно (любое), определяющее его условие.
Таблица истинности для операции ИЛИ имеет вид:
| A | B | X=A v B |
| 0 | 0 | 0 |
| 0 | 1 | |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Действие, связанное с операцией ИЛИ можно записать следующим образом:
X = A + B = A v B
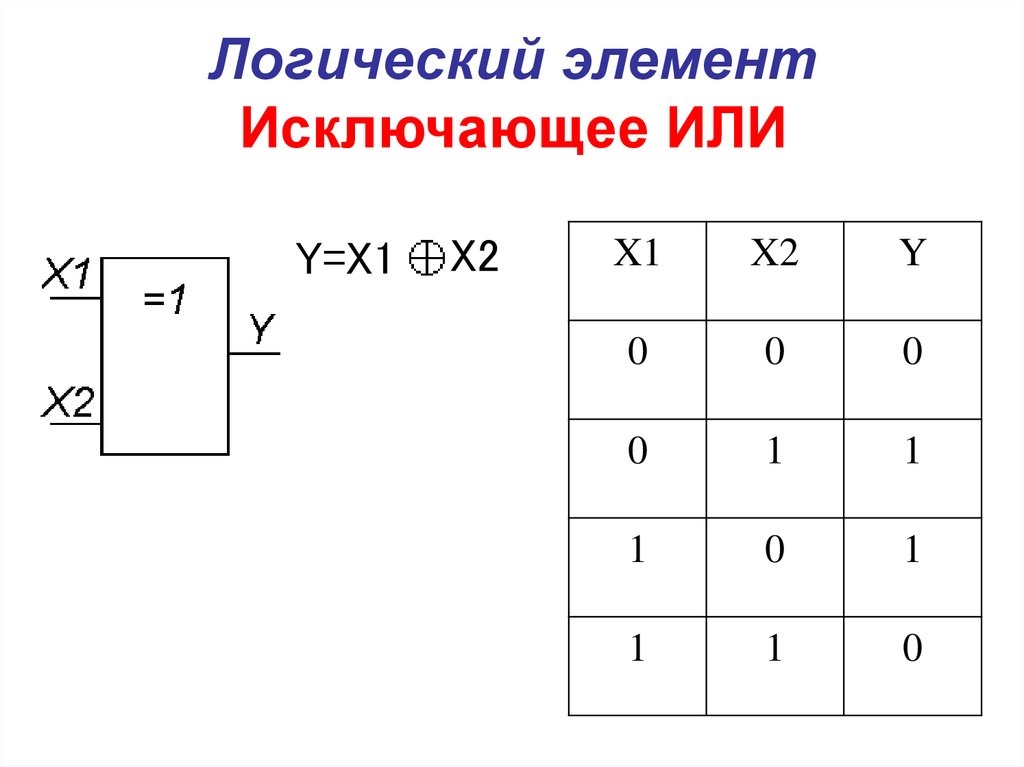
Логическая операция Исключающее ИЛИ. Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.
Операция Исключающее ИЛИ осуществляет суммирование по модулю два т.е. без учета переноса в старший разряд.
Таблица истинности имеет вид:
| A | B | X=AB |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Действие, связанное с операцией Исключающее ИЛИ можно записать следующим образом:
X = A B
Действие, связанное с операцией
X = A → B
Таблица истинности Импликации имеет вид:
| A | B | A → B |
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Операция тождество.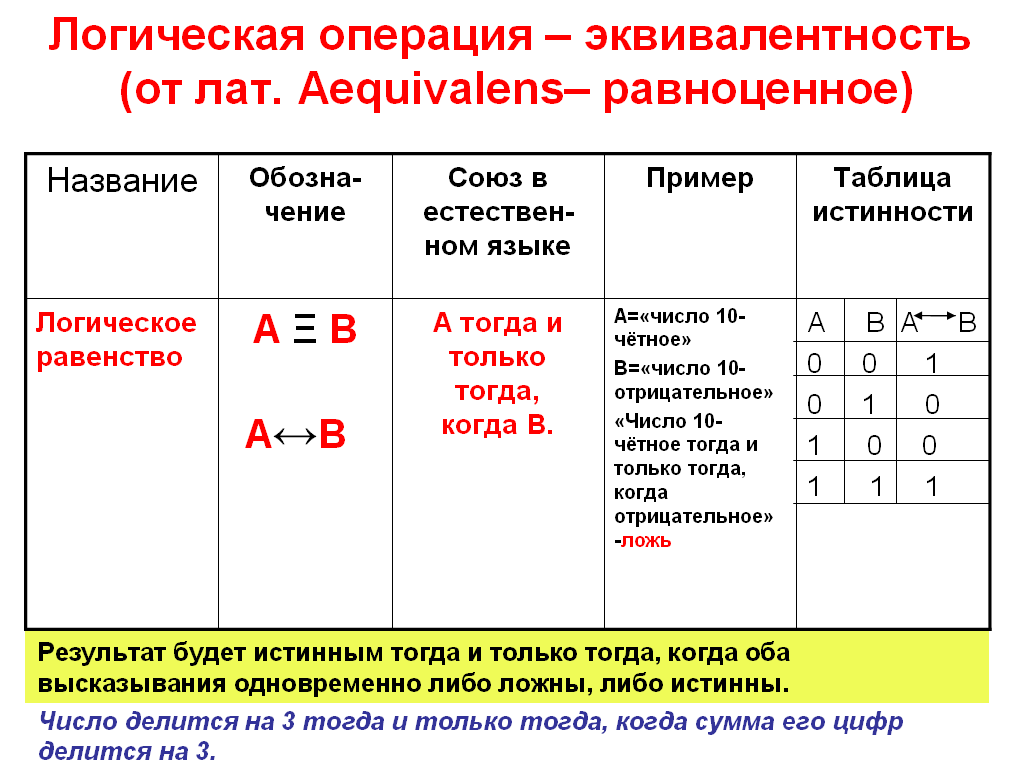 Операция тождество определяет тождественность аргументов.
Операция тождество определяет тождественность аргументов.
Таблица истинности для операции тождество имеет вид:
| A | B | A Ξ B |
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Действие, связанное с операцией тождество можно записать следующим образом:
X = A Ξ B
Диаграммы Венна (круги Эйлера)
Поиск номера сети
Необходимо найти номер сети по IP-адресу 12. 16.196.10 и маске 255.255.224.0.
16.196.10 и маске 255.255.224.0.
| маска сети | 255. | 255. | 224. | 0 | |
| IP-адрес | 12. | 16. | 196. | 10 | — ip-адрес (узла, компьютера и т.п.) |
| IP-адрес | 0000 1100. | 0001 0000. | 1100 0100. | 0000 1010 | |
| маска сети | 1111 1111. | 1111 1111. | 1110 0000. | 0000 0000 | |
| адрес сети | 0000 1100. | 0001 0000. | 110x xxxx. | xxxx xxxx | — эта часть относится к адресу сети — она взята из ip-адреса, но взяты те цифры, напротив которых стоят единицы остальные цифры справа надо дополнить нулями, чтобы общее число цифр стало равным 32. Получится следующее: |
| адрес сети | 0000 1100.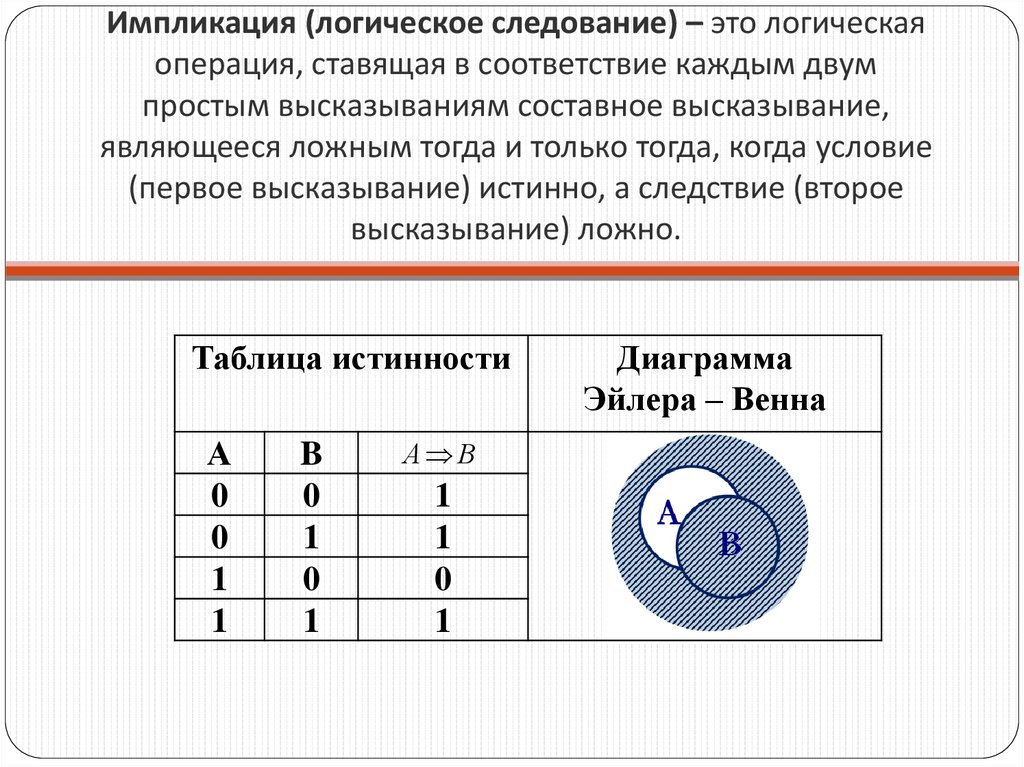 | 0001 0000. | 1100 0000. | 0000 0000 | — полный адрес сети теперь каждую октаду (последовательность из 8 цифр, разделены точками) переводим в десятичный вид. Получаем: |
| адрес сети | 12. | 16. | 192. | 0 | — полный адрес сети (в десятичном виде) |
Логические операторы | Основы Python
Для перемещения по курсу нужно зарегистрироваться
1. Введение ↳ теория
2. Hello, World! ↳ теория / тесты / упражнение
3. Инструкции ↳ теория / тесты / упражнение
4. Арифметические операции ↳ теория / тесты / упражнение
5. Ошибки оформления — синтаксис и линтер ↳ теория / тесты / упражнение
6. Строки ↳ теория / тесты / упражнение
7. Переменные ↳ теория / тесты / упражнение
8. Выражения в определениях ↳ теория / тесты / упражнение
9. Именование ↳ теория / тесты / упражнение
10. Интерполяция
↳
теория
/
тесты
/
упражнение
Интерполяция
↳
теория
/
тесты
/
упражнение
11. Извлечение символов из строки ↳ теория / тесты / упражнение
12. Срезы строк ↳ теория / тесты / упражнение
13. Типы данных ↳ теория / тесты / упражнение
14. Неизменяемость и примитивные типы ↳ теория / тесты / упражнение
15. Функции и их вызов ↳ теория / тесты / упражнение
16. Сигнатура функции ↳ теория / тесты / упражнение
17. Вызов функции — выражение ↳ теория / тесты / упражнение
18. Детерминированность ↳ теория / тесты / упражнение
19. Стандартная библиотека ↳ теория / тесты / упражнение
20. Свойства и методы ↳ теория / тесты / упражнение
21. Цепочка методов ↳ теория / тесты / упражнение
22. Определение функций ↳ теория / тесты / упражнение
23. Возврат значений ↳ теория / тесты / упражнение
24. Параметры функций ↳ теория / тесты / упражнение
25. Необязательные параметры функций ↳ теория / тесты / упражнение
26. Именованные аргументы ↳ теория / тесты / упражнение
27. Окружение
↳
теория
/
тесты
/
упражнение
Окружение
↳
теория
/
тесты
/
упражнение
28. Логика ↳ теория / тесты / упражнение
29. Логические операторы ↳ теория / тесты / упражнение
30. Результат логических операций ↳ теория / тесты / упражнение
31. Условные конструкции ↳ теория / тесты / упражнение
32. Оператор Match ↳ теория / тесты / упражнение
33. Цикл while ↳ теория / тесты / упражнение
34. Агрегация данных ↳ теория / тесты / упражнение
35. Обход строк ↳ теория / тесты / упражнение
36. Условия внутри тела цикла ↳ теория / тесты / упражнение
37. Цикл for ↳ теория / тесты / упражнение
38. Отладка ↳ теория / тесты / упражнение
39. Модули ↳ теория / тесты / упражнение
40. Модули поглубже ↳ теория / тесты / упражнение
41. Пакеты ↳ теория / тесты / упражнение
42. Модуль random ↳ теория / тесты / упражнение
43. Кортежи ↳ теория / тесты / упражнение
44. История развития языка Python ↳ теория / тесты
Испытания
1. Фибоначчи
2. Сумма двоичных чисел
Сумма двоичных чисел
3. Физзбазз
4. Классификация отрезков
5. Вращение троек
6. Разница углов
7. Степени тройки
8. Фасад
9. Счастливый билет
10. Идеальные числа
11. Инвертированный регистр
12. Счастливые числа
13. Шифрование
Порой обучение продвигается с трудом. Сложная теория, непонятные задания… Хочется бросить. Не сдавайтесь, все сложности можно преодолеть. Рассказываем, как
Не понятна формулировка, нашли опечатку?
Выделите текст, нажмите ctrl + enter и опишите проблему, затем отправьте нам. В течение нескольких дней мы улучшим формулировку или исправим опечатку
Что-то не получается в уроке?
Загляните в раздел «Обсуждение»:
- Изучите вопросы, которые задавали по уроку другие студенты — возможно, ответ на ваш уже есть
- Если вопросы остались, задайте свой. Расскажите, что непонятно или сложно, дайте ссылку на ваше решение. Обратите внимание — команда поддержки не отвечает на вопросы по коду, но поможет разобраться с заданием или выводом тестов
- Мы отвечаем на сообщения в течение 2-3 дней.
 К «Обсуждениям» могут подключаться и другие студенты. Возможно, получится решить вопрос быстрее!
К «Обсуждениям» могут подключаться и другие студенты. Возможно, получится решить вопрос быстрее!
Подробнее о том, как задавать вопросы по уроку
Что такое символ логического отрицания?
К
- Рахул Авати
Символ логического отрицания используется в булевой алгебре для обозначения того, что истинностное значение следующего утверждения перевернуто. Символ (¬) напоминает черточку с хвостиком или верхнюю половину прямоугольника. Символ арифметического вычитания (-) и тильда (~) также используются для обозначения логического отрицания.
Символ логического отрицания выглядит как черточка с хвостиком или верхняя половина прямоугольника. Символ отрицания является унарным логическим оператором. Он просто переворачивает истинностное значение данного утверждения. Таким образом, если утверждение представлено как A, то ¬A является логической противоположностью или отрицанием A.
Таким образом, если утверждение представлено как A, то ¬A является логической противоположностью или отрицанием A.
Таким образом, ¬A = не A
Если A = истина, ¬A = ложь
Если A = ложь, ¬A = истина
Кроме того, ¬(¬A) = A
Символ ¬ часто встречается внутри сложных логических выражений или перед ними. Тем не менее, его самое простое использование — с одним предложением.
Если А: Небо голубое, то
¬А: Небо не голубое, или неверно, что небо голубое
Правила использования символа логического отрицания усложняются, когда этот символ появляется в сложных операторах.
Если A: Небо голубое, и
Если B: Трава зеленая, то
¬(AV B): Ни небо голубое, ни трава зеленая
Поскольку символы ~ и ¬ могут использоваться взаимозаменяемо, приведенное выше утверждение также может быть представлено логически как ~(AV B). Вариант использования любого символа зависит от предпочтений пользователя или контекста для обозначения отрицания.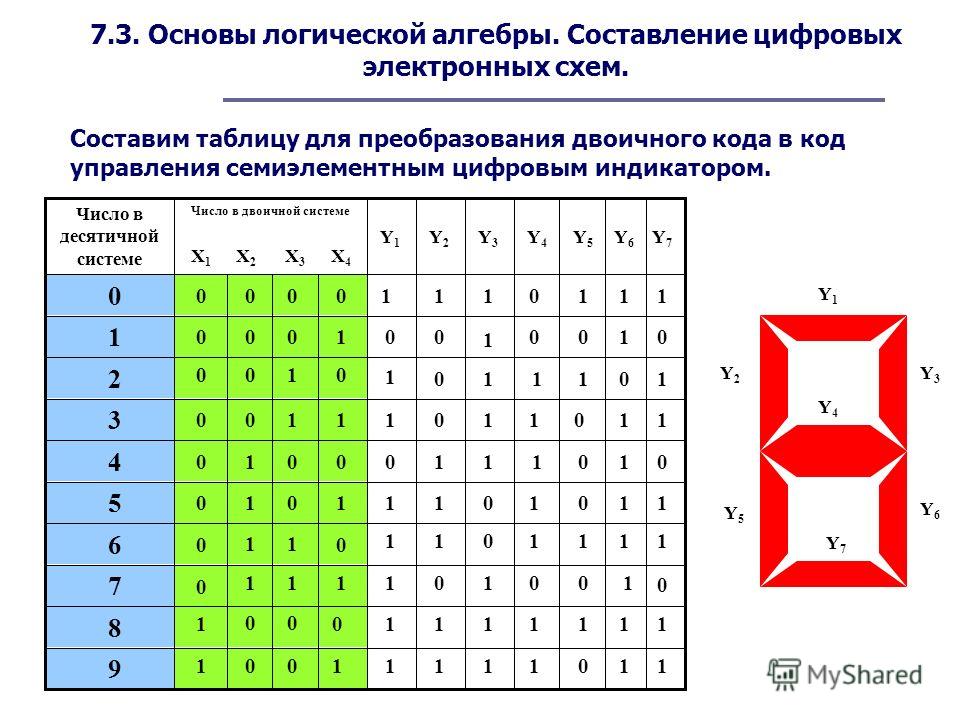
В обычном повседневном языке утверждения могут быть переданы полными повествовательными предложениями, такими как следующие:
- Небо голубое.
- Идет дождь.
- Футбол — популярный во всем мире вид спорта.
Однако, чтобы выразить логические отношения между такими утверждениями, становится обременительным выписывать все предложение при каждом появлении каждого утверждения. Таким образом, конкретные отдельные заявления представлены с использованием заглавных букв как операторные константы .
Таким образом, A, B и C могут использоваться для представления предыдущих утверждений:
- А: Небо голубое.
- Б: Идет дождь.
- C: Футбол — популярный во всем мире вид спорта.
Строчные буквы алфавита, начинающиеся с p, используются в качестве переменных оператора . Таким образом, можно сказать: «Рассмотрите любое утверждение p» или «Предположим, что пара утверждений p и q оба верны».
Символ логического отрицания ¬ или ~ является одним из операторные связки или операторы, которые можно использовать для формирования новых составных операторов из двух или более операторов. Он просто переворачивает истинностное значение любого утверждения, перед которым оно появляется. Это утверждение может быть простым или составным.
Итак, если оригинал верен, утверждение ¬ ложно. Но если оригинал ложен, утверждение ¬ становится истинным. Его значение может быть представлено этой таблицей истинности:
| р | ¬p |
| Правда | Ложь |
| Ложь | Правда |
Примеры ¬ с простыми операторами
p: Лев рычит
¬p: Лев не рычит
p: Солнце не светит
¬p: Солнце светит
Примеры ¬ со сложными операторами
p: Лев рычит
q: Птицы щебечут
¬(p V q): Ни лев не рычит, ни птицы не щебечут
p: лев рычит
q: птицы не щебечут
¬(p V q): лев не рычит, а птицы щебечут
Английское выражение «Это не так, что…» выполняет ту же функцию, что и символ логического отрицания. Однако даже одного слова вместо достаточно, чтобы передать отрицание.
Однако даже одного слова вместо достаточно, чтобы передать отрицание.
В сложных предложениях отрицание всегда выполняется перед логическим И и логическим ИЛИ. Далее, как и в алгебре — по правилу BODMAS, или порядку операций — все операции внутри скобок выполняются первыми.
ASCII-код символа логического отрицанияАмериканский стандартный код для обмена информацией (ASCII), созданный в 1963 году, является широко используемым и общепринятым форматом кодирования символов для текстовых данных в вычислительных системах. С 1969 года ASCII также используется в качестве стандарта для интернет-данных.
В системе ASCII используются уникальные значения для 128 буквенных символов (прописные и строчные буквы от A до Z), цифровых и специальных символов, а также управляющих кодов. Код ASCII для символа логического отрицания — 170. Он является частью группы ASCII 9.0033 расширенных символа . Символу ¬ предшествует ® на 169, а за ним ½ на 171.
Код ASCII для символа логического отрицания — 170. Он является частью группы ASCII 9.0033 расширенных символа . Символу ¬ предшествует ® на 169, а за ним ½ на 171.
Символ ¬ можно ввести на компьютерах под управлением Windows с помощью следующих сочетаний клавиш:
- Удерживайте клавишу Alt на клавиатуре.
- Удерживая нажатой клавишу, введите число 170. (Как упоминалось ранее, 170 — это номер буквы или символа ¬ в таблице ASCII.)
- Отпустите клавишу Alt.
Значение Unicode U+00AC соответствует символу логического отрицания ¬. Альтернативный код определяется как 0172; ввод 0172 при нажатой клавише Alt приведет к вводу этого символа в Word или другом документе. Когда клавиша Alt отпущена, символ вставляется в документ.
Оператор логического отрицания в JavaScript В JavaScript оператор логического отрицания выражается как ! (логическое НЕ). Также известен как логическое дополнение оператор переводит истину в ложь и наоборот. Обычно используется с логическими или булевыми значениями.
Также известен как логическое дополнение оператор переводит истину в ложь и наоборот. Обычно используется с логическими или булевыми значениями.
При использовании с небулевыми значениями возвращает false , если его единственный операнд можно преобразовать в true. В противном случае возвращается true . Если значение можно преобразовать в истинное, оно называется правдивым , а если его можно преобразовать в ложное, оно называется ложным .
Поскольку возвращаемое значение всегда можно преобразовать в логический примитив, оператор ! оператор считается логическим оператором, даже если его можно использовать с операндами, не являющимися логическими значениями.
См. также: Математические символы
Последнее обновление: август 2022 г.
Продолжить чтение О символе логического отрицания- К какому проценту покрытия юнит-тестами должны стремиться команды?
- 5 ярлыков Windows 10 для администраторов рабочего стола
- Почему 8 примитивных типов данных Java не являются объектами
- 11 языков облачного программирования, которые нужно знать разработчикам
- 5 основных языков программирования для специалистов по кибербезопасности
видео с возможностью покупки
Видео с возможностью покупки — это способ, с помощью которого потребители находят товары и совершают покупки по ссылкам в видео.
Сеть
- входная фильтрация
Ingress filtering — это метод, используемый предприятиями и интернет-провайдерами для предотвращения проникновения подозрительного трафика в …
- многопользовательский MIMO
Многопользовательский MIMO или MU-MIMO — это технология беспроводной связи, в которой используется несколько антенн для улучшения связи за счет …
- богон
Богон — это незаконный адрес интернет-протокола, который попадает в набор IP-адресов, которые официально не назначены…
Безопасность
- судо (су ‘делать’)
Sudo — это утилита командной строки для Unix и операционных систем на базе Unix, таких как Linux и macOS.
- E-Sign Act (Закон об электронных подписях в глобальной и национальной торговле)
Закон об электронных подписях (Закон об электронных подписях в глобальной и национальной торговле) — это федеральный закон США, в котором указывается, что в .
 ..
.. - личная информация (PII)
Информация, позволяющая установить личность (PII), — это любые данные, которые потенциально могут идентифицировать конкретное лицо.
ИТ-директор
- управление корпоративными проектами (EPM)
Управление корпоративными проектами (EPM) представляет собой профессиональные практики, процессы и инструменты, используемые для управления несколькими …
- Управление портфелем проектов: руководство для начинающих
Управление портфелем проектов — это формальный подход, используемый организациями для выявления, определения приоритетов, координации и мониторинга проектов …
- SWOT-анализ (анализ сильных и слабых сторон, возможностей и угроз)
SWOT-анализ представляет собой основу для выявления и анализа сильных и слабых сторон организации, возможностей и угроз.

HRSoftware
- проверка сотрудников
Проверка сотрудников — это процесс проверки, проводимый работодателями для проверки биографических данных и проверки информации о новом…
- Эффект хоторна
Эффект Хоторна — это изменение поведения участников исследования в ответ на их знание о том, что они …
- командное сотрудничество
Совместная работа в команде — это подход к общению и управлению проектами, который делает упор на командную работу, новаторское мышление и равенство …
Служба поддержки клиентов
- живой чат (живая поддержка)
Живой чат (поддержка в реальном времени) — это технология, которая предоставляет компаниям возможность взаимодействовать с пользователями, когда они посещают …
- отток клиентов (отток клиентов)
Отток клиентов, также называемый оттоком клиентов, — это количество платящих клиентов, которые не стали постоянными клиентами.

- разрешение личности
Разрешение идентификационных данных — это процесс управления данными, который связывает поведение клиента в Интернете с его уникальной идентификацией путем сбора …
Пропозициональная логика | Brilliant Math & Science Wiki
Содержание
- Основные понятия — определения
- Обзор таблицы истинности
- Связки
- Хорошо сформированные формулы
- Тавтологии, противоречия и случайности
- Логическая эквивалентность
- Валидность и согласованность
- Ограничения пропозициональной логики
- Смотрите также
В логике высказываний высказывание (или высказывание ) представлено символом (или буквой ), связь которого с другими высказываниями определяется набором символов (или связок ). Утверждение описывается его значением истинности , которое либо верно , либо ложно .
Утверждение описывается его значением истинности , которое либо верно , либо ложно .
\(\color{Red} \textbf{Предложения}\)
Предложение — это утверждение, взятое целиком, которое либо истинно, либо ложно. Например, предложение может быть:
Все слоны зеленые.
В отличие от силлогистической логики, в логике высказываний это утверждение берется целиком, обычно представленное символом, и нас интересует только то, истинно оно или ложно, а не отдельные термины в утверждении.
\(\color{Red} \textbf{Буквы предложения}\)
В логике высказываний предложение по соглашению обозначается заглавной буквой, обычно жирным шрифтом. Например, приведенное выше предложение может быть представлено буквой 9.0339 А .
Ответ: Все слоны зеленые.
\(\color{Red} \textbf{Значение истинности}\)
Каждому из утверждений присваивается значение истинности из либо истинно , либо ложно . В других областях (например, в логических элементах компьютера) эти значения задаются двоичными представлениями \(1\) (истина) и \(0\) (ложь).
В других областях (например, в логических элементах компьютера) эти значения задаются двоичными представлениями \(1\) (истина) и \(0\) (ложь).
Мы говорим, что \(v(P)\) оценивает предложение \(P\), т. е. возвращает его значение истинности .
\(\color{Red} \textbf{Connectives}\)
В логике высказываний отношения между предложениями представлены связками .
Существует пять различных соединений , представленных в следующей таблице: \)
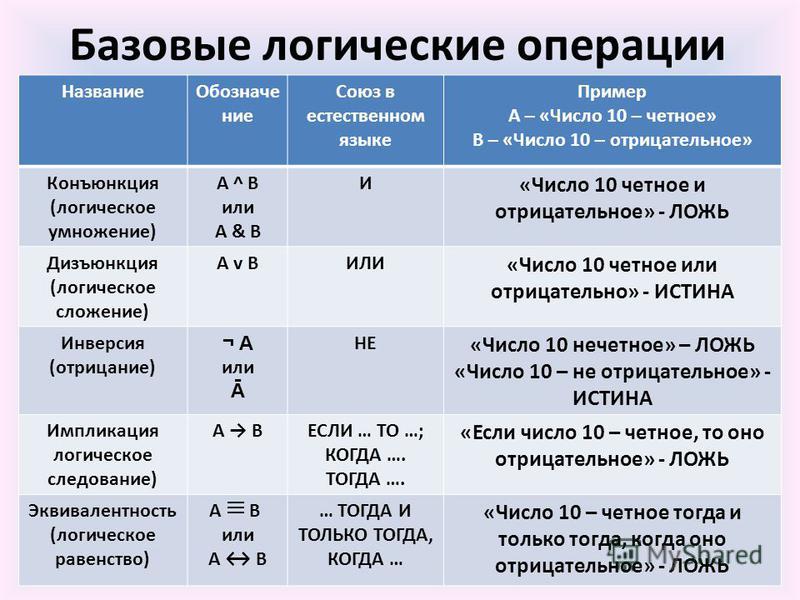 0014
0014Сначала мы представим два предложения в виде письма-предложения :
.- А : Дождь
- B : Джейк не пойдет в школу пешком
Тогда мы будем использовать условную связку, чтобы сделать наше утверждение.
А \(\к\) Б \(_\квадрат\)
Для уточнения смысла предложения или связки используется таблица истинности .
Таблицы истинности — это способ визуализации значений истинности предложений. Значение true представлен как « 1 «, а значение false представлен как « 0 «.
Например, рассмотрим следующие предложения:
- A : Марти носит зеленые ботинки.
- B : У Марти есть собака.
- C : Марти носит зеленые сапоги, и у Марти есть собака.
Предложение C принимает следующие значения истинности:
- Если Марти не носит зеленые сапоги и у него нет собаки, то предложение C равно ложному .

- Если Марти не носит зеленых сапог, но у него есть собака, то предложение C ложно .
- Если Марти носит зеленые сапоги, но у него нет собаки, то предложение C является ложным .
- Если Марти носит зеленые сапоги и у него есть собака, то предложение C верно .
Представленные в таблице истинности , у нас есть по одной строке для каждого из приведенных выше утверждений (включая все возможные комбинации Марти в зеленых ботинках и/или с собакой), и каждый столбец представляет возможные состояния каждого из утверждений. предложения A, B и C выше.
Таким образом, четыре приведенных выше утверждения представлены в следующей таблице истинности:
Соединители — это логические символы, выражающие отношение между предложениями.
Есть пять основных связок:
- Отрицание
- Соединение
- Разделение
- Условный
- Биусловный
Эти концепции более подробно описаны ниже.
\(\color{Red} \textbf{Отрицание}\)
Отрицание является унарной логической связкой. Для любого предложения \(P\) отрицание \(P\), обозначаемое \(\neg P,\), есть предложение, из которого следует, что \(P\) ложно. \(\neg P\) также читается как «не» \(P\).
\[v(\neg B) = \left\{\begin{matrix} 1 &&& \text{если } v(B)= 0\\ 0 &&& \text{иначе.} \ _\квадрат \end{matrix}\right.\]
The truth table (1=true, 0=false) for negation is as follows:
| P | \(\neg\) P |
| 1 | 0 |
| 0 | 1 |
За предложение:
A : Луна сделана из зеленого сыра.
Что такое \(\отрицательный A\)?
Отрицание суждения A было бы утверждением, которое всегда истинно, если A ложно, и всегда ложно, если A истинно. Следующее утверждение соответствует этому критерию::
\(\neg\) A : Луна не из зеленого сыра. \(_\квадрат\)
\(\color{Red} \textbf{Conjugation}\)
Логическая конъюнкция — это ассоциативная бинарная логическая связка, которая оценивается как истинная только в том случае, если оба высказывания, которые она связывает, истинны.
\[ v(A \клин B) = \left\{\begin{matrix} 1 && \text{если } v(B)= 1 \text{ и } v(A)= 1 \\ 0 && \text{иначе}. \ end {matrix} \ right. \]
Таблица истины для сопряжения следующая:
| P | Q | Q | 97 Q | 9 P \ . |
(1 = 1 0,9014
)
Рассмотрим следующий оператор:
Слоны зеленые, а Джордж носит красные сапоги.
Что это за предложение?
Этим высказываниям можно присвоить пропозициональные буквы:
E : Слоны зеленые
G : Джордж носит красные сапоги.
Тогда приведенный выше оператор переписывается как:
E \(\клин\) G
Итак, это предложение является союзом. \(_\квадрат\)
\(\color{Red} \textbf{Дизъюнкция}\)
Логическая дизъюнкция — это ассоциативная бинарная логическая связка, которая оценивается как истинная, если одно из высказываний, которые она связывает, истинно. Примечание : Это «включающее» определение дизъюнкции, не путать с «исключительной» формой, эквивалентной вентилю «исключающее ИЛИ» в компьютерной логике.
\[v(A \vee B) = \left\{\begin{matrix} 0 &&& \text{если } v(B)= 0 \text{ и } v(A)= 0 \\ 1 &&& \text{иначе.} \ _\квадрат \end{matrix}\right.\]
The truth table for disjunction iis as follows:
| P | Q | P \(\vee\) Q |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
(1 = TRUE, 0 = False)
.
Рассмотрим следующий оператор:
Слоны зеленые, или Джордж носит красные сапоги (или и то, и другое).
Перепишите это, используя пропозициональную логику.
Этим высказываниям можно присвоить пропозициональные буквы:
E : Слоны зеленые
G : Джордж носит красные сапоги.
Тогда приведенный выше оператор переписывается как:
E \(\vee\) G \(_\квадрат\)
\(\color{Red} \textbf{Conditional}\)
Логическое условие эквивалентно выражению «Если A, то B». Результат верен, если он согласуется с этим утверждением. Единственная противоречивая ситуация — это если B ложно, когда A истинно. Это противоречит условному утверждению. Таким образом, определение выглядит следующим образом:
\[v(P \to Q) = \left\{\begin{matrix} 0 &&& \text{если } v(P)= 1, v(Q)= 0 \\ 1 &&& \text{иначе.} \ _\квадрат \end{matrix}\right.\]
И это соответствующая таблица истины:
| P | Q | P \ (\) Q | P \ (\) Q 988 | P \ (\) Q 88 | P \ (\).| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | |
(1 = 1 0,9014
)
Предположим, у нас есть следующее утверждение (составное предложение):
Если Ребекка закончит домашнее задание, она сможет смотреть Netflix.
Это логическое условие?
Это состоит из двух простых предложений, которые мы будем называть P и Q :
- P : Ребекка заканчивает домашнее задание.
- Q : Ребекка смотрит Netflix.
Затем мы можем установить следующий условный оператор, используя условную связку:
P \(\к\) Q
Итак, да, это логическое условие. \(_\квадрат\)
8, красный 8, красный, коричневый 8 8, Браун
Это известная проблема в изучении дедуктивных рассуждений и логики.
Вам показывают набор из четырех карточек, разложенных на столе, каждая из которых имеет номер на одной стороне и цветное пятно на другой стороне.
На видимых лицевых сторонах карточек изображены цифры 3, 8, красный и коричневый.
Какие карты нужно перевернуть, чтобы проверить истинность утверждения о том, что если на одной стороне карты изображено четное число, то ее противоположная сторона красная?
\(\color{Red} \textbf{Biconditional}\)
Biconditional — это связка, которая представляет условие «тогда и только если» .
Проверяет, имеют ли оба предложения одно и то же истинностное значение. Его также можно представить как \( (A \to B)\wedge(B \to A).\)
\[v(A \leftrightarrow B) = \left\{\begin{matrix} 1 &&& \text{если } v(A)= v(B) \\ 0 &&& \text{иначе.} \ _\квадрат \end{matrix}\right.\]
Эквивалент логического вентиля XNOR.
The truth table looks like this:
| P | Q | P \(\leftrightarrow\) Q | ||||
| 0 | 0 | 1 | ||||
| 0 | 1 | 0 | ||||
| 1 | 0 | 0 | ||||
| 1 | 1 | 1 | 1 | 1110791 | 71 | 1 | 1 | 1 | 1 | 0014 |
| P | Q | \(\neg\) P | P \(\клин\) Q | P \(\vee\) Q 3\087 | 0P \(\leftrightarrow\) Q | |
| 0 | 0 | 1 | 0 | 0 | 1 | 1 |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 0 | 1 | 0 | 0 |
| 1 | 1 | 0 | 1 | 1 | 1 | 1 |
So far we have обсудили следующие простые предложения:
- А
- \(\нег\) А
- А \(\клин\) Б
- А \(\вее\) Б
- А \(\к\) Б
Однако мы можем построить гораздо более сложные предложения, комбинируя приведенные выше простые предложения для построения бесконечного числа комбинаций правильно построенной формулы, например: \) В ) \(\вее\) С ]
Предложение называется «правильной формулой» (или wff), если оно построено по следующему набору правил:
- Любое атомарное предложение — это правильно построенная формула.
- Если \(A\) — правильно построенная формула, то \(\neg A\) — также правильно построенная формула.
- Если \(A\) и \(B\) — правильно построенные формулы, то \((A \клин B)\) также является правильно построенной формулой.
- Если \(A\) и \(B\) — правильно построенные формулы, то \((A \vee B)\) также является правильно построенной формулой.
- Если \(A\) и \(B\) — правильно построенные формулы, то \((A \to B)\) также является правильно построенной формулой.
- Если \(A\) и \(B\) правильно построенные формулы, то \((A \leftrightarrow B)\) также является правильно построенной формулой. \(_\квадрат\)
- Если предложение построено с использованием только 1-6 выше, то предложение не является правильно построенной формулой.
Ни один из них 3 1 2 и 3 Все они 1 и 2 2 1 и 3
Согласно логике высказываний, что из следующего не является правильно сформулированной формулой?
(1): (\(A \клин B) \к (C \ви D)\)
(2): (\(A \отриц B) \к (C \ви D)\ )
(3): (\(A \leftrightarrow B) \to (\neg D)\)
\(\color{Red} \textbf{Тавтология}\)
A тавтология это то, что верно только с точки зрения логики. Примером может быть «Либо идет дождь, либо нет дождя».
Примером может быть «Либо идет дождь, либо нет дождя».
Формально мы говорим, что предложение является тавтологией , если оно истинно для всех возможных назначений истинности задействованных атомарных предложений. \(_\квадрат\)
Покажите, что это предложение является тавтологией :
.\[ ((A \land B) \to C) \leftrightarrow (A \to (B \to C)).\]
Мы можем построить таблицу истинности, чтобы проверить это:
\(А\) \(Б\) \(С\) \(A \land B\) \(((A \land B) \to C)\) \(B \to C\) \((A \to (B \to C ) \) 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 . 70087 0 0 1 0 0 1 0 1 1 1 0 1 1 1 1 0 0 0 1 1 1 1 0 1 0 1 1 1 1 1 0 1 0 0 0 1 1 1 1 1 1 1 Как видите, столбцы 5 и 7 содержат одинаковые записи для всех комбинаций A, B и C. Следовательно, \(((A \land B) \to C) \leftrightarrow (A \to (B \to C ))\) действительно тавтология . \(_\квадрат\)
\(\color{Red} \textbf{Противоречие}\)
Противоречие — это утверждение, которое является ложным с точки зрения логики.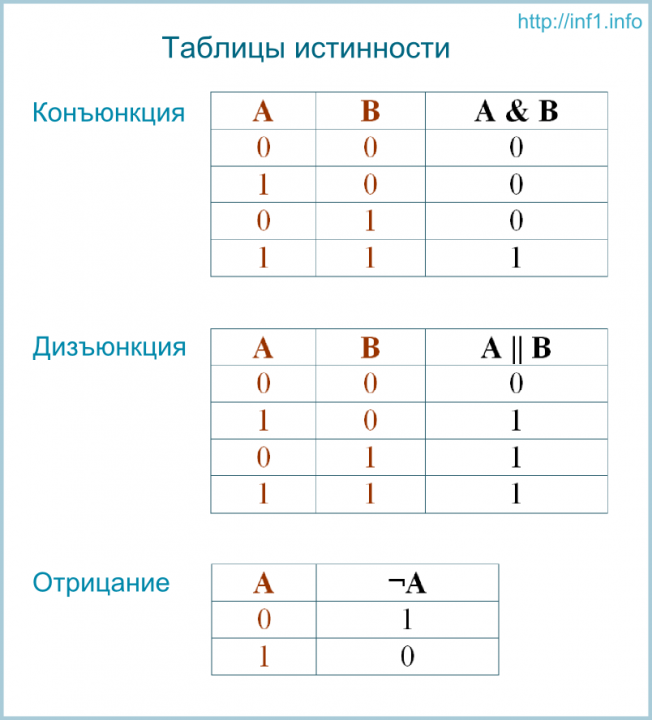 Примером может быть «Идет дождь, и не идет дождь».
Примером может быть «Идет дождь, и не идет дождь».
Формально мы говорим, что предложение является противоречием , если оно ложно для всех возможных назначений истинности задействованных атомарных предложений. \(_\квадрат\)
Отрицание тавтологии определенно есть противоречие .
Поскольку, как показано выше, \(((A \land B) \to C) \leftrightarrow (A \to (B \to C))\) является тавтологией , следующее противоречие :
\[\neg (((A \land B) \to C) \leftrightarrow (A \to (B \to C))). \]
\(\color{Red} \textbf{Непредвиденные обстоятельства}\)
Предложение является контингентным тогда и только тогда, когда оно не является ни противоречием , ни тавтологией . \(_\квадрат\)
Пример непредвиденной ситуации:
\[ (A \land B) \leftrightarrow (A \vee B). \]
\]
Мы можем увидеть это, составив таблицу истинности:
| \( A\) | \(B\) | \(A \land B\) | \(A \vee B\) |
| 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 |
| 1 | 0 | 0 | 1 |
| 1 | 1 | 1 | 1 |
Мы можем видеть, что, поскольку третий и четвертый столбцы не все совпадают, и не все противоречат друг другу, это пример непредвиденного обстоятельства. т. е. является ли предложение действительным, равно зависит от значений \(A\) и \(B\).
Противоречие Контингент Более одного из этих Это не очень хорошо сформулированная формула Тавтология
Согласно пропозициональной логике следует тавтология , противоречие или контингент ?
Два предложения \(A\) и \(B\) эквивалентны тогда и только тогда, когда \(A \leftrightarrow B\) является тавтологией.
\(_\квадрат\)
В то время как бикондиционал проверяет, имеют ли два предложения равную ценность для конкретного назначения значений истинности, эквивалентность является тестом для всех возможных назначений значений истинности.
Вот список нескольких известных логических тождеств:
1 2 3 4 5 Это нерешенная проблема
В пропозициональной логике у нас есть пять связок:
- Отрицание
- Соединение
- Разделение
- Условный
- Биусловный
Билли утверждает, что это слишком много и что любое логическое предложение, которое может быть построено с помощью этих пяти связок, может быть построено с меньшим количеством.
Какое наименьшее количество необходимых связок (включая только перечисленные здесь), чтобы иметь возможность составить любое логическое предложение, которое можно составить из этих пяти?
\(\color{Red} \textbf{Validity}\)
До сих пор мы ничего не делали, чтобы отличить хороший аргумент от ужасного.
Есть два случая, когда аргумент может пойти не так:
- Предпосылка неверна.
- Логическая структура аргумента неверна.
Поскольку в логике высказываний мы ничего не можем сделать, чтобы определить, истинна ли посылка на самом деле, мы определяем достоверность аргумента в терминах второй идеи.
\( \left \{ P_1, P_2, \cdots, P_n \right \} \) говорят, что влекут за собой \(C\) тогда и только тогда, когда не существует назначения истинности, для которого \( P_1, P_2, \cdots , P_n \) все истинны, а \(C\) ложно. \(_\квадрат\)
Обозначим следствие следующим образом:
\[ \left \{ P_1, P_2, \cdots, P_n \right \} \models C. \]
\]
Вот еще один способ определить следствие:
\(\left \{ P_1, P_2, \cdots, P_n \right \} \models C\) тогда и только тогда, когда \( ( \left ( P_1 \клин P_2 \клин \cdots \клин P_n \right ) \to В) \) — тавтология. \(_\квадрат\)
К настоящему моменту читателю должно быть очевидно, что аргумент действителен тогда и только тогда, когда посылка влечет за собой вывод.
\(\color{Red} \textbf{Consistency}\)
Набор предложений является противоречивым , если он не может быть одновременно все истинным. В противном случае соответствует .
Набор предложений \(\phi = \left \{A_1, A_2, \cdots, A_n \right \}\) является противоречивым тогда и только тогда, когда \(\left ( A_1 \wedge A_2 \wedge \cdots \wedge A_n\right )\) есть противоречие.
В противном случае соответствует . \(_\квадрат\)
Несогласованным набором будет
.\[ \phi = \left \{A, A \to B, \neg B, C \right \}. \]
Обратите внимание, что предложение \(C\) не имеет ничего общего с самой несогласованностью. Тем не менее, это часть противоречивого набора в любом случае.
Логика высказываний — лишь один из множества формальных языков. Возможно, что структура аргумента теряется при переводе его с английского языка на пропозициональную логику.
Естественным расширением логики высказываний является квантифицированная логика, также называемая логикой предикатов или логикой первого порядка.
Рассмотрим следующий известный аргумент:
- Все люди смертны.
- Аристотель — человек.
- Следовательно, Аристотель смертен.
Попробуем символизировать это в логике высказываний:
\[\begin{выравнивание} A: &\text{ Все люди смертны.} \\ B: &\text{ Аристотель — человек.} \\ C: &\text{ Аристотель смертен.} \конец{выравнивание}\]
Аргумент становится
\[\frac{A, \; B}{\следовательно C}.
\]
Хотя это явно «логическое» заключение, это совершенно неверный аргумент в логике высказываний , поскольку A , B и C не имеют отношения друг к другу.
Обратите внимание, что проблема не в символизации аргумента. На самом деле, это лучшая символизация, которую логика высказываний может предложить для этих утверждений. По этой причине пропозициональная логика часто упоминается как «логика нулевого порядка», тогда как квантифицированная логика называется «логикой первого порядка», поскольку он просматривает содержание утверждения, чтобы сделать логический вывод, как в приведенном выше примере.
- Логика высказываний с использованием алгебры
- Решение задачи на пропозициональную логику
- Предикатная/квантифицированная логика
- Логические элементы
- Обзор логики
Цитировать как: Логика высказываний.


 К «Обсуждениям» могут подключаться и другие студенты. Возможно, получится решить вопрос быстрее!
К «Обсуждениям» могут подключаться и другие студенты. Возможно, получится решить вопрос быстрее! ..
..





 \(_\квадрат\)
\(_\квадрат\)
 \]
\]