Site Loader
Posted on 08.04.2023

Содержание

НОУ ИНТУИТ | Лекция | Логические основы ЭВМ

Аннотация: Рассматриваются основные логические элементы и принципы их соединения в логические схемы.

Ключевые слова: логический, выражение, истина, ложь, алгебра, представление, переменная, значение, функция, инверсия, дизъюнкция, конъюнкция, таблица, очередь

Любая цифровая вычислительная машина состоит из логических схем — таких схем, которые могут находиться только в одном из двух возможных состояний — либо «логический ноль», либо «логическая единица». За логический 0 и логическую 1 можно принять любое выражение, в том числе и словесное, которое можно характеризовать как «истина» и «ложь». В вычислительной технике логические 0 и 1 — это состояние электрических схем с определенными параметрами. Так, для логических элементов и схем, выполненных по технологии транзисторно-транзисторной логики (ТТЛ-схемы), логический 0 — это напряжение в диапазоне 0 … + 0,4 В, а логическая 1 — это напряжение в диапазоне + 2,4 … + 5 В [1]. Работа логических схем описывается посредством специального математического аппарата, который называется логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 — 1864 гг.), она является основой всех методов упрощения булевых выражений.

Логические переменные и логические функции — это такие переменные и функции, которые могут принимать только два значения — либо логический 0, либо логическая 1.

Основные логические функции и элементы

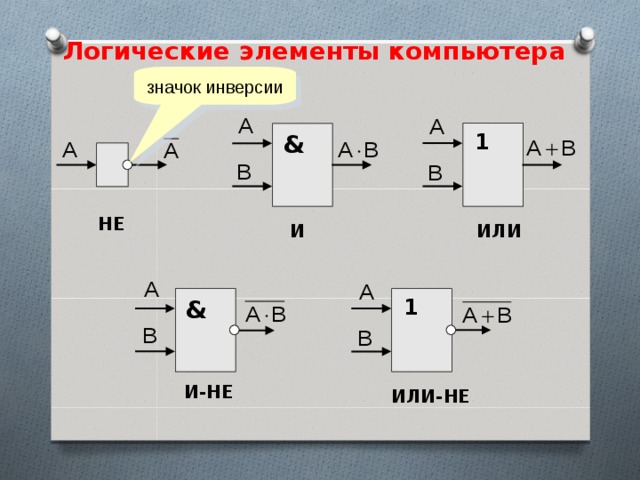
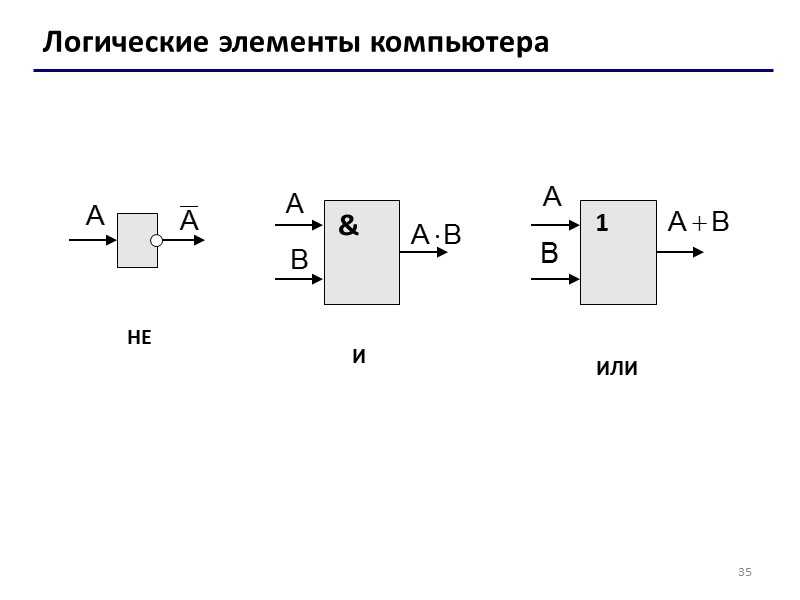
Логический элемент — графическое представление элементарной логической функции.

Логическое умножение (конъюнкция) — функция И

Рассмотрим ключевую схему представленную на рис. 1.1,а. Примем за логический 0 [2]:

  • на входе схемы разомкнутое состояние соответствующего ключа, например, ;
  • intuit.ru/2010/edi»>на выходе схемы ( ) — такое ее состояние, когда через сопротивление R ток
    не протекает    .

Таблица истинности — это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции.

Рис. 1.1. Трёх-входовой логический элемент И

Таблица истинности для логической схемы, представленной на рис. 1.1,б, состоит из 8 строк, поскольку данная схема имеет три входа — , и . Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно . Очевидно, что через сопротивление R ток протекает только тогда, когда замкнуты все три ключа — и , и , и . Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис.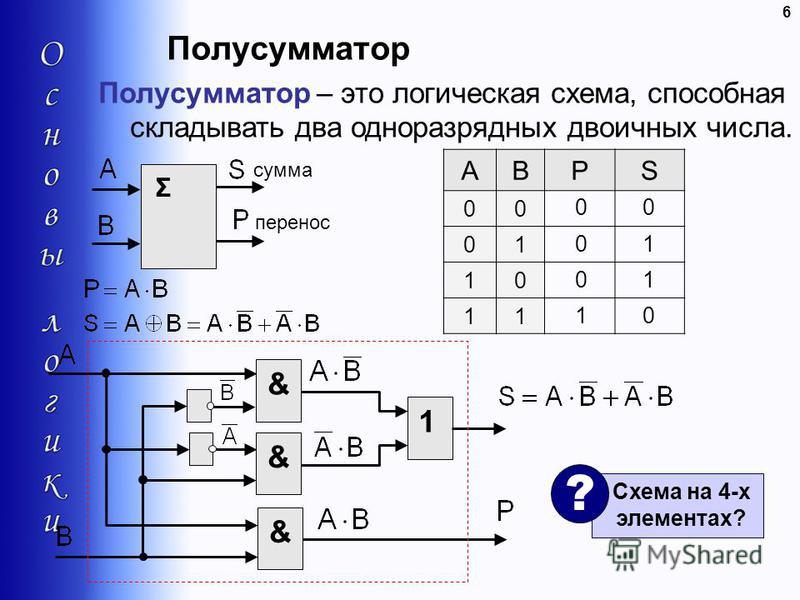

1.1,в.

Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.

Уровень логического 0 является решающим для логического умножения .

В логических выражениях применяется несколько вариантов обозначения логического умножения. Так, для приведенного на рис. 1.1,в трёх-входового элемента И, логическое выражение можно представить в виде:

  • либо , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
  • либо ;
  • либо — с использованием знака конъюнкции;
  • либо , но при этом из контекста должно быть ясно, что между переменными , и производится логическое умножение.
Логическое сложение (дизъюнкция) — функция ИЛИ

Рассмотрим ключевую схему, представленную на рис. 1.2,а. Таблица истинности для данной логической схемы (рис. 1.2,б) состоит из 4 строк, поскольку данная схема имеет два входа — и . Количество сочетаний этих переменных равно . Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или , или . Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах

соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.

Рис. 1.2. Логический элемент ИЛИ на два входа

Правило логического сложения: если на вход логического элемента ИЛИ подается хотя бы одна логическая , то на его выходе будет логическая 1.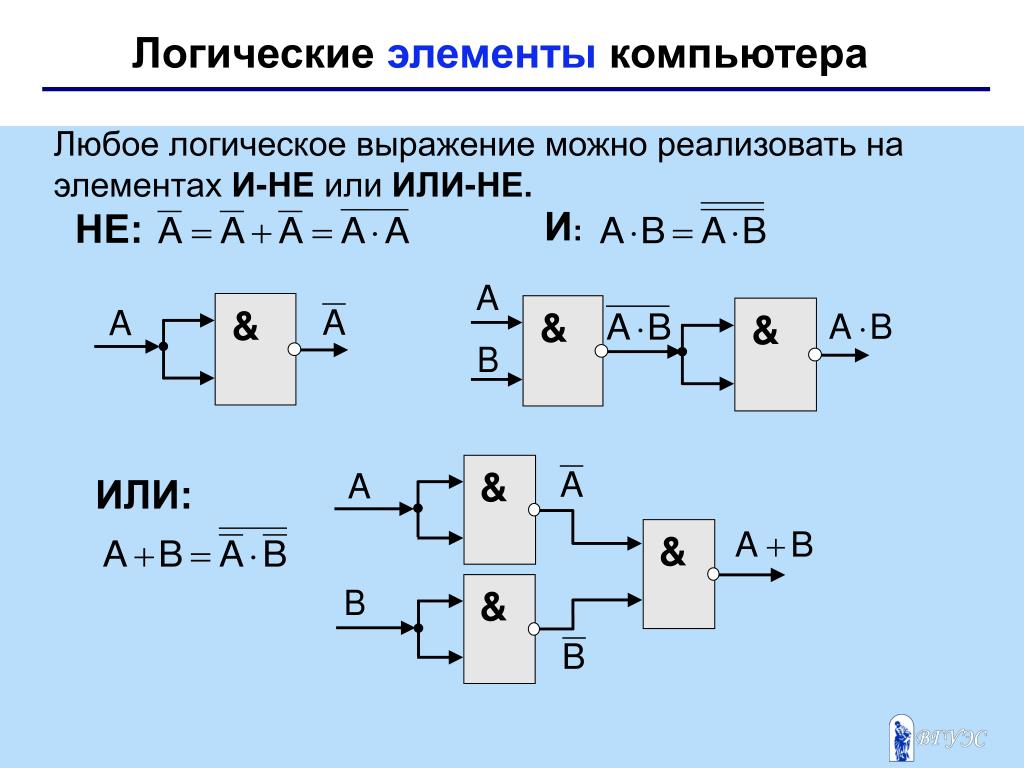

Для логического сложения решающим является уровень логической 1.

В логических выражениях применяется два варианта обозначения логического сложения. Так, для приведенного двух-входового элемента ИЛИ, логическое выражение можно представить в виде:

  • либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
  • либо — с использованием знака дизъюнкции.
Логическое отрицание (инверсия) — функция НЕ

Рассмотрим ключевую схему, представленную на рис. 1.3,а. Таблица истинности для данной схемы (рис. 1.3,б) самая простая и состоит всего из 2 строк, поскольку она (единственная из всех логических элементов) имеет только один вход — . Количество вариантов для единственной

логической переменной равно . Очевидно, что через сопротивление R ток протекает ( ) тогда, когда не замкнут, т.е. . Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.

Рис. 1.3. Логический элемент НЕ

Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.

В логических выражениях применяется единственный вариант обозначения инверсии:

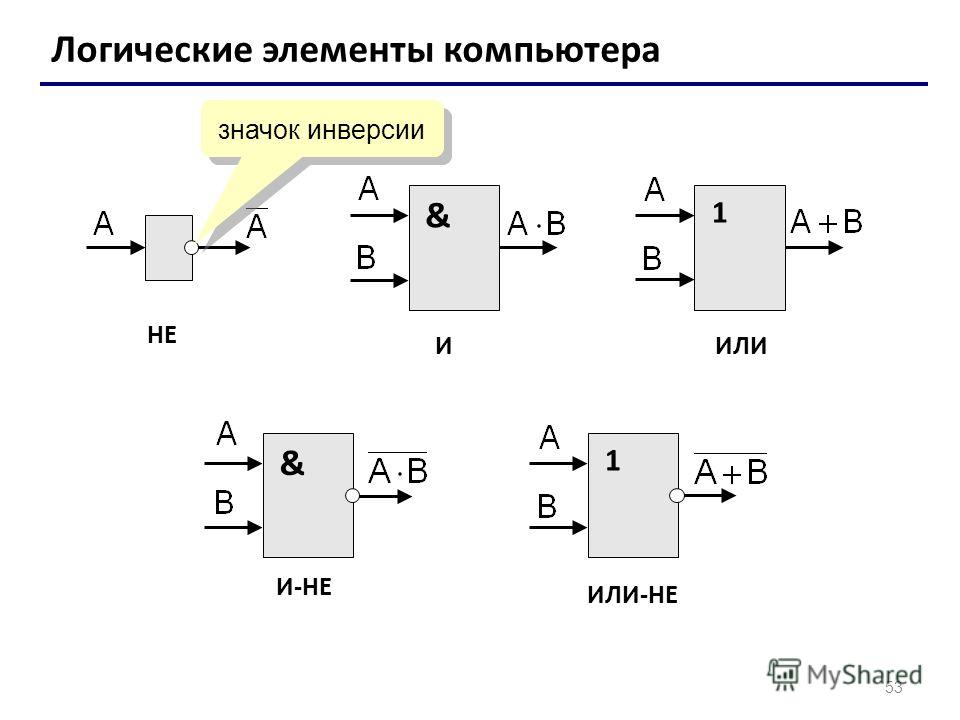
К основным логическим элементам относятся еще два элемента, которые являются комбинацией элементов И, ИЛИ и НЕ: элемент И-НЕ и ИЛИ-НЕ.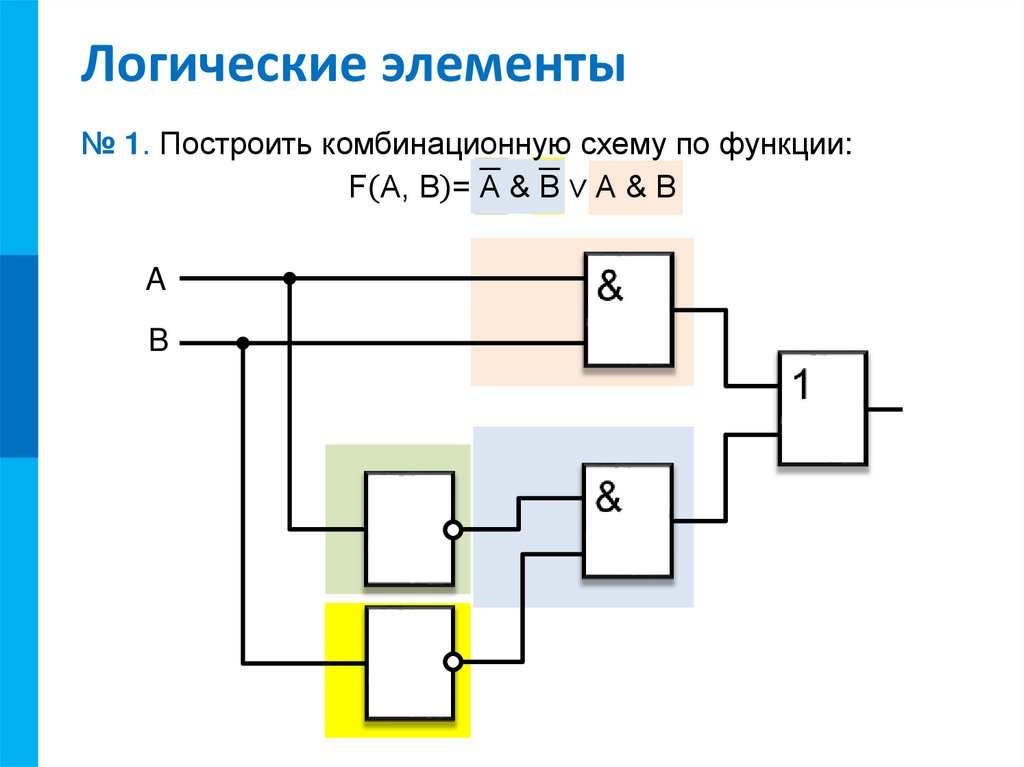

Логическая функция и элемент И-НЕ

Данная функция производит логическое умножение значений входных сигналов, а затем инвертирует результат этого умножения. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.

Рис. 1.4. Логический элемент И-НЕ на три входа

Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1

.

В логических выражениях применяются обозначения:

  • либо , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
  • intuit.ru/2010/edi»>либо ;
  • либо ;
  • либо .
Логическая функция и элемент ИЛИ-НЕ

В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.5,а.

Таблица истинности приведена на рис. 1.5,б.

Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.В логических выражениях применяются обозначения:

  • либо , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
  • либо .

Рис. 1.5. Логический элемент ИЛИ-НЕ на два входа

Микроконтроллеры и логические операции

Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “Радиолюбитель“

В нашей жизни бывают случаи когда нет необходимости вникать в глубину того, или иного вопроса, достаточно и его поверхностного понимания. Иногда это связано с нашим «нежеланием», в другом случае сложностью этого вопроса. Так и сейчас, изучая логические операции, мы не будем лезть в глубину, а просто смиримся с тем фактом, что они существуют и знать их надо.

Основа всего – слово «логика».
Логика (др.-греч. λογική) — «наука о правильном мышлении», «искусство рассуждения» (от λόγος — «речь», «рассуждение», «мысль»).
Как видите, логика это не просто древнегреческое слово, а целая наука, изучение которой позволяет нам правильно и здраво рассуждать, и, соответственно, делать правильные выводы из наших рассуждений, чего, однако, очень не хватает в нашем современном мире.
Рассуждая о чем-либо, мы, на основе логических заключений, делаем соответствующие выводы. К примеру, думая о своем товарище, на основе каких-то фактах, характеризующих его, мы можем сделать вывод – друг он нам, или нет (или: «и не друг, и не враг, – а так»).



В конце 19 века, группа лиц, под названием «математики», решила перевести весь наш мыслительный процесс в более понятную для них форму – математическую. И из простой, человеческой логики, появилась математическая или – символическая логика. То есть, по их разумению, найти истину можно не только путем шевеления «серым веществом», но и применением математических методов. В чем суть этого метода. Любая высказанная нами мысль основывается на каких то фактах – кирпичиках, составляющих ее основу. Так вот, в математической логике эти «кирпичики» имеют только два состояния – «ложь» или «истина». По идее, и в человеческой логике должно быть также. Но на то мы и «человеки».
1+1 равно 2 – истинна, 1+1 не равно 2 – ложь. Все просто и понятно. Но это только в математической логике, а у людей 1+1 может равняться и 3. Так вот, из этих «кирпичиков», а у математиков они называются – «простые выражения», которые могут быть только или «истинной», или «ложью», складываются «сложные выражения», которые, естественно, тоже могут быть только или «истинными» или «ложными». А весь этот процесс получения сложного выражения из простых можно описать «логической формулой» или, как еще говорят, – «логическим выражением».
И вот тут мы подошли к главному – к логическим операциям:
Логическое выражение – это символическая запись высказывания, состоящая из логических величин, объединенных логическими операциями. Логические величины – это или «1», или «0». Если выражение «истинно» – то его величина 1, если «ложно» – то его величина 0 (так уж принято).
Логические операции позволяют складывать, а точнее – связывать, между собой простые выражения (те самые «кирпичики») – логические величины.
К примеру, перефразируя Уильяма, нашего, Шекспира, возьмем вот такое предложение:
«Изучим или не изучим (микроконтроллер), вот в чем вопрос».
Слово «изучим» обозначим как «А», «не изучим» – как «В» и посмотрим как это предложение может выглядеть в символьной записи с использование логической операции:
А or В = ?

Точно также происходит запись логических операций при создании программы. Каждый “язык” программирования имеет соответствующий набор символьных команд, с помощью которых происходит запись логических операций в программе.

Ну а теперь я постараюсь ответить на вопрос – «Зачем нам, простым смертным, далеким от этих философских и математических понятий, это нужно».
Во-первых. Лишними любые знания никогда не бывают. Познавая новое, мы открываем для себя что-то неизвестное, расширяем свой кругозор, пополняем свой скудный словарный запас (что позволяет более внятно излагать свою мысль, а не прибегать через слово к нецензурным связкам для ее озвучивания), а самое главное – учимся мыслить другими, более высокими категориями, тем самым отдаляя себя от «прародителей» – обезьян.
Во-вторых. Труд математиков не пропал даром и не остался только теорией.
Все современные цифровые технологии основываются на логических операциях, без них никуда не деться. Почти все (а может даже и все) цифровые микросхемы в своей работе используют логические схемы (выполняют логические операции, в том числе и микроконтроллер).
Теперь конкретно для нас, изучающих микроконтроллеры и их программирование:
1. Создавая программу, мы прописываем все действия микроконтроллера основываясь на своей логике с применением логических операций, иногда даже и не подозревая об этом (теперь-то, мы не только «не подозреваем»), которые применяем к логическим выражениям.
Пример – «если в ходе выполнения программы получен такой результат, то дальше программа пойдет вот таким путем, а если мы получили другой результат, то программа дальше пойдет вот этим путем» – типичное выполнение логической операции.
2. В программировании логическая операция применяется не только к логическому выражению (смотри п.1), но и для операций с двоичными числами, так называемые «логические побитовые (битовые) операции», которые очень сильно облегчают тяжелую жизнь программиста (этот пункт мы детально рассмотрим при изучении команд микроконтроллера).
3. Нельзя создать конструкцию только на одном микроконтроллере. Она будет бессмысленна. Помимо самого микроконтроллера в схеме должна быть его «обвязка», – резисторы, конденсаторы, диоды, транзисторы, индикаторы, реле и т.д. Очень часто в схемах на микроконтроллерах применяются цифровые микросхемы, в основе работы которых лежит принцип логических операций. Знание логических операций и грамотное применение таких микросхем совместно с микроконтроллером, позволяет создавать более простые и эффективные радиолюбительские конструкции.

Существует три основных логических операции при помощи которых можно записать любое логическое выражение (вот тут, надо сосредоточиться):

1. Инверсия
2. Конъюнкция
3. Дизъюнкция

Конъюнкция, оно же «Логическое И», оно же «Логическое умножение».
Мы выбираем название «Логическое И» – оно чаще встречается в программировании.
Допустим, у нас есть два простых выражения – А и В. Эти выражения могут иметь значения или 1 (истина), или 0 (ложь).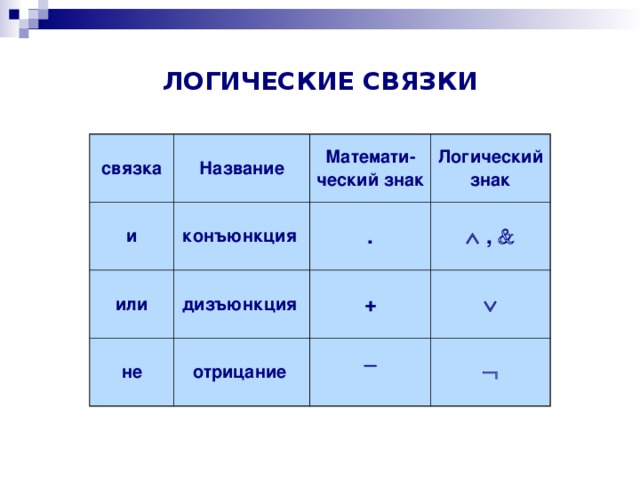 При выполнении операции «Логическое И» мы получим сложное выражение которое примет значение 1 (истина) только в том случае если и А, и В имеют значение 1 (истина), во всех других случаях результат будет 0 (ложь).
Операция «Логическое И» имеет обозначения (в языках программирования): И, &&, AND, &.
Посмотрите на таблицу (такие таблицы называются «таблицы истинности»):
А    В   А&В
1     1      1
0    0      0
1     0     0
0     1     0
Как видите, результат будет «истинной», равным 1, если только и А, и В будут равны 1 (истинны).
К примеру, прописывая алгоритм работы программы, мы можем эту операцию «озвучить» так: «Если в ходе выполнения программы результаты А и В «истинны», то дальше выполняем это, если результаты А и В, оба, или один из них – «ложь», то дальше выполняем вот это».
А третье название операции – «Логическое умножение» (не путайте с арифметическим умножением) применяется для двоичных чисел.

Дизъюнкция, оно же «Логическое ИЛИ», оно же «Логическое сложение».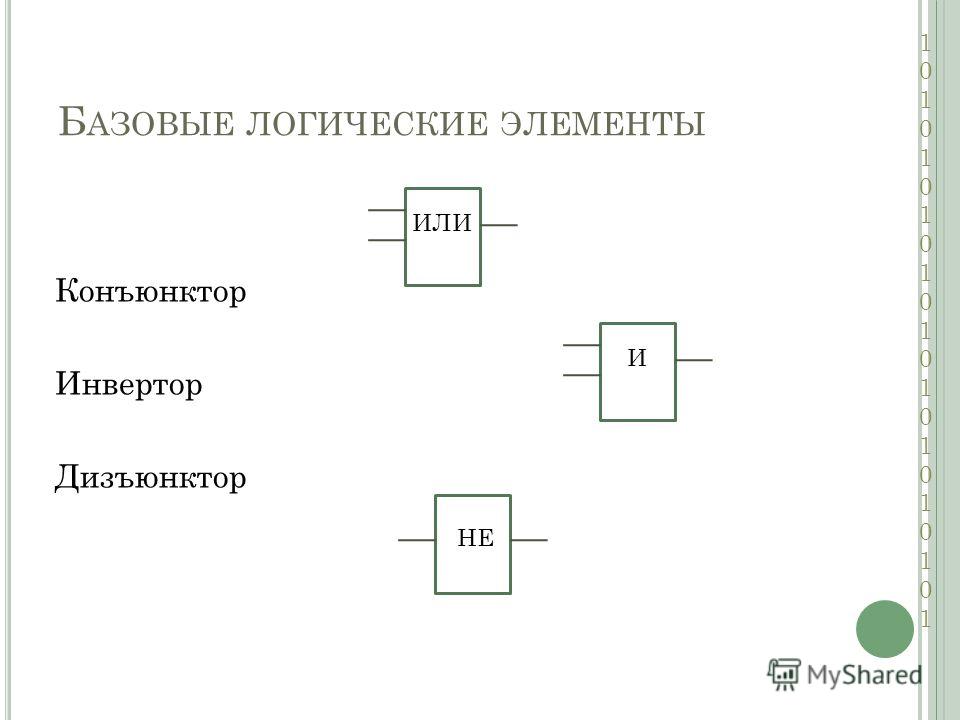
Мы выбираем название «Логическое ИЛИ». Кстати, если логически подумать, то можно и догадаться какие результаты будут при выполнении этой операции.
В «Логическом И» результат равен 1, если и А, и В, равны 1, а в «Логическом ИЛИ» результат будет равен 1, если или А, или В, равны единице.
Операция «Логическое ИЛИ» имеет обозначения: ИЛИ, ||, OR, |.
Посмотрим таблицу истинности:
А    В    А||В
1     1       1
0    0       0
1     0       1
0     1       1
А «Логическое сложение» применяется ….. Я думаю вы догадались где.

Инверсия, оно же «Логическое НЕ», оно же «Отрицание».
Мы выбираем название «Логическое НЕ».
Операция «Логическое НЕ» имеет обозначения: НЕ, !, NOT.
Тут вообще все просто:
Если А=1 (истина), то после выполнения операции «Отрицание» А примет значение 0, то есть становится ложным. И наоборот.
Есть еще одно название этой операции «Инвертор», а применяется оно в отношении цифровых микросхем. .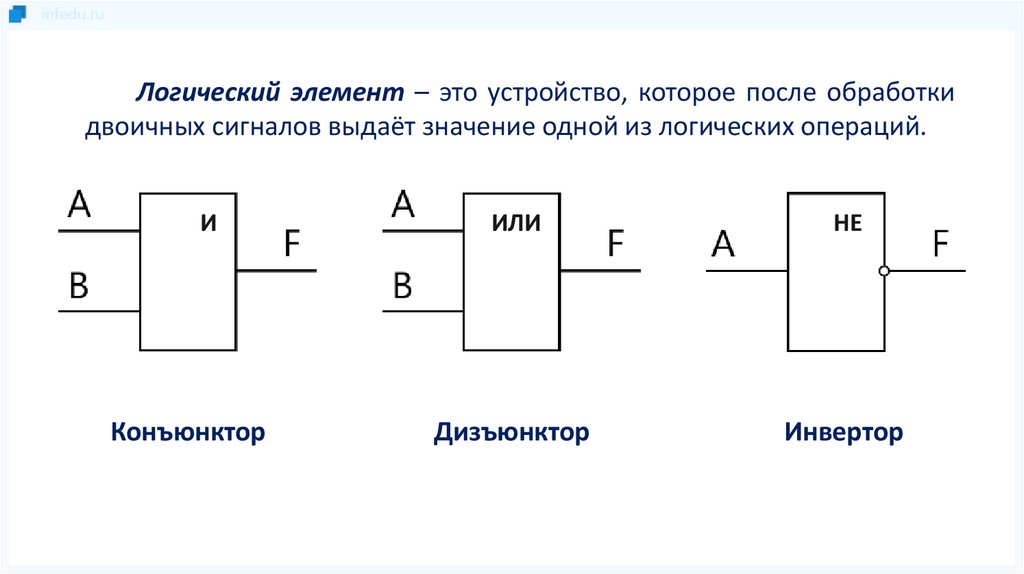
Таблица истинности
А    В    АxorВ
1     1        0
0    0        0
1     0        1
0     1        1
В этом случае, при выполнении операции «Исключающее ИЛИ», результат будет истинен (равен 1), если А не равно В.  В остальных случаях результат будет равен 0 (ложный).

Как я уже говорил, логические операции применяются не только к выражениям, но и к двоичным числам – так называемые логические побитовые (битовые) операции. А повторяюсь я только потому, что в некоторых языках программирования логические операции с выражениями, и логические битовые операции имеют одинаковое написание, и если вы будете пользоваться таким языком, то этот момент надо всегда держать в памяти, чтобы не допустить ошибок.

Также мы уяснили, что логические операции – основа цифровой техники. Даже цифровые микросхемы, которые предназначены только для выполнения логических операций, называют – «логические микросхемы», или еще проще – «логика».
Немного остановимся на микросхемах логики и мы.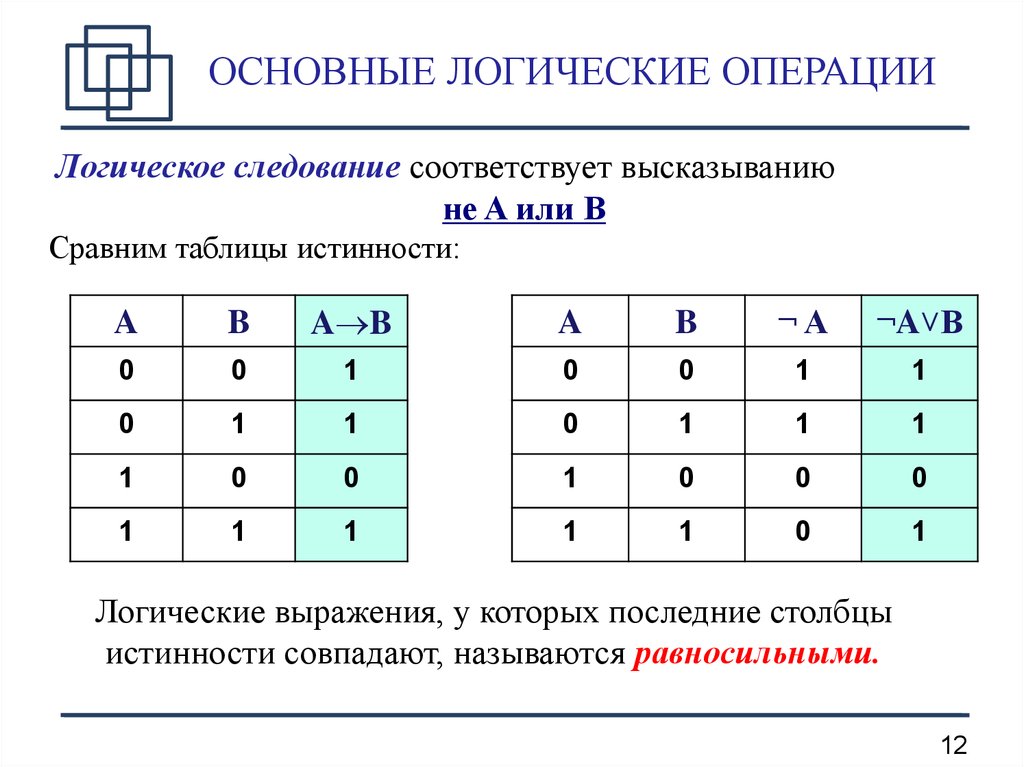
Работы цифровых микросхем логики основана на выполнение трех основных логических операций, с которыми мы ознакомились выше. Сочетание этих логических операций позволило создать великое (ну, может и не совсем великое) множество цифровых микросхем логики.
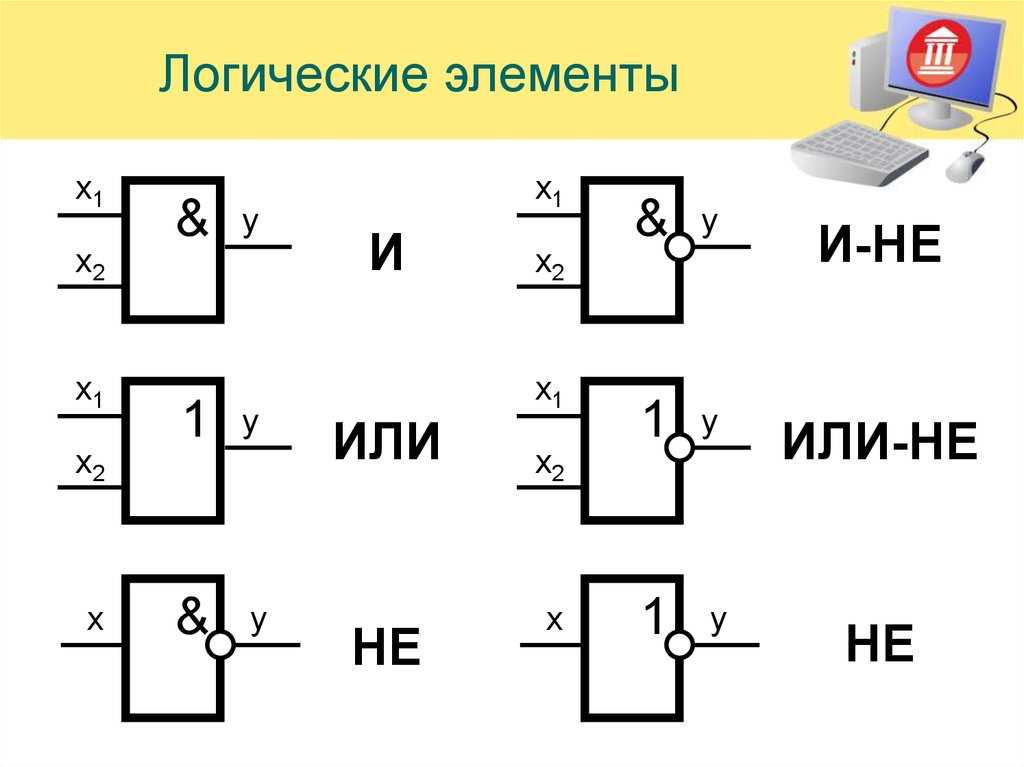
Основа таких микросхем – логический элемент:
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).

1. Логический элемент выполняющий операцию «Логическое И»:
Логический элемент, реализующий функцию конъюнкции («Логическое И»), называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
– «1» тогда и только тогда, когда на всех входах действуют «1»,
– «0» тогда и только тогда, когда хотя бы на одном входе действует «0»


2. Логический элемент, реализующий функцию «Логическое ИЛИ»:
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
– «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
– «0» тогда и только тогда, когда на всех входах действуют «0»


3.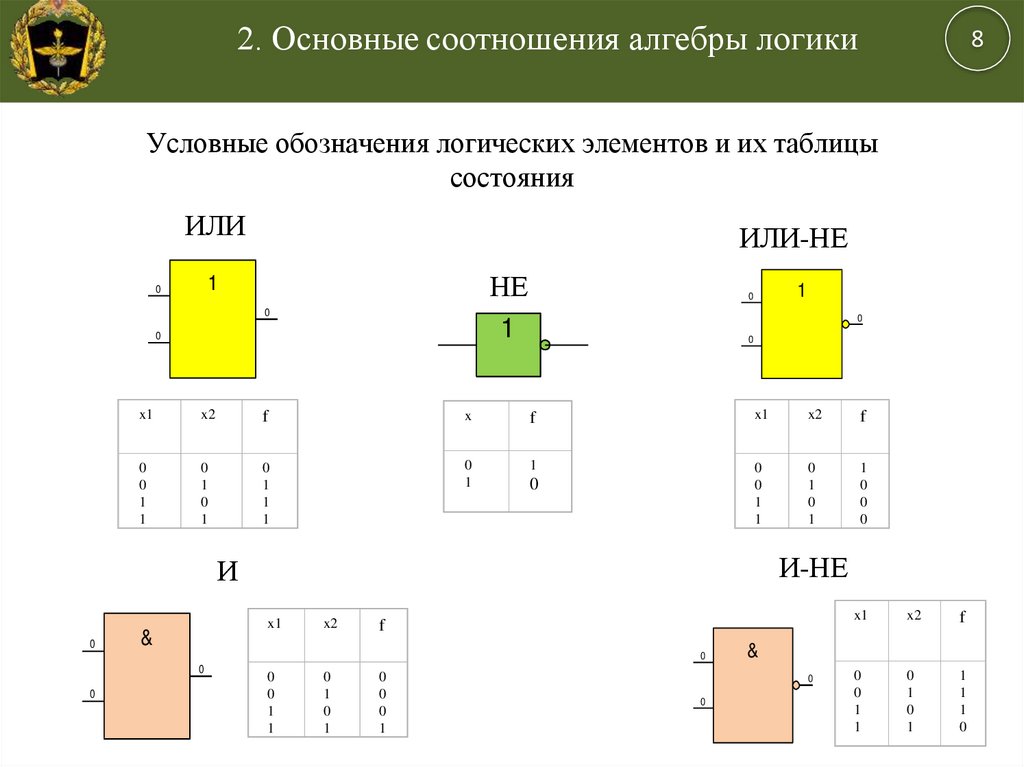 Логический элемент, реализующий функцию «Логическое НЕ»:
Мнемоническое правило для отрицания звучит так: На выходе будет:
– «1» тогда и только тогда, когда на входе «0»,
– «0» тогда и только тогда, когда на входе «1»


Это основные логические элементы.
А вот примеры комбинации основных логических операций:

1. Логический элемент, реализующий функцию «Исключающее ИЛИ» (неравнозначность):
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
– «1» тогда и только тогда, когда на входе действует нечётное количество,
– «0» тогда и только тогда, когда на входе действует чётное количество
Словесное описание: “истина на выходе – только при истине на входе 1, либо только при истине на входе 2″.


2. Логический элемент, реализующий функцию «Логическое ИЛИ-НЕ» (инверсия функции дизъюнкции):
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
– «1» тогда и только тогда, когда на всех входах действуют «0»,
– «0» тогда и только тогда, когда хотя бы на одном входе действует «1»


3.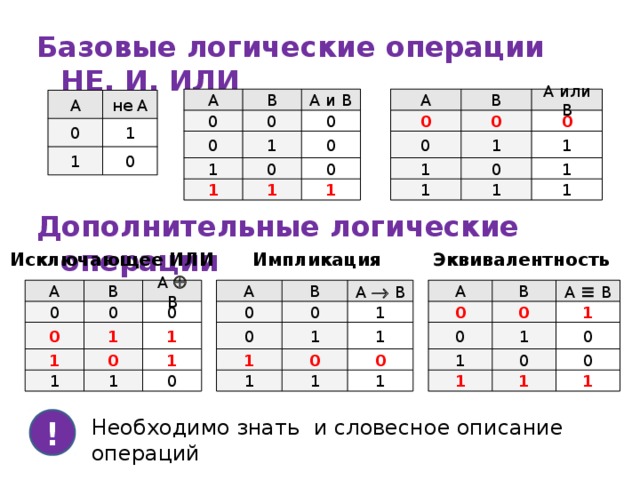 Логический элемент, реализующий функцию «Логическое И-НЕ»:
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
– «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
– «0» тогда и только тогда, когда на всех входах действуют «1»

Кроме таких комбинаций логических операций существует еще много других.

Практический пример использования микросхем логики.
Допустим, собираем охранную сигнализацию для дома. У нас имеется четыре датчика (на дверь и три окна). При срабатывании любого из них должен срабатывать звуковой сигнал.
Без применения дополнительных микросхем нам придется подключить эти четыре датчика к четырем входам микроконтроллера. Затем, программным путем, проверять каждый из четырех входов на наличие сигнала срабатывания датчика. При использовании микросхемы логики, выполняющую «Логическую операцию ИЛИ» и имеющую четыре входа, к примеру К561ЛЕ6 (в данной микросхеме имеется 3 логических четырехвходовых элементов, реализующих логическую функцию «ИЛИ-НЕ»), мы можем подключить датчики к входам одного элемента микросхемы, а единственный его выход подключить к одному входу микроконтроллера.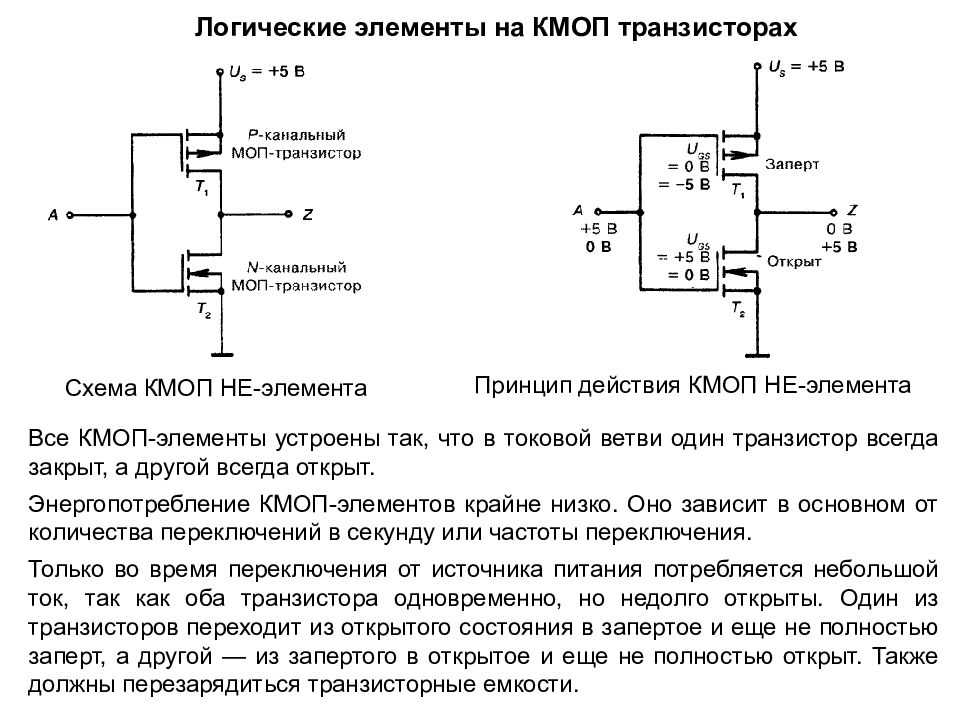 Теперь, при срабатывании любого датчика на выходе микросхемы сформируется сигнал срабатывания, который подастся на вход микроконтроллера. Наш выигрыш:
– задействован всего один вход микроконтроллера (вместо четырех)
– уменьшается объем программы (вместо опроса четырех входов, нам надо контролировать только один вход микроконтроллера).

Кстати, есть еще одна разновидность логики – женская логика. Весьма интересная штука. Но так как она к сегодняшней теме не относится, то придется, к сожалению, этот вопрос опустить.

Предыдущие статьи:

♦ Микроконтроллер и как его победить
♦ Микроконтроллер и системы счисления

Следующие статьи:

♦ Общее устройство микроконтроллера
♦ Арифметико-логическое устройство и организация памяти – память программ, память данных, энергонезависимая память
♦ Регистры общего назначения, регистры ввода/вывода, стек, счетчик команд
♦ Регистр состояния SREG
♦ Порты ввода/вывода микроконтроллера

Руководство по логическим операторам в R (ИЛИ, НЕ и И в R)

Предположим, мы хотим изменить или сравнить результаты сравнений, сделанных с помощью операторов отношения.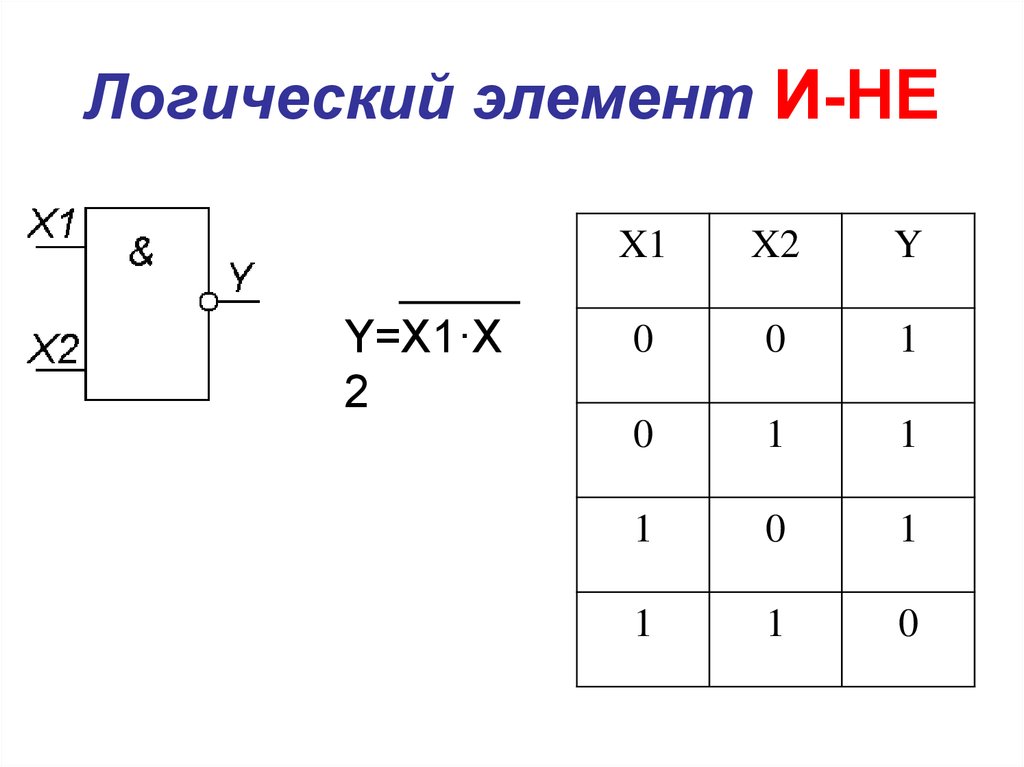 Как бы мы это сделали?

 R делает это с помощью операторов AND, OR и NOT .

Логические операторы в R

  • Оператор И: Представленный с помощью амперсанда, этот оператор принимает два логических значения и возвращает ИСТИНА , только если оба значения ИСТИНА себя.
  • Оператор ИЛИ:  Обозначенный символом пики, этот оператор принимает два логических значения и возвращает ИСТИНА , если только одно значение равно ИСТИНА .
  • Оператор NOT: Представленный восклицательным знаком, этот оператор инвертирует логическое значение, для которого он используется.

 

Оператор И «&»

Оператор И принимает два логических значения и возвращает ИСТИНА , только если оба значения равны ИСТИНА себя. Это означает, что ИСТИНА и ИСТИНА оценивается как ИСТИНА , но ЛОЖЬ и ИСТИНА , ИСТИНА и ЛОЖЬ и ЛОЖЬ и ЛОЖЬ оцениваются как ЛОЖЬ .

Только ИСТИНА и ИСТИНА дадут нам ИСТИНА. | Скриншот: Линда Нго

Вместо использования логических значений мы можем использовать результаты сравнений. Предположим, у нас есть переменная x , равная 12. Чтобы проверить, больше ли эта переменная пяти, но меньше 15, мы можем использовать x больше пяти и x меньше 15.

 x <- 12
x > 5 & x < 15

Первая часть, x > 5 , будет оцениваться как TRUE , поскольку 12 больше пяти. Вторая часть, x < 15 , также будет оцениваться как ИСТИНА , потому что 12 также меньше 15. Таким образом, результатом этого выражения будет ИСТИНА , поскольку ИСТИНА и ИСТИНА равно ИСТИНА . Это имеет смысл, потому что 12 лежит между пятью и 15.

Однако, если бы x было 17, выражение x > 5 & x < 15 упростилось бы до ИСТИНА И ЛОЖЬ , что привело бы к выражению ЛОЖЬ .

Подробнее о R: группировка данных с помощью R: Руководство

 

И Пример задачи оператора

Рассмотрим следующий вектор и переменную:

 linkedin <- c(16, 9, 13, 5, 2, 17, 14 )
last <- tail(linkedin, 1)

The linkedin 9Вектор 0015 представляет собой количество просмотров вашего профиля в LinkedIn за последние семь дней. Последняя переменная представляет последних значений вектора linkedin .

Определите, находится ли переменная last в диапазоне от 15 до 20, исключая 15, но включая 20. last > 15 & last <= 20 Последняя переменная LinkedIn — 14, которая не находится между 15 и 20. | Скриншот: Линда Нго

 

Оператор И Пример задачи 2

Рассмотрим следующие векторы:

 linkedin <- c(16, 9, 13, 5, 2, 17, 14)
facebook <- c(17, 7, 5, 16, 8, 13, 14)

Вектор linkedin представляет просмотры вашего профиля LinkedIn за последние семь дней, а вектор facebook представляет просмотры вашего Профиль Facebook за последние семь дней.

Определите, когда число просмотров LinkedIn превысило 10, а количество просмотров Facebook не достигло 10 за определенный день. Используйте linkedin и facebook векторов.

 

Пример 2 Решение 

 # linkedin больше 10, но facebook меньше 10
linkedin > 10 и facebook < 10
Только на третий день число просмотров в LinkedIn превысило 10, а в Facebook — меньше 10. | Скриншот: Линда Нго

 

И Пример задачи оператора 3

Рассмотрим следующую матрицу:

 просмотров <- matrix(c(linkedin, facebook), nrow = 2, byrow = TRUE)

Переменная linkedin и facebook соответствует тем же векторам в предыдущем примере.

Первая и вторая строки в матрице представлений соответствуют векторам linkedin и facebook соответственно.

Определите, когда матрица просмотров равна числу от 11 до 14, исключая 11 и включая 14.

 

Пример 3 Решение 

 # Когда количество просмотров находится между 11 (исключительно) и 14 (включительно)?
просмотров > 11 и просмотров <= 14
На третий и последний день количество просмотров LinkedIn составляло от 11 (без учета) до 14 (включительно). На шестой и последний день количество просмотров в Facebook составляло от 11 (исключительно) до 14 (включительно). | Скриншот: Линда Нго

 

ИЛИ Оператор «|»

Оператор ИЛИ | работает аналогично оператору И и , но разница в том, что только одно из логических значений должно быть равно ИСТИНА для того, чтобы вся операция ИЛИ оценивалась как ИСТИНА .

Это означает, что ИСТИНА | TRUE равно TRUE , а также TRUE | ЛОЖЬ и ЛОЖЬ | ИСТИНА оценивается как ИСТИНА . Когда обе логические ЛОЖЬ в операции ИЛИ, ЛОЖЬ | ЛОЖЬ , результат ЛОЖЬ . Помните, что операция ИЛИ не является операцией исключающего ИЛИ, поэтому TRUE | ИСТИНА также равна ИСТИНА .

Только ЛОЖЬ и ЛОЖЬ дадут нам ЛОЖЬ. | Скриншот: Линда Нго

С оператором И только ИСТИНА и ИСТИНА дает ИСТИНА , все остальное равно ЛОЖЬ . С оператором ИЛИ только FALSE | ЛОЖЬ дает ЛОЖЬ , все остальное ИСТИНА .

Как и в операциях И, мы можем использовать сравнения вместе с оператором ИЛИ. Предположим, у нас есть переменная y , равная четырем. Чтобы увидеть, меньше ли эта переменная пяти или больше 15, мы можем использовать следующее выражение:

 г <- 4
у < 5 | y > 15

R сначала выполнит сравнение, в результате чего TRUE | FALSE , что, в свою очередь, приводит к TRUE .

Теперь предположим, что y равно 14. Выражение y < 5 | y > 15 теперь оценивается как FALSE | ЛОЖЬ . Ни одно из сравнений не является TRUE , поэтому результатом будет FALSE .

Подробнее о науке о данных: 8 способов фильтрации кадров данных Pandas

 

Пример задачи оператора ИЛИ 1

Используя те же переменные из «Пример задачи оператора И 3», определите, является ли last меньше пяти или больше 10.

 linkedin <- c(16, 9, 13, 5, 2, 17, 14)
last <- tail(linkedin, 1)

 

Пример 1 Решение 

 # Last меньше 5 или больше 10?
последний < 5 | last > 10
Последний элемент LinkedIn имеет номер 14, и хотя он меньше пяти, он больше 10, поэтому выражение оценивается как истинное. | Скриншот: Линда Нго

 

Пример оператора ИЛИ Задача 2

Рассмотрим те же векторы linkedin и facebook из предыдущего примера.

 линкин <- c(16, 9, 13, 5, 2, 17, 14)
facebook <- c(17, 7, 5, 16, 8, 13, 14)

Определите, когда один или оба социальных профиля были посещены не менее 12 раз.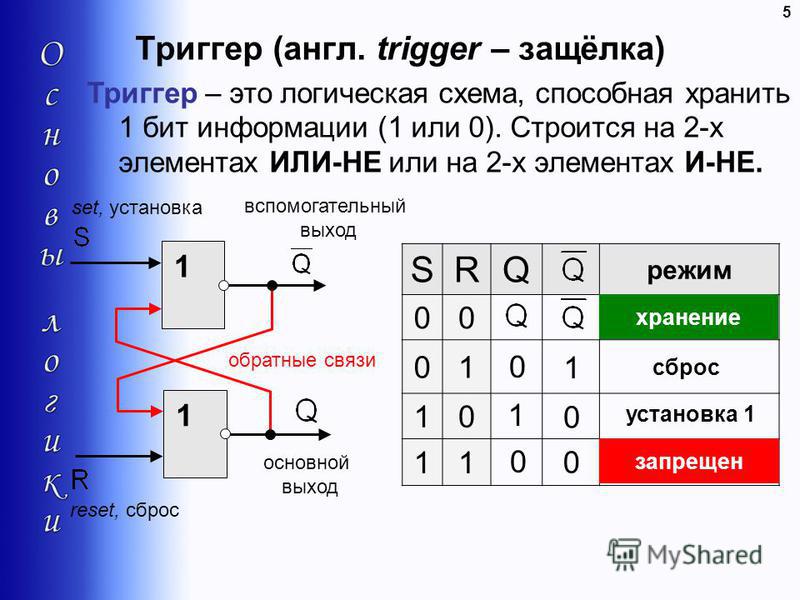

 

Пример 2 Решение 

 # Когда одно или оба посещения были по крайней мере 12 раз?
связанный >= 12 | фейсбук >= 12
В дни 1, 3, 4, 6 и 7 один или оба социальных профиля были посещены не менее 12 раз. | Скриншот: Линда Нго

 

НЕ Оператор «!»

Оператор НЕ, представленный восклицательным знаком ! просто инвертирует логическое значение, для которого оно используется. То есть !TRUE оценивается как FALSE , а !FALSE оценивается как TRUE .

!TRUE оценивается как FALSE, а !FALSE оценивается как TRUE. | Снимок экрана: Линда Нго

Как и операторы ИЛИ и И, мы можем использовать оператор НЕ в сочетании с логическими операторами. Это не всегда необходимо. Например, !(x < 5) совпадает с x >= 5 .

Однако в R есть случаи, когда оператор NOT особенно удобен. Например, встроенная функция R is.numeric() проверяет, является ли объект R числовым.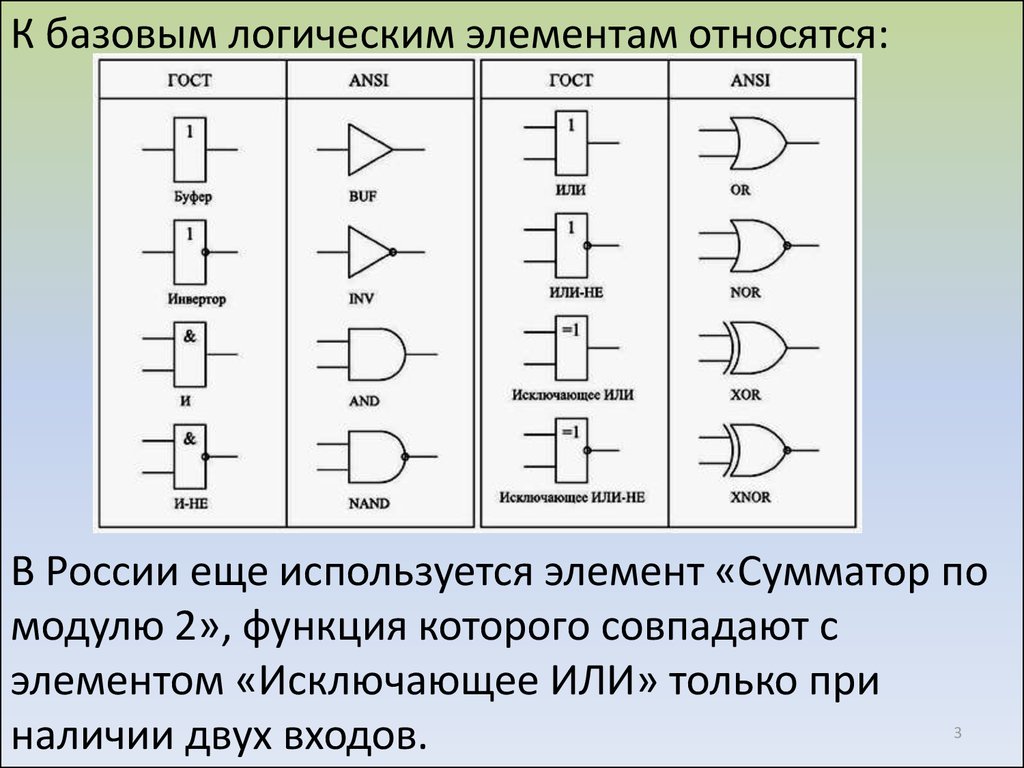 Нет соответствующей встроенной функции, которая проверяет, не является ли это числом. Для проверки нам пришлось бы инвертировать результат ( !is.numeric() ). Таким образом, is.numeric(5) оценивается как TRUE , так как пять является числом. Если мы отрицаем этот результат, используя оператор НЕ ( !is.numeric(5) ), получаем FALSE . Однако если мы используем is.numeric("hello") , мы получаем FALSE . Отрицание этого результата ( !is.numeric("hello") ) дает нам TRUE .

 

Логические операторы и векторы

Итак, как логические операторы работают с векторами и матрицами? Как и реляционные операторы, они выполняют операции поэлементно. Рассмотрим эти два вектора:

 c(ИСТИНА, ИСТИНА, ЛОЖЬ) и c(ИСТИНА, ЛОЖЬ, ЛОЖЬ)

Операция И над этими двумя векторами приводит к вектору с элементами ИСТИНА , ЛОЖЬ и ЛОЖЬ .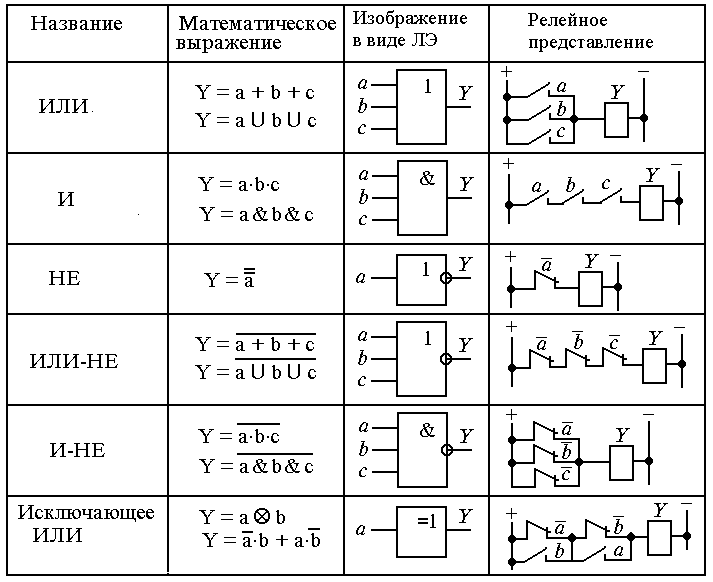

 ИСТИНА ЛОЖЬ ЛОЖЬ

Первыми элементами обоих векторов являются ИСТИНА , поэтому первый элемент результирующего вектора содержит ИСТИНА . То же самое относится ко вторым элементам, где ИСТИНА и ЛОЖЬ приводят к ЛОЖЬ , и к третьим элементам, где ЛОЖЬ и ЛОЖЬ дать ЛОЖЬ .

То же самое происходит с оператором ИЛИ:

 c(ИСТИНА, ИСТИНА, ЛОЖЬ) | c(ИСТИНА, ЛОЖЬ, ЛОЖЬ)

ИСТИНА | ИСТИНА дает ИСТИНА, ИСТИНА | ЛОЖЬ также дает ИСТИНА и ЛОЖЬ | ЛОЖЬ дает ЛОЖЬ . Итак, мы получили бы результат:

 ИСТИНА ИСТИНА ЛОЖЬ

Оператор НЕ работает также с каждым элементом вектора:

 !c(ИСТИНА, ИСТИНА, ЛОЖЬ)

ИСТИНА преобразуются в ЛОЖЬ , а ЛОЖЬ преобразуются в ИСТИНА . Таким образом, мы получили бы результат:

 FALSE FALSE TRUE
Использование логических операторов для утверждений true-false. 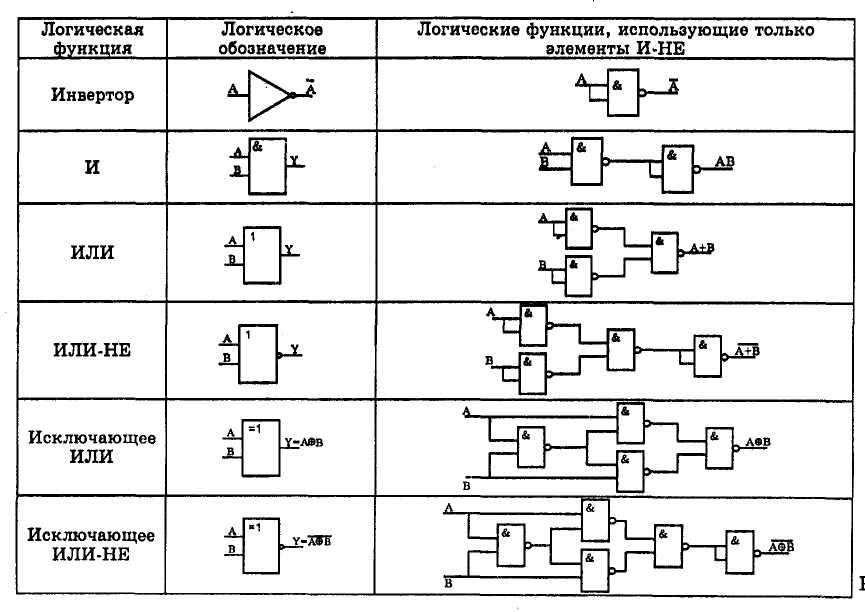| Снимок экрана: Линда Нго

 

Пример задачи логических операторов и векторов

Что вернет следующий набор выражений R:

 x <- 5
у <- 7
!(!(x < 4) & !!!(y > 12))

 

Решение 

 FALSE

Чтобы найти ответ, полезно разбить запрос на более мелкие выражения.

Сначала у нас есть левое выражение !(x < 4) внутреннего выражения (!(x < 4) & !!!(y > 12)) .

  1. x < 4 : Поскольку x равно пяти, а 5 < 4 неверно, это утверждение оценивается как FALSE .
  2. !(x < 4) : Из предыдущего шага мы определили, что x < 4 оценивается как FALSE . Отрицание этого результата дает нам !FALSE , что равно TRUE .

Далее у нас есть правильное выражение !!!(y > 12) внутреннего выражения (!(x < 4) & !!!(y > 12)) .

  1. y > 12 : Поскольку y равно семи, а 7 > 12 неверно, это выражение дает FALSE .
  2. !(y > 12) : Отрицая результат первого шага, получаем !ЛОЖЬ или ИСТИНА .
  3. !!(y > 12) : отрицая результат второго шага, мы получаем !TRUE или FALSE .
  4. !!!(y > 12) : Отрицая результат третьего шага, мы получаем !FALSE или TRUE .

Таким образом, для внутреннего выражения (!(x < 4) & !!!(y > 12)) оно оценивается как TRUE & TRUE , что равно TRUE .

Внешний оператор НЕ ! отрицает это ИСТИНА , что дает !(!(x < 4) & !!!(y > 12)) равно !ИСТИНА или ЛОЖЬ .

Учебник по логическим операторам в R. | Видео: DataCamp

Подробнее о науке о данных: как отобразить все столбцы и строки в Pandas DataFrame

 

Одиночные и двойные операторы «&» против «&&», «|» против «||»

В чем разница между одинарным и двойным амперсандом или вертикальной чертой? В R вы можете использовать как версию с одним знаком, так и версию с двумя знаками, но результат выполняемой вами логической операции может быть другим. Самая большая разница возникает, когда вы используете два типа операций над векторами.

 c(TRUE, TRUE, FALSE) & c(TRUE, FALSE, FALSE)

Как мы видели ранее, приведенное выше выражение оценивается как вектор:

 TRUE FALSE FALSE

Однако, если мы используем && , мы просто получаем TRUE .

 c(TRUE, TRUE, FALSE) && c(TRUE, FALSE, FALSE)

Это связано с тем, что операция двойного И проверяет только первый элемент каждого вектора. В этом случае первые элементы ИСТИНА и ИСТИНА , поэтому выражение возвращает TRUE .

Использование оператора && R. | Скриншот: Линда Нго

Вы можете видеть подобные вещи, происходящие с оператором OR. Версия с одним знаком | возвращает весь вектор. Версия с двойным знаком || возвращает результат оператора ИЛИ для первого элемента каждого вектора.

Использование || оператор в R. | Скриншот Linda Ngo

Так что будьте внимательны при выполнении логических операций над векторами. Скорее всего, вы захотите использовать версию с одним знаком для большинства действий.

Логические операторы Python с примерами

Улучшить статью

Сохранить статью

  • Уровень сложности: Easy
  • Последнее обновление: 09 янв, 2023

  • Читать
  • Обсудить

    • Улучшить статью

    Сохранить статью

    Операторы используются для выполнения операций над значениями и переменными. Это специальные символы, которые выполняют арифметические и логические вычисления. Значение, с которым работает оператор, известно как 9.0585 Операнд .

    Таблица содержимого

    • Логические операторы
      • Логический и оператор
      • Логический или оператор
      • Logical Not Operator
    • Орден Оценки логических операторов
    9008 используется в условных операторах (либо True, либо False). Они выполняют Логическое И , Логическое ИЛИ и Логическое НЕ операций.

    OPERATOR DESCRIPTION SYNTAX
    and Logical AND: True if both the operands are true x and y
    or Logical OR: True if either of операнды истинны x или y
    не Логическое НЕ: Истинно, если операнд ложен не x
    Таблица истинности для всех комбинаций значений X и Y.

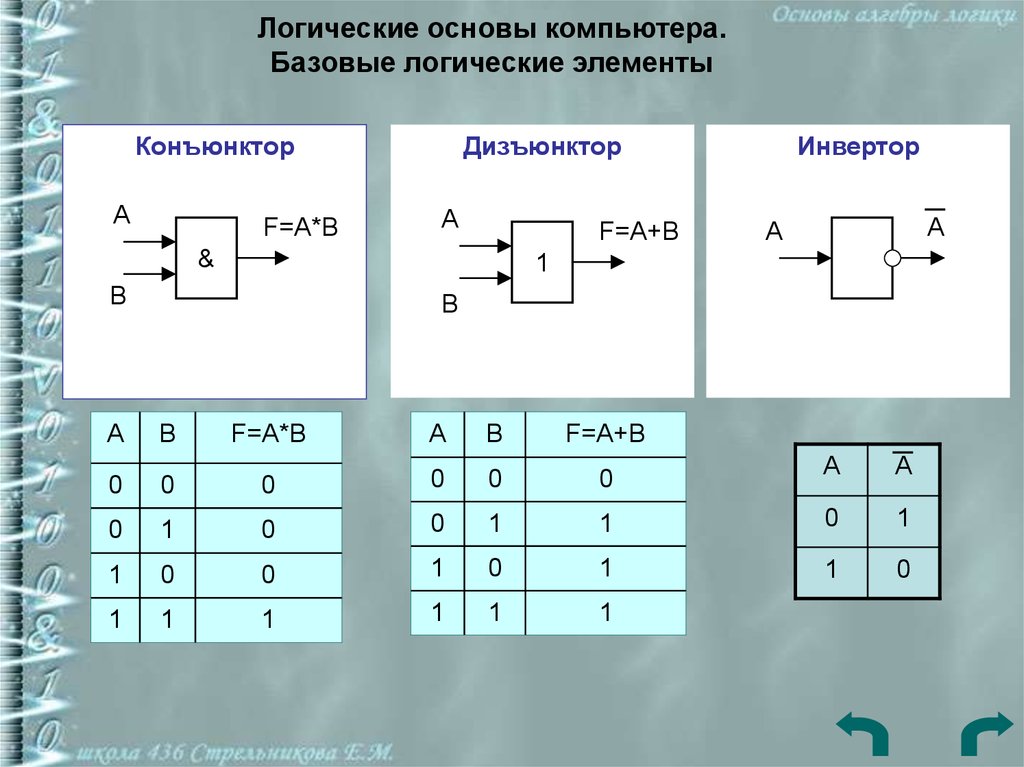
    Таблица истинности

    Логический оператор И

    Логический оператор возвращает значение Истина, если оба операнда имеют значение Истина, в противном случае он возвращает значение Ложь. Example #1:  

    Python3

     

    a = 10

    b = 10

    c = - 10

     

    , если а > 0 и B> 0 :

    Печать ( ». Числа больше 0" ( ". 0 and b > 0 and c > 0 :

         print ( "The numbers are greater than 0" )

    Else :

    Печать ( ». больше 0 Хотя бы одно число не больше 0

    Пример №2:  

    Python3

     

    a = 10

    b = 12

    c = 0

     

    if a and b and c:

    Печать ( «Все цифры имеют логическое значение как истинное» )

    ELS0014 ( "По крайней мере одно число имеет логическое значение как False" )

    Вывод 

     По крайней мере одно число имеет логическое значение как Fal

    Примечание: Если первое выражение оценивается как ложное при использовании оператора и, то последующие выражения не оцениваются.

    Логический оператор ИЛИ

    Логический оператор или возвращает значение Истина, если хотя бы один из операндов имеет значение Истина. Пример №1:  

    Python3

     

    a = 10

    b = - 10

    c = 0

     

    Если a> 0 или B> 0 :

    Печать ( "Ибо по номеру GREAGS ( ".0015 )

    else :

         print ( "No number is greater than 0" )

     

    if b > 0 или C> 0 :

    Печать ( "Любое из числа больше 0" )

    ESHIT )

    и ESH0015 :

         print ( "No number is greater than 0" )

    Output 

     Either of the number is greater than 0
Нет числа больше 0

      Example #2:  

    Python3

     

    a = 10

    b = 12

    c = 0

     

    if a or b or c:

         print ( "Atleast одно число имеет логическое значение как True" )

    else :

         print ( 5 )

    Вывод 

     По крайней мере одно число имеет логическое значение как True

    Примечание: Если первое выражение оценивается как True при использовании оператора или, то последующие выражения не оцениваются.

    Логический оператор "не"

    Логический оператор "не" работает с одним логическим значением. Если логическое значение равно True, оно возвращает False и наоборот. Пример:  

    Python3

     

    a = 10

     

    if not a:

         print ( "Boolean value of a is True" )

     

    if not (a % 3 = = 0 or a % 5 = = 0 ):

         print ( "10 is not divisible by either 3 or 5" )

    else :

    Печать ( "10 делится на 3 или 5" )

    .

    Порядок оценки логических операторов

    В случае нескольких операторов Python всегда оценивает выражение слева направо. В этом можно убедиться на приведенном ниже примере. Пример:

    Python3

    DEF Порядок (x):

    Печать (4 Печать (4 Print (4

    .

         возврат True if x > 0 else False

          

    a = order

    b = order

    c = order

     

    if a( - 1 ) or b( 5 ) или C ( 10 ):

    Печать ( "Atleast Один из числа.

    alexxlab

    Добавить комментарий

    Ваш адрес email не будет опубликован. Обязательные поля помечены *

    Внимание! Внешний вид товара, комплектация и характеристики могут изменяться производителем без предварительных уведомлений. Данный интернет-сайт носит исключительно информационный характер и ни при каких условиях не является публичной офертой, определяемой положениями Статьи 437 (2) Гражданского кодекса Российской Федерации. 2024 © Все права защищены.