НОУ ИНТУИТ | Лекция | Логические основы ЭВМ
Аннотация: Рассматриваются основные логические элементы и принципы их соединения в логические схемы.
Любая цифровая вычислительная машина состоит из логических схем — таких схем, которые могут находиться только в одном из двух возможных состояний — либо «логический ноль», либо «логическая единица». За логический 0 и логическую 1 можно принять любое выражение, в том числе и словесное, которое можно характеризовать как «истина» и «ложь». В вычислительной технике логические 0 и 1 — это состояние электрических схем с определенными параметрами. Так, для логических элементов и схем, выполненных по технологии транзисторно-транзисторной логики (ТТЛ-схемы), логический 0 — это напряжение в диапазоне 0 … + 0,4 В, а логическая 1 — это напряжение в диапазоне + 2,4 … + 5 В [1]. Работа логических схем описывается посредством специального математического аппарата, который называется логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 — 1864 гг.), она является основой всех методов упрощения булевых выражений.
Логические переменные и логические функции — это такие переменные и функции, которые могут принимать только два значения — либо логический 0, либо логическая 1.
Основные логические функции и элементы
Логический элемент — графическое представление элементарной логической функции.
Логическое умножение (конъюнкция) — функция И
Рассмотрим ключевую схему представленную на рис. 1.1,а. Примем за логический 0 [2]:
- на входе схемы разомкнутое состояние соответствующего ключа, например,
 ;
; - на выходе схемы (

Таблица истинности — это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции.
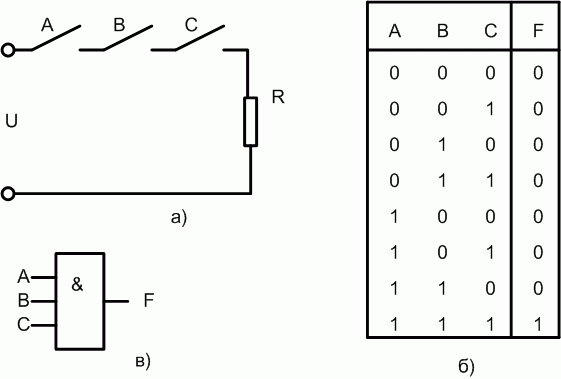
Рис. 1.1. Трёх-входовой логический элемент И
Таблица истинности для логической схемы, представленной на рис. 1.1,б, состоит из 8 строк, поскольку данная схема имеет три входа — 
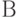 и
и  . Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно
. Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно 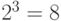
 , и
, и 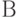 , и
, и  . Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.
. Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.
Уровень логического 0 является решающим для логического умножения .
В логических выражениях применяется несколько вариантов обозначения логического умножения. Так, для приведенного на рис. 1.1,в трёх-входового элемента И, логическое выражение можно представить в виде:
Логическое сложение (дизъюнкция) — функция ИЛИ
Рассмотрим ключевую схему, представленную на рис. 1.2,а. Таблица истинности для данной логической схемы (рис. 1.2,б) состоит из 4 строк, поскольку данная схема имеет два входа —  и
и 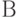 . Количество сочетаний этих переменных равно
. Количество сочетаний этих переменных равно 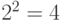 . Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или
. Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или  , или
, или 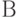 . Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.
. Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.
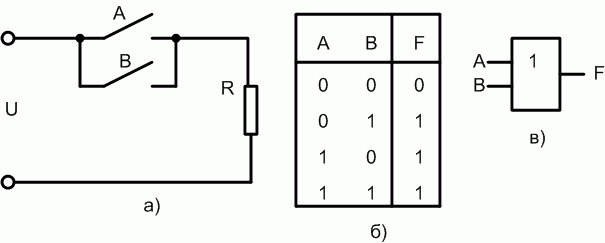
Рис. 1.2. Логический элемент ИЛИ на два входа
Правило логического сложения: если на вход логического элемента ИЛИ подается хотя бы одна логическая 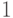 , то на его выходе будет логическая 1.
, то на его выходе будет логическая 1.
Для логического сложения решающим является уровень логической 1.
В логических выражениях применяется два варианта обозначения логического сложения. Так, для приведенного двух-входового элемента ИЛИ, логическое выражение можно представить в виде:
- либо
 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое; - либо
 — с использованием знака дизъюнкции.
— с использованием знака дизъюнкции.
Логическое отрицание (инверсия) — функция НЕ
Рассмотрим ключевую схему, представленную на рис. 1.3,а. Таблица истинности для данной схемы (рис. 1.3,б) самая простая и состоит всего из 2 строк, поскольку она (единственная из всех логических элементов) имеет только один вход —  . Количество вариантов для единственной логической переменной равно
. Количество вариантов для единственной логической переменной равно 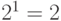 . Очевидно, что через сопротивление R ток протекает (
. Очевидно, что через сопротивление R ток протекает ( 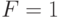 ) тогда, когда
) тогда, когда  не замкнут, т.е.
не замкнут, т.е. 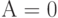 . Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.
. Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.
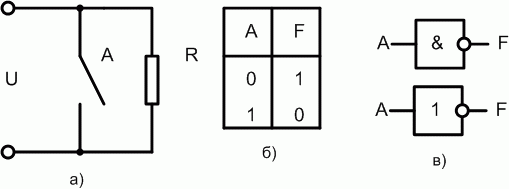
Рис. 1.3. Логический элемент НЕ
Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.
В логических выражениях применяется единственный вариант обозначения инверсии:

К основным логическим элементам относятся еще два элемента, которые являются комбинацией элементов И, ИЛИ и НЕ: элемент И-НЕ и ИЛИ-НЕ.
Логическая функция и элемент И-НЕ
Данная функция производит логическое умножение значений входных сигналов, а затем инвертирует результат этого умножения. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.
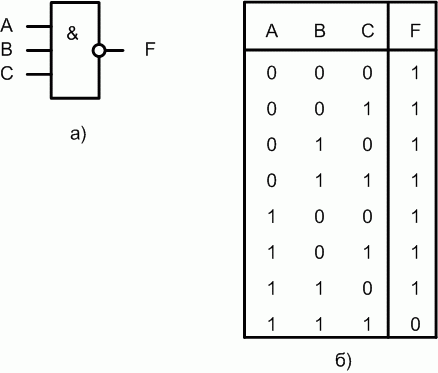
Рис. 1.4. Логический элемент И-НЕ на три входа
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1.
В логических выражениях применяются обозначения:
- либо
 , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
, но при этом из контекста должно быть ясно, что данное умножение именно логическое; - либо
 ;
; - либо
 ;
; - либо
 .
.
Логическая функция и элемент ИЛИ-НЕ
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.5,а. Таблица истинности приведена на рис. 1.5,б.
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.В логических выражениях применяются обозначения:
- либо
 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое; - либо
 .
.
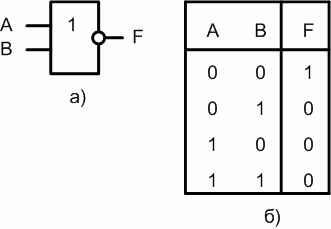
Рис. 1.5. Логический элемент ИЛИ-НЕ на два входа
НОУ ИНТУИТ | Лекция | Логические основы ЭВМ
Аннотация: Рассматриваются основные логические элементы и принципы их соединения в логические схемы.
Любая цифровая вычислительная машина состоит из логических схем — таких схем, которые могут находиться только в одном из двух возможных состояний — либо «логический ноль», либо «логическая единица»
Логические переменные и логические функции — это такие переменные и функции, которые могут принимать только два значения — либо логический 0, либо логическая 1.
Основные логические функции и элементы
Логический элемент — графическое представление элементарной логической функции.
Логическое умножение (конъюнкция) — функция И
Рассмотрим ключевую схему представленную на рис. 1.1,а. Примем за логический 0 [2]:
- на входе схемы разомкнутое состояние соответствующего ключа, например,
 ;
; - на выходе схемы (

Таблица истинности — это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции.

Рис. 1.1. Трёх-входовой логический элемент И
 ,
, 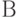 и
и  . Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно
. Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно 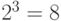
 , и
, и 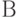 , и
, и  . Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.
. Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.
Уровень логического 0 является решающим для логического умножения .
В логических выражениях применяется несколько вариантов обозначения логического умножения. Так, для приведенного на рис. 1.1,в трёх-входового элемента И, логическое выражение можно представить в виде:
Логическое сложение (дизъюнкция) — функция ИЛИ
Рассмотрим ключевую схему, представленную на рис. 1.2,а. Таблица истинности для данной логической схемы (рис. 1.2,б) состоит из 4 строк, поскольку данная схема имеет два входа —  и
и 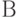 . Количество сочетаний этих переменных равно
. Количество сочетаний этих переменных равно 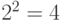 . Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или
. Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или  , или
, или 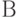 . Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.
. Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.

Рис. 1.2. Логический элемент ИЛИ на два входа
Правило логического сложения: если на вход логического элемента ИЛИ подается хотя бы одна логическая 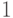 , то на его выходе будет логическая 1.
, то на его выходе будет логическая 1.
Для логического сложения решающим является уровень логической 1.
В логических выражениях применяется два варианта обозначения логического сложения. Так, для приведенного двух-входового элемента ИЛИ, логическое выражение можно представить в виде:
- либо
 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое; - либо
 — с использованием знака дизъюнкции.
— с использованием знака дизъюнкции.
Логическое отрицание (инверсия) — функция НЕ
Рассмотрим ключевую схему, представленную на рис. 1.3,а. Таблица истинности для данной схемы (рис. 1.3,б) самая простая и состоит всего из 2 строк, поскольку она (единственная из всех логических элементов) имеет только один вход —  . Количество вариантов для единственной логической переменной равно
. Количество вариантов для единственной логической переменной равно 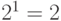 . Очевидно, что через сопротивление R ток протекает (
. Очевидно, что через сопротивление R ток протекает ( 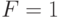 ) тогда, когда
) тогда, когда  не замкнут, т.е.
не замкнут, т.е. 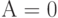 . Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.
. Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.

Рис. 1.3. Логический элемент НЕ
Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.
В логических выражениях применяется единственный вариант обозначения инверсии:

К основным логическим элементам относятся еще два элемента, которые являются комбинацией элементов И, ИЛИ и НЕ: элемент И-НЕ и ИЛИ-НЕ.
Логическая функция и элемент И-НЕ
Данная функция производит логическое умножение значений входных сигналов, а затем инвертирует результат этого умножения. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.

Рис. 1.4. Логический элемент И-НЕ на три входа
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1.
В логических выражениях применяются обозначения:
- либо
 , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
, но при этом из контекста должно быть ясно, что данное умножение именно логическое; - либо
 ;
; - либо
 ;
; - либо
 .
.
Логическая функция и элемент ИЛИ-НЕ
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.5,а. Таблица истинности приведена на рис. 1.5,б.
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.В логических выражениях применяются обозначения:
- либо
 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое; - либо
 .
.

Рис. 1.5. Логический элемент ИЛИ-НЕ на два входа
НОУ ИНТУИТ | Лекция | Логические основы ЭВМ
Аннотация: Рассматриваются основные логические элементы и принципы их соединения в логические схемы.
Любая цифровая вычислительная машина состоит из логических схем — таких схем, которые могут находиться только в одном из двух возможных состояний — либо «логический ноль», либо «логическая единица». За логический 0 и логическую 1 можно принять любое выражение, в том числе и словесное, которое можно характеризовать как «истина» и «ложь». В вычислительной технике логические 0 и 1 — это состояние электрических схем с определенными параметрами. Так, для логических элементов и схем, выполненных по технологии транзисторно-транзисторной логики (ТТЛ-схемы), логический 0 — это напряжение в диапазоне 0 … + 0,4 В, а логическая 1 — это напряжение в диапазоне + 2,4 … + 5 В [1]. Работа логических схем описывается посредством специального математического аппарата, который называется логической (булевой) алгеброй или алгеброй логики. Булева алгебра была разработана Джорджем Булем (1815 — 1864 гг.), она является основой всех методов упрощения булевых выражений.
Логические переменные и логические функции — это такие переменные и функции, которые могут принимать только два значения — либо логический 0, либо логическая 1.
Основные логические функции и элементы
Логический элемент — графическое представление элементарной логической функции.
Логическое умножение (конъюнкция) — функция И
Рассмотрим ключевую схему представленную на рис. 1.1,а. Примем за логический 0 [2]:
- на входе схемы разомкнутое состояние соответствующего ключа, например,
 ;
; - на выходе схемы (
 ) — такое ее состояние, когда через сопротивление R ток не протекает.
) — такое ее состояние, когда через сопротивление R ток не протекает.
Таблица истинности — это таблица, содержащая все возможные комбинации входных логических переменных и соответствующие им значения логической функции.

Рис. 1.1. Трёх-входовой логический элемент И
Таблица истинности для логической схемы, представленной на рис. 1.1,б, состоит из 8 строк, поскольку данная схема имеет три входа —  ,
, 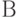 и
и  . Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно
. Каждая из этих логических переменных может находиться либо в состоянии логического 0, либо логической 1. Соответственно количество сочетаний этих переменных равно 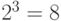 . Очевидно, что через сопротивление R ток протекает только тогда, когда замкнуты все три ключа — и
. Очевидно, что через сопротивление R ток протекает только тогда, когда замкнуты все три ключа — и  , и
, и 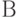 , и
, и  . Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.
. Отсюда еще одно название логического умножения — логический элемент И. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.1,в.
Правило логического умножения :если на вход логического элемента И подается хотя бы один логический 0, то на его выходе будет логический 0.
Уровень логического 0 является решающим для логического умножения .
В логических выражениях применяется несколько вариантов обозначения логического умножения. Так, для приведенного на рис. 1.1,в трёх-входового элемента И, логическое выражение можно представить в виде:
Логическое сложение (дизъюнкция) — функция ИЛИ
Рассмотрим ключевую схему, представленную на рис. 1.2,а. Таблица истинности для данной логической схемы (рис. 1.2,б) состоит из 4 строк, поскольку данная схема имеет два входа —  и
и 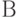 . Количество сочетаний этих переменных равно
. Количество сочетаний этих переменных равно 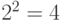 . Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или
. Очевидно, что через сопротивление R ток протекает тогда, когда замкнуты или  , или
, или 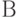 . Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.
. Отсюда еще одно название логического сложения — логическое ИЛИ. В логических схемах соответствующий логический элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.2,в.

Рис. 1.2. Логический элемент ИЛИ на два входа
Правило логического сложения: если на вход логического элемента ИЛИ подается хотя бы одна логическая 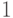 , то на его выходе будет логическая 1.
, то на его выходе будет логическая 1.
Для логического сложения решающим является уровень логической 1.
В логических выражениях применяется два варианта обозначения логического сложения. Так, для приведенного двух-входового элемента ИЛИ, логическое выражение можно представить в виде:
- либо
 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое; - либо
 — с использованием знака дизъюнкции.
— с использованием знака дизъюнкции.
Логическое отрицание (инверсия) — функция НЕ
Рассмотрим ключевую схему, представленную на рис. 1.3,а. Таблица истинности для данной схемы (рис. 1.3,б) самая простая и состоит всего из 2 строк, поскольку она (единственная из всех логических элементов) имеет только один вход —  . Количество вариантов для единственной логической переменной равно
. Количество вариантов для единственной логической переменной равно 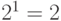 . Очевидно, что через сопротивление R ток протекает (
. Очевидно, что через сопротивление R ток протекает ( 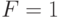 ) тогда, когда
) тогда, когда  не замкнут, т.е.
не замкнут, т.е. 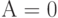 . Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.
. Еще одно название этой логической функции — отрицание, а соответствующий логический элемент называется инвертором. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.3,в. Поскольку он имеет только один вход, в его обозначении допустимым является и знак логического сложения, и знак логического умножения.

Рис. 1.3. Логический элемент НЕ
Правило инверсии: проходя через инвертор, сигнал меняет свое значение на противоположное.
В логических выражениях применяется единственный вариант обозначения инверсии:

К основным логическим элементам относятся еще два элемента, которые являются комбинацией элементов И, ИЛИ и НЕ: элемент И-НЕ и ИЛИ-НЕ.
Логическая функция и элемент И-НЕ
Данная функция производит логическое умножение значений входных сигналов, а затем инвертирует результат этого умножения. В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.4,а. Таблица истинности приведена на рис. 1.4,б.

Рис. 1.4. Логический элемент И-НЕ на три входа
Если на вход логического элемента И-НЕ подается хотя бы один логический 0, то на его выходе будет логическая 1.
В логических выражениях применяются обозначения:
- либо
 , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
, но при этом из контекста должно быть ясно, что данное умножение именно логическое; - либо
 ;
; - либо
 ;
; - либо
 .
.
Логическая функция и элемент ИЛИ-НЕ
В логических схемах этот элемент независимо от того, на какой элементной базе он реализован, обозначается так, как показано на рис. 1.5,а. Таблица истинности приведена на рис. 1.5,б.
Если на вход логического элемента ИЛИ-НЕ подается хотя бы одна логическая 1, то на его выходе будет логический 0.В логических выражениях применяются обозначения:
- либо
 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое; - либо
 .
.

Рис. 1.5. Логический элемент ИЛИ-НЕ на два входа
Аннотация: Рассматривается различные технологии реализации логических элементов.
Логические элементы транзисторно-транзисторной логики
Схемы транзисторно-транзисторной логики (ТТЛ) базируются на биполярных транзисторах npn-структуры. Базовым элементом (рис. 16.1) данной технологии является схема И-НЕ. Логическое умножение осуществляется за счет свойств многоэмиттерного транзистора VT1 [1]. При подаче хотя бы одного логического нуля на эмиттеры этого транзистора замыкается цепь: +5 В, сопротивление R1, переход база-эмиттер, земля на входе. При этом транзисторы VT2 и VT3 остаются закрытыми. Поэтому выходная цепь не замкнута, падения напряжения в ней нет, следовательно, в точке F на выходе схемы будет потенциал источника питания, т.е. логическая единица. Выполняется правило И-НЕ [2]: при подаче хотя бы одного нуля на выходе схемы получили логическую единицу.
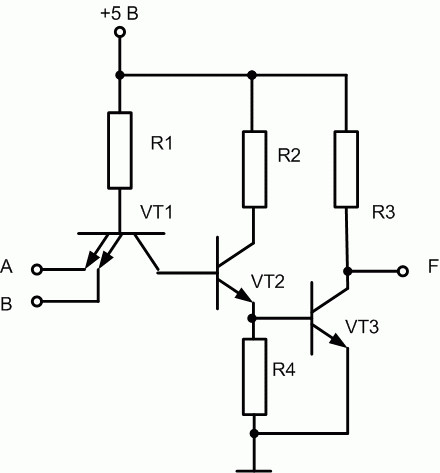
Рис. 16.1. Базовый элемент И-НЕ на ТТЛ
При подаче логической единицы на все входы схемы замыкается цепь: +5 В, сопротивление R2, транзистор VT2, сопротивление R3 , земля. Следовательно, на базу выходного транзистора VT3 подается потенциал, достаточный для его открытия (соответствует падению напряжения на сопротивлении R3). Через открытый транзистор VT3 замыкается буферная цепь: +5 В, сопротивление R4, транзистор VT3, земля. Следовательно, на выходе F будет потенциал, соответствующий падению напряжения на открытом транзисторе VT3, т.е. 0.4 В. Таким образом, F=0.
На рис. 16.2 представлен логический элемент ИЛИ-НЕ. Логическое сложение осуществляется за счет монтажного соединения транзисторов VT3 и VT4. Замыкание буферной цепи (состояние F=0 ) в этом случае возможно при замыкании хотя бы одной из цепей, проходящих через сопротивления R2 и R3. Эти цепи замыкаются в том случае, если на входы подается хотя бы одна логическая единица. Таким образом, выполняется правило ИЛИ-НЕ [2]: при подаче хотя бы одной единицы на выходе схемы получим логический ноль.
При замене в схеме И-НЕ многоэмиттерного транзистора VT1 на одноэмиттерный получается инвертор (рис. 16.3).
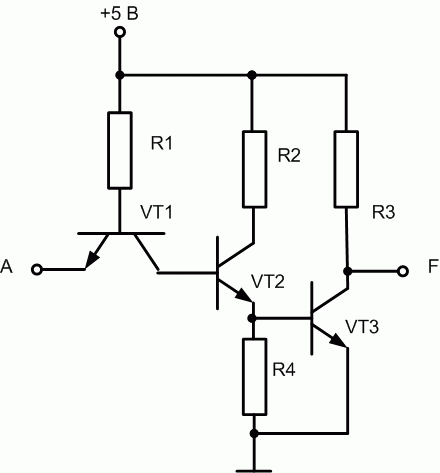
Рис. 16.3. Логический элемент НЕ на ТТЛ
Буферная часть схем логических элементов ТТЛ-технологии может быть реализована по-разному. В частности, резистор в буферной части может быть вынесен за пределы интегральной схемы, при этом существенно уменьшаются потери и нагрев кристалла. Такие схемы называются схемами «с открытым коллектором «. Пример такой схемы приведен на рис. 16.4.
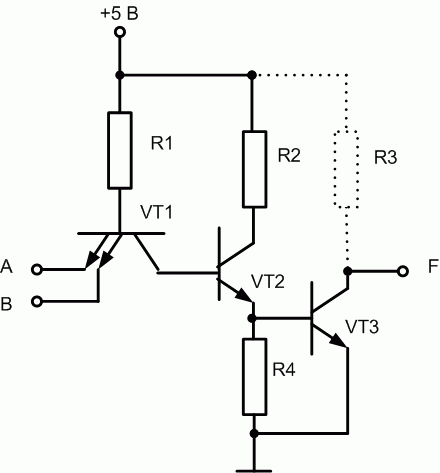
Рис. 16.4. Базовый элемент И-НЕ на ТТЛ с открытым коллектором
В схемах с активной нагрузкой (рис. 16.5) состояние буферной цепи определяется состоянием не одного, а двух транзисторов.
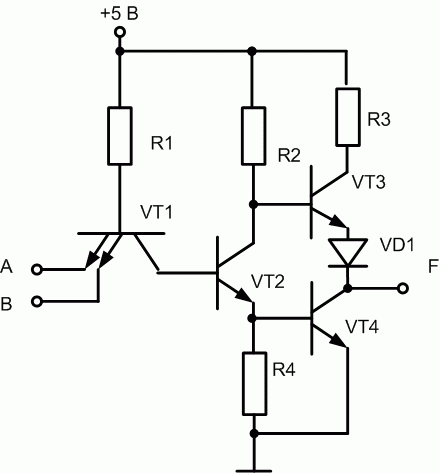
Рис. 16.5. Базовый элемент И-НЕ на ТТЛ с активной нагрузкой
Буферные схемы на три состояния (первые два – логический 0 и логическая 1 ) имеют помимо информационных, разрешающий вход Е (рис. 16.6). При Е=1 диод VD2 подключен на обратное напряжение, поэтому дополнительная цепь, включающая в себя диод VD2 и вход Е, разомкнута и не влияет на работу логического элемента. Таким образом, осуществляется «разрешение» работы элемента. При отсутствии такового разрешения Е=0. Диод VD2 оказывается подключенным на прямое напряжение, замыкается цепь + 5 В, сопротивление R2, открытый диод VD2, земля на входе E. Следовательно, на базу транзистора VT3 в буферной части схемы подается потенциал, соответствующий падению напряжения на открытом диоде, т.е. 0.2 В. При таких условиях данный транзистор закрыт, поэтому выход F оказывается отключенным от источника питания. Кроме того, независимо от состояния информационных входов A и B, замкнется входная цепь +5 В, сопротивление R1, переход база-эмиттер транзистора VT1, земля на входе E. Поэтому, как было описано выше, транзисторы VT2 и VT4 будут закрыты. Вследствие закрытия VT4 выход F будет отключен также и от земли. Таким образом, схема будет не в нулевом и не в единичном, а в «третьем» состоянии, которое называется состоянием высокого сопротивления, Z-состоянием
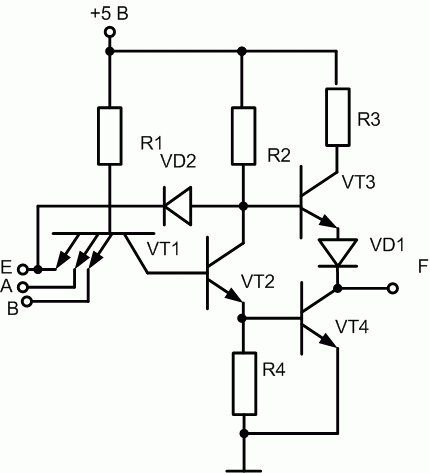
Рис. 16.6. Базовый элемент И-НЕ на ТТЛ с выходом на три состояния
Логические элементы nМОП-технологии
Схемы nМОП-технологии базируются на полевых (МОП) транзисторах с индуцированным каналом n-типа. Базовым элементом (рис. П16.7) данной технологии является схема И-НЕ. Логическое умножение осуществляется за счет последовательного соединения каналов транзисторов VT1 и VT2. Канал между истоком и стоком в nМОП-транзисторе индуцируется в том случае, когда на затвор (вход схемы) подается положительный относительно подложки потенциал. Цепь от +5 В до земли замкнется только в одном случае, когда A=B=1, поскольку в этом случае оба транзистора открываются и образуется единый канал, замыкающий цепь.
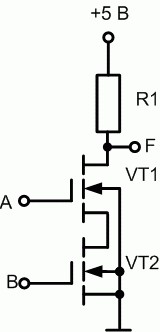
Рис. 16.7. Логический элемент И-НЕ nМОП-технологии
Функция ИЛИ-НЕ осуществляется за счет параллельного соединения таких транзисторов (рис. 16.8): при подаче хотя бы на один вход единицы индуцируется канал в соответствующем транзисторе и замыкается цепь от +5 В до земли. Следовательно, на выходе будет потенциал, соответствующий падению напряжения в канале транзистора, т.е. 0,2 В, при этом F=0.
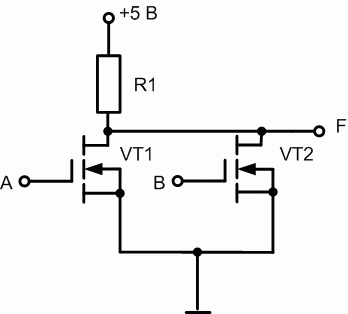
Рис. 16.8. Логический элемент ИЛИ-НЕ nМОП-технологии
Схема инвертора (рис. 16.9) строится на базе одного транзистора.
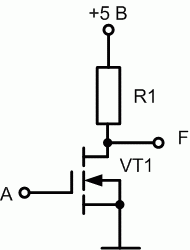
Рис. 16.9. Логический элемент НЕ nМОП-технологии
Логическая функция — это функция логических переменных, которая
может принимать только два значения : 0 или 1. В свою очередь,
сама логическая переменная (аргумент логической функции) тоже может
принимать только два значения : 0 или 1.
Логический элемент — это устройство, реализующее ту или иную
логическую функцию.
Y=f(X1,X2,X3,…,Xn) — логическая функция, она может быть задана
таблицей, которая называется таблицей истинности.
Число строк в таблице — это число возможных наборов значений
аргументов. Оно равно 2n, где n — число переменных.
Число различных функций n переменных равно 22^n.
Логические функции одной переменной
Таблица истинности функции одной переменной Y=f(X) содержит всего
2 строки, а число функций одной переменной равно 4.
1. Функция константа 0, Y=0. Техническая реализация этой функции —
соединение вывода Y с общей шиной с нулевым потенциалом.
Таблица истинности функции константа 0 имеет вид:
2. Функция Y=f(X)=X — функция повторения. Техническая реализация
этой функции — соединение между собой выводов X и Y.
Таблица истинности функции повторения имеет вид:
3. Функция Y=f(X)=NOT(X) — отрицание НЕ или инверсия (NOT(X) — это НЕ X).
Техническая реализация этой функции — инвертор на любом транзисторе
или логическом элементе, или транзисторный ключ.
Таблица истинности функции отрицания имеет вид:
Логический элемент НЕ обозначается на схемах следующим образом:
(пишется X c чертой сверху)
4. Функция константа 1, Y=1. Техническая реализация этой функции —
соединение вывода Y с источником питания.
Таблица истинности функции константа 1 имеет вид:
Важнейшей функцией одной переменной является отрицание НЕ,
остальные функции являются тривиальными.
Логические функции двух переменных
Таблица истинности функции двух переменных Y=f(X1,Х2) содержит 4
строки, а число функций двух переменных равно 16.
Мы рассмотрим только несколько основных функций двух переменных.
1. Логическое ИЛИ (логическое сложение, дизъюнкция):
Y= X1 + X2 = X1VX2
Техническая реализация этой функции — два параллельно соединенных
ключа:
Таблица истинности логического ИЛИ имеет вид:
Логический элемент ИЛИ обозначается на схемах следующим образом:
2. Логическое И (логическое умножение, конъюнкция, схема совпаде-
ний): Y = X1X2 = X1&X2
Техническая реализация этой функции — два последовательно сое-
диненных ключа:
Таблица истинности логического И имеет вид:
Логический элемент И обозначается на схемах следующим образом:
3. Функция стрелка Пирса (ИЛИ-НЕ): Y = NOT(X1+X2)
Таблица истинности функции ИЛИ-НЕ имеет вид:
Логический элемент ИЛИ-НЕ обозначается на схемах следующим образом:
4. Функция штрих Шеффера (И-НЕ): Y = X1|X2 = NOT(X1X2)
Таблица истинности функции И-НЕ имеет вид:
Логический элемент И-НЕ обозначается на схемах следующим образом:
Есть ещё три логические функции двух переменных, имеющие специ-
альные названия: импликация, эквивалентность, неравнозначность
(исключающее ИЛИ, сложение по модулю 2). Последние две функции
являются взаимно обратными, также как, например, функция И и
функция штрих Шеффера.
Элемент памяти — RS-триггер
Триггер — это логическое устройство, способное хранить 1 бит ин-
формации. К триггерам относятся устойства, имеющие два устойчивых
состояния. Простейший триггер — RS-триггер, образован из двух
элементов И-НЕ (или ИЛИ-НЕ). Он позволяет запоминать 1 бит инфор-
мации, поскольку информация в компьютере представляется в двоич-
ном виде. Его схема приведена ниже.
Действие RS-триггера поясняется в приведенной ниже таблице ис-
тинности. S-вход установки (Set), R-вход сброса (Reset).
В обычном (исходном) состоянии на входы триггера поданы 1. Для
записи информации на вход R подан 0. Для сброса информации и под-
готовки к приёму новой информации на вход S подается 0 и триггер
вернётся в исходное состояние.
Поскольку один триггер запоминает 1 бит информации, то для запо-
минания 1 байта (8 бит) нужно 8 триггеров, для запоминания 1 Кб
(1024 байт) надо 8192 триггеров. Современные микросхемы ОЗУ спо-
собны запоминать десятки мегабайт информации.
Элементы математической логики
Существуют такие наборы логических функций, с помощью которых
можно выразить любые другие логические функции. Они называются
функционально полными или базисами. Наиболее известный базис -
это набор функций И, ИЛИ, НЕ. Функция штрих Шеффера является ба-
зисной, также как и функция стрелка Пирса. Поэтому, с помощью ло-
гических элементов ИЛИ-НЕ или И-НЕ можно собрать любую логическую
схему. На таких элементах собран микропроцессор компьютера и дру-
гие логические устройства. Логические схемы состоят из логических
элементов, осуществляющих логические операции.
Логика — наука, изучающая методы установления истинности или лож-
ности одних высказываний на основе истинности или ложности других
высказываний (утверждений). Логика изучает методы доказательств и
опровержений. Логика составляет основу всякого управления, в том
числе технологическими процессами.
Математическая логика — современная форма логики, опирающаяся на
формальные математические методы.
Основные объекты логики — высказывания, то есть предложения, ко-
торые могут быть либо истинными, либо ложными. Существуют два
подхода установления истинности высказываний: эмпирический (опыт-
ный) и логический. При эмпирическом подходе истинность высказыва-
ний устанавливается на основе наблюдений, экспериментов, докумен-
тов и других фактов. При логическом подходе истинность высказыва-
ний доказывается на основе истинности других высказываний, то
есть чисто формально, на основе рассуждений без обращения к фак-
там.
В языках программирования QBasic и Turbo Pascal логические функ-
ции И, ИЛИ, НЕ реализуются в виде логических операций OR (ИЛИ),
AND (И), NOT (НЕ).
Множество всех логических функций, на котором определены три ло-
гические операции И, ИЛИ, НЕ называется булевой алгеброй (по име-
ни основоположника математической логики английского математика
Джорджа Буля). Упрощение формул в булевой алгебре производится на
основе эквивалентных преобразований, опирающихся на следующие ос-
новные законы (эквивалентные соотношения):
Кроме того, применяются ещё три соотношения:
Законы 1,2,3,7 показывают, что свойства конъюнкции очень похожи
на свойства умножения, поэтому её часто называют логическим умно-
жением. Из законов 6 и 8 следует, что используя отрицание, дизъ-
юнкцию можно выразить через конъюнкцию, и наоборот:
Это означает, что наборы И-НЕ и ИЛИ-НЕ также являются функцио-
нально полными или базисными.
Логические элементы — Википедия
Логические элементы — устройства, предназначенные для обработки информации в цифровой форме (последовательности сигналов высокого — «1» и низкого — «0» уровней в двоичной логике, последовательность «0», «1» и «2» в троичной логике, последовательностями «0», «1», «2», «3», «4», «5», «6», «7», «8» и «9» в десятичной логике). Физически логические элементы могут быть выполнены механическими, электромеханическими (на электромагнитных реле), электронными (на диодах и транзисторах), пневматическими, гидравлическими, оптическими и др.
С развитием электротехники от механических логических элементов перешли к электромеханическим логическим элементам (на электромагнитных реле), а затем к электронным логическим элементам на электронных лампах, позже — на транзисторах. После доказательства в 1946 г. теоремы Джона фон Неймана об экономичности показательных позиционных систем счисления стало известно о преимуществах двоичной и троичной систем счисления по сравнению с десятичной системой счисления. От десятичных логических элементов перешли к двоичным логическим элементам. Двоичность и троичность позволяет значительно сократить количество операций и элементов, выполняющих эту обработку, по сравнению с десятичными логическими элементами.
Логические элементы выполняют логическую функцию (операцию) над входными сигналами (операндами, данными).
Всего возможно x ( x n ) ∗ m {\displaystyle \ x^{(x^{n})*m}} логических функций и соответствующих им логических элементов, где x {\displaystyle \ x} — основание системы счисления, n {\displaystyle \ n} — число входов (аргументов), m {\displaystyle \ m} — число выходов, то есть бесконечное число логических элементов. Поэтому в данной статье рассматриваются только простейшие и важнейшие логические элементы.
Всего возможны 2 ( 2 2 ) ∗ 1 = 2 4 = 16 {\displaystyle 2^{(2^{2})*1}=2^{4}=16} двоичных двухвходовых логических элементов и 2 ( 2 3 ) ∗ 1 = 2 8 = 256 {\displaystyle 2^{(2^{3})*1}=2^{8}=256} двоичных трёхвходовых логических элементов (Булева функция).
Кроме 16 двоичных двухвходовых логических элементов и 256 трёхвходовых двоичных логических элементов возможны 19 683 двухвходовых троичных логических элементов и 7 625 597 484 987 трёхвходовых троичных логических элементов (троичные функции).
Логические операции (булева функция) своё теоретическое обоснование получили в алгебре логики.
Логические операции с одним операндом называются унарными, с двумя — бинарными, с тремя — тернарными (триарными, тринарными) и т. д.
Из 2 ( 2 1 ) = 2 2 = 4 {\displaystyle 2^{(2^{1})}=2^{2}=4} возможных унарных операций с унарным выходом интерес для реализации представляют операции отрицания и повторения, причём, операция отрицания имеет большую значимость, чем операция повторения, так как повторитель может быть собран из двух инверторов, а инвертор из повторителей не собрать.
Отрицание, НЕ
 Инвертор, НЕ (IEC)
Инвертор, НЕ (IEC)  Инвертор, НЕ (ANSI)
Инвертор, НЕ (ANSI)| A {\displaystyle A} | ¬ A {\displaystyle A} |
|---|---|
| 0 | 1 |
| 1 | 0 |
Мнемоническое правило для отрицания звучит так: На выходе будет:
Повторение
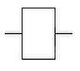
| A {\displaystyle A} | A {\displaystyle A} |
|---|---|
| 0 | 0 |
| 1 | 1 |
Преобразование информации требует выполнения операций с группами знаков, простейшей из которых является группа из двух знаков. Оперирование с большими группами всегда можно разбить на последовательные операции с двумя знаками.
Из 2 ( 2 2 ) = 2 4 = 16 {\displaystyle 2^{(2^{2})}=2^{4}=16} возможных бинарных логических операций с двумя знаками c унарным выходом интерес для реализации представляют 10 операций, приведённых ниже.
Конъюнкция (логическое умножение). Операция И

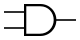
| A {\displaystyle A} | B {\displaystyle B} | A ∧ B {\displaystyle A\land B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Логический элемент, реализующий функцию конъюнкции, называется схемой совпадения. Мнемоническое правило для конъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «1»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «0»
Словесно эту операцию можно выразить следующим выражением: «Истина на выходе может быть при истине на входе 1 И истине на входе 2».
Дизъюнкция (логическое сложение). Операция ИЛИ

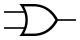
| A {\displaystyle A} | B {\displaystyle B} | A ∨ B {\displaystyle A\lor B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для дизъюнкции с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «1»,
- «0» тогда и только тогда, когда на всех входах действуют «0»
Инверсия функции конъюнкции. Операция И-НЕ (штрих Шеффера)


| A {\displaystyle A} | B {\displaystyle B} | A | B {\displaystyle A|B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для И-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда хотя бы на одном входе действует «0»,
- «0» тогда и только тогда, когда на всех входах действуют «1»
Инверсия функции дизъюнкции. Операция ИЛИ-НЕ (стрелка Пирса)
В англоязычной литературе NOR.
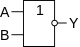
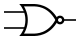
| A {\displaystyle A} | B {\displaystyle B} | A {\displaystyle A} ↓ B {\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для ИЛИ-НЕ с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на всех входах действуют «0»,
- «0» тогда и только тогда, когда хотя бы на одном входе действует «1»
Эквивалентность (равнозначность), ИСКЛЮЧАЮЩЕЕ_ИЛИ-НЕ
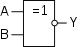 ИСКЛ-ИЛИ-НЕ (IEC)
ИСКЛ-ИЛИ-НЕ (IEC) 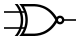 ИСКЛ-ИЛИ-НЕ (ANSI)
ИСКЛ-ИЛИ-НЕ (ANSI)| A {\displaystyle A} | B {\displaystyle B} | A {\displaystyle A} ↔ B {\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило эквивалентности с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует чётное количество,
- «0» тогда и только тогда, когда на входе действует нечётное количество
Словесная запись: «истина на выходе при истине на входе 1 и входе 2 или при лжи на входе 1 и входе 2».
Сложение (сумма) по модулю 2 (Исключающее_ИЛИ, неравнозначность). Инверсия равнозначности.

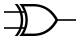
В англоязычной литературе XOR.
| A {\displaystyle A} | B {\displaystyle B} | A ⊕ B {\displaystyle A\oplus B} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для суммы по модулю 2 с любым количеством входов звучит так: На выходе будет:
- «1» тогда и только тогда, когда на входе действует нечётное количество ,
- «0» тогда и только тогда, когда на входе действует чётное количество
Словесное описание: «истина на выходе — только при истине на входе 1, либо только при истине на входе 2».
Импликация от A к B (прямая импликация, инверсия декремента, A<=B)
| A {\displaystyle A} | B {\displaystyle B} | A {\displaystyle A} → B {\displaystyle B} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии декремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» меньше «А»,
- «1» тогда и только тогда, когда на «B» больше либо равно «А»
Импликация от B к A (обратная импликация, инверсия инкремента, A>=B)
| A {\displaystyle A} | B {\displaystyle B} | B {\displaystyle B} → A {\displaystyle A} |
|---|---|---|
| 0 | 0 | 1 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
Мнемоническое правило для инверсии инкремента звучит так: На выходе будет:
- «0» тогда и только тогда, когда на «B» больше «А»,
- «1» тогда и только тогда, когда на «B» меньше либо равно «А»
Декремент. Запрет импликации по B. Инверсия импликации от A к B
| A {\displaystyle A} | B {\displaystyle B} | f ( A , B ) {\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от A к B звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «A» больше «B»,
- «0» тогда и только тогда, когда на «A» меньше либо равно «B»
Инкремент. Запрет импликации по A. Инверсия импликации от B к A
| A {\displaystyle A} | B {\displaystyle B} | f ( A , B ) {\displaystyle f(A,B)} |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 0 |
| 1 | 1 | 0 |
Мнемоническое правило для инверсии импликации от B к A звучит так: На выходе будет:
- «1» тогда и только тогда, когда на «B» больше «A»,
- «0» тогда и только тогда, когда на «B» меньше либо равно «A»
Примечание 1. Элементы импликаций не имеют промышленных аналогов для функций с количеством входов, не равным 2.
Примечание 2. Элементы импликаций не имеют промышленных аналогов.
Этими простейшими логическими операциями (функциями), и даже некоторыми их подмножествами, можно выразить любые другие логические операции. Такой набор простейших функций называется функционально полным логическим базисом. Таких базисов 4:
- И, НЕ (2 элемента)
- ИЛИ, НЕ (2 элемента)
- И-НЕ (1 элемент)
- ИЛИ-НЕ (1 элемент).
Для преобразования логических функций в один из названых базисов необходимо применять Закон (правило) де-Моргана.
Физические реализации
Реализация логических элементов возможна при помощи устройств, использующих самые разнообразные физические принципы:
- механические,
- гидравлические,
- пневматические,
- электромагнитные,
- электромеханические,
- электронные,
- оптические.
Физические реализации одной и той же логической функции, а также обозначения для истины и лжи, в разных системах электронных и неэлектронных элементов отличаются друг от друга.
Классификация электронных транзисторных физических реализаций логических элементов
Логические элементы подразделяются и по типу использованных в них электронных элементов. Наибольшее применение в настоящее время находят следующие логические элементы:
- РТЛ (резисторно-транзисторная логика)
- ДТЛ (диодно-транзисторная логика)
- ТТЛ (транзисторно-транзисторная логика)
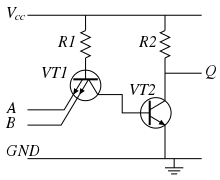 Упрощённая схема двухвходового элемента И-НЕ ТТЛ .
Упрощённая схема двухвходового элемента И-НЕ ТТЛ .Обычно входной каскад логических элементов ТТЛ представляет собой простейшие компараторы, которые могут быть выполнены различными способами (на многоэмиттерном транзисторе или на диодной сборке). В логических элементах ТТЛ входной каскад, кроме функций компараторов, выполняет и логические функции. Далее следует выходной усилитель с двухтактным (двухключевым) выходом.
В логических элементах КМОП входные каскады также представляют собой простейшие компараторы. Усилителями являются КМОП-транзисторы. Логические функции выполняются комбинациями параллельно и последовательно включенных ключей, которые одновременно являются и выходными ключами.
Транзисторы могут работать в инверсном режиме, но с меньшим коэффициентом усиления. Это свойство используется в ТТЛ многоэмиттерных транзисторах. При подаче на оба входа сигнала высокого уровня (1,1) первый транзистор оказывается включённым в инверсном режиме по схеме эмиттерного повторителя с высоким уровнем на базе, транзистор открывается и подключает базу второго транзистора к высокому уровню, ток идёт через первый транзистор в базу второго транзистора и открывает его. Второй транзистор «открыт», его сопротивление мало и на его коллекторе напряжение соответствует низкому уровню (0). Если хотя бы на одном из входов сигнал низкого уровня (0), то транзистор оказывается включённым по схеме с общим эмиттером, через базу первого транзистора на этот вход идёт ток, что открывает его и он закорачивает базу второго транзистора на землю, напряжение на базе второго транзистора мало и он «закрыт», выходное напряжение соответствует высокому уровню. Таким образом, таблица истинности соответствует функции 2И-НЕ.
Для увеличения быстродействия логических элементов в них используются транзисторы Шоттки (транзисторы с диодами Шоттки), отличительной особенностью которых является применение в их конструкции выпрямляющего контакта металл-полупроводник вместо p-n перехода. При работе этих приборов отсутствует инжекция неосновных носителей и явления накопления и рассасывания заряда, что обеспечивает высокое быстродействие. Включение этих диодов параллельно коллекторному переходу блокирует насыщение выходных транзисторов, что увеличивает напряжения логических 0 и 1, но уменьшает потери времени на переключение логического элемента при том же потребляемом токе (или позволяет уменьшить потребляемый ток при сохранении стандартного быстродействия). Так, серия 74хх и серия 74LSxx имеют приблизительно равное быстродействие (в действительности, серия 74LSxx несколько быстрее), но потребляемый от источника питания ток меньше в 4-5 раз (во столько же раз меньше и входной ток логического элемента).
Эта логика, иначе называемая логикой на переключателях тока, построена на базе биполярных транзисторов, объединённых в дифференциальные каскады. Один из входов обычно подключён внутри микросхемы к источнику опорного (образцового) напряжения, примерно посредине между логическими уровнями. Сумма токов через транзисторы дифференциального каскада постоянна, в зависимости от логического уровня на входе изменяется лишь то, через какой из транзисторов течёт этот ток. В отличие от ТТЛ, транзисторы в ЭСЛ работают в активном режиме и не входят в насыщение или инверсный режим. Это приводит к тому, что быстродействие ЭСЛ-элемента при той же технологии (тех же характеристиках транзисторов) гораздо больше, чем ТТЛ-элемента, но больше и потребляемый ток. К тому же, разница между логическими уровнями у ЭСЛ-элемента намного меньше, чем у ТТЛ (меньше вольта), и, для приемлемой помехоустойчивости, приходится использовать отрицательное напряжение питания (а иногда и применять для выходных каскадов второе питание). Зато максимальные частоты переключения триггеров на ЭСЛ более, чем на порядок превышают возможности современных им ТТЛ, например, серия К500 обеспечивала частоты переключения 160—200 МГц, по сравнению с 10-15 МГц современной ей ТТЛ серии К155. В настоящее время и ТТЛ(Ш), и ЭСЛ практически не используются, так как с уменьшением проектных норм КМОП технология достигла частот переключения в несколько гигагерц.
Инвертор
Одним из основных логических элементов является инвертор. Инвертирующими каскадами являются однотранзисторный каскад с общим эмиттером, однотранзисторный каскад с общим истоком, двухтранзисторный двухтактный выходной каскад на комплементарных парах транзисторов с последовательным включением транзисторов по постоянному току (применяется в ТТЛ и КМОП), двухтранзисторный дифференциальный каскад с параллельным включением транзисторов по постоянному току (применяется в ЭСЛ) и др. Но одного условия инвертирования недостаточно для применения инвертирующего каскада в качестве логического инвертора. Логический инвертор должен иметь смещённую рабочую точку на один из краёв проходной характеристики, что делает каскад неустойчивым в середине диапазона входных величин и устойчивым в крайних положениях (закрыт, открыт). Такой характеристикой обладает компаратор, поэтому логические инверторы строят как компараторы, а не как гармонические усилительные каскады с устойчивой рабочей точкой в середине диапазона входных величин. Таких каскадов, как и контактных групп реле, может быть два вида: нормально закрытые (разомкнутые) и нормально открытые (замкнутые).
Применение логических элементов
Логические элементы входят в состав микросхем, например ТТЛ элементы — в состав микросхем К155 (SN74), К133; ТТЛШ — 530, 533, К555, ЭСЛ — 100, К500 и т. д.
Комбинационные логические устройства
Комбинационными называются такие логические устройства, выходные сигналы которых однозначно определяются входными сигналами:
Все они выполняют простейшие двоичные, троичные или n-ичные логические функции.
Последовательностные цифровые устройства
Последовательностными называют такие логические устройства, выходные сигналы которых определяются не только сигналами на входах, но и предысторией их работы, то есть состоянием элементов памяти.
См. также
Примечания
Литература
Ссылки
И, ИЛИ, XOR и НЕ
В этом учебном пособии объясняется суть логических функций Excel И, ИЛИ, XOR и НЕ, а также приводятся примеры формул, демонстрирующие их общее и изобретательское использование.
На прошлой неделе мы рассмотрели логические операторы Excel, которые используются для сравнения данных в разных ячейках. Сегодня вы увидите, как расширить использование логических операторов и построить более сложные тесты для выполнения более сложных вычислений. Логические функции Excel, такие как AND, OR, XOR и NOT, помогут вам в этом.
Логические функции Excel — обзор
Microsoft Excel предоставляет 4 логических функции для работы с логическими значениями. Это функции AND, OR, XOR и NOT. Вы используете эти функции, когда хотите выполнить более одного сравнения в своей формуле или протестировать несколько условий вместо одного. Как и логические операторы, логические функции Excel возвращают либо ИСТИНА, либо ЛОЖЬ при оценке их аргументов.
В следующей таблице приведено краткое описание того, что делает каждая логическая функция, чтобы помочь вам выбрать правильную формулу для конкретной задачи.
| Функция | Описание | Пример формулы | Формула Описание |
| и | Возвращает TRUE, если все аргументы оцениваются как TRUE. | = AND (A2> = 10, B2 <5) | Формула возвращает TRUE, если значение в ячейке A2 больше или равно 10, а значение в B2 меньше 5, иначе FALSE. |
| ИЛИ | Возвращает TRUE, если какой-либо аргумент оценивается как TRUE. | = ИЛИ (A2> = 10, B2 <5) | Формула возвращает TRUE, если A2 больше или равно 10 или B2 меньше 5, или выполнены оба условия. Если ни одно из условий не выполнено, формула возвращает FALSE. |
| XOR | Возвращает логическое исключение или всех аргументов. | = XOR (A2> = 10, B2 <5) | Формула возвращает TRUE, если либо A2 больше или равно 10, либо B2 меньше 5. Если ни одно из условий не выполнено, либо оба условия соблюдены, формула возвращает FALSE. |
| НЕ | Возвращает обратное логическое значение своего аргумента. То есть Если аргумент ЛОЖЬ, то ИСТИНА возвращается, и наоборот. | = НЕ (A2> = 10) | Формула возвращает FALSE, если значение в ячейке A1 больше или равно 10; ИСТИНА в противном случае. |
В дополнение к четырем логическим функциям, описанным выше, Microsoft Excel предоставляет 3 условные функции - IF, IFERROR и IFNA.
логических функций Excel - факты и цифры
- В аргументах логических функций вы можете использовать ссылки на ячейки, числовые и текстовые значения, логические значения, операторы сравнения и другие функции Excel.Однако все аргументы должны соответствовать булевым значениям TRUE или FALSE или ссылкам или массивам, содержащим логические значения.
- Если аргумент логической функции содержит пустых ячеек , такие значения игнорируются. Если все аргументы являются пустыми ячейками, формула возвращает #VALUE! ошибка.
- Если аргумент логической функции содержит числа, то ноль оценивается как ЛОЖЬ, а все остальные числа, включая отрицательные числа, оцениваются как ИСТИНА. Например, если ячейки A1: A5 содержат числа, формула = AND (A1: A5) вернет TRUE, если ни одна из ячеек не содержит 0, иначе FALSE.
- Логическая функция возвращает # ЗНАЧЕНИЕ! ошибка, если ни один из аргументов не соответствует логическим значениям.
- Логическая функция возвращает #NAME? ошибка, если вы неправильно написали имя функции или пытались использовать функцию в более ранней версии Excel, которая ее не поддерживает. Например, функция XOR может использоваться только в Excel 2016 и 2013.
- В Excel 2016, 2013, 2010 и 2007 вы можете включить до 255 аргументов в логическую функцию при условии, что общая длина формулы не превышает 8 192 символа.В Excel 2003 и ниже вы можете указать до 30 аргументов, и общая длина формулы не должна превышать 1024 символов.
Использование функции И в Excel
Функция AND является наиболее популярным членом семейства логических функций. Это удобно, когда нужно проверить несколько условий и убедиться, что все они выполнены. Технически функция AND проверяет указанные вами условия и возвращает TRUE, если все условия оцениваются как TRUE, FALSE в противном случае.
Синтаксис для функции Excel AND следующий:
И (логический1, [логический2],…)
Где логическое - это условие, которое вы хотите проверить и которое может быть оценено как ИСТИНА или ЛОЖЬ. Первое условие (логическое1) является обязательным, последующие условия являются необязательными.
А теперь давайте посмотрим на некоторые примеры формул, которые демонстрируют, как использовать функции AND в формулах Excel.
| Формула | Описание |
= AND (A2 = "Бананы", B2> C2) | Возвращает TRUE, если A2 содержит «Bananas» и B2 больше, чем C2, иначе FALSE. |
= AND (B2> 20, B2 = C2) | Возвращает TRUE, если B2 больше 20, а B2 равно C2, иначе FALSE. |
= AND (A2 = "Бананы", B2> = 30, B2> C2) | Возвращает TRUE, если A2 содержит «Bananas», B2 больше или равно 30 и B2 больше, чем C2, иначе FALSE. |
Функция Excel AND - общее использование
Функция Excel AND сама по себе не очень интересна и имеет узкую полезность.Но в сочетании с другими функциями Excel, AND может значительно расширить возможности ваших рабочих таблиц.
Одно из наиболее распространенных применений функции Excel AND находится в аргументе logic_test функции IF для проверки нескольких условий вместо одного. Например, вы можете вложить любую из функций AND выше в функцию IF и получить результат, подобный следующему:
= ЕСЛИ (И (А2 = "Бананы", В2> С2), "Хорошо", "Плохо")
Дополнительные примеры формул IF / AND можно найти в его учебнике: функция Excel IF с несколькими условиями AND.
Формула Excel для условия МЕЖДУ
Если вам нужно создать формулу между в Excel, которая выбирает все значения между данными двумя значениями, общий подход заключается в использовании функции IF с AND в логическом тесте.
Например, у вас есть 3 значения в столбцах A, B и C, и вы хотите знать, находится ли значение в столбце A между значениями B и C. Чтобы создать такую формулу, достаточно лишь функции IF с вложенным оператором AND и парой операторов сравнения:
Формула для проверки, если X между Y и Z, включительно:
= ЕСЛИ (И (А2> = В2, А2 <= С2), «Да», «Нет»)
Формула для проверки, находится ли X между Y и Z, не включительно:
= ЕСЛИ (И (А2> В2, А2 <С2), «Да», «Нет»)
Как показано на скриншоте выше, формула отлично работает для всех типов данных - чисел, дат и текстовых значений.При сравнении текстовых значений формула проверяет их посимвольно в алфавитном порядке. Например, в нем говорится, что яблок находятся не между абрикосовых и бананов , потому что второе «p» в яблочных стоит перед «r» в абрикосовых . Пожалуйста, смотрите Использование операторов сравнения Excel с текстовыми значениями для более подробной информации.
Как видите, формула IF / AND проста, быстра и почти универсальна. Я говорю «почти», потому что это не охватывает один сценарий.Приведенная выше формула подразумевает, что значение в столбце B меньше, чем в столбце C, т. Е. Столбец B всегда содержит значение нижней границы, а C - значение верхней границы. По этой причине формула возвращает « № » для строки 6, где A6 имеет 12, B6-15 и C6-3, а также для строки 8, где A8 - 24 ноября, B8 - 26 декабря и C8 - 21-октября
Но что, если вы хотите, чтобы ваша формула между работала правильно, независимо от того, где находятся значения нижней и верхней границ? В этом случае используйте функцию Excel MEDIAN, которая возвращает медиану заданных чисел (т.е.е. число в середине набора чисел).
Итак, если вы замените AND в логическом тесте функции IF на MEDIAN, формула будет иметь вид:
= IF (A2 = MEDIAN (A2: C2), «Да», «Нет»)
И вы получите следующие результаты:
Как видите, функция MEDIAN отлично работает с числами и датами, но возвращает #NUM! ошибка для текстовых значений. Увы, никто не идеален 🙂
Если вы хотите получить идеальную формулу Between, которая работает как для текстовых значений, так и для чисел и дат, вам придется создать более сложный логический текст с использованием функций AND / OR, например:
= ЕСЛИ (ИЛИ (И (А2> В2, А2 <С2), И (А2 <В2, А2> С2)), «Да», «Нет»)
Использование функции ИЛИ в Excel
Как и AND, функция Excel OR является базовой логической функцией, которая используется для сравнения двух значений или операторов.Разница в том, что функция OR возвращает TRUE, если хотя бы один, если аргументы оцениваются как TRUE, и возвращает FALSE, если все аргументы являются FALSE. Функция ИЛИ доступна во всех версиях Excel 2016 - 2000.
Синтаксис функции Excel ИЛИ очень похож на AND:
ИЛИ (логический1, [логический2],…)
Где логично это то, что вы хотите проверить, это может быть ИСТИНА или ЛОЖЬ. Требуется первая логика, дополнительные условия (до 255 в современных версиях Excel) являются необязательными.
А теперь давайте напишем несколько формул, чтобы вы могли понять, как работает функция ИЛИ в Excel.
| Формула | Описание |
= ИЛИ (A2 = "Бананы", A2 = "Апельсины") | Возвращает TRUE, если A2 содержит «Bananas» или «Oranges», иначе FALSE. |
= ИЛИ (B2> = 40, C2> = 20) | Возвращает TRUE, если B2 больше или равно 40 или C2 больше или равно 20, иначе FALSE. |
= ИЛИ (B2 = "", C2 = "") | Возвращает TRUE, если либо B2, либо C2 не заполнены, либо оба, FALSE в противном случае. |
Наряду с функцией Excel AND функция OR широко используется для расширения полезности других функций Excel, которые выполняют логические тесты, например функция ЕСЛИ. Вот только несколько примеров:
Функция IF с вложенным ИЛИ
= ЕСЛИ (ИЛИ (B2> 30, C2> 20), «Хорошо», «Плохо»)
Формула возвращает « Good », если число в ячейке B3 больше 30 или число в C2 больше 20, в противном случае « Bad ».
функции Excel И / ИЛИ в одной формуле
Естественно, ничто не мешает вам использовать обе функции, И И ИЛИ, в одной формуле, если ваша бизнес-логика требует этого. Могут быть бесконечные вариации таких формул, которые сводятся к следующим основным схемам:
= И (ИЛИ (Cond1, Cond2), Cond3)
= И (ИЛИ (Cond1, Cond2), ИЛИ (Cond3, Cond4)
= ИЛИ (И (Cond1, Cond2), Cond3)
= ИЛИ (И (Cond1, Cond2), И (Cond3, Cond4))
Например, если вы хотите узнать, какие партии бананов и апельсинов проданы, i.е. Число «На складе» (столбец B) равно числу «Продано» (столбец C), следующая формула ИЛИ / И может быстро показать это вам:
= ИЛИ (И (А2 = "бананы", В2 = С2), И (А2 = "апельсины", В2 = С2))
ИЛИ функция в Excel условного форматирования
= ИЛИ ($ B2 = "", $ C2 = "")
Правило с приведенной выше формулой ИЛИ выделяет строки, которые содержат пустую ячейку либо в столбце B или C, либо в обоих.
Для получения дополнительной информации о формулах условного форматирования см. Следующие статьи:
Использование функции XOR в Excel
В Excel 2013 Microsoft представила функцию XOR, которая является логической функцией Exclusive OR .Этот термин определенно знаком тем из вас, кто знает какой-либо язык программирования или информатику в целом. Для тех, кто этого не делает, поначалу может быть немного сложно понять концепцию «Эксклюзивно или», но, надеюсь, поможет приведенное ниже объяснение, проиллюстрированное примерами формул.
Синтаксис функции XOR идентичен OR:
XOR (логический1, [логический2],…)
Требуется первый логический оператор (логический 1), дополнительные логические значения являются необязательными.Вы можете проверить до 254 условий в одной формуле, и это могут быть логические значения, массивы или ссылки, которые оценивают как ИСТИНА или ЛОЖЬ.
В простейшей версии формула XOR содержит только 2 логических оператора и возвращает:
- ИСТИНА, если любой из аргументов оценивается как ИСТИНА.
- ЛОЖЬ, если оба аргумента ИСТИНА или ни один не ИСТИНА.
Это может быть легче понять из примеров формул:
| Формула | Результат | Описание |
= XOR (1> 0, 2 <1) | ИСТИНА | Возвращает TRUE, поскольку 1-й аргумент равен TRUE, а 2 и - FALSE. |
= XOR (1 <0, 2 <1) | ЛОЖЬ | Возвращает FALSE, потому что оба аргумента FALSE. |
= XOR (1> 0, 2> 1) | ЛОЖЬ | Возвращает FALSE, потому что оба аргумента TRUE. |
Когда добавляется больше логических операторов, функция XOR в Excel приводит к:
- ИСТИНА, если нечетное число аргументов оценивается как ИСТИНА;
- FALSE, если общее число операторов TRUE является четным, или если все операторы FALSE.
Скриншот ниже иллюстрирует точку:
Если вы не уверены, как функцию Excel XOR можно применить к реальному сценарию, рассмотрите следующий пример. Предположим, у вас есть таблица участников и их результаты для первых двух игр. Вы хотите знать, кто из плательщиков должен сыграть в игру 3 rd на следующих условиях:
- Участник, выигравший Игру 1 и Игру 2, автоматически переходит в следующий раунд и не обязан играть в Игру 3.
- Конкурсанты, которые проиграли обе первые игры, выбивают и тоже не играют в игру 3.
- Участники, которые выиграли либо в Игру 1, либо в Игру 2, должны играть в Игру 3, чтобы определить, кто войдет в следующий раунд, а кто нет.
Простая формула XOR работает именно так, как мы хотим:
= XOR (B2 = "Выиграл", C2 = "Выиграл")
И если вы вложите эту функцию XOR в логический тест формулы IF, вы получите еще более разумные результаты:
= ЕСЛИ (XOR (B2 = "Выиграл", C2 = "Выиграл"), "Да", "Нет")
Использование функции НЕ в Excel
Функция NOT является одной из самых простых функций Excel с точки зрения синтаксиса:
НЕ (логично)
Вы используете функцию NOT в Excel, чтобы изменить значение ее аргумента.Другими словами, если логическое значение равно FALSE, функция NOT возвращает TRUE и наоборот. Например, обе приведенные ниже формулы возвращают FALSE:
= НЕ (ИСТИНА)
= НЕ (2 * 2 = 4)
Зачем желать получить такие нелепые результаты? В некоторых случаях вам может быть более интересно узнать, когда определенное условие не выполняется, чем когда оно выполняется. Например, при просмотре списка нарядов вы можете исключить некоторые цвета, которые вам не подходят. Я не особенно люблю черный, поэтому я продолжаю с этой формулой:
= НЕ (C2 = "черный")
Как обычно, в Microsoft Excel существует более одного способа что-то сделать, и вы можете достичь того же результата, используя оператор «Не равно»: = C2 <> «черный».
Если вы хотите проверить несколько условий в одной формуле, вы можете использовать NOT в сочетании с функцией AND или OR. Например, если вы хотите исключить черный и белый цвета, формула будет выглядеть следующим образом:
= НЕ (ИЛИ (C2 = "черный", C2 = "белый"))
И если вы предпочитаете не иметь черное пальто, в то время как вы можете рассмотреть черный пиджак или заднюю шубу, вы должны использовать НЕ в сочетании с функцией Excel AND:
= НЕ (И (C2 = "черный", B2 = "пальто"))
Другое распространенное использование функции NOT в Excel - обратное поведение некоторых других функций.Например, вы можете комбинировать функции NOT и ISBLANK для создания формулы ISNOTBLANK, которой не хватает в Microsoft Excel.
Как вы знаете, формула = ISBLANK (A2) возвращает TRUE, если ячейка A2 пуста. Функция NOT может преобразовать этот результат в FALSE: = NOT (ISBLANK (A2))
А затем вы можете сделать еще один шаг и создать вложенный оператор IF с функциями NOT / ISBLANK для реальной задачи:
= ЕСЛИ (НЕ (ISBLANK (C2)), C2 * 0,15, «Без бонуса :(»)
В формуле, переведенной на простой английский, Excel выполняет следующие действия.Если ячейка C2 не пуста, умножьте число в C2 на 0,15, что дает бонус в 15% каждому продавцу, совершившему дополнительные продажи. Если C2 пусто, появляется текст «Нет бонуса :(».
По сути, именно так вы используете логические функции в Excel. Конечно, эти примеры только поверхностно рассмотрели возможности AND, OR, XOR и NOT. Зная основы, теперь вы можете расширить свои знания, решая свои реальные задачи и составляя умные сложные формулы для своих рабочих листов.
Вы также можете быть заинтересованы в:
,IF, И, ИЛИ, Вложенные логические функции IF & NOT в Excel

- Home
Тестирование
- Назад
- Agile Тестирование
- BugZilla
- Cugumber
- Testing Jmeter
- JIRA
- Назад
- JUnit
- LoadRunner
- Ручное тестирование
- Мобильное тестирование
- Mantis
- Почтальон
- QTP
Тестирование- Selenium
- SoapUI
- Управление тестированием
- TestLink
SAP
- 9000 4 Назад
- ABAP
- APO
- Новичок
- Базис
- BODS
- BI
- BPC
- CO
- Назад
- CRM
- Назад
- PI / PO
- PP
- SD
- SAPUI5
- Безопасность
- Solution Manager
- Successfactors
- SAP Обучение
веб
- Назад
- Apache
- Android
- AngularJS
- ASP.Чистая
- C
- C #
- C ++
- CodeIgniter
- СУБД
- Назад
- Java
- JavaScript
- JSP
- Kotlin
M000
- Back
- Perl
- PHP
- PL / SQL
- PostgreSQL
- Python
- ReactJS
- Ruby & Rails
- Scala
- SQL5000
- SQL000
- UML
- VB.Net
- VBScript
- Веб-сервисы
- WPF
Необходимо учиться!
- Назад
- Учет
- Алгоритмы
- Blockchain
- Бизнес-аналитик
- Сложение Сайт
- CCNA
- Cloud Computing
- COBOL
- Compiler Design
- Embedded Systems
- Назад
- Ethical Hacking
- Excel Учебники
- Go Программирование
- IoT
- ITIL
- Дженкинс
- MIS
- Networking
- Операционная система
- Prep
- Назад
- PMP
- Photoshop Управление
- Проект
- Отзывы
- Salesforce
- SEO
- Разработка программного обеспечения
- VBA
Big Data
- Назад
- AWS
- BigData
- Cassandra
- Cognos
- Складирование данных 000000000 HBB
- Назад
Чтобы визуализировать архитектуру модели , мы используем так называемый вычислительный граф : ориентированный граф, который используется для представления математической функции. И переменные, и операции являются узлами; переменные вводятся в операции, а операции создают переменные.
Вычислительный график нашего перцептрона:
Символ Σ представляет линейную комбинацию входов x с помощью весов w и смещения b .Поскольку эти обозначения довольно тяжелые, отныне я буду упрощать вычислительный граф следующим образом:
Я представляю некоторые примеры того, что персептрон может реализовать с его емкостью (я буду говорить об этом термине в следующих частях этой серии!). Логические функции являются отличной отправной точкой, поскольку они приведут нас к естественному развитию теории перцептрона и, как следствие, нейронных сетей .
НЕ логическая функция
Начнем с очень простой задачи:
Может ли персептрон реализовать НЕ логическую функцию?
NOT (x) - функция с 1 переменной, это означает, что у нас будет один вход за раз: N = 1.Кроме того, это логическая функция , и поэтому и вход, и выход имеют только два возможных состояния: 0 и 1 (т. Е. False и True): пошаговая функция Хевисайда, кажется, соответствует нашему случаю, так как она генерирует двоичный выход ,
Учитывая эти соображения, мы можем сказать, что, если существует персептрон, который может реализовать функцию NOT (x), он будет похож на тот, который показан слева.
Учитывая два параметра, w и b , он выполнит следующие вычисления:
ŷ = ϴ ( wx + b)
Основной вопрос: существуют ли два значения, которые, если они выбраны в качестве параметров, позволяют персептрон для реализации НЕ логической функции? Когда я говорю, что персептрон реализует функцию, я имею в виду, что для каждого входа в домене функции перцептрон возвращает одно и то же число (или вектор), которое функция должна вернуть для того же входа.
Возвращаясь к нашему вопросу: эти значения существуют, поскольку их легко найти: давайте выберем w = -1 и b = 0,5.
И мы получаем:
NOT (0) = 1
NOT (1) = 0
Мы заключаем, что ответ на первый вопрос таков: да, персептрон может реализовать логическую функцию NOT; нам просто нужно правильно установить его параметры . Обратите внимание, что мое решение не уникально; на самом деле, решения, предназначенные как (w, b) точки, для этой конкретной задачи бесконечны! Вы можете использовать свой любимый;)
И логическая функция И
Следующий вопрос:
Может ли персептрон реализовать логическую функцию И?
Логическая функция AND - это функция с двумя переменными, AND (x1, x2) , с двоичными входами и выходами.
Этот график связан со следующими вычислениями:
ŷ = ϴ ( w1 * x1 + w2 * x2 + b )
На этот раз у нас есть три параметра: w1 , w2, и b ,
Можете ли вы угадать, какие три значения для этих параметров позволят персептрону решить проблему И ?
РЕШЕНИЕ:
w1 = 1, w2 = 1, b = -1,5
И это печатает:
И (1, 1) = 1
И (1, 0) = 0
И (0, 1 ) = 0
И (0, 0) = 0
ИЛИ логическая функция ИЛИ
ИЛИ (x1, x2) также является функцией с 2 переменными, и ее выход является одномерным (т.е.одно число) и имеет два возможных состояния (0 или 1). Поэтому мы будем использовать персептрон с той же архитектурой, что и ранее. Какие три параметра решают проблему ИЛИ?
РЕШЕНИЕ:
w1 = 1, w2 = 1, b = -0,5
ИЛИ (1, 1) = 1
ИЛИ (1, 0) = 1
ИЛИ (0, 1) = 1
ИЛИ ( 0, 0) = 0
XOR - ВСЕ (персептроны) ДЛЯ ОДНОГО (логическая функция)
Мы заключаем, что один персептрон с функцией активации Хевисайда может реализовывать каждую из основных логических функций: НЕ, И и ИЛИ.
Они называются фундаментальными , потому что любая логическая функция, какой бы сложной она ни была, может быть получена комбинацией этих трех. Мы можем сделать вывод, что , если мы соответствующим образом соединим три перцептрона, которые мы только что создали, мы сможем реализовать любую логическую функцию! Давайте посмотрим, как:
Как мы можем построить сеть из фундаментальных логических персептронов , чтобы она реализовала функцию XOR?
РЕШЕНИЕ:
И выход:
XOR (1, 1) = 0
XOR (1, 0) = 1
XOR (0, 1) = 1
XOR (0, 0) = 0
Это прогнозы, которые мы искали! Мы только что объединили три перцептрона выше, чтобы получить более сложную логическую функцию.
Некоторым из вас может быть интересно, можно ли, как мы это делали для предыдущих функций, найти значения параметров для одного персептрона, чтобы он самостоятельно решал проблему XOR.
Я не заставлю вас слишком долго искать эти три числа, потому что это будет бесполезно: ответ в том, что они не существуют. Почему? Ответ заключается в том, что проблема XOR не является линейно отделимым , и мы обсудим это подробно в следующей главе этой серии!
Я опубликую его через несколько дней, и мы пройдем через свойство линейной отделимости, которое я только что упомянул.Я изменю темы, которые я представил сегодня, в геометрической перспективе. Таким образом, каждый результат, который мы получили сегодня, получит свое естественное и интуитивное объяснение.
Если вам понравилась эта статья, я надеюсь, вы подумаете над ней! Каждый хлопок мне очень помогает 🙂 Кроме того, не стесняйтесь связаться со мной по телефону Linkedin !
До скорой встречи,
Франк
. В Excel много работы по сравнению данных в разных ячейках. Когда вы делаете сравнение между двумя значениями, вы хотите знать одну из следующих вещей:
- Является ли значение A равным значению B (A = B)
- - это , превышающий B (A> B)
- - это меньше, чем B (A
- A больше или равно B (A> = B)
- A меньше или равно B (A <= B)
- Is A не равно B (A <> B)
Это так называемые логические или логические операторы, потому что в каждом конкретном случае может быть только два возможных ответа - ИСТИНА или ЛОЖЬ.
Использование логических операторов в ваших формулах
Excel очень гибок в использовании этих логических операторов. Например, вы можете использовать их для , сравнить две ячейки или сравнить результаты одной или нескольких формул . Например:
- = A1 = A2
- = A1 = (A2 * 5)
- = (A1 * 10) <= (A2 / 5)
Как показывают эти примеры, вы можете ввести их непосредственно в ячейку в Excel и заставить Excel вычислять результаты формулы так же, как это было бы с любой формулой.С этими формулами Excel всегда будет возвращать либо TRUE, либо FALSE в качестве результата в ячейке.
Широко используется логические операторы в функции IF в Excel (подробнее о функции IF можно прочитать здесь). Функция IF работает следующим образом:
- = IF (логический_тест, value_if_TRUE, value_if_FALSE)
По сути, функция IF выполняет логический тест (все три приведенных выше примера являются логическими тестами) и затем возвращает соответствующий результат в зависимости от того, является ли результат теста истинным или ложным.Например:
- = IF (A1> A2, «Больше чем», «Меньше чем»)
- = IF (A1> A2, A1 * 10%, A1 * 5%)
Однако не всегда нужно использовать формулу IF. Вот версия этой формулы, которая использует логический оператор, а также демонстрирует еще одну полезную функцию логических операторов в целом:
- = (A1> A2) * (A1 * 10 *) + (A1 <= A2) * (A1 * 5%)
Это выглядит запутанно, но на самом деле это очень логично (извините за каламбур). Однако полезно знать, что в Excel значение TRUE равно 1, а значение FALSE равно 0.
Итак, в этом примере:
- Если A1> A2 TRUE, то формула будет кратна (A1 * 10%) на 1.
- Поскольку A1> A2 TRUE, то A1 <= A2 ложно, поэтому он умножится (A1 * 5%) на 0.
- Затем он сложит результаты вместе: (A1 * 10%) * 1 + (A1 * 5%) * 0.
- Окончательный результат равен (A1 * 10%) равному в конкретном примере.
Очевидно, что если A1 меньше A2, то произойдет обратное.
Использование нескольких логических операторов
В некоторых случаях вы можете захотеть выполнить более одного сравнения как часть вашей формулы.Например:
- (сегодня среда) и (небо голубое)
- (сегодня среда) или (небо голубое)
- (сегодня среда и (небо НЕ синее)
- (сегодня среда) или (небо НЕ синее)
В Excel вы можете использовать одну из трех логических функций для построения этих формул:
Функция AND работает, выполняя несколько тестов сравнения, а затем возвращает TRUE, если все тесты были верными, и FALSE, если один или несколько тестов были ложными.Вот пара примеров:
- = И (А1> А2, А1 <А3) (если А1 больше, чем А2, и меньше, чем А3, верните ИСТИНА, в противном случае верните ЛОЖЬ)
- IF (AND (A2> A2, A1
Функция OR работает очень похоже на функцию AND. Однако, хотя AND требует, чтобы все тесты возвращали true, функция OR будет возвращать TRUE, если только один из тестов возвращает true.Например:
- = ИЛИ (А1> А2, А1 <А3) (если или А1> А2 ИЛИ А1> А3 - истина, то вернуть ИСТИНА. Если ни одна из них не верна, вернуть ЛОЖЬ).
- = ЕСЛИ (ИЛИ (A1> A2, A1
Важно отметить, что функции AND и IF могут включать до 255 логических тестов (в моих примерах здесь использовалось только 2). Независимо от количества тестов, которые вы включаете, применяются те же правила, что и в моих простых примерах.
Также стоит отметить, что вы можете объединить функции И и ИЛИ в одну формулу. Например:
- = И (ИЛИ (А1> А2, А1 <А3), А1> А4)
В этом примере функция AND вернет TRUE, только если (A1> A2 ИЛИ A1
Последняя логическая функция, которую вы можете использовать, - это функция НЕ. Функция NOT несколько самоочевидна - она берет любой логический результат теста и делает обратное.Например:
- = (Небо синее) - вернет ИСТИНА, если небо голубое, и ЛОЖЬ, если небо не голубое.
- = НЕ (Небо синее) вернет ЛОЖЬ, если небо синее, и ИСТИНА, если небо не синее.
Обратите внимание, что в этом примере не важно, какими могут быть другие цвета неба!
Конечно, вы можете использовать функцию NOT с функциями AND, OR и IF:
- = НЕ (И (А1> А2, А1 <А3)) - если А1> А2 И А1 <А3, вернуть ЛОЖЬ
- = И (НЕ (А1> А2), А1 <А3) - если А1 НЕ> А2 и А1 <А3, вернуть TRUE.
Обратите внимание, что запись NOT (A1> A2) - это еще один способ записи (A1 <= A2). В этом простом примере использование функции NOT не добавило много значения, но в некоторых случаях функция NOT может быть очень удобной.
Таким образом, многое из того, что вы делаете в Excel, особенно когда вы начинаете использовать функции IF, связано с использованием логических операторов. Логические функции, И, ИЛИ и НЕ являются отличным способом расширить использование логических операторов для выполнения более сложных вычислений.
,


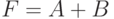 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое;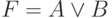 — с использованием знака дизъюнкции.
— с использованием знака дизъюнкции.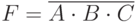 , но при этом из контекста должно быть ясно, что данное умножение именно логическое;
, но при этом из контекста должно быть ясно, что данное умножение именно логическое;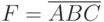 ;
; ;
; .
.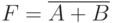 , но при этом из контекста должно быть ясно, что данное сложение именно логическое;
, но при этом из контекста должно быть ясно, что данное сложение именно логическое;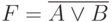 .
.