Логические И и ИЛИ. Краткое введение в программирование на Bash
Логические И и ИЛИ. Краткое введение в программирование на BashВикиЧтение
Краткое введение в программирование на Bash
Родригес Гарольд
Содержание
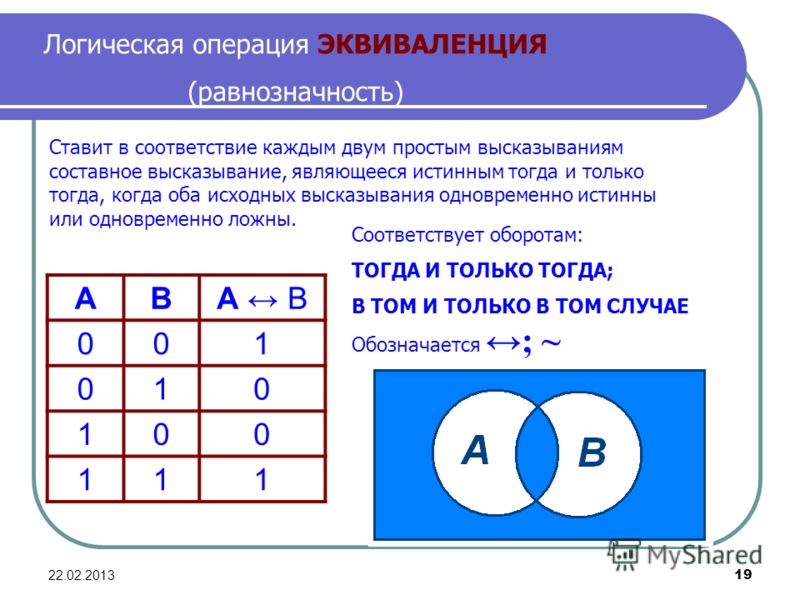
Логические И и ИЛИ
Вы уже видели, что такое управляющие структуры и как их использовать. Для решения тех же задач есть еще два способа. Это логическое И — «&&» и логическое «ИЛИ» — « || ». Логическое И используется следующим образом:
выражение_1&&выражение_2
Сначала выполняется выражение, стоящее слева, если оно истинно, выполняется выражение, стоящее справа. Если выражение_1 возвращает ЛОЖЬ, то выражение_2 не будет выполнено. Если оба выражения возвращают ИСТИНУ, выполняется следующий набор команд. Если какое-либо из выражений не истинно, приведенное выражение считает ложным в целом.
если выражение_1 истинно И выражение_2 истинно, тогда выполнять…[15]
Пример использования:
#!/bin/bash
x=5
y=10
if [ «$x» -eq 5 ] && [ «$y» -eq 10 ]; then
echo «Оба условия верны»
else
echo «Условия не верны»
fi
Здесь мы находим, что переменные х и у содержат именно те значения, которые мы проверяем, поэтому проверяемые условия верны. Если вы измените значение с х = 5 на х = 12, а затем снова запустите программу, она выдаст фразу «Условия не верны».
Логическое ИЛИ используется аналогичным образом. Разница лишь в том, что оно проверяет ошибочность выражения слева. Если это так — оно начинает выполнять следующий оператор:
выражение_1||выражение_2
Данное выражение в псевдокоде выглядит так:
если выражение_1 истинно ИЛИ выражение_2 истинно, выполняем …
Таким образом, любой последующий код будет выполняться, если хотя бы одно из выражений истинно:
#!/bin/bash
x=3
y=2
if [ «$x» -eq 5 ] || [ «$y» -eq 2 ]; then
echo «Одно из условий истинно»
else
echo «Ни одно из условий не является истинным»
fi
Здесь вы видите, что только одно из выражений истинно.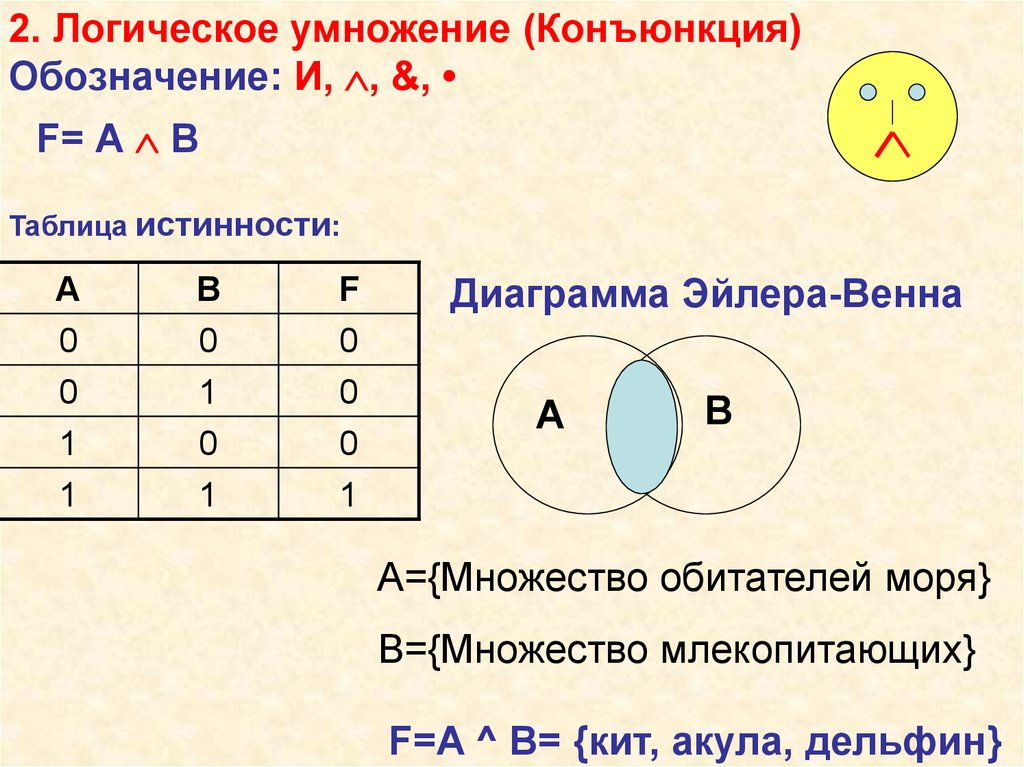 Попробуйте изменить значение у и повторно запустите программу. Вы увидите сообщение, что ни одно из выражений не является истинным.
Попробуйте изменить значение у и повторно запустите программу. Вы увидите сообщение, что ни одно из выражений не является истинным.
Аналогичная реализация условия с помощью оператора if будет большего размера, чем вариант с использованием логического И и ИЛИ, поскольку потребует дополнительного вложенного if. Ниже приведен код, реализующий тот же функционал, но с использованием оператора if:
#!/bin/bash
x=5
y=10
if [ «$x» -eq 5 ]; then
if [ «$y» -eq 10 ]; then
echo «Оба условия верны»
else
echo «Оба условия неверны»
fi
fi
Приведенный код менее нагляден для чтения и требует для своего написания больших усилий. Но у вас остается возможность для избавления себя от всех этих трудностей путем использования операторов логических И и ИЛИ.
Логические данные
Логические данные
Логические данные предназначены для выполнения операций сравнения, а также для использования в условных операторах.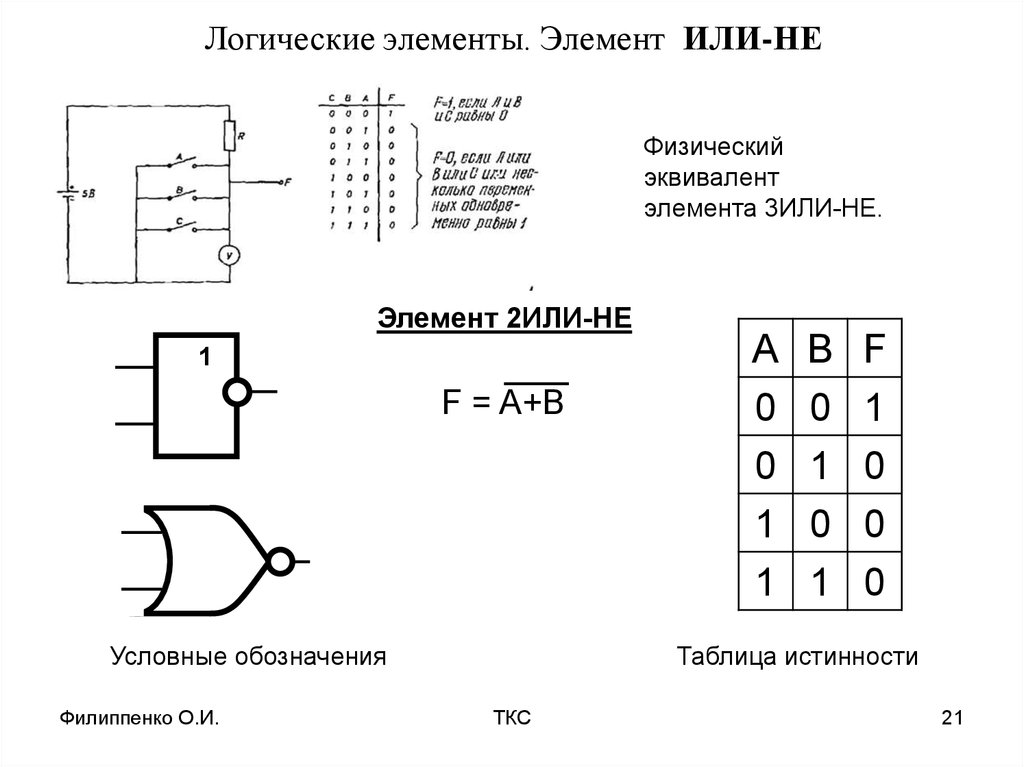 При этом логические данные имеют только два значения: true (истина) и false (ложь). Отметим, что в JScript эти значения никак не соотносятся с
При этом логические данные имеют только два значения: true (истина) и false (ложь). Отметим, что в JScript эти значения никак не соотносятся с
Логические операторы
Логические операторы
Логические операторы Логические операторы выполняют действия над логическими значениями. Все они приведены в табл. 14.5. А в табл. 14.6 и 14.7 показаны результаты выполнения этих операторов.Основная область применения логических операторов — выражения сравнения (о них см.
1. Логические команды
1.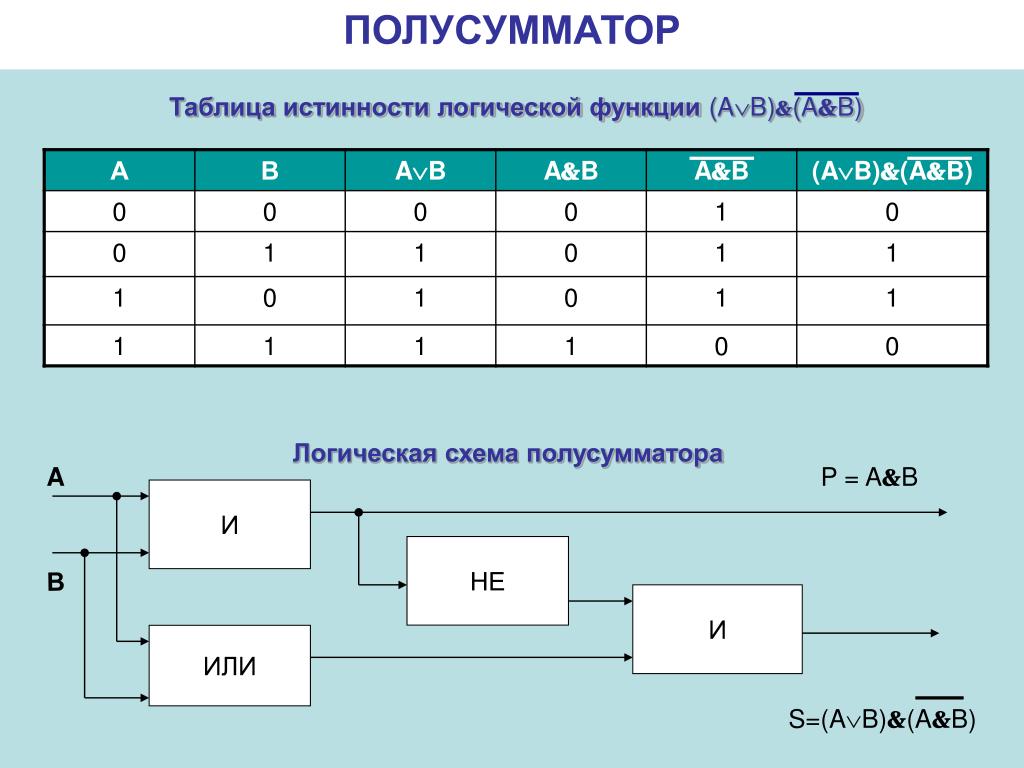 Логические команды
Наряду со средствами арифметических вычислений, система команд микропроцессора имеет также средства логического преобразования данных. Под логическими понимаются такие преобразования данных, в основе которых лежат правила формальной
Логические команды
Наряду со средствами арифметических вычислений, система команд микропроцессора имеет также средства логического преобразования данных. Под логическими понимаются такие преобразования данных, в основе которых лежат правила формальной
Логические операции
Логические операции Для создания объектов более сложных, чем изначальные звезды, прямоугольники и эллипсы, мы можем использовать логические операции. Это гораздо проще, чем полноценная векторная графика, где мы будем создавать фигуры с нуля.Для выполнения логических
Логические И и ИЛИ
Логические И и ИЛИ Вы уже видели, что такое управляющие структуры и как их использовать. Для решения тех же задач есть еще два способа. Это логическое И — «&&» и логическое «ИЛИ» — « || ». Логическое И используется следующим образом:выражение_1&&выражение_2Сначала
Логические функции
Логические функции
Логические функции могут найти применение при математических, инженерных вычислениях или при сравнительном анализе данных.
IV. Логические операции
IV. Логические операции Обычно логические операции «считают» условные выражения операндами. Операция ! имеет один операнд, расположенный справа. Остальные операции имеют два операнда: один слева и один справа. && Логическое И: результат операции имеет значение «истина»,
Логические операции
Логические операции Логические операции выполняют над своими операндами логические функции И (&&) и ИЛИ (||). Операнды логических операций могут иметь целый, плавающий тип, либо быть указателями. Типы первого и второго операндов могут различаться. Сначала всегда
Логические операторы
Логические операторы
Firebird предоставляет три логических оператора, которые могут работать с другими предикатами разными способами. * NOT задает отрицание условия поиска, к которому он применяется. Он имеет наивысший приоритет.* AND создает сложный предикат, объединяет два
* NOT задает отрицание условия поиска, к которому он применяется. Он имеет наивысший приоритет.* AND создает сложный предикат, объединяет два
Логические операции
Логические операции В XSLT имеются две логические операции — or и and. Эти операции бинарны, то есть каждая из них определена для двух операндов. Если операнды не являются булевыми значениями, они неявным образом приводятся к булевому типу.Семантика or и and очевидна — они
Логические операции
Логические операции К логическим относятся бинарные операции and, or и xor, а также унарная операция not, имеющие операнды типа boolean и возвращающие значение типа boolean. Эти операции подчиняются стандартным правилам логики: a and b истинно только тогда, когда истинны a и b, a or b истинно
Логические нарушения
Логические нарушения
Если накопитель исправен физически, но представляется как пустой или неформатированный, а находящиеся на нем данные не видны операционной системе, то в данном случае повреждены служебные таблицы файловой системы. Данные почти всегда остаются на
Данные почти всегда остаются на
55. Логические команды
55. Логические команды Согласно теории, над высказываниями (над битами) могут выполняться следующие логические операции.1. Отрицание (логическое НЕ) – логическая операция над одним операндом, результатом которой является величина, обратная значению исходного
Предметно-логическая и эмоционально-экспрессивная сторона содержания текста — МегаЛекции
Тематика текстов разнообразна, содержание тоже. Но можно выделить общие стороны содержания, которые обнаруживаются если не во всех, то в большинстве текстов. Классификация Гальперина:
Содержательно-фактуальная информация – сообщение о фактах, событиях, которые происходят, происходили или будут происходить в окружающем нас мире, действительном или воображаемом.
Содержательно-концептуальная информация – индивидуально-авторское понимание отношений между явлениями, которые описаны средствами СФИ, понимание их причинно-следственных связей, их значимости в социальной, экономической, политической, культурной жизни народа. Эта информация не всегда выражена ясно в тексте. Она дает возможность и даже требует разных толкований. Любовь сильнее смерти и страха смерти. Информация эстетико-художественного характера: «Любовь сильнее смерти и страха смерти. Только любовью держится и движется жизнь».
Содержательно-подтекстовая информация – скрытая информация, которую извлекается из СФИ благодаря способности языка порождать ассоциативные и коннотативные значения, а также благодаря способности предложений внутри СФИ приращивать смыслы. Пример: воробей камнем упал: камнем обычно падают хищные птицы на добычу. Воробей здесь уподобляется им по своей смелости.
Пример: воробей камнем упал: камнем обычно падают хищные птицы на добычу. Воробей здесь уподобляется им по своей смелости.
+
Предметно-логическая сторона текста – предметные отношения и логические связи. Ряды компонентов, которые непосредственно соотносят текст с действительностью, с трудом могут быть заменены синонимами или другими соотносительными средствами языкового выражения или вовсе не могут быть заменены: вывоз сырья, продажа и перепродажа товаров и т.д. Функция сообщения. Эта сторона всегда присуща тексту.
Эмоционально-экспрессивная сторона текста – отношение автора к теме (оценка), соотнесение текста с адресатом. Компоненты, которые содержат оценку сообщаемого, легко заменимы синонимами. Изрядная доля – солидная доля, кормится продажей – живет продажей. Функция воздействия. Эта сторона может быть в тексте сведена к минимуму.
БИЛЕТ № 22
Композиция словесного произведения и смежные понятия: архитектоника, сюжет, фабула.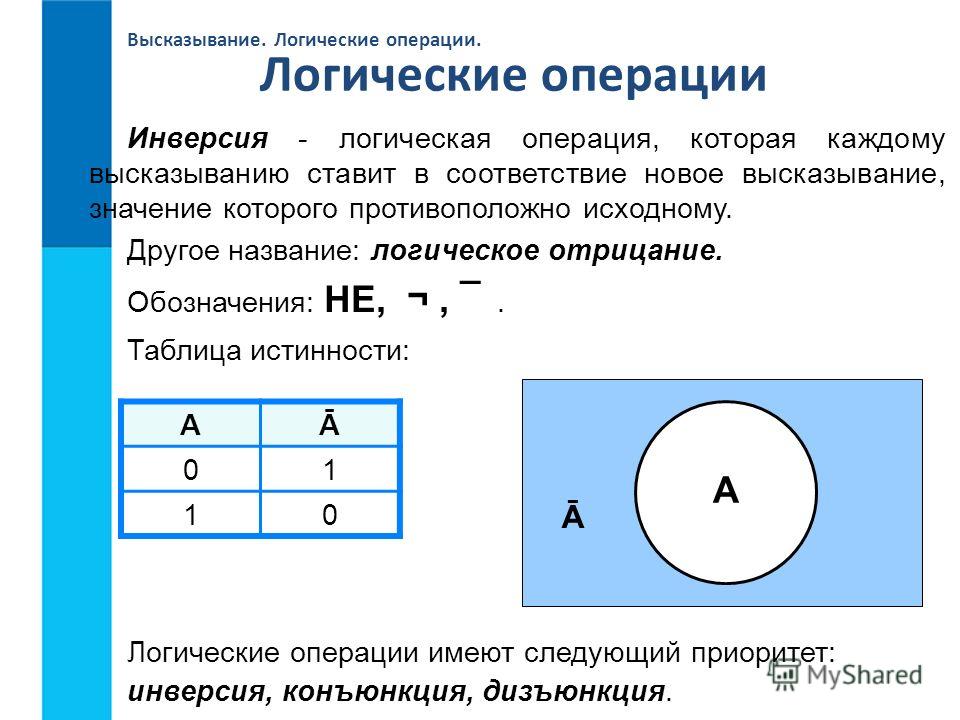 Различные аспекты композиции.
Различные аспекты композиции.
Композиция – по латыни –сочинение, составление, соединение. Композицией в общем плане называют построение, взаимное расположение и соотношение частей какого-либо произведения: словесного, музыкального, живописного. Но нас интересует словесное. С понятием композиции в словесности соотносятся понятия архитектоники, сюжета, фабулы. Отношения между ними не определены с достаточной ясностью, иногда даже композиция смешивается с архитектоникой, не различаются композиция и сюжет и т.д. Поэтому важно понимание этих трех смежных понятий. Архитектоника(гр. строительное искусство) – внешняя форма строения произведения словесности, расположение его частей: пролог, эпилог, глава, часть, том и т.д. в стихотворении – это строфа и твердые формы (сонет, баллада). Архитектоника рассматривается в плане единства внешней формы расположения частей текста с раскрытием его содержания. Фабула (история, рассказ) – совокупность событий, изображаемых в произведении, а Сюжет – последовательное развитие событий, как они изложены в произведении. Композиция словесного произведения понимается по-разному. 1) «Школьное» толкование композиции – развертывание сюжета, в котором выделяются такие обобщенные части: экспозиция – завязка – развитие действия – кульминация – развязка». Именно такое расположение частей необязательно. Много отступлений. 2)Еще одно толкование композиции, более связанное с особенностями словесного творчества: «мотивированное расположение «отрезков» текста.Каждый «отрезок» в составе словесного целого характеризуется или выдержанной на всем его протяжении той или иной формой словесного выражения (повествование, описание, рассуждение, диалог), или точкой видения автора, рассказчика, персонажа, с которой ведется изложение». О случаях сложных отношений архитектоники и сюжета. «Прежде всего, это относится к расположению частей в произведении в отношении к последовательности событий во времени, охватываемом повествованием». Среди возможных видов временных сдвигов «рассказы героев».
Композиция словесного произведения понимается по-разному. 1) «Школьное» толкование композиции – развертывание сюжета, в котором выделяются такие обобщенные части: экспозиция – завязка – развитие действия – кульминация – развязка». Именно такое расположение частей необязательно. Много отступлений. 2)Еще одно толкование композиции, более связанное с особенностями словесного творчества: «мотивированное расположение «отрезков» текста.Каждый «отрезок» в составе словесного целого характеризуется или выдержанной на всем его протяжении той или иной формой словесного выражения (повествование, описание, рассуждение, диалог), или точкой видения автора, рассказчика, персонажа, с которой ведется изложение». О случаях сложных отношений архитектоники и сюжета. «Прежде всего, это относится к расположению частей в произведении в отношении к последовательности событий во времени, охватываемом повествованием». Среди возможных видов временных сдвигов «рассказы героев».
3) Третье определение композиции выдвинул В.В. Виноградов, предложив понимание композиции художественного текста, «как системы динамического развертывания словесных рядов в сложном словесно-художественном единстве». Он определяет слагаемые компоненты композиции словесного произведения как словесные ряды. В качестве слагаемых могут выступать не только слова, но и словосочетания, тропы, фигуры, синтаксические модели. Виноградов не предложил дефиниции словесного ряда. Поэтому Горшков предлагает свои свойства словесного ряда. 1) Поскольку словесный ряд выступает как слагаемое композиции, то является категорией текста. Вне текста словесного ряда нет.2)Определение «словесный» выступает в широком смысле (языковой) и предполагает ряд не только лексический, но и фонетический, морфологический, словообразовательный, синтаксический и т.д. Так что словесный ряд – это последовательность языковых единиц разных ярусов (а не только яруса лексики).
3) Третье свойство – не обязательно непрерывная последовательность языковых единиц, образующих словесный ряд.
4) Словесные ряды могут быть выделены по различным признакам, из которых главные – соотнесенность с определенной сферой языкового употребления (архаизмы, неологизмы, жаргонизмы, профессионализмы, диалектизмы) и с определенным приемом построения текста. Могут быть объединены связанностью с какой-либо стороной построения текста: эмоционально-экспрессивной или предметно-логической.
Словесные ряды. Словесный ряд и контекст СР – это представленная в тексте последовательность (не обязательно непрерывная) языковых единиц разных ярусов объединенных композиционной ролью и соотнесенностью с определенной сферой языкового выражения или с определенным приемом построения текста. Определение композиции, которое выдвинул В.В. Виноградов, — он предложил понимание композиции художественного текста, «как системы динамического развертывания словесных рядов в сложном словесно-художественном единстве».
Он определяет слагаемые компоненты композиции словесного произведения как словесные ряды. В качестве слагаемых могут выступать не только слова, но и словосочетания, тропы, фигуры, синтаксические модели. Виноградов не предложил дефиниции словесного ряда. Поэтому Горшков предлагает свои свойства словесного ряда. 1) Поскольку словесный ряд выступает как слагаемое композиции, то является категорией текста. Вне текста словесного ряда нет. 2) Определение «словесный» выступает в широком смысле (языковой) и предполагает ряд не только лексический, но и фонетический, морфологический, словообразовательный, синтаксический и т.д. Так что словесный ряд – это последовательность языковых единиц разных ярусов (а не только яруса лексики). 3) Третье свойство – не обязательно непрерывная последовательность языковых единиц, образующих словесный ряд. 4) Словесные ряды могут быть выделены по различным признакам, из которых главные – соотнесенность с определенной сферой языкового употребления (архаизмы, неологизмы, жаргонизмы, профессионализмы, диалектизмы) и с определенным приемом построения текста. Могут быть объединены связанностью с какой-либо стороной построения текста: эмоционально-экспрессивной или предметно-логической. Отличается словесный ряд от контекста. Контекст – (тесная связь, соединение) – часть текста, взятая в таком протяжении, которое достаточно для определения смысла входящего в него отдельного слова или предложения. СР же является слагаемым, компонентом текста, а не его частью от и до.
Могут быть объединены связанностью с какой-либо стороной построения текста: эмоционально-экспрессивной или предметно-логической. Отличается словесный ряд от контекста. Контекст – (тесная связь, соединение) – часть текста, взятая в таком протяжении, которое достаточно для определения смысла входящего в него отдельного слова или предложения. СР же является слагаемым, компонентом текста, а не его частью от и до.
Воспользуйтесь поиском по сайту:
∧ — Логическое И: U+2227 and
U+2227
Нажмите, чтобы скопировать и вставить символ
Техническая информация
| Название в Юникоде | Logical And |
| Номер в Юникоде | U+2227 |
| HTML-код | ∧ |
| CSS-код | \2227 |
| Мнемоника | ∧ |
| Раздел | Математические операторы |
| Версия Юникода: | 1. 1 (1993) 1 (1993) |
Значение символа
Логическое И. Математические операторы.
Символ «Логическое И» был утвержден как часть Юникода версии 1.1 в 1993 г.
Свойства
| Версия | 1.1 |
| Блок | Математические операторы |
| Тип парной зеркальной скобки (bidi) | Нет |
| Композиционное исключение | Нет |
| Изменение регистра | 2227 |
| Простое изменение регистра | 2227 |
Кодировка
| Кодировка | hex | dec (bytes) | dec | binary |
|---|---|---|---|---|
| UTF-8 | E2 88 A7 | 226 136 167 | 14846119 | 11100010 10001000 10100111 |
| UTF-16BE | 22 27 | 34 39 | 8743 | 00100010 00100111 |
| UTF-16LE | 27 22 | 39 34 | 10018 | 00100111 00100010 |
| UTF-32BE | 00 00 22 27 | 0 0 34 39 | 8743 | 00000000 00000000 00100010 00100111 |
| UTF-32LE | 27 22 00 00 | 39 34 0 0 | 656539648 | 00100111 00100010 00000000 00000000 |
Наборы с этим символом:
∑
Математические знаки
3.
 ПАУЗА ЛОГИЧЕСКАЯ И ПСИХОЛОГИЧЕСКАЯ. ТЕМП И РИТМ РЕЧИ.. Интонация
ПАУЗА ЛОГИЧЕСКАЯ И ПСИХОЛОГИЧЕСКАЯ. ТЕМП И РИТМ РЕЧИ.. ИнтонацияИнтонация
реферат
Осмысленное произношение предложения требует правильного членения его на звенья, такты. Но «в обыкновенной связной речи нет четкой делимости на слова, так что промежутки, белые пространства, отделяющие слова друг от друга в писаном или печатном тексте, не всегда являются показателями членения речи в произношении» [14].
Знаком, сигналом остановки служит смысловая законченность синтагмы или предложения. При выразительном чтении группировка слов по синтагмам облегчает чтецу анализ текста, а слушателям — правильное восприятие его на слух. Объединение слов по логическим группам придает предложению звуковую цельность, законченность. Восприятие читаемого текста, расчлененного на синтагмы, с обозначением синтагматического (фразового) ударения, гораздо легче уже потому, что при таком чтении мы устанавливаем смысл всех логических связей в предложении и далее в тексте, а тем самым даем истолкование текста, обеспечивая убедительную и правильную его передачу.
Членение речи обозначается паузами. Пауза объединяет слова в непрерывный ряд звуков, но в то же время и разделяет группы слов, ограничивает их. Это логическая пауза. Паузы могут быть разной длительности, в зависимости от высказываемой мысли, от содержания читаемого. Чтец, соблюдая логические паузы, произносит слова, заключенные между ними, слитно, как одно слово. В предложении: Ячмень сеют, I когда молодой скворец I головку в окошке показывает 11 паузы разной длительности. Самая длительная пауза — в конце предложения перед следующим предложением, пауза короче — после слова сеют, на стыке главного и придаточного, очень короткая — после слова скворец. Пауза членит фразу на звенья. Слова в пределах такта произносятся слитно.
При неверной паузе нарушается смысл предложения, содержание его становится неясным, извращается основная мысль. С. Волконский приводит пример, когда неверная постановка паузы нарушает смысл предложения: «И кудри черные до плеч. Остановимся после черные,- совершенно понятно: кудри до плеч . .. Теперь остановимся после кудри,- бессмыслица: черные до плеч (а ниже плеч другого цвета?)»[15]. Известен также пример предложения, в котором от перенесения паузы меняется основной смысл утверждения: Они кормили его I мясом своих собак. Они кормили его мясом I своих собак.
.. Теперь остановимся после кудри,- бессмыслица: черные до плеч (а ниже плеч другого цвета?)»[15]. Известен также пример предложения, в котором от перенесения паузы меняется основной смысл утверждения: Они кормили его I мясом своих собак. Они кормили его мясом I своих собак.
Иногда место логической паузы определяется знаками препинания:
Хотя услуга нам I при нужде дорога,I Но за нее не всяк умеет взяться. II (И. Крыл о в.)
Не дай бог с дураком связаться!II Услужливый дурак I опаснее врага.II (И. Крылов.)
Надо научиться хорошо слышать паузу и соблюдать ее при чтении. Прочтём:
1. Синий, синий,I ходит он плавным разливом I и середь ночи, как середь дня, I виден за столько вдаль, I за сколько видеть может человечье oкo.II
2. Нежась и прижимаясь ближе к берегам от ночного холода, I дает он по себе серебряную струю; I и она вспыхивает, словно полоса дамасской сабли; I а он, I синий, I снова заснул. (Н. Гоголь.)
В первом предложении пауза выделяет обособленное определение, отделяет однородные сказуемые и концовку — придаточное. Во втором пауза отделяет деепричастный оборот, является предупреждением о перечислении действий, противопоставлении их. Пауза наполняется соответствующим содержанием. Логические паузы оформляют речь, придают ей законченность. Иногда логическая пауза переходит в психологическую. Логической паузе «отведено более или менее определенное, очень небольшое время длительности. Если это время затягивается, то бездейственная логическая пауза должна скорее перерождаться в активную психологическую» [16].
Во втором пауза отделяет деепричастный оборот, является предупреждением о перечислении действий, противопоставлении их. Пауза наполняется соответствующим содержанием. Логические паузы оформляют речь, придают ей законченность. Иногда логическая пауза переходит в психологическую. Логической паузе «отведено более или менее определенное, очень небольшое время длительности. Если это время затягивается, то бездейственная логическая пауза должна скорее перерождаться в активную психологическую» [16].
Психологическая пауза — это остановка, которая усиливает, выявляет психологическое значение фразы, отрывка. Она богата внутренним содержанием, активна, так как обусловливается отношением чтеца к событию, к действующему лицу, к его поступкам. Она отражает работу воображения читающего, тотчас же отражается на интонации , иногда даже меняет логическую группировку слов , так как проистекает из внутренней жизни , из жизни воображения. Значение её характеризуется В.Аксёновым так: « Психологическая пауза может возникнуть в начале фразы — перед словами , внутри фразы- между словами и в конце фразы-после прочитанных слов. В первом случае она предупреждает значение слов предстоящих; во втором — проявляет психологическую зависимость (объединяющую или разъединяющую) высказанной мысли от мысли последующей, подчеркивая значение этих мыслей и отношение к ним; в третьем случае она задерживает внимание на отзвучавших словах и образах, как бы продлевая в молчании глубину их значения. Воздействие психологической паузы в последнем случае огромно» [17].
В первом случае она предупреждает значение слов предстоящих; во втором — проявляет психологическую зависимость (объединяющую или разъединяющую) высказанной мысли от мысли последующей, подчеркивая значение этих мыслей и отношение к ним; в третьем случае она задерживает внимание на отзвучавших словах и образах, как бы продлевая в молчании глубину их значения. Воздействие психологической паузы в последнем случае огромно» [17].
Вот одна из заключительных сцен «Тамани», где М. Лермонтов описывает борьбу русского офицера, случайно попавшего «в мирный круг честных контрабандистов», с девушкой-контрабандисткой.
— Ты видел,- отвечала она:- ты донесешь ! — и сверхъестественным усилием повалила меня на борт; мы оба по пояс свесились из лодки; ее волосы касались воды; минута была решительная. Я уперся коленкою во дно, схватил ее одной рукой за косу, другой за горло, она выпустила мою одежду, II и я мгновенно бросил ее в волны. Было уже довольно темно; голова её мелькнула раза два среди морской пены, и больше я ничего не видал.
При чтении этого отрывка первая психологическая пауза перед словами и я мгновенно сбросил ее в волны-пауза ожидания исхода борьбы; в то же время эта пауза — знак перелома; быстро сменяющиеся действия, напряженность этих действий должны же привести к какому-то концу. Вот он, конец: я мгновенно сбросил ее в волны. Что будет? Каково последствие этого действия? Верно, утонет? Таково содержание второй паузы. Эпизод закончен: Голова ее (девушки) мелькнула раза два среди морской пены, и больше я ничего не видал. Третья пауза наполняется ·тоже значительным содержанием: гибель девушки случайна, бессмысленна. Пауза в данном случае заставит слушателя осмыслить прочитанное, задуматься над ним.
Психологическая пауза — выразительное средство при чтении произведения. По выражению К. С. Станиславского, «красноречивое молчание» и есть психологическая пауза. Она является чрезвычайно важным орудием общения» [18]. «Все они (паузы.) умеют досказать то, что недоступно слову, и нередко действуют в молчании гораздо интенсивнее, тоньше и неотразимее, чем сама речь. Их бессловесный разговор может быть интересен, содержателен и убедителен не менее, чем словесный» [19]. «Пауза — важный элемент нашей речи и один из главных ее козырей» [20]. Паузное членение речи (паузировка) очень важно для осмысления читаемого и произносимого текста. Именно между двумя паузами, следующими одна за другой, выделяется отрезок речи, который является основной интонационной единицей. С паузировкой неразрывно связаны темп и ритм речи. Произнесём какую-то фразу или ряд фраз. Самое произнесение займет определенное время. Чем же заполнилось это время? Звуками самой разнообразной длительности. Звуки речи слагаются в слоги и слова, т. е. в ритмические части и группы. Одни ритмические части или группы требуют отрывистого произношения, другие — плавного, растянутого, певучего; одни звуки притягивают ударение, другие лишены его и т. д. Между потоками этих звуков имеются паузы — тоже разной длительности. Таким образом, в устной речи мы замечаем определенный темп и ритм. «Темп есть быстрота чередования условно принятых за единицу одинаковых длительностей в том или другом размере.
Их бессловесный разговор может быть интересен, содержателен и убедителен не менее, чем словесный» [19]. «Пауза — важный элемент нашей речи и один из главных ее козырей» [20]. Паузное членение речи (паузировка) очень важно для осмысления читаемого и произносимого текста. Именно между двумя паузами, следующими одна за другой, выделяется отрезок речи, который является основной интонационной единицей. С паузировкой неразрывно связаны темп и ритм речи. Произнесём какую-то фразу или ряд фраз. Самое произнесение займет определенное время. Чем же заполнилось это время? Звуками самой разнообразной длительности. Звуки речи слагаются в слоги и слова, т. е. в ритмические части и группы. Одни ритмические части или группы требуют отрывистого произношения, другие — плавного, растянутого, певучего; одни звуки притягивают ударение, другие лишены его и т. д. Между потоками этих звуков имеются паузы — тоже разной длительности. Таким образом, в устной речи мы замечаем определенный темп и ритм. «Темп есть быстрота чередования условно принятых за единицу одинаковых длительностей в том или другом размере. Ритм есть количественное отношение действенных длительностей (движения, звука) к длительностям, условно принятым за единицу в определенном темпе и размере» [21]. Так определяет К. С. Станиславский понятия темпа и ритма, необходимые нам для изучения устной выразительной речи. Эти понятия очень близки, а самые явления почти неразделимы в речи. К. С. Станиславский объединяет темп и ритм в одно понятие — «темпо-ритм». «Буквы, слоги и слова,- говорит он,- это музыкальные ноты в речи, из которых создаются такты, арии и целые симфонии. Недаром же хорошую речь называют музыкальной» [22]. Речь диктора (чтеца) должна быть в одних случаях плавной, слитной, в других — быстрой, легкой, четкой, чеканной. Такая гибкость речи приобретается сознательным стремлением выработать в себе чувство темпа и ритма. Темп и ритм в свою очередь определяются смысловой стороной читаемого текста и намерениями читающего или рассказывающего.Для овладения «музыкальной» речью К. С. Станиславский советует: «Берите за образец подлинных певцов и заимствуйте для своей речи их четкость, правильную размеренность и дисциплину в речи.
Ритм есть количественное отношение действенных длительностей (движения, звука) к длительностям, условно принятым за единицу в определенном темпе и размере» [21]. Так определяет К. С. Станиславский понятия темпа и ритма, необходимые нам для изучения устной выразительной речи. Эти понятия очень близки, а самые явления почти неразделимы в речи. К. С. Станиславский объединяет темп и ритм в одно понятие — «темпо-ритм». «Буквы, слоги и слова,- говорит он,- это музыкальные ноты в речи, из которых создаются такты, арии и целые симфонии. Недаром же хорошую речь называют музыкальной» [22]. Речь диктора (чтеца) должна быть в одних случаях плавной, слитной, в других — быстрой, легкой, четкой, чеканной. Такая гибкость речи приобретается сознательным стремлением выработать в себе чувство темпа и ритма. Темп и ритм в свою очередь определяются смысловой стороной читаемого текста и намерениями читающего или рассказывающего.Для овладения «музыкальной» речью К. С. Станиславский советует: «Берите за образец подлинных певцов и заимствуйте для своей речи их четкость, правильную размеренность и дисциплину в речи. Передавайте правильно длительность букв, слогов, слов, остроту ритма при сочетании их звуковых частиц, образуйте из фраз речевые такты, регулируйте ритмическое соотношение целых фраз между собой, любите правильные и четкие акцентуации (ударения), типичные для переживаемых чувств, страсти или для создаваемого образа» [23]. Эти советы молодым актерам как нельзя более пригодны и для чтеца, и для диктора, желающего совершенствовать речь, добиваясь ее большей выразительности. Не только в стихотворной, но и в прозаической речи есть ритм. В этом можно убедиться, слушая хорошее чтение произведений Пушкина, Гоголя, Typгенева и других. Даже в деловой речи — в выступлениях на собрании , по радио, при чтении газетной статьи — отмечается ритмическое произнесение. Самый четкий ритм ощущается при произнесении стихов. На протяжении предложения или всего высказывания темпо-ритм меняется в зависимости от смысла. Если мы хотим привлечь внимание слушателя, то произнесем фразу или ее часть замедленно, подчеркнуто; вводные же слова или предложения, мысли второстепенные, высказываемые между прочим, произнесем в среднем или даже быстром темпе.
Передавайте правильно длительность букв, слогов, слов, остроту ритма при сочетании их звуковых частиц, образуйте из фраз речевые такты, регулируйте ритмическое соотношение целых фраз между собой, любите правильные и четкие акцентуации (ударения), типичные для переживаемых чувств, страсти или для создаваемого образа» [23]. Эти советы молодым актерам как нельзя более пригодны и для чтеца, и для диктора, желающего совершенствовать речь, добиваясь ее большей выразительности. Не только в стихотворной, но и в прозаической речи есть ритм. В этом можно убедиться, слушая хорошее чтение произведений Пушкина, Гоголя, Typгенева и других. Даже в деловой речи — в выступлениях на собрании , по радио, при чтении газетной статьи — отмечается ритмическое произнесение. Самый четкий ритм ощущается при произнесении стихов. На протяжении предложения или всего высказывания темпо-ритм меняется в зависимости от смысла. Если мы хотим привлечь внимание слушателя, то произнесем фразу или ее часть замедленно, подчеркнуто; вводные же слова или предложения, мысли второстепенные, высказываемые между прочим, произнесем в среднем или даже быстром темпе.
4. МЕЛОДИКА.
Кроме ударения, темпа и ритма, в понятие интонации входит также мелодика тона. Стоит сказать, что движение голоса вверх и вниз по звукам разной высоты называют мелодикой речи. Зададим громко вопрос: И всё? Мы услышим подъем голоса на звуке [о]. Ответ: Да, всё. Мы отмечаем понижение голоса на звуке [о]. Схематически движение голоса можно обозначить следующим образом :
— И всё?!
— Да, всё.
Вот ещё мелодический рисунок фразы:
По ниве прохожу я узкою межой,
Поросшей кашкою и цепкой лебедой.
Здесь намеренно обеднена мелодика предложения, чтобы легче было изобразить движение тона. На самом деле мелодика речи гораздо разнообразнее, богаче. Восклицательные, вопросительные знаки, точки, запятые — все это указатели не только пауз, но и мелодических рисунков предложения. Эти рисунки можно назвать фигурами мелодии.
Существуют различные мелодические фигуры. Окончание мысли и вместе с тем завершение фразы требуют понижения голоса (нисходящая фигура). Развитие мысли вместе с развитием высказывания требуют повышения голоса (восходящая фигура). В одном и том же предложении мелодия может идти сначала в качестве восходящей, а затем — в качестве нисходящей, где-то в середине фразы будет перелом — после кульминационного пункта. Возможна также монотонная мелодия фразы.
Развитие мысли вместе с развитием высказывания требуют повышения голоса (восходящая фигура). В одном и том же предложении мелодия может идти сначала в качестве восходящей, а затем — в качестве нисходящей, где-то в середине фразы будет перелом — после кульминационного пункта. Возможна также монотонная мелодия фразы.
Примеры мелодических фигур:
Ты пойдёшь? (восходящая фигура мелодии).
Пойду .(нисходящая фигура мелодии).
Запомни раз и навсегда … (внушение, монотонная мелодия),
Ты опять уснешь!(полная фигура: повышение, кульминация, понижение голоса ).
Мелодика предложений, фраз, синтагм очень разнообразна. Современный синтаксис русского языка сводит мелодические рисунки синтагм к нескольким типам и в первую очередь различает мелодику конечных и неконечных синтагм. Для конечных синтагм в основном характерны два типа мелодики. Повествовательным предложениям свойственно понижение тона в конце. Вопросительные имеют специфическую мелодику. В предложениях без вопросительных местоимений и наречий значение вопроса создается только мелодикой (резкое повышение тона на ударном слоге того слова, к которому ставится вопрос). Мелодика неконечных синтагм более разнообразна и сводится к трем мелодическим типам: 1. Резкое повышение тона на ударном слоге выделяемого слова. Перед этим словом и после него слова произносятся более низким тоном :(Ваша книга I на столе. В ней вы прочитаете — всё).
Мелодика неконечных синтагм более разнообразна и сводится к трем мелодическим типам: 1. Резкое повышение тона на ударном слоге выделяемого слова. Перед этим словом и после него слова произносятся более низким тоном :(Ваша книга I на столе. В ней вы прочитаете — всё).
2. Отсутствие резких интервалов. Интонационным центром неконечной синтагмы выступает ударный слог выделяемого слова :
(Так как это близко,- ты поезжай).
3. Неконечные синтагмы произносятся как законченные в смысловом отношении:
(Это Володя I, наш тракторист).
Конечная синтагма произносится на более низком тоне. Обе синтагмы одинаковы по рисунку мелодики [24].
Следует учитывать, кроме того, еще особенности содержания высказываемой мысли, а также особенности грамматической структуры предложения, целого высказывания. В речевой практике мелодика многих грамматических структур закрепилась.
Так специфическими мелодиками являются: вопросительная, пояснительная, перечислительная, предупредительная, причинной связи, противительной связи, разделительная, мелодика вводности, незаконченности и др.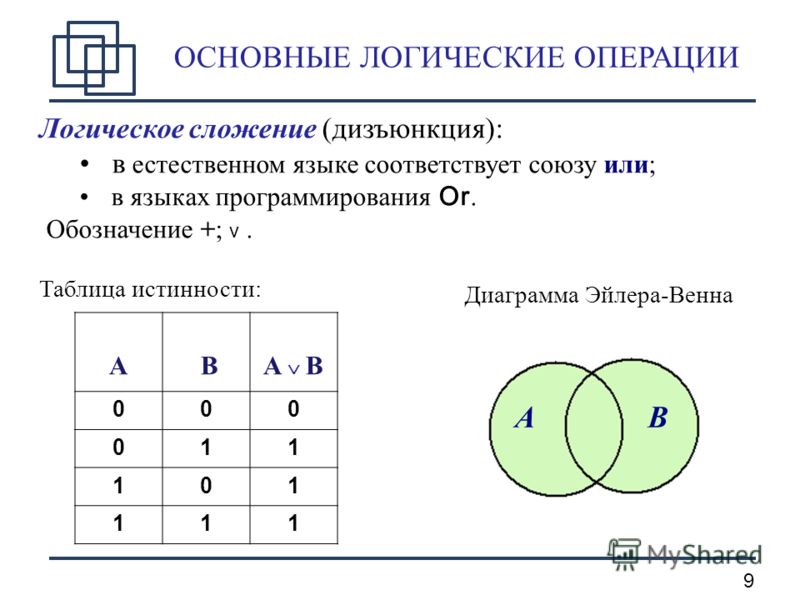 [25]. При чтении художественного произведения мелодика служит одним из ярких выразительных средств звучащей речи: она воздействует на слушателя, облегчает восприятие произведения, раскрывает его эмоциональную сторону. Взволнованной речи присущи смелые подъемы и понижения (падения) мелодии. Вспомним отрывок из произведения А. Гайдара «Чук И Гек», в котором изображается отчаяние матери. Вернувшись домой, в сторожку, она не нашла сына. Гек пропал … Мать выбежала на дорогу, зарядила ружье и выстрелила. Прозвучал ответный выстрел.
[25]. При чтении художественного произведения мелодика служит одним из ярких выразительных средств звучащей речи: она воздействует на слушателя, облегчает восприятие произведения, раскрывает его эмоциональную сторону. Взволнованной речи присущи смелые подъемы и понижения (падения) мелодии. Вспомним отрывок из произведения А. Гайдара «Чук И Гек», в котором изображается отчаяние матери. Вернувшись домой, в сторожку, она не нашла сына. Гек пропал … Мать выбежала на дорогу, зарядила ружье и выстрелила. Прозвучал ответный выстрел.
У крыльца раздался гром и стук. Распахнулась дверь. В избу влетела собака, а за нею вошел окутанный паром сторож.
— Что за беда? Что за стрельба? — спросил он, не здороваясь и не раздеваясь. -Пропал мальчик,- сказала мать. Слезы ливнем хлынули из ее глаз, и она больше не могла сказать ни слова. — Стой, не плачь! — гаркнул сторож.- Когда пропал? Давно? Недавно? .. Назад, Смелый! — крикнул он собаке.- Да говорите же, или я уйду обратно! — Час тому назад,- ответила мать. — Мы ходили за водой. Мы пришли, а его нет. Он оделся и куда-то ушел
— Мы ходили за водой. Мы пришли, а его нет. Он оделся и куда-то ушел
Слова пропал мальчик надо дать с мелодией незаконченности предложения (в восходящей мелодии). Повелительный смысл речи сторожа, добивающегося решения загадки, и настойчивое его требование ответить на вопросы: Давно? Недавно? — обусловлены обстановкой и создавшимся состоянием тревоги. Ударную силу приобретает фраза: Да говорите же, или я уйду обратно!,- которую следует прочесть в сильной, восходящей, а затем нисходящей мелодии.
Да говорите же , или я уйду обратно!
Успокаивающие слова сторожа порождают и соответственное понижение тона. Мелодия становится более спокойной:
-Ну, за час он далеко не уйдет, а в одежде и в валенках сразу не замерзнет.
Обращаясь к собаке и побуждая ее к действию, сторож говорит: Ко мне, Смелый! На, нюхай (калоши и башлык Гека).
Прочитать эти слова надо на более высокой ноте, твердо, в тоне команды, размеренным темпом. Более или менее спокойно звучит повествовательная речь. Мелодия такой речи условно может быть выражена прямой линией с незначительными подъемами и падениями — отклонениями от среднего тона:
Мелодия такой речи условно может быть выражена прямой линией с незначительными подъемами и падениями — отклонениями от среднего тона:
И тогда все люди встали,I еще раз поздравили друг друга с Новым годом и пожелали всем счастья.
Лирическая окрашенность фразы диктуется контекстом: перед этим идут строчки:
Это в далекой-далекой Москве, под красной звездой, на Спасской башне звонили золотые кремлевские часы. И этот звон — перед Новым годом — сейчас слушали люди и в городах, и в горах, в степях, в тайге, на синем море.
Ценным выразительным средством по воле чтеца может стать монотон, т. е. произнесение речи без подъемов и падений. Начало поэмы В. Маяковского «Владимир Ильич Ленин» читается монотонно торжественно:
Время.I Начинаю про Ленина рассказ.
Слова торжественного обещания юных пионеров читаются также монотонно. При переходе от одной части произведенияк другой, иногда сильно отличающейся или даже противоположной по содержанию, чтец делает паузу, во время которой он как бы внутренне перестраивается на новый лад. Мелодика, отзывчивая на психологические задачи, отразит этот переход. Вспомним стихотворение М. Лермонтова «На смерть поэта». Первая часть этого стихотворения по своему основному тону должна быть прочитана в плоскости «низа», вторая часть представляет контраст первой и читается в плоскости «верха» С экспрессией ярко выраженного негодования и угрозы. Нужно не только упражняться в использовании интонации, но постоянно наблюдать за интонацией речи других, особенно мастеров художественного слова — артистов, чтецов, рассказчиков, дикторов. Надо прислушиваться к речи детей. Безыскусственные интонации последних делают их речь, предельно выразительной. «Наблюдайте жизнь, говорит И. Я. Блинов,- и вы убедитесь, что человек без яркого темперамента, «бесчувственный», как принято говорить, звучит в своей речи монотонно, без активных и заметных мелодий. Педант говорит на «одной ноте». Чем ярче эмоциональная отзывчивость человека, тем богаче его речь мелодической выразительностью … Помните: речь, лишенная должных мелодических акцентов,- бесчувственна!» [26]
Мелодика, отзывчивая на психологические задачи, отразит этот переход. Вспомним стихотворение М. Лермонтова «На смерть поэта». Первая часть этого стихотворения по своему основному тону должна быть прочитана в плоскости «низа», вторая часть представляет контраст первой и читается в плоскости «верха» С экспрессией ярко выраженного негодования и угрозы. Нужно не только упражняться в использовании интонации, но постоянно наблюдать за интонацией речи других, особенно мастеров художественного слова — артистов, чтецов, рассказчиков, дикторов. Надо прислушиваться к речи детей. Безыскусственные интонации последних делают их речь, предельно выразительной. «Наблюдайте жизнь, говорит И. Я. Блинов,- и вы убедитесь, что человек без яркого темперамента, «бесчувственный», как принято говорить, звучит в своей речи монотонно, без активных и заметных мелодий. Педант говорит на «одной ноте». Чем ярче эмоциональная отзывчивость человека, тем богаче его речь мелодической выразительностью … Помните: речь, лишенная должных мелодических акцентов,- бесчувственна!» [26]
5. ТЕМБР.
ТЕМБР.
Тембр — это специфическая (сверхсегментная) окраска речи, придающая ей те или другие экспрессивно-эмоциональные свойства. Тембр рассматривается как очень важное, но дополнительное средство обогащения мелодики речи и органически связан с ней, обусловливает ее. У каждого человека есть свои особенности звучания речи, связанные с устройством и работой его речевого аппарата, характером звуков его голоса . По совокупности этих признаков, даже не видя человека, можно узнать, что говорит именно он.
Но окраска речи может меняться, отклоняться от обычной нормы, в зависимости от эмоций. Чем сильнее эмоции, тем больше отклонений от обычного звучания. Выразительность речи и сообщается этим отклонением. «Если вы больны, плохо настроены, наоборот, счастливы и веселы,- обо всем этом «расскажет» тембр вашего голоса. Если вы активны в выражении мысли, если ваши эмоции не скрыты,- снова прежде всего тембр об этом доведет это «до сведения» вашего собеседника» [27]. Причины этого могут быть разные, зависящие или не зависящие от воли говорящего. Замысел писателя в первую очередь должен определять и средства эмоциональной окраски речи. Правильное прочтение произведения, его верное истолкование при подготовке к чтению — основное условие, при котором творческое намерение поэта или писателя безошибочно осуществляется чтецом. Тембр окрашивает все произведение, наделяя его бесконечно разнообразными оттенками. Чем, как не тембральной окраской, можно передать мысли, представления, чувства от имени действующего лица, как бы «сквозь призму» его восприятия и оценки? Прочтем стихотворение А. Барто «Машенька». Вообразим пока еще ограниченный комнатой круг представлений Машеньки, и мы невольно в начале стихотворения примем тон нежной мамаши или нянюшки, нараспев произносящей одну из бесчисленных своих забавок, затем перейдем на точку зрения Машеньки и особым чувством окрасим слова, которые рисуют мир ребенка, как он сам его представляет.
Причины этого могут быть разные, зависящие или не зависящие от воли говорящего. Замысел писателя в первую очередь должен определять и средства эмоциональной окраски речи. Правильное прочтение произведения, его верное истолкование при подготовке к чтению — основное условие, при котором творческое намерение поэта или писателя безошибочно осуществляется чтецом. Тембр окрашивает все произведение, наделяя его бесконечно разнообразными оттенками. Чем, как не тембральной окраской, можно передать мысли, представления, чувства от имени действующего лица, как бы «сквозь призму» его восприятия и оценки? Прочтем стихотворение А. Барто «Машенька». Вообразим пока еще ограниченный комнатой круг представлений Машеньки, и мы невольно в начале стихотворения примем тон нежной мамаши или нянюшки, нараспев произносящей одну из бесчисленных своих забавок, затем перейдем на точку зрения Машеньки и особым чувством окрасим слова, которые рисуют мир ребенка, как он сам его представляет.
Машенька (Отрывок)
Кто, кто в этой комнате живет?
Кто, кто вместе с солнышком встает?
Это Машенька проснулась,
С боку на бок повернулась и, откинув одеяло,
Вдруг сама на ножки встала.
«Здесь не комната большая -здесь огромная страна,
Два дивана-великана,
Вот зеленая поляна — это коврик у окна.
Потянулась Машенька к зеркалу рукой,
Удивилась Машенька: «Кто же там такой?»
Она дошла до стула, немножко отдохнула
Постояла у стола и опять вперед пошла …
Окраска речи может сообщить словам противоположный смысл, например: А наши умники -то что придумали … Слову умники придается иронический смысл особым образом окрашенной мелодики. Продолжим теперь рассказ о том, что же такое сделали упомянутые «умники»,- И вся последующая речь окрасится иронией, например: Книги в сарай снесли, бумаги — в печку! Хорошо! Никакой заботушки! Заключительное одобрение Хорошо! дано с неожиданно сильным повышением голоса на ударном слоге. Теперь весь смысл высказывания понимается не как одобрение, а как порицание, осуждение всех действий «умников». Тембр — выразитель художественной интерпретации текста. Чтец не только передает его в соответствии с пониманием творческих задач автора произведения, но и обогащает звучание собственными творческими замыслами. Каких-либо рецептов «раскраски тембра» нет. Вдумчивое чтение текста, «вживание» в образы писателя, автора — вот что дает основу эмоционально-экспрессивного чтения. «Гармоническое единство интонации речи с ее внутренними корнями должно обеспечить речи ту естественность и простоту, которые дороже необдуманной «красивости» [28].
Каких-либо рецептов «раскраски тембра» нет. Вдумчивое чтение текста, «вживание» в образы писателя, автора — вот что дает основу эмоционально-экспрессивного чтения. «Гармоническое единство интонации речи с ее внутренними корнями должно обеспечить речи ту естественность и простоту, которые дороже необдуманной «красивости» [28].
Ощутимое проявление художественного истолкования произведения — это выражение отношения чтеца к изображаемому, его личные эстетические оценки. В восприятии текста участвует и мышление, и воображение. Описываемые в произведении картины должны возникать во внутреннем видении (в воображении), как живые. Живость придают не только общая обрисовка «предложенных обстоятельств», но и детали. Чтецу в этом помогает и жизненный опыт, и изучение эпохи, и сведения из биографии писателя и многое другое. Образ «звучит» ярче, если «согреть» его воображением, конкретизировать детали. Для примера можно взять стихотворение С. Щипачева
«Пионерский галстук».
Как повяжешь галстук, береги его:
Он ведь с нашим знаменем цвета одного.
А под этим знаменем в бой идут бойцы,
За Отчизну бьются братья и отцы.
Как повяжешь галстук, ты светлей лицом …
На скольких ребятах он пробит свинцом! ..
Пионерский галстук -нет его родней!
Он от юной крови стал еще красней.
Как повяжешь галстук, береги его:
Он ведь с нашим знаменем цвета одного.
Стихотворение представляет собой монолог — напутствие школьнику, вступающему в пионерскую организацию. Монолог можно вложить в уста кого-нибудь из старших в семье: деда, отца, брата-комсомольца. В соответствии с этим чтению должен быть сообщен тембральный колорит. Легко представить себе, что, предположим, монолог произносит дед-ветеран Великой Отечественной войны. В торжественный, праздничный день он провожает внука на пионерский сбор, где тот будет принят в ряды организации и получит впервые свой пионерский галстук. Разговор происходит наедине. Речь деда задушевная, торжественная, небыстрая. Каждое слово этой речи значительно, веско, серьезно. Дед хочет, чтобы мальчик понял и почувствовал, что пионерский галстук — символ борьбы: Он ведь с нашим знаменем цвета одного …
Дед хочет, чтобы мальчик понял и почувствовал, что пионерский галстук — символ борьбы: Он ведь с нашим знаменем цвета одного …
Создание условий для ситуативной речи помогает чтецу найти окраску речи и прочитать людям текст с той степенью волнения, какая может быть свойственна бойцу в «предлагаемых обстоятельствах». Чтец сопереживает, активно живет жизнью того лица, от имени которого ведет речь. Текст как бы одухотворяется и приобретает живые, естественные интонации, окрашенные чувством.
Логическая и синтаксическая структуры различных видов текста. Их построение -Стилистика и литературное редактирование
Кто не делится найденным, подобен свету в дупле секвойи (древняя индейская пословица)
Библиографическая запись:
Логическая и синтаксическая структуры различных видов текста. Их построение . — Текст : электронный // Myfilology.ru – информационный филологический ресурс : [сайт]. – URL: https://myfilology.ru//162/logicheskaya-i-sintaksicheskaya-struktury-razlichnyx-vidov-teksta-ix-postroenie/ (дата обращения: 29.09.2022)
– URL: https://myfilology.ru//162/logicheskaya-i-sintaksicheskaya-struktury-razlichnyx-vidov-teksta-ix-postroenie/ (дата обращения: 29.09.2022)
Содержание
Логическая и синтаксическая структуры различных видов текста. Их построение
Логические структуры повествования и описания однотипны. Их составляющие (узлы повествования и элементы описания) равноправны, а связь между ними сочинительная.
Для синтаксической структуры повествования характерна опора на глагольные формы, прежде всего на формы прошедшего времени совершенного вида. Именно эти глагольные формы обладают наиболее отчётливо проявленной способностью «двигать действие», обозначая достигаемый им предел. Исчерпав себя, действие прекращается и уступает место другому. Таков механизм сочетания глаголов совершенного вида, передающих в повествовании последовательность событий.
В «чистом» виде описания и повествования в газетных материалах встречаются редко.
Ломоносов считал повествование разновидностью описания, представляющей «деяние». В определённых условиях линейная последовательность в перечислении событий может быть нарушена, могут возникнуть добавочные линии повествования, появиться их обрывы, могут включаться фрагменты, в которых описываются результаты действия.
В качестве основы текстовой конструкции может выступить и описание: «постоянное взаимодействие повествования и описания создаёт возможность включить отдельный эпизод в более широкий контекст пространства и времени, подводит к необходимости понять общий смысл отдельного события».
Повествование представляет собой, на первый взгляд, наиболее простой способ изложения. Не случайно, видимо, древнейшие образцы народного творчества – это в основном повествования, рассказы о событиях. Психологи установили, что дети, учась говорить, первую свою связную речь строят обычно как повествование. Педагогические методики учитывают это. «Первые темы, которые самым естественным путём пришли нам в голову, –свидетельствуют воспоминания преподавателей Яснополянской школы Толстого, – были описания простых предметов, как-то хлеба, избы, дерев и т.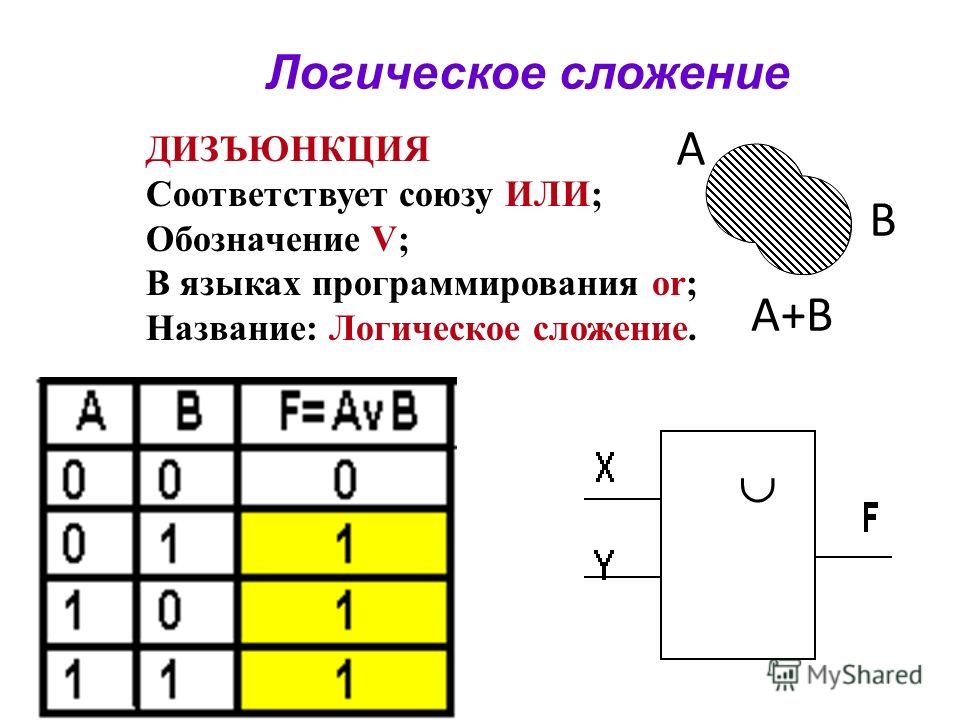 п.; но, к крайнему удивлению нашему, требования эти доводили учеников почти до слёз, и, несмотря на помощь учителя, они решительно отказывались писать на темы такого рода. Мы попробовали предложить описание каких-нибудь событий, и все обрадовались, как будто им сделали подарок. Столь любимые в школах описания так называемых простых предметов – свиньи, горшка, стола – оказались, без сомнения, труднее, чем целые, из воспоминаний взятые рассказы».
п.; но, к крайнему удивлению нашему, требования эти доводили учеников почти до слёз, и, несмотря на помощь учителя, они решительно отказывались писать на темы такого рода. Мы попробовали предложить описание каких-нибудь событий, и все обрадовались, как будто им сделали подарок. Столь любимые в школах описания так называемых простых предметов – свиньи, горшка, стола – оказались, без сомнения, труднее, чем целые, из воспоминаний взятые рассказы».
Строя повествование, каждый узел его мы представляем отдельно и, выявляя характер связей между ними, подчёркиваем лишь смену этих узлов.
В речи повествование и описание взаимодействуют самым непосредственным образом, отражая разнообразные формы пространственно-временных отношений, существующих в действительности. Не случайно в старой риторической традиции было принято рассматривать повествование и описание как единство, «род слова».
Однако психология создания автором этих видов текста и психология восприятия их читателем различны, и это существенно для редактора. В чём причина относительной сложности описания? При чтении мы постепенно движемся по тексту, от одного элемента описания к другому, но в результате этого поэлементного знакомства с предметом описания мы должны представить себе его как целое, как определённое единство, составить о нём целостное представление. Отсюда – конструктивные особенности описаний, характер приёмов, организующих их структуру.
В чём причина относительной сложности описания? При чтении мы постепенно движемся по тексту, от одного элемента описания к другому, но в результате этого поэлементного знакомства с предметом описания мы должны представить себе его как целое, как определённое единство, составить о нём целостное представление. Отсюда – конструктивные особенности описаний, характер приёмов, организующих их структуру.
Строя повествование, каждый узел его мы представляем отдельно и, выявляя характер связей между ними, подчёркиваем лишь смену этих узлов. Строя описание, мы ищем характерные черты предмета, олицетворяющие в нём главное, помогаем читателю преодолеть психологические трудности, апеллируя к его чувствам, вводим в действие дополнительные импульсы, способствующие созданию целостной картины. Очевидно, как важно учитывать это при работе над текстом.
Для описания характерны глаголы несовершенного вида (в прошедшем и настоящем времени), фиксирующие статику фактов и позволяющие достичь эффект «остановленного времени». Не случайно одна из функций настоящего времени глагола в грамматике имеет название «настоящее изобразительное». Оно называет действие, но само по себе лишено движения. Лишь в речи, в смене глагольных форм настоящее время глагола приобретает свойство передавать движение. И тогда, когда в описательных текстах употребляются другие формы сказуемых – ими могут быть различные глагольные формы, – они семантически близки к настоящему изобразительному времени и только называют действия, не определяя ни последовательности, ни длительности их. Иногда в описаниях мы вообще не видим глагольных форм. Однако описательный текст, состоящий целиком из номинативных предложений, т. е. перечисления признаков именительными падежами, сравнительно редок.
Не случайно одна из функций настоящего времени глагола в грамматике имеет название «настоящее изобразительное». Оно называет действие, но само по себе лишено движения. Лишь в речи, в смене глагольных форм настоящее время глагола приобретает свойство передавать движение. И тогда, когда в описательных текстах употребляются другие формы сказуемых – ими могут быть различные глагольные формы, – они семантически близки к настоящему изобразительному времени и только называют действия, не определяя ни последовательности, ни длительности их. Иногда в описаниях мы вообще не видим глагольных форм. Однако описательный текст, состоящий целиком из номинативных предложений, т. е. перечисления признаков именительными падежами, сравнительно редок.
Логическая и физическая необходимость
Остановимся вкратце на логических и физических модальностях, а также на модальностях, связанных с ценностями.
К логическим модальным понятиям относятся «(логически) необходимо», «(логически) возможно», «(логически) невозможно» и «(логически) случайно».
Логическая необходимость — характеристика высказывания, отрицание которого представляет собой логическое противоречие.
Логически необходимым являются, в частности, высказывание «Неверно, что неон — инертный газ и вместе с тем не инертный газ», поскольку отрицание этого высказывания («Неон — инертный газ и неон не является инертным газом») внутренне противоречиво (оно представляет собой отрицание закона противоречия). Логически необходимо высказывание «Трава зеленая или она не зеленая», так как его отрицание («Неверно, что трава зеленая или она не зеленая») противоречиво (отрицание закона исключенного третьего). Логически необходимым является также высказывание «Все холостяки не женаты», поскольку его отрицание («Есть холостяки, являющиеся женатыми») противоречиво.
Истинность логически необходимого высказывания может быть установлена независимо от опыта, на основе простого анализа значений слов, входящих в это высказывание. К примеру, высказывание «Снег бел» фактически истинно, для подтверждения его истинности требуется эмпирическое наблюдение. Высказывания же «Снег есть снег», «Белое есть белое», «Всякий холостяк не является женатым» и т.п. необходимо истинны: для установления их истинности не нужно обращаться к опыту, достаточно знать значения входящих в них слов.
Высказывания же «Снег есть снег», «Белое есть белое», «Всякий холостяк не является женатым» и т.п. необходимо истинны: для установления их истинности не нужно обращаться к опыту, достаточно знать значения входящих в них слов.
Понятие логической необходимости связано с понятием логического закона: логически необходимы законы логики и все, что вытекает из них.
Логическая возможность — характеристика внутренне непротиворечивого высказывания.
Например, высказывание «КПД паровой машины равен 100%» является, очевидно, ложным, но оно внутренне непротиворечиво и, значит, логически возможно. Но высказывание «КПД такой машины выше 100%» противоречиво, и потому логически невозможно.
Логическая возможность может быть разъяснена через понятие логического закона: логически возможно всякое высказывание, не противоречащее законам логики. Скажем, высказывание «Вирусы — живые организмы» совместимо с законами логики и, следовательно, логически возможно. Высказывание же «Неверно, что если человек — юрист, то он юрист» противоречит логическому закону тождества и потому является невозможным.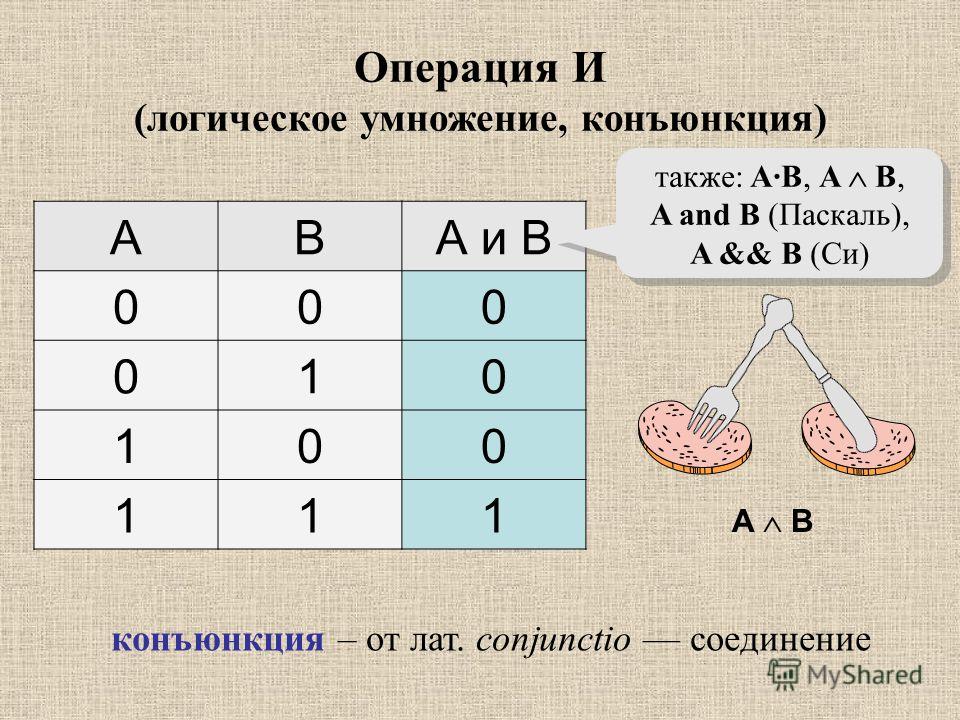
Логическая случайность — «двусторонняя возможность», или логическая возможность как высказывания, так и его отрицания.
Случайно то, что может быть, но может и не быть. С точки зрения логики случайно, например, что все многоклеточные существа смертны: ни утверждение этого факта, ни его отрицание не содержат внутреннего (логического) противоречия.
Логическая невозможность — внутренняя противоречивость высказывания. Логически невозможны, например, высказывания: «Растения дышат и растения не дышат», «Неверно, что если Вселенная бесконечна, то она бесконечна», «Некоторые жены не состоят в браке» и т.п.
Логические модальности можно определить друг через друга.
«Высказывание А логически необходимо» означает «Отрицание А не является логически возможным».
Например, «Необходимо, что холод есть холод» означает «Невозможно, чтобы холод не был холодом».
«А логически возможно» означает «Отрицание А не является логически необходимым».
К примеру, «Возможно, что кадмий — металл» означает «Неверно, что необходимо, что кадмий — не металл».
Физическая необходимость
Смысл логических модальностей легче понять, сопоставляя их с физическими, или онтологическими (бытий-ственными), модальностями.
Физические модальности — понятия, используемые для формулировки высказываний о необходимом, возможном, случайном и невозможном не в мышлении, а в природе.
Например: «Необходимо, что действие равно противодействию», «Случайно, что стекло разбилось», «Невозможно, чтобы дождь лил сорок дней и ночей подряд» и т.п. Логические модальные понятия связаны с «механикой» человеческого мышления и используются для характеристики существенных ее моментов. Физические модальные понятия касаются устройства самого реального мира.
Физическая необходимость — характеристика высказывания, отрицание которого несовместимо с законами природы.
Физически необходимыми являются, к примеру, высказывания: «Все планеты вращаются вокруг своей оси» и «Электрон, движущийся по стационарной орбите, не излучает энергию».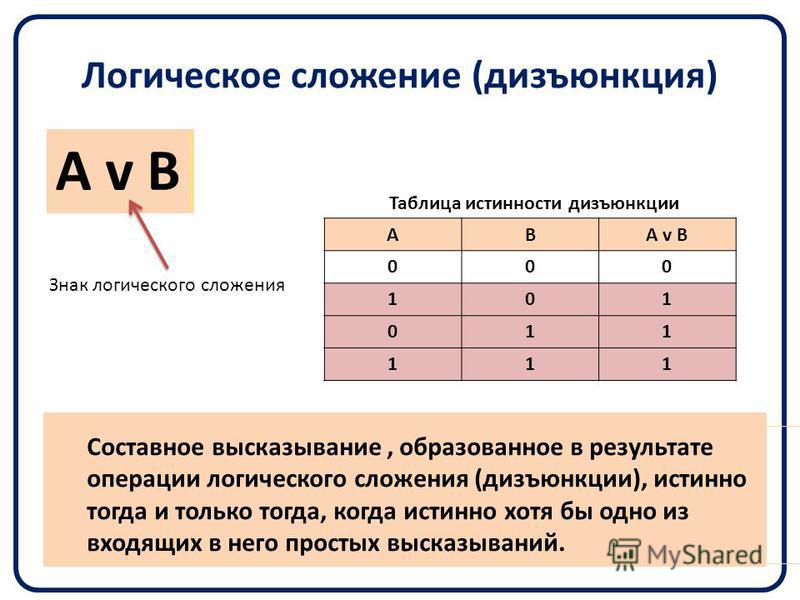 Отрицания этих высказываний противоречили бы законам физики: отрицание первого высказывания несовместимо с законами небесной механики, отрицание второго — с законами квантовой механики.
Отрицания этих высказываний противоречили бы законам физики: отрицание первого высказывания несовместимо с законами небесной механики, отрицание второго — с законами квантовой механики.
Физическая возможность — характеристика высказывания, не противоречащего законам природы.
Например, высказывание «КПД двигателя внутреннего сгорания равен 100%» противоречит законам термодинамики и, значит, физически невозможно. Высказывание же «КПД такого двигателя превышает 20%» не противоречит ограничениям, устанавливаемым термодинамикой, и является физически возможным.
Физически случайно, к примеру, что этот автомобиль выкрашен в зеленый цвет: нет законов природы, которые предписывали бы ему быть зеленым или, скажем, синим.
Логическая необходимость сильнее физической: все логически необходимое является также необходимым физически, но не наоборот. Иначе говоря: законы логики есть также законы природы, но не наоборот. Если, например, планета вращается, то она вращается, — это следствие закона логики и вместе с тем необходимая истина физики.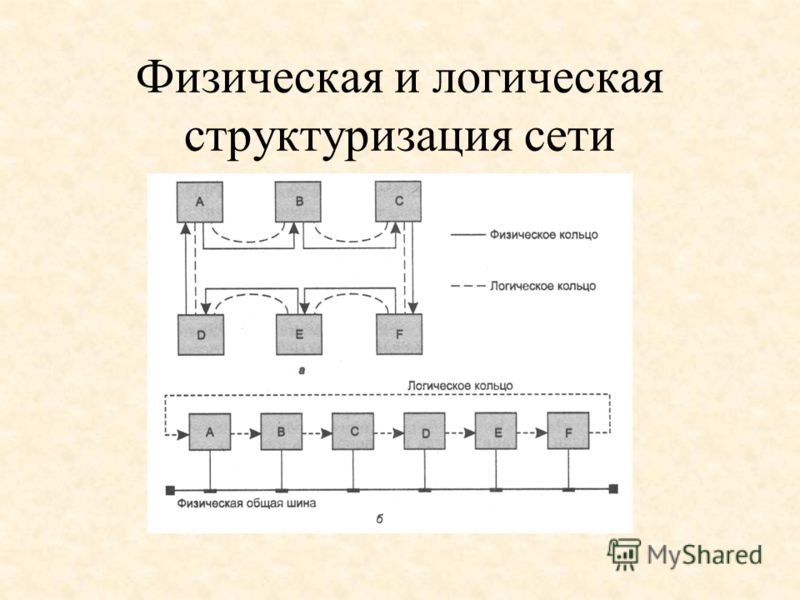 Но то, что у планет эллиптические орбиты, — закон физики, но не логики: логически возможно, чтобы орбиты планет были круговыми.
Но то, что у планет эллиптические орбиты, — закон физики, но не логики: логически возможно, чтобы орбиты планет были круговыми.
Физическая необходимость не сводится к логической. Нельзя, скажем, принципы механики свести к законам логики.
Логическая возможность шире физической возможности: возможное физически является возможным и логически, но не наоборот. К примеру, абсолютно чистое, не содержащее примесей золото возможно логически, но физически невозможно. Круговые орбиты планет возможны логически, но невозможны физически.
Самой широкой категорией является, таким образом, логическая возможность. Она включает физическую возможность и, далее, физическую необходимость и логическую необходимость. Последняя является самой узкой категорией.
И — логическое И
И — Логическое И| Код операции | Инструкция | Оп/Ан | 64-битный режим | Режим совместимости/этапа | Описание |
|---|---|---|---|---|---|
| 24 ib | И АЛ, имм8 | я | Действительный | Действительный | АЛ И имм8.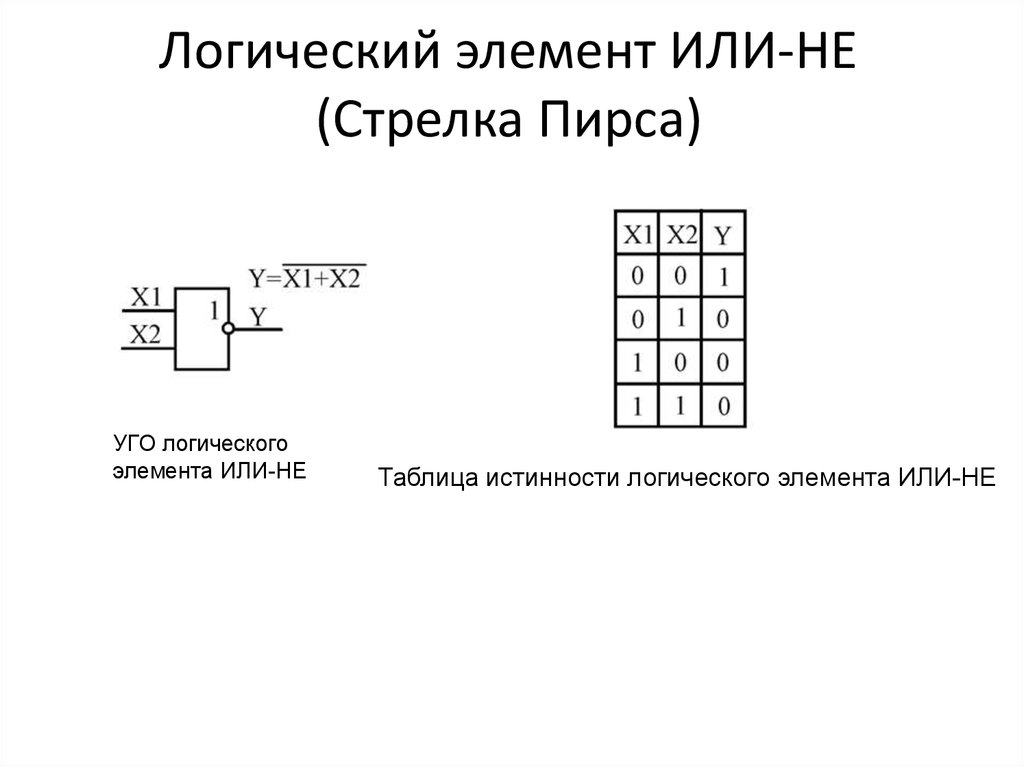 |
| 25 | И ТОПОР, имм16 | я | Действительно | Действительный | ТОПОР И мм16. |
| 25 идентификатор | И ЕАКС, имм32 | я | Действительный | Действительный | EAX И imm32. |
| REX.W + 25 идентификатор | И РАКС, имм32 | я | Действительный | Н.В. | ЗнакRAX И imm32 расширен до 64 бит. |
| 80/4 иб | И р/м8, имм8 | МИ | Действительный | Действительный | об/м8 И имм8. |
| REX + 80/4 ib | И р/м8 * , имм8 | МИ | Действительный | Н.В. | об/м8 И имм8. |
| 81/4 iw | И р/м16, имм16 | МИ | Действительный | Действительный | об/м16 И имм16. |
| 81/4 ID | И об/м32, имм32 | МИ | Действительный | Действительный | об/м32 И имм32. |
| REX.W + 81/4 id | И р/м64, имм32 | МИ | Действительный | Н.В. | r/m64 AND Знак imm32 расширен до 64 бит. |
| 83/4 иб | И р/м16, имм8 | МИ | Действительный | Действительный | об/м16 И имм8 (знак расширенный). |
| 83/4 иб | И об/м32, имм8 | МИ | Действительный | Действительный | об/м32 И имм8 (знак расширенный). |
| REX.W + 83/4 ib | И р/м64, имм8 | МИ | Действительный | Н.В.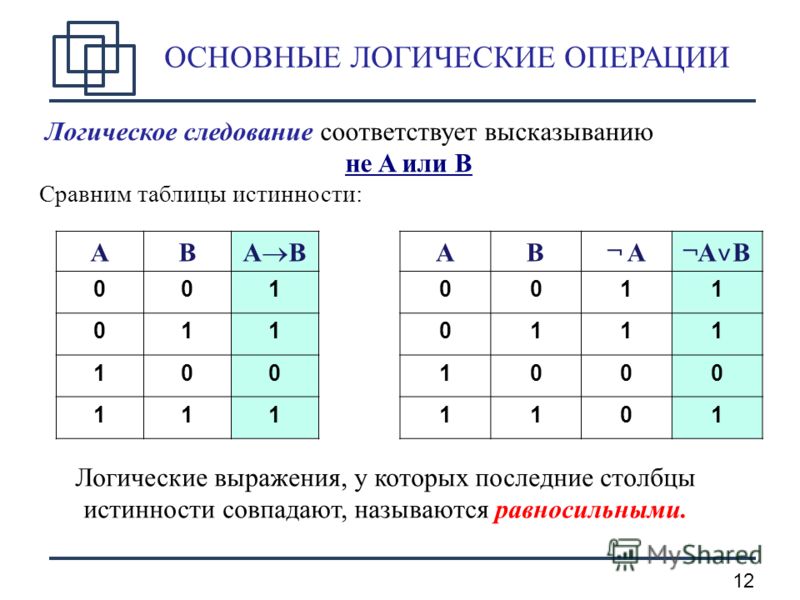 | об/м64 И имм8 (знак расширенный). |
| 20 /р | И р/м8, р8 | МР | Действительный | Действительный | р/м8 И р8. |
| REX + 20 /r | И р/м8 * , р8 * | МР | Действительный | Н.В. | об/м64 И об/м6 (расширенный знак). |
| 21 / р | И р/м16, р16 | МР | Действительный | Действительный | об/м16 И об/м16. |
| 21 / р | И р/м32, р32 | МР | Действительный | Действительный | об/м32 И об/м32. |
| REX.W + 21 / р | И р/м64, р64 | МР | Действительный | Н. В. В. | р/м64 И р32. |
| 22 / р | И р8, р/м8 | ринггитов | Действительный | Действительный | r8 И r/m8. |
| REX + 22 / р | И р8 * , р/м8 * | ринггитов | Действительный | Н.В. | об/м64 И об/м6 (расширенный знак). |
| 23 / р | И р16, р/м16 | ринггитов | Действительный | Действительный | r16 И r/m16. |
| 23 / р | И r32, об/м32 | ринггитов | Действительный | Действительный | r32 И r/m32. |
| REX.W + 23 / р | И р64, р/м64 | ринггитов | Действительный | Н.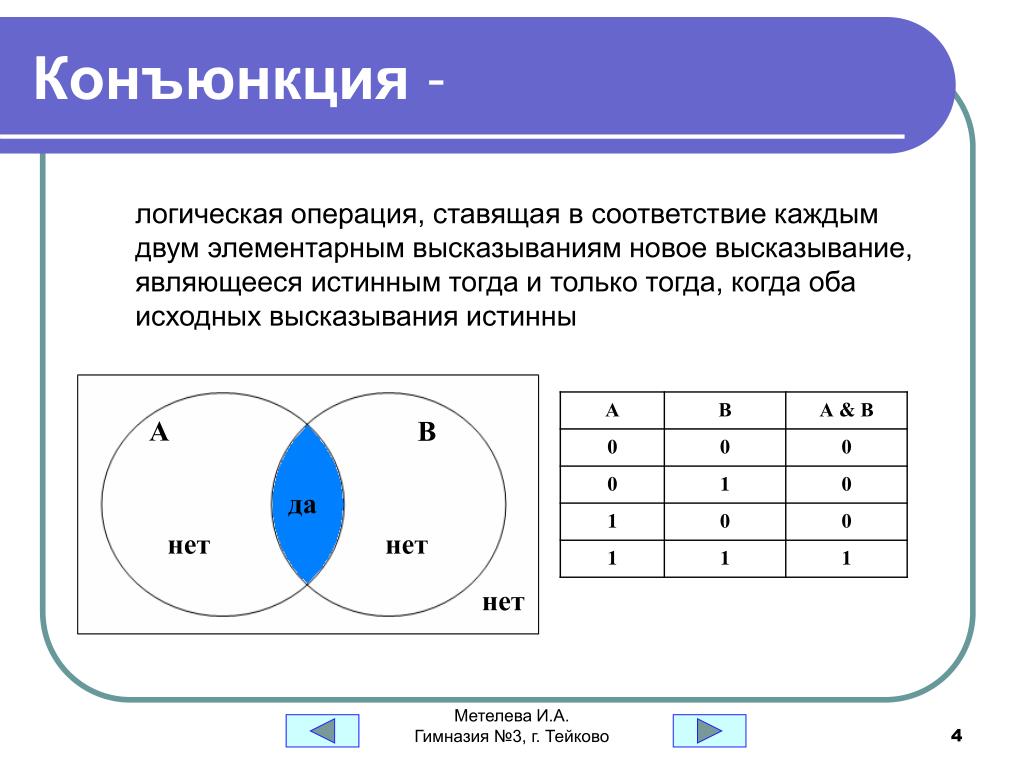 В. В. | r64 И r/m64. |
*В 64-битном режиме r/m8 нельзя закодировать для доступа к следующим байтовым регистрам, если используется префикс REX: AH, BH, CH, DH.
Кодирование операнда инструкции ¶
| Оп/Р | Операнд 1 | Операнд 2 | Операнд 3 | Операнд 4 |
| RM | ModRM:reg (r, w) | ModRM:р/м (р) | нет данных | Нет данных |
| МР | ModRM:r/m (r, w) | ModRM:reg (r) | нет данных | NA |
| MI | ModRM:r/m (r, w) | имм8/16/32 | нет данных | Н/Д |
| I | АЛ/АКС/ЕАКС/РАКС | имм8/16/32 | нет данных | Нет данных |
Описание ¶
Выполняет побитовую операцию И над целевым (первым) и исходным (вторым) операндами и сохраняет результат в ячейке целевого операнда.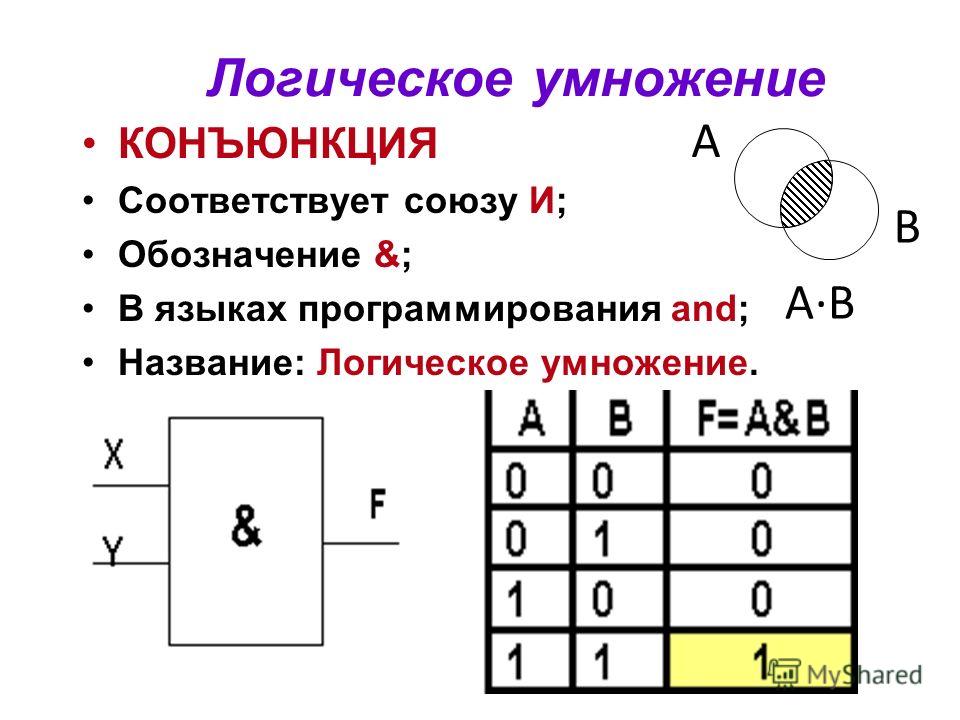 Исходный операнд может быть непосредственным, регистром или ячейкой памяти; операнд назначения может быть регистром или ячейкой памяти. (Однако в одной инструкции нельзя использовать два операнда памяти.) Каждый бит результата устанавливается в 1, если оба соответствующих бита первого и второго операндов равны 1; в противном случае устанавливается на 0,
Исходный операнд может быть непосредственным, регистром или ячейкой памяти; операнд назначения может быть регистром или ячейкой памяти. (Однако в одной инструкции нельзя использовать два операнда памяти.) Каждый бит результата устанавливается в 1, если оба соответствующих бита первого и второго операндов равны 1; в противном случае устанавливается на 0,
Эту инструкцию можно использовать с префиксом LOCK, чтобы разрешить ее выполнение атомарно.
В 64-битном режиме размер операции инструкции по умолчанию составляет 32 бита. Использование префикса REX в форме REX.R разрешает доступ к дополнительным регистрам (R8-R15). Использование префикса REX в виде REX.W повышает скорость работы до 64 бит. См. сводную таблицу в начале этого раздела для кодирования данных и ограничений.
Операция ¶
НАЗНАЧЕНИЕ := НАЗНАЧЕНИЕ И ИСТОЧНИК;
Затронутые флаги ¶
Флаги OF и CF очищены; флаги SF, ZF и PF устанавливаются в соответствии с результатом.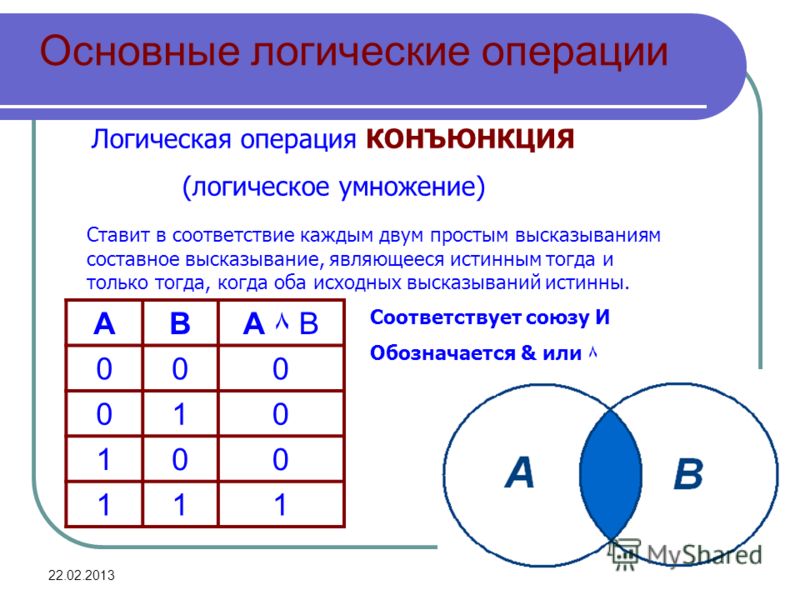 Состояние флага AF не определено.
Состояние флага AF не определено.
Исключения защищенного режима ¶
| #GP(0) | Если операнд назначения указывает на недоступный для записи сегмент. |
| Если эффективный адрес операнда памяти выходит за пределы сегмента CS, DS, ES, FS или GS. | |
| Если регистр DS, ES, FS или GS содержит селектор сегмента NULL. | |
| #СС(0) | Если эффективный адрес операнда памяти выходит за пределы сегмента SS. |
| #PF(код неисправности) | Если происходит ошибка страницы. |
| #AC(0) | Если включена проверка выравнивания и делается невыровненная ссылка на память при текущем уровне привилегий 3. |
| #UD | Если используется префикс LOCK, но назначение не является операндом памяти. |
Исключения режима реального адреса ¶
| #GP | Если эффективный адрес операнда памяти выходит за пределы сегмента CS, DS, ES, FS или GS.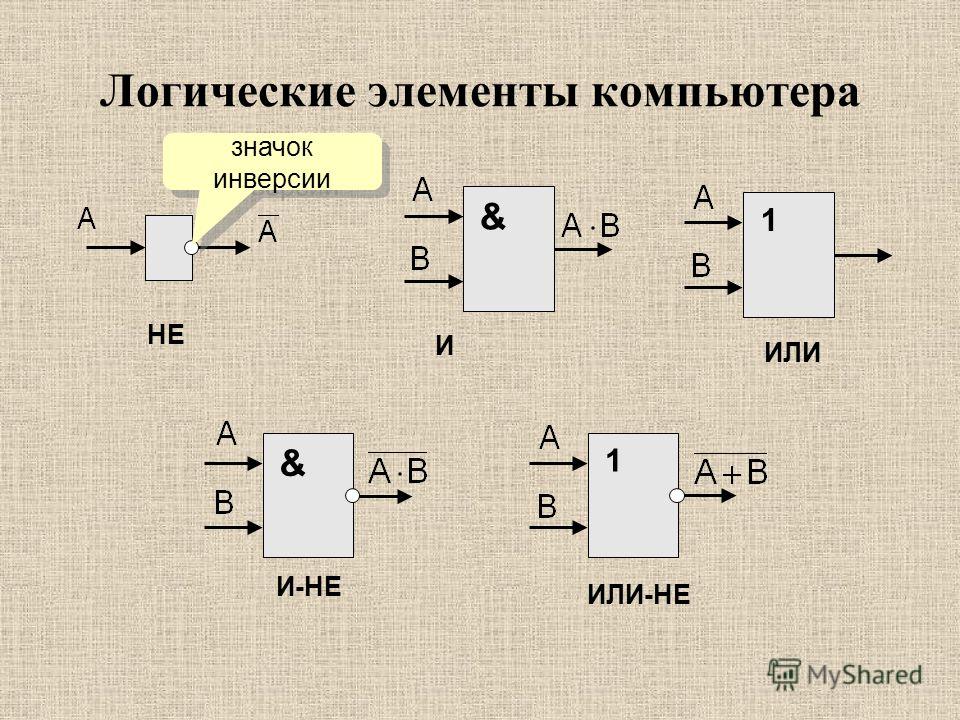 |
| #SS | Если эффективный адрес операнда памяти выходит за пределы сегмента SS. |
| #УД | Если используется префикс LOCK, но назначение не является операндом памяти. |
Исключения режима Virtual-8086 ¶
| #GP(0) | Если эффективный адрес операнда памяти выходит за пределы сегмента CS, DS, ES, FS или GS. |
| #СС(0) | Если эффективный адрес операнда памяти выходит за пределы сегмента SS. |
| #PF(код неисправности) | Если происходит ошибка страницы. |
| #AC(0) | Если включена проверка выравнивания и делается невыровненная ссылка на память. |
| #УД | Если используется префикс LOCK, но назначение не является операндом памяти. |
Исключения режима совместимости ¶
Те же исключения, что и в защищенном режиме.
Исключения 64-битного режима ¶
| #СС(0) | Если адрес памяти, ссылающийся на сегмент SS, имеет неканоническую форму. |
| #GP(0) | Если адрес памяти имеет неканоническую форму. |
| #PF(код неисправности) | Если происходит ошибка страницы. |
| #AC(0) | Если включена проверка выравнивания и делается невыровненная ссылка на память, а текущий уровень привилегий равен 3. |
| #UD | Если используется префикс LOCK, но назначение не является операндом памяти. |
Логическое и критическое мышление — онлайн-курс
Поисковый запросК сожалению, этот курс в настоящее время не проводится. Просмотрите другие курсы по бизнесу и менеджменту.
4.8 (459 отзывов)
Улучшите свои навыки логического и критического мышления в этом бесплатном онлайн-курсе. Определите общие препятствия на пути к эффективному мышлению.
198,522 записаны на этот курс
Другие курсы, которые могут вам понравиться
Этот курс сейчас не проводится. Мы можем отправить вам электронное письмо, когда он снова начнется, или проверить другие курсы, которые могут вам понравиться.
Мы можем отправить вам электронное письмо, когда он снова начнется, или проверить другие курсы, которые могут вам понравиться.
Нам постоянно дают причины делать что-то и верить во что-то: верить, что мы должны покупать товар, поддерживать дело, соглашаться на работу, осуждать кого-то невиновным или виновным, что справедливость требует от нас выполнения какой-либо работы по дому и т. д. на. Оценка причин, по которым нам дано делать или верить в эти вещи, требует от нас критического и логического мышления.
Улучшите свои навыки логического и критического мышления
Несмотря на то, что мы призваны постоянно использовать свои навыки критического и логического мышления, у большинства из нас это не очень хорошо получается. Этот бесплатный онлайн-курс призван помочь вам развить и улучшить эти навыки.
Вы узнаете, как:
- выявлять и избегать типичных ошибок мышления, ведущих к формированию ложных убеждений;
- распознавать, реконструировать и оценивать аргументы;
- использовать базовые логические инструменты для анализа аргументов;
- и применять эти инструменты в таких областях, как наука, моральные теории и право.

Адъюнкт-профессор Тим Дэр и доктор Патрик Жирар из Оклендского университета отправляются с нами в информативное и увлекательное восьминедельное путешествие по мирам логического и критического мышления, помогая нам избежать этих распространенных препятствий и заблуждений и улучшить наши навыки логического и критического мышления. .
На протяжении всего курса Тим и Патрик предоставляют видео, статьи и задания, чтобы провести нас через дебри логического и критического мышления.
Первую половину курса мы посвятим изучению ключевых понятий логического и критического мышления. Во второй половине курса мы будем применять эти концепции в знакомых областях, чтобы помочь вам развить практические и полезные навыки логического и критического мышления.
В первую неделю мы начинаем с введения в логическое и критическое мышление и общие препятствия и заблуждения.
На второй неделе Патрик вводит аргументы. Мы учимся определять посылки и выводы — компоненты хорошего аргумента — и к концу этой недели сможем построить аргумент в стандартной форме.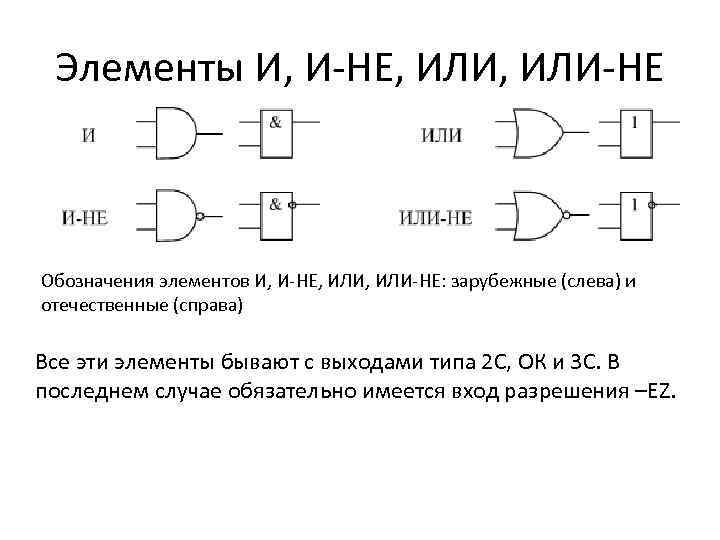
На третьей неделе мы научимся различать дедуктивные и недедуктивные аргументы, а также правильность и несостоятельность, силу и слабость.
На четвертой неделе мы более подробно изучаем хорошие и плохие аргументы, учимся определять, является ли аргумент разумным или убедительным, и как оценивать аргумент.
Недели с пятой по седьмую изучают три знакомые области – науку, право и мораль – которые требуют наших навыков логического и критического мышления способами, соответствующими конкретным требованиям этих областей.
Наконец, на восьмой неделе мы применим уроки курса к спору «в дикой природе», чтобы увидеть, как навыки, которые мы развили за время нашего восьминедельного путешествия, могут быть использованы в нашей собственной жизни.
К концу курса вы приобретете базовые навыки логической и критической оценки аргументов и, таким образом, сможете лучше понять причины своих убеждений.
Вы можете узнать больше в статье Патрика для блога FutureLearn: «Что флаг Новой Зеландии может научить нас логическому и критическому мышлению?»
Не удается воспроизвести видео. Включите JavaScript или рассмотрите возможность обновления вашего браузера.
Включите JavaScript или рассмотрите возможность обновления вашего браузера.
Скачать видео: стандартное или HD
Какие темы вы будете освещать?
- Выявление общих недостатков в построении убеждений
- Распознавать и реконструировать аргументы
- Оценивать аргументы как хорошие или плохие
- Анализ аргументов с использованием основных логических инструментов
- Применять базовые логические стратегии в таких областях, как наука, теории морали и право
Обучение на этом курсе
На каждом этапе курса вы можете встречаться с другими учащимися, делиться своими идеями и участвовать в активных дискуссиях в комментариях.
Чего вы добьетесь?
К концу курса вы сможете…
Изучать ключевые понятия логического и критического мышления
Применять ключевые понятия логического и критического мышления
Выявлять препятствия на пути и критическое мышление
Определите компоненты хорошего аргумента
Приведите аргумент в стандартной форме
Классифицируйте дедуктивные и недедуктивные аргументы
Интерпретация научных, моральных и правовых аргументов
Разработка аргумента «в дикой природе»
Оценка аргументов снисходительно
Для кого предназначен курс?
Этот курс открыт для всех, кто заинтересован в улучшении своих навыков логического и критического мышления. Никаких предварительных знаний или опыта не требуется.
Никаких предварительных знаний или опыта не требуется.
Кто разработал курс?
Университет Окленда
Университет Окленда является ведущим университетом Новой Зеландии и единственным университетом, включенным в список 200 лучших университетов Times Higher Education. . Пожалуйста, обновите страницу для просмотра этого контента.
Познакомьтесь с этим курсом
Узнайте, на что похож этот курс, ознакомившись с некоторыми этапами курса перед тем, как присоединиться:
Эвристика доступности
Пример дерева Похутукавы
9051 против существования БогаВы знаете кого-нибудь, кому понравился бы этот курс? Расскажите им об этом…
Вы можете использовать хэштег #FLcriticalThinking, чтобы рассказать об этом курсе в социальных сетях.
И, ИЛИ, исключающее ИЛИ и НЕ
В учебном пособии объясняется суть логических функций Excel И, ИЛИ, исключающее ИЛИ и НЕ, а также приводятся примеры формул, демонстрирующие их распространенное и изобретательское использование.
На прошлой неделе мы познакомились с логическими операторами Excel, которые используются для сравнения данных в разных ячейках. Сегодня вы увидите, как расширить использование логических операторов и создать более сложные тесты для выполнения более сложных вычислений. В этом вам помогут логические функции Excel, такие как AND, OR, XOR и NOT.
- Логические функции Excel — обзор
- Excel И функция
- Функция ИЛИ в Excel
- Excel XOR функция
- НЕ функция в Excel
Логические функции Excel — обзор
Microsoft Excel предоставляет 4 логические функции для работы с логическими значениями. Функции И, ИЛИ, исключающее ИЛИ и НЕ. Вы используете эти функции, когда хотите выполнить более одного сравнения в своей формуле или проверить несколько условий вместо одного. Как и логические операторы, логические функции Excel возвращают либо ИСТИНА, либо ЛОЖЬ при оценке их аргументов.
В следующей таблице приведены краткие сведения о том, что делает каждая логическая функция, чтобы помочь вам выбрать правильную формулу для конкретной задачи.
| Функция | Описание | Пример формулы | Описание формулы |
| И | Возвращает ИСТИНА, если все аргументы оцениваются как ИСТИНА. | =И(A2>=10, B2<5) | Формула возвращает ИСТИНА, если значение в ячейке A2 больше или равно 10, а значение в ячейке B2 меньше 5, в противном случае — ЛОЖЬ. |
| ИЛИ | Возвращает ИСТИНА, если любой аргумент имеет значение ИСТИНА. | =ИЛИ(A2>=10, B2<5) | Формула возвращает значение ИСТИНА, если A2 больше или равно 10 или B2 меньше 5, или выполняются оба условия. Если ни одно из условий не выполнено, формула возвращает ЛОЖЬ. |
| Исключающее ИЛИ | Возвращает логическое исключающее ИЛИ всех аргументов. | =исключающее ИЛИ(A2>=10, B2<5) | Формула возвращает значение ИСТИНА, если либо A2 больше или равно 10, либо B2 меньше 5.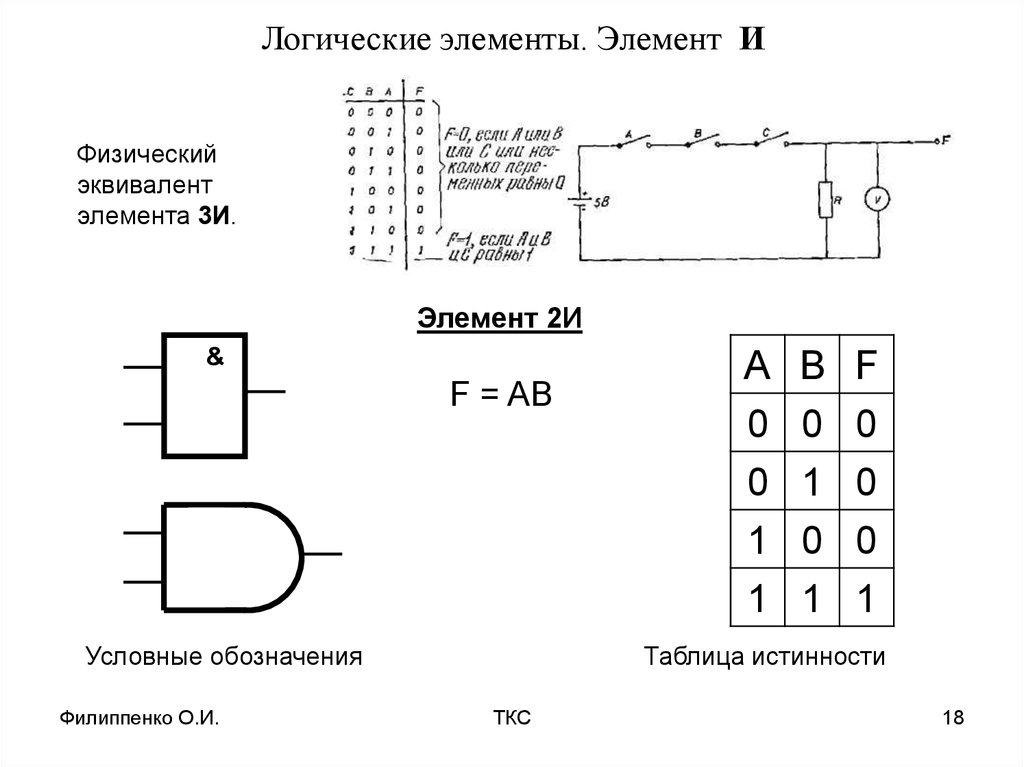 Если ни одно из условий не выполняется или выполняются оба условия, формула возвращает значение FALSE. Если ни одно из условий не выполняется или выполняются оба условия, формула возвращает значение FALSE. |
| НЕ | Возвращает обратное логическое значение своего аргумента. т.е. Если аргумент ЛОЖЬ, то возвращается ИСТИНА и наоборот. | = НЕ(А2>=10) | Формула возвращает ЛОЖЬ, если значение в ячейке A1 больше или равно 10; ИСТИНА в противном случае. |
В дополнение к четырем логическим функциям, описанным выше, Microsoft Excel предоставляет 3 «условные» функции — ЕСЛИ, ЕСЛИОШИБКА и ЕСЛИНА.
Логические функции Excel — факты и цифры
- В аргументах логических функций можно использовать ссылки на ячейки, числовые и текстовые значения, логические значения, операторы сравнения и другие функции Excel. Однако все аргументы должны оцениваться как логические значения TRUE или FALSE или ссылки или массивы, содержащие логические значения.
- Если аргумент логической функции содержит любые пустых ячеек , такие значения игнорируются.
 Если все аргументы являются пустыми ячейками, формула возвращает #ЗНАЧ! ошибка.
Если все аргументы являются пустыми ячейками, формула возвращает #ЗНАЧ! ошибка. - : Если аргумент логической функции содержит числа, то ноль оценивается как ЛОЖЬ, а все остальные числа, включая отрицательные числа, оцениваются как ИСТИНА. Например, если ячейки A1:A5 содержат числа, формула =И(A1:A5) вернет значение ИСТИНА, если ни одна из ячеек не содержит 0, и ЛОЖЬ в противном случае.
- Логическая функция возвращает #ЗНАЧ! ошибка, если ни один из аргументов не имеет логических значений.
- Логическая функция возвращает #ИМЯ? ошибка, если вы допустили ошибку в имени функции или попытались использовать функцию в более ранней версии Excel, которая ее не поддерживает. Например, функцию XOR можно использовать только в Excel 2016 и 2013.
- В Excel 2016, 2013, 2010 и 2007 в логическую функцию можно включить до 255 аргументов при условии, что общая длина формулы не превышает 8 192 символов. В Excel 2003 и более ранних версиях вы можете указать до 30 аргументов, а общая длина вашей формулы не должна превышать 1024 символа.

Использование функции И в Excel
Функция И является наиболее популярным членом семейства логических функций. Это удобно, когда вам нужно протестировать несколько условий и убедиться, что все они соблюдены. Технически функция И проверяет заданные вами условия и возвращает значение ИСТИНА, если все условия оцениваются как ИСТИНА, в противном случае — ЛОЖЬ.
Синтаксис функции И в Excel следующий:
И(логический1, [логический2], …)
Где логическое — это условие, которое вы хотите проверить, которое может быть оценено как ИСТИНА или ЛОЖЬ. Первое условие (логическое1) является обязательным, последующие условия необязательны.
А теперь давайте рассмотрим несколько примеров формул, демонстрирующих использование функций И в формулах Excel.
| Формула | Описание |
=И(A2="Бананы", B2>C2) | Возвращает TRUE, если A2 содержит "бананы" и B2 больше, чем C2, в противном случае FALSE. |
=И(B2>20, B2=C2) | Возвращает TRUE, если B2 больше 20 и B2 равно C2, иначе FALSE. |
=И(A2="Бананы", B2>=30, B2>C2) | Возвращает ИСТИНА, если A2 содержит «бананы», B2 больше или равно 30 и B2 больше C2, в противном случае FALSE. |
Функция И в Excel - обычное использование
Сама по себе функция И в Excel не очень интересна и имеет узкую полезность. Но в сочетании с другими функциями Excel И может значительно расширить возможности ваших рабочих листов.
Одним из наиболее распространенных применений функции И в Excel является аргумент логическая_проверка функции ЕСЛИ для проверки нескольких условий вместо одного. Например, вы можете вложить любую из приведенных выше функций И внутрь функции ЕСЛИ и получить результат, аналогичный этому:
=ЕСЛИ(И(A2="Бананы", B2>C2), "Хорошо", "Плохо")
Дополнительные примеры формул ЕСЛИ/И см.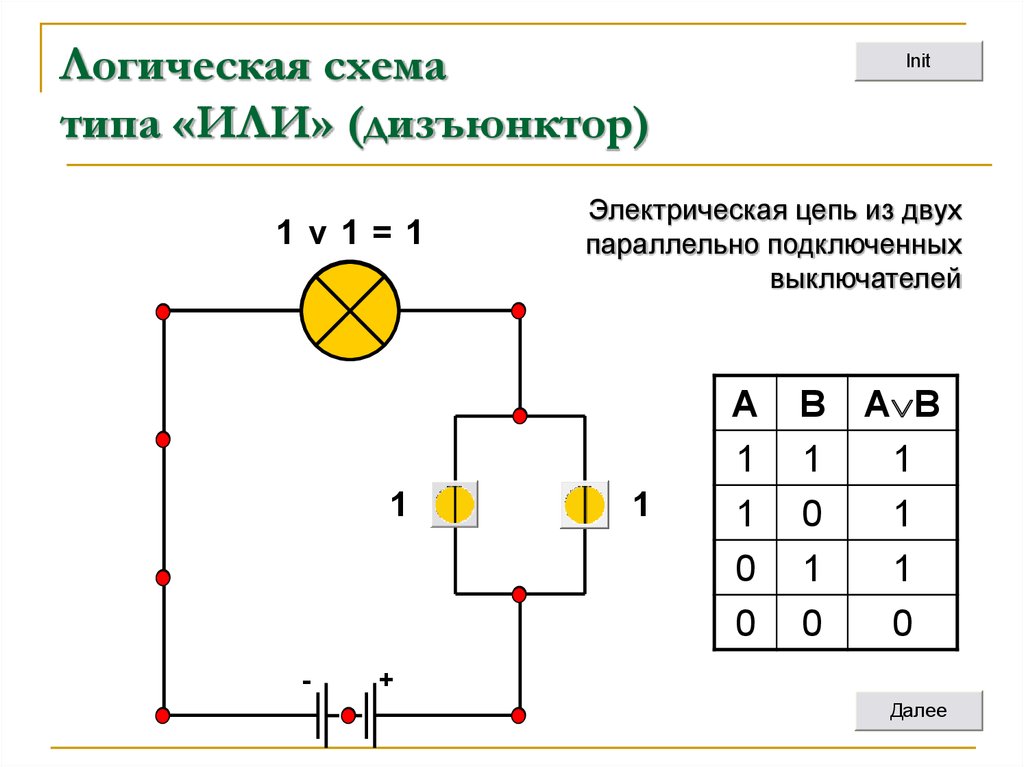 в его руководстве: Функция ЕСЛИ в Excel с несколькими И условия.
в его руководстве: Функция ЕСЛИ в Excel с несколькими И условия.
Формула Excel для условия МЕЖДУ
Если вам нужно создать формулу между в Excel, которая выбирает все значения между заданными двумя значениями, общий подход заключается в использовании функции ЕСЛИ с И в логическом тесте.
Например, у вас есть 3 значения в столбцах A, B и C, и вы хотите знать, находится ли значение в столбце A между значениями B и C. Чтобы составить такую формулу, достаточно функции ЕСЛИ с вложенным И и парой операторов сравнения:
Формула для проверки, находится ли X между Y и Z, включительно:
=ЕСЛИ(И(A2>=B2,A2<=C2),"Да", "Нет")
Формула для проверки, находится ли X находится между Y и Z, не включительно:
=ЕСЛИ(И(A2>B2, A2
Как показано на снимке экрана выше, формула работает отлично для всех типов данных - числа, даты и текстовые значения. При сравнении текстовых значений формула проверяет их посимвольно в алфавитном порядке.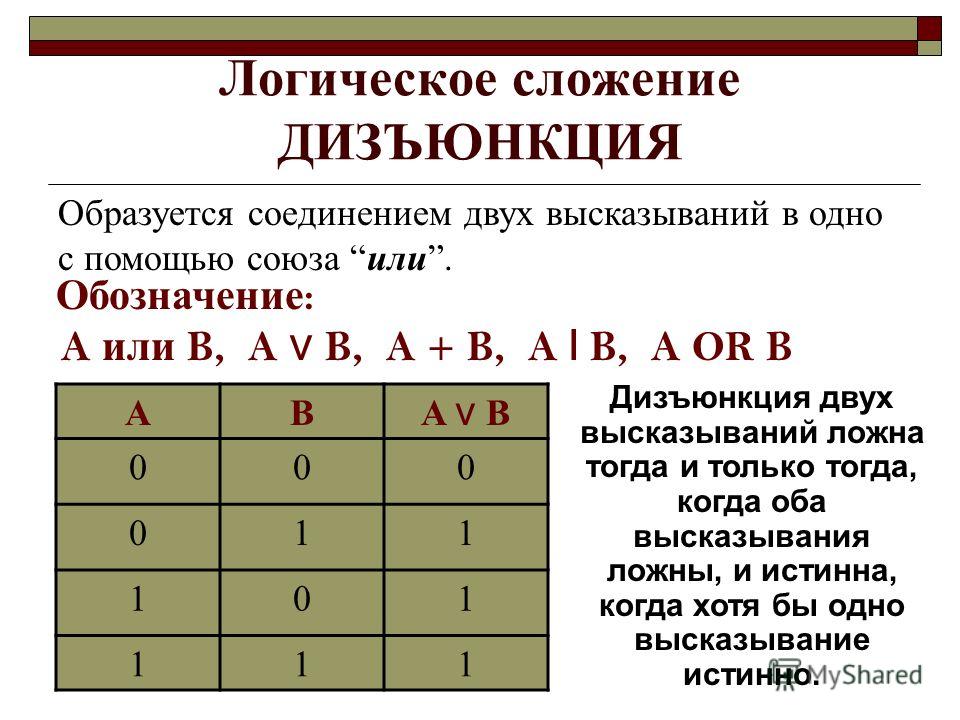 Например, указано, что Яблоки не находятся между Абрикос и Бананы , потому что вторая «р» в Яблоки стоит перед «r» в Абрикос . Дополнительные сведения см. в разделе Использование операторов сравнения Excel с текстовыми значениями.
Например, указано, что Яблоки не находятся между Абрикос и Бананы , потому что вторая «р» в Яблоки стоит перед «r» в Абрикос . Дополнительные сведения см. в разделе Использование операторов сравнения Excel с текстовыми значениями.
Как видите, формула ЕСЛИ/И проста, быстра и почти универсальна. Я говорю «почти», потому что это не относится к одному сценарию. Из приведенной выше формулы следует, что значение в столбце B меньше, чем в столбце C, т. е. столбец B всегда содержит значение нижней границы, а C — значение верхней границы. По этой причине формула возвращает " № " для строки 6, где A6 имеет 12, B6 - 15 и C6 - 3, а также для строки 8, где A8 - 24 ноября, B8 - 26 декабря и C8 - 21 октября.
Но что, если Вы хотите, чтобы формула между интервалами работала правильно независимо от того, где находятся значения нижней и верхней границы? В этом случае используйте функцию МЕДИАНА Excel, которая возвращает медиану заданных чисел (т.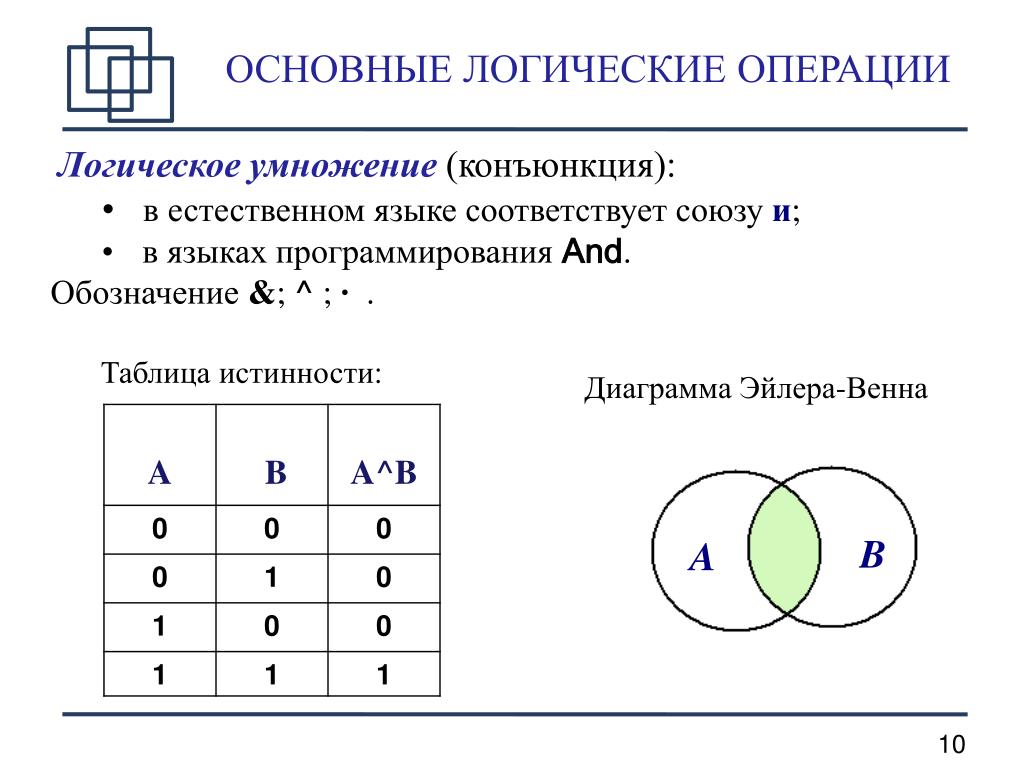 е. число в середине набора
е. число в середине набора
Итак, если заменить И в логической проверке функции ЕСЛИ на МЕДИАНУ, формула будет выглядеть так:
=ЕСЛИ(A2=МЕДИАНА(A2:C2),"Да","Нет")
И вы получите следующие результаты:
Как видите, функция МЕДИАНА отлично работает для чисел и дат , но возвращает #ЧИСЛО! ошибка для текстовых значений. Увы, никто не идеален 🙂
Если вам нужна идеальная формула между, которая работает для текстовых значений, а также для чисел и дат, вам придется построить более сложный логический текст, используя функции И / ИЛИ, как это :
=ЕСЛИ(ИЛИ(И(A2>B2, A2
Использование функции ИЛИ в Excel
Как а также И, функция Excel ИЛИ — это базовая логическая функция, которая используется для сравнения двух значений или утверждений. Разница в том, что функция ИЛИ возвращает ИСТИНА, если хотя бы один из аргументов принимает значение ИСТИНА, и возвращает ЛОЖЬ, если все аргументы равны ЛОЖЬ.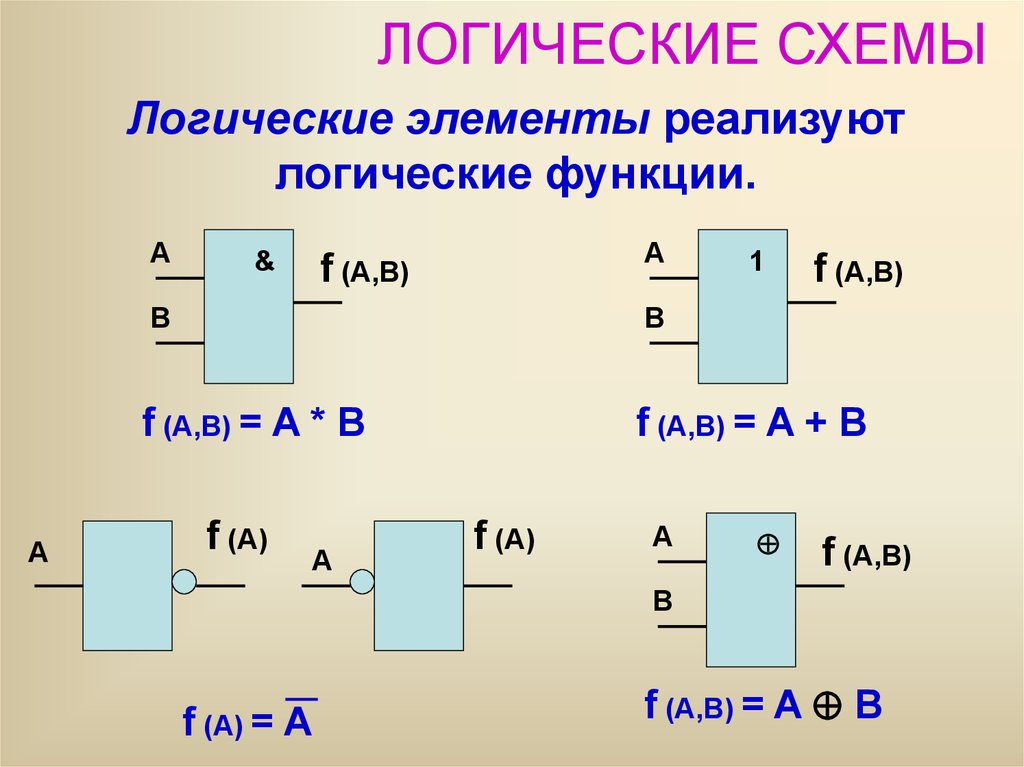 Функция ИЛИ доступна во всех версиях Excel 2016–2000.
Функция ИЛИ доступна во всех версиях Excel 2016–2000.
Синтаксис функции ИЛИ Excel очень похож на И:
ИЛИ(логический1, [логический2], …)
Где логичный — это то, что вы хотите проверить, что может быть либо ИСТИНА, либо ЛОЖЬ. Первое логическое обязательно, дополнительные условия (до 255 в современных версиях Excel) необязательны.
А теперь давайте напишем несколько формул, чтобы вы поняли, как работает функция ИЛИ в Excel.
| Формула | Описание |
=ИЛИ(A2="Банан", A2="Апельсины") | Возвращает ИСТИНА, если A2 содержит "бананы" или "апельсины", в противном случае - ЛОЖЬ. |
=ИЛИ(B2>=40, C2>=20) | Возвращает TRUE, если B2 больше или равно 40 или C2 больше или равно 20, в противном случае FALSE. |
=ИЛИ(B2=" ", C2="") | Возвращает TRUE, если либо B2, либо C2 пусты, либо и то, и другое, в противном случае FALSE.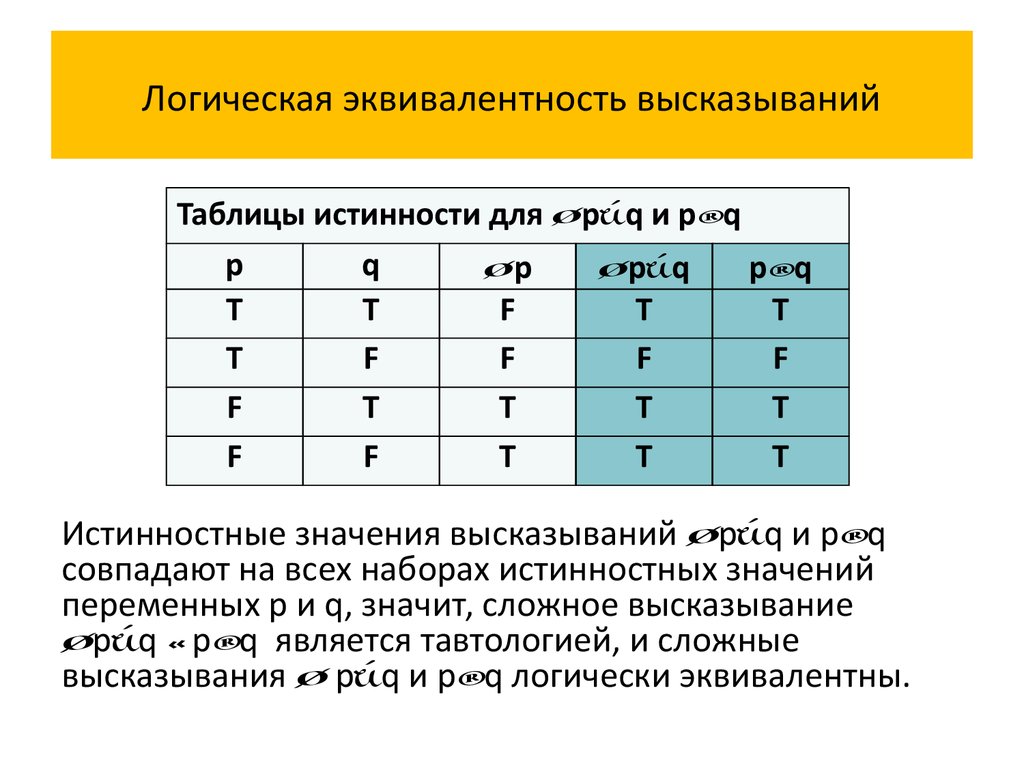 |
Как и функция И в Excel, операция ИЛИ широко используется для расширения возможностей других функций Excel, выполняющих логические тесты, например. функция ЕСЛИ. Вот лишь пара примеров:
Функция ЕСЛИ с вложенным ИЛИ
= ЕСЛИ(ИЛИ(B2>30, C2>20), "Хорошо", "Плохо")
Формула возвращает " Хорошо ", если число в ячейке B3 больше 30 или число в C2 больше 20, иначе " Bad ".
Функции Excel И/ИЛИ в одной формуле
Естественно, ничто не мешает вам использовать обе функции, И и ИЛИ, в одной формуле, если этого требует ваша бизнес-логика. Могут быть бесконечные вариации таких формул, которые сводятся к следующим основным шаблонам:
=И(ИЛИ(Вывод1, Вывод2), Вывод3)
=И(ИЛИ(Вывод1, Вывод2), ИЛИ(Вывод3, Вывод4)
=ИЛИ(И(Вывод1, Вывод2), Вывод3 )
=ИЛИ(И(Условие1,Условие2), И(Условие3,Условие4))
Например, если вы хотите узнать, какие партии бананов и апельсинов распроданы, т.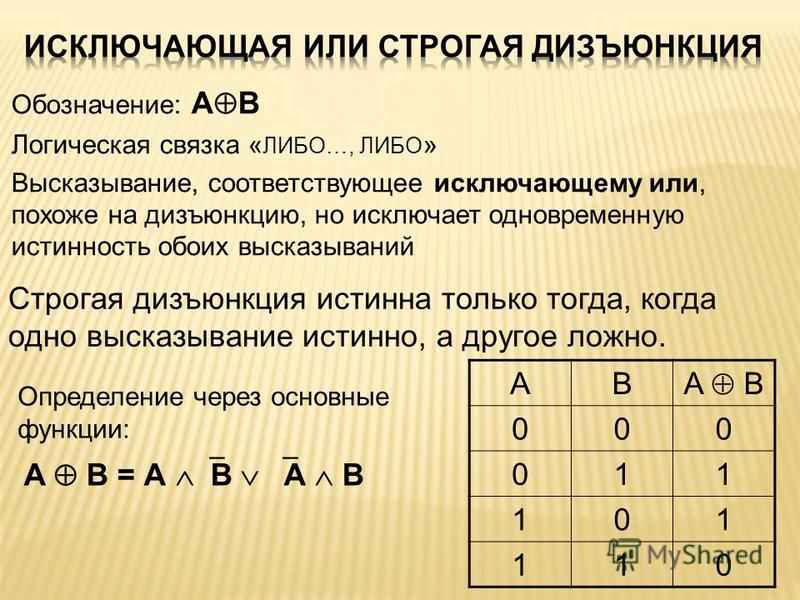 е. номер "В наличии" ( столбец B) равен числу «Продано» (столбец C), следующая формула ИЛИ/И может быстро показать это вам:
е. номер "В наличии" ( столбец B) равен числу «Продано» (столбец C), следующая формула ИЛИ/И может быстро показать это вам:
=ИЛИ(И(A2="бананы", B2=C2), И(A2="апельсины", B2=C2))
Функция ИЛИ в условном форматировании Excel
=ИЛИ($ B2="", $C2="")
Правило с приведенной выше формулой ИЛИ выделяет строки, содержащие пустую ячейку либо в столбце B, либо в столбце C, либо в обоих столбцах.
Дополнительные сведения о формулах условного форматирования см. в следующих статьях:
- Формулы условного форматирования Excel
- Изменение цвета строки на основе значения ячейки
- Изменение цвета ячейки на основе значения другой ячейки
- Как выделить каждую вторую строку в Excel
Использование функции XOR в Excel
В Excel 2013 Microsoft представила функцию XOR, которая является логической функцией Исключающее ИЛИ . Этот термин определенно знаком тем из вас, кто хоть немного знаком с каким-либо языком программирования или информатикой в целом. Для тех, кто этого не делает, концепция «Исключающее ИЛИ» может быть немного трудной для понимания поначалу, но, надеюсь, приведенное ниже объяснение, иллюстрированное примерами формул, поможет.
Для тех, кто этого не делает, концепция «Исключающее ИЛИ» может быть немного трудной для понимания поначалу, но, надеюсь, приведенное ниже объяснение, иллюстрированное примерами формул, поможет.
Синтаксис функции XOR идентичен синтаксис OR:
XOR(логический1, [логический2],…)
Требуется первый логический оператор (логический 1), дополнительные логические значения необязательны. Вы можете проверить до 254 условий в одной формуле, и это могут быть логические значения, массивы или ссылки, которые оцениваются как ИСТИНА или ЛОЖЬ.
В простейшей версии формула XOR содержит всего 2 логических оператора и возвращает:
- ИСТИНА, если любой из аргументов оценивается как ИСТИНА.
- FALSE, если оба аргумента имеют значение TRUE или ни один из них не является TRUE.
Это может быть легче понять из примеров формул:
| Формула | Результат | Описание |
=исключающее ИЛИ(1>0, 2<1) | ИСТИНА | Возвращает ИСТИНА, так как 1-й аргумент равен ИСТИНА, а второй -й -й аргумент — ЛОЖЬ. |
=исключающее ИЛИ(1<0, 2<1) | ЛОЖЬ | Возвращает ЛОЖЬ, так как оба аргумента равны ЛОЖЬ. |
=исключающее ИЛИ(1>0, 2>1) | ЛОЖЬ | Возвращает ЛОЖЬ, поскольку оба аргумента имеют значение ИСТИНА. |
При добавлении дополнительных логических операторов функция XOR в Excel возвращает:
- ИСТИНА, если нечетное число аргументов оценивается как ИСТИНА;
- FALSE, если общее количество операторов TRUE четно или если все операторы имеют значение FALSE.
На приведенном ниже снимке экрана показана эта точка:
Если вы не знаете, как можно применить функцию Excel XOR к реальному сценарию, рассмотрите следующий пример. Предположим, у вас есть таблица участников и их результатов за первые 2 игры. Вы хотите узнать, кто из плательщиков должен сыграть в игру 3 rd , исходя из следующих условий:
- Участники, выигравшие игру 1 и игру 2, автоматически переходят в следующий раунд и не должны играть в игру 3.

- Участники, проигравшие обе первые игры, выбывают из игры и не участвуют в игре 3.
- Участники, выигравшие Игру 1 или Игру 2, должны сыграть Игру 3, чтобы определить, кто пройдет в следующий раунд, а кто нет.
Простая формула XOR работает именно так, как нам нужно:
=XOR(B2="Выиграл", C2="Выиграл")
И если вы вложите эту функцию XOR в логическую проверку формулы IF, вы получите еще более разумные результаты:
=ЕСЛИ(ИСКЛЮЧАЮЩЕЕ ИЛИ(B2="Выиграл", C2="Выиграл"), "Да", "Нет")
Использование функции НЕ в Excel
Функция НЕ является одной из самых простых функций Excel в термины синтаксиса:
НЕ (логическое)
Вы используете функцию НЕ в Excel, чтобы инвертировать значение ее аргумента. Другими словами, если логический результат равен ЛОЖЬ, функция НЕ возвращает значение ИСТИНА, и наоборот. Например, обе приведенные ниже формулы возвращают ЛОЖЬ:
= НЕ(ИСТИНА)
=НЕ(2*2=4)
Зачем хотеть получать такие нелепые результаты? В некоторых случаях вам может быть интереснее узнать, когда определенное условие не выполняется, чем когда оно выполняется. Например, при просмотре списка одежды вы можете исключить какой-то цвет, который вам не подходит. Я не особенно люблю черный цвет, поэтому использую следующую формулу:
Например, при просмотре списка одежды вы можете исключить какой-то цвет, который вам не подходит. Я не особенно люблю черный цвет, поэтому использую следующую формулу:
=НЕ(C2="черный")
Как обычно, в Microsoft Excel есть несколько способов сделать что-то, и того же результата можно добиться, используя оператор Not equal to: =C2<>"black".
Если вы хотите проверить несколько условий в одной формуле, вы можете использовать НЕ в сочетании с функцией И или ИЛИ. Например, если вы хотите исключить черный и белый цвета, формула будет выглядеть так:
= НЕ(ИЛИ(C2="черный", C2="белый"))
иметь черное пальто, в то время как черная куртка или шуба на спине могут быть рассмотрены, вы должны использовать НЕ в сочетании с функцией Excel И:
= НЕ(И(C2="черный", B2="пальто") )
Еще одно распространенное использование функции НЕ в Excel — изменение поведения какой-либо другой функции. Например, вы можете комбинировать функции НЕ и ЕПУСТО, чтобы создать формулу НЕПУСТЬ, которой нет в Microsoft Excel.
Как вы знаете, формула =ЕПУСТО(A2) возвращает ИСТИНА, если ячейка A2 пуста. Функция НЕ может обратить этот результат в ЛОЖЬ: =НЕ(ЕСПУСТО(A2))
Затем вы можете сделать еще один шаг и создать вложенный оператор ЕСЛИ с функциями НЕ/ПУСТО для реальной задачи:
= ЕСЛИ (НЕ (ПУСТО (C2)), C2 * 0,15, «Нет бонуса : (»)
В переводе на простой английский язык формула сообщает Excel сделать следующее. Если ячейка C2 не пуста , умножьте число в C2 на 0,15, что дает бонус в размере 15% каждому продавцу, совершившему дополнительные продажи. Если C2 пуст, появляется текст «Нет бонуса :(».
По сути, это то, как вы используете логические функции в Excel.Конечно, эти примеры лишь поверхностно касаются возможностей И, ИЛИ, исключающего ИЛИ и НЕ. Зная основы, вы теперь можете расширить свои знания, решая свои реальные задачи и записывая сложные сложные формулы для своих рабочих листов.
Вас также может заинтересовать
равно, не равно, больше, меньше
Многие задачи, которые вы выполняете в Excel, включают сравнение данных в разных ячейках.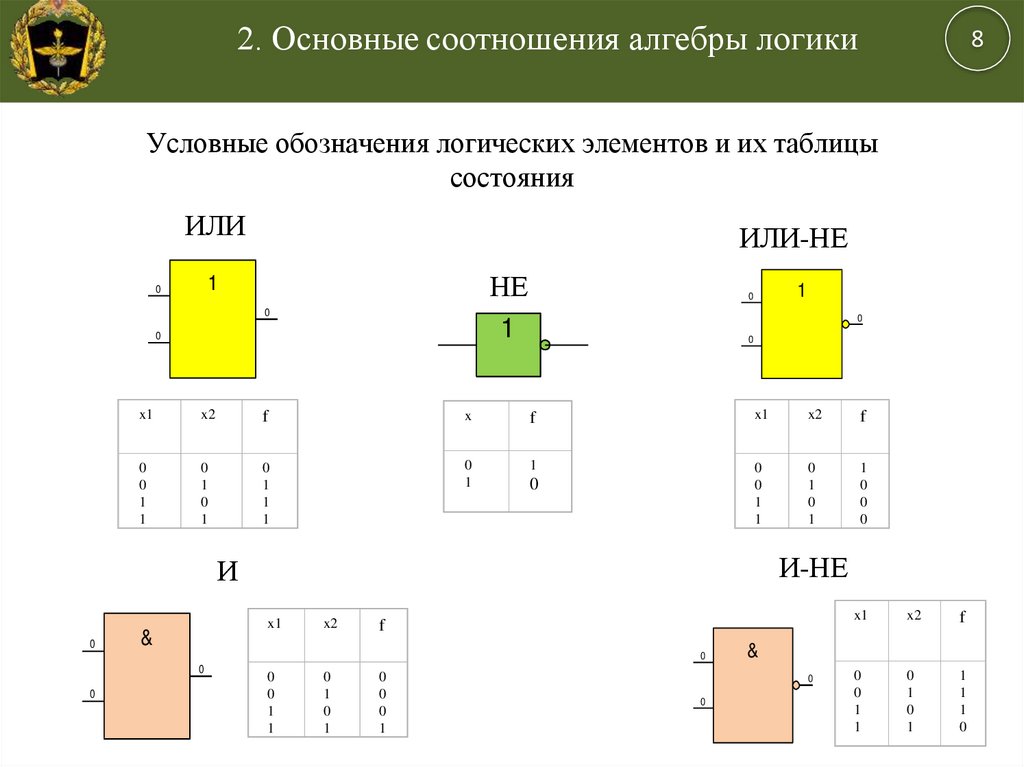 Для этого в Microsoft Excel предусмотрено шесть логических операторов, которые также называются операторами сравнения. Этот учебник призван помочь вам понять суть логических операторов Excel и написать наиболее эффективные формулы для анализа данных.
Для этого в Microsoft Excel предусмотрено шесть логических операторов, которые также называются операторами сравнения. Этот учебник призван помочь вам понять суть логических операторов Excel и написать наиболее эффективные формулы для анализа данных.
- Логические операторы Excel
- Равно
- Не равно
- Больше / меньше / больше или равно / меньше или равно
- Распространенное использование логических операторов в Excel
Логические операторы Excel — обзор
Логический оператор используется в Excel для сравнения двух значений. Логические операторы иногда называют булевыми операторами, потому что результат сравнения в любом конкретном случае может быть либо ИСТИНА, либо ЛОЖЬ.
В Excel доступно шесть логических операторов. В следующей таблице объясняется, что делает каждый из них, и иллюстрируется теория примерами формул.
| Состояние | Оператор | Пример формулы | Описание |
| Равен | = | =А1=В1 | Формула возвращает значение ИСТИНА, если значение в ячейке A1 равно значению в ячейке B1; ЛОЖЬ в противном случае.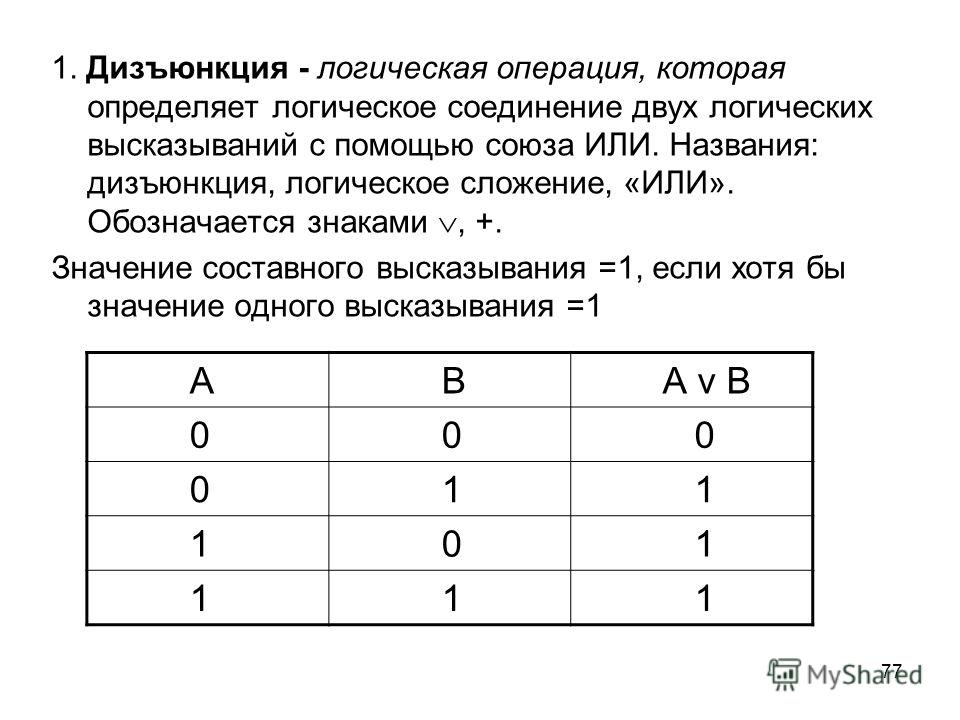 |
| Не равно | <> | =А1<>В1 | Формула возвращает значение ИСТИНА, если значение в ячейке A1 не равно значению в ячейке B1; ЛОЖЬ в противном случае. |
| Больше | > | =А1>В1 | Формула возвращает значение ИСТИНА, если значение в ячейке A1 больше, чем значение в ячейке B1; в противном случае возвращается ЛОЖЬ. |
| Менее | < | =А1<В1 | Формула возвращает значение ИСТИНА, если значение в ячейке A1 меньше, чем в ячейке B1; ЛОЖЬ в противном случае. |
| Больше или равно | >= | =А1>=В1 | Формула возвращает значение ИСТИНА, если значение в ячейке A1 больше или равно значениям в ячейке B1; ЛОЖЬ в противном случае. |
| Меньше или равно | <= | =А1<=В1 | Формула возвращает значение ИСТИНА, если значение в ячейке A1 меньше или равно значениям в ячейке B1; ЛОЖЬ в противном случае.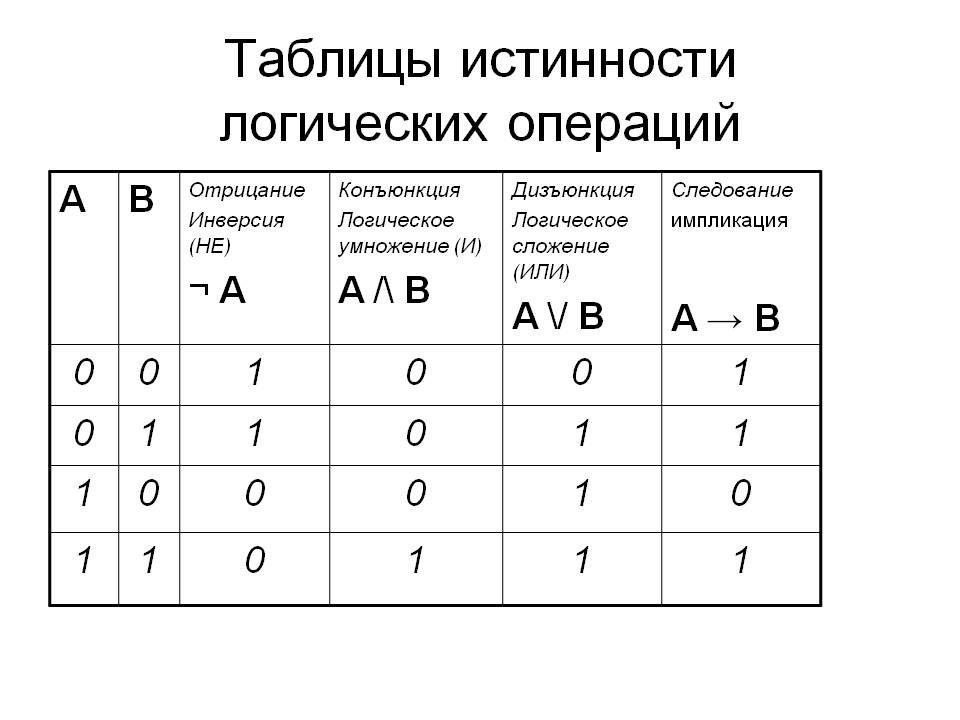 |
На приведенном ниже снимке экрана показаны результаты, возвращаемые логическими операторами Равно , Не равно , Больше и Меньше :
Может показаться, что приведенная выше таблица охватывает все, и говорить больше не о чем. о. Но на самом деле у каждого логического оператора есть свои особенности, и знание их может помочь вам использовать настоящую мощь формул Excel.
Использование логического оператора "Равно" в Excel
Логический оператор "Равно " (=) может использоваться для сравнения всех типов данных - чисел, дат, текстовых значений, логических значений, а также результатов, возвращаемых другими приложениями Excel. формулы. Например:
| =A1=B1 | Возвращает ИСТИНА, если значения в ячейках A1 и B1 совпадают, в противном случае — ЛОЖЬ. |
| =A1="апельсины" | Возвращает ИСТИНА, если ячейки A1 содержат слово «апельсины», в противном случае — ЛОЖЬ. |
| =A1=ИСТИНА | Возвращает ИСТИНА, если ячейки A1 содержат логическое значение ИСТИНА, в противном случае возвращает ЛОЖЬ. |
| =А1=(В1/2) | Возвращает ИСТИНА, если число в ячейке A1 равно частному от деления B1 на 2, в противном случае — ЛОЖЬ. |
Пример 1. Использование оператора "Равно" с датами
Возможно, вы удивитесь, узнав, что логический оператор "Равно " не может сравнивать даты так же легко, как числа. Например, если в ячейках А1 и А2 указана дата «1.12.2014», формула =A1=A2 вернет TRUE, как и должно быть.
Однако, если вы попробуете либо =A1=12/1/2014 , либо =A1="12/1/2014" , вы получите ЛОЖЬ в результате. Немного неожиданно, а?
Дело в том, что Excel хранит даты как числа, начинающиеся с 1 января 1900 года, которые хранятся как 1. Дата 1/12/2014 хранится как 41974. В приведенных выше формулах Microsoft Excel интерпретирует «12/1/ 2014" как обычную текстовую строку, а так как "12.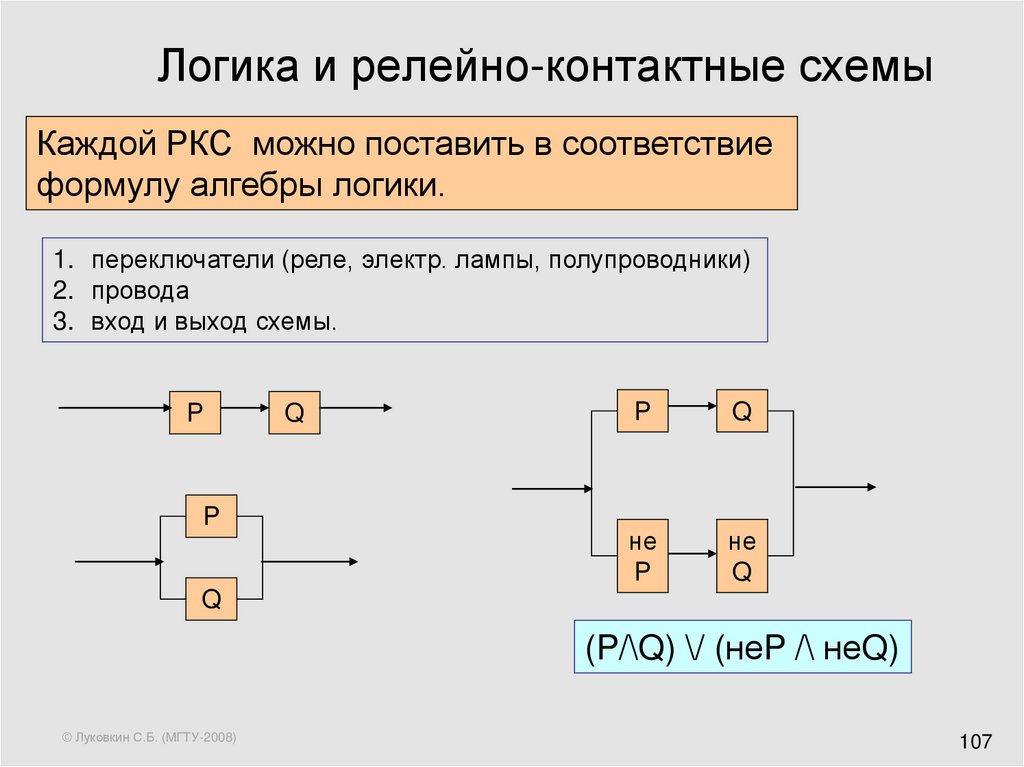 01.2014" не равно 41974, возвращает ЛОЖЬ.
01.2014" не равно 41974, возвращает ЛОЖЬ.
Чтобы получить правильный результат, вы всегда должны заключать дату в функцию ДАТАЗНАЧ, например: =A1=ДАТАЗНАЧ("1/12/2014")
Примечание. Функцию DATEVALUE также необходимо использовать с другим логическим оператором, как показано в следующих примерах.
Тот же подход следует применять при использовании оператора равенства Excel в логической проверке функции ЕСЛИ. Вы можете найти больше информации, а также несколько примеров формул в этом руководстве: Использование функции Excel IF с датами.
Пример 2. Использование оператора "Равно" с текстовыми значениями
Использование оператора Excel "Равно " с текстовыми значениями не требует никаких дополнительных действий. Единственное, что вы должны иметь в виду, это то, что логический оператор Equal to в Excel нечувствителен к регистру , что означает, что различия в регистре игнорируются при сравнении текстовых значений.
Например, если ячейка A1 содержит слово « апельсинов », а ячейка B1 содержит « апельсинов 9».0020 ", формула =A1=B1 вернет ИСТИНА.
Если вы хотите сравнить текстовые значения с учетом их различия в регистре, вы должны использовать функцию EXACT вместо оператора равно . Синтаксис функция EXACT так же проста, как:
EXACT(text1, text2)
Где text 1 и text2 — это значения, которые вы хотите сравнить.Если значения совпадают, включая регистр, Excel возвращает TRUE, в противном случае он возвращает ЛОЖЬ. Вы также можете использовать функцию ТОЧНОЕ в формулах ЕСЛИ, когда вам нужно сравнение текстовых значений с учетом регистра, как показано на снимке экрана ниже:
Примечание. Если вы хотите сравнить длину двух текстовых значений, вы можете вместо этого использовать функцию ДЛСТР, например, =ДЛСТР(A2)=ДЛСТР(B2) или =ДЛСТР(A2)>=ДЛСТР(B2) .
Пример 3. Сравнение логических значений и чисел
Существует распространенное мнение, что в Microsoft Excel логическое значение ИСТИНА всегда равно 1, а ЛОЖЬ - 0.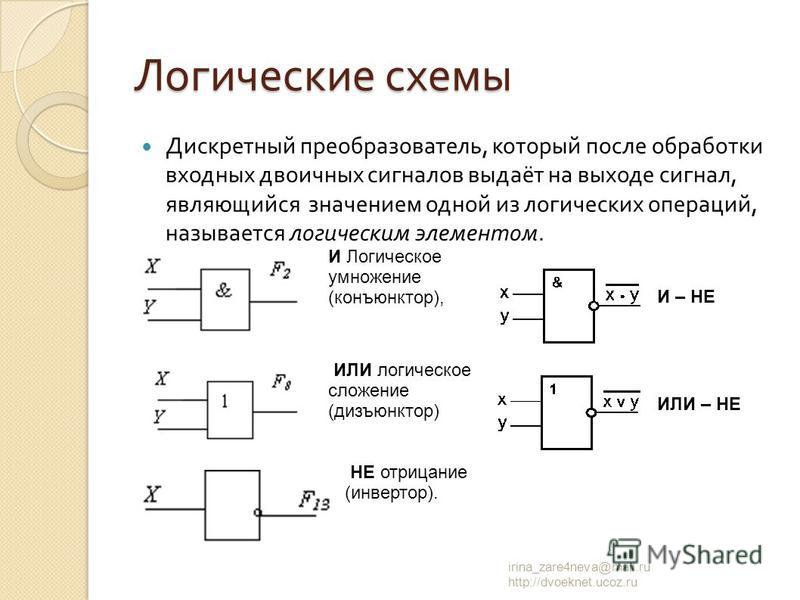 Однако это верно лишь отчасти, и ключевое слово здесь " всегда" или точнее "не всегда" 🙂
Однако это верно лишь отчасти, и ключевое слово здесь " всегда" или точнее "не всегда" 🙂
При написании логического выражения "равно" для сравнения логического значения и числа необходимо специально указать для Excel, что нечисловое логическое значение должно рассматриваться как число. Вы можете сделать это, добавив двойной знак минус перед логическим значением или ссылкой на ячейку, например. грамм. =A2=--ИСТИНА или =A2=--B2 .
Знак минус 1 st , который технически называется унарным оператором, приводит ИСТИНА/ЛОЖЬ к -1/0 соответственно, а второй унарный инвертирует значения, превращая их в +1 и 0. Это, вероятно, будет проще чтобы понять глядя на следующий скриншот:
Примечание. Вы должны добавить двойной унарный оператор перед логическим значением при использовании других логических операторов, таких как не равно , больше или меньше , чтобы правильно сравнивать числовые и логические значения.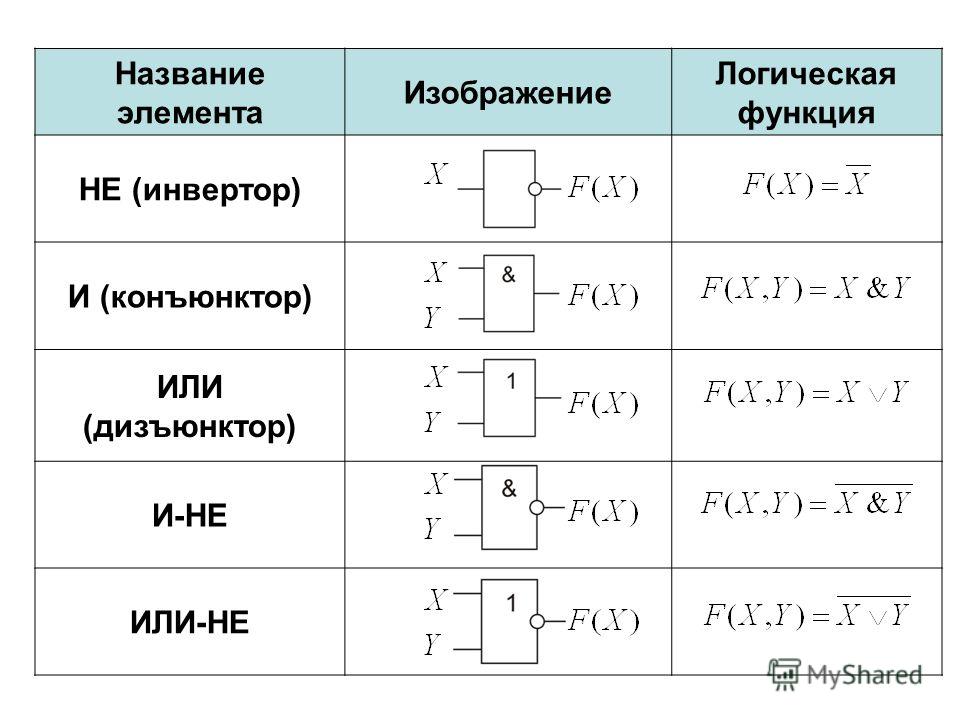
При использовании логических операторов в сложных формулах вам также может понадобиться добавить двойное унарное выражение перед каждым логическим выражением, которое возвращает ИСТИНА или ЛОЖЬ в качестве результата. Вот пример такой формулы: СУММПРОИЗВ и СУММЕСЛИМН в Excel.
Использование логического оператора «Не равно» в Excel
Вы используете оператор Excel Не равно (<>), когда хотите убедиться, что значение ячейки не равно указанному значению. Использование оператора Не равно очень похоже на использование оператора Равно , которое мы только что обсуждали.
Результаты, возвращаемые оператором Не равно , аналогичны результатам, полученным функцией НЕ Excel, которая меняет значение своего аргумента на противоположное. В следующей таблице приведены несколько примеров формул.
| Не равно оператору | Функция НЕ | Описание |
| =А1<>В1 | = НЕ(А1=В1) | Возвращает ИСТИНА, если значения в ячейках A1 и B1 не совпадают, в противном случае — ЛОЖЬ.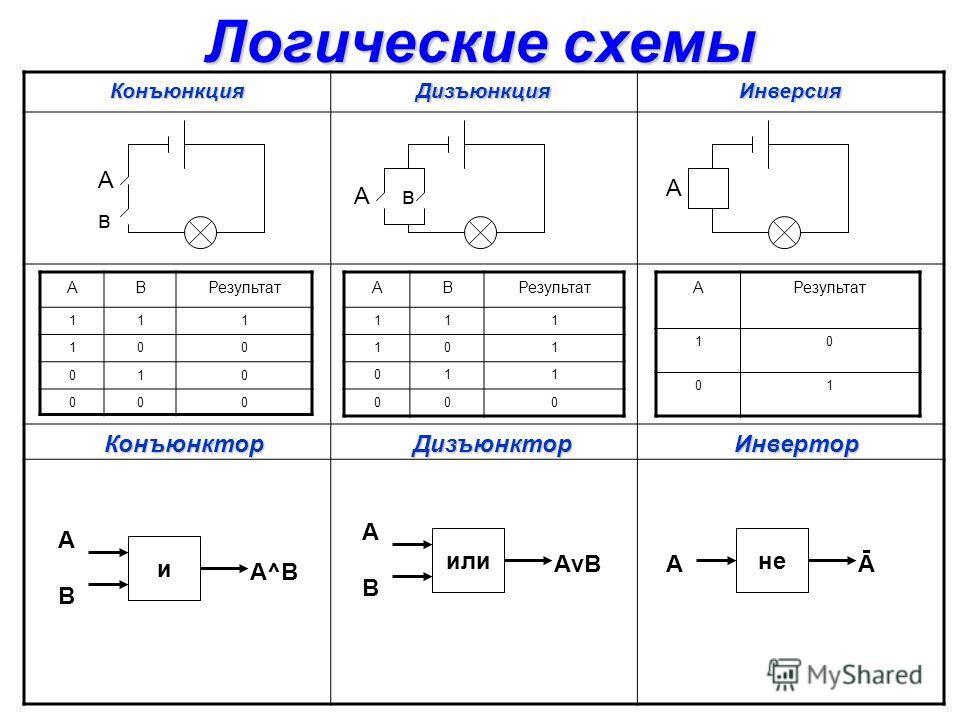 |
| =A1<>"апельсины" | = НЕ(A1="апельсины") | Возвращает ИСТИНА, если ячейка A1 содержит любое значение, кроме «апельсинов», и ЛОЖЬ, если она содержит «апельсины», или «АПЕЛЬСИНЫ», или «апельсины» и т. д. |
| =A1<>ИСТИНА | = НЕ (A1 = ИСТИНА) | Возвращает ИСТИНА, если ячейка A1 содержит любое значение, кроме ИСТИНА, в противном случае - ЛОЖЬ. |
| =А1<>(В1/2) | = НЕ(А1=В1/2) | Возвращает ИСТИНА, если число в ячейке A1 не равно частному от деления B1 на 2, в противном случае - ЛОЖЬ. |
| =A1<>ДАТАЗНАЧ("1/12/2014") | = НЕ(A1=ДАТАЗНАЧ("1/12/2014")) | Возвращает ИСТИНА, если A1 содержит какое-либо значение, кроме даты 1 декабря 2014 г., независимо от формата даты, в противном случае — ЛОЖЬ. |
Больше, меньше, больше или равно, меньше или равно
Эти логические операторы используются в Excel для проверки сравнения одного числа с другим.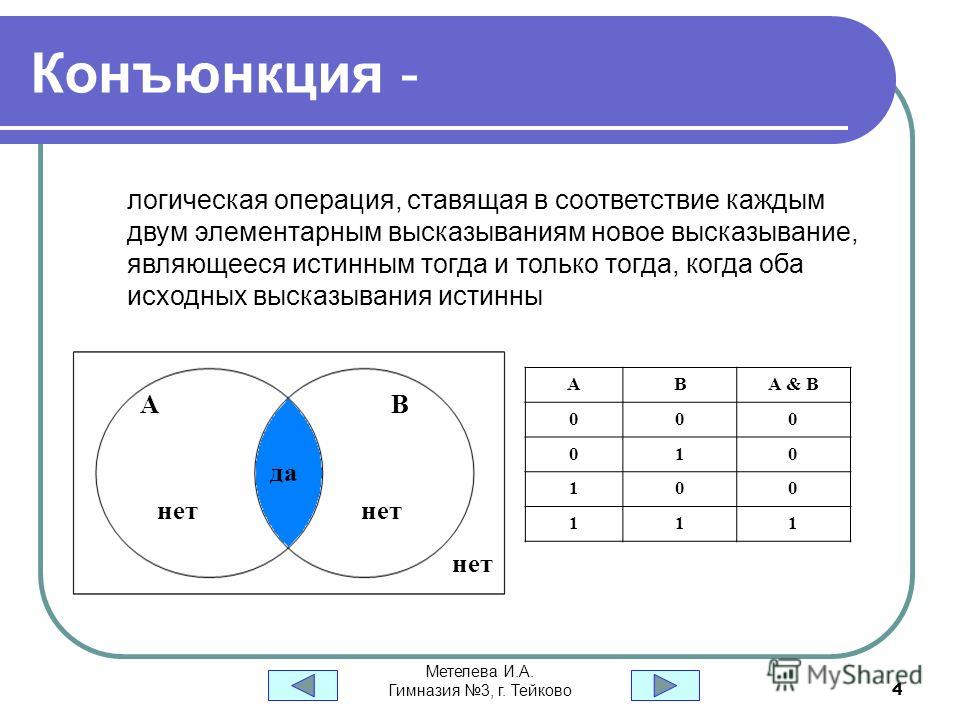 Microsoft Excel предоставляет 4 операции сравнения, названия которых говорят сами за себя:
Microsoft Excel предоставляет 4 операции сравнения, названия которых говорят сами за себя:
- Больше чем (>)
- Больше или равно (>=)
- Меньше чем (<)
- Меньше или равно (<=)
Чаще всего операторы сравнения Excel используются с числами, значениями даты и времени. Например:
| =А1>20 | Возвращает TRUE, если число в ячейке A1 больше 20, иначе FALSE. |
| =А1>=(В1/2) | Возвращает ИСТИНА, если число в ячейке A1 больше или равно частному от деления B1 на 2, в противном случае — ЛОЖЬ. |
| =A1<ДАТАЗНАЧ("1/12/2014") | Возвращает TRUE, если дата в ячейке A1 меньше 1 декабря 2014 г., иначе FALSE. |
| =A1<=СУММ(B1:D1) | Возвращает ИСТИНА, если число в ячейке A1 меньше или равно сумме значений в ячейках B1:D1, в противном случае — ЛОЖЬ. |
Использование операторов сравнения Excel с текстовыми значениями
Теоретически вы также можете использовать операторы больше , больше или равно , а также их аналоги меньше с текстовыми значениями.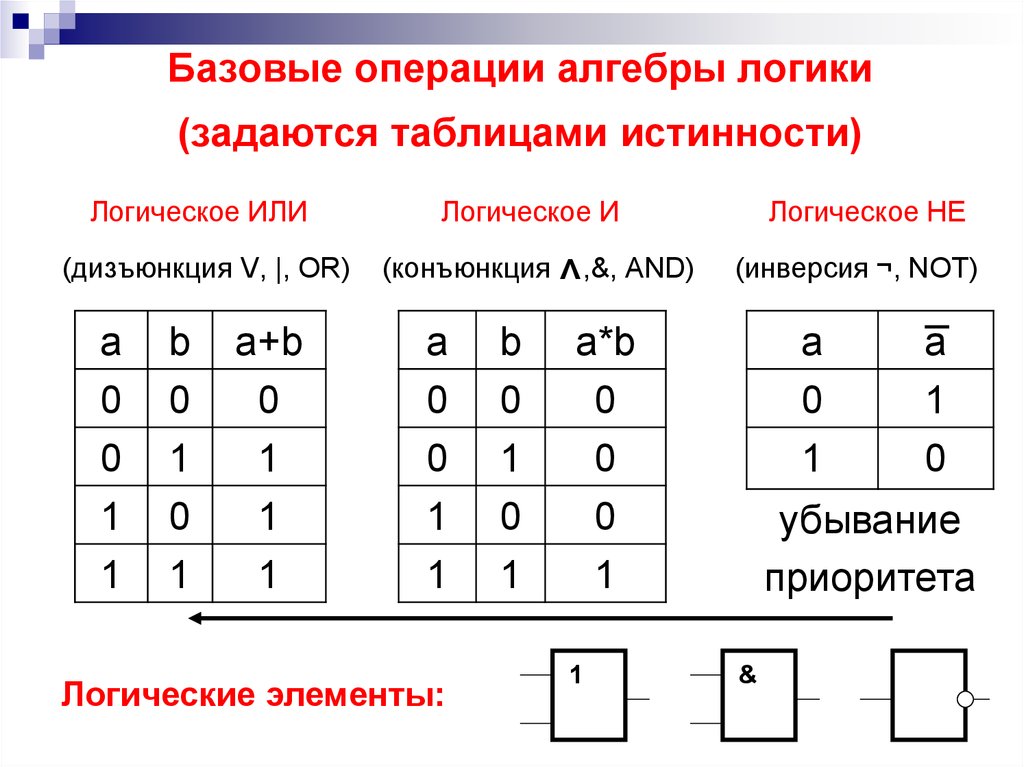 Например, если ячейка A1 содержит « яблок », а ячейка B1 содержит « бананов », угадайте, какая формула
Например, если ячейка A1 содержит « яблок », а ячейка B1 содержит « бананов », угадайте, какая формула =A1>B1 вернется? Поздравляю тех, кто сделал ставку на ЛОЖЬ : )
При сравнении текстовых значений Microsoft Excel игнорирует их регистр и сравнивает значения посимвольно, при этом "a" считается наименьшим текстовым значением, а "z" - наибольшим текстовым значением.
Итак, при сравнении значений « яблок » (A1) и « бананов » (B1) Excel начинается с их первых букв «a» и «b» соответственно, а так как «b» больше чем "а", формула =A1>B1 возвращает ЛОЖЬ.
Если первые буквы совпадают, то сравниваются 2 и буквы, если они тоже совпадают, то Excel попадает в 3 rd , 4 th букв и так далее. Например, если A1 содержит « яблок », а B1 содержит « агавы », формула =A1>B1 вернет TRUE, поскольку «p» больше, чем «g».
На первый взгляд кажется, что использование операторов сравнения с текстовыми значениями имеет очень мало практического смысла, но никогда не знаешь, что тебе может понадобиться в будущем, так что, возможно, эти знания кому-то пригодятся.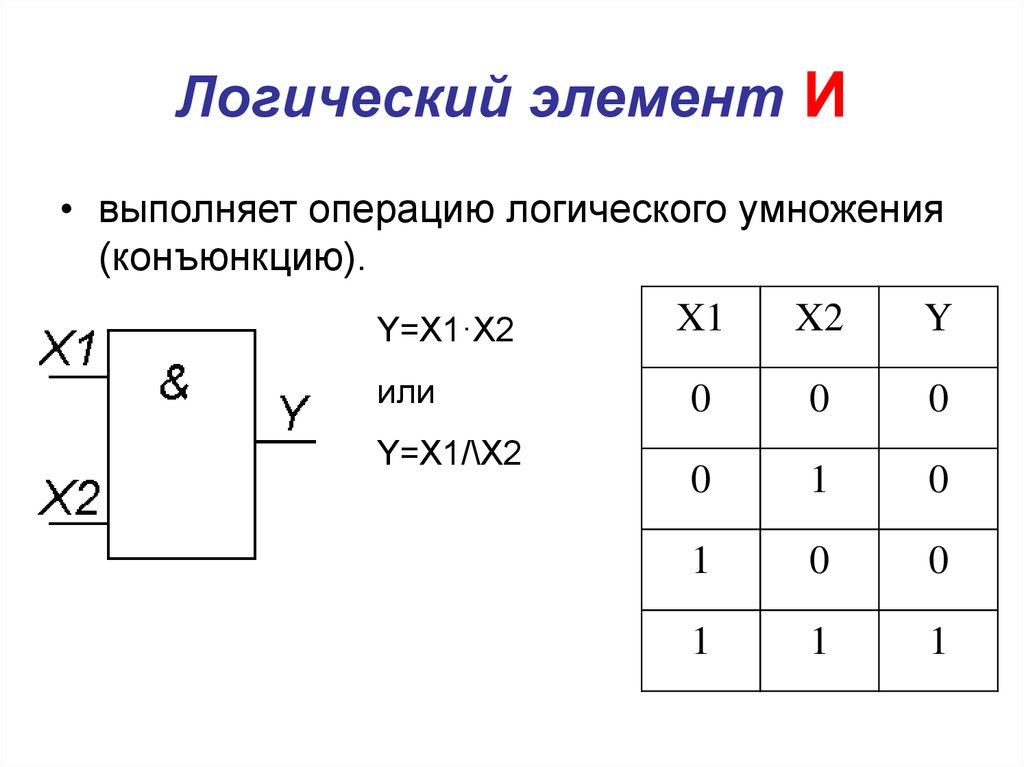
Распространенное использование логических операторов в Excel
В реальной работе логические операторы Excel редко используются сами по себе. Согласитесь, булевы значения TRUE и FALSE, которые они возвращают, хоть и очень истинны (извините за каламбур), но не очень значимы. Чтобы получить более разумные результаты, вы можете использовать логические операторы как часть функций Excel или правил условного форматирования, как показано в приведенных ниже примерах.
1. Использование логических операторов в аргументах функций Excel
Что касается логических операторов, то Excel очень либерален и позволяет использовать их в параметрах многих функций. Одно из наиболее распространенных применений находится в функции ЕСЛИ в Excel, где операторы сравнения могут помочь построить логический тест, а формула ЕСЛИ вернет соответствующий результат в зависимости от того, оценивается ли тест как ИСТИНА или ЛОЖЬ. Например:
=ЕСЛИ(A1>=B1, "ОК", "Неверно")
Эта простая формула ЕСЛИ возвращает ОК, если значение в ячейке A1 больше или равно значению в ячейке B1, "Неверно " в противном случае.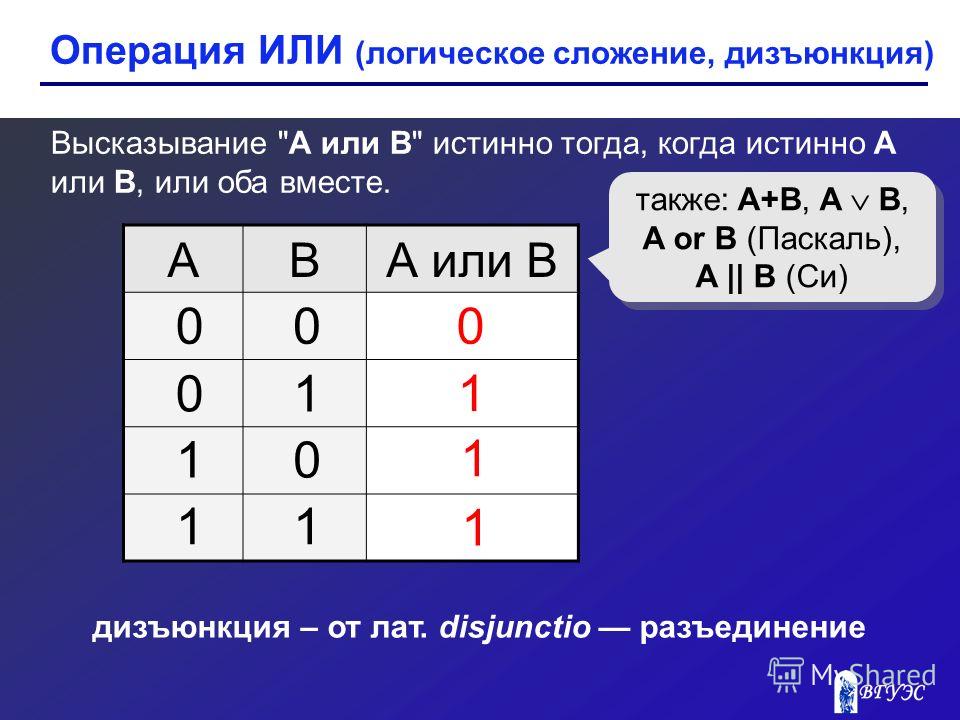
А вот еще пример:
=ЕСЛИ(A1<>B1, СУММ(A1:C1), "")
Формула сравнивает значения в ячейках A1 и B1, и если A1 не равно B1 , возвращается сумма значений в ячейках A1:C1, в противном случае — пустая строка.
Логические операторы Excel также широко используются в специальных функциях ЕСЛИ, таких как СУММЕСЛИ, СЧЁТЕСЛИ, СРЗНАЧЕСЛИ и их эквивалентах во множественном числе, которые возвращают результат на основе определенного условия или нескольких условий.
Вы можете найти множество примеров формул в следующих учебниках:
- Использование функции ЕСЛИ в Excel
- Как использовать СУММЕСЛИ в Excel
- Excel СУММЕСЛИМН и СУММЕСЛИ с несколькими критериями
- Использование СЧЁТЕСЛИ в Excel
- Excel COUNTIFS и COUNTIF с несколькими критериями
2. Использование логических операторов Excel в математических расчетах
Конечно, функции Excel очень эффективны, но не всегда их нужно использовать для достижения желаемого результата. Например, результаты, возвращаемые следующими двумя формулами, идентичны:
Например, результаты, возвращаемые следующими двумя формулами, идентичны:
Функция ЕСЛИ: =ЕСЛИ(B2>C2, B2*10, B2*5)
Формула с логическими операторами: =(B2>C2)*(B2*10)+(B2<=C2)* (B2*5)
Думаю, формулу ЕСЛИ легче интерпретировать, верно? Он говорит Excel умножить значение в ячейке B2 на 10, если B2 больше, чем C2, в противном случае значение в ячейке B1 умножается на 5.
Теперь давайте проанализируем формулу 2 и с больше, чем и меньше или равно логических операторов. Полезно знать, что в математических вычислениях Excel приравнивает логическое значение ИСТИНА к 1, а ЛОЖЬ к 0. Имея это в виду, давайте посмотрим, что на самом деле возвращает каждое из логических выражений.
Если значение в ячейке B2 больше, чем значение в C2, то выражение B2>C2 является ИСТИНА и, следовательно, равно 1. С другой стороны, B2<=C2 является ЛОЖЬ и равно 0. Итак, учитывая что B2>C2, наша формула претерпевает следующее преобразование:
Поскольку любое число, умноженное на ноль, дает ноль, мы можем отбросить вторую часть формулы после знака плюс.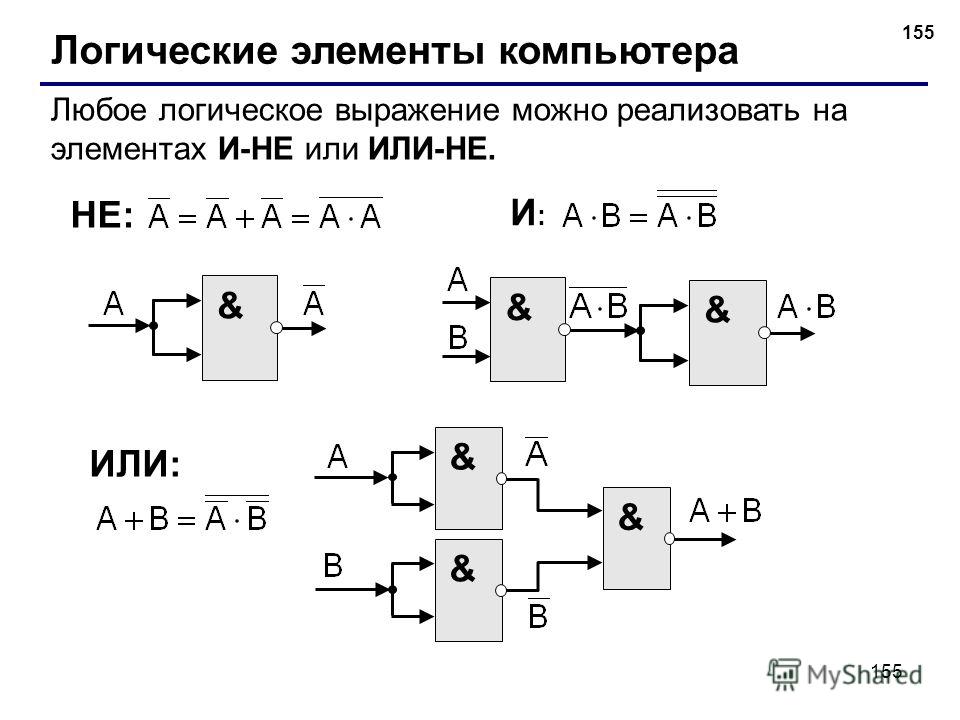 И поскольку любое число, умноженное на 1, является этим числом, наша сложная формула превращается в простую =B2*10, которая возвращает произведение умножения B2 на 10, что и делает приведенная выше формула ЕСЛИ: )
И поскольку любое число, умноженное на 1, является этим числом, наша сложная формула превращается в простую =B2*10, которая возвращает произведение умножения B2 на 10, что и делает приведенная выше формула ЕСЛИ: )
Очевидно, что если значение в ячейке B2 меньше, чем в C2, то выражение B2>C2 оценивается как FALSE (0), а B2<=C2 как TRUE (1), что означает, что произойдет обратное описанному выше.
3. Логические операторы в условном форматировании Excel
Логические операторы также часто используются в условном форматировании Excel, что позволяет быстро выделить наиболее важную информацию в электронной таблице.
Например, следующие простые правила выделяют выбранные ячейки или целые строки на вашем листе в зависимости от значения в столбце A:
Меньше (оранжевый): =A1<5
Больше (зеленый): =A1>20
Подробные пошаговые инструкции и примеры правил см. в следующих статьях. :
- Формулы условного форматирования Excel
- Как изменить цвет строки на основе значения ячейки
- Два способа изменить цвет фона на основе значения ячейки
- Как выделить каждую вторую строку в Excel
Как видите, использование логических операторов в Excel интуитивно понятно и просто.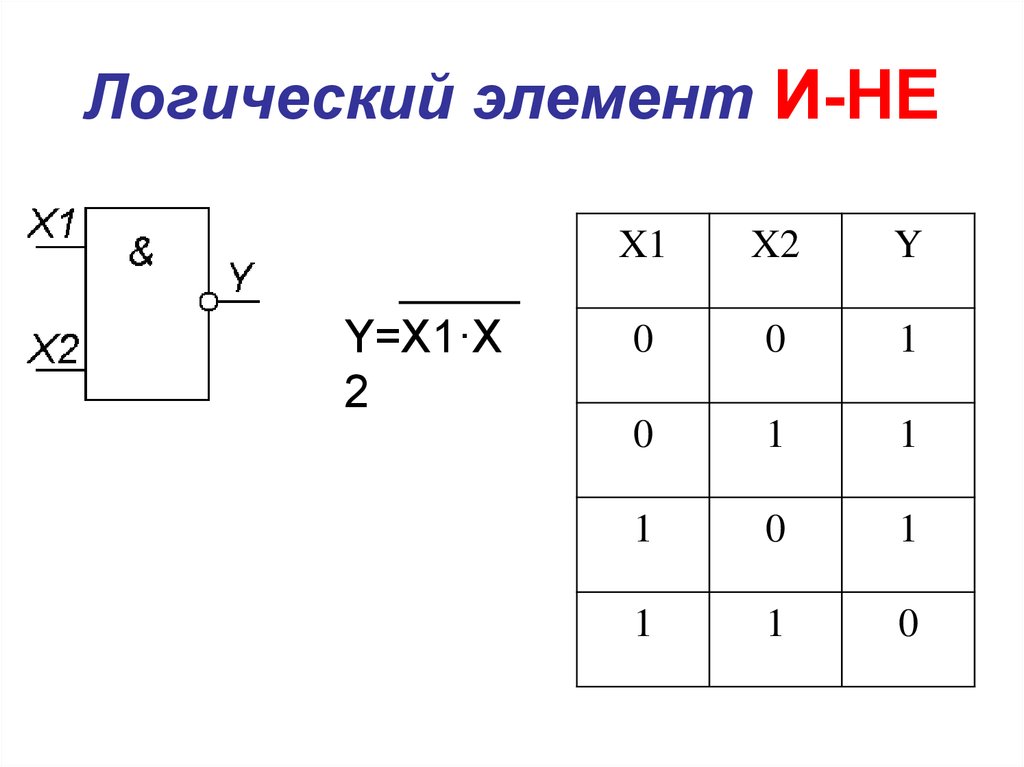 В следующей статье мы изучим азы логических функций Excel, которые позволяют выполнять более одного сравнения в формуле. Пожалуйста, оставайтесь с нами и спасибо за чтение!
В следующей статье мы изучим азы логических функций Excel, которые позволяют выполнять более одного сравнения в формуле. Пожалуйста, оставайтесь с нами и спасибо за чтение!
Вас также может заинтересовать
логических операторов в PowerShell | Список логических операторов с примерами
Мы видели много условий в операторе if, например if($j -lt 10), но если бы мы хотели проверить сразу несколько условий, например, $j -lt 10 и $ i -lt 15. Итак, у нас есть логические операторы для решения подобных ситуаций. Логические операторы в PowerShell объединяют два или более выражений и операторов вместе. Проще говоря, если мы хотим преобразовать несколько условий в одно условие, мы можем использовать логические операторы в PowerShell. Давайте вызовем логический оператор с именем LO для синтаксиса.
Синтаксис:
if(cond1 LO1 cond2 LO2 cond3){
Оператор 1
Оператор 2
...
}
Итак, в приведенном выше синтаксисе cond2 one LO1 cond3 LO1 .
В приведенном выше синтаксисе (cond1 LO1 cond2 LO2 cond3)=одно условие. Поскольку он вернет комбинацию нескольких условий с одним значением.
Примеры логических операторов в PowerShell
Ниже приведены примеры логических операторов в Powershell с подробным описанием.
Пример #1
В этом примере мы комбинируем три условия all ,($a -gt $b) =одно условие,(($a -lt 20) -или ($b -lt 20))=одно условие комбинацией двух и ($a -gt $b) -and (($a -lt 20) -or ($b -lt 20)) = одно условие, комбинацией всех трех получаем одно условие. Таким образом, если все эти условия будут истинными, будет показан только вывод «все комбинированные условия верны».
Код:
$a =14
$b=12
if(($a -gt $b) -и (($a -lt 20) -или ($b -lt 20))
){
Запись-Вывод «все комбинированные условия верны»
}
Вывод:
=одно условие,(($a -lt 20) -или ($b -lt 20))=одно условие,($a -gt $b) -и (($a -lt 20) -или ($b - lt 20)) = одно условие, комбинируя все три, мы получаем одно условие.
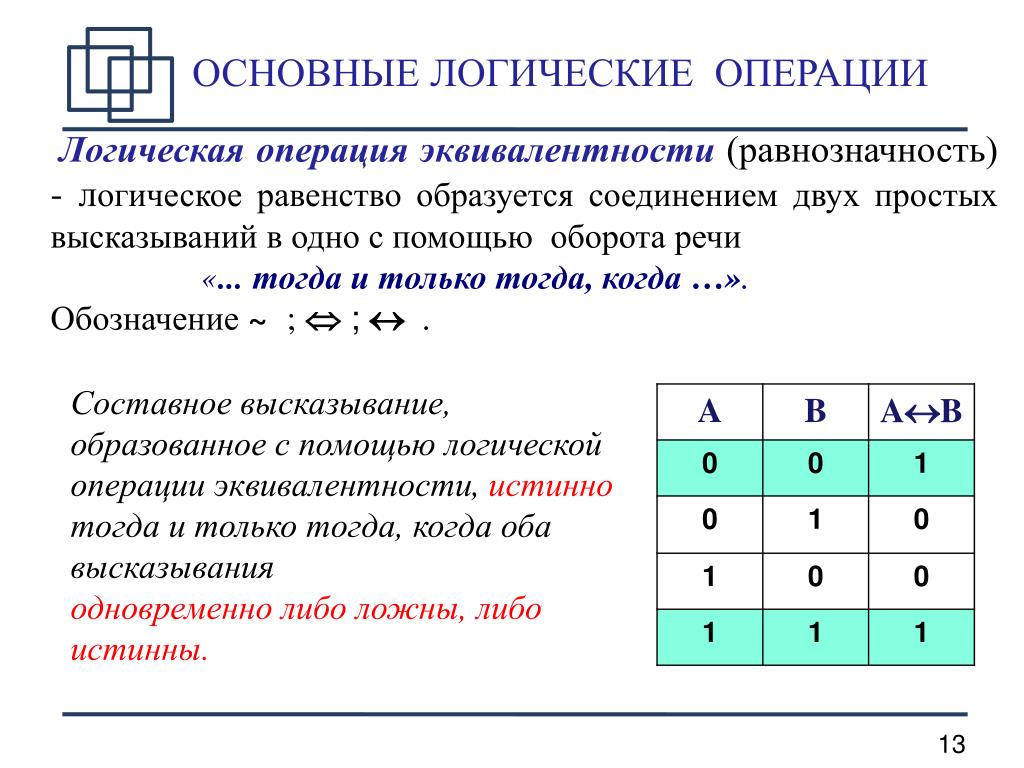 Здесь мы видим, что мы объединяем все три условия, чтобы сформировать одно условие, их вывод будет один.
Здесь мы видим, что мы объединяем все три условия, чтобы сформировать одно условие, их вывод будет один.Код:
$a =20
$b=21
if(($a -gt $b) -и (($a -lt 20) -или ($b -lt 20))
){
Запись-вывод «все комбинированные условия верны»
}else{
Запись-вывод «все комбинированные условия ложны»
}
Вывод:
Список логических операторов в PowerShell
8 5 основных логических операторов в PowerShell: «и», «или», «xor», «not=(!)». давайте обсудим каждый с примером вкратце.1) -и Оператор
и называется логическим И, вывод любого логического и является Истинным, если $a и $b Истинны, в противном случае Ложным, ниже приведены некоторые примеры для логических и операторов.
Код:
$a -и $b //false (если оба ложны)
$a -и $b //ложно (если хотя бы одно из них ложно)
$a -и $b //true (если оба они верны)
Таким образом, логика и оператор истинны только тогда, когда истинны оба. Скрин выполнения приведенных выше примеров приведен ниже.
Скрин выполнения приведенных выше примеров приведен ниже.
Вывод:
В целом и операторы, используемые там, где мы хотим, все условия должны быть полностью заполнены. Например, предположим, что в классе учитель решил допустить к экзаменам только тех учеников, посещаемость которых превышает 100 человек, а также они оплатили стоимость занятия. Так что здесь оба условия должны быть выполнены полностью.
Код:
$посещаемость =101
$оплачено = «да»
если ($посещаемость -gt 100 -и $оплачено -eq «да»){
Запись-вывод «Допустить его на обследование»
}
Вывод:
Мы также можем протестировать эту программу, передав разные входные значения $посещаемости и $оплаты.
2) -или Оператор
Логический или, Ложь, если $a и $b имеют значение Ложь, в противном случае несколько примеров приведены ниже:
Код:
ложны)
$a -or $b //true (если хотя бы одно из них истинно)
$a -or $b //true (если оба они истинны)
Таким образом, в основном логика и только оператор false когда оба ложны.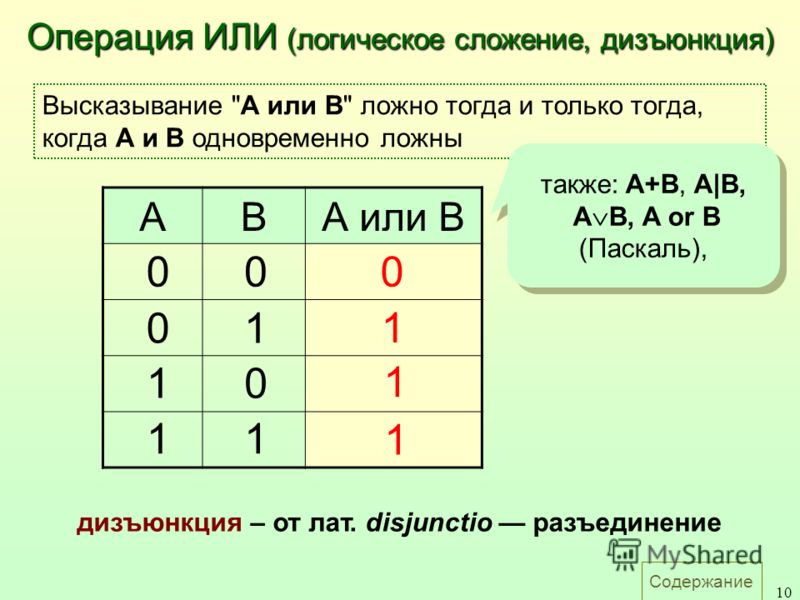 Скрин выполнения приведенных выше примеров приведен ниже.
Скрин выполнения приведенных выше примеров приведен ниже.
Вывод:
В общем, операторы or используются, когда мы хотим считать, что какое-либо условие верно, например, учащиеся, посетившие более 100, получат 5 дополнительных баллов или учащийся, набравший более 200 баллов.
Код:
} 9076 Выход: Мы также можем протестировать эту программу, передав разные входные значения $attendance и $paid. Логическое исключающее или ,True, если $a или $b истинно, иначе Код: Ниже на экране показаны выходные данные приведенного выше примера, Вывод: Логическое not, True, если $a равно False, иначе Код: Экран для приведенного выше примера приведен ниже, Вывод: ! оператор такой же, как и у оператора -not. Код: Экран для приведенного выше примера приведен ниже, Вывод: Примечание: В PowerShell всегда используйте $TRUE и $FALSE для значений true и false, если вы будете использовать true и false, они не будет рассматриваться как логическое значение. Код: Скрин для приведенного выше примера приведен ниже, Вывод: Некоторые примеры из реальной жизни со смешением всех операторов вместе, Предположим, что наш сервер и база данных работают, и мы хотим реализовать определенную проверку, будет ли она постоянно проверять, работают ли сервер и база данных или нет. Код: 1-й ввод: 2-й ввод: В заключение, без логического оператора наше программирование будет пустым, потому что только с помощью логических операторов мы можем писать ситуационный код, мы можем иметь дело с различными условиями. Это руководство по логическим операторам в PowerShell. R имеет несколько операторов для выполнения задач, включая арифметические, логические и побитовые операции. В этой статье вы узнаете о различных операторах R с помощью примеров. R имеет множество операторов для выполнения различных математических и логических операций. Операторы в R в основном можно разделить на следующие категории. Эти операторы используются для выполнения математических операций, таких как сложение и умножение. Операторы сравнения используются для сравнения значений. Вот список реляционных операторов, доступных в R. Пример запуска Вышеупомянутые операторы работают с векторами. Переменные, использованные выше, на самом деле были одноэлементными векторами. Мы можем использовать функцию Все операции выполняются поэлементно. Вот пример. При несовпадении длины (количества элементов) векторов операндов элементы более короткого вектора циклически перерабатываются, чтобы соответствовать длине более длинного. R выдаст предупреждение, если длина более длинного вектора не является целым кратным длины более короткого вектора. Логические операторы используются для выполнения логических операций, таких как Операторы Но Ноль рассматривается как Эти операторы используются для присвоения значений переменным. $посещаемость =101
$оценки =201
if($посещаемость -gt 100 -или $marks -gt 200){
Запись-Вывод «добавить 5 дополнительных оценок» 9052 3) -xor Оператор
('a' -eq 'A') -xor ('a' -eq 'z') //true, поскольку одно из них верно
('a' -eq 'A') -xor ('Z' -eq 'z')//false, поскольку одно из них ложно
(' a' -eq 's') -xor ('Z' -eq 'p') //false, так как оба они ложны 4) -not Оператор
-not /false, так как вывод выражения истинен
-not ('v' -eq 'a')// true, поскольку выходное выражение ложно
-not ('v' -eq 'V') //false, поскольку выходное выражение истинно
-not ('V' -eq 'V1') //true, поскольку выходное выражение ложно 5) ! Оператор
 Просто! оператор преобразует true в false и false в true.
Просто! оператор преобразует true в false и false в true. !('a' -eq 'a') //false, так как вывод выражения верен
!('v' -eq 'a')// true, поскольку выходное выражение ложно
!('v' -eq 'V') //ложно, так как выходное выражение истинно
!('V' -eq 'V1') //истинно, так как выходное выражение ложно $a =false
$b=true
!$a //правда
!($b) //правда
a) //true
!($b) //false 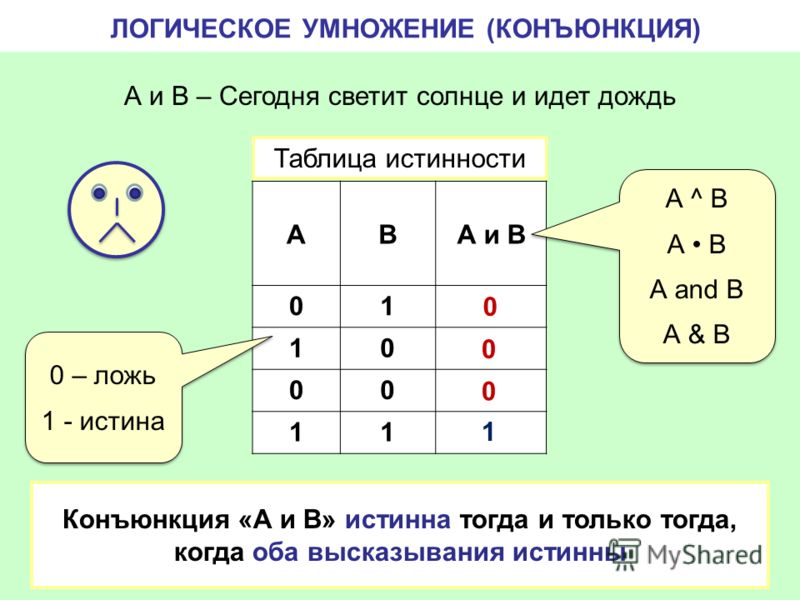
if($server -eq "работает" -and $database -eq "работает"){
Write-Output "сервер работает и база данных работает"
}elseif($server -eq "не работает" - и $database -eq "работает"){
Запись-вывод «сервер не работает, а база данных работает»
}elseif($server -eq «работает» -и $database -eq «не работает»){
Запись-вывод «сервер работает, а база данных не работает»
}else{
Write-Output «сервер и база данных не работают»
} $server = «не работает»;
$database="работает" $server="работает";
$database = «не работает» Заключение
Рекомендуемые статьи
 Здесь мы обсудим введение и 5 лучших логических операторов в Powershell с примерами и реализацией кода. Вы также можете прочитать следующие статьи, чтобы узнать больше –
Здесь мы обсудим введение и 5 лучших логических операторов в Powershell с примерами и реализацией кода. Вы также можете прочитать следующие статьи, чтобы узнать больше – Арифметические, реляционные, логические и др.
Арифметические операторы Реляционные операторы Логические операторы Операторы присваивания R Арифметические операторы
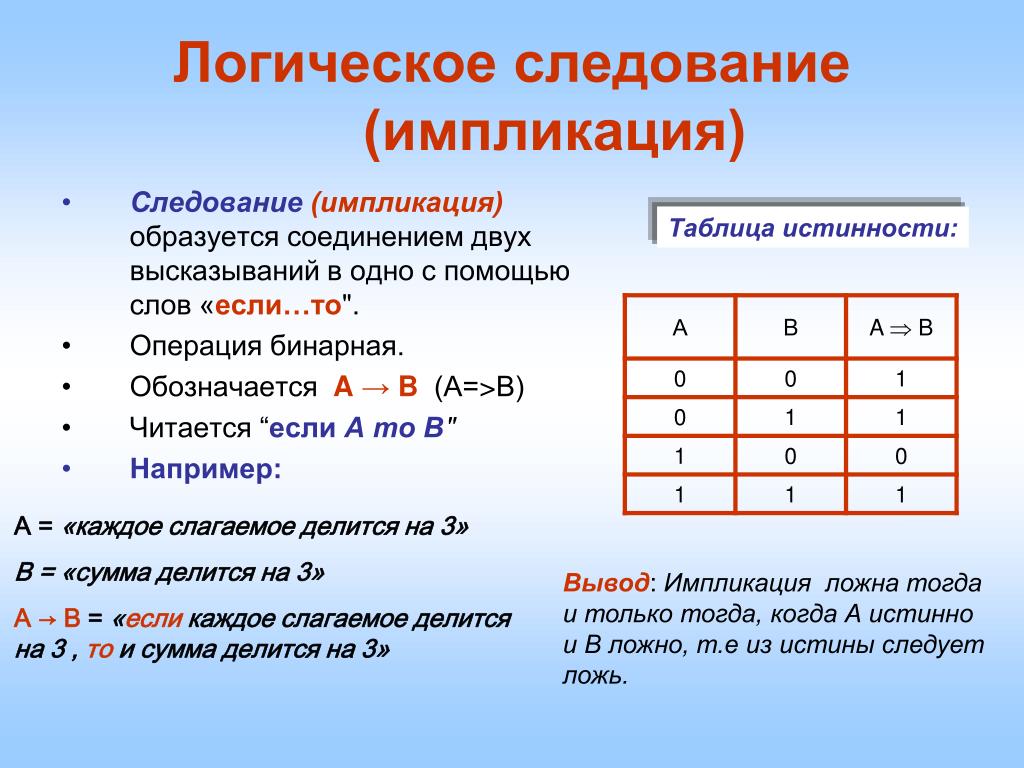 Вот список арифметических операторов, доступных в R. 9Икс
[1] 1048576
Вот список арифметических операторов, доступных в R. 9Икс
[1] 1048576 R Реляционные операторы
Оператор Описание < Менее > Больше <= Меньше или равно >= Больше или равно == равно != Не равно > х <- 5
> у <- 16
> х<у
[1] ИСТИНА
> х>у
[1] ЛОЖЬ
> х<=5
[1] ИСТИНА
> у>=20
[1] ЛОЖЬ
> у == 16
[1] ИСТИНА
> х != 5
[1] ЛОЖЬ
Операции с векторами

c() (как в конкатенации) для создания векторов в R. > х <- с(2,8,3)
> у <- с(6,4,1)
> х+у
[1] 8 12 4
> х>у
[1] ЛОЖЬ ИСТИНА ИСТИНА
> х <- с(2,1,8,3)
> у <- с(9,4)
> x+y # Элемент y перерабатывается в 9,4,9,4
[1] 11 5 17 7
> x-1 # Скаляр 1 перерабатывается в 1,1,1,1
[1] 1 0 7 2
> х+с(1,2,3)
[1] 3 3 11 4
Предупреждение:
В х + с (1, 2, 3):
большая длина объекта не кратна меньшей длине объекта
R Логические операторы
И , ИЛИ и т.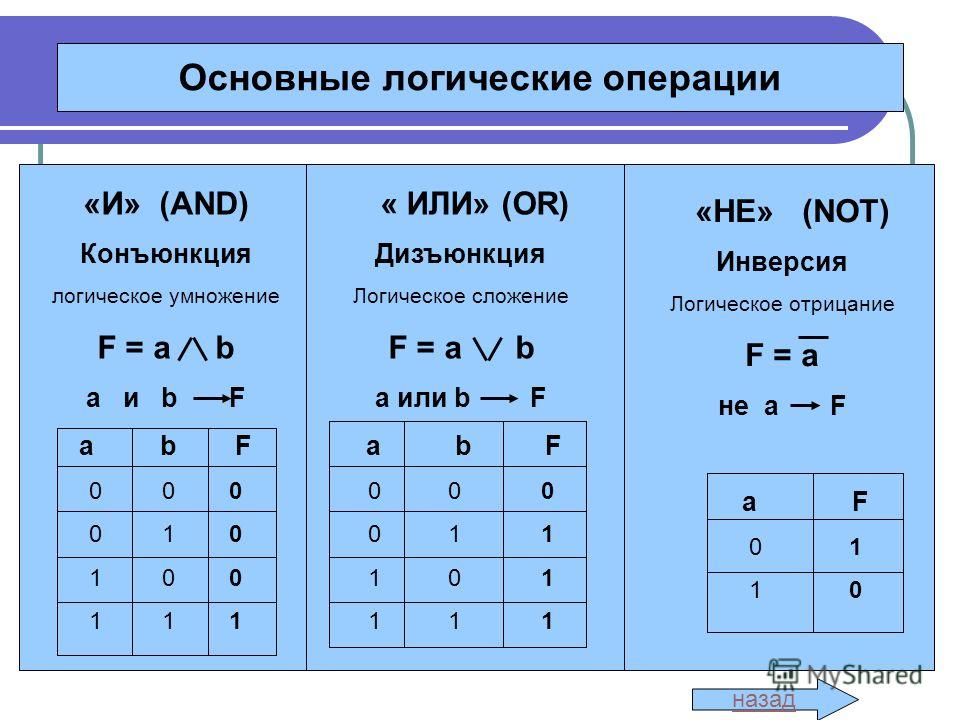 д.
д. Оператор Описание ! Логический НЕ и Поэлементное логическое И && Логический И | Поэлементное логическое ИЛИ || Логическое ИЛИ и и | выполнить поэлементную операцию с результатом, имеющим длину большего операнда. && и || проверяет только первый элемент операндов, что приводит к логическому вектору одинарной длины. ЛОЖЬ , а ненулевые числа принимаются как ИСТИНА . Пример запуска. > х <- с (ИСТИНА, ЛОЖЬ, 0,6)
> y <- c(ЛОЖЬ,ИСТИНА,ЛОЖЬ,ИСТИНА)
> !х
[1] ЛОЖЬ ИСТИНА ИСТИНА ЛОЖЬ
> х&у
[1] ЛОЖЬ ЛОЖЬ ЛОЖЬ ИСТИНА
> х&&у
[1] ЛОЖЬ
> х|у
[1] ИСТИНА ИСТИНА ЛОЖЬ ИСТИНА
> х||у
[1] ИСТИНА
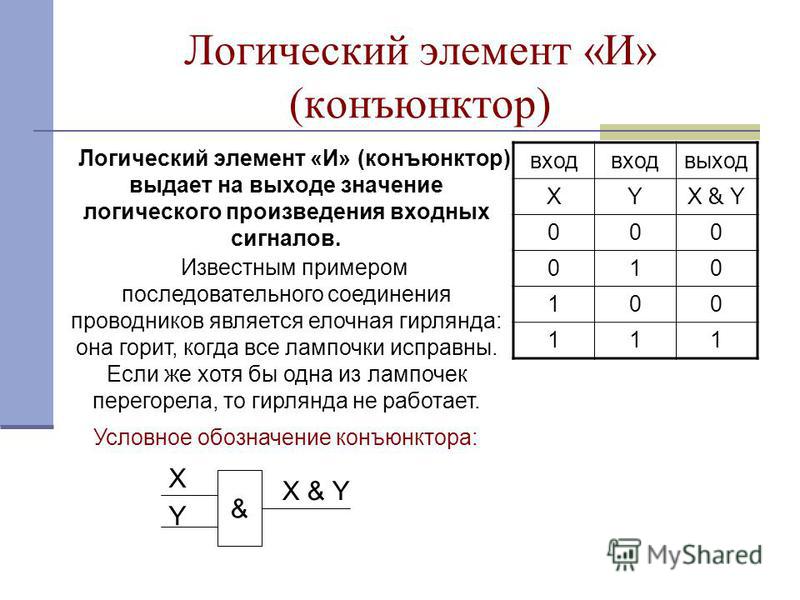




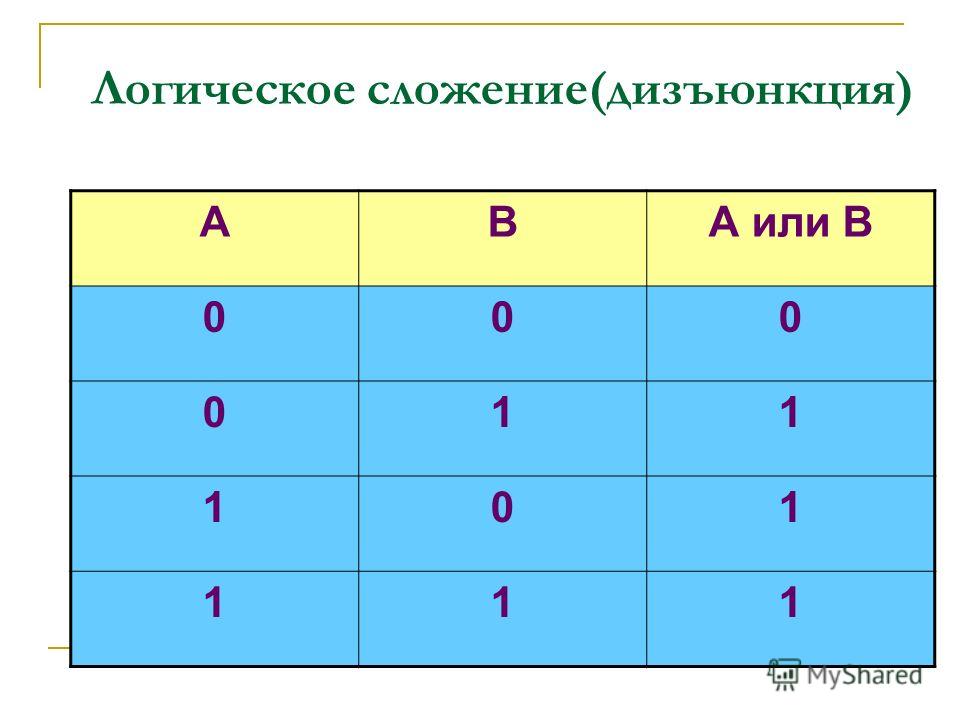 Если все аргументы являются пустыми ячейками, формула возвращает #ЗНАЧ! ошибка.
Если все аргументы являются пустыми ячейками, формула возвращает #ЗНАЧ! ошибка.