ЛИНЗА — это… Что такое ЛИНЗА?
(нем. Linse, от лат. lens — чечевица) — простейший оптич. элемент, изготавливаемый из прозрачного материала, ограниченный двумя преломляющими поверхностями, имеющими общую ось либо две взаимно перпендикулярные плоскости симметрии. При изготовлении Л. для видимой области применяют оптическое стекло или органическое стекло (массовое тиражирование непрецизионных деталей), в УФ-диапазоне — кварц, флюорит и др., в ИК-диапазоне — спец. сорта стёкол, кремний, германий, сапфир, ряд солей и т. д.
Рабочие поверхности Л. обычно имеют сферич. форму, реже — цилиндрическую, тороидальную, конусообразную или с заданными небольшими отступлениями от сферы (асферическую). Л. со сферич. поверхностями наиб. просты в изготовлении и являются осн. элементами большинства оптич. систем.
В параксиальном приближении (углы 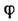 между лучами и оптич. осью столь малы, что можно заменить sin
между лучами и оптич. осью столь малы, что можно заменить sin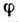
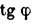 на
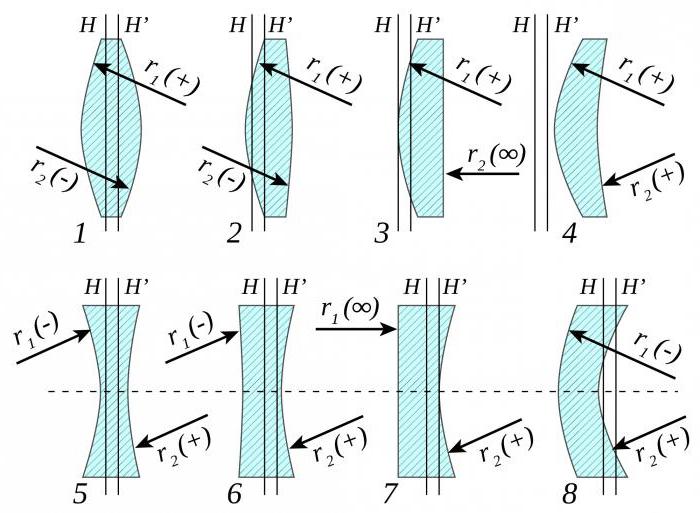
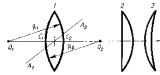
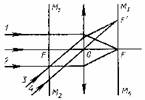
на 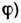 свойства Л. со сферич. поверхностями могут быть однозначно охарактеризованы положением главных плоскостей и оптической силой Ф, представляющей собой выражаемую в диоптриях величину, обратную фокусному расстоянию (в м). Связь этих характеристик с геом. параметрами Л. ясны из рис., в к-ром для наглядности углы наклона лучей изображены преувеличенно большими. Расстояния от первой по ходу лучей поверхности линзы до первой гл. плоскости Я и от второй поверхности до второй гл. плоскости
свойства Л. со сферич. поверхностями могут быть однозначно охарактеризованы положением главных плоскостей и оптической силой Ф, представляющей собой выражаемую в диоптриях величину, обратную фокусному расстоянию (в м). Связь этих характеристик с геом. параметрами Л. ясны из рис., в к-ром для наглядности углы наклона лучей изображены преувеличенно большими. Расстояния от первой по ходу лучей поверхности линзы до первой гл. плоскости Я и от второй поверхности до второй гл. плоскости S1, 2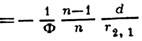
фокусное расстояние от H до переднего фокуса (F)f= -1/Ф, от 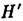 до заднего фокуса I
до заднего фокуса I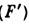
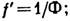 оптич. сила Л., являющаяся мерой её преломляющего действия, равна
оптич. сила Л., являющаяся мерой её преломляющего действия, равна
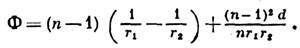
Здесь п — показатель преломления вещества Л. (или отношение этого показателя к показателю преломления окружающей среды, если последний 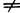 1), d — измеренная вдоль оси толщина Л., r1 и r2 — радиусы кривизны её поверхностей (считаются положительными, если центры кривизны расположены дальше по ходу лучей; так, у изображённой на рис. двояковыпуклой Л. r1>0, r2<0), расстояния отсчитываются вдоль направления распространения света.
1), d — измеренная вдоль оси толщина Л., r1 и r2 — радиусы кривизны её поверхностей (считаются положительными, если центры кривизны расположены дальше по ходу лучей; так, у изображённой на рис. двояковыпуклой Л. r1>0, r2<0), расстояния отсчитываются вдоль направления распространения света.
Способ построения и расчёта траекторий проходящих через Л. меридиональных (лежащих в осевой плоскости) лучей с использованием гл. плоскостей ясен из рис. После прохождения Л. луч кажется исходящим из точки на 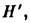 удалённой от оси на то же расстояние h, что и точка пересечения исходного луча с Я. Угол между лучом и осью изменяется на
удалённой от оси на то же расстояние h, что и точка пересечения исходного луча с Я. Угол между лучом и осью изменяется на 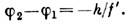 Для нахождения траектории произвольного немеридионального луча последний проецируется на две взаимно перпендикулярные осевые плоскости. Каждая проекция является по существу меридиональным лучом и ведёт себя указанным выше образом.
Для нахождения траектории произвольного немеридионального луча последний проецируется на две взаимно перпендикулярные осевые плоскости. Каждая проекция является по существу меридиональным лучом и ведёт себя указанным выше образом.
Положение даваемого Л. изображения точки определяется ф-лами
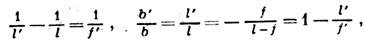
где l и 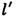 — расстояния от гл. плоскостей до плоскостей предмета и изображения соответственно (рис.), b и
— расстояния от гл. плоскостей до плоскостей предмета и изображения соответственно (рис.), b и 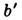 — расстояния точки и её изображения от оси (отсчитываемые вверх).
— расстояния точки и её изображения от оси (отсчитываемые вверх).
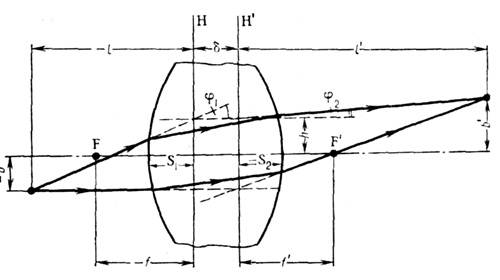
Если 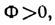 Л. наз. положительной или собирающей, при
Л. наз. положительной или собирающей, при 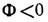 — отрицательной или рассеивающей; линзы с Ф=0 наз. афокальными и используются гл. обр. для исправления аберраций др. оптич. элементов. Положительные Л. дают действительные изображения всех действительных объектов, находящихся до переднего фокуса (на рис.- левее F), и всех мнимых объектов, находящихся за Л. Рассеивающие Л. дают расположенное между Л. и передним фокусом прямое, мнимое, уменьшенное изображение действит. объектов.
— отрицательной или рассеивающей; линзы с Ф=0 наз. афокальными и используются гл. обр. для исправления аберраций др. оптич. элементов. Положительные Л. дают действительные изображения всех действительных объектов, находящихся до переднего фокуса (на рис.- левее F), и всех мнимых объектов, находящихся за Л. Рассеивающие Л. дают расположенное между Л. и передним фокусом прямое, мнимое, уменьшенное изображение действит. объектов.
Расстояние 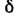 между гл. плоскостями Л. почти не зависит от её оптич. силы и формы и примерно равно d(1-1/n). Когда
между гл. плоскостями Л. почти не зависит от её оптич. силы и формы и примерно равно d(1-1/n). Когда 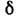 пренебрежимо мало по сравнению с
пренебрежимо мало по сравнению с 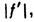 Л. наз. тонкой. У тонких Л. знак оптич. силы Ф совпадает со знаком разности 1/r1-1/r2; при этом толщина собирающих Л. по мере удаления от оси уменьшается, а рассеивающих — возрастает. Обе гл. плоскости тонких Л. можно считать совпадающими с плоскостью Л. и отсчитывать введённые выше расстояния /,
Л. наз. тонкой. У тонких Л. знак оптич. силы Ф совпадает со знаком разности 1/r1-1/r2; при этом толщина собирающих Л. по мере удаления от оси уменьшается, а рассеивающих — возрастает. Обе гл. плоскости тонких Л. можно считать совпадающими с плоскостью Л. и отсчитывать введённые выше расстояния /,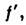
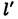 прямо от последней. Чёткой границы между толстыми Л. (когда
прямо от последней. Чёткой границы между толстыми Л. (когда 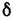 нельзя пренебречь) и тонкими не существует — всё зависит от конкретных применений.
нельзя пренебречь) и тонкими не существует — всё зависит от конкретных применений. Для преобразования высококогерентных световых пучков (обычно лазерного происхождения) используются преим. тонкие Л. Их часто наз. квадратичными фазовыми корректорами: при прохождении когерентного пучка через тонкую Л. к распределению фазы по его сечению добавляется величина 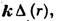
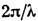 — волновой вектор,
— волновой вектор,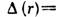 = ( п-1)
= ( п-1)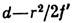 — вносимая Л. дополнит. разность хода, являющаяся квадратичной ф-цией удаления r от оси. Распределение комплексной амплитуды поля в фокальной плоскости Л. с точностью до фазового множителя является
— вносимая Л. дополнит. разность хода, являющаяся квадратичной ф-цией удаления r от оси. Распределение комплексной амплитуды поля в фокальной плоскости Л. с точностью до фазового множителя является 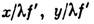 (х, у — поперечные координаты на фокальной плоскости). Распределение интенсивности в той же плоскости подобно угл. распределению излучения с коэф. подобия
(х, у — поперечные координаты на фокальной плоскости). Распределение интенсивности в той же плоскости подобно угл. распределению излучения с коэф. подобия 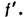 Поэтому Л. широко применяются в системах пространственной фильтрации излучения, обычно представляющих собой комбинацию Л. с установленными в их фокальных плоскостях диафрагмами, растрами,
Поэтому Л. широко применяются в системах пространственной фильтрации излучения, обычно представляющих собой комбинацию Л. с установленными в их фокальных плоскостях диафрагмами, растрами, Л. обладают всеми аберрациями, присущими цент-риров. оптич. системам (см. Аберрации оптических систем). Проблема аберраций особенно важна при использовании широкополосных и обладающих большими угл. апертурами световых пучков обычных (некогерентных) источников. Сферич. и хроматич. аберрации, а также кома могут быть в значит. степени исправлены путём комбинирования двух Л. разл. формы и из материалов с разл. дисперсией. Такие двухлинзовые системы широко используются в качестве объективов для зрительных труб и т. п. Иногда сферич. аберрации уничтожаются с помощью Л. с асферической, в частности параболоидальной, формой поверхности.
Для коррекции разл. дефектов глаза применяются Л. не только со сферическими, но также с цилиндрич. и торич. поверхностями. Цилиндрич. Л. сравнительно часто используются в тех случаях, когда изображение точечного источника должно быть «растянуто» в полосу или линию (напр., в спектральных приборах).
Лит.: Борн М., Вольф Э., Основы оптики, пер. с англ., 2 изд., М., 1973; Гудмен Д ж., Введение в Фурье-оптику, пер. с англ.. М.. 1970. Ю. А. Ананьев.
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия. Главный редактор А. М. Прохоров. 1988.
определение, описание, формула и решение
Существуют объекты, которые способны изменять плотность падающего на них потока электромагнитного излучения, то есть либо увеличивать его, собирая в одну точку, либо уменьшать его путем рассеивания. Эти объекты называются линзами в физике. Рассмотрим подробнее этот вопрос.
Что представляют собой линзы в физике?
Под этим понятием подразумевают абсолютно любой объект, который способен изменять направление распространения электромагнитного излучения. Это общее определение линз в физике, под которое попадают оптические стекла, магнитные и гравитационные линзы.
В данной статье главное внимание будет уделено именно оптическим стеклам, которые представляют собой объекты, изготовленные из прозрачного материала, и ограниченные двумя поверхностями. Одна из этих поверхностей обязательно должна иметь кривизну (то есть являться частью сферы конечного радиуса), в противном случае объект не будет обладать свойством изменения направления распространения световых лучей.
Принцип работы линзы

Суть работы этого незамысловатого оптического объекта заключается в явлении преломления солнечных лучей. В начале XVII века знаменитый голландский физик и астроном Виллеброрд Снелл ван Ройен опубликовал закон преломления, который в настоящее время носит его фамилию. Формулировка этого закона следующая: когда солнечный свет переходит через границу раздела двух оптически прозрачных сред, то произведение синуса угла падения между лучом и нормалью к поверхности на коэффициент преломления среды, в которой он распространяется, является величиной постоянной.

Для пояснения вышесказанного приведем пример: пусть свет падает на поверхность воды, при этом угол между нормалью к поверхности и лучом равен θ1. Затем, световой пучок преломляется и начинает свое распространение в воде уже под углом θ2 к нормали к поверхности. Согласно закону Снелла получим: sin(θ1)*n1 = sin(θ2)*n2, здесь n1 и n2 — коэффициенты преломления для воздуха и воды, соответственно. Что такое коэффициент преломления? Это величина, показывающая, во сколько раз скорость распространения электромагнитных волн в вакууме больше таковой для оптически прозрачной среды, то есть n = c/v, где c и v — скорости света в вакууме и в среде, соответственно.
Физика возникновения преломления заключается в выполнении принципа Ферма, согласно которому свет движется таким образом, чтобы за наименьшее время преодолеть расстояние от одной точки к другой в пространстве.
Виды линз

Вид оптической линзы в физике определяется исключительно формой поверхностей, которые ее образуют. От этой формы зависит направление преломления падающего на них луча. Так, если кривизна поверхности будет положительной (выпуклой), то по выходе из линзы световой пучок будет распространяться ближе к ее оптической оси (см. ниже). Наоборот, если кривизна поверхности является отрицательной (вогнутой), тогда пройдя через оптическое стекло, луч станет удаляться от его центральной оси.
Отметим еще раз, что поверхность любой кривизны преломляет лучи одинаково (согласно закону Стелла), но нормали к ним имеют разный наклон относительно оптической оси, в результате получается разное поведение преломленного луча.
Линза, которая ограничена двумя выпуклыми поверхностями, называется собирающей. В свою очередь, если она образована двумя поверхностями с отрицательной кривизной, тогда она называется рассеивающей. Все остальные виды оптических стекол связаны с комбинацией указанных поверхностей, к которым добавляется еще и плоскость. Каким свойством будет обладать комбинированная линза (рассеивающим или собирающим), зависит от суммарной кривизны радиусов ее поверхностей.
Элементы линзы и свойства лучей

Для построения в линзах в физике изображений необходимо познакомиться с элементами этого объекта. Они приведены ниже:
- Главная оптическая ось и центр. В первом случае имеют в виду прямую, проходящую перпендикулярно линзе через ее оптический центр. Последний, в свою очередь, представляет собой точку внутри линзы, проходя через которую, луч не испытывает преломления.
- Фокусное расстояние и фокус — дистанция между центром и точкой на оптической оси, в которую собираются все падающие на линзу параллельно этой оси лучи. Это определение верно для собирающих оптических стекол. В случае рассеивающих линз собираться в точку будут не сами лучи, а мнимое их продолжение. Эта точка называется главным фокусом.
- Оптическая сила. Так называется величина, обратная фокусному расстоянию, то есть D = 1/f. Измеряется она в диоптриях (дптр.), то есть 1 дптр. = 1 м-1.
Ниже приводятся основные свойства лучей, которые проходят через линзу:
- пучок, проходящий через оптический центр, не изменяет направления своего движения;
- лучи, падающие параллельно главной оптической оси, изменяют свое направление так, что проходят через главный фокус;
- лучи, падающие на оптическое стекло под любым углом, но проходящие через его фокус, изменяют свое направление распространения таким образом, что становятся параллельными главной оптической оси.
Приведенные выше свойства лучей для тонких линз в физике (так их называют, потому что не важно, какими сферами они образованы, и какой толщиной обладают, имеют значение только оптические свойства объекта) используются для построения изображений в них.
Изображения в оптических стеклах: как строить?
Ниже приведен рисунок, где подробно разобраны схемы построения изображений в выпуклой и вогнутой линзах объекта (красной стрелки) в зависимости от его положения.
Из анализа схем на рисунке следуют важные выводы:
- Любое изображение строится всего на 2-х лучах (проходящем через центр и параллельном главной оптической оси).
- Собирающие линзы (обозначаются со стрелками на концах, направленными наружу) могут давать как увеличенное, так и уменьшенное изображение, которое в свою очередь может быть реальным (действительным) или мнимым.
- Если предмет расположен в фокусе, то линза не образует его изображения (см. нижнюю схему слева на рисунке).
- Рассеивающие оптические стекла (обозначаются стрелками на их концах, направленными внутрь) дают независимо от положения предмета всегда уменьшенное и мнимое изображение.
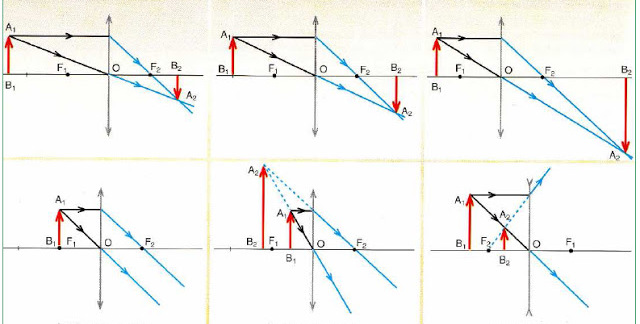
Нахождение расстояния до изображения
Чтобы определять, на каком расстоянии появится изображение, зная положение самого предмета, приведем формулу линзы в физике: 1/f = 1/do + 1/di, где do и di — расстояние до предмета и до его изображения от оптического центра, соответственно, f — главный фокус. Если речь идет о собирающем оптическом стекле, тогда число f будет положительным. Наоборот, для рассеивающей линзы f — отрицательное.
Воспользуемся этой формулой и решим простую задачу: пусть предмет находится на расстоянии do = 2*f от центра собирающего оптического стекла. Где появится его изображение?
Из условия задачи имеем: 1/f = 1/(2*f)+1/di. Откуда: 1/di = 1/f — 1/(2*f) = 1/(2*f), то есть di = 2*f. Таким образом, изображение появится на расстоянии двух фокусов от линзы, но уже с другой стороны, чем сам предмет (об этом говорит положительный знак величины di).
Краткая история
Любопытно привести этимологию слова «линза». Оно ведет происхождение от латинских слов lens и lentis, что означает «чечевица», поскольку оптические объекты по своей форме действительно похожи на плод этого растения.
Преломляющая способность сферических прозрачных тел была известна еще древним римлянам. Для этой цели они применяли круглые стеклянные сосуды, наполненные водой. Сами же стеклянные линзы начали изготавливаться только в XIII веке в Европе. Использовались они в качестве инструмента для чтения (современные очки или лупа).
Активное использование оптических объектов при изготовлении телескопов и микроскопов относится к XVII (в начале этого века Галилей изобрел первый телескоп). Отметим, что математическая формулировка закона преломления Стелла, без знания которой невозможно изготавливать линзы с заданными свойствами, была опубликована голландским ученым в начале того же XVII века.
Другие виды линз
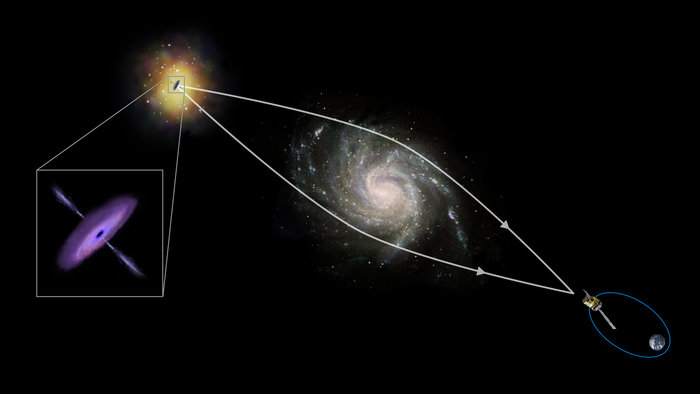
Как было отмечено выше, помимо оптических преломляющих объектов, существуют также магнитные и гравитационные. Примером первых являются магнитные линзы в электронном микроскопе, яркий пример вторых заключается в искажении направления светового потока, когда он проходит вблизи массивных космических тел (звезд, планет).
Линза — это… Что такое Линза?
Линза (нем. Linse, от лат. lens — чечевица) — деталь из оптически (и не только, линзы также применяются в СВЧ технике, и там обычно состоят из непрозрачных диэлектриков или набора металлических пластин) прозрачного однородного материала, ограниченная двумя полированными преломляющими поверхностями вращения, например, сферическими или плоской и сферической. В настоящее время всё чаще применяются и «асферические линзы», форма поверхности которых отличается от сферы. В качестве материала линз обычно используются оптические материалы, такие как стекло, оптическое стекло, оптически прозрачные пластмассы и другие материалы.
Линзами также называют и другие оптические приборы и явления, которые создают сходный оптический эффект, не обладая указанными внешними характеристиками. Например:
История
Первое упоминание о линзах можно найти в древнегреческой пьесе Аристофана «Облака» (424 до н. э.), где с помощью выпуклого стекла и солнечного света добывали огонь.
Из произведений Плиния Старшего (23 — 79) следует, что такой способ разжигания огня был известен и в Римской империи — там также описан, возможно, первый случай применения линз для коррекции зрения — известно, что Нерон смотрел гладиаторские бои через вогнутый изумруд для исправления близорукости.
Сенека (3 до н. э. — 65) описал увеличительный эффект, который даёт стеклянный шар, заполненный водой.
Арабский математик Альхазен (965—1038) написал первый значительный трактат по оптике, описывающий, как хрусталик глаза создаёт изображение на сетчатке. Линзы получили широкое использование лишь с появлением очков примерно в 1280-х годах в Италии.
 Растение, видимое через двояковыпуклую линзу
Растение, видимое через двояковыпуклую линзуХарактеристики простых линз
В зависимости от форм различают собирающие (положительные) и рассеивающие (отрицательные) линзы. К группе собирательных линз обычно относят линзы, у которых середина толще их краёв, а к группе рассеивающих — линзы, края которых толще середины. Следует отметить, что это верно только если показатель преломления у материала линзы больше, чем у окружающей среды. Если показатель преломления линзы меньше, ситуация будет обратной. Например пузырёк воздуха в воде — двояковыпуклая рассеивающая линза.
Линзы характеризуются, как правило, своей оптической силой (измеряется в диоптриях), или фокусным расстоянием.
Для построения оптических приборов с исправленной оптической аберрацией (прежде всего — хроматической, обусловленной дисперсией света, — ахроматы и апохроматы) важны и иные свойства линз и их материалов, например, коэффициент преломления, коэффициент дисперсии, коэффициент пропускания материала в выбранном оптическом диапазоне.
Иногда линзы/линзовые оптические системы (рефракторы) специально рассчитываются на использование в средах с относительно высоким коэффициентом преломления (см. иммерсионный микроскоп, иммерсионные жидкости).
Виды линз:
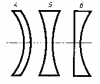
Собирающие:
1 — двояковыпуклая
2 — плоско-выпуклая
3 — вогнуто-выпуклая (положительный(выпуклый) мениск)
Рассеивающие:
4 — двояковогнутая
5 — плоско-вогнутая
6 — выпукло-вогнутая (отрицательный(вогнутый) мениск)

Выпукло-вогнутая линза называется мениском и может быть собирательной (утолщается к середине), рассеивающей (утолщается к краям) или телескопической (фокусное расстояние равно бесконечности). Так, например линзы очков для близоруких — как правило, отрицательные мениски.
Вопреки распространённому заблуждению, оптическая сила мениска с одинаковыми радиусами не равно нулю, а положительна, и зависит от показателя преломления стекла и от толщины линзы. Мениск, центры кривизны поверхностей которого находятся в одной точке называется концентрической линзой (оптическая сила всегда отрицательна).
Отличительным свойством собирательной линзы является способность собирать падающие на её поверхность лучи в одной точке, расположенной по другую сторону линзы.
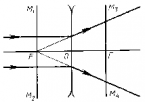
Основные элементы линзы: NN — оптическая ось — прямая линия, проходящая через центры сферических поверхностей, ограничивающих линзу; O — оптический центр — точка, которая у двояковыпуклых или двояковогнутых (с одинаковыми радиусами поверхностей) линз находится на оптической оси внутри линзы (в её центре).Примечание. Ход лучей показан, как в идеализированной (тонкой) линзе, без указания на преломление на реальной границе раздела сред. Дополнительно показан несколько утрированный образ двояковыпуклой линзы
Если на некотором расстоянии перед собирательной линзой поместить светящуюся точку S, то луч света, направленный по оси, пройдёт через линзу не преломившись, а лучи, проходящие не через центр, будут преломляться в сторону оптической оси и пересекутся на ней в некоторой точке F, которая и будет изображением точки S. Эта точка носит название сопряжённого фокуса, или просто фокуса.
Если на линзу будет падать свет от очень удалённого источника, лучи которого можно представить идущими параллельным пучком, то по выходе из неё лучи преломятся под бо́льшим углом и точка F переместится на оптической оси ближе к линзе. При данных условиях точка пересечения лучей, вышедших из линзы, называется фокусом F’, а расстояние от центра линзы до фокуса — фокусным расстоянием.
Лучи, падающие на рассеивающую линзу, по выходе из неё будут преломляться в сторону краёв линзы, то есть рассеиваться. Если эти лучи продолжить в обратном направлении так, как показано на рисунке пунктирной линией, то они сойдутся в одной точке F, которая и будет фокусом этой линзы. Этот фокус будет мнимым.
Мнимый фокус рассеивающей линзы

Сказанное о фокусе на оптической оси в равной степени относится и к тем случаям, когда изображение точки находится на наклонной линии, проходящей через центр линзы под углом к оптической оси. Плоскость, перпендикулярная оптической оси, расположенная в фокусе линзы, называется фокальной плоскостью.
Собирательные линзы могут быть направлены к предмету любой стороной, вследствие чего лучи по прохождении через линзу могут собираться как с одной, так и с другой её стороны. Таким образом, линза имеет два фокуса — передний и задний. Расположены они на оптической оси по обе стороны линзы на фокусном расстоянии от главных точек линзы.
Ход лучей в тонкой линзе
Линза, для которой толщина принята равной нулю, в оптике называется «тонкой». Для такой линзы показывают не две главных плоскости, а одну, в которой как бы сливаются вместе передняя и задняя.
Рассмотрим построение хода луча произвольного направления в тонкой собирающей линзе. Для этого воспользуемся двумя свойствами тонкой линзы:
- Луч, прошедший через оптический центр линзы, не меняет своего направления;
- Параллельные лучи, проходящие через линзу, сходятся в фокальной плоскости.
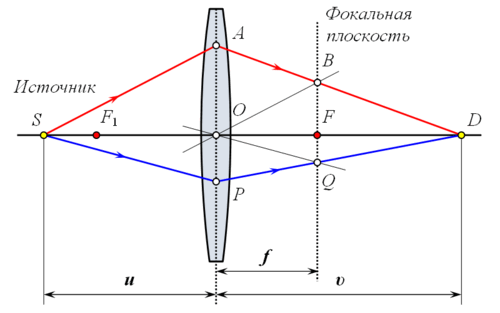
Рассмотрим луч SA произвольного направления, падающий на линзу в точке A. Построим линию его распространения после преломления в линзе. Для этого построим луч OB, параллельный SA и проходящий через оптический центр O линзы. По первому свойству линзы луч OB не изменит своего направления и пересечёт фокальную плоскость в точке B. По второму свойству линзы параллельный ему луч SA после преломления должен пересечь фокальную плоскость в той же точке. Таким образом, после прохождения через линзу луч SA пойдёт по пути AB.
Аналогичным образом можно построить другие лучи, например луч SPQ.
Обозначим расстояние SO от линзы до источника света через u, расстояние OD от линзы до точки фокусировки лучей через v, фокусное расстояние OF через f. Выведем формулу, связывающую эти величины.
Рассмотрим две пары подобных треугольников: 1) SOA и OFB; 2) DOA и DFB. Запишем пропорции
Разделив первую пропорцию на вторую, получим
После деления обеих частей выражения на v и перегруппировки членов, приходим к окончательной формуле
где — фокусное расстояние тонкой линзы.
Ход лучей в системе линз
Ход лучей в системе линз строится теми же методами, что и для одиночной линзы.
Рассмотрим систему из двух линз, одна из которых имеет фокусное расстояние OF, а вторая O2F2. Строим путь SAB для первой линзы и продолжаем отрезок AB до вхождения во вторую линзу в точке C.
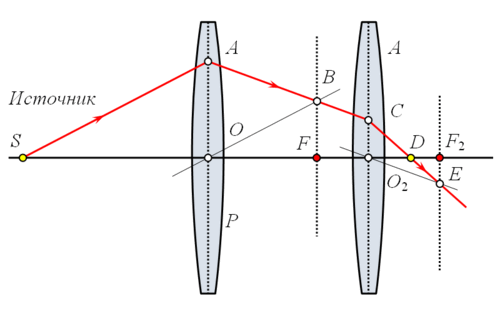
Из точки O2 строим луч O2E, параллельный AB. При пересечении с фокальной плоскостью второй линзы этот луч даст точку E. Согласно второму свойству тонкой линзы луч AB после прохождения через вторую линзу пойдёт по пути CE. Пересечение этой линии с оптической осью второй линзы даст точку D, где сфокусируются все лучи, вышедшие из источника S и прошедшие через обе линзы.
Построение изображения тонкой собирающей линзой
При изложении характеристики линз был рассмотрен принцип построения изображения светящейся точки в фокусе линзы. Лучи, падающие на линзу слева, проходят через её задний фокус, а падающие справа — через передний фокус. Следует учесть, что у рассеивающих линз, наоборот, задний фокус расположен спереди линзы, а передний позади.
Построение линзой изображения предметов, имеющих определённую форму и размеры, получается следующим образом: допустим, линия AB представляет собой объект, находящийся на некотором расстоянии от линзы, значительно превышающем её фокусное расстояние. От каждой точки предмета через линзу пройдёт бесчисленное количество лучей, из которых, для наглядности, на рисунке схематически изображён ход только трёх лучей.
Три луча, исходящие из точки A, пройдут через линзу и пересекутся в соответствующих точках схода на A1B1, образуя изображение. Полученное изображение является действительным и перевёрнутым.
В данном случае изображение получено в сопряжённом фокусе в некоторой фокальной плоскости FF, несколько удалённой от главной фокальной плоскости F’F’, проходящей параллельно ей через главный фокус.
Далее приведены различные случаи построения изображений предмета, помещённого на различных расстояниях от линзы.
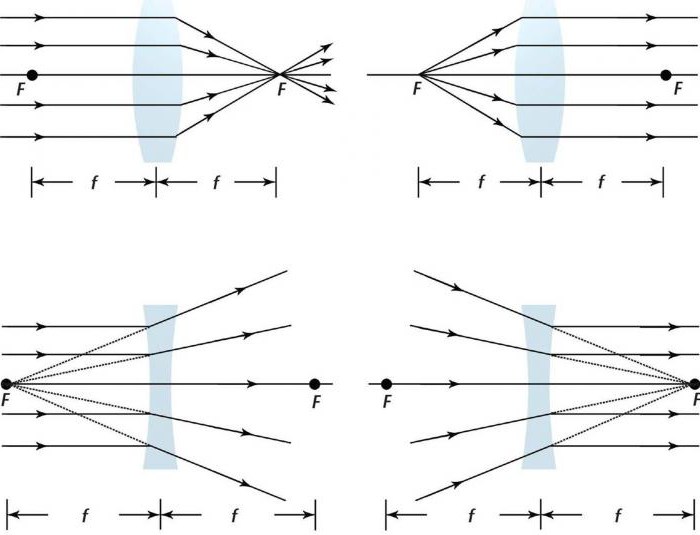
Если предмет находится на бесконечно далёком от линзы расстоянии, то его изображение получается в заднем фокусе линзы F’ действительным, перевёрнутым и уменьшенным до подобия точки.
Если предмет приближён к линзе и находится на расстоянии, превышающем двойное фокусное расстояние линзы, то изображение его будет действительным, перевёрнутым и уменьшенным и расположится за главным фокусом на отрезке между ним и двойным фокусным расстоянием.
Если предмет помещён на двойном фокусном расстоянии от линзы, то полученное изображение находится по другую сторону линзы на двойном фокусном расстоянии от неё. Изображение получается действительным, перевёрнутым и равным по величине предмету.
Если предмет помещён между передним фокусом и двойным фокусным расстоянием, то изображение будет получено за двойным фокусным расстоянием и будет действительным, перевёрнутым и увеличенным.
Если предмет находится в плоскости переднего главного фокуса линзы, то лучи, пройдя через линзу, пойдут параллельно, и изображение может получиться лишь в бесконечности.
Если предмет поместить на расстоянии, меньшем главного фокусного расстояния, то лучи выйдут из линзы расходящимся пучком, нигде не пересекаясь. Изображение при этом получается мнимое, прямое и увеличенное, т. е. в данном случае линза работает как лупа.
Нетрудно заметить, что при приближении предмета из бесконечности к переднему фокусу линзы изображение удаляется от заднего фокуса и по достижении предметом плоскости переднего фокуса оказывается в бесконечности от него.
Эта закономерность имеет большое значение в практике различных видов фотографических работ, поэтому для определения зависимости между расстоянием от предмета до линзы и от линзы до плоскости изображения необходимо знать основную формулу линзы.
Формула тонкой линзы
Расстояния от точки предмета до центра линзы и от точки изображения до центра линзы называются сопряжёнными фокусными расстояниями.
Эти величины находятся в зависимости между собой и определяются формулой, называемой формулой тонкой линзы (открытой Исааком Барроу):
где — расстояние от линзы до предмета; — расстояние от линзы до изображения; — главное фокусное расстояние линзы. В случае толстой линзы формула остаётся без изменения с той лишь разницей, что расстояния отсчитываются не от центра линзы, а от главных плоскостей.
Для нахождения той или иной неизвестной величины при двух известных пользуются следующими уравнениями:
Следует отметить, что знаки величин , , выбираются исходя из следующих соображений — для действительного изображения от действительного предмета в собирающей линзе — все эти величины положительны. Если изображение мнимое — расстояние до него принимается отрицательным, если предмет мнимый — расстояние до него отрицательно, если линза рассеивающая — фокусное расстояние отрицательно.
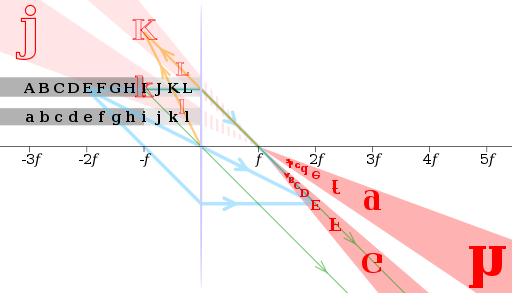
Изображения чёрных букв через тонкую выпуклую линзу с фокусным расстоянием f (отображаются красным цветом). Показаны лучи для букв E, I и K (синим, зеленым и оранжевым соответственно). Размеры реального и перевернутого изображения E (2f) одинаковы. Образ I (f) — в бесконечности. К (при f/2) имеет двойной размер виртуального и прямого изображения
Линейное увеличение
Линейным увеличением (для рисунка из предыдущего раздела) называется отношение размеров изображения к соответствующим размерам предмета. Это отношение может быть также выражено дробью , где — расстояние от линзы до изображения; — расстояние от линзы до предмета.
Здесь есть коэффициент линейного увеличения, т. е. число, показывающее во сколько раз линейные размеры изображения меньше(больше) действительных линейных размеров предмета.
В практике вычислений гораздо удобнее это соотношение выражать в значениях или , где — фокусное расстояние линзы.
.
Расчёт фокусного расстояния и оптической силы линзы
Значение фокусного расстояния для линзы может быть рассчитано по следующей формуле:
- , где
— коэффициент преломления материала линзы, — коэффициент преломления среды, окружающей линзу,
— расстояние между сферическими поверхностями линзы вдоль оптической оси, также известное как толщина линзы,
— радиус кривизны поверхности, которая ближе к источнику света (дальше от фокальной плоскости),
— радиус кривизны поверхности, которая дальше от источника света (ближе к фокальной плоскости),
Для в этой формуле, знак радиуса положителен, если поверхность выпуклая, и отрицателен, если вогнутая. Для наоборот — положителен, если вогнутая, и отрицателен, если выпуклая [1]. Если пренебрежительно мало, относительно её фокусного расстояния, то такая линза называется тонкой, и её фокусное расстояние можно найти как:
(Эту формулу также называют формулой тонкой линзы.) Величина фокусного расстояния положительна для собирающих линз, и отрицательна для рассеивающих. Величина называется оптической силой линзы. Оптическая сила линзы измеряется в диоптриях, единицами измерения которых являются м−1.
Указанные формулы могут быть получены аккуратным рассмотрением процесса построения изображения в линзе с использованием закона Снелла, если перейти от общих тригонометрических формул к параксиальному приближению. Кроме того, для вывода формулы тонкой линзы удобно заменить её треугольной призмой и затем использовать формулу угла отклонения этой призмы[1].
Линзы симметричны, то есть они имеют одинаковое фокусное расстояние независимо от направления света — слева или справа, что, однако, не относится к другим характеристикам, например, аберрациям, величина которых зависит от того, какой стороной линза повёрнута к свету.
Комбинация нескольких линз (центрированная система)
Линзы могут комбинироваться друг с другом для построения сложных оптических систем. Оптическая сила системы из двух линз может быть найдена как простая сумма оптических сил каждой линзы (при условии, что обе линзы можно считать тонкими и они расположены вплотную друг к другу на одной оси):
- .
Если линзы расположены на некотором расстоянии друг от друга и их оси совпадают (система из произвольного числа линз, обладающих таким свойством, называется центрированной системой), то их общую оптическую силу с достаточной степенью точности можно найти из следующего выражения:
- ,
где — расстояние между главными плоскостями линз.
Недостатки простой линзы
В современной фотоаппаратуре к качеству изображения предъявляются высокие требования.
Изображение, даваемое простой линзой, в силу целого ряда недостатков не удовлетворяет этим требованиям. Устранение большинства недостатков достигается соответствующим подбором ряда линз в центрированную оптическую систему — объектив. Недостатки оптических систем называются аберрациями, которые делятся на следующие виды:
Линзы со специальными свойствами
Линзы из органических полимеров
Полимеры дают возможность создавать недорогие асферические линзы с помощью литья.
Линзы контактныеВ области офтальмологии созданы мягкие контактные линзы. Их производство основано на применении материалов, имеющих бифазную природу, сочетающих фрагменты кремний-органического или кремний-фторорганического полимера силикона и гидрофильного полимера гидрогеля. Работа в течение более 20 лет привела к созданию в конце 90-х годов силикон-гидрогелевых линз, которые благодаря сочетанию гидрофильных свойств и высокой кислородопроницаемости могут непрерывно использоваться в течение 30 дней круглосуточно.[2]
Линзы из кварца
Кварцевое стекло — переплавленный чистый кремнезём с незначительными (около 0,01 %) добавками Al2О3, СаО и MgO. Оно отличается высокой термостойкостью и инертностью ко многим химическим реактивам за исключением плавиковой кислоты.
Прозрачное кварцевое стекло хорошо пропускает ультрафиолетовые и видимые лучи света.
Линзы из кремния
Кремний сочетает сверхвысокую дисперсию с самым большим абсолютным значением коэффициента преломления n=3,4 в диапазоне ИК-излучения и полной непрозрачностью в видимом диапазоне спектра.[3]
Кроме того, именно свойства кремния и новейшие технологии его обработки позволили создать линзы для рентгеновского диапазона электромагнитных волн.
Применение линз
Линзы являются универсальным оптическим элементом большинства оптических систем.
Традиционное применение линз — бинокли, телескопы, оптические прицелы, теодолиты, микроскопы и фотовидеотехника. Одиночные собирающие линзы используются как увеличительные стёкла.
Другая важная сфера применения линз офтальмология, где без них невозможно исправление недостатков зрения — близорукости, дальнозоркости, неправильной аккомодации, астигматизма и других заболеваний. Линзы используют в таких приспособлениях, как очки и контактные линзы.
В радиоастрономии и радарах часто используются диэлектрические линзы, собирающие поток радиоволн в приёмную антенну, либо фокусирующие на цели.
В конструкции плутониевых ядерных бомб для преобразования сферической расходящейся ударной волны от точечного источника (детонатора) в сферическую сходящуюся применялись линзовые системы, изготовленные из взрывчатки с разной скоростью детонации (то есть с разным коэффициентом преломления).
См. также
Примечания
Ссылки
Литература
- Краткий фотографический справочник. Под общей редакцией д.т. н. Пуськова В. В., изд. 2-е, М., Искусство, 1953.
- Оптика, Г. С. Ландсберг, изд. 5-ое, М., Наука, 1976.
- Политехнический словарь, глав.ред. А. Ю. Ишлинский, изд. 3-е, М., Советская Энциклопедия, 1989.
- Линза // Фотокинотехника: Энциклопедия / Главный редактор Е. А. Иофис. — М.: Советская энциклопедия, 1981.
виды линз (физика). Виды собирающих, оптических, рассеивающих линз. Как определить вид линзы?
Линзы, как правило, имеют сферическую или близкую к сферической поверхность. Они могут быть вогнутыми, выпуклыми или плоскими (радиус равен бесконечности). Обладают двумя поверхностями, через которые проходит свет. Они могут сочетаться по-разному, образуя различные виды линз (фото приведено далее в статье):
- Если обе поверхности выпуклые (изогнуты наружу), центральная часть толще, чем по краям.
- Линза с выпуклой и вогнутой сферами называется мениском.
- Линза с одной плоской поверхностью носит название плоско-вогнутой или плоско-выпуклой, в зависимости от характера другой сферы.
Как определить вид линзы? Остановимся на этом подробнее.
Собирающие линзы: виды линз
Независимо от сочетания поверхностей, если их толщина в центральной части больше, чем по краям, они называются собирающими. Имеют положительное фокусное расстояние. Различают следующие виды собирающих линз:
- плоско-выпуклые,
- двояковыпуклые,
- вогнуто-выпуклые (мениск).
Их еще называют «положительными».
Рассеивающие линзы: виды линз
Если их толщина в центре тоньше, чем по краям, то они носят название рассеивающих. Имеют отрицательное фокусное расстояние. Существуют такие виды рассеивающих линз:
- плоско-вогнутые,
- двояковогнутые,
- выпукло-вогнутые (мениск).
Их еще называют «отрицательными».

Базовые понятия
Лучи от точечного источника расходятся из одной точки. Их называют пучком. Когда пучок входит в линзу, каждый луч преломляется, изменяя свое направление. По этой причине пучок может выйти из линзы в большей или меньшей степени расходящимся.
Некоторые виды оптических линз изменяют направление лучей настолько, что они сходятся в одной точке. Если источник света расположен, по меньшей мере, на фокусном расстоянии, то пучок сходится в точке, удаленной, по крайней мере, на ту же дистанцию.
Действительные и мнимые изображения
Точечный источник света называется действительным объектом, а точка сходимости пучка лучей, выходящего из линзы, является его действительным изображением.
Важное значение имеет массив точечных источников, распределенных на, как правило, плоской поверхности. Примером может служить рисунок на матовом стекле, подсвеченный сзади. Другим примером является диафильм, освещенный сзади так, чтобы свет от него проходил через линзу, многократно увеличивающую изображение на плоском экране.
В этих случаях говорят о плоскости. Точки на плоскости изображения 1:1 соответствуют точкам на плоскости объекта. То же относится и к геометрическим фигурам, хотя полученная картинка может быть перевернутой по отношению к объекту сверху вниз или слева направо.
Схождение лучей в одной точке создает действительное изображение, а расхождение – мнимое. Когда оно четко очерчено на экране – оно действительное. Если же изображение можно наблюдать, только посмотрев через линзу в сторону источника света, то оно называется мнимым. Отражение в зеркале – мнимое. Картину, которую можно увидеть через телескоп – тоже. Но проекция объектива камеры на пленку дает действительное изображение.
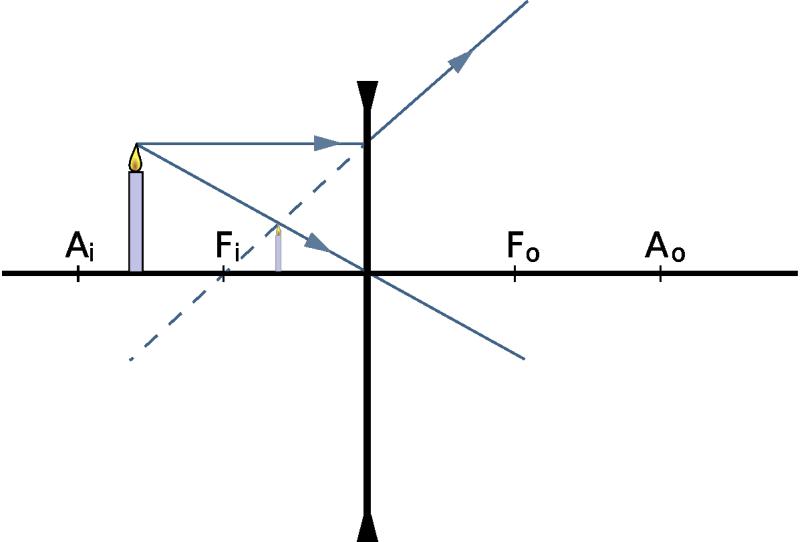
Фокусное расстояние
Фокус линзы можно найти, пропустив через нее пучок параллельных лучей. Точка, в которой они сойдутся, и будет ее фокусом F. Расстояние от фокальной точки до объектива называют его фокусным расстоянием f. Параллельные лучи можно пропустить и с другой стороны и таким образом найти F с двух сторон. Каждая линза обладает двумя F и двумя f. Если она относительно тонка по сравнению с ее фокусными расстояниями, то последние приблизительно равны.
Дивергенция и конвергенция
Положительным фокусным расстоянием характеризуются собирающие линзы. Виды линз данного типа (плоско-выпуклые, двояковыпуклые, мениск) сводят лучи, выходящие из них, больше, чем они были сведены до этого. Собирающие объективы могут формировать как действительное, так и мнимое изображение. Первое формируется только в случае, если расстояние от линзы до объекта превышает фокусное.
Отрицательным фокусным расстоянием характеризуются рассеивающие линзы. Виды линз этого типа (плоско-вогнутые, двояковогнутые, мениск) разводят лучи больше, чем они были разведены до попадания на их поверхность. Рассеивающие линзы создают мнимое изображение. И только когда сходимость падающих лучей значительна (они сходятся где-то между линзой и фокальной точкой на противоположной стороне), образованные лучи все еще могут сходиться, образуя действительное изображение.
Важные различия
Следует быть очень внимательными, чтобы отличать схождение или расхождение лучей от конвергенции или дивергенции линзы. Виды линз и пучков света могут не совпадать. Лучи, связанные с объектом или точкой изображения, называются расходящимися, если они «разбегаются», и сходящимся, если они «собираются» вместе. В любой коаксиальной оптической системе оптическая ось представляет собой путь лучей. Луч вдоль этой оси проходит без какого-либо изменения направления движения из-за преломления. Это, по сути, хорошее определение оптической оси.
Луч, который с расстоянием отдаляется от оптической оси, называется расходящимся. А тот, который к ней становится ближе, носит название сходящегося. Лучи, параллельные оптической оси, имеют нулевое схождение или расхождение. Таким образом, когда говорят о схождении или расхождении одного луча, его соотносят с оптической осью.
Некоторые виды линз, физика которых такова, что луч отклоняется в большей степени к оптической оси, являются собирающими. В них сходящиеся лучи сближаются еще больше, а расходящиеся отдаляются меньше. Они даже в состоянии, если их сила достаточна для этого, сделать пучок параллельным или даже сходящимся. Аналогично рассеивающая линза может развести расходящиеся лучи еще больше, а сходящиеся – сделать параллельными или расходящимися.

Увеличительные стекла
Линза с двумя выпуклыми поверхностями толще в центре, чем по краям, и может использоваться в качестве простого увеличительного стекла или лупы. При этом наблюдатель смотрите через нее на мнимое, увеличенное изображение. Объектив камеры, однако, формирует на пленке или сенсоре действительное, как правило, уменьшенное в размерах по сравнению с объектом.
Очки
Способность линзы изменять сходимость света называется ее силой. Выражается она в диоптриях D = 1 / f, где f – фокусное расстояние в метрах.
У линзы с силой 5 диоптрий f = 20 см. Именно диоптрии указывает окулист, выписывая рецепт очков. Скажем, он записал 5,2 диоптрий. В мастерской возьмут готовую заготовку в 5 диоптрий, полученную на заводе-изготовителе, и отшлифуют немного одну поверхность, чтобы добавить 0,2 диоптрии. Принцип состоит в том, что для тонких линз, в которых две сферы расположены близко друг к другу, соблюдается правило, согласно которому общая их сила равна сумме диоптрий каждой: D = D1 + D2.

Труба Галилея
Во времена Галилея (начало XVII века), очки в Европе были широко доступны. Они, как правило, изготавливались в Голландии и распространялись уличными торговцами. Галилео слышал, что кто-то в Нидерландах поместил два вида линз в трубку, чтобы удаленные объекты казались больше. Он использовал длиннофокусный собирающий объектив в одном конце трубки, и короткофокусный рассеивающий окуляр на другом конце. Если фокусное расстояние объектива равно fo и окуляра fe, то дистанция между ними должна быть fo-fe, а сила (угловое увеличение) fo/fe. Такая схема называется трубой Галилея.
Телескоп обладает увеличением 5 или 6 крат, сравнимым с современными ручными биноклями. Этого достаточно для многих захватывающих астрономических наблюдений. Можно без проблем увидеть лунные кратеры, четыре луны Юпитера, кольца Сатурна, фазы Венеры, туманности и звездные скопления, а также слабые звезды в Млечном Пути.

Телескоп Кеплера
Кеплер услышал обо всем этом (он и Галилей вели переписку) и построил еще один вид телескопа с двумя собирающими линзами. Та, у которой большое фокусное расстояние, является объективом, а та, у которой оно меньше – окуляром. Расстояние между ними равно fo + fe, а угловое увеличение составляет fo/fe. Этот кеплеровский (или астрономический) телескоп создает перевернутое изображение, но для звезд или луны это не имеет значения. Данная схема обеспечила более равномерное освещение поля зрения, чем телескоп Галилея, и была более удобна в использовании, так как позволяла держать глаза в фиксированном положении и видеть все поле зрения от края до края. Устройство позволяло достичь более высокого увеличения, чем труба Галилея, без серьезного ухудшения качества.
Оба телескопа страдают от сферической аберрации, в результате чего изображения не полностью сфокусированы, и хроматической аберрации, создающей цветные ореолы. Кеплер (и Ньютон) считал, что эти дефекты невозможно преодолеть. Они не предполагали, что возможны ахроматические виды линз, физика которых станет известна лишь в XIX веке.

Зеркальные телескопы
Грегори предположил, что в качестве объективов телескопов можно использовать зеркала, так как в них отсутствует цветная окантовка. Ньютон воспользовался этой идеей и создал ньютоновскую форму телескопа из вогнутого посеребренного зеркала и положительного окуляра. Он передал образец Королевскому обществу, где тот находится и по сей день.
Однолинзовый телескоп может проецировать изображение на экран или фотопленку. Для должного увеличения требуется положительная линза с большим фокусным расстоянием, скажем, 0,5 м, 1 м или много метров. Такая компоновка часто используется в астрономической фотографии. Людям, незнакомым с оптикой, может показаться парадоксальной ситуация, когда более слабая длиннофокусная линза дает большее увеличение.
Сферы
Высказывались предположения, что древние культуры, возможно, имели телескопы, потому что они делали маленькие стеклянные шарики. Проблема состоит в том, что неизвестно, для чего они использовались, и они, конечно, не могли бы лечь в основу хорошего телескопа. Шарики могли применяться для увеличения мелких объектов, но качество при этом вряд ли было удовлетворительным.
Фокусное расстояние идеальной стеклянной сферы очень короткое и формирует действительное изображение очень близко от сферы. Кроме того, аберрации (геометрические искажения) значительные. Проблема кроется в расстоянии между двумя поверхностями.
Однако если сделать глубокую экваториальную канавку, чтобы блокировать лучи, которые вызывают дефекты изображения, она превращается из очень посредственной лупы в прекрасную. Такое решение приписывается Коддингтону, а увеличитель его имени можно приобрести сегодня в виде небольших ручных луп для изучения очень маленьких объектов. Но доказательств того, что это было сделано до 19-го века, нет.
Линза. Формула тонкой линзы (Зеленин С.В.). Видеоурок. Физика 11 Класс
Как вы уже знаете, законы преломления и отражения определяют поведение луча при его падении на границу раздела двух прозрачных сред. При этом граница раздела считалась плоской. Однако в жизни нам чаще приходится сталкиваться с криволинейными поверхностями. Одним из представителей таких границ является сфера.
Такой поверхностью, даже двумя, обладает линза. Она представляет собой один из самых важных оптических приборов.
Линзу можно представить как фигуру, образованную пересечением двух сфер. У некоторых линз одна из боковых поверхностей плоская. Эту поверхность можно представить как сферу с бесконечно большим радиусом. Конечно же, две сферы могут пересекаться различным способом (Рис. 1).
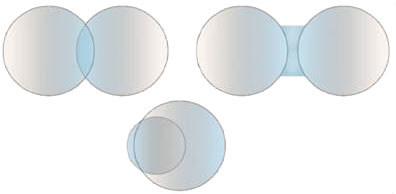
Рис. 1. Способы пересечения двух сфер.
Пересекая две сферы, можно вывести все виды линз (Рис. 2).
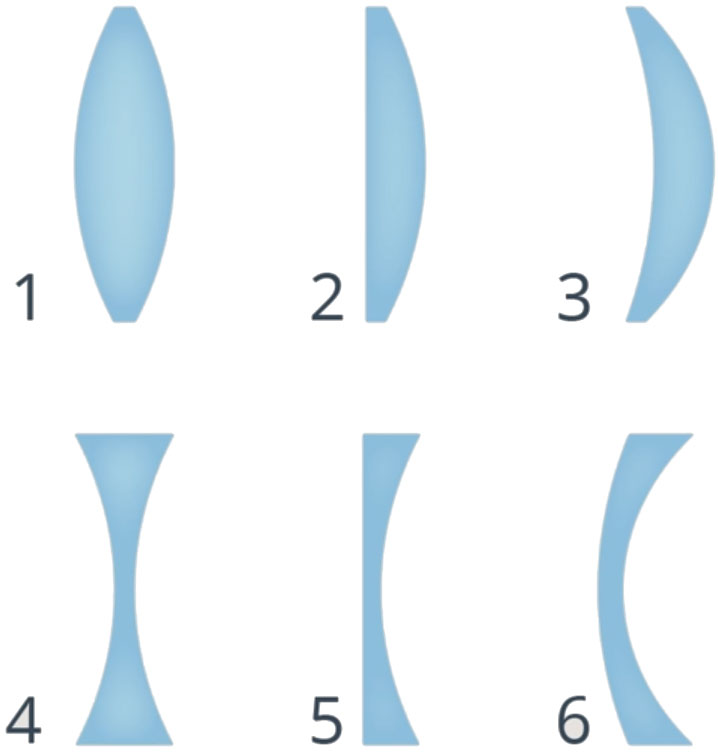
Рис. 2. Виды линз. Собирающие: 1. Двояковыпуклая; 2. Плоско-выпуклая; 3. Вогнуто-выпуклая. Рассеивающие: 4. Двояковогнутая; 5. Плоско-вогнутая; 6. Выпукло-вогнутая
Для первоначального изучения особенности прохождения света через линзы нам будет достаточно рассмотреть первый тип. Рассмотрим двояковыпуклую линзу, ограниченную двумя сферическими преломляющими поверхностями. Эти поверхности обозначим, как 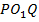 и
и 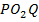 . Центр первой сферы лежит в точке
. Центр первой сферы лежит в точке 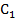 , второй – в точке
, второй – в точке 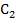
(Рис. 3).
На рисунке для ясности изображена линза с видимой толщиной. В действительности мы будем предполагать, что все рассматриваемые линзы очень тонкие.
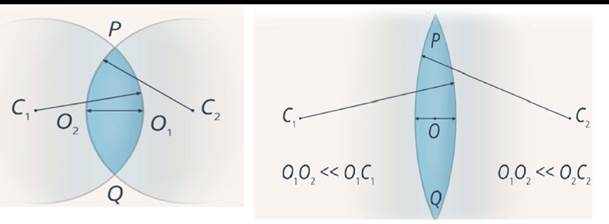
Рис. 3, рис. 4. Двояковыпуклая линза
В таком случае точки  и
и  можно считать практически совпадающими и обозначить одной точкой
можно считать практически совпадающими и обозначить одной точкой  . Точка
. Точка 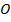 называется оптическим центром линзы. Всякая прямая, проходящая через оптический центр линзы, называется оптической осью линзы. Та из осей, которая проходит через центры обеих преломляющих поверхностей, называется главной оптической осью. Все остальные – побочные оптические оси.
называется оптическим центром линзы. Всякая прямая, проходящая через оптический центр линзы, называется оптической осью линзы. Та из осей, которая проходит через центры обеих преломляющих поверхностей, называется главной оптической осью. Все остальные – побочные оптические оси.
Луч, идущий по какой-либо из оптических осей, проходя через линзу, практически не меняет своего направления. Действительно, для лучей, идущих вдоль оптической оси, участки обеих поверхностей линзы можно считать параллельными, ведь толщину линзы мы считаем малой (Рис. 5).
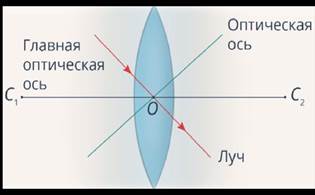
Рис. 5. Элементы линзы
При прохождении луча через плоскопараллельную пластинку световой луч претерпевает лишь параллельное смещение. Но смещением луча в очень тонкой пластинке можно пренебречь.
Если на линзу падает луч, не совпадающий ни с одной оптической осью, то он испытывает двойное преломление. Сначала на первой поверхности, ограничивающей линзу, а затем на второй, при этом луч отклоняется от своего первоначального направления.
Если через линзу пропустить пучок лучей, параллельных главной оптической оси и находящихся от нее на малом расстоянии, то после преломления все лучи пучка соберутся в одной точке, ее называют главным фокусом линзы (Рис. 6).
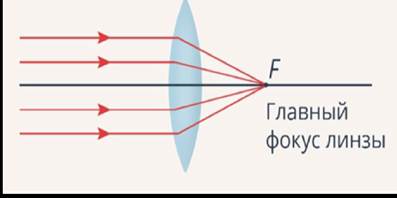
Рис. 6. Главный фокус линзы
Благодаря описанному свойству двояковыпуклую линзу, если она изготовлена из материала с относительным показателем преломления большим единицы, называют собирающей.
Таким образом, мы можем выделить два утверждения касательно собирающей линзы.
1. Луч, идущий вдоль одной из оптических осей собирающей линзы, при прохождении через нее не меняет своего направления.
2. Луч, который идет параллельно главной оптической оси и на небольшом расстоянии от нее, после преломления проходит через главный фокус линзы.
Теперь сделанные утверждения нужно дополнить выводом о том, как будет вести себя луч, который не проходит через оптический центр и не параллелен главной оптической оси. Для этого введем следующее определение.
Фокальной плоскостью линзы называется плоскость, которая проходит через главный фокус и перпендикулярна главной оптической оси линзы. Все точки этой плоскости, за исключением главного фокуса, называют побочными фокусами линзы.
Для чего нам нужна данная плоскость? Оказывается, если на линзу падает пучок света параллельный побочной оси, то после преломления в линзе этот лучок соберется в одном из побочных фокусов линзы.
Тогда возникает вопрос: как же найти побочный фокус, в котором соберется этот пучок (Рис. 7)?
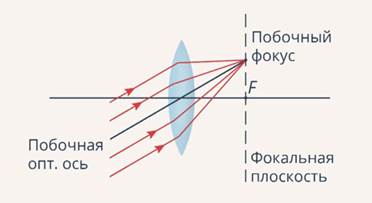
Рис. 7. Нахождение побочного фокуса
На рисунке показан этот побочный фокус, он является пересечением побочной оптической оси, параллельной лучам пучка, с фокальной плоскостью. Попробуем обосновать, почему именно таким способом лучи преломляются в линзе (конкретно в двояковыпуклой).
Данную линзу можно представить как совокупность призм, склеенных в одно целое. Мы знаем, что всякая прима, относительный показатель преломления которой больше единицы, отклоняет луч в сторону своего основания. Поскольку мы имеем дело с набором линз, преломляющие углы которых монотонно уменьшаются при удалении от главной оптической оси, то и углы, на которые эти призмы преломляют лучи параллельного пучка, будут различными.
Чем дальше луч расположен от главной оптической оси, тем больше угол его отклонения. В конечном итоге все лучи попадают в фокус (Рис. 8).
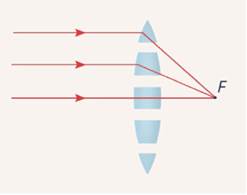
Рис. 8. Преломление пучка света
Мы предполагали, что пучок лучей падает на линзу слева направо, но ничего не изменится, если на линзу направить идентичный пучок лучей справа налево. Этот пучок лучей, направленный параллельно главной оптической оси, вновь соберется в одной точке  во втором фокусе линзы, на некотором расстоянии от ее оптического центра.
во втором фокусе линзы, на некотором расстоянии от ее оптического центра.
Фокус  обычно называют передним фокусом, а
обычно называют передним фокусом, а  – задним фокусом линзы. Соответственно, расстояние до
– задним фокусом линзы. Соответственно, расстояние до 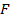 называют передним фокусным расстоянием, а до
называют передним фокусным расстоянием, а до 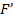 – задним фокусным расстоянием.
– задним фокусным расстоянием.
Рассмотрим, от чего может зависеть фокусное расстояние линзы. Совершенно ясно, что если любой луч, идущий параллельно главной оптической оси, попадает в главный фокус, то фокусное расстояние не зависит от параметров луча. Более общим утверждением будет такое: фокусное расстояние вообще не зависит от параметров источника света, но с той оговоркой, что мы рассматриваем лучи, близкие к главной оптической оси. От чего же тогда может зависеть фокусное расстояние? Во-первых, от материала, из которого изготовлена линза, во-вторых, оно зависит от кривизны поверхностей, ограничивающих линзу. Выражение, определяющее такую зависимость, называется формулой шлифовщика:
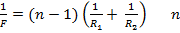 – относительный показатель преломления
– относительный показатель преломления
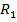 ,
, 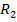 – радиусы боковых поверхностей линзы
– радиусы боковых поверхностей линзы
Еще одной важной характеристикой линзы является ее оптическая сила  .
.
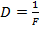
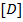 = дптр =
= дптр = 
Понятно, что чем больше фокусное расстояние, тем оптическая сила меньше.
Теперь рассмотрим вопрос практического использования линзы. В первую очередь, для этого нам нужно изобрести алгоритмы, которые позволяют нам строить изображения, даваемые двояковыпуклой линзой.
Для начала введем обозначения, тонкую двояко-выпуклую линзу будем изображать отрезком со стрелочками, главная оптическая ось перпендикулярна линзе и проходит через ее оптический центр  , главные фокусы линзы находятся на одинаковом расстоянии от оптического центра, по обе стороны. Фокусное расстояние, как и саму точку фокуса, обозначим
, главные фокусы линзы находятся на одинаковом расстоянии от оптического центра, по обе стороны. Фокусное расстояние, как и саму точку фокуса, обозначим 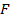 . Предмет, изображение которого нам нужно получить, обозначим стрелочкой. (Пока рассмотрим случай, когда предмет расположен перпендикулярно главной оптической оси.)
. Предмет, изображение которого нам нужно получить, обозначим стрелочкой. (Пока рассмотрим случай, когда предмет расположен перпендикулярно главной оптической оси.)
Для получения изображения предмета нам достаточно построить изображения концов отрезка, более того, если один из концов отрезка лежит на главной оптической оси, то достаточно построить лишь изображение второго конца отрезка, который не принадлежит оси, затем опустить перпендикуляр на главную оптическую ось и получить изображение всего предмета.
Для этого, как уже говорилось, проведем два луча из верхнего конца предмета, найдем точку пересечения этих лучей после преломления в линзе. В качестве первого луча возьмем тот, что проходит через оптический центр, он не преломляется, а в качестве второго – луч, идущий параллельно главной оптической оси. Второй луч после преломления идет в фокус.
Получаем изображение точки, опускаем перпендикуляр на ось, соединяем полученные точки и получаем изображение предмета (Рис. 9).
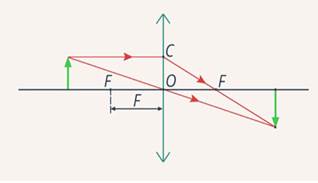
Рис. 9. Построение изображения предмета
Обозначим через 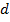 расстояние от предмета до линзы и
расстояние от предмета до линзы и 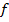 от изображения до линзы. Отношение высоты изображения (
от изображения до линзы. Отношение высоты изображения (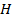 ) к высоте предмета (
) к высоте предмета (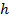 ), назовем увеличением линзы и обозначим через
), назовем увеличением линзы и обозначим через 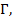 гамма. Тогда можно вывести такую формулу:
гамма. Тогда можно вывести такую формулу:
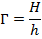
Предмет обозначим 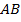 , изображение –
, изображение – 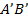 . Рассмотрим две пары подобных треугольников
. Рассмотрим две пары подобных треугольников 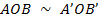 (Рис. 10), и из этого можно вывести еще одну формулу:
(Рис. 10), и из этого можно вывести еще одну формулу:
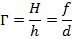
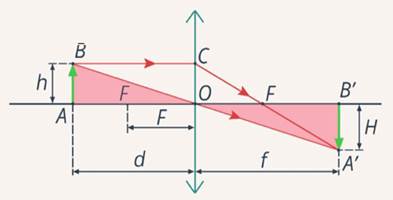
Рис. 10. Геометрическая задача по нахождению изображения
Также из подобия треугольников 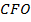 и
и 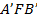 следует, что:
следует, что:
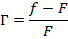
Теперь мы можем приравнять полученные равенства, производим несложные арифметические вычисления и получаем конечную формулу:
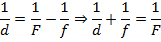
Двояковогнутая линза
Двояковогнутую линзу, изготовленную из материала с коэффициентом преломления большим 1, называют рассеивающей. Такое название обусловлено тем, что лучи, идущие до преломления в линзе параллельно ее главной оптической оси, после преломления отклоняются от своего направлению в сторону от главной оптической оси, в отличие от собирающей линзы. Все утверждения о ходе лучей в рассевающей линзе являются аналогами для соответствующих утверждений в собирательной линзе с той лишь разницей, что теперь говорить стоит не о ходе самих лучей, а об их продолжениях (Рис. 11).
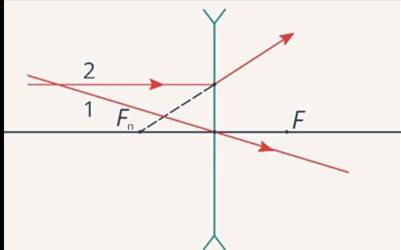
Рис. 11.
1. Луч, проходящий через оптический центр, не преломляется
2. Луч, параллельный главной оптической оси, после преломления идет так, что его продолжение проходит через главный фокус
Луч, параллельный побочной оптической оси, после преломления идет так, что его продолжение проходит через побочный фокус, который является точкой пересечения побочной оптической оси параллельной лучу с фокальной плоскостью (Рис. 12).
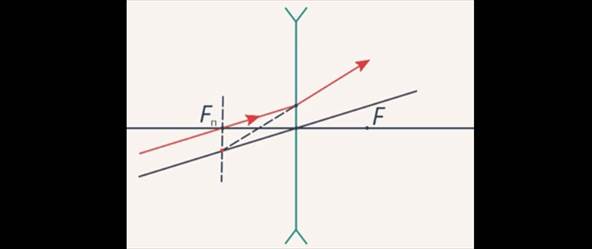
Рис. 12. Преломление луча, идущего параллельно побочной оси
Формула тонкой рассевающей линзы будет иметь вид:
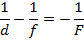
Полученная формула является формулой тонкой линзы, как мы видим, она связывает три величины: расстояние от предмета до линзы, расстояние от изображения до линзы и фокусное расстояние линзы. Зная два из выше приведенных параметров, мы с легкостью можем найти третий.
Важно отметить, что в задачах лишь два из этих параметров могут менять свое значение, а именно расстояние от предмета до линзы и расстояние до изображения.
Пример решения задачи
Задача № 1: определить увеличение, даваемое линзой, фокусное расстояние которой равно 0,26 м, если предмет отстоит от нее на расстоянии 30 см.
Решение: используем выведенные формулы.
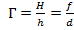 ,
,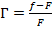 ,
, 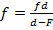
Таким образом, нам не хватает лишь расстояния до предмета. Воспользовавшись формулой тонкой линзы, найдем это расстояние:
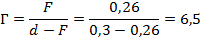
Ответ: 6,5.
Фокусное расстояние линзы, как мы знаем, не зависит от положения предмета и от положения изображения, а определяется только лишь параметрами самой линзы. Об этом мы уже говорили, когда ознакомились с формулой шлифовщика.
Также важно отметить, что в формулу не входит размер предмета и размер изображения. И тут важно сделать еще один вывод: вышеприведенная картинка не изменится, если изображение и предмет поменять местами. Это обусловлено принципом обратимости световых лучей, о котором говорилось на прошлых уроках.
На данном уроке мы рассмотрели одно из самых важных практических приложений геометрической оптики, а именно ход лучей в тонкой линзе. Все выводы, сделанные о ходе лучей через двояковыпуклую линзу, можно применить и к другим разновидностям линз. Кроме того, мы вывели важное соотношение – формулу тонкой линзы, которая позволяет нам делать выводы об изображениях, даваемых линзой в случаях, если нам известно расстояние от предмета до линзы.
Список литературы
1. Жилко В.В., Маркович Я.Г. Физика. 11 класс. – 2011.
2. Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика. 11 класс. Учебник.
1. Касьянов В.А. Физика, 11 класс. – 2004.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
1. Интернет портал «Math Us!» (Источник)
2. Интернет портал «ЗАО «Опто-Технологическая Лаборатория»» (Источник)
3. Интернет портал «ГЕОМЕТРИЧЕСКАЯ ОПТИКА» (Источник)
Домашнее задание
1. С помощью линзы на вертикальном экране получено действительное изображение электрической лампочки. Как изменится изображение, если закрыть верхнюю половину линзы?
2. Постройте изображение предмета, помещенного перед собирающей линзой, в следующих случаях: 1. 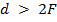 ; 2.
; 2. 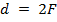 ; 3.
; 3. 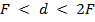 ; 4.
; 4. 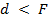 .
.
Линзы | |
Прозрачное для света тело, ограниченное выпуклыми или вогнутыми преломляющими поверхностями, называется линзой. Принцип работы линзы объясняется на основе анализа хода лучей в призме и усеченной призме |
|
Собирающие (положительные) линзы — это линзы, преобразующие пучок параллельных лучей в сходящийся: двояковыпуклые (1), где 0102 — главная оптическая ось, R1R2— радиусы кривизны поверхности, плоско-выпуклые (2),выпукло-вогнутые (3). |
|
Рассеивающие (отрицательные) линзы — это линзы, преобразующие пучок параллельных лучей в расходящийся: вогнуто-выпуклые (4), двояковогнутые(5), плоско-вогнутые (6). |
|
Линзы, у которых середины толще чем края — собирающие, а у которых толще края — рассеивающие. Эти условия выполняются, если показатель преломления стекла, из которого изготовлена линза, больше показателя преломления среды, в которой используется линза. |
|
Линзы, в которых можно пренебречь смещением луча при прохождении внутри линзы, называют тонкими линзами. |
|
Главные фокусы и фокусное расстояние линзы Точка F на главной оптической оси, в которой пересекаются после преломления лучи, параллельные этой оси, называется главным фокусом. Плоскость, которая перпендикулярна главной оптической оси линзы, а также проходит через ее главный фокус, называется фокальной Побочный фокус F’ — это точка на фокальной плоскости, в которой собираются лучи, падающие на линзу параллельно побочной оси. |
|
У собирающей линзы фокусы действительные, у рассеивающей — мнимые.Расстояние между линзой и главным фокусом (OF) — фокусное расстояние. Его обозначают буквой F. У собирающей линзы считают F>0, у рассеивающей — F<0. |
|
Оптическая сила линзы: Единица оптической силы линзы в СИ — диоптрия: 1 дптр =1 м-1. |
|
Оптическая сила линзы определяется кривизной ее поверхности, а также показателем преломления ее вещества относительно окружающей среды:
где r1 и R2 — радиусы сферических поверхностей линзы; n — относительный показатель преломления. |
|
Вывод формулы тонкой линзы |
|
Из подобия треугольников, заштрихованных одинаково, следует
откуда Разделив последнее равенство на произведение dfF, получим:
|
— формула тонкой линзы |
Оптическая сила линзы равна: |
|
При расчетах числовые значения действительных величин всегда подставляются со знаком «плюс», а мнимых—со знаком «минус». |
|
Линейное увеличение |
|
Из подобия заштрихованных треугольников следует: |
|
Построение изображения в тонкой линзе.
|
|
Линза — Класс!ная физика
Линза
«Физика — 11 класс»
Прозрачное тело, ограниченное сферическими поверхностями, называют линзой.
Виды линз
Линза может быть ограничена двумя выпуклыми сферическими поверхностями (двояковыпуклая линза), выпуклой сферической поверхностью и плоскостью (плосковыпуклая линза), выпуклой и вогнутой сферическими поверхностями (вогнуто-выпуклая линза).
Эти линзы посредине толще, чем у краев, и все они называются выпуклыми.
Линзы, которые посредине тоньше, чем у краев, называются вогнутыми.
На рисунке изображены три вида вогнутых линз: двояковогнутая, плосковогнутая и выпукло-вогнутая.
Тонкая линза
Мы рассмотрим наиболее простой случай, когда толщина линзы l = АВ пренебрежимо мала по сравнению с радиусами R1 и R2 сферических поверхностей линзы и расстоянием предмета от линзы.
Такую линзу называют тонкой линзой.
В дальнейшем, говоря о линзе, мы всегда будем подразумевать тонкую линзу.
Точки А и В — вершины сферических сегментов — расположены в тонкой линзе столь близко друг от друга, что их можно принять за одну точку, которую называют оптическим центром линзы и обозначают буквой О.
Луч света, который проходит через оптический центр линзы, не изменяет своего направления, а только смещается, но, так как линза тонкая, этим смещением можно пренебречь.
Прямую O1O2, проходящую через центры сферических поверхностей, которые ограничивают линзу, называют ее главной оптической осью.
Главная оптическая ось тонкой линзы проходит через оптический центр.
Любую другую прямую, проходящую через оптический центр, называют побочной оптической осью.
Изображение в линзе
Подобно плоскому зеркалу, линза создает изображения источников света.
Это означает, что свет, исходящий из какой-либо точки предмета (источника), после преломления в линзе снова собирается в одну точку (изображение) независимо от того, через какую часть линзы прошли лучи.
Если по выходе из линзы лучи сходятся, они образуют действительное изображение.
В случае же, когда прошедшие через линзу лучи расходятся, то пересекаются в одной точке не сами эти лучи, а лишь их продолжения.
Изображение в этом случае мнимое.
Его можно наблюдать глазом непосредственно или с помощью оптических приборов.
Лучи или их продолжения будут пересекаться практически в одной точке, если они образуют малые углы с главной оптической осью
Собирающая линза
Обычно линзы изготавливают из стекла.
Выпуклые линзы являются собирающими.
Любую из них схематично можно себе представить как совокупность стеклянных призм.
В воздухе каждая призма отклоняет лучи к основанию.
Все лучи, идущие через линзу, отклоняются в сторону ее главной оптической оси.
Точка, в которой пересекаются после преломления в собирающей линзе лучи, падающие на нее параллельно главной оптической оси, называется главным фокусом линзы.
Эту точку обозначают буквой F.
Пучки, параллельные главной оптической оси, можно направить на линзу и с противоположной стороны.
Точка, в которой они сойдутся, пройдя линзу, будет другим главным фокусом.
Таким образом, у линзы два главных фокуса.
В однородной среде они располагаются по обе стороны линзы на одинаковых расстояниях от нее.
Эти расстояния называются фокусным расстоянием линзы; его обозначают буквой F (той же буквой, что и фокус).
Направим три узких параллельных пучка лучей от осветителя под углом к главной оптической оси линзы.
Мы увидим, что пересечение лучей произойдет не в главном фокусе, а в другой точке.
Но примечательно то, что точки пересечения независимо от углов, образуемых этими пучками с главной оптической осью, располагаются в плоскости, перпендикулярной главной оптической оси линзы и проходящей через главный фокус.
Эту плоскость называют фокальной плоскостью.
Поместив светящуюся точку в фокусе линзы (или в любой точке ее фокальной плоскости), получим после преломления параллельные лучи.
Если сместить источник дальше от фокуса линзы, лучи за линзой становятся сходящимися и дают действительное изображение.
Когда же источник находится ближе фокуса, преломленные лучи расходятся и изображение получается мнимым.
Рассеивающая линза
Вогнутые линзы, находящиеся в оптически менее плотной среде (по сравнению с материалом линзы), являются рассеивающими.
Направив на такую линзу лучи параллельно главной оптической оси, мы получим расходящийся пучок лучей.
Их продолжения пересекаются в главном фокусе рассеивающей линзы.
В этом случае главный фокус является мнимым и расположен на расстоянии F от линзы.
Другой мнимый главный фокус находится по другую сторону линзы на таком же расстоянии, если среда по обе стороны линзы одна и та же.
Оптическая сила линзы
Величину, обратную фокусному расстоянию, называют оптической силой линзы.
Ее обозначают буквой D:
D > 0, если линза собирающая, D < 0, если линза рассеивающая.
Чем ближе к линзе ее фокусы, тем сильнее линза преломляет лучи, собирая или рассеивая их, и тем больше оптическая сила линзы.
Оптическую силу D линз выражают в диоптриях (дптр).
Оптической силой в 1 дптр обладает линза с фокусным расстоянием 1 м.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Световые волны. Физика, учебник для 11 класса — Класс!ная физика
Оптика — Скорость света — Принцип Гюйгенса. Закон отражения света — Закон преломления света — Полное отражение — Линза — Построение изображения в линзе — Формула тонкой линзы. Увеличение линзы — Примеры решения задач. Геометрическая оптика — Дисперсия света — Интерференция механических волн — Интерференция света — Некоторые применения интерференции — Дифракция механических волн — Дифракция света — Дифракционная решетка — Поперечность световых волн. Поляризация света — Поперечность световых волн и электромагнитная теория света — Примеры решения задач. Волновая оптика — Краткие итоги главы


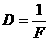
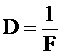
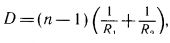
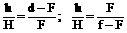
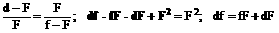
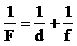 , где d — расстояние предмета от линзы; f — расстояние от линзы до изображения, F — фокусное расстояние.
, где d — расстояние предмета от линзы; f — расстояние от линзы до изображения, F — фокусное расстояние.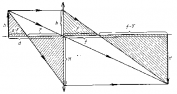
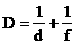
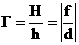 .
.