Линии электрического поля: Ошибка 403 — доступ запрещён — RC74 — интернет-магазин радиоуправляемых моделей

Содержание

Свойства силовых линий электрического поля

Силовые линии электрического поля имеют начало и конец. Они начинаются на положительных зарядах и заканчиваются на отрицательных.
Силовые линии электрического поля всегда перпендикулярны поверхности проводника.
Распределение силовых линий электрического поля определяет характер поля. Поле может быть радиальным (если силовые линии выходят из одной точки или сходятся в одной точке), однородным (если силовые линии параллельны) и неоднородным (если силовые линии не параллельны).

Напряжённость — физическая величина, характеризующая поле:

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда

Также иногда называется силовой характеристикой электрического поля.

Математически зависимость вектора от координат пространства само задаёт векторное поле.

Модуль напряжённости электрического поля в СИ измеряется в В/м (Вольт на метр).

вакууме (или в отсутствии среды, способной к магнитной поляризации, а также в случаях, когда последняя пренебрежима) напряженность магнитного поля совпадает с вектором магнитной индукции.

СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».

В вакууме Н. э. п. удовлетворяет принципу суперпозиции, согласно которому полная напряжённость поля в точке равна геометрической сумме напряжённостей полей, создаваемых отдельными заряженными частицами.

Напряжённость магни́тного по́ля — (стандартное обозначение Н) это векторная

физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M.

В СИ: , где μ₀ — магнитная постоянная

Напряжение. Отношение работы, совершаемой любым электрическим полем при перемещении положительного заряда из одной точки поля в другую, к значению заряда называется напряжением между этими точками:

Отсюда работа сил электрического поля при перемещении заряда равна произведению напряжения U между точками на заряд q:

A = qU. (40.8)

В электростатическом поле напряжение между двумя любыми точками равно разности потенциалов этих точек:

. (40.9)

Как будет показано далее, равенство (40.9) может не выполняться, если электрическое поле непотенциальное. В непотенциальных электрических полях работа сил поля при перемещении электрического заряда зависит от траектории движения заряда из одной точки в другую.

Напряжённость электри́ческого по́ля — векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению

силы действующей на пробный заряд, помещенный в данную точку поля, к величине этого заряда q:

Также иногда называется силовой характеристикой электрического поля.

Математически зависимость вектора от координат пространства само задаёт векторное поле.

Модуль напряжённости электрического поля в СИ измеряется в В/м (Вольт на метр).

В магнетиках (магнитных средах) напряженность магнитного поля имеет физический смысл «внешнего» поля, то есть совпадает (быть может, в зависимости от принятых единиц измерения, с точностью до постоянного коэффициента, как например в системе СИ, что общего смысла не меняет) с таким вектором магнитной индукции, какой «был бы, если магнетика не было».

Для установления связи между силовой характеристикой электрического поля — напряжённостью и его энергетической характеристикой — потенциалом рассмотрим элементарную работу сил электрического поля на бесконечно малом перемещении точечного заряда q: dA = q E dl, эта же работа равна убыли потенциальной энергии заряда

q: dA = — dW_п = — q d , где d — изменение потенциала электрического поля на длине перемещения dl. Приравнивая правые части выражений, получаем: E dl = -d или в декартовой системе координат

E_x dx + E_y dy + E_z dz = -d , (1. 8)

где E_x, E_y, E_z — проекции вектора напряженности на оси системы координат. Поскольку выражение (1.8) представляет собой полный дифференциал, то для проекций вектора напряженности имеем

откуда

Стоящее в скобках выражение является градиентом потенциала j, т. е.

E = — grad = -Ñ .

Напряжённость в какой-либо точке электрического поля равна градиенту потенциала в этой точке, взятому с обратным знаком. Знак «минус» указывает, что напряженность E направлена в сторону убывания потенциала.

Напряженность поля связана с разностью потенциалов формулой E=U/∆d,

Где U-разность потенциалов между двумя точками на одной силовой линии, находящимися на малом расстоянии ∆d друг от друга.

Напряженность поля Ē направлена в сторону убывания потенциала.

Единица измерения напряженности 1В/м.

Все точки поверхности, перпендикулярной силовым линиям, имеют один и тот же6 потенциал. Поверхности равного потенциала называют эквипотенциальными. Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону уменьшения потенциала.

Для измерения разности потенциалов используют прибор электрометр.

?15.Энергия взаимодействия зарядов и энергия заряда во внешнем электрическом поле. Движение заряда во внешнем электрическом поле.

Forceline

Силовые линии

Для графического изображения электрического поля E используются силовые линии. Силовая линия определяется как линия, касательная к которой в любой точке совпадает с E. Густота силовых линий пропорциональна модулю E.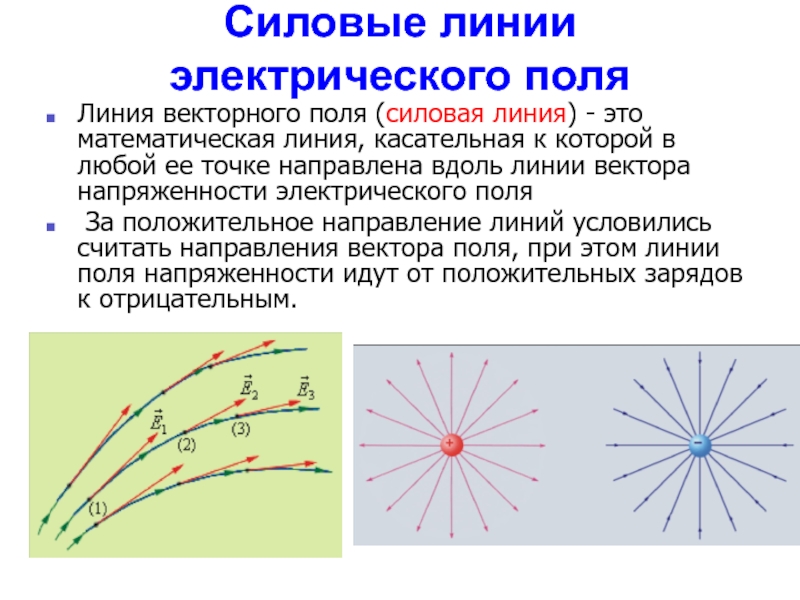

Следует иметь в виду, что в природе никаких силовых линий нет. Электрическое поле непрерывно во всех точках пространства за исключением точек, в которых расположены заряды. Таким образом силовую линию можно провести через любую точку, если только в ней нет заряда (в точках расположения заряда поле не определено).

Если поле создается одним зарядом, то силовые линии имеют вид прямых, выходящих из точки, где находится заряд, или сходящихся в эту точку, в зависимости от того, положителен или отрицателен заряд.

Через каждую точку поля проходит только одна силовая линия, т.е. силовые линии не пересекаются, поскольку направление силы, действующей на помещенный в поле заряд, имеет вполне определенное направление.

Силовые линии электростатического поля не могут быть замкнутыми. Действительно, при перемещении заряда вдоль силовой линии силами поля совершается работа, так как сила направлена все время вдоль пути. Если бы силовая линия была замкнутой, то при перемещении заряда вдоль такой линии с возвращением в исходную точку производилась бы работа, тогда как работа, производимая силами консервативного поля на замкнутом пути, равна нулю.

Таким образом, силовые линии должны обязательно где-то начинаться или кончаться, либо уходить на бесконечность одним из своих концов. Точками начала или конца силовой линии являются создающие поле заряды. Что касается бесконечности, то силовая линия не может уходить туда обоими своими концами. В противном случае при переносе заряда вдоль такой линии из бесконечности в бесконечность производилась бы некоторая работа в противоречии с тем, что на обоих концах пути потенциальная энергия равна нулю. Поэтому одним концом силовой линии должен быть обязательно заряд, другой же ее конец может находиться либо на бесконечности, либо на заряде противоположного знака.

На рисунке изображены силовые линии поля двух зарядов противоположного знака, причем положительный заряд больше отрицательного. Поэтому часть линий исходящих из положительного заряда заканчивается на отрицательном, а часть уходит на бесконечность.

Сайт управляется системой uCoz

19.4 Эквипотенциальные линии – Колледж физики

Резюме

Объясните эквипотенциальные линии и эквипотенциальные поверхности.
Опишите действия по заземлению электроприбора.
Сравните линии электрического поля и эквипотенциальные линии.

Мы можем изображать электрические потенциалы (напряжения) графически, точно так же, как мы рисовали картинки для иллюстрации электрических полей. Конечно, эти два связаны. Рассмотрим рисунок 1, на котором изображен изолированный положительный точечный заряд и линии его электрического поля. Силовые линии электрического поля исходят из положительного заряда и заканчиваются на отрицательном заряде. В то время как мы используем синие стрелки для представления величины и направления электрического поля, мы используем зеленые линии для обозначения мест, где электрический потенциал постоянен. Они называются эквипотенциальными линиями в двух измерениях, или эквипотенциальных поверхностей в трех измерениях. Термин эквипотенциальный также используется как существительное, относящееся к эквипотенциальной линии или поверхности. Потенциал точечного заряда одинаков в любом месте воображаемой сферы радиусом [латекс]\boldsymbol{r}[/латекс], окружающей заряд. Это верно, поскольку потенциал точечного заряда задается формулой [latex]\boldsymbol{V = kQ/r}[/latex] и, таким образом, имеет одинаковое значение в любой точке, находящейся на заданном расстоянии [latex]\boldsymbol {r}[/latex] от оплаты. Эквипотенциальная сфера представляет собой круг на двумерном изображении на рисунке 1. Поскольку линии электрического поля направлены радиально от заряда, они перпендикулярны эквипотенциальным линиям.

Рис. 1. Изолированный точечный заряд Q с линиями электрического поля синего цвета и эквипотенциальными линиями зеленого цвета. Потенциал одинаков вдоль каждой эквипотенциальной линии, а это означает, что для перемещения заряда в любом месте вдоль одной из этих линий не требуется никакой работы. Для перемещения заряда от одной эквипотенциальной линии к другой необходима работа. Эквипотенциальные линии в любом случае перпендикулярны линиям электрического поля.

Важно отметить, что эквипотенциальных линий всегда перпендикулярны силовым линиям электрического поля . Никакой работы не требуется для перемещения заряда по эквипотенциалу, поскольку [латекс]\boldsymbol{\Delta V = 0}[/латекс]. Таким образом, работа равна

[латекс]\boldsymbol{W = — \Delta \;\textbf{PE} = -q \Delta V = 0}. [/latex]

Работа равна нулю, если сила перпендикулярна движению. Сила действует в том же направлении, что и [латекс]\boldsymbol{E}[/латекс], поэтому движение по эквипотенциалу должно быть перпендикулярно [латексу]\boldsymbol{E}[/латекс]. Точнее, работа связана с электрическим полем соотношением

[латекс]\жирныйсимвол{W = Fd \;\textbf{cos} \theta = qEd \;\textbf{cos} \theta = 0.}[/latex]

Обратите внимание, что в приведенном выше уравнении [латекс] \boldsymbol{E}[/latex] и [latex]\boldsymbol{F}[/latex] обозначают величины напряженности и силы электрического поля соответственно. Ни [latex]\boldsymbol{q}[/latex], ни [latex]\textbf{E}[/latex], ни [latex]\boldsymbol{d}[/latex] не равны нулю, поэтому [latex]\boldsymbol{ \textbf{cos} \theta}[/latex] должен быть равен 0, то есть [латекс]\boldsymbol{\theta}[/latex] должен быть равен [латекс]\boldsymbol{9{\circ}}[/латекс]. Другими словами, движение по эквипотенциалу перпендикулярно [латексу]\boldsymbol{E}[/латексу].

Одно из правил для статических электрических полей и проводников состоит в том, что электрическое поле должно быть перпендикулярно поверхности любого проводника. Это означает, что проводник является эквипотенциальной поверхностью в статических ситуациях . На поверхности проводника не может быть разности потенциалов, иначе будут течь заряды. Одно из применений этого факта состоит в том, что проводник можно зафиксировать при нулевом напряжении, подключив его к земле с помощью хорошего проводника — процесс, называемый заземлением. Заземление может быть полезным инструментом безопасности. Например, заземление металлического корпуса электроприбора гарантирует, что он находится при нулевом напряжении относительно земли.

Заземление

Проводник можно зафиксировать при нулевом напряжении, соединив его с землей с помощью хорошего проводника — процесс, называемый заземлением.

Поскольку проводник является эквипотенциальным, он может заменить любую эквипотенциальную поверхность. Например, на рис. 1 заряженный сферический проводник может заменить точечный заряд, а электрическое поле и потенциальные поверхности вне его останутся неизменными, что подтверждает утверждение о том, что распределение сферического заряда эквивалентно точечному заряду в его центре.

На рис. 2 показано электрическое поле и эквипотенциальные линии для двух одинаковых и противоположных зарядов. Имея линии электрического поля, эквипотенциальные линии можно провести, просто сделав их перпендикулярными линиям электрического поля. И наоборот, учитывая эквипотенциальные линии, как на рис. 3(а), линии электрического поля можно нарисовать, сделав их перпендикулярными эквипотенциалам, как на рис. 3(б).

Рис. 2. Линии электрического поля и эквипотенциальные линии для двух равных, но противоположных зарядов. Эквипотенциальные линии можно провести, сделав их перпендикулярными линиям электрического поля, если они известны. Обратите внимание, что потенциал наибольший (наиболее положительный) вблизи положительного заряда и наименьший (наиболее отрицательный) вблизи отрицательного заряда. Рис. 3. (а) Эти эквипотенциальные линии можно измерить вольтметром в лабораторном эксперименте. (b) Соответствующие силовые линии электрического поля находят, проводя их перпендикулярно эквипотенциалам.

Обратите внимание, что эти поля согласуются с двумя равными отрицательными зарядами

. Одним из наиболее важных случаев является знакомые параллельные проводящие пластины, показанные на рис. 4. Между пластинами эквипотенциалы расположены на равном расстоянии друг от друга и параллельны. То же самое поле можно было бы поддерживать, поместив проводящие пластины на эквипотенциальные линии при показанных потенциалах.

Рис. 4. Электрическое поле и эквипотенциальные линии между двумя металлическими пластинами.

Важное применение электрических полей и эквипотенциальных линий связано с сердцем. Сердце полагается на электрические сигналы для поддержания своего ритма. Движение электрических сигналов заставляет камеры сердца сокращаться и расслабляться. Когда у человека сердечный приступ, движение этих электрических сигналов может быть нарушено. Искусственный кардиостимулятор и дефибриллятор могут использоваться для запуска ритма электрических сигналов. Эквипотенциальные линии вокруг сердца, грудного отдела и оси сердца являются полезными способами наблюдения за структурой и функциями сердца. Электрокардиограмма (ЭКГ) измеряет слабые электрические сигналы, генерируемые во время деятельности сердца. Подробнее о взаимосвязи между электрическими полями и сердцем обсуждается в главе 19..7 Энергия, запасенная в конденсаторах.

PhET Explorations: Charges and Fields

Перемещайте точечные заряды по игровому полю, а затем просматривайте электрическое поле, напряжения, эквипотенциальные линии и многое другое. Это красочно, это динамично, это бесплатно.

Рисунок 5. Заряды и поля

Эквипотенциальная линия — это линия, вдоль которой электрический потенциал постоянен.
Эквипотенциальная поверхность представляет собой трехмерную версию эквипотенциальной линии.
Эквипотенциальные линии всегда перпендикулярны линиям электрического поля.
Процесс, с помощью которого проводник может быть зафиксирован при нулевом напряжении, соединив его с землей с помощью хорошего проводника, называется заземлением.

Задачи и упражнения

1: (a) Нарисуйте эквипотенциальные линии вблизи точечного заряда + [латекс]\boldsymbol{q}[/латекс]. Укажите направление возрастания потенциала. (b) Сделайте то же самое для точечного заряда [латекс]\boldsymbol{-3 \; д}[/латекс].

2: Нарисуйте эквипотенциальные линии для двух одинаковых положительных зарядов, показанных на рисунке 6. Укажите направление увеличения потенциала.

Рис. 6. Электрическое поле вблизи двух равных положительных зарядов направлено от каждого из зарядов.

3: На рис. 7 показаны силовые линии электрического поля вблизи двух зарядов [латекс]\boldsymbol{q_1}[/latex] и [латекс]\boldsymbol{q_2}[/латекс], величина первого из которых в четыре раза больше второй. Начертите эквипотенциальные линии этих двух зарядов и укажите направление возрастания потенциала.

4: Нарисуйте эквипотенциальные линии на большом расстоянии от зарядов, показанных на рисунке 7. Укажите направление возрастания потенциала.

Рис. 7. Электрическое поле вблизи двух зарядов.

5: Изобразите эквипотенциальные линии вблизи двух противоположных зарядов, где отрицательный заряд в три раза больше положительного по величине. См. Рисунок 7 для аналогичной ситуации. Укажите направление возрастания потенциала.

6: Нарисуйте эквипотенциальные линии вблизи отрицательно заряженного проводника на рис. 8. Как будут выглядеть эти эквипотенциальные линии на большом расстоянии от объекта?

Рис. 8. Отрицательно заряженный проводник.

7: Нарисуйте эквипотенциальные линии, окружающие две проводящие пластины, показанные на рисунке 9, учитывая, что верхняя пластина имеет положительный заряд, а нижняя пластина имеет одинаковое количество отрицательного заряда. Обязательно укажите распределение заряда на пластинах. Является ли поле самым сильным там, где пластины находятся ближе всего? Почему так должно быть?

Рисунок 9.

8: (a) Нарисуйте линии электрического поля вблизи заряженного изолятора на рисунке 10. Обратите внимание на его неоднородное распределение заряда. (b) Нарисуйте эквипотенциальные линии, окружающие изолятор. 2}[/latex] . а) Чему равно электрическое поле относительно земли на высоте 3,00 м? б) Рассчитайте электрический потенциал на этой высоте. (c) Нарисуйте электрическое поле и эквипотенциальные линии для этого сценария.

10: Малый электрический скат ( Narcine bancroftii ) поддерживает невероятный заряд на голове и заряд, равный по величине, но противоположный по знаку, на хвосте (рис. 11). а) Нарисуйте эквипотенциальные линии, окружающие луч. (b) Нарисуйте эквипотенциали, когда луч находится вблизи корабля с проводящей поверхностью. в) Как это распределение заряда может быть полезно лучу?

Рисунок 11. Малый электрический скат ( Narcine bancroftii ) (кредит: Национальное управление океанических и атмосферных исследований, Коллекция рыболовства NOAA).

эквипотенциальная линия: линия, вдоль которой электрический потенциал постоянен

заземление: фиксация проводника при нулевом напряжении путем соединения его с землей или землей

5.

7: Линии электрического поля — Physics LibreTexts

Последнее обновление
Сохранить как PDF

Идентификатор страницы: 4377

OpenStax
OpenStax

Цели обучения

К концу этого раздела вы сможете:

Объяснять назначение диаграммы электрического поля
Описать взаимосвязь между векторной диаграммой и диаграммой силовых линий
Объясните правила создания диаграммы поля и почему эти правила имеют физический смысл
Зарисовка поля произвольного исходного заряда

Теперь, когда у нас есть некоторый опыт расчета электрических полей, давайте попробуем разобраться в геометрии электрических полей. Как упоминалось ранее, наша модель состоит в том, что заряд на объекте (исходный заряд) изменяет пространство в области вокруг него таким образом, что когда другой заряженный объект (пробный заряд) помещается в эту область пространства, этот пробный заряд испытывает электрическую силу. Концепция электрического линия поля s и диаграммы линий электрического поля позволяют нам визуализировать способ изменения пространства, позволяя нам визуализировать поле. Цель этого раздела — дать вам возможность создавать наброски этой геометрии, поэтому мы перечислим конкретные шаги и правила, связанные с созданием точного и удобного наброска электрического поля.

Важно помнить, что электрические поля трехмерны. Хотя в эту книгу мы включили несколько псевдотрехмерных изображений, некоторые диаграммы, которые вы увидите (как здесь, так и в последующих главах), будут двухмерными проекциями или сечениями. Всегда помните, что на самом деле вы смотрите на трехмерное явление.

Нашей отправной точкой является физический факт, что электрическое поле исходного заряда заставляет пробный заряд в этом поле испытывать силу. По определению, векторы электрического поля указывают в том же направлении, что и электрическая сила, которую испытает (гипотетический) положительный пробный заряд, если поместить его в поле (рис. \(\PageIndex{1}\)).

Рисунок \(\PageIndex{1}\): Электрическое поле положительного точечного заряда. Показано большое количество векторов поля. Как и у всех векторных стрелок, длина каждого вектора пропорциональна величине поля в каждой точке. (а) Поле в двух измерениях; (б) поле в трех измерениях.

Мы нанесли на рисунок множество векторов поля, которые равномерно распределены вокруг заряда источника. Поскольку электрическое поле является вектором, стрелки, которые мы рисуем, соответствуют в каждой точке пространства как величине, так и направлению поля в этой точке. Как всегда, длина нарисованной нами стрелки соответствует величине вектора поля в этой точке. Для заряда точечного источника длина уменьшается на квадрат расстояния от заряда источника. Кроме того, направление вектора поля находится в радиальном направлении от исходного заряда, потому что направление электрического поля определяется направлением силы, с которой положительный пробный заряд будет действовать в этом поле. (Опять же, имейте в виду, что фактическое поле является трехмерным; есть также линии поля, указывающие наружу и внутрь страницы.)

Эта диаграмма верна, но становится менее полезной по мере усложнения распределения заряда источника. Например, рассмотрим диаграмму векторного поля диполя (рис. \(\PageIndex{2}\)).

Рисунок \(\PageIndex{2}\): Векторное поле диполя. Даже имея всего два одинаковых заряда, диаграмму векторного поля становится трудно понять.

Существует более удобный способ представления той же информации. Вместо того, чтобы рисовать большое количество все более мелких векторных стрелок, мы соединяем их все вместе, образуя непрерывные линии и кривые, как показано на рисунке \(\PageIndex{3}\).

Рисунок \(\PageIndex{3}\): (a) Диаграмма силовых линий электрического поля положительного точечного заряда. (б) Диаграмма силовых линий диполя. На обеих диаграммах величина поля указана плотностью силовых линий. Векторы поля (здесь не показаны) касаются всюду линий поля.
Хотя на первый взгляд это может показаться неочевидным, эти диаграммы поля передают ту же информацию об электрическом поле, что и векторные диаграммы. Во-первых, направление поля в каждой точке — это просто направление вектора поля в этой же точке. Другими словами, в любой точке пространства вектор поля в каждой точке касается линии поля в этой же точке. Стрелка, расположенная на линии поля, указывает ее направление.
Что касается величины поля, на это указывает плотность силовых линий — то есть число силовых линий на единицу площади, проходящих через небольшую площадь поперечного сечения, перпендикулярную электрическому полю. Эта плотность силовых линий рисуется пропорциональной величине поля в этом поперечном сечении. В результате, если силовые линии расположены близко друг к другу (то есть плотность силовых линий больше), это указывает на то, что величина поля в этой точке велика. Если силовые линии далеко друг от друга в поперечном сечении, это указывает на малую величину поля. Рисунок \(\PageIndex{4}\) иллюстрирует идею.
Рисунок \(\PageIndex{4}\): Линии электрического поля, проходящие через воображаемые области. Поскольку количество линий, проходящих через каждую область, одинаково, но сами области различны, плотность силовых линий различна. Это свидетельствует о разной величине электрического поля в этих точках.
На рисунке \(\PageIndex{4}\) одинаковое количество силовых линий проходит через обе поверхности ( S и \(S’\)), но поверхность S больше, чем поверхность \(S’ \). Следовательно, плотность силовых линий (количество линий на единицу площади) больше в точке \(S’\), что указывает на то, что электрическое поле сильнее в точке \(S’\), чем в точке С . Правила построения диаграммы электрического поля следующие.
Стратегия решения задач: рисование линий электрического поля
Линии электрического поля либо возникают на положительных зарядах, либо приходят из бесконечности, и либо заканчиваются на отрицательных зарядах, либо уходят в бесконечность.
Количество силовых линий, начинающихся или заканчивающихся зарядом, пропорционально величине этого заряда. Заряд 2 q будет иметь в два раза больше строк, чем заряд д .
В каждой точке пространства вектор поля в этой точке касается линии поля в этой же точке.
Плотность силовых линий в любой точке пространства пропорциональна (и, следовательно, репрезентативна) величине поля в этой точке пространства.
Линии поля никогда не могут пересекаться. Поскольку силовая линия представляет направление поля в данной точке, если две силовые линии пересекаются в какой-то точке, это будет означать, что электрическое поле указывает в двух разных направлениях в одной точке. Это, в свою очередь, предполагает, что (чистая) сила, действующая на пробный заряд, помещенный в эту точку, будет направлена в двух разных направлениях. Поскольку это очевидно невозможно, отсюда следует, что силовые линии никогда не должны пересекаться.
Всегда помните, что силовые линии служат только удобным способом визуализации электрического поля; они не являются физическими лицами. Хотя направление и относительная напряженность электрического поля могут быть определены по набору силовых линий, эти линии также могут вводить в заблуждение. Например, силовые линии, нарисованные для представления электрического поля в области, должны обязательно быть дискретными. Однако фактическое электрическое поле в этой области существует в каждой точке пространства.
Линии поля для трех групп дискретных зарядов показаны на рисунке \(\PageIndex{5}\). Поскольку заряды в частях (а) и (б) имеют одинаковую величину, показано одинаковое количество силовых линий, начинающихся или заканчивающихся на каждом заряде. Однако в (с) мы рисуем в три раза больше силовых линий, выходящих из заряда \(+3q\), чем входящих в заряд \(-q\). Линии поля, которые не заканчиваются на \(-q\), исходят наружу от конфигурации заряда, в бесконечность.
Рисунок \(\PageIndex{5}\): Три типичные диаграммы электрического поля. а) диполь. б) Два одинаковых заряда. в) Два заряда противоположных знаков и разной величины. Можно ли по диаграмме определить, какой заряд имеет большую величину?
Умение построить точную диаграмму электрического поля — важный и полезный навык; это значительно упрощает оценку, прогнозирование и, следовательно, расчет электрического поля заряда источника. Лучший способ развить этот навык — использовать программное обеспечение, которое позволяет вам размещать исходные заряды, а затем рисовать чистое поле по запросу. Мы настоятельно рекомендуем вам поискать программу в Интернете. Как только вы найдете тот, который вам нравится, запустите несколько симуляций, чтобы получить основные идеи построения диаграммы поля. Затем попрактикуйтесь в рисовании диаграмм полей и сверяйте свои прогнозы с компьютерными диаграммами.
PhET: Заряды и поля
Расположите положительные и отрицательные заряды в пространстве и просмотрите результирующее электрическое поле и электростатический потенциал. Постройте эквипотенциальные линии и выясните их связь с электрическим полем. Создавайте модели диполей, конденсаторов и многого другого!
Эта страница под названием 5.7: Electric Field Lines распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована OpenStax с помощью исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Наверх
Была ли эта статья полезной?
Тип изделия
Раздел или страница
Автор
ОпенСтакс
Лицензия
СС BY
Версия лицензии
4,0
Программа OER или Publisher
ОпенСтакс
Показать оглавление
нет
Теги
Электрическое поле
строка поля
строк поля
источник@https://openstax.