Фазное и линейное напряжение

В том случае, если обмотки генератора трехфазного тока соединить между собой специальным образом («звездой» или треугольником), то у такого тока возникают свойства, которые удобны в применении.

Векторная диаграмма напряжений для соединения «звезда»

Схема соединения звездой (рис.1(а)) и соответствующая векторная диаграмма напряжений на обмотках (рис.1(в)) изображены на рис.1. Здесь имеется точка $О$, которая называется точкой одинакового потенциала. Напряжение на каждой обмотке называется фазным (его амплитуда $U_{mf}$). Проводник, который соединен с точкой одинакового потенциала называют нулевым проводом. Проводники, которые соединены со свободными концами обмоток, называются фазными проводами. Получается, что фазные напряжения — это напряжения между нулевым и фазными проводами. Напряжения между фазными проводами называют линейным (его амплитуда $U_{ml}$). Линейное напряжение между проводами 1-2 могут обозначать как $U_{12}$, между проводами 1-3 — $U_{13}$ и так далее.

Рисунок 1.

Векторная диаграмма показывает, что амплитуды $U_{ml}\ $и $U_{mf}$находятся в соотношениях:

Ток, который течет через обмотки генератора называют фазным током ($I_f$), ток который течет в линиях называется током линии ($I_l$). В соединении звездой фазные токи равны токам в линии. Если сопротивления нагрузок не равны нулю, а $R_1=R_2=R_2=R$, то суммарная сила тока через нулевой провод равна нулю:

так как из векторной диаграммы видно, что $\sum\limits_i{U_i=0.}$

Векторная диаграмма напряжений для соединения «треугольник»

Схема соединения обмоток генератора треугольник изображена на рис.2. В этом случае амплитуды напряжений фазного и линейного равны ($U_{mf}=U_{ml}$).

Рисунок 2.

Из векторной диаграммы токов (рис.2(в)) запишем амплитудных значений тока:

В соединении обмоток генератора треугольником ток замыкания в обмотках равен нулю. Однако это справедливо только для основной гармоники. Токи высших гармоник, появляющиеся из-за нелинейности колебаний, в обмотках есть.

Соединение нагрузок тоже может быть в виде звезды и в виде треугольника. На рис. 1 и рис.2 изображены соединения одного типа, как для генератора, так и для нагрузок. Но совсем не обязательно, что соединения обмоток генератора и нагрузок совпадают. Так, можно реализовать четыре возможные комбинации соединения генератора и нагрузок: «звезда» — «звезда», треугольник — треугольник, «звезда» — треугольник, треугольник — «звезда». Каждое из перечисленных соединений имеет свои особенности.

Пример 1

Задание: В чем состоят особенности соединений «звезда» — «звезда» и «звезда» — треугольник?

Решение:

1. При соединении «звезда» — «звезда» (рис.1) на всех нагрузках имеется разное напряжение. При одинаковых сопротивлениях ($R_1=R_2=R_3$) (или примерно равных) сила тока по нулевому проводу равна нулю (или очень мала). Теоретически нулевой провод можно убрать, но без него на каждую из пар нагрузок действует линейное напряжение, амплитудное значение которого равно:

\[U_{ml}=\sqrt{3}U_{mf}\left(1.1\right).\]

Это напряжение распределяется между нагрузками в соответствии с величиной их сопротивлений. Такая зависимость напряжений от нагрузок крайне не удобна, поэтому нулевой провод сохраняют.

1. При соединении «звезда» — треугольник (рис.3). На каждое сопротивление действует линейное напряжение равное:

\[U_{ml}=\sqrt{3}U_{mf}\left(1.2\right).\]

Это линейное напряжение не зависит от величины сопротивления.

Рисунок 3.

Пример 2

Задание: Определите, чему равно фазное напряжение, если линейное $U_{ml}=220\ В$. Чему будет равно линейное напряжение, если 220 В считать фазным напряжением? Считать, что соединение обмоток генератора — «звезда».

Решение:

В том случае, если обмотки генератора соединены звездой, и это соединение имеет нулевой провод, в линии существует две системы напряжений (линейное и фазное), что является достоинством такого соединения.

Для соединения «звезда» мы имеем соотношение:

\[U_{ml}=\sqrt{3}U_{mf}\left(2.1\right).\]

Следовательно, для фазного напряжение имеем:

\[U_{mf}=\frac{U_{ml}}{\sqrt{3}}=\frac{220}{\sqrt{3}}\approx 127\ \left(В\right).\]

Если дано фазное напряжение, то:

\[U_{ml}=\sqrt{3}U_{mf}=\sqrt{3}\cdot 220\approx 380\ (В)\left(2.2\right).\]

Ответ: 1. $U_{mf}=127\ В.$ $U_{ml}=380\ В.$

Линейные и фазные токи и напряжения в трехфазных цепях

Трехфазная система электроснабжения принята в качестве стандарта в большинстве стран мира, Россия не исключение. Каждый дом в стране подключен именно к такой сети, но в отдельную квартиру заходит, как правило, один фазный провод. При желании можно провести и еще две фазы, что часто делается на участках, предназначенных для ИЖС. Они нужны для работы оборудования, содержащего электродвигатель. При подключении к трехфазной цепи часто возникают вопросы, связанные с такими понятиями, как фазный и линейный ток, а также с соответствующими показателями напряжений.

Цепи переменного тока

Как известно, электроснабжение в России осуществляется с помощью цепей переменного тока с частотой 50 Гц. За одну секунду совершается 50 циклов. Полный цикл представляет собой круг, угловой размер которого можно измерить в градусах и радианах — 360 градусов радиан или 2π радиан. Соответственно, половина этого цикла будет 180 или π радиан, треть — 120 или 2 π/3 и т. д. Конкретный момент этого цикла и называется фазой.

Цепи в стране синхронизированы в единую систему.

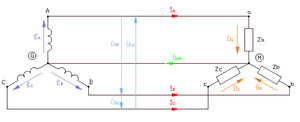
Сдвиг по фазе в цепи

Это выражение не имеет ничего общего со здоровьем головного мозга. Таким термином объясняют несовпадение графиков тока и напряжения, что бывает на участках с катушками или конденсаторами, а также сравнение фаз в разных проводах. При трехфазной системе электроснабжения сдвиг составляет 120 градусов или 2 π/ 3 радиан.

Вот так выглядит наложение графиков напряжений в трех проводах, идущих от трансформаторной будки. Слева даже наглядно показано, как такое можно получить от простой турбины.

Возможно, некоторые помнят подобное упражнение при составление графика функции y=sin (x), когда рисовали ее от круга.

Действующие показатели тока и напряжения

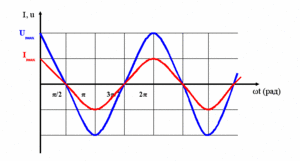
Максимальная амплитуда напряжения в цепи, идущей от трансформаторной подстанции во дворе, составляет 310 В. За 1 с она бывает 100 раз — внизу и вверху графика. Мгновенные значения этого параметра зависят от фазы, в которой находится график. Естественно, для потребителей такое представление крайне неудобно, поэтому в обиходе используется понятие действующего напряжения.

Его формула была выведена экспериментально на основе закона Джоуля-Ленца. Суть вывода этой формулы заключается в том, что действующее значение переменного тока эквивалентно значению постоянного при одинаковом выделении теплоты. Коэффициент, который используется при вычислении, равен √2. Зная это, можно воспользоваться правилом:

I=I m/ √2, U=Um/√2,

где I m и Um — амплитуда. Если подставить во вторую формулу значение амплитуды, то получается, что действующее напряжение фазного провода относительно земли в квартире составит 230 В. Оно еще называется фазным. Ну, а величина тока будет зависеть от нагрузки, согласно закону Ома:

I=U/R.

Ток в фазном проводе тоже будет называться фазным.

Соединения звезда и треугольник

В домашней розетке помимо фазы обязательно присутствует ноль. Правильное его название — нейтраль. Некоторые путают его с заземлением, но на самом деле у него иная функция.

Чтобы ее лучше понять, нужно ознакомиться с таким понятиями, как «звезда» и «треугольник».

Роль нейтрали в цепи

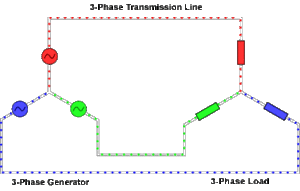На подстанции, откуда в квартиру идет питающий провод, все три фазы одним концом соединены. Второй конец одной из фаз идет в одну квартиру, другой — в другую, третий — в третью. Если в каждой квартире в качестве второго провода использовать заземление, может возникнуть неприятная ситуация.

Но равновесие в этой системе возможно лишь тогда, когда все три потребителя одновременно включают одинаковую нагрузку — она называется симметричной. В реальности же один может включить телевизор, а другой — электрическую духовку. Итогом этого станет перекос фаз, когда у владельца телевизора в розетке будет 380, а у обладателя духовки 30 с небольшим. Чтобы такого не случилось, с места соединения концов фазных проводов выводят нейтраль, которая и идет в каждую квартиру. Для пущей осторожности ее тоже заземляют.

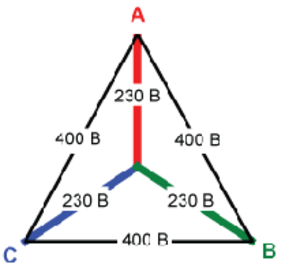
Нейтраль (нулевой провод) является компенсатором несимметричности нагрузки в такой цепи, которую назвали «звездой». В таком соединении между одной из фаз и нейтралью напряжение приблизительно равно 220 В, а между двумя фазами — 380. Это самое межфазное напряжение и называется линейным.

Его значение вычисляется исходя из действующего фазного и значения угла сдвига между ними. Вспомнив уроки геометрии в школе можно вывести:

AB=2x230x√3/2=230х√3=400.

Учитывая, что в цепь постоянно что-то включено, и в чистом виде ЭДС дома не измерить, получим:

220х√3=380.

Таким образом, фазные и линейные напряжения и токи при соединении звездой подчиняются следующим закономерностям:

U (l)=√3U (f), I (l)=I (f) — линейный ток равен фазному.

Соединение звездой с нейтралью очень удобно для распределения проводки по разным потребителям. Его преимущества можно перечислить:

• устойчивость режима работы электроприборов в условиях разных нагрузок;
• двигатели, обмотки которых подключены таким методом, не перегреваются;
• из-за невозможности увеличить ток — пуск двигателя осуществляется плавно;
• возможность использования как линейного, так и фазного напряжения.

Схема треугольник и максимум мощности

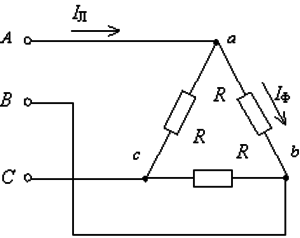
Такая необходимость возникает при желании по максимуму использовать КПД электродвигателя. Это можно достигнуть путем соединения фазных проводов в треугольник. Фазное и линейное напряжение в трехфазных цепях такого типа будут совпадать и равняться 380 В. А вот линейный ток, протекающий в подведенных к двигателю фазах, будет отличаться от того, что протекает через обмотки. Фазный ток можно вычислить, зная сопротивление и напряжение в обмотках, это величины известные. А вот линейный ток вычисляется по такой же диаграмме, как и напряжение в схеме «звезда»:

I (l)=I (f)x√3, U (f)=U (l).

Стоит ли делать такое переключение — отдельный вопрос. Для этого нужно учесть ряд важных моментов:

• Мощность, конечно, увеличится в 1,5 раза. Возможность перегрева — тоже.
• Если у двигателя тяжелый ротор, то при раскрутке ток будет раз в 7 выше, чем при устойчивой работе.
• То же самое будет наблюдаться при попытке дать физическую нагрузку на вращающуюся часть, например, при пилке чего-то жесткого, при подъеме тяжести (если двигатель используется в качестве лебедки).

Поэтому перед проведением экспериментов стоит хорошо ознакомиться с паспортом двигателя и возможностями вашей сети.

Вполне возможно, что лучше будет приобрести электродвигатель с реостатной регулировкой пускового тока.

Соединение фаз потребителей электроэнергии в звезду

Схема соединения фаз электроприемников «звезда» получила очень широкое распространение в электроэнергетике. Принципиальная схема соединения звездой показана ниже:

Из схемы видно, что фазные напряжения приемника U_a, U_b, U_c не равны линейным напряжениям U_ab, U_bc, U_ca. Если применить к контурам aNba, bNcb, cNac второй закон Кирхгофа получим соотношение для фазных и линейных напряжений:

Если сопротивления нейтрального провода и линейных проводов не учитывать, то можно предположить, что напряжение на клеммах генератора и электроприемника равны. Вследствие указанного равенства векторные диаграммы для источника и приемника электрической энергии будут одинаковы.

Фазные и линейные напряжения приемника, как и источника, будут образовывать две симметричные системы напряжений. Соответственно между фазными и линейными значениями напряжений будет существовать определенная зависимость:

Далее будет показано, что соотношение (2) будет справедливо лишь при определенных условиях, а также в случае отсутствия нулевого провода, то есть в трехпроводной сети.

Исходя из указанного выше соотношения (2) можно сделать вывод, что соединение звездой лучше применять в случае, когда каждая фаза трехфазного электроприемника или однофазные приемники рассчитаны на напряжение в раз меньше, чем номинальное линейное напряжение сети.

Также из схемы соединения звезда (смотри схему выше) видно, что при соединении приемников звездой фазные токи будут равны линейным:

Применив первый закон Кирхгофа можно получить соотношение между токами при соединении электроприемников звездой:

Зная фазные токи с помощью формулы (4) можно вычислить ток нейтрального провода I_N. В случае отсутствия нейтрального провода справедливо будет выражение:

Симметричная нагрузка при соединении приемников звездой

Нагрузка считается симметричной тогда, когда реактивные и активные сопротивления каждой фазы будут равны, то есть выполняется равенство:

Условие симметричности также может быть выражено через комплексные сопротивления Z_a = Z_b = Z_c.

Симметричная нагрузка в сети возникает при подключении трехфазных электроприемников. Будем считать, что данная система имеет нейтральный провод.

В отношении любой из фаз при симметричной нагрузке будут справедливы все формулы, полученные для однофазной сети, например для фазы А:

Так как в четырехпроводной цепи U_a = U_b = U_c = U_л /  , то при симметричной нагрузке:

Векторная диаграмма при симметричной активно-индуктивной нагрузке приведена выше. Из приведенных выражений и векторной диаграммы следует, что при симметричной нагрузке образуется симметричная система токов, поэтому ток в нейтральном проводе будет равен I_N = I_a + I_b + I_c = 0.

Отсюда можно сделать вывод, что при симметричной нагрузке отключение нейтрального провода не приведет к серьезным нарушениям работы электроприемников, то есть не произойдет изменение фазных напряжений, углов сдвига, токов, мощностей.

Из сказанного выше следует, что при симметричной нагрузке в нейтральном проводе нет необходимости, и довольно часто в симметричных системах нейтральный провод не применяется.

Мощность трехфазного приемника электрической энергии при симметричной нагрузке можно выразить формулами:

Как правило, для трехфазных приемников электрической энергии в качестве номинальных параметров указываются линейные напряжения и токи. Исходя из этого, целесообразней выражать мощность трехфазной цепи тоже через линейные напряжения и тока, поэтому подставим в формулу (6) линейные значения и получим:

Пример

К трехфазной электрической цепи с линейным напряжением U_л = U_ab = U_bc = U_ca = 380 В необходимо подключить трехфазный электроприемник, каждая фаза которого рассчитывается на фазное напряжение в 220 В и имеет активное сопротивление r_ф = 10 Ом и индуктивное сопротивление х_ф = 10 Ом, которые соединены последовательно. Необходимо определить мощности, углы сдвига между токами и напряжениями (cos φ) и фазные токи.

Решение

Каждая фаза потребителя электрической энергии рассчитана на напряжение в раз меньше номинального, то фазы потребителя нужно соединять в звезду. Поскольку нагрузка в данном случае симметричная, то нулевой провод (нейтраль) к потребителю можно не подводить.

Фазные тока, углы сдвига cos φ, а также полны сопротивления фаз будут иметь вид:

Активная, реактивная и полная мощности  приемника, а также любой фазы будут равны:

Векторная диаграмма для данной системы приводилась выше.

Несимметричная нагрузка при соединении приемников звездой

Нагрузка трехфазной электрической сети будет считаться несимметричной, если хотя бы одно из фазных сопротивлений не равно другим. Проще говоря, сопротивления фаз не равны, например: r_a = r_b = r_c, x_a = x_b ≠ x_c. В общем случае  считают, что несимметричная нагрузка возникает при отключении одной из фаз.

Возникает не симметрия чаще всего при подключении к трехфазной сети однофазных электроприемников. Они могут иметь различные мощности, режимы работы, различное территориальное расположение, что тоже влияет на величину фазной нагрузки.

В случае, когда необходимо подключить однофазные потребители электрической энергии, для более равномерной загрузки их делят на три примерно одинаковые по мощности группы.

Один вывод однофазных потребителей подключают к одной из трех фаз, а второй вывод подключают к нейтральному проводу. Так как все электроприемники рассчитываются на одно напряжение, то в пределах каждой фазы они соединяются параллельно.

Главной особенностью электрической сети несимметричной нагрузкой является то, что она должна в обязательном порядке иметь нейтральный провод. Это объяснимо тем, что при его отсутствии величины фазных напряжений будут в значительной степени зависеть от величины не симметрии сети, то есть от величин и характера сопротивления каждой из фаз. Поскольку сопротивления фаз могут варьироваться довольно в широких пределах в зависимости от количества подключенных электроприемников, также широко будет варьироваться и напряжения на потребителях электрической энергии, а это недопустимо.

Для иллюстрации выше сказанного ниже приведена векторная диаграмма для трехфазной несимметричной цепи при наличии нейтрального провода:

Ниже приведена приведена векторная диаграмма для этой же цепи, но при отсутствии нулевого рабочего (нейтрального) провода:

Также можно посмотреть видео, где объясняется, что может произойти в электрической цепи при обрыве нулевого провода:

Необходимость нулевого провода станет еще более очевидной, если представить, что вам необходимо подключить однофазного потребителя к одной из фаз, при этом остальные две подключать нельзя, так как приемник рассчитан на фазное напряжение 220 В, а не на линейное 380В, как в таком случае получить замкнутый контур для протекания электрического тока? Только использовать нулевой рабочий проводник.

Для повышения надежности соединения электроприемников в цепь нулевого рабочего проводника не устанавливают коммутационную аппаратуру (автоматические выключатели, предохранители или разъединители).

Фазные токи, углы сдвига, а также фазные мощности при несимметричной нагрузке будут различными. Для вычисления их фазных значений можно применить формулу (5), а вот для вычисления трехфазной мощности формула (6) уже не подходит. Для определения мощностей необходимо пользоваться выражением:

Если существует необходимость определения тока нейтрального провода, то необходимо решать задачу комплексным методом. Если существует векторная диаграмма, то определить ток можно по ней.

Пример

В осветительной электрической сети с напряжением в 220 В в фазе А включено 20 ламп, фазе В – 10 ламп, а в фазе С – 5 ламп. Параметры лампы U_ном = 127 В, Р_ном = 100 Вт. Необходимо определить ток нейтрального провода и каждой лампы.

Решение

Если учесть, что лампы накаливания имеют только активное сопротивление (реактивное слишком мало и им пренебрегают), то по формуле мощности определим ток лампы, а по закону Ома ее сопротивление:

Зная число и сопротивление ламп нетрудно определить сопротивления фаз, а также фазные токи:

Для определения тока в нейтральном проводе I_N решим задачу комплексным методом. Так как при сделанных ранее допущениях комплексные напряжения приемника равны комплексным ЭДС источника, получим:

Где комплексные значения фазных сопротивлений будут равны Z_a = 8,05 Ом, Z_b = 16,1 Ом, Z_с = 32,2 Ом.

Комплексные значения токов, а также действующее значение тока нейтрального провода будут иметь вид:

Какое будет фазное напряжение на 3-хфазном асинхр. двигателе при соединении треугольником, если линейное напряж=220В?

Бытовая электросеть имеет 3 фазы по 380 вольт и это ЛИНЕЙНОЕ напряжение (это тот кАбель, который в дом/ в в электрощиток на лестничной площадке заходит) . А в квартиру заводится ОДНА фаза и «ноль» и получаемое ФАЗНОЕ напряжение равно 220В. При соединении треугольником фозное напряжение равно линейному. Ты чего куда подключить хочешь? Спроси-отвечу, у меня работа с движками и их подключением связана. А так… ты некорректно вопрос сформулировал.

не прав. в треугольнике линейное напряжение= фазному. если соединить статор в треугольник и вкл в сеть 380/220 то двигатель сгорит, т. к. расчетное напряжение обмотки 220В. двигатели с маркировкой 380/220 пригодны для сетей с лин напряжением 380В, статор соед в звезду, и для сетей с лин напряжением 220В, тогда статор соед в треугольник

при соединении треугольником на каждой обмотке 220 звездой 380

линейный ток — это… Что такое линейный ток?

 

линейный ток
Ток, протекающий в линейном проводнике трехфазной электрической цепи, соединяющем источник и приемник электрической энергии.

EN

phase current, I
value of the current flowing in each phase of an electrical distribution system
[IEC 61557-12, ed. 1.0 (2007-08)]

FR

courant de phase, I
valeur du courant circulant dans chaque phase d’un réseau de distribution électrique
[IEC 61557-12, ed. 1.0 (2007-08)]

Четырехпроводная система трехфазного тока

Нейтраль — обшая точка соединенных концов фазных обмоток генератора (источника питания). То же самое относится и к потребителю (нагрузке).
Линейные провода (проводники) — проводники, присоединенные к началу фазных обмоток  (А, В и С).
Звезда (соединение звездой) — представленное на рисунке соединение, в котором начала обмоток соединены в одну общую точку.
Нулейвой провод (проводник) или нулевой рабочий провод (проводник) — проводник соединяющий нейтрали генератора (источника питания) и потребителя (нагрузки). Нулевой провод выполняет роль обратного провода.
Линейное напряжение — напряжение между линейными проводами.
Фазное напряжение — напряжение между линейным и нулевым проводом.
Фазный ток — ток, протекающий по фазной обмотке генератора (источника питания) или потребителя.
Линейный ток — ток, протекающий по линейному проводу.
При соединении звездой линейный ток равен фазному.
При работе по нулевому проводу протекает ток, равный векторной сумме трех линейных токов: I_А, I_B и I_C.
Если фазы нагружены равномерно, то ток нулевого провода равен нулю.

[На основе книги Кузнецов М. И. Основы электротехники. М, «Высшая Школа», 1964]

22. Как рассчитать фазный ток, если известны линейное напряжение и сопротивление нагрузки в схеме треугольник.

Схема треугольник

В этой схеме (рис. 10.2,) токи в фазах при несимметричной нагрузке различны 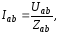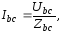но напряжения остаются неизменными (номинальные). Линейные токи определяют по закону Кирхгофа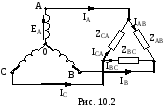

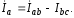
Мощность трехфазной несимметричной цепи.

Для измерения активной мощности трехфазной нагрузки в общем случае, когда нагрузка несимметрична, используют 3 ваттметра (рис. 10.3, а), и тогда полная мощность равна сумме показаний ваттметров. При симметричной нагрузке достаточно одного ваттметра, включенного в одну из фаз.

Трехфазную цепь с тремя проводами, соединяющими генератор с потребителем, всегда можно рассматривать как две двухпроводные линии, имеющие один общий провод, например как линии АВ и СВ с общим проводом В (рис.  10.3, б), в котором ток 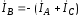. При этом по первой линии при напряжении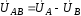идет ток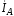, а по второй линии при напряженииидет ток.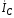

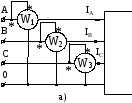
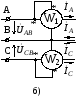
Рис. 10.3

Мощность, передаваемая по первой линии ,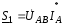

а мощность, передаваемая по второй линии,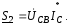

Полная мощность, передаваемая по трехпроводной линии, S = S₁ + S₂.

Из сказанного вытекает возможность измерять мощность, передаваемую по трехпроводной линии трехфазной системы, двумя ваттметрами, каждый из которых определяет мощность, передаваемую по одной из двух двухпроводных линий. Такая схема включения ваттметров (схема Арона) изображена на рис. 10.3, б.

При выводе не делалось никаких предположений о симметрии системы, следовательно, найденный метод измерения мощности двумя ваттметрами применим как в случае симметричной, так и в случае несимметричной трехфазной трехпроводной системы.

При чисто активной нагрузке (=0) показания обоих ваттметров одинаковы.

Полное значение передаваемой (активной) мощности равно алгебраической сумме показаний обоих ваттметров. На практике часто два ваттметра ставятся на общую ось. Показания такого сдвоенного ваттметра непосредственно равны всей (активной) мощности, передаваемой по трехпроводной линии.

Если определить разность показаний ваттметров W₂–W₁=U_ЛI_Лsin, то по ней можно определить реактивную мощность 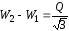. На основании последних выражений легко вывести формулу, позволяющую определить угол по показаниям ваттметров:

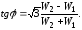
23. Как определяется мощность в трёхфазных цепях?.

Вычисление величины полной мощности. Расчет полной мощности электрической цепи требует знания ее активной и реактивной составляющих, соотношение которых в любой схеме описывается треугольником мощностей.

Для вычисления активной (Р) и реактивной (Q) составляющих 3-х фазной цепи проводится суммирование их величин в каждой фазе по формулам:

   Р=Р_A+Р_B+Р_C=U_AI_Acosφ_A+U_ВI_Вcosφ_В+U_СI_AСcosφ_С;    Q=Q_A+Q_B+Q_C=U_AI_Asinφ_A+U_ВI_Вsinφ_В+U_СI_AСsinφ_С.

I_A, I_В, I_С, U_A, U_В, U_С – вектора токов и напряжений в фазах, Φ – угол сдвига фаз векторов тока относительно напряжения.

Для симметричного режима работы схемы во всех фазах выполняется равенство мощностей. Поэтому общую величину мощности можно получить простым умножением фазной составляющей на количество фаз в системе:

   Р=3Р_Ф=3U_Ф∙I_Ф∙cosφ;    Q=3Q=3U_Ф∙I_Ф∙sinφ;    S=3S_Ф=(Р2+Q2)=3U_ФI_Ф.

Делаем замену фазных составляющих линейными по их соотношениям для схемы звезды: I_Л=I_Ф, U_Ф=U_Л/√3.

В результате получаем:

   Р=3U_Ф∙I_Ф∙cosφ=(3U_Л∙I_Л/√3)∙cosφ=√3∙U_Л∙I_Л∙cosφ.

Заменяем фазные составляющие линейными для схемы треугольника по их соотношениям: I_Ф=I_Л/√3, U_Ф=U_Л.

Итог вычисления:

   Р=3U_Ф∙I_Ф∙cosφ=(3U_Л∙I_Л/√3)∙cosφ=√3∙U_Л∙I_Л∙cosφ.

Таким образом, получилось, что зависимость от вариантов соединения элементов цепи схемой γ либо Δ в 3-х фазной симметричной системе значения мощностей отсутствует. Они вычисляются по одним и тем же формулам:

   Р=√3∙U∙I∙cosφ [Вт];    Q=√3∙U∙I∙sinφ [вар];    S=√(Р²+Q²) [ВА].

Для данных выражений сложилось правило: подставлять линейные значения векторов U и I без указания их линейных индексов.

Способы измерений мощности В энергетике существует постоянная необходимость измерения электрических величин. Активная составляющая полной мощности замеряется ваттметром, а реактивная – варметром. Ваттметр работает по алгоритму, описанному формулой:

   W=U_W∙I_W∙cos(U_W^I_W)=Re│U_W∙I_W*│.

U_W, I_W – те вектора, которые подвели к клеммам прибору для замера активной составляющей.

Практика электрических измерений предлагает несколько вариантов подключения к электросети ваттметров. Они выбираются в зависимости от схемы выполненный коммутации нагрузок и ее характеристик.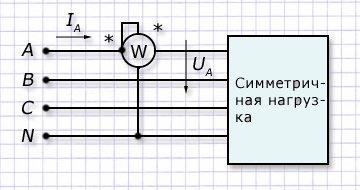

В симметричной 3-х фазной системе достаточно включить один ваттметр в любую фазу для постоянного замера активной мощности с последующим утроением полученного результата по алгоритму Р=3W=3U_Ф∙I_Ф∙cosφ.

Однако, этот простой способ только ориентировочно оценивает замеряемые величины, имеет большие погрешности. Поэтому, он малоприемлем для выполнения замеров, требующих высокой точности и в решении коммерческих задач.

Более точные замеры активной составляющей для звезды с нейтральным проводом обеспечивает использование в измерении трех ваттметров.