Первая электронная вычислительная машина с двоичной системой счисления. Забытый проект ABC

До 70 годов считалось, что первый электронный цифровой компьютер (ENIAC) был создан Джоном Мокли и Джоном П. Эккертом еще в далеких 40 годах. В 1973 году завершился судебный процесс между корпорацией Sperry Rand и компанией Honeywell за авторство изобретения электронной вычислительной машины. Корпорацией Sperry был приобретен патент на ENIAC и после этого компания взыскивала процент от других компаний, которые занимались разработкой ЭВМ. Honeywell платить не захотели, после чего корпорация Sperry подала на них в суд, но не тут то было: им был предьявлен встречный иск. Обвинялась Sperry в том, что использовала недействительный патент и этим самым нарушала антитрестовский закон. Представители компании Honeywell привели как довод созданную до ENIAC конструкцию ЭВМ Атанасова. Атанасов был разыскан, что самое интересное, он не был хорошо знаком с устройством ENIAC. Конструктивные особенности его компьютера ABC были использованы в ЭВМ ENIAC. Джон В. Атанасов — ученый из Айовы, еще в 30 годах создал первую электронную вычислительную машину, которая работала на основе двоичной системы счисления.

4 октября 1903 года Джон Винсент Атанасов родился в нескольких милях к западу от Гамильтона, штат Нью-Йорк, на ферме, принадлежавшей его деду, в семье эмигрантов из Болгарии. Он был первым ребенком в семье Джона (Ивана) Атанасова (1876-1956) и Ив Лаусен Парди (1881-1983). Его отец был инженером, а мать — учительницей математики в школе. В семье было девять детей (один из них умер): Джон, Этелин, Маргарет, Теодор, Авис, Раймонд, Мельва и Ирвинг.

Джон писал о своих родителях:

«Мой отец родился 6 января в 1876 году, наш народ как раз готовился к восстанию против турок (апрельское антиосманское восстание в Болгарии, произошло 18 апреля — 23 мая 1876 года и было жестоко подавлено турками, оно считается кульминацией болгарского национально освободительного движения против османского гнета, в ходе восстания погибло от 25 до 50 тысяч болгар). Людям, проживавшим в нашем поселке было предложено покинуть свои дома вместе с семьями, после чего дома были сожжены. Моя бабушка бежала с ребенком (моим отцом) на руках за дедушкой… прозвучал выстрел… один из турецких солдат выстрелил моему дедушке прямо в грудь, он упал замертво, рикошетом пуля задела моего отца и на всю жизнь оставила шрам, как ужасное напоминание о тех событиях. Бабушка вышла второй раз замуж. В 15 лет мой отец прибыл в США, в 15 лет он остался сиротой. Здесь он закончил Университет Колгейт (американский гуманитарный колледж в г. Хамильтоне, округ Мэдисон штата Нью-Йорк). Позже женился на моей матери-американке, дед по линии матери принимал участие в гражданской войне между Севером и Югом».

с матерью

Происшествие, случившееся в то время, является задокументированным фактом в истории болгарского народа (так называемая Резня в Бояджик). 11 мая 1876 года турецкая армия напала и разграбила деревню Бояджик, убив почти две сотни невооруженных людей, в основном женщин и детей. Только лишь чудо уберегло отца Атанасова от верной гибели.

«… сотни, тысячи болгар всех возрастов и обоего пола погибли при самых страшных обстоятельствах; подробности совершенных жестокостей ужасны; в Перуштице, Батаке, Ветрене вырезано все население. Недавно деревня Бояджик около Ямбола испытала ту же судьбу. Женщин и девушек насиловали, убивали и уводили в рабство, убивали детей, убивали крестьян, убегающих при приближении войска, убивали и тех, кто оставался при них, убивали тех, кто прятался, и тех, что сдавали оружие, — за то, что оно у них было; и тех, у которых его не было, — за то, что они его не сдавали; стреляли из вагонов по служащим на линии железной дороги… вооруженные банды бродят по стране, отнимая у крестьян все, что можно отнять, и регулярные войска появляются при малейшем сопротивлении, чтобы предать все огню и меч».

Иван Атанасов прибыл в США со своим дядей в 1889 году, имя Иван было изменено иммиграционной службой на — Джон. После окончания колгейтского университета в 1890 году родители Атанасова поженились и переехали в Нью-Джерси, где отец получил работу инженера. Отец продолжил свою учебу в вечернее и ночное время, посещал курсы, увлекался электротехникой и электроникой. После рождения Джона семья переехала во Флориду, где отец получил работу в новом городке Brewster инженером на электростанции, на данный момент это город-призрак.

городок Brewster

Джон закончил здесь начальную школу, уже в то время его интересовало все, что было связано с электричеством) В 9 лет он обнаружил неисправность в электропроводке на заднем крыльце дома и смог починить ее. К слову, его отец был первым в округе, кто провел электрическую проводку в своем доме. Джон был развит не по годам, рано научился читать и любил все, что мог узнать из книг. Учился он хорошо, был прилежным учеником, интересовался спортом, особенно был увлечен бейсболом. Но увлечение бейсболом растаяло как туман, после того как отец подарил ему логарифмическая линейку, считается, что до появления карманных калькуляторов этот инструмент был просто незаменим для инженеров при расчетах.

«Эта логарифмическая линейка была моей самой любимой игрушкой, бейсбол был почти забыт, когда я приступил к серьезному изучению логарифмов». В 10 лет он изучал физику и химию, занимался математикой, как-то его мать дала ему книгу, в которой шла речь о вычислениях в других системах счисления, отличных о десятичной.

Еще во время учебы в школе, Атанасов освоил дифференциальное исчисление, а отец взял его как-то на завод и показал работу генератора. Это все определило его дальнейший выбор. Когда мальчику нужно было переходить в старшие классы, семья переехала на ферму в Old Chicora, Флорида. За два года в возрасте 15 лет Атанасов окончил Mulberry High School с отличием по математическим дисциплинам. Он решил, что быть физиком-теоретиком его призвание. Но ему пришлось год проработать в фосфатных шахтах, чтобы заработать денег. В 1921 году Джон поступил в университет во Флориде на электротехнический факультет.

Много времени Атанасов проводил в механических и литейных мастерских университета. Он закончил университет в 1925 году со степенью бакалавра с наилучшими баллами и получил стипендию на обучение в магистратуре по математике и физике от штата Айова. Ему предлагали обучение многие высшие заведения, такие как Гарвард, но он решил все же продолжить обучение в Эймсе.

Летом 1925 года Джон закончил обучение в Айове и получил диплом инженера — электрика, тут же занимался преподавательской деятельностью и вел два математических класса. В 1926 году Джон женился на молодой голубоглазой брюнетке Луре Микс из Оклахомы. Через год у них родилась дочь Эльзи и семья переехала в Висконсин, где Атанасов (май 1930 год) защитил свою докторскую диссертацию. Двое других детей, двойнята Джоан и Джон, родились через год.

В марте 1929 года он стал аспирантом Университета в штате Висконсин и продолжил свою учебу в области теоретической физики. Работая над своей докторской диссертацией, Атанасову приходилось делать много вычислений, его тема была о гелии поляризующемся в электрическом поле, он часами проводил расчеты с помощью калькулятора Монро, одним из самых современных вычислительных устройств того времени. В то время аналоговые методы решения с помощью дифференциального анализатора Ванневара-Буша не могли уже удовлетворять запросы из-за допускаемых неточностей, а устройств, которые реализовали бы цифровой подход, просто — напросто не существовало. И вот, в такие моменты Атанасов понимал, что пришло время разработать что-то, что сможет помочь делать расчеты намного быстрее, точнее, его не покидала мысль о автоматизации решения больших линейных алгебраических уравнений. Атанасов даже попытался модифицировать калькулятор фирмы IBM.

Поэтому после возвращении в Государственный колледж штата Айова, где он работал ассистентом профессора по математике и физике, он всерьез занялся разработкой и созданием быстродействующей вычислительной машины. Он проводил эксперименты с вакуумными трубками, радио, изучал электронику. Атанасов изучил многие доступные на то время вычислительные устройства, и пришел к выводу, что их можно разделить на два класса аналоговые устройства и вычислительные машины (но термин «цифровая вычислительная машина» начал использовался позже). В 1936 году Атанасов попытался создать небольшой аналоговый калькулятор. В Айове никто кроме Джона не занимался созданием новых вычислительных машин, здесь он спокойно обдумывал свои идеи, но с другой стороны и не было людей специалистов с которыми он мог бы обсудить на месте свои задумки, разобраться в возникших технических и теоретических проблемах. Такой себе одинокий изобретатель.

Джон Атанасов изначально думал создать аналоговое устройство, что-то похожее на его любимые логарифмические линейки, но очевидным стал тот факт, что длина таких линейных пленок для точного решения линейных алгебраических уравнений была бы сотни метров. Ограниченность аналоговых средств вычисления толкали ученого на создание чего-то «революционного». Как сохранить числа в машине — вот была первая задача, которую Атанасов попытался решить. Вот так возник термин «память» для описания данной функции в машине. Какие виды памяти только не перебрал Атанасов и механические штырьки, и электромагнитные реле, и электронные лампы. Так как электронные лампы на то время были дорогие, он решил использовать конденсаторы. Конденсаторы сами по себе небольшие и недорогие компоненты, которые могли на некоторое время сохранять электрический заряд, но вот о маленьких размерах машины и ее быстродействии с таким видом памяти можно было забыть.

Вторая задача, которую следовало решить он назвал «вычислительным механизмом». Для этого механизма Атанасов решил использовать электронные лампы, которые использовались бы в качестве двухпозиционных переключателей с функциями включить/выключить. На данном этапе и возникла дилемма, какую систему исчисления использовать в машине (даже система исчисления с основанием на сто показалась ученому многообещающей). В конце-концов была выбрана двоичная система счисления.

Еще была у Атанасова одна страсть — автомобили. Он старался каждый год покупать новый (вот не известно продавал ли предыдущие). Одним из зимних вечеров 1937 года в придорожной таверне, куда заехал Атанасов на новом форде c мощным двигателем V8, его посетила идея и то, по каким принципам должен быть создан новый вычислительный аппарат. Суть этих принципов была сформулирована им позже, а именно она состояла в том, что для работы компьютера будет использоваться электричество, и основана она будет не на привычной десятичной системе счисления, а на двоичной.

«… однажды зимним вечером 1937 года я почувствовал, что совершенно измучен невозможностью найти решение проблем, связанных с конструкцией машины. Я сел в автомобиль, разогнался и ехал так долгое время, пока не стал контролировать свои эмоции. Это было моей привычкой — у меня получалось восстанавливать контроль над собой, после того как проедусь по дороге, сосредоточившись на управлении автомобилем. Но в ту ночь я был слишком измучен и продолжал мчаться, пока не пересек реку Миссисипи и не оказался в штате Иллинойс, в 300 километрах от того места, где сел в машину…(зашел в таверну и заказал выпивку) я почувствовал, что уже не так нервничаю, и мои мысли снова обратились к вычислительным машинам. Я не знаю, почему моя голова тогда заработала и почему она не работала раньше, но там было симпатично, прохладно и тихо».

Принципы работы будущей вычислительной машины Атанасов набросал на салфетке, он думал о том, какой будет конструкция регенеративной памяти, назвал ее «дискретной», он придумал поместить конденсаторы на вращающиеся цилиндрические барабаны (из под банок сока), каждую секунду они бы вступали в контакт со щетками (в виде кабелей) и заряжались бы. Память, состоящая из конденсаторов, «встряхивалась» бы щетками при повороте вращающихся цилиндров, а при необходимости снимались бы старые данные и вводились новые. Придуманная логическая электронная схема позволяла считывать числа с двух разных цилиндров с конденсаторами.

Началась работа над создание прототипа. Нужен был помощник, так в 1939 году произошло знакомство Атанасова с Берри, который на тот момент был выпускником электротехнического отделения, хорошо разбирался в электронике.

Работа над ABC (Atanasoff— Berry Computer) длилась три года, а первый прототип был продемонстрирован еще в 1939 году и его целью было решение системы линейных уравнений, система могла работать с 29 переменными, она обрабатывала два уравнения и убирала одну из переменных, а получившиеся уравнение выводила на двоичные перфокарты размеров 8Х11, после этого карты с более простой системой уравнений подавались обратно в машину, процесс начинался заново. Все это сокращало бы такие расчеты с 29 переменными. На калькуляторе это заняло бы 10 недель, а на вычислительной машине всего 7! дней. Но все равно это был бы очень длительный процесс.

В ABC использовалась двоичная арифметика. Длина слова составляла 50 бит. Перфокарты с промежуточными результатами содержали тридцать 50-разрядных двоичных чисел. В машине было два запоминающихся устройства, которые состояли из вращающихся барабанов, к которым были прикреплены небольшие конденсаторы, подключенные к латунному контакту на поверхности барабана.

5/6 периферийной поверхности барабана было занято латунными контактами, а 1/6 оставалась пустой, что предоставляло время для выполнения других операций. Скорость прохождения контактов мимо считывающей щетки составляла 60 в секунду.

По словам Берри:
«… полярность заряда на конденсаторе указывала “единицу” или “ноль”, и каждый конденсатор сразу же после считывания перезаряжался, чтобы заряд никогда не оставался на нем более одной секунды. Все слова обрабатывались параллельно, но внутри каждого слова цифры обрабатывались последовательно. Интересно отметить, что прежде чем проектировать память на конденсаторах, мы серьезно рассматривали идею использования магнитных барабанов, но отказались от нее из-за низкого уровня сигналов. Имелось 30 идентичных арифметических устройств, которые по существу были двоичными сумматорами. Каждое состояло из серии электровакуумных ламп с прямой связью (семь сдвоенных триодов), соединенных между собой таким образом, что они выполняли двоичное сложение. Каждое устройство имело три входа (два — для складываемых или вычитаемых чисел и один — для переноса с предыдущего места) и два выхода (один — для результата на том месте, а другой — для переноса на другое место)».

Преобразование десятичных чисел в двоичные осуществлялось с помощью вращающегося барабана, на котором находились контакты, представляющие двоичные эквиваленты 1,2 — 9,10,20 — 9х14. На выходе тот же аппарат в обратном порядке преобразовывал и выдавал на механический счетчик десятичный результат.

Атанасов напечатал на 35 страницах описание такой машины в надежде получить финансирование данного проекта. Сумма расходов составила чуть больше 5 тысяч долларов, но финансирование он позже получил от частного фонда. Адвокат, который был нанят Айовским университетом, по каким-то причинам не подал заявку на патент.

В 1940 году Атанасов и Берри пригласили Мокли (физик из колледжа Урсинуса) в Айову «на помощь», после того как Атанасов прослушал его лекцию о «возможности использования аналоговых компьютеров для решения проблем метеорологии» в Пенсильвании. В 1941 году Мокли посетил дом Атанасова и они втроем 5 дней общались на тему цифровой вычислительной машины ABC, но материалы Атанасов попросил оставить все же в секрете. Так состоялась эта судьбоносная встреча Атанасова и Мокли.

Мокли

Мокли прибыл вечером в пятницу 13 июня из Вашингтона. Атанасов был готов показать свою частично собранную машину, не смотря на предупреждения жены о том, что Мокли ей показался не совсем честным человеком, а ABC не была еще запатентована. Мокли впечатлили пару вещей — идея использования конденсаторов в блоке памяти и метод пополнять их заряд раз в секунду, поместив их на вращающийся цилиндр.

Вот, что вспоминал Мокли о этой встрече и увиденной машине Атанасова — Берри:

«Я думал, что его машина гораздо хитроумнее, но так как она оказалась частично механической, в том числе в ней использовались вращающиеся коммутирующие переключатели, она никоим образом не была похожа на то, что я имел ввиду. Я больше не интересовался подробностями. Полумеханический характер машины Атанасова вызвал у меня довольно сильное разочарование. У него не было в планах ничего, что могло бы сделать машину более универсальной и позволило бы ей решать какие-либо другие задачи, кроме решения системы линейных уравнений».

«Поэтому, когда началось судебное разбирательство за первенство среди электронных вычислительных машин, в своих свидетельствах Мокли сказал, что данный визит для него значил не больше, чем посещение выставки, на которой он просто почерпнул кое-какие идеи». Главным отличием Мокли от Атанасова было его желание и умение работать в коллективе. В результате Мокли и его талантливая команда вошли в историю как изобретатели первого электронного компьютера. Да и потом, как утверждал Мокли это были его идеи, которые были дополнены идеями, опытом других талантливых ученых, во время беседы с ними, при посещении разных выставок. После посещения Атанасова, Мокли был приглашен пройти курс электроники в университете Пенсильвании. Все это сподвигло его на создание компьютера и уже к осени 1941 года Мокли доделал свою версию компьютера. Здесь уже начинается история ENIAK. Первым полностью электронный цифровой компьютер, который собирали при строгой секретности для военных целей в университете Пенсильвании.

Вернемся к Атанасову и его машине.

И так уже через три года к 1942 году машина была почти готова. Размер такой вычислительной машины был с письменный стол и насчитывала такая машина 300 электронных ламп. Проблемой был механизм для прожигания отверстий в перфокартах с помощью искры (он срабатывал через раз).

Пришел 1942 год, военные годы заставили отложить работу Атанасова над проектом ABC. Он был призван на службу на флот и был назначен главой Отдела акустики при Военно-морской Артиллерийской лаборатории (NOL) в Вашингтоне, штат Колумбия. Его зарплата составила 10 тысяч долларов и работал он тут над проблемой акустических мин, участвовал в испытании атомной бомбы на атолле Бикини. В это время вычислительная машина Атанасова пылилась в подвале в университете Айовы, была разобрана каким-то аспирантом, так как занимала много места. О ней было позабыто. Ни Атанасов, ни Берри не были уведомлены о том, что их детище было разобрано и только лишь третья его часть сохранилась.

В 1949 году Атанасов развелся со своей первой женой. Лура переехала с детьми в Денвер. В том же году Джон женился во второй раз на Алисе Гросби.

Даже если бы о АВС вспомнили, у данной машины были ограничения: процесс замедлялся за счет механически поворачивающихся ячеек памяти да и система прожигания отверстий в перфокарте тормозила работу такого компьютера. Для того, чтобы ускорить быстродействие такой вычислительной машины нужно было сделать ее полностью электронной и программируемой.

В 1945 году Артиллерийское ведомство обратилось к Джону Атанасову с запросом помочь в конструировании компьютера для Военно-морской Артиллерийской лаборатории. Атанасов отказался от проекта, аргументируя это тем, что он не сможет одновременно работать над компьютерным проектом и заканчивать работу в Отделе акустики NOL.

После окончания войны Атанасов вернулся к компьютерам. Он сожалел о том, что закинул работу над созданием компьютера, так как его работа была поистине революционной. До 1949 года он был главой отдела акустики NOL. В 1950-1951 году он был директором программы взрывов при NOL.

В 1952 году Джон Атанасов открыл фирму «Артиллерийская инженерная корпорация» в городе Фредерик, штат Мериленд, позже Атанасов работал консультантом по автоматизации в упаковочной фирме.

В один прекрасный день в 1954 году к Атанасову пришел адвокат фирмы IBM, с предложение доказать то, что именно он — Атанасов был первым, кто создал электронный компьютер, а проект ENIAC просто напросто был заимствован у проекта ABC. Атанасов решил побороться за первенство своего проекта.

«… Атанасов все более убеждался, что ENIAC была заимствована от его ABC и что стоит продолжать это дело. Более того, ему придавало силы признание его заслуг в других странах, в частности на родине его предков — Болгарии, которая в 1970 году наградила его орденом Кирилла и Мефодия I степени».

Приговор судьи звучал так:

«Эккерт и Мокли, — читал судья Ларсон, — не сами изобрели этот автоматический электронный цифровой компьютер, но вместо того позаимствовали эту идею у доктора Джона В. Атанасова, а поэтому патент ENIAC является недействительным».

Остаток жизни Джон Винсент Атанасов (после сердечного удара в 1975 году) провел на своей ферме около Монровил, штат Мериленд. Он умер 15 июня в 1995 году в возрасте 92 лет.

Хоть машина Атанасова и не была ни универсальной, ни программируемой, ни полностью электронной, ученый заслуживает считаться первопроходцем, тем, кто придумал первый частично электронный цифровой компьютер.

Переводим числа между двоичной и десятичной системами «на лету», объяснение «на пальцах»

Здравствуйте, Хабровцы.
Пост можно было бы назвать: «Для любителей посчитать на пальцах», но это мы узнаем дальше.

Вступление: А что-же тянуть. Все что будет дальше, пойдет на тему подсчета в двоичной системе на пальцах. Кто еще не знает, постараюсь обьяснить, что это, как и зачем это осваивать.
Начну, пожалуй, с преимуществ:
1. Удобно переводить любое число с десятичной в двоичную системы и наоборот, не используя калькулятор.
2. Развивается моторика пальцев.
3. Развивается визуальное восприятие двоичных чисел.
Минусы:
1. Немного тренировки.
2. Нельзя в публичных местах показывать числа 26,27,352,378 и 891.

Суть:
Многим, наверняка, приходилось переводить между системами. И я думаю многие запомнили, что:
2-10
3-11
4-100
5-101
и т.д.
Логично, что исходя из того что каждая разрядность имеет два состояния, мы можем изобразить это дело на пальцах.
Поставьте перед собой руку (ладонью к себе), согните большой палец. Вот и есть единица. Разогните большой и согните указательный, вот и два. Тоесть разогнутый палец — это 0, а согнутый — 1. Так как начальные нули отбросились, мы имеем отсчет от «самой левой» единицы.
Названия пальцев — те которые загнуты:
средний, большой — 101 — 5
безымянный, средний -1100 — 12
мизинец, средний — 10100 — 20
Чтобы загибать мизинец, понадобиться некоторая практика. Но суть в другом. Представим разрядность каждого пальца руки, как 2^n (на фото)

То есть,

Теперь, представим, что нам нужно перевести число 25 в двоичную. Загибаем Мизинец — 16, Безымянный — 8 и большой — 1. т.к. 16+8+1=25.

Если не поняли, то вот еще пример, число 14, думаем: Мизинец — это много, средний нормально, но можно взять больше, поэтому — загибаем безымянный, это 8. Запомнили, далее средний — +4, єто уже 12 и указательный — +2, итог 14.

Так же поступаем с двоичными. Вот например видим где-то: 1011101. Представляем это на руках с разрядностями (уже две руки).

64+16+8+4+1=93
Имеем: 1011101(2) = 93(10)

Заключение: Таким образом мы можем использовать данный метод от 0 до 1023, используя пальцы и обладая элементарной арифметикой. Но при добавлении, хотя бы, одного разряда, можно будет считать до 2047, и далее до 4095, 8191 и т.д. А это могут быть руки, ноги, веки, либо что-то еще что может иметь два состояния 1 и 0.

Троичный компьютер: Да, Нет, Может быть: judgesuhov — LiveJournal

В принципе, у троичной системы счисления было не меньше шансов, чем у двоичной. Кто знает, по какому пути развития пошел бы технический прогресс, если бы «трайты» одержали победу над «байтами»?

Информация, которой оперирует компьютер, так или иначе раскладывается на единицы и нули — графика, музыка, тексты, алгоритмы программ. Все просто и понятно: «включено» — «выключено», «есть сигнал» — «нет сигнала». Либо «истина», либо «ложь» — двоичная логика. А между тем еще в 1961-м, в год первого полета человека в космос, в Советском Союзе наладили производство необычных вычислительных машин, оперировавших не двоичной, а троичной логикой.

История создания
Строго говоря изобретателем первой вычислительной машины с троичной логикой в далеком 1840 году был английский изобретатель-самоучка Томас Фоулер. Его машина была механической и полностью деревянной.
Ну а первыми, кто вернулся к этой идее (более чем через сто лет), были инженеры с кафедры вычислительной математики механико-математического факультета МГУ.

Все началось в 1954 году: кафедре должны были передать электронно-вычислительную машину М-2, но не сложилось. А машину-то ждали, готовились ее устанавливать и налаживать, с нею связывались определенные ожидания и планы. И кто-то предложил: давайте построим свою.

Взяли — и построили, благо в то время в МГУ существовали некоторые теоретические наработки. Руководителем группы, осуществлявшей проектирование и изготовление машины, был назначен Николай Петрович Брусенцов. Задача была такая: сделать машину предельно простой и недорогой (потому что никакого специального финансирования у проекта не было). Поначалу собирались делать двоичную ЭВМ, но позже — как раз из соображений экономичности и простоты архитектуры — пришли к решению, что она будет троичной, использующей «естественный» троичный симметричный код, простейший из симметричных кодов.

К концу 1958 года был закончен первый экземпляр машины, которой дали имя «Сетунь» — по названию московской речки. «Сетунь» была относительно невелика для вычислительных машин того поколения и занимала площадь 25−30 квадратных метров. Благодаря своей изящной архитектуре она была способна выполнять 2000−4500 операций в секунду, обладала оперативной памятью в 162 девятитритных ячейки и запоминающим устройством на магнитном барабане емкостью 36−72 страницы по 54 ячейки каждая. Машинных команд было всего 27 (причем три так и остались невостребованными), благодаря чему программный код получался весьма экономным; программирование непосредственно в машинных кодах было настолько простым, что для «Сетуни» даже не разрабатывали свой ассемблер. Данные вводили в машину с перфоленты, результаты выводились на телетайп (причем, что любопытно, отрицательные цифры печатались как обычные, но перевернутые кверху ногами). При эксплуатации машина показывала 95−98% полезного времени (расходуемого на решение задач, а не на поиск неисправностей и устранение неполадок), а в те времена очень хорошим результатом считалось, если машина могла дать хотя бы 60%.

На межведомственных испытаниях 1960 года машину признали пригодной для массового использования в КБ, лабораториях и вузах, последовало распоряжение о серийном выпуске «Сетуни» на Казанском заводе математических машин. С 1961 по 1965 год было построено 50 экземпляров, которые работали по всей стране. Затем производство свернули. Почему перестали выпускать «Сетунь», если она успешно использовалась всюду от Калининграда до Якутска? Одна из возможных причин в том, что компьютер оказался слишком дешевым в производстве и потому невыгодным для завода. Другая причина- косность бюрократических структур, противодействие ощущалось на каждом из этапов.

Впоследствии Николай Брусенцов и Евгений Жоголев разработали более современную версию машины, использовавшую те же принципы троичности, — «Сетунь-70″, но она так и не пошла в серийное производство, единственный опытный образец работал в МГУ до 1987 года.

«Сетунь» — единственный в мире серийный компьютер с троичной логикой.

Трехзначная логика
Если погрузиться в теорию, то у придуманной схоластами двоичной логики, т. е. логики, построенной на двух элементах (например, «истина» и «ложь»), есть глубокий недостаток: набор некоторых утверждений в ней приводит к парадоксам, то есть имеет противоречивое решение. От этого порока свободна троичная логика, которую исходно развивал великий гений древнего мира Аристотель.
С древним ученым философом согласен и создатель троичного компьютера Николай Брусенцов, по мнению которого двухзначная математическая логика не соответствует здравому смыслу: «закон исключенного третьего» отрезает иные заключения, кроме «истины» и «не-истины», а между тем процесс познания реальности человеком отнюдь не сводится к дихотомии «да/нет». Поэтому, утверждает Брусенцов, чтобы стать интеллектуальным, компьютеру следует быть троичным.

Трехзначная логика отличается от двухзначной тем, что кроме значений «истина» и «ложь» существует третье, которое понимается как «не определено», «нейтрально» или «может быть». При этом сохраняется совместимость с двухзначной логикой — логические операции с «известными» значениями дают те же результаты.

Логике, оперирующей тремя значениями, естественным образом соответствует троичная система счисления — троичная симметричная, если говорить точнее, простейшая из симметричных систем. К этой системе впервые обратился Фибоначчи для решения своей «задачи о гирях».

В троичной симметричной системе используются цифры: -1, 0 и 1 (или, как их еще обозначают, -, 0 и +). Преимущества ее как симметричной системы состоят в том, что, во-первых, не нужно как-то особо отмечать знак числа — число отрицательно, если его ведущий разряд отрицателен, и наоборот, а инвертирование (смена знака) числа производится путем инвертирования всех его разрядов; во-вторых, округление здесь не требует каких-то специальных правил и производится простым обнулением младших разрядов.

Кроме того, из всех позиционных систем счисления троичная наиболее экономична — в ней можно записать большее количество чисел, нежели в любой другой системе, при равном количестве используемых знаков: так, например, в десятичной системе, чтобы представить числа от 0 до 999, потребуется 30 знаков (три разряда, десять возможных значений для каждого), в двоичной системе теми же тридцатью знаками можно закодировать числа в диапазоне от 0 до 32767, а в троичной — от 0 до 59048. Самой экономичной была бы система счисления с основанием, равным числу Эйлера (e = 2,718…), и 3 — наиболее близкое к нему целое.

Если в привычных нам двоичных компьютерах информация измеряется в битах и байтах, то компьютеры на троичной системе счисления оперируют новыми единицами: тритами и трайтами. Трит — это один троичный разряд; подобно тому, как бит может принимать значения 0 и 1 («ложь» и»истина»), трит может быть (+), (0) или (-) (то есть «истина», «неизвестно» или «ложь»).

Один трайт традиционно (так было на «Сетуни») равен шести тритам и может принимать 729 различных значений (байт — только 256). Впрочем, возможно, в будущем трайты станут 9- или 27-разрядными, что естественнее, так как это степени тройки.

Троичная система счисления
В чем же плюсы троичной системы счисления (далее – СС) над двоичной?

1) Меньше разрядов
(Написано разжевано, чтобы каждый смог понять суть этого пункта)
Возьмем число 10 в десятичной СС и переведем его в двоичную СС, получим 1010, переведем в троичную симметричную СС, получим +0+, ну а если в троичную несимметричную СС, то получим 101. Из этого мы видим, что в некоторых числах в троичной симметричной и несимметричной СС-ах меньше разрядов, чем в двоичной СС.
Возьмем число 5 в десятичной СС и переведем его в двоичную СС, получим 101, переведем в троичную симметричную СС, то получим +—, ну а если в троичную несимметричную СС, то получим 12. Из этого мы видим, что в некоторых числах в троичной несимметричной СС меньше разрядов, чем в двоичной и троичной симметричной СС-ах.

2) Емкость
Троичная СС вмещает больший диапазон чисел, т.к. 3^n>2^n (где n-натуральное число). Например, если n=9, то 3^9=19683>2^9=512.

3) Экономичность системы счисления
Экономичность системы счисления — запас чисел, который можно записать в данной системе с помощью определенного количества знаков. Чем больше запас тем экономичнее система. По затратам числа знаков (в трёхразрядном десятичном числе 3*10=30 знаков) наиболее экономична из позиционных показательных несимметричных систем счисления. Обозначим p основание системы счисления, n количество требуемых знаков. Тогда получим n/p разрядов требуемых для записи этого набора знаков в заданной системе счисления, а количество чисел которое при этом можно записать будет равно pn/p.

Настоящее и будущее троичных компьютеров
После «Сетуни» было несколько экспериментальных проектов, осуществлявшихся энтузиастами (таких, например, как американские Ternac и TCA2), однако это были либо весьма несовершенные машины, далекие от двоичных аналогов, либо и вовсе программные эмуляции на двоичном «железе».

Основная причина состоит в том, что использование в компьютерах троичных элементов пока не дает никаких существенных преимуществ перед двоичными: выпуск последних налажен массово, они проще и дешевле по себестоимости. Даже будь сейчас построен троичный компьютер, недорогой и по своим характеристикам сравнимый с двоичными, он должен быть полностью совместим с ними. Уже разработчики «Сетуни-70» столкнулись с необходимостью обеспечить совместимость: чтобы обмениваться информацией с другими университетскими машинами, пришлось добавить возможность читать с перфолент двоичные данные и при выводе также конвертировать данные в двоичный формат.

Однако нельзя сказать, что троичный принцип в компьютеростроении — это безнадежный анахронизм. В последнее десятилетие возникла необходимость в поиске новых компьютерных технологий, и некоторые из этих технологий лежат в области троичности.

Одно из таких исследовательских направлений — поиск альтернативных способов увеличения производительности процессоров. Каждые 24 месяца число транзисторов в кристалле процессора увеличивается примерно вдвое — эта тенденция известна как «закон Мура», и вечно продолжаться она не может: масштабы элементов и связей можно измерить в нанометрах, и очень скоро разработчики столкнутся с целым рядом технических сложностей. Кроме того, есть и экономические соображения — чем меньше, тем дороже разработки и производство. И с какого-то момента окажется дешевле поискать альтернативные способы делать процессоры мощнее, нежели продолжать гонку за нанометрами, — обратиться к технологиям, от которых раньше отказывались как от нерентабельных. Переход от однородных кремниевых структур к гетеропереходным проводникам, состоящим из слоев различных сред и способным генерировать несколько уровней сигнала вместо привычных «есть» и «нет», — это возможность повысить интенсивность обработки информации без увеличения количества элементов (и дальнейшего уменьшения их размеров). При этом от двухзначной логики придется перейти к многозначным — трехзначной, четырехзначной и т. д.

Другое направление, также нацеленное на увеличение производительности, — разработки в области асинхронных процессоров. Известно, что обеспечение синхронности процессов в современных компьютерах изрядно усложняет архитектуру и расходует процессорные ресурсы — до половины всех транзисторов в чипе работает на обеспечение этой самой синхронности. Компания Theseus Logic предлагает использовать «расширенную двоичную» (фактически — троичную) логику, где помимо обычных значений «истина» и «ложь» есть отдельный сигнал «NULL», который используется для самосинхронизации процессов. В этом же направлении работают еще несколько исследовательских групп.
Есть и более фантастические направления, где оправдано использование трехзначной логики: оптические и квантовые компьютеры.

Наиболее перспективным мне представляется последнее.

[Квантовый компьютер]

Квантовый компьютер — вычислительное устройство, работающее на основе квантовой механики. Квантовый компьютер принципиально отличается от классических компьютеров, работающих на основе классической механики.

Благодаря огромной скорости разложения на простые множители, квантовый компьютер позволит расшифровывать сообщения, зашифрованные при помощи популярного асимметричного криптографического алгоритма RSA. До сих пор этот алгоритм считается сравнительно надёжным, так как эффективный способ разложения чисел на простые множители для классического компьютера в настоящее время неизвестен. Для того, например, чтобы получить доступ к кредитной карте, нужно разложить на два простых множителя число длиной в сотни цифр. Даже для самых быстрых современных компьютеров выполнение этой задачи заняло бы больше времени, чем возраст Вселенной, в сотни раз. Если компьютер будет построен — эта задача становится осуществимой благодаря алгоритму Шора.

Канадская компания D-Wave заявила в феврале 2007 года о создании образца квантового компьютера, состоящего из 16 кубит. Это устройство работает на кубитах — квантовых аналогах битов.

Но можно построить компьютеры не на битах, а на кутритах — аналогах трита в квантовом компьютере.

Кутрит (квантовый трит) — квантовая ячейка, имеющая три возможных состояния.

При использовании в универсальных квантовых вентилях кутриты вместо кубитов, исследователи могут существенно снизить количество необходимых вентилей.

Утверждают, что компьютер, который в обычном случае использовал бы 50 традиционных квантовых вентилей, сможет обойтись всего девятью, если будет основан на троичном представлении.

Также, согласно некоторым исследованиям, использование кутритов вместо кубитов позволит упростить реализацию квантовых алгоритмов и компьютеров.

Источники:
1. Еженедельник IT Weekly № 02/2012 http://www.it-weekly.ru/analytics/products/41910.html
2. «Популярная механика» №107 http://www.popmech.ru/technologies/11918-troichnyy-kompyuter-da-net-mozhet-byt-logika/
3. Замена двоичной логики — увеличит ли это производительность? http://habrahabr.ru/post/166679/

Разработка урока по информатике «Двоичная система счисления»

Урок № 2 «Двоичная система счисления»

Цель урока:  Формировать практические навыки перевода чисел из десятичной системы счисления в двоичную и наоборот.

Задачи урока:

1.Образовательная: осознанное понимание представления чисел в двоичной системе счисления, перевода десятичных чисел в двоичную систему счисления, арифметических операций с двоичными числами.

2.Развивающая: развивать мышление учащихся посредством анализа, сравнения и обобщения изучаемого материала.

3.Воспитательная: активизация познавательной и творческой активности учащихся, воспитание чувства ответственности, коммуникабельности.

Тип урока: комбинированный.

Метод обучения: словесный, наглядный, практический.

Формы организации деятельности обучающихся: фронтальная, индивидуальная.

Оборудование: компьютер, проектор, интерактивная доска.

Электронно-образовательные ресурсы: Презентация «Двоичная система счисления», раздаточный материал.

Универсальные учебные действия:

• умение ориентироваться в межличностных отношениях;

• установление связи между целью и мотивом деятельности;

• целеполагание;

• работать по плану, инструкции;

• осуществлять самоконтроль;

• оценка результата;

• самостоятельное формулирование познавательной цели;

• умение структурировать знания;

• умение осознанно и произвольно строить речевое высказывание в устной форме;

• умение слушать и вступать в диалог;

• умение с достаточной полнотой и точностью выражать свои мысли в соответствии с поставленной задачей;

Планируемые результаты:

личностные:

• формирование ответственного отношения к учению на основе мотивации к обучению и познанию;

• формирование осознанного, уважительного и доброжелательного отношения к другому человеку, его мнению;

• формирование коммуникативной компетентности в общении и сотрудничестве со сверстниками и взрослыми в процессе учебной деятельности.

метапредметные:

• умение определять понятия, создавать обобщения, классифицировать, строить рассуждение, умозаключение и делать выводы;

• умение создавать, применять различные продукты для решения учебной задачи;

• умение оценивать правильность выполнения учебной задачи, собственные возможности её решения;

• развитие ИКТ–компетенции.

предметные:

• знать: определения: системы счисления, основания системы счисления, алгоритм перевода числа из десятичной системы счисления в двоичную, применение двоичной системы в жизни;

• уметь: переводить числа из десятичной системы счисления в двоичную и наоборот.

Структура занятия:

1. 1. 1. Организационный этап (1 мин)

      2. Повторение предыдущих знаний. (4 мин)

      3. Подготовка к восприятию нового материала, мотивация.

      4. Первичное усвоение новых знаний (25 мин)

      5. Первичное осмысление и закрепление изученного (7 мин)

      6. Информация о домашнем задании, инструктаж по его выполнению (2 мин).

      7. Рефлексия (подведение итогов занятия) (1 мин).

Ход урока

1. Организационный момент урока (1мин).

Подготовка учащихся к уроку, проверка присутствующих на уроке.

2. Повторение предыдущих знаний. Проверка домашнего задания. (4 мин).

3. Подготовка к восприятию нового материала, мотивация. (5 мин).

Сегодня на уроке вы имеете возможность показать свои знания не только по информатике, но и по математике.

— Вопросы ученикам:

1. С каким универсальным техническим устройством мы работаем на уроках информатики? (Это устройство называется компьютер).

2. Для чего была изобретена ЭВМ? (ЭВМ изобретена для работы с числами).

3. Зачем нужны числа? (Для практических вычислений)

4. На каком школьном учебном предмете вас учат работать с числами?

(С числами работаем на математике).

5. Сколько цифр используется для представления чисел? (10: 0,1,2,3,4,5,6,7,8,9)

6. Какие сигналы используются в компьютере и как они обозначаются?

(включено, выключено; 0,1)

7. Сколько цифр используется? (Используется 2 цифры: 0 и 1).

8. Какая это система счисления? (Это двоичная система счисления).

4. Первичное усвоение новых знаний (25 мин)

— Итак, тема сегодняшнего урока:   “Двоичная система счисления”.

 

Сегодня мы с вами познакомимся с 2СС и научимся  работать с двоичными числами:

Из всех систем счисления особенно проста и поэтому интересна для технической реализации в ЭВМ двоичная система счисления.

В ЭВМ используют двоичную систему, потому что она имеет ряд преимуществ перед другими системами:

для ее реализации нужны технические элементы с двумя возможными состояниями (есть ток, нет тока; включено, выключено и т.д., одному из состояний ставится в соответствие 1, другому – 0), а не десять, как в десятичной системе;

представление информации посредством только двух состояний надежно и помехоустойчиво;

упрощается выполнение арифметических действий;

возможность использовать аппарат булевой алгебры для выполнения логической преобразований информации.

— В двоичной системе счисления используются всего две цифры 0 и 1. Другими словами, двойка является основанием двоичной системы счисления. (Аналогично у десятичной системы основание 10.).Двоичная система счисления аналогична десятичной за исключением того, что в формировании числа участвуют всего лишь две знака-цифры: 0 и 1. Как только разряд достигает своего предела (т.е. единицы), появляется новый разряд, а старый обнуляется.

Попробуем считать в двоичной системе:
0 – это ноль
1 – это один (и это предел разряда)
10 – это два
11 – это три (и это снова предел)
100 – это четыре
101 – пять
110 – шесть
111 – семь и т.д.

Перевод чисел из двоичной системы счисления в десятичную СС.

Не трудно заметить, что в двоичной системе счисления длины чисел с увеличением значения растут быстрыми темпами. Как определить, что значит вот это: 1001001? Непривычный к такой форме записи чисел человеческий мозг обычно не может понять сколько это. Неплохо бы уметь переводить двоичные числа в десятичные.

Запишем в развёрнутой форме двоичное число 1001001.

Если посчитать сумму составляющих, то в итоге мы получим десятичное число, соответствующее 1001001:

Т.е. число 1001001 по основанию 2 равно числу 73 по основанию 10. Записать это можно так:

1001001₂ = 73₁₀

Составляют таблицу перевода десятичных чисел от 0 до 20 в двоичную систему счисления.

десятичное

число

двоичное число

десятичное

число

двоичное число

0

0000

11

1011

1

0001

12

1100

2

0010

13

1101

3

0011

14

1110

4

0100

15

1111

5

0101

16

10000

6

0110

17

10001

7

0111

18

10010

8

1000

19

10011

9

1001

20

10100

10

1010

и т.д.

 

Вывод: недостаток двоичной системы – это быстрый рост числа разрядов, необходимых для записи чисел.

Физкультминутка.

Перевод десятичного числа в двоичное

Может потребоваться перевести десятичное число в двоичное. Один из способов – это деление на два и формирование двоичного числа из остатков. Например, нужно получить из числа 26 его двоичную запись: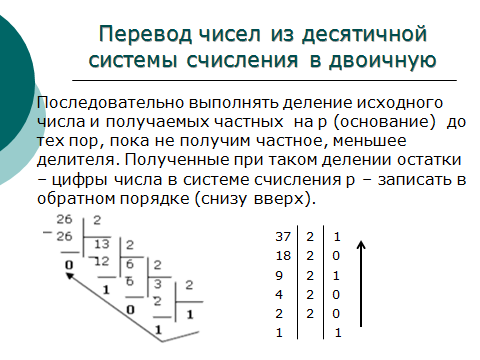

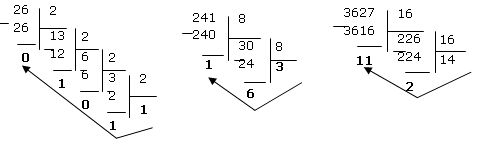
Собираем остатки вместе, начиная с конца: 11010. Это и есть число 26 в двоичном представлении. Проверим:

11010₂ = 1*2⁴ + 1*2³ + 0*2² + 1*2¹ + 0*2⁰ = 16 + 8 + 0 + 2 + 0 = 26₁₀.

5. Первичное осмысление и закрепление изученного (7 мин)

— Что такое двоичная система счисления?

-Чем хороша двоичная система счисления?

-Недостаток двоичной системы счисления.

Решить самостоятельно Проверка

6. Информация о домашнем задании, инструктаж по его выполнению (2 мин).

Параграф № 2 п. 2.1.1 — 2.1.2., стр. 12-14, стр.43 ЭОР № 2,3

1) Переведите число 61 из десятичной в ДВОИЧНУЮ

2) Переведите число 922 из десятичной в ДВОИЧНУЮ

3) Переведите число 1001100 из ДВОИЧНОЙ в десятичную

4) Переведите число 1110011100 из ДВОИЧНОЙ в десятичную

7. Рефлексия (подведение итогов занятия) (1 мин).

• Какое задание было самым интересным? 

• Какое задание, по вашему мнению, было самым сложным? 

• С какими трудностями вы столкнулись, выполняя задания?