«Дизъюнкция. Инверсия. Логические выражения. Таблицы истинности»
Урок 49-50, 9 класс
Учитель: Брух Т.В.
Дата: __________
Тема: «Дизъюнкция. Инверсия. Логические выражения. Таблицы истинности»
Цели: Познакомить с основными логическими операциями: инверсия, конъюнкция, дизъюнкция.
Задачи:
Сформировать у учащихся понятие “логическая операция»;
Способствовать формированию логического мышления, интереса к изучаемому материалу.
Ход урока
I. Организационный момент.
II. Проверка домашнего задания.
III. Изложение нового материала.
В алгебре высказываний над высказываниями можно производить логические операции, в результате которых получаются новые, составные (сложные) высказывания.
Логическая операция — способ построения сложного высказывания из данных высказываний, при котором значение истинности сложного высказывания полностью определяется значениями истинности исходных высказываний.
Рассмотрим три базовых логических операций — инверсию, конъюнкцию, дизъюнкцию и дополнительные — импликацию и эквивалентность.
Логическая операция | Название | Обозначение знаками | Таблица истинности | Определение | |||||||||||||||
Инверсия | Логическое отрицание |
| Инверсия логической переменной истина, если переменная ложна, и, наоборот, инверсия ложна, если переменная истинна. | ||||||||||||||||
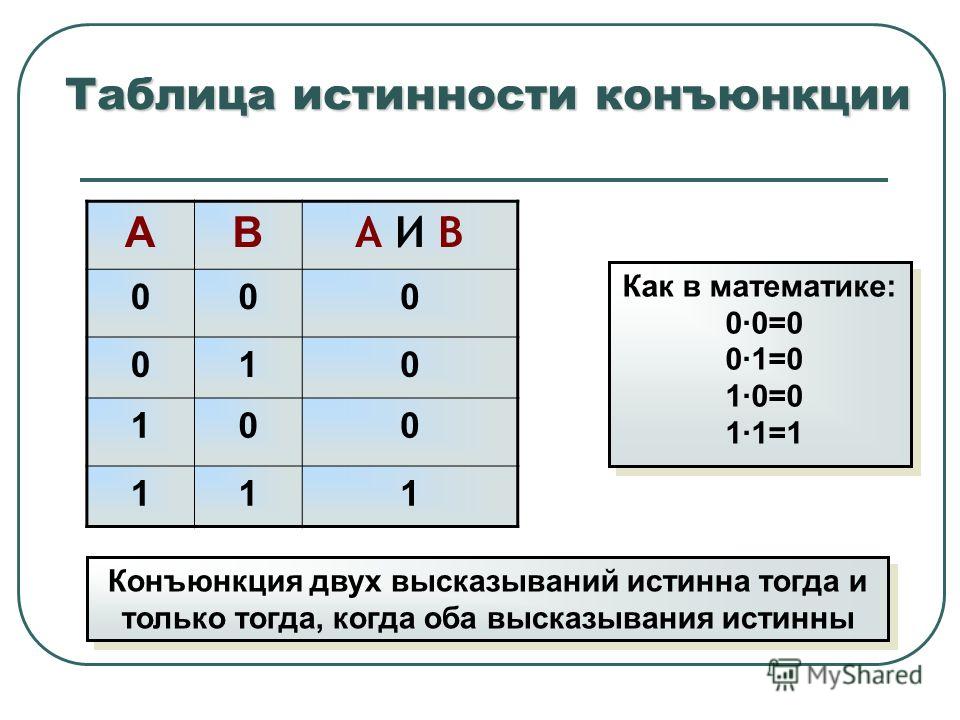
Конъюнкция | Логическое умножение |
| Конъюнкция двух логических переменных истинна тогда и только тогда, когда оба высказывания, истинны | ||||||||||||||||
Дизъюнкция | Логическое сложение |
| Дизъюнкция двух логических переменных ложна тогда и только тогда, когда оба высказывания ложны. | ||||||||||||||||
Импликация | Логическое следование |
А — условие В — следствие |
| Импликация двух логических переменных ложна тогда и только тогда, когда из истинного основания следует ложное следствие | |||||||||||||||
Эквивалентность | Логическое равенство |
| Эквивалентность двух логических переменных истинна тогда и только тогда, когда оба высказывания одновременно либо ложны, либо истинны |
Упражнение 1. D— конъюнкция
D— конъюнкция
— дизъюнкция.
Упражнение 2.
Дана формула B=(AΛB)V(¬AΛ¬B). Составьте предложение.
IV. Закрепление изученного материала.
1. Среди следующих высказываний укажите составные, выделите в них простые, обозначьте их каждое из них буквой. Запишите с помощью логических операций каждое составное высказывание.
Число 456 трехзначное и четное.
Неверно, что Солнце движется вокруг Земли.
Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
Луна — спутник Земли.
На уроке химии ученики выполняли лабораторную работу, и результаты исследований записывали в тетрадь.
Если число оканчивается на 0, то оно делится на 10.
Чтобы погода была солнечной, достаточно, чтобы не было ни ветра, ни дождя.
Если у меня будет свободное время и не будет дождя, тоя не буду писать сочинения, а пойду на дискотеку.
Если человек с детства и юности своей не давал нервам властвовать над собой, то они не привыкнут раздражаться, и будут ему послушны.
2. Постройте отрицания следующих высказываний.
На улице сухо.
Сегодня выходной день.
Ваня не был готов сегодня к урокам.
Неверно, что число 3 не является делителем числа 198.
Некоторые млекопитающие не живут на суше.
Неверно, что число 17 — простое.
3. Из каждых трех выберите пару высказываний, являющихся отрицаниями друг друга.
“Луна — спутник Земли”, “Неверно, что Луна спутник Земли”, “Неверно, что Луна не является спутником Земли”;
“2007 2008”, “2007 ? 2008”;
“Прямая а перпендикулярна прямой с”; “Прямая а не параллельна прямой с”; “Прямая а не пересекается с прямой с”.
4. По данным формам сложных высказываний запишите высказывания на русском языке.
Из двух простых высказываний постройте сложное высказывание, используя логические связки «и», «или»:
а) В кабинете есть парты. В кабинете есть стулья.
б) Одна половина класса изучает английский язык. Вторая половина изучает французский язык.
в) Антон старше Лили. Сережа старше Лили.
Определите тип высказывания и вид логической операции с соответствующей логической связкой:
a) Всякий прямоугольник имеет прямые углы и параллельные противоположные стороны;
б) Треугольники с равными сторонами не являются равнобедренными;
в) На следующем уроке будет либо история, либо химия;
г) Завтра я пойду в школу и библиотеку;
д) Либо он заболел, либо забыл о нашей договорённости;
е) Утром мы обычно ходим на лыжах или катаемся на коньках.
V. Итог урока.
Обобщить пройденный материал, оценить работу активных учеников.
VI. Домашнее задание.
1. Выучить определения, знать обозначения.
2. Даны высказывания:
А = {На улице светит солнце},
В = {На улице дождь},
С = {На улице пасмурная погода},
D = {На улице идет снег}.
Составьте два сложных высказывания, одно из которых в любой ситуации всегда будет ложным, а другое истинным.
Практическая работа
1. Среди следующих высказываний укажите составные, выделите в них простые, обозначьте их каждое из них буквой. Запишите с помощью логических операций каждое составное высказывание.
Число 456 трехзначное и четное.
Неверно, что Солнце движется вокруг Земли.
Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.
Луна — спутник Земли.
На уроке химии ученики выполняли лабораторную работу, и результаты исследований записывали в тетрадь.
Если число оканчивается на 0, то оно делится на 10.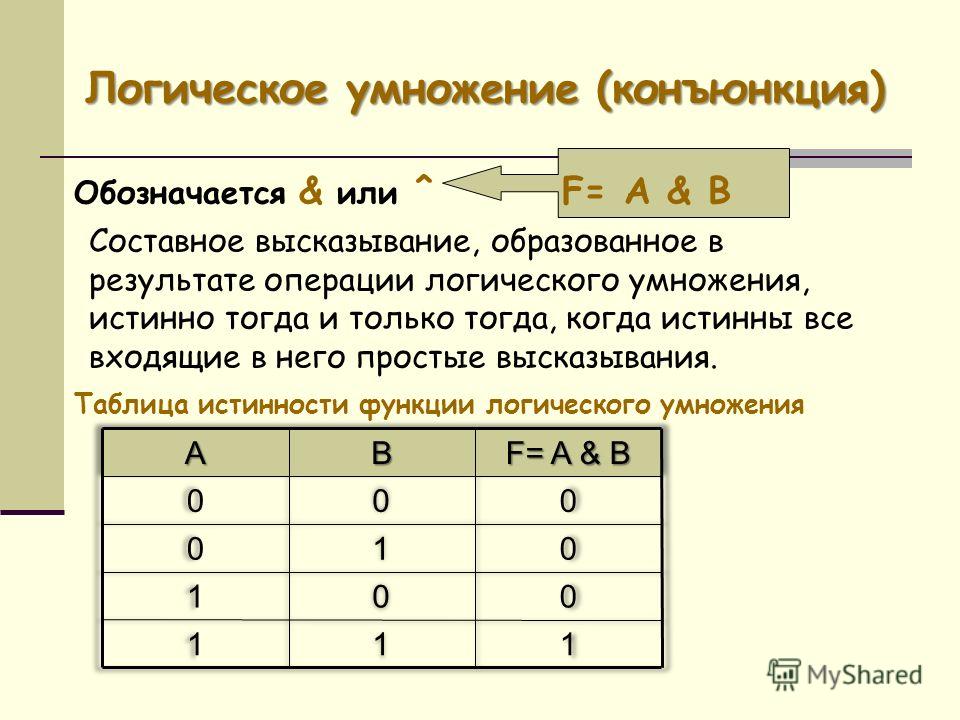
Чтобы погода была солнечной, достаточно, чтобы не было ни ветра, ни дождя.
Если у меня будет свободное время и не будет дождя, тоя не буду писать сочинения, а пойду на дискотеку.
Если человек с детства и юности своей не давал нервам властвовать над собой, то они не привыкнут раздражаться, и будут ему послушны.
2. Постройте отрицания следующих высказываний.
На улице сухо.
Сегодня выходной день.
Ваня не был готов сегодня к урокам.
Неверно, что число 3 не является делителем числа 198.
Некоторые млекопитающие не живут на суше.
Неверно, что число 17 — простое.
3. Из каждых трех выберите пару высказываний, являющихся отрицаниями друг друга.
“Луна — спутник Земли”, “Неверно, что Луна спутник Земли”, “Неверно, что Луна не является спутником Земли”;
“2007 2008”, “2007 ? 2008”;
“Прямая а перпендикулярна прямой с”; “Прямая а не параллельна прямой с”; “Прямая а не пересекается с прямой с”.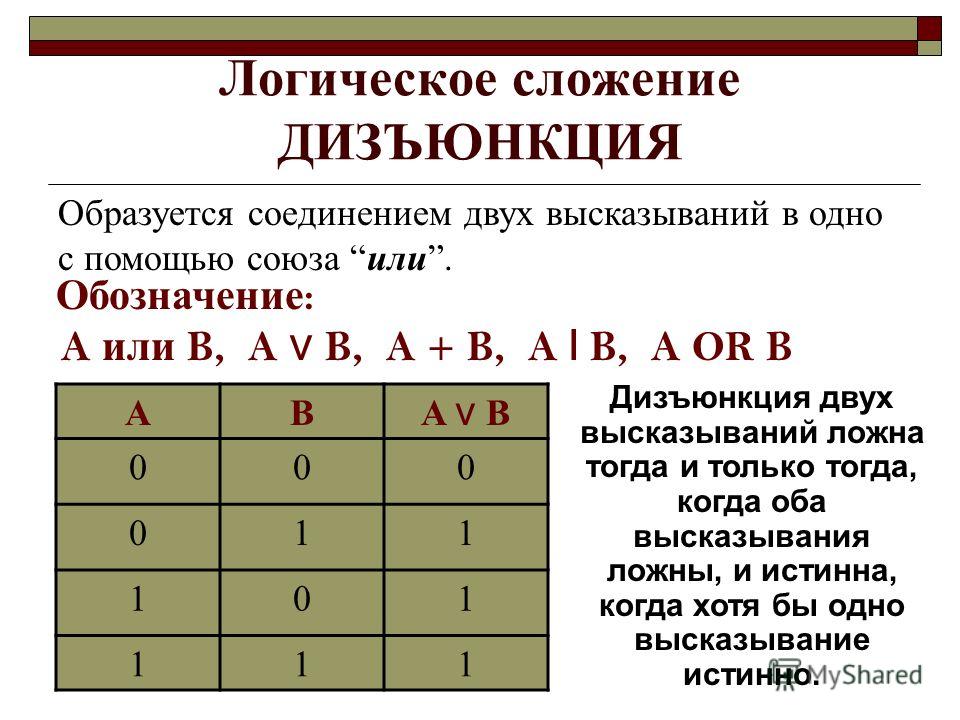
4. По данным формам сложных высказываний запишите высказывания на русском языке.
Из двух простых высказываний постройте сложное высказывание, используя логические связки «и», «или»:
а) В кабинете есть парты. В кабинете есть стулья.
б) Одна половина класса изучает английский язык. Вторая половина изучает французский язык.
в) Антон старше Лили. Сережа старше Лили.
Определите тип высказывания и вид логической операции с соответствующей логической связкой:
a) Всякий прямоугольник имеет прямые углы и параллельные противоположные стороны;
б) Треугольники с равными сторонами не являются равнобедренными;
в) На следующем уроке будет либо история, либо химия;
г) Завтра я пойду в школу и библиотеку;
д) Либо он заболел, либо забыл о нашей договорённости;
е) Утром мы обычно ходим на лыжах или катаемся на коньках.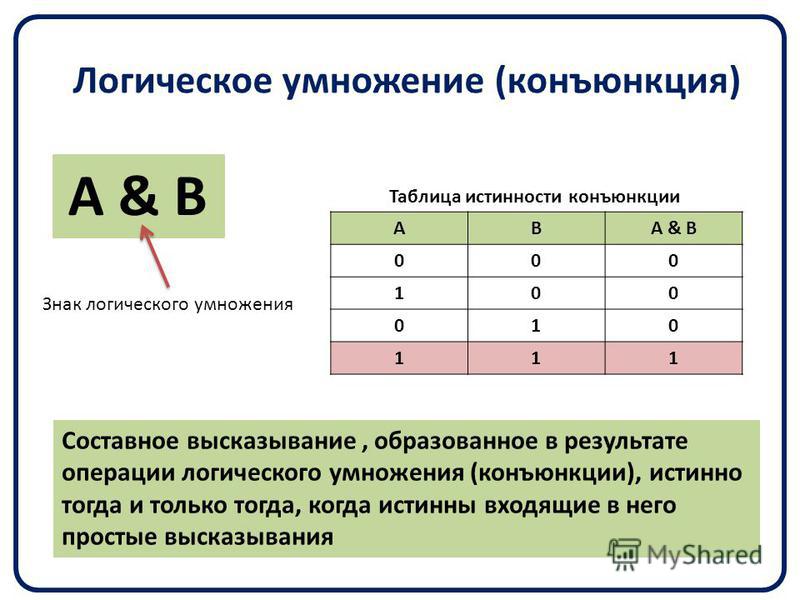
7.2. Логические операции (отрицание, конъюнкция, дизъюнкция, импликация, эвиваленция). Правила записи и истинности.
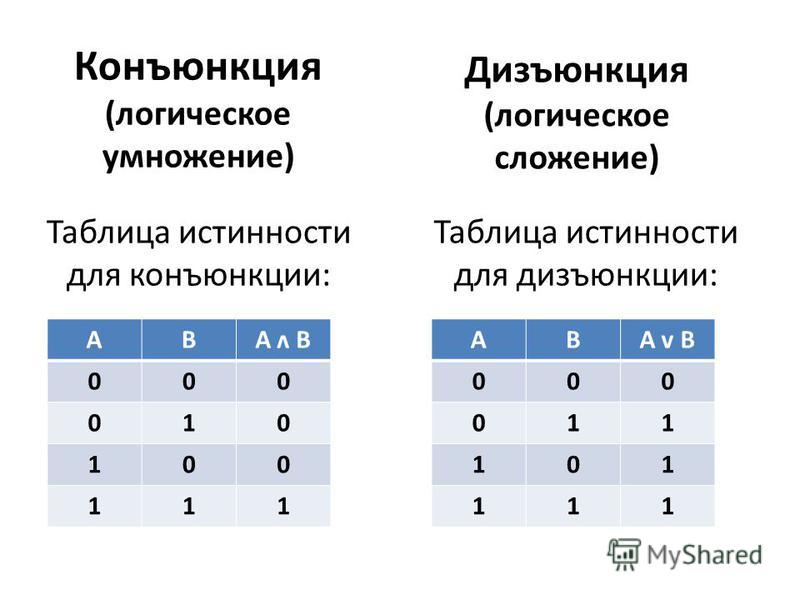
1) Логическое умножение или конъюнкция:
Конъюнкция — это сложное логическое выражение, которое считается истинным в том и только том случае, когда оба простых выражения являются истинными, во всех остальных случаях данное сложеное выражение ложно.
Обозначение: F = A & B.
2) Логическое сложение или дизъюнкция:
Дизъюнкция — это сложное логическое выражение, которое истинно, если хотя бы одно из простых логических выражений истинно и ложно тогда и только тогда, когда оба простых логических выраженныя ложны.
Обозначение: F = A + B.
3) Логическое отрицание или инверсия:
Инверсия
— это сложное логическое выражение, если
исходное логическое выражение истинно,
то результат отрицания будет ложным, и
наоборот, если исходное логическое
выражение ложно, то результат отрицания
будет истинным. Другими простыми слова,
данная операция означает, что к исходному
логическому выражению добавляется
частица НЕ или слова НЕВЕРНО, ЧТО.
4) Логическое следование или импликация:
Импликация — это сложное логическое выражение, которое истинно во всех случаях, кроме как из истины следует ложь. Тоесть данная логическая операция связывает два простых логических выражения, из которых первое является условием (А), а второе (В) является следствием.
5)Логическая равнозначность или эквивалентность:
Эквивалентность — это сложное логическое выражение, которое является истинным тогда и только тогда, когда оба простых логических выражения имеют одинаковую истинность.
Порядок выполнения логических операций в сложном логическом выражении.
1. Инверсия;
2. Конъюнкция;
3. Дизъюнкция;
4. Импликация;
5. Эквивалентность.
7.3. Логическая формула. Тождественно истинные и тождественно лонные формулы
7.4. Связь между алгеброй логики и двоичным кодированием.
7.5. Логические элементы компьютера и их таблицы истинности
7. 5.1.
Схема «И»
5.1.
Схема «И»
7.5.2. Схема «ИЛИ»
7.5.3. Схема «НЕ»
7.5.4. Схема «И-НЕ»
7.5.5. Схема «ИЛИ-НЕ»
7.5.6. RS-триггер и его таблица истинности.
Особенность RS-триггера заключается в том, что при подаче одновременно на входы R и S сигнала, соответствующего логической 1, состояние триггера становится неопределенным: на обоих выходах Q и `Q установится уровень “1”, а после снятия со входов управляющих сигналов, в силу случайных причин, триггер может установиться в состояние “0” либо “1”. Очевидно, что для нормальной работы триггера необходимо исключить указанное сочетание входных сигналов, приводящее к неопределенному состоянию, что можно осуществить, предусмотрев выполнения запрещающего условия R × S=0.
7.5.7. Сумматор и его таблица истинности.
7.6. Основные законы алгебры логики и упрощение логических формул.
7.7. Переключательная схема
8. 1.
Понятие алгоритма
1.
Понятие алгоритма
8.2. Свойства алгоритма (понятность, дискретность, определенность, результативность, массовость)
Дискретность (прерывность, раздельность) — алгоритм должен представлять процесс решения задачи как последовательное выполнение простых (или ранее определенных) шагов. Каждое действие, предусмотренное алгоритмом, исполняется только после того, как закончилось исполнение предыдущего.
Определенность — каждое правило алгоритма должно быть четким, однозначным. Благодаря этому свойству выполнение алгоритма носит механический характер и не требует никаких дополнительных указаний или сведений о решаемой задаче.
Результативность (конечность) — алгоритм должен приводить к решению задачи за конечное число шагов.
Массовость
— алгоритм решения задачи разрабатывается
в общем виде, то есть он должен быть
применим для некоторого класса задач,
различающихся только исходными данными.
При этом исходные данные могут выбираться
из некоторой области, которая называется
областью применимости алгоритма.
8.3. Формы представления алгоритмов
8.4. Составление блок-схем.
8.5. Линейная алгоритмическая конструкция
8.6. Ветвящаяся алгоритмическая конструкция
8.7. Цикл с предусловием
8.8. Цикл с постусловием
8.9. Массив
9. Основы программирования
9.1. Машинный код процессора (триггеры, венили)
9.2. Общее понятие языка программирования (метаязык, синтаксис, семантика, операторы, отладка)
Программи́рование
— в обычном понимании, это процесс
создания компьютерных программ. Иногда
под программированием понимают настройку
электронных устройств и программно-аппаратных
комплексов (например, программирование
цифровых АТС, программирование бытовых
приборов конечным пользователем, запись
информации в ПЗУ). Разработку логической
схемы для ПЛИСтоже называют
программированием. В общем понимании,
программирование — это процесс создания
алгоритма функционирования устройства,
который может быть выражен либо в
структуре самого устройства, либо в
виде последовательности выполняемых
устройством элементарных инструкций.
Обычно,
основным инструментом программирования
является среда программирования, которая
включает себя текстовый редактор и
компилятор или интерпретатор. Текстовый
редактор среды программирования может
иметь специфичную функциональность,
такую как индексация имен, отображение
документации, средства визуального
создания пользовательского интерфейса.
С помощью текстового редактора программист
производит набор программы в виде
текста, который называют исходным кодом.
Язык программирования определяет
синтаксис и изначальную семантику
исходного кода, семантика языка
программирования может расширяться
текстом программы, дополнительными
библиотеками и программно-аппаратным
окружением, в котором исполняется
программа. Компилятор преобразует текст
программы в машинный код, непосредственно
исполняемый электронными компонентам
и компьютера. Интерпретатор либо явно
не преобразует текст программы в машинный
код, либо делает такое преобразование
в процессе выполнения программы.
Программирование можно разбить логически на несколько стадий:
Анализ
Проектирование — разработка комплекса алгоритмов
Кодирование и компиляцию — написание исходного текста программы и преобразование его в исполнимый код с помощью компилятора
Тестирование и отладку — выявление и устранение ошибок в программах
Испытания и сдачу программ
Сопровождение
9.3. Компиляторы и интерпретаторы
9.4. Уровни языков программирования (низкий, высокий)
Основы цифровой и вычислительной техники
Всего логических операций три: одна унарная – инверсия и две бинарных – дизъюнкция и конъюнкция (табл. 1.12).
Таблица 1.12
Названия и обозначения логических операций
|
Название операции |
Слово |
Знак |
|
Инверсия, отрицание, дополнение |
НЕ (NOT) |
ˉ, −, ~ |
|
Дизъюнкция, логическое сложение, объединение |
ИЛИ (OR) |
,, + |
|
Конъюнкция, логическое умножение, пересечение |
И (AND) |
,, · |
Чаще всего инверсия (inversio – перестановка) обозначается чертой над аргументом (х′), дизъюнкция (disjunctio – разобщение) – значком v, а конъюнкция (conjunctio – союз, связь) – символом обычного умножения (∙).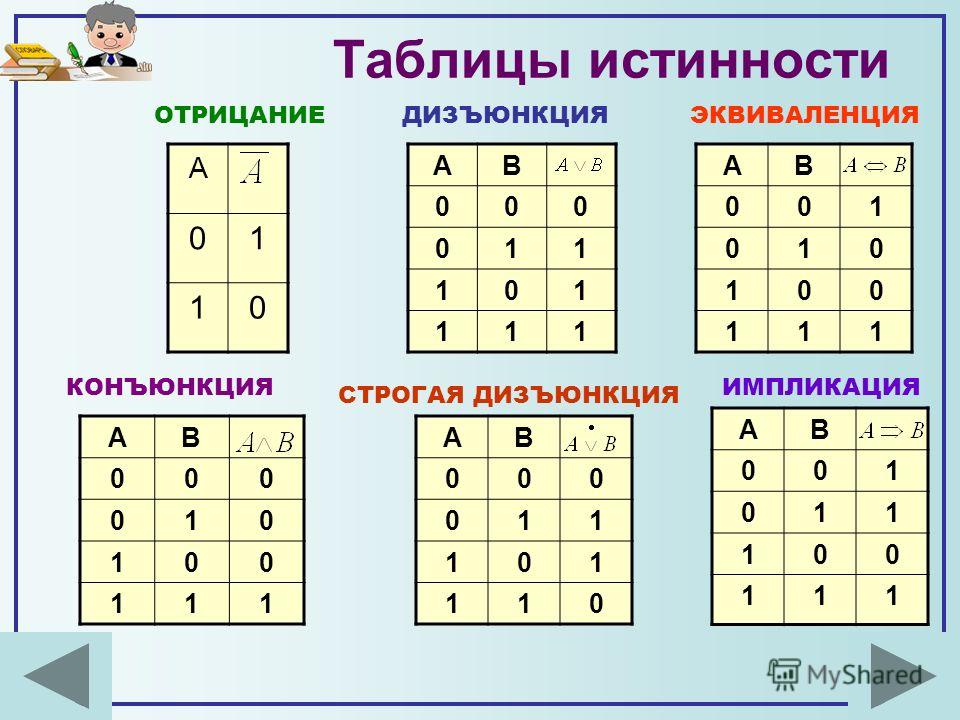
Смысл логических операций раскрывается с помощью диаграмм Эйлера (рис. 1.1) и перебора всех возможных значений аргументов, над которыми проводятся эти операции (табл. 1.13).
Рис. 1.1. Диаграммы Эйлера для основных операций алгебры логики: а – инверсия; б – дизъюнкция; в – конъюнкция
Проанализируем данные табл. 1.13.
Таблица 1.13
Таблица истинности логических операций
|
Аргумент |
Логическая операция |
||||
|
х1 |
х0 |
|
|
х1х0 |
х1^х0 |
|
0 |
0 |
1 |
1 |
0 |
0 |
|
0 |
1 |
1 |
0 |
1 |
0 |
|
1 |
0 |
0 |
1 |
1 |
0 |
|
1 |
1 |
0 |
0 |
1 |
1 |
Сопоставление столбцов таблицы х1 с х1′ и х0 с х0′ показывает, что операцию инверсии можно выполнять чисто арифметически: 0′ = 1 – 0; 1′ = 1 – 1 иалгебраически: х′ = 1 – х.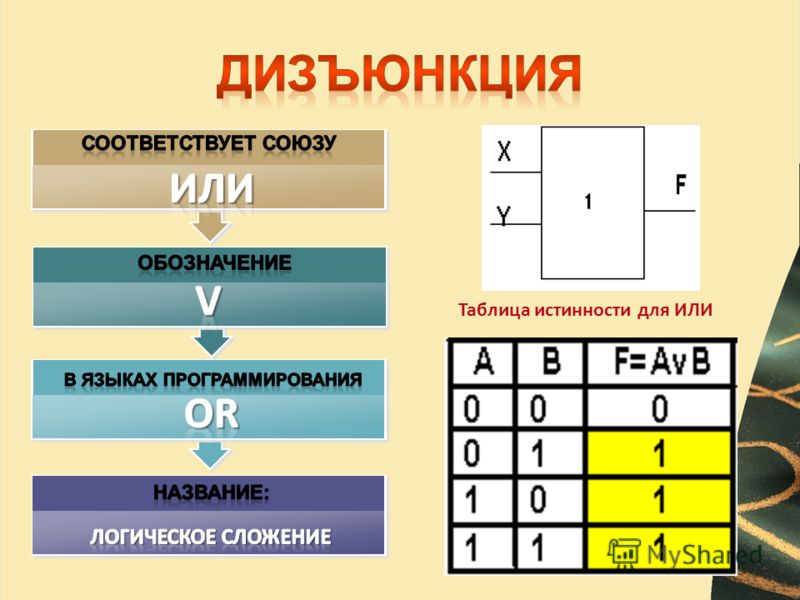 Отсюда и возникло еще одно название этой операции – дополнение. В случае неопределенности (если ее обозначить ½) получим ½ = 1 – ½ = ½, т.е. инверсия неопределенности равна самой неопределенности, что очевидно. Отсюда же можно сделать вывод, что двойная инверсия приводит к исходному аргументу, т.е. x» = l — x′ = l – (1 – x) = x, иэто называется законом двойного отрицания.
Отсюда и возникло еще одно название этой операции – дополнение. В случае неопределенности (если ее обозначить ½) получим ½ = 1 – ½ = ½, т.е. инверсия неопределенности равна самой неопределенности, что очевидно. Отсюда же можно сделать вывод, что двойная инверсия приводит к исходному аргументу, т.е. x» = l — x′ = l – (1 – x) = x, иэто называется законом двойного отрицания.
Закон ложного положения, т.е. если х1 = х0, то и х1′ =x0′, может быть доказан следующим образом. Поскольку 1 = 1, то вычитая из левой и правой единицы равные значения х1 и x0 получим 1 – х1 = 1 – x0 что и соответствует х1′ =x0′.
Дизъюнкция.В отличие от обычного арифметического или алгебраического суммирования здесь наличие двух единиц дает в результате единицу. Именно поэтому при обозначении логического суммирования не рекомендуется использовать знак сложения (+). Операцией, эквивалентной дизъюнкции, является выбор максимального значения из двух: МАХ(х1; х0).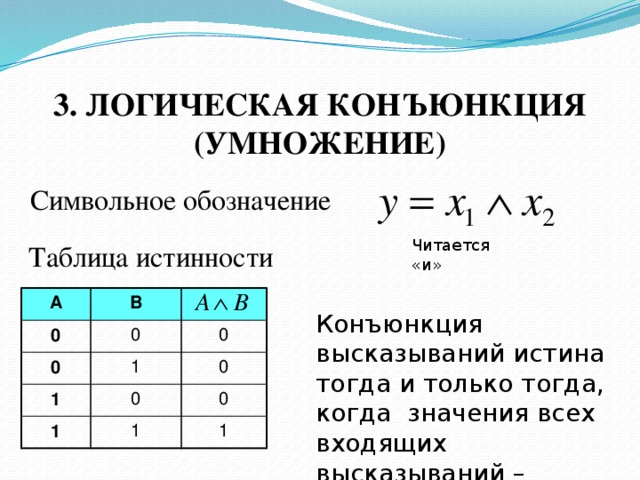 Это справедливо и при обозначении неопределенности числом ½.
Это справедливо и при обозначении неопределенности числом ½.
Анализ табл.1.3 позволяет перейти к сокращенной ее форме – алгебраической таблице истинности (табл. 1.14). Первые две строки табл. 1.13 (х1 = 0) определяют закон сложения с нулем x v 0 = x, а вторые две строки (х1 = 1) – закон сложения с единицей x v 1 = 1.
Таблица 1.14
Алгебраическая таблица истинности дизъюнкции и конъюнкции
|
х1 |
х1х0 |
х1·х0 |
|
0 |
х0 |
0 |
|
1 |
1 |
х0 |
Конъюнкция.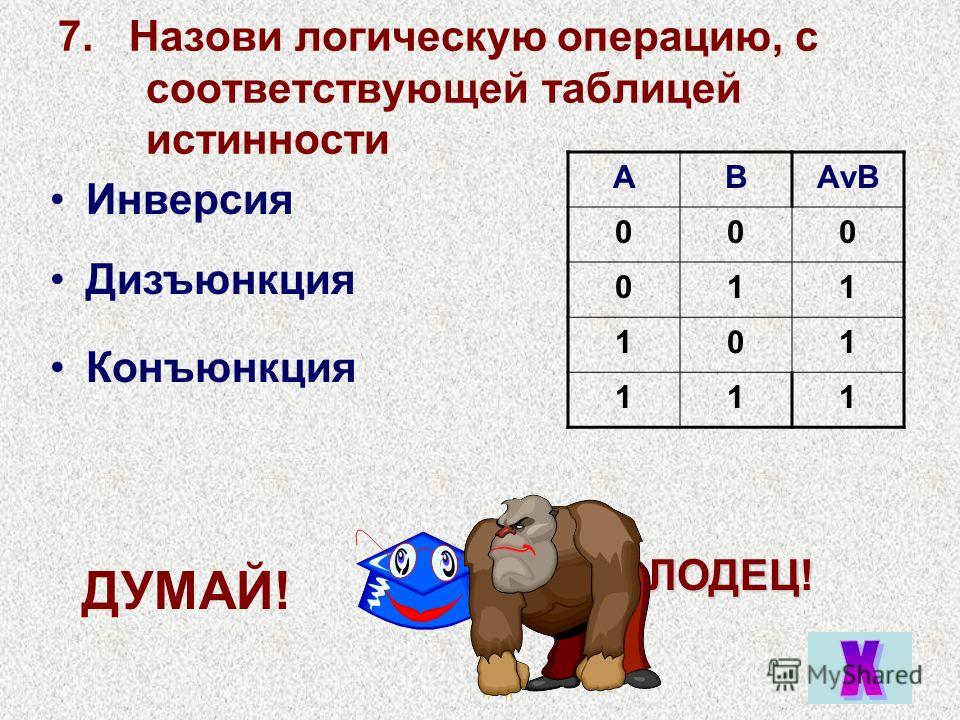 Табл. 1.13 убедительно показывает тождественность операций обычного и логического умножений. Эквивалентной операцией в данном случае является выбор наименьшего значения из двух: MIN(x1; x0), что также справедливо и при обозначении неопределенности через ½. В этом случае уместен переход к сокращенной – алгебраической табл. 1.14. Первые две строки табл. 1.13 доказывают закон умножения на нуль: х∙0= 0 и вторые две – закон умножения на единицу: х∙1=х.
Табл. 1.13 убедительно показывает тождественность операций обычного и логического умножений. Эквивалентной операцией в данном случае является выбор наименьшего значения из двух: MIN(x1; x0), что также справедливо и при обозначении неопределенности через ½. В этом случае уместен переход к сокращенной – алгебраической табл. 1.14. Первые две строки табл. 1.13 доказывают закон умножения на нуль: х∙0= 0 и вторые две – закон умножения на единицу: х∙1=х.
Еще несколько законов можно извлечь из анализа табл. 1.13, приравняв в одном случае оба аргумента друг другу: x1 = x0 = х – это закон идемпотентности, или тавтологии, а вдругом случае – один аргумент инверсному значению другого: x1 = х0′ (табл. 1.15).
Таблица 1.15
Законы тавтологии и дополнительности
|
Название закона |
Дизъюнкция |
Конъюнкция |
|
|
Идемпотентный, тавтологии |
хх = х |
х ·х = х |
|
|
Дополнительности |
исключенного третьего |
хх = 1 |
– |
|
противоречия |
– |
х ·х = 0 |
|
Следует обратить внимание на то, что в табл.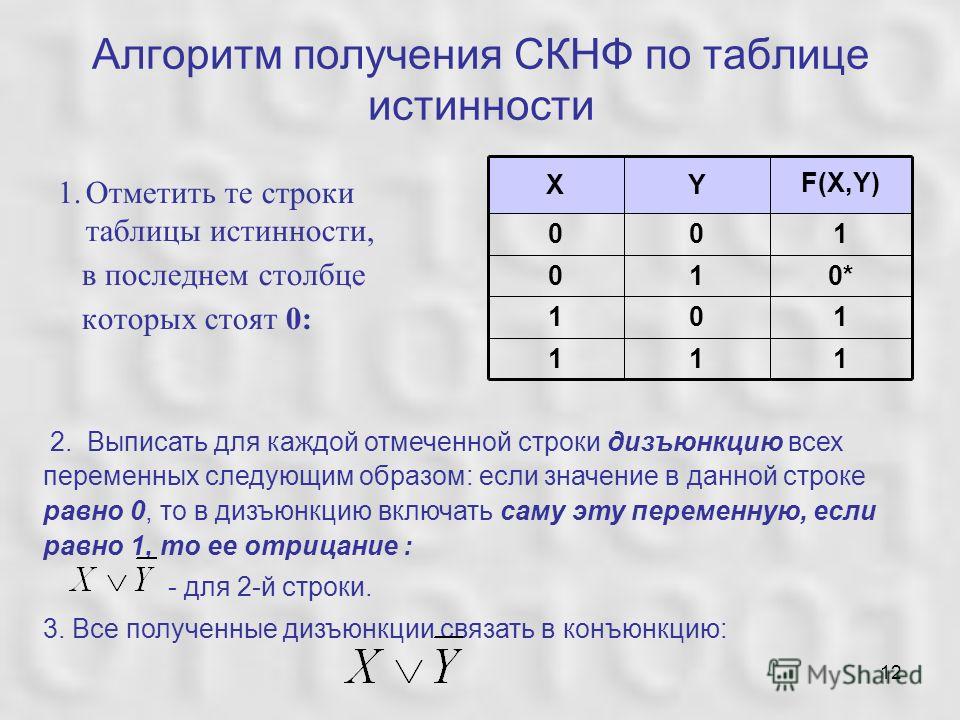 1.15 приведены данные, справедливые только для определенных значений переменной х. Однако закон тавтологии выполняется также и в случае неопределенного значения х=½. Законы же исключенного третьего и противоречия при х=½ не действуют, поскольку неопределенность сохраняется: х v x′ = ½ и х∙х′ = ½.
1.15 приведены данные, справедливые только для определенных значений переменной х. Однако закон тавтологии выполняется также и в случае неопределенного значения х=½. Законы же исключенного третьего и противоречия при х=½ не действуют, поскольку неопределенность сохраняется: х v x′ = ½ и х∙х′ = ½.
Для доказательства справедливости замены операции инверсии х на 1 – х, дизъюнкции на определение максимума и конъюнкции на вычисление минимума приведена табл. 1.16.
Таблица 1.16
Таблица истинности, подтверждающая законность замены операций инвертирования, дизъюнкции и конъюнкции
|
х1 |
х0 |
х1х0 (х1;х0) |
MAX |
х1·х0 |
MIN (х1;х0) |
1 |
1 – х1 |
0 |
1 – х0 |
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
0 |
½ |
½ |
½ |
0 |
0 |
1 |
1 |
½ |
½ |
|
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
|
½ |
0 |
½ |
½ |
0 |
0 |
½ |
½ |
1 |
1 |
|
½ |
½ |
½ |
½ |
½ |
½ |
½ |
½ |
½ |
½ |
|
½ |
1 |
1 |
1 |
½ |
½ |
½ |
½ |
0 |
0 |
|
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
1 |
|
1 |
½ |
1 |
1 |
½ |
½ |
0 |
0 |
½ |
½ |
|
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
17.
 5: Таблицы истинности: союз (и), дизъюнкция (или), отрицание (не)
5: Таблицы истинности: союз (и), дизъюнкция (или), отрицание (не)- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 34286
- Дэвид Липпман
- Колледж Пирса через OpenTextBookStore
Прежде чем мы сосредоточимся на таблицах истинности, мы собираемся ввести некоторые символы, которые обычно используются для и , или , и , а не .
Символы
Символ \(\клин\) используется для и: \( A\) и \(B\) обозначается \(A \клин B\)
Используется символ \(\vee\) для or: \(A\) или \(B\) обозначается \(A \vee B\)
Символ \(\sim\) используется для not: не \(A\) обозначается \(\ sim A\)
Вы можете запомнить первые два символа, связав их с фигурами объединения и пересечения. \(A \клин B\) будет элементами, которые существуют в обоих множествах, в \(A \cap B\). Точно так же \(A \vee B\) будут элементами, которые существуют в любом наборе, в \(A \cup B\). Когда мы работаем с наборами, мы используем закругленную версию символов; когда мы работаем с операторами, мы используем заостренную версию. 9{\ text {«Я люблю кока-колу»}}\).
\(A \клин B\) будет элементами, которые существуют в обоих множествах, в \(A \cap B\). Точно так же \(A \vee B\) будут элементами, которые существуют в любом наборе, в \(A \cup B\). Когда мы работаем с наборами, мы используем закругленную версию символов; когда мы работаем с операторами, мы используем заостренную версию. 9{\ text {«Я люблю кока-колу»}}\).
- Мне нравится пепси или кока-кола.
- Я люблю пепси и кока-колу.
- Я не люблю пепси.
- Дело не в том, что я люблю пепси или кока-колу.
- Я люблю пепси и не люблю кока-колу.
Раствор
- \(P \vee C\)
- \(П \клин С\)
- \(\сим П\)
- \(\sim(P \vee C)\)
- \(P \клин \sim C\)
Как видите, мы можем использовать круглые скобки для организации более сложных операторов.
Попробуйте сейчас 2
Переведите фразу «У нас есть морковь, иначе мы не будем варить суп» в символы.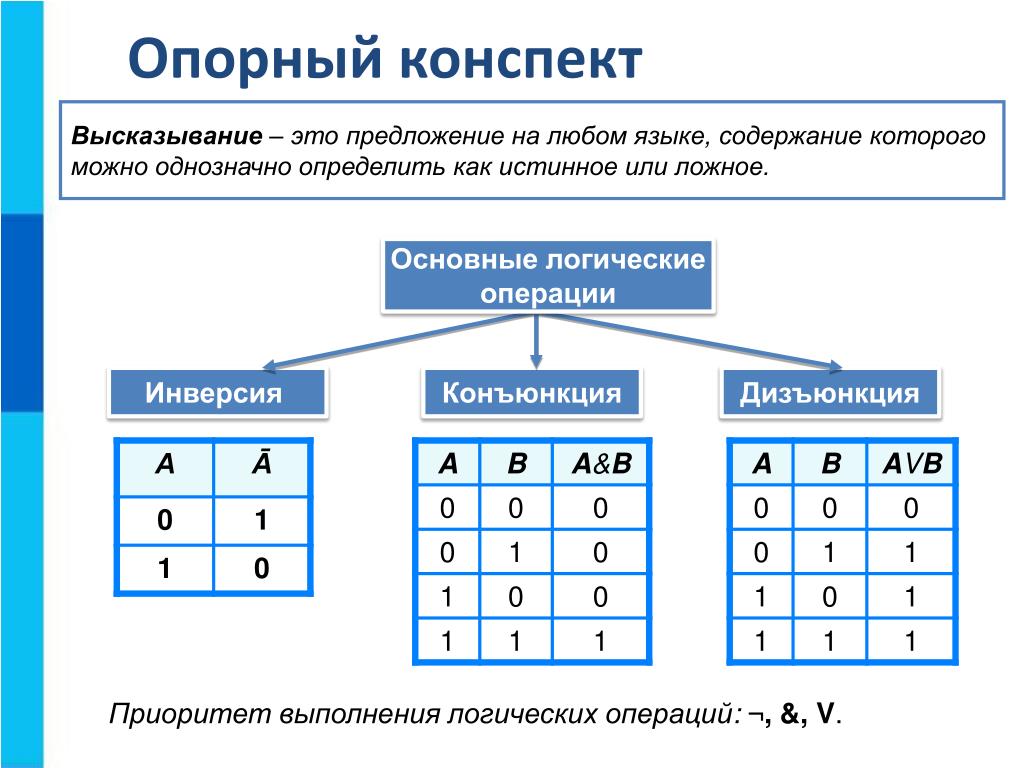 Пусть \(C\) представляет «у нас есть морковь», а \(S\) представляет «мы будем варить суп».
Пусть \(C\) представляет «у нас есть морковь», а \(S\) представляет «мы будем варить суп».
- Ответить
\(C \vee \sim S\)
Поскольку сложные логические утверждения могут быть сложными для понимания, мы можем создать таблицу истинности , чтобы отслеживать, какие значения истинности для простых утверждений делают сложное утверждение истинным и ложным.
Таблица истинности
Таблица, показывающая результирующее значение истинности сложного утверждения для всех возможных значений истинности для простых утверждений.
Пример 16
Предположим, вы выбираете новый диван, и ваша вторая половинка говорит: «Купите секционный или что-нибудь с шезлонгом».
Это сложное утверждение, состоящее из двух более простых условий: «является секционным» и «имеет фаэтон». Для простоты давайте использовать S для обозначения «является секционным», а C для обозначения «имеет шезлонг».
Таблица истинности для этой ситуации будет выглядеть так:
\(\begin{array}{|c|c|c|}
\hline S & C & S \text { or } C \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\ \hline
\end{массив}\)
В таблице , T используется для true, а F для false. В первой строке, если S истинно и C также истинно, то сложное утверждение « S или C » истинно. Это будет секционная, в которой также есть шезлонг, что соответствует нашему желанию. (Помните, что или в логике не являются исключающими; если кушетка имеет обе функции, она удовлетворяет условию.)
В предыдущем примере с кушеткой таблица истинности на самом деле просто суммировала то, что мы уже знаем о том, как или ведомость работы. Таблицы истинности для основных 9Операторы 0032 и , или и , а не показаны ниже.
Базовые таблицы истинности
Конъюнкция
\(\begin{array}{|c|c|c|}
\hline A & B & A \wedge B \\
\hline \mathrm{T} & \ mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \ mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline
\end{массив}\)
Дизъюнкция
\(\begin{array}{|c|c|c|}
\hline A & B & A \vee B \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline
\end{массив}\)
Отрицание
\(\begin{array}{ |c|c|}
\hline A & \sim A \\
\hline \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} \\
\hline
\end{array}\)
Таблицы истинности становятся действительно полезными, когда мы анализируем более сложные логические операторы.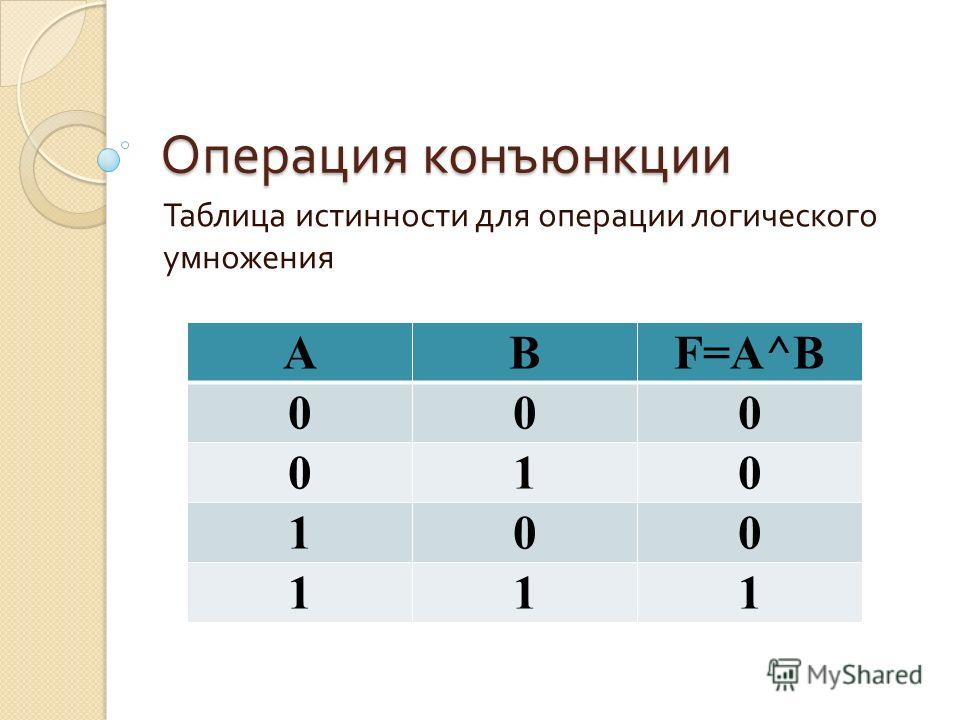
Пример 17
Создайте таблицу истинности для утверждения \(A \vee \sim B\)
Решение
Когда мы создаем таблицу истинности, нам нужно перечислить все возможные комбинации значений истинности для \(A\) и \(В\). Обратите внимание, что первый столбец содержит 2 T, за которыми следуют \(2 ~\mathrm{Fs}\), а второй столбец чередует \(\mathrm{T}, \mathrm{F}, \mathrm{T}\), F , Этот шаблон гарантирует, что будут учтены все 4 комбинации.
\(\begin{array}{|c|c|}
\hline A & B \\
\hline \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \ mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} \\
\hline
\end{массив}\)
После создания столбцов с этими начальными значениями мы создаем третий столбец для выражения \(\sim B\). Теперь мы временно проигнорируем столбец для \(A\) и запишем истинные значения для \(\sim B\)
\(\begin{array}{|c|c|c|}
\hline A & B & \sim B \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \ mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline
\end{array}\)
Далее мы можем найти истинностные значения \(A \vee \sim B,\), используя первый и третий столбцы.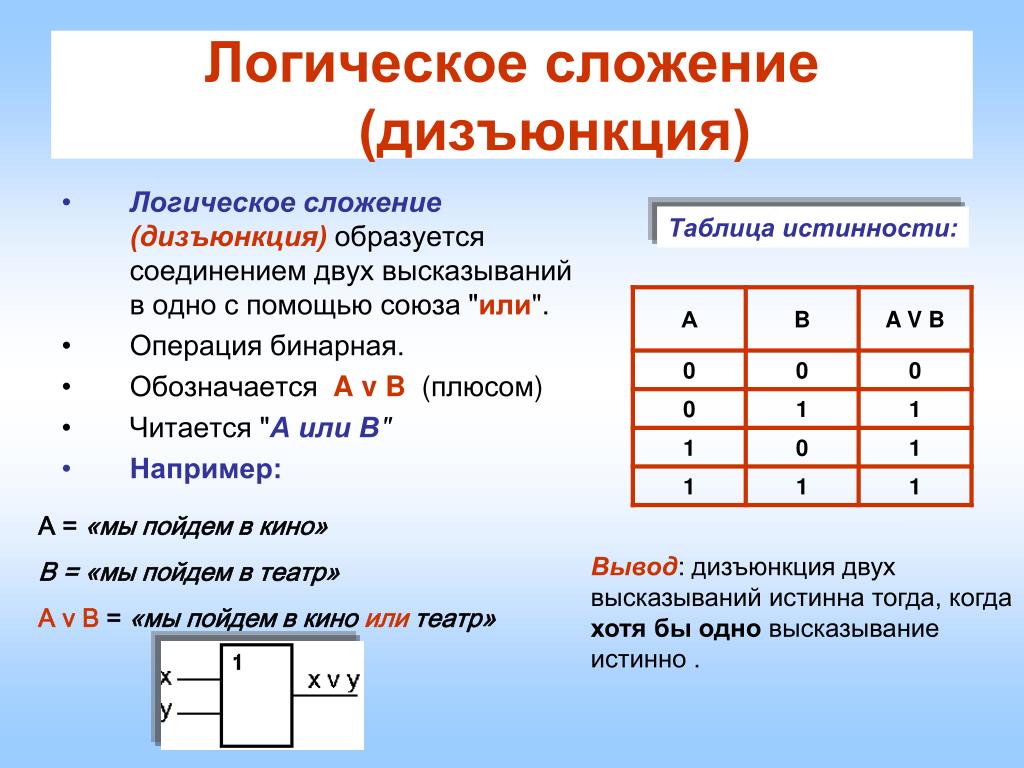
\(\begin{array}{|c|c|c|c|}
\hline A & B & \sim B & A \vee \sim B \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \ mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \ mathrm{T} & \mathrm{T} \\
\hline
\end{array}\)
Таблица истинности показывает, что \(A \vee \sim B\) верно в трех случаях и ложно в одном случае . Если вам интересно, в чем смысл этого, предположим, что это последний день бейсбольного сезона, и две команды, которые не играют друг с другом, соревнуются за финальное место в плей-офф. Анахайм выйдет в плей-офф, если выиграет свою игру или , если Бостон не выиграет свою игру. (Анахайм владеет тай-брейком; если обе команды выигрывают или если обе команды проигрывают, то Анахайм получает место в плей-офф.) Если \(A=\) Анахайм выигрывает свою игру и \(B=\) Бостон выигрывает свою игру, тогда \(A \vee\) \(\sim B\) представляет ситуацию «Анахайм выигрывает свою игру или Бостон не выигрывает свою игру».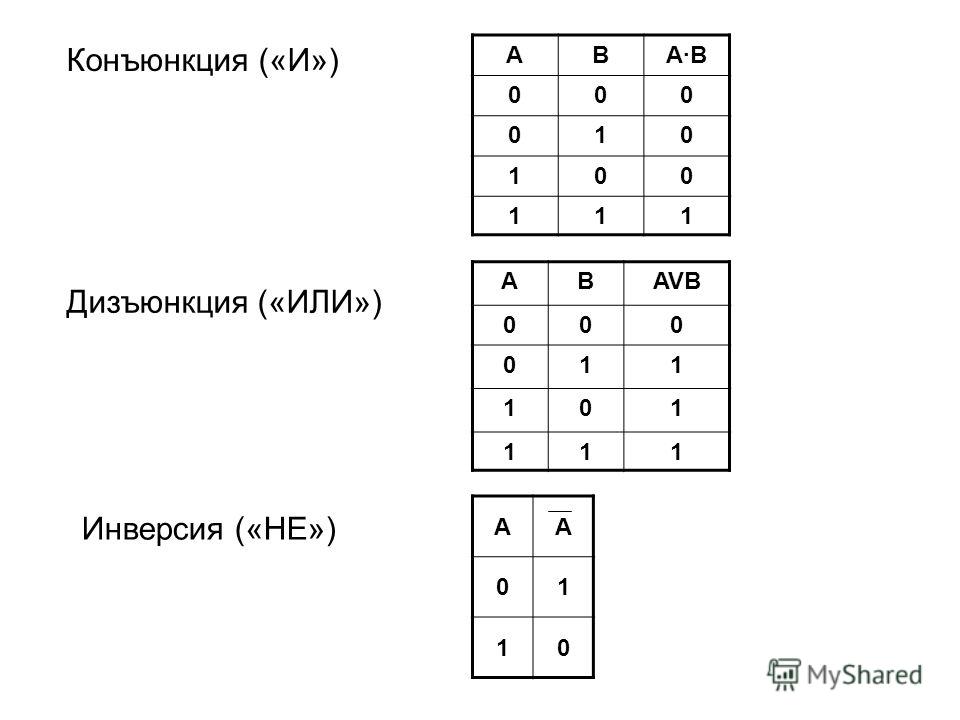 Таблица истинности показывает нам различные сценарии, связанные с выходом Анахайма в плей-офф. В первом ряду Анахайм выигрывает свою игру, а Бостон выигрывает свою игру, так что это правда, что Анахайм выходит в плей-офф. Во втором ряду выигрывает Анахайм, а не Бостон, так что это правда, что Анахайм выходит в плей-офф. В третьем ряду Анахайм не выигрывает свою игру, а Бостон выигрывает свою игру, так что это 9.0228 false что Анахайм выходит в плей-офф. В четвертом ряду Анахайм не побеждает, а Бостон не побеждает, так что это правда, что Анахайм выходит в плей-офф.
Таблица истинности показывает нам различные сценарии, связанные с выходом Анахайма в плей-офф. В первом ряду Анахайм выигрывает свою игру, а Бостон выигрывает свою игру, так что это правда, что Анахайм выходит в плей-офф. Во втором ряду выигрывает Анахайм, а не Бостон, так что это правда, что Анахайм выходит в плей-офф. В третьем ряду Анахайм не выигрывает свою игру, а Бостон выигрывает свою игру, так что это 9.0228 false что Анахайм выходит в плей-офф. В четвертом ряду Анахайм не побеждает, а Бостон не побеждает, так что это правда, что Анахайм выходит в плей-офф.
Попробуйте сейчас 3
Создайте таблицу истинности для этого утверждения: \(\sim A \wedge B\)
- Ответ
\(\begin{array}{|c|c|c|c|}
\hline A & B & \sim A & \sim A \wedge B \\
\hline \mathrm{T} & \mathrm{ T} и \mathrm{F} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \ mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline
\end{массив}\)
Пример 18
Создайте таблицу истинности для утверждения \(A \клин \sim(B \vee C)\)
Решение
Это помогает работать изнутри наружу при создании таблицы истинности, а также создавать столбцы в таблице для промежуточных операций. Начнем с перечисления всех возможных комбинаций значений истинности для \(A, B,\) и \(C.\). Обратите внимание, что первый столбец содержит 4 T, за которыми следуют \(4 \mathrm{Fs}\), второй столбец содержит \(2 \mathrm{Ts}, 2 \mathrm{Fs}\), затем повторяется, и последний столбец чередуется \(\mathrm{T}, \mathrm{F}, \mathrm{T}, \mathrm{ F} \ldots\) Этот шаблон гарантирует, что будут учтены все 8 комбинаций. После создания столбцов с этими начальными значениями мы создаем четвертый столбец для самого внутреннего выражения, \(B \vee C .\). Теперь мы временно проигнорируем столбец для \(A\) и сосредоточимся на \(B\) и \ (C\), записывая значения истинности для \(B \vee C\)
Начнем с перечисления всех возможных комбинаций значений истинности для \(A, B,\) и \(C.\). Обратите внимание, что первый столбец содержит 4 T, за которыми следуют \(4 \mathrm{Fs}\), второй столбец содержит \(2 \mathrm{Ts}, 2 \mathrm{Fs}\), затем повторяется, и последний столбец чередуется \(\mathrm{T}, \mathrm{F}, \mathrm{T}, \mathrm{ F} \ldots\) Этот шаблон гарантирует, что будут учтены все 8 комбинаций. После создания столбцов с этими начальными значениями мы создаем четвертый столбец для самого внутреннего выражения, \(B \vee C .\). Теперь мы временно проигнорируем столбец для \(A\) и сосредоточимся на \(B\) и \ (C\), записывая значения истинности для \(B \vee C\)
\(\begin{array}{|c|c|c|}
\hline A & B & C \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{ T} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{ T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{ Ф}\
\hline
\end{массив}\)
\(\begin{array}{|c|c|c|c|}
\hline A & B & C & B \vee C \\
\hline \ mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{T} & \ mathrm{T} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline
\end{array}\)
Далее мы можем найдите отрицание \(B \vee C\), работая с столбцом \(B \vee\) C, который мы только что создали. (Игнорируйте первые три столбца и просто инвертируйте значения в столбце \(B \vee C\).)
(Игнорируйте первые три столбца и просто инвертируйте значения в столбце \(B \vee C\).)
\(\begin{array}{|c|c|c|c|c|}
\hline A & B & C & B \vee C & \sim(B \vee C) \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{ F} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \ mathrm{T} & \mathrm{T} & \mathrm{F} \\
\hline \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} \\
\hline
\end{array}\)
Наконец, мы находим значения \(A\) и \(\sim(B \vee C)\). (Второй, третий и четвертый столбцы игнорируйте.)
\(\begin{array}{|c|c|c|c|c|c|}
\hline A & B & C & B \vee C & \sim B \vee C) & A \wedge \sim B \vee C \text { ) } \\
\hline \text { T } & \text { T } & \text { T } & \text { T } & \text { F } & \text { F } \\
\hline \text { T } & \ текст { T } & \text { F } & \text { T } & \text { F } & \text { F } \\
\hline \text { T } & \text { F } & \text { T } & \text { T } & \text { F } & \text { F } \\
\hline \text { T } & \text { F } & \text { F } & \text { F } & \text { T } & \text { T } \\
\hline \text { F } & \text { T } & \text { T } & \text { T } & \text { F } & \text { F } \\
\hline \text { F } & \text { T } & \text { F } & \text { T } & \text { F } & \text { F } \\
\hline \text { F } & \ текст { F } & \text { T } & \text { T } & \text { F } & \text { F } \\
\hline \text { F } & \text { F } & \text { F } & \text { F } & \text { T } & \text { F } \\
\hline
\end{array}\)
Оказывается, это сложное выражение верно только в одном случае: когда \( А\) верно, \(В\) ложно и \(С\) ложно. Чтобы проиллюстрировать эту ситуацию, предположим, что Анахайм выйдет в плей-офф, если: (1) Анахайм выиграет и (2) ни Бостон, ни Кливленд не выиграют. IFF — единственный сценарий, при котором «Анахайм» выйдет в плей-офф.
Чтобы проиллюстрировать эту ситуацию, предположим, что Анахайм выйдет в плей-офф, если: (1) Анахайм выиграет и (2) ни Бостон, ни Кливленд не выиграют. IFF — единственный сценарий, при котором «Анахайм» выйдет в плей-офф.
Попробуйте сейчас 4
Создайте таблицу истинности для этого утверждения: \((\sim A \wedge B) \vee \sim B\)
- Ответ
\(\begin{array}{|c|c|c|c|c|c|}
\hline A & B & \sim A & \sim A \wedge B & \sim B & (\sim A \ клин B) \vee \sim B \\
\hline \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{F} \\
\hline \mathrm{T} & \mathrm{F} & \mathrm{F} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline \mathrm{F} & \mathrm{T} & \mathrm{T} & \mathrm{T} & \mathrm{F} & \mathrm{T} \\
\hline \mathrm{F} & \ mathrm{F} & \mathrm{T} & \mathrm{F} & \mathrm{T} & \mathrm{T} \\
\hline
\end{массив}\)
Эта страница под заголовком 17.5: Таблицы истинности: соединение (и), дизъюнкция (или), отрицание (не) используется в соответствии с лицензией CC BY-SA 3. 0 и была создана, изменена и/или курирована Дэвидом Липпманом (The OpenTextBookStore) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
0 и была создана, изменена и/или курирована Дэвидом Липпманом (The OpenTextBookStore) через исходный контент, отредактированный в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или Страница
- Автор
- Дэвид Липпман
- Лицензия
- CC BY-SA
- Версия лицензии
- 3,0
- Показать страницу TOC
- нет
- Теги
- источник@http://www.
 opentextbookstore.com/mathinsociety
opentextbookstore.com/mathinsociety
- источник@http://www.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Домашняя страница > Логика > Символика Логика > Логические связки | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Философия 103: Введение в логику Конъюнкция, отрицание и дизъюнкция Abstract: Логические операции конъюнкции, отрицания и дизъюнкции (альтерации) обсуждаются относительно их табличных определений истинности.
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Отправляйте исправления или предложения по адресу webmaster@philosophy. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Аргументы | Язык | Заблуждения | Предложения | Силлогизмы | Перевод | Символический | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| . | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Союзы и дизъюнкции в математике (видео, определение и примеры)
Содержание
В математической логике слова имеют точное значение. Логика пытается показать правдивые выводы, вытекающие из правдивых предпосылок, или надежно выявляет ложь. Математические и логические операторы соединяются соединителями; конъюнкции и дизъюнкции — это два типа логических соединителей.
- Логические операторы
- Логические разъемы
- Союзы в математике
- Дизъюнкции в математике
- Примеры конъюнкции и дизъюнкции
Логические утверждения
С помощью логики утверждения могут быть помечены как истинные или ложные, например:
- Все числа целые
- Некоторые отрицательные числа являются целыми числами
- Квадраты являются прямоугольниками
- Некоторые четырехугольники являются параллелограммами
- Четырехугольники имеют 11 сторон
- Прямоугольники имеют четыре стороны
Ясно, что некоторые из этих шести утверждений ложны, но дело в том, что их можно проверить. Они не высказывают мнения. Сравните их, скажем, «Мне нравятся чизбургеры», что показывает мнение.
Они не высказывают мнения. Сравните их, скажем, «Мне нравятся чизбургеры», что показывает мнение.
Логические соединители
Операторы часто обозначаются буквами p и q. Они связаны вместе с помощью соединителей, поэтому вы можете комбинировать идеи, используя «и» или «или» между утверждениями. Два оператора, соединенные соединителями, создают составной оператор . Соединение логических утверждений — это не то же самое, что связывание идей в обычном английском разговоре. Сравните:
- Я люблю чизбургеры, а мой друг любит банановые молочные коктейли
- Все числа целые, а квадраты прямоугольники
Первые связанные утверждения, одно составное утверждение, являются мнениями. Второе составное утверждение является логическим утверждением (но составное утверждение ложно).
Два типа соединителей называются союзами («и») и дизъюнкциями («или»). В союзах используется математический символ ∧, а в дизъюнкциях — математический символ ∨.
Союзы в математике
Соединение двух утверждений с помощью «и» является соединением , что означает, что оба утверждения должны быть истинными, чтобы составное утверждение было истинным в целом. Соединения обозначаются символом ∧, поэтому эти два отдельных утверждения можно объединить в составное утверждение:
- Утверждение p: Квадраты — это прямоугольники
- Утверждение q: прямоугольники имеют четыре стороны
- Составное утверждение (на английском языке): Квадраты — это прямоугольники, а прямоугольники имеют четыре стороны.
- Составной оператор (в математических символах): p∧q
Только если обе части составного утверждения верны, все утверждение истинно.
Дизъюнкция в математике
Когда связующим звеном между двумя операторами является «или», у вас есть дизъюнкция . В этом случае только одно утверждение в составном утверждении должно быть истинным, чтобы все составное утверждение было истинным.
Давайте еще раз посмотрим на исходные утверждения:
- Все числа целые
- Некоторые отрицательные числа являются целыми числами
- Квадраты являются прямоугольниками
- Некоторые четырехугольники являются параллелограммами
- Четырехугольники имеют 11 сторон
- Прямоугольники имеют четыре стороны
Если мы свяжем одно истинное и одно ложное утверждение в составное утверждение с помощью соединителя «или» (обозначается ∨), мы все равно получим истинное составное утверждение:
- p: Квадраты — это прямоугольники
- q: Четырехугольники имеют 11 сторон
- p∨q: все квадраты являются прямоугольниками или четырехугольниками с 11 сторонами
Примеры конъюнкции и дизъюнкции
Вот четыре других составных утверждения, взятых из наших исходных утверждений. Определите символы и определите, верны или нет составные утверждения:
- p: Некоторые отрицательные числа являются целыми числами
- q: Квадраты являются прямоугольниками
- Некоторые отрицательные числа являются целыми числами, а квадраты — прямоугольниками.

Вы сказали p∧q и оценили ли вы это как истину? Оба утверждения верны, поэтому составное утверждение, соединенное союзом «и», истинно.
- p: Некоторые четырехугольники являются параллелограммами
- q: Четырехугольники имеют 11 сторон
- Некоторые четырехугольники являются параллелограммами, или четырехугольники имеют 11 сторон.
Вы сказали p∨q и оценили это составное утверждение как истинное? Хотя у четырехугольников нет 11 сторон, союз «или» делает составное утверждение верным, поскольку некоторые четырехугольники являются параллелограммами.
- p: Четырехугольники имеют 11 сторон
- q: Прямоугольники имеют четыре стороны
- Четырехугольники имеют 11 сторон, а прямоугольники имеют четыре стороны.
Вы сказали p∧q? Что еще более важно, вы сказали, что это составное утверждение было ложным? Поскольку у четырехугольников нет 11 сторон, конъюнкция неверна.
- p: Все числа целые
- q: Квадраты являются прямоугольниками
- Все числа являются целыми числами или квадраты являются прямоугольниками.



 opentextbookstore.com/mathinsociety
opentextbookstore.com/mathinsociety
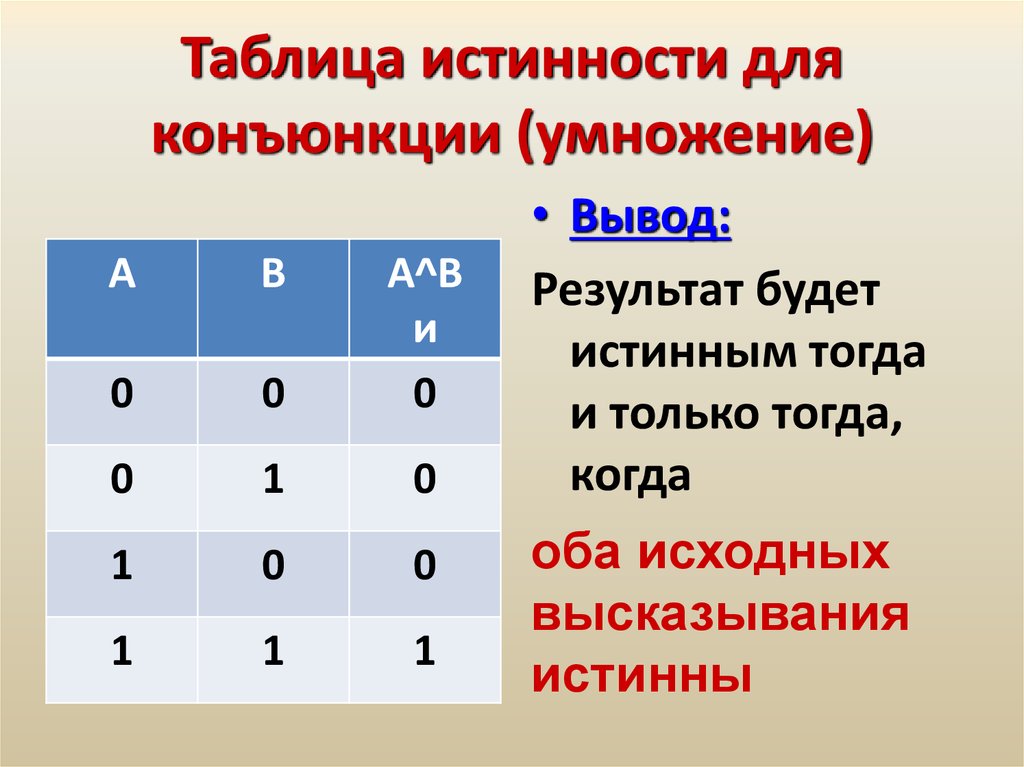 Эти случаи могут быть
перечислены ниже в том, что называется таблица истинности .
Эти случаи могут быть
перечислены ниже в том, что называется таблица истинности .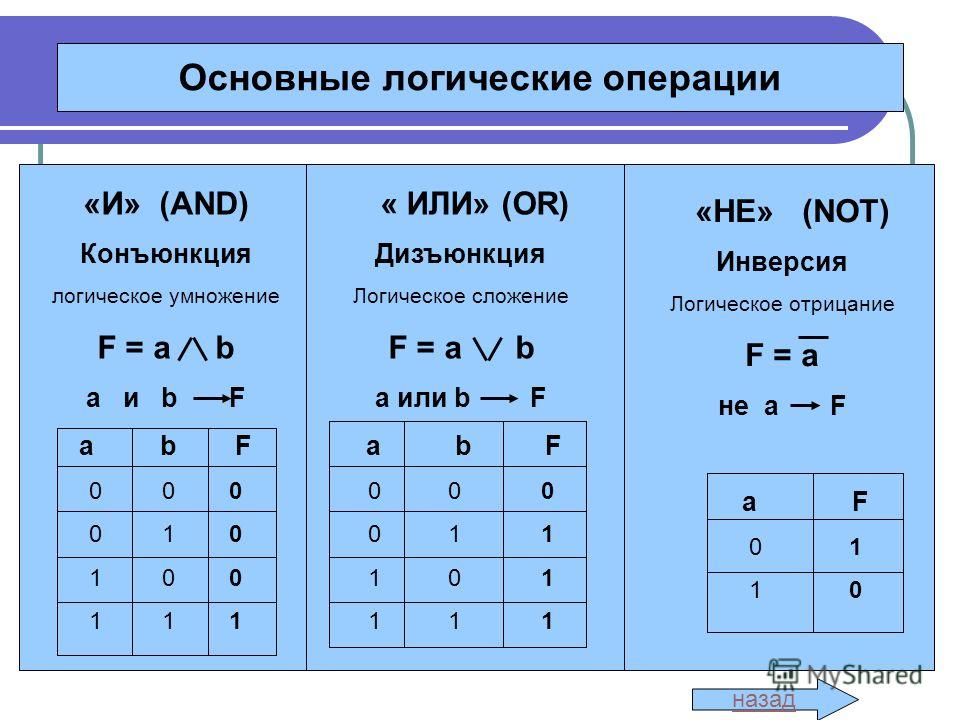 Его можно рассматривать как «минимальный
общее логическое значение» для соединенных утверждений.
Его можно рассматривать как «минимальный
общее логическое значение» для соединенных утверждений.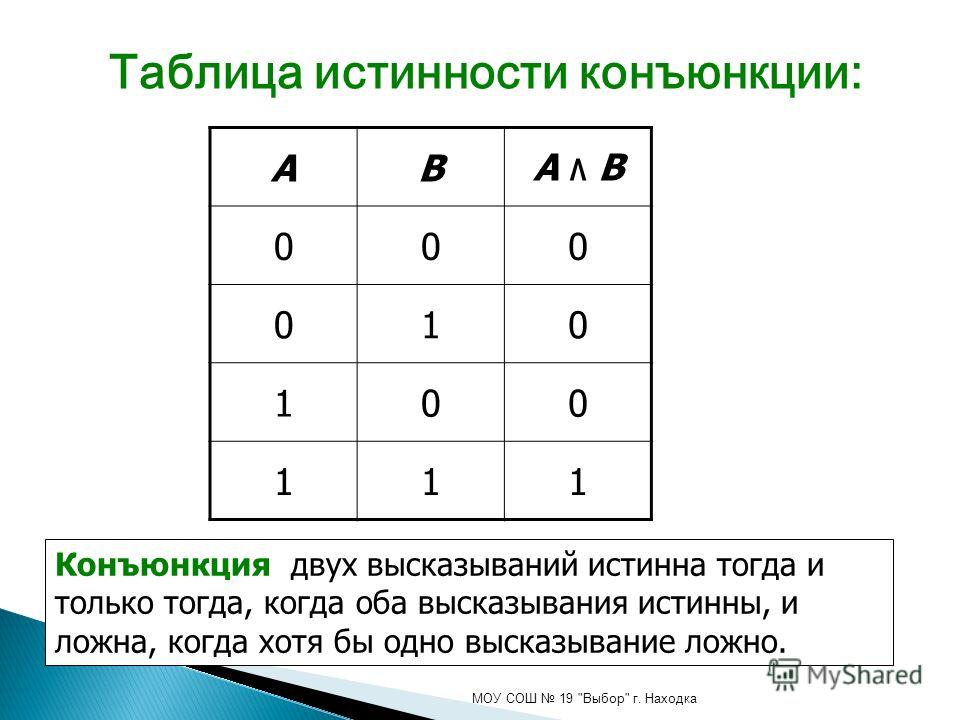
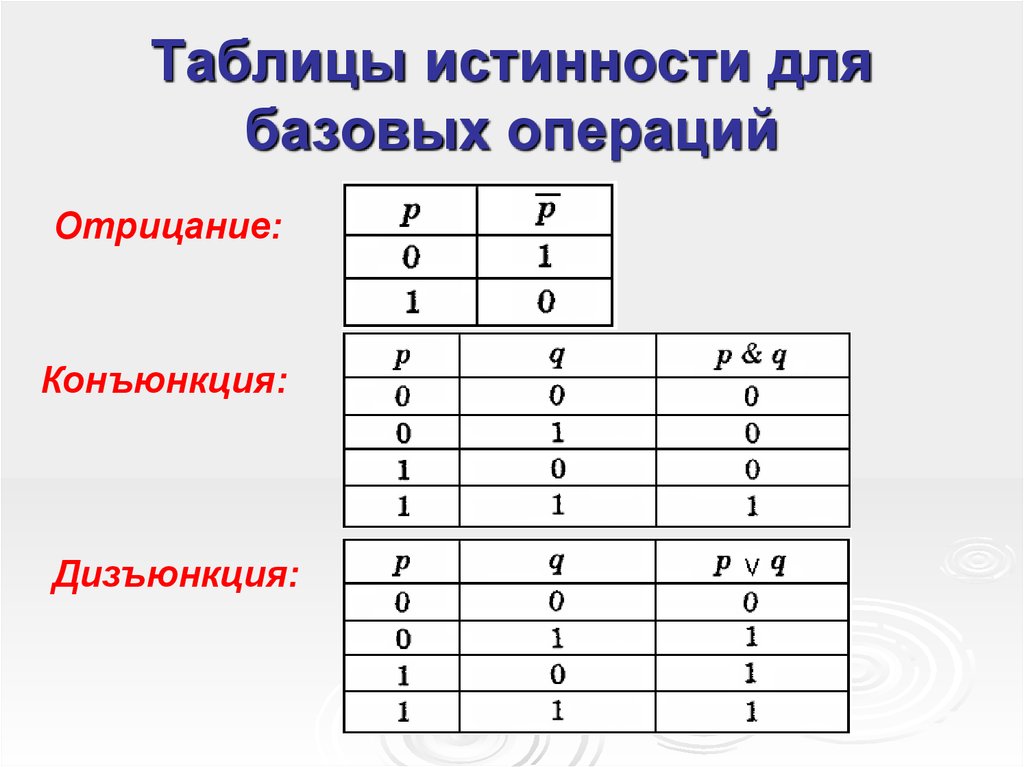
 которые ложны, только если оба утверждения (дизъюнкты) ложны.
которые ложны, только если оба утверждения (дизъюнкты) ложны. » Если в этом примере Джон не на
библиотека и Джон не учится, то истинность сложного утверждения
неверно:
» Если в этом примере Джон не на
библиотека и Джон не учится, то истинность сложного утверждения
неверно: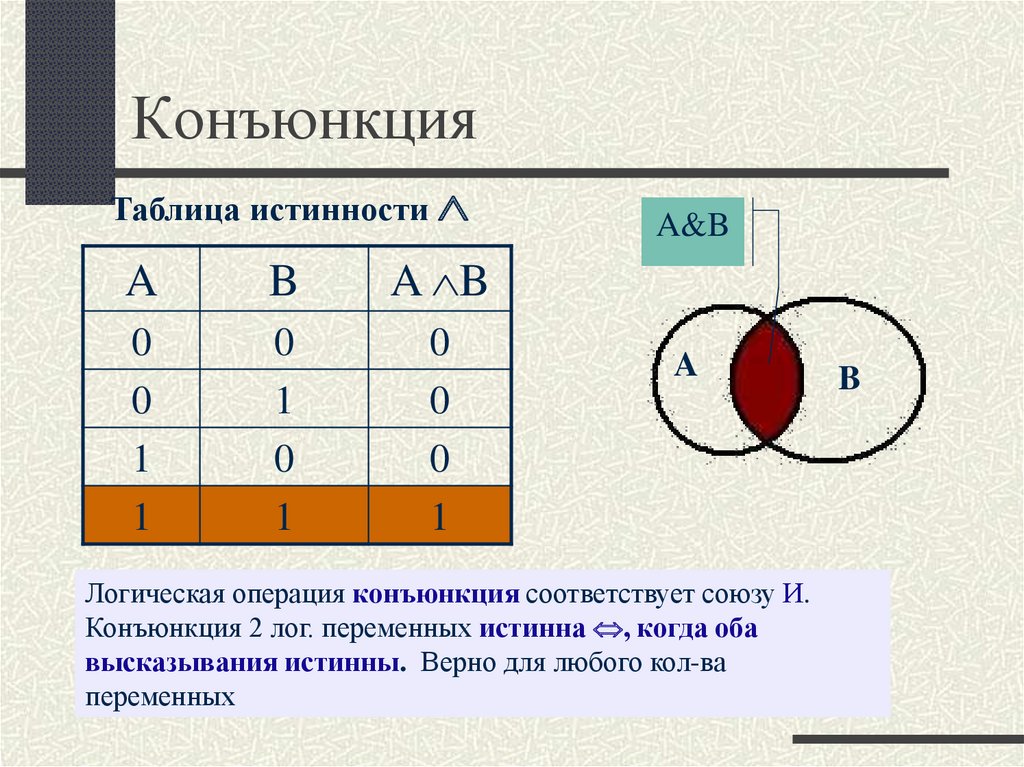
 lander.edu
lander.edu