Цепь переменного тока с емкостью
Если в цепь постоянного тока включить конденсатор (идеальный – без потерь), то в течение короткого времени после включения по цепи потечет зарядный ток. После того как конденсатор зарядится до напряжения, соответствующего напряжению источника, кратковременный ток в цепи прекратится. Следовательно, для постоянного тока конденсатор представляет собой разрыв цепи или бесконечно большое сопротивление.
Если же конденсатор включить в цепь переменного тока, то он будет заряжаться попеременно то в одном, то в другом направлении.
При этом в цепи будет проходить переменный ток. Рассмотрим это явление подробнее.
В момент включения напряжение на конденсаторе равно нулю. Если включить конденсатор к переменному напряжению сети, то в течение первой четверти периода, когда напряжение сети будет возрастать (рисунок 1), конденсатор будет заряжаться.
Рисунок 1. Графики и векторная диаграмма для цепи переменного тока, содержащей емкость
По мере накопления зарядов на обкладках конденсатора напряжение конденсатора увеличивается. Когда напряжение сети к концу первой четверти периода достигнет максимума, заряд конденсатора прекращается и ток в цепи становится равным нулю.
Когда напряжение сети к концу первой четверти периода достигнет максимума, заряд конденсатора прекращается и ток в цепи становится равным нулю.
Ток в цепи конденсатора можно определить по формуле:
где q – количество электричества, протекающее по цепи.
Из электростатики известно:
q = C × uC = C × u ,
где C – емкость конденсатора; u – напряжение сети; uC – напряжение на обкладках конденсатора.
Окончательно для тока имеем:
Из последнего выражения видно, что, когда
максимально (положения а, в, д), i также максимально. Когда (положения б, г на рисунке 1), то i также равно нулю.
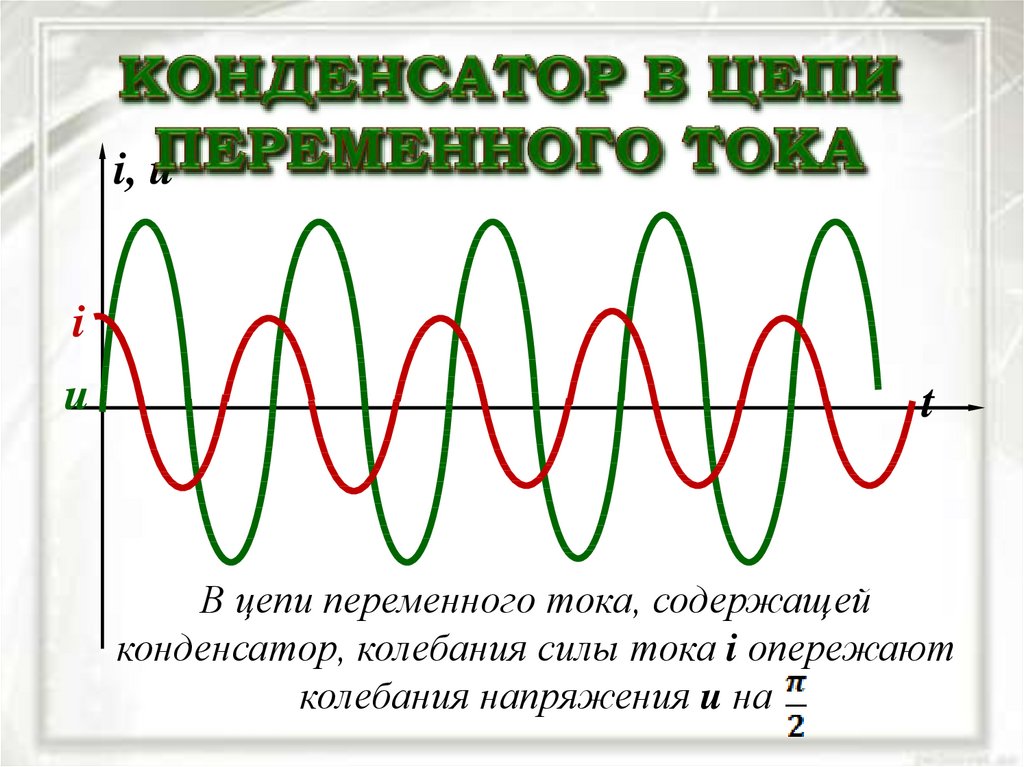
Во вторую четверть периода напряжение сети будет уменьшаться, и конденсатор начнет разряжаться. Ток в цепи меняет свое направление на обратное. В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд. Из рисунка 1 видно, что ток в цепи с емкостью в своих изменениях опережает по фазе на 90°
В следующую половину периода напряжение сети меняет свое направление и наступает перезаряд конденсатора и затем снова его разряд. Из рисунка 1 видно, что ток в цепи с емкостью в своих изменениях опережает по фазе на 90°
напряжение на обкладках конденсатора.
Сравнивая векторные диаграммы цепей с индуктивностью и емкостью, мы видим, что индуктивность и емкость на фазу тока влияют прямо противоположно.
Поскольку мы отметили выше, что скорость изменения тока пропорциональна угловой частоте ω, из формулы
получаем аналогично, что скорость изменения напряжения также пропорциональна угловой частоте ω и для действующего значения тока имеем
I = 2 × π × f × C × U .
Обозначая
, где xC называется емкостным сопротивлением, или реактивным сопротивлением емкости. Итак мы получили формулу емкостного сопротивления при включении емкости в цепи переменного тока. Отсюда, на основании выражения закона Ома, мы можем получить ток для цепи переменного тока, содержащей емкость:
Отсюда, на основании выражения закона Ома, мы можем получить ток для цепи переменного тока, содержащей емкость:
Напряжение на обкладках конденсатора
UC = IC × xC .
Та часть напряжения сети, которая имеется на конденсаторе, называется емкостным падением напряжения, или реактивной слагающей напряжения, и обозначается UC.
Емкостное сопротивление xC, так же как индуктивное сопротивление xL, зависит от частоты переменного тока.
Но если с увеличением частоты индуктивное сопротивление увеличивается, то емкостное сопротивление, наоборот, будет уменьшаться.
Пример 1. Определить емкостное реактивное сопротивление конденсатора емкостью 5 мкФ при разных частотах сетевого напряжения. Расчет емкостного сопротивления произведем при частоте 50 и 40 Гц:
при частоте 50 Гц:
при частоте 400 Гц:
Применим формулу средней или активной мощности для рассматриваемой цепи:
P = U × I × cos φ .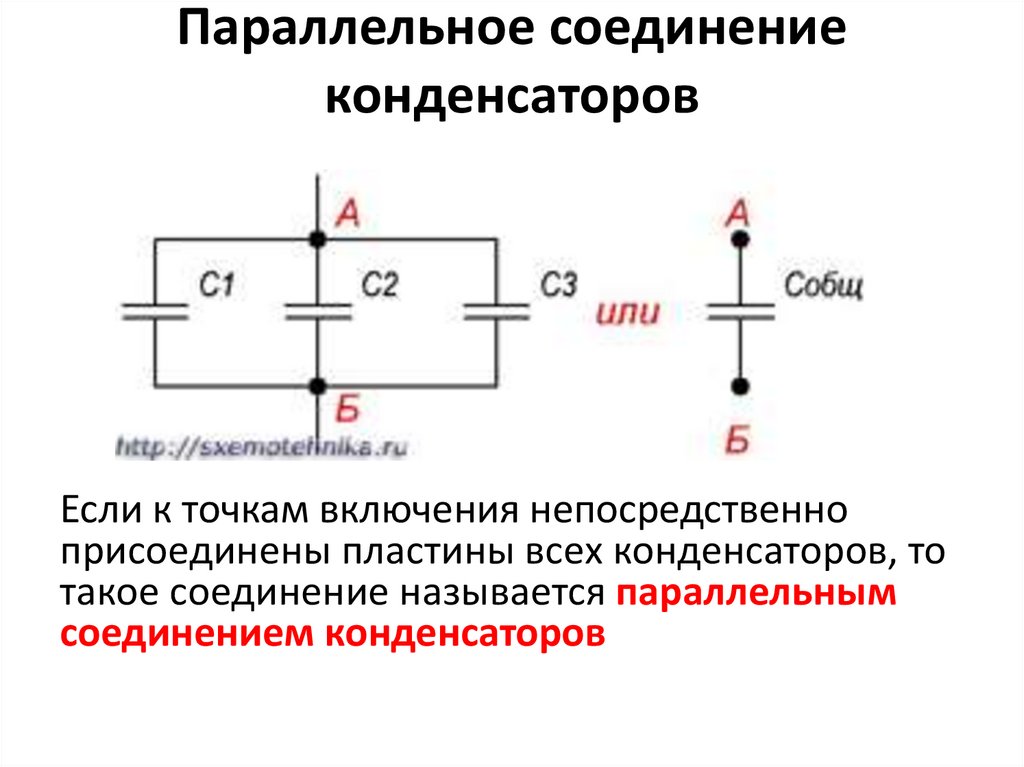
Так как в цепи с емкостью ток опережает напряжение на 90°, то
φ = 90°; cos φ = 0 .
Поэтому активная мощность также равна нулю, то есть в такой цепи, как и в цепи с индуктивностью, расхода мощности нет.
На рисунке 2 показана кривая мгновенной мощности в цепи с емкостью. Из чертежа видно, что в первую четверть периода цепь с емкостью забирает из сети энергию, которая запасается в электрическом поле конденсатора.
Рисунок 2. Кривая мгновенной мощности в цепи с емкостью
Энергию, запасаемую конденсатором к моменту прохождения напряжения на нем через максимум, можно определить по формуле:
В следующую четверть периода конденсатор разряжается на сеть, отдавая ей ранее запасенную в нем энергию.
За вторую половину периода явление колебаний энергии повторяется. Таким образом, в цепи с емкостью происходит лишь обмен энергией между сетью и конденсатором без потерь.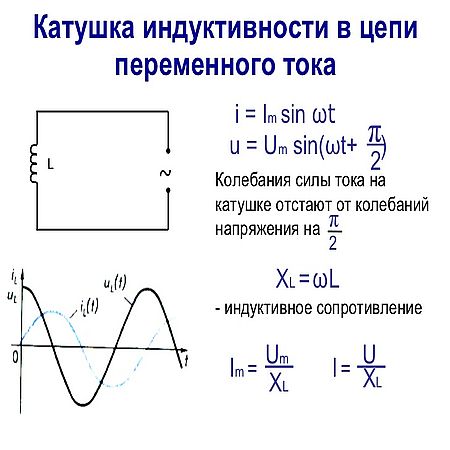
Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.
5 важных факторов, связанных с ней
Пункты обсуждения- Введение в цепь переменного тока
- Важная терминология, относящаяся к цепи переменного тока
- Чисто резистивная цепь переменного тока
- Фазорная диаграмма чисто резистивной цепи
- Питание в чисто резистивной цепи
- Чистая емкостная цепь переменного тока
- Фазорная диаграмма чистой емкостной цепи
- Мощность в чисто емкостной цепи
- Чистая индуктивная цепь переменного тока
- Фазорная диаграмма чистой индуктивной цепи
- Мощность в чисто индуктивной цепи
AC означает переменный ток.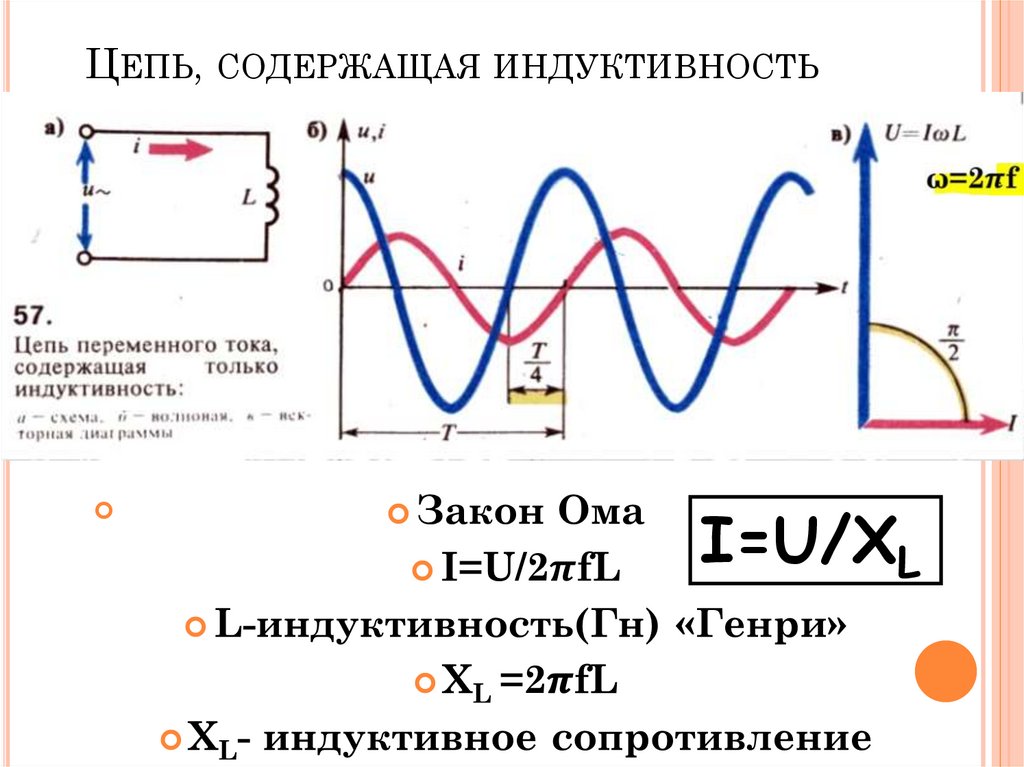 Если поток заряда от источника энергии периодически изменяется, цепь будет называться цепью переменного тока. Напряжение и ток (как величина, так и направление) в цепи переменного тока изменяются со временем.
Если поток заряда от источника энергии периодически изменяется, цепь будет называться цепью переменного тока. Напряжение и ток (как величина, так и направление) в цепи переменного тока изменяются со временем.
Цепь переменного тока имеет дополнительное сопротивление протеканию тока, поскольку в цепях переменного тока также присутствуют полное сопротивление и реактивное сопротивление. В этой статье мы обсудим три элементарных, но важных и фундаментальных схемы переменного тока. Мы найдем для них уравнения напряжения и тока, векторные диаграммы, форматы мощности. Более сложные, но базовые схемы могут быть получены из этих схем, например — последовательные RC-цепи, последовательные LC-схемы, последовательные RLC-схемы и т. Д.
Что такое цепь постоянного тока? Узнайте о KCL, KVL! Нажмите здесь!Важная терминология, относящаяся к цепи переменного токаДля анализа цепей переменного тока и их изучения необходимы базовые знания в области электротехники. Некоторые из часто используемых терминов приведены ниже для справок. Кратко изучите их, прежде чем исследовать семейство цепей переменного тока.
Некоторые из часто используемых терминов приведены ниже для справок. Кратко изучите их, прежде чем исследовать семейство цепей переменного тока.
- Амплитуда: Мощность течет в цепи переменного тока в виде синусоидальных волн. Амплитуда относится к максимальной величине волны, которая может быть достигнута как в положительной, так и в отрицательной областях. Максимальная величина представлена как Vm и Im (для напряжения и тока соответственно).
- Чередование: Синусоидальные сигналы имеют период 360o. Это означает, что волна повторяется после 360o промежуток времени. Половина этого цикла называется чередованием.
- Мгновенное значение: Величина напряжения и тока, заданные в любой момент времени, называется мгновенным значением.
- Частота: Частота определяется количеством циклов, созданных волной за один второй промежуток времени.
 Единица измерения частоты — Герц (Гц).
Единица измерения частоты — Герц (Гц). - Временной период: Период времени можно определить как промежуток времени, за который волна завершила один полный цикл.
- Форма волны: Форма волны — это графическое представление распространения волн.
- Значения RMS: Среднеквадратичное значение означает «среднеквадратическое значение». Среднеквадратичное значение любых компонентов переменного тока представляет собой эквивалентное значение величины постоянного тока.
Если цепь переменного тока состоит только из чистого сопротивления, то эта цепь будет называться чистой резистивной цепью переменного тока. В этом типе нет катушки индуктивности или конденсатора. Цепь переменного тока. В этой цепи мощность, генерируемая сопротивлением, и компоненты энергии, напряжение и ток, остаются в одной и той же фазе. Это обеспечивает одновременное повышение напряжения и тока на пиковое значение или максимальное значение.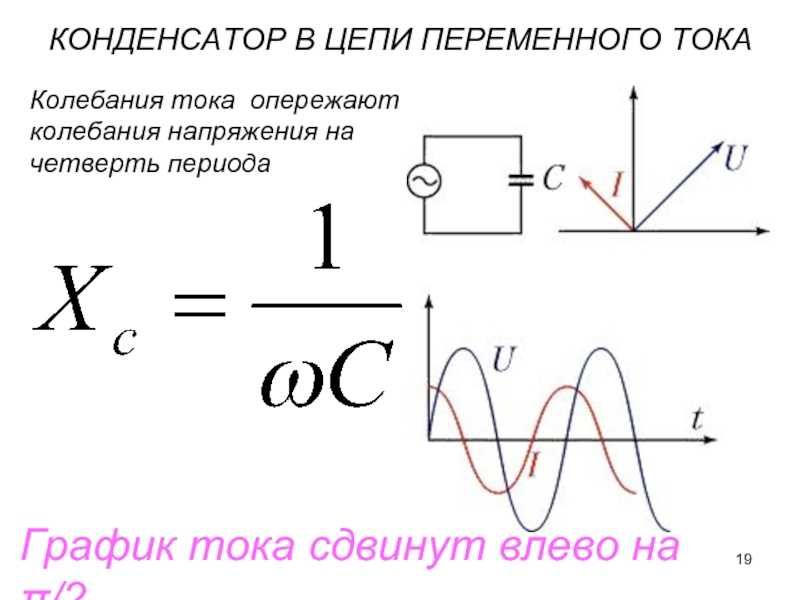
Предположим, что напряжение источника равно V, значение сопротивления равно R, а ток, протекающий по цепи, равен I. Сопротивление включено последовательно. Приведенное ниже уравнение дает напряжение в цепи.
В = Вm Sinωt
Теперь из закона Ома мы знаем, что V = IR или I = V / R
Итак, ток я буду,
я = (Вm / R) Sinωt
Или я = яm Sinωt; яm V =m / Р
Максимальное значение тока и напряжения будет при ωt = 90o.
Фазорная диаграмма чисто резистивной цепиНаблюдая за уравнениями, можно сделать вывод об отсутствии разности фаз между током и напряжением в цепи. Это означает, что разность фазовых углов между двумя компонентами энергии будет равна нулю. Таким образом, нет никакого запаздывания или опережения между напряжением и током чисто резистивной цепи переменного тока.
Как упоминалось ранее, ток и напряжение остаются в одной и той же фазе в цепи. мощность дается как произведение напряжения и текущий. Предложенные для цепей переменного тока мгновенные значения напряжения и тока учитываются из соображений, предназначенных для расчета мощности.
Итак, мощность можно записать как — P = Vm Sinωt * Im Синωт.
Или P = (Vm * Im / 2) * 2 Sinω2t
Или P = (Vm / √2) * (Im/ √2) * (1 — Cos2ωt)
Или P = (Vm / √2) * (Im/ √2) — (Vm / √2) * (Im/ √2) * Cos2ωt
Теперь о средней мощности в цепи переменного тока.
P = среднее значение [(Vm / √2) * (Im/ √2)] — Среднее значение [(Vm / √2) * (Im/ √2) * Cos2ωt]
Теперь Cos2ωt становится равным нулю.
Итак, сила приходит как — P = Vсреднеквадратичное значение *Iсреднеквадратичное значение.
Здесь P означает среднюю мощность, Всреднеквадратичное значение обозначает среднеквадратичное напряжение, а Iсреднеквадратичное значение обозначает среднеквадратичное значение тока.
Чистая емкостная цепь переменного токаЕсли цепь переменного тока состоит только из чистого конденсатора, то эта цепь будет называться чисто емкостной цепью переменного тока. В этой форме нет никакого резистора или катушки индуктивности. Цепь переменного тока. Типичный конденсатор представляет собой пассивное электрическое устройство, которое накапливает электрическую энергию в электрическом поле. Это двухполюсное устройство. Емкость известна как эффект конденсатора. Емкость имеет единицу измерения – Фарад (Ф).
Чистая емкостная цепьКогда на конденсатор подается напряжение, конденсатор заряжается и через некоторое время начинает разряжаться, когда источник напряжения убирается.
Предположим, что напряжение источника равно V; в конденсатор имеет емкость C, ток, протекающий по цепи, равен I.
Приведенное ниже уравнение дает напряжение в цепи.
В = Вm Sinωt
Заряд конденсатора определяется выражением Q = CVи I = dQ / dt дает ток внутри цепи.
Итак, I = C dV / dt; как I = dQ / dt.
Или, I = С д (Вm Sinωt) / dt
Или I = Vm C d (Sinωt) / dt
Или I = ω Vm C Косωt.
Или I = [Vm / (1 / ωC)] sin (ωt + π / 2)
Или I = (Vm / Xc) * sin (ωt + π / 2)
Xc известен как реактивное сопротивление цепи переменного тока (в частности, емкостное реактивное сопротивление). Максимальный ток будет наблюдаться, когда (ωt + π / 2) = 90o.
Таким образом, Im = Vm / Хс
Фазорная диаграмма чистой емкостной цепиСоблюдая уравнения, можно сделать вывод, что напряжение в цепи превышает текущее значение на угол 90 градусов. Векторная диаграмма схемы приведена ниже.
Векторная диаграмма схемы приведена ниже.
Как упоминалось ранее, фаза напряжения имеет опережение тока в цепи на 90 градусов. Мощность задается как произведение напряжения и тока. При расчетах цепей переменного тока учитываются мгновенные значения напряжения и тока, предназначенные для расчета мощности.
Итак, мощность для этой схемы может быть записана как — P = Vm Sinωt * Im Sin (ωt + π / 2)
Или P = (Vm * Im * Sinωt * Cosωt)
Или P = (Vm / √2) * (Im/ √2) * Sin2ωt
Или, P = 0
Итак, исходя из выводов, можно сказать, что средняя мощность емкостной цепи равна нулю.
Чистая индуктивная цепь переменного тока Если цепь переменного тока состоит только из чистого индуктора, то эта цепь будет называться чисто индуктивной цепью переменного тока. Там вообще нет резисторов или Конденсаторы участвуют в этом типе цепи переменного тока. Типичный индуктор представляет собой пассивное электрическое устройство, которое накапливает электрическую энергию в магнитных полях. Это двухполюсное устройство. Индуктивность известна как эффект индуктора. Индуктивность имеет единицу измерения – Генри (Гн). Накопленная энергия также может быть возвращена в цепь в виде тока.
Там вообще нет резисторов или Конденсаторы участвуют в этом типе цепи переменного тока. Типичный индуктор представляет собой пассивное электрическое устройство, которое накапливает электрическую энергию в магнитных полях. Это двухполюсное устройство. Индуктивность известна как эффект индуктора. Индуктивность имеет единицу измерения – Генри (Гн). Накопленная энергия также может быть возвращена в цепь в виде тока.
Предположим, что напряжение источника равно V; индуктивность индуктора равна L, ток, протекающий по цепи, равен I.
Приведенное ниже уравнение дает напряжение в цепи.
В = Вm Sinωt
Индуцированное напряжение определяется как — E = — L dI / dt
Итак, V = — E
Или V = — (- L dI / dt)
Или, Vm Sinωt = L dI / dt
Или dI = (Vm / L) Sinωt dt
Теперь, применив интеграцию с обеих сторон, мы можем писать.
Или dI = ∫ (Vm / L) Sinωt dt
Или I = (Vm / ωL) * (- Cosωt)
Или I = (Vm / ωL) sin (ωt — π / 2)
Или I = (Vm / XL) sin (ωt — π / 2)
Здесь, XL = ωL и известен как индуктивное реактивное сопротивление цепи.
Максимальный ток будет наблюдаться при (ωt — π / 2) = 90o.
Таким образом, Им = Вм / ХL
Фазорная диаграмма чистой индуктивной цепиСоблюдая уравнения, можно сделать вывод, что ток в цепи опережает значение напряжения на угол 90 градусов. Векторная диаграмма схемы приведена ниже.
Векторная диаграмма индуктивной цепиМощность в чисто индуктивной цепиКак упоминалось ранее, фаза тока имеет опережение напряжения в цепи на 90 градусов. Мощность задается как произведение напряжения и тока. Для цепей переменного тока принимаются во внимание мгновенные значения напряжения и тока, используемые для расчета мощности.
Итак, мощность для этой схемы может быть записана как — P = Vm Sinωt * Im Sin (ωt — π / 2)
Или P = (Vm * Im * Sinωt * Cosωt)
Или P = (Vm / √2) * (Im/ √2) * Sin2ωt
Или, P = 0
Итак, исходя из выводов, можно сказать, что средняя мощность индуктивного контура равна нулю.
электромагнетизм. Ток через конденсатор в цепях переменного тока
$\begingroup$
Я немного запутался в уравнении для мгновенного тока через конденсатор в цепях переменного тока.
В моем учебнике это выглядит так:
$$i_C = \omega CV \ cos(\omega t + \pi/2) = -\omega CV \ sin(\omega t)$$
где $\omega$ = угловая частота, $C$ — емкость, $V$ — напряжение на конденсаторе.
Я также вижу это в некоторых местах в Интернете (и в задаче «подсказки» для моего домашнего задания) без части «+ $\pi/2$», и я не уверен, почему. Любые идеи?
Любые идеи?
Чтобы добавить к моему замешательству, уравнение для тока через индуктор в задаче «подсказки», согласуется с учебником:
$$i_L = (V/\omega L) \ cos(\omega t — \ pi/2) = (V/\omega L) \ sin(\omega t)$$
Рассматриваемая задача относится к этой схеме:
- электромагнетизм
- емкость
- индуктивность
$\endgroup$
5
$\begingroup$
Число пи/2 возникает при преобразовании угловой меры из градусов в радианы, где 2(пи) радиан равняется 360 градусам.
Кстати, вот простой способ визуализировать протекание тока через конденсатор:
Представьте себе две плоские металлические пластины, обращенные друг к другу, между которыми нет ничего, кроме воздуха. Каждая пластина соединена с проводом, в который мы можем впрыснуть дополнительные электроны или высосать часть.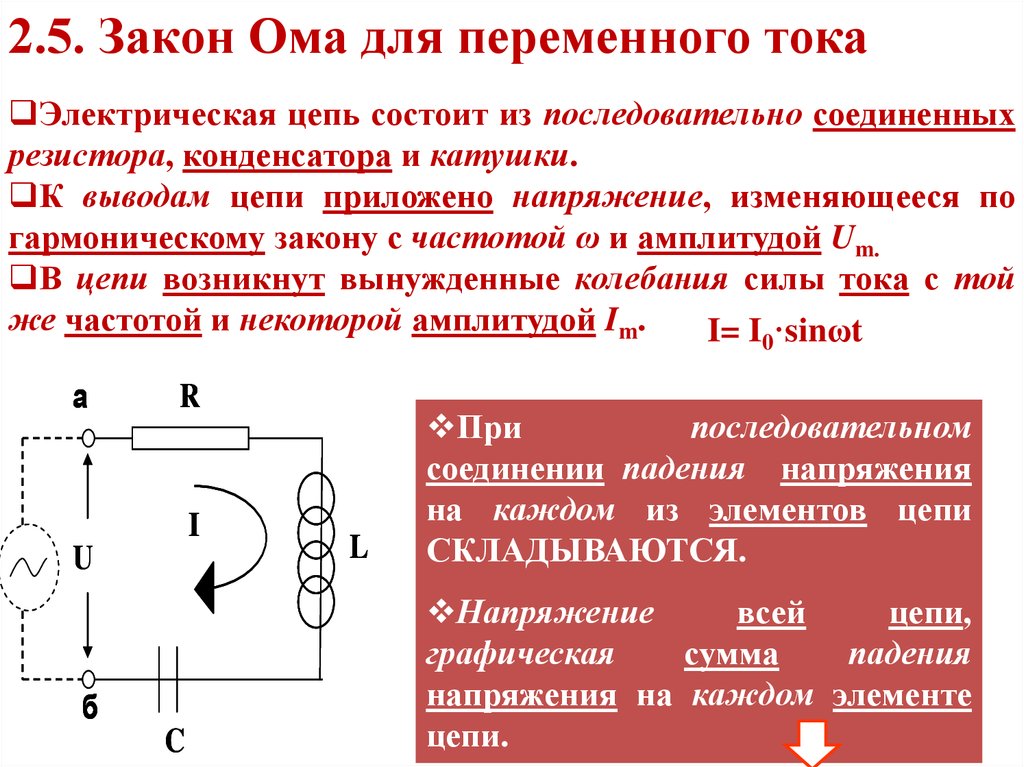
Теперь мы внезапно впрыскиваем несколько дополнительных электронов в одну из пластин, и эти дополнительные электроны затем перетекают в пластину и «столкнутся» с электронами, сидящими на другой пластине, через зазор.
Теперь на одной пластине электронов больше, чем на другой, и в ответ некоторые электроны на другой пластине отталкиваются от нее и вытекают через прикрепленный к ней провод, образуя краткий всплеск тока, который гаснет, когда потенциалы на обеих пластинах становятся равными и противоположными.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Основы работы с конденсаторами — Учебные пособия по электронике
Опубликовано
Конденсаторы — невероятно полезный компонент, который используется в самых разных схемах по самым разным причинам. Действительно, разнообразие применений просто ошеломляет. . В этом уроке мы узнаем, что такое конденсатор, как обращаться с конденсатором в цепи постоянного тока, как обращаться с конденсатором в цепи переходного процесса, как работать с конденсаторами в цепи переменного тока и попытаемся понять, что такое происходит с конденсатором на физическом уровне.
Что такое конденсатор?
Конденсатор представляет собой устройство для накопления электрической энергии, состоящее из двух пластин, находящихся как можно ближе друг к другу, но не соприкасаясь, которые накапливают энергию в электрическом поле. Обычно это устройства с двумя клеммами, и их символ представляет собой идею двух пластин, скрепленных вместе.
Но на самом деле конденсаторы выглядят совсем не так, и даже один конденсатор может выглядеть совершенно по-разному — от почти микроскопических до размеров семейного фургона.
Емкость измеряется емкостью в фарадах, которая связана с количеством заряда на проводящих пластинах по отношению к напряжению. между проводниками. Если один кулон заряда дает один вольт на пластинах, то емкость конденсатора составляет один фарад.
В действительности большинство конденсаторов находятся в диапазоне от пикофарад до миллифарад, хотя специальные конденсаторы могут иметь гораздо более высокую емкость (с другими компромиссами в производительности).
Как работают конденсаторы в цепи постоянного тока?
В стабильной цепи постоянного тока, при отсутствии изменений напряжения в течение длительного времени, конденсаторы крайне просты. Вы можете относиться к ним так, как будто их нет. При моделировании цепи постоянного тока без переходных процессов вы можете удалить конденсатор и заменить его открытым, и схема останется точно такой же. Дополнительный бонус: если последовательно с конденсатором есть какие-либо другие элементы цепи, вы также можете их игнорировать. Хотя это может вызвать аплодисменты у учащихся схемы 1, это довольно бесполезно, поэтому давайте рассмотрим цепи постоянного тока, в которых есть изменение напряжения.
Вы можете относиться к ним так, как будто их нет. При моделировании цепи постоянного тока без переходных процессов вы можете удалить конденсатор и заменить его открытым, и схема останется точно такой же. Дополнительный бонус: если последовательно с конденсатором есть какие-либо другие элементы цепи, вы также можете их игнорировать. Хотя это может вызвать аплодисменты у учащихся схемы 1, это довольно бесполезно, поэтому давайте рассмотрим цепи постоянного тока, в которых есть изменение напряжения.
В переходных процессах в цепи постоянного тока, когда вы моделируете размыкание или замыкание переключателя, конденсатор будет сопротивляться изменению напряжения. Это сопротивление связано с тем, что ток, протекающий через конденсатор, «заполняет» конденсатор, он не может заряжаться или разряжаться мгновенно. Это изменение напряжения является последовательным и может быть точно рассчитано, если вы знаете емкость, а также любое последовательное сопротивление. Он моделируется следующими уравнениями:
Где:
v c — напряжение на конденсаторе
В 1 — входное напряжение
t — время, прошедшее с момента подачи входного напряжения
𝜏 — постоянная времени
Мы рассмотрим эти типы цепей более подробно в другом руководстве, но на данный момент, полезно взглянуть на уравнение и увидеть, как оно отражает реальное поведение заряда или разряда конденсатора. Обратите особое внимание на экспоненциальный рост и спад и подумайте, почему он не является линейным, а что изменение замедляется по мере того, как фактическое напряжение приближается к целевому напряжению.
Обратите особое внимание на экспоненциальный рост и спад и подумайте, почему он не является линейным, а что изменение замедляется по мере того, как фактическое напряжение приближается к целевому напряжению.
Как работают конденсаторы в цепи переменного тока?
При обсуждении работы конденсатора в цепи постоянного тока вы либо сосредотачиваетесь на сценариях устойчивого состояния, либо смотрите на изменения во времени. Однако с цепью переменного тока вы обычно смотрите на реакцию цепи в отношении частоты. Это связано с тем, что импеданс конденсатора не установлен — он зависит от частоты. Этот импеданс описывается следующим уравнением:
Напомню, омега (ω) = 2π*частота. Кроме того, j — это символ инженера-электрика для квадратного корня из -1, поэтому представление мнимых чисел. Имея это в виду, давайте посмотрим, что означает это уравнение. J — это воображаемый термин, который помогает нам понять фазовые сдвиги и то, сколько реальной мощности мы получаем. Мы не будем слишком беспокоиться о том, что это значит сейчас, но это важная концепция, которую мы будем доводить до тошноты при обсуждении цепей переменного тока. *Омега* — это представление частоты, которая применяется к цепи, а «с» — это измеренная емкость конденсатора. Поскольку эти члены находятся в знаменателе, мы видим, что если вы увеличиваете либо частоту, либо емкость, сопротивление конденсатора уменьшается. Если частота равна 0, импеданс будет бесконечен (поэтому мы рассматриваем конденсатор как обрыв в цепях постоянного тока), но импеданс также будет равен 0, если частота бесконечна.
Мы не будем слишком беспокоиться о том, что это значит сейчас, но это важная концепция, которую мы будем доводить до тошноты при обсуждении цепей переменного тока. *Омега* — это представление частоты, которая применяется к цепи, а «с» — это измеренная емкость конденсатора. Поскольку эти члены находятся в знаменателе, мы видим, что если вы увеличиваете либо частоту, либо емкость, сопротивление конденсатора уменьшается. Если частота равна 0, импеданс будет бесконечен (поэтому мы рассматриваем конденсатор как обрыв в цепях постоянного тока), но импеданс также будет равен 0, если частота бесконечна.
Важные сведения о цепях переменного тока
Хотя я не хочу бомбардировать вас слишком большим количеством деталей, я хочу кратко остановиться на нескольких важных моментах цепей переменного тока, на которые влияют конденсаторы. Это будет повторено в обзоре катушек индуктивности, поскольку они также влияют на цепи переменного тока. В частности, есть два пункта, которые я хотел бы рассмотреть и которые станут основополагающими моментами анализа цепи переменного тока. Эти элементы относятся к выходному напряжению по сравнению с входным напряжением.
Эти элементы относятся к выходному напряжению по сравнению с входным напряжением.
Величина: при изменении импеданса конденсатора выходное напряжение будет увеличиваться или уменьшаться в зависимости от конфигурации схемы. Эта взаимосвязь между выходным и входным напряжением является величиной и является важным фактором, который следует учитывать.
Величина входного/выходного напряжения Фазовый сдвиг: В то время как величина довольно проста, фазовый сдвиг может быть немного сложнее представить. Тот факт, что конденсатору требуется некоторое время для зарядки и разрядки, означает, что форма выходного напряжения может быть задержана. Величина задержки считается фазовым сдвигом, который может быть еще больше сбит с толку тем фактом, что он измеряется в градусах, что в основном представляет собой процент от полного цикла переменного сигнала.
Последовательные и параллельные конденсаторы
Когда конденсаторы соединены последовательно и параллельно, их можно комбинировать для упрощения расчетов и некоторых моделей моделирования. Это очень просто, и если вы знаете, как рассчитать последовательные и параллельные резисторы, вам нужно помнить только одну вещь. Они противоположны резисторам. При параллельном подключении конденсаторов можно просто сложить емкости. С конденсаторами, соединенными последовательно, вы обращаетесь с ними так же, как с параллельным резистором, используя следующее уравнение.
Это очень просто, и если вы знаете, как рассчитать последовательные и параллельные резисторы, вам нужно помнить только одну вещь. Они противоположны резисторам. При параллельном подключении конденсаторов можно просто сложить емкости. С конденсаторами, соединенными последовательно, вы обращаетесь с ними так же, как с параллельным резистором, используя следующее уравнение.
Это также можно упростить в двух сценариях. Если есть только два последовательно соединенных конденсатора, вы можете использовать это более простое уравнение:
А если есть только два последовательных конденсатора с одинаковой емкостью, вы можете просто разделить емкость на два, что еще проще.
Как конденсатор работает физически?
Как упоминалось ранее, конденсатор состоит из двух металлических пластин, скрепленных вместе, разделенных диэлектриком, который может быть практически любым. Чаще всего эти металлические «тарелки» на самом деле скручены вместе, как один из тех желейных рулетов, о которых я узнал, когда смотрел British Baking Show, но два куска, а не один.
Еще проще представить, и с точки зрения физики то же самое, рассматривать как две параллельные пластины. На этих пластинах по мере того, как конденсатор заряжается и напряжение на пластинах увеличивается, положительные и отрицательные заряды собираются на разных пластинах.
Теперь давайте посмотрим на уравнение, которое используется для расчета емкости плоского конденсатора:
ε — абсолютная диэлектрическая проницаемость диэлектрика между двумя пластинами, и я не буду Не беспокойтесь об этом слишком много. Просто знайте, что если у вас есть вакуум между двумя пластинами или другой материал, это повлияет на общую емкость. «A» представляет собой площадь пластин — это должно иметь смысл, поскольку большая площадь дает большую емкость. «d» представляет собой расстояние между двумя пластинами и показывает, что чем ближе пластины друг к другу, тем больше емкость. Это должно иметь смысл, поскольку, если пластины расположены ближе, положительные и отрицательные заряды сильнее притягиваются друг к другу и еще больше хотят перепрыгнуть через диэлектрик на другую пластину. Но не могут — не считая квантовых эффектов, никакие электроны не могут напрямую переходить с одной пластины на другую. Вот почему в цепи постоянного тока, когда электроны текут в одном направлении, конденсатор действует как открытый. Но как тогда протекает ток в цепи переменного тока? Давайте обсудим это, используя метафору.
Но не могут — не считая квантовых эффектов, никакие электроны не могут напрямую переходить с одной пластины на другую. Вот почему в цепи постоянного тока, когда электроны текут в одном направлении, конденсатор действует как открытый. Но как тогда протекает ток в цепи переменного тока? Давайте обсудим это, используя метафору.
Надеюсь, потрясающая метафора работы конденсатора
Должен признаться, я придумал эту метафору и думал, что я гениален. Затем я увидел страницу Википедии о конденсаторах, и там была почти такая же метафора, так что это было ударом по моему и без того хрупкому эго. В любом случае, вот моя метафора о воде и резиновом барьере.
Помните, что в метафорах воды/электричества давление воды эквивалентно напряжению, а расход воды эквивалентен току. Теперь представьте круглый трубопровод с реверсивным насосом и гибким резиновым барьером, блокирующим поток воды. По мере того, как насос постоянно проталкивает воду в одном направлении, подобно напряжению постоянного тока, резина растягивается, и в этом растяжении накапливается энергия. Но после определенного момента сопротивление резины сравняется с усилием насоса, и движение воды прекратится. Если вы измените направление насоса, в конечном итоге вы достигнете того же равновесия в другом направлении. Это похоже на зарядку и разрядку конденсатора напряжением постоянного тока. Так как насчет сигналов переменного тока?
Но после определенного момента сопротивление резины сравняется с усилием насоса, и движение воды прекратится. Если вы измените направление насоса, в конечном итоге вы достигнете того же равновесия в другом направлении. Это похоже на зарядку и разрядку конденсатора напряжением постоянного тока. Так как насчет сигналов переменного тока?
Если насос регулярно переключается медленно, то равновесие будет достигаться часто, и вода перестанет поступать в течение длительного периода времени. Однако по мере того, как частота чередований увеличивается, у резинового барьера будет меньше времени для полного изгиба. В конце концов, когда насос достаточно быстро меняет направление, создается впечатление, что барьера даже нет, а вода движется вперед и назад. Таким образом, даже несмотря на то, что вода на самом деле не проходит через барьер, энергия проходит без проблем. Таким образом, конденсатор пропускает переменный ток, так как это просто передача энергии, а не реальное физическое перемещение электронов с одной пластины на другую.
Неидеальные соображения для конденсаторов
Хотя мы предполагаем, что конденсаторы работают идеально большую часть времени, существуют некоторые реальные соображения, которые могут быть или не быть достаточно важными, чтобы их нужно было учитывать при проектировании или исправление проблем. Кратко рассмотрим их:
- Эквивалентное последовательное сопротивление (ESR). Хотя мы предполагаем, что конденсатор не имеет сопротивления, на самом деле оно есть. Это заметно, когда конденсатор заряжается и разряжается, так как во время процесса рассеивается некоторая мощность. Это также замедляет скорость, с которой конденсатор может заряжаться и разряжаться.
- Индуктивность. Обычно это гораздо меньшая проблема, чем ESR, в любом конденсаторе есть небольшая индуктивность, которая сопротивляется изменениям тока. Не имеет большого значения большую часть времени.
- Пределы напряжения. У каждого конденсатора есть предел того, какое напряжение вы можете подать на него, прежде чем он сломается.
 Будьте осторожны, чтобы дать себе немного дополнительного свободного пространства с ограничением напряжения, чтобы учесть любые потенциальные скачки напряжения.
Будьте осторожны, чтобы дать себе немного дополнительного свободного пространства с ограничением напряжения, чтобы учесть любые потенциальные скачки напряжения. - Обратное напряжение. Некоторые конденсаторы не заботятся о полярности напряжения, но некоторые, особенно электролитические конденсаторы, не могут работать с обратным напряжением, иначе они взорвутся. Взрыв может быть сильным словом, обычно они просто немного пукают и перестают работать.
- Срок службы. Со временем конденсаторы стареют и их емкость падает. Некоторые технологии борются с этим больше, чем другие. Для некоторых конфигураций это уменьшение емкости может не сказаться на производительности, но если есть настроенная схема, зависящая от определенной емкости, это может вызвать проблемы.
Области применения конденсаторов
Мы углубимся в особенности использования конденсаторов, но хотели бы воспользоваться моментом, чтобы обсудить их использование на высоком уровне. Вот несколько наиболее распространенных вариантов использования:
Вот несколько наиболее распространенных вариантов использования:
- Управление потоком сигналов переменного/постоянного тока. Как упоминалось ранее, конденсатор пропускает сигналы переменного тока и блокирует сигналы постоянного тока. Поэтому, если вы подключите конденсатор последовательно с чем-либо, он блокирует сигнал постоянного тока, устраняя нежелательные смещения постоянного тока. Если вы подключите конденсатор параллельно чему-либо, он шунтирует сигналы переменного тока, часто он подключается к земле, чтобы вы могли шунтировать любые нежелательные сигналы переменного тока на землю (например, электрические помехи).
- Гладкие блоки питания. Поскольку конденсаторы накапливают энергию, общепринятой практикой является размещение конденсатора как можно ближе к нагрузке (тому, что потребляет энергию), чтобы в случае падения напряжения в линии конденсатор мог обеспечивать короткие всплески тока, чтобы противостоять этому падению напряжения.
- Настройка резонансных частот.
 Для электромагнитных систем, антенн и линий передачи емкость системы влияет на то, на какой частоте они резонируют.
Для электромагнитных систем, антенн и линий передачи емкость системы влияет на то, на какой частоте они резонируют. - Коррекция фазового сдвига. Если вы не знакомы с цепями переменного тока, это не будет иметь особого смысла, но если нагрузка слишком индуктивная, это может снизить эффективность системы. Чтобы противодействовать этому, вы можете добавить емкость к нагрузке.
Резюме
Конденсаторы невероятно просты по своей концепции, но детали, то, как они работают с сигналами постоянного и переменного тока, и их несовершенства обеспечивают невероятно разнообразное количество применений и соображений. Можно написать десятки руководств о различных способах использования конденсаторов, и мы посмотрим, сколько из них мы сможем собрать вместе. Если у вас есть какие-либо вопросы, не стесняйтесь оставлять комментарии ниже или заходить на наш канал Discord, чтобы задать их!
- Конденсатор (1)
Автор:
Джош Бишоп
Интересуясь встраиваемыми системами, туризмом, кулинарией и чтением, Джош получил степень бакалавра электротехники в Университете штата Бойсе.


 Единица измерения частоты — Герц (Гц).
Единица измерения частоты — Герц (Гц).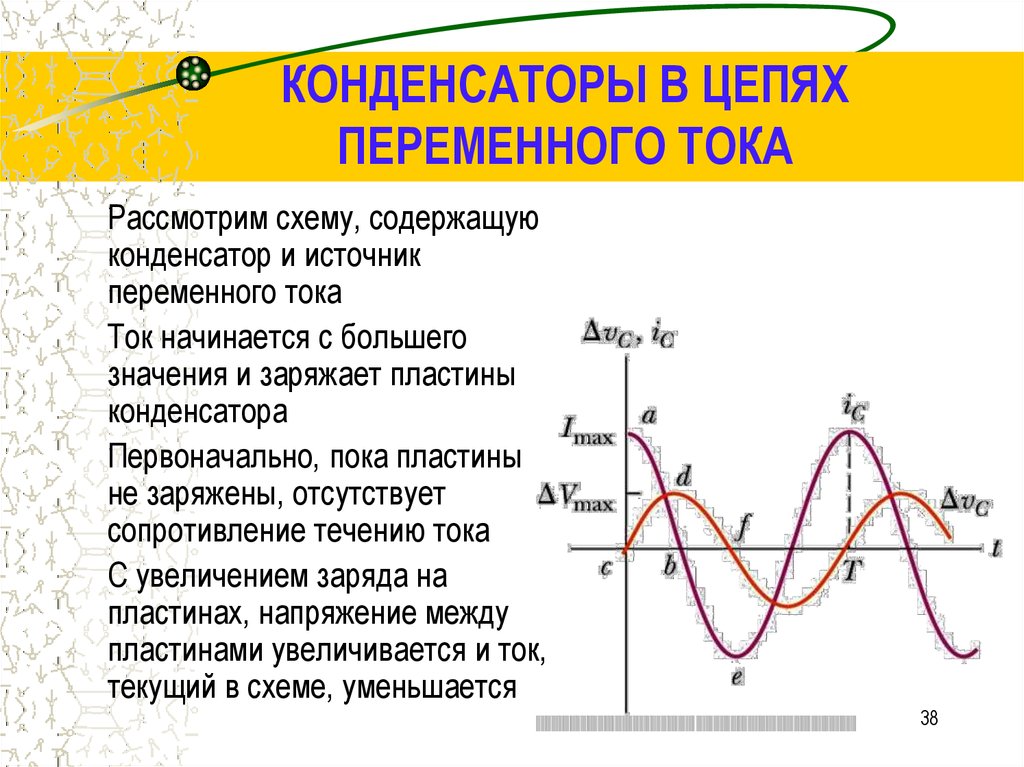 Будьте осторожны, чтобы дать себе немного дополнительного свободного пространства с ограничением напряжения, чтобы учесть любые потенциальные скачки напряжения.
Будьте осторожны, чтобы дать себе немного дополнительного свободного пространства с ограничением напряжения, чтобы учесть любые потенциальные скачки напряжения. Для электромагнитных систем, антенн и линий передачи емкость системы влияет на то, на какой частоте они резонируют.
Для электромагнитных систем, антенн и линий передачи емкость системы влияет на то, на какой частоте они резонируют.