Конденсаторы постоянного тока
Калькуляторы рассчитывают параметры разрядки и зарядки конденсатора от источника постоянной ЭДС через сопротивление. Формулы, по которым идет расчет, приведены под калькуляторами. Понять приводимые ниже формулы поможет картинка, изображающая электрическую схему заряда конденсатора от источника постоянной ЭДС батареи :. Итак, при замыкании ключа К в цепи пойдет электрический ток, который будет приводить к заряду конденсатора. По закону Ома сумма напряжений на конденсаторе и резисторе равна ЭДС источника, таким образом: При этом заряд и сила тока зависят от времени. В начальный момент времени на конденсаторе нет заряда, сила тока максимальна, также как и максимальна мощность, рассеиваемая на резисторе.
Поиск данных по Вашему запросу:
Схемы, справочники, даташиты:
Прайс-листы, цены:
Обсуждения, статьи, мануалы:
Дождитесь окончания поиска во всех базах.

По завершению появится ссылка для доступа к найденным материалам.
Содержание:
- Конденсатор постоянного тока
- §52. Конденсаторы, их назначение и устройство
- Конденсатор в цепи постоянного тока
- Конденсатор в цепи постоянного тока
- Конденсатор в цепи постоянного и переменного тока
- Вы точно человек?
- Конденсатор в электрической цепи
- Как работает конденсатор. Емкость конденсатора.
ПОСМОТРИТЕ ВИДЕО ПО ТЕМЕ: Урок 359. Конденсатор и катушка индуктивности в цепи переменного тока.
Конденсатор постоянного тока
На рис. После включения цепи вольтметр, включенный в цепь, покажет полное напряжение генератора. Стрелка амперметра установится на нуле — ток через изоляцию конденсатора протекать не может.
Но проследим внимательно за стрелкой амперметра при включении незаряженного конденсатора. Если амперметр достаточно чувствителен, а емкость конденсатора велика, то нетрудно обнаружить колебание стрелки: сразу после включения стрелка сойдет с нуля, а затем быстро вернется в исходное положение.
Цепь электрического генератора, содержащая конденсатор Этот опыт показывает, что при включении конденсатора при его зарядке в цепи протекал ток — в ней происходило передвижение зарядов: электроны с пластины, присоединенной к положительному полюсу источника, перешли на пластину, присоединенную к отрицательному полюсу. Как только конденсатор зарядится, движение зарядов прекращается.
Как только конденсатор зарядится, движение зарядов прекращается.
Отключая генератор и повторно замыкая его на конденсатор, мы уже не обнаружим движения стрелки: конденсатор остается заряженным, и при повторном включении движения зарядов в цепи не происходит. Для того чтобы вновь наблюдать отклонение стрелки, нужно замыкать генератор на разряженный конденсатор. С этой целью, предварительно отключив генератор, замкнем пластины конденсатора проволокой, при этом между зажимами конденсатора и подносимой к ним проволокой проскочит искра, тем самым легко убедиться, что при разряде конденсатора в его цепи опять протекал ток.
Если замыкание проволокой произвести так, чтобы путь зарядов проходил через амперметр, то легко увидеть, что его стрелка кратковременно отклонится. Отклонение стрелки теперь должно происходить, конечно, в другую сторону. После разряда конденсатора можно повторить первый опыт — стрелка амперметра вновь покажет, что в цепи конденсатора передвигаются электрические заряды проходит ток.
Попытаемся вычислить ток, протекающий в проводах, присоединенных к конденсатору. Если за промежуток времени напряжение конденсатора увеличивается на , то, значит, за это же время его заряд увеличится на т. Предположим, что напряжение на конденсаторе емкостью возросло на 50 В за время в одну десятую долю секунды.
В таком случае за это же время заряд положительной пластины конденсатора увеличился на Но для того чтобы такой заряд прошел по проводам за время с, нужно, чтобы по ним протекал средний ток Заряд конденсатора через резистор. Представим себе, что генератор с постоянным напряжением замыкается через резистор с сопротивлением на незаряженный конденсатор емкостью рис.
В начальный момент, пока еще конденсатор не заряжен, его напряжение равно нулю. Значит все напряжение источника приходится на сопротивление R. А это значит, что по закону Ома в цепи будет протекать ток С течением времени, напротив, конденсатор зарядится, его напряжение будет равно напряжению генератора, в цепи не будет тока, на резисторе не будет никакого напряжения.
Эти графики построены в предположении, что конденсатор емкостью мкФ заряжается от источника постоянного напряжения В через сопротивление 10 Ом. В этом случае заряд происходит очень медленно. Если бы емкость составила всего 1 мкФ, а сопротивление 1 Ом, все происходило бы в миллион раз скорее. Для того чтобы приведенные графики оказались пригодными и для второго случая, нужно считать, что время выражено не в секундах, а в миллионных долях секунды в общем случае при любых R и С указанные на графике значения времени следует умножить на произведение С и Я.
Если напряжение источника остается В, то значения тока должны быть увеличены в 10 раз. Например, в начальный момент будет протекать ток не 10 мА, а А. Длительность и характер процесса не зависят от напряжения источника; б — разряд конденсатора С через резистор сопротивлением R.
Слева показана электрическая схема. После заряда конденсатор отключается. Справа показано, как изменяются ток и напряжение конденсатора с течением времени. Графики построены для случая. Уменьшение емкости и сопротивления до значений и 1 Ом увеличило бы скорость разряда в миллион раз. Начальное; значение тока при неизменности начального напряжения при этом возросло бы в 10 раз и составило бы А вместо 10 мА.
Графики построены для случая. Уменьшение емкости и сопротивления до значений и 1 Ом увеличило бы скорость разряда в миллион раз. Начальное; значение тока при неизменности начального напряжения при этом возросло бы в 10 раз и составило бы А вместо 10 мА.
При других значениях R и С время, показанное на графике, нужно умножить на произведение При этом заряд конденсатора должен быть равен Поставим такой вопрос: как скоро заряд в одну сотую кулона может быть сообщен конденсатору? Если бы в цепи ток не уменьшался, а оставался равным т. Но сообразим, может ли долго протекать такой ток, как Если бы такой ток протекал четверть секунды, он уже сообщил бы конденсатору четверть полного заряда, а значит, поднял бы его напряжение до четверти от полных В.
Но когда напряжение конденсатора возрастет до 25 В, ток должен уменьшиться до 7,5 мА. В самом деле, если напряжение генератора В, а напряжение на конденсаторе 25 В, то разность между ними приходится на резистор. Опять же по закону Ома Но такой ток будет заряжать конденсатор медленнее, чем его заряжал ток в 10 мА.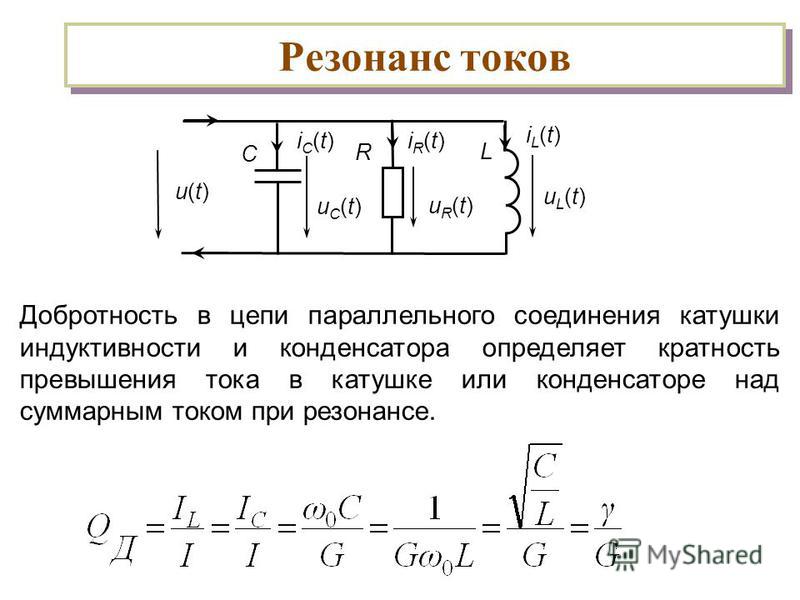
Из приведенного рассуждения ясно, что: нарастание напряжения на конденсаторе будет происходить, постепенно замедляясь; ток, достигнув наибольшего значения в начальный момент, потом постепенно уменьшится; чем больше емкость больше заряд и чем больше сопротивление цепи, тем медленнее происходит заряд конденсатора.
Разряд конденсатора на резистор. Если отключить генератор и через резистор с сопротивлением R замкнуть пластины конденсатора, начнется процесс его разряда. Энергия электрического поля в конденсаторе. Заряженный конденсатор обладает определенным запасом энергии, заключенной в его электрическом поле. Об этом можно судить по тому, что заряженный конденсатор, отключенный от сети, способен некоторое время поддерживать электрический ток — об этом можно судить и по искре, наблюдаемой при разряде конденсаторов.
Энергия, заключенная в конденсаторе, подводится к нему в то время, когда он заряжается от генератора. В самом деле, во время его заряда в цепи течет ток и к его зажимам приложено напряжение, а это значит, что ему сообщается энергия. Полное количество энергии, запасенной конденсатором, может быть выражено формулой Энергия равна половине квадрата напряжения, умноженного на емкость.
Полное количество энергии, запасенной конденсатором, может быть выражено формулой Энергия равна половине квадрата напряжения, умноженного на емкость.
Если напряжение выражено в вольтах, а емкость — в фарадах, то энергия окажется выраженной в джоулях. Так, энергия, запасенная в конденсаторе емкостью мкФ при напряжении В, Это, конечно, не очень большая энергия такая энергия поглощается лампочкой 50 Вт за каждую секунду.
Но если конденсатор быстро разряжается скажем, за одну тысячную долю секунды , то мощность происходящего разряда энергии, конечно, очень велика: Поэтому понятно, что при разряде большого конденсатора звук похож на выстрел. Быстрым разрядом энергии, запасенной в конденсаторе, иногда пользуются для сварки маленьких металлических изделий. При разряде конденсатора на резистор энергия, заключавшаяся в электрическом конденсаторе, переходит в тепло нагреваемого резистора.
Применение конденсаторов. Применения конденсаторов в электротехнике очень разнообразны. Рассмотрим здесь некоторые из них. Конденсаторы широко применяют для целей изоляции двух цепей по постоянному напряжению при сохранении связи между ними на переменном токе.
Конденсаторы широко применяют для целей изоляции двух цепей по постоянному напряжению при сохранении связи между ними на переменном токе.
Конденсаторы изолируют постоянное напряжение, не пропуская постоянный ток. В то же время малейшее изменение напряжения изменяет их заряд и, следовательно, пропускает через них соответствующий переменный ток рис. На входе схемы между точками а и б приложено постоянное напряжение и маленькое, изменяющееся во времени напряжение — его форма Соответствует передаваемому сигналу. Конденсатор не пропускает постоянный ток соответствующий. Маленькое изменяющееся напряжение А и меняет заряд конденсатора.
Протекающий зарядный ток создает падение напряжения на большом сопротивлении цепи. Это падение напряжения очень близко к значению переменного напряжения Таким образом, напряжение на выходе схемы между точками в и г приблизительно равно 2. На свойствах конденсатора пропускать ток под действием изменяющегося напряжения и не пропускать ток под действием постоянного напряжения основаны сглаживающие устройства фильтры, не пропускающие переменное напряжение.
На выходе схемы напряжение сглажено — оно близко к постоянному. Еще более сильное сглаживание можно получить, включая вместо резисторов индуктивные катушки L. Сглаживающее устройство, содержащее R и С.
Колебания напряжения на входе схемы не передаются на выход. Напряжение на выходе близко к постоянному Как было показано в гл. Такое сглаживающее устройство показано на рис. Сглаживающее устройство, содержащее L и С. На вход подано напряжение, заметно колеблющееся во времени. Напряжение на нагрузке почти постоянно Ток от батареи проходит через первичную обмотку катушки. В нужный момент он прерывается специальными подвижными контактами.
Быстрое изменение тока наводит ЭДС взаимоиндукции во вторичной обмотке катушки. Число витков вторичной обмотки очень велико, и разрыв тока производится быстро.
Поэтому ЭДС, наводимая во вторичной обмотке, может достигать 10—12 тыс. Прерывание контакта происходит очень часто: так, в четырехцилиндровом двигателе один разрыв контактов происходит за каждый оборот двигателя.
На схеме на рис. Объясним его назначение. При отсутствии конденсатора разрыв цепи сопровождался бы образованием искры между контактами прерывателя. Схема цепи, служащей для электрического зажигания горючей смеси в цилиндрах автомобильного двигателя: — прерыватель. Внизу показан разрез цилиндра с поршнем, над которым смесь воздуха с бензином воспламеняется электрической искрой, проскакивающей между электродами свечи Не говоря уже о том, что часто появляющаяся искра быстро привела бы к износу контактов, наличие искры препятствует резкому разрыву тока: ток, после того как контакты разойдутся, еще остается замкнутым через искру и лишь постепенно спадает до нуля.
Если между контактами прерывателя включен конденсатор как это показано на рис. Когда контакты начинают расходиться, цепь тока не разрывается — ток замыкается через еще не заряженный конденсатор.
Но конденсатор быстро заряжается, и дальнейшее протекание тока оказывается невозможным. Напряжение на заряженном конденсаторе может намного превысить 12 В, так как уменьшение тока в первичной обмотке катушки наводит в ней большую ЭДС самоиндукции.
Несмотря на это между контактами прерывателя искра уже не возникает, так как к этому моменту контакты прерывателя успевают достаточно далеко отойти один от другого. Когда контакты прерывателя вновь замкнутся, конденсатор быстро разрядится и будет готов к работе при новом разрыве контактов. Таким образом, конденсатор предохраняет контакты от обгорания и улучшает работу системы зажигания.
Его назначение станет ясным после того, как мы рассмотрим электрические колебания в системе индуктивность — конденсатор. Разряд конденсатора на индуктивность. В такой цепи возникают электрические колебания см. Оно рассмотрено в гл. О применении конденсаторов в колебательных контурах генераторов рассказано в гл. Эти применения конденсаторов основаны на электрических колебаниях в системе LC индуктивность и емкость.
Электрические колебания.
§52. Конденсаторы, их назначение и устройство
Регистрация Вход. Ответы Mail. Вопросы — лидеры Магнитный воин -какие силы стоят за эффектом Джанибекова? Решите задачу по физике 1 ставка. Какая польза народному хозяйству от астрономии и теории эволюции?
Какая польза народному хозяйству от астрономии и теории эволюции?
Поскольку между пластинами изолятор, не проводящий постоянный электрический ток, то зачем бы нам конденсатор в цепи постоянного тока? Рис.
Конденсатор в цепи постоянного тока
Конденсаторы постоянного тока, также известные как конденсаторы постоянного тока. Конденсаторы постоянного тока являются одним из типов пассивных компонентов. Поддерживающие конденсаторы постоянного тока, в основном, с использованием полипропиленовых пленочных поддерживающих конденсаторов постоянного тока, которые имеют высокое выдерживаемое напряжение, высокое сопротивление по току, низкий импеданс, низкую индуктивность, небольшую потерю емкости, небольшой ток утечки, хорошие температурные характеристики, быструю скорость зарядки и разрядки, а также длительный срок службы жизнь. Длительный около часов , хорошая безопасность и взрывозащищенная стабильность, а также простота установки без полярности. Широко используется в индустрии силовой электроники. После испытания: UR следует применять в течение 30 минут, от 24 до 48 часов до измерения. Поглотите пульсирующий ток высокой амплитуды от инвертора к DC-Link, чтобы он не генерировал пульсирующее напряжение высокой амплитуды на импедансе DC-Link, чтобы вызвать колебания напряжения на шине постоянного тока. Держите его в допустимых пределах. Номинальная емкость, номинальное напряжение, номинальный пульсационный ток и таблица размеров корпуса.
После испытания: UR следует применять в течение 30 минут, от 24 до 48 часов до измерения. Поглотите пульсирующий ток высокой амплитуды от инвертора к DC-Link, чтобы он не генерировал пульсирующее напряжение высокой амплитуды на импедансе DC-Link, чтобы вызвать колебания напряжения на шине постоянного тока. Держите его в допустимых пределах. Номинальная емкость, номинальное напряжение, номинальный пульсационный ток и таблица размеров корпуса.
Конденсатор в цепи постоянного тока
Конденсаторы — это электрические накопители заряда, электронные пассивные компоненты, применяющиеся во всех электронных, радиотехнических конструкциях. Различные типы конденсаторов отличаются между собой конструктивным диэлектриком, что сказывается на области их применения, и схематическим предписанием в те или иные конструктивные приложения. При выборе и покупке компонента необходимо учитывать его основные характеристики, такие как, емкость, рабочее напряжение и тип конденсатора, а так же, конструктивное исполнение, выводной или чип-конденсатор, элемент поверхностного монтажа. Именно чип-конденсаторы являются лидерами производства таких компаний, как Epcos и Murata , совершенствующие конструктивные новации микроэлектроники.
Именно чип-конденсаторы являются лидерами производства таких компаний, как Epcos и Murata , совершенствующие конструктивные новации микроэлектроники.
На рис. После включения цепи вольтметр, включенный в цепь, покажет полное напряжение генератора.
Конденсатор в цепи постоянного и переменного тока
Конденсатор является пассивным электронным компонентом. В чем же отличие между конденсаторами переменного тока и постоянного? Полярность определяет различие конденсаторов постоянного тока и переменного. Многие конденсаторы с оксидным диэлектриком электролитические. При обратной полярности напряжения электролитические конденсаторы обычно выходят из строя из-за химического разрушения диэлектрика с последующим увеличением тока, вскипанием электролита внутри и, как следствие, с вероятностью взрыва корпуса.
Вы точно человек?
Конденсатор является пассивным электронным компонентом. Ёмкость конденсатора измеряется в фарадах. Первые конденсаторы, состоящие из двух проводников, разделенных непроводником диэлектриком , упоминаемые обычно как конденсатор Эпинуса или электрический лист, были созданы ещё раньше [3]. Конденсатор является пассивным электронным компонентом [4]. В простейшем варианте конструкция состоит из двух электродов в форме пластин называемых обкладками , разделённых диэлектриком , толщина которого мала по сравнению с размерами обкладок см. Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами из-за намотки.
Конденсатор является пассивным электронным компонентом [4]. В простейшем варианте конструкция состоит из двух электродов в форме пластин называемых обкладками , разделённых диэлектриком , толщина которого мала по сравнению с размерами обкладок см. Практически применяемые конденсаторы имеют много слоёв диэлектрика и многослойные электроды, или ленты чередующихся диэлектрика и электродов, свёрнутые в цилиндр или параллелепипед со скруглёнными четырьмя рёбрами из-за намотки.
Высоковольтные конденсаторы постоянного тока торговой марки Lifasa серии HVDC предназначены для использования в источниках питания.
Конденсатор в электрической цепи
Последний раз редактировалось profrotter Убрал лишний мягкий знак в «зарядиться». Здравствуйте, уважаемые форумчане. Хочу понять, как будет вести себя конденсатор в цепи постоянного тока.
Как работает конденсатор. Емкость конденсатора.
ВИДЕО ПО ТЕМЕ: Y конденсатор, зачем он нужен и как выбрать правильный
youtube.com/embed/OYdSoHO5bpg» frameborder=»0″ allowfullscreen=»»/>На практике же, все выпускаемые конденсаторы представляют собой многослойные рулоны лент электродов в форме цилиндра или параллелепипеда, разделенных между собой слоями диэлектрика. По принципу работы он схож с батарейкой только на первый взгляд, но все же он сильно отличается от него по принципу и скорости заряда-разряда, максимальной емкости. Заряд конденсатора. В момент подключения к источнику питания оказывается больше всего места на электродах, поэтому и ток будет зарядки максимальным, но по мере накопления заряда, ток будет уменьшаться и пропадет полностью после полного заряда.
Алюминиевые электролитические конденсаторы широко используются в различных электро- и радиотехнических приборах теле-, радио-, аудиоустройствах, стиральных машинах, кондиционерах воздуха и т. Применение на постоянном напряжении с наложенной переменной составляющей пульсирующее напряжение :.
Заряд и разряд конденсатора. Конденсатор представляет собой устройство, способное накапливать электрические заряды. Простейшим конденсатором являются две металлические пластины электроды , разделенные каким-либо диэлектриком. Конденсатор 2 можно зарядить, если соединить его электроды с источником 1 электрической энергии постоянного тока рис. При заряде конденсатора свободные электроны, имеющиеся на одном из его электродов, устремляются к положительному полюсу источника, вследствие чего этот электрод становится положительно заряженным. Электроны с отрицательного полюса источника устремляются ко второму электроду и создают на нем избыток электронов, поэтому он становится отрицательно заряженным.
Конденсатор представляет собой устройство, способное накапливать электрические заряды. Простейшим конденсатором являются две металлические пластины электроды , разделенные каким-либо диэлектриком. Конденсатор 2 можно зарядить, если соединить его электроды с источником 1 электрической энергии постоянного тока рис. При заряде конденсатора свободные электроны, имеющиеся на одном из его электродов, устремляются к положительному полюсу источника, вследствие чего этот электрод становится положительно заряженным. Электроны с отрицательного полюса источника устремляются ко второму электроду и создают на нем избыток электронов, поэтому он становится отрицательно заряженным.
Заряд конденсатора. Для того чтобы зарядить конденсатор, необходимо включить его в цепь постоянного тока. На рис. Конденсатор С присоединен к зажимам генератора.
Конденсаторы в цепи постоянного тока
Похожие презентации:
Расчет цепи постоянного тока
Электрические цепи постоянного тока
Электрические цепи постоянного тока
Линейные электрические цепи постоянного тока
Электрические цепи постоянного тока
Электротехника и электроника. Электрические цепи постоянного тока. (Лекция 1)
Электрические цепи постоянного тока. (Лекция 1)
Электрические цепи постоянного тока
Электрические цепи постоянного тока
Линейные электрические цепи постоянного тока. (Лекция 1)
Постоянный ток
1. Задача № 1
Определить энергию конденсатора емкостьюС =200 мкф, включенного в цепь, схема которой
изображена на рисунке. ЭДС источника 5 В, его
внутреннее сопротивление 0,5 Ом. Сопротивление
резистора
R1 = 2 Ом,
R2 =2,5 Ом.
С
R2
R1
2. Решение задачи №1:
В стационарном режиме через конденсатор ток не идет.Поэтому электрическую цепь можно представить проще:
Ток в этой цепи определяется
I = E/ R1 +R2 + r.
Напряжение на участке ав – напряжение на резисторе R2 , а значит и на конденсаторе:
U = IR2.=R2 E/ R1 +R2 + r.
W= СU2/2
W= С(R 2) 2E2/2(R1 +R2 +r )2=
6,25/10000Дж
Ответ:
а
Е
R2
R1
в
W =6,25/10000Дж
3. Задача № 2 Попробуйте решить самостоятельно.
 Конденсаторы С1 и С2 и резисторы, сопротивления
Конденсаторы С1 и С2 и резисторы, сопротивлениякоторых равны R1, R2, R3 включены в электрическую цепь,
как показано на рисунке. Найдите установившийся заряд
на конденсаторе С, если ЕДС источника Е, а его
внутреннее сопротивление равно нулю.
C1
R3
R2
R1
C2
E
4. Решение задачи №2 Ток в стационарном режиме идет по цветной ветке. I =E/ R1+R2+R3 = 1A Напряжение на конденсаторе С2 равно
напряжению на резисторах R2 и R3q2=C2U23 = C2 I R23 = 2мкф 1А 10ом = 20мкКл
Ответ:q2 = 20мкКл
С1
R3
R3
R2
R1
R2
R1
С2
Е
Е
5. Следующий тип задач позволяет определить разность потенциалов в электрической цепи содержащей конденсаторы.
Задача № 3Найти разность потенциалов между точками А и В в
цепи. Внутренним сопротивлением источника можно
пренебречь. ЭДС источника равна Е=10В, R1 = 2 ом, R2 = 3
ом. Емкость конденсаторов С1 = 0,5мкф,
С1
С2
С2 = 2 мкф
А
+
+
R1
R2
В
—
+
E
6.
 Решение задачи №3:Ток в стационарном режиме идет от источника через сопротивление R1 и R2
Решение задачи №3:Ток в стационарном режиме идет от источника через сопротивление R1 и R2I = E/R1 +R2 = 10B/5ом = 2А . Ur1 = I R1 = 4В
По верхней ветке, через конденсаторы ток не идет.
Правые пластины конденсатора заряжены положительно, левые отрицательно от источника
тока. Если идти от точки А против часовой стрелки до точки В потенциал изменяется:
при переходе через конденсатор С1 потенциал (энергия) уменьшается от + к -, при переходе по
резистору R1 к точке В потенциал возрастает:
Yа – Uc1 + Ur1 = Yв :
Yа –Yв = Uc1 — Ur1
По законам последовательного соединения конденсаторов:
q1 = q2,
следовательно: С1U1 = C2U2, Откуда: U1 С1/ C2 = U2
Е = U1 +U2 = U1 + U1 С1/ C2 = U1 ( 1 + С1/ C2 ).
Uc1 = Е/ ( 1 + С1/ C2 ) = 10В /( 1+ 0,5мкф/2мкф) = 8В
Yа –Yв = Uc1 — Ur1 = 8В – 4В = 4В
Ответ: Yа –Yв = 4В
7. Задача №4.Определить заряд конденсатора С в схеме, представленной на рисунке. Внутренним сопротивлением батареи пренебречь.
 E
EРешение задачи:
—
+
3C
2C
+
Обозначим заряды
конденсаторов С, 2С и
3С через q1,q2 и q3
соответственно.
2R
+
C
+
R
Предположим, что у конденсатора С положительный заряд находится на нижней пластине.
Тогда из закона сохранения заряда
–q2 – q1 + q3 = 0
( в выделенном квадрате пластины конденсаторов не соединены с источником, значит
заряд этих пластин до зарядки конденсаторов и после зарядки остается равны нулю
1) q2 + q1 = q3
В стационарном режиме ток идет только через источник тока R и 2R. Через конденсаторы
ток не идет. R и 2R соединены последовательно, поэтому ток в цепи:
I = E/3R
8. Продолжение решения задачи №4
Выберем обход в правом контуре по часовой стрелке, тогда по 2 –му правилу Кирхгоффа:2) – Uc+ U2c = IR = E/3; q2/2c — q1/c = E/3; q2/2C — q1/C = E/3; — 2q1 + q2 =2CE/3
q2 = 2q1 +2CE/3
( конденсатор — накопитель энергии, здесь в роли источника тока)
Аналогично в левом контуре:
3C
3) U3c + Uc = I2R = 2E/3
q3/3c + q1/c = 2 E/3
2C
+
2R
+
C
+
R
С учетом первого уравнения:
(q2 + q1 = q3)
3) q 1 /3c + q2/3c + q1/c = 2E/3;
q2 + q1 +3q1 = 2CE
4q1 + 2 q1 + 2CE/3 = 2CE
6q1 =2CE – 2CE/3 = 6CE/3 -2CE/3 = 4CE/3
q1 = 4CE/18 = 2CE/9
Ответ: Заряд на конденсаторе С: q1 = 2CE/9
Примечание: Следует обратить внимание на то, что q1 положительный.
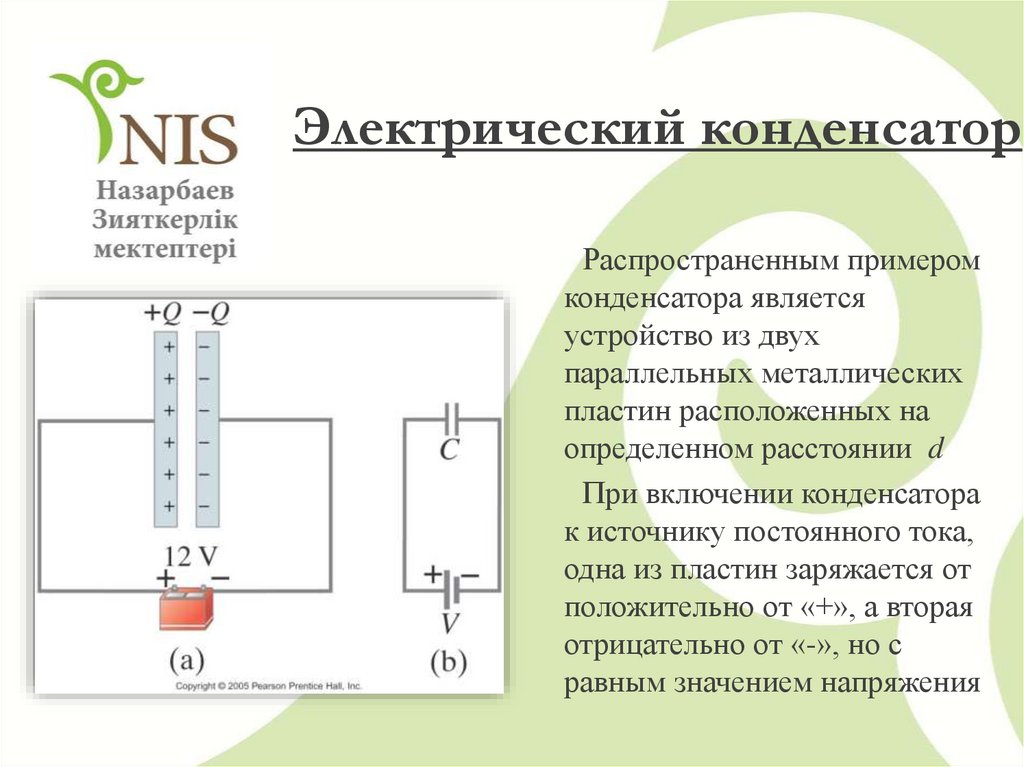 Это означает, что предположение о знаке
Это означает, что предположение о знакезаряда на обкладках конденсатора С было правильным (от этого предположения зависит расстановка знаков в
первом уравнении). Понятно, что если бы было сделано другое предположение, ответ имел бы другой знак.
English Русский Правила
Переходные процессы в цепях постоянного тока с конденсатором
ПЕРЕХОДНЫМ ПРОЦЕССОМ называется процесс перехода от одного установившегося в цепи режима к другому. Примером такого процесса является зарядка и разрядка конденсатора. В ряде случаях законы постоянного тока можно применять и к изменяющимся токам, когда изменение тока происходит не слишком быстро. В этих случаях мгновенное значение силы тока будет практически одно и то же во всех поперечных сечениях цепи. Такие токи называют квазистационарными
РАЗРЯДКА КОНДЕНСАТОРА. Если обкладки заряженного конденсатора ёмкости С замкнуть через сопротивление R, то через это сопротивление потечёт ток. Согласно закону Ома для однородного участка цепи
Согласно закону Ома для однородного участка цепи
IR=U,
где I и U – мгновенные значения силы тока в цепи и напряжения на обкладках конденсатора. Учитывая, что и , преобразуем закон Ома к виду
(1)
В этом дифференциальном уравнении переменные разделяются, и после интегрирования получим закон изменения заряда конденсатора со временем
, (2)
где q0 — начальный заряд конденсатора, е — основание натурального логарифма. Произведение RC, имеющее размерность времени, называется время релаксации t . Продифференцировав выражение (2) по времени, найдём закон изменения тока:
, (3)
где I0 — сила тока в цепи в момент времени t = 0. Из уравнения (3) видно, что t есть время, за которое сила тока в цепи уменьшается в е раз.
Зависимость от времени количества теплоты, выделившегося на сопротивлении R при разряде конденсатора можно найти из закона Джоуля-Ленца:
(4)
ЗАРЯДКА КОНДЕСАТОРА.

Считаем, что первоначально конденсатор не заряжен. В момент времени t = 0 ключ замкнули, и в цепи пошёл ток, заряжающий конденсатор. Увеличивающиеся заряды на обкладках конденсатора будут всё в большей степени препятствовать прохождению тока, постепенно уменьшая его. Запишем закон Ома для этой замкнутой цепи:
.
После разделения переменных уравнение примет вид:
Проинтегрировав это уравнение с учётом начального условия
q = 0 при t = 0 и с учётом того, что при изменении времени от 0 до t заряд изменяется от 0 до q, получим
, или после потенцирования
q = . (4)
Анализ этого выражения показывает, что заряд приближается к своему максимальному значению, равному С, асимптотически при t ® ?.
Подставляя в формулу (4) функцию I(t) = dq/dt, получим
. (5)
(5)
Из закона сохранения энергии следует, что при зарядке конденсатора для любого момента времени работа источника тока dАист рана сумме количества джоулевой теплоты dQ, выделившейся на резисторе R и изменению энергии конденсатора dW:
dAист= dQ + dW,
где dAист =Idt, dQ =I2Rdt, dW =d. Тогда для произвольного момента времени t имеем:
Аист(t)===С. (6)
Q(t)==С. (7)
W(t) ==. (8)
МЕТОДИКА И ПОРЯДОК ИЗМЕРЕНИЙ:
В реальных электрических цепях постоянного тока, содержащих конденсаторы, переходные процессы разрядки и зарядки конденсаторов проходят за время порядка 10–6 – 10-3 с. Для того,чтобы сделать доступными для наблюдения и измерения электрические параметры при переходных процессах в настоящей компьютерной модели это время значительно увеличено за счёт увеличения ёмкости конденсатора.
Для того,чтобы сделать доступными для наблюдения и измерения электрические параметры при переходных процессах в настоящей компьютерной модели это время значительно увеличено за счёт увеличения ёмкости конденсатора.
ЭКСПЕРИМЕНТ 1
Определение ёмкости конденсатора методом разрядки
1.Соберите на рабочей части экрана замкнутую электрическую цепь, показанную ниже на рис.2. Для этого сначала щёлкните мышью на кнопке э.д.с.,расположенной в правой части окна эксперимента. Переместите маркер мыши на рабочую часть экрана, где расположены точки, и щёлкните маркером мыши в виде вытянутого указательного пальца в том месте, где должен быть расположен источник тока. Подведите маркер мыши к движку появившегося регулятора э.д.с., нажмите на левую кнопку мыши, удерживая её в нажатом состоянии, меняйте величину э.д.с. и установите 10 В. Аналогичным образом включите в цепь 4 других источника тока. Суммарная величина э.д.с. батареи должна соответствовать значению, указанному в таблице 1 для вашего варианта.
Таким же образом разместите далее на рабочей части экрана 7 ламп Л1-Л7 ( кнопка ), Ключ К (кнопка ), вольтметр (кнопка ), амперметр (кнопка ), конденсатор (кнопка ). Все элементы электрической цепи соедините по схеме рис.1 с помощью монтажных проводов (кнопка ).
2. Щёлкните мышью на кнопке «Старт». Должна засветиться лампа Л7, а надпись на кнопке измениться на «Стоп». Курсором мыши замкните ключ К.
3. После установления в цепи стационарного тока ( должны погаснуть лампы Л5 и Л6 и светиться лампы Л1-Л4) запишите показания электроизмерительных приборов в таблицу 2.
4. Нажмите на кнопку «Стоп» и курсором мыши разомкните ключ К.
5. Двумя короткими щелчками мыши на кнопке «Старт» запустите и остановите процесс разрядки конденсатора. Показания амперметра будут соответствовать начальному току разрядки конденсатора I0. Запишите это значение в таблицу 3.
6. Вновь замкните ключ, зарядите конденсатор и повторите п.п. 5, 6 ещё 4 раза.
7. Для каждого опыта рассчитайте It= I0/2,7- силу тока, которая должна быть в цепи разрядки конденсатора через время релаксации t и запишите эти значения в таблицу 3.
Для каждого опыта рассчитайте It= I0/2,7- силу тока, которая должна быть в цепи разрядки конденсатора через время релаксации t и запишите эти значения в таблицу 3.
8. При разомкнутом ключе нажатием кнопки «Старт» запустите процесс разрядки конденсатора и одновременно включите секундомер.
9. Внимательно наблюдайте за изменением показаний амперметра в процессе разрядки конденсатора. Остановите секундомер и синхронно нажмите кнопку «Стоп» при показании амперметра, равном или близким к It. Запишите это значение времени t1 в таблицу 3.
10. Проделайте опыты п.п.8, 9 ещё 4 раза.
Таблица 1. Суммарное значение э.д.с. источников тока
|
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
Э. |
50 |
49 |
48 |
47 |
46 |
45 |
44 |
43 |
Таблица 2. Определение сопротивления лампы.
|
№п/п |
I, А |
U, В |
R, Ом |
|
Номер опыта |
1 |
2 |
3 |
4 |
5 |
Среднее значение |
|
I0, А |
||||||
|
It, А |
||||||
|
t, с |
||||||
|
C, Ф |
Таблица 3. Результаты измерений и расчётов.
Результаты измерений и расчётов.
ОБРАБОТКА РЕЗУЛЬТАТОВ:
1. По закону Ома для участка цепи Л1-Л4: и результатам измерений, приведённым в таблице 2, определите сопротивление одной лампы.
2. По формуле (при разрядке конденсатора квазистационарный ток протекает по 6 последовательно соединённым лампам) определите ёмкость конденсатора и запишите эти значения в таблицу 3.
3. Рассчитайте погрешности измерений и сформулируйте выводы по результатам проделанной работы.
ЭКСПЕРИМЕНТ 2
Изучение зависимости от времени количества тепла, выделившегося на нагрузке при разряде конденсатора
- Выполняя действия, аналогичные описанным в эксперименте 1, зарядите конденсатор до напряжения, соответствующего суммарному значению э.д.с. для вашего варианта.
- Нажмите кнопку «Стоп» и отключите ключ К.
- Проведите 5-ти секундный процесс частичного разряда конденсатора через подключённые лампы.
 Для этого нажмите синхронно кнопку «Старт» и кнопку запуска секундомера и через 5 секунд нажатием кнопки «Стоп» остановите процесс разрядки конденсатора.
Для этого нажмите синхронно кнопку «Старт» и кнопку запуска секундомера и через 5 секунд нажатием кнопки «Стоп» остановите процесс разрядки конденсатора. - Запишите показания амперметра в таблицу 4 и вновь зарядите конденсатор до первоначального напряжения.
- Последовательно увеличивая длительность процесса разрядки конденсатора на 5 с, проделайте эти опыты до времени разрядки, соответствующему полному исчезновению заряда на конденсаторе. (Напряжение на конденсаторе и ток разрядки через лампы должен быть близким к нулю). Результаты измерений тока разрядки запишите в соответствующие ячейки таблицы 4.
Таблица 4. Результаты измерений и расчетов
|
Время разрядки t, с |
5 |
10 |
15 |
20 |
… |
5n |
|
Ток разряда I через t с, А |
||||||
|
Кол-во тепла Q за t с, Дж |
ОБРАБОТКА РЕЗУЛЬТАТОВ:
- Для каждого времени разрядки вычислите по формуле (4) количество тепла, выделившегося на шести лампах и запишите эти значения в соответствующие ячейки третьей строки табл.
 4. Полезный совет: для расчёта Q воспользуйтесь программой MS Exсel.
4. Полезный совет: для расчёта Q воспользуйтесь программой MS Exсel. - Постройте график зависимости количества выделившегося тепла Q к данному моменту времени от длительности процесса разрядки конденсатора t.
- Сравните рассчитанное количество тепла, выделившееся к моменту полного разряда конденсатора с его теоретическим значением, равным .
- Сделайте выводы по графику и ответу и проведите расчёт погрешностей измерений.
ЭКСПЕРИМЕНТ 3
Проверка закона сохранения энергии в процессе зарядки конденсатора через сопротивление
Рис.3
- Соберите в рабочей части экрана опыта схему, показанную на рис.3. Вольтметр, включённый параллельно 5-ти лампам, будет показывать напряжение на внешнем сопротивлении, а амперметр – силу тока через нагрузку и источники тока. Напряжение на конденсаторе определяется программой автоматически и указывается в вольтах на экране монитора над конденсатором.

- Установите суммарную э.д.с. источников тока, соответствующую значению, приведённому в табл.1 для вашего варианта.
- При разомкнутом ключе К нажмите кнопку «Старт».
- Нажатием кнопки мыши замкните ключ К и начните процесс зарядки конденсаторов. Одновременно с замыканием ключа включите секундомер.
- Через время релаксации t = RС нажатием кнопки «Стоп» остановите процесс и запишите показания электроизмерительных приборов в таблицу 5.
- Нажмите кнопку «Выбор» и обнулите показания напряжений на всех конденсаторах и на электроизмерительных приборах.
- Повторите эти измерения ещё 4 раза и заполните две верхних строки таблицы 5.
Таблица 5. Результаты измерений и расчетов
|
№ опыта |
1 |
2 |
3 |
4 |
5 |
Среднее |
|
I, A |
||||||
|
Uc, B |
||||||
|
UR, B |
||||||
|
Аист, Дж |
||||||
|
DW, Дж |
||||||
|
Q, Дж |
ОБРАБОТКА РЕЗУЛЬТАТОВ:
- По формулам 6, 7, 8 и измеренным значениям напряжения на конденсаторе Uc рассчитайте величины работу источника тока Аист, изменение энергии конденсатора DW и выделившегося на нагрузке количества тепла Q через время заряда, равного времени релаксации.

- Проверьте выполнение закона сохранения энергии в процессе зарядки конденсатора по формуле: Аист =DW + Q.
- Сделайте выводы по итогам работы.
Вопросы и задания для самоконтроля
Вопросы и задания для самоконтроля
- Что представляет собой конденсатор и от чего зависит его ёмкость?
- Выведите формулы ёмкости плоского, цилиндрического и сферического конденсаторов.
- Как изменяется разность потенциалов на обкладках конденсатора при его зарядке и разрядке?
- Какой ток называется квазистационарным?
- Выведите формулы электроёмкости батареи последовательно и параллельно соединённых конденсаторов
- Что такое время релаксации?
- Объясните принцип работы экспериментальной установки.
- Нарисуйте графики зависимости силы тока и напряжения от времени при зарядке и разрядке конденсатора.

- Соберите на мониторе такую цепь, состоящую из источника тока, двух ламп, выключателя и соединительных проводов, чтобы с выключением лампы в одной цепи загоралась лампа в другой.
- Определите заряд, который пройдёт через гальванометр в схеме, показанной на рис. 2, при замыкании ключа.
- Конденсатор ёмкости С = 300 пФ подключается через сопротивление R =500 Ом к источнику постоянного напряжения U0. Определите: а) время, по истечению которого напряжение на конденсаторе составит 0,99 U0; в) количество тепла, которое выделится на этом сопротивлении при разрядке конденсатора за это же время.
- Имеется ключ, соединительные провода и две электрические лампочки. Составьте на мониторе электрическую схему включения в сеть этих лампочек, которая должна удовлетворять следующему условию: при замкнутом ключе горит только первая лампочка, при размыкании ключа первая гаснет, а вторая загорается.

- Конденсатору ёмкостью С сообщают заряд q, после чего обкладки конденсатора замыкают через сопротивление R. Определите: а) закон изменения силы тока, текущего через сопротивление; б) заряд, прошедший через сопротивление за время t; в) количество тепла, выделившееся в сопротивлении за это время.
- Определите количество тепла, выделившегося в цепи (рис. 4-6) при переключении ключа К из положения 1 в положение 2. Параметры цепи обозначены на рисунках.
Как конденсатор работает с постоянным током
В предыдущем посте мы рассмотрели концепцию, конструкцию и работу конденсатора как источника постоянного напряжения. Этот пост посвящен теме . Как работает конденсатор с DC . Конденсаторы широко используются в электронике постоянного тока. Вопросы приходят на ум, когда мы думаем о постоянном токе и конденсаторе:
- Как конденсатор работает с входом постоянного тока?
- Какое конечное напряжение конденсатора после зарядки?
- Сколько времени требуется конденсатору для зарядки/разрядки?
Давайте обсудим решение вышеуказанных вопросов.
Конденсатор выполняет три задачи в цепях постоянного тока: принимает заряд, удерживает заряд и отдает заряд в определенное время. Когда конденсатор подключен к источнику постоянного напряжения, конденсатор начинает процесс приобретения заряда. Это создаст напряжение на конденсаторе. Как только конденсатор приобретает достаточный заряд, начинает течь ток, и вскоре напряжение на конденсаторе достигает значения, приблизительно равного напряжению источника постоянного тока. Когда на конденсаторе почти полное напряжение, ток через конденсатор больше не течет. Это займет некоторое время. Но есть интересный факт. Конденсатор не будет заряжаться на 100% в тот же момент, когда на него подается постоянное напряжение. Конденсатор получает первую часть полного заряда быстро, вторую часть медленнее, третью часть медленнее и так далее. Следовательно, мы можем сказать, что конденсатор заряжается нелинейно.
Вы можете представить себе эту ситуацию с аналогией шины . Сравните автобус с конденсатором, свободное место с пространством и людей с электронами. В автобусе каждый пытается занять место. Если осталось меньше мест, людям нужно больше времени, чтобы найти свободное место. Точно так же электроны пытаются занять место на пластине конденсатора. Здесь электронам требуется некоторое время, чтобы попасть на пластины. Перемотать конструкцию конденсатора. Для входного постоянного напряжения первая пластина заряжается до входного напряжения. Поскольку между двумя пластинами нет проводящего пути, второй пластине требуется некоторое время, чтобы получить заряд.
Сравните автобус с конденсатором, свободное место с пространством и людей с электронами. В автобусе каждый пытается занять место. Если осталось меньше мест, людям нужно больше времени, чтобы найти свободное место. Точно так же электроны пытаются занять место на пластине конденсатора. Здесь электронам требуется некоторое время, чтобы попасть на пластины. Перемотать конструкцию конденсатора. Для входного постоянного напряжения первая пластина заряжается до входного напряжения. Поскольку между двумя пластинами нет проводящего пути, второй пластине требуется некоторое время, чтобы получить заряд.
Это время определяет время зарядки конденсатора. Итак, нам необходимо выяснить параметры, от которых зависит время заряда конденсатора. Согласно закону Ома, если сопротивление цепи увеличивается, меньший ток доступен для зарядки конденсатора. Это увеличивает время, необходимое для зарядки конденсатора. Поскольку емкость и напряжение обратно пропорциональны друг другу, увеличение значения емкости требует больше времени для зарядки конденсатора. Таким образом, с этими соотношениями мы можем сказать, что время зарядки конденсатора зависит как от сопротивления цепи, так и от емкости конденсатора. это постоянная времени конденсатора. Но процесс измерения времени зарядки конденсатора сложен, поскольку конденсатор никогда не будет заряжаться с одинаковой скоростью.
Таким образом, с этими соотношениями мы можем сказать, что время зарядки конденсатора зависит как от сопротивления цепи, так и от емкости конденсатора. это постоянная времени конденсатора. Но процесс измерения времени зарядки конденсатора сложен, поскольку конденсатор никогда не будет заряжаться с одинаковой скоростью.
Время зарядки или постоянная времени обозначается как τ (тау). Он определяет время, за которое конденсатор емкостью «С» фарад, включенный последовательно с сопротивлением «R» Ом, приобретает первую часть полного заряда. Постоянная времени может быть математически определена следующим образом:
Время зарядки = сопротивление x емкость
τ = R x C
Постоянная времени – это время, необходимое конденсатору для увеличения напряжения или тока до 63,21 % от максимума или уменьшение до 36,79 % от начального значения.
Почему конденсатор заряжается до 63% приложенного напряжения? Вот уравнение для напряжения на конденсаторе в любой момент времени во время зарядки.
Where V c = capacitor voltage, V i = input voltage , t = время зарядки, R = сопротивление, C = емкость
Цепь зарядки конденсатора Напр. для R = 10 МОм и C = 0,1 мкФ постоянная времени составляет 1 секунду. Это не означает, что конденсатор полностью зарядится за 1 секунду. Это означает, что конденсатор будет заряжаться до 63% входного напряжения за 2 секунды. Если мы продолжим подавать напряжение, конденсатор займет 63% разницы между текущим напряжением и входным напряжением. Этот процесс будет повторяться до тех пор, пока конденсатор не зарядится полностью. Мы получаем значение 63% или 0,63, когда подставляем одну постоянную времени в приведенное выше уравнение. Мы можем рассчитать ток в любой момент (время) в конденсаторе, используя закон Ома. Рассмотрим ту же схему, что обсуждалась ранее. Вот уравнение тока во время заряда конденсатора.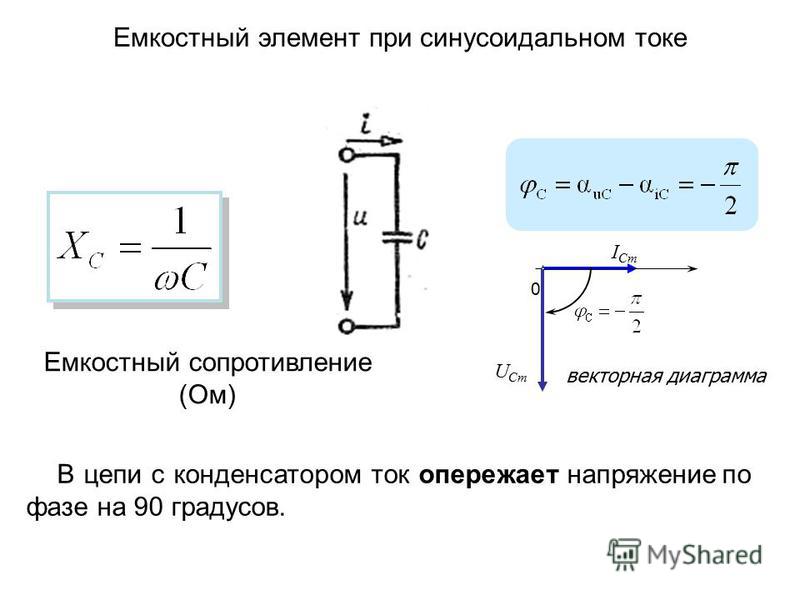
В таблице ниже показаны значения для зарядной зарядки для контакта.
| Положение переключателя | Постоянная времени (τ) (в секундах) | Напряжение заряда конденсатора ( В c ) (в вольтах) | Ток заряда конденсатора ( I с ) |
| ВЫКЛ | 0 | 0 | 10 мкА |
| НА | 1RC | 63.2120 | 3,6787 мкА |
| НА | 2RC | 86.4664 | 1,3533 мкА |
| НА | 3RC | 95.0212 | 0,4978 мкА |
| НА | 4RC | 98.1684 | 0,1831 мкА |
| НА | 5RC | 99. 3262 3262 | 0,0673 мкА |
| НА | 8RC | 99,9664 | 3,3546 нД |
| НА | 11RC | 99,9983 | 0,1670 нА |
| НА | 14RC | 99,9999 | 8,3152 пА |
| НА | 17RC | 99,9999 | 0,4139 пА |
Термин 1RC, 2RC и т. д. определяет, сколько раз постоянное напряжение должно быть приложено к конденсатору. Приведенная выше таблица напоминает важный факт, связанный с конденсатором, т.е. конденсатор никогда не будет хранить полный заряд, данный ему . Каждый раз постоянное напряжение на конденсаторе медленно увеличивается (кроме первого), но оно никогда не будет равно входному напряжению. Ток, протекающий через цепь резистора-конденсатора, уменьшается с увеличением времени (τ). Вот график, показывающий поведение зарядного напряжения и тока конденсатора.
График зарядного тока и напряжения конденсатора График зарядного напряжения и тока конденсатора имеет экспоненциальный рост и падение соответственно.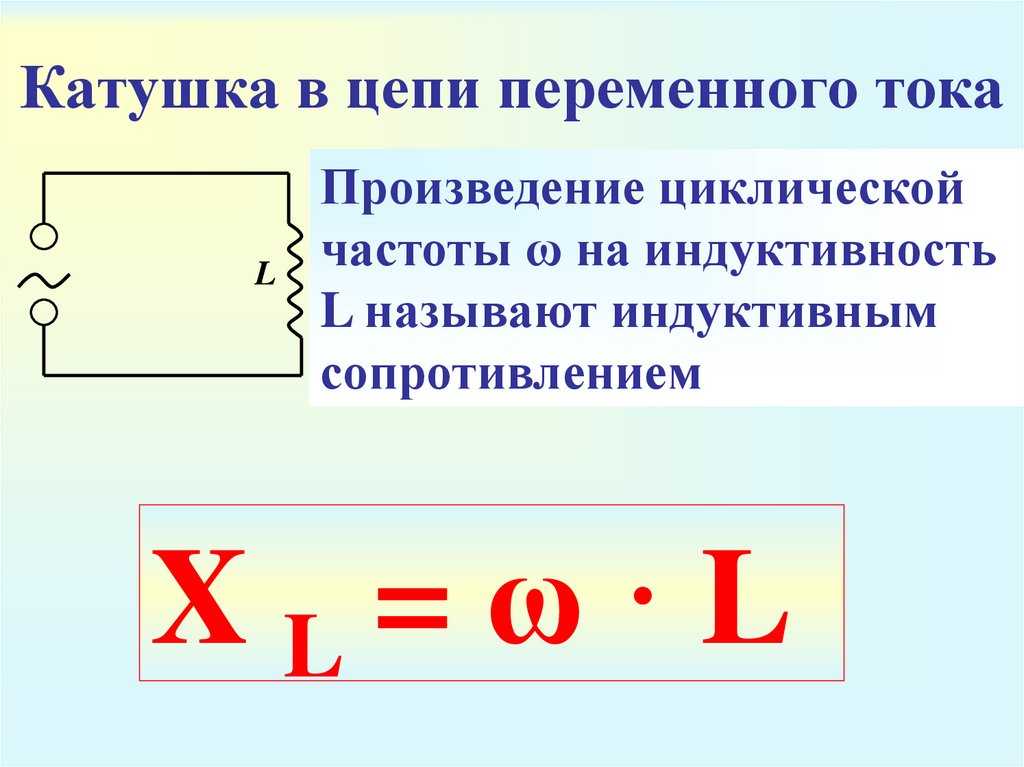 Кривая показывает, сколько времени требуется конденсатору, чтобы получить почти полный заряд. Экспоненциальный рост напряжения и экспоненциальный спад тока в емкостной цепи не совпадают или не совпадают в фазе . Обратите внимание, что ось x графика изменена относительно значения по оси y, чтобы иметь четкое представление об изменении напряжения или тока. График не соответствует определенному масштабу. За 5RC секунд зарядный ток I c ≈ 0 и напряжение зарядки В c ≈ входное напряжение.
Кривая показывает, сколько времени требуется конденсатору, чтобы получить почти полный заряд. Экспоненциальный рост напряжения и экспоненциальный спад тока в емкостной цепи не совпадают или не совпадают в фазе . Обратите внимание, что ось x графика изменена относительно значения по оси y, чтобы иметь четкое представление об изменении напряжения или тока. График не соответствует определенному масштабу. За 5RC секунд зарядный ток I c ≈ 0 и напряжение зарядки В c ≈ входное напряжение.
Существует несколько способов разрядить заряженный конденсатор. Самый простой способ — использовать светодиод или резистор последовательно с конденсатором. Мы должны проявлять крайнюю осторожность при выборе резистора или светодиода для разряда конденсатора. Перед использованием рекомендуется ссылаться на такие характеристики, как мощность, значение в случае резистора и прямого тока, напряжение в случае светодиода. Схема разрядки конденсатора показана ниже.
Схема разрядки конденсатора показана ниже.
Вот уравнения для напряжения на конденсаторе и тока в конденсаторе в любой момент времени во время разрядки.
V D = V I ( E -τ / RC ) I D = V D = V D = V D 88888888888 гг. показывает значения напряжения и тока разрядки конденсатора для соответствующей постоянной времени. Во время разрядки напряжение, при котором конденсатор начинает разряжаться, соответствует последнему заряду| Положение переключателя | Постоянная времени (τ) (в секундах) | Напряжение заряда конденсатора ( В d ) | Ток заряда конденсатора ( I d ) |
| ВЫКЛ | 0 | ≈ 100 В | 10 мкА |
| НА | 1RC | 36,7879 В | 3,6787 мкА |
| НА | 2RC | 13,5335 В | 1,3533 мкА |
| НА | 3RC | 4,9877 В | 0,4978 мкА |
| НА | 4RC | 1,8315 В | 0,1831 мкА |
| НА | 5RC | 0,6737 В | 0,0673 мкА |
| НА | 8RC | 0,0335 В | 3,3546 нД |
| НА | 11RC | 1,6701 мВ | 0,1670 нА |
| НА | 14RC | 30,5902 мкВ | 8,3152 пА |
| НА | 17RC | 4,1399 мкВ | 0,4139 пА |
Во время разрядки напряжение и ток конденсатора быстро уменьшаются в течение 1RC секунды, после чего происходит медленное уменьшение обеих величин. Вот график напряжения и тока разряда конденсатора. Оба графика имеют экспоненциально падающий характер. Через 5RC секунд ток разряда I d ≈ 0 и напряжение разрядки В d ≈ 0.
Вот график напряжения и тока разряда конденсатора. Оба графика имеют экспоненциально падающий характер. Через 5RC секунд ток разряда I d ≈ 0 и напряжение разрядки В d ≈ 0.
На данный момент это все. Надеюсь, теперь вы знаете, как конденсатор работает с постоянным током. В следующем посте мы узнаем о конденсаторе в цепях переменного тока. Спасибо за чтение и не забудьте оставить комментарий.
О Ганеше Патиле
Ганеш Гопал Патил получил степень магистра в области встроенных систем. Он получил степень бакалавра технических наук в области электроники и телекоммуникаций. Его текущие интересы включают проектирование встраиваемых систем на основе микроконтроллеров.
Previous What is Capacitor
Next Eagle PCB Design Tutorial
DC Bus Capacitor for Drive Inverters
Jih-Sheng Lai and Heath Kouns
Virginia Polytechnic and State University
668 Whittemore Hall
Blacksburg, VA 24061-0111
Joseph Bond
Electronic Concepts, Inc.
526 Industrial Way West
Eatontown, NJ 07724
РЕФЕРАТ
Для привода тягового двигателя с батарейным питанием шина постоянного тока инвертора представляет высокочастотный пульсирующий ток из-за переключения устройств. Конденсатор шины постоянного тока в традиционной конструкции инвертора, рассчитанный на основе пульсаций напряжения, больше не эффективен. Чтобы выдерживать большие токи в высокотемпературной среде, предлагается использовать сильноточные пленочные конденсаторы с малой индуктивностью для замены обычных электролитических конденсаторов большой емкости в инверторе привода тягового двигателя мощностью 75 кВт. Предлагаемая конструкция приводит к значительному уменьшению размеров и повышению производительности по сравнению с существующей. Представлены характеристики малоиндуктивного сильноточного пленочного конденсатора, демонстрирующие его превосходство над обычными электролитическими конденсаторами. Приведены экспериментальные результаты, подтверждающие необходимость использования предлагаемого конденсатора.
Ключевые слова: конденсаторы, тяговые электроприводы, конструкция инвертора
I. ВВЕДЕНИЕ
В последнее время в промышленности все больше внимания уделяется конденсаторной технологии. Для приложений с низким энергопотреблением, особенно в компьютерах и телекоммуникациях, критерии выбора и доступности обсуждались и резюмировались в [1]. Ожидаемый срок службы конденсатора звена постоянного тока применительно к приводам тяговых двигателей обсуждался в [2]. В связи с успешным развитием использования недавно разработанного сильноточного пленочного конденсатора с низкой индуктивностью в приводе тягового двигателя большой мощности (75 кВт) цель этой статьи состоит в том, чтобы предоставить теоретические основы и данные полевых экспериментов для потенциально лучшей шины постоянного тока. вариант конструкции конденсатора.
Конденсатор звена постоянного тока является наиболее важным пассивным компонентом привода тягового двигателя. В традиционных конструкциях используется набор электролитических конденсаторов большой емкости для сглаживания напряжения на шине постоянного тока.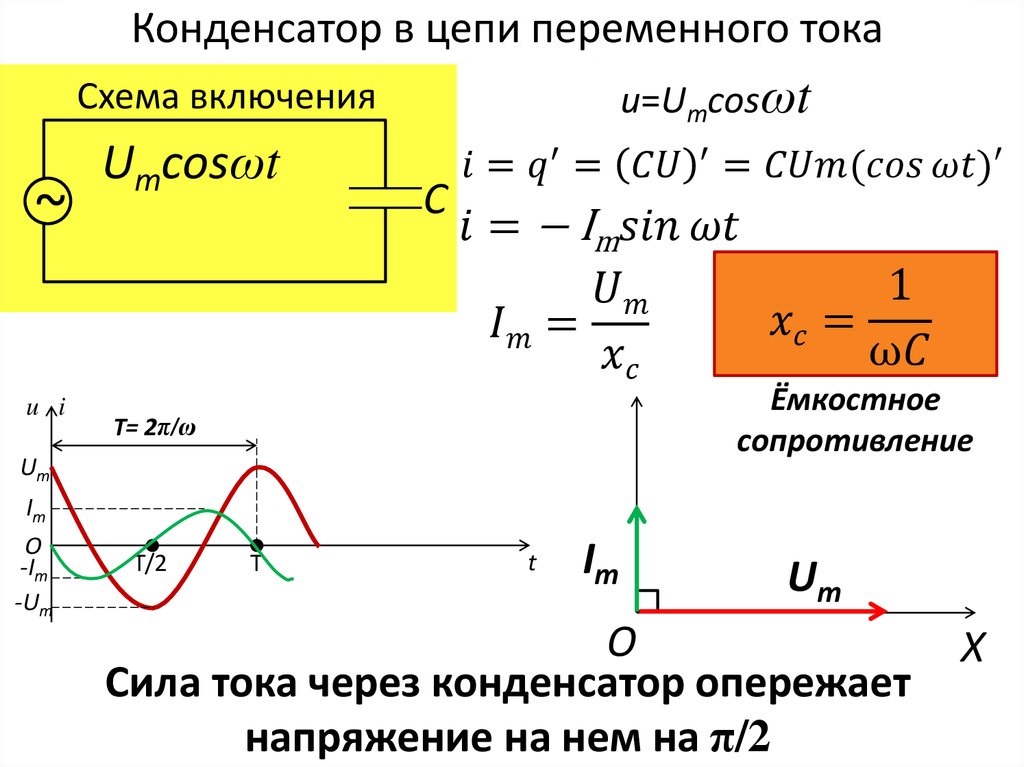 В результате исследования напряжения на шине постоянного тока и пульсаций тока было обнаружено, что один высокочастотный пленочный конденсатор с низкой индуктивностью можно использовать для замены оригинальной конструкции инвертора привода тягового двигателя мощностью 75 кВт, в которой использовались три громоздких электролитических конденсатора. Значительными результатами являются (1) уменьшение размера, (2) снижение стоимости и (3) повышение надежности. С использованием предлагаемого пленочного конденсатора большой мощности весь тяговый двигатель и инвертор могут быть интегрированы в компактный корпус, что устраняет значительное количество кабелей и связанные с ними затраты и потери.
В результате исследования напряжения на шине постоянного тока и пульсаций тока было обнаружено, что один высокочастотный пленочный конденсатор с низкой индуктивностью можно использовать для замены оригинальной конструкции инвертора привода тягового двигателя мощностью 75 кВт, в которой использовались три громоздких электролитических конденсатора. Значительными результатами являются (1) уменьшение размера, (2) снижение стоимости и (3) повышение надежности. С использованием предлагаемого пленочного конденсатора большой мощности весь тяговый двигатель и инвертор могут быть интегрированы в компактный корпус, что устраняет значительное количество кабелей и связанные с ними затраты и потери.
Конденсатор шины постоянного тока в мощных тяговых электроприводах должен решать следующие проблемы: (1) пульсации тока из-за переключения инвертора, (2) флуктуации напряжения из-за индуктивности вывода источника, (3) переходные процессы напряжения из-за индуктивность рассеяния и быстрое переключение устройств, а также (4) перенапряжение из-за регенерации. Емкость, необходимая для решения первых трех проблем, может быть невелика, но основные проблемы вызывают способность выдерживать ток и частотная характеристика конденсатора. Для регенерации, если батарея напрямую подключена к шине постоянного тока, размер емкости не имеет значения. Таким образом, общая конструкция должна быть ориентирована на текущие возможности обработки в широком температурном диапазоне.
Емкость, необходимая для решения первых трех проблем, может быть невелика, но основные проблемы вызывают способность выдерживать ток и частотная характеристика конденсатора. Для регенерации, если батарея напрямую подключена к шине постоянного тока, размер емкости не имеет значения. Таким образом, общая конструкция должна быть ориентирована на текущие возможности обработки в широком температурном диапазоне.
Наш инвертор привода тягового двигателя пережил несколько поколений. В нашей конструкции инвертора первого поколения шина постоянного тока состоит из четырех электролитических конденсаторов с номиналом 450 В, 6800 мкФ каждый. В нашей конструкции инвертора второго поколения шина постоянного тока состоит из трех электролитических конденсаторов, каждый на 450 В, 4700 мкФ. Размер каждого инверторного конденсатора второго поколения составляет 3 дюйма в диаметре и 5,125 дюйма в высоту, а ток пульсаций составляет 12,3 А при 85 °C [3]. При параллельном подключении трех из них общий ток составляет всего 36,9О.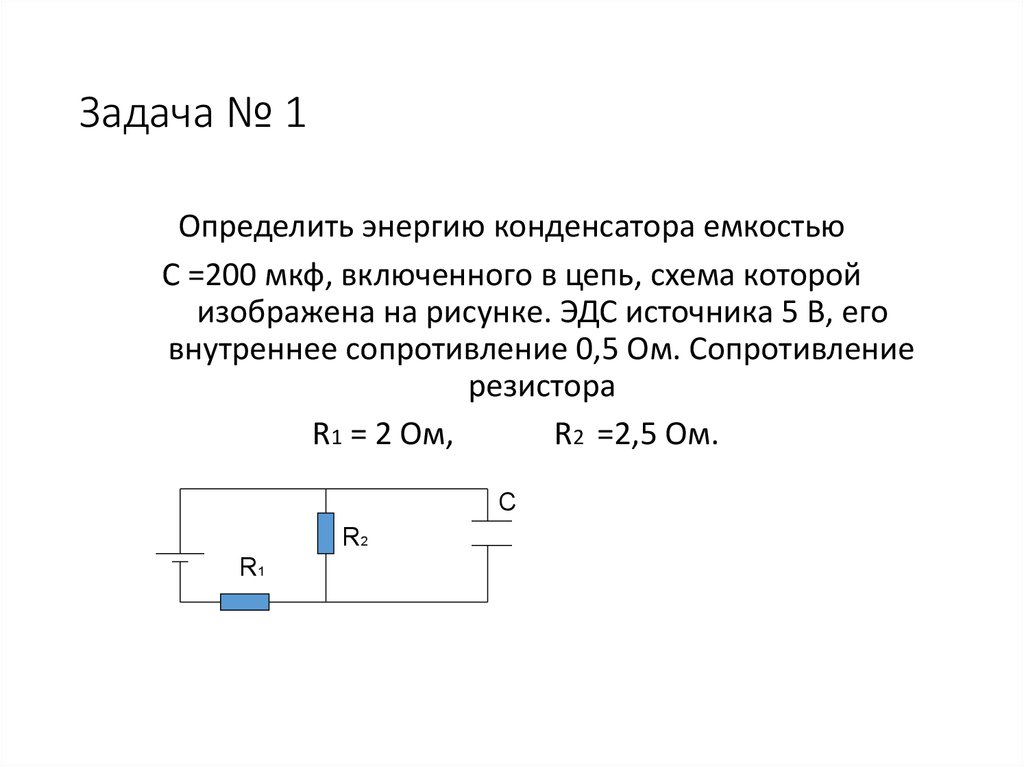 Несмотря на то, что рейтинг кажется низким, причина, по которой разрешено уменьшение емкости и размеров, заключается в том, что весь инвертор, включая конденсатор, охлаждался вентилятором мощностью 26 Вт, а температура не превышала предела. Пульсации напряжения на шине постоянного тока никогда не были проблемой при разработке первых двух поколений.
Несмотря на то, что рейтинг кажется низким, причина, по которой разрешено уменьшение емкости и размеров, заключается в том, что весь инвертор, включая конденсатор, охлаждался вентилятором мощностью 26 Вт, а температура не превышала предела. Пульсации напряжения на шине постоянного тока никогда не были проблемой при разработке первых двух поколений.
Для нового поколения идея конструкции инвертора состоит в том, чтобы интегрировать инвертор и двигатель вместе с одним комплектом жидкостного охлаждения, чтобы можно было еще больше уменьшить размер и вес всего привода тягового двигателя и, таким образом, увеличить запас хода. расширенный. Таким образом, недавно разработанный инвертор привода тягового двигателя использует один пленочный конденсатор 500 В, 200 мкФ для замены оригинальных громоздких электролитических конденсаторов. Имея физические размеры 3,6” × 4,5” × 1,4”, этот конденсатор имеет ток пульсаций 140 А при 85°C. Таким образом, этот новый инвертор не только уменьшает физический размер, но и улучшает способность обработки высокочастотных пульсаций тока.
В дополнение к значительному улучшению устойчивости к току пульсации и уменьшению размера, недавно принятый пленочный конденсатор с низкой индуктивностью также продемонстрировал значительное снижение скачков напряжения по сравнению с традиционной конструкцией, в которой использовалась комбинация силовой шины и громоздких электролитических конденсаторов. Наш инвертор второго поколения на шинной основе с тремя электролитическими конденсаторами показал скачок напряжения более 33% во время переходного процесса выключения устройства. Благодаря пленочному конденсатору с низкой индуктивностью, интегрированному с толстой медной печатной платой (PCB), скачок напряжения снижается до 14 %, что позволяет отказаться от дополнительных снабберных конденсаторов на шине постоянного тока.
Также хорошо известно, что электролитический конденсатор имеет ограниченный срок службы, поскольку его электролит имеет тенденцию высыхать после 10 000 часов использования. Замена громоздкого электролитического конденсатора пленочным конденсатором позволяет увеличить ожидаемый срок службы до более чем 100 000 часов — улучшение на порядок.
В этой статье полная принципиальная схема инвертора привода тягового двигателя будет подробно описана с учетом причин пульсаций тока и всплесков напряжения, что обосновывает необходимость использования пленочного конденсатора с низкой индуктивностью. На основе информации о напряжении и токе инвертора можно определить характеристики конденсатора звена постоянного тока и выбрать тип конденсатора. Будут показаны характеристики выбранного пленочного конденсатора, чтобы увидеть, соответствует ли он проектным требованиям. Будет показана фотография силовой части инвертора тягового электропривода мощностью 75 кВт, чтобы показать все связанные компоненты и характер его низкой паразитной индуктивности. Наконец, будут показаны экспериментальные результаты, указывающие на преимущество использования предложенного сильноточного файлового конденсатора с малой индуктивностью.
II. НЕОБХОДИМАЯ ЦЕПЬ ИНВЕРТОРА И КОНДЕНСАТОРЫ
На рис. 1 показана упрощенная принципиальная схема инвертора с батарейным питанием для привода трехфазного двигателя переменного тока. По этой схеме нужен только один конденсатор. Строго говоря, даже этот конденсатор является избыточным, поскольку он подключен параллельно жесткому источнику постоянного тока. Вопрос зачем и какой конденсатор нужен при таком аргументе. Чтобы ответить на этот вопрос, необходимо хорошо разбираться в механизме переключения инвертора и паразитных компонентах схемы.
По этой схеме нужен только один конденсатор. Строго говоря, даже этот конденсатор является избыточным, поскольку он подключен параллельно жесткому источнику постоянного тока. Вопрос зачем и какой конденсатор нужен при таком аргументе. Чтобы ответить на этот вопрос, необходимо хорошо разбираться в механизме переключения инвертора и паразитных компонентах схемы.
Рис. 1. Упрощенная принципиальная схема инвертора.
Синтез плавного синусоидального тока для привода двигателя переменного тока с источником жесткого постоянного напряжения должен иметь высокую скорость переключения в различных комбинациях переключателей инвертора, чтобы выходной ток мог отслеживать требуемый синусоидальный ток для уменьшения пульсирующее содержимое. Величина этой пульсации зависит от напряжения постоянного тока, индуктивности двигателя, противоэлектромагнитной силы двигателя (ЭДС) и периода переключения. Каждый период переключения имеет напряжение на обмотке двигателя либо +V DC , 0 или –V DC . При подаче +V dc ток двигателя возрастает. С другой стороны, когда применяется 0 или –V dc , ток двигателя падает. Частота переключения в современных инверторах на основе биполярных транзисторов с изолированным затвором (IGBT) обычно составляет от 10 кГц до 20 кГц. В зависимости от индуктивности обмотки двигателя и схемы модуляции пульсации колеблются от нескольких процентов до тока, близкого к полной нагрузке. В тяговом приводе электромобиля на базе асинхронного двигателя эта пульсация составляет от 25 до 65% от номинального тока нагрузки. В тяговом приводе электромобиля на основе двигателя с постоянными магнитами пульсации обычно выше, потому что индуктивность двигателя по своей природе ниже. Дело обстоит хуже на низких скоростях, когда противо-ЭДС двигателя также мала. Пульсирующие токи всех трехфазных ветвей в сумме весьма значительны и не приветствуются аккумуляторным источником. Следовательно, конденсатор шины постоянного тока C dc , показанный на рис.
При подаче +V dc ток двигателя возрастает. С другой стороны, когда применяется 0 или –V dc , ток двигателя падает. Частота переключения в современных инверторах на основе биполярных транзисторов с изолированным затвором (IGBT) обычно составляет от 10 кГц до 20 кГц. В зависимости от индуктивности обмотки двигателя и схемы модуляции пульсации колеблются от нескольких процентов до тока, близкого к полной нагрузке. В тяговом приводе электромобиля на базе асинхронного двигателя эта пульсация составляет от 25 до 65% от номинального тока нагрузки. В тяговом приводе электромобиля на основе двигателя с постоянными магнитами пульсации обычно выше, потому что индуктивность двигателя по своей природе ниже. Дело обстоит хуже на низких скоростях, когда противо-ЭДС двигателя также мала. Пульсирующие токи всех трехфазных ветвей в сумме весьма значительны и не приветствуются аккумуляторным источником. Следовательно, конденсатор шины постоянного тока C dc , показанный на рис. 1, необходим для поглощения вышеупомянутого пульсирующего тока из-за переключения инвертора, которое имеет ±V dc , приложенное к обмоткам двигателя, так что ток батареи является плавным постоянным током, и более длинная батарея жизни можно ожидать. Однако нагрузка по поглощению пульсирующего тока, по-видимому, смещается на C dc .
1, необходим для поглощения вышеупомянутого пульсирующего тока из-за переключения инвертора, которое имеет ±V dc , приложенное к обмоткам двигателя, так что ток батареи является плавным постоянным током, и более длинная батарея жизни можно ожидать. Однако нагрузка по поглощению пульсирующего тока, по-видимому, смещается на C dc .
Пульсации тока конденсатора можно получить путем компьютерного моделирования всей системы тягового привода, включая инвертор и асинхронный двигатель. На рис. 2 показаны смоделированные входной постоянный и выходной переменный токи инвертора. Без сглаживающего конденсатора C dc , ток батареи I в равен току звена постоянного тока I dc , который пульсирует между 0 и максимальным током нагрузки. На рисунке показано, что конденсатор шины постоянного тока потребляет ток I cap , который поглощает значительную высокочастотную составляющую тока от I dc и, таким образом, сглаживает входной ток батареи.
Рис. 2. Моделирование входного постоянного и выходного переменного тока в трех основных циклах. 9[4] .
Обратите внимание, что инвертор управляется схемой пространственно-векторной модуляции (SVM), при которой одна фаза остается непереключенной в течение одной шестой цикла сети, а две другие фазы переключаются с предварительно рассчитанным рабочим циклом. схему для обеспечения синусоидального тока на выходе.
На рис. 3 показаны подробные формы сигналов тока для пяти циклов переключения. Также показаны управляющие сигналы переключающих устройств, чтобы объяснить, как выходные переменные токи отражаются обратно в звено постоянного тока. Когда все верхние переключатели (S 1 , S 3 , S 5 ) включены, как показано в узкой заштрихованной области, напряжения на клеммах двигателя равны нулю, а токи циркулируют через диоды. Таким образом, в этой узкой заштрихованной области ток в звене постоянного тока равен нулю.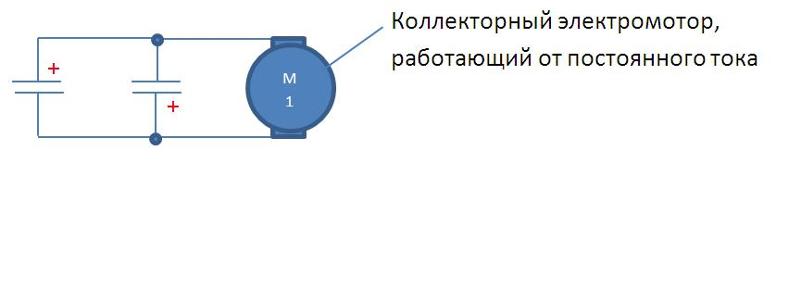 В широкой заштрихованной области переключите S 5 остается включенным, но переключатель S 3 выключается, а переключатель S 6 включается. Это позволяет току нагрузки течь обратно в звено постоянного тока, т. е. ток звена постоянного тока равен току нагрузки, который является максимальным током среди трех фаз. Таким образом, ток звена постоянного тока I dc всегда колеблется между нулем и максимальным током нагрузки в каждом периоде переключения. При батарее, потребляющей почти постоянный входной ток I в , ток конденсатора шины постоянного тока I cap , видит высокочастотный пульсирующий переменный ток, который представляет собой разницу между I в и I в постоянном токе . При смоделированной выходной мощности 37,5 кВт, которая является постоянной мощностью испытанного двигателя, среднеквадратичное значение тока конденсатора составляет 80 А, а входной ток батареи составляет 130 А. Соотношение тока конденсатора шины постоянного тока I cap и постоянного тока входной ток I в оказался равным 61,5%.
В широкой заштрихованной области переключите S 5 остается включенным, но переключатель S 3 выключается, а переключатель S 6 включается. Это позволяет току нагрузки течь обратно в звено постоянного тока, т. е. ток звена постоянного тока равен току нагрузки, который является максимальным током среди трех фаз. Таким образом, ток звена постоянного тока I dc всегда колеблется между нулем и максимальным током нагрузки в каждом периоде переключения. При батарее, потребляющей почти постоянный входной ток I в , ток конденсатора шины постоянного тока I cap , видит высокочастотный пульсирующий переменный ток, который представляет собой разницу между I в и I в постоянном токе . При смоделированной выходной мощности 37,5 кВт, которая является постоянной мощностью испытанного двигателя, среднеквадратичное значение тока конденсатора составляет 80 А, а входной ток батареи составляет 130 А. Соотношение тока конденсатора шины постоянного тока I cap и постоянного тока входной ток I в оказался равным 61,5%. Можно легко спроектировать, чтобы показать, что при максимальной выходной мощности привода 75 кВт среднеквадратичное значение тока конденсатора составит 160 А.
Можно легко спроектировать, чтобы показать, что при максимальной выходной мощности привода 75 кВт среднеквадратичное значение тока конденсатора составит 160 А.
Рис. 3. Сигналы управления и входные постоянные токи инвертора.
Традиционно размер C dc выбирался произвольно. Для серийных тяговых электроприводов мощностью 75 кВт найдено значение от 15 мФ до 25 мФ с электролитическими конденсаторами. Философия конструкции с электролитическими конденсаторами большой емкости обычно унаследована от конструкции промышленных приводов, где C dc рассчитывается для сглаживания 6 th гармонические пульсации, вызванные линией электропередач. Согласно приведенному выше исследованию с помощью моделирования необходимость сглаживания 6-й гармоники -й -й больше не требуется, когда источником является жесткая аккумуляторная батарея, и критерий выбора конденсатора теперь должен быть сосредоточен на способности выдерживать ток, а не на пульсациях напряжения.
В дополнение к C dc есть еще несколько конденсаторов, которые традиционно используются в инверторе для борьбы с паразитными компонентами и проблемами переключения. На рис. 4 подробно показаны паразитные компоненты тягового электропривода. Пассивные компоненты, обведенные пунктиром на рис. 4, являются паразитными компонентами, которые не показаны на принципиальной схеме, но вызывают некоторые нежелательные эффекты при переключении.
Рис. 4. Полная схема тягового инвертора, включая необходимые конденсаторы и все паразитные индуктивности рассеяния.
В качестве примера возьмем паразитную индуктивность. Паразитная индуктивность существует между фазами L lk и всеми соединениями устройства. Эти индуктивности вызовут всплеск напряжения во время переключения устройств. Величина всплеска напряжения зависит от величины сосредоточенной паразитной индуктивности и скорости изменения тока. Ограничение по физическим размерам делает почти невозможным устранение паразитной индуктивности в инверторе большой мощности. Таким образом, снабберный конденсатор постоянного тока C dc-sn , обычно добавляется к верхней и нижней шинам постоянного тока на каждой фазе для локального подавления всплесков напряжения. Требования к C dc-sn — способность выдерживать высокие пиковые токи и чрезвычайно низкая индуктивность. В зависимости от компоновки и упаковки, сосредоточенная паразитная индуктивность находится в диапазоне от десятков до сотен нГн. Индуктивность рассеяния и его межблочная индуктивность С dc-sn должны быть не менее чем на порядок меньше сосредоточенной паразитной индуктивности; в противном случае это не поможет подавлению скачков напряжения.
Таким образом, снабберный конденсатор постоянного тока C dc-sn , обычно добавляется к верхней и нижней шинам постоянного тока на каждой фазе для локального подавления всплесков напряжения. Требования к C dc-sn — способность выдерживать высокие пиковые токи и чрезвычайно низкая индуктивность. В зависимости от компоновки и упаковки, сосредоточенная паразитная индуктивность находится в диапазоне от десятков до сотен нГн. Индуктивность рассеяния и его межблочная индуктивность С dc-sn должны быть не менее чем на порядок меньше сосредоточенной паразитной индуктивности; в противном случае это не поможет подавлению скачков напряжения.
Когда электролитические конденсаторы используются как C dc , вышеупомянутый C dc-sn неизбежен, поскольку паразитная индуктивность в электролите весьма значительна. Однако с использованием предложенного пленочного конденсатора с низкой индуктивностью и встроенной печатной платы принтера (печатной платы) из толстой меди также можно исключить демпфирующий конденсатор постоянного тока.
III. ХАРАКТЕРИСТИКИ КОНДЕНСАТОРОВ
Хотя критерии выбора в первую очередь основаны на возможностях пульсаций тока и низкой индуктивности. Существуют и другие важные функции, которые необходимо включить в приложения тягового привода. Ключевые особенности включают в себя:
- Диапазон рабочих температур от –55 °C до +105 °C.
- Диэлектрическая прочность (максимум): 650 В пост. тока испытано при 25 °C в течение 60 секунд.
- СОЭ (максимум): 0,003 Ом, испытано при 10 кГц, 25 °C
- E.S.L. (Типичный): 21 нГн
- Пиковый ток (Максимальный): 9818 А
- Среднеквадратичное значение тока: 207 А при 10 кГц, 25 °C и 147 А при 10 кГц, 85 °C
На рис. вышеописанные особенности. Ключевые особенности его механической конструкции:
- Пластина радиатора: нижняя алюминиевая пластина позволяет радиатору отводить тепло и поддерживать рабочую температуру конденсатора ниже максимальной температуры радиатора.
- Низкий профиль: прямоугольный блок имеет форм-фактор, аналогичный большинству мощных модулей IGBT, что позволяет значительно упростить компоновку шины постоянного тока, поскольку конденсатор и модули IGBT могут быть установлены на одной и той же пластине радиатора, чтобы избежать изгиба силовая шина.

- Шпильки повышенной прочности: Шпильки диаметром 5/8 дюйма изготовлены из меди с никелированным покрытием. Он обеспечивает непрерывный ток 200 А без значительного повышения температуры.
Рис. 5. Фотография сильноточного манипуляционного пленочного конденсатора.
На рис. 6 показана зависимость максимально допустимого тока конденсатора от рабочей частоты при температуре 55°C. Кривая показывает, что действующее значение номинального тока увеличивается с увеличением частоты. В источнике постоянного тока или инверторе с батарейным питанием конденсатор звена постоянного тока не должен выдерживать низкочастотные токи, но беспокоят высокочастотные пульсации. Разработанный пленочный конденсатор показывает допустимый ток более 200 А (среднеквадратичное значение) в диапазоне рабочих частот и температур и является желательным для конкретного применения в приводе тягового двигателя мощностью 75 кВт.
Рис. 6. Максимально допустимый ток.
6. Максимально допустимый ток.
На рис. 7 показано, что среднеквадратичное значение номинального тока конденсатора ухудшается с температурой точки перегрева. Следует отметить, что с помощью теплоотводящей пластины можно избежать горячих точек, а токовую способность можно поддерживать на желаемом уровне.
На рис. 8 показано сопротивление конденсатора в зависимости от частоты. Самая низкая точка импеданса — это резонансная частота, которая превращает характеристику конденсатора в характеристику катушки индуктивности. Любой высокочастотный шум или пульсирующие токи, особенно токи, связанные с электромагнитными помехами (EMI), не будут фильтроваться этим конденсатором звена постоянного тока. Таким образом, необходимо иметь дополнительные меньшие дифференциальные конденсаторы и синфазные конденсаторы для фильтрации шумовых токов, частота которых превышает 80 кГц.
Рис. 7. Номинальный ток в зависимости от точки перегрева.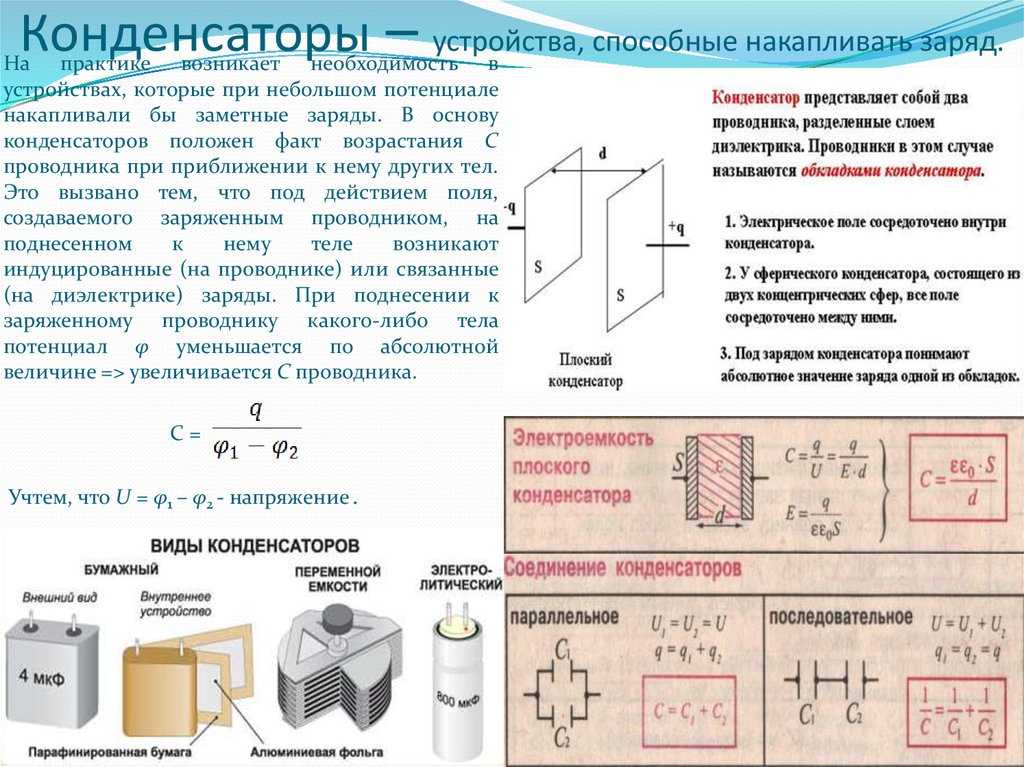
Рис. 8. Импеданс как функция частоты.
На рис. 9 показан ожидаемый срок службы конденсатора звена постоянного тока. Инверторы привода тяговых двигателей обычно работают при температуре окружающей среды или радиатора 65°C. При повышении температуры от 10 до 15 °C ожидаемый срок службы сокращается примерно вдвое, или до 100 000 часов. Такой срок службы Cy по-прежнему намного выше, чем у электролитических конденсаторов, срок службы которых обычно составляет всего 10 000 часов. Фактически срок службы разработанного пленочного конденсатора намного превышает срок службы транспортного средства [2].
Рис. 9. Ожидаемая продолжительность жизни в зависимости от температуры.
IV. ИНВЕРТОР НА ОСНОВЕ НИЗКОИНДУКТИВНОГО КОНДЕНСАТОРА И РЕЗУЛЬТАТЫ ЭКСПЕРИМЕНТОВ
На рис. 10 представлена фотография инвертора мощностью 75 кВт на полностью пленочных конденсаторах, реализующего схему, показанную на рис. обычная силовая шина. Все необходимые конденсаторы крепятся на печатной плате либо шпильками, либо пайкой. Заметил, что С dc-sn и C CM являются готовыми продуктами, и их номинальное напряжение не оптимизировано. Ключом к этому блоку является конденсатор звена постоянного тока C dc , специально изготовленный для работы с большими токами в условиях высокой рабочей температуры. Он имеет опорную пластину, которая позволяет устанавливать радиатор для удобного управления температурой.
обычная силовая шина. Все необходимые конденсаторы крепятся на печатной плате либо шпильками, либо пайкой. Заметил, что С dc-sn и C CM являются готовыми продуктами, и их номинальное напряжение не оптимизировано. Ключом к этому блоку является конденсатор звена постоянного тока C dc , специально изготовленный для работы с большими токами в условиях высокой рабочей температуры. Он имеет опорную пластину, которая позволяет устанавливать радиатор для удобного управления температурой.
Рис. 10. Фотография инвертора в сборе.
На рис. 11 показаны кривые экспериментального выходного тока инвертора и тока конденсатора звена постоянного тока при выходной нагрузке 13,7 кВт. Выходной ток нагрузки представляет собой коммутационные пульсации 10 кГц поверх синусоидальной волны. При напряжении на шине постоянного тока 217 В измеренный входной постоянный ток и ток конденсатора составляют 69А и 42,3 А соответственно. Соотношение I cap и I в составляет 61,3%, что согласуется с результатами моделирования.
Соотношение I cap и I в составляет 61,3%, что согласуется с результатами моделирования.
Рис. 11. Экспериментальный выход инвертора и токи конденсаторов шины постоянного тока.
На рис. 12 показан экспериментальный ток конденсатора звена постоянного тока в расширенном временном масштабе. Верхняя кривая верхнего окна показывает ток конденсатора в течение 2/3 основного цикла, а верхняя кривая нижнего окна показывает ток конденсатора в течение двух циклов переключения. Конденсатор заряжается, когда все верхние выключатели инвертора включены; он разряжается при включении одного верхнего переключателя и включении хотя бы одного нижнего переключателя. Форма волны тока конденсатора очень хорошо согласуется с смоделированным результатом.
Рис. 12. Экспериментальный ток конденсатора шины постоянного тока.
Ток конденсатора зависит от различных условий тока нагрузки. На рис. 13 показаны измеренные значения тока конденсатора шины постоянного тока в зависимости от входного постоянного тока. Как правило, в этом приводе тягового двигателя на базе асинхронной машины среднеквадратичное значение тока пульсаций конденсатора шины постоянного тока составляет приблизительно 61% от входного постоянного тока. Этот процент согласуется с результатами моделирования, показанными на рис. 2 и 3. Результат дает хорошее представление о конструкции конденсатора звена постоянного тока. При использовании инвертора мощностью 75 кВт, 300 В в качестве проектной цели необходим конденсатор звена постоянного тока с допустимой нагрузкой по току 150 А при рабочей температуре 65 °C.
На рис. 13 показаны измеренные значения тока конденсатора шины постоянного тока в зависимости от входного постоянного тока. Как правило, в этом приводе тягового двигателя на базе асинхронной машины среднеквадратичное значение тока пульсаций конденсатора шины постоянного тока составляет приблизительно 61% от входного постоянного тока. Этот процент согласуется с результатами моделирования, показанными на рис. 2 и 3. Результат дает хорошее представление о конструкции конденсатора звена постоянного тока. При использовании инвертора мощностью 75 кВт, 300 В в качестве проектной цели необходим конденсатор звена постоянного тока с допустимой нагрузкой по току 150 А при рабочей температуре 65 °C.
Рис. 13. Измеренный ток конденсатора звена постоянного тока в зависимости от входного постоянного тока.
Всплеск напряжения из-за переключения устройств и паразитной индуктивности можно свести к минимуму за счет хорошей компоновки схемы и конденсаторов звена постоянного тока с низкой индуктивностью. В традиционной компоновке на основе медных стержней с электролитическим конденсатором с высоким ESL в качестве конденсатора шины постоянного тока скачок напряжения составляет более 30% от напряжения на шине постоянного тока. С использованием многослойной печатной платы в качестве силовой шины и комбинации высокочастотного конденсатора шины постоянного тока C dc и демпферный конденсатор постоянного тока C dc-sn , всплески напряжения значительно уменьшаются. На рис. 14 показаны экспериментальные результаты с различными конфигурациями C dc и C dc-sn .
В традиционной компоновке на основе медных стержней с электролитическим конденсатором с высоким ESL в качестве конденсатора шины постоянного тока скачок напряжения составляет более 30% от напряжения на шине постоянного тока. С использованием многослойной печатной платы в качестве силовой шины и комбинации высокочастотного конденсатора шины постоянного тока C dc и демпферный конденсатор постоянного тока C dc-sn , всплески напряжения значительно уменьшаются. На рис. 14 показаны экспериментальные результаты с различными конфигурациями C dc и C dc-sn .
На рис. 14(а) показано, что при работе схемы без C dc-sn , но с вышеупомянутым сильноточным малоиндуктивным C dc выброс напряжения составляет 56 В или 14 % от напряжения на шине постоянного тока. напряжение, которое составляет 400 В. На рис. 14(b) показаны результаты с C dc + C DC-SN . C dc-sn состоит из двух соединенных параллельно высокочастотных пленочных конденсаторов емкостью 1 мкФ [5]. Каждый используемый здесь демпферный конденсатор имеет удлиненные, но приспособленные площадки, которые можно установить на модуль IGBT. Всплеск напряжения при такой конфигурации падает до 38 В или 9,5%. На рис. 14(c) снова показаны результаты испытаний с C dc + C dc-sn , но C dc-sn не имеет соединительной площадки. Вместо этого он имеет набор монтажных отверстий, что позволяет монтировать конденсатор непосредственно поверх модуля IGBT [6], как показано на рис. 10. Значение емкости этого прямого монтажа C dc-sn составляет 2 мкФ, а результирующее перенапряжение дополнительно снижается до 30 В или 7,5%. Сравнение результатов этих испытаний указывает на значимость компоновки и снижения паразитной индуктивности для снижения выбросов напряжения.
Каждый используемый здесь демпферный конденсатор имеет удлиненные, но приспособленные площадки, которые можно установить на модуль IGBT. Всплеск напряжения при такой конфигурации падает до 38 В или 9,5%. На рис. 14(c) снова показаны результаты испытаний с C dc + C dc-sn , но C dc-sn не имеет соединительной площадки. Вместо этого он имеет набор монтажных отверстий, что позволяет монтировать конденсатор непосредственно поверх модуля IGBT [6], как показано на рис. 10. Значение емкости этого прямого монтажа C dc-sn составляет 2 мкФ, а результирующее перенапряжение дополнительно снижается до 30 В или 7,5%. Сравнение результатов этих испытаний указывает на значимость компоновки и снижения паразитной индуктивности для снижения выбросов напряжения.
Рис. 14. Выброс напряжения при отключении устройства: (а) с C dc , но без C dc-sn ; (б) с C dc и 2 × 1 мкФ C dc-sn . (б) с C dc и низкомк C dc-sn .
(б) с C dc и низкомк C dc-sn .
В таблице 1 сравниваются пики напряжения в трех различных конфигурациях. Первая конфигурация относится к нашей конструкции инвертора первого поколения с тремя электролитическими конденсаторами емкостью 4700 мкФ и традиционной компоновкой медных шин. Его скачок напряжения составляет более 33 % при номинальном напряжении и токе. Поскольку этот всплеск напряжения слишком велик, он не тестировался в условиях 400 В. Вторая конфигурация заключается в использовании рекомендуемого сильноточного пленочного конденсатора с малой индуктивностью. Результат показывает 15% при номинальном напряжении и токе. Условия испытаний были расширены до напряжения шины 400 В, и всплеск напряжения не превышал номинального напряжения конденсатора. Последняя конфигурация заключается в добавлении 2-мкФ C dc-sn поверх IGBT, скачок напряжения был снижен до уровня менее 8%.
Таблица 1. Сравнение всплесков напряжения с различными конденсаторами звена постоянного тока
В таблице 2 сравниваются всплески напряжения с одним и тем же конденсатором C dc емкостью 200 мкФ, но с тремя различными конфигурациями C dc 900sn. Первая конфигурация имеет только один конденсатор на 1 мкФ. Результирующий скачок напряжения составляет 11,5%. Вторая конфигурация имеет два параллельно установленных конденсатора емкостью 1 мкФ, и результирующий всплеск напряжения уменьшен до 9.5%. Последняя конфигурация заключается в добавлении сквозного монтажа 2-мкФ C dc-sn поверх IGBT, а скачок напряжения был снижен до 30 В или 7,5%.
Первая конфигурация имеет только один конденсатор на 1 мкФ. Результирующий скачок напряжения составляет 11,5%. Вторая конфигурация имеет два параллельно установленных конденсатора емкостью 1 мкФ, и результирующий всплеск напряжения уменьшен до 9.5%. Последняя конфигурация заключается в добавлении сквозного монтажа 2-мкФ C dc-sn поверх IGBT, а скачок напряжения был снижен до 30 В или 7,5%.
Таблица 2. Сравнение всплесков напряжения с различными демпфирующими конденсаторами sc
и многослойная компоновка печатной платы, производительность уже выдающаяся. Судя по таблицам 1 и 2, уменьшение выброса напряжения за счет замены электролитического конденсатора предлагаемым высокочастотным пленочным конденсатором является достаточно значительным, поэтому дальнейшее снижение выброса напряжения от снаббер-конденсатора постоянного тока может не понадобиться. Из соображений производительности предпочтительно дальнейшее снижение скачков напряжения, но из соображений стоимости оказывается, что C dc-sn можно исключить.![]()
V. ВЫВОДЫ
В работе продемонстрировано использование малоиндуктивных сильноточных пленочных конденсаторов в мощном инверторе для приводов тяговых электродвигателей с батарейным питанием. Как смоделированные, так и экспериментальные формы сигналов тока конденсатора звена постоянного тока инвертора с пространственно-векторной модуляцией показывают, что конденсатор должен выдерживать высокочастотный ток со среднеквадратичным значением примерно 61% от среднего тока звена постоянного тока. Хотя этот процент отличается для разных машин и разных схем модуляции, его величина всегда нетривиальна в большинстве приводных систем инвертор-двигатель. Очевидно, что с таким высоким током, протекающим в конденсаторе постоянного тока, традиционная конструкция с использованием электролитического конденсатора не только громоздка по размеру, но и неадекватна по току.
В результате тщательного компьютерного моделирования и проверки аппаратной реализации можно сделать несколько выводов:
- Выбор конденсатора шины постоянного тока должен основываться на способности выдерживать ток, а не на пульсациях напряжения в инверторной приводной системе с батарейным питанием.
 Таким образом, традиционная конструкция, использующая несколько громоздких электролитических конденсаторов, может быть полностью заменена одним сильноточным пленочным конденсатором. №
Таким образом, традиционная конструкция, использующая несколько громоздких электролитических конденсаторов, может быть полностью заменена одним сильноточным пленочным конденсатором. № - Сильноточный пленочный конденсатор удовлетворяет не только требованиям по току пульсаций, но и ожидаемому сроку службы, необходимому для привода тягового двигателя.
- Сильноточный пленочный конденсатор имеет низкую индуктивность, что позволяет существенно снизить выбросы напряжения при переключении устройства.
- Благодаря конструкции силовой шины с малой индуктивностью и использованию пленочного конденсатора шины постоянного тока с низкой индуктивностью можно отказаться от демпфирующего конденсатора постоянного тока, что позволяет увеличить размер и снизить стоимость.
БЛАГОДАРНОСТЬ
Авторы хотели бы поблагодарить доктора Чарльза Э. (Бада) Конрада из VPT Inc. и г-на Джеймса А. Мерритта из Министерства энергетики США (DOE) за их решительную поддержку в рамках программы DOE Cooperative Automotive. Программа исследований в области передовых технологий (CARAT).
Программа исследований в области передовых технологий (CARAT).
ССЫЛКИ
[1] И. В. Клелланд, «Последние достижения в технологии конденсаторов с применением высокочастотной силовой электроники и преобразования напряжения», в конференции. Рек. конференции IEEE по прикладной силовой электронике, Даллас, Техас, март 1999 г., стр. 685–691. Рек. конференции специалистов по силовой электронике IEEE, Бавено, Италия, июнь 1996 г., стр. 432–437.
[3] Nichicon, Каталог электронных компонентов, CAT8100L, 1998.
[4] Т. Нергаард, Дж. С. Лай, Х. Коунс, К. Э. Конрад, «Оптимальная системная эффективность работы асинхронного двигателя», будет представлено на Ежегодном собрании IEEE IAS, октябрь 2002 г.
[5 ] https://www.eccaps.com/ECI_LOHENRY.htm, Electronic Concepts MP88 — Спецификация металлизированного полипропиленового IGBT-конденсатора.
[6] https://www.ecicaps.com/ECI_MP80.htm, Электронные концепции MP80 Металлизированный полипропиленовый IGBT монтируемый конденсатор.
Конденсаторы в цепях переменного и постоянного тока
Хотите создать сайт? Найдите бесплатные темы и плагины WordPress.
Конденсаторы в цепях постоянного токаКогда конденсатор помещается в замкнутую цепь постоянного тока (течет ток), он начинает заряжаться. Зарядка — это когда напряжение на пластинах быстро нарастает, чтобы сравняться с напряжением источника. Как только конденсатор достигает своего полностью заряженного состояния, ток прекращается.
После отключения заряженного конденсатора от цепи он остается заряженным. до разрядить конденсатор, его нужно будет поместить в замкнутую цепь без источника напряжения. В большинстве случаев провод используется для соединения двух концов конденсатора для быстрой разрядки. Однако это опасно, и при разрядке конденсатора следует соблюдать осторожность.
RC-цепи или резисторно-конденсаторные цепи являются основным типом схем. Зарядка или разрядка конденсатора требует времени, и разные конденсаторы имеют разное время зарядки. Постоянная времени RC — фиксированный временной интервал, равный произведению сопротивления на емкость в последовательной RC-цепи. Постоянная времени определяет скорость зарядки/разрядки конденсатора. Смотрите следующее уравнение:
Зарядка или разрядка конденсатора требует времени, и разные конденсаторы имеют разное время зарядки. Постоянная времени RC — фиксированный временной интервал, равный произведению сопротивления на емкость в последовательной RC-цепи. Постоянная времени определяет скорость зарядки/разрядки конденсатора. Смотрите следующее уравнение:
R — сопротивление,
C — емкость,
τ — постоянная времени RC
Конденсаторы в цепях постоянного тока Пример 1Найдите постоянную времени для следующей RC-цепи: резистор 500 Ом и конденсатор 20 мкФ.
Подставьте значения в уравнение.
\[\tau =500\text{ }\Omega \text{ }\times \text{ }20\text{ }\mu F\]
Решить. Единицей постоянной времени являются секунды.
\[\mathbf{\tau }\text{ }=0,01\text{ }s\]
Конденсаторы в цепях постоянного тока Пример 4 4002 Если резистор 3,5 кОм соединить с конденсатором 0,5 мкФ, какой будет постоянная времени?
Умножьте сопротивление и емкость.
\[\mathbf{\tau }\text{ }=3500\text{ }\Omega \text{ }\times .5\text{ }\mu F\]
Решить.
\[\text{ }\tau \text{ = 0}\text{.00175 с или 1}\text{.75 мс}\]
Зарядка и разрядка конденсатора на графике нелинейны . Он имеет экспоненциальную кривую зарядки и разрядки. См. рис. 1 для кривой зарядки.
Рисунок 1 Напряжение конденсатора RC серии
Обратите внимание, что график разбит на пятикратные постоянные. За пять постоянных времени конденсатор достигает 99% (с округлением до 100%) заряда или разряда. Время переходного процесса — пятикратная константа времени или время полной зарядки/разрядки конденсатора.
Для расчета зарядного/разрядного напряжения и тока конденсатора используйте следующие уравнения:
\[\begin{matrix} \mathbf{v}\text{ }=\text{ }{{\mathbf{V}} _{\mathbf{F}}}+\text{ }\left( {\mathbf{V}}_{\mathbf{i}}}\text{ – }{{\mathbf{V}}_{\ mathbf{F}}} \right)\text{ }. {t}/{}_{RC}}} \right) & {} & \left( 3 \right) \\\end{ матрица}\]
{t}/{}_{RC}}} \right) & {} & \left( 3 \right) \\\end{ матрица}\]
Где,
V — мгновенное напряжение,
V F — окончательное напряжение
E — экспоненциальное число
T —
τ
T
τ0004. . stist.
Конденсаторы в цепях постоянного тока Пример 3Через 2 секунды какое напряжение заряжено в RC-цепи: резистор 200 Ом, конденсатор 4 мкФ и источник напряжения 6 В (см. рис. 2).
Рисунок 2 Схема цепи с резистором, подключенным к конденсатору и источнику постоянного напряжения } \ Omega \ times \ text {} 4 \ text {} \ mu f \ right)} \]
Использование показателя, рассчитайте, что внутри ()
1 -E -2500
Умножьте, что на источник напряжения (конечное напряжение.)
6 В x 1
Решить.
v = 6 В
Конденсаторы в цепях постоянного тока Пример 4конденсатор (см. рис. 3). Чему равен заряд конденсатора?
Рис. 3: Схема цепи Напряжение постоянного тока, подключенное к RC-цепи
Найти показатель степени ( Уравнение 3 )
\[-\frac{0.5}{\left( 3500\text{ }\Omega \times \text{ }15\text{ }\mu F \right)}~\]
Вычислить, что внутри ( )
1 – e -9,5238
Умножить на конечное напряжение.
9 В x 0,9999
Решить.
v = 8,999 В
Расчет разрядки аналогичен расчету зарядки, но уравнение другое. Поскольку разрядка заканчивается на нуле, уравнение упрощается до: 9{t}}{{/}_{RC}}}} \right) & {} & \left( 4 \right) \\\end{matrix}\]
Где
v — мгновенное напряжение ,
V I — начальное напряжение
E — экспоненциальное число
T IS Time
τ — постоянная времени
в DC Circuits. Конденсатор, заряженный до 5 В, разряжается за 0,2 секунды. Конденсатор рассчитан на 5 мкФ, а резистор на 1000 Ом. Конденсатор полностью разряжен?
Конденсатор, заряженный до 5 В, разряжается за 0,2 секунды. Конденсатор рассчитан на 5 мкФ, а резистор на 1000 Ом. Конденсатор полностью разряжен?Вычислить показатель степени ( Уравнение 4 )
\[-\frac{0.2}{\left( 1000\text{ }\Omega \times \text{ }5\text{ }\mu F \right)} \]
Подставьте значения.
5 В x e -40
Найти остаточное напряжение.
2,124 x 10 -17 В
Поскольку оставшееся напряжение практически равно нулю, конденсатор разряжен.
Конденсаторы в цепях постоянного тока Пример 6Конденсатор емкостью 35 мкФ имеет заряд 10 В. Если его подключить к резистору 2 кОм на 0,1 секунды, каков оставшийся заряд?
Найти показатель степени ( Уравнение 4 )
\[-\frac{0.1}{\left( 2000\text{ }\Omega \times \text{ }35\text{ }\mu F \right)} \]
Подставьте значения.
10 В x e -1,4286
Решить.
v = 2,397 В
На рис. 4 показано влияние конденсатора на прямоугольную волну. Вместо пульсации волна медленно заряжается до максимального значения. Затем он медленно разряжает напряжение, а не падает до нуля.
Рис. 4 Конденсатор прямоугольной формы при зарядке-разрядке
Конденсаторы в цепях переменного тока Конденсаторы в цепях переменного тока сложнее, чем в цепях постоянного тока. Это связано с переменным током. В цепях переменного тока конденсаторы сопротивляются току. емкостное реактивное сопротивление — это конденсатор, сопротивляющийся синусоидальному току и обозначенный X C . Поскольку он сопротивляется потоку тока, единицей измерения емкостного сопротивления является ом. Это зависит как от частоты, так и от емкости, см. следующее уравнение:
следующее уравнение:
\[\begin{matrix} {{X}_{C}}=\frac{1}{2\text{ }\pi fC} & {} & \left( 5 \right) \\\end{matrix}\]
X C — емкостное сопротивление (Ом),
f — частота (Гц)
C — емкость (Ф).
Конденсаторы в цепях переменного тока Пример 7Конденсатор емкостью 8 мкФ подключен к с рабочим напряжением 6 В и частотой 400 Гц (см. рис. 5). Что такое емкостное сопротивление?
Рисунок 5 Схема цепи с одним конденсатором, подключенным к источнику переменного напряжения \text{ }Hz\text{ }\times \text{ }8\text{ }\mu F\]
Затем разделите единицу на то, что вы вычислили.
\[\frac{1}{0.02011}\]
Решить. 6 В среднеквадратичное значение не имело значения для решения емкостного реактивного сопротивления.
X C =49,74 Ом
Конденсаторы в цепях переменного тока Пример 8реактивное сопротивление быть? 9Рисунок 6
Схема цепи переменного напряжения, подключенного к одному конденсатору \text{ }\times \text{ }60\text{ }\mu F\] Единица, деленная на знаменатель.
\[\frac{1}{1.13097}\]
Решить.
X C =0,884 Ом
Всякий раз, когда конденсаторы соединены последовательно и подается переменный ток, емкостное сопротивление каждого конденсатора ведет себя так же, как резисторы. X C суммируется для последовательно включенных конденсаторов. См. следующее уравнение: {C1}}}+\text{ }{{\mathbf{X}}_{\mathbf{C2}}}+\text{ }{{\mathbf{X}}_{\mathbf{C3}}}+ \ldots .+\text{ }{{\mathbf{X}}_{\mathbf{Cn}}}\]
Конденсаторы в цепях переменного тока Пример 9Источник напряжения имеет частоту 700 Гц и два конденсатора номиналом 2 мкФ и 0,03 мкФ соединены последовательно (см. рис. 7). Чему равно полное емкостное сопротивление?
Рисунок 7 Принципиальная схема источника переменного напряжения с двумя последовательными конденсаторами
Рассчитайте емкостное реактивное сопротивление для обоих конденсаторов.
\[{{X}_{C1}}=\frac{1}{2\text{ }\pi \times 700\text{ }Hz\text{ }\times 2\text{ }\mu F} ~~=113.68\Omega\]
\[{{X}_{C2}}=\frac{1}{2\text{ }\pi \times 700\text{ }Hz\times .03\text{ }\mu F}~=7578.81\Omega \]
Сложите их вместе, чтобы получить X C (всего)
\[{{\mathbf{X}}_{\mathbf{C}\left( Total \right)}}=113,68\Omega +\text{ }7578.81\Omega =\text{ }7692.49\Omega \]
Поскольку емкостное реактивное сопротивление действует так же, как резисторы, при параллельном подключении конденсаторов емкостное реактивное сопротивление рассчитывается по следующей формуле:
Уравнение для расчета полного емкостного сопротивления 3 или более конденсаторов параллельно
9{1}/{}_{{{\mathbf{X}}_{\mathbf{C}n}}}}\]Для двух конденсаторов можно использовать следующее уравнение:
\[{{\ mathbf{X}}_{C\left( Total \right)}}=\frac{{{\mathbf{X}}_{\mathbf{C1}}}\times {{\mathbf{X}}_{ \mathbf{C2}}}}{{{\mathbf{X}}_{\mathbf{C1}}}+\text{ }{{\mathbf{X}}_{\mathbf{C2}}}}\ ]
Конденсаторы в цепях переменного тока Пример 10Каково емкостное сопротивление для следующей цепи (рисунок 8), конденсаторы 4 мкФ и 0,06 мкФ, подключенные параллельно к источнику напряжения, имеющему 900 Гц частота?
Рисунок 8 Схема подключения двух конденсаторов, подключенных параллельно к источнику переменного напряжения
Найдите реактивное сопротивление емкости для каждого конденсатора.
\[{{X}_{C1}}=\frac{1}{2\text{ }\pi \times 900\times 4\text{ }\mu F}=44.21\Omega \]
\ [{{X}_{C2}}=\frac{1}{2\text{ }\pi \times 900\times 0,06\text{ }\mu F}=2947,31\Omega \]
Вычислите сумму.
\[{{X}_{C(Всего)}}=\frac{44.21\Omega \text{ }\times \text{ 2947}\text{.31}\Omega }{44.21\Omega \text{ + 2947}\text{.31}\Omega }=43.56\Omega \]
Закон Ома по-прежнему применяется для определения схемы. В конденсаторах вместо сопротивления используется емкостное сопротивление (хотя в основном они одинаковы). Таким образом, уравнение выглядит так:
\[\begin{align} & I=\frac{V}{{{X}_{C}}} \\ & V=I{{X}_{C}} \\\end{align}\]
Конденсаторы в цепях переменного тока Пример 11Какой ток при 6 В rms с частотой 2 кГц подается на конденсатор 0,2 мкФ (см. рис. 9)?
Рис. 9 Принципиальная схема одного конденсатора, подключенного к источнику переменного напряжения
Вычислите X C .
\[\frac{1}{2\text{ }\pi \times 2000\text{ }Hz\text{ }\times \text{ }.2\text{ }\mu F}\]
Текущий напряжение на X C .
\[\frac{6\text{ }V}{397.89\Omega }\]
Решить. Имейте в виду, является ли это среднеквадратичным значением, значением pp или p.
I =0,015 A rms
Ранее напряжение на одном конденсаторе рассчитывалось с использованием емкости. Вы можете добиться тех же результатов, используя емкостное реактивное сопротивление. См. следующее уравнение:
\[{{V}_{x}}=\left( \frac{{{X}_{Cx}}}{{{X}_{C(total)}}} \ right){{V}_{s}}\]
Где X Cx — емкостное реактивное сопротивление конденсатора с неизвестным напряжением.
Конденсаторы в цепях переменного тока Пример 12 Каково напряжение на конденсаторе емкостью 4 мкФ, соединенном последовательно с конденсатором емкостью 0,75 мкФ, с источником напряжения 6 В, , среднеквадратичное значение, , и частотой 850 Гц (см. рисунок 10). ).
рисунок 10). ).
Рисунок 10 Принципиальная схема двух последовательно соединенных конденсаторов с источником переменного напряжения
Рассчитайте X C для конденсаторов.
\[\begin{align} & {{X}_{C1}}=\text{ }\frac{1}{2\text{ }\pi \times 850\text{ }Hz\times 4\text { }\mu F}=46,81\Omega \\ & {{X}_{C2}}=\text{ }\frac{1}{2\text{ }\pi \times 850\text{ }Hz\times 0,75\текст{ }\мкФ}=249.65\Omega \\ & {{X}_{C\left( Total \right)}}=46,81\Omega +249,65\Omega =296,46\Omega \\\end{align}\]
Подставьте значения в уравнение.
\[{{V}_{x}}=\frac{46,81\Omega }{296,46\Omega }\times 6\text{ }{{V}_{rms}}=0,947{{V}_{ rms}}\]
Мгновенная мощность – это произведение мгновенного тока на мгновенное напряжение. Это позволяет вам видеть мощность в любой точке, если известны ток и напряжение.
В идеале вся энергия должна быть сохранена, а затем возвращена в цепь.


 д.с.,В
д.с.,В Для этого нажмите синхронно кнопку «Старт» и кнопку запуска секундомера и через 5 секунд нажатием кнопки «Стоп» остановите процесс разрядки конденсатора.
Для этого нажмите синхронно кнопку «Старт» и кнопку запуска секундомера и через 5 секунд нажатием кнопки «Стоп» остановите процесс разрядки конденсатора. 4. Полезный совет: для расчёта Q воспользуйтесь программой MS Exсel.
4. Полезный совет: для расчёта Q воспользуйтесь программой MS Exсel.
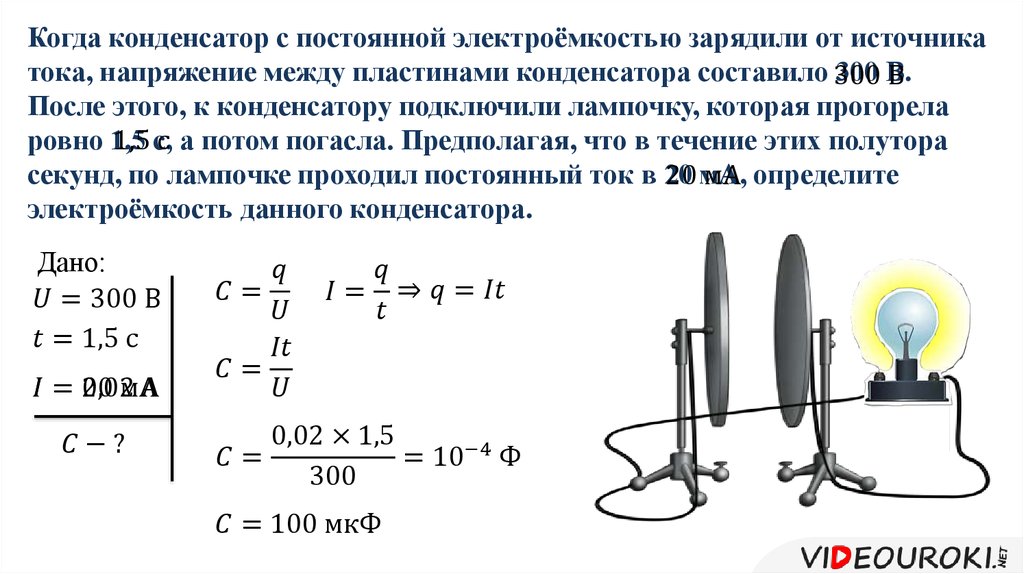



 Таким образом, традиционная конструкция, использующая несколько громоздких электролитических конденсаторов, может быть полностью заменена одним сильноточным пленочным конденсатором. №
Таким образом, традиционная конструкция, использующая несколько громоздких электролитических конденсаторов, может быть полностью заменена одним сильноточным пленочным конденсатором. №