влияние на переменный и постоянный ток, формулы для расчета

Обновлено: 22.06.2023

Чем больше частота переменного тока, тем лучше пропускает конденсатор ток (тем меньше сопротивление конденсатора переменному току).

Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и емкостной нагрузкой. Такая нагрузка наз. реактивной.

Индуктивное сопротивление в цепи переменного тока

В катушке, включенной в цепь переменного напряжения, си­ла тока меньше силы тока в цепи постоянного напряжения для этой же катушки. Следовательно, катушка в цепи переменного напряжения создает большее сопротивление, чем в цепи посто­янного напряжения.

Мгновенное значение силы тока:

Мгновенное значение напряжения можно установить, учиты­вая, что u = — ε_i , где u — мгновенное значение напряжения, а ε_i — мгновенное значение эдс самоиндукции, т. е. при изменении тока в цепи возникает ЭДС самоиндукции, которая в соответствии с законом электромагнитной индукции и правилом Ленца равна по величине и противоположна по фазе приложенному напряжению.

Следовательно , где амплитуда напряжения.

Напряжение опережает ток по фазе на π/2.

Т.к. согласно закону Ома сила тока прямо пропорциональна напряжению и обратно пропорциональная сопротивлению, то приняв величину ωL за сопротивление катушки переменному току, получим: — закон Ома для цепи с чисто индуктивной нагрузкой.

Величина — индуктивное сопротивление.

Т.о. в любое мгновение времени изменению силы тока противодействует ЭДС самоиндукции. ЭДС самоиндукции — причина индуктивного сопротивления.

В отличие от активного сопротивления, индуктивное не является характеристикой проводника, т.к. зависит от параметров цепи (частоты): чем больше частота переменного тока, тем больше сопротивление, которое ему оказывает катушка.

Т.к. разность фаз между колебаниями тока и напряжения равна π/2, то мощность в цепи равна 0: энергия не расходуется, а происходит обмен энергией между источником напряжения и индуктивной нагрузкой. Такая нагрузка наз. реактивной.

При проектировании электрический цепей, оборудования и электроприборов учитываются многие свойства проводников. Одним из важных свойств считается емкостное сопротивление.

В данной статье будет подробно описано — что такое емкостное сопротивление конденсатора. Так же будет приведена формула расчета такого параметра, описана работа конденсатора в цепи переменного тока и сферы применения ёмкостного сопротивления.

Определение

Сопротивлением называют физический эффект противодействия протеканию тока по любой электрической цепи. Этим свойством обладают все проводники электрического тока. Данная величина измеряется в Ом.

Емкостное электрическое сопротивление является величиной, благодаря которой можно понять, что в цепи присутствует конденсатор. Емкостные сопротивления конденсатора рассчитываются только для цепей переменного тока, без учета наличия в них резисторов.

Конденсатор обозначается на схеме буквой «С», а его ёмкостное сопротивление «Xc».

Принцип работы

Конденсатор с определенной ёмкостью работает по принципу периода, который состоит из заряда и разряда элемента. Период делится на 4 части:

1. Первая часть предполагает рост напряжения. В этот момент сопротивление конденсатора минимально, а зарядный ток очень высокий.
2. Во второй четверти происходит наполнение его ёмкости за счет зарядного тока.
3. В третьей четверти конденсатор полностью заряжается, при этом происходит снижение тока вплоть до 0. ЭДС возрастает с эффектом смены своей направленности.
4. В последней четверти происходит разряд элемента. На этом этапе ЭДС будет в пределах 0, а ток постепенно нарастать.

Все описанные процессы за один период определяют дальнейший фазный сдвиг на 90 градусов.

Природа возникновения емкостного сопротивления полностью зависит от нескольких факторов:

1. Обязательно наличие конденсатора в цепи.
2. По цепи должен течь только переменный ток.
3. Сопротивление проводника должно быть меньше емкости конденсатора.

Все эти факторы помогают рассчитать наиболее правильное значение ёмкостных характеристик для наиболее эффективной работы электроцепи.

Расчет

Расчет электрического емкостного сопротивления цепи делается по формуле. Она состоит из следующих значений:

1. «Xc» — является емкостным сопротивлением в Омах.
2. «1» — период полного заряда и разряда элемента.
3. «w» — круговая частота переменного тока с емкостью, рад/сек.
4. «C» — емкость конденсатора, единицы измерения Фарад.

Сама формула при этом выглядит следующим образом:

При помощи этой формулы легко рассчитывается Xc. Для этого требуется просто умножить циклическую частоту переменного тока на известную величину емкости конденсатора. Далее необходимо будет один период разделить на полученное значение. Таким образом можно всегда найти сопротивление конденсатора в Ом.

Рассчитываться емкостное сопротивление может так же с помощью и другой формулы, которая приведена на рисунке ниже.

При расчетах по данной формуле прослеживаются следующие зависимости:

1. Емкость конденсатора и частота тока всегда выше сопротивления.
2. От величин емкости и частоты зависит скорость одного периода заряда/разряда конденсатора.

Также стоит учесть, что после подключения конденсатора в цепь постоянного тока, его сопротивление сильно увеличивается. Объясняется причина такого явления довольно просто — отсутствует частота протекания электричества.

Характеристики элемента

Для того чтобы понять, что такое емкостное сопротивление, необходимо разобраться с его основной характеристикой, которая называется емкостью. Емкостью называется накопительная способность элемента. Она заключается в накоплении определенной доли электрического тока за определённый промежуток времени. Единицей измерения этой величины является Фарад (Ф или F).

Элемент заряжается электричеством до определенного момента, после которого он начинает разряжаться и отдавать ток дальше по электроцепи. Время полного разряда напрямую зависит от величины сопротивления цепи. Чем выше это значение, тем меньше времени тратится на разрядку элемента. Для расчета ёмкостной характеристики используется следующее выражение:

Так же конденсаторы обладают рядом дополнительных характеристик. К ним относят:

1. Общую удельную емкость. Является отношением массы диэлектрических пластин и емкостных параметров.
2. Напряжение. Параметр определяется как рабочее напряжение, которое способен выдержать элемент.
3. Температурная стойкость или стабильность. Это температурный параметр, который не влияет на изменение емкости.
4. Изоляционное сопротивление. Является величиной точки утечки и саморазряда.
5. Эквивалентная нагрузка. Значение, определяющее потери на выводе или контактах устройства.
6. Абсорбция. Разность потенциалов в момент разряда до 0.
7. Полярность. Параметр свойственен элементам, которые работают строго при подаче на обкладку потенциала определенного значения (плюс или минус).
8. Индуктивность. Свойство конденсатора образовывать на контактах индуктивное сопротивление. Такое свойство может наделить элемента параметрами колебательного контура.

Все эти значения строго учитываются при проектировании цепей или схем электрического оборудования.

Импеданс

Кроме емкостного, конденсатор еще имеет общее сопротивление или импеданс. Данное значение определяется с учетом значений трех параметров: индуктивного, резистивного и емкостного сопротивления.

Для вычисления импеданса применяется следующая формула:

В данном выражении используются следующие сопротивления:

1. xL — индуктивное;
2. xC — емкостное;
3. R — активное.

Активное сопротивление цепи появляется вследствие возникновения в ней ЭДС. Так как переменный ток по своей природе импульсный, то электромагнитный поток может довольно незначительно изменяться, а это приводит к сдвигу постоянного значения ЭДС.

Емкостные и индуктивные величины взаимосвязаны.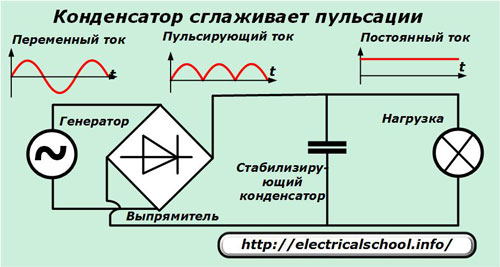 По разнице между ними легко находят реактивную составляющую цепи.

Отсюда легко проследить, от чего зависит само реактивное сопротивление:

1. Если реактивная величина больше 0, то устройство больше нагружено индуктивным значением.
2. Если реактивное значение равно 0, то емкость не нагружается активным сопротивлением.
3. Если реактивность меньше 0, то элемент имеет высокое емкостное сопротивление.

Активное сопротивление считается невосполнимой величиной. Она тратится на преобразование тока в иной вид энергии. Реактивная величина неизменна для актуальной цепи переменного тока.

Узнав, по какой формуле делаются необходимые вычисления и поняв смысл емкостного сопротивления, можно заняться расчетом данной величины.

Например, сделаем расчет на основе следующих данных:

• Емкость конденсатора C=1мкФ;
• В цепи также имеется активное сопротивление R, которое равно 5 кОм;
• Индуктивное сопротивление цепи xL составляет 4. 5 кОм;
• Частота переменного тока равна 50 Гц;
• Напряжение 50 вольт.

На основе этих данных необходимо будет найти сопротивление конденсатора.

Емкостное сопротивление определим следующим образом:

xC=1/(2πfC)=1/(2×3.14×50×1×10 -6 )=3184 Ом или округленно 3.2 кОм.

Для определения величины тока в этой цепи воспользуемся законом Ома:

I=U/xC=50/3184=0.0157 ампер или 15.7мА.

После этого определяются параметры общего сопротивления:

Z=(R²+(xL-xC)²)½=(5000²+(4500-3184)²)½=5170 Ом или 5.1 кОм.

По данным расчётам можно определить влияние емкостного элемента на электроцепь. Главное понимать, какие физические величины используются в данных формулах для выполнения правильных вычислений.

Применение

В электронных цепях очень часто конденсатор используется в качестве фильтрующего элемента. При этом инженеры учитывают способ подключения данного элемента:

1. При параллельном соединении конденсатора с цепью, устройство способно задерживать ток высокой частоты. Такой фильтр работает по принципу зависимости сопротивления от частоты тока. Чем выше частота, тем ниже будет сопротивление.
2. При последовательном включении фильтр уже отсеивает низкочастотные импульсы. Вторым свойством такого фильтра является возможность не пропускать постоянный ток.

Также большая доля использования таких устройств приходится на звуковые усилители. Конденсатор способен отделить переменный и постоянный ток, а значит работать в качестве усилителя низкой частоты. При этом подбираются элементы с наименьшей емкостью.

Так же устройства используются для блоков питания постоянного тока или стабилизаторов. Тут применяется свойство разделения постоянной и переменной составляющей. Например, разделение ее между потребителями с помощью отдельных выходов для постоянного и переменного тока. В таких устройствах конденсатор разряжается, если нагрузка на цепь увеличивается за счет подключения нового устройства. Тем самым общая пульсация в цепи сглаживается. При необходимости можно передать ток обоих значений по одному проводнику. Делается это следующим образом — контакты с постоянным напряжением подключают к выводу емкости для прямого контакта с переменным напряжением. Таким образом происходит фильтрация частоты, сглаживание импульсов и передача постоянного тока потребителю. Такая схема используется в антенных усилителях, которые подключаются к телевизорам.

Измерение и проверка

Измерить целостность конденсатора и его сопротивление можно при помощи мультиметра. Перед этим элемент обязательно необходимо отсоединить от цепи.

Проверка

Диагностика целостности конденсатора начинается с визуально осмотра его состояния. Любые трещины, вздутия или деформации корпуса можно считать неисправностью элемента. Если визуальный осмотр не дал никаких результатов, то элемент проверяется на пробой при помощи тестера.

Делается такая проверка следующим образом:

1. Элемент необходимо выпаять из схемы, а его контактные выводы замкнуть металлическим предметом для разрядки.
2. Мультиметр перемести в режим замера сопротивления.
3. Измерительные щупы соединить с контактами устройства.
4. Сопротивление исправного элемента будет измеряться бесконечным значением, которое будет превышать значение сопротивления утечки. Величина этой утечки при этом составляет 2 кОм.

Если показания меньше этого значения, значит элемент неисправен и пробит.

Замер

Замерить сопротивление можно так же с помощью мультиметра. Его надо будет перевести в режим измерения сопротивлений более 100 кОм. Далее необходимо соединить щупы прибора с контактами устройства. Некоторое время потребуется на полную зарядку элемента. После этого он покажет конечный результат, который не должен быть выше 100 кОм. Если этот порог преодолен, то можно сделать однозначный вывод о неисправности элемента.

Измерение емкости

Для замера емкости потребуется тестер с режимом СX. Если такого режима нет, проверить элемент будет невозможно. Далее требуется:

1. Полностью разрядить конденсатор.
2. На мультиметре выбирается режим СX.
3. Измерительные щупы соединить с контактными выводами устройства, строго соблюдая полярность.
4. Прибор должен показать величину больше 1, но при этом ее значение должно быть в пределах тех значений, которые указаны на корпусе детали. Если значение равняется 0 или находится за пределами указанных значений, то конденсатор можно признать неисправным.

Полученные мультиметром данные также можно считать ёмкостным значением, так как в момент проверки элемент проходит зарядку током.

Емкостным сопротивлением обладают все цепи, в которых задействованы конденсаторы. Зная, какой по параметрам элемент включен в данную цепь, можно легко рассчитать его емкостное влияние на цепь, используя представленные в статье формулы для расчётов.

Конденсатор емкостью C имеет в цепи постоянного тока бесконечно большое сопротивление. Если же приложить к конденсатору переменное напряжение, то он будет периодически перезаряжаться, и в цепи потечет ток. Напряжение на конденсаторе достигает максимального значения в те моменты, когда ток равен нулю.

Если R = 0, то напряжение на конденсаторе совпадает с приложенным напряжением и u = q/C. Мгновенное значение тока определяется выражением:

Между напряжением и током имеется разность фаз —π/2.

В чисто емкостной цепи переменного тока ток опережает напряжение на π/2 (или Т/4).

В соответствии с приведенным выше уравнением амплитуда тока I_m = ωCU_m. Сравнение с законом Ома U = RI показывает, что величина 1/ωС играет роль сопротивления.

Цепь переменного тока, содержащая емкость C, обладает сопротивлением переменному току; оно называется емкостным сопротивлением Х_C.

Единица СИ емкостного сопротивления: [X_C] = Ом.

ХC	емкостное сопротивление цепи переменного тока,	Ом
ω = 2πf	круговая частота переменного тока,	радиан/Секунда
C	емкость,	Фарад

При увеличении частоты емкостное сопротивление уменьшается. Для постоянного тока (f = 0) оно бесконечно велико.

Ток в цепи, обладающей только емкостным сопротивлением, определяется выражением

Читайте также:

  
• Драйвер для светодиодов своими руками с питанием от 220 В: как сделать, схема простого самодельного стабилизатора напряжения для работы лед светильника от сети
  
• Катушка индуктивности — что это такое? Магнитные поля. Электрическая индуктивность и ее применение.
  
• Мигает светодиодный прожектор: во включенном состоянии и после выключения, не горит, причина, мерцает, стал тускло светить

2.2 Емкостное сопротивление конденсатора

Лабораторная работа № 2

Прохождение гармонического сигнала через конденсатор

1. Целью лабораторной работы является:

1.1 Экспериментальное определение фазовых соотношений между токами и напряжениями в процессе прохождение гармонического сигнала через конденсатор и ее соответствие теоретическим представлениям

1.

2.Экспериментальное определение амплитудных соотношений между токами и напряжениями в процессе прохождение гармонического сигнала через конденсатор и ее соответствие теоретическим представлениям

2. Содержание работы

Содержанием практической части работы является экспериментальное определение фазовых и амплитудных соотношений между токами и напряжениями в процессе прохождение гармонического сигнала через конденсатор и их соответствие теоретическим представлениям

Выполнение лабораторной работы проводится на ПЭВМ с использованием прикладных программ «EWB5.12» или «Micro-CaP8».

Правила безопасности при выполнении лабораторной работы являются типовыми.

2 Краткие теоретические сведения

2.1 Конденсатор в цепи переменного тока

Самой распространенной формой сигнала в схемотехнике аналоговых электронных устройств является гармонический (синусоидальный или косинусоидальный) сигнал, а в цифровой схемотехнике – сигнал в виде прямоугольных импульсов.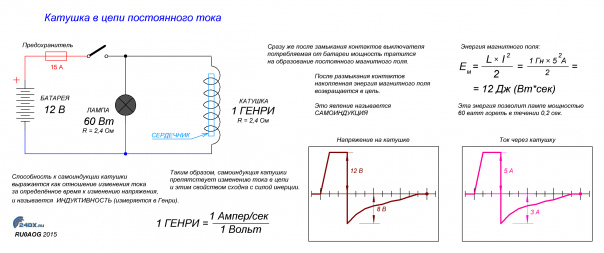 Однако прямоугольные импульсы также являются суммой гармонических сигналов (ряд Фурье). Поэтому в радиотехнике такое большое внимание уделяется изучению прохождения гармонических сигналов через различные цепи.

В этот раз рассмотрим прохождение гармонического сигнала через реальный конденсатор.

Известно , что конденсатор не пропускает через себя постоянного тока. Поэтому в электрической цепи, в которой последовательно с источником тока включен конденсатор, постоянный ток протекать не может.

Совершенно иначе ведет себя конденсатор в цепи переменного тока (рисунок 1).

Рисунок 1 – Напряжение и ток через идеальный конденсатор

 

В течение первой четверти периода, когда переменная ЭДС нарастает, конденсатор заряжается, и поэтому по цепи проходит зарядный электрический ток i, сила которого будет наибольшей вначале, когда конденсатор не заряжен. По мере приближения заряда к концу сила зарядного тока будет уменьшаться.

Заряд конденсатора заканчивается и зарядный ток прекращается в тот момент, когда переменная ЭДС перестает нарастать, достигнув своего амплитудного значения. Этот момент соответствует концу первой четверти периода.

После этого переменная ЭДС начинает убывать, одновременно с чем конденсатор начинает разряжаться. Следовательно, в течение второй четверти периода по цепи будет протекать разрядный ток. Так как убывание ЭДС происходит вначале медленно, а затем все быстрее и быстрее, то и сила разрядного тока, имея в начале второй четверти периода небольшую величину, будет постепенно возрастать.

К концу второй четверти периода конденсатор разрядится, ЭДС будет равна нулю, а ток в цепи достигнет наибольшего, амплитудного, значения.

С началом третьей четверти периода ЭДС, переменив свое направление, начнет опять возрастать, а конденсатор — снова заряжаться. Заряд конденсатора будет происходить теперь в обратном направлении, соответственно изменившемуся направлению ЭДС. Поэтому направление зарядного тока в течение третьей четверти периода будет совпадать с направлением разрядного тока во второй четверти, т.

е. при переходе от второй четверти периода к третьей ток в цепи не изменит своего направления.

Вначале, пока конденсатор не заряжен, сила зарядного тока имеет наибольшее значение. По мере увеличения заряда конденсатора сила зарядного тока будет убывать. Заряд конденсатора закончится и зарядный ток прекратится в конце третьей четверти периода, когда ЭДС достигнет своего амплитудного значения и нарастание ее прекратится.

К концу третьей четверти периода конденсатор окажется опять заряженным, но уже в обратном направлении, т. е. на той пластине, где был прежде плюс, будет минус, а где был минус, будет плюс. При этом ЭДС достигнет амплитудного значения (противоположного направления), а ток в цепи будет равен нулю.

В течение последней четверти периода ЭДС начинает опять убывать, а конденсатор разряжаться; при этом в цепи появляется постепенно увеличивающийся разрядный ток. Направление этого тока совпадает с направлением тока в первой четверти периода и противоположно направлению тока во второй и третьей четвертях.

Из всего изложенного выше следует, что по цепи с конденсатором проходит переменный ток и что сила этого тока зависит от величины емкости конденсатора и от частоты тока. Кроме того, из рисунка 1, который мы построили на основании наших рассуждений, видно, что

 в чисто емкостной цепи фаза переменного тока опережает фазу напряжения на 90°. Диэлектрик же, как нам известно, поляризуется под действием электрического поля, возникающего в нем при заряде конденсатора, и поляризация его исчезает, когда конденсатор разряжается. При этом диэлектрик с возникающим в нем током смещения служит для переменного тока своего рода продолжением цепи, а для постоянного разрывает цепь. Но ток смещения образуется только в пределах диэлектрика конденсатора, и поэтому сквозного переноса зарядов по цепи не происходит.

 

Конденсатор, включенный в цепь переменного тока, влияет на силу протекающего по цепи тока, т. е. ведет себя как сопротивление Ток в цепи с конденсатором может протекать лишь при изменении приложенного к ней напряжения, причем сила тока, протекающего по цепи при заряде и разряде конденсатора, будет тем больше, чем больше емкость конденсатора и чем быстрее происходят изменения ЭДС.

Сопротивление, оказываемое конденсатором переменному току, зависит от величины емкости конденсатора и от частоты тока. Чем больше емкость конденсатора, тем больший заряд переносится по цепи за время заряда и разряда конденсатора, а следовательно, и тем больший будет ток в цепи. Увеличение же тока в цепи свидетельствует о том, что уменьшилось ее сопротивление. Следовательно, с увеличением емкости уменьшается сопротивление цепи переменному току.

Увеличение частоты тока увеличивает величину переносимого по цепи заряда, так как заряд (а равно и разряд) конденсатора должен произойти быстрее, чем при низкой частоте. В то же время увеличение величины переносимого в единицу времени заряда равносильно увеличению тока в цепи, а следовательно, уменьшению ее сопротивления. Если же мы будем постепенно уменьшать частоту переменного тока и сведем ток к постоянному, то сопротивление конденсатора, включенного в цепь, будет постепенно возрастать и станет бесконечно большим (разрыв цепи) к моменту появления в цепи постоянного тока. Следовательно, с увеличением частоты уменьшается сопротивление конденсатора переменному току.

Рисунок 2 —  Зависимость емкостного сопротивления конденсатора от частоты

Для постоянного тока, т. е. когда частота его равна нулю, сопротивление емкости бесконечно велико; поэтому постоянный ток по цепи с емкостью проходить не может.

Величина емкостного сопротивления определяется по следующей формуле

где Хс — емкостное сопротивление конденсатора в ом;

f—частота переменного тока в гц;

ω — угловая частота переменного тока;

С — емкость конденсатора в ф. С помощью конденсаторов, например, достигается необходимое для работы схем разделение постоянных токов и токов низкой частоты от токов высокой частоты. Если нужно преградить путь току низкой частоты в высокочастотную часть схемы, последовательно включается конденсатор небольшой емкости.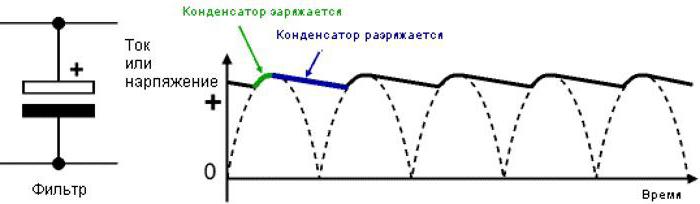 Он оказывает большое сопротивление низкочастотному току и в то же время легко пропускает ток высокой частоты. Если же надо не допустить ток высокой частоты, например, в цепь питания радиостанции, то используется конденсатор большой емкости, включаемый параллельно источнику тока. Ток высокой частоты в этом случае проходит через конденсатор, минуя цепь питания радиостанции.

При включении конденсатора в цепь переменного тока, в последнем не затрачивается мощность, так как фазы тока и напряжения сдвинуты друг относительно друга на 90°. Энергия в течение одной четверти периода— при заряде конденсатора — запасается в электрическом поле конденсатора, а в течение другой четверти периода — при разряде конденсатора — отдается обратно в цепь. Поэтому емкостное сопротивление является реактивным или безваттным.

Нужно, однако, отметить, что практически в каждом конденсаторе при прохождении через него переменного тока затрачивается бóльшая или меньшая активная мощность, обусловленная происходящими изменениями состояния диэлектрика конденсатора. Кроме того, абсолютно совершенной изоляции между пластинами конденсатора никогда не бывает; утечка в изоляции между пластинами приводит к тому, что параллельно конденсатору как бы оказывается включенным некоторое активное сопротивление, по которому течет ток и в котором, следовательно, затрачивается некоторая мощность. И в первом и во втором случае мощность затрачивается совершенно бесполезно на нагревание диэлектрика, поэтому ее называют мощностью потерь.

Потери, обусловленные изменениями состояния диэлектрика, называются диэлектрическими, а потери, обусловленные несовершенством изоляции между пластинами, — потерями утечки.

 

Зарядка конденсатора

Иторы похожи на аккумуляторы, хранящие электрическую энергию. Сумма, которую они хранят, измеряется в фарадах. Они пригодятся, потому что они могут высвобождать энергию, когда это необходимо. Вместе с другими компонентами схемы конденсаторы могут служить фильтром, который пропускает одни электрические импульсы и останавливает другие.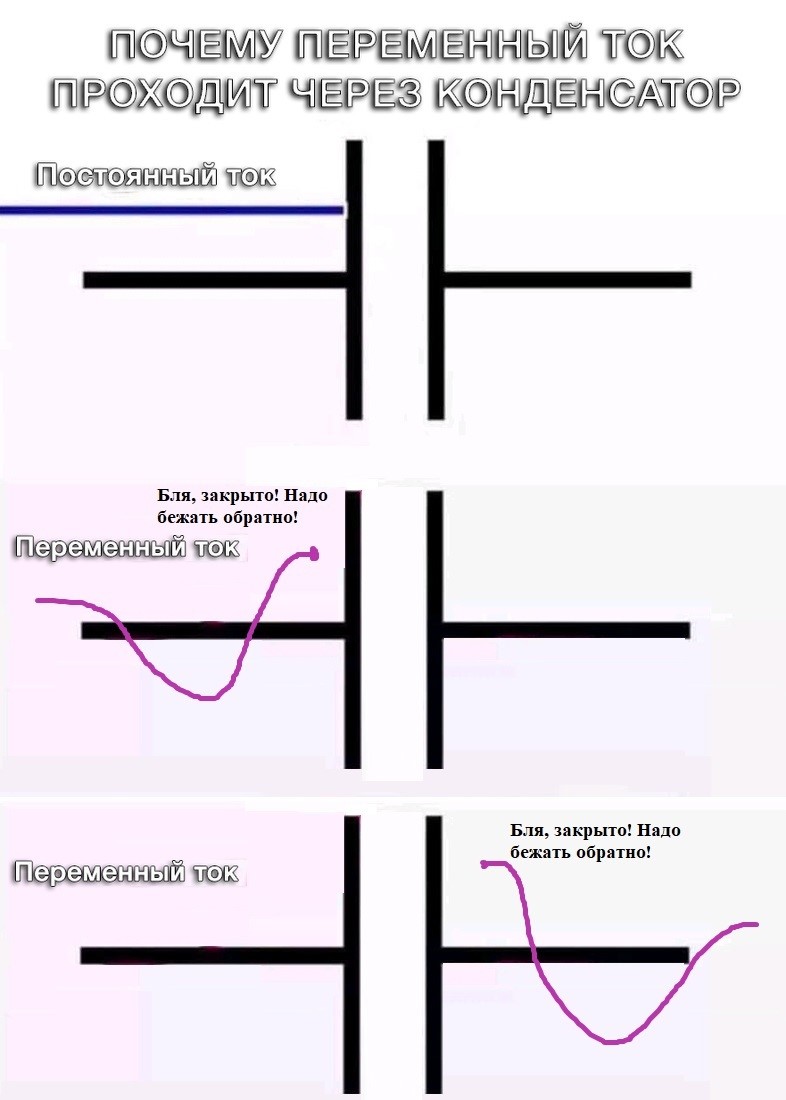 Многие электронные устройства, которые мы используем каждый день, такие как кардиостимуляторы, телефоны и компьютеры, зависят от работы конденсаторов.

Как заряжается конденсатор?

В проводящих материалах есть множество крошечных отрицательно заряженных частиц, называемых электронами, которые составляют электрический ток. Эти электроны могут легко перемещаться в электрическом поле и отделяться от атома. Но в изоляционных материалах всего несколько электронов, и они прочно привязаны к атомному ядру. Поэтому они не могут легко отделиться от атома.

Знание этого поможет нам понять, как заряжаются конденсаторы. Конденсаторы могут накапливать энергию благодаря электрическому полю, которое толкает или притягивает электроны. Когда положительные и отрицательные заряды встречаются на противоположных пластинах конденсатора, конденсатор заряжается.

‍

Схема заряженного конденсатора

‍

Пластины внутри конденсатора имеют положительные и отрицательные заряды, которые притягиваются друг к другу, но никогда не соприкасаются. Это заставляет их постоянно толкать и тянуть электрическое поле между двумя пластинами. Так конденсатор удерживает свой заряд.

Как ведет себя заряд конденсатора в цепях переменного и постоянного тока?

Давайте теперь рассмотрим различия в том, как конденсатор заряжается в цепях постоянного тока, по сравнению с его поведением при зарядке в цепях переменного тока.

Поведение конденсатора при зарядке в цепях постоянного тока

Чтобы понять, как работает конденсатор и как ведет себя его заряд в цепях постоянного тока, взгляните на приведенную ниже базовую схему.

Простая схема заряда конденсатора

‍

Когда переключатель находится в положении 2, на конденсатор не подается напряжение и, следовательно, отсутствует электрическое поле. Это означает, что электроны в проводящих пластинах неподвижны, и пластины не имеют положительного или отрицательного заряда. Разность потенциалов между обкладками равна нулю, а вольтметр покажет значение 0,

Однако, когда вы переместите переключатель в положение 1, вы заметите, что стрелка амперметра движется вверх, а затем быстро опускается обратно. Это связано с тем, что при перемещении переключателя в положение 1 происходит движение электронов.

Положительный полюс источника постоянного тока притягивает электроны к верхней проводящей пластине, а отрицательный полюс отталкивает электроны к нижней проводящей пластине. В результате верхняя пластина становится положительно заряженной, потеряв электроны, а нижняя пластина становится отрицательно заряженной, приобретя электроны.

Между двумя обкладками конденсатора существует разность потенциалов, противоположная направлению постоянного потенциала. Это изменение разности потенциалов отражается на показаниях амперметра и вольтметра. Вы можете увидеть, как эти показания меняются на диаграммах разброса ниже.

Рассеянный заряд значения напряжения конденсатора в течение периода времени

‍

Период, в течение которого конденсатор заряжается, называется временным состоянием. Именно в этот период стрелка амперметра движется вверх, а затем снова вниз. Когда конденсатор полностью заряжен, он достигает устойчивого состояния. В этот момент вольтметр показывает V, что является значением напряжения источника постоянного тока.

Рассеянный заряд текущего значения конденсатора в течение периода времени

‍

Показания амперметра противоположны значению напряжения. Причина этого в том, что конденсатор заряжается во временном состоянии, поэтому ток продолжает проходить через него. По мере зарядки разность потенциалов между обкладками конденсатора возрастает, приближаясь к разности потенциалов источника постоянного тока. По мере приближения ток начинает уменьшаться, потому что разность потенциалов между источником постоянного тока и конденсатором уменьшается. Когда конденсатор полностью заряжен, он входит в устойчивое состояние, и разность потенциалов источника постоянного тока и конденсатора одинакова. Электрическая нагрузка, которую конденсатор может накапливать в цепи постоянного тока, составляет:

Здесь:

В = напряжение на конденсаторе.

C = емкость конденсатора.

Q = электрическая нагрузка конденсатора.

Чтобы понять концепцию зарядки конденсатора в цепи переменного тока, нам нужно посмотреть на процесс в разные периоды периода зарядки.

Ток и напряжение конденсатора имеют разность фаз 90 градусов в цепях переменного тока

‍

Мы рассмотрим поведение цепи в 4 различных частях периода зарядки. Эти части предназначены для угла, называемого а, между 0 — π/2, π/2 — π, π — 3π/2 и 3π/2 — 2π.

0 < a < π/2 Заряд конденсатора А переменным током (диаграмма 1)

‍

При замыкании ключа в момент времени t = 0 конденсатор начинает заряжаться. Поскольку напряжение изменяется с высокой скоростью, существует большой поток электронов, а это означает, что ток находится на максимальном уровне. По мере приближения к π/2 напряжение на конденсаторе приближается к Um (пиковое значение источника переменного тока), поток электронов уменьшается, а также уменьшается ток.

Заряд конденсатора переменным током (Диаграмма 2)

‍

π < a < 3π/2

 

Несмотря на то, что он включает дифференцирование, объяснение довольно простое. Ток, проходящий через конденсатор, прямо пропорционален значению его емкости и скорости изменения напряжения во времени.

Заряд конденсатора переменным током (диаграмма 3)

‍

После точки a = π напряжение конденсатора начинает увеличиваться по мере увеличения напряжения источника переменного тока. Электроны нижней пластины притягиваются источником, а лишние электроны движутся к верхней пластине. По мере продвижения к точке a = 3π/2, поскольку скорость изменения напряжения уменьшается, а напряжение на конденсаторе приближается к -Vm, значение тока уменьшается.

3π/2 < a < 2π Заряд конденсатора переменным током (диаграмма 4)

‍

Таким образом, напряжение конденсатора изменяется в зависимости от источника, к которому он подключен. Когда напряжение источника уменьшается, напряжение конденсатора также уменьшается. Чем быстрее меняется напряжение, тем больше ток, проходящий через конденсатор. В точке, где напряжение источника переменного тока равно 0, ток, протекающий через конденсатор, максимален, и конденсатор полностью разряжен.

В цепях переменного тока ток, проходящий через конденсатор, прямо пропорционален значению его емкости и скорости изменения напряжения во времени. Уравнения для нахождения максимального напряжения и максимального тока конденсатора в цепи переменного тока включают пиковое значение напряжения и значение емкости. В целом поведение конденсатора в цепях постоянного и переменного тока различно, при этом напряжение, ток и нагрузка конденсатора постоянно меняются в цепях переменного тока.

Заряд конденсатора

Как долго конденсатор может удерживать заряд?

Это зависит от схемы и качества изолятора между двумя токопроводящими пластинами, поскольку на практике через изоляторы проходят небольшие токи утечки.

Когда конденсатор полностью заряжен?

Конденсатор считается полностью заряженным, если он больше не может удерживать электрическую нагрузку. Мы понимаем, когда конденсатор полностью заряжен, исходя из того, когда он начинает не пропускать через себя ток.

Как рассчитать заряд конденсатора?

Мы можем рассчитать заряд конденсатора, глядя на его емкость и приложенное к нему напряжение в соответствии с уравнением: Q = CV.

Что такое зарядка конденсатора?

Заряд конденсатора происходит при последовательном подключении резистора и конденсатора к источнику напряжения. Начальное значение тока, проходящего через конденсатор, находится на максимальном уровне и постепенно уменьшается вплоть до нуля. Когда вы считаете, что ток, проходящий через конденсатор, равен нулю, это означает, что конденсатор заряжен.

Какова формула конденсатора?

Общая формула для определения значения емкости в цепи постоянного тока может быть математически выражена как Q=CV. Где V — напряжение, приложенное к конденсатору, C — емкость конденсатора, а Q — электрическая нагрузка на конденсатор.

‍

Конденсаторы

Конденсатор представляет собой устройство, в котором две проводящие поверхности накапливают электрический заряд. Однако у него есть зазор между двумя поверхностями, который изолирует их друг от друга. Расстояние между зазором и материалом в зазоре (воздух, стекло, минерал, жидкость и т. д.) не слишком велико, чтобы предотвратить достаточно сильное электрическое поле, которое толкает электрические заряды и заставляет их собираться на поверхностях.

Из чего состоит конденсатор?

В простом конденсаторе используются две параллельные пластины из проводящего материала, разделенные изолятором. Изолятор называется диэлектрик и представляет собой материал, который предотвращает прохождение через него электрического тока. Способность электрического поля проходить через диэлектрический материал определяется значением измерения, известным как ε , называемым диэлектрической проницаемостью . Это, наряду с размерами пластин конденсатора, определяет, сколько заряда он может хранить. Важна площадь пластин ( A ) и расстояние между ними ( d ). Вот иллюстрация того, как части конденсатора связаны вместе с их важными свойствами:

Величина емкости ( C ) конденсатора зависит от способности электрического поля влиять на заряды на его пластин, умноженное на площадь проводящей поверхности, деленную на расстояние между пластинами.

С = ε * А / д

Емкость измеряется в единицах Фарад (F) . Большинство конденсаторов, используемых в небольших современных электронных схемах, имеют емкость микрофарад (мкФ) или пикофарад (пФ) . Пикофарад очень мал, это 1/1000000000000 фарада.

Электрическое поле

Сначала конденсатор имеет одинаковое количество положительных и отрицательных зарядов на каждой пластине. Заряды не могут перейти на другую пластину из-за зазора между ними, который изолирует пластины друг от друга. Зазор может быть воздухом или другим непроводящим материалом. Однако внутри зазора есть электрическое поле ( E ), который направляет силу от батареи, чтобы подтолкнуть противоположный электрический заряд к пластинам.

Зарядка

Наличие электрического поля между этими поверхностями заставляет заряды на пластинах располагаться ближе всего к направлению противоположного заряда. Это происходит до тех пор, пока пластины конденсатора не заполнятся противоположными зарядами. На приведенном ниже рисунке показан конденсатор с двумя пластинами, которые заряжаются противоположно за счет силы приложенного к ним напряжения. Заряды перемещаются и движутся к пластине в направлении своего притяжения.

Время RC

На самом деле конденсатор не заряжается сразу. Для зарядки требуется время из-за некоторого сопротивления току, протекающему к его пластинам или от них. При любом напряжении на обкладках конденсатора потребуется некоторое время, пока он полностью зарядится. Как только конденсатор полностью зарядится, к нему перестанет поступать ток, потому что больше нет места для новых зарядов. На следующей схеме показана простая схема для зарядки конденсатора.

Специальная величина для цепи зарядки конденсатора находится путем умножения ее сопротивления на емкость.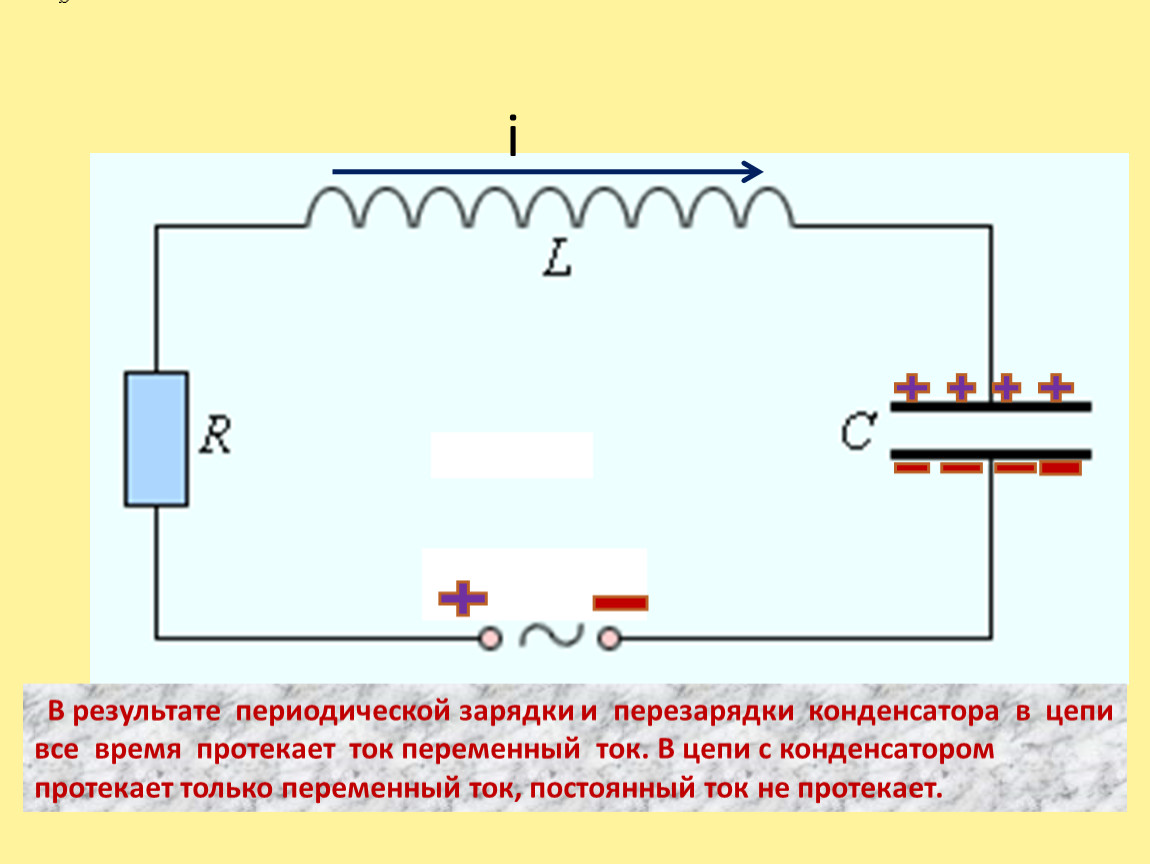 Результатом является значение времени, называемое постоянной времени RC . Например, если сопротивление резистора 20 кОм, а конденсатора 200 пФ (пФ), постоянная времени RC-цепи равна:

20000 Ом * 2e-10 фарад = 4 микросекунды

Используя свойства времени заряда , мы можем определить, что конденсатор будет иметь более 99% его заряда через 5 постоянных времени, или 5 * RC секунд. На этой диаграмме первая цепь показывает момент замыкания цепи. Ток только начинает течь с 0 вольт через конденсатор, и он имеет сбалансированный заряд. На второй диаграмме показан полный заряд и отсутствие тока после периода 5 постоянных времени RC.

На второй схеме вы видите, что когда конденсатор полностью заряжен и ток прекращается, напряжение на нем становится таким же, как напряжение питания, обеспечивающее заряд. Используя значения сопротивления и емкости, упомянутые в предыдущем примере, конденсатор будет заряжаться примерно за 20 микросекунд:

5 * RC = 5 * 4 микросекунды = 20 микросекунд

Следующие графики показывают, как конденсатор заряжается и разряжается во времени:

А конденсатор не не заряжается и не разряжается с одинаковой скоростью время идет.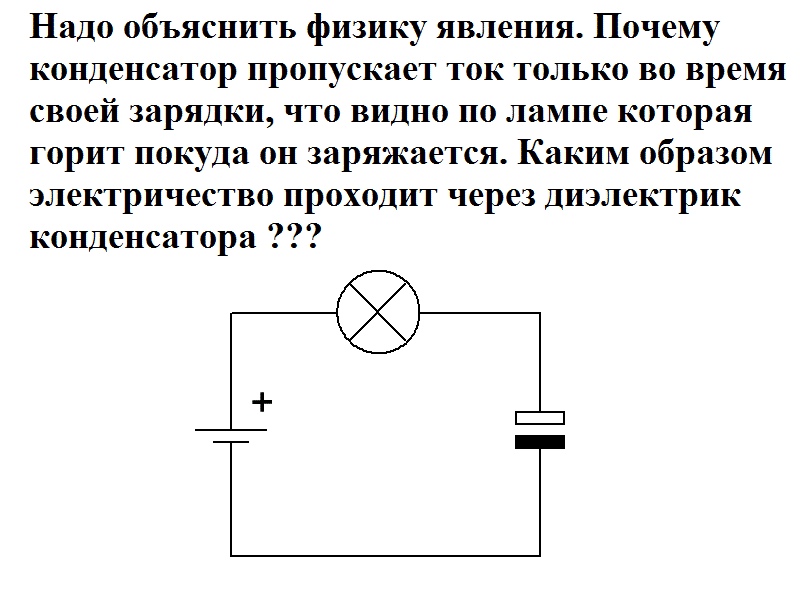 Напряжение на конденсаторе с течением времени следует «естественной» схеме, пока конденсатор полностью не зарядится или не разрядится. Из графиков видно, что скорость заряда или разряда действительно замедляется по мере приближения к 5 * RC количество времени, в данном случае 20 микросекунд .

Специальный номер, называемый и , используется для расчета напряжения конденсатора в любой конкретный момент после начала зарядки или разрядки. Это число известно как число Эйлера и используется в математических формулах для моделирования поведения в естественном мире. Значение этого числа приблизительно равно 2,71828 и в сочетании с R и C значений в цепи зарядки, используется для определения напряжения на конденсаторе. Напряжение на конденсаторе рассчитывается по следующим формулам:

• Зарядка: В пост. заряжать с
• Разрядка: Vc = Vstart*(e**(t/(R*C))) , где Vstart напряжение перед разрядом

Эксперимент: моделирование заряда и разряда

---

Используя значения для R и C вместе с числом Эйлера, вы можете составить график заряда и разряда конденсатора, чтобы увидеть, как он ведет себя во времени.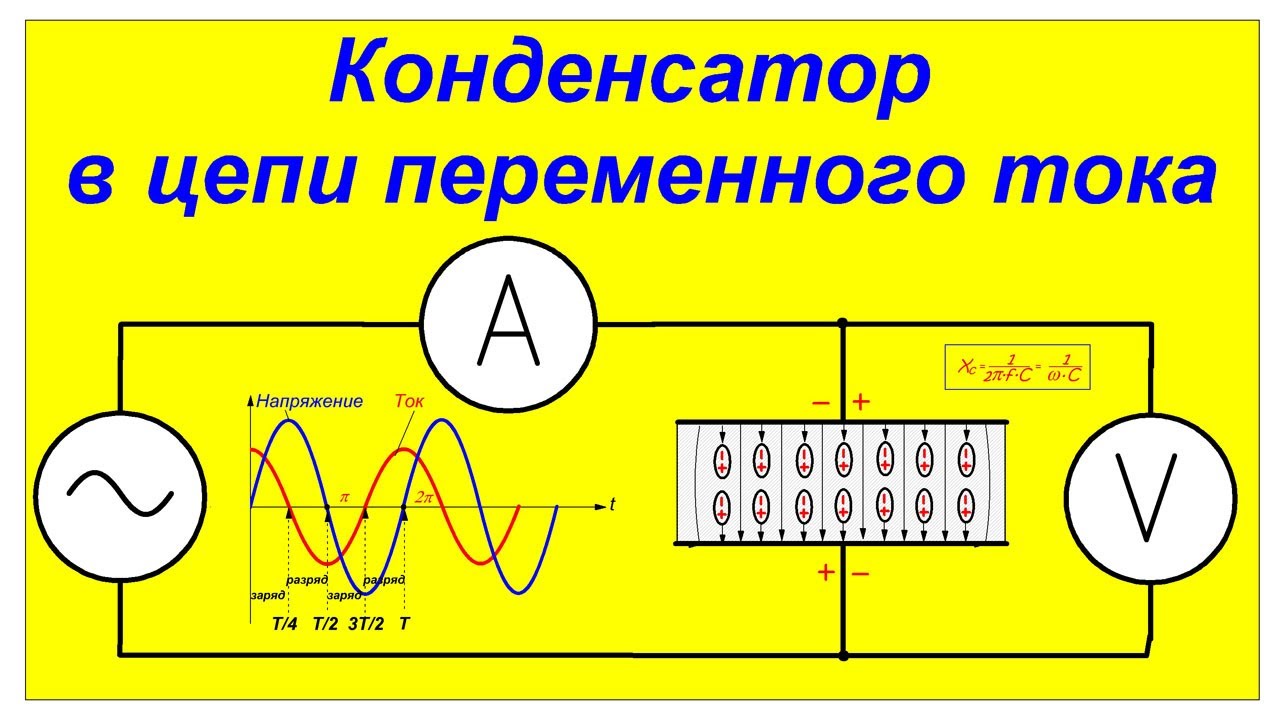 Кроме того, множители постоянной времени RC можно сопоставить с уровнем напряжения, чтобы увидеть, когда конденсатор почти полностью заряжен. Для моделирования модели значение 20 кОм используется для R и 200 пФ используется для C . Зарядное и пусковое напряжение 3.3v .

Настройка : Скопируйте следующий код в редактор.

 пусть е = 2,71828
пусть R = 20000
пусть С = 2e-10
пусть Vc = 0
пусть Вин = 3,3
пусть т = 0
для (пусть я = 0; я < 75; я ++) {
    Vc = Vin*(1 - e**(t/(R*C)))
    т += -0,0000005
    console.logValue("ВК", ВК)
    пауза(100)
}
т = 0
Вин = Вк
для (пусть я = 0; я < 75; я ++) {
    Vc=Vin*(e**(t/(R*C)))
    т += -0,0000005
    console.logValue("ВК", ВК)
    пауза(100)
} 

Тест : Запустите код и переключитесь на представление данных, чтобы увидеть вывод консоли на диаграмме.

Результат : Диаграмма показывает характер заряда и разряда в течение 37,5 микросекунд каждый. Форма графика показывает, как работает «естественная» скорость заряда и разряда.

Эксперимент: Детектор заряда

---

Уровень заряда конденсатора можно отслеживать, проверяя, какое напряжение на нем в данный момент. Цифровой выходной контакт может служить источником заряда, а аналоговый входной контакт может измерять напряжение на конденсаторе. Конденсатор заряжается через резистор. Чтобы иметь возможность наблюдать за изменением уровня заряда, используется конденсатор на 100 мкФ и сопротивление от 10 кОм до 40 Ом. Если вы сделали свой собственный резистор, он будет хорошо работать в этом эксперименте.

Материалы :

• (4) Провода типа «крокодил»
• Резистор с сопротивлением от 10 кОм до 40 кОм — используйте собственный графитовый резистор
• Конденсатор 100 мкФ

Настройка :

1. Подсоедините один конец зажима типа «крокодил» к выводу (-) конденсатора (на некоторых конденсаторах это более короткий провод). Подключите другой конец провода типа «крокодил» к контакту GND на плате.
2. Подсоедините один конец другого провода типа «крокодил» к выводу (+) конденсатора (на некоторых конденсаторах это более длинный провод). Подключите другой конец провода типа «крокодил» к одному концу вашего резистора.
3. Возьмите третий провод типа «крокодил» и подключите один его конец к выводу (+) конденсатора. Подключите другой конец этого провода типа «крокодил» к контакту A5 на плате.
4. Возьмите еще один провод типа «крокодил» и прикрепите его к другому концу резистора. Прикрепите несвязанный конец шнура «крокодил» к A4 пин на плате.

6. Загрузите на плату следующий код:

 контактов.A4.digitalWrite(false)
input.buttonA.onEvent (ButtonEvent.Click, функция () {
    контакты.A4.digitalWrite(true)
})
input.buttonB.onEvent (ButtonEvent. Click, функция () {
    контакты.A4.digitalWrite(false)
})
навсегда (функция () {
    light.graph(pins.A5.analogRead(), 1010)
    пауза(200)
}) 

Тест : Нажмите кнопку A , чтобы зарядить конденсатор, и наблюдайте, как загораются пиксели, показывающие уровень заряда. Нажмите кнопку B , чтобы разрядить конденсатор и наблюдать, как пиксели гаснут, когда заряд уходит.

Дополнительный тест : Измените значение сопротивления и повторите тест. Обратите внимание, как время заряда и разряда отличается от первого теста.

Результат : Пиксели на плате загорятся, показывая уровень заряда конденсатора. Каждый пиксель представляет еще 10% заряда. Каждый пиксель будет светиться (или отключаться при разрядке) дольше, чем предыдущий, поскольку скорость заряда замедляется. Последнему пикселю требуется гораздо больше времени, чтобы загореться, чем другим пикселям. Это будет относиться ко времени зарядки последних 10%, как показано на плоской части графика из предыдущего эксперимента.