Как найти силу тока в цепи — Инженерные технологии Коломна

Одной из основных характеристик электрической цепи является сила тока. Она измеряется в амперах и определяет нагрузку на токопроводящие провода, шины или дорожки плат. Эта величина отражает количество электричества, которое протекло в проводнике за единицу времени. Определить её можно несколькими способами в зависимости от известных вам данных. Соответственно студенты и начинающие электрики из-за этого часто сталкиваются с проблемами при решении учебных заданий или практических ситуаций. В этой статье мы и расскажем, как найти силу тока через мощность и напряжение или сопротивление.

Если известна мощность и напряжение

Допустим вам нужно найти силу тока в цепи, при этом вам известны только напряжение и потребляемая мощность. Тогда чтобы её определить без сопротивления воспользуйтесь формулой:

P=UI

После несложных мы получаем формулу для вычислений

I=P/U

Следует отметить, что такое выражение справедливо для цепей постоянного тока. Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:

Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88:

Р1 = Р2/η

Здесь P2 – активная полезная мощность на валу, η – КПД, оба этих параметра обычно указывают на шильдике.

Находим полную мощность с учетом cosФ (он также указывается на шильдике):

S = P1/cosφ

Определяем потребляемый ток по формуле:

Iном = S/(1,73·U)

Здесь 1,73 – корень из 3 (используется для расчетов трёхфазной цепи), U – напряжение, зависит от включения двигателя (треугольник или звезда) и количества вольт в сети (220, 380, 660 и т.д.). Хотя в нашей стране чаще всего встречается 380В.

Если известно напряжение или мощность и сопротивление

Но встречаются задачи, когда вам известно напряжение на участке цепи и величина нагрузки, тогда чтобы найти силу тока без мощности воспользуйтесь законом Ома, с его помощью проводим расчёт силы тока через сопротивление и напряжение.

I=U/R

Но иногда случается так, что нужно определить силу тока без напряжения, то есть когда вам известна только мощность цепи и её сопротивление. В этом случае:

P=UI

При этом согласно тому же закону Ома:

U=IR

То:

 P=I2*R

Значит расчёт проводим по формуле:

I2=P/R

Или возьмем выражение в правой части выражения под корень:

I=(P/R)1/2

Если известно ЭДС, внутреннее сопротивление и нагрузка

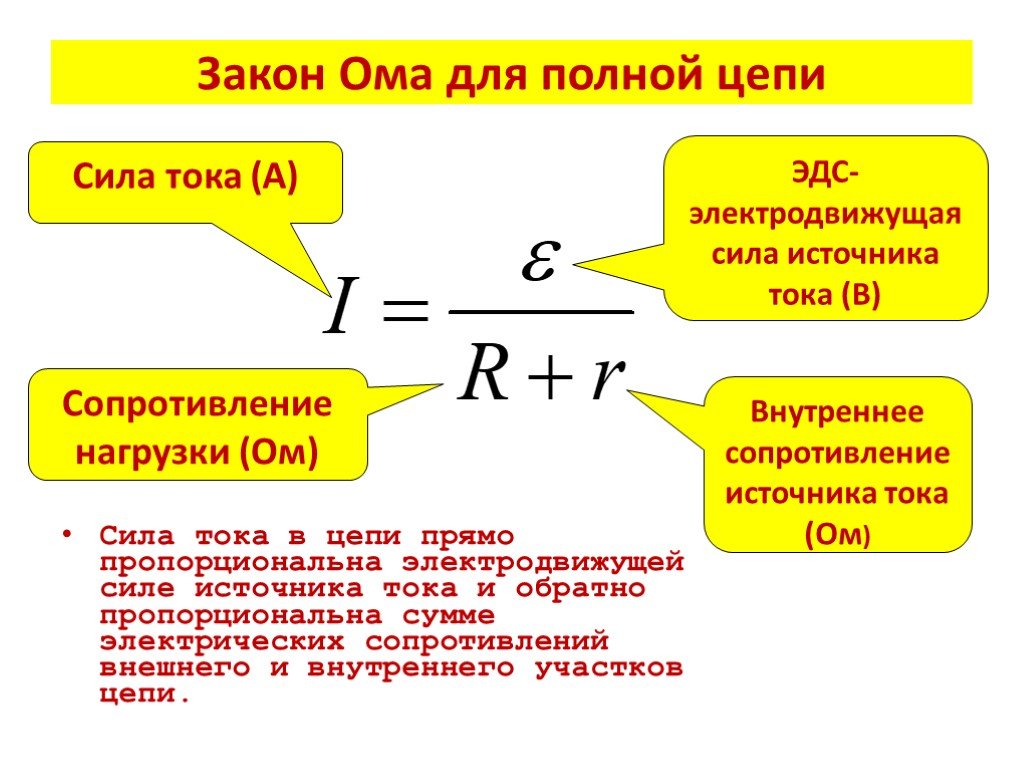
Ко студенческим задачам с подвохом можно отнести случаи, когда вам дают величину ЭДС и внутреннее сопротивление источника питания. В этом случае вы можете определить силу тока в схеме по закону Ома для полной цепи:

I=E/(R+r)

Здесь E – ЭДС, r – внутреннее сопротивление источника питания, R – нагрузки.

Закон Джоуля-Ленца

Еще одним заданием, которое может ввести в ступор даже более-менее опытного студента – это определить силу тока, если известно время, сопротивление и количество выделенного тепла проводником.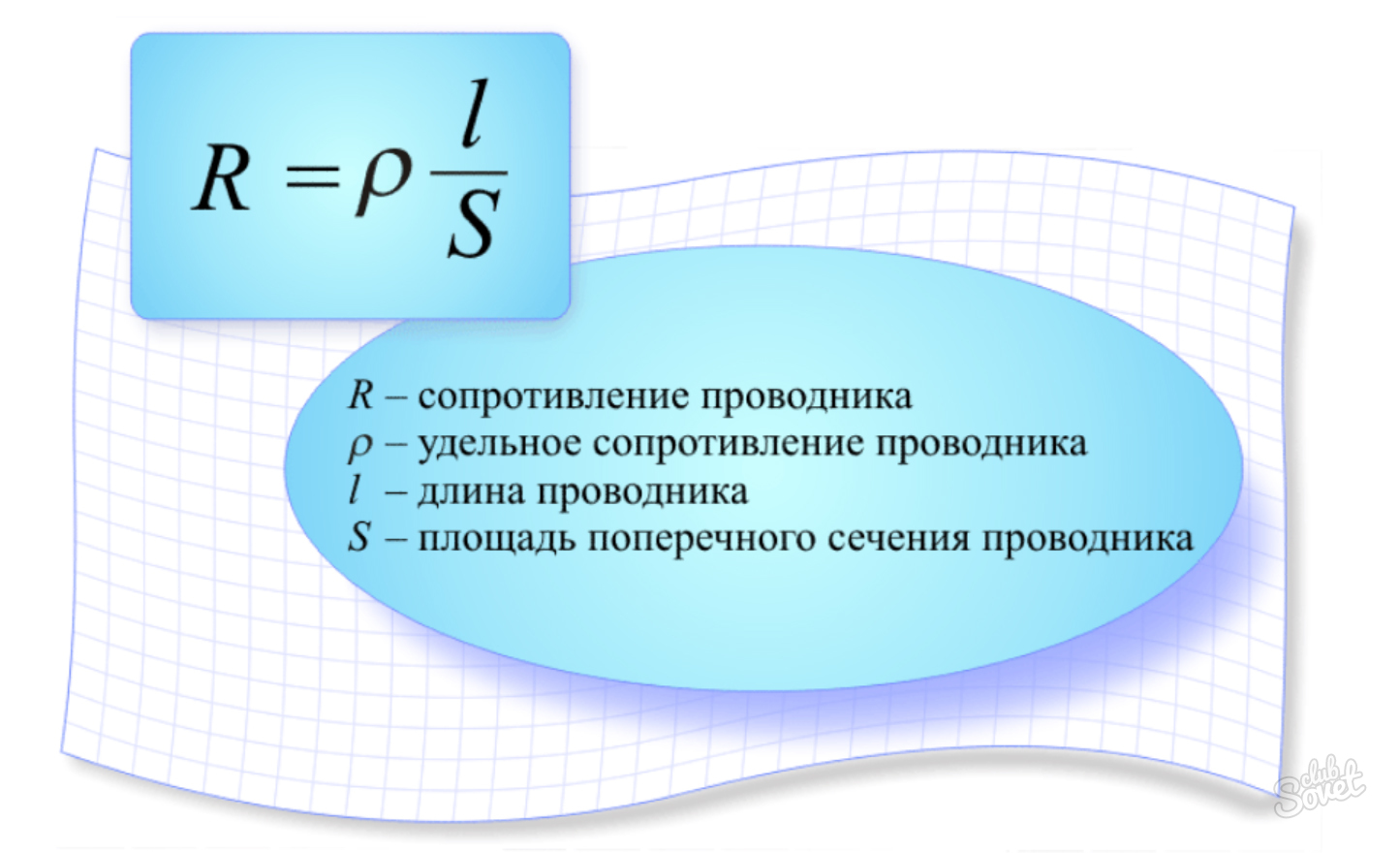 Для этого вспомним закон Джоуля-Ленца.

Его формула выглядит так:

Q=I2Rt

Тогда расчет проводите так:

I2=QRt

Или внесите правую часть уравнения под корень:

I=(Q/Rt)1/2

Несколько примеров

В качестве заключения предлагаем закрепить полученную информацию на нескольких примерах задач, в которых нужно найти силу тока.

1 задача: Рассчитать I в цепи из двух резисторов при последовательном соединении и при параллельном соединении. R резисторов 1 и 2 Ома, источник питания на 12 Вольт.

Из условия ясно, что нужно привести два варианта ответа для каждого из вариантов соединений. Тогда чтобы найти ток при последовательном соединении, сначала складывают сопротивления схемы, чтобы получить общее.

R1+R2=1+2=3 Ома

Тогда рассчитать силу тока можно по закону Ома:

I=U/R=12/3=4 Ампера

При параллельном соединении двух элементов Rобщее можно рассчитать так:

Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67

Тогда дальнейшие вычисления можно проводить так:

I=12*0,67=18А

2 задача: рассчитать ток при смешанном соединении элементов. На выходе источника питания 24В, а резисторы на: R1=1 Ом, R2=3 Ома, R3=3 Ома.

В первую очередь нужно найти R общее параллельно соединенных R2 и R3, по той же формуле, что мы использовали выше.

Rприв=(R2*R3)/(R2+R3)=(3*3)|(3+3)=9/6=3/2=1,5 Ома

Теперь схема примет вид:

Далее находим ток по тому же закону Ома:

I=U/(R1+Rприв)=24/(1+1,5)=24/2,5=9,6 Ампер

Теперь вы знаете, как найти силу тока, зная мощность, сопротивление и напряжение. Надеемся, предоставленные формулы и примеры расчетов помогли вам усвоить материал!

Наверняка вы не знаете:

Источник

Сила тока

Сила тока – отношение заряда, пронесенного через поперечное сечение проводника за интервал времени, к этому интервалу времени.

Сила тока, как и заряд, величина скалярная. Она может быть как положительной, так и отрицательной. За положительное направление силы тока принято движение положительных зарядов.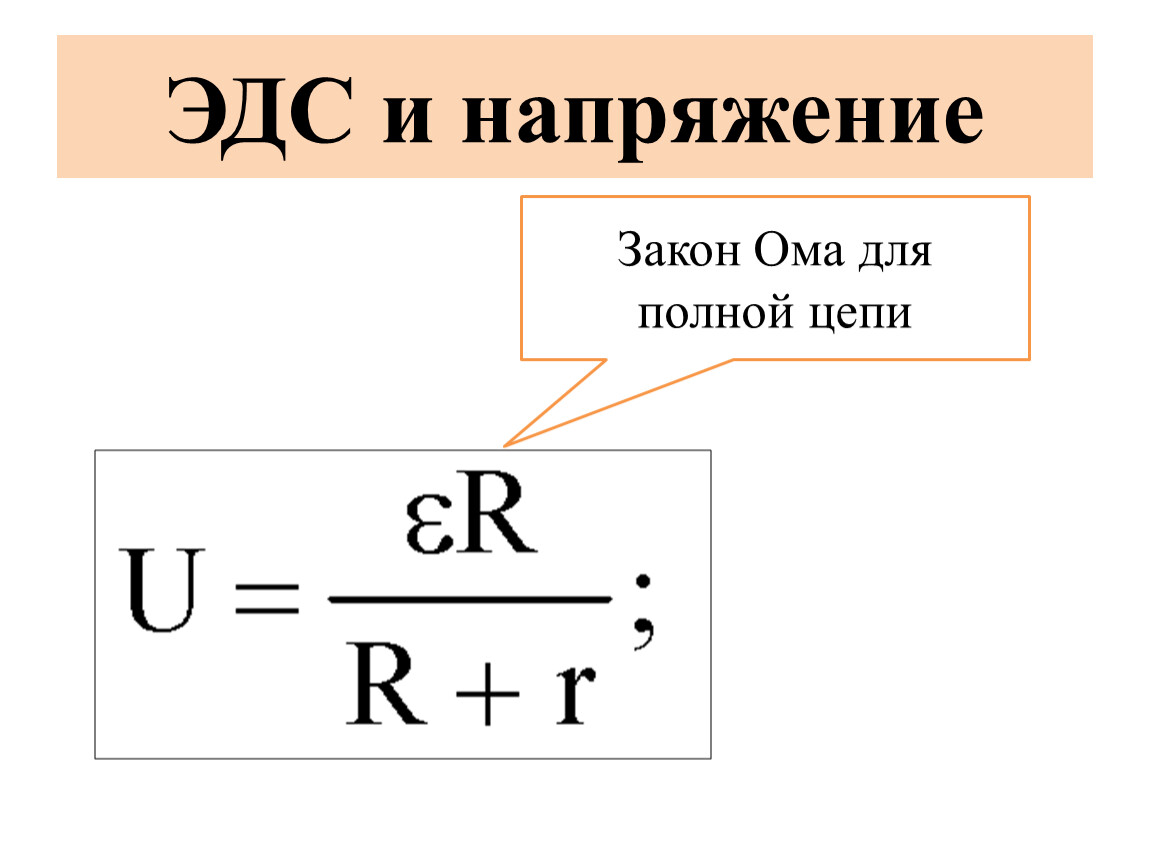 Если с течением времени сила тока не меняется, то ток называется постоянным.

За единицу принимают силу тока, при которой отрезки пар. проводников длиной 1м. Взаимодействуют с силой 2*10^-7 Н. Единица — 1Ампер. 1Кл=1А*1сек. Кулон равен эл. заряду, преходящему сквозь поперечное сечение проводника при силе тока 1А за время 1сек. Амперметр включают в цепь последовательно с прибором силу тока которого измеряют.

Электродвижущая сила

Для того, чтобы в проводнике существовал электрический ток длительное время, необходимо поддерживать неизменными условия, при которых возникает электрический ток.

Во внешней цепи электрические заряды движутся под действием сил электрического поля. Но, чтобы поддерживать разность потенциалов на концах внешней цепи, необходимо перемещать электрические заряды внутри источника тока против сил электрического поля. Такое перемещение может осуществляться только под действием сил неэлектростатической природы.

Силы, вызывающие перемещение электрических зарядов внутри источника постоянного тока против направления действия сил электростатического поля, называются

сторонними силами. Сторонние силы в гальваническом элементе или аккумуляторе возникают в результате электрохимических процессов, происходящих на границе раздела электрод – электролит. В машине постоянного тока сторонней силой является сила Лоренца.

Полная работа сил электростатического поля при движении зарядов по замкнутой цепи постоянного тока равна нулю. Следовательно, вся работа электрического тока в замкнутой электрической цепи оказывается совершенной за счет действия сторонних сил, вызывающих разделение зарядов внутри источника и поддерживающих постоянное напряжение на выходе источника тока.

Отношение работы сторонних сил по перемещению заряда вдоль цепи называется электродвижущей силой источника:

Электродвижущая сила выражается в тех же единицах, что и напряжение, т.  е. в вольтах.

ЭДС численно равна работе по перемещению единичного положительного заряда. Работа сторонних сил не может быть выражена через разность потенциалов, так как сторонние силы не консервативные (потенциальные) и их работа зависит от траектории.

13. Закон Ома. Сопротивление проводников. См. 3 случая. Сопротивление проводников

Сопротивление является основной электрической характеристикой проводника.

Сопротивление проводника можно определить из закона Ома:

Единица электрического сопротивления в СИ – Ом. Электрическим сопротивлением 1 Обладает такой участок цепи, на котором при силе тока 1 А напряжение равно 1 В.

Опыт показывает, что электрическое сопротивление проводника прямо пропорционально его длине и обратно пропорционально площади поперечного сечения:

Зависимость удельного электрического сопротивления от температуры – см. стр. 16

Постоянный для данного вещества параметр называетсяудельным электрическим сопротивлением вещества. Удельное сопротивление зависит от рода вещества и его состояния (в первую очередь от температуры).

6.3 ЭДС движения | Texas Gateway

Цели обучения

К концу этого раздела вы сможете делать следующее:

• Расчет ЭДС, силы, магнитного поля и работы, связанной с движением объекта в магнитном поле

Как мы видели, любое изменение магнитного потока индуцирует противодействующую этому изменению ЭДС — процесс, известный как индукция. Движение является одной из основных причин индукции. Например, магнит, перемещаемый по направлению к катушке, создает ЭДС, а катушка, перемещаемая по направлению к магниту, создает аналогичную ЭДС. В этом разделе мы сосредоточимся на движении в магнитном поле, стационарном относительно Земли, производя то, что условно называется ЭДС движения .

Одна из ситуаций, когда возникает ЭДС движения, известна как эффект Холла и уже исследовалась. На заряды, движущиеся в магнитном поле, действует магнитная сила F=qvBsinθ,F=qvBsinθ, размер 12{F= ital «qvB»»sin»θ} {}, которая перемещает противоположные заряды в противоположных направлениях и создает ЭДС=Bℓv.ЭДС= Бℓв. size 12{«emf»=Bℓv} {} Мы видели, что эффект Холла имеет приложения, включая измерения размера BB 12{B} {} и v.v. size 12{v} {} Теперь мы увидим, что эффект Холла является одним из аспектов более широкого явления индукции, и мы обнаружим, что ЭДС движения можно использовать в качестве источника энергии.

Рассмотрим ситуацию, показанную на рис. 6.11. Стержень движется со скоростью vv по паре проводящих рельсов, разделенных расстоянием ℓℓ, в однородном магнитном поле ВВ размера 12{B} {} Рельсы неподвижны относительно ВВ размера 12{B} {} и соединены с постоянный резистор R. R. размером 12 {R} {} Резистор может быть любым, от лампочки до вольтметра. Рассмотрим область, окруженную движущимся стержнем, рельсами и резистором.

BB размером 12{B} {} перпендикулярна этой области, и площадь увеличивается по мере движения стержня. Таким образом, магнитный поток, заключенный между рельсами, стержнем и резистором, увеличивается. При изменении потока индуцируется ЭДС в соответствии с законом индукции Фарадея.

Рисунок 6.11 (a) ЭДС движения=Bℓvemf=Bℓv size 12{«ЭДС»=Bℓv} {} индуцируется между рельсами, когда этот стержень движется вправо в однородном магнитном поле. Магнитное поле ВВ размером 12{B} {} направлено внутрь страницы, перпендикулярно движущимся стержню и рельсам и, следовательно, к ограниченной ими области. (b) Закон Ленца дает направления индуцированного поля и тока, а также полярность индуцированной ЭДС. Поскольку поток увеличивается, индуцированное поле направлено в противоположном направлении или выходит за пределы страницы. RHR-2 дает показанное направление тока, и полярность стержня будет управлять таким током. RHR-1 также указывает на ту же полярность стержня. Обратите внимание, что буква E, используемая в эквивалентной схеме в нижней части части (b), представляет ЭДС.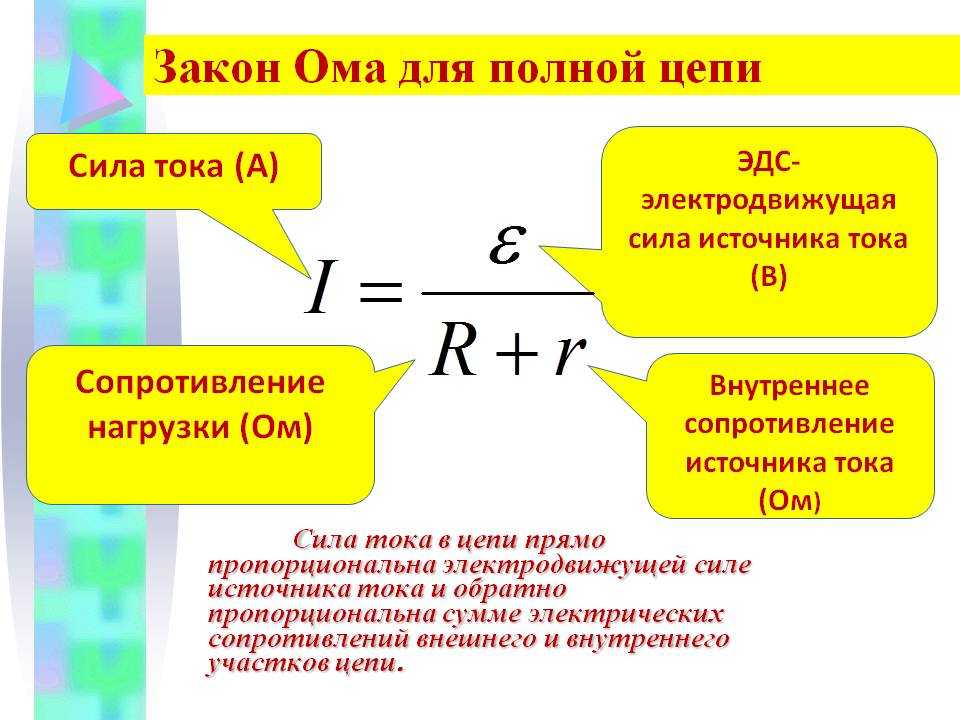

Чтобы найти величину ЭДС, индуцированной вдоль движущегося стержня, воспользуемся законом индукции Фарадея без знака.

6.7 ЭДС=NΔΦΔтемс=NΔΦΔt размер 12{«ЭДС»=N { {ΔΦ} над {Δt} } } {}

Здесь и далее ЭДС подразумевает величину ЭДС. В этом уравнении N=1N=1 размер 12{N=1} {} и поток Φ=BAcosθ.Φ=BAcosθ. size 12{Φ= ital «BA»»cos»θ} {} Имеем θ=0ºθ=0º и cosθ=1,cosθ=1, так как BB перпендикулярна A.A. Теперь ΔΦ=Δ(BA)=BΔA, ΔΦ=Δ(BA)=BΔA, размер 12{ΔΦ=Δ \(итал. «BA» \) =BΔA} {}, так как размер BB 12{B} {} равномерен. Обратите внимание, что площадь, заметаемая стержнем, составляет ΔA=ℓΔx. ΔA=ℓΔx. size 12{ΔA=ℓΔx} {} Ввод этих величин в выражение для ЭДС дает

6,8 ЭДС=BΔAΔt=BℓΔxΔt.ЭДС=BΔAΔt=BℓΔxΔt. size 12{«ЭДС»= { {BΔA} над {Δt} } =B { {ℓΔx} над {Δt} } } {}

стержня. Ввод этого в последнее выражение показывает, что

6,9 ЭДС = Bℓv (B, ℓ, и v перпендикулярно) ЭДС = Bℓv (B, ℓ, и v перпендикулярно) size 12 {«ЭДС» = Bℓv} {}

— ЭДС движения . Это то же самое выражение, которое было дано ранее для эффекта Холла.

Установление связей: объединение сил

Существует много связей между электрической и магнитной силами. Тот факт, что движущееся электрическое поле создает магнитное поле и, наоборот, движущееся магнитное поле создает электрическое поле, является частью того, почему электрические и магнитные силы теперь считаются разными проявлениями одной и той же силы. Это классическое объединение электрических и магнитных сил в то, что называется электромагнитной силой, является источником вдохновения для современных усилий по объединению других основных сил.

Чтобы найти направление индуцируемого поля, направление тока и полярность индуктируемой ЭДС, мы применяем закон Ленца, как описано в Законе Фарадея об индукции: Закон Ленца. (См. рис. 6.11[b].) Поток увеличивается, так как увеличивается площадь охвата. Таким образом, индуцированное поле должно противодействовать существующему и быть за пределами страницы. Таким образом, RHR-2 требует, чтобы I было направлено против часовой стрелки, что, в свою очередь, означает, что вершина стержня положительна, как показано на рисунке.

ЭДС движения также возникает, если магнитное поле движется, а стержень (или другой объект) неподвижен относительно Земли (или какого-либо наблюдателя). Мы видели пример этого в ситуации, когда движущийся магнит индуцирует ЭДС в неподвижной катушке. Важно относительное движение. В этих наблюдениях проявляется связь между магнитными и электрическими полями. Движущееся магнитное поле создает электрическое поле за счет ЭДС индукции. Мы уже видели, что движущееся электрическое поле создает магнитное поле — движущийся заряд подразумевает движущееся электрическое поле, а движущийся заряд создает магнитное поле.

ЭДС движения в слабом магнитном поле Земли обычно не очень велики, иначе мы заметили бы напряжение вдоль металлических стержней, таких как отвертка, во время обычных движений. Например, простой расчет ЭДС движения стержня длиной 1 м, движущегося со скоростью 3,0 м/с перпендикулярно полю Земли, дает ЭДС = Bℓv = (5,0 × 10–5T) (1,0 м) (3,0 м/с) = 150 мкВ. .ЭДС=Bℓv=(5,0×10-5T)(1,0 м)(3,0 м/с)=150 мкВ. size 12{«emf»=Bℓv= \( 5 «.» 0 раз «10» rSup { size 8{ — 5} } T \) \( 1 «.» 0`m \) \( 3 «.» 0 `»м/с» \) =»150″`»мкВ»} {} Это небольшое значение соответствует опыту. Однако есть эффектное исключение. В 1992 и 1996, с помощью космического корабля «Шаттл» были предприняты попытки создать большие ЭДС движения. Привязанный спутник должен был быть выпущен по проводу длиной 20 км, как показано на рис. 6.12, для создания ЭДС 5 кВ за счет движения с орбитальной скоростью через поле Земли. Эту ЭДС можно было бы использовать для преобразования части кинетической и потенциальной энергии шаттла в электрическую энергию, если бы удалось создать полную цепь. Чтобы завершить цепь, неподвижная ионосфера должна была обеспечить обратный путь для протекания тока. (Ионосфера — это разреженная и частично ионизированная атмосфера на орбитальных высотах. Она проводит ток из-за ионизации. Ионосфера выполняет ту же функцию, что и неподвижные рельсы и соединительный резистор на рис. 6.11, без которых не было бы полной цепи.) на ток в кабеле за счет магнитной силы F=IℓBsinθF=IℓBsinθ размер 12{F=IℓB»sin»θ} {} совершает работу, которая уменьшает кинетическую и потенциальную энергию челнока и позволяет преобразовать ее в электрическую энергию. Оба теста оказались неудачными. В первом кабель болтался и его можно было протянуть только на пару сотен метров; во втором трос оборвался при почти полном вытягивании. Пример 6.2 указывает на принципиальную возможность.

Пример 6.2 Расчет большой ЭДС движения объекта на орбите

Рис. 6.12 ЭДС движения как преобразование электроэнергии для космического челнока является мотивом для эксперимента с привязанным спутником. Было предсказано, что ЭДС 5 кВ будет индуцироваться в тросе длиной 20 км при движении с орбитальной скоростью в магнитном поле Земли. Цепь завершается обратным путем через стационарную ионосферу.

Рассчитайте ЭДС движения вдоль проводника длиной 20,0 км, движущегося с орбитальной скоростью 7,80 км/с перпендикулярно Земле 5,00×10−5T5,00×10−5T размером 12{5 «.» «00» умножить на «10» rSup { размер 8{ — 5} } T} {} магнитное поле.

Стратегия

Это прямое применение выражения для ЭДС движения — ЭДС=Bℓv.ЭДС=Bℓv. size 12{«emf»=Bℓv} {}

Решение

Ввод заданных значений в emf=Bℓvemf=Bℓv size 12{«emf»=Bℓv} {} дает

6.10 emf = B ℓv      = (5,00 × 10−5T)(2,0×104 м)(7,80×103 м/с)     = 7,80 × 103 В.э.д.с. = Bℓv      = (5,00 × 10-5T)(2,0 × 104 м)(7,80 × 103 м/с)      = 7,80 × 103 В.

Обсуждение

Полученное значение превышает измеренное напряжение 5 кВ для эксперимента с челноком, поскольку фактическое орбитальное движение троса не перпендикулярно полю Земли. Значение 7,80 кВ является максимальной ЭДС, полученной при θ=90ºθ=90º размера 12{θ=»90″°} {} и sinθ=1.sinθ=1. размер 12{«sin»θ=1} {}

Переменный ток и ЭДС: определение, формула и объяснение

Переменный ток

Мы уже знали, что постоянный ток (DC) создается источником напряжения, полюса которого не меняют своей полярности со временем.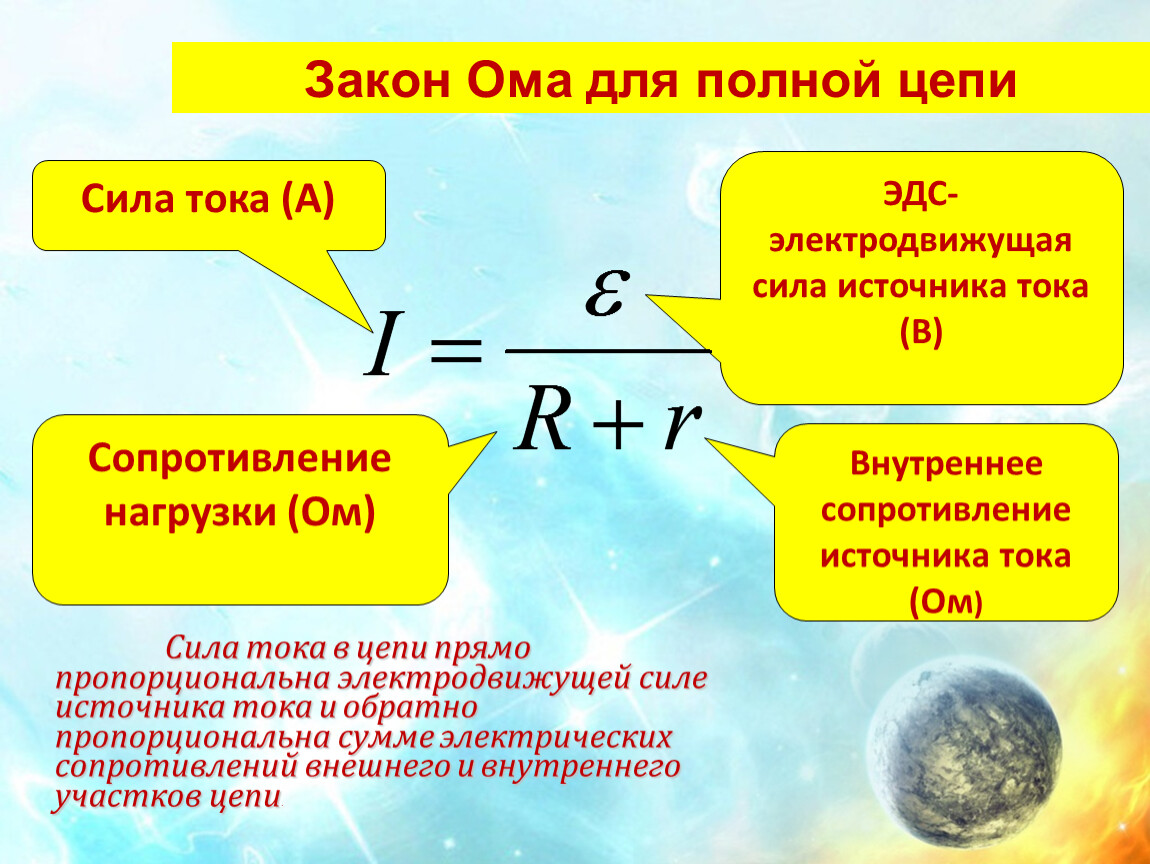 Следовательно, направление потока постоянного тока не меняется со временем.

С другой стороны, переменный ток создается источником напряжения, полярность клемм которого постоянно меняется со временем, т. е. клемма, которая была положительной в один момент времени, через какое-то время становится отрицательной, и наоборот.

Из-за изменения полярности источника напряжения направление протекания тока также продолжает меняться.

В этой главе «Переменный ток и электрические машины» мы узнаем, как напряжение и ток, изменяющиеся во времени, связаны друг с другом в различных цепях с компонентами, а именно резисторами, конденсатором и катушкой индуктивности.

Переменный ток Определение

Переменный ток – это ток, величина которого постоянно меняется со временем, а направление периодически меняется на противоположное.

Переменный ток – это ток, величина которого изменяется по синусоидальному закону во времени. Таким образом, переменный ток определяется как
$$I=I_0sin\left(\omega t\right)\tag{1}$$ Или это также может быть представлено уравнением
$$I=I_0cos\left(\omega t\right)$$ Где
$I_0=$ амплитуда тока или пиковое значение переменного тока.
Оба эти представления приводят к одному и тому же результату.

Если $T$ — период переменного тока, а $f$ — частота, то
$$\omega=\frac{2\pi}{T}=2\pi f \tag{2}$$ Где $\omega$ называется угловой частотой переменного тока, а $\phi$ называется фазовой постоянной. Полный набор изменений тока за один период времени T называется цикл .

Вместо функции синуса AC также может быть представлен функцией косинуса, и каждое представление приводит к одинаковым результатам. Мы обсудим схемы с синусоидальным представлением переменного тока

На приведенном ниже рисунке показан контраст между переменным и постоянным током. Он показывает изменение переменного и постоянного тока во времени.

Переменный ток, меняющийся во времени по синусоидальному закону. Эта цифра представляет изменение переменного тока во времени.

Из этого рисунка ясно видно, что переменный ток возрастает от 0 до максимума в одном направлении, затем падает до нуля в момент Т/2, затем возрастает от 0 до максимума в противоположном направлении и снова падает до нуля в момент времени Т, завершая один полный цикл.

Здесь важно отметить, что
Поскольку переменный ток положительный в одной половине цикла и отрицательный в другой, его среднее значение за весь цикл равно нулю. Это будет доказано в следующем разделе статьи.

Что такое переменная ЭДС?

Полная форма переменной ЭДС – переменная электродвижущая сила. Давайте теперь поймем значение переменной ЭДС, сначала определив ее.

Переменная ЭДС определение

ЭДС или напряжение, величина которого изменяется синусоидально со временем, известна как переменная ЭДС и представлена ​​соотношением
$$E=E_0sin\left(\omega t\right)\tag{3}$$ Или это также может быть представлено
$$E=E_0cos\left(\omega t\right)$$ где $E_0$ — пиковое значение переменной ЭДС.
Вышеупомянутое уравнение представляет мгновенное значение переменной ЭДС.

Так вот, например, величина ЭДС меняется со временем и ее направление периодически меняется на противоположное.

Важные термины, относящиеся к AC

Давайте начнем наше обсуждение с того, что сначала посмотрим, как генерируется переменная ЭДС? При вращении катушки в магнитном поле возникает переменная ЭДС. Соотношение (1) и (3) дает нам соотношение для переменного тока и переменной ЭДС и показывает нам, как они меняются со временем.

Теперь предположим, что эта ЭДС приложена к электрической цепи сопротивлением $R$. Тогда ток, протекающий по этой цепи, будет $$I=\frac{E}{R}=\frac{E_0}{R}sin\left(\omega t\right)$$ Или, $$I=I_0sin\влево(\омега т\вправо)$$ Как мы знаем, это соотношение для переменного тока в цепи. Это уравнение представляет мгновенное значение переменного тока.
Здесь
$I= $ мгновенное значение переменного тока
$I_0=\frac{E_0}{R}=$ пиковое или максимальное значение переменного тока, также известное как амплитуда тока.

Амплитуда переменного тока

Это максимальное значение, достигаемое переменным током в любом направлении. Оно также известно как пиковое значение тока и обозначается $I_0$.

Формула амплитуды тока

Он определяется соотношением $$I_0=\frac{E_0}{R}$$

Период времени переменного тока

Время, за которое переменный ток совершает один цикл своих изменений, называется его периодом времени и обозначается $T$.
$$\text{Период времени} = \frac{\text{Угловое смещение за полный цикл}}{\text{Угловая скорость}}$$ Или, $$T=\frac{2\pi}{\omega}$$

Частота переменного тока

Число циклов, совершаемых АС в секунду, называется его частотой и обозначается $f$. $$f=\frac{1}{T}=\frac{\omega}{2\pi}$$

Среднее значение переменного тока за один полный цикл

Важный вывод: Докажите математически, что среднее значение переменного тока за один полный цикл равно нулю.

Мы знаем, что мгновенное значение AC в любой момент времени $t$ определяется как
$I=I_0 \sin\omega t$
Предположим, что этот ток постоянен в течение очень малого промежутка времени $dt$, тогда количество заряда который протекает по контуру за этот небольшой промежуток времени $dt$, составляет 9{Т}\\ &=-\frac{I_0 T}{2\pi}\left [ \cos 2\pi — \cos 0\right ]\\ &=-\frac{I_0 T}{2\pi}\left [ 1 — 1 \right ]=0 \конец{выравнивание*} Это доказывает, что среднее значение AC за один полный цикл равно
$\langle I\rangle_{full\;cycle}=\frac{q}{T}=0$
, что равно нулю.