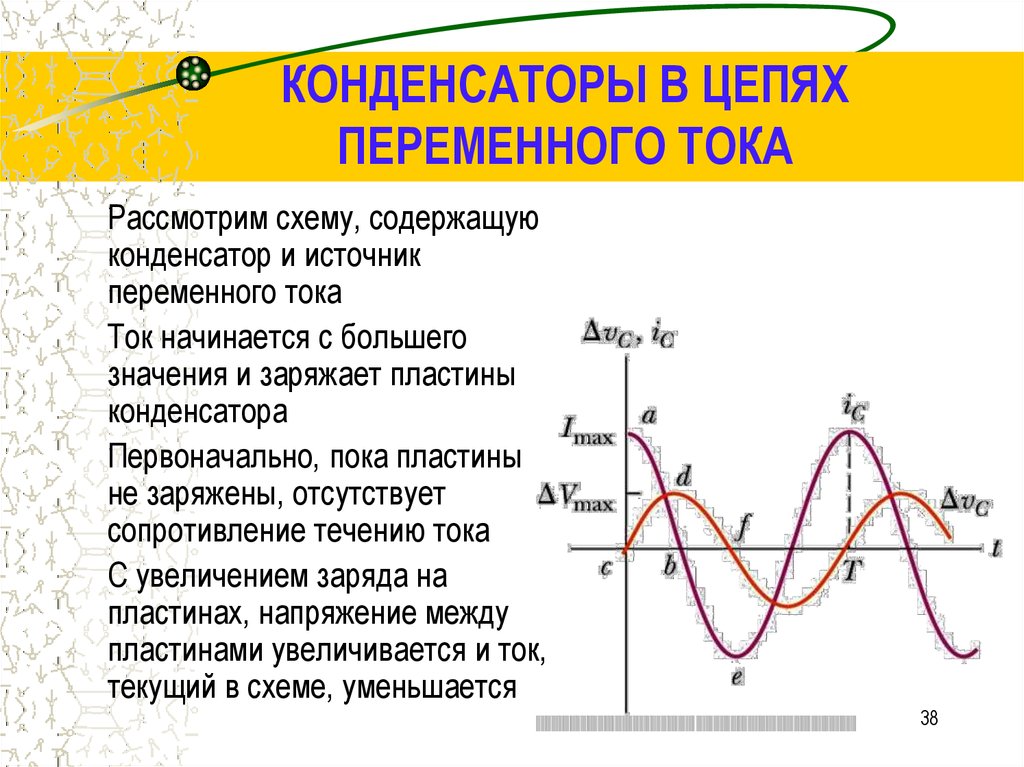
Цепь переменного тока с конденсатором

При переменном напряжении на реальном конденсаторе кроме тока смещения имеются небольшие токи проводимости, через толщу диэлектрика (объемный ток) и по поверхности (поверхностный ток).Токи проводимости и поляризацию диэлектрика сопровождают потери энергии.

Таким образом, в реальном конденсаторе наряду с изменением энергии электрического поля (это характеризует реактивная мощность Q) из-за несовершенства диэлектрика идет необратимый процесс преобразования электрической энергии в тепло, скорость которого выражается активной мощностью Р. Поэтому в схеме замещения реальный конденсатор должен быть представлен активным и реактивным элементами.

Деление реального конденсатора на два элемента — это расчетный прием, так как конструктивно их выделить нельзя. Однако такую же схему замещения имеет реальная цепь из двух элементов, один из которых характеризуется только активной мощностью Р (Q = 0), другой — реактивной (емкостной) мощностью Q(P = 0).

Схема замещения конденсатора с параллельным соединением элементов

Реальный конденсатор (с потерями) можно представить эквивалентной схемой параллельного соединения активной G и емкостной B_с проводимостей (рис. 13.15), причем активная проводимость определяется мощностью потерь в конденсаторе G = Р/U_c², а емкость — конструкцией конденсатора. Предположим, что проводимости G и В_с для такой цепи известны, а напряжение имеет уравнение

u = Umsinωt.

Требуется определить токи в цепи и мощность. Исследование цепи с активным сопротивлением и цепи с емкостью показало, что при синусоидальном напряжении токи в них так же синусоидальны. При параллельном соединении ветвей G и В_с , согласно первому закону Кирхгофа, общий ток i равен сумме токов в ветвях с активной и емкостной проводимостями:

i = i_G + i_c,                                                      (13. 30)

Учитывая, что ток i_G совпадает по фазе с напряжением, а ток i_c опережает напряжение на четверть периода, уравнение общего тока можно записать в следующем виде:

 

Векторная диаграмма токов в цепи с конденсатором

Для определения действующей величины общего тока I методом векторного сложения построим векторную диаграмму согласно уравнению

I = I_G + I_C

 

Действующие величины составляющих тока:

 

I_G = GU                                                       (13.31)

 

I_C = B_CU                                                      (13.32)

Первым на векторной диаграмме изображается вектор напряжения U (рис. 13.16, а), его направление совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза напряжения φ_a =0). Вектор I_G совпадает по направлению с вектором U, а вектор I_C направлен перпендикулярно вектору U с положительным углом. Из векторной диаграммы видно, что вектор общего напряжения отстает от вектора общего тока на угол φ, величина которого больше нуля, но меньше 90º. Вектор I является гипотенузой прямоугольного треугольника, катеты которого — составляющие его векторы I_G и I_C : При напряжении u = U_msinωt соответствии с векторной диаграммой уравнение тока

i = I_msin(ωt + φ)

 

Треугольник проводимостей для конденсатора

Стороны треугольников токов, выраженные в единицах тока, разделим на напряжение U. Получим подобный треугольник проводимостей (рис. 13.16, б), катетами которого являются активная G = I_G/U и емкостная В_с = I_с/U проводимости, а гипотенузой — полная проводимость цепи Y = I/U. Из треугольника проводимостей

Связь между действующими величинами напряжения и тока выражается формулами

I = UY

 

U = I/Y                                                        (13.35)

 

Из треугольников токов и проводимостей определяют величины

 

cosφ = I_G/I = G/Y;                sinφ = I_c/I = B_c/Y;              tgφ = I_C/I_G = B_c/G.               (13.36)

 

Мощность цепи с конденсатором

Выражение мгновенной мощности реального конденсатора

p = ui = U_msinωt * I_msin(ωt+φ)

совпадает с выражением мгновенной мощности катушки. Рассуждения, аналогичные тем, которые сделаны при рассмотрении графика мгновенной мощности катушки (см. рис.13. 11), можно провести и для реального конденсатора на основе графика рис. 13.17. Величины активной, реактивной и полной мощностей выражаются теми же формулами, какие были получены для катушки [см. (13.19) — (13.22)]. Это нетрудно показать, если стороны треугольника токов, выраженные в единицах тока, умножить на напряжение U. В результате умножения получится подобный треугольник мощностей (рис. 13.16, в), катетами которого являются мощности; активная

 P = UI_G = UIcosφ

реактивная

Q = UI_C = UIsinφ

полная

 

Схема замещения конденсатора с последовательным соединением элементов

Реальный конденсатор, так же как и катушка, на расчетной схеме может быть представлен последовательным соединением двух участков: с активным R и емкостным Х_с сопротивлениями. На рис. 13.18, а такая схема показана в сравнении со схемой параллельного соединения активной и емкостной проводимостей (рис.13. 18,6). Все выводы и формулы, полученные для катушки, остаются в силе и для конденсатора при условии замены индуктивного сопротивления емкостным. Конденсаторы, применяемые на практике, имеют относительно малые потери энергии. Поэтому в схемах замещения они представлены чаще всего только реактивной частью, т. е.

емкостью С[B_C = ωC, X_c = 1/(ωC)] Участки цепи, где последовательно соединены отдельные элементы — резистор R и конденсатор С, имеют такую схему замещения, как показано на рис. 13.18, а. Если вам интересно прочитайте статью о настоящих конденсаторах которые применяются в промышленности.

27.03.2014

ТОЭ,Переменный ток

Расчет цепей синусоидального тока

Физика — 11

Таблица 3.3. Цепь переменного тока с активным сопротивлением.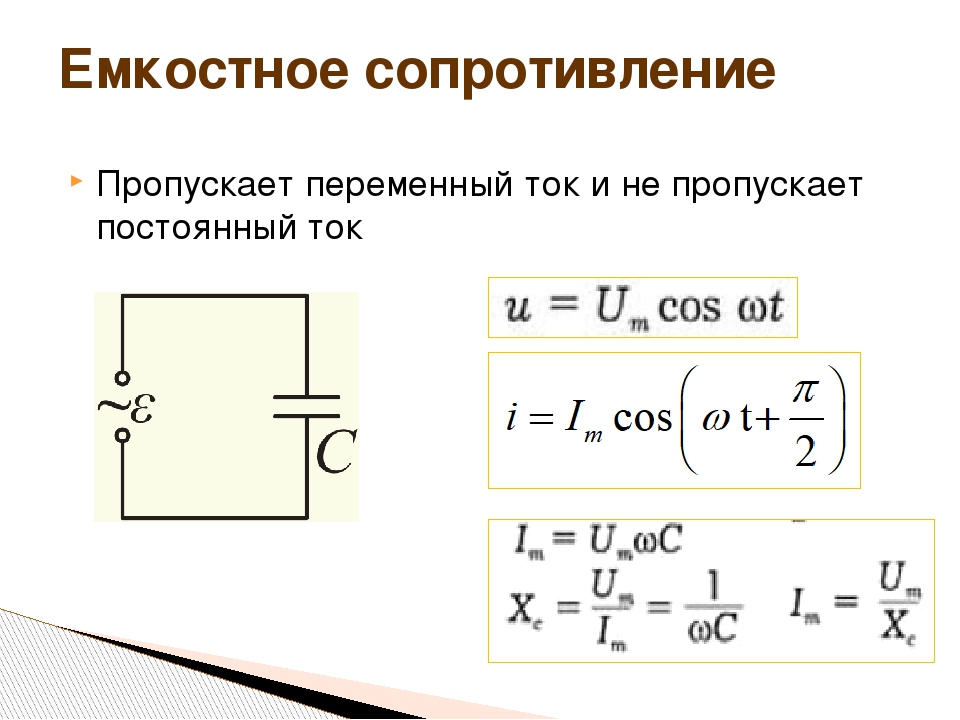

Соотношения между характеристиками

Графики характеристик

Согласно закону Ома: i = u R = Um R sinωt = Imsinωt. В цепи, состоящей только из резистора, сила тока i и напряжение u колеблются в одинаковых фазах. Поэтому: φ0 = 0 и cos φ0 = 1 В этом случае средняя мощность: = Im ⋅ Um 2 ⋅ cosφ0 = Im ⋅ Um 2 = I2mR 2 Мгновенная мощность: P = iu = i2R = I 2mRsin2ωt. • В цепи переменного тока, содержащей только резистор, активное сопротивление, амплитудные значения силы тока и напряжения не зависят от частоты переменного тока.

Конденсатор в цепи переменного тока. Как будут меняться величины, характеризующие переменный ток, в цепи переменного тока с конденсатором?

ИССЛЕДОВАНИЕ

1

В каком случае в цепи с конденсатором существует ток?

Оборудование: конденсатор (100 мкФ), лампа (4В), источники постоянного и переменного тока, ключ (2 пгг.), соединительные провода.

Ход работы:

1.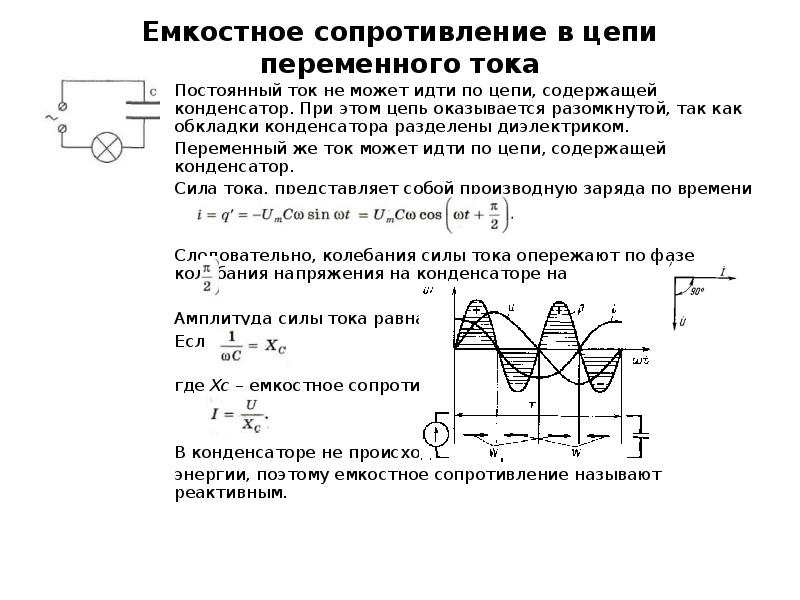 Соберите цепь, руководствуясь схемой (b). 2. Замкнув ключ 1, подсоедините конденсатор к источнику постоянного напряжения и наблюдайте за происходящим.

3. Разомкните ключ 1 и затем, замкнув ключ 2, подсоедините конденсатор к источнику переменного тока, одновременно продолжая наблюдать за происходящим.

4. Подсоедините лампу непосредственно к источнику переменного тока без конденсатора и сравните ее свечение (излучение) со свечением в цепи с конденсатором.

Обсуждение результата:

• При соединении конденсатора в какой цепи электрический ток существовал, и лампа светилась? Почему?
• В какой цепи переменного тока лампа светила ярче: с конденсатором или без? Почему?

При подсоединении конденсатора к источнику постоянного тока по цепи проходит кратковременный ток, лампа на миг загорается и сразу гаснет. Причиной кратковременности тока является наличие диэлектрика между пластинами конденсатора.

Конденсатор, подсоединенный к источнику переменного тока, периодически перезаряжаясь, обеспечивает ток в цепи и свечение лампы. Если лампа подсоединена к источнику переменного тока напрямую без конденсатора, то она светит ярче, чем в той же цепи с конденсатором. Уменьшение яркости свечения лампы свидетельствует о сопротивлении, которое создает конденсатор в этой цепи. Сопротивление, созданное конденсатором, называют ёмкостным сопротивлением и обозначают символом X_c. Соотношения между величинами, характеризующими цепь переменного тока с конденсатором, систематизированы в таблице 3.4.

Конденсатор напряжения переменного тока — 88Guru

Введение

Мы знаем, что конденсатор состоит из двух пластин проводников, разделенных изолированным расстоянием, и также известен как диэлектрик. Конденсатор ограничивает или регулирует ток при подключении к источнику переменного тока, но полностью не предотвращает дрейф заряда.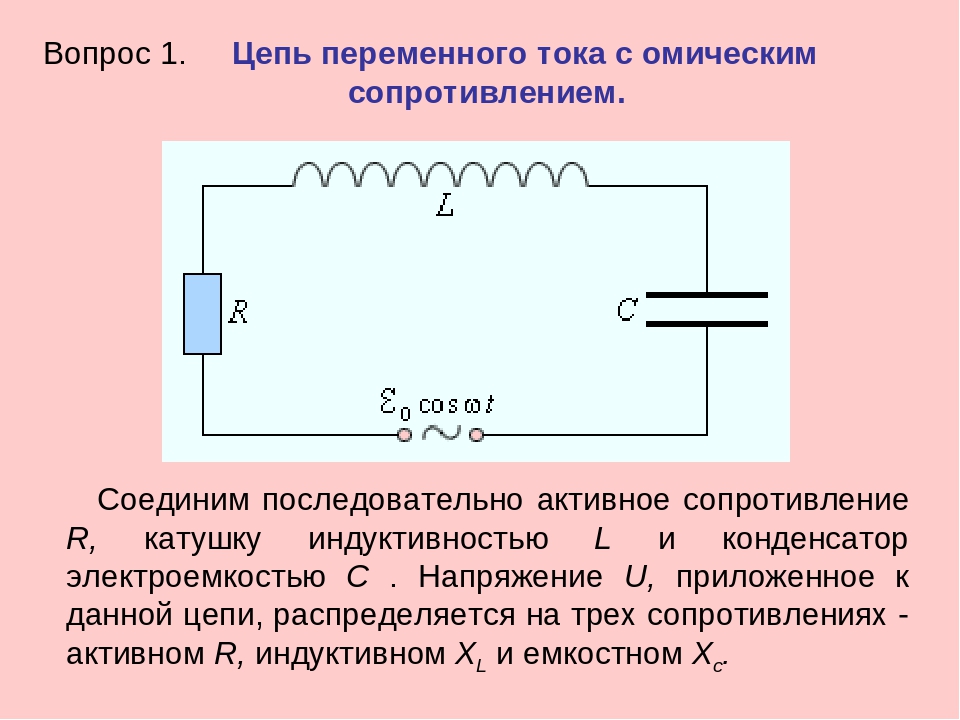 Конденсатор постепенно заряжается и разряжается по мере изменения направления тока в течение каждого полупериода. Наибольший зарядный ток возникает, когда пластины конденсатора не заряжается , поэтому процесс зарядки не является линейным или мгновенным. Подобно конденсатору, когда он полностью заряжен , его заряд начинает резко падать. Способность конденсатора удерживать заряд на своих пластинах называется емкостью. Когда конденсатор подключен к источнику напряжения в цепи постоянного тока, ток течет в течение короткого периода времени, необходимого для зарядки конденсатора. Напряжение на проводящих пластинах увеличивается по мере накопления на них заряда, уменьшая ток. Ток цепи обнуляется после того, как конденсатор полностью разрядится.0003 заряжено .

Емкость в цепях переменного тока и емкостное реактивное сопротивление

Расчетная способность конденсатора накапливать энергию в цепи переменного тока называется емкостью. Отношение электрического заряда к соответствующей разности его электрических потенциалов называется емкостью.

$$C=\frac{d Q}{d V}$$

Где dQ и dV — заряд и разность потенциалов на конденсаторах соответственно. Емкость также может быть определена как свойство конденсатора накапливать заряд. Соотношение между зарядным током (I) и конденсаторами, при которых изменяется напряжение питания конденсаторов, определяется выражением

$$I=C \frac{d Q}{d V}$$

Емкостное реактивное сопротивление

Емкостное реактивное сопротивление сопротивление потоку электричества через конденсатор переменного тока. Он рассчитывается в омах, обозначается \(X_C\) и измеряется в единицах Ω. Он рассчитывается математически по приведенной формуле.

$$X_C=\frac{1}{2 \pi f C}=\frac{1}{\omega C}$$

Где f — частота, C — емкость, ⍵=2πf.

Отношение эффективного тока к напряжению на конденсаторе — еще один способ описания емкостного реактивное сопротивление . Получаем вывод, что емкостное реактивное сопротивление обратно пропорционально частоте из вышеупомянутой связи. Это означает, что падение частоты на конденсаторе приведет к уменьшению емкостного реактивного сопротивления и наоборот.

Как конденсатор работает при переменном токе?

Конденсатор напрямую связан с источником переменного тока в цепи переменного тока. Конденсатор проходит через процесс зарядки или разрядки и блокирует постоянный ток, когда применяется источник переменного тока. Конденсатор также частично препятствует прохождению сигнала переменного тока. Реактивное сопротивление — это термин, используемый для описания свойств конденсатора в ответ на сигнал переменного тока. Конденсатор имеет короткое замыкание по переменному току.

Цепи конденсаторов переменного тока?

Конденсаторная цепь переменного тока напрямую соединяет источник переменного тока с конденсатором, позволяя току течь по цепи. Пластины конденсатора постоянно заряжаются и разряжаются в результате подачи переменного тока.

Конденсатор подключен к цепи переменного тока.

Роль конденсатора в цепи переменного тока

Пока есть источник, конденсатор будет постоянно заряжаться и разряжаться. Однако постоянная времени определяет, будет ли он полностью заряжаться (преобразовывать электрическую энергию в заряд для хранения между двумя пластинами) или полностью разряжаться (заряжаться в электрическую энергию). Мы должны использовать нагрузку для зарядки конденсатора. Постоянная времени равна RC, где C — емкость, а R — сопротивление нагрузки цепи. Конденсатор начинает заряжаться, когда на его пути находится источник питания. Когда полностью зарядил , он будет ждать подходящего времени, чтобы высвободить накопленную энергию.

Роль конденсатора в цепи постоянного тока

Конденсатор начинает заряжаться, как только подключается источник постоянного тока, поскольку источники постоянного тока имеют постоянное напряжение. Как только полностью зарядит , он будет ждать подходящего момента, чтобы снять накопленный заряд. В результате получается разомкнутая цепь после полной зарядки . В результате конденсатор действует как компонент разомкнутой цепи. Зарядка постоянно заряжал и разряжал переменным током, правда, из-за переменного напряжения. Конденсатор, таким образом, выполняет роль резистора. В этом случае вместо сопротивления используется реактивное сопротивление , а реактивное сопротивление конденсатора равно

$$
\frac{1}{2 \pi f C} .
$$

Функция конденсатора в цепи переменного тока

Электрические цепи содержат конденсаторы, которые накапливают электрическую энергию и повышают коэффициент мощности цепи.

$$
\text { Коэффициент мощности }=\frac{\text { Активная мощность }}{\text { Полная мощность }}
$$

Переменный ток через конденсатор (вывод)

заряд на конденсаторе в данный момент времени t, и мгновенное напряжение V на конденсаторе, то мы можем написать,

$$
V=\frac{Q}{C}
$$

Напряжение на источнике и конденсатор однородный. Тогда по правилу цикла Кирхгофа

$$
V=V_m \sin \omega t
$$

Из приведенных выше двух уравнений можно написать, что

$$
V_m \sin \omega t=\frac{Q}{C}
$$

Опять же,

$$
I= \frac{d Q}{d t}
$$

$$
I=\frac{d}{d t}\left(C V_m \sin (\omega t)\right)=\omega C V_m \cos ( \omega t)
$$

Теперь, как мы знаем,

$$
\begin{gathered}
\cos (\omega t)=\sin \left(\omega t+\frac{\pi}{2 }\right) \\
I=I_m \sin \left(\omega t+\frac{\pi}{2}\right) \\
I_m=\frac{V_m}{\left(\frac{1}{\omega C}\right)}
\end{собран}
$$

\(\frac{1}{2 \pi f C } \) является емкостным реактивным сопротивлением и обозначается \(X_C\).

Итак,

$$
I_m=\frac{V_m}{X_C}
$$

Резюме

Конденсатор представляет собой электрическую деталь, создающую прямую связь с напряжением источника переменного тока. Конденсатор изменяет свой заряд или разряд в ответ на изменение напряжения питания. Без реального тока, проходящего через конденсатор, ток цепи сначала будет течь в одном направлении, прежде чем переключаться в другом. В цепи с постоянным током все обстоит иначе. Пластина конденсатора содержит как положительные, так и отрицательные заряды, когда через нее проходит ток, когда она подключена к цепи постоянного тока. Во многих различных секторах, включая накопители энергии , фильтры, выпрямители и прочее, конденсаторы используются. Кроме того, он используется в цепях для повышения напряжения и сглаживания колебаний тока.

Часто задаваемые вопросы

1. Что такое емкостное сопротивление?

Ответ: Емкостное реактивное сопротивление в электрической цепи – это сопротивление, которое конденсатор оказывает потоку переменного тока

2. Сформулируйте закон Кирхгофа для напряжения.

Ответ: Алгебраическая сумма разностей потенциалов и электродвижущих сил равна нулю в замкнутом контуре.

3. Укажите роль конденсатора в цепи переменного тока.

Ответ: Заряд непрерывно заряжается и разряжается в цепи переменного тока из-за переменного напряжения. Конденсатор, таким образом, выполняет роль резистора. В этом случае вместо сопротивления используется реактивное сопротивление , а конденсатор .0003 реактивное сопротивление равно \(\frac{1}{2 \pi f C} \).

4. Укажите роль конденсатора в цепи постоянного тока.

Ответ: Конденсатор начинает заряжаться, как только подключается источник постоянного тока, поскольку напряжение источника постоянного тока постоянно. Как только полностью зарядит , он будет ждать подходящего момента, чтобы снять накопленный заряд. В результате получается разомкнутая цепь после полной зарядки . В результате конденсатор действует как компонент разомкнутой цепи.

5. Что такое электролитический конденсатор?

Ответ: Электролитический конденсатор — это конденсатор, в котором подвижность ионов обеспечивает проводимость. Жидкость или гель с высокой концентрацией ионов называют электролитом.

Теги : Напряжение переменного тока , Конденсатор , Зарядка , Разрядка , Электропитание , Реактивное сопротивление , Сопротивление

Компания 88Guru была создана с социальной целью сделать качественные обучающие видео материалы доступными для всех индийских студентов. Технологии, возможности подключения и социальные сети быстро меняют мир образования, и мы хотим возглавить трансформацию индустрии обучения в Индии.

88Guru — идеальное дополнение к текущей модели обучения. 88Guru создает прекрасную возможность для детей и родителей сблизиться, участвуя в ценной учебной деятельности. Он также предоставляет полную учебную программу на кончиках ваших пальцев для тех моментов, когда вам нужна помощь в короткие сроки. Мы считаем, что этот способ обучения может быть трансформационным, добавляя часы к дню ребенка, обеспечивая при этом полный контроль над процессом обучения.

Каждый курс преподается лучшими учителями из лучших школ Индии и проводится в увлекательной манере, чтобы заинтересовать учащихся. Процесс электронного обучения состоит из видеоинструкций, заданий с компьютерной оценкой и информационной панели, которая позволяет ученику и родителю отслеживать прогресс.

8.10 Реактивное, индуктивное и емкостное сопротивление – Колледж Дугласа, физика 1207

Глава 8 Электромагнитная индукция, цепи переменного тока и электрические технологии

Резюме

• График зависимости напряжения и тока от времени в простых индуктивных, емкостных и резистивных цепях.
• Рассчитать индуктивное и емкостное сопротивление.
• Расчет тока и/или напряжения в простых индуктивных, емкостных и резистивных цепях.

Многие схемы также содержат конденсаторы и катушки индуктивности в дополнение к резисторам и источнику переменного напряжения. Мы видели, как конденсаторы и катушки индуктивности реагируют на постоянное напряжение при его включении и выключении. Теперь мы рассмотрим, как катушки индуктивности и конденсаторы реагируют на синусоидальное переменное напряжение.

Предположим, что катушка индуктивности подключена непосредственно к источнику переменного напряжения, как показано на рис. 1. Разумно предположить пренебрежимо малое сопротивление, так как на практике мы можем сделать сопротивление катушки индуктивности настолько малым, что оно окажет незначительное влияние на цепь. Также показан график зависимости напряжения и тока от времени.

Рис. 1. (a) Источник переменного напряжения, включенный последовательно с катушкой индуктивности, имеющей незначительное сопротивление. (б) График тока и напряжения на катушке индуктивности в зависимости от времени.

График на рис. 2(b) начинается с максимального напряжения. Обратите внимание, что ток начинается с нуля и достигает своего пика 90 251 после 90 252 управляющего им напряжения, как это было в случае, когда в предыдущем разделе было включено постоянное напряжение. Когда напряжение в точке а становится отрицательным, ток начинает уменьшаться; он становится равным нулю в точке b, где напряжение является самым отрицательным.

Затем ток становится отрицательным, снова следуя за напряжением. Напряжение становится положительным в точке с и начинает делать ток менее отрицательным. В точке d ток проходит через нуль как раз в тот момент, когда напряжение достигает своего положительного пика, чтобы начать новый цикл. Это поведение резюмируется следующим образом:

Напряжение переменного тока в катушке индуктивности

Когда синусоидальное напряжение подается на катушку индуктивности, напряжение опережает ток на одну четвертую периода или на фазовый угол 90 ^o .

Ток отстает от напряжения, так как катушки индуктивности препятствуют изменению тока. Изменение тока индуцирует противо-ЭДС 90 167 V = -L ( ΔI / Δt) 90 168   Это считается эффективным сопротивлением катушки индуктивности переменному току. Действующее значение тока

I через катушку индуктивности L определяется вариантом закона Ома:

, где В — среднеквадратичное напряжение на катушке индуктивности, а X _L  определено как

.

X _Д = 2 π f Д

с f частотой источника переменного напряжения в герцах (анализ цепи с использованием правила контура Кирхгофа и исчисления фактически дает это выражение). X _L называется индуктивным реактивным сопротивлением, потому что индуктор препятствует протеканию тока. Х _Д имеет единицы измерения в омах ( 1 Гн = 1 Ом•с ), так что частота, умноженная на индуктивность, имеет единицы измерения сопротивления как (циклы/с)( Ом•с) = Ом, что согласуется с его ролью эффективного сопротивления. Имеет смысл, что X _L пропорционально L , поскольку чем больше индукция, тем больше ее сопротивление изменению. Также разумно, что X _L пропорционально частоте f , поскольку большая частота означает большее изменение тока. то есть ΔI/Δt большое для больших частот (большое f , маленькое Δt ). Чем больше изменение, тем больше сопротивление индуктора.

Пример 1. Расчет индуктивного реактивного сопротивления, а затем тока

(a) Рассчитайте индуктивное сопротивление катушки индуктивности 3,00 мГн при подаче переменного напряжения 60,0 Гц и 10,0 кГц . (b) Чему равно среднеквадратичное значение тока на каждой частоте, если приложенное среднеквадратичное напряжение равно 120 В ?

Стратегия

Индуктивное сопротивление находится непосредственно из выражения X _L = 2 π fL. После того, как X _L найдено на каждой частоте, можно использовать закон Ома, сформулированный в уравнении I=V/X _L , для определения тока на каждой частоте.

Решение для (a)

Ввод частоты и индуктивности в уравнение X _L = 2 π фл0272 L = 2 π fL = 6,28 (60,0 /с) (3,00 мГн) = 1,13 Ом при 60 Гц.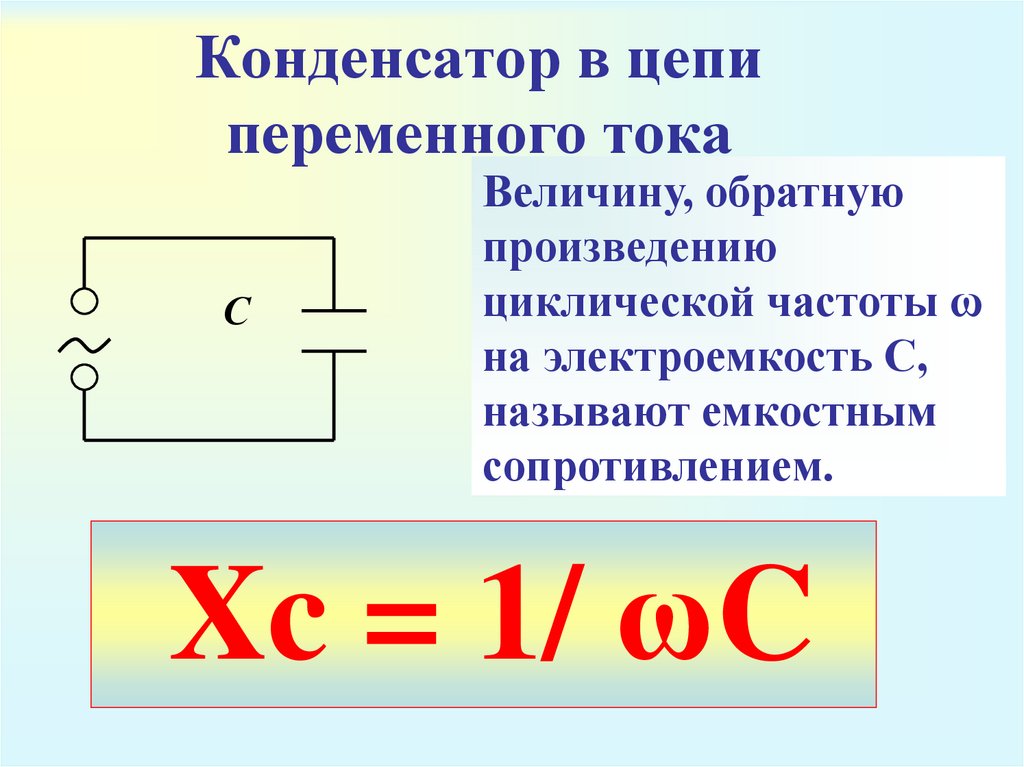

Аналогично, при 10 кГц

X _L = 2 π fL = 6,28 (10 x 10 ³  /с) (3,00 мГн) = 188 Ом при 10 кГц.

Решение для (b)

Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в уравнении I = V/X _L , при условии, что приложенное среднеквадратичное напряжение равно 120 В. Для первой частоты , это дает

Аналогично, при 10 кГц

Обсуждение

Катушка индуктивности очень по-разному реагирует на двух разных частотах. На более высокой частоте его реактивное сопротивление велико, а ток мал, что соответствует тому, как индуктор препятствует быстрому изменению. Таким образом, высокие частоты препятствуют больше всего. Индукторы можно использовать для фильтрации высоких частот; например, большой индуктор можно включить последовательно с системой воспроизведения звука или последовательно с вашим домашним компьютером, чтобы уменьшить высокочастотный звук, выходящий из ваших динамиков, или высокочастотные скачки мощности в вашем компьютере.

Обратите внимание, что хотя сопротивление в рассматриваемой цепи незначительно, переменный ток не очень велик, поскольку индуктивное сопротивление препятствует его протеканию. При переменном токе нет времени для того, чтобы ток стал чрезвычайно большим.

Рассмотрим конденсатор, подключенный непосредственно к источнику переменного напряжения, как показано на рис. 2. Сопротивление такой цепи можно сделать настолько малым, что оно оказывает незначительное влияние по сравнению с конденсатором, поэтому мы можем предположить пренебрежимо малое сопротивление. Напряжение на конденсаторе и ток представлены на рисунке как функции времени.

Рис. 2. (a) Источник переменного напряжения, включенный последовательно с конденсатором C , имеющим незначительное сопротивление. (б) График тока и напряжения на конденсаторе в зависимости от времени.

График на рис. 2 начинается с максимального напряжения на конденсаторе. В этот момент ток равен нулю, потому что конденсатор полностью заряжен и останавливает поток. Затем напряжение падает, а ток становится отрицательным по мере разряда конденсатора. В точке а конденсатор полностью разряжен (Q=0 на нем) и напряжение на нем равно нулю. Ток между точками a и b остается отрицательным, что приводит к изменению напряжения на конденсаторе. Это завершается в точке b, где ток равен нулю, а напряжение имеет самое отрицательное значение. Ток становится положительным после точки b, нейтрализуя заряд конденсатора и сводя напряжение к нулю в точке c, что позволяет току достигать своего максимума. Между точками c и d ток падает до нуля, когда напряжение достигает своего пика, и процесс начинает повторяться. На протяжении всего цикла напряжение следует за током на одну четвертую цикла:

Напряжение переменного тока в конденсаторе

Когда на конденсатор подается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на фазовый угол 90 ^o .

Конденсатор влияет на ток, имея возможность полностью остановить его при полной зарядке. Поскольку применяется переменное напряжение, существует среднеквадратичное значение тока, но оно ограничено конденсатором. Это считается эффективным сопротивлением конденсатора переменному току, поэтому среднеквадратичное значение тока I n цепь, содержащая только конденсатор C согласно другой версии закона Ома равна

, где В — среднеквадратичное значение напряжения, а X _c определяется (как и X _L , это выражение для X _C ) является результатом анализа схемы с использованием правил Кирхкулуса быть

, где X _C называется емкостным реактивным сопротивлением, потому что конденсатор препятствует протеканию тока. X _C измеряется в омах (проверка оставлена ​​читателю в качестве упражнения). X _C обратно пропорциональна емкости C Чем больше конденсатор, тем больший заряд он может хранить и тем больший ток может протекать. Оно также обратно пропорционально частоте f ; чем больше частота, тем меньше времени остается для полной зарядки конденсатора, и поэтому он меньше препятствует току.

Пример 2. Расчет емкостного реактивного сопротивления, а затем тока

(a) Рассчитайте емкостное реактивное сопротивление конденсатора емкостью 5,00 мФ при подаче переменного напряжения частотой 60,0 Гц и 10,0 кГц. б) Чему равно среднеквадратичное значение тока, если приложенное среднеквадратичное напряжение равно 120 В?

Стратегия

Емкостное реактивное сопротивление находится непосредственно из выражения в . Как только X _C найдено на каждой частоте, можно использовать закон Ома, сформулированный как I = V/X _C , чтобы найти ток на каждой частоте.

Раствор для (а)

Ввод частоты и емкости в дает

Аналогично, при 10 кГц,

Решение для (b)

Среднеквадратичное значение тока теперь находится с использованием версии закона Ома в I = V/X _C , при условии, что приложенное среднеквадратичное значение напряжения составляет 120 В. Для первой частоты это дает

Аналогично, при 10 кГц, наоборот индуктор реагирует. На более высокой частоте его реактивное сопротивление мало, а ток велик. Конденсаторы способствуют изменениям, тогда как индукторы сопротивляются изменениям. Конденсаторы больше всего препятствуют низким частотам, поскольку низкая частота дает им время зарядиться и остановить ток. Конденсаторы можно использовать для фильтрации низких частот. Например, конденсатор, включенный последовательно со звуковоспроизводящей системой, избавляет ее от гула частотой 60 Гц.

Хотя конденсатор в основном представляет собой разомкнутую цепь, в цепи с переменным напряжением, приложенным к конденсатору, существует среднеквадратичное значение тока. Это связано с тем, что напряжение постоянно меняется, заряжая и разряжая конденсатор. Если частота стремится к нулю (постоянный ток), X _C , стремится к бесконечности, а ток равен нулю после зарядки конденсатора. На очень высоких частотах реактивное сопротивление конденсатора стремится к нулю — он имеет пренебрежимо малое реактивное сопротивление и не препятствует протеканию тока (он действует как простой провод). Конденсаторы оказывают противоположное воздействие на цепи переменного тока по сравнению с катушками индуктивности .

Напомню, что на рис. 3 показано напряжение переменного тока, приложенное к резистору, и график зависимости напряжения и тока от времени. Напряжение и ток равны в фазе в резисторе. Поведение простого сопротивления в цепи не зависит от частоты:

Рис. 3. (a) Источник переменного напряжения последовательно с резистором. (b) График зависимости тока и напряжения на резисторе от времени, показывающий, что они точно совпадают по фазе.

Напряжение переменного тока в резисторе

Когда на резистор подается синусоидальное напряжение, оно точно совпадает по фазе с током — они имеют фазовый угол 0 ^o .

• Для катушек индуктивности в цепях переменного тока мы обнаружили, что, когда к катушке индуктивности приложено синусоидальное напряжение, напряжение опережает ток на одну четвертую периода или на фазовый угол 90 ^o .
• Противодействие катушки индуктивности изменению тока выражается как вид сопротивления переменному току.
• Закон Ома для катушки индуктивности

  , где В — среднеквадратичное напряжение на катушке индуктивности.

• X _L  определяется как индуктивное реактивное сопротивление, определяемое формулой

  X _L = 2 π fL

  с f частотой источника переменного напряжения в герцах.

• Индуктивное сопротивление X _L измеряется в омах и имеет наибольшее значение на высоких частотах.
• Для конденсаторов мы обнаружили, что когда к конденсатору прикладывается синусоидальное напряжение, напряжение следует за током на одну четвертую периода или на 90 ^o фазовый угол.
• Поскольку конденсатор может останавливать ток при полной зарядке, он ограничивает ток и предлагает другую форму сопротивления переменному току; Закон Ома для конденсатора

  , где В — среднеквадратичное напряжение на конденсаторе.

• X _C  определяется как емкостное реактивное сопротивление, определяемое выражением
• X _C   измеряется в омах и максимальна на низких частотах.

Задачи и упражнения

1: При какой частоте дроссель 30,0 мГн будет иметь реактивное сопротивление 100 Ом.

2: Какое значение индуктивности следует использовать, если требуется реактивное сопротивление 20,0 кОм на частоте 500 Гц?

3: Какую емкость следует использовать для получения реактивного сопротивления 2,00 МОм при 60,0 Гц ?

4: При какой частоте конденсатор 80,0 мФ будет иметь реактивное сопротивление 0,250 Ом ?

5: (a) Найдите ток через катушку индуктивности 0,500 Гн , подключенную к источнику 60,0 Гц, 480 В переменного тока . (b) Какой будет ток на частоте 100 кГц ?

6: (a) Какой ток протекает, когда источник переменного тока с частотой 60,0 Гц, 480 В подключен к конденсатору 0,250 мкФ ? (b) Какой ток будет на частоте 25,0 кГц?

7: A 20,0 кГц, 16,0 В источник, подключенный к катушке индуктивности, дает 2,00 А ток. Индуктивность какая?

8: A 20,0 Гц, 16,0 В источник производит ток 2,00 мА при подключении к конденсатору. Какова емкость?

9: (a) Катушка индуктивности, предназначенная для фильтрации высокочастотных помех от питания, подаваемого на персональный компьютер, устанавливается последовательно с компьютером. Какая минимальная индуктивность должна быть у него, чтобы создать реактивное сопротивление 2,00 кОм для шума 15,0 кГц ? б) Каково его реактивное сопротивление при частоте 60,0 Гц?

10: Конденсатор на рис. 4(а) предназначен для фильтрации низкочастотных сигналов, препятствуя их передаче между цепями. а) Какая емкость необходима для получения реактивного сопротивления 100 кОм на частоте 120 Гц? (b) Каким будет его реактивное сопротивление при частоте 1,00 МГц ? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

11: Конденсатор на рис. 4(b) фильтрует высокочастотные сигналы, замыкая их на землю. а) Какая емкость необходима для получения реактивного сопротивления 10,0 м Ом для сигнала 5,00 кГц ? б) Каким будет его реактивное сопротивление при частоте 3,00 Гц ? (c) Обсудите последствия ваших ответов на вопросы (a) и (b).

12: необоснованные результаты

При записи напряжений, вызванных активностью головного мозга (ЭЭГ), сигнал 10,0 мВ с частотой 0,500 Гц подается на конденсатор, производящий ток 100 мА. Сопротивление незначительно.