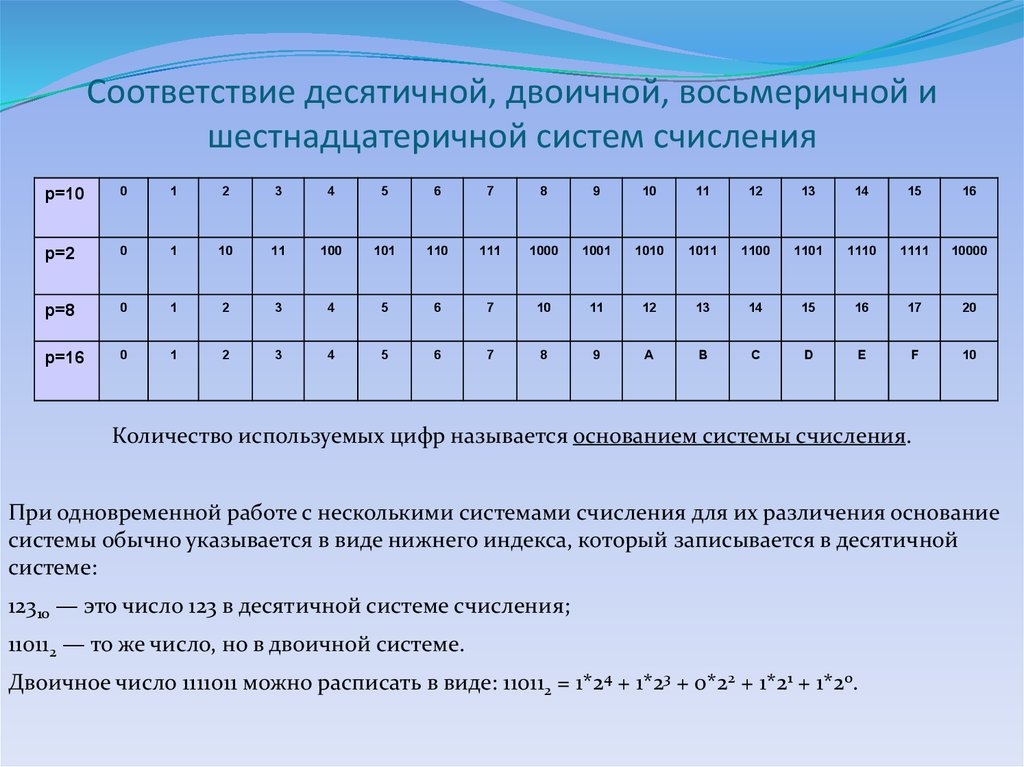
Pr2_9kl-системы счисления

Практическая работа № 1-2 (9 кл.)

ТЕМА: Работа с системами счисления.

ЦЕЛЬ: Выработать первичные навыки работы с системами счисления.

Теоретические сведения.

Система счисления – это совокупность правил для обозначения и наименования чисел.

Непозиционной называется такая система счисления, в которой количественный эквивалент каждой цифры не зависит от ее положения (места, позиции) в записи числа.

Основанием системы счисления называется количество знаков или символов, используемых для изображения числа в данной системе счисления.

Наименование системы счисления соответствует ее основанию (например, десятичной называется система счисления так потому, что ее основание равно 10, т.е. используется десять цифр).

Система счисления называется позиционной, если значение цифры зависит от ее места (позиции) в записи числа.

Системы счисления, используемые в компьютерах.

Двоичная система счисления. Для записи чисел используются только две цифры – 0 и 1. Выбор двоичной системы объясняется тем, что электронные элементы, из которых строятся ЭВМ, могут находиться только в двух хорошо различимых состояниях. По существу эти элементы представляют собой выключатели. Как известно выключатель либо включен, либо выключен. Третьего не дано. Одно из состояний обозначается цифрой 1, другое – 0. Благодаря таким особенностям двоичная система стала стандартом при построении ЭВМ.

Восьмеричная система счисления. Для записи чисел используется восемь чисел 0,1,2,3,4,5,6,7.

Шестнадцатеричная система счисления. Для записи чисел в шестнадцатеричной системе необходимо располагать шестнадцатью символами, используемыми как цифры. В качестве первых десяти используются те же, что и в десятичной системе. Для обозначения остальных шести цифр (в десятичной они соответствуют числам 10,11,12,13,14,15) используются буквы латинского алфавита – A,B,C,D,E,F.

Перевод целых чисел из десятичной системы счисления в другую.

Правило перевода целых чисел из десятичной системы счисления в систему с основанием q:

1. Последовательно выполнять деление исходного числа и получаемых частных на q до тех пор, пока не получим частное, меньшее делителя.

2. Полученные при таком делении остатки – цифры числа в системе счисления q – записать в обратном порядке (снизу вверх).

П ример1. Перевести 26₁₀ в двоичную систему счисления. А₁₀→А₂

Решение:

Ответ: 26₁₀=110102

П

19

18

1

3

ример2.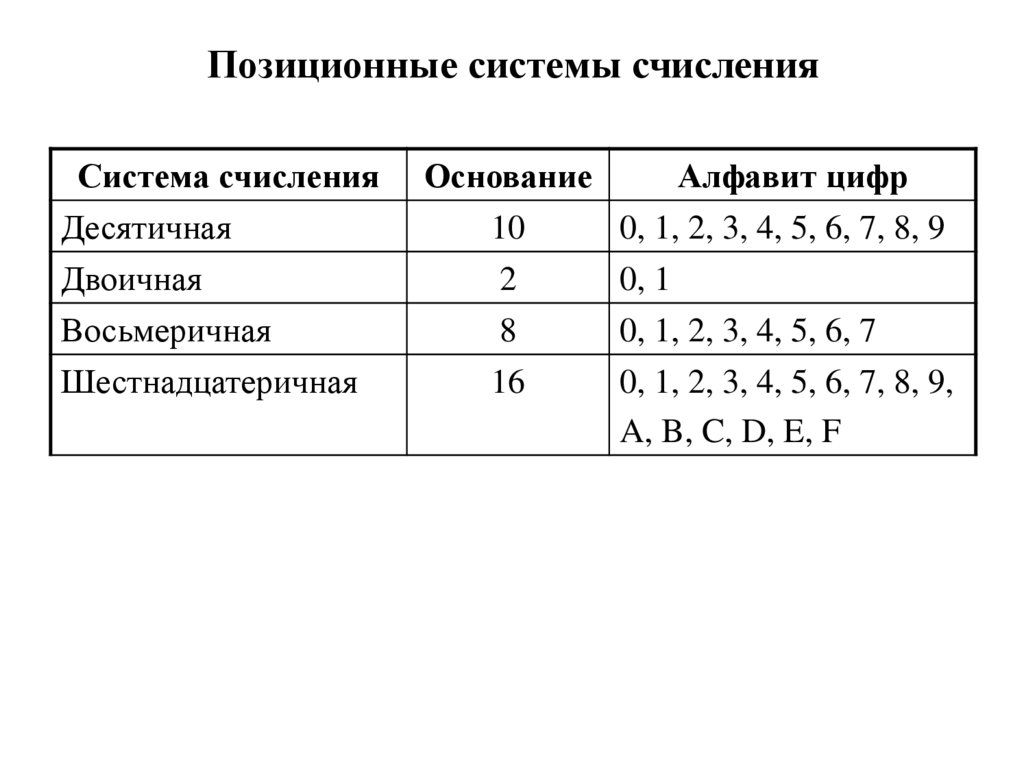 Перевести 19₁₀ в троичную систему счисления. А₁₀→А₃

Р ешение:

6

6

0

3

2

Ответ:

19₁₀=201₃

П ример3. Перевести 241₁₀ в восьмеричную систему счисления. А₁₀→А₈

Решение:

Ответ: 241₁₀=361₈

Пример4. Перевести 3627₁₀ в шестнадцатеричную систему счисления. А₁₀→А₁₆

Р ешение: Т.к. в шестнадцатеричной системе счисления 14 – Е,

а 11 – В, то получаем ответ Е2В₁₆.

Ответ: 3627₁₀=E2B₁₆

Перевод чисел из любой системы счисления в десятичную.

Правило Для того чтобы число из любой системы счисления перевести в десятичную систему счисления, необходимо его представить в развернутом виде и произвести вычисления.

Пример1. Перевести число 110110

2 из двоичной системы счисления в десятичную.

Решение:

5 4 3 2 1 0

1 1 0 1 1 0 ₂ = 1*2⁵ + 1*2⁴ + 0*2³+1*2²+1*2¹+0*2⁰ =32+16+4+2=54₁₀

Ответ: 110110₂ = 54₁₀

Пример2. Перевести число 101,01₂ из двоичной системы счисления в десятичную.

Решение:

2 1 0 -1 -2

1 0 1, 0 1 ₂ = 1*2² + 0*2¹ + 1*2⁰+0*2^-1+1*2^-2 =4+0+1+0+0,25=5,25₁₀

Ответ: 101,01₂ = 5,25₁₀

Пример3. Перевести число 122100₃ из троичной системы счисления в десятичную.

Решение:

4 3 2 1 0

1 2 2 0 1 ₃=1*3⁴ + 2*3³ + 2*3² + 0*3¹ + 1*3⁰ = 81+54+18+1 = 154₁₀

Ответ: 12201₃ = 154

10

Пример4. Перевести число 163₇ из семеричной системы счисления в десятичную.

Решение: 163₇ = 1*7² + 6*7¹ + 3*7⁰ = 49+42+3= 94₁₀.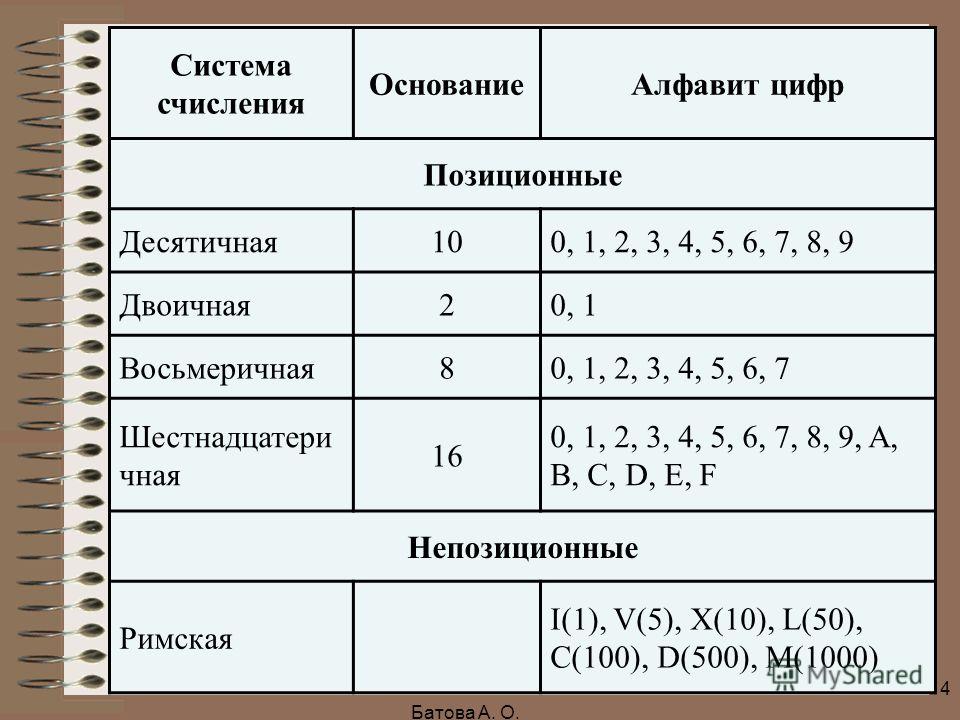

Ответ: 163₇ = 94_10.

Пример6. Перевести число 2Е₁₆ в десятичную систему счисления.

Решение:

2 1

2 Е₁₆ = 2*16¹ +14*16⁰

= 32 +14 = 46₁₀.

Ответ: 2Е₁₆ = 46_10.

Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную системы счисления.

Перевод целых чисел.

Правило. Чтобы перевести целое двоичное число в восьмеричную (8=2³) систему счисления необходимо:

Пример1. Перевести число 11101010₂ в восьмеричную систему счисления.

Решение:

1 1101010

3 5 2

О твет: 11101010₂ = 352₈

Пример. Перевести число 11110000010110₂ в восьмеричную систему счисления.

Решение:

1 11 110 000 010 110

7 6 0 2 6

Ответ: 11110000010110₂= 76026₈

Правило Чтобы перевести целое двоичное число в шестнадцатеричную (16=2⁴) систему счисления необходимо:

Пример. Перевести число 11100010₂ в шестнадцатеричную систему счисления.

Решение:

1 110 0010

Е 2

Ответ: 11100010₂ = Е2₁₆

Перевод чисел из восьмеричной и шестнадцатеричной систем счисления в двоичную систему счисления.

Правило Для того, чтобы восьмеричное (шестнадцатеричное) число перевести в двоичную систему счисления, необходимо каждую цифру этого числа заменить соответствующим числом, состоящим из 3 (4) цифр двоичной системы счисления.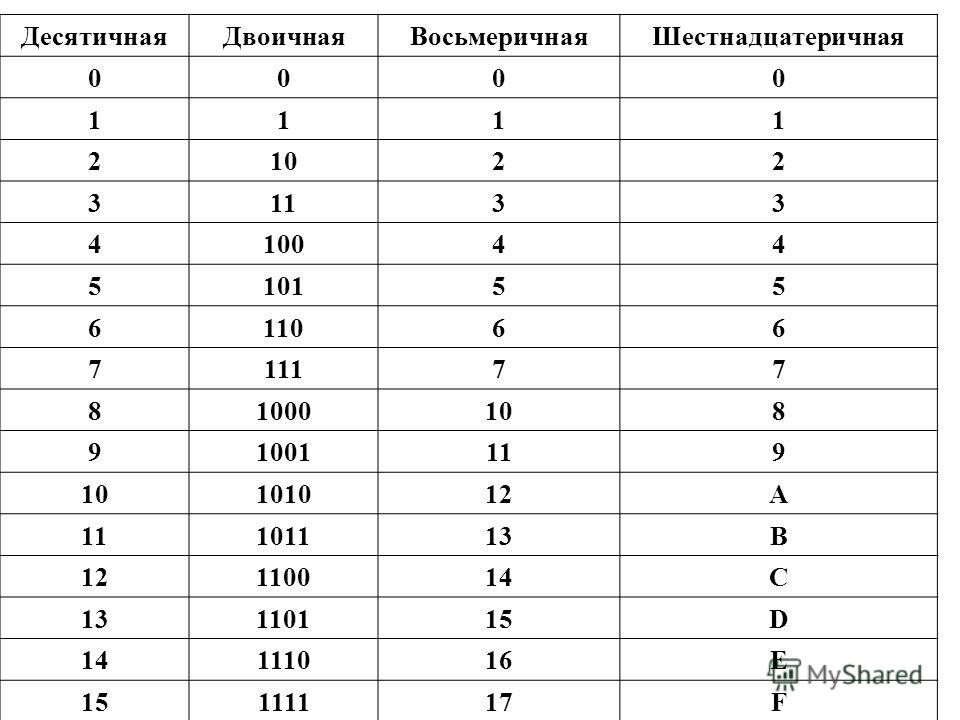

Пример

. Перевести число 523₈ перевести в двоичную систему счисления.

Решение:

5 2 3

101 010 011

О твет: 528₈ = 101010011₂

Пример. Перевести число 4ВА35₁₆ перевести в двоичную систему счисления.

Р ешение:

4 В А 3 5

100 1011 1010 0011 0101

Ответ: 4ВА35₁₆ = 100 1011 1010 0011 0101₂

Математические операции в различных системах счисления

Сложение

Сложение чисел 15 и 6 в различных системах счисления

Ответ: 15+6 = 21₁₀ = 10101₂ = 25₈ = 15₁₆.  

Вычитание

Вычитание чисел 45 и 18 в различных системах счисления

Десятичная: 45₁₀–18₁₀Двоичная: 101101₂–10010₂ Восьмеричная: 55₈–22₈

1 1 1 Заем

4 5 101101 55

18 10010 22

27 11011 33

Ответ: 45–18 = 27₁₀ = 11011₂ = 33₈

Умножение

Перемножим числа 115 и 51

Ответ: 115^.51 = 5865₁₀ = 1011011101001₂ = 13351₈.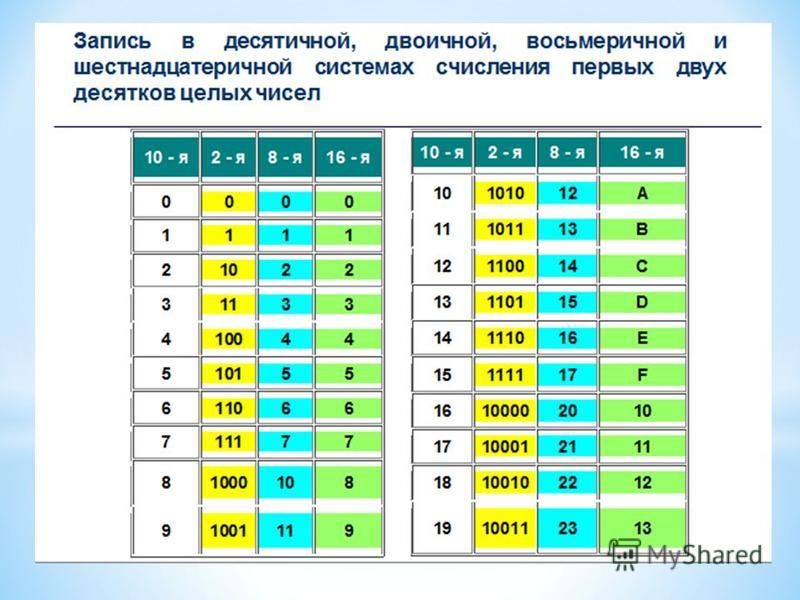

Задание 1.

(3 балла)

1. Составить в тетради таблицу соответствия систем счисления от 0 до 30

Десятичная	Двоичная	Восьмеричная	Шестнадцатеричная
0	0	0	0
1	1	1	1
2	10	2	2
3	11	3	3
4	100	4	4
…	…	…	…
30	11110	36	1Е

2. Перевести десятичные числа (345, 1023, 678) в двоичную (345), восьмеричную(1023) и шестнадцатеричную(678) системы счисления.

Задание 2.

(6 баллов)

1. Произвести сложение чисел 15, 7 и 3 в двоичной, восьмеричной и шестнадцатиричной системах счисления. Порядок действий и ответы записать в тетрадь.

2. Произвести вычитание чисел 56 и 21 в двоичной, восьмеричной и шестнадцатиричной системах счисления. Порядок действий и ответы записать в тетрадь.

3. Перевести числа 34 ₈ , 25₈ , 89₁₆ и 16₁₆ в двоичную систему счисления и выполнить произведение 34 ₈ и 25₈ , 89₁₆ и 16₁₆ в двоичной системе счисления. Порядок действий и ответы записать в тетрадь.

Задание 3.

(3 балла)

Выполняются задания на перевод чисел из одной системы счисления в другую, математические действия над числами по индивидуальным карточкам.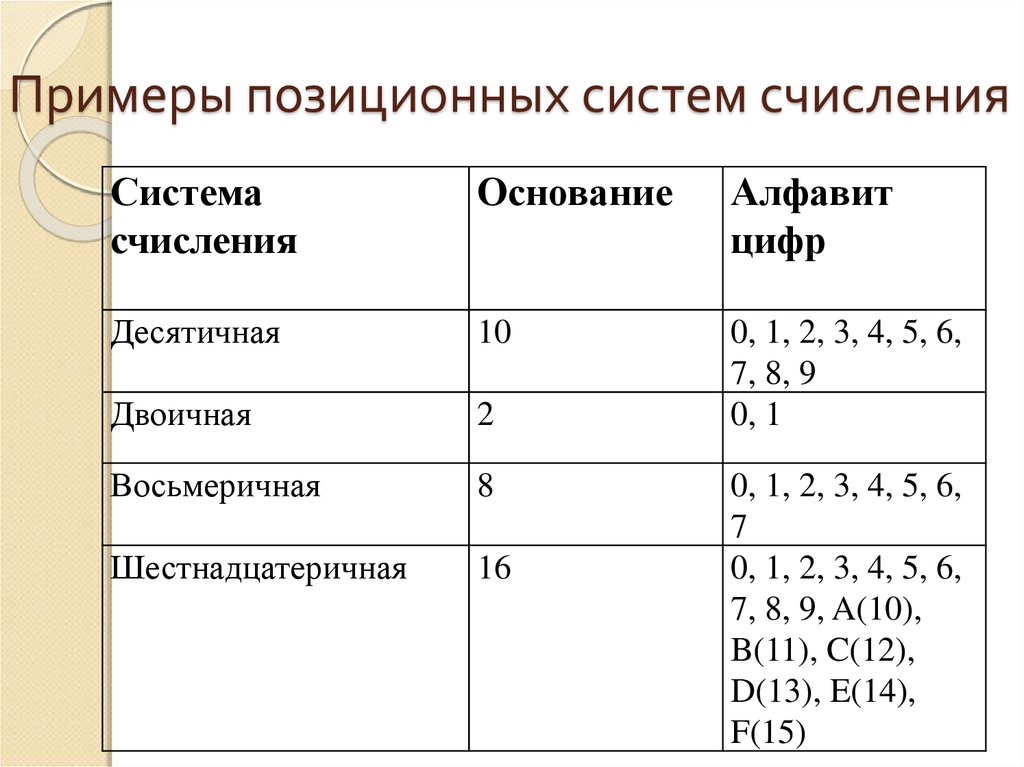

Вопросы к защите практической работы:

1. Что такое система счисления?

2. Что такое основание системы счисления?

3. Что такое непозиционная система счисления?

4. Что такое позиционная система счисления?

5. Из каких знаков состоит алфавит десятичной и двоичной систем?

6. Почему в вычислительной технике взята за основу двоичная система счисления?

7. Каковы правила сложения двоичных чисел?

8. Из каких символов состоят алфавиты восьмеричной и шестнадцатеричной систем?

9. В чем заключается преимущество восьмеричной или шестнадцатеричной системы по сравнению с двоичной?

10. Как перевести двоичное число в восьмеричное и шестнадцатиричное?

11. Как перевести восьмеричное число в десятичное?

12. Как перевести шестнадцатиричное число в десятичное?

13. Какие целые числа следуют за числами: 1111₂; 177₈; 9AFF₁₆?

14. Какие целые числа предшествуют числам: 10000₂; 110₈; A10₁₆?

15. Какой цифрой заканчивается четное двоичное число?

16. Какой цифрой заканчивается нечетное двоичное число?

17. Какое наибольшее десятичное число можно записать тремя цифрами:

а) в двоичной системе;

б) в восьмеричной системе;

в) в шестнадцатеричной системе?

Лекция 2 — Информатика и ИКТ

Тема: Подходы к понятию информации и измерению информации

Термин информация имеет множество определений. «Информация» происходит от латинского слова «informatio», что означает разъяснение, изложение, осведомление. Информация всегда представляется в виде сообщения. Сообщение – это форма представления каких-либо сведений в виде речи, текста, изображения, цифровых данных, графиков, таблиц и т.д. В широком смысле информация – это сведения, совокупность каких-либо данных, знаний. Наряду с понятие информация в информатике часто употребляется понятие данные. Данные – это результаты наблюдений над объектами и явлениями, которые по каким-то причинам не используются, а только хранятся. Как только данные начинают использовать в каких-либо практических целях, они превращаются в информацию.

1. Представление и кодирование информации с помощью знаковых систем.

 С древних времен знаки используются человеком для долговременного хранения информации и ее передачи на большие расстояния.

Форма знаков. В соответствии со способом восприятия знаки можно разделить на зрительные, слуховые, осязательные, обонятельные и вкусовые, причем в человеческом общении используются знаки первых трех типов.

К зрительным знакам, воспринимаемым с помощью зрения, относятся буквы и цифры, которые используются в письменной речи, знаки химических элементов, музыкальные ноты, дорожные знаки и т. д.

К слуховым знакам, воспринимаемым с помощью слуха, относятся звуки, которые используются в устной речи, а также звуковые сигналы, которые производятся с помощью звонка, колокола, свистка, гудка, сирены и т. д.

Для слепых разработана азбука Брайля, которая использует осязательный способ восприятия текстовой информации.

В коммуникации многих видов животных особую роль играют обонятельные знаки. Например, медведи и другие дикие животные помечают место обитания клочьями шерсти, сохраняющей запах, чтобы отпугнуть чужака и показать, что данная территория уже занята.

Для долговременного хранения знаки записываются на носители информации.

Для передачи информации на большие расстояния используются знаки в форме сигналов. Всем известны световые сигналы светофора, звуковые сигналы школьного звонка оповещают о начале или конце урока, электрические сигналы передают информацию по телефонным и компьютерным сетям, электромагнитные волны передают сигналы радио и телевидения.

Значение знаков. Знаки отображают объекты окружающего мира или понятия, т. е. имеют определенное значение (смысл).

Знаки различаются по способу связи между их формой и значением. Иконические знаки позволяют догадаться об их смысле, так как они имеют форму, похожую на отображаемый объект. Примером таких знаков являются значки на Рабочем столе операционной системы компьютера, например, значок Мой компьютер.

Символами называются знаки, для которых связь между формой и значением устанавливается по общепринятому соглашению.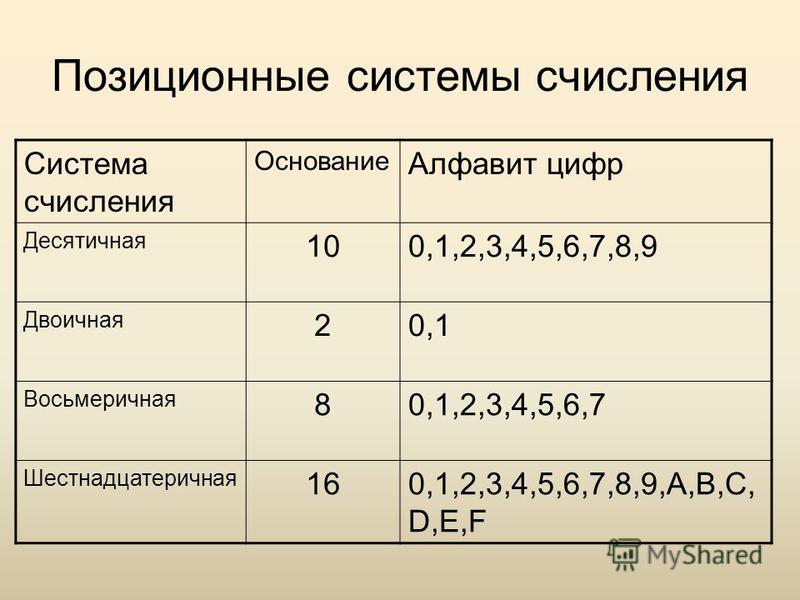 Примером таких знаков являются символы химических элементов, отображающие атомы химических веществ (табл. 2).

Если неизвестно соглашение о связи формы и значения символов, то ничего нельзя сказать о смысле информации, записанной такими знаками. Существуют найденные археологами и до сих пор нерасшифрованные тексты на древних языках, так как неизвестно значение знаков, которыми они записаны.

Таблица 2. Иконические знаки и символы

В современном мире широко применяется шифрование, которое использует секретный ключ в качестве соглашения о связи формы символов с их значениями. Если секретный ключ неизвестен, то содержание передаваемого текста понять невозможно.

Один и тот же символ может иметь различное значение в разных знаковых системах. Например, знак «О» используется в качестве:

— буквы «О» в русском алфавите;

— буквы «О» [ou] в английском алфавите;

— цифры 0 в системах счисления;

— символа химического элемента «О» (кислорода) в таблице Д. И. Менделеева.

Знаковые системы являются наборами знаков определенного типа. С некоторыми знаковыми системами вы хорошо знакомы и постоянно ими пользуетесь (языки и системы счисления), с другими познакомитесь в этом пункте.

Каждая знаковая система строится на основе определенного алфавита (набора знаков) и правил выполнении операций над знаками.

Естественные языки. Человек широко использует для представления информации знаковые системы, которые называются языками. Естественные языки начали формироваться еще в древнейшие времена в целях обеспечения обмена информацией между людьми. В настоящее время существуют сотни естественных языков (русский, английский, китайский и др.).

В устной речи, которая используется как средство коммуникации при непосредственном общении людей, в качестве знаков языка используются различные звуки (фонемы).

В основе письменной речи лежит алфавит, т. е. набор знаков (букв), которые человек различает по их начертанию. В большинстве современных языков буквы соответствуют определенным звукам устной речи. Алфавит русского языка называется кириллицей и содержит 33 знака, английский язык использует латиницу и содержит 26 знаков.

На основе алфавита по правилам грамматики образуются основные объекты языка — слова. Правила, согласно которым из слов данного языка строятся предложения, называются синтаксисом. Необходимо отметить, что в естественных языках грамматика и синтаксис языка формулируются с помощью большого количества правил, из которых существуют исключения, так как такие правила складывались исторически.

Формальные языки. В процессе развития науки были разработаны формальные языки (системы счисления, алгебра, языки программирования и др.), основное отличие которых от естественных языков состоит в существовании строгих правил грамматики и синтаксиса.

Например, десятичную систему счисления можно рассматривать как формальный язык, имеющий алфавит (цифры) и позволяющий не только именовать и записывать объекты (числа), но и выполнять над ними арифметические операции по строго определенным правилам.

Существуют формальные языки, в которых в качестве знаков используют не буквы и цифры, а другие символы, например, музыкальные ноты, изображения элементов электрических или логических схем, дорожные знаки, точки и тире (код азбуки Морзе).

Физическая реализация знаков в естественных и формальных языках может быть различной. Например, текст и числа могут быть напечатаны на бумаге, высвечены на экране монитора компьютера, записаны на магнитном или оптическом диске.

Генетический алфавит. Генетический алфавит является «азбукой», на которой строится единая система хранения и передачи наследственной информации живыми организмами.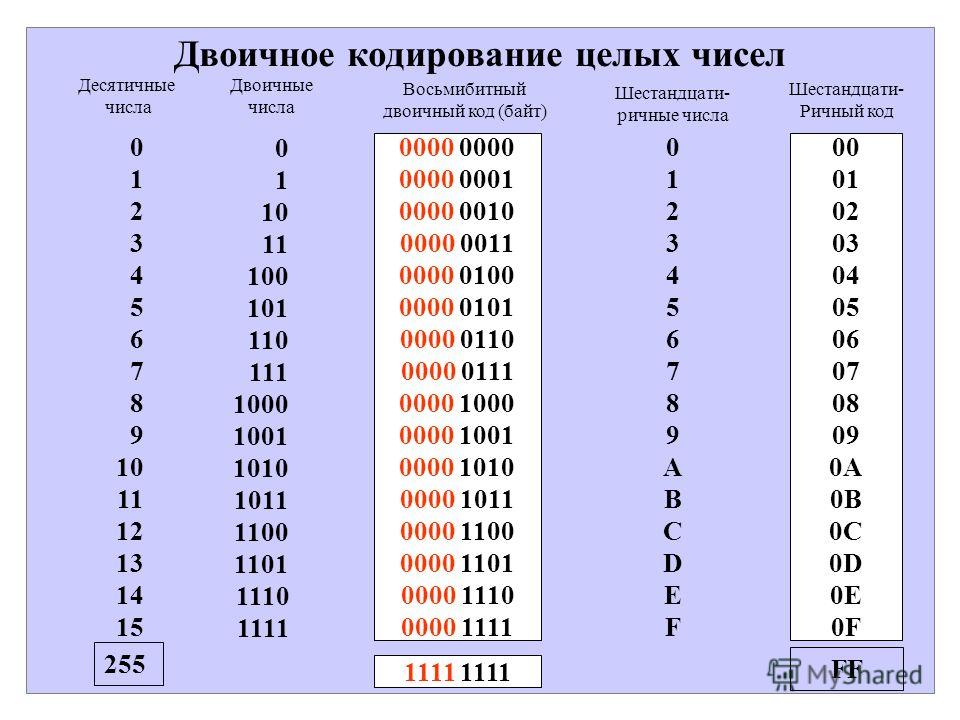

Как слова в языках образуются из букв, так и гены состоят из знаков генетического алфавита. В процессе эволюции от простейших организмов до человека количество генов постоянно возрастало, так как было необходимо закодировать все более сложное строение и функциональные возможности живых организмов.

Генетическая информация хранится в клетках живых организмов в специальных молекулах. Эти молекулы состоят из двух длинных скрученных друг с другом в спираль цепей, построенных из четырех различных молекулярных   фрагментов (рис. 1.6). Фрагменты образуют генетический алфавит и обычно обозначаются латинскими прописными буквами {A, G, С, Т}.

Рис 1. Модель молекулы генетического кода

Двоичная знаковая система. В процессах хранения, обработки и передачи информации в компьютере используется двоичная знаковая система, алфавит которой состоит всего из двух знаков {0, 1}. Физически знаки реализуются в форме электрических импульсов (нет импульса — 0, есть импульс — 1), а также состояний ячеек оперативной памяти и участков поверхностей носителей информации (одно состояние — 0, другое состояние — 1).

Именно двоичная знаковая система используется в компьютере, так как существующие технические устройства могут надежно сохранять и распознавать только два различных состояния (знака).

В 60-е годы XX века в СССР учеными Московского государственного университета была разработана и запущена в производство ЭВМ «Сетунь» (всего было произведено 50 экземпляров) (рис. 1.7). «Сетунь» использовала троичное кодирование информации и, соответственно, состояла из устройств, способных находиться в одном из трех возможных состояний.

Рис. 2. ЭВМ «Сетунь»

2. Двоичное кодирование текстовой, графической и звуковой информации.

Код — это набор условных обозначений (или сигналов) для записи (или передачи) некоторых заранее определенных понятий.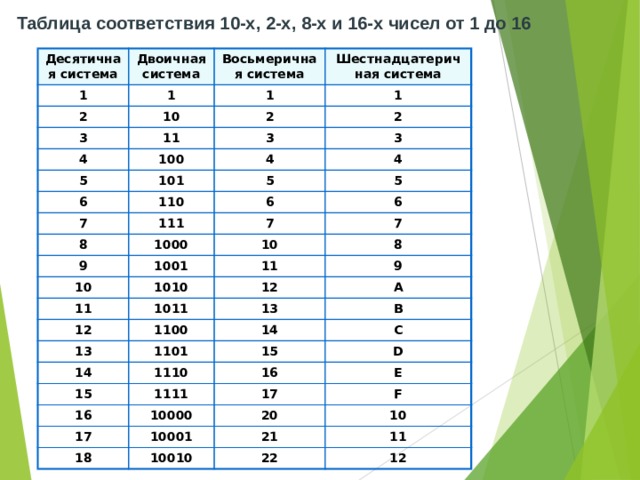

            Кодирование информации – это процесс формирования определенного представления информации. В более узком смысле под термином «кодирование» часто понимают переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки.

            Обычно каждый образ при кодировании (иногда говорят — шифровке) представлении отдельным знаком.

            Знак — это элемент конечного множества отличных друг от друга элементов.

            В более узком смысле под термином «кодирование» часто понимают переход от одной формы представления информации к другой, более удобной для хранения, передачи или обработки.

            Компьютер может обрабатывать только информацию, представленную в числовой форме. Вся другая информация (например, звуки, изображения, показания приборов и т. д.) для обработки на компьютере должна быть преобразована в числовую форму. Например, чтобы перевести в числовую форму музыкальный звук, можно через небольшие промежутки времени измерять интенсивность звука на определенных частотах, представляя результаты каждого измерения в числовой форме. С помощью программ для компьютера можно выполнить преобразования полученной информации, например, «наложить» друг на друга звуки от разных источников.

            Аналогичным образом на компьютере можно обрабатывать текстовую информацию. При вводе в компьютер каждая буква кодируется определенным числом, а при выводе на внешние устройства (экран или печать) для восприятия человеком по этим числам строятся изображения букв. Соответствие между набором букв и числами называется кодировкой символов.

            Как правило, все числа в компьютере представляются с помощью нулей и единиц (а не десяти цифр, как это привычно для людей). Иными словами, компьютеры обычно работают в двоичной системе счисления, поскольку при этом устройства для их обработки получаются значительно более простыми.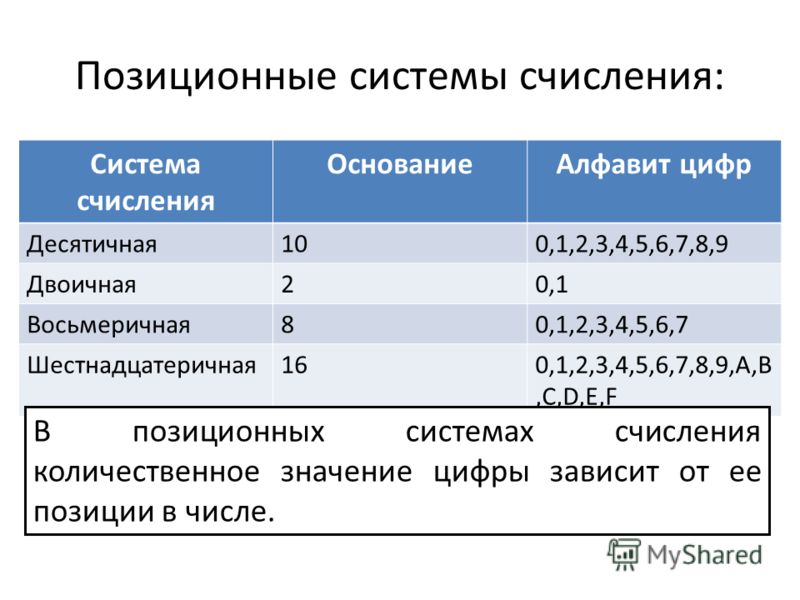 Ввод чисел в компьютер и вывод их для чтения человеком может осуществляться в привычной десятичной форме, а все необходимые преобразования выполняют программы, работающие на компьютере.

            Способы кодирования информации.

            Одна и та же информация может быть представлена (закодирована) в нескольких формах. C появлением компьютеров возникла необходимость кодирования всех видов информации, с которыми имеет дело и отдельный человек, и человечество в целом. Но решать задачу кодирования информации человечество начало задолго до появления компьютеров. Грандиозные достижения человечества — письменность и арифметика — есть не что иное, как система кодирования речи и числовой информации. Информация никогда не появляется в чистом виде, она всегда как-то представлена, как-то закодирована.

            Двоичное кодирование – один из распространенных способов представления информации. В вычислительных машинах, в роботах и станках с числовым программным управлением, как правило, вся информация, с которой имеет дело устройство, кодируется в виде слов двоичного алфавита.

            Кодирование символьной (текстовой) информации.

            Основная операция, производимая над отдельными символами текста — сравнение символов.

            При сравнении символов наиболее важными аспектами являются уникальность кода для каждого символа и длина этого кода, а сам выбор принципа кодирования практически не имеет значения.

            Для кодирования текстов используются различные таблицы перекодировки. Важно, чтобы при кодировании и декодировании одного и того же текста использовалась одна и та же таблица.

            Таблица перекодировки — таблица, содержащая упорядоченный некоторым образом перечень кодируемых символов, в соответствии с которой происходит преобразование символа в его двоичный код и обратно.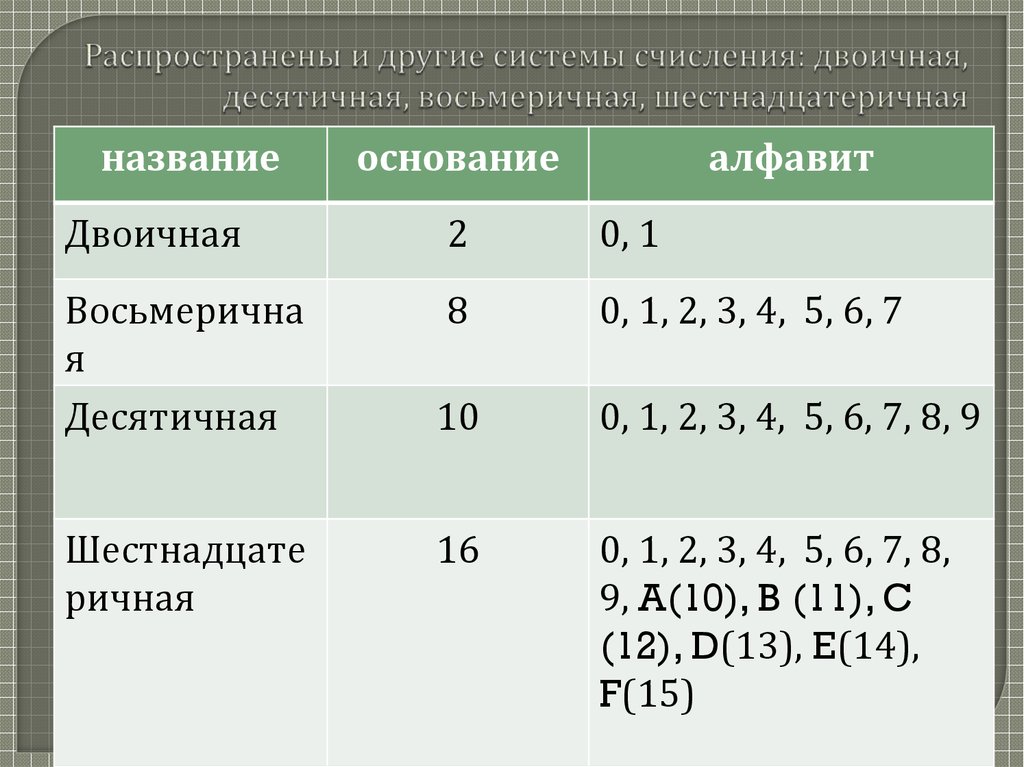

            Наиболее популярные таблицы перекодировки: ДКОИ-8, ASCII, CP1251, Unicode.

Можно поступить следующим образом: измерять амплитуду сигнала через равные промежутки времени и записывать полученные числовые значения в память компьютера.

3. Представление числовой информации с помощью систем счисления.

Для записи информации о количестве объектов используются числа. Числа записываются с использованием особых знаковых систем, которые называются системами счисления. Алфавит систем счисления состоит из символов, которые называются цифрами. Например, в десятичной системе счисления числа записываются с помощью десяти всем хорошо известных цифр: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.

Система счисления — это знаковая система, в которой числа записываются по определенным правилам с помощью символов некоторого алфавита, называемых цифрами.

Все системы счисления делятся на две большие группы: позиционные и непозиционные системы счисления.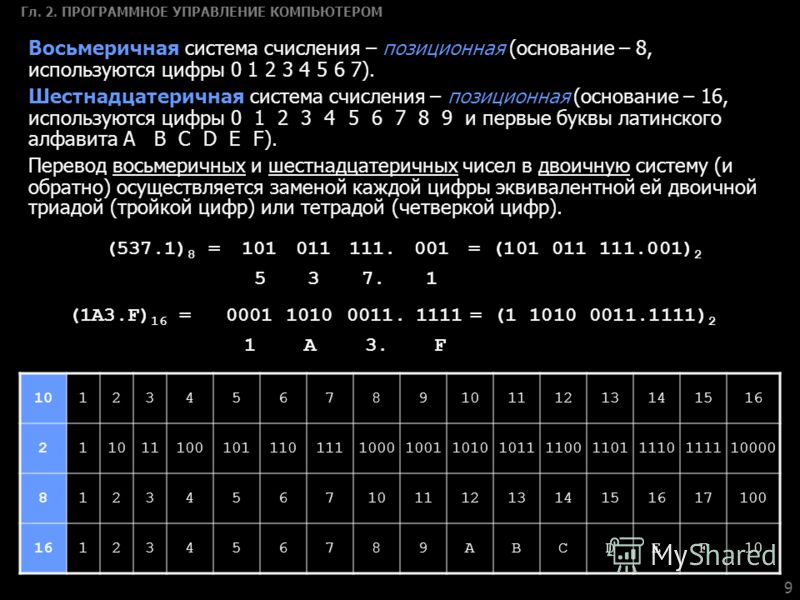 В позиционных системах счисления значение цифры зависит от ее положения в числе, а в непозиционных — не зависит.

Римская непозиционная система счисления. Самой распространенной из непозиционных систем счисления является римская. В качестве цифр в ней используются: I (1), V (5), X (10), L (50), С (100), D (500), М (1000).

Значение цифры не зависит от ее положения в числе. Например, в числе XXX (30) цифра X встречается трижды и в каждом случае обозначает одну и ту же величину — число 10, три числа по 10 в сумме дают 30.

Величина числа в римской системе счисления определяется как сумма или разность цифр в числе. Если меньшая цифра стоит слева от большей, то она вычитается, если справа — прибавляется. Например, запись десятичного числа 1998 в римской системе счисления будет выглядеть следующим образом:

MCMXCVIII = 1000 + (1000 — 100) + (100 -10)+ 5 + 1 + 1 + 1.

Позиционные системы счисления.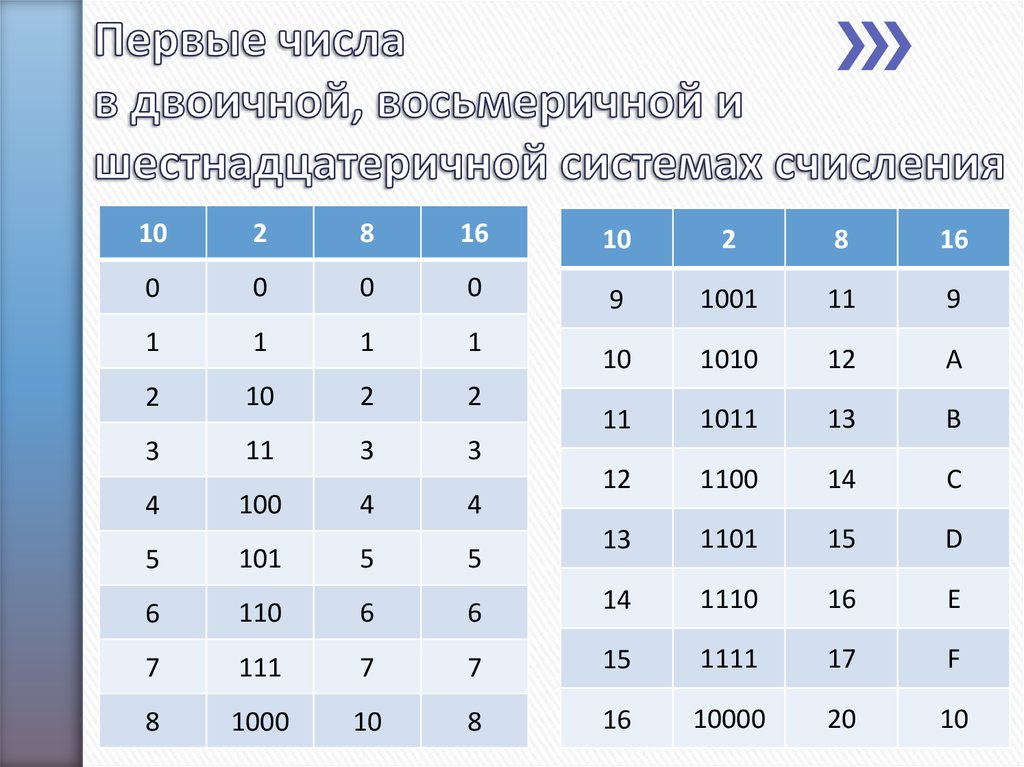  Первая позиционная система счисления была придумана еще в Древнем Вавилоне, причем вавилонская нумерация была шестидесятеричной, то есть в ней использовалось шестьдесят цифр! Интересно, что до сих пор при измерении времени мы используем основание, равное 60 (в 1 минуте содержится 60 секунд, а в 1 часе — 60 минут).

В XIX веке довольно широкое распространение получила двенадцатеричная система счисления. До сих пор мы часто употребляем дюжину (число 12): в сутках две дюжины часов, круг содержит тридцать дюжин градусов и так далее.

В позиционных системах счисления количественное значение цифры зависит от ее позиции в числе.

Наиболее распространенными в настоящее время позиционными системами счисления являются десятичная, двоичная, восьмеричная и шестнадцатеричная. Каждая позиционная система имеет определенный алфавит цифр и основание.

В позиционных системах счисления основание системы равно количеству цифр (знаков в ее алфавите) и определяет, во сколько раз различаются значения одинаковых цифр, стоящих в соседних позициях числа.

Десятичная система счисления имеет алфавит цифр, который состоит из десяти всем известных, так называемых арабских, цифр, и основание, равное 10, двоичная — две цифры и основание 2, восьмеричная — восемь цифр и основание 8, шестнадцатеричная — шестнадцать цифр (в качестве цифр используются и буквы латинского алфавита) и основание 16 (табл. 3).

Таблица 3. Позиционные системы счисления

Система счисления Основание Алфавит цифр Десятичная 10 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 Двоичная 2 0, 1 Восьмеричная 8 0, 1, 2, 3, 4, 5, 6, 7 Шестнадцатеричная 16 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, А(10), В(11), C(12), D(13), E(14), F(15)

Десятичная система счисления.  Рассмотрим в качестве примера десятичное число 555. Цифра 5 встречается трижды, причем самая правая цифра 5 обозначает пять единиц, вторая справа — пять десятков и, наконец, третья справа — пять сотен.

Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим. В десятичной системе цифра, находящаяся в крайней справа позиции (разряде), обозначает количество единиц, цифра, смещенная на одну позицию влево, — количество десятков, еще левее — сотен, затем тысяч и так далее. Соответственно имеем разряд единиц, разряд десятков и так далее.

Число 555 записано в привычной для нас свернутой форме. Мы настолько привыкли к такой форме записи, что уже не замечаем, как в уме умножаем цифры числа на различные степени числа 10.

В развернутой форме записи числа такое умножение записывается в явной форме. Так, в развернутой форме запись числа 555 в десятичной системе будет выглядеть следующим образом:

555₁₀ = 5 × 10² + 5 × 10¹ + 5 × 10⁰.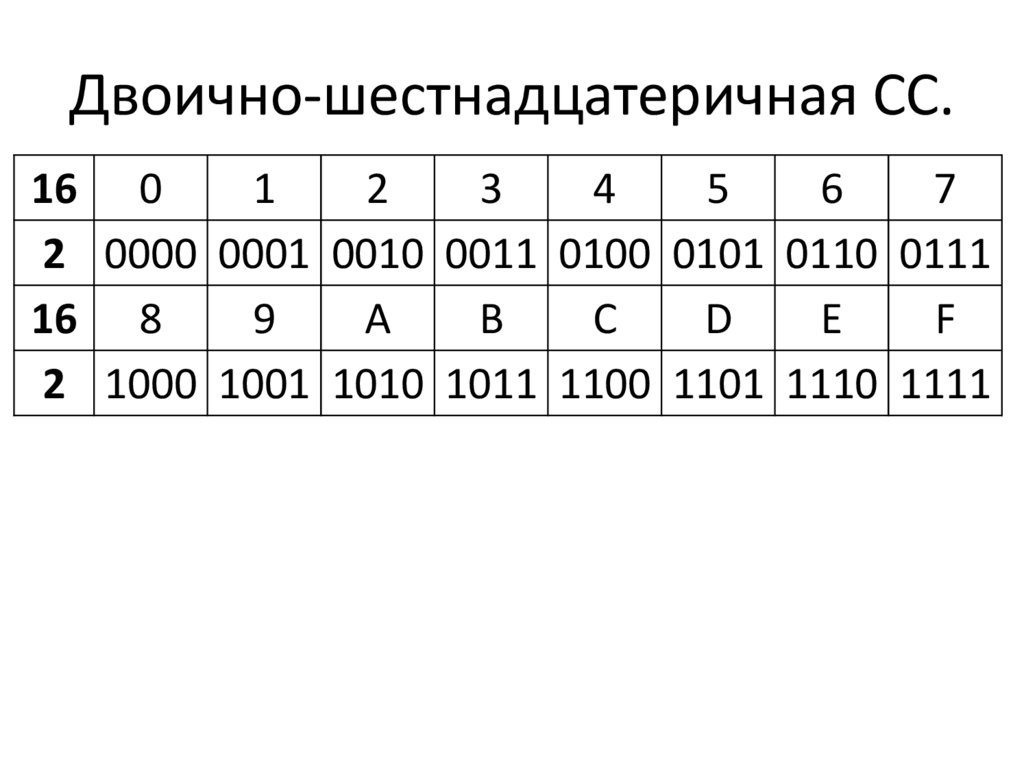

Как видно из примера, число в позиционной системе счисления записывается в виде суммы числового ряда степеней основания (в данном случае 10), в качестве коэффициентов которых выступают цифры данного числа.

Для записи десятичных дробей используются отрицательные значения степеней основания. Например, число 555,55 в развернутой форме записывается следующим образом:

555,55₁₀ = 5 × 10² + 5 × 10¹ + 5 × 10⁰ + 5 × 10^-1 + 5 × 10^-2 .

В общем случае в десятичной системе счисления запись числа А₁₀, которое содержит n целых разрядов числа и m дробных разрядов числа, выглядит так:

A₁₀ = a_n-1 × 10^n-1 + … + a₀ × 10⁰ + a_-1 × 10^-1 + … + a_-m × 10^-m

Коэффициенты a_i в этой записи являются цифрами десятичного числа, которое в свернутой форме записывается так:

А₁₀ = a_n-1 a_n-2 . .. a₀, a_-1 … a_-m.

Из вышеприведенных формул видно, что умножение или деление десятичного числа на 10 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной, на один разряд соответственно вправо или влево. Например:

555,55₁₀ × 10 = 5555,5₁₀; 
555,55₁₀ : 10 = 55,555₁₀.

Двоичная система счисления. В двоичной системе счисления основание равно 2, а алфавит состоит из двух цифр (0 и 1). Следовательно, числа в двоичной системе в развернутой форме записываются в виде суммы степеней основания 2 с коэффициентами, в качестве которых выступают цифры 0 или 1.

Например, развернутая запись двоичного числа может выглядеть так:

А₂ = 1 × 2² + 0 × 2¹ + 1 × 2⁰ + 0 × 2^-1 + 1 × 2^-2.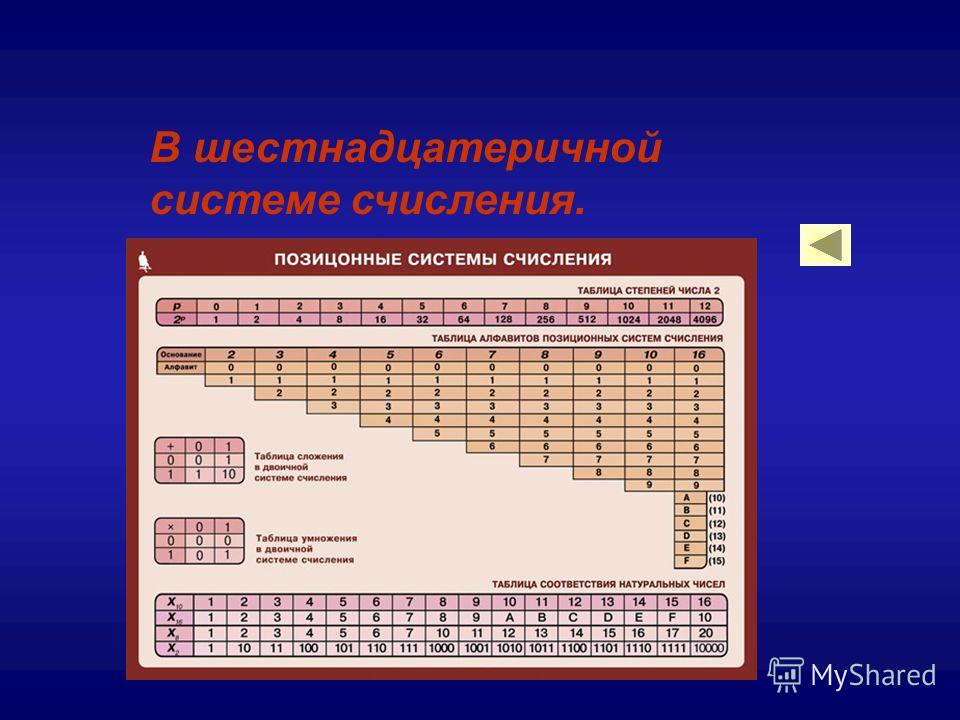

Свернутая форма этого же числа:

А₂ = 101,01₂.

В общем случае в двоичной системе запись числа А₂, которое содержит n целых разрядов числа и m дробных разрядов числа, выглядит так:

А₂ = a_n-1 × 2^n-1 + a_n-2 × 2^n-2 + … + a₀ × 2⁰ + a_-1 × 2^-1 + … + a_-m × 2^-m

Коэффициенты а_i в этой записи являются цифрами (0 или 1) двоичного числа, которое в свернутой форме записывается так:

А₂ = а_n-1 а_n-2 … а₀, а_-1 а_-2 … а_-m

Из вышеприведенных формул видно, что умножение или деление двоичного числа на 2 (величину основания) приводит к перемещению запятой, отделяющей целую часть от дробной на один разряд соответственно вправо или влево.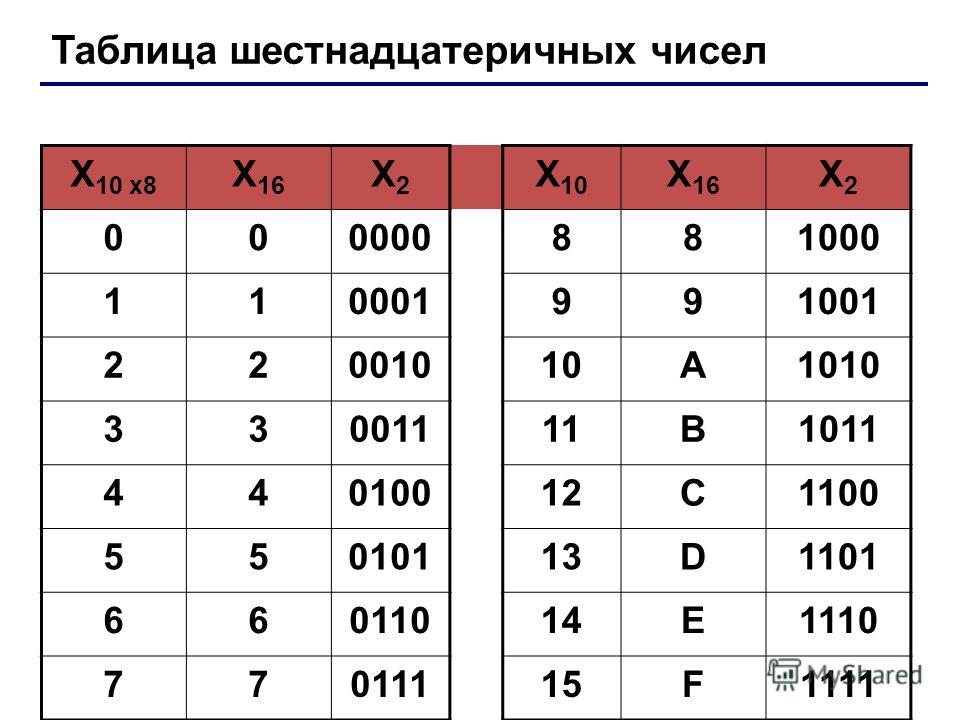 Например:

101,01₂ × 2 = 1010,1₂; 
101,01₂ : 2 = 10,101₂.

Позиционные системы счисления с произвольным основанием. Возможно использование множества позиционных систем счисления, основание которых равно или больше 2. В системах счисления с основанием q (q-ичная система счисления) числа в развернутой форме записываются в виде суммы степеней основания q с коэффициентами, в качестве которых выступают цифры 0, 1, q — 1:

A_q = a_n-1 × q^n-1 + a_n-2 × q^n-2 + … + a₀ × q⁰ + a_-1 × q^-1 + … + a_-m × q^-m

Коэффициенты а_i в этой записи являются цифрами числа, записанного в q-ичной системе счисления.

Так, в восьмеричной системе основание равно восьми (q = 8). Тогда записанное в свернутой форме восьмеричное число А₈ = 673,2₈ в развернутой форме будет иметь вид:

А₈ = 6 × 8² + 7 × 8¹ + 3 × 8⁰ + 2 × 8^-1.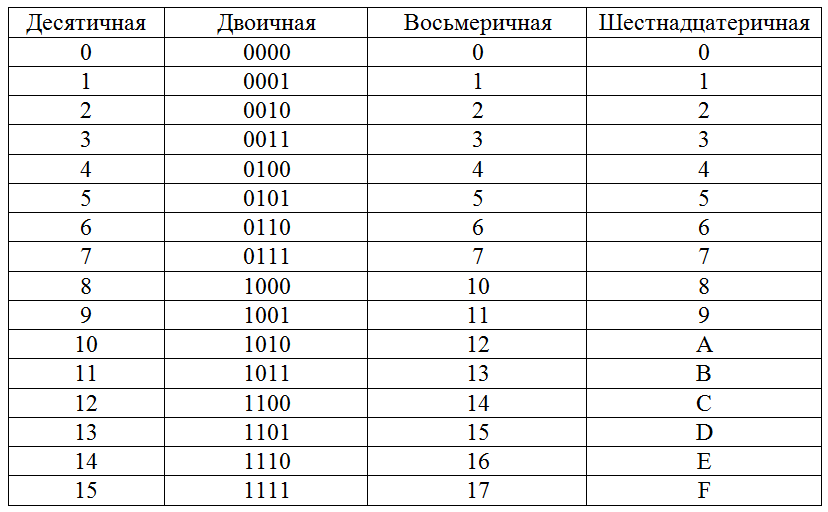

В шестнадцатеричной системе основание равно шестнадцати (q = 16), тогда записанное в свернутой форме шестнадцатеричное число А₁₆ = 8A,F₁₆ в развернутой форме будет иметь вид:

А₁₆ = 8 × 16¹ + А × 16⁰ + F × 16^-1.

Если выразить шестнадцатеричные цифры через их десятичные значения (А=10, F=15), то запись числа примет вид:

А₁₆ = 8 × 16¹ + 10 × 16⁰ + 15 × 16^-1.

цифр и символов

цифр и символов
Далее: Настоящий компьютер вверх: хо Предыдущий: Выполнение инструкции на MU0

Подразделы

• Двоичные, восьмеричные и шестнадцатеричные числа
• Биты, байты, слова и символы
• Степени числа 10 и числа 2
• Скорость

---

Числа и символы

Почти все компьютеры хранят числа как двоичные , т. е. по основанию 2. чем десятичное по основанию 10. Каждое число состоит из строки бит (двоичные цифры), каждая из которых может быть либо 0, либо 1. например. используя 16-битный строки, одна хранится как двоичное число 0000000000000001, два как 0000000000000010, три как 0000000000000011, четыре как 0000000000000100, десять как 0000000000001010, сто как 0000000001100100, одна тысяча как 0000001111101000, и десять тысяч как 0010011100010000.
(Обычно мы также используем специальный способ кодирования отрицательных чисел, известный как 2s дополнение, что упрощает арифметику с их использованием. Это будет описано в CS1031.)

Двоичные числа не так просто использовать людям, поскольку мы привыкли к основанию 10. Чтобы немного облегчить жизнь, мы обычно группируем биты вместе. например мы могли бы написать десять тысяч как 0 010 011 100 010 000 или 0010 0111 0001 0000. Чтобы сделать жизнь еще проще, мы обычно заменяем группы битов на соответствующее десятичное значение для каждой группы, поэтому 0 010 011 100 010 000 обычно записывается как 023420 ( восьмеричное обозначение) и 0010 0111 0001 0000 обычно записывается как 2710 ( шестнадцатеричное число обозначение, обычно называемое просто hex ).
Как насчет 4-битных групп со значениями 1010–1111 (с десяти до пятнадцати)? Поскольку больше нет десятичных цифр, начинаем использовать буквы алфавита, заменяя 1010 (десять) по А, 1011 (одиннадцать) по Б, 1100 (двенадцать) по С, 1101 (тринадцать) D, 1110 (четырнадцать) на E и 1111 (пятнадцать) Ф. (В качестве альтернативы мы можем использовать от A до F вместо A до F.)

Итак, шестнадцатеричное число 1A5E эквивалентно двоичному числу 0001 1010 0101 1110, что совпадает с 0 001 101 001 011 110, что эквивалентно восьмеричному числу 015136. Мы можем преобразовать каждое из них в десятичное:
0001101001011110 (двоичный, справа налево) = 0*1 + 2 + 4 + 8 + 16 + 0*32 + 64 + 0*128 + 0*256 + 512 + 0*1024 + 2048 + 4096 + 0*8192 + 0*16384 + 0*32768 (десятичное) = 6750
015136 (восьмеричный, справа налево) = 6*1 + 3*8 + 1*64 + 5*512 + 1*4096 + 0*32768 = 6750
015136 (восьмеричное, слева направо) = ((((0*8 + 1)*8 + 5)*8 + 1)*8 + 3)*8 + 6 = 6750
1A5E (шестнадцатеричный, справа налево, A=10, E=14) = 14*1 + 5*16 + 10*256 + 1*4096 = 6750
1A5E (шестнадцатеричный, слева направо, A=10, E=14) = (((1*16 + 10)*16) + 5)*16 + 14 = 6750

Чтобы преобразовать десятичное число в двоичное (или восьмеричное, или шестнадцатеричное), просто разделите его повторно на 2 (или 8, или 16), при этом остаток на каждом этапе является следующим цифра: 6750/2 = 3375 r 0 (поэтому 0 — младший значащий бит ответа), 3375/2 = 1687 r 1 (поэтому 1 — это следующий значащий бит ответа), 1687/2 = 843 р 1, 843/2 = 421 р 1, 421/2 = 210 р 1, 210/2 = 105 р 0, 105/2 = 52 р 1, 52/2 = 26 р 0, 26/2 = 13 р 0, 13/2 = 6 р 1, 6/2 = 3 р 0, 3/2 = 1 р 1, 1/2 = 0 r 1, и перечисление всех остатков дает нам эквивалентное двоичное значение 1 1010 0101 1110, и мы можем поставить дополнительные 0 впереди, чтобы получить 0001 1010 0101 1110.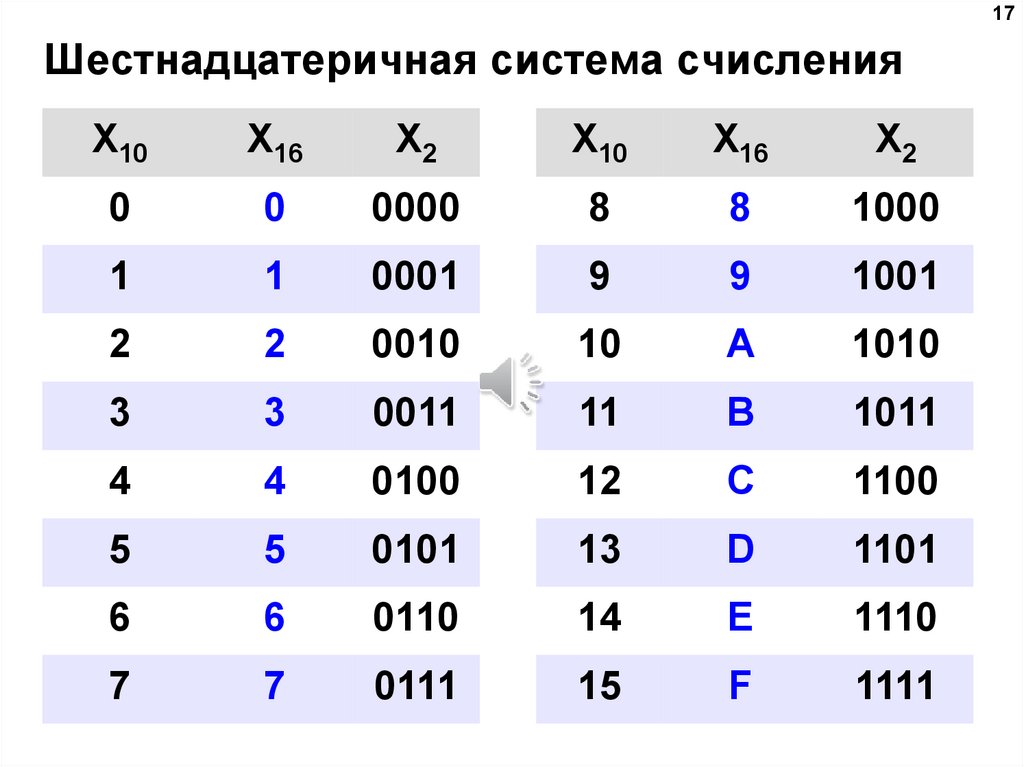

[Уильямс, разделы 2.8 и 3.6]

Бит — это двоичная цифра, т. е. нечто, значение которого может быть 0 или 1. Если мы соберем несколько битов вместе, мы сможем представить намного больше разные значения — 1 бит может представлять 2 разных значения, 2 бита могут представляют 4 разных значения, 3 бита могут представлять 8 разных значений, и поэтому on — n бит могут представлять разные значения.

Обычно мы принимаем эти значения за разные числа (например, от 0 до , или к ). Однако, пока мы согласны в значениях, любое могут быть представлены различные значения, такие как буквы алфавита или любые другие персонажи. А байт состоит из 8 бит и может использоваться для представления Европейские персонажи. Ранним стандартом был ASCII , который определяет только 128 различных английских и американских символов. (Альтернативная кодировка, теперь по сути заброшен, был EBCDIC.) Он был расширен за счет включения 128 дополнительных Европейские символы по стандарту ISO 8859. (Мы иногда называем их «7-битный ASCII» и «8-битный ASCII» соответственно.) Это, в свою очередь, было расширено до поддерживают наборы символов, используемые остальным миром в Юникод стандартный — однако для этого требуется 16-битная и более длинная кодировка. Например 8-битной кодировки во всех трех стандартах буква «А» представлена `0100 0001′. (Для получения дополнительной информации используйте `man ascii’ или `man iso_8859_1′ или `man unicode’ или `man utf-8′ на компьютере с Linux.)

Слово может состоять из любого количества битов, но на большинстве компьютеров обычно означает самый большой размер, который помещается в регистры и т. д. Раньше это было 16 бит (например, MU0), и в настоящее время обычно 32-битный. Потому что 16-битные компьютеры когда-то были такими распространено, вы можете найти 16-битное слово, а 32-битное длинное слово, даже на 32-битные компьютеры.

Килограмм	1К	=	1000=	=	1 тысяча		=	1 024
Мега	1М	=		=	1 миллион		=	1 048 567
Гига	1G	=		=	1 миллиард долларов США		=	1 073 741 824
Тера	1T	=		=	1 британский миллиард		=	1 099 511 627 776

В вычислениях степени 10 часто аппроксимируются степенями 2, поэтому мы говорим о напр. Мегабайт памяти означает байты. Однако мы также говорить о MegaFLOPS означает FLOPS. Первоначально обычный компьютер числа были Ks, а вносимые ошибки составляли всего около 2%. В настоящее время мы обычно говорят о М и Г, а начинают говорить о Т, где различия намного больше, поэтому, наверное, лучше избегать степени 2, когда есть какая-либо двусмысленность.

милли: 1м = 0,001 = = 1 тысячная
микро: = 1 миллионная
нано: 1n = = 1 миллиардная доля США

b/s, часто обозначаемый как bps, означает бит в секунду.
Б/с, часто записывается как Б/с, означает количество байтов в секунду.
Гц, сокращение от Hertz, означает количество циклов в секунду.

Если компьютер передает информацию по кабелю 32-битными словами, отправка другое слово каждую тысячную секунды, оно работает на частоте 1 кГц, принимая 1 мс для каждой передачи и максимальная скорость отправки 32 КБ/с или 4 КБ/с.

---

Далее: Настоящий компьютер вверх: хо Предыдущий: Выполнение инструкции на MU0

Пит Джинкс 2003-09-25

Характеристики восьмеричных и шестнадцатеричных символов

Редактировать

Твиттер LinkedIn Фейсбук Эл. адрес

• Статья
• 03.08.2021
• 2 минуты на чтение

Последовательность \ ooo означает, что вы можете указать любой символ из набора символов ASCII в виде трехзначного восьмеричного кода. Числовое значение восьмеричного целого числа определяет значение желаемого символа или расширенного символа.

Аналогично, последовательность \x ччч позволяет указать любой символ ASCII как шестнадцатеричный код символа. Например, вы можете указать символ возврата ASCII как обычную управляющую последовательность C ( \b ), или вы можете закодировать его как \010 (восьмеричное) или \x008 (шестнадцатеричное).

В восьмеричной управляющей последовательности можно использовать только цифры от 0 до 7. Восьмеричные escape-последовательности никогда не могут быть длиннее трех цифр и заканчиваются первым символом, который не является восьмеричной цифрой. Хотя вам не обязательно использовать все три цифры, вы должны использовать хотя бы одну. Например, восьмеричное представление равно 9.0010\10 для символа возврата ASCII и \101 для буквы A, как указано в диаграмме ASCII.

Точно так же вы должны использовать по крайней мере одну цифру для шестнадцатеричной управляющей последовательности, но вы можете опустить вторую и третью цифры. Поэтому вы можете указать шестнадцатеричную escape-последовательность для символа возврата на одну позицию как \x8 , \x08 или \x008 .

Значение восьмеричной или шестнадцатеричной управляющей последовательности должно быть в диапазоне представляемых значений для типа unsigned char для символьной константы и введите wchar_t для широкосимвольной константы.