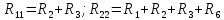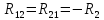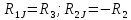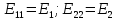Метод законов кирхгофа примеры решения задач

Прочитав статейки про первый и второй законы Кирхгофа, уважаемый читатель может сказать: «Хорошо, MyElectronix, ты рассказал мне, конечно, интересные штуки, но что мне дальше с ними делать? Пока по твоим словам я заключил, что если я соберу ручками схему, то я смогу в каждом ее узле и в каждом контуре намерить вот такие вот зависимости. Это здорово, но я хотел бы рассчитывать схемы, а не просто наблюдать зависимости!»
Господа, все эти замечания абсолютно верные и в ответ на них можно лишь рассказать о расчете электрических схем с помощью законов Кирхгофа. Без лишних слов перейдем сразу к делу!
Начнем с самого простейшего случая. Он изображен на рисунке 1. Допустим, ЭДС источника питания равна Е1=5 В, а сопротивления R1=100 Ом, R2=510 Ом, R3=10 кОм. Требуется рассчитать напряжения на резисторах и ток через каждый резистор.
Господа, замечу сразу, эту задачу можно решить гораздо более простым способом, чем с применением законов Кирхгофа. Однако сейчас наша задача не искать оптимальные способы решения, а на наглядном примере рассмотреть методику применения законов Кирхгофа при расчете схем.

Рисунок 1 – Простая схема
В этой схеме мы можем видеть три контура. Если возник вопрос – а почему три, то рекомендую посмотреть статью про второй закон Кирхгофа . В той статье имеется практически такая же схема с наглядным пояснением методики расчета числа контуров.
Господа, хочу отметить один тонкий момент. Хоть контура и три,
Итак, будем использовать два независимых контура. Для этого зададимся в каждом контуре направлением обхода контура. Как мы уже говорили, это некоторое направление в контуре, которое мы принимаем за положительное. Можно в какой-то степени назвать это аналогом осей координат в математике. Направление обхода каждого контура нарисуем синей стрелкой.
Далее зададимся направлением токов в ветвях: просто проставим его наугад. Не важно, угадаем мы сейчас направление или нет. Если угадали, то в конце расчета мы получим ток со знаком плюс, а если ошиблись – со знаком минус. Итак, обозначим токи в ветвях черными стрелочками с подписями I
Мы видим, что в контуре №1 направление токов I1 и I3, а также направление источника питания совпадают с направлением обхода, поэтому будем считать их со знаком плюс. В контуре №2 ток I2 совпадет с направлением обхода, поэтому будет со знаком плюс, а ток I3 направлен в другую сторону, поэтому будет со знаком минус. Запишем второй закон Кирхгофа для контура №1:

А теперь запишем этот же закон для контура №2:

Видим, что в контуре №2 нет источников питания, поэтому в левой части (где у нас согласно второму закону Кирхгофа стоит сумма ЭДС) у нас нолик. Итак, у нас есть два уравнения, а неизвестных-то у нас три (I1, I2, I3). А нам известно, что для нахождения трех неизвестных нужна система с тремя независимыми уравнениями. Где же взять третье недостающее уравнение? А, например, из первого закона Кирхгофа ! Согласно этому закону мы можем записать

Господа, теперь полный порядок, у нас есть три уравнения и три неизвестных и нам остается только решить вот такую вот систему уравнений

Подставим конкретные числа. Все расчеты будем вести в кошерной системе СИ. Рекомендую всегда считать только в ней. Не поддавайтесь искушению подставлять куда-то миллиметры, мили, килоамперы и прочее. Возможно возникновение путаницы.

Решение таких систем рассматривается чуть ли не в начальной школе и, полагаю, не должно вызывать трудностей . Если что, есть куча математических пакетов, которые сделают это за вас, если вам лень самим ручками считай. Поэтому мы опустим процесс решения, а сразу приведем результат

Видим, что все токи получились у нас со знаком плюс. Это значит, что мы верно угадали их направление. Да, то есть токи в схеме текут именно в том направлении, как мы нарисовали стрелочки на рисунке 1. Однако из условия задачи необходимо найти не только токи через резисторы, но и падение напряжения на них. Как это сделать? Например, с помощью уже изученного нами закона Ома . Как мы помним, закон Ома связывает между собой ток, напряжение и сопротивление. Если нам известны любые две из этих величин, мы легко можем найти третью. В данном случае мы знаем сопротивление и ток, который течет через это сопротивление. Поэтому, используя вот эту формулу

находим напряжение на каждом резисторе

Заметим, господа, что напряжения на резисторах R2 и R3 равны между собой. Это и логично, поскольку они соединены между собой параллельно. Однако пока не будем на этом акцентировать большое внимание, рассмотрим это лучше в другой раз.
Итак, господа, мы решили эту простую задачку с помощью двух законов Кирхгофа и закона Ома . Но это был совсем простой пример. Давайте попробуем решить более сложную задачу. Взгляните на рисунок 2.

Рисунок 2 – Схема посложнее
Схема выглядит внушительно, не правда ли? Возможно, вам даже не верится, что эту схему можно легко рассчитать. Однако, господа, уверяю вас, вы обладаете всеми необходимыми знаниями для расчета этой схемы, если уже изучили мои предыдущие статьи. Сейчас вы в этом убедитесь.
Для начала зададимся конкретными цифрами значений сопротивлений резисторов и напряжений источников.
Пусть Е1=15 В, Е2=24 В, R1= 10 Ом, R2 = 51 Ом, R3=100 Ом, R4=1 кОм, R5=10 Ом, R6=18 Ом, R7=10 кОм.
Найти, как и в прошлой задаче, требуется все токи в схеме и напряжения на всех резисторах.
В этой схеме мы можем видеть три независимых контура. Обозначим их римскими цифрами I, II, III. В каждом контуре зададимся направлением обхода. Они показаны синими стрелками.
Дальше как и в прошлый раз наугад расставим направления токов во всех ветвях и подпишем где какой ток. Видно, что всего у нас 6 ветвей и, соответственно, 6 разных токов (I1…I6).
Теперь запишем второй закон Кирхгофа для всех трех независимых контуров.
Второй закон Кирхгофа для контура I:

Второй закон Кирхгофа для контура II:

Второй закон Кирхгофа для контура III:

У нас есть три уравнения, однако неизвестных токов аж 6. Как и в прошлой задаче для получения недостающих уравнений запишем первые законы Кирхгофа для узлов.
Первый закон Кирхгофа для узла А:

Первый закон Кирхгофа для узла В:

Первый закон Кирхгофа для узла С:

Собственно, у нас теперь есть система из 6 уравнений с 6 неизвестными. Остается только решить эту систему

Подставляя числа, заданные в условии, получаем

Опуская решения за пределами статьи, приведем итоговый результат

Господа, мы видим, что почти все токи, кроме I4 получились у нас со знаками «минус». Это значит, что мы не угадали их направление, когда рисовали стрелочки на рисунке 2 . То есть все токи, кроме тока I4 на самом деле текут в противоположные стороны. А ток I
Теперь все по тому же закону Ома ровно как в прошлом примере рассчитаем напряжения на резисторах:

Вот и все, господа: схема рассчитана, а задачка решена. Таким образом, вы теперь обладаете весьма мощным инструментом по расчету электрических схем. С помощью двух законов Кирхгофа и закона Ома вы сможете рассчитать весьма непростые схемы, найти величины токов и их направления, а также напряжения на всех нагрузках цепи. Более того, зная токи и напряжения вы легко сможете рассчитать и мощности, которые на этих резисторах выделяются, если воспользуетесь рекомендациями из моей предыдущей статьи .
На этом на сегодня все господа. Огромной вам всем удачи и успешных расчетов!
Вступайте в нашу группу Вконтакте
Вопросы и предложения админу: This email address is being protected from spambots. You need JavaScript enabled to view it.
Пример решения задачи
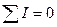 -первый закон Кирхгофа
-первый закон Кирхгофа
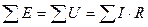 — второй закон Кирхгофа
— второй закон Кирхгофа
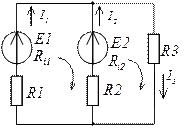
Составляем уравнения по законам Кирхгофа для данной схемы

Пример решения задачи:
Подставляя исходные данные
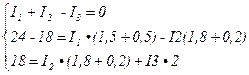
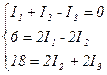
Сокращаем коэффициенты в уравнениях
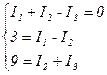
Выражаем I1 из первого уравнения и подставляем во второе
Совместно записываем второе и третье уравнение и вычитаем почленно
Подставляем найденные I2=2A в третье уравнение
Подставляем I2 и I3 в первое уравнение
Оба источника работают в режиме генератора, так как ток и ЭДС совпадают по направлению
| Задание | Схема к заданию |
| 1.Составьте в общем виде необходимое количество уравнений по законам Кирхгофа. | 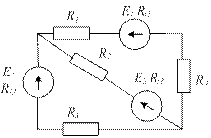 |
МЕТОД КОНТУРНЫХ ТОКОВ
Этот метод позволяет уменьшать количество уравнений в системе.
1. Выбираем производное направление контурного тока;
2. Составляем уравнение по второму закону Кирхгофа для контурных токов. При записи учитываем падение напряжения от собственного контурного тока и контурных токов соседних контуров;
3. Решаем полученную систему уравнений и определяем контурные токи;
4. Рассчитываем действительные токи ветвей по правилу:
если в ветви течёт один контурный ток, то действительный ток равен этому контурному; если течет несколько, то действительный равен алгебраической сумме.

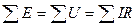 — второй закон Кирхгофа
— второй закон Кирхгофа
Пусть при решении получилось
Тогда I1 = I1к=3A и направлен вверх
Пример решения задачи
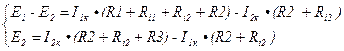
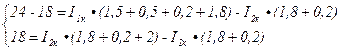
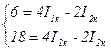
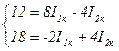
| Задание | Схема к заданию |
| 1.Составьте в общем виде необходимое количество уравнений по методу контурных токов. | 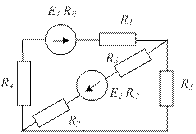 |
МЕТОД ДВУХ УЗЛОВ

1.Обозначим узлы (А;В)
Под узлом А обозначим узел, к которому направлено больше ЭДС
2.Все токи направляем к узлу А
3. Рассчитываем проводимость каждой ветви по формуле единица разделить на сумму всех сопротивлений ветви.
G1= 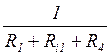 См
См
G2= 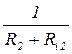 См
См
G3= 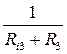 См
См
G4= 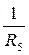 См
См
4) Определяем напряжение между двумя узлами, в эту формулу Е входит со знаком «плюс» если она направлена к узлу А и со знаком «минус» , если от узла
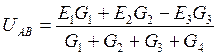 ∙
∙
5) Записываем токи ветвей
6) Меняем направлен отрицательных токов (I3, I4)
Пример решения задачи
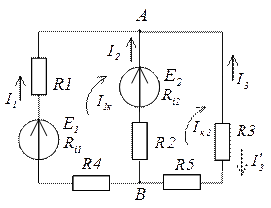 G1
G1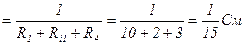
G2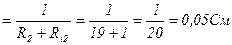
G3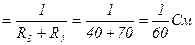
UAB= 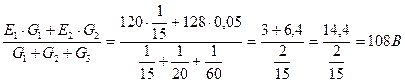
I1=(E1-UАВ)∙G1=(120-108)∙ 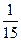 =
= 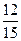 =
= 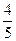 =0,8A
=0,8A
I2=( E2-UАВ )∙G2=(128-108)∙ 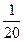 =1A
=1A
I3=- UАВ∙G3 =(-108)∙ 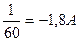
| Задание | Схема к заданию |
| 1.Составьте в общем виде решение задачи по методу двух узлов. | 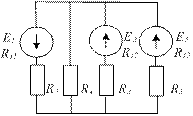 |
МЕТОД ЭКВИВАЛЕНТНОГО ГЕНЕРАТОРА
Этим методом удобно рассчитывать ток в одной ветви, особенно, если сопротивление этой ветви меняется.
Цель называется активной, если она содержит внутри себя источники или усилительные элементы и пассивной, если нет (R, L, C).
Согласно теории об эквивалентном генераторе любой активный двухполюсник можно заменить эквивалентным ЭДС с эквивалентным внутренним сопротивлением.
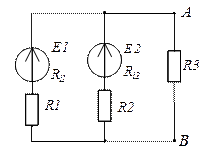
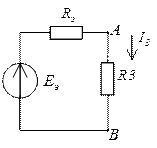
Схема с активным двухполюсником из нее следует 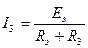
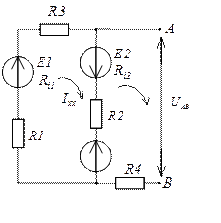
Чтобы найти Еэ надо разомкнуть ветвь АВ и найти напряжение на зажимах разомкнутой ветви.
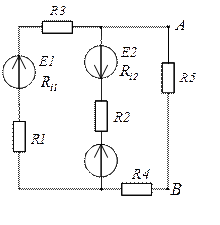
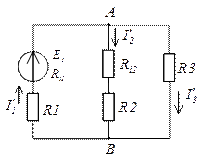
Пример решения задачи методом эквивалентного генератора.
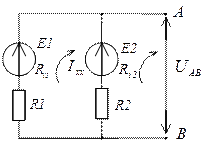
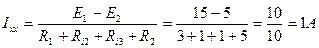
Обходим контур, который замыкается через UAB по второму закону Кирхгофа.
Чтобы найти Rэ надо разомкнуть ветвь АВ, исключить все ЭДС, оставив их внутренне сопротивление и рассчитать входное сопротивление цепи по отношению к зажимам разомкнутой ветви.
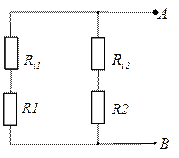 Ri2,2=Ri2+R2=1+5=6 Ом
Ri2,2=Ri2+R2=1+5=6 Ом
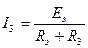
I3= 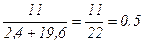 A
A
 Пример решения задачи.
Пример решения задачи.
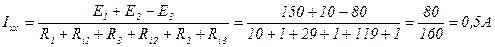
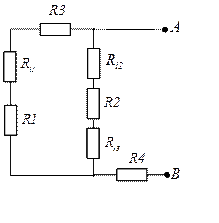
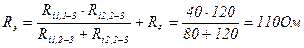 I5=
I5= 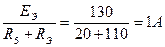
ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ
Активные элементы — это источники и усилительные элементы.
Пассивные — резисторы, катушки индуктивности и конденсаторы.
Операционный усилитель — активный резистивный элемент, который выполняет в технике связи основной усилительный эффект. Представляет собой то или иное число транзисторов (до 20) и резисторов. Выполняется в виде интегральных микросхем.
Схемное изображение операционного усилителя:
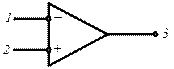
Операционный усилитель имеет 8 выводов: 2 входных, 1 выходной, 1 заземлённый и 2 для регулировки, 2 источника питания. Напряжение питания 12-15 В.
1) очень высокий коэффициент усиления μ = 10 4 — 10 5 ;
2) очень высокое входное сопротивление Rвх = 10 5 и выше;
3) маленькое выходное сопротивление Rвых = единицы Ом.
Неинвертируемый (положительный) вход операционного усилителя — это такой вход, при подаче на который напряжения одной полярности на выходе получается напряжение той же полярности.
Инвертируемый (отрицательный) вход операционного усилителя — это такой вход, при подаче на который напряжения одной полярности на выходе получается напряжение другой полярности.
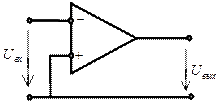
Работа операционного усилителя сводится к тому, что напряжение источника питания преобразуется по закону входного напряжения, но напряжение на выходе не может быть больше, чем напряжение источника питания. Поэтому, если операционный усилитель работает без обратной связи, то на его выходе всегда будет сигнал прямоугольной формы, равный напряжению источника питания.
Схема включения операционного усилителя без обратной связи:
Понятие об обратной связи
Обратная связь — это цепи, через которые часть напряжения с выхода четырёхполюсника снова подаётся на вход того же четырехполюсника.
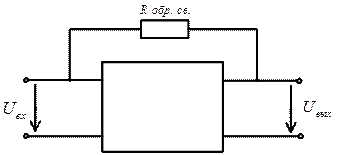
ООС — отрицательная обратная связь — это когда выходное напряжение подаётся на вход со знаком противоположным знаку входного.
ПОС — когда выходное напряжение подаётся на вход с тем же знаком, что и знак входного напряжения.
Операционный усилитель всегда работает с глубокой отрицательной обратной связью. Поэтому его коэффициент передачи уменьшается, но зато улучшаются его другие свойства (стабильность, полоса пропускания).
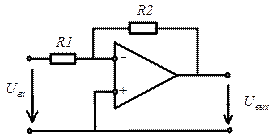
Схема операционного усилителя с обратной связью:
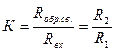
| Задание | Варианты ответов |
| 1.Является ли операционный усилитель активным элементом? | Да; Нет. |
| 2.Можно ли на выходе операционного усилителя получить напряжение больше чем напряжение питания? | Да; Нет. |
| 3.Является ли очень высокий коэффициент передачи операционного усилителя его достоинством? | Да; Нет. |
МЕТОД НАЛОЖЕНИЯ
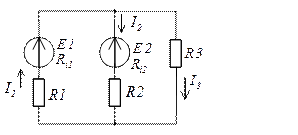
Основан на принципе, согласно которому, ток в которой ветви может быть найден, как алгебраическая сумма токов от действия каждой ЕДС в отдельности
1. Поочередно оставляем в схеме по одному источнику
2. Внутренние сопротивления исключаемых источников остаются
3. Получаем расчет схемы для нахождения частичных токов. Эти токи обозначаем со « ′ » и рассчитываем по закону Ома
4. Находим действительные токи ветви, как алгебраическую сумму частичных токов. Действительный ток направлен в сторону большего действительного
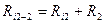
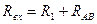
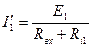
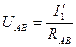
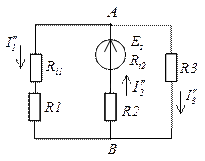
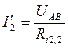
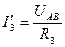
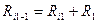
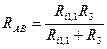
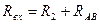
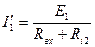

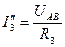
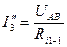
Пусть при решении получилось
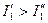 ,
, 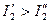 ,
, 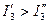 . Тогда
. Тогда
Рассмотрим на примерах как можно использовать законы Кирхгофа при решении задач.
Задача 1
Дана схема, и известны сопротивления резисторов и ЭДС источников. Требуется найти токи в ветвях, используя законы Кирхгофа.

Используя первый закон Кирхгофа, можно записать n-1 уравнений для цепи. В нашем случае количество узлов n=2, а значит нужно составить только одно уравнение.
Напомним, что по первому закону, сумма токов сходящихся в узле равна нулю. При этом, условно принято считать входящие токи в узел положительными, а выходящими отрицательными. Значит для нашей задачи

Затем используя второй закон (сумма падений напряжения в независимом контуре равна сумме ЭДС в нем) составим уравнения для первого и второго контуров цепи. Направления обхода выбраны произвольными, при этом если направление тока через резистор совпадает с направлением обхода, берем со знаком плюс, и наоборот если не совпадает, то со знаком минус. Аналогично с источниками ЭДС.
На примере первого контура – ток I1 и I3 совпадают с направлением обхода контура (против часовой стрелки), ЭДС E1 также совпадает, поэтому берем их со знаком плюс.
Уравнения для первого и второго контуров по второму закону будут:

Все эти три уравнения образуют систему

Подставив известные значения и решив данную линейную систему уравнений, найдем токи в ветвях (способ решения может быть любым).

Проверку правильности решения можно осуществить разными способами, но самым надежным является проверка балансом мощностей.
Задача 2
Зная сопротивления резисторов и ЭДС трех источников найти ЭДС четвертого и токи в ветвях.

Как и в предыдущей задаче начнем решение с составления уравнений на основании первого закона Кирхгофа. Количество уравнений n-1= 2
 Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче.
Затем составляем уравнения по второму закону для трех контуров. Учитываем направления обхода, как и в предыдущей задаче.

На основании этих уравнений составляем систему с 5-ью неизвестными

Решив эту систему любым удобным способом, найдем неизвестные величины
 Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками.
Для этой задачи выполним проверку с помощью баланса мощностей, при этом сумма мощностей, отданная источниками, должна равняться сумме мощностей полученных приемниками.
 Баланс мощностей сошелся, а значит токи и ЭДС найдены верно.
Баланс мощностей сошелся, а значит токи и ЭДС найдены верно.
Тема 3. Законы Кирхгофа и их применение для расчета электрических цепей
1. Ток I3 при I1 = 5A, I2 = 7A равен:
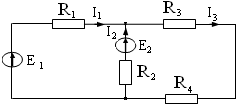
1) 12 А
2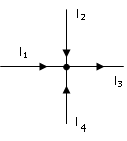 .
Первый закон Кирхгофа имеет вид:
.
Первый закон Кирхгофа имеет вид:
3) I1 + I2 — I3 + I4 = 0
3. Уравнение по второму закону Кирхгофа для цепи постоянного тока имеет вид:
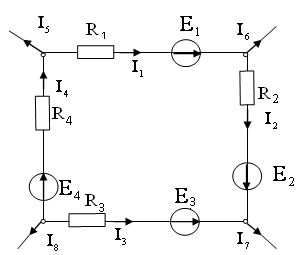
1) I1 R 1+ I2R2 – I3R3+ I4R4= E1+ E2 – E3 + E4
4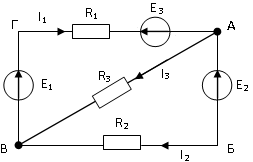 .
Для внешнего контура АБВГ электрической
цепи справедливо уравнение:
.
Для внешнего контура АБВГ электрической
цепи справедливо уравнение:
1) E1 – E2 – Е3= I2R2 + I1R1
5. Для внутреннего контура АВГ электрической цепи справедливо уравнение:
2) E1 – Е3= I3R3 + I1R1
6. Для внешнего контура АБВ электрической цепи справедливо уравнение:
1) E2 = -I2R2 + I3R3
7. Для узла А электрической цепи справедливо уравнение:
1 )
)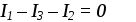
8. Для узла B электрической цепи справедливо уравнение:
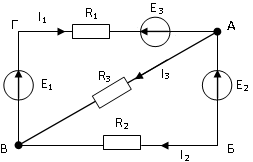
3) 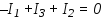
9. Для электрической цепи указать неправильное уравнение:
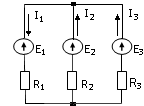
4) 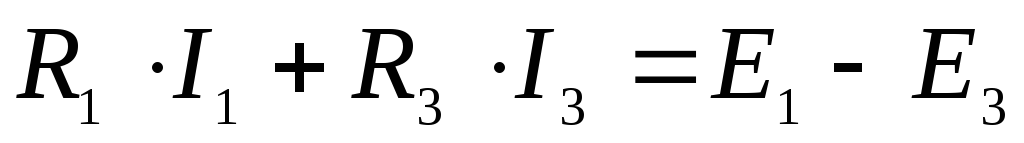 ;
;
10. Уравнение по 2-ому закону Кирхгофа для контура adb имеет вид:
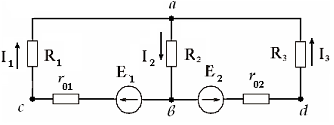
4) 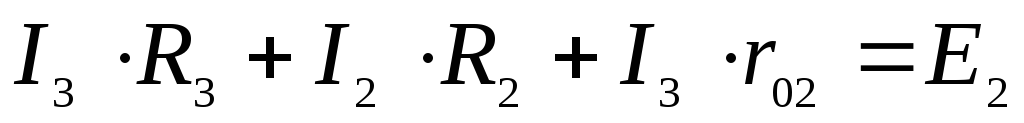
11. Уравнение по первому закону Кирхгофа для узла а имеет вид:.

3) 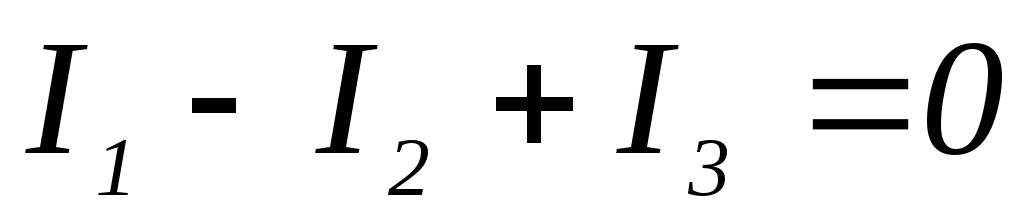
1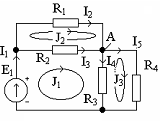 2.
Уравнение по первому закону Кирхгофа
для узла А имеет вид:
2.
Уравнение по первому закону Кирхгофа
для узла А имеет вид:
2) I2+I3-I4-I5=0
1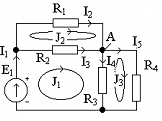 3.
Уравнение по 2-ому закону Кирхгофа для
контураJ1 имеет вид:
3.
Уравнение по 2-ому закону Кирхгофа для
контураJ1 имеет вид:
5) I3R2+I4R3 =E1
1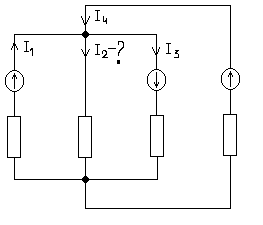 4.
ТокI2,
если I1=0,5А,
I3=0,3А,
I4=0,6А.
4.
ТокI2,
если I1=0,5А,
I3=0,3А,
I4=0,6А.
4) I2 =0,8А
15. Первый закон Кирхгофа формулируется следующим образом
2) алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю;
16. Второй закон Кирхгофа формулируется следующим образом
1) алгебраическая сумма падений напряжений в контуре равна алгебраической сумме ЭДС в том же контуре;
1 7.
Общее количество независимых уравнений
по законам Кирхгофа, необходимое для
расчета токов в ветвях заданной цепи,
составит…
7.
Общее количество независимых уравнений
по законам Кирхгофа, необходимое для
расчета токов в ветвях заданной цепи,
составит…
4) 5
18. Количество уравнений, которые необходимо составить по первому закону Кирхгофа для заданной цепи, составляет…
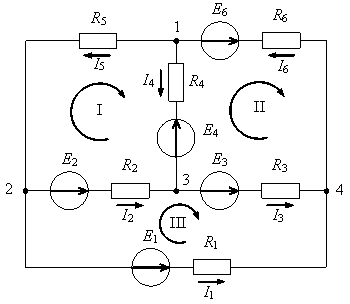
1) 3
Тема 4. Анализ цепей постоянного тока с одним источником энергии
1. Эквивалентное сопротивление цепи относительно источника ЭДС составит…
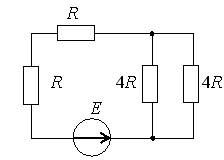
2) 4R
2. Если пять резисторов c сопротивлениями R1= 100 Ом,
R2 = 10 Ом, R3= 20 Ом, R4= 500 Ом, R5= 1000 Ом соединены последовательно, то ток будет …
один и тот же.
3. Внутренние сопротивления rА, rБ, rВ источников энергии находятся в соотношении
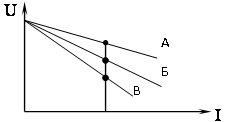
1) rА = rБ = rВ 2) rА < rБ < rВ 3) rА > rБ > rВ
4. К.П.Д. ηА, ηБ, ηВ источников электрической энергии находятся в соотношении …

1) А = Б = В 2) А < Б < В 3) А > Б >В
5. Источник ЭДС работает в генераторном режиме, когда
2) ток, протекающий через источник, совпадает по направлению с ЭДС;
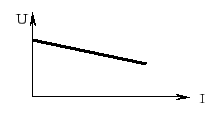
6. Внешняя характеристика источника ЭДС имеет вид:
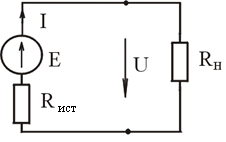
1) 
7. Источник ЭДС работает в режиме потребления энергии, когда
3)ток, протекающий через источник, противоположен по направлению ЭДС.
8 . Показание амперметра при U = 90 В, R = 30 Ом равно …
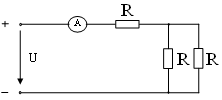 1)
1,5 A 2)
3 A
3) 2 А 4) 9 A 5)
1 A
1)
1,5 A 2)
3 A
3) 2 А 4) 9 A 5)
1 A
9. Показание амперметра при U = 90 B, R = 30 Ом равно…
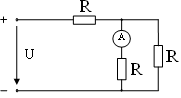
1) I = 1 A
10. Показание вольтметра при U = 90 B, r = 30 Ом равно …
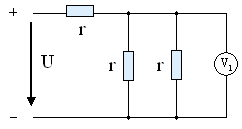
2) U = 30B
11. Ток I в электрической цепи при U = 10 B, E = 20 B, R = 5 Ом равен
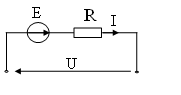
2А
12. Показание амперметра при R1 = R4 = 20 Ом, R2 = R3 = 30 Ом, E = 50В равно
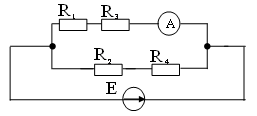
2) 1A
13. Если ток I3 = 0, E1 = 10 В, R1 = 2 Ом, R2 = 4 Ом, E2 равно…
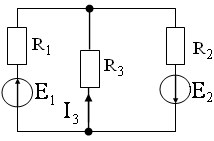
1) 20B 2) 40B 3) 5B 4) 10B 5) 50B
14. Метод эквивалентного генератора применяют, когда необходимо определить
1) контурные токи;
2) потенциалы узлов;
3) ток в выделенной ветви;
4) частичные токи.
15. ЭДС источника энергии Е при сопротивлениях цепи R1 = R4 = 20 Ом, R2 = R3 = 30 Ом и показании амперметра 2 А равна
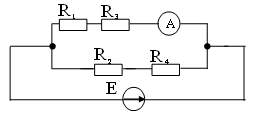
2) 100 В
16. Сопротивление лампы накаливания с номинальными параметрами Uн =220В и Рн = 100 Вт равно …
1) 484 Ом
17. Общее сопротивление двух ламп накаливания мощностью по 100 Вт включенных, параллельно на напряжение U = 200 В, равно …
1) 200 Ом
18. Ток лампы накаливания номинальной мощностью Рн = 200 Вт, включенной на номинальное напряжение Uн = 200B, равен …
3) 1 А
19. Напряжение сети U при падениях напряжения на соответствующих сопротивлениях U1=80B, U2=140B, U3=140B равно …
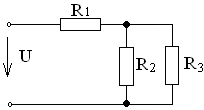
1) 220 В
20. Ток I при потребляемой мощности Р=125 Вт и сопротивлениях цепи R1=10 Ом, R2=2 Ом, R3=8 Ом равен …
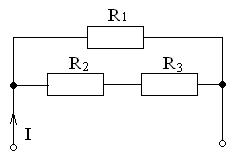
3) I=5 A
21. Показание вольтметра при U = 90 B, R = 30 Ом равно …
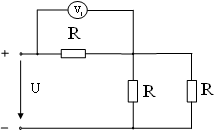
2) 60 В
22. Эквивалентное сопротивление цепи, если R1= R2 = R3= R4= R5= R6= R, равно …
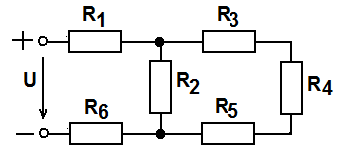
1) 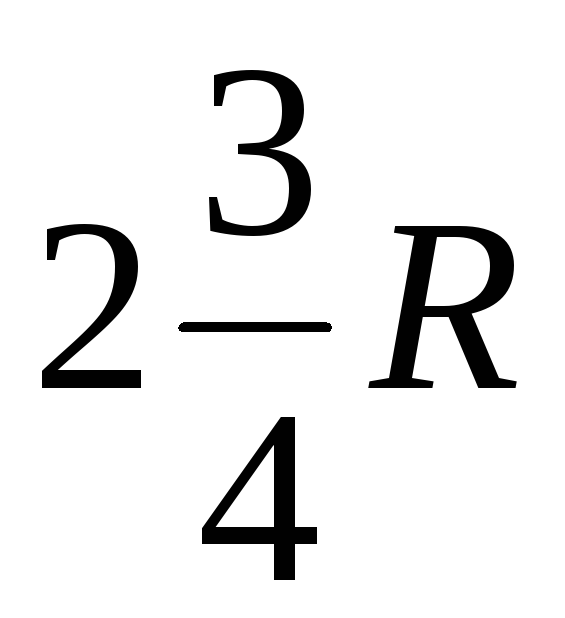
23. Эквивалентное сопротивление R электрической цепи при R = 2Ом равно …
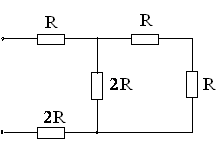
1) 8 Ом
24. Эквивалентное сопротивление RЭ электрической цепи при R = 2 Ом равно …
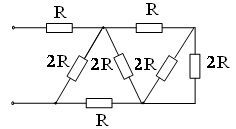
2) 4 Ом
25. Выражение для определения эквивалентного (входного) сопротивления RЭ цепи имеет вид:
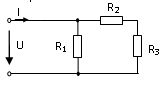
1) 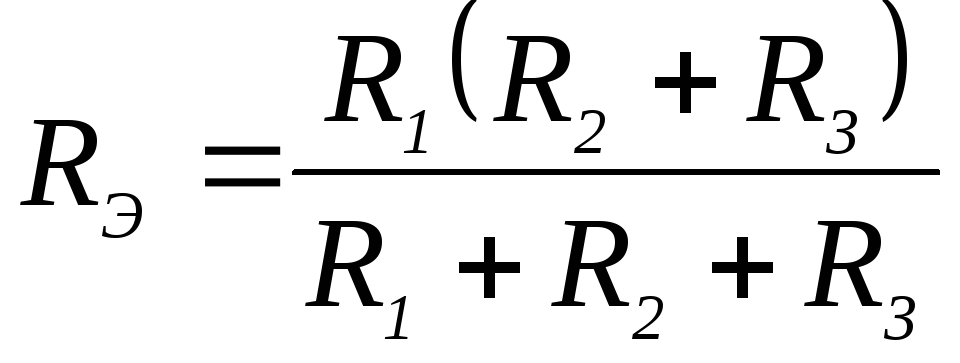
2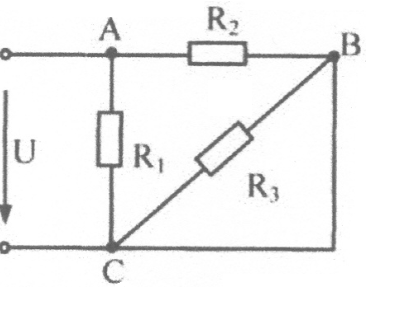 6.
Выражение для определения эквивалентного
(входного)
сопротивления RЭ цепи имеет вид:
6.
Выражение для определения эквивалентного
(входного)
сопротивления RЭ цепи имеет вид:
1) 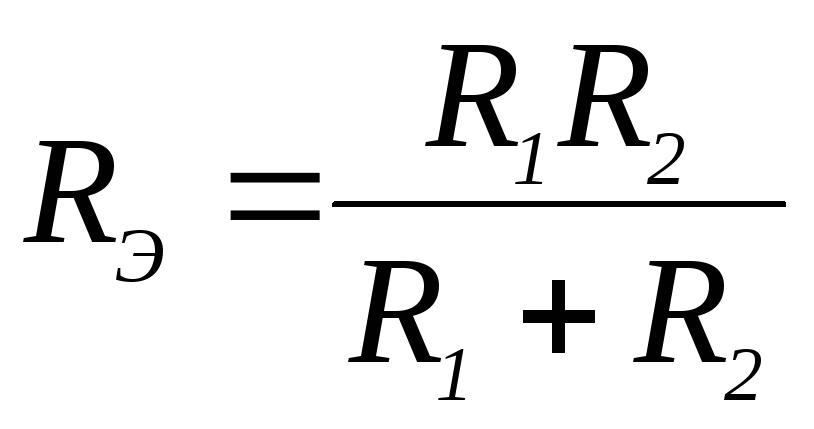
27. Выражение для определения эквивалентного (входного) сопротивления RЭ цепи имеет вид:
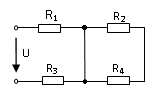
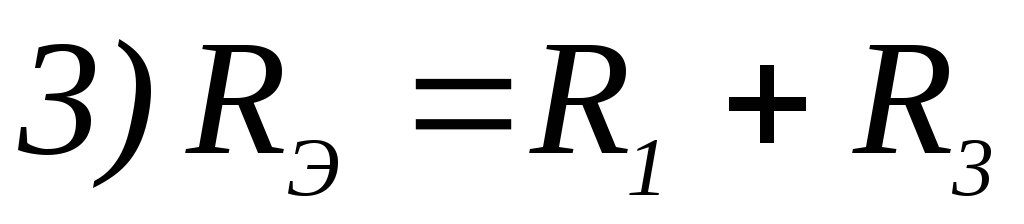
28. Выражение для определения эквивалентного (входного) сопротивления RЭ цепи имеет вид:
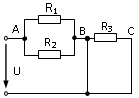
2) 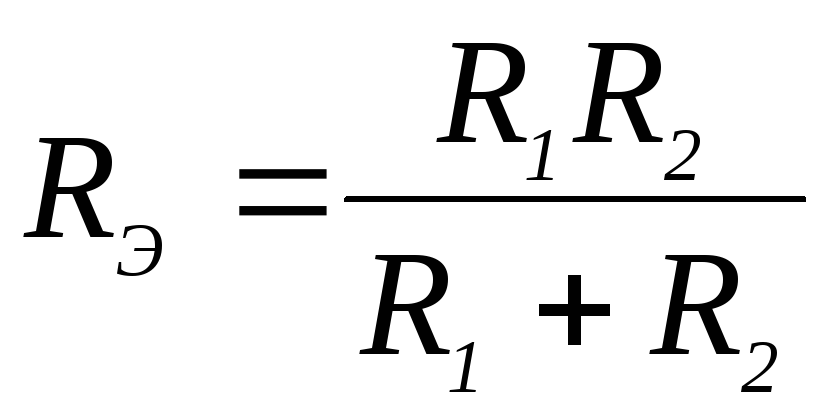
29. Выражение для определения эквивалентного (входного) сопротивления RЭ цепи имеет вид:
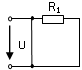
2)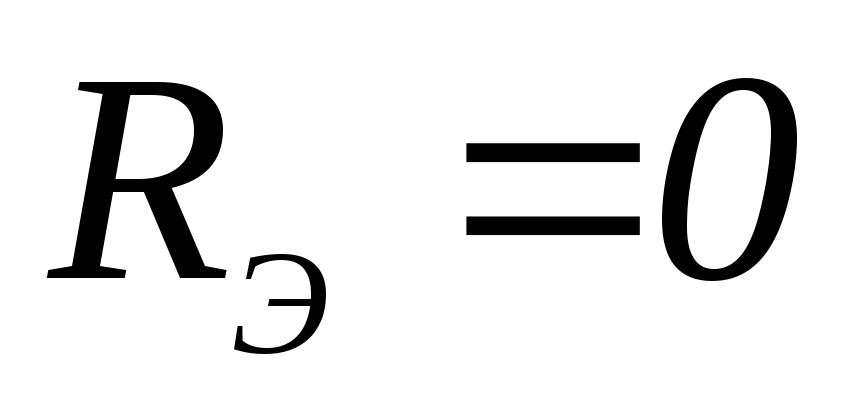
3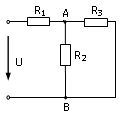 0.
Выражение для определения эквивалентного
(входного)
сопротивления RЭ цепи имеет вид:
0.
Выражение для определения эквивалентного
(входного)
сопротивления RЭ цепи имеет вид:
3) 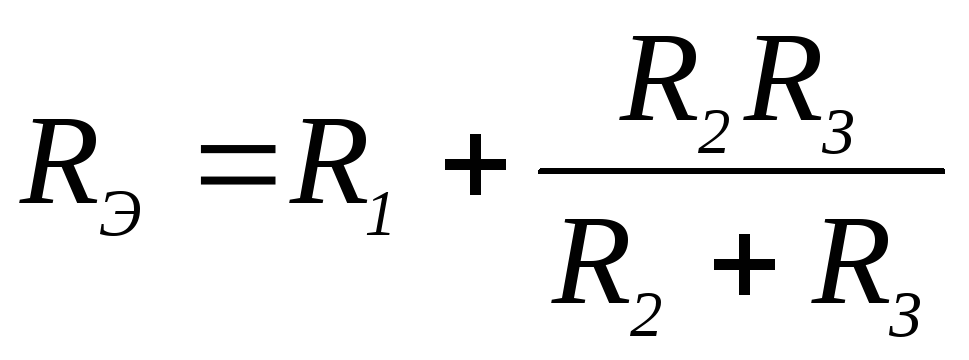
31. Выражение для определения эквивалентного (входного) сопротивления RЭ цепи имеет вид:
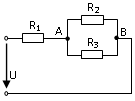
2) 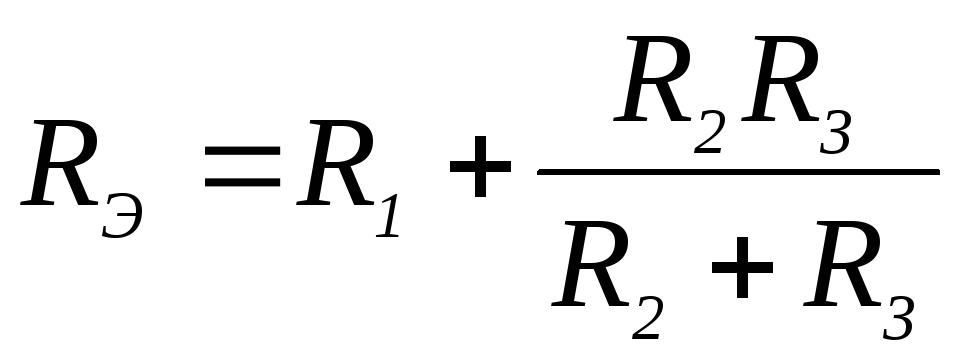
32. Выражение для эквивалентного сопротивления RЭ электрической цепи имеет вид:
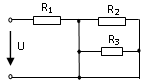 2)
2) 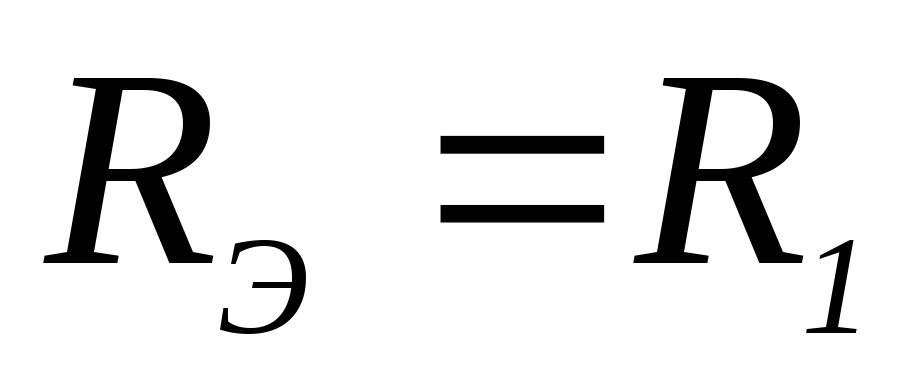
33. Выражение для эквивалентного сопротивления RЭ электрической цепи имеет вид:
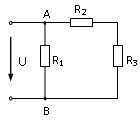
1) 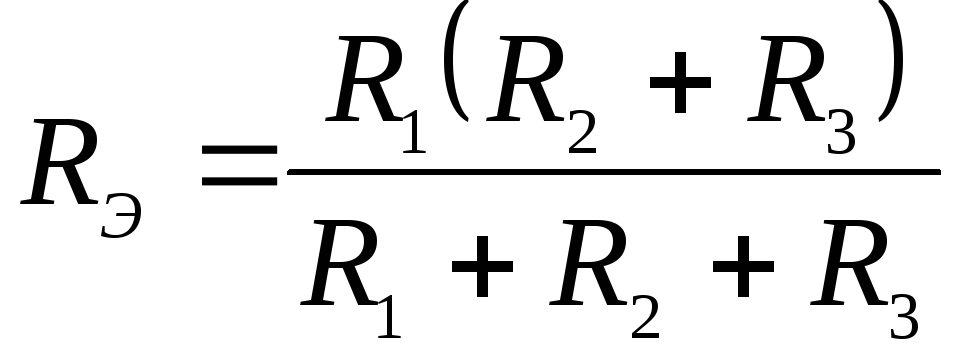
34. Входное сопротивление RЭ электрической цепи при R1 = R2 = R3 = R4 = 50 Ом равно …
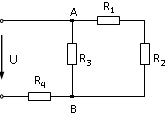
4) 83 Ом
35. Входное сопротивление RЭ цепи R1 = R2 = R3 = R4 = R5 = 50 Ом равно…
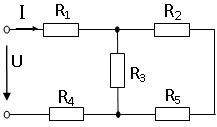
5) 133 Ом
36. Входное сопротивление RЭ электрической цепи при R1 = R2 = R3 = 50 Ом равно …
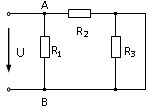
3) 25 Ом
37. Входное сопротивление RЭ электрической цепи при R1 = R2 = R3 = 50 Ом равно …
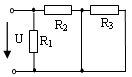
2) 25 Ом
38. Входное сопротивление RЭ электрической цепи при R1 = R2 = R3 = R4 = 50 Ом равно …
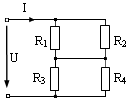
1) 50 Ом
39. Входное сопротивление RЭ электрической цепи при R1 = R2=0,5Ом, R3 = R5 = 10 Ом, R4 =R6 = R7 = 5 Ом равно …
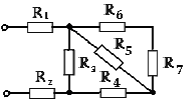
4) 6 Ом
1) Составить уравнения по законам Кирхгофа.
Некоммерческое акционерное общество
«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ»
Кафедра теоретических основ электротехники

РАСЧЕТНО-ГРАФИЧЕСКАЯ РАБОТА №1
По дисциплине «Основы теории цепей»
На тему «Расчет линейных электрических цепей постоянного тока с зависимыми источниками»
Специальность «Информационные системы»
Выполнил Ануарбеков Шыңғыс Группа ИС-16-2
Принял доцент каф. ТОЭ Айтжанов Н.М.
_________ «____»____________2017г.
Алматы 2017
Содержание
Введение……………………………………………………………………………………………………3
Задание………………………………………………………………………………………………………4
Расчетная часть………………………………………………………………………………………….6
Уравнения по законам Кирхгофа………………………………………………………..6
Метод контурных токов……………………………………………………………………..7
Метод узловых потенциалов………………………………………………………………9
Сравнение результатов МКТ и МУП…………………………………………………10
Метод эквивалентного генератора……………………………………………………..11
Напряжение на зажимах источника тока……………………………………………13
Баланс мощностей…………………………………………………………………………….13
Заключение………………………………………………………………………………………………14
Список литературы…………………………………………………………………………………..15
Введение
Цель работы: умение составлять систему уравнений по законам Кир-хгофа; применение закона Ома; получение навыков расчётов электрических цепей постоянного тока с зависимыми источниками методами контурных токов, методом узловых потенциалов, эквивалентного генератора.
В цепи действуют независимые источники напряжения с ЭДС Е1, Е2, Е3, источник тока J и зависимый источник напряжения Еи , управляемый током. Номер схемы определяется по таблице 1.1, числовые значения параметров цепи приведены в таблицах 1.2 и 1.3.
Таблица 1.1
Год поступления | Первая буква фамилии | |||||||||
Четный | А БЯ | ГЭЕ | ЖЗЩ | КЛ | МН | ОПР | СТУ | ФЧЦ | ХШИ | ДЮВ |
№ схемы | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | 1.10 |
МЭГ | I1 | I3 | I4 | I2 | I1 | I4 | I3 | I3 | I1 | I2 |
Таблица 1.2
Год поступления | Последняя цифра номера студенческого билета | |||||||||
Четный | 0 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
E1, В | 25 | 20 | 30 | 40 | 20 | 25 | 15 | 35 | 40 | 15 |
E2, В | 10 | 15 | 25 | 20 | 30 | 20 | 15 | 10 | 20 | 25 |
E3, В | 25 | 30 | 35 | 20 | 30 | 20 | 25 | 15 | 30 | 10 |
J, А | 3 | 5 | 2 | 6 | 4 | 10 | 8 | 5 | 3 | 5 |
r, Ом | 10 | 20 | 15 | 16 | 25 | 30 | 35 | 40 | 15 | 20 |
Таблица 1.3
Год поступления | Предпоследняя цифра номера студенческого билета | |||||||||
Четный | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 0 |
R1, Ом | 25 | 20 | 15 | 20 | 10 | 30 | 20 | 10 | 30 | 15 |
R2, Ом | 15 | 30 | 20 | 12 | 20 | 10 | 20 | 25 | 40 | 20 |
R3, Ом | 20 | 16 | 25 | 35 | 30 | 20 | 30 | 16 | 10 | 30 |
R4, Ом | 30 | 20 | 30 | 40 | 15 | 40 | 15 | 25 | 20 | 30 |
R, Ом | 6 | 10 | 8 | 10 | 10 | 15 | 20 | 15 | 5 | 8 |

Рисунок 1.1
Задание:
1) Составить уравнения по законам Кирхгофа.
2) Рассчитать токи во всех ветвях методом контурных токов.
3) Рассчитать токи во всех ветвях методом узловых потенциалов. 4) Сравнить результаты, полученные в пунктах 2, 3 и свести их в
одну таблицу.
5) Рассчитать ток в одной ветви методом эквивалентного генератора (см. таблицу 1.1).
6) Определить напряжение на зажимах источника тока.
7) Проверить выполнение баланса мощности.
Расчетная часть
Первый
закон Кирхгофа: алгебраическая сумма
токов в узле электрической цепи равна
нулю: 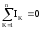 .
Со знаком «+» записываются токи,
направленные к узлу, со знаком «-»
записываются токи, направленные от узла
(или наоборот). Число уравнений,
составляемых по первому закону Кирхгофа,
равно
.
Со знаком «+» записываются токи,
направленные к узлу, со знаком «-»
записываются токи, направленные от узла
(или наоборот). Число уравнений,
составляемых по первому закону Кирхгофа,
равно 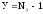 ,
где
,
где 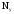 —
число узлов в цепи. В цепи (рис 1.1) имеются
4 узла, исходя из этого У = 4-1 = 3 (количество
уравнений по I
закону Кирхгофа). Следовательно,
достаточно записать уравнения для узлов
1, 2 и 3.
—
число узлов в цепи. В цепи (рис 1.1) имеются
4 узла, исходя из этого У = 4-1 = 3 (количество
уравнений по I
закону Кирхгофа). Следовательно,
достаточно записать уравнения для узлов
1, 2 и 3.
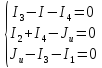
Второй
закон Кирхгофа: в любом замкнутом контуре
электрической цепи алгебраическая
сумма напряжений на сопротивлениях,
входящих в этот контур равна алгебраической
сумме ЭДС: 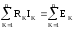 .
Напряжения записываются со знаком «+», если
положительное направление тока
.
Напряжения записываются со знаком «+», если
положительное направление тока 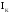 совпадает с направлением обхода контура,
со знаком «-», если направление тока
совпадает с направлением обхода контура,
со знаком «-», если направление тока 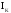 противоположно
направлению обхода контура; ЭДС
противоположно
направлению обхода контура; ЭДС 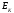 ,
направления, которых совпадают с
направлением обхода контура, записываются
со знаком «+», а ЭДС
,
направления, которых совпадают с
направлением обхода контура, записываются
со знаком «+», а ЭДС 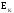 ,
направленные против обхода контура –
со знаком «-». Число уравнений, составляемых
по второму закону Кирхгофа, равно:
,
направленные против обхода контура –
со знаком «-». Число уравнений, составляемых
по второму закону Кирхгофа, равно: 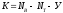 ,
где
,
где 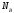 — число ветвей,
— число ветвей, 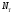 — число источников тока. Исходя из этого,
в цепи (рис 1.1) 6 ветвей, 1 источник тока
и как было выше сказано – 4 узла.
Следовательно, для второго закона
Кирхгофа понадобится К = 6-1-3=2 уравнения.
Выбираем два независимых контура, не
имеющих источника тока, затем произвольно
выбираем обход контура (рис 1.1). И для
каждого контура (внешний контур и контур
1241) запишем уравнение по II
закону Кирхгофа:
— число источников тока. Исходя из этого,
в цепи (рис 1.1) 6 ветвей, 1 источник тока
и как было выше сказано – 4 узла.
Следовательно, для второго закона
Кирхгофа понадобится К = 6-1-3=2 уравнения.
Выбираем два независимых контура, не
имеющих источника тока, затем произвольно
выбираем обход контура (рис 1.1). И для
каждого контура (внешний контур и контур
1241) запишем уравнение по II
закону Кирхгофа:
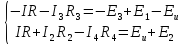
Общая система уравнений по законам Кирхгофа будет выглядеть следующим образом
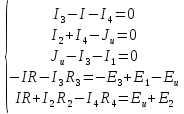
2) Рассчитать токи во всех ветвях методом контурных токов.
Составим систему уравнений по методу контурных токов для цепи постоянного тока (рис 1.2):
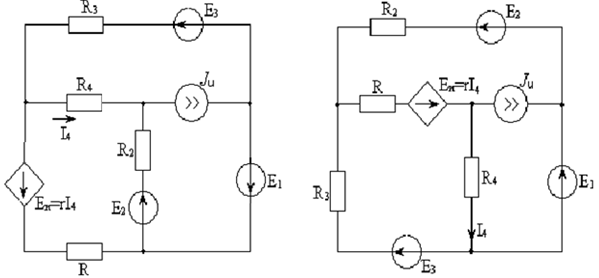
Рисунок 1.2.
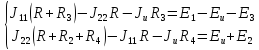
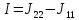
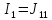
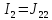
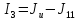
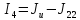 ,
где
,
где 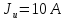
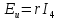 =
=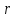 (
(
Решение: 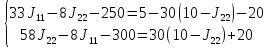
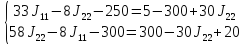
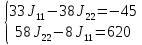 =
=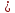
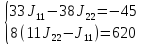 =
=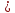
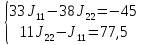 =
=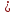
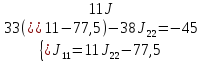 =
=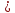
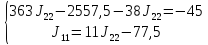 =
=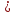
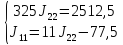 =
=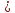
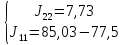 =
=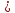
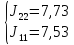 =
=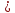
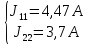 ,
тогда
,
тогда
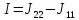 =7,73
– 7,53 = 0,2А
=7,73
– 7,53 = 0,2А
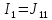 =
7,53А
=
7,53А
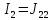 =
7,73А
=
7,73А
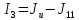 =
10 – 7,53 = 2,47А
=
10 – 7,53 = 2,47А
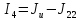 =
010– 7,73 = 2,27А
=
010– 7,73 = 2,27А
3) Рассчитать токи во всех ветвях методом узловых потенциалов.
Метод
узловых потенциалов позволяет уменьшить
число уравнений системы до числа 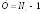 .
Суть метода
узловых потенциалов заключается в
определении потенциалов узлов
электрической цепи, токи рассчитываются
по закону Ома. При составлении уравнений
по методу узловых потенциалов, потенциал
одного из узлов принимают равным нулю,
для определения потенциалов оставшихся
узлов составляются уравнения.
.
Суть метода
узловых потенциалов заключается в
определении потенциалов узлов
электрической цепи, токи рассчитываются
по закону Ома. При составлении уравнений
по методу узловых потенциалов, потенциал
одного из узлов принимают равным нулю,
для определения потенциалов оставшихся
узлов составляются уравнения.
Возьмем
узел 3 за базовый и будем считать, что
он равен нулю. Автоматически значение
потенциала в узле 4 становится равным 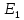 .
.
(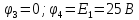 ).
).
Составим систему уравнений по методу узловых потенциалов для цепи постоянного тока (рис 1.3), так как значения потенциалов в узлах 3 и 4 известны, то нам необходимо составить систему из 2 уравнений для узлов 1 и 2:
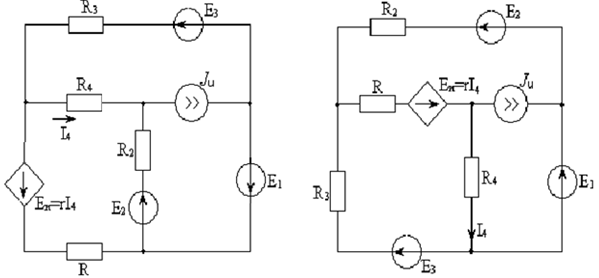
Рисунок 1.3
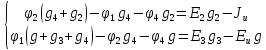

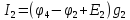
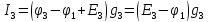
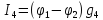
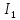 найдем,
применив I
закон Кирхгофа
найдем,
применив I
закон Кирхгофа 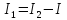
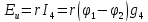
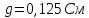
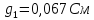
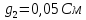
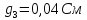
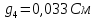
Решение: 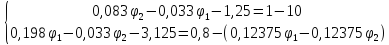
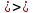
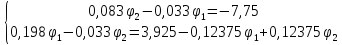
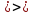


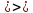
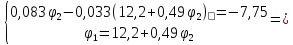
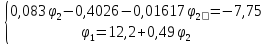
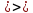
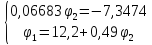

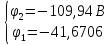 ,
тогда
,
тогда
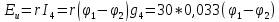 =0,99*68,2694
= 67,586706В
=0,99*68,2694
= 67,586706В
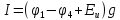 =
0,115 А
=
0,115 А
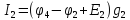 =
7,47А
=
7,47А
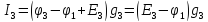 =
2,46А
=
2,46А
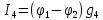 =
2,25А
=
2,25А
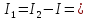 7,35А
7,35А
Вопрос 19. Первый закон Кирхгофа, узловые уравнения. Второй закон Кирхгофа, контурные уравнения.
Узел— точка, в которой сходятся не менее 3-х токов.
Ветвь— участок цепи, по которому течёт один и тот же ток.
Контур— любой замкнутый путь в схеме.
Первый закон Кирхгофа
Для любого узла сумма токов, приходящих к узлу, равна сумме токов, отходящих от узла.
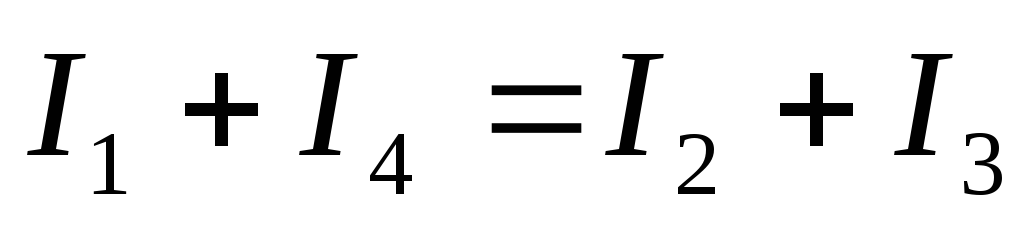
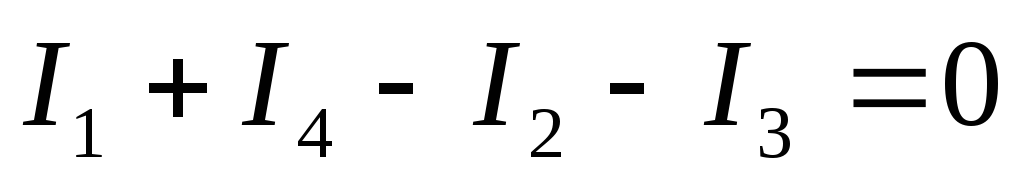
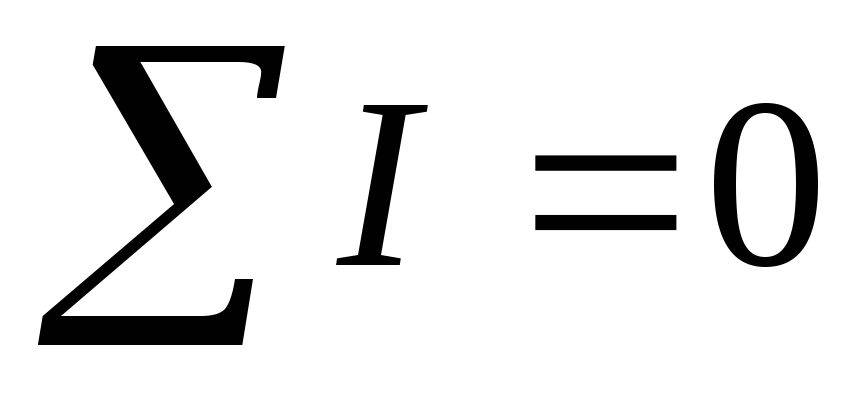
Для любого узла электрической цепи алгебраическая сумма токов равна нулю. Ток, который притекает к узлу, берётся со знаком “+”, который оттекает — со знаком “–”.
Второй закон Кирхгофа
Для любого замкнутого контура алгебраическая сумма ЭДС равна алгебраической сумме падений напряжений на участках этого контура.

Порядок составления контурных уравнений:
Выбираем произвольное направление тока ветвей.
Если в схеме n узлов, то составляем n – 1 уравнение по первому закону Кирхгофа.
Выбираем произвольное направление обхода контура.
Если направление обхода и ЭДС совпадают, то она входит в уравнение со знаком “+”, если нет — со знаком “–”.
Если ток ветви и направление обхода совпадают, то падение напряжения входит в уравнение со знаком “+”, если нет — со знаком “–”.
Если при расчёте получился отрицательный ток, значит его направление противоположно выбранному.
Задача
С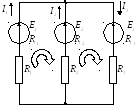 оставить
контурные уравнения для решения сложной
электрической цепи.
оставить
контурные уравнения для решения сложной
электрической цепи.
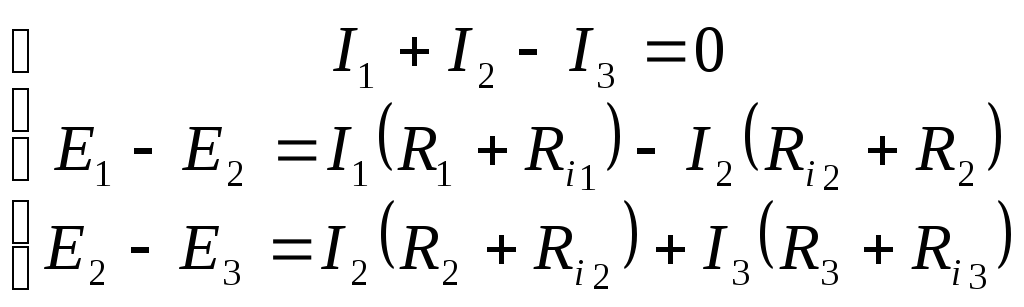
Вопрос 20. Расчёт сложных электрических цепей методом контурных токов.
Метод контурных токовпозволяет решать меньшее количество уравнений, чем при расчёте сложных электрических цепей методом уравнений Кирхгофа.
Порядок расчёта:
Выбираем произвольное направление контурного (расчётного) тока.
Составляем уравнение по второму закону Кирхгофа для контурных токов. При записи учитываем падение напряжения от контурного (собственного) тока и контурных токов соседних контуров.
Решаем полученную систему уравнений и рассчитываем контурные токи.
Рассчитываем действительные токи ветвей по правилу:
Если в ветви течёт один контурный ток, то действительный ток равен контурному току. Если два и более — то действительный равен их алгебраической сумме и направлен в сторону большего.
Задача
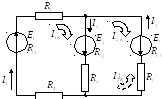
Найти и направить все токи в электрической цепи методом контурных токов.
Используя алгоритм, составляется система уравнений:
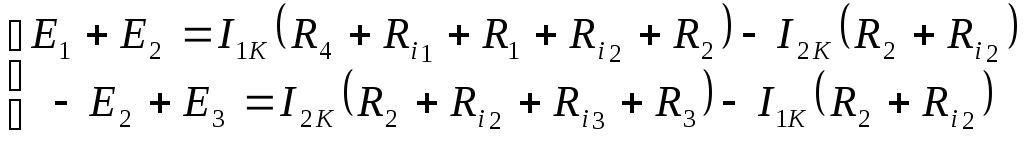
Пусть при решении получили контурные токи:
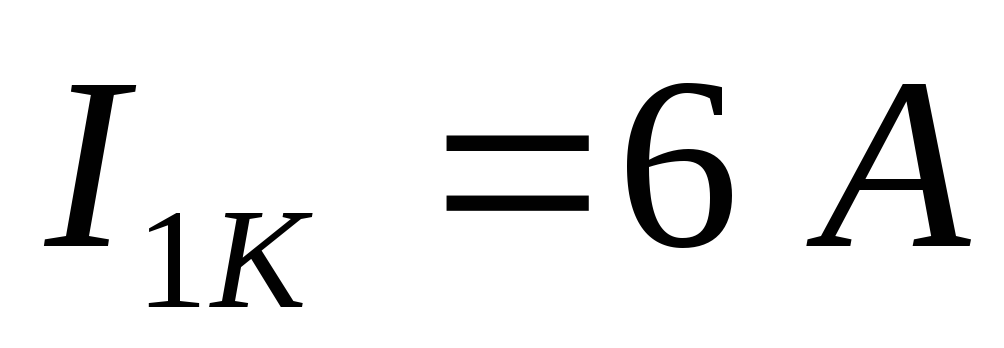
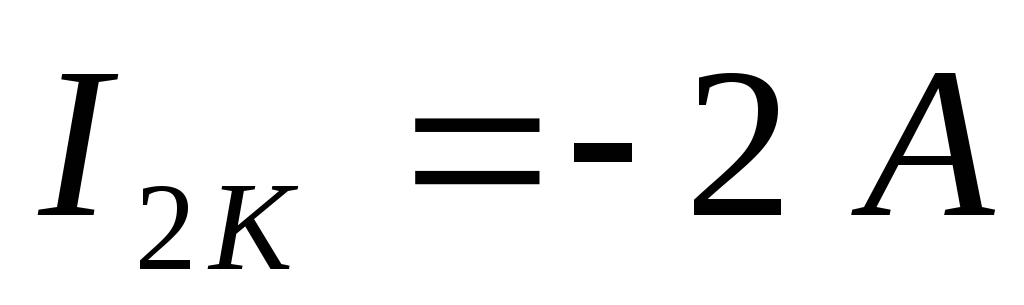
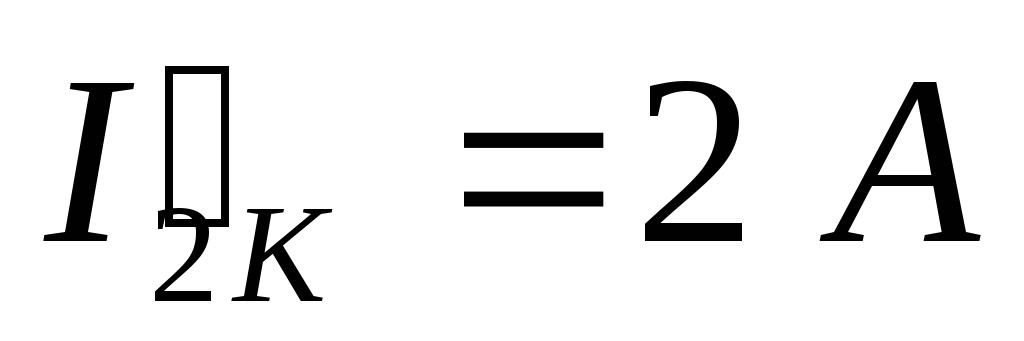
Тогда можно рассчитать действительные токи:
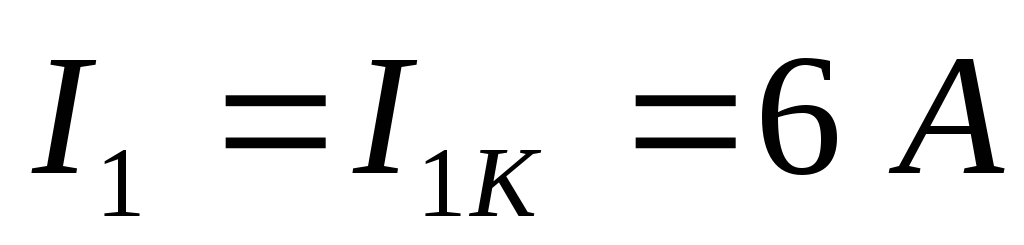
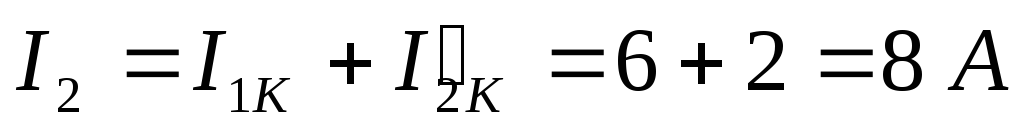
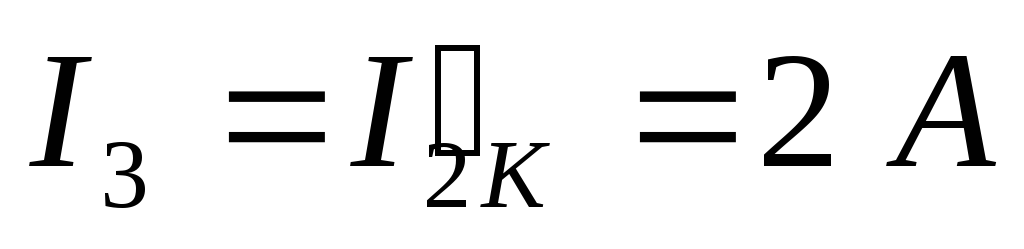
Вопрос 21. Расчёт сложных электрических цепей методом двух узлов.
Рассмотрим метод узловых напряжений(двух узлов) на примере.
Задача
Определить токи ветвей и направить их.
Порядок расчёта:
обозначаем узлы А и Б: под узлом А обозначаем узел, к которому направлена большая ЭДС;
все токи направляем к узлу А;
рассчитываем проводимость каждой ветви по формуле
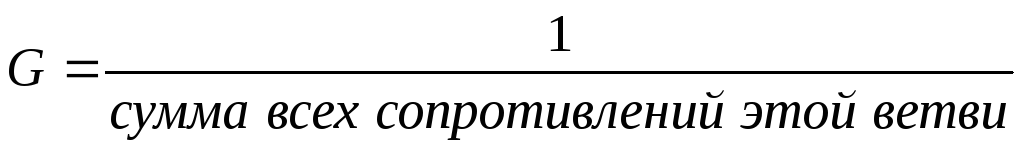 :
:
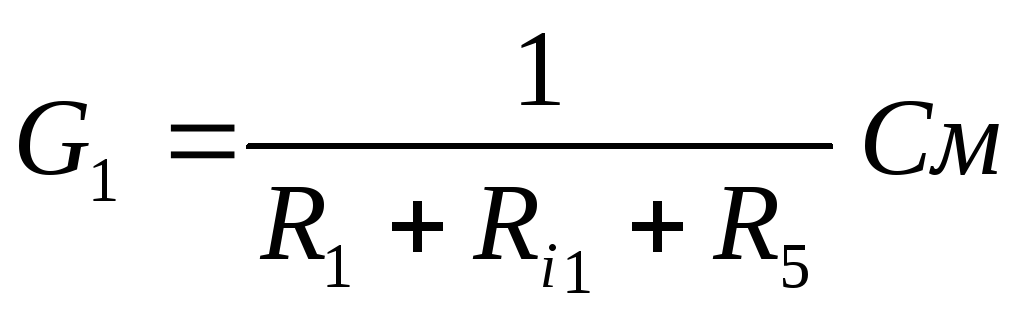
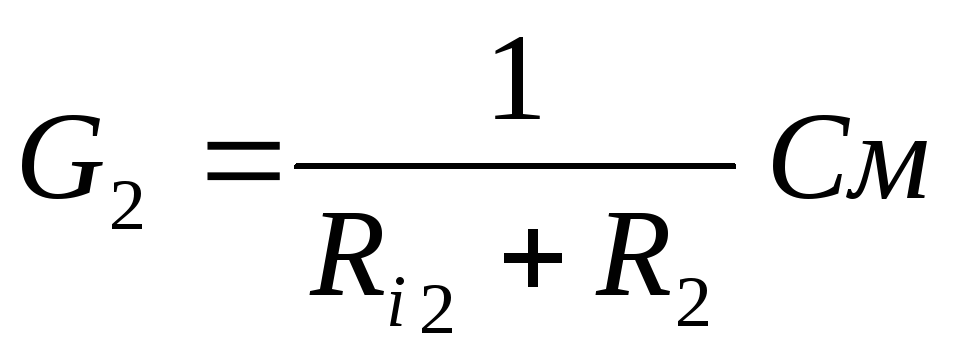
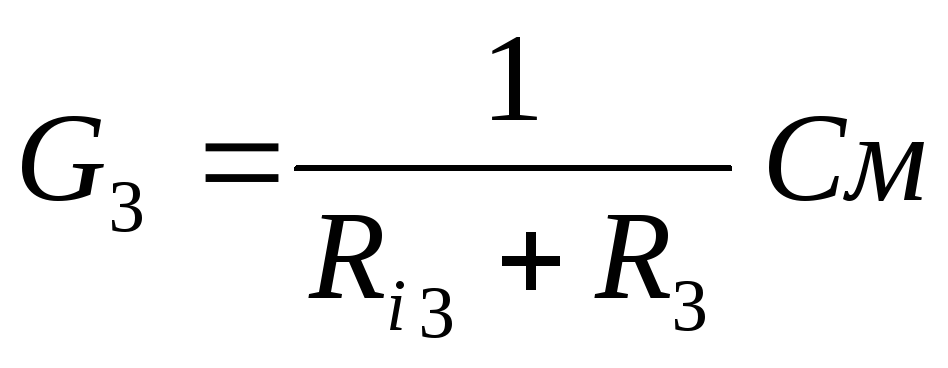
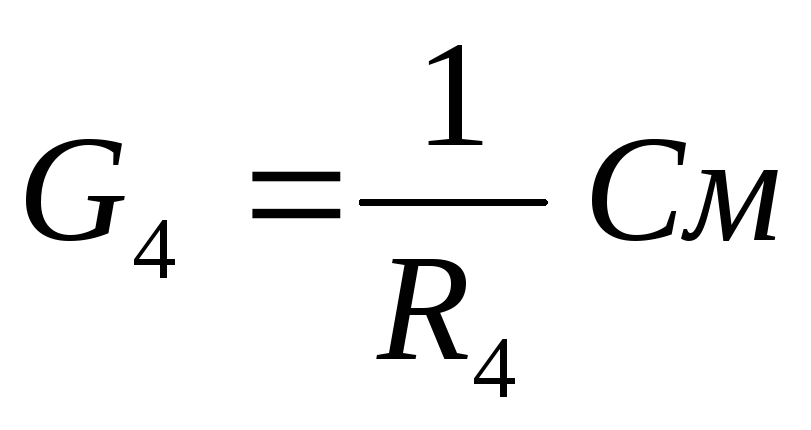
Рассчитываем напряжение
 между двумя узлами по формуле:
между двумя узлами по формуле:
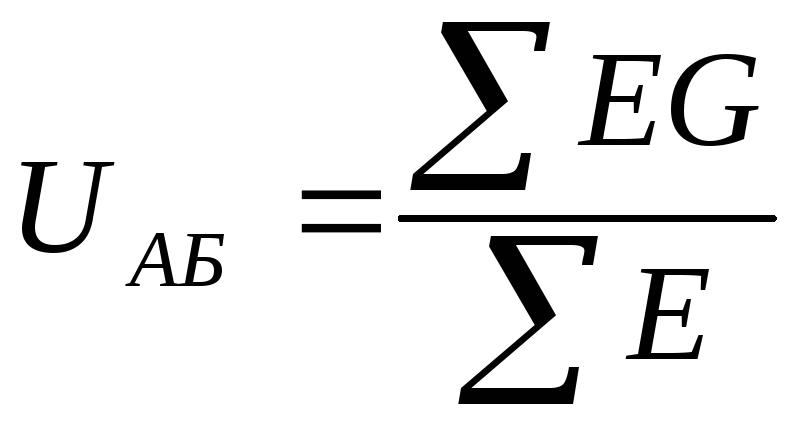
В формулу Eвходит со знаком “+”, если она направлена к узлу А; если от узла — то со знаком “–”.
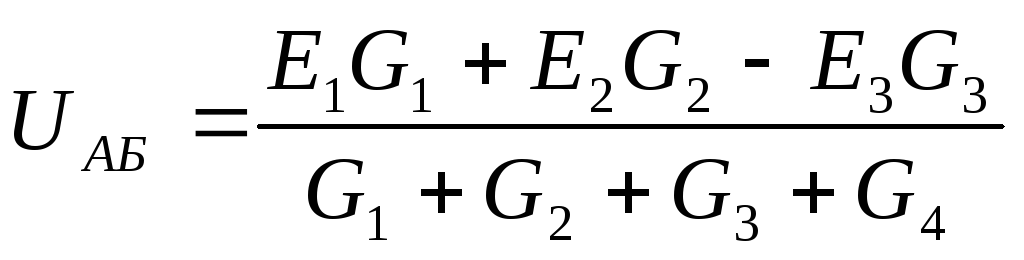
Находим токи ветвей:
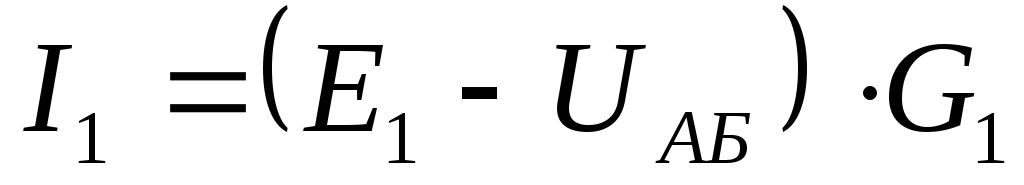
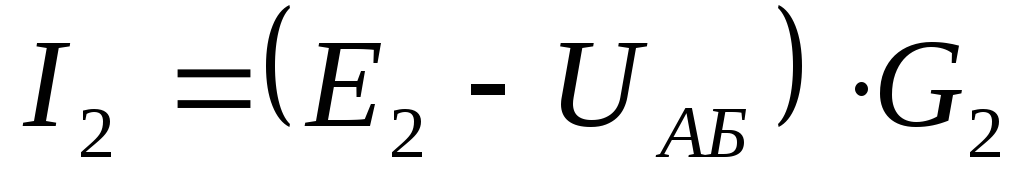
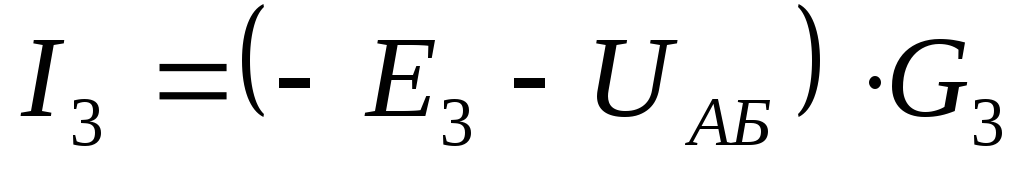
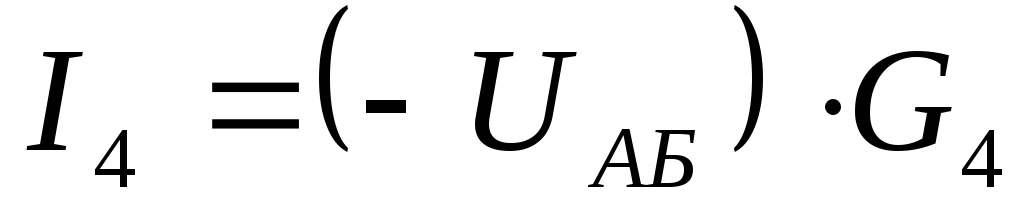
Изменяем направление отрицательных токов.
Вопрос 22. Расчёт сложных электрических цепей методом эквивалентного генератора.
Методом эквивалентного генераторанаходят ток в одной ветви. Особенно удобно, если сопротивление этой ветви изменяется.
Согласно теореме об эквивалентном
генераторе, любой активный двухполюсник
можно заменить эквивалентной ЭДС ( )
и эквивалентным внутренним сопротивлением
(
)
и эквивалентным внутренним сопротивлением
(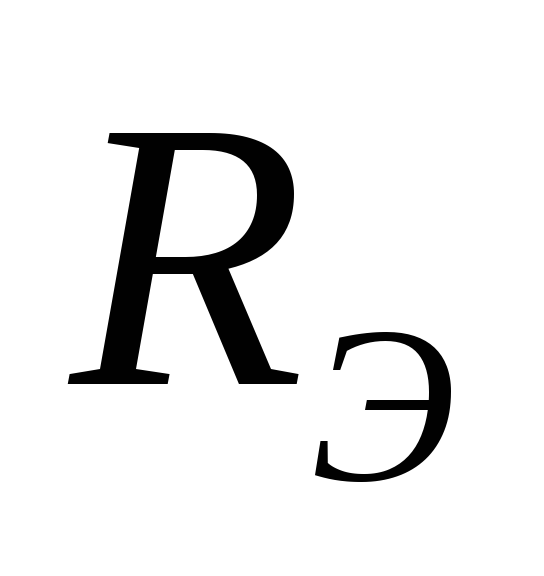 ).
То, что обведено пунктиром на схеме 1,
— активный двухполюсник:
).
То, что обведено пунктиром на схеме 1,
— активный двухполюсник:
Схема 1А | Схема 1Б |
Чтобы найти 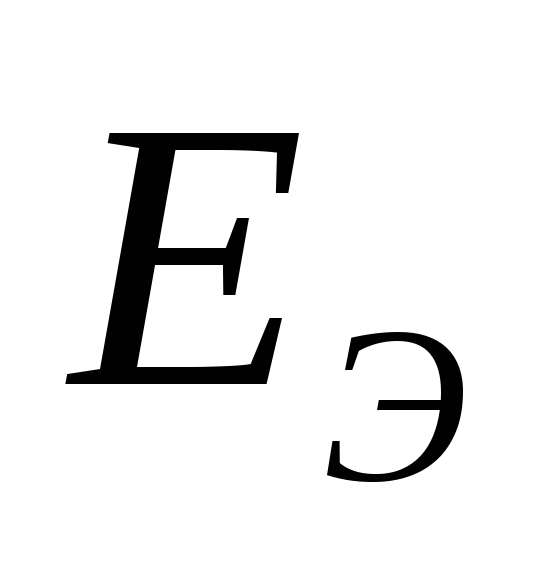 ,
надо разомкнуть ветвь АБ и найти
напряжение на зажимах разомкнутой
ветви. Оно будет равно
,
надо разомкнуть ветвь АБ и найти
напряжение на зажимах разомкнутой
ветви. Оно будет равно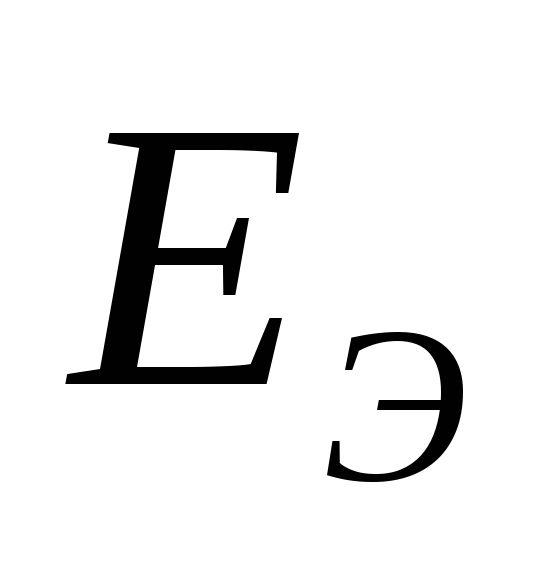 :
:
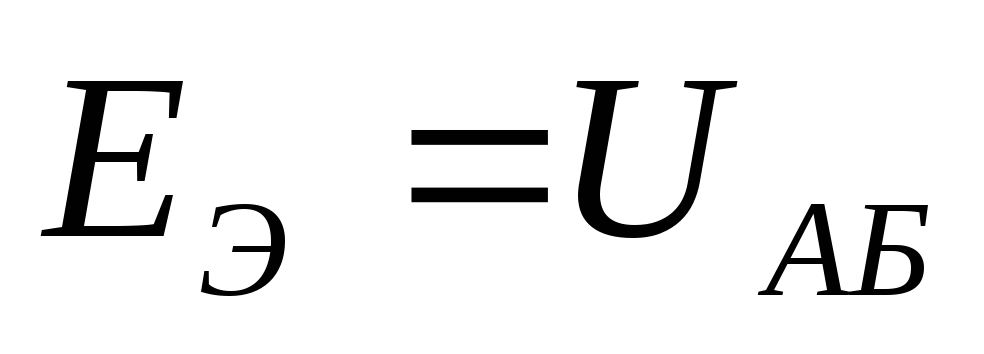
Чтобы найти 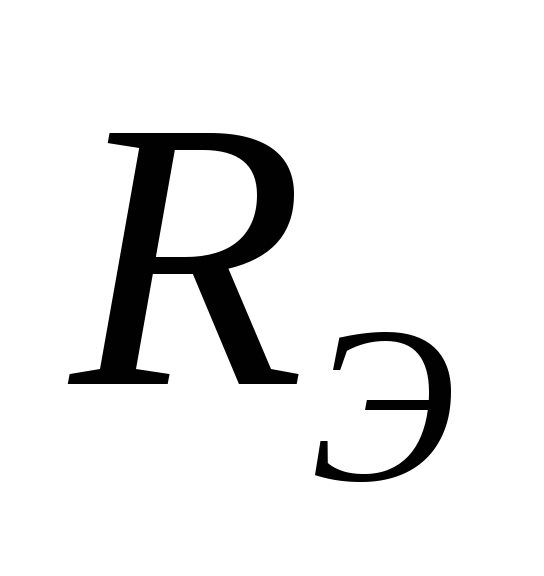 ,
надо разомкнуть ветвь АБ, убрать все
источники, оставив их внутренние
сопротивления. Далее необходимо
рассчитать сопротивление цепи по
отношению к зажимам АБ. Это и будет
,
надо разомкнуть ветвь АБ, убрать все
источники, оставив их внутренние
сопротивления. Далее необходимо
рассчитать сопротивление цепи по
отношению к зажимам АБ. Это и будет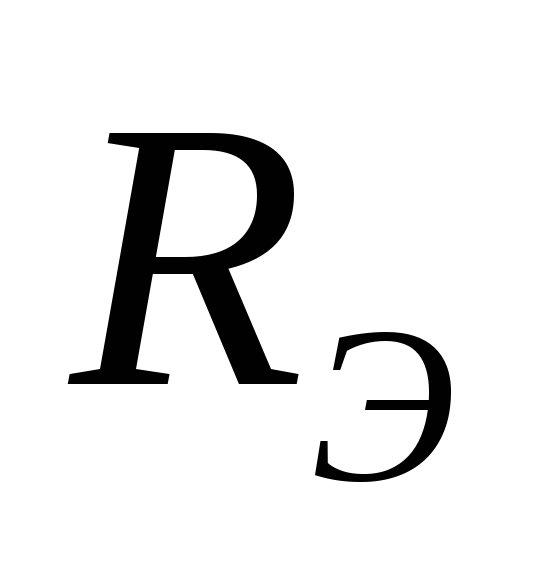 .
.
Если известны 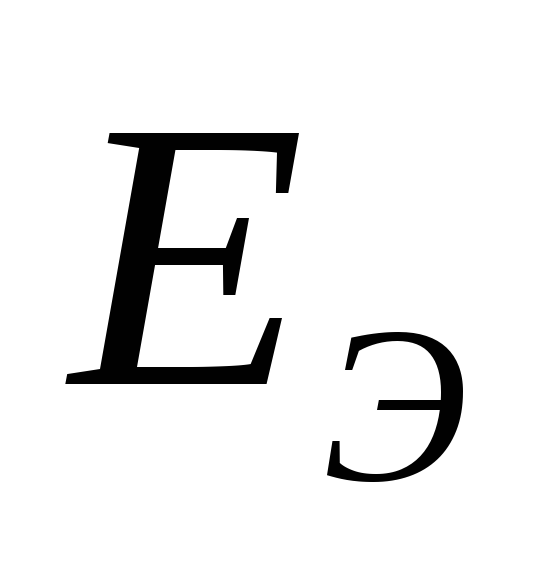 и
и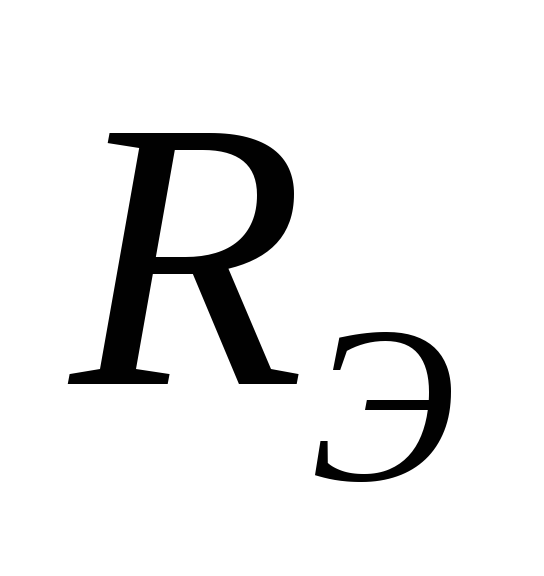 ,
то:
,
то:
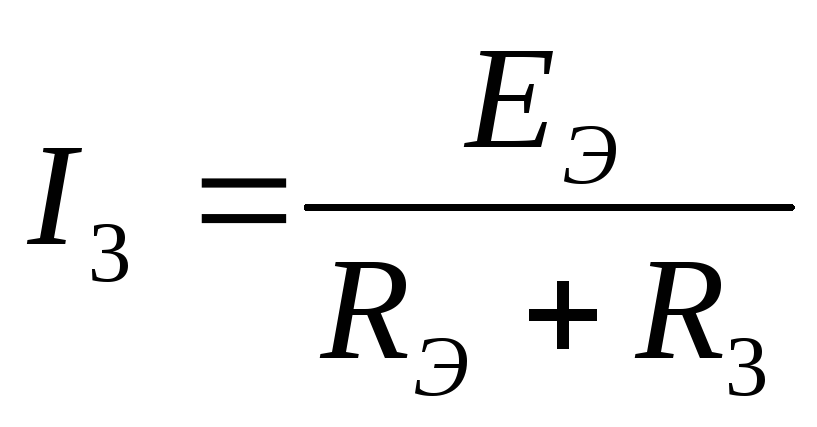
Задача
Дано (для схемы 1А):

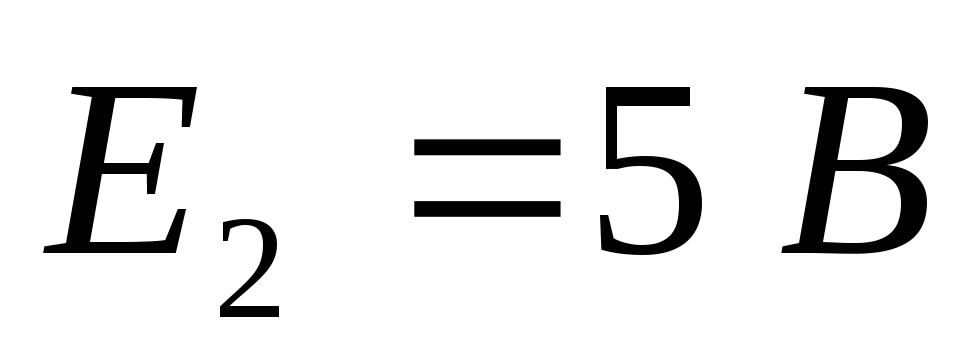
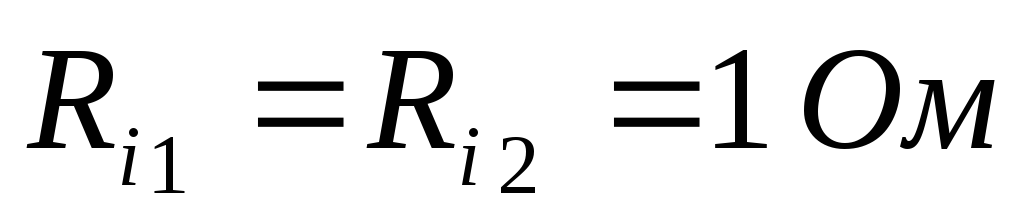
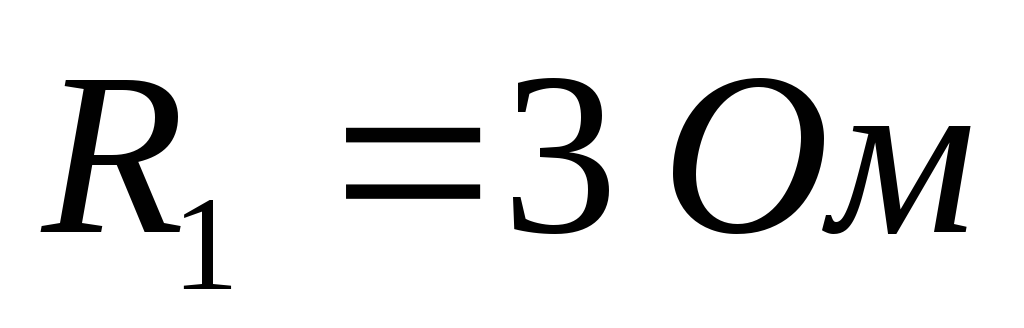
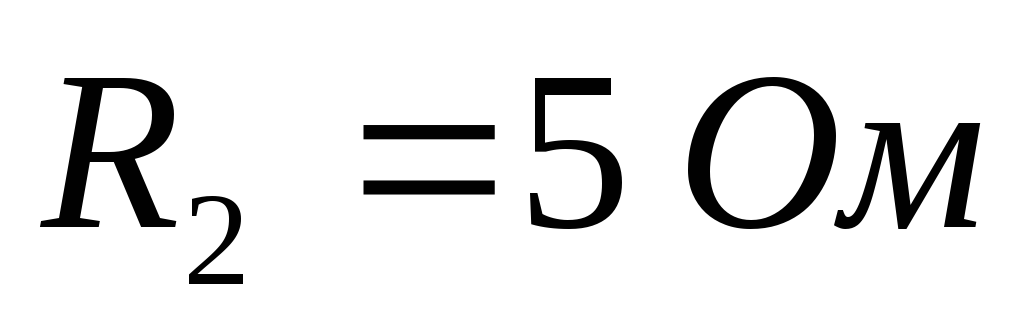
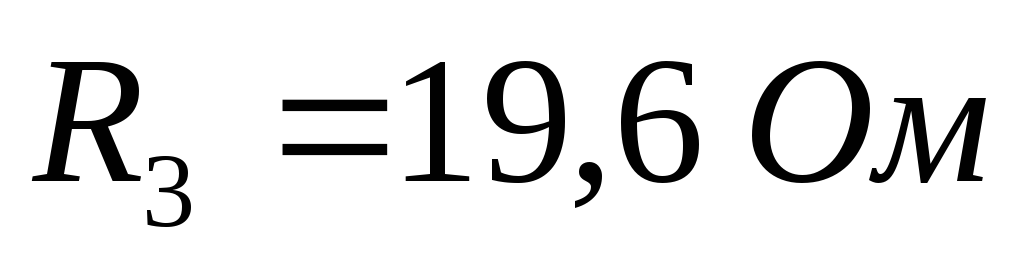
Найти ток 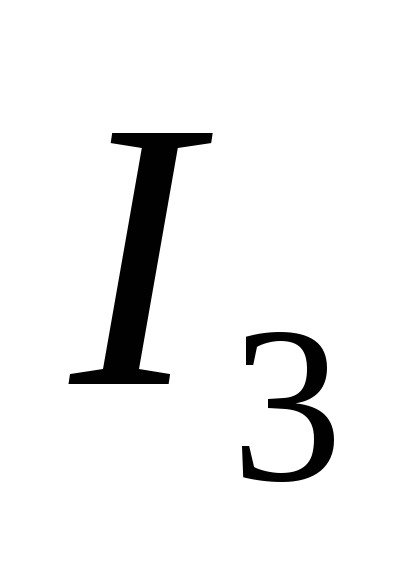 в цепи (методом эквивалентного
генератора).
в цепи (методом эквивалентного
генератора).
Разомкнутая цепь приведена на схеме:
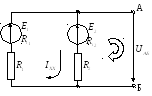
Находим ток холостого хода:
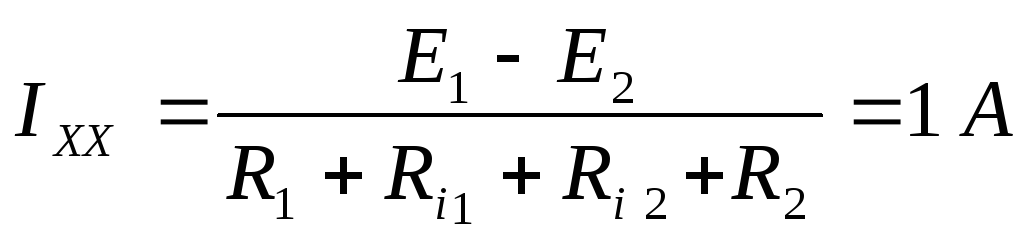
Найдём 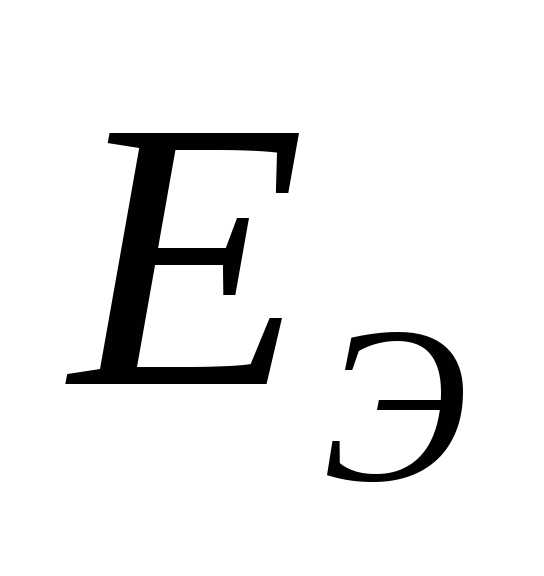 :
:
Обходим контур по второму закону
Кирхгофа так, чтобы он замкнулся через
напряжение 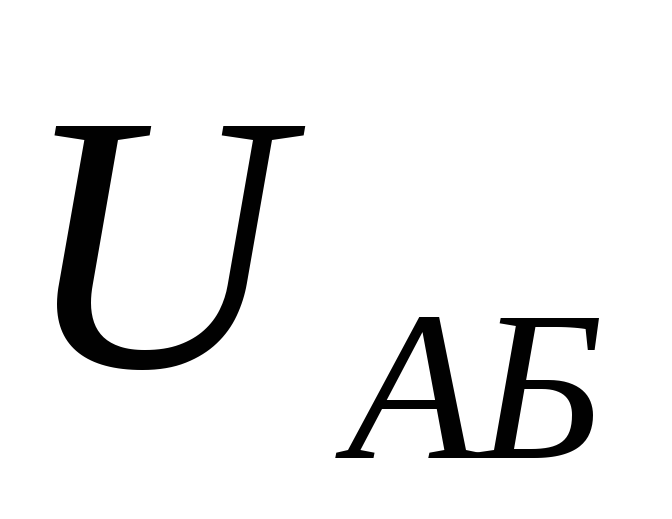 (лучше взять такой контур, где меньше
элементов):
(лучше взять такой контур, где меньше
элементов):
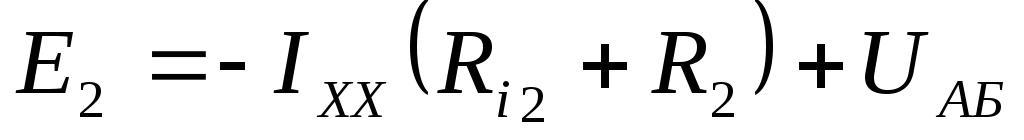
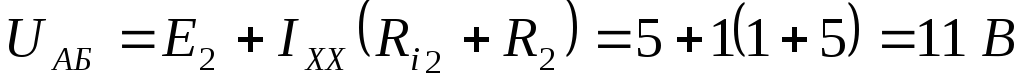
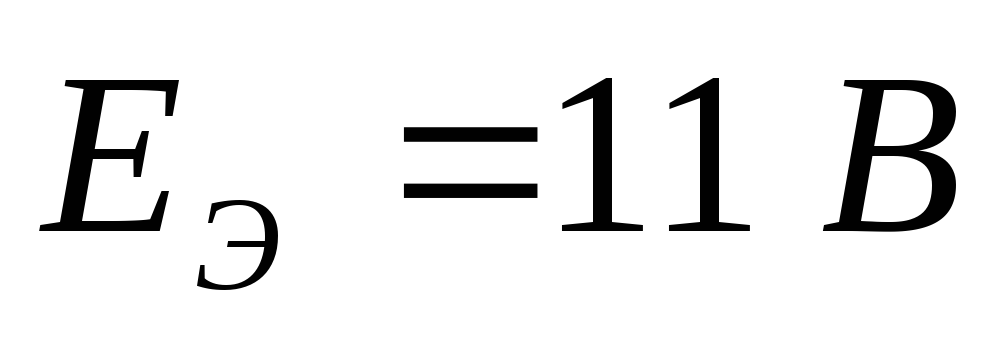
Находим 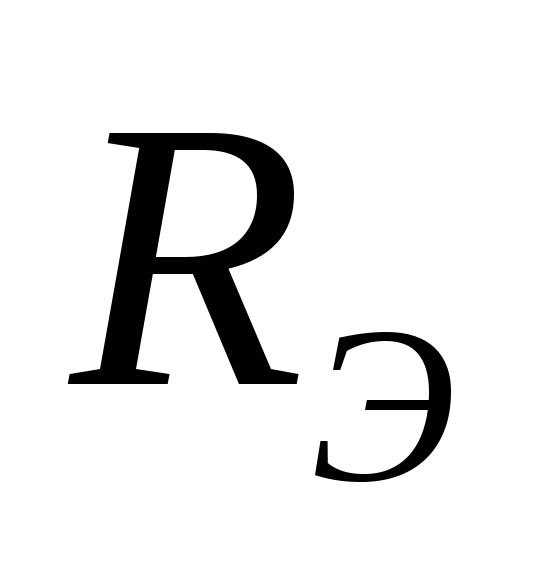 :
:
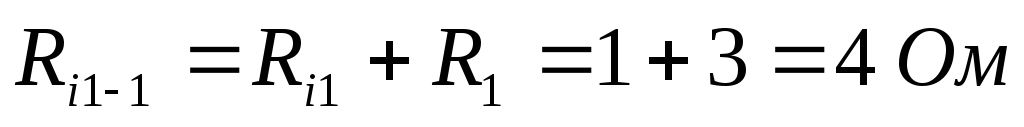
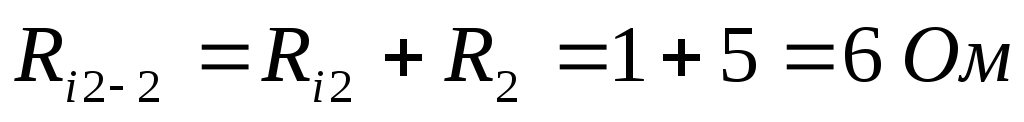
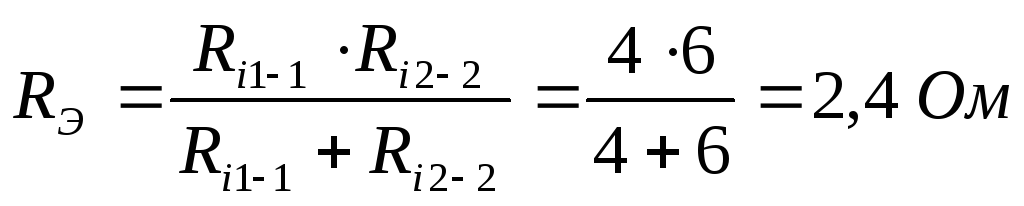
Далее можно выразить искомый ток:
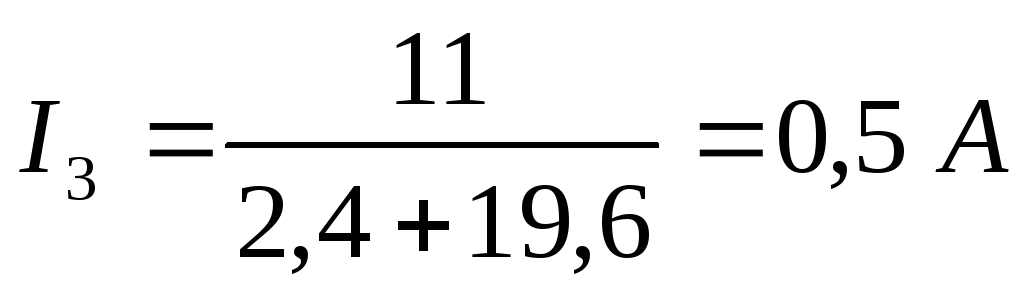
11. Расчёт сложных схем по уравнениям Кирхгофа.
Предположим, перед нами стоит задача по расчету сложной электрической цепи, состоящей из k узлов, l ветвей и m идеальных источников тока (под идеальным источником тока подразумевается такой источник тока, для которого Rт равен бесконечности). Суть метода сводится к решению системы линейных уравнений c l неизвестными. В качестве неизвестных выступают токи ветвей. Решив такую систему мы получим значения токов во всех ветвях электрической цепи, зная которые очень просто рассчитать все другие параметры цепи (напряжения на отдельных элементах, мощность и т.д.)
Перед началом расчета будет нелишним, по возможности, упростить электрическую схему с целью уменьшения количества ветвей. Это может существенно упростить расчеты и уменьшить вероятность ошибки. Например, решение системы линейных уравнений с 4 неизвестными гораздо проще решения системы с 5 неизвестными.
Порядок расчета цепей, связанный с использованием законов Кирхгофа следующий:
Выбирают положительные направления токов в ветвях электрической цепи.
Составляют (k-1) независимых уравнений по первому закону Кирхгофа. Уравнения составленные по первому закону Кирхгофа гораздо проще уравнений, составленных по второму закону Кирхгофа. Поэтому их составляют максимально возможное количество.
Выбирают (l-k+1-m) независимых контуров электрической цепи. Контуры необходимо выбирать так, чтобы в них вошли все ветви схемы. Контуры взаимно независимы, если каждый последующий выбираемый контур содержит не менее одной новой ветви.
Для каждого из выбранных независимых контуров выбирают направления обхода и составляют уравнение по второму закону Кирхгофа.
Решают систему из (l-m) линейных уравнений любым удобным способом.
Пример.
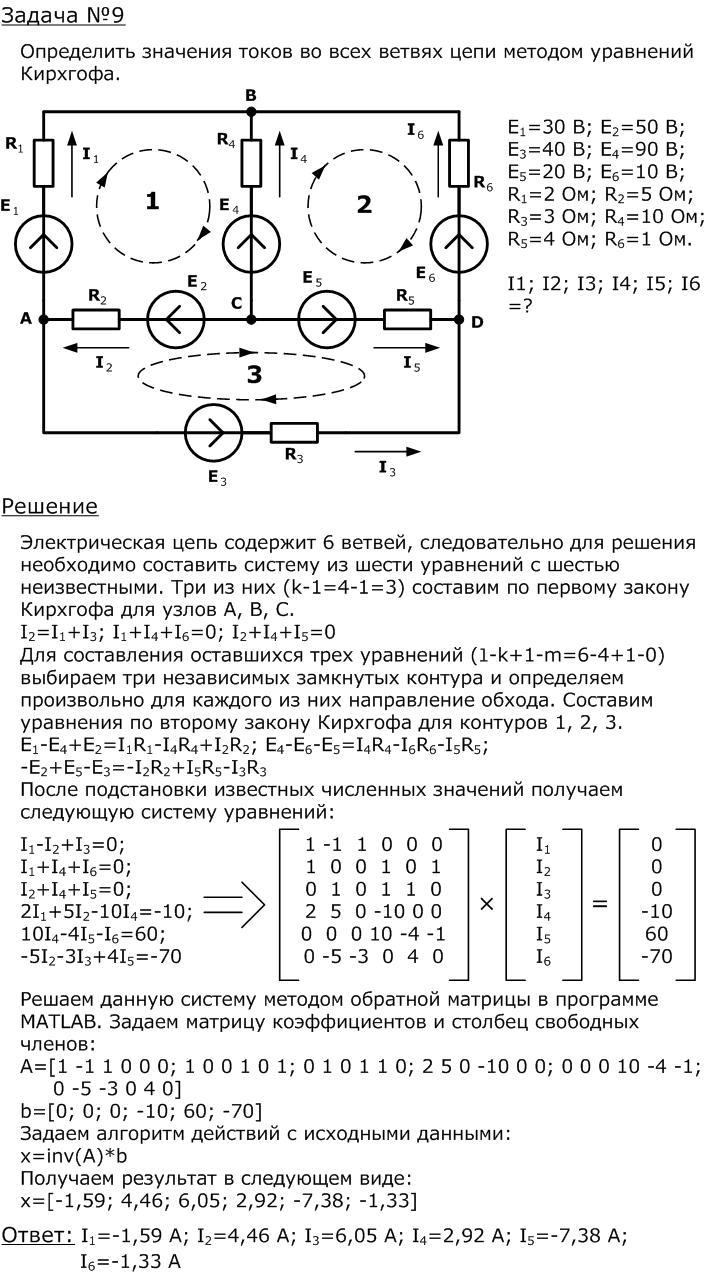
На
рисунке изображена схема сложной
электрической цепи, содержащей 4 узла
и 6 ветвей (k=4, l=6). Для расчета цепи
необходимо составить систему из 6
линейных уравнений. Предварительно
выберем направления токов в каждой из
ветвей. По первому закону Кирхгофа 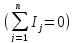 составляем
3 уравнения (k-1=4-1=3), например для узлов
A, B и C. Вместо любого из этих узлов для
составления уравнения можно взять узел
D, на результат расчетов это не повлияет.
Оставшиеся 3 уравнения (l-k+1-m=6-4+1-0=3)
придется составлять по второму закону
Кирхгофа (
составляем
3 уравнения (k-1=4-1=3), например для узлов
A, B и C. Вместо любого из этих узлов для
составления уравнения можно взять узел
D, на результат расчетов это не повлияет.
Оставшиеся 3 уравнения (l-k+1-m=6-4+1-0=3)
придется составлять по второму закону
Кирхгофа (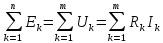 )
)
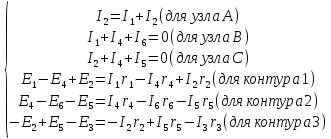
Подставляем известные значения
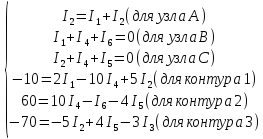
Решаем получившуюся систему.
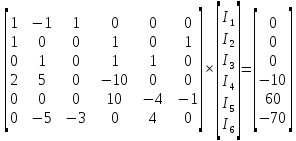
Получаем ответы в матричном виде.
12. Метод контурных токов.
Теоретические сведения.
В данном методе расчета полагают, что в каждом контуре протекает свой контурный ток. Контурные токи и принимают за неизвестные, находят их, и уже затем через контурные токи определяют токи в ветвях. Чтобы сократить количество неизвестных, источник тока включают в контур, но только в один. Ток данного контура считают известным и равным току источника. Если в схеме несколько источников тока, количество неизвестных можно существенно сократить, включая источники в разные контура. В таких схемах применение этого метода наиболее рационально. Число неизвестных в данном методе равно количеству уравнений, которые необходимо было бы составить по второму закону Кирхгофа для данной схемы. Уравнения составляют только для контуров, не содержащих источников тока.
Алгоритм расчета цепи методом контурных токов.
Определяем общее число ветвей p*
Определяем число ветвей с источниками тока pит.
Определяем число ветвей с неизвестными токами p*-pит
Определяем число контуров, необходимое и достаточное для определения всех неизвестных токов m= p*-(q-1).
Произвольно наносим на схему номера и направления неизвестных токов.
Обозначаем на схеме контура и выбираем направления их обхода. Необходимо, чтобы каждая ветвь входила хотя бы в один из обозначаемых контуров. При этом ветви с источниками тока обязательно включаем, но каждую в свой контур. Токи данных контуров считаем известными и равными токам источников – таким образом, число неизвестных сокращается.
Записываем выражения для токов в ветвях через контурные токи. Контурные токи в ветвях, не являющихся смежными, и будут истинными токами. Для ветвей, входящих в несколько контуров (смежных ветвей) истинный ток будет являться суммой либо разностью контурных токов данных контуров. При этом те контурные токи, которые совпадают по направлению с током в ветви, берем со знаком плюс, а те, направления которых противоположны – со знаком минус. Определяем собственные сопротивления контуров как сумму всех сопротивлений, входящих в контур (только для контуров без источников тока). Эти сопротивления обозначаются двойным повторяющимся индексом: и т.д.
Определяем сопротивления смежных ветвей и их знаки: плюс – если контурные токи сонаправлены в данной ветви, и минус, если их направления встречны. Эти сопротивления обозначаются двойным индексом, цифры которого указывают номера смежных контуров и т.д.
Аналогично определяем сопротивления ветвей, являющихся смежными с контурами, содержащими источники тока.
Определяем суммарную ЭДС контура (также обозначается двойным повторяющимся индексом — и т.д.). Это алгебраическая сумма ЭДС, входящих в данный контур, причем со знаком плюс берут те ЭДС, направления которых совпадают с выбранным направлением обхода, и наоборот, со знаком минус те, что направлены встречно.
Записываем систему уравнений по форме, приведенной ниже:

Решаем данную систему относительно контурных токов.
Определяем токи в ветвях, подставляя контурные токи в выражения п. 7
Пример.
Найти токи в схеме рис. 35 с применением метода контурных токов.
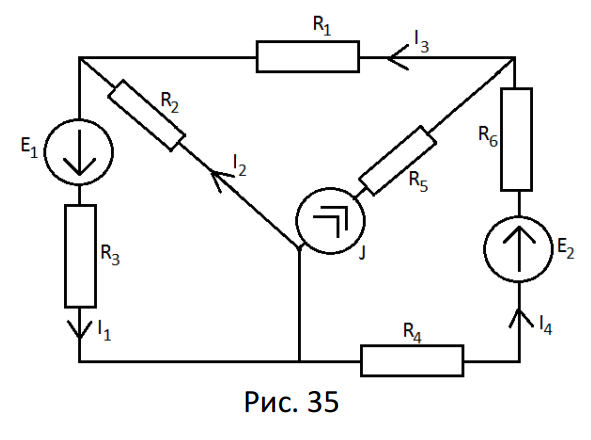
Дано: 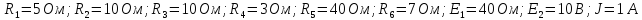
1.2.1.1. Топология цепи.
Определяем общее число ветвей: p*=5
Определяем число ветвей с источниками тока: pит=1.
Определяем число ветвей с неизвестными токами: p*- pит=4.Количество узлов – 3
Определяем необходимое и достаточное число контуров: 3
Произвольно наносим на схему номера и направления неизвестных токов (рис. 36)
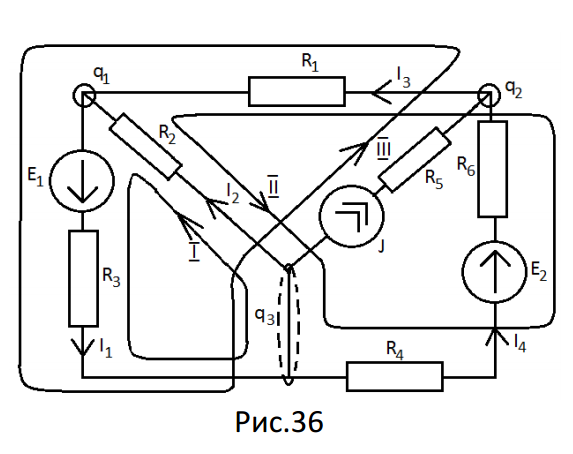
Определяем собственные сопротивления контуров (для контуров без источников тока):

Определяем сопротивления смежных ветвей и их знаки:

Аналогично определяем сопротивления ветвей, являющихся смежными с контуром, содержащим источник тока:

Определяем суммарную ЭДС контуров:

Записываем систему уравнений по форме:
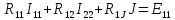
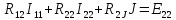
Если произвести подстановку сопротивлений, то видно, что данная система полностью совпала с системой, полученной в п. 7:
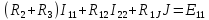
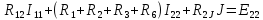
Решаем данную систему относительно контурных токов:

Определяем токи в ветвях, подставляя контурные токи в выражения п. 7
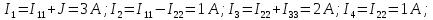
Первый и второй законы Кирхгофа и их практическое применение
Уравнения, или правила, Кирхгофа относят к основным законам электрических цепей.
Они вытекают из таких фундаментальных законов как, закон сохранения заряда и безвихревости электростатического поля, в своё время описанных уравнениями Максвелла. Уравнения Кирхгофа довольно часто используются благодаря своей универсальности, пригодности для решения многих задач в теории электротехники, в том числе и связанных с расчётами сложных электрических цепей, практичности. Применяя правила Кирхгофа к линейной электрической цепи можно получить систему линейных уравнений, из которых в свою очередь, можно найти значения токов на всех ветвях цепи и все межузловые напряжения.
В правилах Кирхгофа применяют такие понятия электрической цепи, как: узел, ветвь, контур. Участок электрической цепи с одним и тем же током называют ветвью, например отрезок 1-4, на рисунке 1, с протекающим по нему током i1 , есть ветвь. Точку, соединяющую три и более ветви называют узлом, например точки 1,2,3,4 на рисунке 1 есть узлы. Замкнутый путь, проходящий через несколько ветвей и узлов разветвлённой электрической цепи называют контуром. Начав с некоторого узла цепи и однократно пройдя по нескольким ветвям и узлам, и возвратившись в исходный узел, мы пройдём путь, который и называют замкнутым. Проходимые при таком обходе ветви и узлы принято называть принадлежащими данному контуру, при этом надо принимать во внимание, что ветвь и узел могут принадлежать одновременно нескольким контурам.
 Рисунок 1
Рисунок 1Первое правило Кирхгофа построено на основании утверждения о непрерывности электрического тока для любого узла электрической цепи или замкнутого контура.
Первое правило Кирхгофа трактует, что алгебраическая сумма токов ветвей , для любого узла или замкнутого сечения электрической цепи, равна нулю:

Выше сказанное говорит о том, что электрические заряды в узле (например, S2 на рисунок 1) или сечении (например, S14 на рисунке 1) любой электрической цепи накапливаться не могут. Иными словами, сколько тока втекает в узел, столько из него и вытекает.
Второе правило Кирхгофа основано на утверждении, что любая электрическая цепь является потенциальной, а работа по перемещению электрических зарядов в замкнутом контуре равна нулю:

где U – работа(электрическое напряжение), k – число источников выполняющих работу;
Рассмотрим цепь, изображённую на рисунке1, образованную двухполюсными элементами, где ветви в местах соединений образуют узлы 1,2,3,4 и где направления напряжений и токов в ветвях совпадают. Для составления уравнений Кирхгофа выберем произвольно узел S2 , замкнутое сечение S14 (”несколько узлов”) и замкнутый контур 1, направление обхода которого изображено на рисунке 1.
Если принять, что выходящие из сечений и узлов токи считать положительными, а входящие отрицательными, то тогда уравнения составленные по первому правилу Кирхгофа будут иметь вид:

Для составления уравнения по второму правилу Кирхгофа, напряжения совпадающие с направлением обхода контура считаем положительными, а не совпадающие отрицательными. При этом уравнение примет вид:

Рассмотрим второе правило Кирхгофа на более наглядном примере (рисунке 2, см. ниже) и с более понятной для практического применения трактовкой, утверждающей что: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii, Ri – ток и сопротивление i-й ветви.
 Рисунок 2
Рисунок 2Применяя второе правило Кирхгофа составляем уравнение для замкнутого контура схемы(рисунок 2) :

При составлении полученного уравнения знаки учитывались как:
— ЭДС (E) положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;
— падение напряжения (IR) на резисторе положительно, если направление тока в нем совпадает с направлением обхода.
Мы рассмотрели применение правил Кирхгофа на простых примерах цепей постоянного тока и напряжений. На самом деле электрические цепи бывают значительно сложнее и состоять из различных элементов (источников ЭДС и тока , нелинейных и т.п.). Например, для второго правила Кирхгофа физическое представление уравнения для переменного тока уже будет иметь вид:
Следует отметить, что для цепей синусоидального(переменного) тока правила Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений. Чтобы решать уравнения Кирхгофа для цепей синусоидального тока их составляют в комплексной форме, в которой учитываются ”мгновенные” изменения значений токов и напряжений.
Но какие сложные уравнения не приходилось бы составлять и решать, следует помнить, что физически второе правило(закон) Кирхгофа характеризует равновесие напряжений в любом контуре цепи.
Пример составления уравнений по законам Кирхгофа для разветвленной цепи
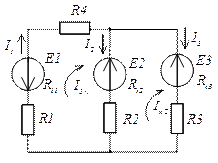
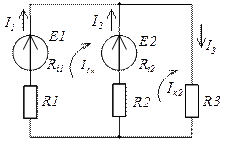
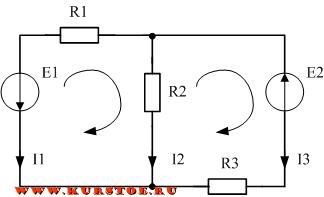
Рассмотрим пример составления уравнений по законам Кирхгофа для разветвленной электрической цепи постоянного тока. Для данной электрической цепи необходимо рассчитать токи в каждой ветви. Для расчета токов будет пользоваться законами Кирхгофа.
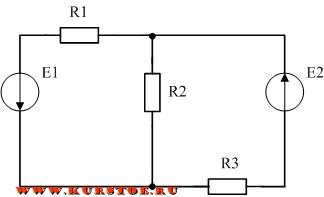
Составляем уравнения по первому закону кирхгофа. Согласно алгоритма задаемся направлением токов в ветвях электрической схемы.
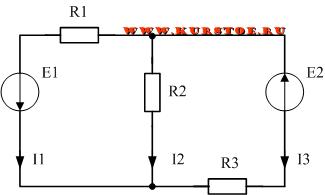
Количество уравнений равно количеству узлов минус один. У нас в схеме два узла. Значит будет одно уравнение. Т.к. все токи втекают в узел, то берем их с одним знаком, например плюс. В результате уравнение по первому закону будет таким.
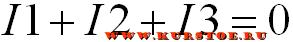
Составим уравнения по второму правилу Кирхгофа. По алгоритму необходимо задаться обходом независимых контуров.
В электрической цепи три контура. Контура обозначены стрелочками.
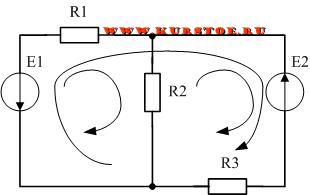
Из них только любые два являются независимыми контурами.
Для каждого независимого контура составляем уравнение по второму закону Кирхгофа.
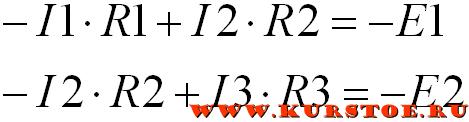
В первом уравнении перед током I1 поставлен минус, т.к. направление обхода первого (слева) контура не совпадает с направление протекающего тока I1.
Перед током I2 в первом уравнении поставлен плюс, т.к. направление обхода первого контура совпадает с направление протекающего тока I2.
Перед ЭДС 1 поставлен минус, т.к. направление действия ЭДС 1 не совпадает с направление обхода первого контура.
Во втором уравнении перед током I2 поставлен минус, т.к. направление обхода второго контура не совпадает с направление протекающего тока I2.
Перед током I3 во втором уравнении поставлен плюс, т.к. направление обхода второго контура совпадает с направление протекающего тока I3.
Перед ЭДС 2 поставлен минус, т.к. направление действия ЭДС 2 не совпадает с направление обхода второго контура.
Выполняем объединение уравнений в систему. Решаем систему уравнений с тремя неизвестными I1, I2, I3 любым известным способом.
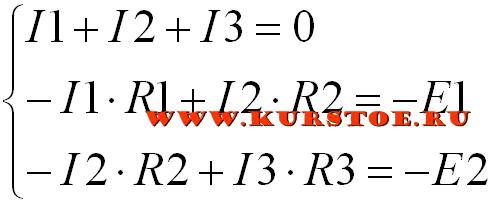


 между двумя узлами по формуле:
между двумя узлами по формуле: