|
Заглавная страница
КАТЕГОРИИ: Археология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Балочные системы. Определение реакций опор и моментов защемления |
⇐ ПредыдущаяСтр 3 из 8Следующая ⇒ Момент силы относительно точки Моментом силы относительно точки называется произведение величины силы на длину перпендикуляра, опущенного из точки на линию действия силы (рис. а). · Если бы тело было закреплено в точке О, то сила Р стремилась бы вращать момента, а перпендикуляр а называется плечом силы относительно центра момента. Таким образом, М = сила×плечо. Момент силы Р относительно Ообозначается М0(Р) = Ра. Моменты сил измеряют в ньютоно метрах (Нм) или килограммометрах (кГм Принято считать момент положительным, если сила стремится вращать тело по часовой стрелке (рис. а), и отрицательным — против часовой стрелки (рис. б). Установленное правило знаков для моментов сил, как и для моментов пар, условно. Когда линия действия силы проходит через данную точку, ее момент относительно этой точки равен нулю, так как в рассматриваемом случае плечо равно нулю а = 0 (рис. Между моментом пары и моментом силы есть одно существенное различие. У момента пары сил величина и направление не зависят от положения этой пары в пространстве. Свойства пар сил Пара, приложенная к ТТ, стремится вызвать его вращение. Вращательное действие пары определяется ее моментом, который равен произведению одной из сил пары на ее плечо, то есть расстояние между линиями действия сил пары: M(P,P′)=P⋅d=P′⋅d Нетрудно убедиться в справедливости следующих утверждений: 1. Сумма проекций сил пары на любую ось равна нулю; 2. Сумма моментов сил пары относительно любой точки равна моменту этой пары. В общем случае действие пары сил на ТТ определяется тремя факторами: 1. плоскостью действия; 2. направлением вращения в этой плоскости; 3. величиной момента. Чтобы однозначно определить все эти факторы, вводят понятие вектор-момента пары. Определение. Вектор-моментом пары сил называется вектор, который: · перпендикулярен плоскости действия пары · направлен по правилу правого винта; · равен по модулю моменту пары (Рис. Нетрудно убедиться, что вектор-момент пары сил можно представить в виде векторных произведений: ММ→(P→,P′→)=AB→×P′→=BA→×P→ Рис.1
15.Сложение пар сил и условие равновесия Теорема о сложении пар сил: Две пары сил, произвольно расположенные в пространстве, эквивалентны одной паре с моментом равным геометрической сумме моментов слагаемых пар. Если на тело действует произвольная система (М1,М2,…,Мn) пар, то вектор момента результирующей пары равен векторной сумме моментов, составляющих пары. M=M1+M2+…+Mn=ΣMk (сверху векторы) Если две пары сил расположены в одной плоскости, то векторы моментов пар направлены перпендикулярно этой плоскости в ту или иную стороны. Поэтому моменты пар можно складывать алгебраически. M=M1+M2+…+Mn=ΣMk Условие равновесия системы пар сил: Для равновесия тела, находящегося под действием системы произвольно расположенных в пространстве пар, необходимо и достаточно, чтобы момент результирующей (эквивалентной) пары был равен 0. M=ΣMk=0 В случае, если все пары сил расположены в одной плоскости (или в параллельных плоскостях), то для равновесия необходимо равенство 0 алгебраической суммы моментов составляющих пар. ⇐ Предыдущая12345678Следующая ⇒ Читайте также: Коммуникативные барьеры и пути их преодоления Рынок недвижимости. Сущность недвижимости Решение задач с использованием генеалогического метода История происхождения и развития детской игры |
|
Последнее изменение этой страницы: 2021-03-09; просмотров: 330; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. |
Момент силы относительно центра (точки)
Похожие презентации:
Влияния состава и размера зерна аустенита на температуру фазового превращения и физико-механические свойства сплавов
Газовая хроматография
Геофизические исследования скважин
Искусственные алмазы
Трансформаторы тока и напряжения
Транзисторы
Воздушные и кабельные линии электропередач
Создание транспортно-энергетического модуля на основе ядерной энергодвигательной установки мегаваттного класса
Магнитные аномалии
Нанотехнологии
1. ТЕОРЕТИЧЕСКАЯ МЕХАНИКА СТАТИКА
Лекция №22. 2.1 Момент силы относительно центра (точки)
3. Момент силы относительно центра
Z
mO r F
B
mO F h
F
mO
h
O
r
A
Моментом силы F относительно центра
(точки) О называется вектор mO F равный векторному произведению радиуса вектора r , проведенного из центра О в точку А приложения силы, и
вектора силы F :
mO F r F
B
Z
F
mO
h
A
r
O
Вектор mO F приложен в точке О и направлен плоскости, проходящей через центр О и силу F , в ту сторону, откуда сила видна стремящейся повернуть
тело вокруг центра О против хода часовой стрелки.

Модуль mO F равен произведению модуля силы F на плечо h:
mO
= F·h,
где плечо h перпендикуляр, опущенный из центра О на линию действия
силы F .
Момент mO F характеризует вращательный эффект силы
но центра (точки) О.
F
относитель-
5. Свойства момента силы:
Момент силы относительно центра не изменяется при переносе силы вдольлинии ее действия в любую точку.
Если линия действия силы проходит через центр О (h = 0), то момент силы
относительно центра О равен нулю.
Для плоской системы сил при вычислении моментов сил относительно точки
(центра), находящейся в той же плоскости, пользуются понятием алгебраического момента силы относительно точки.
Алгебраический момент силы F относительно
точки О равен взятому с соответствующим знаком
произведению модуля силы на ее плечо:
mО( F ) = F h.
Момент считается положительным, если сила
стремится повернуть тело вокруг точки О против хода
часовой стрелки, и отрицательным по ходу часовой
стрелки:
mO ( F1 ) F1 h2 ;
mO ( F2 ) F2 h3 .
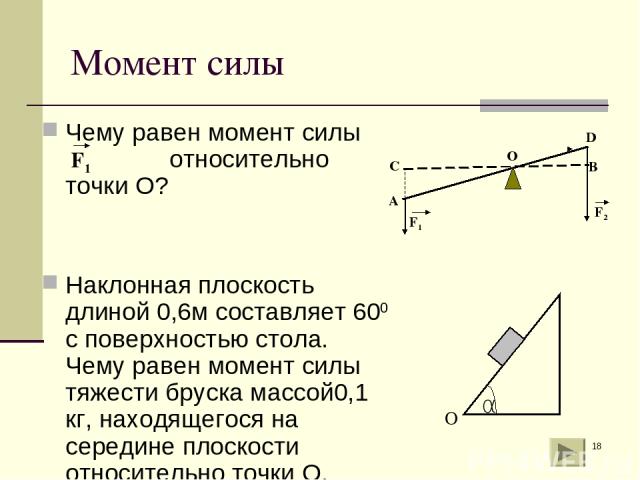
F1
h2 О
h3
F2
6. Теорема Вариньона
При определении алгебраического момента силы относительноточки в случае, когда сложно найти плечо h, следует разложить
силу на составляющие, плечи которых найти проще, (часто параллельно осям координат), и применить теорему Вариньона:
если данная система сил имеет равнодействующую, то момент равнодействующей относительно любой точки О равен
сумме моментов составляющих сил, относительно той же
точки
mO ( R ) mO ( Fk ), где R Fk .
7. 2.2 Теория пар сил, свойства пар сил
Парой сил называется система двух равныхпо модулю, параллельных и направленных в
противоположные стороны сил ( F F ).
Плоскость, в которой лежат силы F и F , называется плоскостью пары, а кратчайшее расстояние d между линиями действия сил плечом пары.
Пара сил не может быть заменена одной эквивалентной ей силой, т.е. не имеет равнодействующей, так как R F F 0.
Пара может быть уравновешена только
другой парой сил.

Под действием пары сил тело вращается.
Вращательный эффект пары, характеризуется
моментом пары.
F
B
A
F
d
8. Момент пары сил
Моментом пары называется вектор равный векторному произведениюm r F
,
модуль которого равен произведению модуля одной из сил пары на ее плечо
m F d.
Вектор m направлен перпендикулярно
плоскости пары в ту сторону, откуда пара
видна стремящейся повернуть тело против
хода часовой стрелки. Момент пары m
свободный вектор, т. е. его можно прикладывать в любой точке тела.
m
B
F d
F
r
A
9. Свойства пар сил
1. Момент пары равен сумме моментов сил пары относительно произвольного центра (точки) О:mO mO ( F ) mO ( F ) .
2. Момент пары относительно любого центра
F
mO равен моменту пары m:
mO F h F (h d ) F d m.
mO m
d
B
A
F
O
3. Момент пары равен моменту одной из сил пары относительно точки
приложения другой силы пары:
m mB ( F ) mA ( F ).
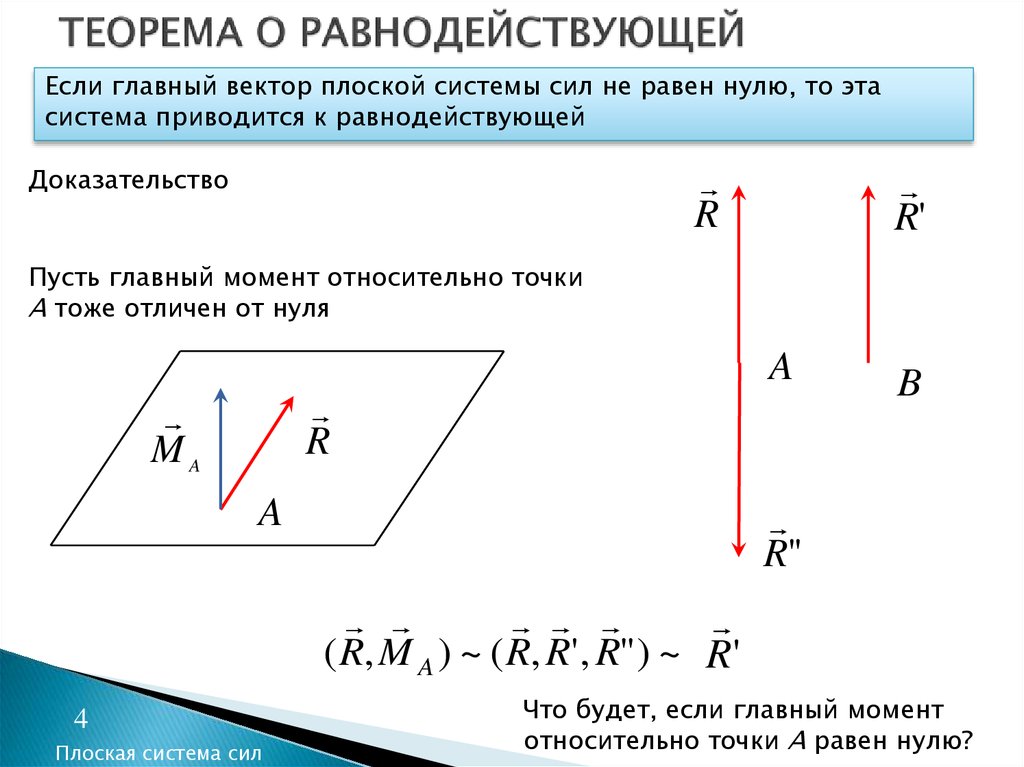
4. Теорема. Пары сил с равными моментами эквивалентны.
Следствия:
Пару сил, приложенную к твердому телу, можно заменить другой
парой в той же плоскости, если при такой замене не изменяется величина момента пары и его направление:
Пару сил можно переносить в плоскость, параллельную плоскости
пары.
5. Теорема. Совокупность нескольких пар с моментами m1 , m2, mn
эквивалентна одной паре, момент
сумме моментов данных пар:
m m1 m2 mn .
6. Если на тело действует пространственная система пар, то тело находится в равновесии, если векторная сумма моментов пар равна нулю:
m 0.
7. Если пары лежат в одной плоскости, то
момент пары считают величиной алгебраической,
так как в этом случае все вектора моментов пар
параллельны.
Алгебраический момент пары равен взятому
с соответствующим знаком произведению модуля
одной из сил пары на плечо пары:
Z
m1
mn
Y
X
m2
m F d .

Знак «+» соответствует повороту тела под действием пары против хода часовой
стрелки,
«─» по ходу часовой стрелки.
Пары сил на плоскости часто изображается
Y
дуговой стрелкой, показывающей направление
поворота тела парой.
8. Если на тело действует плоская система пар, то
тело находится в равновесии, если сумма моментов пар
равна нулю:
m
k
0.
m1
O
m2
X
English Русский Правила
Карта механики — Момент относительно точки
Для любой точки протяженного тела, если на это тело действует сила, которая не проходит через эту точку, то эта сила вызовет момент относительно этой точки. Как обсуждалось на странице моментов, момент — это тенденция силы вызывать вращение.
Альтернативой расчету момента через скалярные величины является использование векторного метода или метода векторного произведения . Для простых двумерных задач обычно проще использовать скалярные величины, но для более сложных задач обычно проще использовать метод векторного произведения. Метод векторного произведения для вычисления моментов говорит, что вектор момента силы относительно точки будет равен векторному произведению вектора r из точки в любую точку на линии действия силы и самого вектора силы.
Метод векторного произведения для вычисления моментов говорит, что вектор момента силы относительно точки будет равен векторному произведению вектора r из точки в любую точку на линии действия силы и самого вектора силы.
| \[\vec{M}=\vec{r}\times \vec{F}\] |
Большое преимущество этого метода в том, что r не обязательно должно быть кратчайшим расстоянием между точкой и линией действия, оно идет от точки до любой части линии действия. Для любой задачи существует много возможных векторов r , хотя из-за того, как работает перекрестное произведение, все они должны в конце концов давать один и тот же вектор моментов.
Вектор момента силы F относительно точки A будет равен векторному произведению вектора r и вектора силы. Вектор r — это вектор из точки А в любую точку на линии действия силы. Здесь важно отметить, что все величины ( r , F и M ) являются векторами.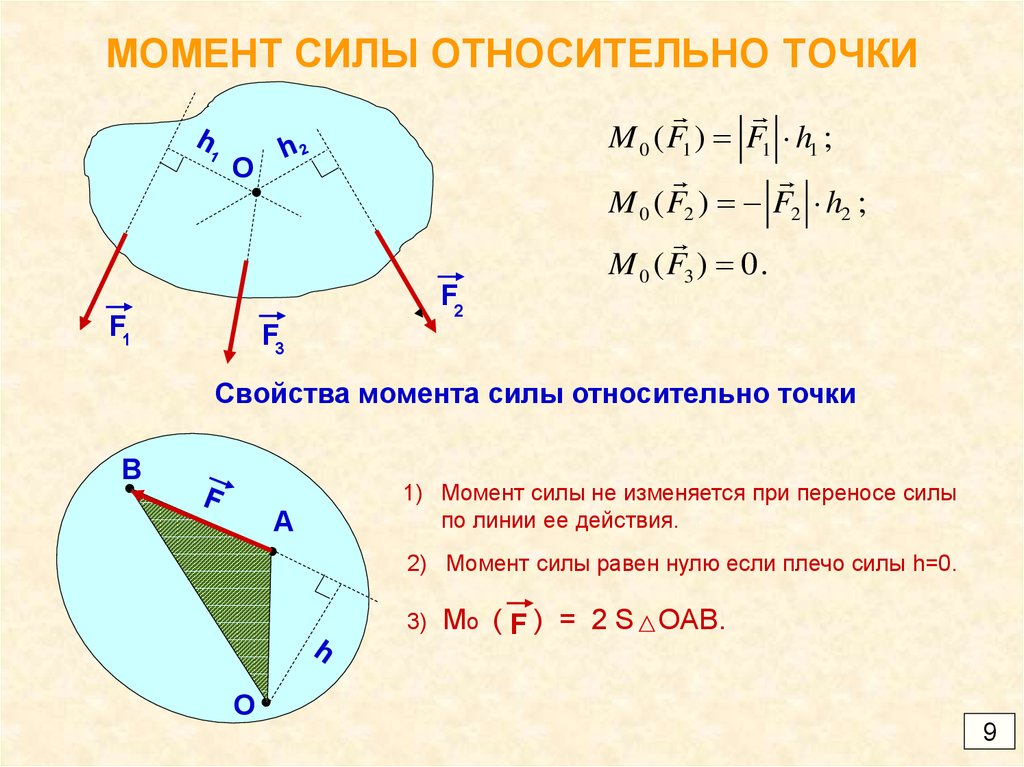 Прежде чем вы сможете найти векторное произведение, вам нужно будет записать r и F в векторной компонентной форме. Кроме того, даже для двумерных задач вам нужно будет выписать все три компонента r и F векторы. Для двумерных задач компоненты z векторов r и F будут просто равны нулю, но эти значения необходимы для расчетов.
Прежде чем вы сможете найти векторное произведение, вам нужно будет записать r и F в векторной компонентной форме. Кроме того, даже для двумерных задач вам нужно будет выписать все три компонента r и F векторы. Для двумерных задач компоненты z векторов r и F будут просто равны нулю, но эти значения необходимы для расчетов.
Полученный вектор момента совпадет с осью вращения для данного момента, где вы можете использовать правило правой руки, чтобы определить, движется ли момент по часовой стрелке или против часовой стрелки вокруг этой оси.
Результат пересечения r F даст нам вектор момента. Для этой двумерной задачи вектор момента указывает в положительном направлении z. Мы можем использовать правило правой руки, чтобы определить направление вращения с момента (выровняйте большой палец правой руки с вектором момента, и наши согнутые пальцы будут указывать в направлении вращения с момента).
Наконец, также важно отметить, что перекрестное произведение, в отличие от умножения, не является коммуникативным. Это означает, что порядок векторов имеет значение, и r пересечение F не будет таким же, как F пересечение r . Важно всегда использовать r крест F при расчете моментов.
Момент силы — Mini Physics
от Mini Physics
Показать/скрыть подтемы (Силы и вращательное действие сил | Уровень O) Показать/Скрыть подтемы (Силы и динамика | Уровень A) Момент силы или крутящий момент, r определяется как эффект поворота силы вокруг оси вращения и является произведением силы (F) и перпендикулярного расстояния (d) от линии действия силы до оси вращения.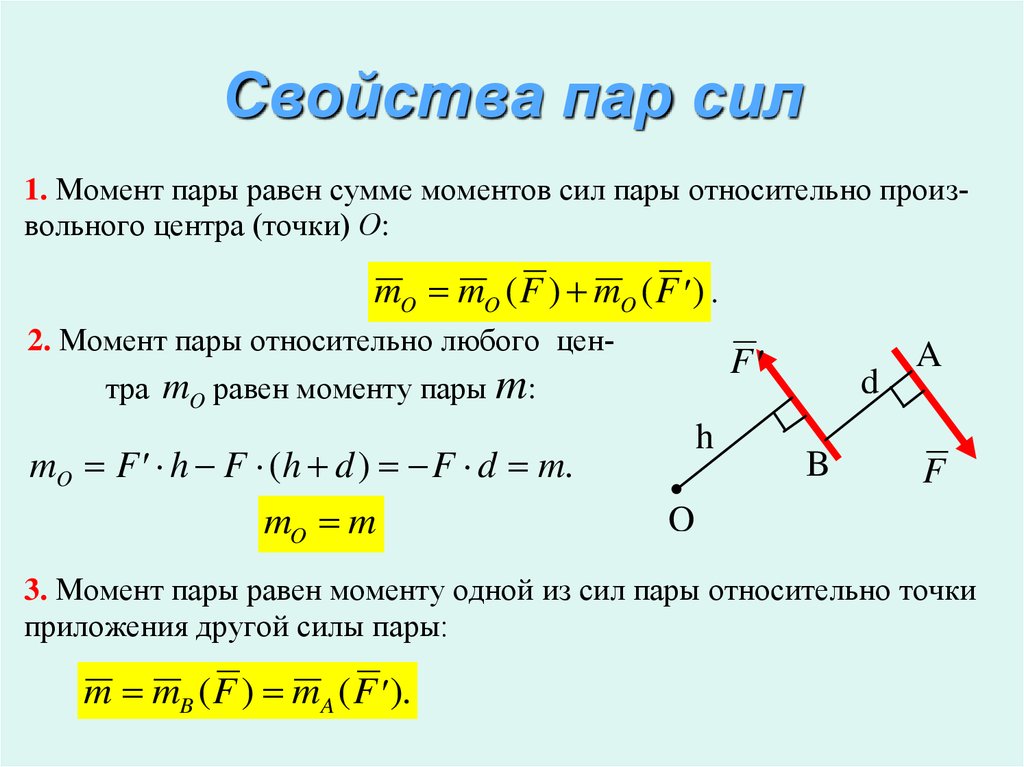
- Единицей момента силы в системе СИ является ньютон-метр (Нм). Это векторная величина.
- Его направление задается правилом правой руки, перпендикулярным плоскости действия силы, и точкой вращения, параллельной оси вращения.
$$r = F \times d$$
,где
r – момент силы/крутящего момента
F – сила
d – расстояние по перпендикуляру от линии действия силы до оси вращения
Пара
Пара – это пара сил, равных по величине, но противоположных по направлению, линии движения которых не совпадают.
- Будет продолжать вращаться, так как есть результирующий момент
- Поскольку силы равны и противоположны, результирующая сила равна нулю и, следовательно, нет линейного ускорения
- $r = F \times d$
Крутящий момент(Момент пары) есть произведение одной из сил и перпендикулярного расстояния между их линиями действия сил.
- Может снимать момент с любой точки
Вопросы для самопроверки
Рассмотрим рисунок выше.
 Учитывая, что вес кота 150 Н, а расстояние от кота до оси вращения равно 30 см, вычислить момент силы относительно оси вращения. Показать/скрыть ответ
Учитывая, что вес кота 150 Н, а расстояние от кота до оси вращения равно 30 см, вычислить момент силы относительно оси вращения. Показать/скрыть ответ $$\begin{aligned} r &= F \times d \\ &= 150 \times 0.30 \\ &= 45 \text{ Nm} \end{aligned}$$
Почему крышку контейнера легче открыть ложкой, чем монетой?
Показать/скрыть ответЛожка длиннее монеты. Если вы используете их, чтобы открыть крышку контейнера путем поворота, перпендикулярное расстояние (d) будет больше для ложки, чем для монеты.
Предположим, что для открытия крышки требуется момент силы $x \text{ Нм}$, и что $d_{\text{ложка}} = 2 d_{\text{монета}}$.
Найдите силу, необходимую для открытия крышки, если мы используем ложка :
$$\begin{align} r &= F \times d \\ x &= F_{\text{ложка}} \times d_{\text{ложка}} \\ F_{\text{ ложка}} &= \frac{x}{d_{\text{ложка}}} \end{aligned}$$
Найдите силу, необходимую для открытия крышки, если мы используем монету :
$$ \begin{align} r &= F \times d \\ x &= F_{\text{coin}} \times d_{\text{coin}} \\ F_{\text{coin}} &= \frac{ x}{d_{\text{coin}}} \end{align}$$
Так как $d_{\text{ложка}} = 2 d_{\text{coin}}$,
$$\begin{align} F_{\text{coin}} &= \frac{x}{\frac{d_{\text{spoon}}}{2}} \\ &= 2 \frac{x }{d_{\text{ложка}}} \\ &= 2 F_{\text{ложка}} \end{aligned}$$
Из вычислений выше ($F_{\text{coin}} = 2 F_ {\text{ложка}}$), вам потребуется в два раза больше силы, чтобы открыть крышку контейнера, если вы используете монету.


 Все правила по сольфеджио
Все правила по сольфеджио
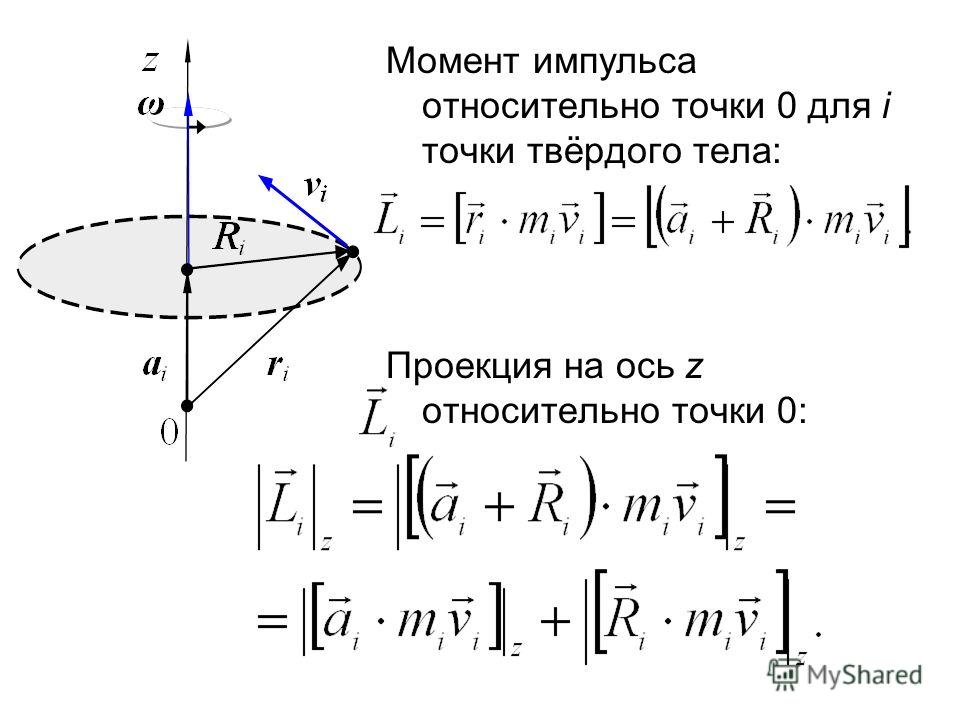
 У момента силы величина и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент.
У момента силы величина и направление (знак) момента силы зависят от положения точки, относительно которой определяется момент. 1).
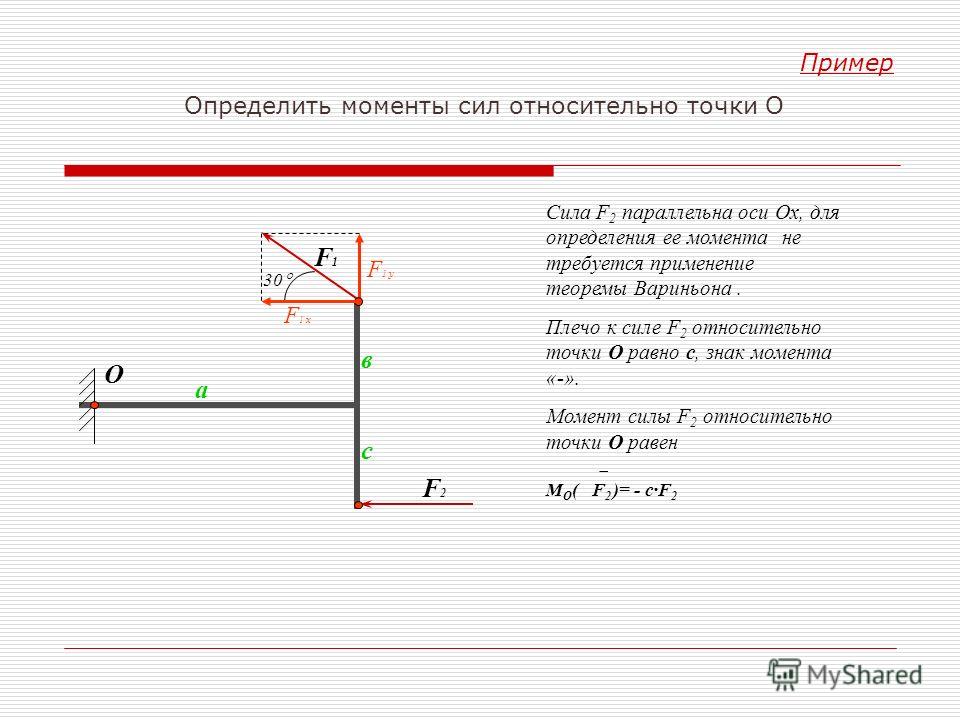
1).
 su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)
su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 161.97.168.212 (0.004 с.)