Коэффициент индуктивной связи
Степень (интенсивность) индуктивной связи двух катушек принято характеризовать коэффициентом индуктивной связи kМ.
Коэффициент связи kМ определяется как среднее геометрическое отношений потоков взаимной индукции к собственным полным потокам катушек. Для N1: или и для N2: или .
Среднее геометрическое соответствующих отношений будет определяться выражением:
. (5.15)
С учетом (5.4) и (5.9) выражение (5.15) имеет вид:
. (5.16)
Следует отметить, что для реальных
катушек (контуров) имеет место неравенство
0 < kМ < 1,
т. к. всегда существуют потоки рассеяния ,
приводящие к выполнению соотношения .
Применение ферромагнитных сердечников
с высокими значениями магнитной
проницаемости
позволяет существенно увеличить
магнитную проводимость для потоков
взаимной индукции ,
замыкающихся по сердечнику и уменьшить
относительную долю потоков в общем потоке каждой катушки, что в
соответствии с выражениями (5. 4) и (5.15)
приводит к увеличению значения kМ.
4) и (5.15)
приводит к увеличению значения kМ.
Если в линейной цепи с индуктивно связанными элементами (катушками, контурами) действуют источники синусоидальных сигналов одинаковой частоты, то в установившемся режиме все реакции цепи (токи и напряжения) будут являться синусоидальными функциями той же частоты, отличающимися только амплитудами и начальными фазами.
В этом отношении линейные индуктивно связанные цепи полностью аналогичны линейным цепям без индуктивной связи, рассмотренным в разделе 3. Вполне очевидно, что при анализе установившихся процессов в индуктивно связанных цепях справедливы все рассмотренные ранее особенности применения метода комплексных амплитуд.
Взаимная индуктивность LМ отображается в область » » как комплексный резистор . Эквивалентные схемы индуктивно связанных катушек (контуров) рис.5.4 в области » » представлены на рис. 5.7.
Уравнения цепей для схем рис. 5.7 относительно
комплексных амплитуд:
5.7 относительно
комплексных амплитуд:
(5.17)
Рис.5.7. Эквивалентные схемы индуктивно связанных катушек в области » «:
а – согласное включение; б – встречное включение
Для схем рис. 5.5 в области » » уравнения цепей (5.12) относительно комплексных амплитуд имеют вид:
(5.18)
где .
В уравнениях (5.17) и (5.18) знак плюс соответствует согласному включению, знак минус – встречному включению.
В общем случае в индуктивной связи может находиться n катушек (контуров), причем каждая попарная взаимосвязь со своим значением взаимной индуктивности (коэффициент связи ).
При таком варианте взаимно индуктивных
связей в уравнения цепей для каждой
катушки (контура) необходимо включить
соответствующие слагаемые – напряжения
взаимной индукции от остальных, связанных
с ней катушек (контуров).
Рис.5.8. Эквивалентная схема трех индуктивно связанных катушек
Уравнения цепей относительно комплексных амплитуд имеют вид:
(5.19)
В уравнениях (5.19) обозначено:
На рис.5.8 первая и вторая катушки включены согласно, а катушки: первая и третья, вторая и третья включены встречно.
В уравнениях (5.19) для первой катушки
имеем напряжения взаимной индукции: от второй и от третьей катушек. Аналогично для
второй катушки: от первой
Пример расчета
Линейная электрическая цепь содержит
идеальный источник синусоидального
напряжения и потребитель, представляющий собой
две индуктивно связанных катушки,
соединенных последовательно и в магнитном
отношении встречно.
Известны расположение и ориентация катушек в пространстве. Заданы параметры сигнала и параметры катушек: В; рад/с; Гц; . Первая катушка имеет число витков
Требуется определить все реакции цепи, коэффициент связи и комплексную мощность потребителя.
Эквивалентная схема цепи в области » » представлена на рис.5.9.
Рис.5.9. Эквивалентная схема цепи для комплексных амплитуд
Уравнение цепи относительно комплексных амплитуд составляется аналогично выражению (5.14):
(5.20)
Очевидно, что полное комплексное сопротивление цепи при встречном включении катушек описывает соотношение
. (5.21)
(5.21)
Для заданных значений параметров элементов
Ом.
Комплексная амплитуда тока:
А.
Можно ввести полные комплексные сопротивления первой и второй катушек при их встречном включении:
Комплексные амплитуды напряжений на выводах катушек:
В;
В.
Коэффициент индуктивной связи катушек:
.
Комплексные мощности катушек:
ВА;
ВА.
Комплексная мощность потребителя:
ВА.
Комплексная мощность на выходе источника:
ВА.
Баланс мощностей: .
Реакции цепи в области » t«:
— ток А;
— напряжения на выводах катушек:
|
Random converter |
Калькулятор взаимной индукцииЭтот калькулятор определяет взаимоиндукцию двух связанных катушек индуктивности. Пример. Рассчитать взаимную индуктивность двух расположенных рядом катушек индуктивности 10 мкГн и 5 мкГн с коэффициентом связи 0,5. Входные данные Индуктивность первой катушки, L1 генри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн) Индуктивность второй катушки, L2 миллигенри (мГн) Коэффициент связи, k 0 ≤ k ≤ 1 Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данные Взаимоиндукция M миллигенри (мГн) Введите величины индуктивностей и коэффициента связи, выберите единицы индуктивности в генри (Гн), миллигенри (мГн), микрогенри (мкГн) или пикогенри (пГн) и нажмите кнопку Рассчитать. В токоизмерительных клещах с разъемным магнитопроводом для безопасного измерения тока без необходимости подключать прибор к схеме используется измерительный трансформатор. В приборе используется явление взаимной индукции. На разъемном магнитопроводе надета катушка, являющаяся вторичной обмоткой измерительного трансформатора. Первичной «обмоткой» является охватываемый магнитопроводом провод с током. Электродвижущая сила, возникающая в катушке на магнитопроводе, пропорциональна току, текущему в проводнике, охваченном клещами. Прибор измеряет напряжение на зажимах катушки и указывает на дисплее значение измеряемого тока. Калькулятор определит взаимоиндукцию M двух связанных катушек индуктивности по формуле: где k — коэффициент связи, L₁ — индуктивность первой катушки и L₂ — индуктивность второй катушки. Коэффициент связи определяется как отношение взаимоиндукции двух катушек к максимально возможному значению их взаимоиндукции. Коэффициент связи изменяется в пределах от 0 до 1 и зависит от близости катушек или обмоток, материала их сердечника, их взаимной ориентации, формы и количества витков. Тороидальные трансформатор и дроссель в импульсном блоке питания Пример расчетов. Коэффициент связи двух катушек с индуктивностью 2 мкГн и 3 мкГн равен 0,5. Взаимоиндукция в микрогенри определяется как Две катушки с взаимной индукцией на принципиальной схеме При увеличении силы тока, протекающего через катушку индуктивности L₁ от внешней цепи, вокруг катушки создается увеличивающееся магнитное поле, в котором сохраняется энергия. При уменьшении тока магнитное поле также уменьшается. При этом на выводах катушки возникает напряжение (ЭДС самоиндукции) в направлении, противоположном направлению тока, и сохраняемая в магнитном поле энергия отдается обратно во внешнюю цепь. Взаимоиндукция в вашем автомобиле: для создания искры в свечах зажигания используется катушка зажигания, представляющая собой трансформатор с высоким коэффициентом трансформации. Когда ток через первичную обмотку с малым числом витков прерывается, очень большая ЭДС возникает во вторичной обмотке с большим числом витков, которая достаточна для создания искры в зазоре автомобильной свечи зажигания В обратной ситуации, если ток течет в катушке L₂, а наводится ток в катушке L₁, взаимоиндукция будет той же. Отметим, что электродвижущая сила (ЭДС) возникает только при изменении тока, причем чем быстрее изменяется ток, тем больше будет ЭДС. То есть, ЭДС взаимной индукции прямо пропорциональна скорости изменения тока Явление взаимной индукции используется в трансформаторах, электродвигателях, генераторах и других устройствах, в которых для функционирования необходимо взаимодействие с магнитным полем. Автор статьи: Анатолий Золотков Примеры расчетовРасчет взаимоиндукции двух катушек индуктивности 62 мкГн и 75 мкГн с коэффициентом связи 0,5 Расчет взаимоиндукции двух катушек индуктивности 4,3 микрогенри и 5,1 микрогенри с коэффициентом связи 0,25 Расчет взаимоиндукции двух катушек индуктивности 110 микрогенри и 130 микрогенри с коэффициентом связи 0,5 Расчет взаимоиндукции двух катушек индуктивности 1,3 микрогенри и 1,6 микрогенри с коэффициентом связи 0,25 Расчет взаимоиндукции двух катушек индуктивности 180 мГн и 220 мГн с коэффициентом связи 0,25 Расчет взаимоиндукции двух катушек индуктивности 4,7 мГн и 5,6 мГн с коэффициентом связи 0,5 Расчет взаимоиндукции двух катушек индуктивности 5,6 миллигенри и 6,8 миллигенри с коэффициентом связи 0,25 Расчет взаимоиндукции двух катушек индуктивности 30 мкГн и 36 мкГн с коэффициентом связи 0,75 Расчет взаимоиндукции двух катушек индуктивности 43 микрогенри и 51 микрогенри с коэффициентом связи 0,25 Расчет взаимоиндукции двух катушек индуктивности 16 мкГн и 20 мкГн с коэффициентом связи 0,75 Вас могут заинтересовать и другие калькуляторы из группы «Электротехнические и радиотехнические калькуляторы»:Калькулятор резистивно-емкостной цепи Калькулятор параллельных сопротивлений Калькулятор параллельных индуктивностей Калькулятор емкости последовательного соединения конденсаторов Калькулятор импеданса конденсатора Калькулятор импеданса катушки индуктивности Калькулятор взаимоиндукции параллельных индуктивностей Калькулятор взаимной индукции — последовательное соединение индуктивностей Калькулятор импеданса параллельной RC-цепи Калькулятор импеданса параллельной LC-цепи Калькулятор импеданса параллельной RL-цепи Калькулятор импеданса параллельной RLC-цепи Калькулятор импеданса последовательной RC-цепи Калькулятор импеданса последовательной LC-цепи Калькулятор импеданса последовательной RL-цепи Калькулятор импеданса последовательной RLC-цепи Калькулятор аккумуляторных батарей Калькулятор литий-полимерных аккумуляторов для дронов Калькулятор индуктивности однослойной катушки Калькулятор индуктивности плоской спиральной катушки для устройств радиочастотной идентификации (RFID) и ближней бесконтактной связи (NFC) Калькулятор расчета параметров коаксиальных кабелей Калькулятор светодиодов. Калькулятор цветовой маркировки резисторов Калькулятор максимальной дальности действия РЛС Калькулятор зависимости диапазона однозначного определения дальности РЛС от периода следования импульсов Калькулятор радиогоризонта и дальности прямой радиовидимости РЛС Калькулятор радиогоризонта Калькулятор эффективной площади антенны Симметричный вибратор Калькулятор частоты паразитных субгармоник (алиасинга) при дискретизации Калькулятор мощности постоянного тока Калькулятор мощности переменного тока Калькулятор пересчета ВА в ватты Калькулятор мощности трехфазного переменного тока Калькулятор преобразования алгебраической формы комплексного числа в тригонометрическую Калькулятор коэффициента гармонических искажений Калькулятор законов Ома и Джоуля — Ленца Калькулятор времени передачи данных Калькулятор внутреннего сопротивления элемента питания батареи или аккумулятора |
Какой коэффициент связи индуктора?
Ответить
Проверено
203,7 тыс.+ просмотров
Подсказка: Коэффициент связи дает взаимодействие между двумя катушками с точки зрения взаимной индукции. Взаимная индуктивность — это свойство двух катушек, при котором каждая катушка противодействует любому изменению силы тока в другой катушке из-за ЭДС индукции. Взаимная индуктивность между двумя катушками будет одинаковой.
Полное пошаговое решение:
Катушка индуктивности представляет собой электронный компонент с двумя выводами, который накапливает энергию в магнитном поле, когда через него протекает электрический ток.
Коэффициент связи можно определить как долю магнитного потока, создаваемого током в одной катушке, которая связана с другой катушкой. Он представлен символом (k), а величина связи между двумя индуктивно связанными катушками выражается в терминах коэффициента связи. Это может быть задано как-
\[K=\dfrac{M}{\sqrt{{{L}_{1}}{{L}_{2}}}}\]
Где,
М \[=\] взаимная индуктивность между двумя катушками
\[{{L}_{1}}=\] самоиндукция первой катушки
\[{{L}_{2}}= \]самоиндукция второй катушки
Теперь докажем коэффициент связи катушки индуктивности, который равен
Имеются две магнитно связанные катушки, имеющие виток \[{{N}_{1}}\] и \[ {{N}_{2}}\] соответственно
Ток \[{{I}_{1}}\], протекающий в первой катушке, создает магнитный поток \[{{\phi}_{1 }}\] ,имеющих оборот \[{{N}_{1}}\], то их самоиндукция будет задана как-
\[{{L}_{1}}=\dfrac{{{N}_{1}}{{\phi }_{1}}}{{{I}_{1}}}\] ( Уравнение 1)
Предположим, что коэффициент связи между двумя катушками равен k. вторая катушка имеет вид-
вторая катушка имеет вид-
\[{{M}_{12}}=\dfrac{k{{\phi}_{1}}{{N}_{2}}}{{{I}_ {1}}}\] (Уравнение 2)
Ток \[{{I}_{2}}\], протекающий во второй катушке, создаст магнитный поток \[{{\phi}_{2 }}\], имеющих несколько витков \[{{N}_{2}}\], то их самоиндукция будет равна –
\[{{L}_{2}}=\dfrac{{{\phi}_{2}}{{N}_{2}}}{{{I}_{2}}}\]( Уравнение 3)
Поскольку коэффициент связи между двумя катушками равен k, то \[k{{\phi}_{2}}\] представляет собой магнитный поток, связанный с первой катушкой, а затем взаимную индуктивность во второй катушке из-за первая катушка определяется как —
\[{{M}_{21}}=\dfrac{k{{\phi}_{2}}{{N}_{1}}}{{{I}_{ 2}}}\]Уравнение (4)
При умножении Уравнения (2) и Уравнения (4) друг на друга мы получаем
\[{{M}_{12}}\times {{M}_{21}} =\left( \dfrac{k{{\phi}_{1}}{{N}_{2}}}{{{I}_{1}}} \right)\times \left( \dfrac{ k{{\phi }_{2}}{{N}_{1}}}{{{I}_{2}}} \right)\]Уравнение (5) 9{2}}}{{{L}_{1}}{{L}_{2}}} \\
& \Rightarrow k=\dfrac{M}{\sqrt{{{L}_{1} }{{L}_{2}}}} \\
\end{align}\]
Примечание: Коэффициент связи всегда оказывается меньше единицы, и его максимальное значение равно единице. Если коэффициент связи равен единице, то это называется идеальной связью, когда весь поток одной катушки связывает другую. Если коэффициент связи между двумя индукторами больше, то их взаимная индуктивность также будет больше.
Если коэффициент связи равен единице, то это называется идеальной связью, когда весь поток одной катушки связывает другую. Если коэффициент связи между двумя индукторами больше, то их взаимная индуктивность также будет больше.
Дата последнего обновления: 16 мая 2023
•
Всего просмотров: 203.7k
•
Просмотров сегодня: 5.65k
Недавно обновленные страницы
900 02 Большинство эубактериальных антибиотиков получают из биологии Rhizobium класса 12 NEET_UGСаламиновые биоинсектициды были извлечены из биологии класса 12 NEET_UG
Какое из следующих утверждений относительно бакуловирусов класса 12 биологии NEET_UG
Канализационные или городские канализационные трубы не должны быть непосредственно классом биологии 12 NEET_UG
Очистка сточных вод осуществляется A Микробами B Удобрения класса 12 биологии NEET_UG
Иммобилизация ферментов – это A Превращение активного фермента класса 12 биологии NEET_UG
Большинство эубактериальных антибиотиков получают из A Rhizobium класса 12 биологии NEET_UG 900 03
Биоинсектициды Саламин экстрагированы из 12-го класса биологии NEET_UG
Какое из следующих утверждений относительно бакуловирусов 12-го класса биологии NEET_UG
Канализационные или муниципальные канализационные трубы не должны относиться непосредственно к 12-му классу биологии NEET_UG
Очистка сточных вод осуществляется A Микробами B Удобрения класса 12 биологии NEET_UG
Иммобилизация ферментов – это A Преобразование активного фермента класса 12 биологии NEET_UG
Тенденции сомнения 900 03
индукция — Как измерить коэффициент связи?
спросил
Изменено 1 год, 5 месяцев назад
Просмотрено 2к раз
\$\начало группы\$
У меня есть сердечник EE с одной обмоткой на одном внешнем стержне и второй обмоткой на другом внешнем стержне.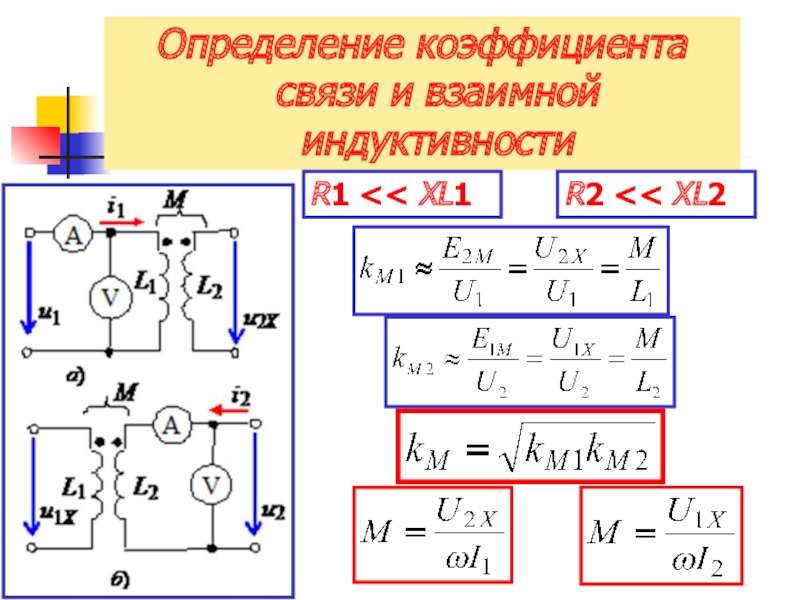 Я измеряю индуктивность одной обмотки при открытой другой обмотке и наоборот.
Я измеряю индуктивность одной обмотки при открытой другой обмотке и наоборот.
Для взаимной индуктивности я измеряю вспомогательную последовательную индуктивность (L_aiding = L_1 + L_2 + 2M) и встречную последовательную индуктивность (L_opposing = L_1 + L_2 — 2M) и заменяю эти две, чтобы получить M = 1/4 * ( L_aiding — L_opposing), что дает мне взаимную индуктивность.
Теперь я могу рассчитать коэффициент связи, используя следующее уравнение: K = M / sqrt(L_1 * L_2).
Проблема в том, что без воздушного зазора я получаю связь около 0,2, а с воздушным зазором 0,4 мм я получаю связь 0,32, что не имеет никакого смысла, так как воздушный зазор даст мне большую индуктивность рассеяния, следовательно, более низкий коэффициент связи .
Что я могу делать не так?
- индукция
\$\конечная группа\$
1
\$\начало группы\$
Что я могу делать не так?
Когда центральная часть сердечника EE действует как «короткий» путь для возбуждаемого магнитного поля, большая часть магнитного потока обходит неуправляемую катушку, и, следовательно, связь кажется низкой. Когда вы вводите зазор между половинами EE, «короткий» маршрут становится менее жизнеспособным быстрее, чем маршрут через вторичную катушку. Оба маршрута, конечно, менее жизнеспособны, но по отношению друг к другу их соответствующие противодействия становятся ближе. Это означает, что связь будет увеличиваться по мере добавления небольшого зазора.
Когда вы вводите зазор между половинами EE, «короткий» маршрут становится менее жизнеспособным быстрее, чем маршрут через вторичную катушку. Оба маршрута, конечно, менее жизнеспособны, но по отношению друг к другу их соответствующие противодействия становятся ближе. Это означает, что связь будет увеличиваться по мере добавления небольшого зазора.
То, что вы видите, соответствует моим ожиданиям.
\$\конечная группа\$
3
\$\начало группы\$
Коэффициент связи можно определить с помощью индуктивности рассеяния.
$$ K знак равно {\sqrt{{L_P — L_{lP}}\над {L_P}}}$$
Где:
\$ L_P =\$ первичная индуктивность при разомкнутой вторичной обмотке
\$ L_{lP} =\$ первичная индуктивность при закороченной вторичной обмотке (индуктивность рассеяния)
Это уравнение выполняется, если обмотки не имеют потерь. Вы также можете измерить K со вторичной стороны.



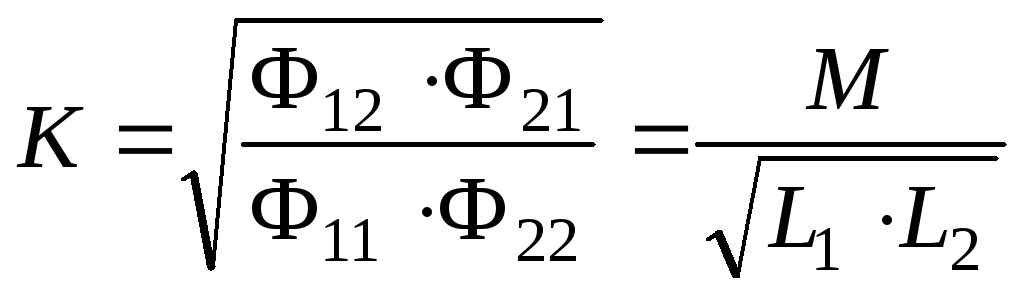 У слабо связанных катушек или обмоток коэффициент связи k 0.5. Если две катушки плотно намотаны одна над другой на общем ферромагнитном сердечнике, их связь почти идеальна и значение коэффициента связи k приближается к единице. Если же расстояние между катушками велико, значение k очень мало и приближается к нулю.
У слабо связанных катушек или обмоток коэффициент связи k 0.5. Если две катушки плотно намотаны одна над другой на общем ферромагнитном сердечнике, их связь почти идеальна и значение коэффициента связи k приближается к единице. Если же расстояние между катушками велико, значение k очень мало и приближается к нулю. Если рядом с первой катушкой поместить вторую катушку L₂, то магнитное поле, возникшее в первой катушке, создаст напряжение во второй катушке. Если общее магнитное поле пронизывает несколько катушек, говорят, что у них имеется взаимная индукция. Она обычно обозначает буквой M и измеряется в единицах индуктивности (генри).
Если рядом с первой катушкой поместить вторую катушку L₂, то магнитное поле, возникшее в первой катушке, создаст напряжение во второй катушке. Если общее магнитное поле пронизывает несколько катушек, говорят, что у них имеется взаимная индукция. Она обычно обозначает буквой M и измеряется в единицах индуктивности (генри). В то же время взаимоиндукция часто бывает нежелательной, когда возникает паразитная индуктивная связь между проводниками в схеме или даже между силовыми кабелями и металлическими кабельными каналами, в которых они помещены.
В то же время взаимоиндукция часто бывает нежелательной, когда возникает паразитная индуктивная связь между проводниками в схеме или даже между силовыми кабелями и металлическими кабельными каналами, в которых они помещены. Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов
Расчет ограничительных резисторов для одиночных светодиодов и светодиодных массивов
 com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.
com, однако мы не можем гарантировать, что они не содержат ошибок и неточностей. Вся информация предоставляется «как есть», без каких-либо гарантий. Условия.