Коэффициент трения скольжения – формула, минимальное значение
4
Средняя оценка: 4
Всего получено оценок: 89.
4
Средняя оценка: 4
Всего получено оценок: 89.
Физическая величина, характеризующая трущиеся поверхности, называется коэффициентом трения скольжения. Величина обозначается буквой μ. Коэффициент трения определяют опытным путём.
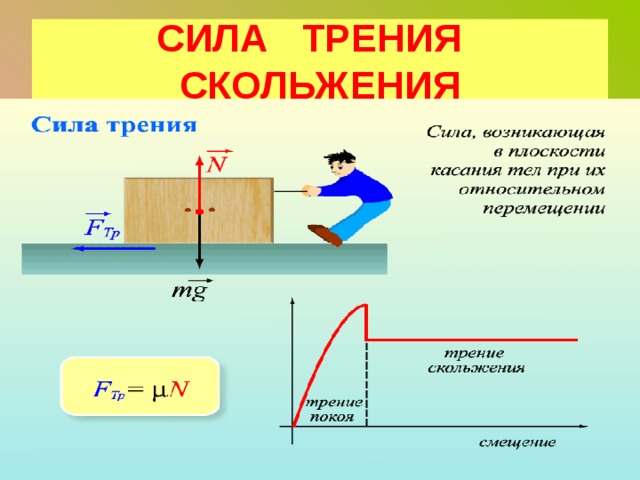
Сила трения скольжения
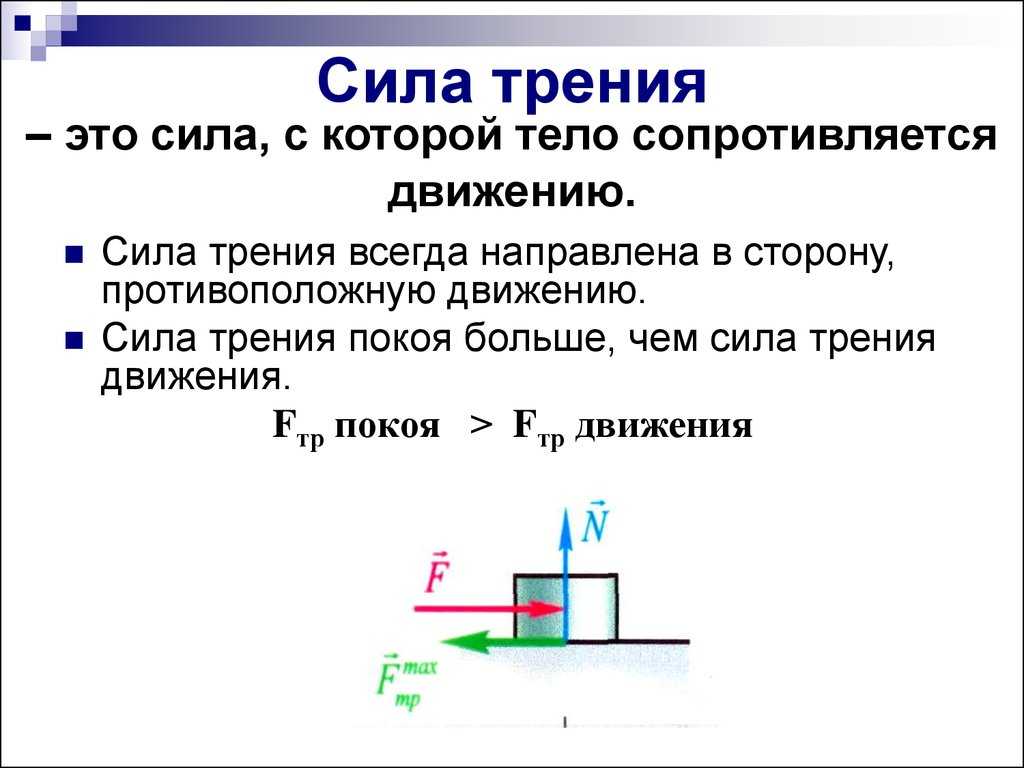
На покоящиеся и движущиеся тела всегда действуют силы трения. Они возникают при соприкосновении твердых тел, твердых тел и жидкостей или газов и подчиняются законам Ньютона. Направление сил трения противоположно движению тела и силам, стремящимся изменить его положение.
В случае, когда тело движется относительно другого, говоря о трении скольжения. Она зависит от:
- Силы нормальной реакции опоры $\vec N$,
- От скорости движения (но в вычислениях этой зависимостью пренебрегают),
- От безразмерного коэффициента трения скольжения $\mu$, который характеризует свойства и состояние поверхностей соприкосновения.

Коэффициент зависит от свойств материала. Чем больше шероховатость поверхности, тем больше значение коэффициента и, соответственно, больше сила трения. Коэффициент трения смазанных поверхностей будет меньше, чем у несмазанных для одной и той же пары материалов. Также коэффициент трения зависит от скорости. Однако эта зависимость минимальна и ей пренебрегают, если не требуется точность измерения. Поэтому коэффициент трения считается постоянным.
Рис. 2. Поверхность трения.Расчет коэффициента трения скольжения
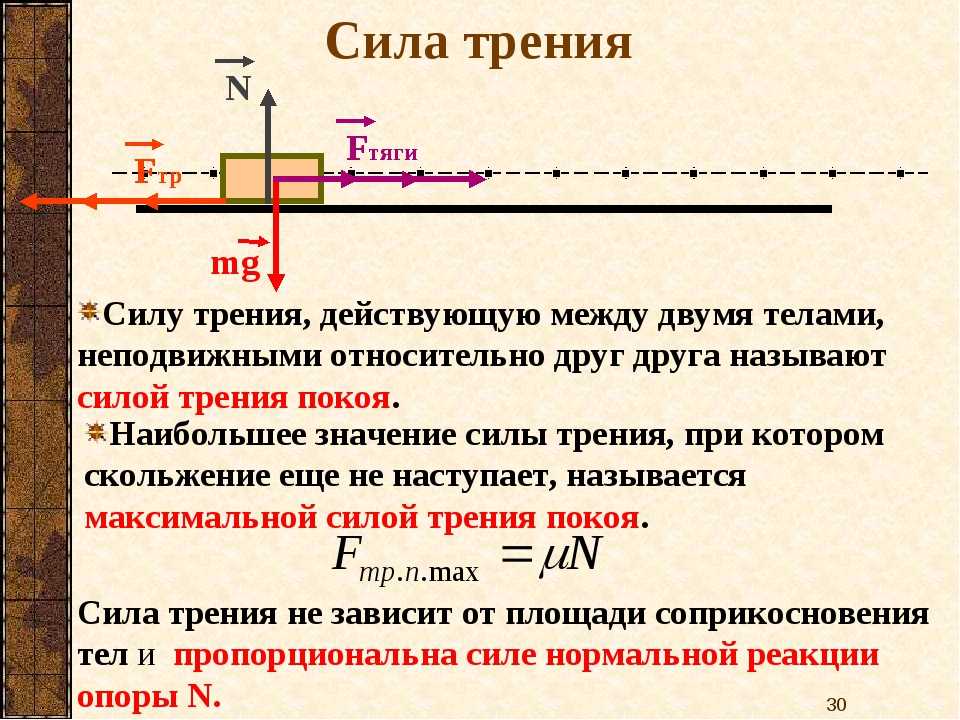
С достаточно большой точностью силу трения скольжения рассчитывают как предельную силу трения покоя по формуле:
$F_{тр} = \mu \cdot N$.
Тогда формула коэффициента трения скольжения:
$\mu ={{F_{тр}} \over {N}}$
Значение N рассчитывается как произведение массы тела на ускорение свободного падения и на косинус угла к поверхности приложения:
$N = m \cdot g \cdot cos \alpha$
Рис. 3. Сила нормальной реакции опоры для тел, скатывающихся по наклонной поверхности.
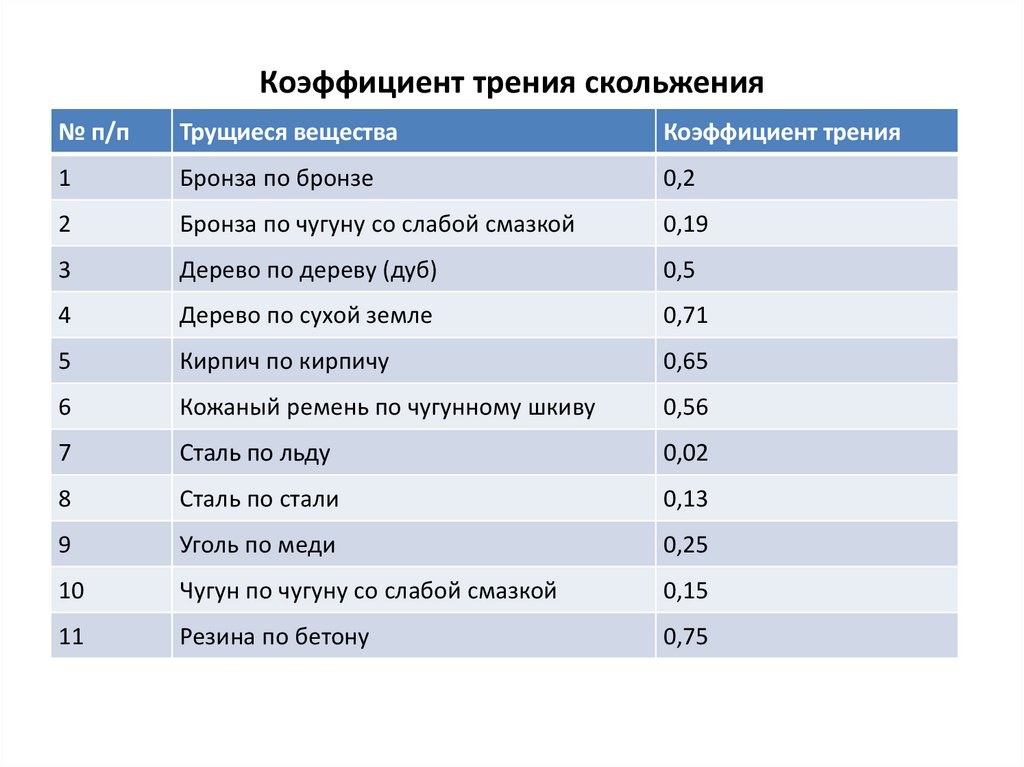
Для большинства пар материалов коэффициент рассчитан опытным путём. Значения находятся в пределах 0,1…0,5. Некоторые значения представлены в таблице.
Трущиеся материалы | ||
Покоя | При движении | |
Алюминий по алюминию | 0,94 | |
Бронза по бронзе | 0,20 | |
Бронза по чугуну | 0,21 | |
Дерево по дереву | 0,65 | 0,33 |
Дерево по камню | 0,46-0,60 | |
Дуб по дубу (вдоль волокон) | 0,62 | 0,48 |
Дуб по дубу (перпендикулярно волокнам) | 0,54 | 0,34 |
Железо по бронзе | 0,19 | 0,18 |
Железо по железу | 0,15 | 0,14 |
Железо по чугуну | 0,19 | 0,18 |
Каучук по дереву | 0,80 | 0,55 |
Каучук по металлу | 0,80 | 0,55 |
Кирпич по кирпичу (гладко отшлифованные) | 0,5-0,7 | |
Лёд по льду | 0,028 | |
Медь по чугуну | 0,27 | |
Металл по дереву | 0,60 | 0,40 |
Металл по камню | 0,42-0,50 | |
Металл по металлу | 0,18-0,20 | |
Олово по свинцу | 2,25 | |
Полозья деревянные по льду | 0,035 | |
Обитые железом полозья по льду | 0,02 | |
Резина (шина) по твёрдому грунту | 0,40-0,60 | |
Резина (шина) по чугуну | 0,83 | |
Сталь (коньки) по льду | 0,02-0,03 | 0,015 |
Сталь по железу | 0,19 | |
Сталь по стали | 0,15-0,25 | 0,09 при 3 м/с, 0,03 при 27 м/с |
Чугун по дубу | 0,65 | 0,30-0,50 |
Чугун по стали | 0,33 | 0,13 |
Чугун по чугуну | 0,15 | |
Коэффициент трения – переменная величина.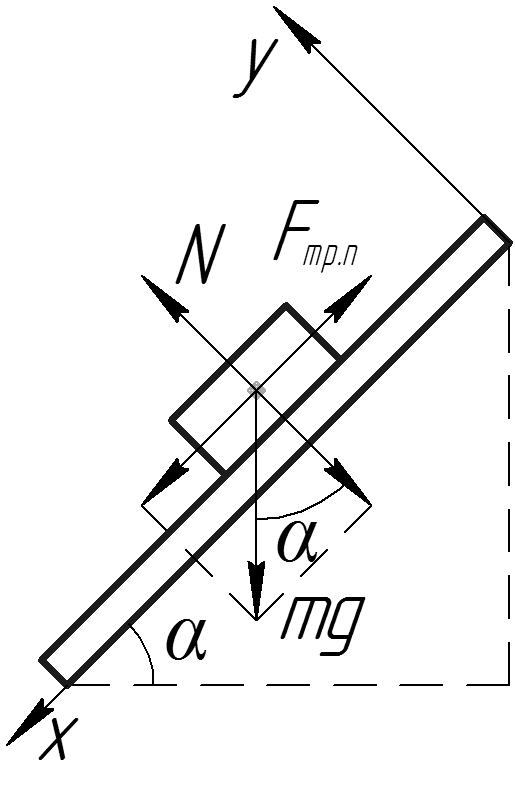
Что мы узнали?
Коэффициент трения скольжения – физическая величина, характеризующая трущиеся поверхности. Как найти: $\mu = {{F_{тр}} \over {N}}$. На практике коэффициент рассчитывается исходя из свойств материала эмпирическим путём.
Тест по теме
Доска почёта
Чтобы попасть сюда — пройдите тест.
Пока никого нет. Будьте первым!
Оценка доклада
4
Средняя оценка: 4
Всего получено оценок: 89.
А какая ваша оценка?
Формула для определения коэффициента трения скольжения. Коэффициент трения скольжения. Б. Вывод «расчётной формулы»
Различных материалов по поверхности.
Цель работы:
определение коэффициентов трения качения и трения скольжения.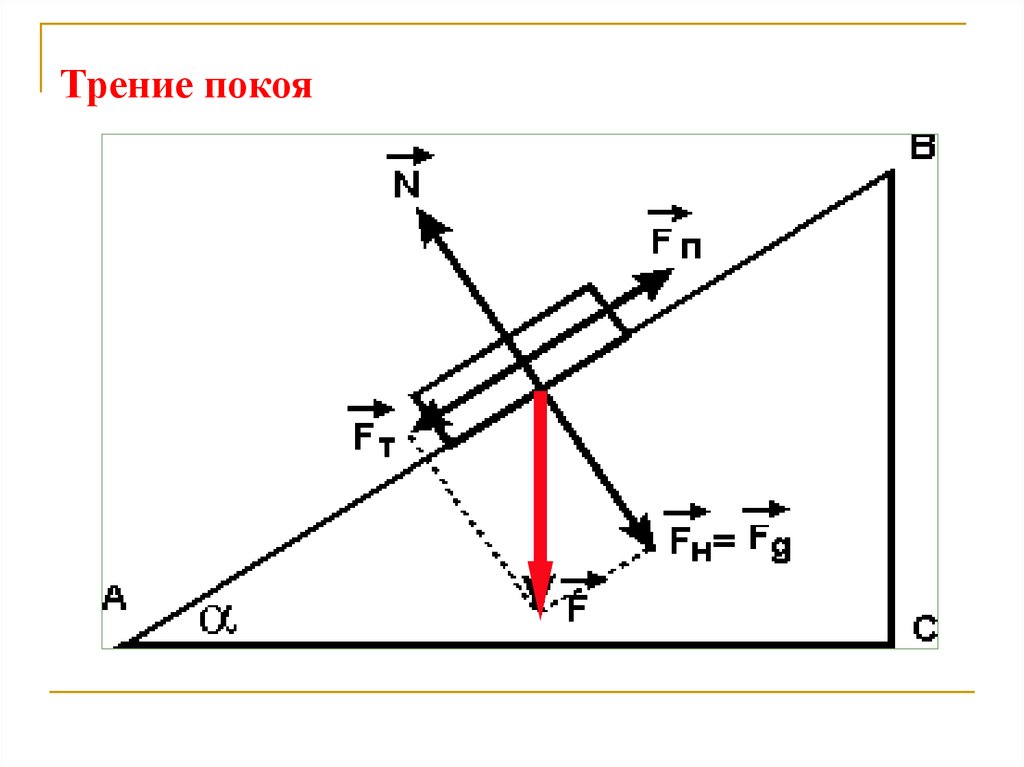
Краткая теория к изучению движения тела по наклонной плоскости
При относительном перемещении двух соприкасающихся тел или при попытке вызвать такое перемещение возникают силы трения. Различают три вида трения, возникающего при контакте твердых тел: трение скольжения, покоя и качения. Трение скольжения и трение качения всегда связаны с необратимым процессом – превращением механической энергии в тепловую.
Рис. 5.15.1
Сила трения скольжения действует на контактирующие друг с другом тела и направлена в сторону, противоположную скорости относительного движения. Сила нормальной реакции опоры и сила трения являются нормальной и тангенциальной составляющими одной и той же силы , которая называется силой реакции опоры (рис. 5.15.1). Модули сил F тр. и N связаны между собой приближенным эмпирическим законом Амонтона-Кулона:
(5.15.1) |
В этой формуле µ — коэффициент трения, зависящий от материала и качества обработки соприкасающихся поверхностей, слабо зависящий от скорости скольжения и практически не зависящий от площади контакта.
Рис. 5.15.2
Сила трения покоя принимает значение, обеспечивающее равновесие, т.е. состояние покоя тела. Угол α между направлением силы и нормалью к поверхности может принимать значения в промежутке от нуля до максимального, обусловленного законом Амонтона-Кулона.
Сила трения качения возникает из-за деформации материалов поверхностей катящегося тела и опоры, а также из-за разрыва временно образующихся молекулярных связей в месте контакта.
Рассмотрим лишь первую из названных причин, поскольку вторая играет заметную роль только при хорошей полировке тел. При качении цилиндра или шара по плоской поверхности в месте контакта и перед ним возникает деформация катящегося тела или опоры. Тело оказывается в ямке (рис.3.2) и вынуждено все время из нее выкатываться. Из-за этого точка приложения силы реакции опоры
смещается немного вперед по ходу движения, а линия действия этой силы отклоняется немного назад. Нормальная составляющая силы
есть сила упругости, а тангенциальная – сила трения качения.
F тр кач . = k (N n / R ). | (5.15.2) |
В этом выражении R — радиус катящегося тела, а k -коэффициент трения качения, имеющий размерность длины.
Движение тела по наклоной плоскости под действием сил тяжести и трения
При движении одиночного тела по наклоной плоскости движущей силой является сила тяжести F=mg (Рис.5.15.3)
Рис. 5.15.3
Распределим все силы действующие на тело по осям OX и OY. Ось OX направим вдоль наклоной плоскости, а OY перпендикулярно ей.
- OX: m a = mg sin a – F тр ; F тр = µN;
- OY: 0 = mg cos a –N; N = mg cos a;
- m a = mg sin a – mg µ cos a;
- a = g sin a – g µ cos a; g µ cos a = g sin a – a ;
- µ = (g sin a – a )/ (g cos a)
- µ=tg a – a/g cos a
Последние уравнение определяет коэффициент трения
Движение тела по наклоной плоскости под действием сил тяжести, трения и силы натяжения нити направленной вдоль скорости движения
Рис. 5.15.4
5.15.4
Распишем все силы действующие на тело по осям OX и OY. Ось OX направим вдоль наклоной плоскости, а OY перпендикулярно ей.
- OX: m 1 a = -m 1 g sin a – F тр + T; F тр = µN;
- OY: 0 = m 1 g cos a –N; N = m 1 g cos a;
- m 1 a =- m 1 g sin a – m 1 g µ cos a+m 2 g;
- m 1 a =m 2 g – m 1 g sin a – m 1 g µ cos a;
- m 1 g µ cos a =m 2 g – m 1 g sin α – m 1 a ;
- µ = (m 2 g – m 1 g sin a – m 1 a )/ (m 1 g cos a)
Движение тела по наклоной плоскости под действием сил тяжести, трения и силы натяжения нити направленной перепендикулярно скорости движения
Рис. 5.15.5
Движение тела по дугообразной траектории качественно отличается от движения тела по прямолинейной в первую очередь за счет появления центростремительного ускорения. В данной лабораторной работе предлагается рассчитать тангенсальное
α
τ
и нормальное
α
n
ускорение тела на основе снятых прибором измерений. Коэффициент трения взять из предыдущих опытов.
Описания и правила пользования:
Установка состоит из платформы с рабочей длиной 140 см с расположенной вверху шкалой из черно-белых штрихов и электронного устройства для снятия данных, выступающего в качестве. Платформа может устанавливаться в любом положении от горизонтального положения до 45 0 . Отсчет угла наклона производится по шкале (рис.5.15.6). Для проведения эксперимента, электронное устройство счета помещается под специально отведенные широкие штрихи на шкале для калибровки. После проведения эксперимента электронное устройство через специальный кабель подключают к компьютеру.
Рис. 5.15.6. Общий вид установки
Методика проведения лабораторной работы.
При определении коэффициента трения скольжения, платформа устанавливается под углом большим, чем угол трения.
Образец после калибровки из исходного положения освобождается рукой для свободного движения. При прохождении, устройство фиксирует время между двумя последними штрихами на шкале.
По полученным результатам испытаний рассчитывается, путь, скорость, коэффициент трения скольжения. Строится график пути и скорости от времени.
Расчет погрешности провести по правилам расчета погрешностей косвенных измерений.
Контрольные вопросы:
- Силы трения. Объясните причину возникновения силы трения скольжения.
- Сила трения качения.
Глава 15. Теорема об изменении кинетической энергии.
15.3. Теорема об изменении энергии кинетической точки и твердого тела при поступательном движении.
15.3.1. Какую работу совершают действующие на материальную точку силы, если ее кинетическая энергия уменьшается с 50 до 25 Дж? (Ответ -25)
15.3.2. Свободное падение материальной точки массой m начинается из состояния покоя. Пренебрегая сопротивлением воздуха, определить путь, пройденный точкой к моменту времени, когда она имеет скорость 3 м/с. (Ответ 0,459)
15.3.3. Материальная точка массой m = 0,5 кг брошена с поверхности Земли с начальной скоростью v о = 20 м/с и в положении М имеет скорость v = 12 м/с. Определить работу силы тяжести при перемещении точки из положения М о в положение М (Ответ -64)
Определить работу силы тяжести при перемещении точки из положения М о в положение М (Ответ -64)
15.3.4. Материальная точка массой m брошена с поверхности Земли под углом α = 60° к горизонту с начальной скоростью v 0 = 30 м/с. Определить наибольшую высоту h подъема точки. (Ответ 34,4)
15.3.5. Тело массой m = 2 кг от толчка поднимается по наклонной плоскости с начальной скоростью v о = 2 м/с. Определись работу силы тяжести на пути, пройденном телом до остановки. (Ответ -4)
15.3.6. Материальная точка М массой m, подвешенная на нити длиной ОМ = 0,4 м к неподвижной точке О, отведена на угол α = 90° от положения равновесия и отпущена без начальной скорости. Определить скорость этой точки во время ее прохождения через положение равновесия. (Ответ 2,80)
15.3.7. Кабина качелей подвешена на двух стержнях длиной l = 0,5 м. Определить скорость кабины при прохождении ею нижнего положения, если в начальный момент стержни были отклонены на угол φ = 60° и отпущены без начальной скорости. (Ответ 2,21)
(Ответ 2,21)
15.3.8. Материальная точка М массой m движется под действием силы тяжести по внутренней поверхности полуцилиндра радиуса r = 0,2 м. Определить скорость материальной точки в точке В поверхности, если ее скорость в точке A равна нулю. (Ответ 1,98)
15.3.9. По проволоке АВС, расположенной в вертикальной плоскости и изогнутой в виде дуг окружностей радиусов r 1 , = 1 м, r 2 = 2 м, может скользить без трения кольцо D массой m. Определить скорость кольца в точке С, если его скорость в точке А равна нулю. (Ответ 9,90)
15.3.10. По горизонтальной плоскости движется тело массой m = 2 кг, которому была сообщена начальная скорость v 0 = 4 м/с. До остановки тело прошло путь, равный 16 м. Определить модуль силы трения скольжения между телом и плоскостью. (Ответ 1)
15.3.11. Тело массой m = 100 кг начинает движение из состояния покоя по горизонтальной шероховатой плоскости под действием постоянной силы F. Пройдя путь, равный 5 м, скорость тела становится равной 5 м/с. Определить модуль силы F, если сила трения скольжения F тр = 20 Н. (Ответ 270)
Определить модуль силы F, если сила трения скольжения F тр = 20 Н. (Ответ 270)
15.3.12. Хоккеист, находясь на расстоянии 10 м от ворот, клюшкой сообщает шайбе, лежащей на льду, скорость 8 м/с. Шайба, скользя по поверхности льда, влетает в ворота со скоростью 7,7 м/с. Определить коэффициент трения скольжения между шайбой и поверхностью льда.
(Ответ 2,40 10 -2)
15.3.13. По наклонной плоскости спускается без начальной скорости тело массой m = 1кг. Определить кинетическую энергию тела в момент времени, когда оно прошло путь, равный 3 м, если коэффициент трения скольжения между телом и наклонной плоскостью f = 0,2. (Ответ 9,62)
15.3.14. По наклонной плоскости спускается без начальной скорости груз массой m. Какую скорость v будет иметь груз, пройдя путь, равный 4м от начала движения, если коэффициент трения скольжения между грузом и наклонной плоскостью равен 0,15? (Ответ 5,39)
15.3.15. К ползуну 1 массой m = 1 кг прикреплена пружина 2.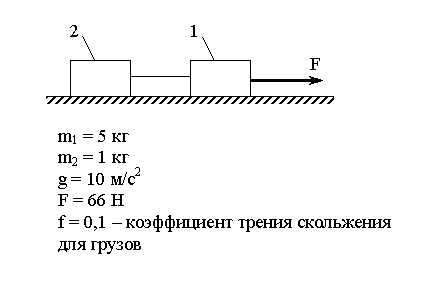 Пружину сжимают из свободного состояния на величину 0,1 м, после чего груз отпускают без начальной скорости. Определить жесткость пружины, если груз, пройдя путь, равный 0,1 м, приобретает скорость 1 м/с.
Пружину сжимают из свободного состояния на величину 0,1 м, после чего груз отпускают без начальной скорости. Определить жесткость пружины, если груз, пройдя путь, равный 0,1 м, приобретает скорость 1 м/с.
(Ответ 100)
Физический практикум
Задача № 3
Определение коэффициента трения скольжения
При подготовке к выполнению этой задачи следует ознакомиться с теорией по учебным пособиям :
1. Глава 2, И.В. Савельев «Курс общей физики», т.1, М., «Наука».
2. § 1 и 2. П.К. Кашкаров, А.В. Зотеев, А.Н. Невзоров, А.А. Склянкин «Задачи по курсу общей физики с решениями. « Механика. Электричество и магнетизм » , М., изд. МГУ.
- Цель работы
Экспериментально проверить законы кинематики и динамики на примере поступательного движения твёрдого тела при наличии сухого трения.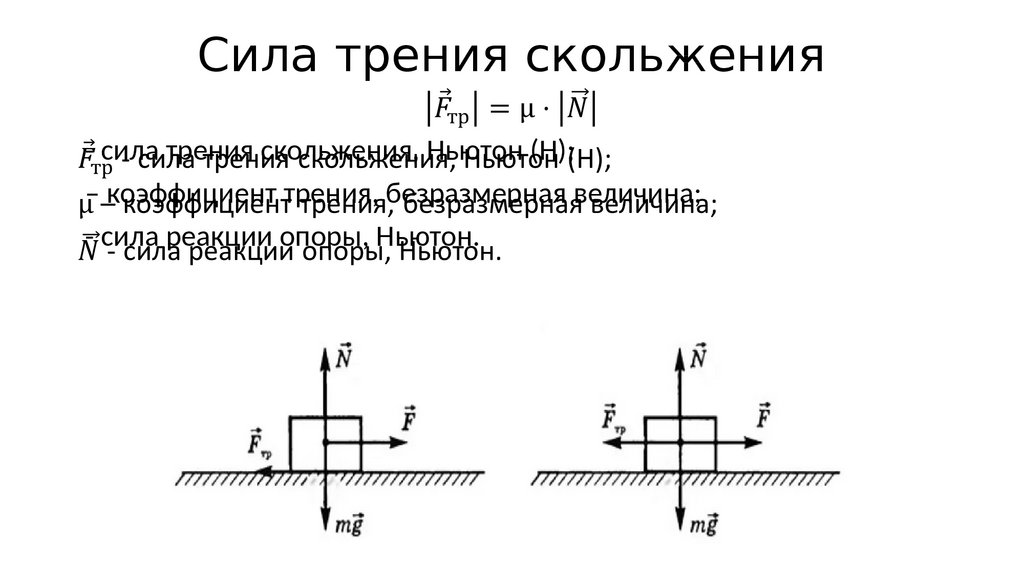 Познакомиться с методом определения коэффициента трения скольжения – трибометрией. На основании опытных данных провести расчёт коэффициента трения скольжения.
Познакомиться с методом определения коэффициента трения скольжения – трибометрией. На основании опытных данных провести расчёт коэффициента трения скольжения.
2. Экспериментальное оборудование, приборы и принадлежности
Л
абораторный стенд (рис. 3.1) включает наклонную направляющую скамью (1) с прикреплённой к ней измерительной линейкой, подвижный брусок (2) (2 шт.), оптические датчики (3) (3 шт.), транспортир для измерения угла наклона направляющей скамьи и модуль сбора сигналов от оптических датчиков (4).
К приборам и принадлежностям относятся компьютер с необходимым программным обеспечением и концентратор для подключения модуля сбора сигналов к компьютеру.
3. Теоретическая частьА. Общие положения
При анализе движения тел с использованием законов Ньютона приходится иметь дело со следующими видами сил:
Cила тяжести – проявление гравитационного взаимодействия тел;
Сила натяжения нитей, пружин, реакции опор и подвесов, и т.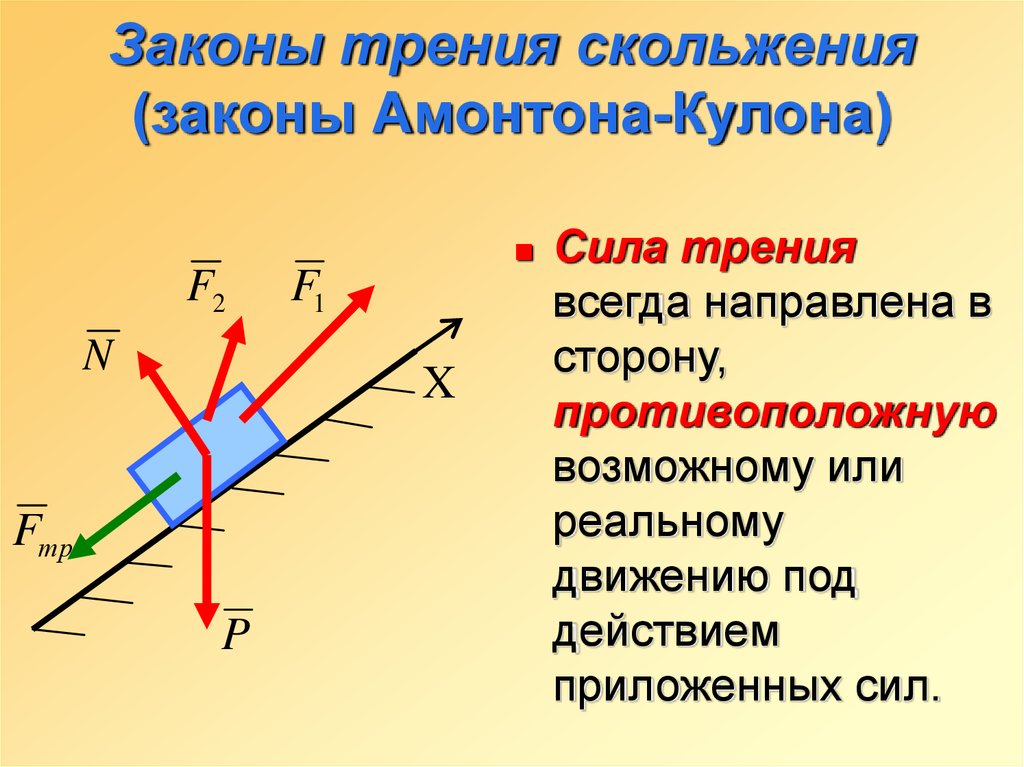 д. («силы реакции связей») – проявление сил упругости, возникающих при деформации тел;
д. («силы реакции связей») – проявление сил упругости, возникающих при деформации тел;
Сила трения . Различают силы сухого и вязкого трения. Сухое трение возникает при возможности движения твёрдого тела по поверхности другого твёрдого тела.
В условиях, когда на тело, соприкасающееся с некоторой поверхностью, действуют силы, но оно не движется относительно этой поверхности, со стороны последней на тело действует сила трения покоя . Её величина находится из условия отсутствия относительного движения:
(3.1),
где – силы, приложенные к телу, за исключением
. Т.е. пока тело находится в покое, сила трения покоя в точности равна по величине и противоположна по направлению касательной составляющей результирующей сил
. Максимальное значение силы трения покоя равно
, где N – нормальная (т.е. перпендикулярная поверхностям) составляющая силы реакции опоры *) , – коэффициент трения скольжения. Коэффициент трения зависит от материала и состояния поверхностей соприкасающихся тел. Для шероховатых поверхностей коэффициент трения больше, чем для отшлифованных. На рис. 3.2 показано как меняется сила сухого трения при нарастании величины силы F . Наклонный участок графика (F тр N ) соответствует покоящемуся телу (F тр пок = F ), а горизонтальный – скольжению.
Коэффициент трения зависит от материала и состояния поверхностей соприкасающихся тел. Для шероховатых поверхностей коэффициент трения больше, чем для отшлифованных. На рис. 3.2 показано как меняется сила сухого трения при нарастании величины силы F . Наклонный участок графика (F тр N ) соответствует покоящемуся телу (F тр пок = F ), а горизонтальный – скольжению.
. (3.2)
* По своей природе силы сухого трения обусловлены электромагнитным взаимодействием молекул поверхностных слоёв соприкасающихся твёрдых тел. Независимость силы трения от скорости соблюдается лишь при не очень больших скоростях, не для всех тел и не при всех качествах обработки поверхностей.
Сила трения скольжения всегда направлена противоположно вектору скорости тела. Этому соответствует векторная запись закона для силы трения скольжения, установленного опытным путем французскими физиками Ш. Кулоном и Г. Амонтоном:
. (3.3)
Здесь – скорость относительного движения тел, v – её модуль.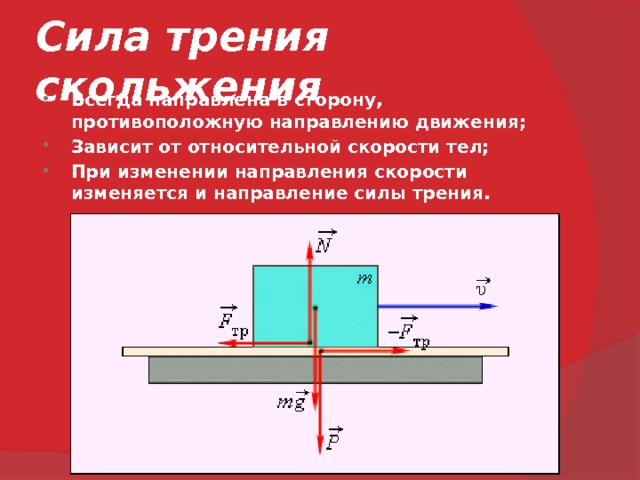
При движении тел в жидких или газообразных средах возникает сила вязкого трения . При малых скоростях она пропорциональна скорости движения тела относительно среды:
, (3.4)
где r – коэффициент вязкого трения (зависит от размеров и формы тела, от вязких свойств среды).
Система методов измерения сил, коэффициентов трения и износостойкости трущихся тел составляет содержание особого раздела механики – трибометрии. В данной работе для экспериментального определения коэффициента трения скольжения используется трибометр в виде наклонной плоскости с регулируемым углом наклона и системой оптических датчиков для регистрации кинематических характеристик тела, соскальзывающего с неё.
Б. Вывод «расчётной формулы»
Брусок, находящийся на наклонной плоскости направляющей скамьи лабораторного стенда (рис. 3.1) испытывает действие двух сил: силы тяжести
и силы реакции опоры со стороны клина. Последнюю, как обычно, удобно сразу представить в виде двух составляющих – силы трения
вдоль поверхности и «нормальной» составляющей (т. е. перпендикулярной к поверхности) – (см. рис. 3.3). В общем случае сила трения может оказаться направленной как вверх, так и вниз вдоль наклонной плоскости. Однако нас будет интересовать случай, когда брусок либо скользит, либо находится на грани соскальзывания вниз по наклонной плоскости. Тогда сила трения направлена наклонно вниз.
е. перпендикулярной к поверхности) – (см. рис. 3.3). В общем случае сила трения может оказаться направленной как вверх, так и вниз вдоль наклонной плоскости. Однако нас будет интересовать случай, когда брусок либо скользит, либо находится на грани соскальзывания вниз по наклонной плоскости. Тогда сила трения направлена наклонно вниз.
Будем предполагать, что стенд неподвижен относительно инерциальной системы отсчёта, связанной с Землей. Тогда, пока брусок не соскальзывает, сумма действующих на него сил равна нулю. Удобно оси О X и О Y системы координат выбираемой нами инерциальной системы отсчёта расположить вдоль наклонной плоскости и перпендикулярно к ней соответственно (см. рис. 3.3). Условия равновесия для бруска покоящегося на наклонной плоскости имеют вид:
0 = N – mg cos . (3.5)
0 = mg sin – F тр . (3.6)
Пока угол наклона направляющей мал составляющая силы тяжести вдоль неё («скатывающая сила») уравновешивается силой трения покоя (!).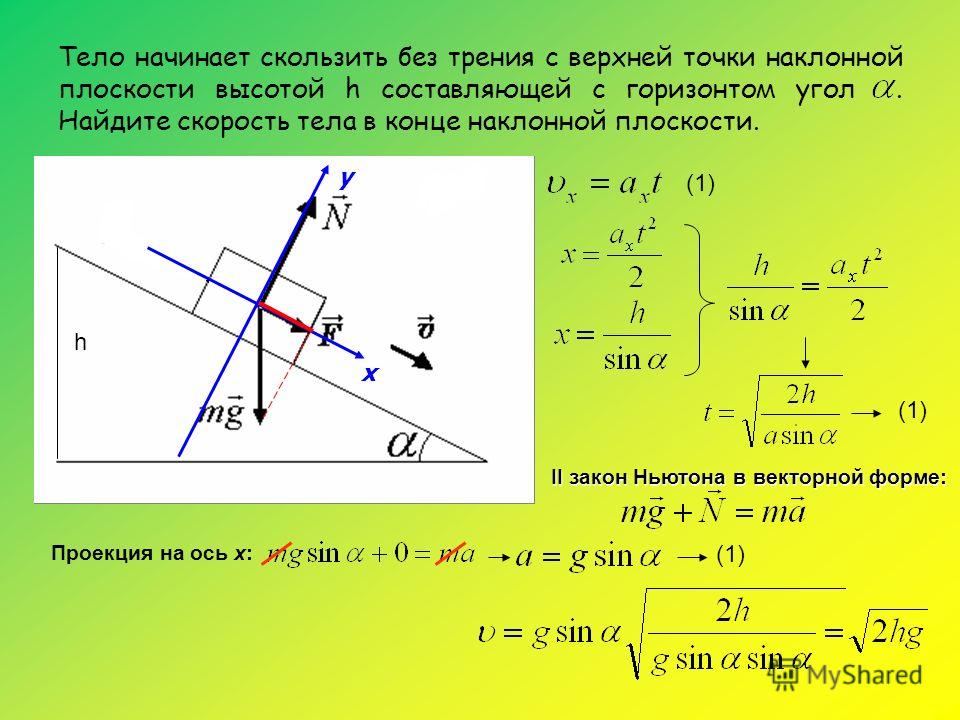 С ростом угла она также растёт (по «закону синуса»). Однако её рост не беспределен. Её максимальное значение, как мы знаем, равно
С ростом угла она также растёт (по «закону синуса»). Однако её рост не беспределен. Её максимальное значение, как мы знаем, равно
= N . (3.7)
Этим и определяется максимальное значение угла, при котором брусок не соскальзывает с наклонной плоскости. Совместное решение уравнений (3.5) – (3.7) приводит к условию:
. (3.8)
Иначе говоря, коэффициент трения равен тангенсу угла наклона плоскости к горизонту, при котором начинается соскальзывание тела с наклонной плоскости. На этом основан принцип действия одного из возможных вариантов трибометров.
Однако установить с достаточной точностью предельный угол начала соскальзывания тела с наклонной плоскости («статический метод») довольно сложно. Поэтому в данной экспериментальной работе используется динамический метод определения коэффициента трения скольжения при поступательном движении твёрдого тела (бруска) по наклонной плоскости с ускорением.
При соскальзывании бруска вниз по наклонной плоскости уравнение движения (второй закон Ньютона) в проекциях на координатные оси будет выглядеть следующим образом:
ma = mg sin – F тр , (3.9)
0 = N mg cos . (3.10)
Сила трения скольжения равна при этом
F тр = N . (3.11)
Эти уравнения динамики позволяют найти ускорение тела:
a = (sin – cos )g . (3.12)
Координата тела, соскальзывающего по наклонной плоскости, меняется по закону равноускоренного движения:
. (3.13)
Оптические датчики, размещённые на фиксированных расстояниях на пути движения бруска, позволяют измерять времена прохождения телом соответствующих участков пути. Используя равенство (3.13), путём численной аппроксимации экспериментальных данных, можно найти величину ускорения a .
По значению рассчитанного ускорения, используя равенство (3.12), можно получить «расчётную формулу» для определения коэффициента трения :
(3.14)
Таким образом, для экспериментального определения коэффициента трения необходимо измерить две величины: угол наклона плоскости и ускорение тела а .
- Описание лабораторной установки
Д
Рис. 3.4
Еревянный брусок 1 (рис. 3.4) с приклеенной к нему визирной планкой (2) длиной ℓ , скользит по наклонной плоскости, пересекая оптические оси датчиков (3), фиксирующих моменты начала и завершения перекрытия их оптических осей скользящим по наклонной плоскости бруском. Передний фронт импульса оптической оси датчика связан с началом перекрытия оптической оси визирной планкой, а задний фронт – с завершением перекрытия планкой оптической оси. За это время брусок перемещается на расстояние ℓ . Таким образом, при последовательном пресечении бруском оптических осей трёх датчиков, фиксируются времена прохождений 6 координатных отметок на оси ОХ (см. рис. 3.5): x 1 , x 1 +ℓ , x 2 , x 2 +ℓ , x 3 , x 3 +ℓ . Экспериментально измеренные значения времени их прохождений t 1 , t 2 , t 3 , t 4 , t 5 , t 6 служат основой для аппроксимации кривой квадратичной зависимости (3.13). В программу аппроксимации необходимо заложить значения координат этих точек x 1 , x 1 +ℓ , x 2 , x 2 +ℓ , x 3 , x 3 +ℓ , которые вносятся в таблицу 1 после фиксации положений 3-х оптических датчиков.
рис. 3.5): x 1 , x 1 +ℓ , x 2 , x 2 +ℓ , x 3 , x 3 +ℓ . Экспериментально измеренные значения времени их прохождений t 1 , t 2 , t 3 , t 4 , t 5 , t 6 служат основой для аппроксимации кривой квадратичной зависимости (3.13). В программу аппроксимации необходимо заложить значения координат этих точек x 1 , x 1 +ℓ , x 2 , x 2 +ℓ , x 3 , x 3 +ℓ , которые вносятся в таблицу 1 после фиксации положений 3-х оптических датчиков.
- Порядок проведения работы
Параметры установки:
Длина визирной планки бруска: ℓ = (110 1) мм ;
Углы наклона направляющей скамьи для брусков №1 и №2:
α 1 = (24 ± 1) град ;
α 2 = (27 ± 1) град .Таблица 1
Координата 1-го датчика x 1 , мм | x 1 +ℓ , | Координата 2-го датчика x 2 , мм | x 2 +ℓ , | Координата 3-го датчика x 3 , мм | x 3 +ℓ , |
Упражнение 1 (брусок №1)
1. Собрать лабораторную установку, установив направляющую скамью под углом α 1 = 24 (контролируется с помощью транспортира) и поместив 3 оптических датчика на пути перемещения бруска вдоль направляющей скамьи.
Собрать лабораторную установку, установив направляющую скамью под углом α 1 = 24 (контролируется с помощью транспортира) и поместив 3 оптических датчика на пути перемещения бруска вдоль направляющей скамьи.
2. Установить брусок №1 на наклонную направляющую и удерживать его в верхнем, начальном, положении.
Запустить измерения, нажав кнопку (Ctrl+S) (запустить измерения для выбранных датчиков) и сразу, непосредственно вслед за запуском, отпустить брусок, после чего он начнет скользить по наклонной плоскости из верхнего положения.
3. После прохождения бруском всей наклонной плоскости, остановить измерения, нажав кнопку (Ctrl+T) (остановить измерения). На экране будут видны три импульса, показывающие моменты перекрытия оптических осей 3-х датчиков при скольжении деревянного бруска по наклонной плоскости (рис. 3.6) (цифры условные).
Р
ис. 3.6
4. Провести обработку полученных данных в соответствии со сценарием:
t , с | x , м | |
правую колонку таблицы, обозначенную «x , м », необходимо заполнить вручную. Если три датчика установлены на отметках 15 см , 40 см и 65 см соответственно (данные берутся из таблицы 1), то, после введения всех шести значений координат датчиков, таблица на экране будет выглядеть следующим образом:
Если три датчика установлены на отметках 15 см , 40 см и 65 см соответственно (данные берутся из таблицы 1), то, после введения всех шести значений координат датчиков, таблица на экране будет выглядеть следующим образом:
t , с | x , м | |
цифра в центральной колонке таблицы (под обозначением «А») равна удвоенному коэффициенту при квадратичной степени в уравнении (3.13), т.е.
, поэтому в данном случае величина ускорения будет равна a 1 = 2A = 0,13×2 = 0,26 м /с 2 . Записать это значение в таблицу 2.
5. Повторить эксперимент по пп. 2-4 ещё четыре раза. Все результаты записать в таблицу 2.
6. Установить направляющую скамью под углом α 2 = 27, поместив три оптических датчика на пути перемещения бруска вдоль направляющей скамьи. Повторить весь эксперимент по пп.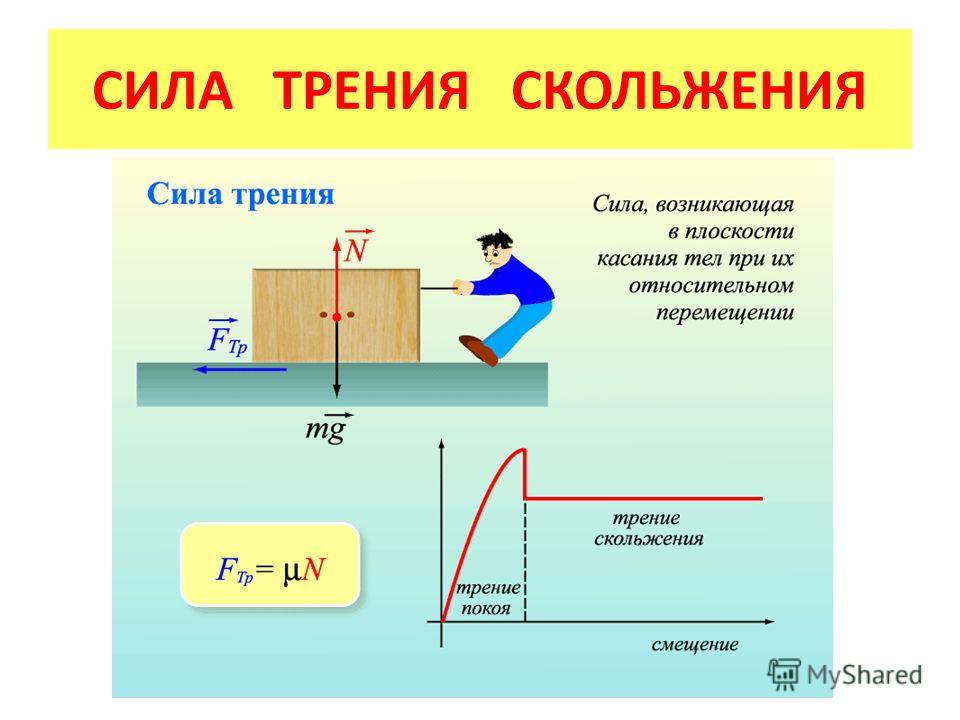 2–4. Все результаты записать в таблицу 3.
2–4. Все результаты записать в таблицу 3.
Таблица 2, брусок №1 (α 1 = 24)
| Таблица 3, брусок №1(α 2 = 27)
|
После таблиц оставить место для записи расчётных результатов (примерно половину страницы).
Упражнение 2 (брусок №2)
1. Взять брусок №2 с другим материалом опорной поверхности скольжения и повторить для него весь эксперимент по пп. 1–6. Все результаты записать в таблицы 4 и 5 соответственно.
Таблица 4, брусок №2 (α 1 = 24)
| Таблица 5, брусок №2 (α 2 = 27)
|
После таблиц оставить место для расчетных результатов (примерно половину страницы).
Используя полученные результаты и расчётное соотношение (3.14), найти среднее значение коэффициента трения I>μ> для каждого бруска и условий проведения опыта (угла наклона плоскости):
…
Частные отклонения записать в таблицы 2–4. Найти погрешность измерений для каждого случая
Для бруска №1:
1 > =…; 2 > = …;Для бруска №2:
3 > = …; 4 > = …2. Оценить погрешность эксперимента (погрешность измерений + погрешность метода).
Погрешность измерений (средняя из модулей частных отклонений):
= …
Погрешность метода:
/B> a 1 > = … м/с 2 ;Δ a 1 = … м/с 2
ε µ = … Δ µ 1 мет. = ε µ · 1 > = …
= ε µ · 1 > = …
Δ µ 1 = …
/B> a 2 > = … м/с 2 ;Δ a 2 = … м/с 2
ε µ = … Δ µ 2 мет. = ε µ · 2 > = …
Δ µ 2 = …
/B> a 3 > = … м/с 2 ;Δ a 3 = … м/с 2
ε µ = … Δ µ 3 мет. = ε µ · 3 > = . ..
..
Δ µ 3 =
/B> a 4 > = … м/с 2 ;Δ a 4 = … м/с 2 ε µ = … Δ µ 4 мет. = ε µ · 4 > = Δ µ 4 = …Записать результат экспериментального определения коэффициента трения μ для бруска №1 и для бруска №2 в стандартной форме:
Что такое сила трения?
Какие виды сил трения вы знаете?
Что такое сила трения покоя? Чему равна сила трения покоя?
Нарисуйте графики зависимости силы сухого трения от касательной к поверхности опоры составляющей результирующей остальных сил, действующих на тело.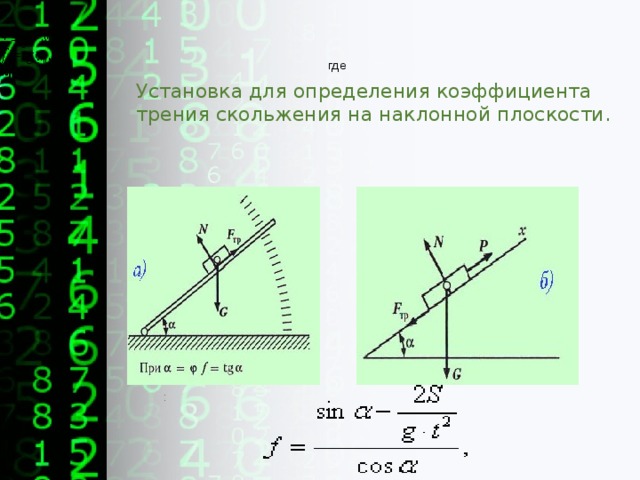
От чего зависит коэффициент трения скольжения?
Как можно экспериментально определить коэффициент трения скольжения из условий равновесия тела на наклонной плоскости?
Как в данной работе экспериментально определяется коэффициент трения скольжения?
Что представляет собой лабораторный стенд?
Расскажите о порядке выполнения работы и проведении измерений.
Как оценить погрешность косвенного измерения коэффициента трения скольжения?
Перед выполнением работы получить инструктаж у лаборанта.
Соблюдать общие правила техники безопасности работы в лаборатории «;Физика»;.
Приложение 1. Оценка погрешности измерений.коэффициентамиУрок
Числе с целью набора статистических данных): определение коэффициента трения скольжения тела по используемой поверхности (использовать… нами задачи ? – Ускорение тела должно быть равно нулю.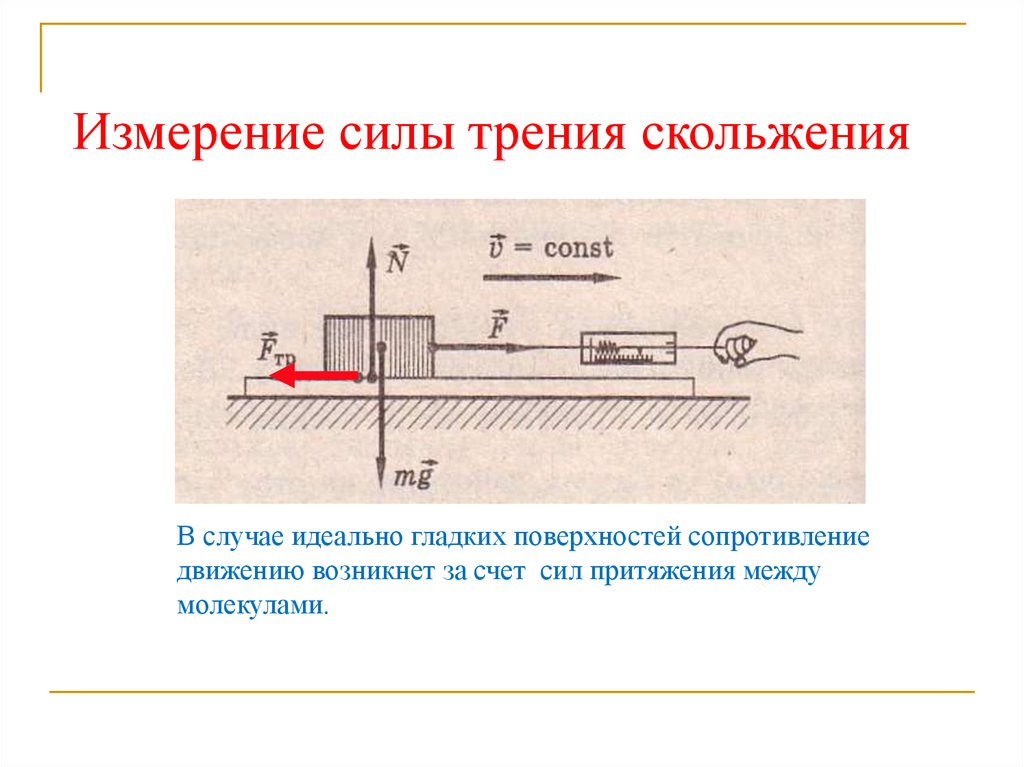 – При каком значении коэффициента трения …
– При каком значении коэффициента трения …
Прямолинейное движение» 1 3 Решение графических задач 1 4 Решение задач
Если брусок тянут с помощью динамометра с постоянной скоростью, то динамометр показывает модуль силы трения скольжения (F тр). Здесь сила упругости пружины динамометра уравновешивает силу трения скольжения.
С другой стороны, сила трения скольжения зависит от силы нормальной реакции опоры (N), которая возникает в следствие действия веса тела. Чем вес больше, тем больше сила нормальной реакции. И чем больше сила нормальной реакции, тем больше сила трения . Между этими силами существует прямая пропорциональная зависимость, которую можно выразить формулой:
Здесь μ – это коэффициент трения . Он показывает, как именно сила трения скольжения зависит от силы нормальной реакции (или, можно сказать, от веса тела), какую долю от нее составляет. Коэффициент трения — безразмерная величина. Для разных пар поверхностей μ имеет разное значение.
Для разных пар поверхностей μ имеет разное значение.
Так, например, деревянные предметы трутся друг о друга с коэффициентом от 0,2 до 0,5 (в зависимости от вида деревянных поверхностей). Это значит, что если сила нормальной реакции опоры 1 Н, то при движении сила трения скольжения может составить значение, лежащее в промежутке от 0,2 Н до 0,5 Н.
Из формулы F тр = μN следует, что зная силы трения и нормальной реакции, можно определить коэффициент трения для любых поверхностей:
Сила нормальной реакции опоры зависит от веса тела. Она равна ему по модулю, но противоположна по направлению. Вес тела (P) можно вычислить, зная массу тела. Таким образом, если не учитывать векторность величин, можно записать, что N = P = mg. Тогда коэффициент трения находится по формуле:
μ = F тр / (mg)
Например, если известно, что сила трения тела массой 5 кг, движущегося по поверхности, равна 12 Н, то можно найти коэффициент трения: μ = 12 Н / (5 кг ∙ 9,8 Н/кг) = 12 Н / 49 Н ≈ 0,245.
2.2.4. Сила трения
Сила трения действует не только на движущееся тело, но и на тело, находящееся в покое, если существуют силы, которые стремятся этот покой нарушить. На тело, которое катится по опоре, также действует сила трения.
Сила трения покоя численно равна составляющей силы, направленной вдоль поверхности, на которой находится данное тело, и стремящейся сдвинуть его с места (рис. 2.7):
F тр.пок = F x .
Рис. 2.7
При достижении указанной составляющей некоторого критического значения (F x = F крит) тело начинает двигаться. Критическое значение силы, которое соответствует началу движения, определяется формулой
F x = F крит = µ пок N ,
где µ пок — коэффициент трения покоя; N — модуль силы нормальной реакции опоры (эта сила численно равна весу тела).
В момент начала движения сила трения покоя достигает максимального значения:
F тр. пок max = μ пок N .
Сила трения скольжения постоянна и определяется произведением:
F
тр. ск = µ ск N
,
ск = µ ск N
,
где µ ск — коэффициент трения скольжения; N — модуль силы нормальной реакции опоры.
При решении задач считают, что коэффициенты трения покоя µ пок и скольжения µ ск равны между собой:
µ пок = µ ск = µ.
На рис. 2.8 изображен график зависимости величины силы трения F тр от проекции силы F x , стремящейся сдвинуть тело, на ось, направленную вдоль поверхности предполагаемого движения.
Рис. 2.8
Для того чтобы определить, будет ли данное тело находиться в покое или начнет двигаться под действием приложенной силы определенной величины и направления, необходимо:
F крит = µN ,
где µ — коэффициент трения; N — модуль силы нормальной реакции опоры;
3) сравнить значения F крит и F x :
- если F x > F крит, то тело движется под действием приложенной силы; в этом случае сила трения скольжения рассчитывается как
F тр.ск = µN ;
- если F x
F тр.пок = F x .
Модуль силы трения качения
F
тр. кач пропорционален коэффициенту трения качения µ кач, модулю силы нормальной реакции опоры N
и обратно пропорционален радиусу R
катящегося тела:
кач пропорционален коэффициенту трения качения µ кач, модулю силы нормальной реакции опоры N
и обратно пропорционален радиусу R
катящегося тела:
F тр. кач = μ кач N R .
Пример 13. К телу массой 6,0 кг, лежащему на горизонтальной поверхности, приложена сила 25 Н, направленная вдоль поверхности. Найти силу трения, если коэффициент трения равен 0,5.
Решение. Произведем оценку величины силы, способной вызвать движение тела, по формуле
F кр = µN ,
где µ — коэффициент трения; N — модуль силы нормальной реакции опоры, численно равной весу тела (P = mg ).
Величина критической силы, достаточной для начала движения тела, составляет
F кр = μ m g = 0,5 ⋅ 6,0 ⋅ 10 = 30 Н.
Проекция силы, приложенной к телу в горизонтальном направлении, на ось предполагаемого движения Ox (см. рисунок) равна
F x = F = 25 Н.
F x
т.е. величина приложенной к телу силы меньше величины силы, способной вызвать его движение. Следовательно, тело находится в состоянии покоя.
Искомая сила трения — сила трения покоя — равна внешней горизонтальной силе, стремящейся этот покой нарушить:
F тр.пок = F x = 25 Н.
Пример 14. Тело находится на наклонной плоскости с углом при основании 30°. Вычислить силу трения, если коэффициент трения равен 0,5 3 . Масса тела равна 3,0 кг.
Решение. На рисунке стрелкой показано направление предполагаемого движения.
Выясним, останется ли тело в покое или начнет двигаться. Для этого рассчитаем величину критической силы, способной вызвать движение, т.е.
F кр = µN ,
где µ — коэффициент трения; N = mg cos α — величина силы нормальной реакции наклонной плоскости.
Расчет дает значение указанной силы:
F кр = μ m g cos 30 ° = 0,5 3 ⋅ 3,0 ⋅ 10 ⋅ 3 2 = 22,5 Н.
Из состояния покоя тело стремится вывести проекция силы тяжести на ось Ox , величина которой составляет
F x = mg sin 30° = 15 Н.
Таким образом, имеет место неравенство
F x
т.е. проекция силы, стремящейся вызвать движение тела, меньше величины силы, способной это сделать. Следовательно, тело сохраняет состояние покоя.
Следовательно, тело сохраняет состояние покоя.
Искомая сила — сила трения покоя — равна
F тр = F x = 15 Н.
Пример 15. Шайба находится на внутренней поверхности полусферы на высоте 10 см от нижней точки. Радиус полусферы составляет 50 см. Вычислить коэффициент трения шайбы о сферу, если известно, что указанная высота является максимально возможной.
Решение. Проиллюстрируем условие задачи рисунком.
Шайба, согласно условию задачи, находится на максимально возможной высоте. Следовательно, сила трения покоя, действующая на шайбу, имеет максимальное значение, совпадающее с проекцией силы тяжести на ось Ox :
F тр. пок max = F x ,
где F x = mg cos α — модуль проекции силы тяжести на ось Ox ; m — масса шайбы; g — модуль ускорения свободного падения; α — угол, показанный на рисунке.
Максимальная сила трения покоя совпадает с силой трения скольжения:
F тр. пок max = F тр. ск,
где F
тр.ск = µN
— модуль силы трения скольжения; N
= mg
sin α — величина силы нормальной реакции поверхности полусферы; µ — коэффициент трения.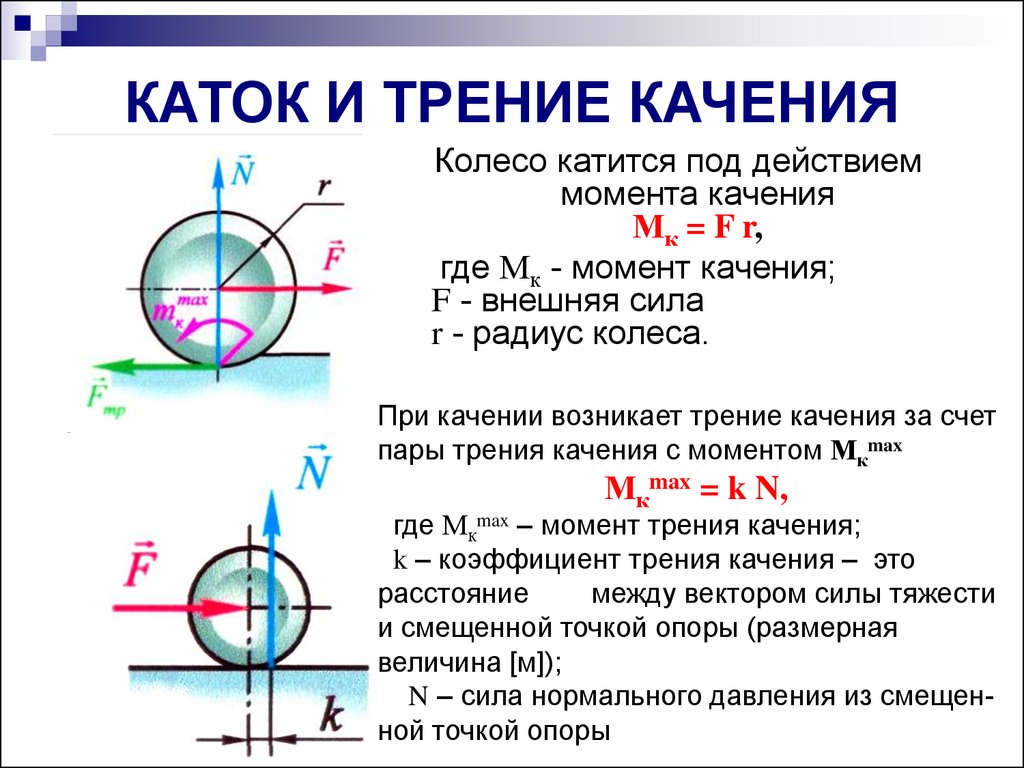
Коэффициент трения определим, записав указанное равенство в явном виде:
mg cos α = µmg sin α.
Отсюда следует, что искомый коэффициент трения определяется тангенсом угла α:
Указанный угол определим из дополнительного построения:
tg α = R − h 2 h R − h 2 ,
где h — предельная высота, на которой может находиться шайба; R — радиус полусферы.
Расчет дает значение тангенса:
tg α = 0,5 − 0,1 2 ⋅ 0,1 ⋅ 0,5 − (0,1) 2 = 4 3
и позволяет вычислить искомый коэффициент трения.
Коэффициент трения. Как найти силу трения скольжения Найти коэффициент трения если сила
Сила трения – величина, с которой взаимодействуют две поверхности при движении. Она зависит от характеристики тел, направления движения. Благодаря трению скорость тела уменьшается, и вскоре оно останавливается.
Сила трения – направленная величина, независящая от площади опоры и предмета, так как при движении и увеличении площади повышается сила реакции опоры. Эта величина участвует в расчете силы трения. В итоге Fтр=N*m. Здесь N – реакция опоры, а m – коэффициент, который является постоянной величиной, если нет необходимости в очень точных расчетах. При помощи этой формулы можно вычислить силу трения скольжения, которую обязательно стоит учитывать при решении задач, связанных с движением.
Если тело вращается на поверхности, то в формулу необходимо включить силу качения. Тогда трение можно найти по формуле Fтркач = f*N/r. Согласно формуле, при вращении тела имеет значение его радиус. Величина f – коэффициент, который можно найти, зная, из какого материала изготовлено тело и поверхность. Это коэффициент, который находится по таблице.
Эта величина участвует в расчете силы трения. В итоге Fтр=N*m. Здесь N – реакция опоры, а m – коэффициент, который является постоянной величиной, если нет необходимости в очень точных расчетах. При помощи этой формулы можно вычислить силу трения скольжения, которую обязательно стоит учитывать при решении задач, связанных с движением.
Если тело вращается на поверхности, то в формулу необходимо включить силу качения. Тогда трение можно найти по формуле Fтркач = f*N/r. Согласно формуле, при вращении тела имеет значение его радиус. Величина f – коэффициент, который можно найти, зная, из какого материала изготовлено тело и поверхность. Это коэффициент, который находится по таблице.Существуют три силы трения:
- покоя;
- скольжения;
- качения.
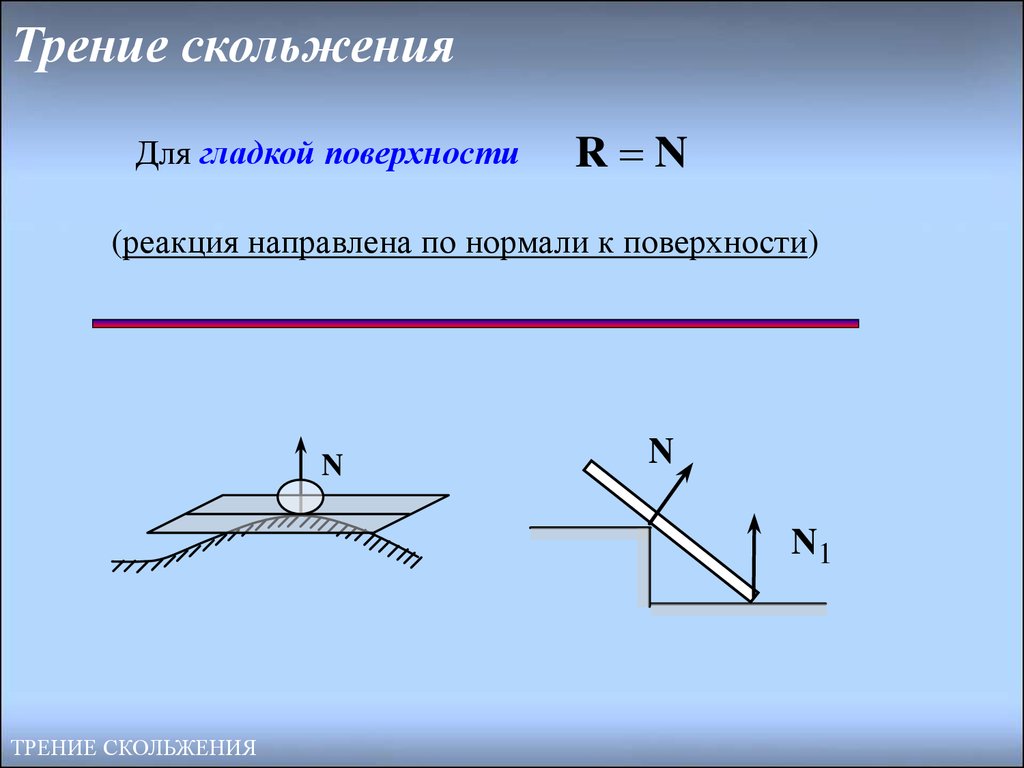 В идеале при взаимодействии двух абсолютно гладких поверхностей не должно возникать силы трения. На самом деле невозможно, чтобы предмет находился в состоянии покоя или движения без сопротивления поверхностей.
Во время движения в жидкости возникает вязкое сопротивление. В отличие от воздушной среды, тело в жидкости не может находиться в состоянии покоя. Оно под воздействием воды начинает движение, соответственно в жидкости не существует трения покоя. Во время перемещения в воде сопротивление движению возникает благодаря разной скорости потоков, окружающих тело. Чтобы снизить сопротивление при перемещении в жидкостях, телу придают обтекаемую форму. В природе для преодоления сопротивления в воде на теле рыб имеется смазка, снижающая трение при движении. Помните, при движении одного тела в жидкостях возникает разное значение сопротивления.
В идеале при взаимодействии двух абсолютно гладких поверхностей не должно возникать силы трения. На самом деле невозможно, чтобы предмет находился в состоянии покоя или движения без сопротивления поверхностей.
Во время движения в жидкости возникает вязкое сопротивление. В отличие от воздушной среды, тело в жидкости не может находиться в состоянии покоя. Оно под воздействием воды начинает движение, соответственно в жидкости не существует трения покоя. Во время перемещения в воде сопротивление движению возникает благодаря разной скорости потоков, окружающих тело. Чтобы снизить сопротивление при перемещении в жидкостях, телу придают обтекаемую форму. В природе для преодоления сопротивления в воде на теле рыб имеется смазка, снижающая трение при движении. Помните, при движении одного тела в жидкостях возникает разное значение сопротивления. На трение в жидкости влияет ее температура. Для того чтобы автомобиль во время мороза нормально ездил, его необходимо предварительно разогреть. В результате этого вязкость масла уменьшается, что снижает сопротивление и уменьшает износ деталей. Во время перемещения в жидкости сопротивление может увеличиваться из-за возникновения турбулентных потоков. В таком случае направление движения становится хаотичным. Тогда формула приобретает вид: F=v2*k. Здесь v – скорость, а k – коэффициент, зависящий от свойств тела и жидкости.
На трение в жидкости влияет ее температура. Для того чтобы автомобиль во время мороза нормально ездил, его необходимо предварительно разогреть. В результате этого вязкость масла уменьшается, что снижает сопротивление и уменьшает износ деталей. Во время перемещения в жидкости сопротивление может увеличиваться из-за возникновения турбулентных потоков. В таком случае направление движения становится хаотичным. Тогда формула приобретает вид: F=v2*k. Здесь v – скорость, а k – коэффициент, зависящий от свойств тела и жидкости.Зная физические свойства тел и сопутствующие силы, воздействующие на предмет, вам легко удастся рассчитать силу трения.
Определение
Силой трения называют силу, которая возникает при относительном перемещении (или попытке перемещения) тел и является результатом сопротивления движению окружающей среды или других тел.
Силы трения возникают тогда, когда соприкасающиеся тела (или их части) перемещаются относительно друг друга. При этом трение, которое появляется при относительном перемещении соприкасающихся тел, называют внешним. Трение, возникающее между частями одного сплошного тела (газ, жидкость) названо внутренним.
Трение, возникающее между частями одного сплошного тела (газ, жидкость) названо внутренним.
Сила трения – это вектор, который имеет направление вдоль касательной к трущимся поверхностям (слоям). При этом эта сила направлена в сторону противодействия относительному смещению этих поверхностей (слоев). Так, если два слоя жидкости перемещаются друг по другу, при этом движутся с различными скоростями, то сила, которая приложена к слою, перемещающемуся с большей скоростью, имеет направление в сторону, которая противоположна движению. Сила же, которая воздействует на слой, который движется с меньшей скоростью, направлена по движению.
Виды трения
Трение, которое возникает между поверхностями твердых тел, называют сухим. Оно возникает не только при скольжении поверхностей, но и при попытке вызвать перемещение поверхностей. При этом возникает сила трения покоя. Внешнее трение, которое появляется между движущимися телами, называют кинематическим.
Законы сухого трения говорят о том, что максимальная сила трения покоя и сила трения скольжения не зависят от площади поверхностей соприкосновения соприкасающихся тел, подверженных трению.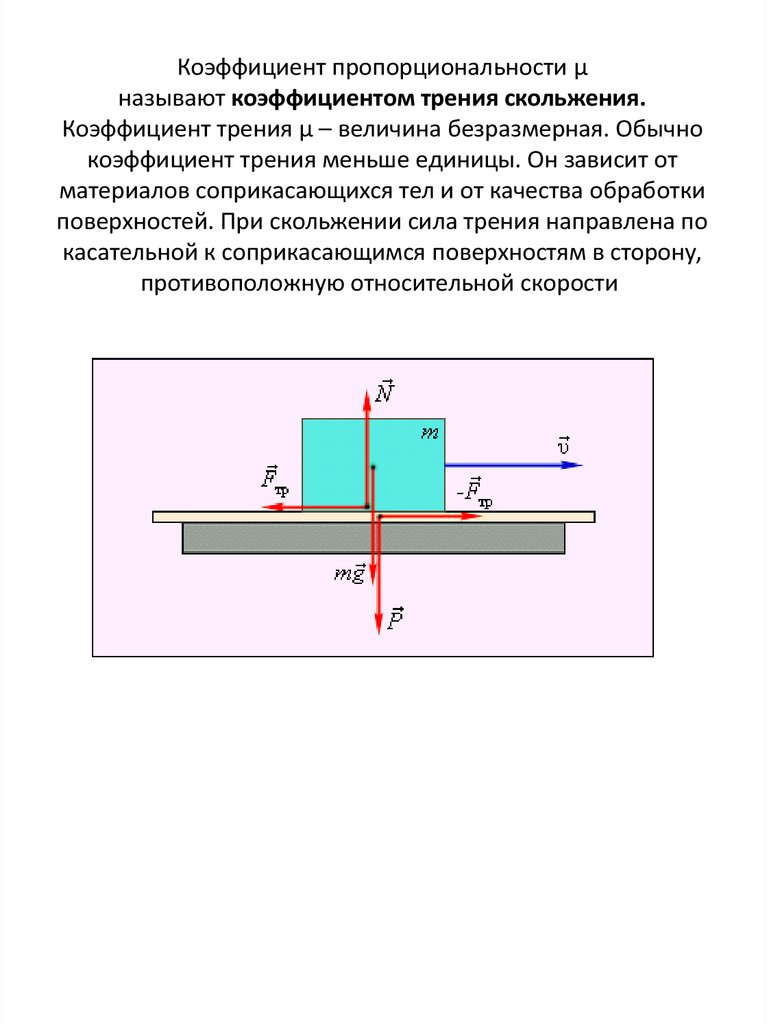 Эти силы пропорциональны модулю силы нормального давления (N), которая прижимает трущиеся поверхности:
Эти силы пропорциональны модулю силы нормального давления (N), которая прижимает трущиеся поверхности:
где – безразмерный коэффициент трения (покоя или скольжения). Данный коэффициент зависит от природы и состояния поверхностей трущихся тел, например от наличия шероховатостей. Если трение возникает как результат скольжения, то коэффициент трения является функцией скорости. Довольно часто вместо коэффициента трения применяют угол трения, который равен:
Угол равен минимальному углу наклона плоскости к горизонту, при котором тело, лежащее на этой плоскости, начинает скользить, под воздействие силы тяжести.
Более точным считают закон трения, который принимает во внимание силы притяжения между молекулами тел, которые подвергаются трению:
где S – общая площадь контакта тел, p 0 – добавочное давление, которое вызывается силами молекулярного притяжения, – истинный коэффициент трения.
Трение между твердым телом и жидкостью (или газом) называют вязким (жидким). Сила вязкого трения становится равной нулю, если скорость относительного движения тел обращается в нуль.
Сила вязкого трения становится равной нулю, если скорость относительного движения тел обращается в нуль.
При движении тела в жидкости или газе появляются силы сопротивления среды, которые могут стать существенно больше, чем силы трения. Величина силы трения скольжения зависит от формы, размеров и состояния поверхности тела, скорости движения тела относительно среды, вязкости среды. При не очень больших скоростях сила трения вычисляется при помощи формулы:
где знак минус означает, что сила трения имеет направление в сторону противоположную направлению вектора скорости. При увеличении скоростей движения тел в вязкой среде линейный закон (4) переходит в квадратичный:
Коэффициенты и существенно зависимы от формы, размеров, состояния поверхностей тел, вязкости среды.
Помимо этого выделяют трение качения.В первом приближении трение качения рассчитывают, применяя формулу:
где k – коэффициент трения качения, который имеет размерность длины и зависит от материала тел, подверженных контакту и качеств поверхностей и т. д. N – сила нормального давления, r – радиус катящегося тела.
д. N – сила нормального давления, r – радиус катящегося тела.
Единицы измерения силы трения
Основной единицей измерения силы трения (как и любой другой силы) в системе СИ является: [P]=H
В СГС: [P]=дин.
Примеры решения задач
Пример
Задание. На горизонтальном диске лежит маленькое тело. Диск вращается вокруг оси, которая проходит через его центр, перпендикулярно плоскости с угловой скоростью . На каком расстоянии от центра диска может находиться в состоянии равновесия тело, если коэффициент трения между диском и телом равен ?
Решение. Изобразим на рис.1 силы, которые будут действовать на тело, положенное на вращающийся диск.
В соответствии со вторым законом Ньютона имеем:
В проекции на ось Yиз уравнения (1.1) получим:
В проекции на ось X имеем:
где ускорение движения маленького тела равно по модуль нормальной составляющей полного ускорения. Силутрения покоя найдем как:
примем во внимание выражение (1. 2), тогда имеем:
2), тогда имеем:
приравняем правые части выражений (1.3) и (1.5):
где маленькое тело (так как оно находится в состоянии покоя на диске) движется со скоростью, равной.
Коэффициент трения — это основная характеристика трения как явления. Он определяется видом и состоянием поверхностей трущихся тел.
ОПРЕДЕЛЕНИЕ
Коэффициентом трения называют коэффициент пропорциональности, связывающий силу трения () и силу нормального давления (N) тела на опору. Чаще всего коэффициент трения обозначают буквой . И так, коэффициент трения входит в закон Кулона — Амонтона:
Данный коэффициент трения не зависит от площадей, соприкасающихся поверхностей.
В данном случае речь идет о коэффициенте трения скольжения, который зависит от совокупных свойств трущихся поверхностей и является безразмерной величиной. Коэффициент трения зависит от: качества обработки поверхностей, трущихся тел, присутствия на них грязи, скорости движения тел друг относительно друга и т. д. Коэффициент трения определяют эмпирически (опытным путем).
д. Коэффициент трения определяют эмпирически (опытным путем).
Коэффициент трения, который соответствует максимальной силе трения покоя в большинстве случаев больше, чем коэффициент трения движения.
Для большего числа пар материалов величина коэффициента трения не больше единицы и лежит в пределах
Угол трения
Иногда вместо коэффициента трения применяют угол трения (), который связан с коэффициентом соотношением:
Так, угол трения соответствует минимальному углу наклона плоскости по отношению к горизонту, при котором тело, лежащее на этой плоскости, начнет скользить вниз под воздействием силы тяжести. При этом выполняется равенство:
Истинный коэффициент трения
Закон трения, который учитывает влияние сил притяжения между молекулами, трущихся поверхностей записываю следующим образом:
где — называют истинным коэффициентом трения, — добавочное давление, которое вызывается силами межмолекулярного притяжения, S — общая площадь непосредственного контакта трущихся тел.
Коэффициент трения качения
Коэффициент трения качения (k) можно определить как отношение момента силы трения качения () к силе с которой тело прижимается к опоре (N):
Отметим, что коэффициент трения качения обозначают чаще буквой . Этот коэффициент, в отличие от выше перечисленных коэффициентов трения, имеет размерность длины. То есть в системе СИ он измеряется в метрах.
Коэффициент трения качения много меньше, чем коэффициент трения скольжения.
Примеры решения задач
ПРИМЕР 1
| Задание | Веревка лежит частично на столе, часть ее свешивается со стола. Если треть длины веревки свесится со стола, то она начинает скользить. Каков коэффициент трения веревки о стол? |
| Решение | Веревка скользит со стола под действием силы тяжести. Обозначим силу тяжести, которая действует на единицу длины веревки как . В таком случае в момент начала скольжения сила тяжести, которая действует на свешивающуюся часть веревки, равна: До начала скольжения эта сила уравновешивается силой трения, которая действует на часть веревки, которая лежит на столе: Так как силы уравновешиваются, то можно записать (): |
| Ответ |
ПРИМЕР 2
| Задание | Каков коэффициент трения тела о плоскость (), если зависимость пути, которое оно проходит задано уравнением: где Плоскость составляет угол с горизонтом.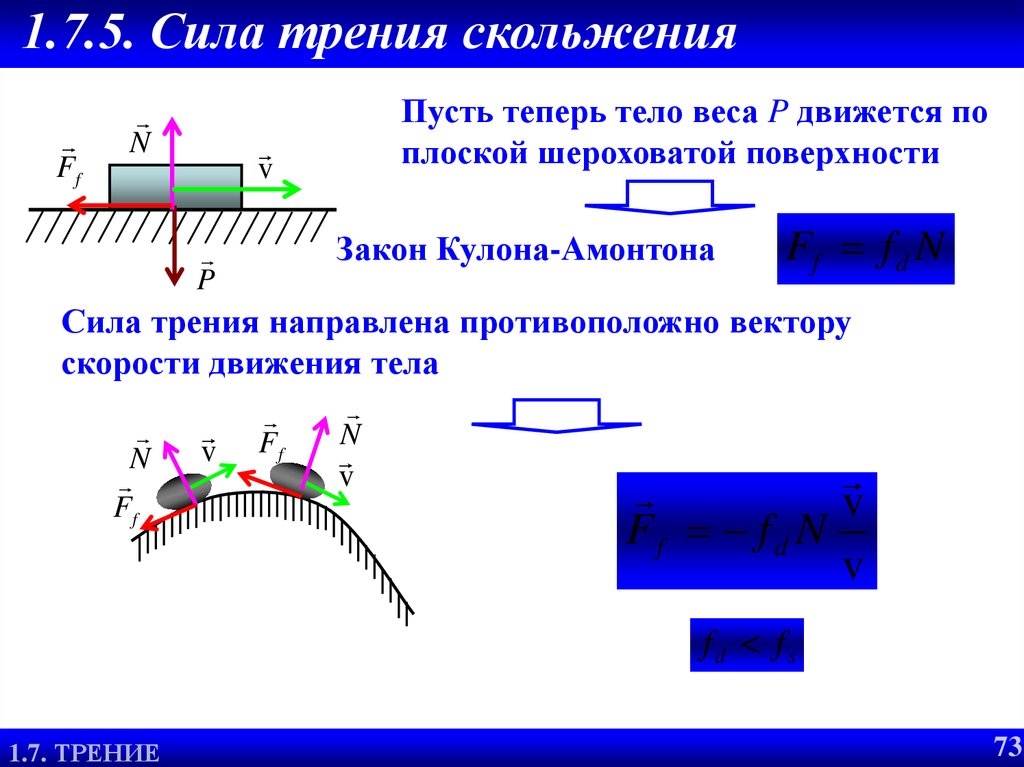 |
| Решение | Запишем второй закон Ньютона для сил, приложенных к движущемуся телу: |
Трение является тем физическим процессом, без которого не могло бы существовать само движение в нашем мире. В физике для вычисления абсолютного значения силы трения необходимо знать специальный коэффициент для рассматриваемых трущихся поверхностей. На этот вопрос ответит данная статья.
Трение в физике
Прежде чем отвечать на вопрос, как коэффициент трения находить, необходимо рассмотреть, что такое трение и какой силой оно характеризуется.
В физике выделяют три вида этого процесса, что протекает между твердыми объектами. Это скольжения и качения. Трение покоя возникает всегда, когда внешняя сила пытается сдвинуть с места объект. Скольжения трение, судя по названию, возникает при скольжении одной поверхности по другой. Наконец, качения трения появляется, когда круглый объект (колесо, шарик) катится по некоторой поверхности.
Объединяет все виды тот факт, что они препятствуют любому движению и точка приложения их сил находится в области контакта поверхностей двух объектов. Также все эти виды переводят механическую энергию в тепло.
Также все эти виды переводят механическую энергию в тепло.
Причинами сил трения скольжения и покоя являются шероховатости микроскопического масштаба на поверхностях, которые трутся. Кроме того, эти виды обусловлены диполь-дипольным и другими видами взаимодействий между атомами и молекулами, которые образуют трущиеся тела.
Причина качения трения связана с гистерезисом упругой деформации, которая появляется в точке контакта катящегося объекта и поверхности.
Сила трения и коэффициент трения
Все три вида сил твердого трения описываются выражениями, имеющими одну и ту же форму. Приведем ее:
Здесь N — сила, действующая перпендикулярно поверхности на тело. Она называется реакцией опоры. Величина µ t — называется коэффициентом соответствующего вида трения.
Коэффициенты для трения скольжения и покоя являются величинами безразмерными. Это можно понять, если посмотреть на равенство силы трения и трения коэффициента. Левая часть равенства выражается в ньютонах, правая часть также выражается в ньютонах, поскольку величина N — это сила.
Что касается качения трения, то коэффициент для него тоже будет величиной безразмерной, однако он определяется в виде отношения линейной характеристики упругой деформации к радиусу катящегося объекта.
Следует сказать, что типичными значениями коэффициентов трения скольжения и покоя являются десятые доли единицы. Для этот коэффициент соответствует сотым и тысячным долям единицы.
Как находить коэффициент трения?
Коэффициент µ t зависит от ряда факторов, которые сложно учесть математически. Перечислим некоторые из них:
- материал трущихся поверхностей;
- качество обработки поверхности;
- наличие на ней грязи, воды и так далее;
- температуры поверхностей.
Поэтому формулы для µ t не существует, и его приходится измерять экспериментально. Чтобы понять, как коэффициент трения находить, следует его выразить из формулы для F t . Имеем:
Получается, что для знания µ t необходимо найти трения силу и реакцию опоры.
Соответствующий эксперимент выполняют следующим образом:
- Берут тело и плоскость, например, изготовленные из дерева.

- Цепляют динамометр к телу и равномерно перемещают его по поверхности.
При этом динамометр показывает некоторую силу, которая равна F t . равна весу тела на горизонтальной поверхности.
Описанный способ позволяет понять, чему равен коэффициент трения покоя и скольжения. Аналогичным образом можно экспериментально определить µ t качения.
Другой экспериментальный метод определения µ t приводится в форме задачи в следующем пункте.
Задача на вычисление µt
Деревянный брус находится на стеклянной поверхности. Наклоняя плавно поверхность, установили, что скольжение бруса начинается при угле наклона 15 o . Чему равен коэффициент трения покоя для пары дерево-стекло?
Когда брус находился на наклонной плоскости при 15 o , то покоя сила трения для него имела максимальное значение. Она равна:
Сила N определяется по формуле:
Применяя формулу для µ t , получаем:
µ t = F t /N = m*g*sin(α)/(m*g*cos(α)) = tg(α).
Подставляя угол α, приходим к ответу: µ t = 0,27.
Если брусок тянут с помощью динамометра с постоянной скоростью, то динамометр показывает модуль силы трения скольжения (F тр). Здесь сила упругости пружины динамометра уравновешивает силу трения скольжения.
С другой стороны, сила трения скольжения зависит от силы нормальной реакции опоры (N), которая возникает в следствие действия веса тела. Чем вес больше, тем больше сила нормальной реакции. И чем больше сила нормальной реакции, тем больше сила трения . Между этими силами существует прямая пропорциональная зависимость, которую можно выразить формулой:
Здесь μ – это коэффициент трения . Он показывает, как именно сила трения скольжения зависит от силы нормальной реакции (или, можно сказать, от веса тела), какую долю от нее составляет. Коэффициент трения — безразмерная величина. Для разных пар поверхностей μ имеет разное значение.
Так, например, деревянные предметы трутся друг о друга с коэффициентом от 0,2 до 0,5 (в зависимости от вида деревянных поверхностей). Это значит, что если сила нормальной реакции опоры 1 Н, то при движении сила трения скольжения может составить значение, лежащее в промежутке от 0,2 Н до 0,5 Н.
Это значит, что если сила нормальной реакции опоры 1 Н, то при движении сила трения скольжения может составить значение, лежащее в промежутке от 0,2 Н до 0,5 Н.
Из формулы F тр = μN следует, что зная силы трения и нормальной реакции, можно определить коэффициент трения для любых поверхностей:
Сила нормальной реакции опоры зависит от веса тела. Она равна ему по модулю, но противоположна по направлению. Вес тела (P) можно вычислить, зная массу тела. Таким образом, если не учитывать векторность величин, можно записать, что N = P = mg. Тогда коэффициент трения находится по формуле:
μ = F тр / (mg)
Например, если известно, что сила трения тела массой 5 кг, движущегося по поверхности, равна 12 Н, то можно найти коэффициент трения: μ = 12 Н / (5 кг ∙ 9,8 Н/кг) = 12 Н / 49 Н ≈ 0,245.
Коэффициент трения. Как найти силу трения Как определить коэффициент трения формула
Научно-практическая конференция
Коэффициент трения и м етоды его расчета
Пенза
2010 г.
I глава. Теоретическая часть
1. Виды трения, коэффициент трения
II глава. Практическая часть
Расчет трения покоя, скольжения, и качения
Расчет коэффициента трения покоя
Список литературы
I глава. Теоретическая часть
1. Виды трения, коэффициент трения
С трением мы сталкиваемся на каждом шагу. Вернее было бы сказать, что без трения мы и шагу ступить не можем. Но несмотря на ту большую роль, которую играет трение в нашей жизни, до сих пор не создана достаточно полная картина возникновения трения. Это связано даже не с тем, что трение имеет сложную природу, а скорее с тем, что опыты с трением очень чувствительны к обработке поверхности и поэтому трудно воспроизводимы.
Существует внешнее и внутреннее
трение (иначе называемое вязкостью ). Внешним называют такой вид трения, при котором
в местах соприкосновения твердых тел
возникают силы, затрудняющие взаимное
перемещение тел и направленные по
касательной к их поверхностям.
Внутренним трением (вязкостью) называется вид трения, состоящий в том, что при взаимном перемещении. слоев жидкости или газа между ними возникают касательные силы, препятствующие такому перемещению.
Внешнее трение подразделяют на трение покоя (статическое трение ) и кинематическое трение . Трение покоя возникает между неподвижными твердыми телами, когда какое-либо из них пытаются сдвинуть с места. Кинематическое трение существует между взаимно соприкасающимися движущимися твердыми телами. Кинематическое трение, в свою очередь, подразделяется на трение скольжения и трение качения .
В жизни человека силы трения играют важную роль. В одних случаях он их использует, а в других борется с ними. Силы трения имеют электромагнитную природу.
Если тело скользит по какой-либо поверхности, его движению препятствует сила трения скольжения.
Где N — сила реакции опоры, a μ — коэффициент трения скольжения. Коэффициент μ зависит от материала и качества обработки
соприкасающихся поверхностей и не
зависит от веса тела. Коэффициент трения
определяется опытным путем.
Коэффициент μ зависит от материала и качества обработки
соприкасающихся поверхностей и не
зависит от веса тела. Коэффициент трения
определяется опытным путем.
Сила трения скольжения всегда направлена противоположно движению тела. При изменении направления скорости изменяется и направление силы трения.
Сила трения начинает действовать на тело, когда его пытаются сдвинуть с места. Если внешняя сила F меньше произведения μN, то тело не будет сдвигаться — началу движения, как принято говорить, мешает сила трения покоя . Тело начнет движение только тогда, когда внешняя сила F превысит максимальное значение, которое может иметь сила трения покоя
Трение покоя – сила трения, препятствующая возникновению движению одного тела по поверхности другого.
II глава. Практическая часть
1. Расчет трения покоя, скольжения и качения
Основываясь
на вышесказанное, я, опытном путем,
находил силу трения покоя, скольжения
и качения. Для этого я использовал
несколько пар тел, в результате
взаимодействия которых будет возникать
сила трения, и прибор для измерения силы
– динамометр.
Для этого я использовал
несколько пар тел, в результате
взаимодействия которых будет возникать
сила трения, и прибор для измерения силы
– динамометр.
Вот следующие пары тел:
деревянный брусок в виде прямоугольного параллепипеда определенной массы и лакированный деревянный стол.
деревянный брусок в виде прямоугольного параллепипеда с меньшей чем первый массой и лакированный деревянный стол.
деревянный брусок в виде цилиндра определенной массы и лакированный деревянный стол.
деревянный брусок в виде цилиндра с меньшей чем первый массой и лакированный деревянный стол.
После того как были проведены опыты – можно было сделать следующий вывод –
Сила трения покоя, скольжения и качения определяется опытном путем.
Трение покоя:
Для 1) Fп=0.6 Н, 2) Fп=0.4 Н, 3) Fп=0.2 Н, 4) Fп=0.15 Н
Трение скольжение:
Для 1) Fс=0.52 Н, 2) Fс=0.33 Н, 3) Fс=0.15 Н, 4) Fс=0.11 Н
Трение качение:
Для
3) Fк=0. 14 Н, 4) Fк=0.08 Н
14 Н, 4) Fк=0.08 Н
Тем самым я определил опытным путем все три вида внешнего трения и получил что
Fп> Fс > Fк для одного и того же тела.
2. Расчет коэффициента трения покоя
Но в большей степени интересна не сила трения, а коэффициент трения. Как его вычислить и определить? И я нашел только два способа определения силы трения.
Первый способ: очень простой. Зная формулу и определив опытным путем и N, можно определить коэффициент трения покоя, скольжения и качения.
1) N 0,81 Н, 2) N 0,56 Н, 3) N 2,3 Н, 4) N 1,75
Коэффициент трения покоя:
= 0,74; 2) = 0,71; 3) = 0,087; 4) = 0,084;
Коэффициент трения скольжения:
= 0,64; 2) = 0,59; 3) = 0,063; 4) = 0,063
Коэффициент трения качения:
3) = 0,06; 4) = 0,055;
Сверяясь с табличными данными я подтвердил верность своих значений.
Но также очень интересен второй
способ нахождения коэффициента трения.
Но этот способ хорошо определяет коэффициент трения покоя, а для вычисления коэффициента трения скольжения и качения возникают ряд затруднений.
Описание: Тело находится с другим телом в покое. Затем конец второго тела на котором лежит первое тело начинают поднимать до тех пор пока первое тело не сдвинется с места.
= sin /cos =tg =BC/AC
На основе второго способа мной были вычислены некоторое число коэффициентов трения покоя.
Дерево по дереву:
АВ = 23,5 см; ВС = 13,5 см.
П = BC/AC = 13,5/23,5 = 0,57
2. Пенопласт по дереву:
АВ = 18,5 см; ВС = 21 см.
П = BC/AC = 21/18,5 = 1,1
3. Стекло по дереву:
АВ = 24,3 см; ВС = 11 см.
П = BC/AC = 11/24,3 = 0,45
4. Алюминий по дереву:
АВ = 25,3 см; ВС = 10,5 см.
П = BC/AC = 10,5/25,3 = 0,41
5. Сталь по дереву:
АВ = 24,6 см; ВС = 11,3 см.
П = BC/AC = 11,3/24,6 = 0,46
6. Орг. Стекло по дереву:
Орг. Стекло по дереву:
АВ = 25,1 см; ВС = 10,5 см.
П = BC/AC = 10,5/25,1 = 0,42
7. Графит по дереву:
АВ = 23 см; ВС = 14,4 см.
П = BC/AC = 14,4/23 = 0,63
8. Алюминий по картону:
АВ = 36,6 см; ВС = 17,5 см.
П = BC/AC = 17,5/36,6 = 0,48
9. Железо по пластмассе:
АВ = 27,1 см; ВС = 11,5 см.
П = BC/AC = 11,5/27,1 = 0,43
10. Орг. Стекло по пластику:
АВ = 26,4 см; ВС = 18,5 см.
П = BC/AC = 18,5/26,4 = 0,7
На основе своих расчетов и проведенных экспериментах я сделал вывод что П > C > К , что неоспоримо соответствовало теоретической базе взятой из литературы. Результаты моих вычислений не вышли за рамки табличных данных, а даже дополнили их, в результате чего я расширил табличные значения коэффициентов трений различных материалов.
Литература
1.
Крагельский И.В., Добычин М.Н., Комбалов
В.С. Основы расчетов на трение и износ.
М.: Машиностроение, 1977. 526 с.
526 с.
Фролов, К. В. (ред.): Современная трибология: Итоги и перспективы . Изд-во ЛКИ, 2008 г.
Елькин В.И.“Необычные учебные материалы по физике”. “Физика в школе” библиотека журнала, №16, 2000.
Мудрость тысячелетий. Энциклопедия. Москва, Олма – пресс, 2006.
Если брусок тянут с помощью динамометра с постоянной скоростью, то динамометр показывает модуль силы трения скольжения (F тр). Здесь сила упругости пружины динамометра уравновешивает силу трения скольжения.
С другой стороны, сила трения скольжения зависит от силы нормальной реакции опоры (N), которая возникает в следствие действия веса тела. Чем вес больше, тем больше сила нормальной реакции. И чем больше сила нормальной реакции, тем больше сила трения . Между этими силами существует прямая пропорциональная зависимость, которую можно выразить формулой:
Здесь μ – это коэффициент трения . Он показывает, как именно сила трения скольжения зависит от силы нормальной реакции (или, можно сказать, от веса тела), какую долю от нее составляет. Коэффициент трения — безразмерная величина. Для разных пар поверхностей μ имеет разное значение.
Коэффициент трения — безразмерная величина. Для разных пар поверхностей μ имеет разное значение.
Так, например, деревянные предметы трутся друг о друга с коэффициентом от 0,2 до 0,5 (в зависимости от вида деревянных поверхностей). Это значит, что если сила нормальной реакции опоры 1 Н, то при движении сила трения скольжения может составить значение, лежащее в промежутке от 0,2 Н до 0,5 Н.
Из формулы F тр = μN следует, что зная силы трения и нормальной реакции, можно определить коэффициент трения для любых поверхностей:
Сила нормальной реакции опоры зависит от веса тела. Она равна ему по модулю, но противоположна по направлению. Вес тела (P) можно вычислить, зная массу тела. Таким образом, если не учитывать векторность величин, можно записать, что N = P = mg. Тогда коэффициент трения находится по формуле:
μ = F тр / (mg)
Например, если известно, что сила трения тела массой 5 кг, движущегося по поверхности, равна 12 Н, то можно найти коэффициент трения: μ = 12 Н / (5 кг ∙ 9,8 Н/кг) = 12 Н / 49 Н ≈ 0,245.
(Занятие каникулярной школы для учащихся 8–9 кл.)
- Активизация мыслительной деятельности учащихся.
- Формирование обобщенного умения проводить физические измерения.
- Формирование обобщенного умения проводить экспериментальную проверку физических закономерностей.
- Формирование умения систематизировать полученные результаты в виде таблицы, умение делать вывод на основе эксперимента.
Организация проведения практикума: Все учащиеся принимающие участие в работе практикума делятся на группы. Каждая группа учащихся получает задание с кратким описанием работы.
По окончании выполнения работы учащимся необходимо составить отчет. Отчет состоит из таблицы, вычисления искомой величины и ее погрешности, вывода по работе.
Ход работы
I. Вступительное слово учителя:
Если положить на горизонтальную поверхность брусок и подействовать на него с
достаточной силой в горизонтальном направлении, то брусок станет двигаться.
Нетрудно убедиться, что в этом случае на брусок действуют четыре силы: в
вертикальном направлении – сила тяжести P и сила реакции опоры Q, равные по
модулю противоположные по направлению; в горизонтальном направлении – сила тяги F и
противоположная по направлению сила трения F mp .
Чтобы брусок двигался равномерно и прямолинейно, нужно, чтобы модуль силы тяги был равен модулю силы трения.
На этом основан метод измерения силы трения. Следует приложить к бруску силу тяги, которая будет поддерживать равномерное прямолинейное движение этого тела. По этой силе тяги определяют модуль силы трения.
II. Практикум.
Задание группе I.
Определите коэффициент трения скольжения при движении бруска по горизонтальной поверхности стола.
Оборудование: трибометр, деревянная линейка, деревянный бруска с тремя отверстиями; динамометр; набор грузов по механике.
Порядок выполнения работы.
- Вычислите цену деления шкалы динамометра.
- Измерьте вес бруска при помощи динамометра. Результат измерения веса запишите в таблицу.
- Измерьте силу трения скольжения бруска с грузами по столу. Для этого перемещайте брусок с грузами равномерно по столу при помощи динамометра.
- Результат измерения запишите в таблицу.

- Нагружая брусок одним, двумя и тремя грузами, измерьте в каждом случае силу трения. Данные занесите в таблицу.
- Вычислите коэффициент трения скольжения
- Определите инструментальную погрешность коэффициента трения.
- Сделайте вывод.
Легко убедиться, что в случае движения тела по горизонтальной поверхности сила нормального давления равна силе тяжести, действующей на это тело: N = P . Это позволяет вычислить коэффициент трения:
Цена деления шкалы динамометра, ц.д = 0,1 Н.
1. Определили вес бруска и груза с помощью динамометра, записали в таблицу.
2. Двигая брусок равномерно по деревянной линейке, определили силу тяги, которая равна силе трения. Записали ее значение в таблицу.
3. Определили коэффициент трения для каждого измерения силы трения, занесли их в таблицу.
4. Определили погрешность измерения для каждого значения коэффициента силы трения.
1. Коэффициент трения равен 0,2.
2. Инструментальная погрешность измерения равна 0,06.
3. Коэффициент трения скольжения при взаимном движении тела по поверхности стола
является величиной постоянной не зависящей от силы нормального давления.
2. Сравните коэффициент трения покоя, скольжения и качения. Сделайте вывод.
Оборудование: динамометр, брусок деревянный, грузы с двумя крючками – 2 шт., карандаши круглые – 2 шт.
Порядок выполнения работы.
2. Измерьте вес бруска с двумя грузами при помощи динамометра. Результат измерения веса запишите в тетрадь.
3. Измерьте максимальную силу трения покоя бруска по столу. Для этого положите брусок на стол, а на брусок два груза; к бруску прицепите динамометр и приведите брусок с грузами в движение. Запишите показания динамометра, соответствующее началу движения бруска.
4. Измерьте силу трения скольжения бруска с грузами по столу. Для этого
перемещайте брусок с грузами равномерно по столу при помощи динамометра.
Результат измерения силы запишите в тетрадь.
5. Измерьте силу трения качения бруска по столу. Для этого положите брусок с двумя грузами на два круглых карандаша и перемещайте равномерно брусок по столу при помощи динамометра. Результат измерения силы запишите в тетрадь.
6. Сделайте вывод о том, какая сила больше:
а) вес тела или максимальная сила трения покоя?
б) максимальная сила трения покоя или сила трения скольжения?
в) сила трения скольжения или сила трения качения?
7. Сравните коэффициент трения покоя, трения скольжения и трения качения.
а) Вес тела больше чем максимальная сила трения покоя.
б) Максимальная сила трения покоя больше чем сила трения скольжения.
в) Сила трения скольжения больше чем сила трения качения.
г) При неизменном весе тела, наименьшее значение коэффициент трения имеет при качении тела, а наибольшее в случае покоя.
3. Определите коэффициент трения скольжения при движении бруска вдоль
поверхности резины, нешлифованной деревянной рейки, наждачной бумаги.
Оборудование: динамометр, брусок деревянный, грузы с двумя крючками – 2 шт., отрез линолеума, деревянная нешлифованная рейка, наждачная бумага.
Порядок выполнения работы.
1. Вычислите цену деления шкалы динамометра.
2. Измерьте вес бруска при помощи динамометра. Результат измерения веса запишите
в таблицу.
3. Измерьте силу трения скольжения бруска с грузами по поверхности резины,
деревянной нешлифованной линейки и по поверхности наждачной бумаги. Для этого
перемещайте брусок с грузами равномерно по столу при помощи динамометра.
Результат измерения запишите в таблицу.
4. Вычислите коэффициент трения скольжения.
5. Сделайте вывод.
Цена деления шкалы динамометра, ц.д = 0,1 Н.
1. Сила трения:
а) зависит от рода трущихся поверхностей.
б) зависит от шероховатости трущихся поверхностей.
в) чем больше шероховатости поверхности, тем коэффициент трения больше.
2. Способы увеличения или уменьшения силы трения скольжения:
Увеличить: увеличить шероховатость трущихся поверхностей, насыпать между
трущихся поверхностей частицы (стружку, опилки, песок).
Уменьшить: шлифовка, полировка трущихся поверхностей, нанесение смазки.
Задание группе II.
Измерение коэффициент трения скольжения, используя наклонную плоскость
Оборудование : линейка деревянная от трибометра, брусок деревянный, линейка измерительная, штатив.
Порядок выполнения работы .
1. Используя штатив, закрепите линейку под углом к столу.
2. Положите брусок на закрепленную под углом деревянную линейку.
3. Меняя угол наклона линейки, найдите такой максимальный угол, при котором
брусок еще покоится.
4. Измерьте длину основания линейки и высоту подъема линейки.
5. Рассчитайте значение коэффициента трения скольжения дерева о дерево по
формуле:
6. Рассчитайте погрешность измерения.
7. Вывод.
Экспериментальные данные.
Измерили высоту подъема и длину основания линейки.
1. Коэффициент трения равен 0,3.
2. Погрешность измерения равна 0,0016.
2. Измерение коэффициента трения скольжения, через опрокидывание
бруска
Измерение коэффициента трения скольжения, через опрокидывание
бруска
Оборудование: брусок деревянный, линейка деревянная от трибометра, нить, линейка ученическая.
Порядок выполнения работы.
Теоретическое обоснование: Брусок с привязанной к длинной грани нитью поставьте торцом на горизонтальную поверхность стола и тяните за нить. Если нить закреплена невысоко над поверхностью стола, то брусок будет скользить. При определенной высоте h точки А крепления нити сила натяжения нити F опрокидывает брусок.
Условия равновесия для этого случая относительно точки – угла опрокидывания:
Fh – mga/2 = 0;
Согласно II закону Ньютона: F – Fтр = 0;
Обработка результатов.
4. Сделайте вывод.
Экспериментальный расчет.
a = 45 ± 1 мм, h = 80 ± 1 мм.
1. Коэффициент трения равен 0,28.
2. Инструментальная погрешность измерения равна 0,0098.
3. Измерение коэффициента трения скольжения с помощью карандаша.
Оборудование: карандаш, линейка деревянная от трибометра, линейка ученическая.
Порядок выполнения работы.
Теоретическое обоснование: Поставьте карандаш на стол вертикально, нажмите на него, наклоните и наблюдайте характер его падения. При небольших углах наклона к вертикали карандаш не проскальзывает относительно поверхности стола при любой величине силы, прижимающей его к столу. Проскальзывание начинается с некоторого критического угла, зависящего от силы трения.
Записываем второй закон Ньютона в проекциях на координатные оси при угле наклона, равном критическому. (Силой тяжести mg, действующей на карандаш, по сравнению с большой силой F пренебрегаем).
Обработка результатов:
1. Рассчитайте по формуле значение коэффициента трения скольжения дерева о
дерево.
2. Определите погрешность измерений.
3. Запишите полученный ответ с учетом допущенных погрешностей измерений.
4. Сделайте вывод.
Экспериментальный расчет.
1. Обработка результатов
α = 30 0 ,
µ= tgα = sina /cosa
1. Коэффициент трения равен 0,58.
III. Подведение итогов практикума:
Сила трения скольжения зависит:
а) От рода трущихся поверхностей.
б) От шероховатости трущихся поверхностей.
в) Прямо пропорционально от силы давления.
г) Коэффициент трения скольжения при взаимном движении тела по поверхности
является величиной постоянной не зависящей от силы нормального давления.
д) Чем больше шероховатости поверхности, тем коэффициент трения больше.
Скольжения: Fтр = мN, где м – коэффициент трения скольжения, N – сила реакции опоры, Н. Для тела, скользящего по горизонтальной плоскости, N = G = mg, где G — вес тела, Н; m – масса тела, кг; g – ускорение свободного падения, м/с2. Значения безразмерного коэффициента м для данной пары материалов даны в справочной . Зная массу тела и пару материалов. скользящих друг относительно друга, найдите силу трения.
скользящих друг относительно друга, найдите силу трения.
Случай 2. Рассмотрите тело, скользящее по горизонтальной поверхности и двигающееся равноускоренно. На него действуют четыре силы: сила, приводящее тело в движение, сила тяжести, сила реакции опоры, сила трения скольжения. Так как поверхность горизонтальная, сила реакции опоры и сила тяжести направлены вдоль одной прямой и уравновешивают друг друга. Перемещение описывает уравнение: Fдв — Fтр = ma; где Fдв – модуль силы, приводящей тело в движение, Н; Fтр – модуль силы трения, Н; m – масса тела, кг; a – ускорение, м/с2. Зная значения массы, ускорения тела и силы, воздействующей на него, найдите силу трения. Если эти значения не заданы прямо, посмотрите, есть ли в условии данные, из которых можно найти эти величины.
Пример задачи 1: на брусок массой 5 кг, лежащий на поверхности, воздействуют силой 10 Н. В результате брусок двигается равноускоренно и проходит 10 за 10 . Найдите силу трения скольжения.
Уравнение для движения бруска:Fдв — Fтр = ma. 2 = 0,8 м/с2. Теперь найдите силу трения: Fтр = ma = 0,8*1 = 0,8 Н.
2 = 0,8 м/с2. Теперь найдите силу трения: Fтр = ma = 0,8*1 = 0,8 Н.
Случай 4. На тело, самопроизвольно скользящее по наклонной плоскости, действуют три силы: сила тяжести (G), сила реакции опоры (N) и сила трения (Fтр). Сила тяжести может быть записана в таком виде: G = mg, Н, где m – масса тела, кг; g – ускорение свободного падения, м/с2. Поскольку эти силы направлены не вдоль одной прямой, запишите уравнение движения в векторном виде.
Сложив по правилу параллелограмма силы N и mg, вы получите результирующую силу F’. Из рисунка можно сделать выводы: N = mg*cosα; F’ = mg*sinα. Где α – угол наклона плоскости. Силу трения можно записать формулой: Fтр = м*N = м*mg*cosα. Уравнение для движения принимает вид: F’-Fтр = ma. Или: Fтр = mg*sinα-ma.
Случай 6. Тело двигается по наклонной поверхности равномерно. Значит, по второму закону Ньютона система находится в равновесии. Если скольжение самопроизвольное, движение тела подчиняется уравнению: mg*sinα = Fтр.
Если же к телу приложена дополнительная сила (F), препятствующая равноускоренному перемещению, выражение для движения имеет вид: mg*sinα–Fтр-F = 0. Отсюда найдите силу трения: Fтр = mg*sinα-F.
Отсюда найдите силу трения: Fтр = mg*sinα-F.
Определение
Силой трения называют силу, которая возникает при относительном перемещении (или попытке перемещения) тел и является результатом сопротивления движению окружающей среды или других тел.
Силы трения возникают тогда, когда соприкасающиеся тела (или их части) перемещаются относительно друг друга. При этом трение, которое появляется при относительном перемещении соприкасающихся тел, называют внешним. Трение, возникающее между частями одного сплошного тела (газ, жидкость) названо внутренним.
Сила трения – это вектор, который имеет направление вдоль касательной к трущимся поверхностям (слоям). При этом эта сила направлена в сторону противодействия относительному смещению этих поверхностей (слоев). Так, если два слоя жидкости перемещаются друг по другу, при этом движутся с различными скоростями, то сила, которая приложена к слою, перемещающемуся с большей скоростью, имеет направление в сторону, которая противоположна движению. Сила же, которая воздействует на слой, который движется с меньшей скоростью, направлена по движению.
Сила же, которая воздействует на слой, который движется с меньшей скоростью, направлена по движению.
Виды трения
Трение, которое возникает между поверхностями твердых тел, называют сухим. Оно возникает не только при скольжении поверхностей, но и при попытке вызвать перемещение поверхностей. При этом возникает сила трения покоя. Внешнее трение, которое появляется между движущимися телами, называют кинематическим.
Законы сухого трения говорят о том, что максимальная сила трения покоя и сила трения скольжения не зависят от площади поверхностей соприкосновения соприкасающихся тел, подверженных трению. Эти силы пропорциональны модулю силы нормального давления (N), которая прижимает трущиеся поверхности:
где – безразмерный коэффициент трения (покоя или скольжения).
Данный коэффициент зависит от природы и состояния поверхностей трущихся тел, например от наличия шероховатостей.
Если трение возникает как результат скольжения, то коэффициент трения является функцией скорости.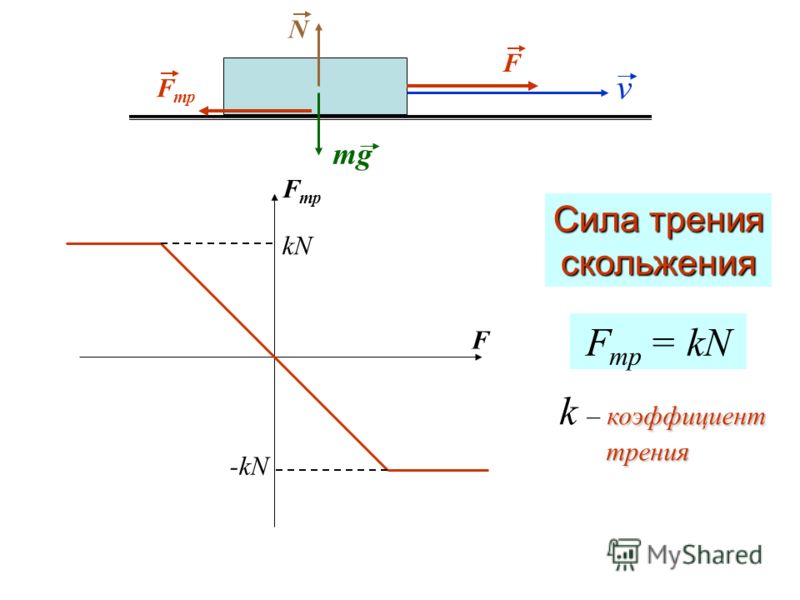 Довольно часто
вместо коэффициента трения применяют угол трения, который равен:
Довольно часто
вместо коэффициента трения применяют угол трения, который равен:
Угол равен минимальному углу наклона плоскости к горизонту, при котором тело, лежащее на этой плоскости, начинает скользить, под воздействие силы тяжести.
Более точным считают закон трения, который принимает во внимание силы притяжения между молекулами тел, которые подвергаются трению:
где S – общая площадь контакта тел, p 0 – добавочное давление, которое вызывается силами молекулярного притяжения, – истинный коэффициент трения.
Трение между твердым телом и жидкостью (или газом) называют вязким (жидким). Сила вязкого трения становится равной нулю, если скорость относительного движения тел обращается в нуль.
При движении тела в жидкости или газе появляются силы сопротивления среды, которые могут стать существенно больше, чем силы трения. Величина силы трения скольжения зависит от формы, размеров и состояния поверхности тела, скорости движения тела относительно среды, вязкости среды.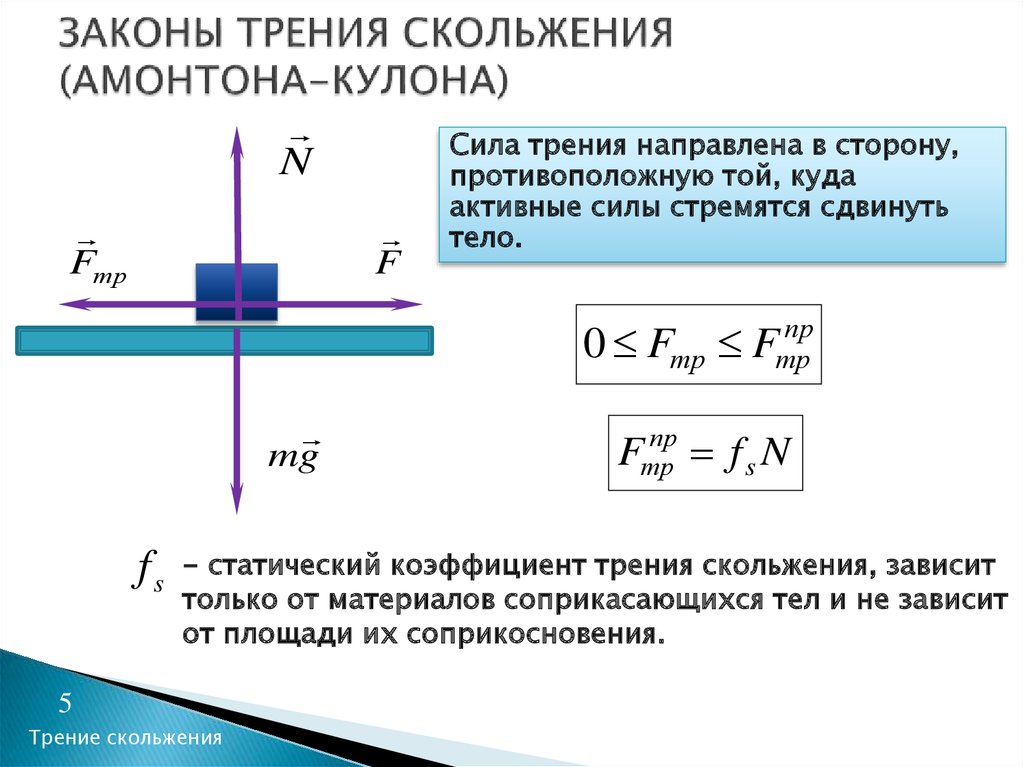 При не очень больших скоростях сила трения вычисляется при помощи формулы:
При не очень больших скоростях сила трения вычисляется при помощи формулы:
где знак минус означает, что сила трения имеет направление в сторону противоположную направлению вектора скорости. При увеличении скоростей движения тел в вязкой среде линейный закон (4) переходит в квадратичный:
Коэффициенты и существенно зависимы от формы, размеров, состояния поверхностей тел, вязкости среды.
Помимо этого выделяют трение качения.В первом приближении трение качения рассчитывают, применяя формулу:
где k – коэффициент трения качения, который имеет размерность длины и зависит от материала тел, подверженных контакту и качеств поверхностей и т.д. N – сила нормального давления, r – радиус катящегося тела.
Единицы измерения силы трения
Основной единицей измерения силы трения (как и любой другой силы) в системе СИ является: [P]=H
В СГС: [P]=дин.
Примеры решения задач
Пример
Задание. На горизонтальном диске лежит маленькое тело. Диск вращается вокруг оси,
которая проходит через его центр, перпендикулярно плоскости с угловой скоростью
. На каком расстоянии от центра диска может находиться в
состоянии равновесия тело, если коэффициент трения между диском и телом равен
?
Диск вращается вокруг оси,
которая проходит через его центр, перпендикулярно плоскости с угловой скоростью
. На каком расстоянии от центра диска может находиться в
состоянии равновесия тело, если коэффициент трения между диском и телом равен
?
Решение. Изобразим на рис.1 силы, которые будут действовать на тело, положенное на вращающийся диск.
В соответствии со вторым законом Ньютона имеем:
В проекции на ось Yиз уравнения (1.1) получим:
В проекции на ось X имеем:
где ускорение движения маленького тела равно по модуль нормальной составляющей полного ускорения. Силутрения покоя найдем как:
примем во внимание выражение (1.2), тогда имеем:
приравняем правые части выражений (1.3) и (1.5):
где маленькое тело (так как оно находится в состоянии покоя на диске) движется со скоростью, равной.
Определение коэффициентов трения качения и скольжения методом наклонного маятника — Учись Как На Парах!
Цель работы: изучение силы трения качения и трения скольжения, определение коэффициентов трения качения и трения скольжения методом наклонного маятника.
Приборы и принадлежности: лабораторная установка “Маятник наклонный” ФМ 16, набор сменных шаров и пластин для проведения эксперимента.
Общие теоретические сведения
Упругие силы, силы всемирного тяготения, а также силы притяжения и отталкивания электрически заряженных тел зависят только от конфигурации тел, то есть от их взаимного расположения, но не от их скоростей. Силы трения, помимо конфигурации, зависят ещё от относительных скоростей тел, между которыми они действуют.
Силы трения могут действовать между соприкасающимися телами или их частями как при их относительном движении, так и при их относительном покое. Трение называется Внешним, если оно действует между различными соприкасающимися телами, не образующими единого тела (например, трение между бруском и наклонной плоскостью, на которой он лежит или с которой он соскальзывает). Если же трение проявляется между различными частями одного и того же тела, например между различными слоями жидкости или газа, скорости которых непрерывно меняются от слоя к слою, то трение называется Внутренним.
Характерной особенностью внешнего трения является наличие силы трения покоя, определяемой как предельная тангенциальная сила, под действием которой начинается относительное перемещение соприкасающихся тел. Внешнее трение возникает и между перемещающимися чистыми поверхностями твёрдых тел, а также между поверхностями, покрытыми оксидными слоями.
Практически трудно получить чистые поверхности. Оставшиеся на поверхности адсорбированные поверхностно активные молекулы образуют на поверхности так называемые граничные слои, сильно влияющие на процесс трения. В этом случае внешнее трение можно назвать Граничным трением.
Внешнее трение — диссипативный процесс, сопровождающийся выделением теплоты, электризацией тел, их разрушением.
Трение между поверхностью твёрдого тела и окружающей его жидкой или газообразной средой, в которой оно движется, а также трение между различными слоями такой среды называется Вязким. Трение между поверхностями двух соприкасающихся твёрдых тел при отсутствии между ними жидкой или газообразной прослойки называется Сухим.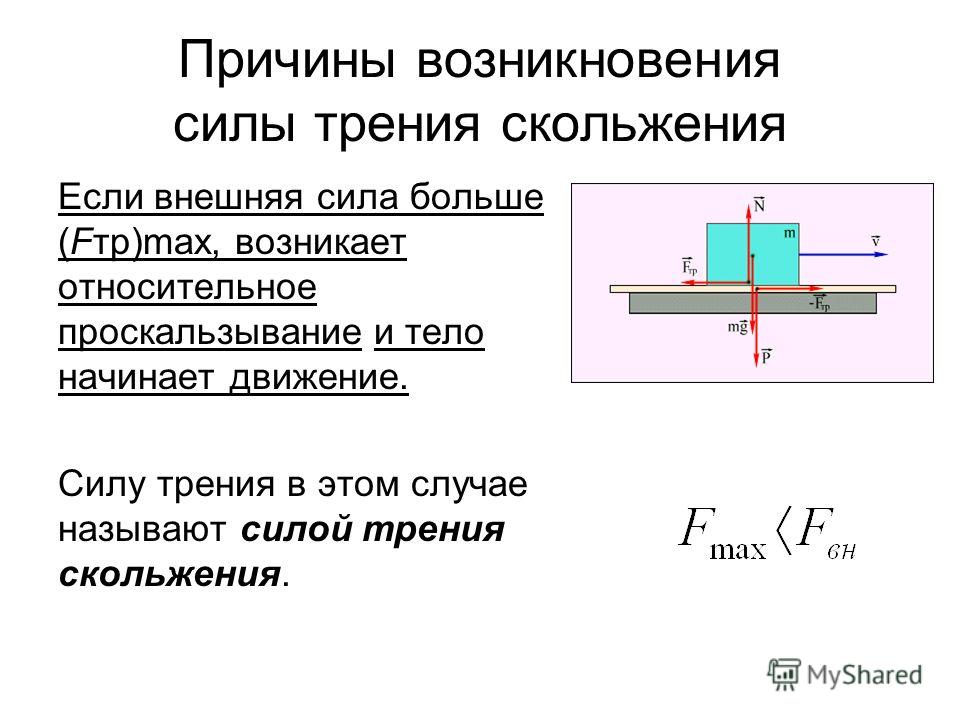 Применительно к этому случаю, когда соприкасающиеся тела движутся друг относительно друга, различают трение скольжения и трение качения.
Применительно к этому случаю, когда соприкасающиеся тела движутся друг относительно друга, различают трение скольжения и трение качения.
Рассмотрим законы сухого трения. Такое трение возникает не только при скольжении одного тела по поверхности другого, но и при всякой попытке вызвать такое скольжение. В последнем случае трение называется Трением покоя или Трением сцепления. Наличие трения покоя — характерная особенность сухого трения. В более общем смысле, безотносительно к тому, между какими телами возникает трение, оно называется Сухим, если силы трения не исчезают при обращении в нуль относительных скоростей соприкасающихся тел. В противоположном случае трение называется жидким. Положим тяжёлый брусок на поверхность горизонтального стола (см. рис. 1). В состоянии покоя вес бруска уравновешен силой нормального давления , с которой на брусок действует стол (). Приложим затем к бруску горизонтальную силу , лежащую в вертикальной плоскости, проходящей через его центр масс, как можно ближе к поверхности стола, чтобы предотвратить опрокидывание бруска, когда он придёт в движение. Опыт показывает, что если сила не превосходит некоторой определённой величины (), то брусок не приходит в движение. Отсюда следует сделать вывод, что на брусок со стороны стола действует равная и противоположно направленная сила , уравновешивающая силу . Это и есть сила трения, а именно трения покоя. Такая же сила трения, но в противоположном направлении действует на поверхность стола со стороны бруска. Сила трения покоя автоматически принимает значения, равные внешней силе . Максимальное значение силы трения покоя равно .
Опыт показывает, что если сила не превосходит некоторой определённой величины (), то брусок не приходит в движение. Отсюда следует сделать вывод, что на брусок со стороны стола действует равная и противоположно направленная сила , уравновешивающая силу . Это и есть сила трения, а именно трения покоя. Такая же сила трения, но в противоположном направлении действует на поверхность стола со стороны бруска. Сила трения покоя автоматически принимает значения, равные внешней силе . Максимальное значение силы трения покоя равно .
Сила трения Зависит от скорости . Характер этой зависимости графически изображён на рис. 2. Сила трения, приложенная к поверхности бруска, всегда действует против направления движения последнего. Как экспериментально установил Кулон, сила трения не зависит от площади поверхности, вдоль которой тела соприкасаются, и пропорциональна силе нормального давления , с которой одно тело действует на другое, то есть
. (1)
Постоянная называется Коэффициентом трения и зависит от природы и состояния трущихся деталей. Если тело действительно скользит по поверхности другого тела, то называют Коэффициентом трения скольжения. Если же тела покоятся друг относительно друга, то его называют Коэффициентом трения покоя.
Если тело действительно скользит по поверхности другого тела, то называют Коэффициентом трения скольжения. Если же тела покоятся друг относительно друга, то его называют Коэффициентом трения покоя.
При качении цилиндра (шара) всегда имеет место сила трения качения — сила, связанная с “потерями” энергии, т. е. с переходом механической энергии в тепловую. Поэтому цилиндр, катящийся без скольжения, постепенно останавливается. В этом случае сила трения качения зависит от свойств материала цилиндра (шара) и плоскости. Трение качения обусловлено взаимной деформацией тел, которая при качении без скольжения является неупругой и поэтому несимметрична относительно катящегося тела (цилиндр, шар, колесо).
Ввиду такой несимметричности деформации (рис. 3) сила реакции имеет и горизонтальную , и вертикальную составляющие, причем вертикальная составляющая силы равна силе тяжести . Точка приложения силы реакции должна находиться впереди цилиндра, а линия действия силы должна проходить выше центра масс цилиндра (рис. 3).
3).
Только в этом случае возможно качение тела без скольжения, т. е. выполняется условие , где – радиус катящегося шара или цилиндра. При этом возникающий вращательный момент сообщает телу отрицательное ускорение, что согласуется с уменьшением величины скорости .
Обозначим расстояние, соответствующее смещению точки приложения силы , через . Так как это смещение обычно очень мало по сравнению с радиусом и угол наклона мал (рис. 3), имеем
, (2)
Где — момент силы .
Расстояние и называется Коэффициентом трения качения. Коэффициент трения качения имеет размерность длины, в отличие от безразмерного коэффициента трения скольжения.
Записанное выше выражение (2) следует рассматривать как первое приближение. Теоретическое рассмотрение процесса перекатывания с учетом величин, характеризующих материал тел, скорости их движения, давления на них приводит к сложным выражениям для величины силы трения качения.
Описание лабораторной установки
Общий вид установки показан на рис. 4.
4.
Маятник наклонный включает в свой состав основание 1 со стойкой, в верхней части которой установлен верхний кронштейн 2 с платформой 3, а также маятник скольжения и маятник качения, которые устанавливаются на верхнем кронштейне 2 поочерёдно.
Платформа 3 имеет прямоугольное окно, в котором устанавливаются сменные образцы в виде пластин из латуни, стали, алюминия и фторопласта. В нижней части платформы нанесена шкала отсчёта угла 4 отклонения маятника. С помощью винта 5 платформа отклоняется от вертикального положения. Угол отклонения платформы определяется с помощью шкалы, закреплённой сзади в нижней части платформы.
Маятник скольжения представляет собой металлический стержень 6, снабжённый призматической опорой 7 и обоймой 8, в которую устанавливаются сменные образцы в виде усечённого шара.
Маятник качения представляет собой металлический шар 9, подвешенный на капроновой нити 10. Шары являются сменными. Они выполнены из алюминия, латуни и стали.
Методика эксперимента
Для исследования процесса трения в данной работе используется метод наклонного маятника.
Шар, закрепленный на металлическом стержне в обойме, может скользить по наклонной плоскости. Если шар отвести из положения равновесия (ось ОО’) На угол и затем отпустить, то он будет колебаться около положения равновесия (рис. 5, а). Из-за трения колебания будут постепенно затухать.
Пусть А — точка поворота (рис. 5, а). В этом положении стержень маятника составляет угол с осью ОО’. Если бы трения не было, то через половину периода маятник оказался бы в точке C, а угол отклонения был бы равен . Но из-за трения шар немного не дойдёт до точки С И остановится в точке В. Это и будет точка поворота. В этой точке угол стержня с осью ОО’ Будет . За половину периода угол поворота маятника уменьшился на . Точка В Расположена несколько ниже, чем точка А, и поэтому потенциальная энергия маятника в точке В Меньше, чем в точке А. Следовательно, маятник потерял высоту при перемещении из А В В.
а б
Рис.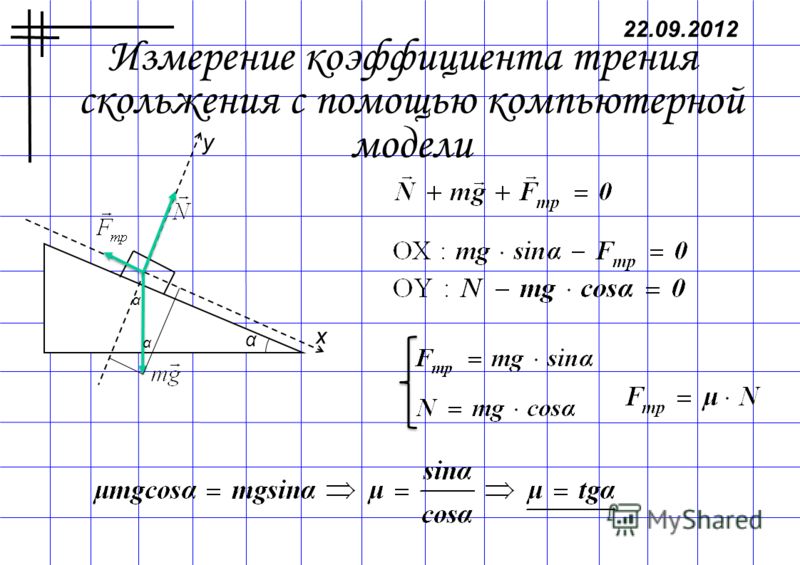 5. Метод наклонного маятника
5. Метод наклонного маятника
Найдем связь между потерей угла и потерей высоты . Для этого спроецируем точки А И В На ось ОО’ (рис. 5, б). Это будут точки А’ И В’ соответственно. Очевидно, что длина отрезка
,
Где L — длина стержня маятника, равная радиусу дуги АВ окружности. При этом угол этой дуги равен , длина дуги .
Так как ось ОО’ Наклонена под углом к горизонту, то проекция отрезка на вертикальную ось есть потеря высоты :
. (3)
При этом изменение потенциальной энергии маятника между точками А И В
, (4)
Где Т — Масса шара, G — Ускорение свободного падения.
Вычислим теперь работу силы трения.
, (5)
Где — коэффициент трения. Сила нормального давления шара на плоскость
. (6)
Тогда работа силы трения на пути между точками А И В Равна
. (7)
Так как , то из выражений (3), (4) и (7) получаем:
. (8)
(8)
Выражение (8) можно существенно упростить, если учесть, что угол очень мал. Так как , то , а
.
Тогда формулу (8) можно записать так:
,
Откуда
. (9)
Из формулы (9) видно, что потеря угла за половину периода определяется величиной и углом . Однако можно найти такие условия, при которых от угла не зависит.
Так как достаточно мало, порядка , то, рассматривая достаточно большие амплитуды так, чтобы
, (10)
Слагаемым в знаменателе формулы (9) можно пренебречь и тогда
.
С другой стороны, пусть углы будут малыми, т. е. и , тогда за половину колебания потеря угла составит:
. (11)
Заметим, что формула (11) справедлива при условии
. (12)
Поскольку , угол будет удовлетворять неравенству (12). Очевидно, что за одно полное колебание потеря угла будет , а за П Колебаний потеря угла составит
,
Откуда коэффициент трения скольжения
. (13)
Для получения выражения, определяющего коэффициент трения качения, рассмотрим процесс трения шара, закреплённого на нити и катящегося по наклонной плоскости. Если отклонить шарик из положения равновесия на угол , а затем отпустить, маятник начнёт совершать затухающие колебания. Через некоторое время, когда маятник совершит полных колебаний, угол его отклонения от положения равновесия примет значение .
Если отклонить шарик из положения равновесия на угол , а затем отпустить, маятник начнёт совершать затухающие колебания. Через некоторое время, когда маятник совершит полных колебаний, угол его отклонения от положения равновесия примет значение .
Уменьшение потенциальной энергии маятника можно определить по выражению (4), где — разность высот положения его центра тяжести относительно начального. Это изменение энергии равно работе при качении тела по плоскости
, (14)
Где — сумма всех углов отклонения шара от равновесного положения за колебаний, — вращательный момент.
В итоге получим:
. (15)
Разность высот положений маятника определяется выражением (3), а сила нормального давления шарика – формулой (6).
Сумма всех углов отклонений маятника за колебаний будет равна
, (16)
Где — расстояние, проходимое шаром при качении вдоль дуги за колебаний, — радиус шара. Учитывая, что достаточно мал, расстояния и можно определить следующим образом:
, (17)
. (18)
(18)
Выразим величину момента трения качения из (15), учитывая (3), (6), (16) — (18):
.
И окончательно:
. (19)
Выражение, стоящее в фигурных скобках в (19), есть коэффициент трения качения :
. (20)
Подготовка лабораторной установки к работе
1. Установить угол наклона платформы равным .
2. Используя маятник качения в качестве отвеса, с помощью регулировочных опор основания выставить стойку установки в строго вертикальном положении.
3. Протереть исследуемые поверхности сменных пластин, усечённые шары и шары маятника качения.
4. Установить одну из сменных пластин по указанию преподавателя на платформу 3.
5. Вставить усечённый стальной шар в обойму 8 маятника скольжения сферической поверхностью наружу. Повесить маятник скольжения с помощью призматической опоры на верхний кронштейн 2 таким образом, чтобы усечённый шар соприкоснулся с установленной на платформу пластиной и ось маятника была параллельна лицевой поверхности платформы.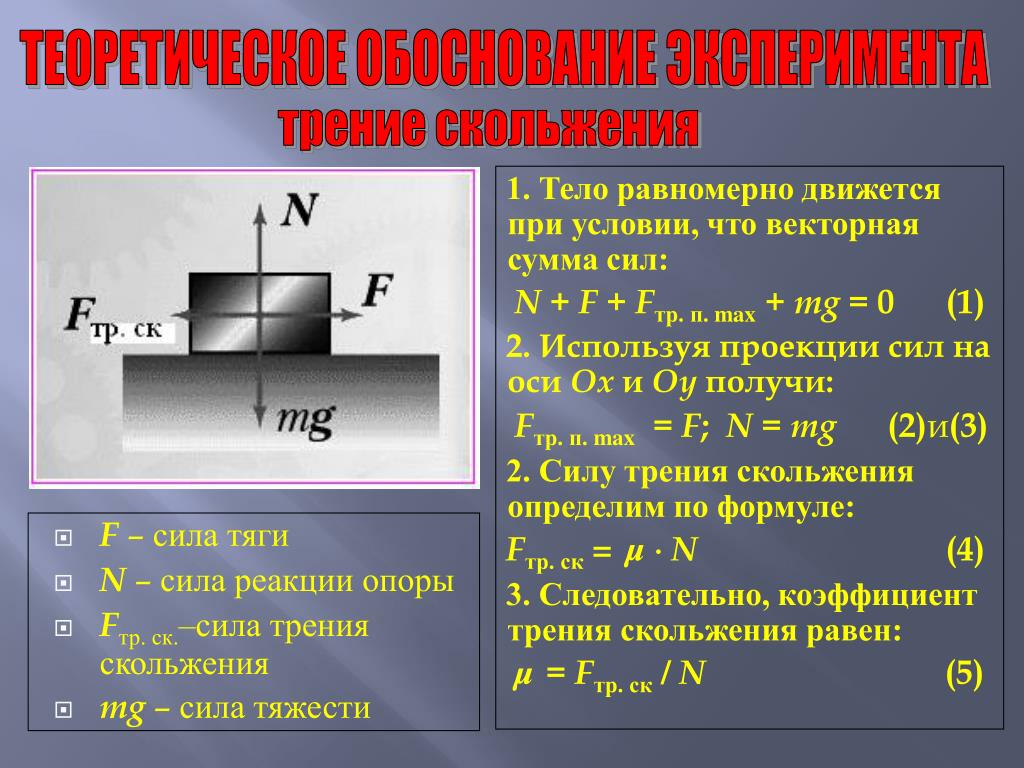 При необходимости подрегулировать положение основания так, чтобы указатель маятника оказался напротив нулевого деления шкалы отсчёта угла отклонения маятника, но без нарушения вертикального положения стойки.
При необходимости подрегулировать положение основания так, чтобы указатель маятника оказался напротив нулевого деления шкалы отсчёта угла отклонения маятника, но без нарушения вертикального положения стойки.
Порядок выполнения работы
Задание 1. Определение коэффициента трения скольжения
1. Установить наклонную плоскость в положение, соответствующее углу наклона .
2. Отвести маятник скольжения на угол , отпустить и зафиксировать угол отклонения маятника при совершении одного полного колебания . Рассчитать уменьшение угла поворота маятника и занести в табл. 1.
3. Повторить п. 2 ещё 2 раза.
4. Повторить пп. 2-3 при совершении маятником двух и трёх полных колебаний .
5. Установить наклонную плоскость в положение, соответствующее углу наклона .
6. Повторить пп. 2-4.
7. Рассчитать среднее значение уменьшения угла поворота маятника в радианах для каждого и абсолютную погрешность по формулам:
, , , ,
Где — число опытов для одного ; мин – точность определения уменьшения амплитуды колебаний маятника; — коэффициент Стьюдента ( при ).
8. Рассчитать коэффициент трения скольжения для каждого из значений и по формуле (13), подставляя значения углов в радианах. Определить среднюю величину коэффициента трения для каждого угла наклона .
.
Таблица 1
, | , | № Опыта | , | , рад | , рад | ||||
10 | 2 | 1 | 1 | ||||||
2 | |||||||||
3 | |||||||||
2 | 1 | ||||||||
2 | |||||||||
3 | |||||||||
3 | 1 | ||||||||
2 | |||||||||
3 | |||||||||
2,5 | 1 | 1 | |||||||
2 | |||||||||
3 | |||||||||
2 | 1 | ||||||||
2 | |||||||||
3 | |||||||||
3 | 1 | ||||||||
2 | |||||||||
3 |
9. Оценить погрешность расчёта коэффициента трения скольжения по формуле
Оценить погрешность расчёта коэффициента трения скольжения по формуле
,
Где , , , , , — цена деления шкалы отсчёта угла наклона платформы.
10. Результаты расчётов записать в виде
, ; , .
Задание 2. Определение коэффициента трения качения
1. Снять маятник скольжения и установить маятник качения (материал шарика и сменной пластины выбрать по указанию преподавателя).
2. Установить наклонную плоскость в положение, соответствующее углу наклона .
3. Отвести маятник качения на угол , отпустить и зафиксировать конечный угол отклонения маятника при совершении двух полных колебаний . Занести значение в табл. 2.
4. Повторить пункт 3 ещё 2 раза.
5. Повторить пп. 3-4 при совершении маятником четырёх и шести полных колебаний ().
6. Установить наклонную плоскость в положение, соответствующее углу наклона .
7. Повторить пп. 3-5.
8. Установить наклонную плоскость в положение, соответствующее углу наклона .
9. Повторить пп. 3-5.
10. Рассчитать среднее значение конечного угла отклонения маятника в радианах для каждого , а также абсолютную погрешность
, , , ,
Где мин – точность определения угла отклонения маятника.
11. Рассчитать коэффициент трения качения для каждого из значений и по соотношению (20), подставляя значения углов в радианах и учитывая, что радиус шара м. Определить среднюю величину коэффициента трения для каждого угла наклона :
.
Таблица 2
, | № опыта | , | , рад | , рад | , м | , м | , м | |
3 | 2 | 1 | ||||||
2 | ||||||||
3 | ||||||||
4 | 1 | |||||||
2 | ||||||||
3 | ||||||||
6 | 1 | |||||||
2 | ||||||||
3 | ||||||||
5 | 2 | 1 | ||||||
2 | ||||||||
3 | ||||||||
4 | 1 | |||||||
2 | ||||||||
3 | ||||||||
6 | 1 | |||||||
2 | ||||||||
3 | ||||||||
7 | 2 | 1 | ||||||
2 | ||||||||
3 | ||||||||
4 | 1 | |||||||
2 | ||||||||
3 | ||||||||
6 | 1 | |||||||
2 | ||||||||
3 |
12. Оценить погрешность расчёта коэффициента трения качения по формуле:
Оценить погрешность расчёта коэффициента трения качения по формуле:
,
Где , , .
13. Результаты расчётов записать в виде
, ; , ;
, .
Вопросы и задания для самоконтроля
1. Дать понятия внутреннего и внешнего трения.
2. Сформулировать определения сухого и вязкого трения.
3. Определить силу трения покоя и зависимость её от скорости движения тела.
4. Что называется коэффициентом трения скольжения? Его размерность?
5. Объяснить механизм возникновения силы трения качения при движении тела без проскальзывания.
6. Что называется коэффициентом трения качения? Его размерность?
7. Сущность метода наклонного маятника.
8. Вывести выражения, определяющие коэффициенты трения скольжения и качения.
Коэффициент трения шин таблица — Altarena.ru — технологии и ответы на вопросы
Содержание
- Коэффициенты трения и сцепления колеса автомобиля с покрытием
- Всё о коэффициенте сцепления шин с дорогой
- Измерение коэффициента сцепления дорожного покрытия по ГОСТ 50597-93
- Силы воздействия на участок поверхности шины во время торможения
- Коэффициенты трения покоя и скольжения
- Коэффициенты трения покоя и трения качения
- Сила трения скольжения
- Содержание
- Типы трения скольжения
- Измерение
- Таблица коэффициентов трения скольжения
- Примечания
- Видео
Коэффициенты трения и сцепления колеса автомобиля с покрытием
Реализация силы тяги Т ведущим колесом зависит от значения трения между шиной колеса и поверхностью дороги:
где фт— коэффициент трения протектора шины по дорожной поверхности; QK, — нагрузка на колесо автомобиля.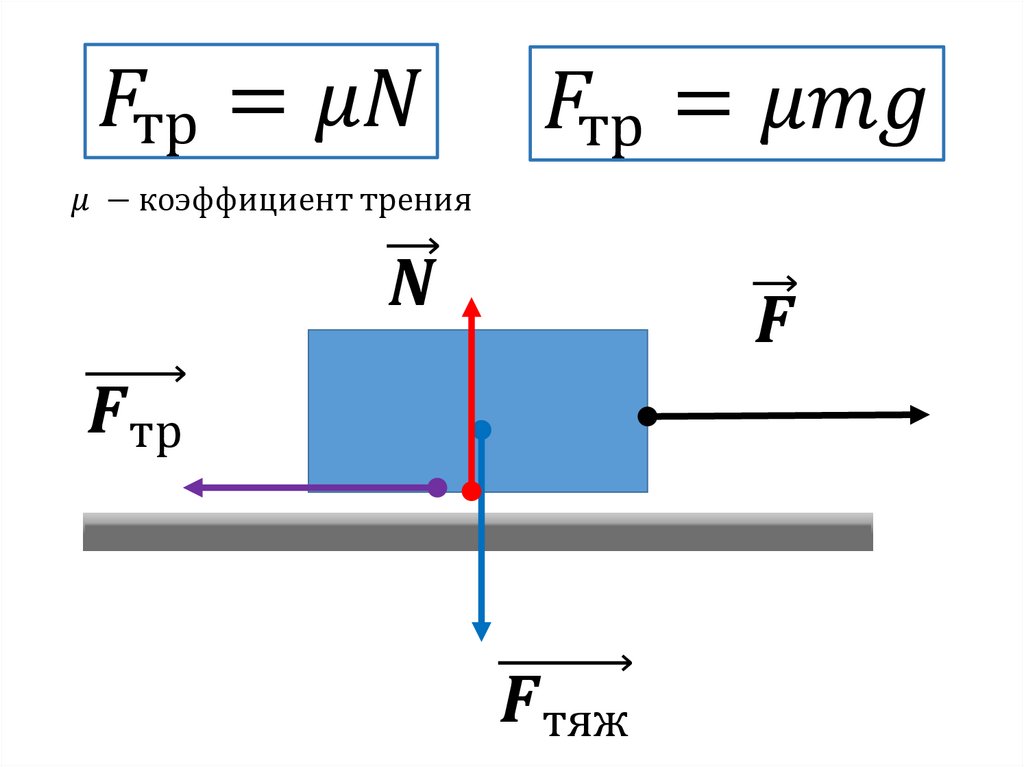
Сила трения при торможении колеса может быть определена через площадь контакта шины с покрытием:
где Т — сила трения колеса с покрытием;
S — площадь контакта колеса с покрытием;
фт — коэффициент трения протектора шины с покрытием;
Кж — коэффициент жесткости шины; рв — давление воздуха в шине.
В дорожной практике вместо понятия силы сцепления применяют понятие коэффициента сцепления:
Коэффициентом сцепления называют отношение реактивной силы, действующей на колесо автомобиля в плоскости его контакта с покрытием, к вертикальной нагрузке, передаваемой колесом на покрытие. По физической сущности коэффициент сцепления представляет собой коэффициент трения пары резина протектора автомобильной шины — покрытие проезжей части дороги.
Отличие этих довольно близких понятий состоит в соотношении адгезионной (Та) и гистерезисной (Td), или деформационной, долей, силы трения — сцепления (рис.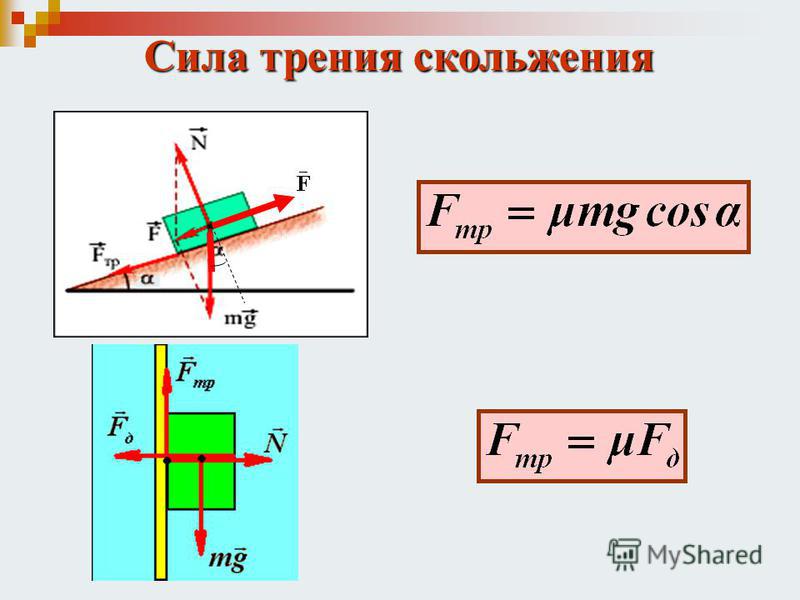 10.7).
10.7).
Рис. 10.7. Зависимость адгезионной (Та) и деформационной (Td) долей силы трения (Т) от шероховатости покрытия: а — на сухом покрытии; б — на мокром покрытии; 2 — высота выступов шероховатости
Адгезионные силы — это силы слипания (склеивания) поверхностей двух разнородных твердых тел, в данном случае поверхности шины колеса и дорожного покрытия.
Адгезионная составляющая является результатом молекулярного взаимодействия контактирующих материалов. Ее значение зависит от материала дорожного покрытия (например, асфальтобетон или цементобетон) и продолжительность контакта (т.е. скорости движения взаимодействующей пары относительно друг друга).
Деформационная составляющая формируется в результате затрат энергии на взаимную деформацию контактирующих тел выступами неровностей, находящимися на их поверхности. На сухих дорожных покрытиях сила трения в контакте шины формируется в основном за счет молекулярной составляющей. На покрытиях, имеющих на своей поверхности пленку воды, автомобильного масла или топлива, пыли, сила трения в основном формируется ее деформационной составляющей. Молекулярная составляющая появляется только после разрыва пленки смазки неровностями на поверхности контактирующих тел и вступления их в непосредственное соприкосновение.
На покрытиях, имеющих на своей поверхности пленку воды, автомобильного масла или топлива, пыли, сила трения в основном формируется ее деформационной составляющей. Молекулярная составляющая появляется только после разрыва пленки смазки неровностями на поверхности контактирующих тел и вступления их в непосредственное соприкосновение.
При скольжении одного гладкого твердого тела по другому основную роль играют адгезионные силы, т.е. собственно трение. При движении эластичной шины по дорожному покрытию характер взаимодействия меняется. Дорожная поверхность всегда имеет шероховатости и поэтому доля гистерезисной (деформационной) составляющей значительно больше, чем адгезионной. Такое взаимодействие характеризуется силой сцепления [4].
Коэффициент сцепления зависит от многих факторов:
Наибольшее влияние на коэффициент сцепления оказывают тип, ровность и состояние поверхности покрытия, а также скорость движения.
При движении автомобиля по неровной поверхности с возрастанием скорости деформация шины происходит не полностью.
Если принять коэффициент сцепления ф при высокой ровности за 100%, то при увеличении неровности покрытий Sc сцепление снижается:
Источник
Всё о коэффициенте сцепления шин с дорогой
Как шины влияют на безопасность, когда вы ведете машину по шоссе? Какие факторы помогают предотвратить занос и позволяют контролировать ваш автомобиль при повороте и остановке?
Вопросы безопасности на дорогах включают не только выбор правильной резины, но и учитывают фактор дорожного покрытия, технические характеристики транспортного средства ТС, другие факторы о которых узнаете ниже.
Измерение коэффициента сцепления дорожного покрытия по ГОСТ 50597-93
Исследования проводились динамометрическим приборомПКРС-2, результаты сведены в таблицу, где указаны виды дорожного покрытия и их состояние в зависимости от погодных и климатических условий. С момента ввода этих коэффициентов прошло много лет. Изменились технологии строительства дорог, в частности контактная поверхность дорожного покрытия. Данные таблицы надо рассматривать, как ориентировочные.
Данные таблицы надо рассматривать, как ориентировочные.
Сцепление шин с дорогой
Совершенно ясно, что эти коэффициенты не есть величина постоянная, а зависят от многих факторов:
Коэффициент сцепления между шиной и дорогой является одним из важных факторов, влияющих на безопасность дорожного движения. Состояние деформации шины различается в зависимости от силы торможения, вертикальной нагрузки на колесо.
Силы воздействия на участок поверхности шины во время торможения
Есть классическая формула в физике F =µN =µmg, которая связывает прямо пропорциональную зависимость силы трения от коэффициента сцепления контактирующих областей и прижимной силы. N равна произведению массы нагруженного колеса на ускорение свободного падения. Конечно распределение веса на переднюю ось будет больше при торможении, но эта классическая формула дает возможность понять какие факторы рассматриваются производителями шин, чтобы обеспечить безопасность автомобиля.
Зависимость тормозного пути от коэффициента сцепления шин с дорогой
Рисунок протектора колеса играет важную роль в определении трения или сопротивления скольжению. В сухих условиях на дорогах с твердым покрытием гладкая шина дает лучшую тягу, чем рифленый или узорчатый протектор, потому что имеется большая площадь контакта для создания сил трения. По этой причине резина, используемая для автогонок, имеет гладкую поверхность без рисунка протектора. К сожалению, гладкая шина развивает очень мало сцепления при влажных условиях, потому что фрикционный механизм уменьшается благодаря смазочной пленке воды между протектором и дорогой.
Рисунок канавки или каналы, по которым идет водоотвод, обеспечивает область прямого контакта между шиной и дорогой. Типовая шина дает коэффициенты сухого и влажного сцепления около 0,7 и 0,4 соответственно. Эти значения представляют собой компромисс между экстремальными значениями около 0,9 (сухих) и 0,1 (влажных), полученными с гладкой шиной.
Торможение на мокрой дороге
Когда автомобиль заторможен до жесткой остановки на сухой дороге, максимальная сила трения может быть больше, чем прочность протектора. В результате, вместо того, чтобы шина просто скользила по дороге, резина отрывается от протектора в области контакта шины и дороги. Несомненно, сопротивление протектора этому разрыву представляет собой сочетание прочности резины, канавок и щелей, составляющих дизайн протектора. Это тоже учитывают производители шин.
Сцепление шин таблица
Кроме того, размер контактной зоны очень важен в автомобильных шинах, потому что тяга является динамической, а не статической; то есть она изменяется по мере того, как колесо катится вперед. Максимальный коэффициент трения может происходить где угодно в области контакта, и чем больше площадь, тем больше вероятность максимальной тяги.
Таким образом, при одинаковой нагрузке и на одной и той же сухой поверхности более широкий профиль имеет большую площадь контакта и развивает более высокую тягу, что приводит к большей тормозной способности. Хотя некоторые специалисты считают, что большая площадь снижает давление на единицу поверхности и таким образом прижимная сила становится меньше, а потому выигрыш в тормозной способности остается под вопросом.
Хотя некоторые специалисты считают, что большая площадь снижает давление на единицу поверхности и таким образом прижимная сила становится меньше, а потому выигрыш в тормозной способности остается под вопросом.
Источник
Трением называется сопротивление, возникающее при относительном перемещении двух соприкасающихся тел в плоскости их касания. Сила сопротивления, направленная противоположно сдвигающему усилию, называется силой трения. По величине перемещения и зависимости его от приложенной силы различают:
а) силу трения движения,
б) неполную силу трения покоя и
в) полную силу трения покоя, которую обычно называют силой трения покоя.
Сила трения движения соответствует очень большим необратимым относительным перемещениям, величина которых не зависит от приложенной силы. В этом случае последняя в случае равномерного движения уравновешивается силой трения движения.
Неполная сила трения покоя соответствует очень малым частично обратимым перемещениям, величина которых пропорциональна приложенной силе. Величина перемещения, соответствующего неполной силе трения, называется предварительным смещением. Обычно визуально обнаружить предварительное смещение не удаётся, так как оно измеряется микронами. В случае предварительного смещения приложенная сила уравновешивается неполной силой трения, и тело находится в покое. Неполная сила трения зависит от приложенной силы и изменяется с увеличением последней от нуля до некоторого максимального значения, при котором она получает название силы трения покоя. В этом случае предварительное смещение переходит в относительное.
Величина перемещения, соответствующего неполной силе трения, называется предварительным смещением. Обычно визуально обнаружить предварительное смещение не удаётся, так как оно измеряется микронами. В случае предварительного смещения приложенная сила уравновешивается неполной силой трения, и тело находится в покое. Неполная сила трения зависит от приложенной силы и изменяется с увеличением последней от нуля до некоторого максимального значения, при котором она получает название силы трения покоя. В этом случае предварительное смещение переходит в относительное.
В зависимости от кинематических признаков относительного перемещения различают следующие виды трения:
а) Трение скольжения, при котором одни и те же точки одного тела приходят в соприкосновение всё с новыми и новыми точками другого тела.
б) Трение качения, при котором следующие одна за другой точки одного тела приходят в соприкосновение со следующими одна за другой точками другого тела, причём мгновенная ось вращения одного тела относительно другого проходит через одну из точек касания.
в) Трение верчения, при котором все точки, расположенные в плоскости касания двух тел, описывают концентрические окружности с центром, лежащим на оси верчения.
Трение верчения является разновидностью трения скольжения. Приведённые выше определения характеризуют трение идеальных тел; для реальных деформированных тел касание будет происходить не в точках, а в зонах. Часто один вид трения сопровождается другим: например, качение сопровождается скольжением (качение с проскальзыванием).
По признаку состояния поверхностей трущихся тел в зависимости от смазки различают:
а) Чистое трение, возникающее на фрикционных поверхностях при полном отсутствии на них посторонних примесей (жидкостей и газов в адсорбированном состоянии). br>Практически чистое трение очень трудно осуществимо; оно может быть реализовано лишь в вакууме.
б) Сухое трение, возникающее при отсутствии смазки и загрязнений между поверхностями. Часто его называют трением несмазанных поверхностей. (Термин применять не рекомендуется. )
)
в) Граничное трение, при котором поверхности разделены слоем смазки настолько незначительной толщины, что он обладает особыми свойствами, отличными от объёмных свойств смазки и зависящими от природы и состояния трущихся поверхностей. Обычные уравнения гидродинамики вязкой жидкости в этом случае неприменимы.
Пограничный слой имеет слоистое строение. Ближе к металлу располагаются более активные молекулы, которые, прикрепляясь своими активными концами к поверхности металла, образуют как бы ворс из молекул смазки.
г) Жидкостное трение, при котором поверхности полностью разделены слоем жидкости, причём внешнее давление вследствие специфичной формы зазора воспринимается слоем вязкой движущейся жидкости.
д) Полусухое трение, смешанное трение, одновременно граничное и сухое.
е) Полужидкостное трение, смешанное трение, одновременно жидкостное и граничное или жидкостное и сухое.
Как указывалось выше, на величину коэфициента трения всякой трущейся пары влияет ряд обычно не учитываемых параметров (давление, шероховатость, размер поверхности, степень загрязнённости и др. ). В связи с этим значения коэфициентов трения, предложенные данными таблицами, пригодны лишь для тех частных условий, при которых они были получены. Очевидно, что определённую таким образом величину коэфициента трения нельзя считать неизменной для данной трущейся пары.
). В связи с этим значения коэфициентов трения, предложенные данными таблицами, пригодны лишь для тех частных условий, при которых они были получены. Очевидно, что определённую таким образом величину коэфициента трения нельзя считать неизменной для данной трущейся пары.
КОЭФФИЦИЕНТЫ ТРЕНИЯ ПОКОЯ и СКОЛЬЖЕНИЯ
для ПАР МАТЕРИАЛОВ
| Комбинация материалов | Коэффициент трения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| сухие поверхности | со смазкой КОЭФФИЦИЕНТЫ ТРЕНИЯ ПРИ СЛАБОЙ СМАЗКЕ КОЭФФИЦИЕНТЫ ТРЕНИЯ СКОЛЬЖЕНИЯ ПО СТАЛИ КОЭФФИЦИЕНТЫ ТРЕНИЯ И ИЗНОСА
КОЭФФИЦИЕНТ ТРЕНИЯ КАЧЕНИЯ ТРЕНИЕ В БОЛТОВЫХ СОЕДИНЕНИЯХ КОЭФФИЦИЕНТЫ СКОЛЬЖЕНИЯ Источник Коэффициенты трения покоя и трения каченияКоэффициенты трения скольжения для различных материалов
Таблица коэффициентов трения покоя (коэффициентов сцепления) для различных пар материалов. Материал Химически чистые металл по металлу | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| совсем без окисных пленок (тщательно очищенные) | 100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| несмазанные на воздухе | 1,0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| смазанные минеральным маслом | 0,2-0,4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| смазанные растительными и животными маслами | 0,1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| медно-свинцовый несмазанный | 0,2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| медно-свинцовый смазанный минеральным маслом | 0,1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сплав Вуда, белый металл = white metall несмазанный | 0,7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сплав Вуда, белый металл смазанный минеральным маслом | 0,1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Фосфористая бронза, латунь несмазанная | 0,35 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Фосфористая бронза, латунь смазанная минеральным маслом | 0,15-0,2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сталь обычная несмазанная | 0,4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сталь обычная смазанная минеральным маслом | 0,1-0,2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Стальные поверхности высокой твердости несмазанные | 0,6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Стальное колесо по стали | 0,001-0,05 |
| Дереянное колесо по дереву | 0,05-0,08 |
| Стальное колесо по дереву | 0,15-0,25 |
| Пневматичекая шина по асфальту | 0,006-0,02 |
| Деревянное колесо по стали | 0,03-0,04 |
| Шарикоподшипник (подшипник качения) | 0,001-0,004 |
| Роликоподшипник (тоже качения) | 0,0025-0,01 |
| Шарик твердой стали по стали | 0,0005-0,001 |
Сила трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.
В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.
Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. (Это можно объяснить тем, что никакое тело не является абсолютно ровным. Поэтому истинная площадь соприкосновения гораздо меньше наблюдаемой. Кроме того, увеличивая площадь, мы уменьшаем удельное давление тел друг на друга.) Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается чаще всего латинской буквой «k» или греческой буквой «μ». Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то «k» можно считать постоянным.
В первом приближении величина силы трения скольжения может быть рассчитана по формуле:
, где
— коэффициент трения скольжения,
— сила нормальной реакции опоры.
По физике взаимодействия трение принято разделять на:
В связи со сложностью физико-химических процессов, протекающих в зоне фрикционного взаимодействия, процессы трения принципиально не поддаются описанию с помощью методов классической механики.
При механических процессах всегда происходит в большей или меньшей степени преобразование механического движения в другие формы движения материи (чаще всего в тепловую форму движения). В последнем случае взаимодействия между телами носят названия сил трения.
Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости тангенциально к поверхности соприкосновения. При этом всегда происходит нагревание взаимодействующих тел.
При этом всегда происходит нагревание взаимодействующих тел.
Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении. Силы трения возникающие при относительном перемещении различных тел, называются силами внешнего трения.
Силы трения возникают и при относительном перемещении частей одного и того же тела. Трение между слоями одного и того же тела называется внутренним трением.
В реальных движениях всегда возникают силы трения большей или меньшей величины. Поэтому при составлении уравнений движения, строго говоря, мы должны в число действующих на тело сил всегда вводить силу трения F тр.
Тело движется равномерно и прямолинейно, когда внешняя сила уравновешивает возникающую при движении силу трения.
Для измерения силы трения, действующей на тело, достаточно измерить силу, которую необходимо приложить к телу, чтобы оно двигалось без ускорения.
Источник
Сила трения скольжения
Сила трения скольжения — сила, возникающая между соприкасающимися телами при их относительном движении.
Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении.
Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости тангенциально к поверхности соприкосновения. При этом всегда в большей или меньшей степени происходит преобразование механического движения в другие формы движения материи — чаще всего в тепловую форму движения, и происходит нагревание взаимодействующих тел.
Содержание
Типы трения скольжения
Если между телами отсутствует жидкая или газообразная прослойка (смазочный материал), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.
По физике взаимодействия трение скольжения принято разделять на:
Также можно классифицировать трение по его области. Силы трения, возникающие при относительном перемещении различных тел, называются силами внешнего трения. Силы трения возникают и при относительном перемещении частей одного и того же тела. Трение между слоями одного и того же тела называется внутренним трением.
Измерение
В связи со сложностью физико-химических процессов, протекающих в зоне фрикционного взаимодействия, процессы трения принципиально не поддаются описанию с помощью методов классической механики. Поэтому нет точной формулы для коэффициента трения. Его оценка производится на основе эмпирических данных: так как по первому закону Ньютона тело движется равномерно и прямолинейно, когда внешняя сила уравновешивает возникающую при движении силу трения, то для измерения действующей на тело силы трения достаточно измерить силу, которую необходимо приложить к телу, чтобы оно двигалось без ускорения.
Таблица коэффициентов трения скольжения
Значения таблицы взяты из справочника по физике [2]
Примечания
Что такое wiki2.info Вики является главным информационным ресурсом в интернете. Она открыта для любого пользователя. Вики это библиотека, которая является общественной и многоязычной.
Основа этой страницы находится в Википедии. Текст доступен по лицензии CC BY-SA 3.0 Unported License.
Wikipedia® — зарегистрированный товарный знак организации Wikimedia Foundation, Inc. wiki2.info является независимой компанией и не аффилирована с Фондом Викимедиа (Wikimedia Foundation).
wiki2.info является независимой компанией и не аффилирована с Фондом Викимедиа (Wikimedia Foundation).
Источник
Видео
Урок 39 (осн). Сила трения. Коэффициент трения
Физика. Решение задач. Коэффициент трения. Выполнялка 23
Коэффициент трения
СИЛА ТРЕНИЯ | коэффициент трения | ДИНАМИКА
Лабораторная работа «Измерение коэффициента трения скольжения»
Коэффициент трения скольжения
Почему у широкой покрышки больше сцепления? (by Engineering Explained)
MXD-02, Прибор для определения коэффициента трения
13. Сила трения. Сила трения покоя. Сила трения скольжения. Коэффициент трения.
Сила трения (для чайников)
Как найти коэффициент кинетического трения: подробная информация и часто задаваемые вопросы – Lambda Geeks
Безразмерная физическая величина, определяющая взаимодействие двух объектов, называется коэффициентами.
Величина коэффициента кинетического трения изменяется в зависимости от природы используемого материала. Как правило, коэффициенты дают отношение двух величин, участвующих в действии. В этом посте давайте обсудим, как найти коэффициент кинетического трения и его последствия.
Как правило, коэффициенты дают отношение двух величин, участвующих в действии. В этом посте давайте обсудим, как найти коэффициент кинетического трения и его последствия.
Рассмотрим две поверхности, одна из которых движется, соприкасаясь с другой. Трение всегда сопротивляется движению и в конце концов останавливает движение поверхности в направлении, противоположном движению.
Общая формула для определения коэффициента трения представляет собой соотношение силы трения и нормальной реакции, действующей на поверхности в перпендикулярном направлении.
Изображение предоставлено: изображение Pexels из Pixabay 9.0005 Диаграмма свободного тела кинетической силы тренияПреобразовав приведенное выше выражение, мы также можем найти кинетическое трение.
Как рассчитать неопределенность коэффициента кинетического трения Неопределенность возникает из-за рассогласования осей координат по направлению движения. Наряду с нормальной силой на систему действует тангенциальная сила. Эта тангенциальная сила объясняет возникновение неопределенности коэффициента кинетического трения.
Наряду с нормальной силой на систему действует тангенциальная сила. Эта тангенциальная сила объясняет возникновение неопределенности коэффициента кинетического трения.
Значение коэффициента не измеряется непосредственно в ходе эксперимента. Его определяют путем расчета всех сил, действующих на систему, и угла наклона объекта с поверхностью.
Общее выражение для коэффициента кинетического трения имеет вид
Рассмотрим скольжение тела по плоскости. Скольжение объекта принимается за различный угол наклона объекта по плоскости для разных случаев. Затем рассчитайте коэффициент кинетического трения для всех углов.
Неопределенность из-за тангенциальной силы и перекоса Приведенное выше утверждение говорит о том, что значение коэффициента кинетического трения изменяется с изменением угла. Это отклонение связано с неопределенностью кинетического коэффициента трения. Давайте изучим, как найти коэффициент кинетического трения с неопределенностью.
Наряду с нормальной силой F N тангенциальная сила также вносит свой вклад в развитие силы трения. Это приводит к ошибке в расчете коэффициента кинетического трения. Измерение неопределенности компенсирует ошибку, возникшую во время расчета.
Нормальная сила действует вдоль оси Y, угол смещения равен β. И тангенциальная сила действует вдоль оси X со смещенным углом α. Эти нормальные и тангенциальные силы соприкасаются, и результирующая сила по осям X и Y определяется как F N cosα + F N sinα
F X = F N (µ K cosα + sinα)
Similarly for Y axis
F Y = F N cosβ – F F sin β
F Y = F N (cosβ – µ K sinβ) Путем решения равнодействующих сил неопределенность трения определяется как коэффициент. Закон «распространение неопределенности» помогает нам дать стандартное значение неопределенности трения. Он дается уравнением.
Он дается уравнением.
Где u — неопределенность данной системы.
Дифференцируя отдельные переменные, мы получаем стандартное значение неопределенности коэффициента кинетического трения.
Это дает стандартное значение неопределенности для входных сил, действующих на систему. Подставив эти значения в уравнение в частных производных, мы получим значение неопределенности.
Как рассчитать коэффициент кинетического трения без учета массыЧтобы рассчитать коэффициент кинетического трения без учета массы, рассмотрим блок, движущийся по плоской поверхности. Брусок массой m движется с ускорением a в направлении действия силы. Нормальная сила, действующая между блоком и поверхностью, равна F N , которая перпендикулярна движению блока. Мы знаем, что сила трения, действующая между блоком и поверхностью и замедляющая движение, определяется уравнением
F K = µ K F N
Согласно второму закону Ньютона сила, действующая на движущееся тело, равна массе, умноженной на ускорение.
F = m* a
На нормальную силу влияет сила тяжести, заданная как
F Н = m*g
µ K m*g
Поскольку тело движется и сила, действующая на брусок, является кинетической силой трения, закон Ньютона можно изменить следующим образом:0003
F K = m* a
Приравнивая два приведенных уравнения, получаем
Это дает значение коэффициента кинетического трения.
Часто задаваемые вопросы Дает ли расчет кинетического трения без учета массы то же значение коэффициента, что и при учете массы?Да, значение коэффициента кинетического трения с учетом или без учета массы одинаково.
Поскольку трение является величиной, не зависящей от абсолютной массы системы, масса не влияет на величину трения, участвующего в процессе. Следовательно, коэффициент кинетического трения остается неизменным независимо от массы объекта.
Влияет ли природа материала на коэффициент кинетического трения? Коэффициент кинетического трения – числовая величина, свидетельствующая о наличии силы трения между объектами.
Поскольку на трение влияет природа материала, очевидно, что его коэффициент также в значительной степени зависит от природы материала.
Что необходимо для нахождения коэффициента кинетического трения движущегося тела?Без коэффициента кинетического трения довольно сложно измерить силу, заставляющую объект тормозить его движение.
Трение всегда пропорционально нормальной перпендикулярной реакции между поверхностями. Это отношение пропорциональности определяется безразмерной величиной, называемой коэффициентом. Коэффициент кинетического трения измеряет абсолютное значение силы трения, которая останавливает движущийся объект.
Может ли значение коэффициента кинетического трения быть больше 1?Обычно значение кинетического коэффициента трения колеблется от 0 до 1. Иногда значение коэффициента превышает 1.
Если влияние силы трения больше, чем перпендикулярная реакция между двумя движущимися поверхностями, то значение коэффициента кинетического трения имеет значение больше 1. Максимальная сила трения заставляет объект ограничивать свое движение, так что коэффициент кинетического трения автоматически увеличивается пропорционально.
Максимальная сила трения заставляет объект ограничивать свое движение, так что коэффициент кинетического трения автоматически увеличивается пропорционально.
Рассеивание энергии из-за трения можно описать в терминах закона сохранения энергии.
Чем выше коэффициент кинетического трения, тем больше сила трения, чем приложенная сила. Сложная задача состоит в том, чтобы удерживать тело в движении при наличии трения. Следовательно, для удержания тела в движении требуется большое усилие. Максимальная сила, приложенная для удержания тела в движении, вызывает рассеивание кинетической энергии, выделяющееся в виде тепла.
6.2 Трение | University Physics Volume 1
Цели обучения
К концу раздела вы сможете:
- Описывать общие характеристики трения
- Перечислите различные типы трения
- Рассчитайте величину статического и кинетического трения и используйте их в задачах, связанных с законами движения Ньютона
Когда тело движется, оно оказывает сопротивление, потому что тело взаимодействует с окружающей средой. Это сопротивление есть сила трения. Трение препятствует относительному движению между соприкасающимися системами, но также позволяет нам двигаться — концепция, которая становится очевидной, если вы попытаетесь пройтись по льду. Трение — распространенная, но сложная сила, и ее поведение до сих пор полностью не изучено. Тем не менее, можно понять обстоятельства, в которых он себя ведет.
Это сопротивление есть сила трения. Трение препятствует относительному движению между соприкасающимися системами, но также позволяет нам двигаться — концепция, которая становится очевидной, если вы попытаетесь пройтись по льду. Трение — распространенная, но сложная сила, и ее поведение до сих пор полностью не изучено. Тем не менее, можно понять обстоятельства, в которых он себя ведет.
Статическое и кинетическое трение
Основное определение трения сформулировать относительно просто.
Трение
Трение – это сила, противодействующая относительному движению между контактирующими системами.
Существует несколько форм трения. Одной из самых простых характеристик трения скольжения является то, что оно параллельно контактным поверхностям между системами и всегда находится в направлении, противодействующем движению или попытке движения систем друг относительно друга. Если две системы находятся в контакте и движутся относительно друг друга, то трение между ними называется кинетическим трением. Например, трение замедляет скольжение хоккейной шайбы по льду. Когда объекты неподвижны, между ними может действовать статическое трение; статическое трение обычно больше, чем кинетическое трение между двумя объектами.
Например, трение замедляет скольжение хоккейной шайбы по льду. Когда объекты неподвижны, между ними может действовать статическое трение; статическое трение обычно больше, чем кинетическое трение между двумя объектами.
Статическое и кинетическое трение
Если две системы находятся в контакте и неподвижны друг относительно друга, то трение между ними называется трением покоя . Если две системы находятся в контакте и движутся друг относительно друга, то трение между ними называется кинетическим трением .
Представьте, например, что вы пытаетесь сдвинуть тяжелый ящик по бетонному полу — вы можете очень сильно надавить на ящик и вообще не сдвинуть его. Это означает, что статическое трение реагирует на то, что вы делаете — оно увеличивается, чтобы быть равным вашему толчку и в противоположном направлении. Если вы, наконец, нажмете достаточно сильно, ящик внезапно соскользнет и начнет двигаться. Теперь статическое трение уступает место кинетическому трению. Находясь в движении, его легче поддерживать в движении, чем было запустить, что указывает на то, что кинетическая сила трения меньше статической силы трения. Если вы добавляете массу к ящику, скажем, кладете на него коробку, вам нужно давить еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться. Кроме того, если вы смазаете бетон маслом, вам будет легче запустить ящик и поддерживать его в рабочем состоянии (как и следовало ожидать).
Находясь в движении, его легче поддерживать в движении, чем было запустить, что указывает на то, что кинетическая сила трения меньше статической силы трения. Если вы добавляете массу к ящику, скажем, кладете на него коробку, вам нужно давить еще сильнее, чтобы он начал двигаться, а также чтобы он продолжал двигаться. Кроме того, если вы смазаете бетон маслом, вам будет легче запустить ящик и поддерживать его в рабочем состоянии (как и следовало ожидать).
(рисунок) — грубое графическое изображение того, как возникает трение на границе раздела двух объектов. При ближайшем рассмотрении этих поверхностей видно, что они шероховатые. Таким образом, когда вы нажимаете, чтобы заставить объект двигаться (в данном случае ящик), вы должны поднимать объект до тех пор, пока он не сможет прыгать вместе с ударом только кончиков поверхности, отломом точек или и тем, и другим. Значительной силе можно сопротивляться трением без видимого движения. Чем сильнее прижимаются поверхности друг к другу (например, если на ящик кладут еще одну коробку), тем больше усилий требуется для их перемещения. Часть трения обусловлена силами сцепления между поверхностными молекулами двух объектов, что объясняет зависимость трения от природы веществ. Например, обувь на резиновой подошве меньше скользит, чем на кожаной. Адгезия зависит от контактирующих веществ и представляет собой сложный аспект физики поверхности. Когда объект движется, становится меньше точек соприкосновения (меньше прилипающих молекул), поэтому для удержания объекта в движении требуется меньшее усилие. При малых, но отличных от нуля скоростях трение почти не зависит от скорости.
Часть трения обусловлена силами сцепления между поверхностными молекулами двух объектов, что объясняет зависимость трения от природы веществ. Например, обувь на резиновой подошве меньше скользит, чем на кожаной. Адгезия зависит от контактирующих веществ и представляет собой сложный аспект физики поверхности. Когда объект движется, становится меньше точек соприкосновения (меньше прилипающих молекул), поэтому для удержания объекта в движении требуется меньшее усилие. При малых, но отличных от нуля скоростях трение почти не зависит от скорости.
Рисунок 6.10 Силы трения, такие как [латекс] \перемещение{\к }{f}, [/латекс] всегда препятствуют движению или попытке движения между соприкасающимися объектами. Трение возникает отчасти из-за шероховатости соприкасающихся поверхностей, как видно на увеличенном виде. Чтобы объект двигался, он должен подняться туда, где пики верхней поверхности могут перескакивать по нижней поверхности. Таким образом, сила требуется только для того, чтобы привести объект в движение. Некоторые из пиков будут сломаны, что также потребует силы для поддержания движения. На самом деле большая часть трения возникает из-за сил притяжения между молекулами, составляющими два объекта, так что даже идеально гладкие поверхности не лишены трения. (На самом деле идеально гладкие, чистые поверхности из подобных материалов будут склеиваться, образуя соединение, называемое «холодной сваркой».)
Некоторые из пиков будут сломаны, что также потребует силы для поддержания движения. На самом деле большая часть трения возникает из-за сил притяжения между молекулами, составляющими два объекта, так что даже идеально гладкие поверхности не лишены трения. (На самом деле идеально гладкие, чистые поверхности из подобных материалов будут склеиваться, образуя соединение, называемое «холодной сваркой».)
Величина силы трения имеет две формы: одна для статических ситуаций (статическое трение), другая для ситуаций, связанных с движением (кинетическое трение). Далее следует только приблизительная эмпирическая (экспериментально определенная) модель. Эти уравнения статического и кинетического трения не являются векторными уравнениями.
Величина статического трения
Величина статического трения [латекс] {f}_{\text{s}} [/латекс] равна
[латекс] {f}_{\text{s}}\le {\ mu } _ {\ text {s}} N, [/ латекс]
где [латекс] {\mu }_{\text{s}} [/латекс] — коэффициент трения покоя , и Н, — величина нормальной силы.
Символ [латекс] \le [/латекс] означает меньшее или равное , подразумевая, что максимальное значение статического трения может составлять [латекс] {\mu }_{\text{s}}N. [/latex] Статическое трение — это реактивная сила, которая увеличивается, чтобы быть равной и противоположной любой прилагаемой силе, вплоть до ее максимального предела. Когда приложенная сила превышает
[латекс] {f}_{\text{s}}\text{(max),} [/latex] объект перемещается. Таким образом,
[латекс] {f}_{\text{s}}(\text{max})={\mu }_{\text{s}}N. [/latex]
Величина кинетического трения
Величина кинетического трения [латекс] {f}_{\text{k}} [/latex] определяется выражением
[латекс] {f}_{\text {k}}={\mu }_{\text{k}}N, [/latex]
, где [latex] {\mu }_{\text{k}} [/latex] — коэффициент кинетическое трение.
Система, в которой [латекс] {f}_{\text{k}}={\mu }_{\text{k}}N [/latex], описывается как система, в которой трение ведет себя просто . Переход от статического трения к кинетическому трению показан на (рис.).
Переход от статического трения к кинетическому трению показан на (рис.).
Рисунок 6.11 (a) Сила трения [латекс] \overset{\to }{f} [/латекс] между блоком и шероховатой поверхностью противоположна направлению приложенной силы [латекс] \overset{\ до {F}. [/latex] Величина статического трения уравновешивает приложенную силу. Это показано в левой части графика (с). б) В какой-то момент величина приложенной силы больше силы кинетического трения, и брусок движется вправо. Это показано в правой части графика. в) график зависимости силы трения от приложенной силы; обратите внимание, что [латекс] {f} _ {\ text {s}} (\ text {max}) > {f} _ {\ text {k}}. [/latex] Это означает, что [латекс] {\ mu } _ {\ text {s}}> {\ mu } _ {\ text {k}}. [/латекс]
Как вы можете видеть на (Рисунок), коэффициенты кинетического трения меньше, чем их статические аналоги. Приблизительные значения [латекс] \мю [/латекс] указаны только с одной или двумя цифрами, чтобы указать приблизительное описание трения, данное двумя предыдущими уравнениями.
| Система | Статическое трение [латекс] {\mu}_{\text{s}} [/латекс] | Кинетическое трение [латекс] {\mu }_{\text{k}} [/латекс] |
|---|---|---|
| Резина на сухом бетоне | 1,0 | 0,7 |
| Резина на мокром бетоне | 0,5-0,7 | 0,3-0,5 |
| Дерево на дереве | 0,5 | 0,3 |
| Вощеная древесина на мокром снегу | 0,14 | 0,1 |
| Металл на дереве | 0,5 | 0,3 |
| Сталь по стали (сухая) | 0,6 | 0,3 |
| Сталь по стали (промасленный) | 0,05 | 0,03 |
| Тефлон на стали | 0,04 | 0,04 |
| Кость, смазанная синовиальной жидкостью | 0,016 | 0,015 |
| Обувь на дереве | 0,9 | 0,7 |
| Обувь на льду | 0,1 | 0,05 |
| Лед на льду | 0,1 | 0,03 |
| Сталь на льду | 0,4 | 0,02 |
(Рисунок) и (Рисунок) включают зависимость трения от материалов и нормальную силу. Направление трения всегда противоположно движению, параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с усилием, параллельным полу), имеет массу 100 кг, то нормальная сила равна его весу, 9{2})=980\,\text{N,} [/latex]
Направление трения всегда противоположно движению, параллельно поверхности между объектами и перпендикулярно нормальной силе. Например, если ящик, который вы пытаетесь толкнуть (с усилием, параллельным полу), имеет массу 100 кг, то нормальная сила равна его весу, 9{2})=980\,\text{N,} [/latex]
перпендикулярно полу. Если коэффициент статического трения равен 0,45, вам придется приложить параллельно полу силу, превышающую
[латекс] {f} _ {\ text {s}} (\ text {max}) = {\ mu } _{\text{s}}N=(0,45)(980\,\text{N})=440\,\text{N} [/latex]
, чтобы переместить ящик. Когда есть движение, трение меньше, а коэффициент кинетического трения может быть 0,30, так что сила всего
[латекс] {f} _ {\ text {k}} = {\ mu } _ {\ text { к}}N=(0,30)(980\,\text{N})=290\,\text{N} [/latex]
поддерживает его движение с постоянной скоростью. Если пол смазан, оба коэффициента значительно меньше, чем без смазки. Коэффициент трения представляет собой безразмерную величину, величина которой обычно находится в диапазоне от 0 до 1,0. Фактическое значение зависит от двух соприкасающихся поверхностей.
Фактическое значение зависит от двух соприкасающихся поверхностей.
Многие люди испытывают скользкость при ходьбе по льду. Однако многие части тела, особенно суставы, имеют гораздо меньший коэффициент трения — часто в три-четыре раза меньше, чем лед. Сустав образован концами двух костей, которые соединены толстыми тканями. Коленный сустав образован костью голени (голенью) и бедренной костью (бедренной костью). Тазобедренный сустав представляет собой шаровидный (на конце бедренной кости) и впадинный (часть таза) сустав. Концы костей в суставе покрыты хрящом, что обеспечивает гладкую, почти стекловидную поверхность. Суставы также вырабатывают жидкость (синовиальную жидкость), которая уменьшает трение и износ. Поврежденный или пораженный артритом сустав можно заменить искусственный сустав ((Рисунок)). Эти заменители могут быть изготовлены из металлов (нержавеющая сталь или титан) или пластмассы (полиэтилен), также с очень низкими коэффициентами трения.
Рисунок 6. 12 Искусственная замена коленного сустава — это процедура, которая проводится уже более 20 лет. Эти послеоперационные рентгеновские снимки показывают замену правого коленного сустава. (кредит: Майк Бэрд)
12 Искусственная замена коленного сустава — это процедура, которая проводится уже более 20 лет. Эти послеоперационные рентгеновские снимки показывают замену правого коленного сустава. (кредит: Майк Бэрд)
Натуральные смазки включают слюну, вырабатываемую во рту, чтобы помочь в процессе глотания, и скользкую слизь, находящуюся между органами в теле, позволяющую им свободно перемещаться друг мимо друга во время сердцебиения, во время дыхания и когда человек движется. Больницы и врачебные кабинеты обычно используют искусственные смазки, такие как гели, для уменьшения трения.
Приведенные уравнения статического и кинетического трения представляют собой эмпирические законы, описывающие поведение сил трения. Хотя эти формулы очень полезны для практических целей, они не имеют статуса математических утверждений, представляющих общие принципы (например, второй закон Ньютона). Фактически, есть случаи, для которых эти уравнения не являются даже хорошими приближениями. Например, ни одна из формул не является точной для смазанных поверхностей или для двух поверхностей, расположенных параллельно друг другу на высоких скоростях. Если не указано иное, мы не будем касаться этих исключений.
Если не указано иное, мы не будем касаться этих исключений.
Пример
Статическое и кинетическое трение
Ящик весом 20,0 кг покоится на полу, как показано на (Рисунок). Коэффициент статического трения между ящиком и полом равен 0,700, а коэффициент кинетического трения равен 0,600. К ящику приложена горизонтальная сила [латекс] \overset{\to }{P} [/латекс]. Найдите силу трения, если (a) [латекс] \overset{\to }{P}=20,0\,\text{N,} [/latex] (b) [латекс] \overset{\to }{P} = 30,0 \, \ text {N,} [/ латекс] (c) [латекс] \ overset {\ to {P} = 120,0 \, \ text {N,} [/ латекс] и (d) [латекс] \overset{\to}}{P}=180,0\,\text{N}\text{.} [/latex]
Рис. 6.13 (a) Ящик на горизонтальной поверхности толкают с силой [латекс] \overset{\to }{P}. [/latex] (b) Силы, действующие на ящик. Здесь [латекс] \overset{\to }{f} [/латекс] может представлять либо статическую, либо кинетическую силу трения.
Стратегия
Схема свободного тела ящика показана на (Рисунок)(b). Применим второй закон Ньютона в горизонтальном и вертикальном направлениях, включая силу трения против направления движения ящика.
Применим второй закон Ньютона в горизонтальном и вертикальном направлениях, включая силу трения против направления движения ящика.
Решение
Второй закон Ньютона дает
[латекс] \begin{array}{cccc}\sum {F}_{x}=m{a}_{x}\hfill & & & \sum { F}_{y}=m{a}_{y}\hfill \\ P-f=m{a}_{x}\hfill & & & N-w=0.\hfill \end{array} [/latex]
Здесь мы используем символ f для обозначения силы трения, поскольку мы еще не определили, подвергается ли ящик трению на станции или кинетическому трению. Мы делаем это всякий раз, когда не уверены, какой тип трения действует. Теперь вес ящика 9{2})=196\,\text{N,} [/latex]
, что также равно N . Таким образом, максимальная сила статического трения составляет [латекс] (0,700)(196\,\text{N})=137\,\text{N}\text{.} [/latex] Пока [латекс] \overset {\to }{P} [/latex] меньше 137 Н, сила статического трения удерживает ящик в неподвижном состоянии и [латекс] {f}_{\text{s}}=\overset{\to }{P }. [/latex] Таким образом, (a) [латекс] {f}_{s}=20,0\,\text{N,} [/latex] (b) [латекс] {f}_{s}=30,0\, \text{N,} [/latex] и (c) [латекс] {f}_{s}=120,0\,\text{N}\text{. {2}\text{.} [/латекс]
{2}\text{.} [/латекс]
Значение
Этот пример иллюстрирует, как мы рассматриваем трение в задаче динамики. Обратите внимание, что статическое трение имеет значение, соответствующее приложенной силе, пока мы не достигнем максимального значения статического трения. Кроме того, движение не может произойти, пока приложенная сила не сравняется с силой статического трения, но тогда сила кинетического трения станет меньше.
Проверьте свои знания
Брусок массой 1,0 кг лежит на горизонтальной поверхности. Коэффициенты трения для блока и поверхности составляют [латекс] {\ mu } _ {s} = 0,50 [/латекс] и [латекс] {\ mu } _ {k} = 0,40. [/latex] (а) Какова минимальная горизонтальная сила, необходимая для перемещения блока? б) Каково ускорение бруска под действием этой силы?
Показать решение
Трение и наклонная плоскость
Одной из ситуаций, когда трение играет очевидную роль, является объект на склоне. Это может быть ящик, поднимаемый по пандусу к погрузочной площадке, или скейтбордист, спускающийся с горы, но основная физика остается той же. Обычно мы обобщаем наклонную поверхность и называем ее наклонной плоскостью , но затем делаем вид, что поверхность плоская. Рассмотрим пример анализа движения по наклонной плоскости с учетом трения.
Обычно мы обобщаем наклонную поверхность и называем ее наклонной плоскостью , но затем делаем вид, что поверхность плоская. Рассмотрим пример анализа движения по наклонной плоскости с учетом трения.
Пример
Горнолыжник
Лыжник массой 62 кг скользит по заснеженному склону с постоянной скоростью. Найдите коэффициент кинетического трения для лыжника, если известно, что трение равно 45,0 Н.
Стратегия
Величина кинетического трения равна 45,0 Н. Кинетическое трение связано с нормальной силой [латекс] Н [/латекс] by [латекс] {f}_{\text{k}}={\mu}_{\text{k}}N [/latex]; таким образом, мы можем найти коэффициент кинетического трения, если мы можем найти нормальную силу, действующую на лыжника. Нормальная сила всегда перпендикулярна поверхности, а поскольку движение перпендикулярно поверхности отсутствует, нормальная сила должна равняться составляющей веса лыжника, перпендикулярной склону. (См. (Рисунок), который повторяет рисунок из главы о законах движения Ньютона. )
)
Рис. 6.14 Движение лыжника и трение параллельны склону, поэтому удобнее всего проецировать все силы на систему координат, где одна ось параллельна склону, а другая перпендикулярна (оси показаны слева лыжника). Нормальная сила [латекс] \overset{\to }{N} [/latex] перпендикулярна склону, а сила трения [латекс] \overset{\to }{f} [/latex] параллельна наклону, но вес лыжника [латекс] \overset{\to }{w} [/latex] имеет компоненты по обеим осям, а именно [латекс] {\overset{\to }{w}}_{y} [/latex] и [ латекс] {\ overset {\ to} {w}} _ {x}. [/latex] Нормальная сила [латекс] \overset{\to }{N} [/latex] равна по модулю [латекс] {\overset{\to }{w}}_{y}, [/latex ], поэтому движение перпендикулярно склону отсутствует. Однако [латекс] \overset{\to }{f} [/latex] меньше, чем [латекс] {\overset{\to }{w}}_{x} [/latex] по величине, так что есть ускорение вниз по склону (вдоль оси x).
У нас есть
[латекс] N={w}_{y}=w\,\text{cos}\,25\text{°}=mg\,\text{cos}\,25\text{ °}. [/latex]
[/latex]
Подставив это в наше выражение для кинетического трения, мы получим
[латекс] {f}_{\text{k}}={\mu}_{\text{k}}мг\,\ text{cos}\,25\text{°}, [/latex]
, который теперь может быть решен для коэффициента кинетического трения [латекс] {\mu}_{\text{k}}. [/latex]
Решение
Решение для [латекс] {\mu }_{\text{k}} [/latex] дает
[латекс] {\mu }_{\text{k}}=\ frac {{f} _ {\ text {k}}} {N} = \ frac {{f} _ {\ text {k}}} {w \, \ text {cos} \, 25 \ text {°} }=\frac{{f}_{\text{k}}}{мг\,\text{cos}\,25\text{°}}. [/латекс] 9{2})(0,906)}=0,082. [/latex]
Значимость
Этот результат немного меньше, чем коэффициент, указанный на (Рисунок) для вощеной древесины на снегу, но все же разумен, так как значения коэффициентов трения могут сильно различаться. В подобных ситуациях, когда объект массой 90 262 м 90 263 скользит вниз по склону, образующему угол [латекс] \тета [/латекс] с горизонтом, трение определяется как [латекс] {f} _ {\ text {k }} = {\ mu } _ {\ text {k}} мг \, \ text {cos} \, \ theta . [/latex] В этих условиях все объекты скользят вниз по склону с постоянным ускорением.
[/latex] В этих условиях все объекты скользят вниз по склону с постоянным ускорением.
Мы обсуждали, что когда объект лежит на горизонтальной поверхности, нормальная сила, поддерживающая его, равна по величине его весу. Кроме того, простое трение всегда пропорционально нормальной силе. Когда предмет находится не на горизонтальной поверхности, как при наклонной плоскости, мы должны найти силу, действующую на предмет, которая направлена перпендикулярно поверхности; это составляющая веса.
Теперь выведем полезное соотношение для расчета коэффициента трения на наклонной плоскости. Обратите внимание, что результат применим только к ситуациям, в которых объект скользит с постоянной скоростью вниз по пандусу.
Объект скользит по наклонной плоскости с постоянной скоростью, если результирующая сила, действующая на объект, равна нулю. Мы можем использовать этот факт для измерения коэффициента кинетического трения между двумя объектами. Как показано на (рис.), кинетическое трение на склоне составляет [латекс] {f}_{k}={\mu }_{k}mg\,\text{cos}\,\theta [/latex]. Компонент веса вниз по склону равен [латекс] мг\,\текст{sin}\,\тета [/латекс] (см. диаграмму свободного тела на (рис.)). Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Записывая это,
Компонент веса вниз по склону равен [латекс] мг\,\текст{sin}\,\тета [/латекс] (см. диаграмму свободного тела на (рис.)). Эти силы действуют в противоположных направлениях, поэтому, когда они имеют одинаковую величину, ускорение равно нулю. Записывая это,
[латекс] {\ mu } _ {\ text {k}} мг \, \ text {cos} \, \ theta = mg \, \ text {sin} \, \ theta . [/latex]
Решая для [латекс] {\ mu } _ {\ text {k}}, [/latex] находим, что
[латекс] {\ mu } _ {\ text {k}} =\ frac{mg\,\text{sin}\,\theta }{mg\,\text{cos}\,\theta }=\text{tan}\,\theta . [/latex]
Положите монету на книгу и наклоняйте ее, пока монета не будет скользить по книге с постоянной скоростью. Возможно, вам придется слегка постучать по книге, чтобы заставить монету двигаться. Измерьте угол наклона относительно горизонтали и найдите [латекс] {\mu }_{\text{k}}. [/latex] Обратите внимание, что монета вообще не начинает скользить до тех пор, пока не будет достигнут угол, больший, чем [латекс]\тета [/латекс], поскольку коэффициент статического трения больше, чем коэффициент кинетического трения. Подумайте, как это может повлиять на значение [латекс] {\mu }_{\text{k}} [/латекс] и его неопределенность.
Подумайте, как это может повлиять на значение [латекс] {\mu }_{\text{k}} [/латекс] и его неопределенность.
Объяснение трения в атомном масштабе
До сих пор рассматривались более простые аспекты трения, связанные с его макроскопическими (крупномасштабными) характеристиками. За последние несколько десятилетий были достигнуты большие успехи в объяснении трения на атомном уровне. Исследователи обнаружили, что атомарная природа трения, по-видимому, имеет несколько фундаментальных характеристик. Эти характеристики не только объясняют некоторые из более простых аспектов трения, они также несут в себе потенциал для разработки сред, почти свободных от трения, которые могли бы сэкономить сотни миллиардов долларов энергии, которая в настоящее время преобразуется (без необходимости) в тепло.
(рисунок) иллюстрирует одну макроскопическую характеристику трения, которая объясняется микроскопическими (мелкомасштабными) исследованиями. Мы заметили, что трение пропорционально нормальной силе, но не площади контакта, что несколько противоречит здравому смыслу. Когда соприкасаются две шероховатые поверхности, фактическая площадь контакта составляет ничтожную долю от общей площади, потому что соприкасаются только выступающие точки. Когда действует большая нормальная сила, фактическая площадь контакта увеличивается, и мы обнаруживаем, что трение пропорционально этой площади.
Когда соприкасаются две шероховатые поверхности, фактическая площадь контакта составляет ничтожную долю от общей площади, потому что соприкасаются только выступающие точки. Когда действует большая нормальная сила, фактическая площадь контакта увеличивается, и мы обнаруживаем, что трение пропорционально этой площади.
Рисунок 6.15 Две соприкасающиеся шероховатые поверхности имеют гораздо меньшую площадь фактического контакта, чем их общая площадь. Когда нормальная сила больше в результате большей приложенной силы, площадь фактического контакта увеличивается, как и трение.
Однако представление в атомном масштабе обещает объяснить гораздо больше, чем простые особенности трения. В настоящее время определяется механизм образования тепла. Другими словами, почему поверхности нагреваются при трении? По сути, атомы связаны друг с другом, образуя решетки. Когда поверхности трутся, поверхностные атомы прилипают и вызывают вибрацию атомных решеток, по существу создавая звуковые волны, которые проникают в материал. Звуковые волны уменьшаются с расстоянием, и их энергия преобразуется в тепло. Химические реакции, связанные с фрикционным износом, также могут происходить между атомами и молекулами на поверхностях. (Рисунок) показывает, как кончик зонда, проведенного по другому материалу, деформируется за счет трения атомного масштаба. Сила, необходимая для перетаскивания наконечника, может быть измерена и связана с 9{12} [/latex]) и трудно поддающееся теоретическому прогнозированию, но касательное напряжение дает фундаментальное понимание масштабного явления, известного с древних времен, — трения.
Звуковые волны уменьшаются с расстоянием, и их энергия преобразуется в тепло. Химические реакции, связанные с фрикционным износом, также могут происходить между атомами и молекулами на поверхностях. (Рисунок) показывает, как кончик зонда, проведенного по другому материалу, деформируется за счет трения атомного масштаба. Сила, необходимая для перетаскивания наконечника, может быть измерена и связана с 9{12} [/latex]) и трудно поддающееся теоретическому прогнозированию, но касательное напряжение дает фундаментальное понимание масштабного явления, известного с древних времен, — трения.
Рис. 6.16 Наконечник зонда деформируется вбок под действием силы трения, когда зонд тащит по поверхности. Измерения того, как сила меняется для разных материалов, дают фундаментальное представление об атомной природе трения.
Описать модель трения на молекулярном уровне. Описывать материю с точки зрения молекулярного движения. Описание должно включать диаграммы для поддержки описания; как температура влияет на изображение; каковы различия и сходства между движением твердых, жидких и газообразных частиц; и как размер и скорость молекул газа соотносятся с повседневными объектами.
Пример
Скользящие блоки
Два блока (рисунок) прикреплены друг к другу безмассовой нитью, которая намотана на блок без трения. Когда нижний блок массой 4,00 кг тянет влево под действием постоянной силы [латекс] \overset{\to }{P}, [/латекс] верхний блок массой 2,00 кг скользит по нему вправо. Найдите величину силы, необходимой для перемещения блоков с постоянной скоростью. Предположим, что коэффициент кинетического трения между всеми поверхностями равен 0,400.
Рис. 6.17 (a) Каждый блок движется с постоянной скоростью. (b) Диаграммы свободного тела для блоков.
Стратегия
Анализируем движения двух блоков по отдельности. На верхний блок действует контактная сила, создаваемая нижним блоком. Составляющими этой силы являются нормальная сила [латекс] {N}_{1} [/латекс] и сила трения [латекс] -0,400{Н}_{1}. [/latex] Другими силами, воздействующими на верхний блок, являются натяжение [латекс] T\text{i} [/latex] в струне и вес самого верхнего блока, 19. 6 Н. На нижний блок действуют контактные усилия верхнего блока и пола. Первая контактная сила имеет компоненты [латекс] \text{−}{N}_{1} [/latex] и [латекс] 0,400{N}_{1}, [/latex] которые представляют собой просто силы реакции на контакт сила, с которой нижний блок действует на верхний блок. Составляющими контактной силы пола являются [латекс] {N}_{2} [/латекс] и [латекс] 0,400{N}_{2}. [/latex] Другими силами, воздействующими на этот блок, являются [латекс] \text{−}P, [/latex] натяжение [латекс] T\text{i}, [/latex] и вес –39.2 N.
6 Н. На нижний блок действуют контактные усилия верхнего блока и пола. Первая контактная сила имеет компоненты [латекс] \text{−}{N}_{1} [/latex] и [латекс] 0,400{N}_{1}, [/latex] которые представляют собой просто силы реакции на контакт сила, с которой нижний блок действует на верхний блок. Составляющими контактной силы пола являются [латекс] {N}_{2} [/латекс] и [латекс] 0,400{N}_{2}. [/latex] Другими силами, воздействующими на этот блок, являются [латекс] \text{−}P, [/latex] натяжение [латекс] T\text{i}, [/latex] и вес –39.2 N.
Решение
Поскольку верхний блок движется горизонтально вправо с постоянной скоростью, его ускорение равно нулю как в горизонтальном, так и в вертикальном направлениях. Из второго закона Ньютона
[латекс] \begin{array}{cccccccc}\hfill \sum {F}_{x}& =\hfill & {m}_{1}{a}_{x}\hfill & & & \hfill \sum {F}_{y}& =\hfill & {m}_{1}{a}_{y}\hfill \\ \hfill T-0.400{N}_{1}& =\hfill & 0\hfill & & & \hfill {N}_{1}-19.6\,\text{N}& =\hfill & 0.\hfill \end{массив} [/latex]
Решая два неизвестных, получаем [латекс] {N}_{1}=19,6\,\text{N} [/латекс] и [латекс] T=0,40{N}_{1}=7,84\ ,\text{N}\text{. } [/latex] Нижний блок тоже не ускоряется, поэтому применение второго закона Ньютона к этому блоку дает
} [/latex] Нижний блок тоже не ускоряется, поэтому применение второго закона Ньютона к этому блоку дает
[латекс] \begin{array}{cccc}\sum { F}_{x}={m}_{2}{a}_{x}\hfill & & & \sum {F}_{y}={m}_{2}{a}_{y} \hfill \\ T-P+0,400\,{N}_{1}+0,400\,{N}_{2}=0\hfill & & & {N}_{2}-39,2\,\text{ N}-{N}_{1}=0.\hfill \end{массив} [/latex]
Значения [латекс] {N}_{1} [/латекс] и T были найдены с помощью первого набора уравнений. Когда эти значения подставляются во второй набор уравнений, мы можем определить [латекс] {N}_{2} [/латекс] и P . Они
[латекс] {N}_{2}=58,8\,\text{N}\enspace\text{и}\enspaceP=39,2\,\text{N}\text{.} [/latex]
Значение
Понимание того, в каком направлении направить силу трения, часто бывает затруднительным. Обратите внимание, что каждая сила трения, отмеченная на (рис.), действует в направлении, противоположном движению соответствующего блока.
Пример
Ящик на разгоняющемся грузовике
Ящик весом 50,0 кг стоит на кузове грузовика, как показано на (Рисунок). Коэффициенты трения между поверхностями равны [латекс] {\ mu } _ {\ text {k}} = 0,300 [/latex] и [латекс] {\ mu } _ {\ text {s}} = 0,400. [/latex] Найдите силу трения на ящике, когда грузовик ускоряется вперед относительно земли со скоростью (a) 2,00 м/с 2 и (b) 5,00 м/с 2 .
Коэффициенты трения между поверхностями равны [латекс] {\ mu } _ {\ text {k}} = 0,300 [/latex] и [латекс] {\ mu } _ {\ text {s}} = 0,400. [/latex] Найдите силу трения на ящике, когда грузовик ускоряется вперед относительно земли со скоростью (a) 2,00 м/с 2 и (b) 5,00 м/с 2 .
Рисунок 6.18 (a) Ящик лежит на платформе грузовика, который ускоряется вперед. (b) Диаграмма свободного тела ящика.
Стратегия
Силы, действующие на ящик, включают его вес, а также нормальные силы и силы трения, связанные с контактом с кузовом грузовика. Начнем с , предполагая , что ящик не скользит. В этом случае на обрешетку действует статическая сила трения [латекс] {f}_{\text{s}} [/латекс]. Кроме того, ускорения ящика и грузовика равны.
Решение
- Применение второго закона Ньютона к ящику с использованием системы отсчета, прикрепленной к земле, дает
9{0} [/latex] по горизонтали. Коэффициент кинетического трения между доской и снегом равен [латекс] {\mu }_{\text{k}}=0,20.
 [/latex] Каково ускорение сноубордиста?
[/latex] Каково ускорение сноубордиста?Рис. 6.19 (a) Сноубордист скользит вниз по склону, наклоненному под углом 13° к горизонтали. (b) Диаграмма свободного тела сноубордиста.
Стратегия
Силами, действующими на сноубордиста, являются его вес и контактная сила склона, которая имеет составляющую по нормали к склону и составляющую вдоль склона (сила кинетического трения). Поскольку она движется по склону, наиболее удобной системой отсчета для анализа ее движения является система с x — ось вдоль и y — ось перпендикулярно наклону. В этой системе отсчета нормальные силы и силы трения лежат вдоль осей координат, компоненты веса равны [латекс] mg\,\text{sin}\,\theta \,\text{по наклону и}\,mg \,\text{cos}\,\theta \,\text{под прямым углом к склону} [/latex], и единственное ускорение происходит вдоль оси x [латекс] ({a}_{y }=0). [/latex]
Решение
Теперь мы можем применить второй закон Ньютона к сноубордисту:
[латекс] \begin{array}{cccccc}\hfill \sum {F}_{x}& =\hfill & m{a}_{x}\hfill & & & \sum {F}_{y }=m{a}_{y}\hfill \\ \hfill mg\,\text{sin}\,\theta -{\mu }_{k}N& =\hfill & m{a}_{x} \hfill & & & \hfill N-mg\,\text{cos}\,\theta =m(0)\text{.
 }\end{array} [/latex]
}\end{array} [/latex]Из второго уравнения [латекс] N=mg\,\text{cos}\,\theta . [/latex] Подставив это в первое уравнение, мы находим
[латекс] \begin{array}{cc}\hfill {a}_{x}& =g(\text{sin}\,\theta — {\ mu } _ {\ text {k}} \, \ text {cos} \, \ theta ) \ hfill \\ & = g (\ text {sin} \, 13 \ text {°} -0,20 \, \ текст {cos} \, 13 \ текст {°}) = 0,29{2}\text{.}\hfill \end{array} [/latex]
Значимость
Обратите внимание на это уравнение, что если [latex] \theta [/latex] достаточно мало или [latex] {\mu } _{\text{k}} [/latex] достаточно велико, [latex] {a}_{x} [/latex] отрицательно, то есть сноубордист замедляется.
Проверьте свое понимание
Сноубордист сейчас движется вниз по склону с уклоном [латекс] 10,0\текст{°} [/латекс]. Чему равно ускорение лыжника?
Показать решение
Резюме
- Трение – это контактная сила, противодействующая движению или попытке движения между двумя системами.
 Простое трение пропорционально нормальной силе Н , поддерживающей две системы.
Простое трение пропорционально нормальной силе Н , поддерживающей две системы. - Величина силы трения покоя между двумя материалами, неподвижными друг относительно друга, определяется с помощью коэффициента трения покоя, который зависит от обоих материалов.
- Сила кинетического трения между двумя движущимися относительно друг друга материалами определяется с помощью коэффициента кинетического трения, который также зависит от обоих материалов и всегда меньше коэффициента трения покоя.
Концептуальные вопросы
Клей на куске ленты может оказывать воздействие. Могут ли эти силы быть разновидностью простого трения? Объясните, особенно учитывая, что лента может приклеиваться к вертикальным стенам и даже к потолку.
Когда вы учитесь водить машину, вы обнаружите, что вам нужно слегка отпустить педаль тормоза, когда вы останавливаетесь, иначе машина остановится рывком. Объясните это с точки зрения связи между статическим и кинетическим трением.

Показать решение
Когда вы водите мелом по классной доске, он иногда скрипит, потому что быстро то соскальзывает, то прилипает к доске. Опишите этот процесс более подробно, в частности объяснив, как он связан с тем, что кинетическое трение меньше статического трения. (Тот же процесс проскальзывания происходит, когда шины визжат по асфальту.)
Студентка-физик готовит завтрак, когда замечает, что сила трения между ее стальной лопаткой и тефлоновой сковородой составляет всего 0,200 Н. Зная коэффициент кинетического трения между два материала, она быстро вычисляет нормальную силу. Что это? 9{2} [/latex] Сила N для вставки сухого стального поршня в стальной цилиндр. Чему равна нормальная сила между поршнем и цилиндром? б) Какую силу ему пришлось бы приложить, если бы стальные детали были смазаны маслом?
(a) Какова максимальная сила трения в коленном суставе человека, который удерживает 66,0 кг своей массы на этом колене? (б) Во время напряженной работы можно приложить к суставам усилия, которые легко в 10 раз превышают поддерживаемый вес.
 {3}\text{-kg} [/latex] грузового автомобиля поддерживается двумя ведущими колесами, что какое максимальное ускорение он может достичь на сухом бетоне? б) Будет ли металлический шкаф, лежащий на деревянном кузове грузовика, скользить, если он будет двигаться с такой скоростью? (c) Решите обе задачи, предполагая, что грузовик имеет полный привод.
{3}\text{-kg} [/latex] грузового автомобиля поддерживается двумя ведущими колесами, что какое максимальное ускорение он может достичь на сухом бетоне? б) Будет ли металлический шкаф, лежащий на деревянном кузове грузовика, скользить, если он будет двигаться с такой скоростью? (c) Решите обе задачи, предполагая, что грузовик имеет полный привод.Показать решение
Упряжка из восьми собак тянет нарты с полозьями из вощеного дерева по мокрому снегу (месиво!). Собаки имеют среднюю массу 19,0 кг, а загруженные сани с всадником имеют массу 210 кг. (a) Рассчитайте ускорение собак, начиная с состояния покоя, если каждая собака действует на снег со средней силой 185 Н, направленной назад. (b) Рассчитайте силу сцепления между собаками и санями.
Рассмотрим фигуриста весом 65,0 кг, которого толкают два других фигуриста, показанных ниже. (a) Найдите направление и величину [латекса] {F}_{\text{tot}}, [/латекс] суммарной силы, действующей на нее со стороны других, учитывая, что величины [латекса] {F}_{ 1} [/латекс] и [латекс] {F}_{2} [/латекс] составляют 26,4 Н и 18,6 Н соответственно.
 (b) Каково ее начальное ускорение, если она изначально неподвижна и носит коньки со стальными лезвиями, направленными в направлении [латекса] {F}_{\text{tot}}? [/latex] (c) Каково ее ускорение, если предположить, что она уже движется в направлении [латекс] {F}_{\text{tot}}? [/latex] (Помните, что трение всегда действует в направлении, противоположном движению или попытке движения между контактирующими поверхностями.)
(b) Каково ее начальное ускорение, если она изначально неподвижна и носит коньки со стальными лезвиями, направленными в направлении [латекса] {F}_{\text{tot}}? [/latex] (c) Каково ее ускорение, если предположить, что она уже движется в направлении [латекс] {F}_{\text{tot}}? [/latex] (Помните, что трение всегда действует в направлении, противоположном движению или попытке движения между контактирующими поверхностями.)Показать решение
Показать, что ускорение любого объекта вниз по склону без трения, образующему угол [латекс] \тета [/латекс] с горизонтом, равно [латекс] a=g\,\text{sin}\,\theta [/латекс ]. (Обратите внимание, что это ускорение не зависит от массы.)
Покажите, что ускорение любого объекта вниз по склону, где трение ведет себя просто (то есть, где [латекс] {f} _ {\ text {k}}={ \ mu } _ {\ text {k}} N) [/ латекс] есть [латекс] a = g (\ text {sin} \, \ theta — {\ mu } _ {\ text {k}} \, \ текст {cos}\,\theta ).
 [/latex] Обратите внимание, что ускорение не зависит от массы и сводится к выражению, найденному в предыдущей задаче, когда трение становится пренебрежимо малым [латекс] ({\ mu } _ {\ text {k}} = 0). [/латекс]
[/latex] Обратите внимание, что ускорение не зависит от массы и сводится к выражению, найденному в предыдущей задаче, когда трение становится пренебрежимо малым [латекс] ({\ mu } _ {\ text {k}} = 0). [/латекс]Показать решение
Рассчитайте замедление сноубордиста, поднимающегося по склону [латекс] 5.00\text{°} [/латекс], принимая во внимание коэффициент трения вощеной древесины по мокрому снегу. Результат предыдущей задачи может быть полезен, но будьте осторожны, принимая во внимание тот факт, что сноубордист движется в гору.
Машина в почтовом отделении отправляет посылки по желобу и вниз по пандусу для загрузки в транспортные средства доставки. (a) Рассчитайте ускорение ящика, движущегося вниз по склону [латекс] 10,0\текст{°} [/латекс], предполагая, что коэффициент трения пакета о вощеное дерево равен 0,100. б) Найдите угол наклона, под которым этот ящик мог бы двигаться с постоянной скоростью. Сопротивлением воздуха в обеих частях можно пренебречь.
 9{-1}\,{\mu}_{\text{s}}. [/latex] Вы можете использовать результат предыдущей задачи. Предположим, что [латекс] а=0 [/латекс] и что статическое трение достигло своего максимального значения.
9{-1}\,{\mu}_{\text{s}}. [/latex] Вы можете использовать результат предыдущей задачи. Предположим, что [латекс] а=0 [/латекс] и что статическое трение достигло своего максимального значения.Рассчитайте максимальное ускорение автомобиля, движущегося по склону [латекс] 6,00\text{°} [/latex] (угол которого составляет [латекс] 6,00\текст{°} [/latex] с горизонталью) при следующих дорожных условиях. Вы можете предположить, что вес автомобиля равномерно распределяется на все четыре шины и что учитывается коэффициент статического трения, то есть шины не могут проскальзывать во время замедления. (Качение не учитывать.) Рассчитайте для автомобиля: (a) На сухом бетоне. (b) На мокром бетоне. (c) На льду, предполагая, что [латекс] {\ mu } _ {\ text {s}} = 0,100 [/латекс], то же, что и для обуви на льду.
Показать решение
Рассчитайте максимальное ускорение автомобиля, движущегося вверх по склону [latex] 4,00\text{°} [/latex] (который образует угол [latex] 4,00\text{°} [/latex] с горизонтально) при следующих дорожных условиях.
 Предположим, что только половина веса автомобиля приходится на два ведущих колеса и что учитывается коэффициент статического трения, то есть шины не могут проскальзывать во время ускорения. (Не обращайте внимания на прокатку.) (a) На сухом бетоне. (b) На мокром бетоне. (c) На льду, предполагая, что [латекс] {\ mu } _ {\ text {s}} = 0,100 [/латекс], то же, что и для обуви на льду. 9{5}\text{N} [/latex], если предположить, что двигатели действуют одинаково? Это не большая сила трения для такой массивной системы. Трение качения для поездов невелико, и, следовательно, поезда являются очень энергоэффективными транспортными системами. б) Какова сила сцепления между 37-м и 38-м вагонами (это сила, с которой каждый из них действует на другой), если предположить, что все вагоны имеют одинаковую массу и что трение равномерно распределено между всеми вагонами и двигателями?
Предположим, что только половина веса автомобиля приходится на два ведущих колеса и что учитывается коэффициент статического трения, то есть шины не могут проскальзывать во время ускорения. (Не обращайте внимания на прокатку.) (a) На сухом бетоне. (b) На мокром бетоне. (c) На льду, предполагая, что [латекс] {\ mu } _ {\ text {s}} = 0,100 [/латекс], то же, что и для обуви на льду. 9{5}\text{N} [/latex], если предположить, что двигатели действуют одинаково? Это не большая сила трения для такой массивной системы. Трение качения для поездов невелико, и, следовательно, поезда являются очень энергоэффективными транспортными системами. б) Какова сила сцепления между 37-м и 38-м вагонами (это сила, с которой каждый из них действует на другой), если предположить, что все вагоны имеют одинаковую массу и что трение равномерно распределено между всеми вагонами и двигателями?Рассмотрим альпиниста весом 52,0 кг, показанного ниже. а) Найдите натяжение веревки и силу, которую альпинист должен прикладывать ногами к вертикальной скале, чтобы оставаться неподвижным.
 Предположим, что сила приложена параллельно ее ногам. Кроме того, предположим, что сила, действующая на ее руки, незначительна. б) Каков минимальный коэффициент трения между ее туфлями и скалой?
Предположим, что сила приложена параллельно ее ногам. Кроме того, предположим, что сила, действующая на ее руки, незначительна. б) Каков минимальный коэффициент трения между ее туфлями и скалой?Показать решение
Участник зимних спортивных соревнований толкает глыбу льда весом 45,0 кг по замерзшему озеру, как показано ниже. (a) Вычислите минимальную силу F , которую он должен приложить, чтобы сдвинуть блок. б) Каково его ускорение в начале движения, если эта сила сохраняется?
Теперь участник тянет блок льда с веревкой через плечо под тем же углом над горизонталью, как показано ниже. Рассчитать минимальную силу F он должен приложить усилия, чтобы сдвинуть блок. б) Каково его ускорение в начале движения, если эта сила сохраняется?
Показать решение
В почтовом отделении посылка, представляющая собой коробку весом 20,0 кг, соскальзывает по пандусу, наклоненному под углом [латекс] 30,0\text{°} [/латекс] к горизонтали.
 Коэффициент кинетического трения между ящиком и плоскостью равен 0,0300. а) Найдите ускорение ящика. б) Найдите скорость ящика в момент достижения им конца плоскости, если длина плоскости равна 2 м, а ящик с самого начала покоится.
Коэффициент кинетического трения между ящиком и плоскостью равен 0,0300. а) Найдите ускорение ящика. б) Найдите скорость ящика в момент достижения им конца плоскости, если длина плоскости равна 2 м, а ящик с самого начала покоится.Глоссарий
- трение
- сила, противодействующая относительному движению или попыткам движения между контактирующими системами
- кинетическое трение
- сила, противодействующая движению двух систем, находящихся в контакте и движущихся относительно друг друга
- статическое трение
- сила, противодействующая движению двух систем, находящихся в контакте и не движущихся относительно друг друга
Калькулятор трения f = мкН
Использование калькулятора
Калькулятор трения находит неизвестную переменную, используя уравнение трения f = мкН . Рассчитайте трение f , коэффициент трения μ или нормальную силу Н .
 Введите два значения, чтобы вычислить третье.
Введите два значения, чтобы вычислить третье.Вы можете вводить числа, десятичные дроби или экспоненциальное представление, как в 3.45e22.
Сила трения – это сила сопротивления движению, когда две поверхности соприкасаются друг с другом. Если две поверхности не движутся относительно друг друга, это называется статическим трением. Когда две поверхности движутся и скользят друг относительно друга, это называется кинетическим трением.
Уравнение трения
\( f = \mu N \)
Переменные в уравнении трения
- \( f \) = сила трения, в ньютонах
- \( \mu \) = коэффициент трения
- \( Н \) = нормальная сила, в ньютонах
Трение можно описать как коэффициент трения, умноженный на нормальную силу. Калькулятор трения использует формулу f = µN , или трение f равно коэффициенту трения μ раза больше нормальной силы Н .
Обратите внимание, что стандартными единицами измерения уравнения трения являются ньютоны.
 Если вы введете другие единицы измерения для расчета, калькулятор произведет преобразование единиц за вас. Коэффициент трения является множителем и не имеет единицы измерения.
Если вы введете другие единицы измерения для расчета, калькулятор произведет преобразование единиц за вас. Коэффициент трения является множителем и не имеет единицы измерения.Формулы трения
Определите трение, коэффициент трения или нормальную силу, используя следующие формулы:
Рассчитайте f При данных μ и N
Рассчитайте силу трения, зная коэффициент трения и нормальную силу:\( f = \mu N \)
Вычислить µ Учитывая f и f
Рассчитайте коэффициент трения, зная силу трения и нормальную силу:\( \mu = \dfrac{f}{N} \)
Вычислить N Учитывая µ и f
Рассчитайте нормальную силу, зная коэффициент трения и силу трения:\( N = \dfrac{f}{\mu} \)
Нормальная сила как функция массы и гравитации
Простая форма уравнения нормальной силы: Н = мг , где нормальная сила Н равна массе м , умноженной на гравитацию г .
 Этот калькулятор позволяет вам вводить массу и гравитацию вместо нормальной силы, которая затем также рассчитывается.
Этот калькулятор позволяет вам вводить массу и гравитацию вместо нормальной силы, которая затем также рассчитывается.Решите для силы трения и коэффициента трения, где уравнение нормальной силы:
\( N = mg \)
Переменные в уравнении нормальной силы
- \( Н \) = нормальная сила
- \(м\) = масса
- \(г\) = сила тяжести
Рассчитать f При заданных μ, m и g
Рассчитайте силу трения, зная коэффициент трения, массу и силу тяжести:\( f = \mu mg \)
Вычислить µ Учитывая f, m и g
Рассчитайте коэффициент трения, зная силу трения, массу и гравитацию:\( \mu = \dfrac{f}{mg} \)
Пример: Сравните силы трения резины и банановой кожуры на линолеуме
Вы с другом решили сравнить силы трения резины и банановой кожуры. на напольном материале линолеум.
 Вы можете использовать первое уравнение нормальной силы , приведенное выше, для расчета f с заданными μ, m и g.
Вы можете использовать первое уравнение нормальной силы , приведенное выше, для расчета f с заданными μ, m и g.Проведя небольшое исследование, вы и ваш друг обнаружили, что коэффициент трения подошв его кроссовок по линолеуму составляет 0,53. А коэффициент трения внутренней части банановой кожуры о линолеум составляет 0,07. Ваш друг весит 65 кг, и вы можете видеть из таблицы планетарного тяготения ниже, что стандартная гравитация на Земле равна 9.0,81 м/с 2 .
Сначала составьте уравнение, чтобы найти силу трения резины о линолеум. Вы хотите использовать формулу f = мкг .
f резина = 0,53 * 65 кг * 9,81 м/с 2
f резина = 337,95
Значит, сила трения вашего друга в кроссовках по линолеуму составляет 95 ньютонов. Обратите внимание, что ваше использование кг и м/с 2 является стандартным для того, чтобы уравнение приводило к некоторому числу ньютонов. Если вы хотите использовать другие единицы измерения, обязательно конвертируйте их в кг, м/с 2 и ньютонов, прежде чем подставлять числа в уравнения.

Затем составьте уравнение, чтобы найти силу трения внутренней поверхности банановой кожуры о линолеум:
f банановая кожура = 0,07 * 65 кг * 9,81 м/с = 44,64 Н
Итак, сила трения вашего друга, наступившего на банановую кожуру на линеолеум, составляет 44,64 ньютона.
Что это значит? Ньютон определяется как сила, необходимая для перемещения груза массой 1 кг со скоростью 1 м/с 2 . Глядя на силу трения вашего друга в кроссовках по линолеуму, потребуется 337,95 ньютона, чтобы ваш друг начал скользить по линолеуму (в кроссовках, стоя на одной ноге).
Если бы ваш друг стоял на банановой кожуре скользкой стороной вниз, потребовалось бы 44,64 ньютона, чтобы ваш друг начал скользить. Если вы разделите 337,95 на 44,64, вы увидите, что потребуется примерно в 7,5 раз больше силы, чтобы протащить вашего друга через линолеум с помощью кроссовок, а не банановой кожуры.
Если бы вы были на другой планете, сила гравитации была бы иной, чем на Земле.
 В этой справочной таблице указана гравитационная сила Солнца, Луны и каждой планеты в нашей Солнечной системе.
В этой справочной таблице указана гравитационная сила Солнца, Луны и каждой планеты в нашей Солнечной системе.Планетарная гравитационная таблица
Источник таблицы: Информационный бюллетень о планетах — НАСА
Стандартная гравитация (g n ): 1,00g n равно 9,80665 м/с 2 силы тяжести на Земле.
Проникновение в сухую пористую породу: Численное исследование моделирования трения скольжения (Технический отчет)
Проникновение в сухую пористую породу: Численное исследование моделирования трения скольжения (Технический отчет) | ОСТИ.GOVперейти к основному содержанию
- Полная запись
- Другие родственные исследования
Проникновение стальных пенетраторов в цель из туфа Антилопы является предметом обсуждения в настоящем исследовании.
 В частности, исследуется влияние трения скольжения между снарядом и целью на проникающую способность. Код конечных элементов PRONTO 2D используется для параметрического исследования коэффициента трения. В настоящее исследование включены как постоянный, так и зависящий от скорости коэффициент трения. Результаты показывают, что увеличение коэффициента трения увеличивает сопротивление проникновению, хотя эта зависимость носит нелинейный характер. С точки зрения пикового замедления и глубины проникновения как постоянный, так и зависящий от скорости коэффициент трения дают почти идентичные результаты. Однако только случаи, зависящие от скорости, показывают характеристику увеличения замедления до завершения события проникновения. По этой причине представление коэффициента трения, зависящее от скорости, предпочтительнее, чем представление постоянного коэффициента трения. 8 ссылок, 13 рис., 1 табл.
В частности, исследуется влияние трения скольжения между снарядом и целью на проникающую способность. Код конечных элементов PRONTO 2D используется для параметрического исследования коэффициента трения. В настоящее исследование включены как постоянный, так и зависящий от скорости коэффициент трения. Результаты показывают, что увеличение коэффициента трения увеличивает сопротивление проникновению, хотя эта зависимость носит нелинейный характер. С точки зрения пикового замедления и глубины проникновения как постоянный, так и зависящий от скорости коэффициент трения дают почти идентичные результаты. Однако только случаи, зависящие от скорости, показывают характеристику увеличения замедления до завершения события проникновения. По этой причине представление коэффициента трения, зависящее от скорости, предпочтительнее, чем представление постоянного коэффициента трения. 8 ссылок, 13 рис., 1 табл.- Авторов:
- Чен, ЭП
- Дата публикации:
- Исследовательская организация:
- Sandia National Labs.
 , Альбукерке, Нью-Мексико (США)
, Альбукерке, Нью-Мексико (США)
- Идентификатор ОСТИ:
- 6710755
- Номер(а) отчета:
- ПЕСОК-88-2485
НА: DE894
- Номер контракта с Министерством энергетики:
- AC04-76DP00789
- Тип ресурса:
- Технический отчет
- Отношение ресурсов:
- Дополнительная информация: Части этого документа неразборчивы в микрофишах
- Страна публикации:
- США
- Язык:
- Английский
- Тема:
- 42 МАШИНОСТРОЕНИЕ; 99 ОБЩЕЕ И РАЗНОЕ // МАТЕМАТИКА, ВЫЧИСЛИТЕЛЬНАЯ И ИНФОРМАЦИОННАЯ НАУКА; ГОРЯЧИЕ-СУХИЕ-СКАЛЬНЫЕ СИСТЕМЫ; ГЛУБИНА ПРОНИКНОВЕНИЯ; ПЕНЕТРАТОРЫ; КОМПЬЮТЕРНОЕ МОДЕЛИРОВАНИЕ; МЕТОД КОНЕЧНЫХ ЭЛЕМЕНТОВ; ЧИСЛЕННЫЕ ДАННЫЕ; Р-КОДЫ; ТРЕНИЕ СКОЛЬЖЕНИЯ; ТЕХНИЧЕСКИЕ ХАРАКТЕРИСТИКИ; КОМПЬЮТЕРНЫЕ КОДЫ; ДАННЫЕ; ЭНЕРГЕТИЧЕСКИЕ СИСТЕМЫ; ТРЕНИЕ; ГЕОТЕРМАЛЬНЫЕ СИСТЕМЫ; ИНФОРМАЦИЯ; ЧИСЛЕННОЕ РЕШЕНИЕ; МОДЕЛИРОВАНИЕ; Геотермальное наследие
Форматы цитирования
- MLA
- АПА
- Чикаго
- БибТекс
Чен, Э. П. Проникновение в сухую пористую породу: численное исследование моделирования трения скольжения . США: Н. П., 1988.
Веб. дои: 10.2172/6710755.
П. Проникновение в сухую пористую породу: численное исследование моделирования трения скольжения . США: Н. П., 1988.
Веб. дои: 10.2172/6710755. Копировать в буфер обмена
Чен, Э. П. Проникновение в сухую пористую породу: численное исследование моделирования трения скольжения . Соединенные Штаты. https://doi.org/10.2172/6710755Копировать в буфер обмена
Чен, Э. П. 1988. «Проникновение в сухую пористую породу: численное исследование моделирования трения скольжения». Соединенные Штаты. https://doi.org/10.2172/6710755. https://www.osti.gov/servlets/purl/6710755.Копировать в буфер обмена
@статья{osti_6710755,
title = {Проникновение в сухую пористую породу: численное исследование моделирования трения скольжения},
автор = {Чен, ЭП},
abstractNote = {Проникновение стальных пенетраторов в цели из туфа Антилопы является предметом обсуждения в настоящем исследовании. В частности, исследуется влияние трения скольжения между снарядом и целью на проникающую способность. Код конечных элементов PRONTO 2D используется для параметрического исследования коэффициента трения. В настоящее исследование включены как постоянный, так и зависящий от скорости коэффициент трения. Результаты показывают, что увеличение коэффициента трения увеличивает сопротивление проникновению, хотя эта зависимость носит нелинейный характер. С точки зрения пикового замедления и глубины проникновения как постоянный, так и зависящий от скорости коэффициент трения дают почти идентичные результаты. Однако только случаи, зависящие от скорости, показывают характеристику увеличения замедления до завершения события проникновения. По этой причине представление коэффициента трения, зависящее от скорости, предпочтительнее, чем представление постоянного коэффициента трения. 8 исх., 13 рис., 1 таб.},
В частности, исследуется влияние трения скольжения между снарядом и целью на проникающую способность. Код конечных элементов PRONTO 2D используется для параметрического исследования коэффициента трения. В настоящее исследование включены как постоянный, так и зависящий от скорости коэффициент трения. Результаты показывают, что увеличение коэффициента трения увеличивает сопротивление проникновению, хотя эта зависимость носит нелинейный характер. С точки зрения пикового замедления и глубины проникновения как постоянный, так и зависящий от скорости коэффициент трения дают почти идентичные результаты. Однако только случаи, зависящие от скорости, показывают характеристику увеличения замедления до завершения события проникновения. По этой причине представление коэффициента трения, зависящее от скорости, предпочтительнее, чем представление постоянного коэффициента трения. 8 исх., 13 рис., 1 таб.},
дои = {10.2172/6710755},
URL-адрес = {https://www.osti.gov/biblio/6710755}, журнал = {},
номер =,
объем = ,
место = {США},
год = {1988},
месяц = {10}
}Копировать в буфер обмена
Посмотреть технический отчет (1,28 МБ)
https://doi.
 org/10.2172/6710755
org/10.2172/6710755Экспорт метаданных
Сохранить в моей библиотеке
Вы должны войти в систему или создать учетную запись, чтобы сохранять документы в своей библиотеке.
Аналогичных записей в сборниках OSTI.GOV:
- Аналогичные записи
ньютоновская механика — Как рассчитывается коэффициент трения?
$\begingroup$
Как рассчитывается коэффициент статического трения и коэффициент кинетического трения в реальной жизни без знания силы трения?
- ньютоновская механика
- классическая механика
- экспериментальная физика
- трение
$\endgroup$
0
$\begingroup$
Я не могу привести пример для всех поверхностей, но для наклонной плоскости формула довольно проста.
 Предположим, вы хотите найти коэффициент трения между блоком и наклоном. Держите блок под наклоном, и если блок неподвижен, попробуйте увеличить угол наклона, пока блок не начнет скользить. В этот момент сила на объекте равна просто равно максимальному значению трения покоя, т.е. $\mu\ mg\ \text{cos}\ \theta$, где $\theta$ — угол наклона. И какая сила действует на объект? Ну, это другая составляющая веса, то есть $mg\\text{sin}\\theta$.
Предположим, вы хотите найти коэффициент трения между блоком и наклоном. Держите блок под наклоном, и если блок неподвижен, попробуйте увеличить угол наклона, пока блок не начнет скользить. В этот момент сила на объекте равна просто равно максимальному значению трения покоя, т.е. $\mu\ mg\ \text{cos}\ \theta$, где $\theta$ — угол наклона. И какая сила действует на объект? Ну, это другая составляющая веса, то есть $mg\\text{sin}\\theta$.
Для условия равновесия вы приравниваете эти два $$\mu\ mg\ \text{cos}\ \theta=mg\ \text{sin}\ \theta$$ из которого вы просто получаете- $$\mu=\text{tan}\ \theta$$Для большей точности повторите вышеописанный эксперимент с более тяжелыми/легкими блоками, разными углами наклона одного и того же материала, а также позаботьтесь о том, чтобы Держите поверхность достаточно гладкой, чтобы обеспечить равномерный наклон. Возьмите среднее значение, и вы получите действительно близкое значение. Обратите внимание, что в этом ответе я просто показал действительно общий метод, который далек от строгости, но я надеюсь, что он все же поможет
$\endgroup$
4
$\begingroup$
Статический коэффициент
В простом эксперименте нужно взять пандус из материала $A$ и блок из материала $B$.
 2}{2gD}$$
2}{2gD}$$$\endgroup$
$\begingroup$
Во-первых, я думаю, что термин «динамический коэффициент трения» более широко принят, чем термин «кинематический коэффициент трения», который, как я предполагаю, относится к тому же понятию.
В любом случае, судя по моему беглому библиографическому поиску, широко используемых методов не существует. Хотя недостатка в предложениях нет. Проверить, например:
Определение динамического трения модифицированным методом Кольского
или
Динамические измерения трения при скоростях скольжения, характерных для высокоскоростных процессов обработки
и в контексте отрасли, в которой я фактически работал (и нет, о стандартном методе не было и речи),
Динамический Измерение коэффициента трения частиц гранулированного удобрения
А также патенты:
Прибор для измерения динамического коэффициента трения
$\endgroup$
Твой ответ
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя адрес электронной почты и пароль
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
.
Коэффициент кинетического трения — DewWool
Главная Физика Коэффициент кинетического трения
Существует много типов трения, таких как трение скольжения, трение качения, статическое трение и т. д. Коэффициент трения, связанный с кинетическим трением, называется коэффициентом кинетического трения. Силу трения можно разделить на две категории в зависимости от состояния движения: статическое трение и кинетическое трение. Кинетическое трение — это трение между двумя скользящими телами, когда они находятся в относительном движении. В этой статье мы обсудим формулу для коэффициента кинетического трения и увидим несколько примеров того, как рассчитать коэффициент кинетического трения. Для получения более подробной информации вы можете прочитать наш пост в блоге о коэффициенте трения.
Уравнение для коэффициента кинетического трения Формула для кинетического тренияF k = μ k * N [уравнение силы трения, где N — нормальная сила]
1k 0 = F k / N [Коэффициент кинетического трения обозначается символом mu с нижним индексом k.
 ( μ k )]
( μ k )]Из приведенного выше уравнения коэффициент кинетического трения может быть определен как отношение между кинетическое трение и нормальная сила. Итак, когда нормальная сила имеет единичное значение, тогда коэффициент кинетического трения равен самому кинетическому трению. Коэффициент кинетического трения уникален для пары материалов.
Коэффициент кинетического трения применим только тогда, когда объект находится в движении. Когда объект находится в состоянии покоя, используется коэффициент трения покоя. Коэффициент кинетического трения обычно меньше значения коэффициента статического трения.
По этой ссылке можно посмотреть примеры значений коэффициента кинетического трения для разных пар материалов.
Решенные примеры по расчету кинетического трения1. Деревянный ящик скользит по стеклянной поверхности. Коэффициент трения между деревянным ящиком и стеклянной поверхностью равен 0,5.
 Нормальная сила, действующая между коробкой и стеклянной поверхностью, равна 50 Н. Рассчитайте кинетическое трение между поверхностями.
Нормальная сила, действующая между коробкой и стеклянной поверхностью, равна 50 Н. Рассчитайте кинетическое трение между поверхностями. Мы знаем формулу кинетической силы трения как F k = μ k * N
Отсюда значение кинетического трения будет = 0,5 * 50 = 25 N
2. Книга равна отдыхая на столе. Вес книги 20 Н. Коэффициент трения между столом и книгой 0,3. Рассчитать коэффициент кинетического трения?
В этом случае книга находится в стационарном состоянии, поэтому мы не можем рассчитать кинетическое трение. Кинетического трения нет, а приведенный выше коэффициент трения является статическим трением, поскольку книга находится в состоянии покоя.
3. Автомобиль движется вниз по склону с углом наклона 60 градусов. вес автомобиля равен 1500 Н. Рассчитайте коэффициент кинетического трения, если кинетическое трение равно 750 Н. нормальная сила как mg cos θ. Таким образом, уравнение кинетического трения изменяется следующим образом:
F k = μ k * mg cos θ
750 = μ K * 1500 * COS 60
µ K = 1
См. Также
Также - 6
- 9000 9000. и DIDES 9000 и DIDES 9000 и DIDES 9000. Кинетическое трение – Определение|формула|примеры
- Примеры трения качения
- Коэффициент трения – Определение0006
- Sliding friction
- Angular friction
- Causes of friction
- Examples of static friction
- Examples of fluid friction
- БИРКИ
- класс 11
- класс 9
Предыдущая статья20 Примеры движения снаряда
Следующая статья15 Различия кислот и оснований
Поиск
Видео дня
youtube.com/embed/MFqwADnUwwM» frameborder=»0″ allow=»accelerometer; autoplay; encrypted-media; gyroscope; picture-in-picture» allowfullscreen=»»>Поддержите нас
Мы хотим сделать науку интересной и в то же время бесплатной! Ваш вклад в эту страницу поможет нам донести качественный контент до детей, которые больше всего в нем нуждаются. Если вам нравится, что мы делаем, и вы хотите поддержать нас, вы можете посетить нашу страницу пожертвований ko-fi на www.ko-fi.com/dewwool.
Категории
- Анимация
- Биология
- Блог
- Химия
- Органическая химия
- Математика
- Физика
- Оптика и акустика
- Викторина
- Без категории
- Рабочие листы
Комикс дня
Архив
Архивы Выбрать месяц Август 2022 Июль 2022 Июнь 2022 Май 2022 Апрель 2022 Март 2022 Январь 2022 Декабрь 2021 Ноябрь 2021 Октябрь 2021 Сентябрь 2021 Август 2021 Июль 2021 Июнь 2021 Май 2021 Апрель 2021 Март 2021 Февраль 2021 Январь 2021 2 Сентябрь 2021 Декабрь 2020 Октябрь 2020 Ноябрь 2020 июль 2020 г. июнь 2020 г. май 2020 г. март 2020 г.
июнь 2020 г. май 2020 г. март 2020 г.Последние сообщения
Рабочие листы по умножению для 2-го класса
админ — 0
В этой статье мы представляем простое умножение однозначных и однозначных чисел методом столбцов, подходящее для учащихся 2 класса. Ответы на приведенный выше рабочий лист умножения: 1) 10,…
Рабочие листы на вычитание 1-й класс
админ — 0
Рабочий лист «Живое вычитание» 1-й класс: Ответы на приведенный выше рабочий лист вычитания на основе изображений: 1) 2, 2) 4, 3) 2, 4) 0. Ответы на приведенные выше вычитания на основе изображений…
Рабочие листы по формам энергии
администратор — 0
В этой статье мы представляем рабочие листы по формам энергии.

- Трение – это контактная сила, противодействующая движению или попытке движения между двумя системами.