Что такое коэффициент трения для масла АTF?
Внимательные читатели нашего блога наверняка заметили, что мы часто упоминаем фрикционное число масла ATF, оно же коэффициент трения. А все потому, что это очень важный показатель с точки зрения состояния масла. Сегодня мы расскажем подробнее, почему.
Срок службы муфты сцепления и максимальная способность передавать усилие от двигателя к колесам зависят, главным образом, от характеристик трения между дисками сцепления. Иначе говоря, сцепляемость дисков между собой имеет критическое значение и является одним из важнейших свойств коробки передач. Коэффициент трения масла (или фрикционное число, англ. friction coefficient) показывает, насколько хорошо или плохо диски сцепляются между собой, когда между ними присутствует тонкий слой масла ATF.
На самом деле различают статический и динамический коэффициенты трения. Динамический КТ показывает сопротивление трению между движущимися дисками сцепления. Статический КТ показывает силу трения между дисками сцепления в покое.
Статический КТ показывает силу трения между дисками сцепления в покое.
Когда диски сцепления скользят?
Диски сцепления скользят в начале переключения передачи. С этого момента диски начинают все сильнее прижиматься друг к другу. Чем выше динамический коэффициент трения масла, тем лучше диски сцепляются друг с другом, то есть быстрее уравниваются их скорости, — и передача включается.
Чем ниже динамический коэффициент трения, тем дольше диски скользят, и передача включается очень долго. Разумеется, передача не должна включаться слишком быстро, но и не слишком медленно. В первом случае вы почувствуете сильный толчок, во втором — при каждой смене передачи диски слишком сильно разогреваются и изнашиваются.
Статический коэффициент трения — это свойство масла удерживать диски сцепления вместе в покое. Как ни странно, статический и динамический коэффициенты зачастую не равны, но они и не должны совпадать!
Приведем пример из обычной жизни, когда статическое трение (трение в покое) выше динамического. Прижмите подушечку пальца к мокрой гладкой поверхности раковины и попробуйте проскользить — наверняка это будет сопровождаться скрипом. Скрип вы слышите потому, что динамический коэффициент трения между вашим пальцем и поверхностью раковины меньше статического: движущийся палец скользит легче, а пальцу, стоящему на месте, труднее начать скольжение. Никому не нужен автомобиль, у которого скачут обороты во время движения или передачи переключаются со скрипом. Поэтому производители стараются «подтянуть» статический и динамический КТ масел для коробки передач при помощи химикатов, которые повышают или понижают фрикционное число.
Прижмите подушечку пальца к мокрой гладкой поверхности раковины и попробуйте проскользить — наверняка это будет сопровождаться скрипом. Скрип вы слышите потому, что динамический коэффициент трения между вашим пальцем и поверхностью раковины меньше статического: движущийся палец скользит легче, а пальцу, стоящему на месте, труднее начать скольжение. Никому не нужен автомобиль, у которого скачут обороты во время движения или передачи переключаются со скрипом. Поэтому производители стараются «подтянуть» статический и динамический КТ масел для коробки передач при помощи химикатов, которые повышают или понижают фрикционное число.
Что означает высокий статический коэффициент трения в коробке передач?
В момент включения передачи диски сцепления скользят относительно друг друга (влияет динамический коэффициент трения). Непосредственно перед выравниванием скорости вращения (замыканием) дисков в игру вступает статический коэффициент трения. Если он выше динамического, диски сцепления тормозятся резко и с толчком. Вы почувствуете это по рывку при смене передач.
Вы почувствуете это по рывку при смене передач.
Таким образом, лучше всего, когда статический и динамический коэффициенты относительно одинаковы (статический чуть ниже), а динамический КТ растет с увеличением скольжения. Последнее означает, что чем быстрее диски будут вращаться, тем больше они будут тормозиться.
Тот и другой показатель можно менять при помощи различных присадок. К сожалению, со временем свойства масла меняются, и вместе с этим меняется статический коэффициент трения (особенно при высоких температурах при длительной эксплуатации). Старое изношенное масло сопровождает одна распространенная особенность — вибрация или дрожание дисков сцепления. Это как раз и обусловлено изменениями, произошедшими с маслом и дисками с течением времени.
Важно отметить, что фрикционное число зависит не только от масла, но и от материала дисков сцепления и программного обеспечения коробки передач. Поэтому крайне важно использовать в коробке правильное масло, совместимое по свойствам с материалами коробки и системами управления. Например, аналогичные коробки передач в BMW и Audi требуют разных масел, что обусловлено программным обеспечением, которое управляет коробкой передач. В одном случае оно учитывает высокую скользкость применяемого масла, в другом — нет.
Например, аналогичные коробки передач в BMW и Audi требуют разных масел, что обусловлено программным обеспечением, которое управляет коробкой передач. В одном случае оно учитывает высокую скользкость применяемого масла, в другом — нет.
Мы надеемся, что вам удалось немного разобраться во «внутреннем мире» масел ATF и впредь вы не будете заливать в свой «автомат» универсальные масла. Масло для коробки передач — это высокотехнологичный продукт, поэтому следует использовать только лицензионные товары.
Проложить путь
Где мы находимся
Таллин
Тяхназе теэ, 2/3, поселок Пеэтри, уезд Раэ, 75312
Tел: +372 5191 5001
Пн-Пт 8:00-17:00
Показать на карте
Кадрина
Флора, деревня Кадапику, уезд Кадрина, 45212
Tел: +372 5191 5001 (Обслуживание)
Tел: +372 5191 0067 (Pемонт)
Пн-Пт 8:00-17:00
Показать на карте
Тарту
Вана-Канди теэ 1, Кандикюла, Тартуская волость 61404
Tел: +372 522 7858
Пн-Пт 8:00-17:00
Показать на карте
Коэффициент трения не зависит от.
 Коэффициент трения и ситуации, в которых он возникает. Сила трения и ее виды
Коэффициент трения и ситуации, в которых он возникает. Сила трения и ее видыКоэффициент трения — отношение силы трения F к реакции Т, направленной по нормали к поверхности касания, возникающей при приложении нагрузки, прижимающей одно тело к другому: f = F/T.
Коэффициент трения — характеристика, применяемая при выполнении технических расчётов, характеризующих фрикционное взаимодействие двух тел. В зависимости от вида перемещения одного тела по другому различают: коэффициент трения при сдвиге — скольжении и коэффициент трения при качении. В свою очередь, при скольжении в зависимости от величины тангенциальной силы различают коэффициент неполного трения скольжения, коэффициент трения покоя и коэффициент трения скольжения. Все эти коэффициенты трения могут изменяться в широких пределах в зависимости от шероховатости и волнистости поверхностей, характера плёнок, покрывающих поверхности. Для протяжённого контакта они мало изменяются с изменением нагрузки. В зависимости от величины коэффициент трения скольжения пары трения делят на 2 группы: фрикционные материалы, имеющие большой коэффициент трения- обычно 0,3-0,35, редко 0,5-0,6, и антифрикционные, имеющие коэффициент трения без смазки 0,15-0,12, при граничной смазке 0,1-0,05.
Коэффициент трения зависит от рода грунта и скорости относительного перемещения трущихся поверхностей.
Коэффициент трения — это основная характеристика трения как явления. Он определяется видом и состоянием поверхностей трущихся тел.
ОПРЕДЕЛЕНИЕ
Коэффициентом трения называют коэффициент пропорциональности, связывающий силу трения () и силу нормального давления (N) тела на опору. Чаще всего коэффициент трения обозначают буквой . И так, коэффициент трения входит в закон Кулона — Амонтона:
Данный коэффициент трения не зависит от площадей, соприкасающихся поверхностей.
В данном случае речь идет о коэффициенте трения скольжения, который зависит от совокупных свойств трущихся поверхностей и является безразмерной величиной. Коэффициент трения зависит от: качества обработки поверхностей, трущихся тел, присутствия на них грязи, скорости движения тел друг относительно друга и т.д. Коэффициент трения определяют эмпирически (опытным путем).
Коэффициент трения, который соответствует максимальной силе трения покоя в большинстве случаев больше, чем коэффициент трения движения.
Для большего числа пар материалов величина коэффициента трения не больше единицы и лежит в пределах
Угол трения
Иногда вместо коэффициента трения применяют угол трения (), который связан с коэффициентом соотношением:
Так, угол трения соответствует минимальному углу наклона плоскости по отношению к горизонту, при котором тело, лежащее на этой плоскости, начнет скользить вниз под воздействием силы тяжести. При этом выполняется равенство:
Истинный коэффициент трения
Закон трения, который учитывает влияние сил притяжения между молекулами, трущихся поверхностей записываю следующим образом:
где — называют истинным коэффициентом трения, — добавочное давление, которое вызывается силами межмолекулярного притяжения, S — общая площадь непосредственного контакта трущихся тел.
Коэффициент трения качения
Коэффициент трения качения (k) можно определить как отношение момента силы трения качения () к силе с которой тело прижимается к опоре (N):
Отметим, что коэффициент трения качения обозначают чаще буквой . Этот коэффициент, в отличие от выше перечисленных коэффициентов трения, имеет размерность длины. То есть в системе СИ он измеряется в метрах.
Коэффициент трения качения много меньше, чем коэффициент трения скольжения.
Примеры решения задач
ПРИМЕР 1
| Задание | Веревка лежит частично на столе, часть ее свешивается со стола. Если треть длины веревки свесится со стола, то она начинает скользить. Каков коэффициент трения веревки о стол? |
| Решение | Веревка скользит со стола под действием силы тяжести. Обозначим силу тяжести, которая действует на единицу длины веревки как . В таком случае в момент начала скольжения сила тяжести, которая действует на свешивающуюся часть веревки, равна: До начала скольжения эта сила уравновешивается силой трения, которая действует на часть веревки, которая лежит на столе: Так как силы уравновешиваются, то можно записать (): |
| Ответ |
ПРИМЕР 2
| Задание | Каков коэффициент трения тела о плоскость (), если зависимость пути, которое оно проходит задано уравнением: где Плоскость составляет угол с горизонтом.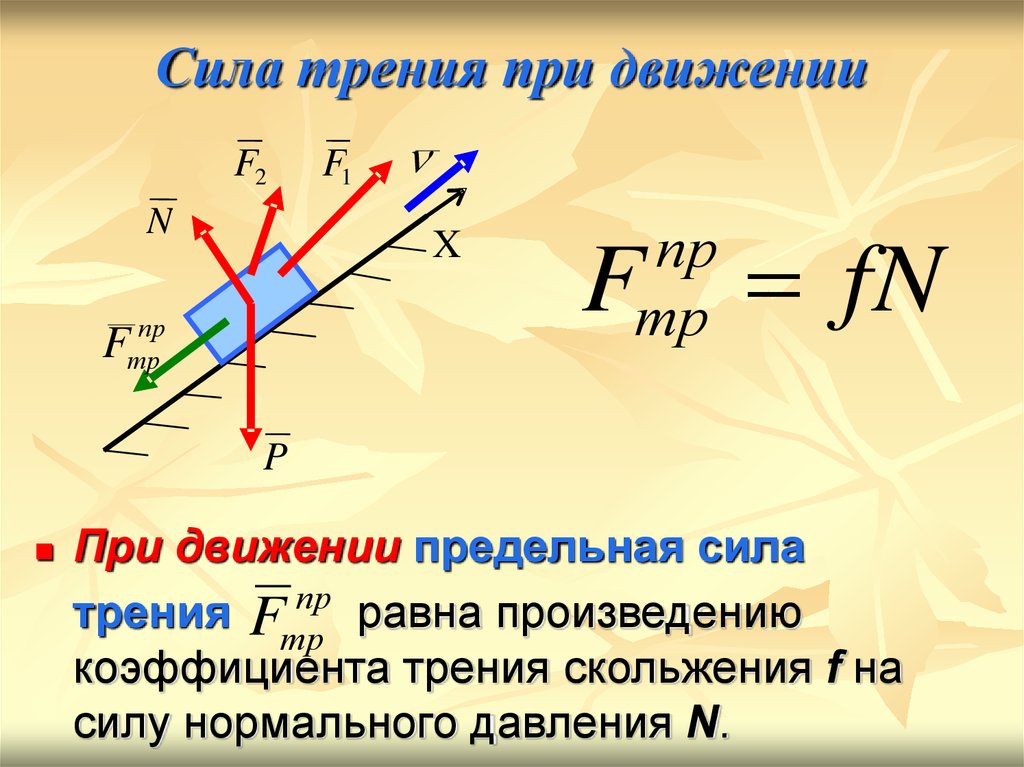 |
| Решение | Запишем второй закон Ньютона для сил, приложенных к движущемуся телу: |
Цель работы :познакомиться с явлением трения качения, определить коэффициент трения качения четырехколесной тележки..
Оборудование : тележка как модель вагона, горизонтальная рельсовая колея с набором фотоэлементов, секундомер, набор грузов.
ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ
Сила трения качения – это касательная к поверхности контакта сила сопротивления движению, возникающая при качении цилиндрических тел.
При качении колеса по рельсу происходит деформация как колеса, так и рельса. Вследствие неидеальной упругости материала в зоне контакта происходят процессы пластической деформации микробугорков, поверхностных слоев колеса и рельса. Из-за остаточной деформации уровень рельса за колесом оказывается ниже, чем перед колесом и колесо при движении постоянно закатывается на бугорок. В наружной части зоны контакта происходит частичное проскальзывание колеса по рельсу. Во всех этих процессах совершается работа силой трения качения. Работа этой силы приводит к рассеянию механической энергии, переходу ее в теплоту, поэтому сила трения качения является диссипативной силой.
Во всех этих процессах совершается работа силой трения качения. Работа этой силы приводит к рассеянию механической энергии, переходу ее в теплоту, поэтому сила трения качения является диссипативной силой.
В центральной части зоны контакта возникает еще одна касательная сила – это сила трения покоя или сила сцепления материала колеса и рельса. Для ведущего колеса локомотива сила сцепления является силой тяги, а при торможении колодочным тормозом – силой торможения. Так как в центре зоны контакта перемещения колеса относительно рельса отсутствует, то работа силой сцепления не совершается.
Распределение давления на колесо со стороны рельса оказывается несимметричным. Спереди давление больше, а сзади меньше (рис.1). Поэтому точка приложения равнодействующей силы на колесо смещена вперед на некоторое небольшое расстояние
 Другая составляющая Q направлена по нормали к поверхности контакта и проходит через ось колеса.
Другая составляющая Q направлена по нормали к поверхности контакта и проходит через ось колеса.Разложим, в свою очередь, силу нормального давления Q на две составляющие: силу N , которая перпендикулярна рельсу и компенсирует силу тяжести, и силу F кач , которая направлена вдоль рельса против движения. Эта сила препятствует движению колеса и является силой трения качения. Сила давления Q вращающего момента сил не создает. Поэтому моменты составляющих ее сил относительно оси колеса должны компенсировать друг друга: . Откуда . Сила трения качения пропорциональна силе N , действующей на колесо перпендикулярно рельсу:
. (1)
Здесь – коэффициент трения качения. Он зависит от упругости материала рельса и колеса, состояния поверхности, размеров колеса. Как видно, чем больше колесо, тем сила трения качения меньше. Если бы за колесом форма рельса восстанавливалась, то эпюра давления была бы симметрична, и трение качения отсутствовало. При качении стального колеса по стальному рельсу коэффициент трения качения достаточно мал: 0,003–0,005, в сотни раз меньше коэффициента трения скольжения. Поэтому катить легче, чем тащить.
При качении стального колеса по стальному рельсу коэффициент трения качения достаточно мал: 0,003–0,005, в сотни раз меньше коэффициента трения скольжения. Поэтому катить легче, чем тащить.
Экспериментальное определение коэффициента трения качения производится на лабораторной установке. Пусть тележка, являющаяся моделью вагона, катится по горизонтальным рельсам. На нее со стороны рельсов действуют горизонтальные силы трения качения и сцепления (рис. 2). Запишем уравнение второго закона Ньютона для замедленного движения тележки массой m в проекции на направление ускорения:
. (2)
Поскольку масса колес составляет значительную часть от массы тележки, то нельзя не учесть вращательного движения колес. Представим качение колес как сумму двух движений: поступательного движения вместе с тележкой и вращательного движения относительно осей колесных пар. Поступательное движение колес объединим с поступательным движением тележки с их общей массой m в уравнении (1).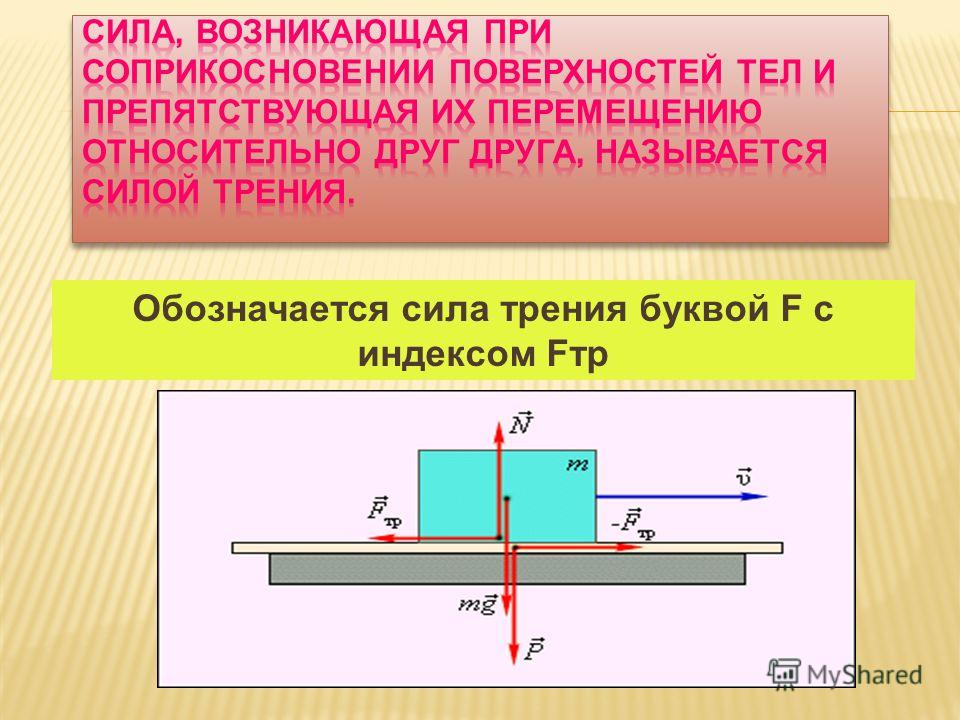 Вращательное движение колес происходит под действием только момента сил сцепления F сц R . Уравнение основного закона динамики вращательного движения (произведение момента инерции всех колес на угловое ускорение равно моменту силы) имеет вид
Вращательное движение колес происходит под действием только момента сил сцепления F сц R . Уравнение основного закона динамики вращательного движения (произведение момента инерции всех колес на угловое ускорение равно моменту силы) имеет вид
. (3)
При отсутствии проскальзывания колеса относительно рельса скорость точки контакта равна нулю. Значит, скорости поступательного и вращательного движений равны и противоположны: . Если это равенство продифференцировать, то получим соотношение между поступательным ускорением тележки и угловым ускорениями колеса: . Тогда уравнение (3) примет вид . Сложим это уравнение с уравнением (2) для исключения неизвестной силы сцепления. В результате получим
. (4)
Полученное уравнение совпадает с уравнением второго закона Ньютона для поступательного движения тележки с эффективной массой: , в которой уже учтен вклад инертности вращения колес в инертность тележки. В технической литературе уравнение вращательного движения колес (3) не применяют, а учитывают вращение колес введением эффективной массы. Например, для груженого вагона коэффициент инертности γ равен 1,05, а для порожнего вагона влияние инертности колес больше: γ = 1,10.
Например, для груженого вагона коэффициент инертности γ равен 1,05, а для порожнего вагона влияние инертности колес больше: γ = 1,10.
Подставив силу трения качения в уравнение (4), получим для коэффициента трения качения расчетную формулу
. (5)
| |
Для определения коэффициента трения качения по формуле (5) следует экспериментально измерить ускорение тележки. Для этого толкнем тележку с некоторой скоростью V 0 по горизонтальным рельсам. Уравнение кинематики равнозамедленного движения имеет вид .
Путь S и время движения t можно измерить, но неизвестна начальная скорость движения V 0 . Однако установка (рис. 3) имеет семь секундомеров, измеряющих время движения от стартового фотоэлемента до следующих семи фотоэлементов. Это позволяет либо составить систему семи уравнений и исключить из них начальную скорость, либо решить эти уравнения графически. Для графического решения перепишем уравнение равнозамедленного движения, поделив его на время: .
Для графического решения перепишем уравнение равнозамедленного движения, поделив его на время: .
Средняя скорость движения до каждого фотоэлемента линейно зависит от времени движения до фотоэлементов. Поэтому график зависимости V> (t ) является прямой линией с угловым коэффициентом, равным половине ускорения (рис.4)
. (6)
Момент инерции четырех колес тележки, которые имеют форму цилиндров радиуса R при общей их массе m кол, можно определить по формуле . Тогда поправка на инертность вращения колес примет вид .
ВЫПОЛНЕНИЕ РАБОТЫ
1. Определить взвешиванием массу тележки вместе с некоторым грузом. Измерить радиус колес по поверхности катания. Записать результаты измерений в табл. 1.
Таблица 1 Таблица 2
| S, м | t, с | , м/с |
| 0,070 | ||
| 0,140 | ||
| 0,210 | ||
| 0,280 | ||
| 0,350 | ||
| 0,420 | ||
| 0,490 |
2. Проверить горизонтальность рельсов. Поставить тележку у начала рельсов так, чтобы стержень тележки был перед отверстиями стартового фотоэлемента. Включить блок питания в сеть 220 В.
Проверить горизонтальность рельсов. Поставить тележку у начала рельсов так, чтобы стержень тележки был перед отверстиями стартового фотоэлемента. Включить блок питания в сеть 220 В.
3. Толкнуть тележку вдоль рельсов так, чтобы она доехала до ловушки и упала в нее. Каждый секундомер покажет время движения тележки от стартового фотоэлемента до его фотоэлемента. Повторить опыт несколько раз. Записать показания семи секундомеров в одном из опытов в табл. 2.
4. Произвести расчеты. Определить среднюю скорость движения тележки на пути от старта до каждого фотоэлемента
5. Построить график зависимости средней скорости движения до каждого фотоэлемента от времени движения. Размер графика не менее половины страницы. На осях координат указать равномерный масштаб. Около точек провести прямую линию.
6. Определить среднее значение ускорения. Для этого на экспериментальной линии как на гипотенузе построить прямоугольный треугольник. По формуле (6) найти среднее значение ускорения.
7. Рассчитать поправку на инертность вращения колес, считая их однородными дисками . Определить по формуле (5) среднее значение коэффициента трения качения .
8. Оценить погрешность измерения графическим способом
. (7)
Записать результат μ = ± δμ, Р = 90%.
Сделать выводы.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Объяснить причину возникновения силы трения качения. Какие факторы влияют на величину силы трения качения?
2. Записать закон для силы трения качения. От чего зависит коэффициент трения качения?
3. Записать уравнения динамики поступательного движения тележки по горизонтальным рельсам и вращательного движения колес. Получить уравнение движения тележки с эффективной массой.
4. Вывести формулу для определения коэффициента трения качения.
5. Объяснить суть графического метода определения ускорения тележки при качении по рельсам. Вывести формулу ускорения.
6. Объяснить влияние вращения колес на инертность тележки.
Работа 17-б
Похожая информация.
Угол и конус трения. Многие задачи на равновесие тела на шероховатой поверхности при наличии силы трения, удобно решать геометрически. Для этой цели используют понятие угла и конуса трения.
Пусть твёрдое тело под действием активных сил находится на шероховатой поверхности в предельном состоянии равновесия, т.е. таком состоянии, когда сила трения достигает своего наибольшего значения при данном значении нормальной реакции (рис. 8.4). В этом случае полная реакция шероховатой поверхности отклонена от нормали к общей касательной плоскости трущихся поверхностей на наибольший угол.
Угол φ между полной реакцией шероховатого тела и направлением нормальной реакции называют углом трения. Угол трения φ зависит от коэффициента трения, т.е.
следовательно, tgφ=ƒ, т.е. тангенс угла трения равен коэффициенту трения скольжения.
Конусом трения называют конус, описанный полной реакцией вокруг направления нормальной реакции. Его можно получить, изменяя активные силы так, чтобы тело на шероховатой поверхности находилось в предельных положениях равновесия, стремясь выйти из равновесия по всем возможным направлениям, лежащим в общей касательной плоскости соприкасающихся поверхностей. Если коэффициент трения во всех направлениях одинаков, то конус трения круговой.
Его можно получить, изменяя активные силы так, чтобы тело на шероховатой поверхности находилось в предельных положениях равновесия, стремясь выйти из равновесия по всем возможным направлениям, лежащим в общей касательной плоскости соприкасающихся поверхностей. Если коэффициент трения во всех направлениях одинаков, то конус трения круговой.
Если неодинаков, то конус трения некруговой, например в случае, когда свойства соприкасающихся поверхностей различны (вследствие определенного направления волокон или в зависимости от направления обработки поверхности тел, если обработка происходит на строгальном станке и т.п.).
Для равновесия тела на шероховатой поверхности необходимо и достаточно, чтобы линия действия равнодействующей активных сил, действующих на тело, проходила внутри конуса трения или в предельном состоянии по его образующей через его вершину (рис. 8.5).
Тело нельзя вывести из равновесия любой по модулю активной силой, если её линия действия проходит внутри конуса трения, т. е. a
е. a
Если линия действия равнодействующей активных сил не проходит внутри конуса трения или по его образующей, т.е. a > φ (рис. 8.5), то тело на шероховатой поверхности не может находиться в равновесии, Q> F.
Задача 1. На тело, находящееся на шероховатой горизонтальной поверхности, действует сила под углом а = 10°. Определить, выйдет ли тело из положения равновесия, если коэффициент трения f = 0,2 (рис. 4).
Решение. Для уравновешенной плоской системы сходящихся сил можно составить два уравнения равновесия:
Находим из (2)
,
.
Так как , то , или . Тогда .
Так как сила приложена под углом, меньшим угла трения, то тело не выйдет из положения равновесия.
Задача 2. Тело весом 100 Н удерживается на шероховатой наклонной плоскости силой Т (рис. 5). Коэффициент трения скольжения между телом и плоскостью f = 0,6. Определить значение силы Т при равновесии тела на плоскости, если a = 45°.
Решение. Возможны два случая предельного равновесия тела и соответственно два предельных значения силы Т при двух направлениях силы трения:
,
где — коэффициент, учитывающий направление движения, = ±1.
Составим для плоской произвольной системы сил два уравнения равновесия.
Научно-практическая конференция
Коэффициент трения и м етоды его расчета
Пенза 2010 г.
I глава. Теоретическая часть
1. Виды трения, коэффициент трения
II глава. Практическая часть
Расчет трения покоя, скольжения, и качения
Расчет коэффициента трения покоя
Список литературы
I глава. Теоретическая часть
1. Виды трения, коэффициент трения
С
трением мы сталкиваемся на каждом шагу.
Вернее было бы сказать, что без трения
мы и шагу ступить не можем. Но несмотря
на ту большую роль, которую играет трение
в нашей жизни, до сих пор не создана
достаточно полная картина возникновения
трения. Это связано даже не с тем, что
трение имеет сложную природу, а скорее
с тем, что опыты с трением очень
чувствительны к обработке поверхности
и поэтому трудно воспроизводимы.
Это связано даже не с тем, что
трение имеет сложную природу, а скорее
с тем, что опыты с трением очень
чувствительны к обработке поверхности
и поэтому трудно воспроизводимы.
Существует внешнее и внутреннее трение (иначе называемое вязкостью ). Внешним называют такой вид трения, при котором в местах соприкосновения твердых тел возникают силы, затрудняющие взаимное перемещение тел и направленные по касательной к их поверхностям.
Внутренним трением (вязкостью) называется вид трения, состоящий в том, что при взаимном перемещении. слоев жидкости или газа между ними возникают касательные силы, препятствующие такому перемещению.
Внешнее
трение подразделяют на трение
покоя (статическое
трение )
и кинематическое
трение .
Трение покоя возникает между неподвижными
твердыми телами, когда какое-либо из
них пытаются сдвинуть с места.
Кинематическое трение существует между
взаимно соприкасающимися движущимися
твердыми телами. Кинематическое трение,
в свою очередь, подразделяется на трение
скольжения и трение
качения .
Кинематическое трение,
в свою очередь, подразделяется на трение
скольжения и трение
качения .
В жизни человека силы трения играют важную роль. В одних случаях он их использует, а в других борется с ними. Силы трения имеют электромагнитную природу.
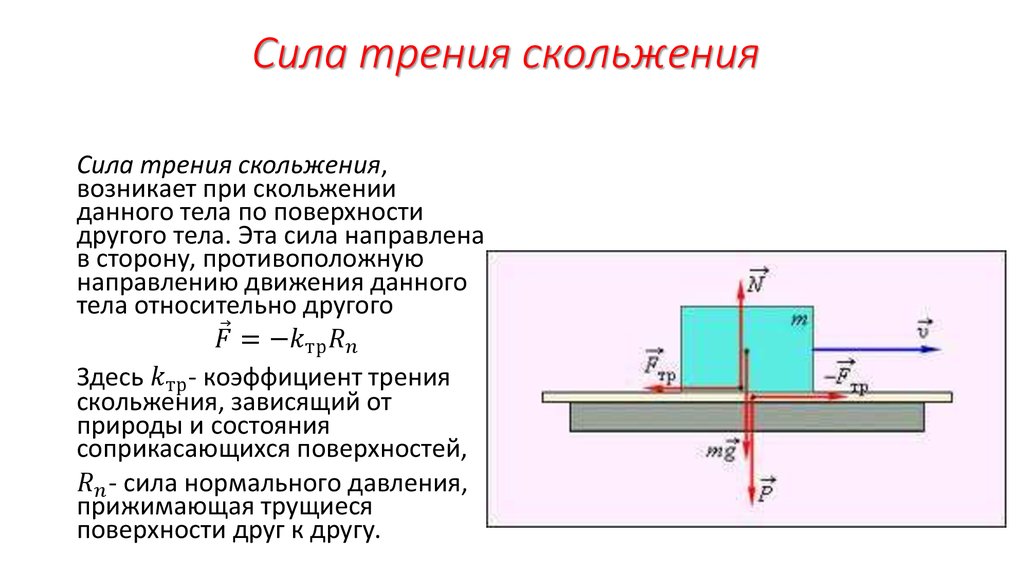
Если тело скользит по какой-либо поверхности, его движению препятствует сила трения скольжения.
Где N — сила реакции опоры, a μ — коэффициент трения скольжения. Коэффициент μ зависит от материала и качества обработки соприкасающихся поверхностей и не зависит от веса тела. Коэффициент трения определяется опытным путем.
Сила трения скольжения всегда направлена противоположно движению тела. При изменении направления скорости изменяется и направление силы трения.
Сила
трения начинает действовать на тело,
когда его пытаются сдвинуть с места.
Если внешняя сила F меньше произведения μN, то тело не будет сдвигаться — началу
движения, как принято говорить, мешает
сила трения покоя . Тело начнет движение только тогда, когда
внешняя сила F превысит максимальное значение, которое
может иметь сила трения покоя
Тело начнет движение только тогда, когда
внешняя сила F превысит максимальное значение, которое
может иметь сила трения покоя
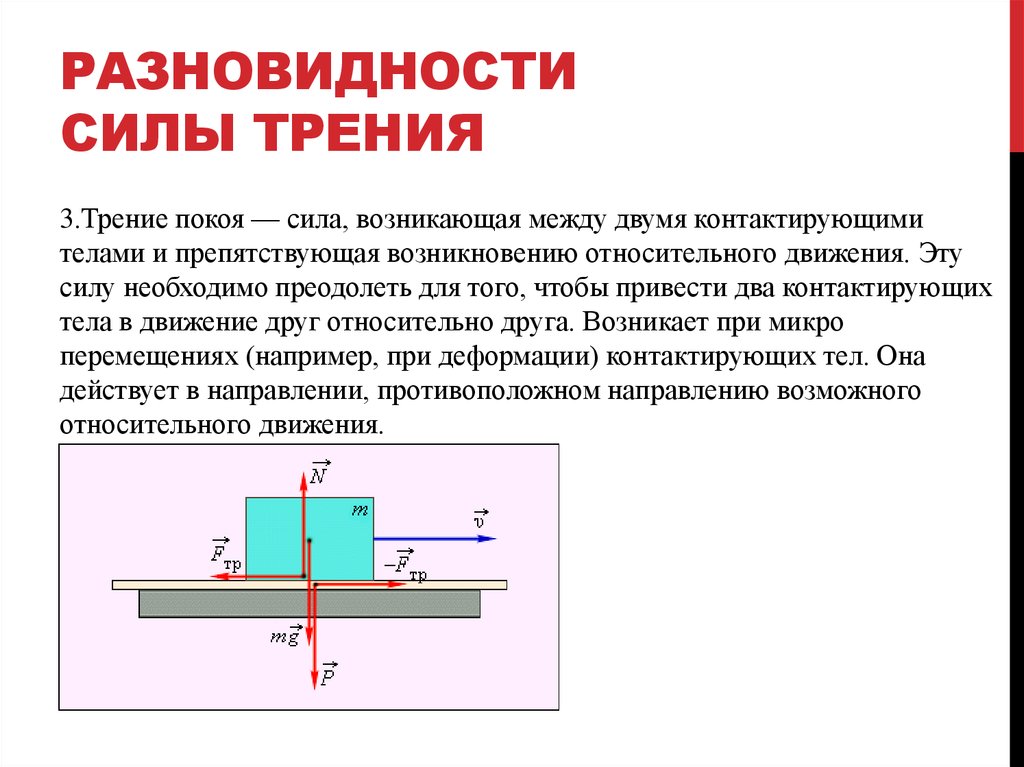
Трение покоя – сила трения, препятствующая возникновению движению одного тела по поверхности другого.
II глава. Практическая часть
1. Расчет трения покоя, скольжения и качения
Основываясь на вышесказанное, я, опытном путем, находил силу трения покоя, скольжения и качения. Для этого я использовал несколько пар тел, в результате взаимодействия которых будет возникать сила трения, и прибор для измерения силы – динамометр.
Вот следующие пары тел:
деревянный брусок в виде прямоугольного параллепипеда определенной массы и лакированный деревянный стол.
деревянный брусок в виде прямоугольного параллепипеда с меньшей чем первый массой и лакированный деревянный стол.
деревянный брусок в виде цилиндра определенной массы и лакированный деревянный стол.
деревянный брусок в виде цилиндра
с меньшей чем первый массой и лакированный
деревянный стол.
После того как были проведены опыты – можно было сделать следующий вывод –
Сила трения покоя, скольжения и качения определяется опытном путем.
Трение покоя:
Для 1) Fп=0.6 Н, 2) Fп=0.4 Н, 3) Fп=0.2 Н, 4) Fп=0.15 Н
Трение скольжение:
Для 1) Fс=0.52 Н, 2) Fс=0.33 Н, 3) Fс=0.15 Н, 4) Fс=0.11 Н
Трение качение:
Для 3) Fк=0.14 Н, 4) Fк=0.08 Н
Тем самым я определил опытным путем все три вида внешнего трения и получил что
Fп> Fс > Fк для одного и того же тела.
2. Расчет коэффициента трения покоя
Но в большей степени интересна не сила трения, а коэффициент трения. Как его вычислить и определить? И я нашел только два способа определения силы трения.
Первый способ: очень простой. Зная формулу и определив опытным путем и N, можно определить коэффициент трения покоя, скольжения и качения.
1) N 0,81 Н, 2) N 0,56 Н, 3) N 2,3 Н, 4) N 1,75
Коэффициент трения покоя:
= 0,74; 2) = 0,71; 3) = 0,087; 4) = 0,084;
Коэффициент трения скольжения:
= 0,64; 2) = 0,59; 3) = 0,063; 4) = 0,063
Коэффициент трения качения:
3) = 0,06; 4) = 0,055;
Сверяясь
с табличными данными я подтвердил
верность своих значений.
Но также очень интересен второй способ нахождения коэффициента трения.
Но этот способ хорошо определяет коэффициент трения покоя, а для вычисления коэффициента трения скольжения и качения возникают ряд затруднений.
Описание: Тело находится с другим телом в покое. Затем конец второго тела на котором лежит первое тело начинают поднимать до тех пор пока первое тело не сдвинется с места.
= sin /cos =tg =BC/AC
На основе второго способа мной были вычислены некоторое число коэффициентов трения покоя.
Дерево по дереву:
АВ = 23,5 см; ВС = 13,5 см.
П = BC/AC = 13,5/23,5 = 0,57
2. Пенопласт по дереву:
АВ = 18,5 см; ВС = 21 см.
П = BC/AC = 21/18,5 = 1,1
3. Стекло по дереву:
АВ = 24,3 см; ВС = 11 см.
П = BC/AC = 11/24,3 = 0,45
4. Алюминий по дереву:
АВ = 25,3 см; ВС = 10,5 см.
П = BC/AC = 10,5/25,3 = 0,41
5. Сталь по дереву:
АВ =
24,6 см; ВС = 11,3 см.
П = BC/AC = 11,3/24,6 = 0,46
6. Орг. Стекло по дереву:
АВ = 25,1 см; ВС = 10,5 см.
П = BC/AC = 10,5/25,1 = 0,42
7. Графит по дереву:
АВ = 23 см; ВС = 14,4 см.
П = BC/AC = 14,4/23 = 0,63
8. Алюминий по картону:
АВ = 36,6 см; ВС = 17,5 см.
П = BC/AC = 17,5/36,6 = 0,48
9. Железо по пластмассе:
АВ = 27,1 см; ВС = 11,5 см.
П = BC/AC = 11,5/27,1 = 0,43
10. Орг. Стекло по пластику:
АВ = 26,4 см; ВС = 18,5 см.
П = BC/AC = 18,5/26,4 = 0,7
На основе своих расчетов и проведенных экспериментах я сделал вывод что П > C > К , что неоспоримо соответствовало теоретической базе взятой из литературы. Результаты моих вычислений не вышли за рамки табличных данных, а даже дополнили их, в результате чего я расширил табличные значения коэффициентов трений различных материалов.
Литература
1.
Крагельский И.В., Добычин М.Н., Комбалов
В. С. Основы расчетов на трение и износ.
М.: Машиностроение, 1977. 526 с.
С. Основы расчетов на трение и износ.
М.: Машиностроение, 1977. 526 с.
Фролов, К. В. (ред.): Современная трибология: Итоги и перспективы . Изд-во ЛКИ, 2008 г.
Елькин В.И.“Необычные учебные материалы по физике”. “Физика в школе” библиотека журнала, №16, 2000.
Мудрость тысячелетий. Энциклопедия. Москва, Олма – пресс, 2006.
Определение коэффициента трения скольжения. Теоретическая механика Описание лабораторной установки
2.2.4. Сила трения
Сила трения действует не только на движущееся тело, но и на тело, находящееся в покое, если существуют силы, которые стремятся этот покой нарушить. На тело, которое катится по опоре, также действует сила трения.
Сила трения покоя численно равна составляющей силы, направленной вдоль поверхности, на которой находится данное тело, и стремящейся сдвинуть его с места (рис. 2.7):
F тр.пок = F x .
Рис. 2.7
При достижении указанной составляющей некоторого критического значения (F
x
= F
крит) тело начинает двигаться. Критическое значение силы, которое соответствует началу движения, определяется формулой
Критическое значение силы, которое соответствует началу движения, определяется формулой
F x = F крит = µ пок N ,
где µ пок — коэффициент трения покоя; N — модуль силы нормальной реакции опоры (эта сила численно равна весу тела).
В момент начала движения сила трения покоя достигает максимального значения:
F тр. пок max = μ пок N .
Сила трения скольжения постоянна и определяется произведением:
F тр.ск = µ ск N ,
где µ ск — коэффициент трения скольжения; N — модуль силы нормальной реакции опоры.
При решении задач считают, что коэффициенты трения покоя µ пок и скольжения µ ск равны между собой:
µ пок = µ ск = µ.
На рис. 2.8 изображен график зависимости величины силы трения F тр от проекции силы F x , стремящейся сдвинуть тело, на ось, направленную вдоль поверхности предполагаемого движения.
Рис. 2.8
Для того чтобы определить, будет ли данное тело находиться в покое или начнет двигаться под действием приложенной силы определенной величины и направления, необходимо:
F крит = µN ,
где µ — коэффициент трения; N — модуль силы нормальной реакции опоры;
3) сравнить значения F крит и F x :
- если F x > F крит, то тело движется под действием приложенной силы; в этом случае сила трения скольжения рассчитывается как
F
тр.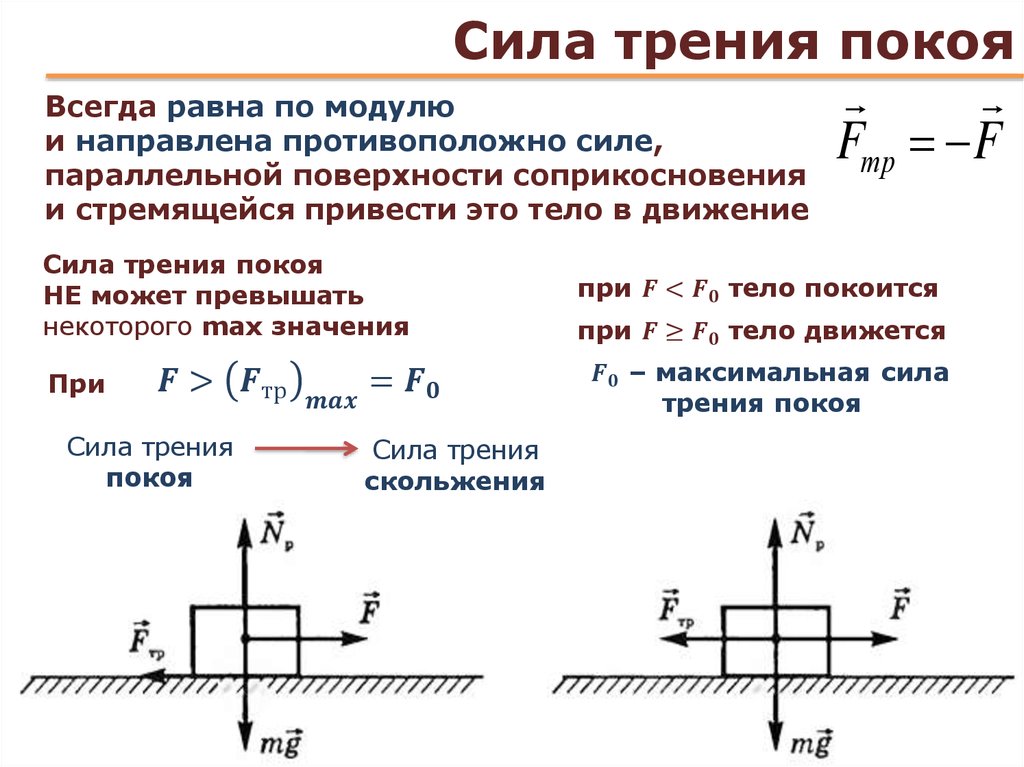 ск = µN
;
ск = µN
;
- если F x
F тр.пок = F x .
Модуль силы трения качения F тр.кач пропорционален коэффициенту трения качения µ кач, модулю силы нормальной реакции опоры N и обратно пропорционален радиусу R катящегося тела:
F тр. кач = μ кач N R .
Пример 13. К телу массой 6,0 кг, лежащему на горизонтальной поверхности, приложена сила 25 Н, направленная вдоль поверхности. Найти силу трения, если коэффициент трения равен 0,5.
Решение. Произведем оценку величины силы, способной вызвать движение тела, по формуле
F кр = µN ,
где µ — коэффициент трения; N — модуль силы нормальной реакции опоры, численно равной весу тела (P = mg ).
Величина критической силы, достаточной для начала движения тела, составляет
F кр = μ m g = 0,5 ⋅ 6,0 ⋅ 10 = 30 Н.
Проекция силы, приложенной к телу в горизонтальном направлении, на ось предполагаемого движения Ox (см. рисунок) равна
F x = F = 25 Н.
F x
т.е. величина приложенной к телу силы меньше величины силы, способной вызвать его движение. Следовательно, тело находится в состоянии покоя.
величина приложенной к телу силы меньше величины силы, способной вызвать его движение. Следовательно, тело находится в состоянии покоя.
Искомая сила трения — сила трения покоя — равна внешней горизонтальной силе, стремящейся этот покой нарушить:
F тр.пок = F x = 25 Н.
Пример 14. Тело находится на наклонной плоскости с углом при основании 30°. Вычислить силу трения, если коэффициент трения равен 0,5 3 . Масса тела равна 3,0 кг.
Решение. На рисунке стрелкой показано направление предполагаемого движения.
Выясним, останется ли тело в покое или начнет двигаться. Для этого рассчитаем величину критической силы, способной вызвать движение, т.е.
F кр = µN ,
где µ — коэффициент трения; N = mg cos α — величина силы нормальной реакции наклонной плоскости.
Расчет дает значение указанной силы:
F кр = μ m g cos 30 ° = 0,5 3 ⋅ 3,0 ⋅ 10 ⋅ 3 2 = 22,5 Н.
Из состояния покоя тело стремится вывести проекция силы тяжести на ось Ox , величина которой составляет
F
x
= mg
sin 30° = 15 Н.
Таким образом, имеет место неравенство
F x
т.е. проекция силы, стремящейся вызвать движение тела, меньше величины силы, способной это сделать. Следовательно, тело сохраняет состояние покоя.
Искомая сила — сила трения покоя — равна
F тр = F x = 15 Н.
Пример 15. Шайба находится на внутренней поверхности полусферы на высоте 10 см от нижней точки. Радиус полусферы составляет 50 см. Вычислить коэффициент трения шайбы о сферу, если известно, что указанная высота является максимально возможной.
Решение. Проиллюстрируем условие задачи рисунком.
Шайба, согласно условию задачи, находится на максимально возможной высоте. Следовательно, сила трения покоя, действующая на шайбу, имеет максимальное значение, совпадающее с проекцией силы тяжести на ось Ox :
F тр. пок max = F x ,
где F
x
= mg
cos α — модуль проекции силы тяжести на ось Ox
; m
— масса шайбы; g
— модуль ускорения свободного падения; α — угол, показанный на рисунке.
Максимальная сила трения покоя совпадает с силой трения скольжения:
F тр. пок max = F тр. ск,
где F тр.ск = µN — модуль силы трения скольжения; N = mg sin α — величина силы нормальной реакции поверхности полусферы; µ — коэффициент трения.
Коэффициент трения определим, записав указанное равенство в явном виде:
mg cos α = µmg sin α.
Отсюда следует, что искомый коэффициент трения определяется тангенсом угла α:
Указанный угол определим из дополнительного построения:
tg α = R − h 2 h R − h 2 ,
где h — предельная высота, на которой может находиться шайба; R — радиус полусферы.
Расчет дает значение тангенса:
tg α = 0,5 − 0,1 2 ⋅ 0,1 ⋅ 0,5 − (0,1) 2 = 4 3
и позволяет вычислить искомый коэффициент трения.
Силой трения () называют силу, возникающую при относительном движении тел. Эмпирически установлено, что сила трения скольжения зависит от силы взаимного давления тел (реакции опоры) (N), материалов поверхностей трущихся тел, скоростей относительного движения.
ОПРЕДЕЛЕНИЕ
Физическая величина, которая характеризует трущиеся поверхности, называется коэффициентом трения . Чаще всего коэффициент трения обозначают буквами k или .
В общем случае коэффициент трения зависит от скорости движения тел относительно друг друга. Надо отметить, что зависимость обычно не принимается во внимание и коэффициент трения скольжения считают постоянным. В большинстве случаев силу трения
Коэффициент трения скольжения величина безразмерная. Коэффициент трения зависит от: качества обработки поверхностей, трущихся тел, присутствия на них грязи, скорости движения тел друг относительно друга и т.д. Коэффициент трения определяют эмпирически (опытным путем).
Коэффициент трения, который соответствует максимальной силе трения покоя в большинстве случаев больше, чем коэффициент трения скольжения.
Для большего числа пар материалов величина коэффициента трения не больше единицы и лежит в пределах
На значение коэффициента трения любой пары тел, между которыми рассматривается сила трения, оказывает влияние давление, степень загрязненности, площади поверхности тел и другое, что обычно не учитывается. Поэтому те значения коэффициентов сил трения, которые указаны в справочных таблицах, полностью совпадают с действительностью лишь при условиях, в которых они были получены. Следовательно, значения коэффициентов сил трения нельзя считать неизменной для одной и той де пары трущихся тел. Так, различают коэффициенты терния для сухих поверхностей и поверхностей со смазкой. Например, коэффициент терния скольжения для тела из бронзы и тела из чугуна, если поверхности материалов сухие равен Для этой же пары материалов коэффициент терния скольжения при наличии смазки
Поэтому те значения коэффициентов сил трения, которые указаны в справочных таблицах, полностью совпадают с действительностью лишь при условиях, в которых они были получены. Следовательно, значения коэффициентов сил трения нельзя считать неизменной для одной и той де пары трущихся тел. Так, различают коэффициенты терния для сухих поверхностей и поверхностей со смазкой. Например, коэффициент терния скольжения для тела из бронзы и тела из чугуна, если поверхности материалов сухие равен Для этой же пары материалов коэффициент терния скольжения при наличии смазки
ПРИМЕР 1
| Задание | Тонкая металлическая цепь лежит на горизонтальном столе (рис.1). Ее длина равна , масса . Конец цепи свешивается с края стола. Если длина свешивающейся части цепи составит часть от длины всей цепи, она начинает скользить вниз со стола. Каков коэффициент трения цепи о стол, если цепь считать однородной по длине? |
| Решение | Цепь движется под действием силы тяжести. Пусть сила тяжести, действующая на единицу длины цепи равна . В таком случае в момент начала скольжения сила тяжести, которая действует на свешивающуюся часть, будет: Пусть сила тяжести, действующая на единицу длины цепи равна . В таком случае в момент начала скольжения сила тяжести, которая действует на свешивающуюся часть, будет:До начала скольжения эта сила уравновешивается силой трения, которая действует на часть цепи, которая лежит на столе: Так как силы уравновешиваются, то можно записать (): |
| Ответ |
ПРИМЕР 2
| Задание | Каков коэффициент трения тела о наклонную плоскость, если угол наклона плоскости равен а ее длина равна . Тело по плоскости двигалось с постоянным ускорением в течение времени t. |
| Решение | В соответствии со вторым законом Ньютона равнодействующая сил приложенных к движущемуся с ускорением телу равна: В проекциях на оси X и Y уравнения (2.1), получим: |
Если брусок тянут с помощью динамометра с постоянной скоростью, то динамометр показывает модуль силы трения скольжения (F тр). Здесь сила упругости пружины динамометра уравновешивает силу трения скольжения.
С другой стороны, сила трения скольжения зависит от силы нормальной реакции опоры (N), которая возникает в следствие действия веса тела. Чем вес больше, тем больше сила нормальной реакции. И чем больше сила нормальной реакции, тем больше сила трения . Между этими силами существует прямая пропорциональная зависимость, которую можно выразить формулой:
Здесь μ – это коэффициент трения . Он показывает, как именно сила трения скольжения зависит от силы нормальной реакции (или, можно сказать, от веса тела), какую долю от нее составляет. Коэффициент трения — безразмерная величина. Для разных пар поверхностей μ имеет разное значение.
Так, например, деревянные предметы трутся друг о друга с коэффициентом от 0,2 до 0,5 (в зависимости от вида деревянных поверхностей). Это значит, что если сила нормальной реакции опоры 1 Н, то при движении сила трения скольжения может составить значение, лежащее в промежутке от 0,2 Н до 0,5 Н.
Из формулы F тр = μN следует, что зная силы трения и нормальной реакции, можно определить коэффициент трения для любых поверхностей:
Сила нормальной реакции опоры зависит от веса тела. Она равна ему по модулю, но противоположна по направлению. Вес тела (P) можно вычислить, зная массу тела. Таким образом, если не учитывать векторность величин, можно записать, что N = P = mg. Тогда коэффициент трения находится по формуле:
Она равна ему по модулю, но противоположна по направлению. Вес тела (P) можно вычислить, зная массу тела. Таким образом, если не учитывать векторность величин, можно записать, что N = P = mg. Тогда коэффициент трения находится по формуле:
μ = F тр / (mg)
Например, если известно, что сила трения тела массой 5 кг, движущегося по поверхности, равна 12 Н, то можно найти коэффициент трения: μ = 12 Н / (5 кг ∙ 9,8 Н/кг) = 12 Н / 49 Н ≈ 0,245.
Глава 15. Теорема об изменении кинетической энергии.
15.3. Теорема об изменении энергии кинетической точки и твердого тела при поступательном движении.
15.3.1. Какую работу совершают действующие на материальную точку силы, если ее кинетическая энергия уменьшается с 50 до 25 Дж? (Ответ -25)
15.3.2. Свободное падение материальной точки массой m начинается из состояния покоя. Пренебрегая сопротивлением воздуха, определить путь, пройденный точкой к моменту времени, когда она имеет скорость 3 м/с. (Ответ 0,459)
(Ответ 0,459)
15.3.3. Материальная точка массой m = 0,5 кг брошена с поверхности Земли с начальной скоростью v о = 20 м/с и в положении М имеет скорость v = 12 м/с. Определить работу силы тяжести при перемещении точки из положения М о в положение М (Ответ -64)
15.3.4. Материальная точка массой m брошена с поверхности Земли под углом α = 60° к горизонту с начальной скоростью v 0 = 30 м/с. Определить наибольшую высоту h подъема точки. (Ответ 34,4)
15.3.5. Тело массой m = 2 кг от толчка поднимается по наклонной плоскости с начальной скоростью v о = 2 м/с. Определись работу силы тяжести на пути, пройденном телом до остановки. (Ответ -4)
15.3.6. Материальная точка М массой m, подвешенная на нити длиной ОМ = 0,4 м к неподвижной точке О, отведена на угол α = 90° от положения равновесия и отпущена без начальной скорости. Определить скорость этой точки во время ее прохождения через положение равновесия. (Ответ 2,80)
(Ответ 2,80)
15.3.7. Кабина качелей подвешена на двух стержнях длиной l = 0,5 м. Определить скорость кабины при прохождении ею нижнего положения, если в начальный момент стержни были отклонены на угол φ = 60° и отпущены без начальной скорости. (Ответ 2,21)
15.3.8. Материальная точка М массой m движется под действием силы тяжести по внутренней поверхности полуцилиндра радиуса r = 0,2 м. Определить скорость материальной точки в точке В поверхности, если ее скорость в точке A равна нулю. (Ответ 1,98)
15.3.9. По проволоке АВС, расположенной в вертикальной плоскости и изогнутой в виде дуг окружностей радиусов r 1 , = 1 м, r 2 = 2 м, может скользить без трения кольцо D массой m. Определить скорость кольца в точке С, если его скорость в точке А равна нулю. (Ответ 9,90)
15.3.10. По горизонтальной плоскости движется тело массой m = 2 кг, которому была сообщена начальная скорость v 0 = 4 м/с. До остановки тело прошло путь, равный 16 м. Определить модуль силы трения скольжения между телом и плоскостью. (Ответ 1)
Определить модуль силы трения скольжения между телом и плоскостью. (Ответ 1)
15.3.11. Тело массой m = 100 кг начинает движение из состояния покоя по горизонтальной шероховатой плоскости под действием постоянной силы F. Пройдя путь, равный 5 м, скорость тела становится равной 5 м/с. Определить модуль силы F, если сила трения скольжения F тр = 20 Н. (Ответ 270)
15.3.12. Хоккеист, находясь на расстоянии 10 м от ворот, клюшкой сообщает шайбе, лежащей на льду, скорость 8 м/с. Шайба, скользя по поверхности льда, влетает в ворота со скоростью 7,7 м/с. Определить коэффициент трения скольжения между шайбой и поверхностью льда.
(Ответ 2,40 10 -2)
15.3.13. По наклонной плоскости спускается без начальной скорости тело массой m = 1кг. Определить кинетическую энергию тела в момент времени, когда оно прошло путь, равный 3 м, если коэффициент трения скольжения между телом и наклонной плоскостью f = 0,2. (Ответ 9,62)
15.3.14. По наклонной плоскости спускается без начальной скорости груз массой m. Какую скорость v будет иметь груз, пройдя путь, равный 4м от начала движения, если коэффициент трения скольжения между грузом и наклонной плоскостью равен 0,15? (Ответ 5,39)
Какую скорость v будет иметь груз, пройдя путь, равный 4м от начала движения, если коэффициент трения скольжения между грузом и наклонной плоскостью равен 0,15? (Ответ 5,39)
15.3.15. К ползуну 1 массой m = 1 кг прикреплена пружина 2. Пружину сжимают из свободного состояния на величину 0,1 м, после чего груз отпускают без начальной скорости. Определить жесткость пружины, если груз, пройдя путь, равный 0,1 м, приобретает скорость 1 м/с.
(Ответ 100)
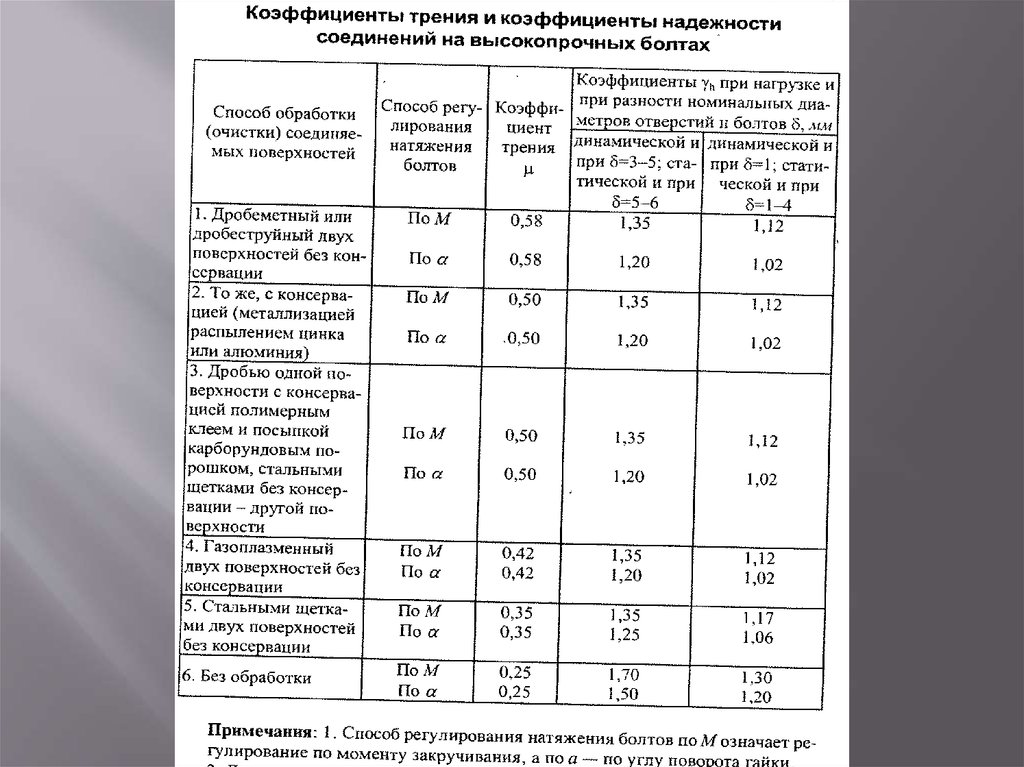
ISO 8295 Определение коэффициентов трения (COF)
Переход к содержанию страницы
- Отрасли
(Показать субменю)
- Испытание материалов
- Пластмассы
(Показать субменю)
- термопластичные и термореактивные формовочные массы
- Полуфабрикаты и готовые изделия
- Тонкие материалы и пленки
- Испытания жестких и мягких полимерных пенных материалов
- Пластиковые трубы
- Композиты
- Металлы
(Показать субменю)
- Стандарты, металлы
- Толстолистовая сталь
- Стальные листы и ленты
- Тонколистовая сталь
- Штанги и стержни
- Проволока и кабели
- Литые и кованые изделия
- Крепежные элементы
- Трубы
- Автомобильная промышленность
(Показать субменю)
- Кузов
- Двигатель и привод
- Ходовая часть
- Компоненты интерьера и систем безопасности
- Технология изготовления аккумуляторов
- Медицина/фармацевтика
(Показать субменю)
- Американская рецептурная книга / United States Pharmacopeia
- Терапевтические системы
- Катетеры и стенты
- Биоматериалы и клинические исследования
- Стоматология
- Бедренные имплантаты
- Биомеханика и ортопедия
- Латекс, резина, силикон
- Текстильные медицинские продукты
- Хирургические инструменты
- Медицинская упаковка
- Автоматизированные испытания
- ВУЗы
- Энергия
(Показать субменю)
- Водородная технология
- Технология изготовления аккумуляторов
- Гелиоиндустрия
- Бумага, картон, санитарно-гигиеническая бумага
(Показать субменю)
- Бумага
- Гофрированный и сплошной картон
- Санитарно-гигиеническая бумага
- Продукты питания и упаковка
- Текстильные изделия
- Мехатроника — электроника
- Стройматериалы
- Пружины
- Продукция
(Показать субменю)
- Статические испытательные машины
(Показать субменю)
- Универсальные испытательные машины
(Показать субменю)
- Машины для испытаний на растяжение
- zwickiLine
- ProLine
- AllroundLine
- Машина для больших усилий испытаний (модельный ряд E)
- Высокотемпературные испытательные системы
- teachXpert
- cLine
- Гидравлические испытательные машины (модельный ряд H)
- Электромеханический испытательный сервоцилиндр
- Испытательные машины с центральным шпинделем
- Машины для усталостных испытаний
(Показать субменю)
- Kappa SS-CF
- Kappa SS
- Kappa DS
- Kappa LA-Spring
- Kappa LA-DW
- Машина Kappa Multistation
- Машины BUP для испытаний на глубокую вытяжку
- Машины для испытаний на кручение TorsionLine
- Двухосные / трехосные испытательные машины
(Показать субменю)
- Испытательные машины с торсионным приводом
- Машина для испытаний на многовекторное растяжение
- Двухосная машина для испытаний биоматериалов
- Испытательная машина для трехосного нагружения
- Машина для испытаний тубулярных биоматериалов
- Системы для испытаний автоинъекторов
- Универсальные испытательные машины
(Показать субменю)
- Динамические машины и машины для усталостных испытаний
(Показать субменю)
- Сервогидравлические испытательные машины
(Показать субменю)
- Модельный ряд HA
- Модельный ряд HB
- Модельный ряд HC
- HC-kompakt
- Вращательное качание, HCT HBT
- Высокоскоростная испытательная машина HTM
- Высокочастотный пульсатор Vibrophore
- Электродинамическая испытательная машина LTM
- Машина для испытаний на изгиб с вращением
- Сервогидравлические испытательные машины
(Показать субменю)
- Автоматизированные испытательные системы
(Показать субменю)
- roboTest N
- roboTest L
- roboTest C
- roboTest P
- roboTest F
- roboTest R
- roboTest H
- roboTest I
- roboTest X
- Оборудование для ударных испытаний
- Приборы для определения индекса расплава
(Показать субменю)
- Пластометр Cflow
- Пластометр Mflow
- Пластометр Aflow
- Испытательные приборы HDT и Вика
(Показать субменю)
- Amsler HDT/Вика Allround
- HDT/Вика Allround
- HDT/Вика Standard
- Вика Dry
- Машины для определения твердости
(Показать субменю)
- Универсальные машины для определения твердости
(Показать субменю)
- ZHU/zwickiLine+
- ZHU250CL
- ZHU250 для универсального определения твердости
- Твердомеры Виккерса
(Показать субменю)
- ZHVμ
- Твердомер Виккерса ZHV30 для малых нагрузок
- ZHV30/zwickiLine
- ZHV10
- Твердомеры Роквелла
(Показать субменю)
- ZHR
- ZHR8150CLK
- Инструментированное испытание на вдавливание
(Показать субменю)
- Наноиндентор ZHN
- ZHN/SEM
- Твердомеры по Шор / IRHD
(Показать субменю)
- Аналоговые и цифровые твердомеры по Шор
- ZwickRoell 3103
- ZwickRoell 3105 combi test
- Универсальные машины для определения твердости
(Показать субменю)
- Модернизация испытательных систем
(Показать субменю)
- Электромеханические статические испытательные машины
- Гидравлические статические испытательные машины
- Сервогидравлические испытательные машины
- Высокочастотные пульсаторы
- Роботизированные испытательные системы
- Испытательные машины фирмы Instron
- Испытательные машины Hegewald & Peschke
- Статические испытательные машины
(Показать субменю)
- testXpert
- Аксессуары
(Показать субменю)
- Программное обеспечение testXpert
- Измерительная, управляющая, регулирующая электроника
- Датчики силы X-force
- Захваты
- Испытательные приспособления
- Экстензометры
(Показать субменю)
- videoXtens
(Показать субменю)
- 2D DIC
- videoXtens biax 2-150 HP
- videoXtens 2-120 HP
- videoXtens 1-120
- videoXtens 1-270
- videoXtens T-160 HP
- videoXtens 3-300
- videoXtens 1-32 HP/TZ
- videoXtens Array
- laserXtens
(Показать субменю)
- laserXtens 7-220 HP
- laserXtens 2-220 HP
- laserXtens 1-15 HP
- laserXtens 2-120 HP/TZ
- laserXtens 1-32 HP/TZ
- Датчик lightXtens 2-1000
- multiXtens II HP
- makroXtens II
- Длинноходовой экстензометр
- Экстензометры digiClip
- Экстензометр Clip-On
- Контактные датчики DMS
- Экстензометры для испытаний на сжатие, изгиб, а также для испытаний готовых изделий
- videoXtens
(Показать субменю)
- Температура и климат
- Подготовка образцов и снятие размеров
- Сервис
(Показать субменю)
- Калибровка
- ZwickRoell Академия
(Показать субменю)
- Индивидуальная стажировка
- Испытательная лаборатория
- Горячая линия и служба поддержки
- Техобслуживание и инспекция
- Ремонт и запчасти
- Перевозка машин
- Аттестация DQ IQ OQ
- Измерение соосности
- ПО, сервис
- Консультации и технология применения
- Фирма
(Показать субменю)
- О нас
- Филиалы по всему миру
- Качество
- Экология и социальные вопросы / CSR
- История
- Надежные результаты испытаний
- Карьера
(Показать субменю)
- Почему именно ZwickRoell?
- Вакансии
- Новости & события
Контакты
TopКоэффициент трения шины по асфальту
Содержание
- Коэффициенты трения и сцепления колеса автомобиля с покрытием
- Коэффициенты трения покоя и скольжения
- Тормозим на широких шинах — результат вас удивит
- Что такое сила трения покоя?
- Тормозим по другим законам
- Шире шины — выше трение
- Еще раз о коэффициенте трения
- Коэффициенты трения покоя и трения качения
- Видео
Коэффициенты трения и сцепления колеса автомобиля с покрытием
Реализация силы тяги Т ведущим колесом зависит от значения трения между шиной колеса и поверхностью дороги:
где фт— коэффициент трения протектора шины по дорожной поверхности; QK, — нагрузка на колесо автомобиля.
Сила трения при торможении колеса может быть определена через площадь контакта шины с покрытием:
где Т — сила трения колеса с покрытием;
S — площадь контакта колеса с покрытием;
фт — коэффициент трения протектора шины с покрытием;
Кж — коэффициент жесткости шины; рв — давление воздуха в шине.
В дорожной практике вместо понятия силы сцепления применяют понятие коэффициента сцепления:
Коэффициентом сцепления называют отношение реактивной силы, действующей на колесо автомобиля в плоскости его контакта с покрытием, к вертикальной нагрузке, передаваемой колесом на покрытие. По физической сущности коэффициент сцепления представляет собой коэффициент трения пары резина протектора автомобильной шины — покрытие проезжей части дороги.
Отличие этих довольно близких понятий состоит в соотношении адгезионной (Та) и гистерезисной (Td), или деформационной, долей, силы трения — сцепления (рис. 10.7).
10.7).
Рис. 10.7. Зависимость адгезионной (Та) и деформационной (Td) долей силы трения (Т) от шероховатости покрытия: а — на сухом покрытии; б — на мокром покрытии; 2 — высота выступов шероховатости
Адгезионные силы — это силы слипания (склеивания) поверхностей двух разнородных твердых тел, в данном случае поверхности шины колеса и дорожного покрытия.
Адгезионная составляющая является результатом молекулярного взаимодействия контактирующих материалов. Ее значение зависит от материала дорожного покрытия (например, асфальтобетон или цементобетон) и продолжительность контакта (т.е. скорости движения взаимодействующей пары относительно друг друга).
Деформационная составляющая формируется в результате затрат энергии на взаимную деформацию контактирующих тел выступами неровностей, находящимися на их поверхности. На сухих дорожных покрытиях сила трения в контакте шины формируется в основном за счет молекулярной составляющей. На покрытиях, имеющих на своей поверхности пленку воды, автомобильного масла или топлива, пыли, сила трения в основном формируется ее деформационной составляющей. Молекулярная составляющая появляется только после разрыва пленки смазки неровностями на поверхности контактирующих тел и вступления их в непосредственное соприкосновение.
На покрытиях, имеющих на своей поверхности пленку воды, автомобильного масла или топлива, пыли, сила трения в основном формируется ее деформационной составляющей. Молекулярная составляющая появляется только после разрыва пленки смазки неровностями на поверхности контактирующих тел и вступления их в непосредственное соприкосновение.
При скольжении одного гладкого твердого тела по другому основную роль играют адгезионные силы, т.е. собственно трение. При движении эластичной шины по дорожному покрытию характер взаимодействия меняется. Дорожная поверхность всегда имеет шероховатости и поэтому доля гистерезисной (деформационной) составляющей значительно больше, чем адгезионной. Такое взаимодействие характеризуется силой сцепления [4].
Коэффициент сцепления зависит от многих факторов:
Наибольшее влияние на коэффициент сцепления оказывают тип, ровность и состояние поверхности покрытия, а также скорость движения.
При движении автомобиля по неровной поверхности с возрастанием скорости деформация шины происходит не полностью.
Если принять коэффициент сцепления ф при высокой ровности за 100%, то при увеличении неровности покрытий Sc сцепление снижается:
Источник
Трением называется сопротивление, возникающее при относительном перемещении двух соприкасающихся тел в плоскости их касания. Сила сопротивления, направленная противоположно сдвигающему усилию, называется силой трения. По величине перемещения и зависимости его от приложенной силы различают:
а) силу трения движения,
б) неполную силу трения покоя и
в) полную силу трения покоя, которую обычно называют силой трения покоя.
Сила трения движения соответствует очень большим необратимым относительным перемещениям, величина которых не зависит от приложенной силы. В этом случае последняя в случае равномерного движения уравновешивается силой трения движения.
Неполная сила трения покоя соответствует очень малым частично обратимым перемещениям, величина которых пропорциональна приложенной силе. Величина перемещения, соответствующего неполной силе трения, называется предварительным смещением. Обычно визуально обнаружить предварительное смещение не удаётся, так как оно измеряется микронами. В случае предварительного смещения приложенная сила уравновешивается неполной силой трения, и тело находится в покое. Неполная сила трения зависит от приложенной силы и изменяется с увеличением последней от нуля до некоторого максимального значения, при котором она получает название силы трения покоя. В этом случае предварительное смещение переходит в относительное.
Обычно визуально обнаружить предварительное смещение не удаётся, так как оно измеряется микронами. В случае предварительного смещения приложенная сила уравновешивается неполной силой трения, и тело находится в покое. Неполная сила трения зависит от приложенной силы и изменяется с увеличением последней от нуля до некоторого максимального значения, при котором она получает название силы трения покоя. В этом случае предварительное смещение переходит в относительное.
В зависимости от кинематических признаков относительного перемещения различают следующие виды трения:
а) Трение скольжения, при котором одни и те же точки одного тела приходят в соприкосновение всё с новыми и новыми точками другого тела.
б) Трение качения, при котором следующие одна за другой точки одного тела приходят в соприкосновение со следующими одна за другой точками другого тела, причём мгновенная ось вращения одного тела относительно другого проходит через одну из точек касания.
в) Трение верчения, при котором все точки, расположенные в плоскости касания двух тел, описывают концентрические окружности с центром, лежащим на оси верчения.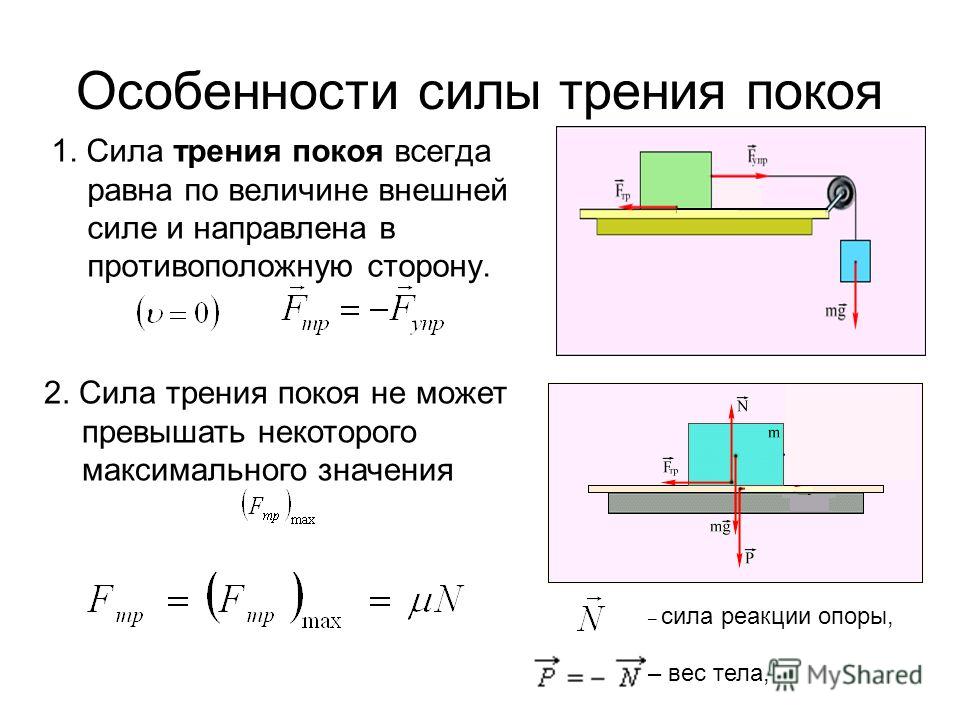
Трение верчения является разновидностью трения скольжения. Приведённые выше определения характеризуют трение идеальных тел; для реальных деформированных тел касание будет происходить не в точках, а в зонах. Часто один вид трения сопровождается другим: например, качение сопровождается скольжением (качение с проскальзыванием).
По признаку состояния поверхностей трущихся тел в зависимости от смазки различают:
а) Чистое трение, возникающее на фрикционных поверхностях при полном отсутствии на них посторонних примесей (жидкостей и газов в адсорбированном состоянии). br>Практически чистое трение очень трудно осуществимо; оно может быть реализовано лишь в вакууме.
б) Сухое трение, возникающее при отсутствии смазки и загрязнений между поверхностями. Часто его называют трением несмазанных поверхностей. (Термин применять не рекомендуется.)
в) Граничное трение, при котором поверхности разделены слоем смазки настолько незначительной толщины, что он обладает особыми свойствами, отличными от объёмных свойств смазки и зависящими от природы и состояния трущихся поверхностей.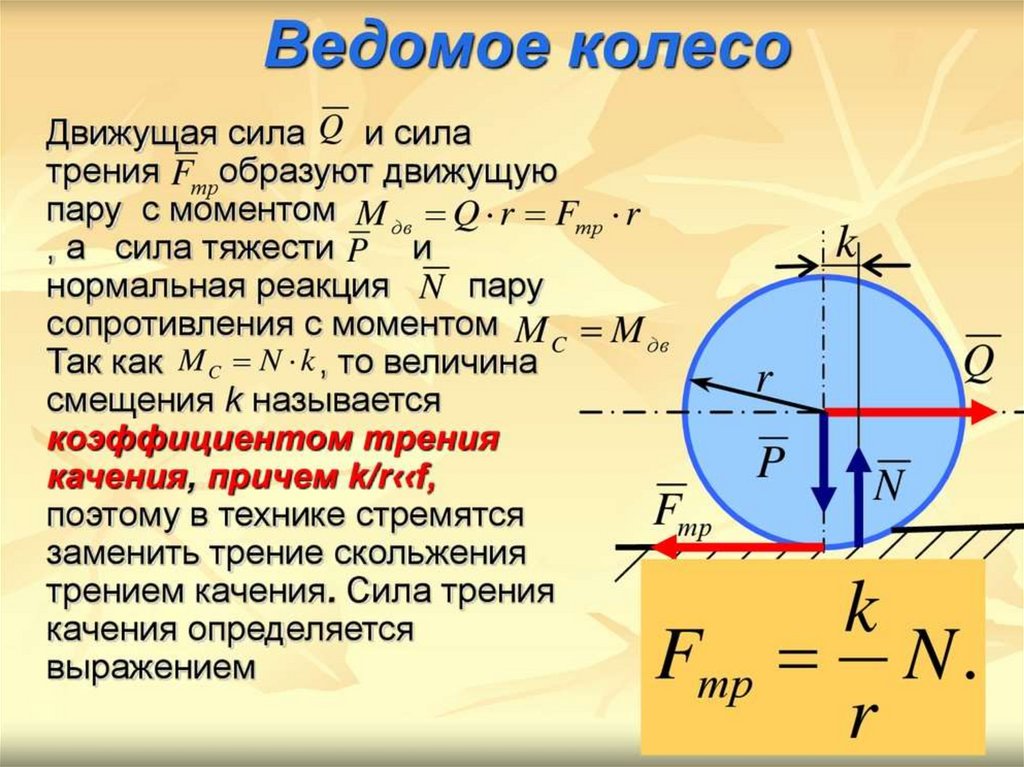 Обычные уравнения гидродинамики вязкой жидкости в этом случае неприменимы.
Обычные уравнения гидродинамики вязкой жидкости в этом случае неприменимы.
Пограничный слой имеет слоистое строение. Ближе к металлу располагаются более активные молекулы, которые, прикрепляясь своими активными концами к поверхности металла, образуют как бы ворс из молекул смазки.
г) Жидкостное трение, при котором поверхности полностью разделены слоем жидкости, причём внешнее давление вследствие специфичной формы зазора воспринимается слоем вязкой движущейся жидкости.
д) Полусухое трение, смешанное трение, одновременно граничное и сухое.
е) Полужидкостное трение, смешанное трение, одновременно жидкостное и граничное или жидкостное и сухое.
Как указывалось выше, на величину коэфициента трения всякой трущейся пары влияет ряд обычно не учитываемых параметров (давление, шероховатость, размер поверхности, степень загрязнённости и др.). В связи с этим значения коэфициентов трения, предложенные данными таблицами, пригодны лишь для тех частных условий, при которых они были получены. Очевидно, что определённую таким образом величину коэфициента трения нельзя считать неизменной для данной трущейся пары.
Очевидно, что определённую таким образом величину коэфициента трения нельзя считать неизменной для данной трущейся пары.
КОЭФФИЦИЕНТЫ ТРЕНИЯ ПОКОЯ и СКОЛЬЖЕНИЯ
для ПАР МАТЕРИАЛОВ
| Комбинация материалов | Коэффициент трения | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| сухие поверхности | со смазкой КОЭФФИЦИЕНТЫ ТРЕНИЯ ПРИ СЛАБОЙ СМАЗКЕ КОЭФФИЦИЕНТЫ ТРЕНИЯ СКОЛЬЖЕНИЯ ПО СТАЛИ КОЭФФИЦИЕНТЫ ТРЕНИЯ И ИЗНОСА
КОЭФФИЦИЕНТ ТРЕНИЯ КАЧЕНИЯ ТРЕНИЕ В БОЛТОВЫХ СОЕДИНЕНИЯХ КОЭФФИЦИЕНТЫ СКОЛЬЖЕНИЯ Источник Тормозим на широких шинах — результат вас удивитНе спешите с выводами. Что такое сила трения покоя?Представьте автомобиль, неподвижно стоящий на ровном асфальте. Водитель изо всех сил давит на педаль тормоза. Автомобиль прицеплен к тягачу через динамометр, измеряющий силу тяги. Тягач начинает движение, а динамометр фиксирует значение силы, которая будет максимальной в тот момент, когда автомобиль с заторможенными колесами тронется с места. Если выполнить такие замеры, поочередно устанавливая комплекты шин с протекторами разной ширины, но из одинаковой резиновой смеси, то значения максимальной силы будут схожими. В этом случае идеально работает закон Кулона — расхождения полученных значений будут минимальными, в пределах погрешности измерений. Но как только автомобиль начинает двигаться, зависимость, установленная Кулоном, теряет актуальность, поскольку вместо силы трения покоя, удерживающей заторможенную машину от движения, вступят в действие другие силы трения. Тормозим по другим законамТорможение (читай: преобразование энергии) происходит за счет трения тормозных колодок о поверхность тормозного диска (барабана), внутреннего трения резины протектора (в основном при его деформации в пятне контакта), а также трения протектора об асфальт даже при незначительном проскальзывании. Максимальная эффективность торможения достигается, когда проскальзывание колес составляет около 15% (так называемое рабочее скольжение). На летних шинах такой эффект возникает благодаря сочетанию внутреннего трения резины при деформации протектора, сдвига мелких фракций на поверхности дороги, а также поглощения энергии подвеской — и используется при работе АБС, которая допускает незначительное проскальзывание шины относительно дороги. Таким образом, торможение происходит в переходной стадии трения скольжения. Нужно выйти далеко за пределы элементарной физики, чтобы описать такое сложное взаимодействие различных видов трения. Трение неминуемо приводит к нагреву поверхности протектора, а изменение температуры существенно влияет на сцепные свойства резины. Перегрев протектора приводит к снижению его прочности и последующим микроразрушениям (плавлениям) поверхности, дополнительно ослабляя «держак». Характерный пример — торможение на автомобилях без АБС с полной блокировкой колес, с дымком и характерным запахом, оставляющее на асфальте черные следы горелой резины. Шире шины — выше трениеЧто мы имеем на практике? Чем шире протектор шины, тем больше площадь ее пятна контакта с дорогой, а значит, и поверхность трения больше. Следовательно, большее количество кинетической энергии будет преобразовываться в тепловую. К тому же интенсивнее станет рассеивание тепловой энергии и снизится опасность перегрева. Всё это в совокупности обеспечивает более эффективное торможение. Переохлаждение шины тоже негативно сказывается на ее сцепных свойствах. Это особенно хорошо видно по ухудшению результатов «холодного» торможения на мокром асфальте при +6 °C (ЗР, № 3 и № 4, 2018). Резина не имеет возможности прогреться до рабочей температуры, а потому остается недостаточно эластичной и хуже цепляется за микронеровности асфальта. В этой ситуации способность широких шин лучше охлаждаться, наоборот, неблагоприятно отражается на рабочих характеристиках — в холодную погоду их сцепные свойства ухудшаются заметнее, чем у узких. Еще раз о коэффициенте тренияКак вычислить коэффициент трения? По формуле k = v²/2gs (где v — скорость начала торможения, g — ускорение свободного падения, s — тормозной путь). Значение тормозного пути для каждой шины получаем экспериментальным путем — замеряем при торможении на асфальте. Разные шины обеспечивают разный тормозной путь — следовательно, по своим сцепным свойствам они отличаются друг от друга. Понравилась заметка? Подпишись и будешь всегда в курсе! Источник Коэффициенты трения покоя и трения каченияКоэффициенты трения скольжения для различных материалов
Таблица коэффициентов трения покоя (коэффициентов сцепления) для различных пар материалов. Материал Химически чистые металл по металлу | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| совсем без окисных пленок (тщательно очищенные) | 100 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| несмазанные на воздухе | 1,0 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| смазанные минеральным маслом | 0,2-0,4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| смазанные растительными и животными маслами | 0,1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| медно-свинцовый несмазанный | 0,2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| медно-свинцовый смазанный минеральным маслом | 0,1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сплав Вуда, белый металл = white metall несмазанный | 0,7 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сплав Вуда, белый металл смазанный минеральным маслом | 0,1 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Фосфористая бронза, латунь несмазанная | 0,35 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Фосфористая бронза, латунь смазанная минеральным маслом | 0,15-0,2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сталь обычная несмазанная | 0,4 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Сталь обычная смазанная минеральным маслом | 0,1-0,2 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Стальные поверхности высокой твердости несмазанные | 0,6 | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Стальное колесо по стали | 0,001-0,05 |
| Дереянное колесо по дереву | 0,05-0,08 |
| Стальное колесо по дереву | 0,15-0,25 |
| Пневматичекая шина по асфальту | 0,006-0,02 |
| Деревянное колесо по стали | 0,03-0,04 |
| Шарикоподшипник (подшипник качения) | 0,001-0,004 |
| Роликоподшипник (тоже качения) | 0,0025-0,01 |
| Шарик твердой стали по стали | 0,0005-0,001 |
Сила трения скольжения — силы, возникающие между соприкасающимися телами при их относительном движении. Если между телами отсутствует жидкая или газообразная прослойка (смазка), то такое трение называется сухим. В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.
В противном случае, трение называется «жидким». Характерной отличительной чертой сухого трения является наличие трения покоя.
Опытным путём установлено, что сила трения зависит от силы давления тел друг на друга (силы реакции опоры), от материалов трущихся поверхностей, от скорости относительного движения и не зависит от площади соприкосновения. (Это можно объяснить тем, что никакое тело не является абсолютно ровным. Поэтому истинная площадь соприкосновения гораздо меньше наблюдаемой. Кроме того, увеличивая площадь, мы уменьшаем удельное давление тел друг на друга.) Величина, характеризующая трущиеся поверхности, называется коэффициентом трения, и обозначается чаще всего латинской буквой «k» или греческой буквой «μ». Она зависит от природы и качества обработки трущихся поверхностей. Кроме того, коэффициент трения зависит от скорости. Впрочем, чаще всего эта зависимость выражена слабо, и если большая точность измерений не требуется, то «k» можно считать постоянным.
В первом приближении величина силы трения скольжения может быть рассчитана по формуле:
, где— коэффициент трения скольжения,— сила нормальной реакции опоры.По физике взаимодействия трение принято разделять на:
В связи со сложностью физико-химических процессов, протекающих в зоне фрикционного взаимодействия, процессы трения принципиально не поддаются описанию с помощью методов классической механики.
При механических процессах всегда происходит в большей или меньшей степени преобразование механического движения в другие формы движения материи (чаще всего в тепловую форму движения). В последнем случае взаимодействия между телами носят названия сил трения.
Опыты с движением различных соприкасающихся тел (твёрдых по твёрдым, твёрдых в жидкости или газе, жидких в газе и т. п.) с различным состоянием поверхностей соприкосновения показывают, что силы трения проявляются при относительном перемещении соприкасающихся тел и направлены против вектора относительной скорости тангенциально к поверхности соприкосновения. При этом всегда происходит нагревание взаимодействующих тел.
При этом всегда происходит нагревание взаимодействующих тел.
Силами трения называются тангенциальные взаимодействия между соприкасающимися телами, возникающие при их относительном перемещении. Силы трения возникающие при относительном перемещении различных тел, называются силами внешнего трения.
Силы трения возникают и при относительном перемещении частей одного и того же тела. Трение между слоями одного и того же тела называется внутренним трением.
В реальных движениях всегда возникают силы трения большей или меньшей величины. Поэтому при составлении уравнений движения, строго говоря, мы должны в число действующих на тело сил всегда вводить силу трения F тр.
Тело движется равномерно и прямолинейно, когда внешняя сила уравновешивает возникающую при движении силу трения.
Для измерения силы трения, действующей на тело, достаточно измерить силу, которую необходимо приложить к телу, чтобы оно двигалось без ускорения.
Источник
Видео
что такое #хват моторезины Круг Камма / #Пятно контакта шин мотоцикла
Урок 39 (осн). Сила трения. Коэффициент трения
Сила трения. Коэффициент трения
Коэффициент трения
На сколько км пробега рассчитана резина? Коэффициент износостойкости автомобильных шин!
Что будет если ездить летом на зимней резине? Это должен знать каждый водитель!
Какое давление качать в колеса велосипеда?
ЧТО ОЗНАЧАЕТ МАРКИРОВКА НА ШИНАХ?! ВСЁ О ШИРИНЕ, ВЫСОТЕ ПРОФИЛЯ И ПОСАДОЧНОГО ДИАМЕТРА
УПРАВЛЯЕМОСТЬ АВТО И ШИРИНА ШИН
Почему шины разные? Асимметричный тип протектора! Шинный РАЙ
Правильное давление в шинах авто. Какое должно быть давление в колесах? Обзор от Avtozvuk.ua
Поделиться или сохранить к себе:
Определение коэффициент трения скольжения
Министерство образования и науки Республики Казахстан
Карагандинский Государственный Технический Университет
Кафедра: Физики
Лабораторная работа №1
Тема: Определение коэффициент трения скольжения
Выполнил:
Принял:
Караганда 2010г.
Цель работы: Определение коэффициента трения скольжения
Задание:
Вычислить коэффициент трения скольжения :
Найти среднее значение коэффициента трения скольжения : ,
среднюю квадратичную ошибку среднего значения коэффициента трения :
Вычислить доверительные интервалы: , .
Таблица 1.
Материал | Pн | Fтр | |||||
Дерево (брусок) |
69,4 | 15,1 | 0,22 |
0,22 |
0,01 |
0,03 |
0,25;
0,19 |
13,1 | 0,19 | ||||||
13,12 | 0,2 | ||||||
16,1 | 0,23 | ||||||
17,1 | 0,25 | ||||||
Дерево (брусок+доп. |
269,4 | 50,1 | 0,19 |
0,21 |
0,01 |
0,03 |
0,24;
0,18
|
60,1 | 0,22 | ||||||
55,1 | 0,21 | ||||||
57,1 | 0,21 | ||||||
58,1 | 0,22 |
Вычислить коэффициент трения по формуле: . Найти среднее арифметическое значение : , среднюю квадратичную ошибку среднего арифметического значения : . Вычислить доверительный интервал .
Таблица 2
Материал | ||||||
Дерево (брусок) | 22 | 0,4 |
0,45 |
0,02 |
0,06 |
0,51;
0,39 |
25 | 0,47 | |||||
23 | 0,43 | |||||
24 | 0,45 | |||||
26 | 0,49 |
Вывод:
В результате вычислений мы определили коэффициент трения скольжения, погрешности и доверительный интервал, в котором находится коэффициент трения.
Контрольные вопросы
1.Объяснить причину возникновения внешнего трения?
Внешним тернием называется трение, возникающее в плоскости касания двух соприкасающихся тел при их относительном перемещении. Это трение обусловлено шероховатостью соприкасающихся поверхностей.
2.Как возникает и от чего зависит сила трения покоя?
Сила трения покоя возникает при попытке вывести тело из состояния покоя. Поскольку в этом случае нужно в первый момент преодолеть не только сцепление тел (силу трения скольжения), но и инерцию тела, сила трения покоя самая большая из всех сил трения.
3.От чего зависит коэффициент трения скольжения и как это согласуется с результатами Вашего опыта?
Зависит от материала соприкасающихся поверхностей и степени их обработки. Из моего опыта: брусок деревянный, имеет шероховатую поверхность, поэтому возникают силы трения.
4. Какова роль смазки при движении тел?
Для уменьшения силы трения на трущиеся поверхности наносят смазку (сила трения уменьшается примерно в10 раз), которая заполняет неровности между этими поверхностями и располагается тонким слоем между ними так, что поверхности как бы перестают касаться друг друга, а скользят друг относительно друга отдельные слои жидкости.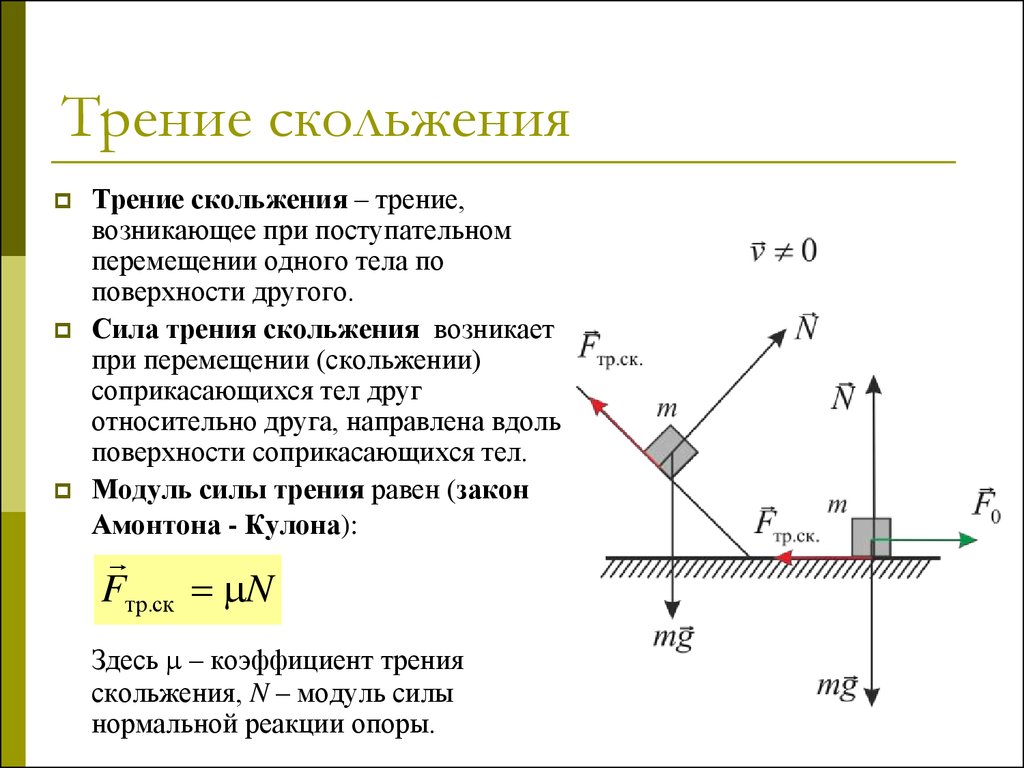
5.Если по горизонтальному трибометру брусок будет двигаться ускоренно, будет ли, сила натяжения нити равна весу чашки с разновесами?
Нет, не будет, т.к. тело придет в движение только тогда, когда приложенная сила F будет больше силы трения Fтр.
6.Зависит ли коэффициент трения от угла наклона трибометра?
Да, зависит. Коэффициент трения равен тангенсу угла , при котором начинается скольжение тела по наклонной плоскости. Чем больше угол , тем больше коэффициент трения.
7. Какие превращения энергии наблюдаются при скольжении одного тел по поверхности другого?
Механическая энергия всегда превращается во внутреннюю энергию.
Может ли коэффициент трения быть больше 1?
Коэффициент трения зависит от объектов, вызывающих трение. Значение обычно составляет в диапазоне от 0 до 1 , но может быть и больше 1. … Коэффициент трения, превышающий единицу, просто означает, что сила трения больше, чем нормальная сила.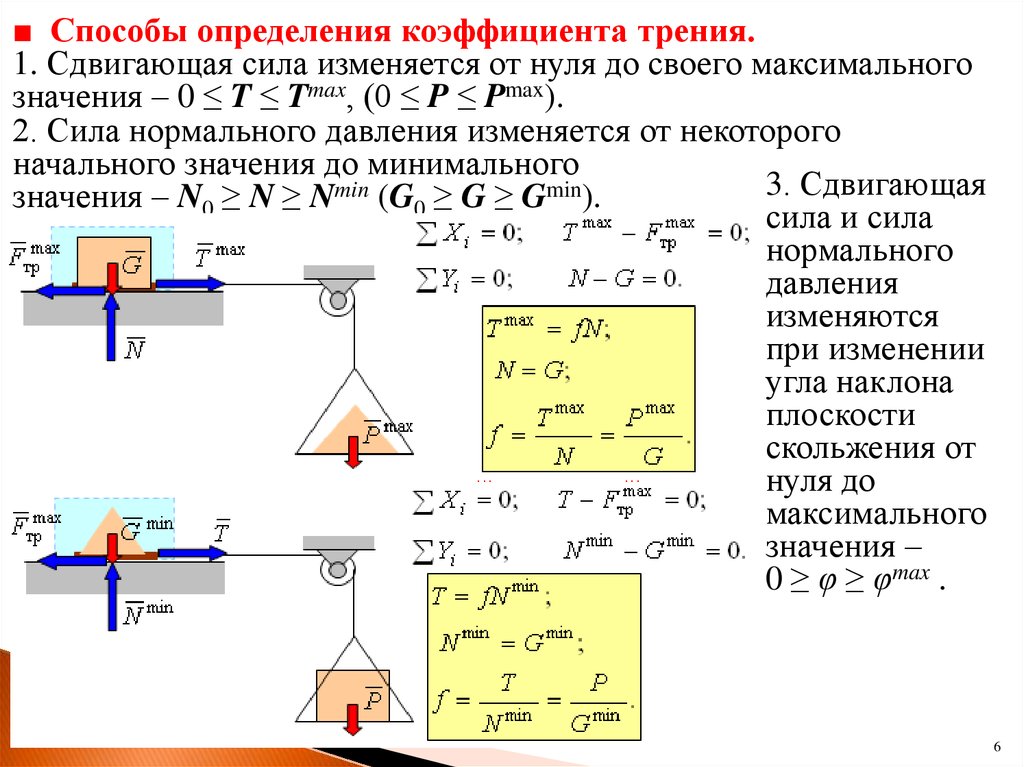
Может ли коэффициент трения быть больше 1,0 поясните на примере?
Значение 1 означает, что сила трения равна нормальной силе. … Коэффициент трения больше единицы просто означает, что сила трения больше, чем нормальная сила. Такой объект, как силиконовый каучук, например , может иметь коэффициент трения намного больше единицы.
Может ли коэффициент трения быть выше 1 класса 11?
Коэффициент трения безразмерен и не имеет единиц измерения. Это скаляр, означающий, что направление силы не влияет на физическую величину. Коэффициент трения зависит от объектов, вызывающих трение. Значение обычно находится в диапазоне от 0 до 1, но может быть больше 1 9.0004 .
Всегда ли необходимо, чтобы коэффициент трения был меньше 1?
Нет необходимости , чтобы коэффициент трения всегда был меньше 1. Когда трение сильнее, чем нормальная сила реакции, коэффициент трения больше 1. Например, силиконовый каучук имеет коэффициент трения больше 1.
Может ли коэффициент трения быть больше единицы?
Коэффициент трения говорит нам о том, насколько меньше или больше нормальной силы является сила трения. Для большинства объектов коэффициент трения находится между 0 и 1. … Так как это значение может быть больше 1 , отношение силы трения и нормальной реакции также может превышать единицу.
Что имеет самый высокий коэффициент трения?
Ладонь руки имеет самый высокий коэффициент трения во всех измеренных местах. Из всех протестированных материалов силикон имеет самый высокий коэффициент трения. На рис. 2 показано изменение коэффициента трения при нормальной силе, приложенной к поверхности кожи, в 10 опытах.
Каков максимальный коэффициент статического трения?
Максимальная сила трения покоя равна: (f s ) max = μ s Н , где μ s — коэффициент трения покоя. Статическое трение малозаметно, поскольку сила статического трения непостоянна и зависит от внешних сил, действующих на объект. То есть f с ≤ μ с Н, а (f с ) max = μ с Н. В общем, μ с ≥ μ k .
То есть f с ≤ μ с Н, а (f с ) max = μ с Н. В общем, μ с ≥ μ k .
Всегда ли MU меньше 1?
Иногда утверждают, что мк всегда меньше 1 , но это неверно. Хотя в большинстве соответствующих приложений μ < 1, значение выше 1 просто означает, что сила, необходимая для скольжения объекта по поверхности, больше, чем нормальная сила поверхности на объекте.
Какова единица коэффициента статического трения?
Обычно обозначается греческой буквой мю (μ) . Математически μ = F/N, где F — сила трения, а N — нормальная сила. Поскольку и F, и N измеряются в единицах силы (например, в ньютонах или фунтах), коэффициент трения безразмерен.
Зачем нужен коэффициент трения при трении?
Согласно Карманному справочнику по инженерным и физическим наукам Newnes, коэффициент трения представляет собой величину трения, существующую между двумя поверхностями. Низкое значение коэффициента трения означает, что для скольжения требуется меньшее усилие . Более высокое значение означает, что требуется большее усилие.
Более высокое значение означает, что требуется большее усилие.
Может ли коэффициент реституции быть больше 1?
Обычно принимает значения от 0 до 1, где 1 означает абсолютно упругое столкновение. … Это может быть больше 1, если во время столкновения происходит прирост энергии в результате химической реакции, уменьшения энергии вращения или другого уменьшения внутренней энергии, которое способствует увеличению скорости после столкновения.
Что такое коэффициент трения?
Коэффициент трения µ является мерой величины трения между двумя поверхностями . Низкое значение коэффициента трения указывает на то, что сила, необходимая для скольжения, меньше, чем сила, необходимая при высоком коэффициенте трения.
Может ли коэффициент трения быть отрицательным?
Отрицательные коэффициенты трения возникают, когда сила трения увеличивается с уменьшением нагрузки . … Таким образом, отрицательный коэффициент трения является частным случаем общего явления гистерезиса в адгезионном взаимодействии между двумя поверхностями во время цикла загрузки-разгрузки 4 , 5 .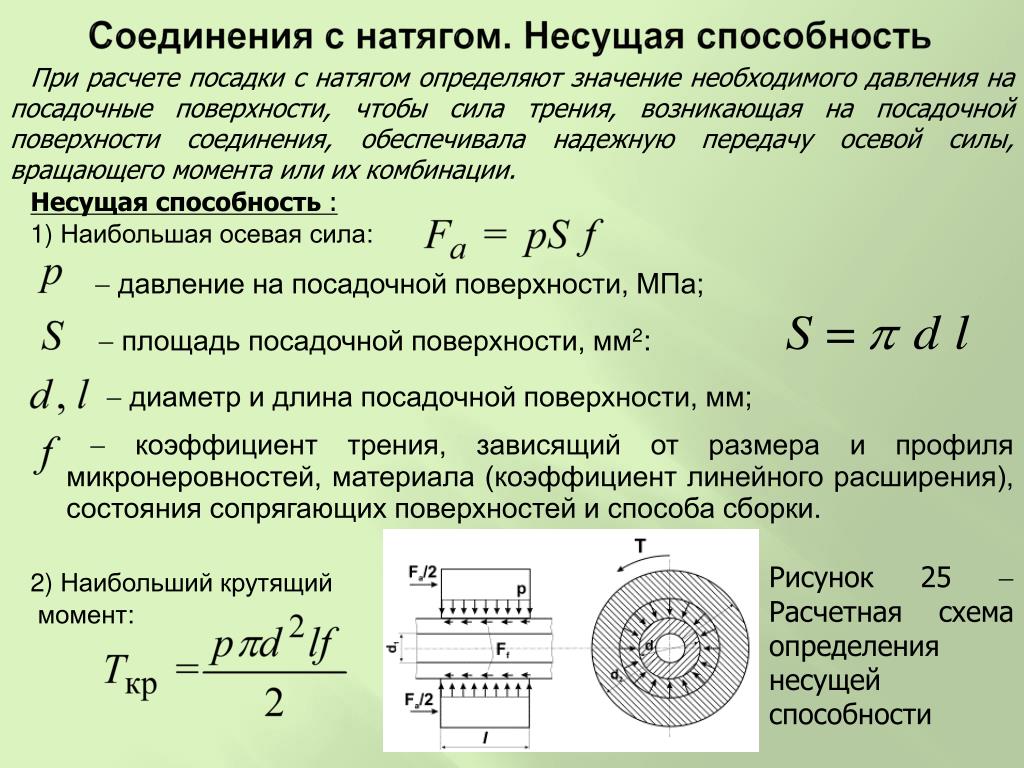
Какой самый низкий коэффициент трения?
На самом деле, с точки зрения широкой доступности различных конструкционных материалов, ПТФЭ предлагает самый низкий коэффициент трения при предполагаемом COH 0,04 как для кинетического, так и для статического трения по сравнению со сталью со смазкой при 0,05 (кинетическое) или 0,1 (статическое).
Является ли коэффициент трения постоянным?
Поскольку и F, и N измеряются в единицах силы (например, в ньютонах или фунтах), коэффициент трения безразмерен . Коэффициент трения имеет разные значения для статического трения и кинетического трения.
Как рассчитать коэффициент трения?
Коэффициент трения, отношение силы трения, противодействующей движению двух контактирующих поверхностей, к нормальной силе, прижимающей две поверхности друг к другу. Обычно его обозначают греческой буквой мю (μ). Математически μ = F/N , где F — сила трения, а N — нормальная сила.
Может ли коэффициент трения быть больше 1,0 Объясните на примере?
Значение 1 означает, что сила трения равна нормальной силе. … Коэффициент трения больше единицы просто означает, что сила трения больше, чем нормальная сила. Такой объект, как силиконовый каучук, например , может иметь коэффициент трения намного больше единицы.
… Коэффициент трения больше единицы просто означает, что сила трения больше, чем нормальная сила. Такой объект, как силиконовый каучук, например , может иметь коэффициент трения намного больше единицы.
Может ли коэффициент трения быть больше 1 класса 11?
Коэффициент трения безразмерен и не имеет единиц измерения. Это скаляр, означающий, что направление силы не влияет на физическую величину. Коэффициент трения зависит от объектов, вызывающих трение. Обычно это значение находится в диапазоне от 0 до 1, но может быть больше 1 .
Может ли коэффициент трения быть больше 1?
Коэффициент трения зависит от объектов, вызывающих трение. Значение обычно равно между 0 и 1, но может быть больше 1 . Значение 0 означает, что между объектами вообще нет трения; такое возможно с помощью сверхтекучести. … Значение 1 означает, что сила трения равна нормальной силе.
Что имеет самый высокий коэффициент трения?
Ладонь руки имеет самый высокий коэффициент трения во всех измеренных местах.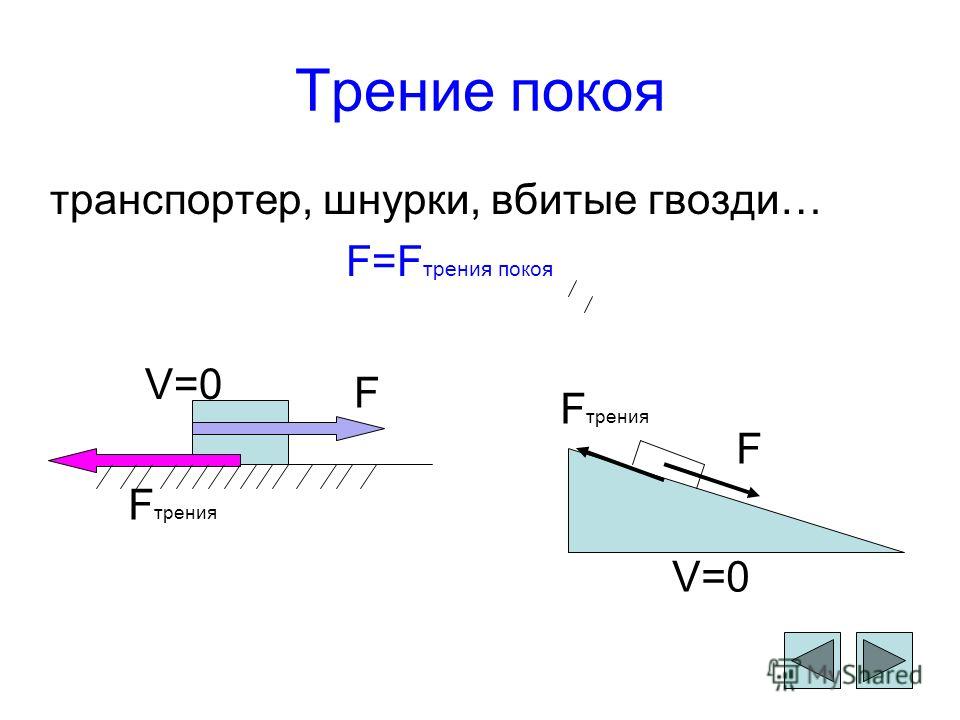 Из всех протестированных материалов силикон имеет самый высокий коэффициент трения. На рис. 2 показано изменение коэффициента трения при нормальной силе, приложенной к поверхности кожи, в 10 опытах.
Из всех протестированных материалов силикон имеет самый высокий коэффициент трения. На рис. 2 показано изменение коэффициента трения при нормальной силе, приложенной к поверхности кожи, в 10 опытах.
Всегда ли необходимо, чтобы коэффициент трения был меньше 1?
Нет необходимости , чтобы коэффициент трения всегда был меньше 1. Когда трение сильнее, чем нормальная сила реакции, коэффициент трения больше 1. Например, силиконовый каучук имеет коэффициент трения больше 1.
Каков максимальный коэффициент статического трения?
Максимальная статическая сила трения: (f s ) max = μ с N , где μ с — коэффициент статического трения. Статическое трение малозаметно, поскольку сила статического трения непостоянна и зависит от внешних сил, действующих на объект. То есть f с ≤ μ с Н, а (f с ) max = μ с Н. В общем, μ с ≥ μ k .
Может ли коэффициент трения быть отрицательным?
Отрицательные коэффициенты трения возникают, когда сила трения увеличивается с уменьшением нагрузки . … Таким образом, отрицательный коэффициент трения является частным случаем общего явления гистерезиса в адгезионном взаимодействии между двумя поверхностями во время цикла загрузки-разгрузки 4 , 5 .
Какой самый низкий коэффициент трения?
ПТФЭ имеет один из самых низких коэффициентов трения среди всех твердых тел. Политетрафторэтилен используется в качестве антипригарного покрытия для сковородок и другой посуды.
В какой единице измеряется коэффициент трения?
Коэффициент трения — это отношение силы к силе, поэтому не имеет единиц измерения .
Всегда ли MU меньше 1?
Иногда утверждают, что мк всегда меньше 1 , но это неверно. Хотя в большинстве соответствующих приложений μ < 1, значение выше 1 просто означает, что сила, необходимая для скольжения объекта по поверхности, больше, чем нормальная сила поверхности на объекте.
Зачем нужен коэффициент трения при трении?
Согласно Карманному справочнику Newnes по инженерным и физическим наукам, коэффициент трения — это величина трения между двумя поверхностями. Низкое значение коэффициента трения означает, что для скольжения требуется меньшее усилие . Более высокое значение означает, что требуется большее усилие.
Коэффициент трения при полировке двух поверхностей?
При полировке двух поверхностей коэффициент трения между ними уменьшается . Но коэффициент трения увеличивается и становится очень большим, если поверхности сделаны очень гладкими.
Является ли коэффициент трения постоянным?
Коэффициент трения равен безразмерной скалярной величине . Это отношение силы трения между двумя телами к силе, прижимающей их друг к другу.
Как рассчитать коэффициент трения?
Коэффициент трения, отношение силы трения, противодействующей движению двух контактирующих поверхностей, к нормальной силе, прижимающей две поверхности друг к другу. Обычно его обозначают греческой буквой мю (μ). Математически μ = F/N , где F — сила трения, а N — нормальная сила.
Обычно его обозначают греческой буквой мю (μ). Математически μ = F/N , где F — сила трения, а N — нормальная сила.
Как найти коэффициент статического трения?
Объединение физики трения с геометрией наклонной плоскости дает простую формулу для коэффициента статического трения: μ = tan(θ) , где μ — коэффициент трения, а θ — угол.
Могут ли коэффициенты быть отрицательными?
Коэффициенты могут быть дробями, целыми числами, положительными числами, отрицательными числами, мнимыми числами и т.д. Отрицательные коэффициенты равны просто коэффициенты, которые являются отрицательными числами . Примером отрицательного коэффициента может быть -8 в термине -8z или -11 в термине -11xy.
Влияние температуры на коэффициент трения
Гугл
Отзывы
Дом
Классический пользовательский
Ресурсы
Физические тесты
лаборатория Физические тесты
1.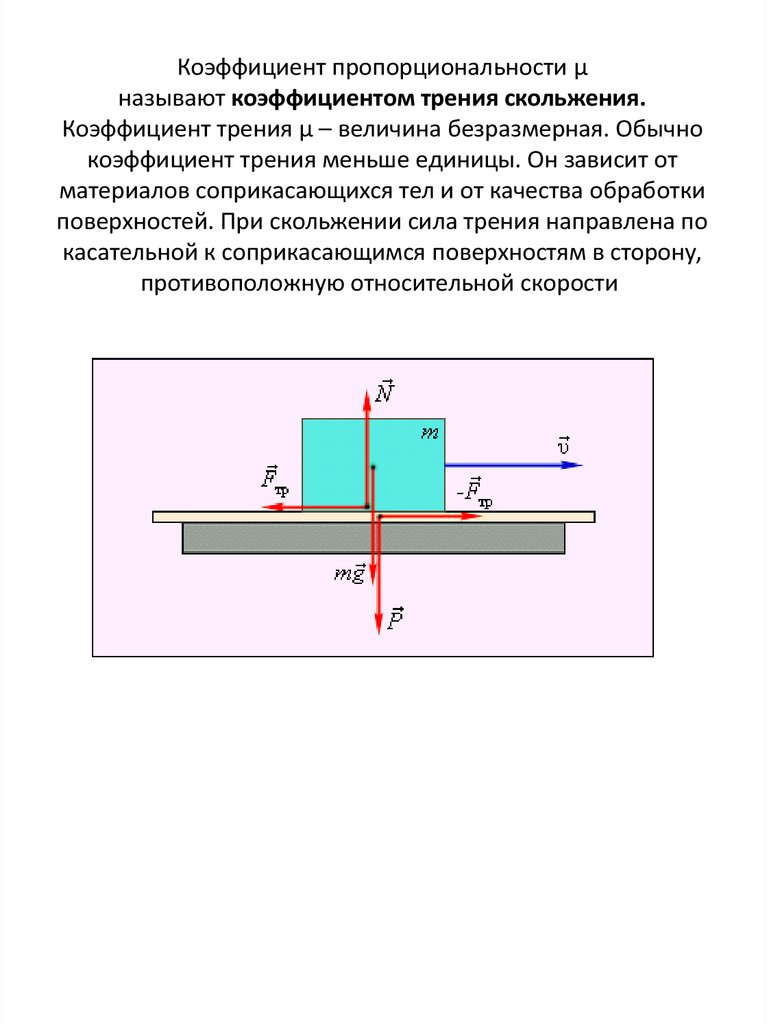 Коэффициент трения
Коэффициент трения
Коэффициент трения является мерой силы трения между двумя поверхностями. Это показатель фрикционного поведения материала. Коэффициент трения пленки зависит от поверхностной адгезии (поверхностное натяжение и кристалличность), добавки (сглаживающее средство, пигмент и т. д.) и полировки поверхности. Коэффициент трения должен контролироваться строго в следующей последовательности операций: пересечение пленки свободным валиком, формование мешков, обвязка изделий шпагатом и укладка тары и другой тары. Помимо внутренних переменных факторов, факторы окружающей среды (такие как рабочая скорость, температура, накопление статического электричества и влажность машины) также могут влиять на результат испытания коэффициента трения.
2. Влияние температуры на коэффициент трения
Изменение состояния движения молекул высокополимера с точки зрения динамики называется разрыхлением. Повышение температуры может, с одной стороны, улучшить способность движущихся частей к теплу. С другой стороны, из-за теплового расширения расстояние между молекулами увеличивается. А именно, увеличивается внутренний объем свободы в высоком полимере, что может увеличить пространство активности движущейся единицы, ускорить движение молекул, сократить время релаксации и ускорить процесс релаксации. После релаксации высокополимера его термодинамическая природа, вязкопластичность и другие физические свойства также резко изменятся. На коэффициент трения, как на один из наиболее часто используемых показателей механики, также может влиять повышение температуры. Вообще говоря, с повышением температуры окружающей среды коэффициент поверхностного трения материала будет иметь определенное изменение, но величина изменения будет различаться от материала к материалу.
С другой стороны, из-за теплового расширения расстояние между молекулами увеличивается. А именно, увеличивается внутренний объем свободы в высоком полимере, что может увеличить пространство активности движущейся единицы, ускорить движение молекул, сократить время релаксации и ускорить процесс релаксации. После релаксации высокополимера его термодинамическая природа, вязкопластичность и другие физические свойства также резко изменятся. На коэффициент трения, как на один из наиболее часто используемых показателей механики, также может влиять повышение температуры. Вообще говоря, с повышением температуры окружающей среды коэффициент поверхностного трения материала будет иметь определенное изменение, но величина изменения будет различаться от материала к материалу.
3. Эксперимент с повышением температуры
Чтобы проверить влияние колебаний температуры на коэффициент трения, коэффициент трения нескольких групп материалов с определенной репрезентативностью испытывают при различных температурах.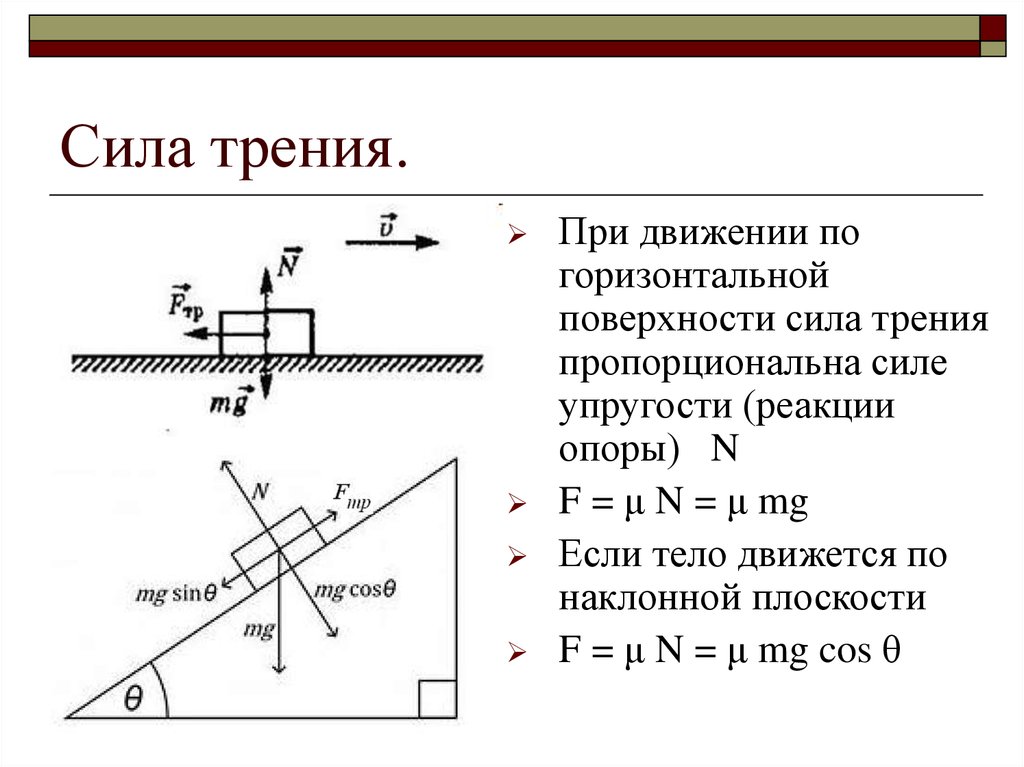 Подробная информация об испытаниях и результаты испытаний приведены ниже:
Подробная информация об испытаниях и результаты испытаний приведены ниже:
Образец: поликарбонатная пленка, комплексная пленка из алюминиевой фольги
Прибор: Labthink FPT-F1 коэффициент трения / тестер отслаивания
Температура испытания: комнатная температура~90,0 ° C
Данные тестирования:
Таблица 1. Данные тестирования пленки ПК
| Тестирование ° C | .||||||||
|---|---|---|---|---|---|---|---|---|
| 32.1 | 0.285 | 0.244 | ||||||
| 45.5 | 0.336 | 0.212 | ||||||
| 62.0 | 0.387 | 0. 319 319 | ||||||
| 74.1 | 0,435 2 | 0,322 2 | ||||||
| 87,5 | 0,433 2 | 0,300 2 |
| Температура испытания, °C0099 1 | ||
|---|---|---|
| 29.6 | 0.314 | 0.239 |
| 46.2 | 0.355 | 0.277 |
74.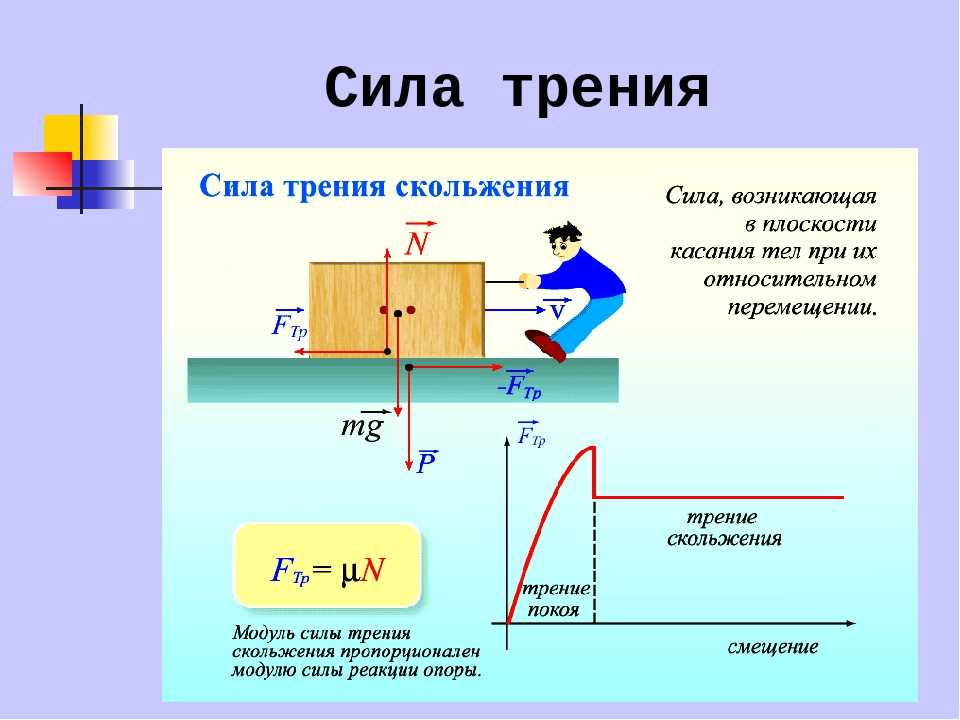 3 3 | 0.343 2 | 0.253 2 |
| 89.5 | 0.429 2 | 0.241 2 |
Примечание 1: данные испытаний являются средними значениями нескольких групп
2: явление прерывистого скольжения
Кривая данных с повышением температуры показана на рис. 1:
Рис. 1. Повышение температуры явно повлияло на коэффициент трения материала
Из рис. 1 видно, что повышение температуры явно повлияло на коэффициент трения материала. Но на разные образцы при повышении температуры эффекты воздействия различны. Причем для одного и того же образца тенденция изменения кинетического коэффициента трения, скорее всего, будет отличаться от тенденции статического коэффициента трения. Например, для поликарбонатной пленки тенденция роста коэффициента статического трения с повышением температуры достаточно устойчива. Но тенденция изменения коэффициента кинетического трения очень велика. Однако общая тенденция изменения кинетического коэффициента трения также увеличивается. Что касается составной пленки из алюминиевой фольги, то тенденция роста коэффициента трения не так очевидна, как у пленки из поликарбоната. А его коэффициент кинетического трения остается практически стабильным при повышении температуры. Здесь необходимо отметить одну вещь: когда тестирование проводится при температуре выше 74 градусов по Цельсию, в процессе тестирования возникает очевидное явление прерывистого скольжения. То есть скольжение прерывистое, а не устойчивое.
Но тенденция изменения коэффициента кинетического трения очень велика. Однако общая тенденция изменения кинетического коэффициента трения также увеличивается. Что касается составной пленки из алюминиевой фольги, то тенденция роста коэффициента трения не так очевидна, как у пленки из поликарбоната. А его коэффициент кинетического трения остается практически стабильным при повышении температуры. Здесь необходимо отметить одну вещь: когда тестирование проводится при температуре выше 74 градусов по Цельсию, в процессе тестирования возникает очевидное явление прерывистого скольжения. То есть скольжение прерывистое, а не устойчивое.
4. Фактическое требование
В реальном процессе упаковки сила трения часто действует как сила сопротивления и сопротивление. Следовательно, коэффициент трения должен эффективно контролироваться в надлежащем диапазоне.
Рулонный материал для автоматической упаковки обычно требует меньшего коэффициента трения внутреннего слоя и умеренного коэффициента трения внешнего слоя. Коэффициент трения внутреннего слоя не может быть слишком мал; в противном случае это приведет к смещению краев в результате нестабильной укладки набивки во время формирования мешка. Слишком большой внешний коэффициент трения вызовет появление пятен при растяжении материала из-за чрезмерного сопротивления в процессе упаковки. В то время как он слишком мал, это приведет к наклону тянущегося компонента, что, в свою очередь, может привести к неточности трассировки электрического глаза и позиционированию обрезки. Содержание раскрывающегося вещества и сглаживающего вещества внутреннего слоя вместе с жесткостью и гладкостью пленки будут влиять на коэффициент трения сложной пленки.
Коэффициент трения внутреннего слоя не может быть слишком мал; в противном случае это приведет к смещению краев в результате нестабильной укладки набивки во время формирования мешка. Слишком большой внешний коэффициент трения вызовет появление пятен при растяжении материала из-за чрезмерного сопротивления в процессе упаковки. В то время как он слишком мал, это приведет к наклону тянущегося компонента, что, в свою очередь, может привести к неточности трассировки электрического глаза и позиционированию обрезки. Содержание раскрывающегося вещества и сглаживающего вещества внутреннего слоя вместе с жесткостью и гладкостью пленки будут влиять на коэффициент трения сложной пленки.
При изучении коэффициента трения материала особое внимание следует обратить на влияние температуры. Как указано выше, различная температура вызовет заметное изменение коэффициента трения. Измеренные данные должны быть получены путем реальных испытаний. Коэффициент трения некоторых материалов может заметно увеличиваться или уменьшаться при изменении температуры.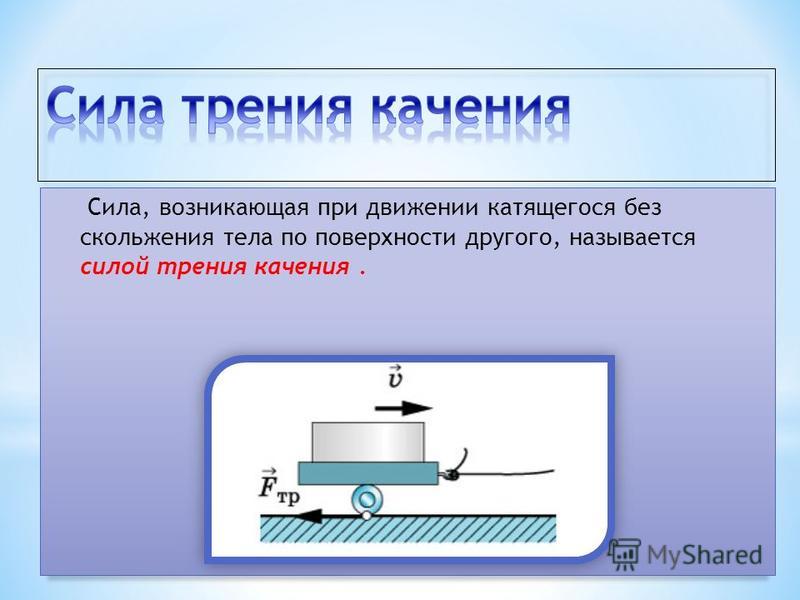 Он также может в некоторой степени поддерживать стабильность данных. Учитывая тот факт, что фактическую температуру производственной линии трудно поддерживать на уровне комнатной температуры, коэффициент трения материала упаковки следует проверять не только при нормальной температуре воздуха, но и при реальной рабочей температуре. Испытание можно выполнить, изменив температуру в лаборатории (когда требуемая температура близка к комнатной) или используя функцию самоконтроля температуры испытательного прибора. Например, Labthink может упростить тест, контролируя температуру тестирования между комнатной температурой и температурой FPT-F19.9,9°С.
Он также может в некоторой степени поддерживать стабильность данных. Учитывая тот факт, что фактическую температуру производственной линии трудно поддерживать на уровне комнатной температуры, коэффициент трения материала упаковки следует проверять не только при нормальной температуре воздуха, но и при реальной рабочей температуре. Испытание можно выполнить, изменив температуру в лаборатории (когда требуемая температура близка к комнатной) или используя функцию самоконтроля температуры испытательного прибора. Например, Labthink может упростить тест, контролируя температуру тестирования между комнатной температурой и температурой FPT-F19.9,9°С.
Кинетика коэффициента трения эластомеров
Abstract
Теоретически и численно исследуется кинетика коэффициента трения эластомера при скачкообразных изменениях скорости скольжения. Численное моделирование обнаруживает такое же качественное поведение, которое наблюдалось экспериментально на разных классах материалов: коэффициент трения сначала скачет, а затем релаксирует до нового стационарного значения.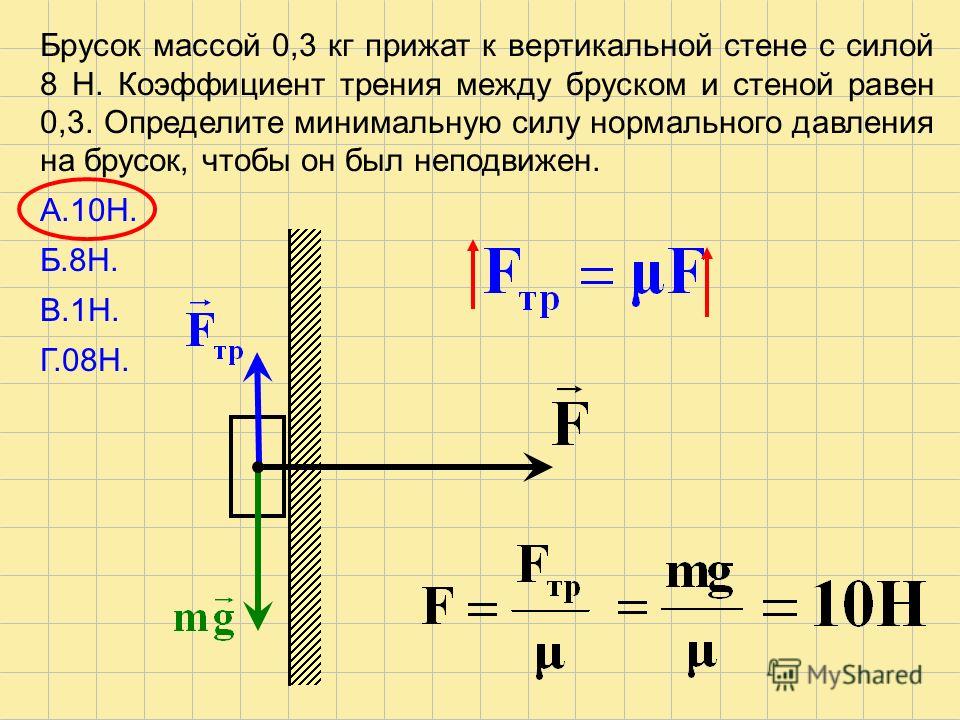 Эластомер моделируется простым телом Кельвина, а поверхность – самоаффинным фракталом с показателем Херста в диапазоне от 0 до 1. Параметры скачка коэффициента трения и времени релаксации определяются в зависимости от материала и параметры загрузки. В зависимости от скорости и показателя Херста наблюдается релаксация трения с характерной длиной или характерным временем.
Эластомер моделируется простым телом Кельвина, а поверхность – самоаффинным фракталом с показателем Херста в диапазоне от 0 до 1. Параметры скачка коэффициента трения и времени релаксации определяются в зависимости от материала и параметры загрузки. В зависимости от скорости и показателя Херста наблюдается релаксация трения с характерной длиной или характерным временем.
Введение
Сухое трение играет решающую роль в самых разнообразных физических процессах и приложениях 1,2 . Очень часто для описания сухого трения используют простейший «закон» трения (закон Амонтона 3 ). Он утверждает, что сила трения F пропорциональна нормальной силе F N : F = мкФ N μ , являясь коэффициентом пропорциональности μF . . Общеизвестно, что «закон» Амонтона является лишь очень грубым «приближением нулевого порядка». Уже кулон 4 знал, что коэффициент трения скольжения зависит от скорости скольжения и нормальной силы и что трение покоя приблизительно логарифмически зависит от времени 1 . Явная зависимость коэффициента трения от времени стала горячей темой в 1970-х годах в контексте динамики землетрясений. На основе экспериментальной работы по горным породам Дитериха 5,6 , Райса и Руины 7 было сформулировано кинетическое уравнение для трения, которое стало одной из наиболее влиятельных обобщенных «моделей скорости-состояния». Подобное кинетическое поведение коэффициента трения наблюдалось на множестве различных материалов, включая металлы, бумагу и полимеры 9.0099 8,9,10,11,12 . Большинство физических интерпретаций трения в зависимости от скорости основаны на концепции Боудена и Табора 13 , подчеркивающей влияние взаимодействия шероховатых поверхностей; они включают прямые наблюдения за контактирующими поверхностями 14 , а также теоретический анализ 15,16 . Были предложены и другие модели кинетики коэффициента трения, основанные на развитии топографии поверхности вследствие износа (Ostermeyer 17,18 ) или сдвигового плавления тонких поверхностных слоев 19 .
Явная зависимость коэффициента трения от времени стала горячей темой в 1970-х годах в контексте динамики землетрясений. На основе экспериментальной работы по горным породам Дитериха 5,6 , Райса и Руины 7 было сформулировано кинетическое уравнение для трения, которое стало одной из наиболее влиятельных обобщенных «моделей скорости-состояния». Подобное кинетическое поведение коэффициента трения наблюдалось на множестве различных материалов, включая металлы, бумагу и полимеры 9.0099 8,9,10,11,12 . Большинство физических интерпретаций трения в зависимости от скорости основаны на концепции Боудена и Табора 13 , подчеркивающей влияние взаимодействия шероховатых поверхностей; они включают прямые наблюдения за контактирующими поверхностями 14 , а также теоретический анализ 15,16 . Были предложены и другие модели кинетики коэффициента трения, основанные на развитии топографии поверхности вследствие износа (Ostermeyer 17,18 ) или сдвигового плавления тонких поверхностных слоев 19 . Хеслот и др. др. 20 предоставил очень подробный экспериментальный анализ динамики систем, подчиняющихся закону трения скорости-состояния. Кинетика коэффициента трения является существенным фактором для устойчивости систем с трением 21,22,23 , неустойчивости прорыва 24 , а также для проектирования систем управления с обратной связью 25,26,27 и остается предметом большого научного и технического интереса. Большинство формулировок законов трения в скоростных состояниях содержат характерную шкалу длины, на которой происходит переход от прилипания к скольжению. Наличие такой длины, как правило, связано с характерным размером неровностей или с другими структурными особенностями на микроуровне 28,29 .
Хеслот и др. др. 20 предоставил очень подробный экспериментальный анализ динамики систем, подчиняющихся закону трения скорости-состояния. Кинетика коэффициента трения является существенным фактором для устойчивости систем с трением 21,22,23 , неустойчивости прорыва 24 , а также для проектирования систем управления с обратной связью 25,26,27 и остается предметом большого научного и технического интереса. Большинство формулировок законов трения в скоростных состояниях содержат характерную шкалу длины, на которой происходит переход от прилипания к скольжению. Наличие такой длины, как правило, связано с характерным размером неровностей или с другими структурными особенностями на микроуровне 28,29 .
Несмотря на интенсивные исследования в области обобщенных законов трения, как вид уравнений трения скорость-состояние, так и их параметры до сих пор могут быть определены только эмпирически. В настоящей работе проведен теоретический анализ кинетики коэффициента трения для одного класса материалов – эластомеров.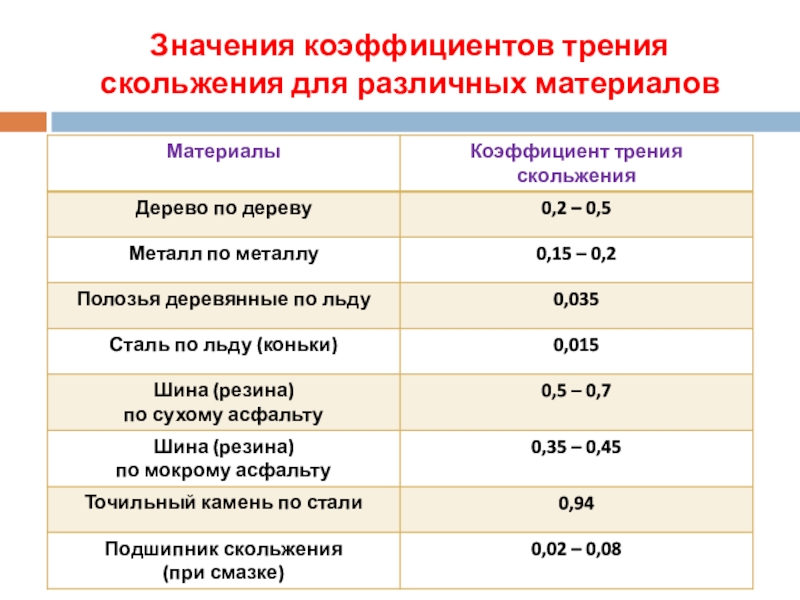 Для этих материалов параметры кинетического закона коэффициента трения связаны с параметрами материала, нагрузки и поверхности. Мы моделируем стандартный тип нагружения, используемый для экспериментального определения параметров скоростно-состоятельных законов: одно из контактирующих тел сначала скользит с постоянной скоростью; в некоторый момент времени происходит скачкообразное изменение скорости скольжения и наблюдается скачок трения и последующая релаксация. Из этих симуляций мы получаем замкнутые соотношения для скачка трения и характерного времени последующей релаксации.
Для этих материалов параметры кинетического закона коэффициента трения связаны с параметрами материала, нагрузки и поверхности. Мы моделируем стандартный тип нагружения, используемый для экспериментального определения параметров скоростно-состоятельных законов: одно из контактирующих тел сначала скользит с постоянной скоростью; в некоторый момент времени происходит скачкообразное изменение скорости скольжения и наблюдается скачок трения и последующая релаксация. Из этих симуляций мы получаем замкнутые соотношения для скачка трения и характерного времени последующей релаксации.
При изучении трения эластомеров мы исходим из концепции Гринвуда и Табора о реологической природе трения эластомеров 30 , которая получила широкое распространение после классической работы Гроша 31 . Чтобы прийти к базовому пониманию динамического поведения коэффициента трения, мы используем одномерную модель, описанную в ссылке 32 : (а) эластомер моделируется как простое тело Кельвина, которое полностью характеризуется своей статический модуль сдвига G и вязкостью η, (б) невозмущенная поверхность эластомера плоская и лишенная трения, (в) твердое контртело предполагается случайным образом шероховатым, самоаффинным, фрактальным, без длинноволновой отсечки, г) не учитываются эффекты адгезии и капиллярности, д) пренебрегаются тепловыми эффектами в микроконтактах.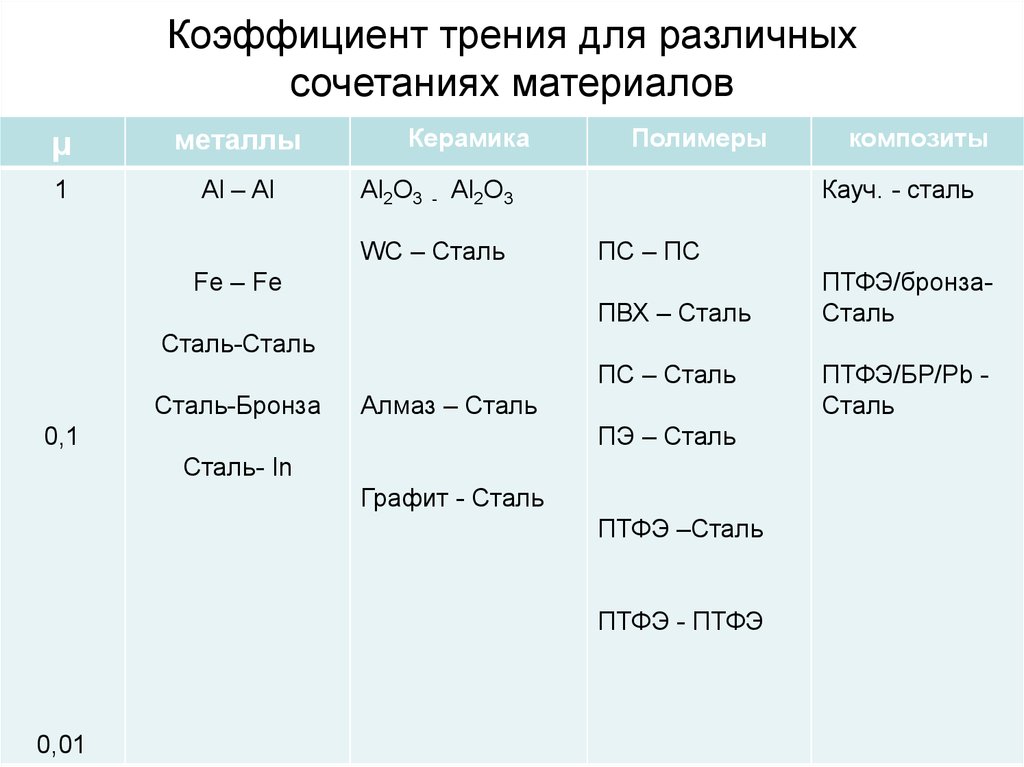
Основываясь на контактной механике как вращательно-симметричных профилей 33 , так и самоаффинных фрактальных поверхностей 34 , недавно было высказано предположение, что результаты, полученные с одномерными основаниями, могут иметь широкую область применимости, если правила метод уменьшения размерности (MDR) 35,36,37 наблюдаются. МЛУ раскритиковали Ляшенко и др. др. в комментарии 38 . Контраргументы представлены в ответе 39 , а также в разделах, посвященных областям применения МЛУ обзорной статьи 35 и монографии 36 . Здесь же отметим только, что одномерная МДР-модель сохраняет все существенные характеристики исходной трехмерной модели, такие как среднеквадратичная шероховатость, градиент и кривизна поверхности, свойства самоподобия (показатель Херста), нормальная жесткость и релаксационные свойства (в случае тела Кельвина время релаксации) и, таким образом, подходит, по крайней мере, для качественного анализа лежащей в основе трехмерной модели трения.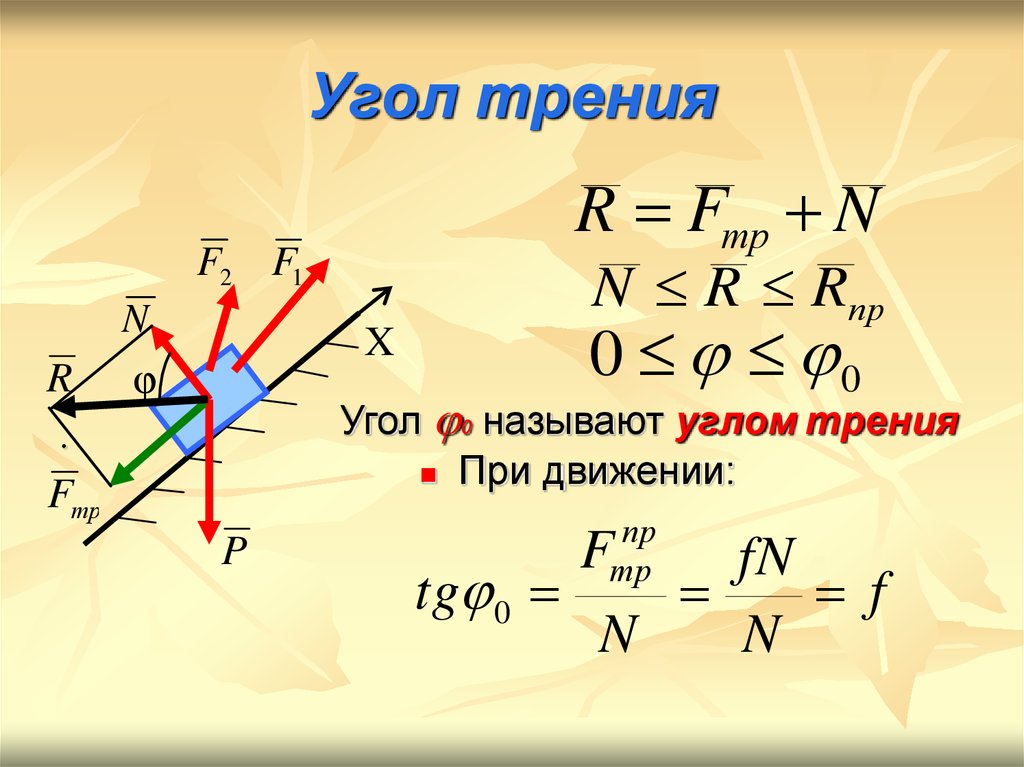
Результаты
Одномерная модель
Согласно МДР тело Кельвина может быть смоделировано как ряд параллельных пружин с жесткостью Δ k z и амортизаторов с постоянной демпфирования Δ05 9002, где 9002 Тело счетчика моделируется в виде грубой линии со спектральной плотностью мощности C 1 D ∝ q −2 H −1 , где q – волновой вектор 43, а H 90 показатель Херста. Этот спектр мощности соответствует двумерной шероховатости со спектром мощности C 2 D ∝ q −2 H −2 35,40 . Спектральная плотность определяется в интервале от q min = 2π/ L , где L — размер системы, до верхнего волнового вектора отсечки q max = π/Δ х . Разнос Δ x определяет верхний волновой вектор отсечки и является важным физическим параметром модели. Топография поверхности характеризуется среднеквадратичной шероховатостью, в которой преобладают длинноволновые компоненты спектра мощности, и среднеквадратичным градиентом поверхности, в котором преобладает коротковолновая часть спектра. Жесткая поверхность создавалась по правилам, описанным в ссылке 9.0099 34 и периодические граничные условия. Жесткая поверхность прижималась к эластомеру с нормальной силой F N и перемещалась по касательной с постоянной скоростью v (рис. 1).
Жесткая поверхность создавалась по правилам, описанным в ссылке 9.0099 34 и периодические граничные условия. Жесткая поверхность прижималась к эластомеру с нормальной силой F N и перемещалась по касательной с постоянной скоростью v (рис. 1).
Контакт эластомера с жестким шероховатым индентором, движущимся со скоростью v .
Изображение в натуральную величину
Модель подробно описана в ссылке 32 . Здесь мы воспроизводим для удобства только основные уравнения. Если жесткий профиль задается z = z ( x — vt ) и профиль эластомера по u = u ( x , 9 т 904 ), тогда удельная сила вязкоупругая основа определяется как
. Для элементов, контактирующих с жесткой поверхностью, это означает, что
, где d — глубина вдавливания, а z ′( x ) обозначает производную по отношению к x . Для этих элементов условие сохранения контакта f > 0, проверяется на каждом временном шаге. Элементы, не соприкасающиеся, релаксируют согласно уравнению z проверяется. Глубина вдавливания d определяется для удовлетворения условия постоянной нормальной силы
Для этих элементов условие сохранения контакта f > 0, проверяется на каждом временном шаге. Элементы, не соприкасающиеся, релаксируют согласно уравнению z проверяется. Глубина вдавливания d определяется для удовлетворения условия постоянной нормальной силы
, где интегрирование производится только по точкам контакта. Типичная конфигурация контакта показана на рисунке 1. Тангенциальная сила рассчитывается путем умножения локальной нормальной силы в каждом отдельном элементе на локальный уклон поверхности и последующего суммирования по всем контактирующим элементам:
Коэффициент трения μ рассчитывался как отношение тангенциальной и нормальной силы.
Из-за независимости степеней свободы алгоритм не является итеративным и проблем сходимости не возникает. Длина системы составляла L = 0,01 м, а количество элементов N = L /Δ x обычно составляло 5000. Модуль сдвига составлял G = 10 7 , время релаксации τ = η/ G = 10 −3 с.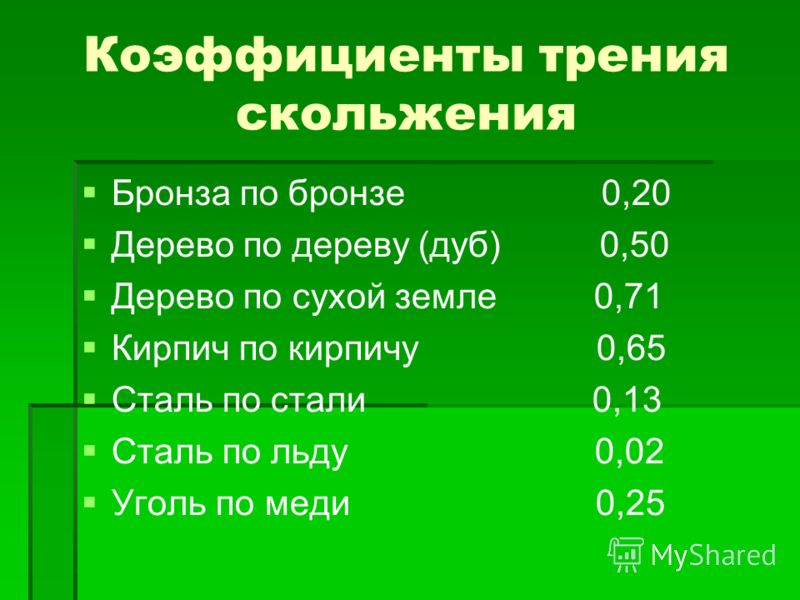 В настоящем исследовании были охвачены следующие диапазоны параметров: 11 значений показателя Херста в диапазоне от 0 до 1; Нормальные силы F Н в пределах от 10 −2 до 10 2 Н; Δ x в диапазоне от 10 −7 до 10 −5 м; шероховатость от 10 −6 до 10 −4 мкм; скорости v 1 от 10 −4 до 10 1 м/с; скачки скорости Δ v от −0,2 v 1 до 0,3 v 1 . Все приведенные ниже значения были получены путем усреднения по 200 реализациям шероховатой поверхности для каждого набора параметров.
В настоящем исследовании были охвачены следующие диапазоны параметров: 11 значений показателя Херста в диапазоне от 0 до 1; Нормальные силы F Н в пределах от 10 −2 до 10 2 Н; Δ x в диапазоне от 10 −7 до 10 −5 м; шероховатость от 10 −6 до 10 −4 мкм; скорости v 1 от 10 −4 до 10 1 м/с; скачки скорости Δ v от −0,2 v 1 до 0,3 v 1 . Все приведенные ниже значения были получены путем усреднения по 200 реализациям шероховатой поверхности для каждого набора параметров.
Релаксация трения после скачка скорости
С помощью модели, описанной ранее, были проведены следующие численные эксперименты: твердое тело сначала перемещалось со скоростью v 1 , в момент времени t 0 скорость была резко изменена на новое значение v 2 которое могло быть больше или меньше начального значения. Типичное поведение коэффициента трения до, во время и после скачка скорости показано на рис.2. v 1 и отрицательное (б) v 2 = 0,8 V 1 Прыгание скорости для параметров: F N = 0,1 N, V 1 = 0,1 м/с, V = 0,01401439 = =9 =9 =9 =9 =9 =9 =9 =9 =
Типичное поведение коэффициента трения до, во время и после скачка скорости показано на рис.2. v 1 и отрицательное (б) v 2 = 0,8 V 1 Прыгание скорости для параметров: F N = 0,1 N, V 1 = 0,1 м/с, V = 0,01401439 = =9 =9 =9 =9 =9 =9 =9 =9 =
Изображение в полный размер
Начальное значение коэффициента трения до прыжка и конечное значение после релаксации, конечно, являются только значениями коэффициента трения для стационарного скольжения, которые были изучены в ссылке 32 и воспроизведены для одного набора параметров материала и нагрузки на рисунке 3а. При тех же параметрах на рис. 3б показаны изменяющиеся во времени кинетические коэффициенты трения для нескольких скоростей во всем диапазоне, использованном на рис. 3а, где скорость скольжения увеличена на 20 % в момент t /τ = 10. В настоящее время В работе мы исследовали весь диапазон скоростей: область I, где коэффициент трения возрастает приблизительно линейно со скоростью, переходную область II и плато III (рис. 3а).
3а, где скорость скольжения увеличена на 20 % в момент t /τ = 10. В настоящее время В работе мы исследовали весь диапазон скоростей: область I, где коэффициент трения возрастает приблизительно линейно со скоростью, переходную область II и плато III (рис. 3а).
(а) Зависимость коэффициента трения от скорости скольжения при стационарном скольжении; (b) кинетический коэффициент трения для 30 скоростей на рисунке 3a с Δ v = 0,2 v 1 .
Другие параметры: F N = 0,1 N, L = 0,01 м, H = 10 — 5 M, G = 100099 , g = 100099 , G = 100099 м. 3 с и H = 0,7.
Изображение в натуральную величину
Релаксация коэффициента трения после прыжка может быть точно описана экспоненциальной функцией вида
где
Пример подгонки показан на рисунке 4. Согласно уравнению (6), коэффициент трения в момент t = t 0 равен µ( t 0 ) = µ*+µ 2 = µ 1 090 49 + 40 , то имеем
Таким образом, кинетическое поведение полностью определяется значением Δμ 0 скачка коэффициента трения и времени его релаксации.
Изображение полного размера
Сначала рассмотрим значение Δμ 0 в момент скачка t = t 0 . При очень малых скачках скорости как непосредственное увеличение коэффициента трения Δμ 0 , так и разность между асимптотическими значениями μ 2 − μ 1 пропорциональны изменению скорости:
В пределе малых скоростях, (область I, соответствующая линейной зависимости коэффициента трения от скорости), как ζ, так и ξ близки к 1. Это означает, что µ скачет прямо к значению µ 2 , так что последующая релаксация практически отсутствует. Это поведение можно ясно наблюдать на рисунке 3b.
На рис. 5 видно, что зависимость Δμ 0 от скорости аналогична зависимости коэффициента трения μ 1 , изученной в эталоне 32 .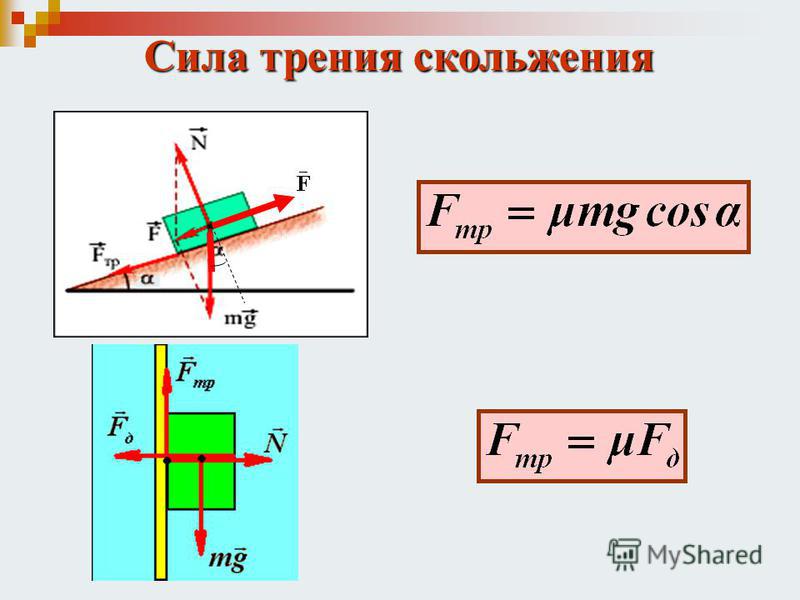 В частности, Δμ 0 сначала линейно возрастает со скоростью, а затем выходит на плато. Результаты моделирования с разными Δ v и разными показателями Херста доказывают, что линейная часть этой зависимости может быть универсально описана уравнением:0005
В частности, Δμ 0 сначала линейно возрастает со скоростью, а затем выходит на плато. Результаты моделирования с разными Δ v и разными показателями Херста доказывают, что линейная часть этой зависимости может быть универсально описана уравнением:0005
, а на плато действует соотношение
. Эти уравнения можно объединить в следующее интерполяционное уравнение
, где мы ввели нормированные величины и . Качество этого приближения показано на рис. 6 в сравнении с численными результатами для 11 показателей Херста.
Рисунок 5и как функции скорости для 20 экспоненциально возрастающих нормальных сил F N от 10 −2 9От 0100 до 10 2 N.
Другие параметры: L = 0,01 м, H = 10 — 5 M, G = 10 7 PA, τ = 109009 –3 9019 = 10 7 PA, τ = 10 –3 = 10 7 PA, τ = 109009 –3 9019 = 10 7 PA, τ = 100438 G .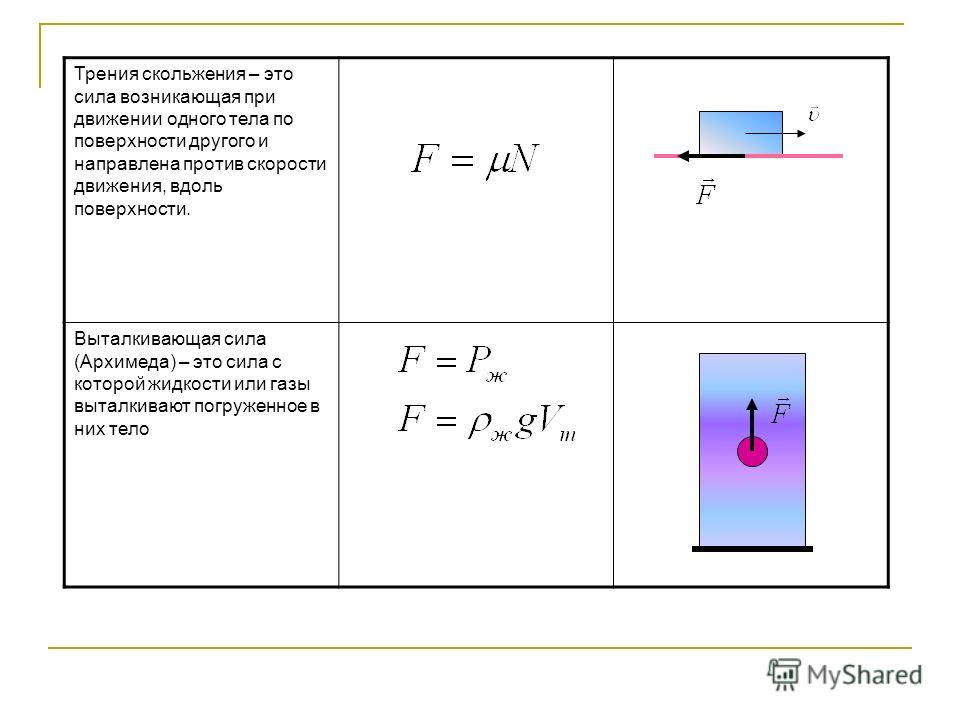 Δ v = 0,2 v 1 и H = 0,7.
Δ v = 0,2 v 1 и H = 0,7.
Изображение в натуральную величину
Рисунок 6Аппроксимация уравнения (12) для 11 показателей Херста от 0 до 1.= 0,01 м, H = 10 −5 м, G = 10 7 PA, τ = 10 −3 S и Δ V = 0,2 V 40404041414141.
Изображение полного размера
Теперь рассмотрим поведение релаксации после скачка. Мы обнаружили, что результаты моделирования для коэффициента b в уравнении (6) могут быть точно описаны эмпирическим уравнением
, где α — коэффициент, зависящий только от показателя Херста. На рис. 7 представлена зависимость коэффициента b в комбинации v 1 τq max для разных показателей Херста. Для v 1 τq max < 1 (левая часть на рис. 7) коэффициент α практически постоянен: α ≈ 1, а для v 1 9 max
его можно аппроксимировать как α ≈ 1 − H (рис.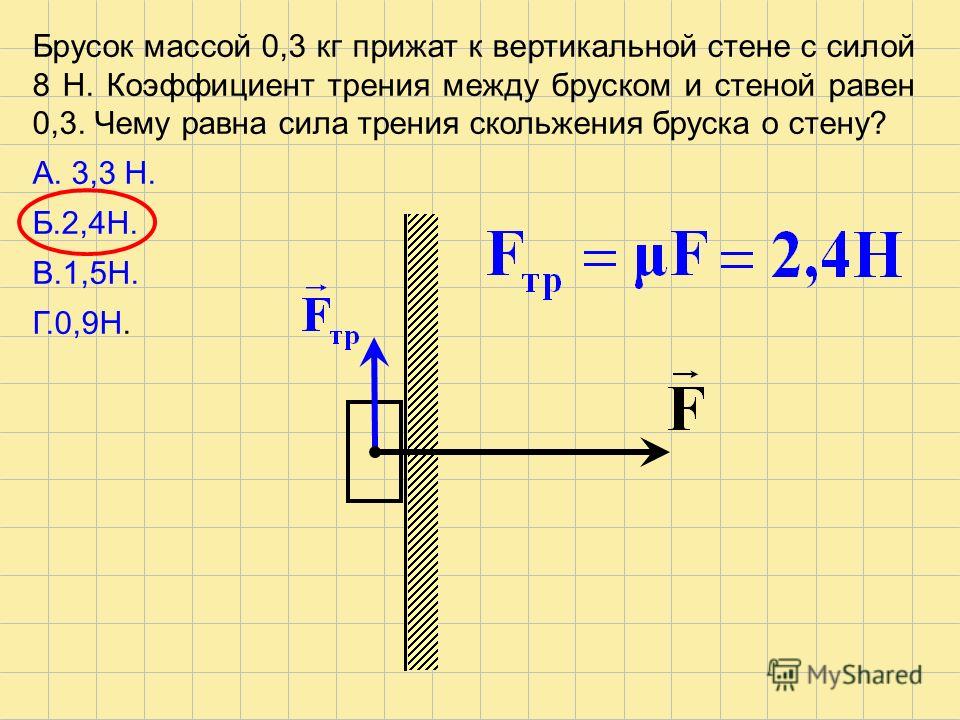 8).
8).
Зависимость коэффициента б от V 1 τq MAX для различных показателей Hurst с набором данных: L = 0,01 м, H = 10 — 5 M, h = 10 — 5 м, h = 10 — 5 м, h = 10 — 5 м, h = — 5 м, h = 10 — 5 м, h = 10 — 5 м, h = 10 — 5 м. Нормальные силы F N в диапазоне от 10 -2 до 10 2 N, 20 скоростей В 1 от 10 –4 до 100099 0. 0 –19099. 0 –19099 –19099 –19099 –19099 –19099 –19099 –19099 –19099 –19099 — 2 . Δ x в диапазоне от 10 −7 до 10 −5 м.
Полноразмерное изображение
Рисунок 8 Зависимость мощности α в уравнении (13) от экспонента Hurst для V 1 τq MAX > 1.
Изображение полного размера
9
. MAX > 1..
Исследована кинетика коэффициента трения после скачка скорости скольжения для модельного эластомера. Мы обнаружили простую общую структуру кинетики: коэффициент трения испытывает сначала скачок, а затем релаксацию по экспоненциальному закону к новому стационарному значению. Скачок Δμ 9Таким образом, 0040 0
коэффициента трения и время релаксации являются единственными величинами, полностью описывающими кинетику коэффициента трения. Для исследуемого модельного эластомера найдены замкнутые зависимости как для Δμ 0 , так и для времени релаксации в зависимости от материала и параметров нагружения. Характер релаксации определяется величиной v 1 τq max , которую можно рассматривать как отношение двух характерных времен системы: времени релаксации τ эластомера и характерного времени контакт микронеровностей 1/( v 1 q макс ). Для V 1 τq MAX <1, коэффициент B в уравнении (6) примерно равен B ≈ V 8 B ≈ V 8 B ≈ V 8 B ≈ V 8 B ≈ V 8 B ≈ V . B ≈ V . коэффициента трения определяется уравнением
Для V 1 τq MAX <1, коэффициент B в уравнении (6) примерно равен B ≈ V 8 B ≈ V 8 B ≈ V 8 B ≈ V 8 B ≈ V 8 B ≈ V . B ≈ V . коэффициента трения определяется уравнениемОтметим, что в этой области релаксация коэффициента трения происходит на характерной длине D c = 1/ q max , что имеет тот же порядок величины, что и размер микроконтактов между телами, в соответствии с исходной концепцией Dieterich et. др. 14 . Для v 1 τq max > 1 релаксация коэффициента трения описывается как
с характерным временем релаксации
Уравнение (15) охватывает предельные случаи релаксации на характерной длине 1 / q max (в пределе H = 0) и релаксации за характерное время τ (в пределе H = 1).
Методы
Для построения одномерных моделей использовался метод уменьшения размерности (МДР). С помощью этого метода трехмерный контакт отображается на одномерный с правильно определенными упругими или вязкоупругими основаниями. Он дает точные решения нормальной контактной задачи осесимметричных и самоаффинных фрактальных поверхностей, а также точные решения тангенциальной контактной задачи с постоянным коэффициентом трения. С помощью этого метода можно анализировать все свойства, которые зависят от соотношения силы и смещения, такие как контактная жесткость, электрическое сопротивление и теплопроводность, а также сила трения для эластомеров. Основы и основные правила подробно описаны в статье 35 и в книжке 36,41 . Дополнительные описания, связанные с вязкоупругим контактом, также можно найти во введении и в начале раздела «Результаты». В исх. 38 было заявлено, что МДР не может правильно описать эффекты упругих взаимодействий в среде. Это неверно: в реальности МДР точно учитывает дальнодействующие взаимодействия за счет изменения формы контактирующих тел 36 . Однако MDR считает процесс скольжения квазистатический. Хотя это допущение выполняется для трения эластомеров при скоростях, намного меньших скорости звука, оно не всегда справедливо для сухого трения или трения при наличии сцепления 42 . Как было показано в Ref. 42 , для таких систем важную роль может играть межфазная динамика. Однако для рассматриваемой в данной статье задачи мы заключаем, что все существенные взаимодействия в среде учитываются корректно.
Однако MDR считает процесс скольжения квазистатический. Хотя это допущение выполняется для трения эластомеров при скоростях, намного меньших скорости звука, оно не всегда справедливо для сухого трения или трения при наличии сцепления 42 . Как было показано в Ref. 42 , для таких систем важную роль может играть межфазная динамика. Однако для рассматриваемой в данной статье задачи мы заключаем, что все существенные взаимодействия в среде учитываются корректно.
Ссылки
Перссон, Б. Н. Дж. Трение скольжения: физические принципы и приложения. (Спрингер, Берлин, 2000).
Попов В. Л. Контактная механика и трение: физические основы и приложения. (Спрингер, Берлин, 2010 г.).
Амонтон Г. О сопротивлении, вызываемом машинами (о сопротивлении и силе в машинах). Мем. l’Acedemie R. A , 257–282 (1699).
Кулон, К. А. Теория простых машин (теория простых машин).
 (Башелье, Париж, 1821 г.).
(Башелье, Париж, 1821 г.).Дитрих, Дж. Х. Трение, зависящее от времени, и механика прерывистого скольжения. Чистое приложение Геофиз. 116, 790–806 (1978).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Дитрих, Дж. Х. Моделирование трения горных пород: 1. Экспериментальные результаты и определяющие уравнения. Дж. Геофиз. Рез. Твердая Земля 84, 2161–2168 (1979).
Артикул Google ученый
Райс, Дж. Р. и Руина, А. Л. Устойчивость устойчивого фрикционного проскальзывания. Дж. Заявл. мех. 50, 343–349 (1983).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Мароне, К. Лабораторные законы трения и их применение к сейсмическим разломам. Анну. Преподобный Планета Земля. науч. 26, 643–696 (1998).
КАС Статья ОБЪЯВЛЕНИЯ Google ученый
Дитрих, Дж.
 Х. и Килгор, Б. Д. Непосредственное наблюдение фрикционных контактов: новое понимание свойств, зависящих от состояния. Чистое приложение Геофиз. 143, 283–30 (1994).
Х. и Килгор, Б. Д. Непосредственное наблюдение фрикционных контактов: новое понимание свойств, зависящих от состояния. Чистое приложение Геофиз. 143, 283–30 (1994).Артикул ОБЪЯВЛЕНИЯ Google ученый
Baumberger, T., Caroli, C., Perrin, B. & Ronsin, O. Нелинейный анализ бифуркации прерывистого скольжения в управляемом ползучести режиме сухого трения. физ. Ред. Е. 51, 4005 (1995).
КАС Статья ОБЪЯВЛЕНИЯ Google ученый
Baumberger, T. Контактная динамика и трение на границе твердое тело-твердое: материальные и статистические аспекты. Твердотельный коммун. 102, 175–185 (1997).
КАС Статья ОБЪЯВЛЕНИЯ Google ученый
Попов В.Л., Грземба Б., Старчевич Дж. и Попов М. Законы трения, зависящие от скорости и состояния, и предсказание землетрясений: что мы можем узнать из лабораторных моделей? Тектонофизика 532–535, 291–300 (2012).

Артикул ОБЪЯВЛЕНИЯ Google ученый
Боуден Ф. П. и Табор Д. Трение и смазка твердых тел. (Кларендон Пресс, Оксфорд, 1986).
Дитрих, Дж. Х. и Килгор, Б. Д. Контактная поверхность для визуализации: распределение контактов по степенному закону и контактные напряжения в кварце, кальците, стекле и акриловом пластике. Тектонофизика 256, 219–239 (1996).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Мюзер, М. Х., Урбах, М. и Роббинс, М. О. Статистическая механика статического и низкоскоростного кинетического трения. Доп. хим. Физ-ра. Пригожин И., Райс С.А., 126 (2003).
Баумбергер, Т., Берту, П. и Кароли, К. Физический анализ закона трения, зависящего от состояния и скорости. II. Динамическое трение. физ. Rev. B 60, 3928 (1999).
КАС Статья ОБЪЯВЛЕНИЯ Google ученый
Остермейер Г.
 П. О динамике коэффициента трения. Носите 254, 852–858 (2003).
П. О динамике коэффициента трения. Носите 254, 852–858 (2003).КАС Статья Google ученый
Остермейер Г. П. и Мюллер М. Динамическое взаимодействие трения и рельефа поверхности в тормозных системах. Трибол. Междунар. 39, 370–380 (2006).
Артикул Google ученый
Попов В. Л. Термодинамика и кинетика сдвигового плавления тонкого слоя смазки, заключенного между твердыми телами. Тех. физ. 46, 605–615 (2001).
MathSciNet КАС Статья Google ученый
Хеслот Ф., Баумбергер Т., Перрин Б., Кароли Б. и Кароли С. Динамика ползучести, прерывистого скольжения и сухого трения: эксперименты и эвристическая модель. физ. Ред. Е. 49, 4973 (1994).
КАС Статья ОБЪЯВЛЕНИЯ Google ученый
Райс Дж. Р., Лапуста Н. и Ранджит К.
 Трение, зависящее от скорости и состояния, и устойчивость скольжения между упруго деформируемыми твердыми телами. Дж. `Мех. физ. Твердые тела 49, 1865–189 гг.8 (2001).
Трение, зависящее от скорости и состояния, и устойчивость скольжения между упруго деформируемыми твердыми телами. Дж. `Мех. физ. Твердые тела 49, 1865–189 гг.8 (2001).Артикул ОБЪЯВЛЕНИЯ Google ученый
Филиппов А.Е., Попов В.Л. Модифицированная модель Берриджа–Кнопова с трением, зависящим от состояния. Трибол. Междунар. 43, 1392–1399 (2010).
Артикул Google ученый
Попов В.Л. Теория перехода от статического к кинетическому трению в граничных слоях смазки. Твердотельный коммун. 115, 369–373 (2000).
КАС Статья ОБЪЯВЛЕНИЯ Google ученый
Шарготт, М. и Попов, В. Л. Механизмы прерывистого скольжения и потери устойчивости. Трибол. und Schmierungstechnik 5, 11–17 (2003).
Google ученый
Канудас де Вит, К. и Ищински, П.
 Адаптивная компенсация трения с частично известной динамической моделью трения. Междунар. Дж. Адаптировать. Процесс управляющих сигналов. 11, 65–80 (1997).
Адаптивная компенсация трения с частично известной динамической моделью трения. Междунар. Дж. Адаптировать. Процесс управляющих сигналов. 11, 65–80 (1997).MathSciNet Статья Google ученый
Дюпон П., Хейворд В., Армстронг Б. и Альтпетер Ф. Модели упругопластического трения в одном состоянии. IEEE транс. вкл., автомат. Контроль 47, 787–792 (2002).
MathSciNet Статья Google ученый
Ламперт, В., Аль-Бендер, Ф. и Суверс, Дж. Экспериментальная характеристика сухого трения при низких скоростях на разработанной установке трибометра для макроскопических измерений. Трибол. лат. 16, 95–105 (2004).
Артикул Google ученый
Попов В.Л., Старцевич Дж., Филиппов А.Е. Влияние ультразвуковых колебаний в плоскости на статическое трение и трение скольжения и собственный масштаб процессов сухого трения.
 Трибол. лат. 39, 25–30 (2010).
Трибол. лат. 39, 25–30 (2010).КАС Статья Google ученый
Филиппов А.Е., Попов В.Л. Фрактальная модель Томлинсона для мезоскопического трения: от микроскопического демпфирования, зависящего от скорости, к макроскопическому кулоновскому трению. физ. Ред. E.2 75, 027103 (7AD).
Гринвуд, Дж. А. и Табор, Д. Трение твердых ползунков по смазанной резине – важность потерь при деформации. проц. Рой. соц. 71, 989–1001 (1958).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Грош, К. А. Связь между трением и вязкоупругими свойствами резины. проц. Р. Соц. Лондон, сер. А, мат. физ. науч. 274, 21–39 (1963).
КАС Статья ОБЪЯВЛЕНИЯ Google ученый
Li, Q. et al. Трение между вязкоупругим телом и твердой поверхностью со случайной самоаффинной шероховатостью. физ. Преподобный Летт.
 111, 034301 (2013).
111, 034301 (2013).КАС Статья ОБЪЯВЛЕНИЯ Google ученый
Хесс М. О методе уменьшения размерности: точное отображение осесимметричных контактных задач с прилипанием и без него. физ. мезомех. 15, 264–269 (2012).
Артикул Google ученый
Порт Р., Попов В. Л., Филиппов А. Е. Нормальная контактная жесткость упругих тел с фрактальными шероховатыми поверхностями для одно- и трехмерных систем. физ. Ред. Е. 86, 026710 (2012).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Попов В. Л. Метод редукции размерности в механике контакта и трения: Связь микро- и макромасштабов. Трение 1, 41–62 (2013).
КАС Статья Google ученый
Попов В.Л. и Хесс М. Methode der Dimensionsreduction in Kontaktmechanik und Reibung (Метод уменьшения размерности в контактной механике и трении).
 (Springer-Verlag, Берлин, 2013 г.).
(Springer-Verlag, Берлин, 2013 г.).Кюршнер С., Попов В. Л. Проникновение самоаффинных фрактальных шероховатых твердых тел в модельный эластомер с линейно-вязкой реологией. физ. Ред. Е. 87, 042802 (2013).
Артикул ОБЪЯВЛЕНИЯ Google ученый
Ляшенко И. А., Пастевка Л., Перссон Б. Н. Дж. Комментарий к статье «Трение между вязкоупругим телом и жесткой поверхностью со случайной самоаффинной поверхностью». Преподобный Летт. 111, 189401 (2013).
КАС Статья ОБЪЯВЛЕНИЯ Google ученый
Li, Q. et al. Ли и др. Отвечать. физ. Преподобный Летт. 111, 189402 (2013).
КАС Статья ОБЪЯВЛЕНИЯ Google ученый
Скараджи, М., Путиньяно, К. и Карбоне, Г. Упругий контакт шероховатых поверхностей: простой критерий, позволяющий сделать двумерную изотропную шероховатость эквивалентной одномерной.
 Носите 297, 811–817 (2013).
Носите 297, 811–817 (2013).КАС Статья Google ученый
Попов В. Л. и Хесс М. Метод уменьшения размерности в контактной механике и трении. (Springer-Verlag, Берлин, 2014 г.).
Браун О.М., Барел И. и Урбах М. Динамика перехода от статического к кинетическому трению. физ. Преподобный Летт. 103, 194301 (2009).
КАС Статья ОБЪЯВЛЕНИЯ Google ученый
Скачать ссылки
Благодарности
Работа выполнена при поддержке Федерального министерства экономики и технологий (Германия) по контракту 03EFT9BE55, Министерства образования Российской Федерации и Deutsche Forschungsgemeinschaft (DFG), Q. Li был при поддержке стипендии Китайского стипендиального совета (CSC).
Информация об авторе
Авторы и организации
Берлинский технологический университет, Берлин, 10623, Германия
Цян Ли, Михаил Попов и Валентин Л.
 Попов
ПоповИнститут физики прочности и материаловедения, Томск, Российская академия наук Россия
Андрей Димаки и Сергей Г. Псахье
Сколковский институт науки и технологий, Москва, 143025, Россия
Сергей Г. Псахье
Томский государственный университет, Томск, 634050, Россия
Андрей Димаки, Михаил Попов, Сергей Григорьевич Псахье и Валентин Львович Попов
Томский политехнический университет Томск, Томск, 634050, Россия
Сергей Г. Димаки & Валентин Л. Попов
Авторы
- Цян Ли
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Андрей Димаки
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Михаил Попов
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
- Сергей Г.
 Псахье
ПсахьеПросмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Попов Валентин Львович
Посмотреть публикации автора
Вы также можете искать этого автора в PubMed Google Scholar
Взносы
V.L.P. и С.Г.П. задумал исследование, Q.L. провели численное моделирование, А.Д. и М.П. разработал исходный программный код. В.Л.П. и К.Л. обсудили результаты и внесли свой вклад в подготовку рукописи. Все авторы рассмотрели рукопись.
Заявление об этике
Конкурирующие интересы
Авторы не заявляют об отсутствии конкурирующих финансовых интересов.
Права и разрешения
Эта работа находится под лицензией Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons для статьи, если иное не указано в кредитной строке; если материал не включен в лицензию Creative Commons, пользователям необходимо будет получить разрешение от держателя лицензии, чтобы воспроизвести материал. Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by-nc-sa/4.0/
Чтобы просмотреть копию этой лицензии, посетите http://creativecommons.org/licenses/by-nc-sa/4.0/
Перепечатка и разрешения
Об этой статье
Эта статья цитируется
Масштабная теория трения скольжения резины
- Рейнхард Хенчке
- Ян Плагге
Научные отчеты (2021)
О роли чешуи в контактной механике и трении между эластомерами и случайно-шероховатыми самоаффинными поверхностями
- Попов Валентин Леонидович
- Андрей Димаки
- Михаил Попов
Научные отчеты (2015)
Комментарий к «Контактной механике для случайно шероховатых поверхностей: о справедливости метода уменьшения размерности» Бо Перссона в Tribology Letters
- В.
 Л. Попова
Л. Попова
Трибологические письма (2015)
- В.
Контактная механика случайно-шероховатых поверхностей: о применимости метода понижения размерности
- Бо Н. Дж. Перссон
Трибологические письма (2015)
Комментарии
Отправляя комментарий, вы соглашаетесь соблюдать наши Условия и Правила сообщества. Если вы обнаружите что-то оскорбительное или не соответствующее нашим условиям или правилам, отметьте это как неприемлемое.
Предельный коэффициент статического трения
Шаблон:Основной коэффициент
Содержание
- 1 Определение
- 2 Единицы и размеры
- 3 Составляющие факторы и измерение
- 3.1 Составляющие факторы
- 3.2 Зависимость от направления
- 3.3 Эмпирические измерения
- 4 Коэффициент статического трения для композитных поверхностей
- 5 Диапазон значений
- 6 Тонкости
- 6.1 Коэффициент трения покоя имеет смысл только для однородной поверхности контакта
- 7 Внешние ссылки
- 7.1 Ссылки на обучающие видео
Определение
Для двух поверхностей предельный коэффициент статического трения (также называемый коэффициентом статического трения или коэффициентом статического трения ) между ними, обозначаемый или , определяется как число, такое, что статическое трение между любыми двумя телами с этими двумя поверхностями соответственно, поскольку поверхности контакта не могут превышать , где нормальная сила между двумя телами.
Для блока, лежащего на столе, предельный коэффициент статического трения между нижней поверхностью блока и верхней поверхностью стола определяется как максимально возможное отношение приложенной горизонтальной силы к нормальной силе, при которой блок не скользить по столу.
Понятие предельного коэффициента статического трения возникает как часть кулоновской модели трения.
Угол, определяемый как угол трения.
Единицы и размеры
Предельный коэффициент статического трения является безразмерным скаляром и не нуждается в единицах измерения.
Определяющие факторы и измерения
Определяющие факторы
Предельный коэффициент статического трения между двумя поверхностями зависит от двух поверхностей и, как таковой, должен быть одинаковым для одной и той же пары поверхностей. Однако коэффициент зависит от ряда факторов, таких как влажность, прилипание пыли к поверхностям, царапины или незначительные изменения поверхности, поэтому измерения для одной и той же пары поверхностей могут отличаться со временем.
Зависимость от направления
Предельный коэффициент трения покоя может несколько меняться в зависимости от направления, если сами поверхности не изотропны, т. е. кажутся разными в разных направлениях. Микроскопические гофры таких поверхностей, как древесина, могут быть разными в разных направлениях.
Эмпирическое измерение
По этой причине предельный коэффициент статического трения для пары поверхностей должен определяться эмпирически путем измерения. Тем не менее, разумное приблизительное значение может быть оценено на основе характера поверхностей.
Коэффициент статического трения для составных поверхностей
Поскольку поверхности могут быть неоднородными, предельный коэффициент статического трения может быть разным для разных частей поверхности. В этом случае нет единого выбора среднего предельного коэффициента статического трения. Скорее, предельное значение статического трения, которое может быть приложено, также зависит от того, как нормальная сила распределяется по различным частям поверхности. Если обозначает давление, то предельное значение трения покоя представляет собой интеграл по элементам площади:
Если обозначает давление, то предельное значение трения покоя представляет собой интеграл по элементам площади:
Диапазон значений
Предельный коэффициент статического трения обычно принимает значения в диапазоне от до . В большинстве случаев предельный коэффициент статического трения меньше , но могут быть ситуации, когда он больше . Для очень скользких поверхностей предельный коэффициент статического трения может быть меньше .
| Первая поверхность | Вторая поверхность | Состояние | (радиан) | (градусы) | (радиан) | (градусы) | ||
|---|---|---|---|---|---|---|---|---|
| Алюминий | Мягкая сталь | Сухая и чистая | ||||||
| Алюминий | Алюминий | Сухая и чистая | ||||||
| Медь | Сталь | Сухая и чистая | ||||||
| Медь | Медь | Сухая и чистая | ? | ? | ? | |||
| Древесина | Бетон | Сухая и чистая | ? | ? | ? | |||
| Древесина | Металл | Сухая и чистая | ? | ? | ? | |||
| Древесина | Металл | Влажный | ? | |||||
| Дерево | Дерево | Сухая и чистая | ? | ? | ? | |||
| Древесина | Дерево | Влажный | ? | ? | ? | |||
| Мягкая сталь | Мягкая сталь | Сухая и чистая | ||||||
| Твердая сталь | Твердая сталь | Сухая и чистая |
Для получения дополнительной информации см. Справочник инженера и Набор инструментов для проектирования.
Справочник инженера и Набор инструментов для проектирования.
Тонкости
Коэффициент трения покоя имеет смысл только при однородной поверхности контакта
Коэффициент трения покоя имеет смысл только тогда, когда характер поверхностей контакта однороден по всей площади контакта. Если поверхность неоднородна, разные части поверхности могут давать разные вклады. В этом случае максимально возможное значение трения покоя зависит не только от суммарного значения нормальной силы, но и от того, как нормальная сила распределена по поверхности контакта. Если давление, то:
и максимально допустимая статическая сила трения:
Внешние ссылки
Ссылки на обучающее видео
- Коэффициент статического трения (видео на Youtube)
Что такое формула коэффициента трения?
Что такое формула коэффициента трения?
коэффициент трения, отношение силы трения, противодействующей движению двух соприкасающихся поверхностей, к нормальной силе, прижимающей две поверхности друг к другу.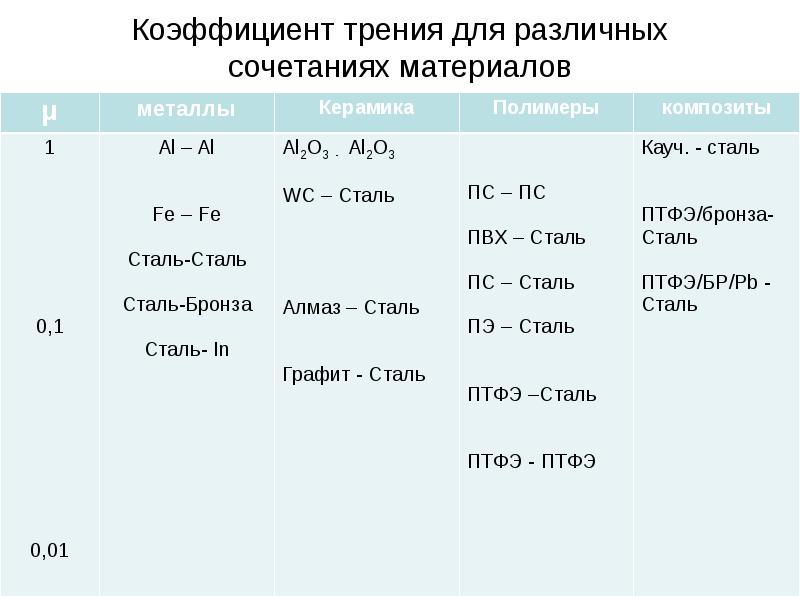 Обычно его обозначают греческой буквой мю (μ). Математически μ = F/N , где F — сила трения, а N — нормальная сила.
Обычно его обозначают греческой буквой мю (μ). Математически μ = F/N , где F — сила трения, а N — нормальная сила.
Что такое коэффициент трения примеров?
Например, лед по стали имеет низкий коэффициент трения — два материала легко скользят друг относительно друга — в то время как резина по дорожному покрытию имеет высокий коэффициент трения — материалы не скользят друг мимо друга легко. Коэффициенты трения колеблются от почти 0 до больше 1.
Как узнать коэффициент?
Формула для коэффициента вариации: Коэффициент вариации = (Стандартное отклонение / Среднее) * 100 .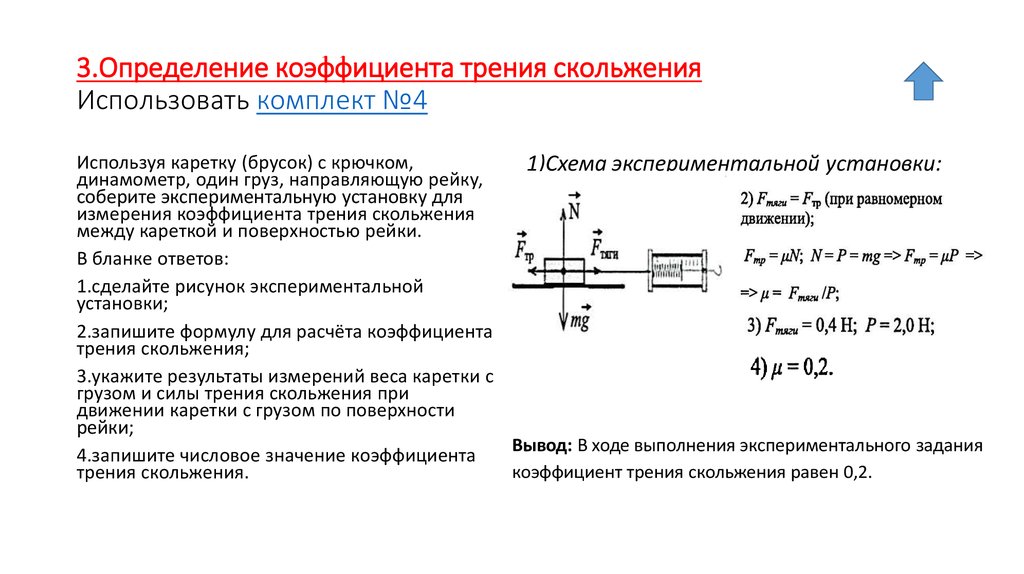 В символах: CV = (SD/x̄) * 100. Умножение коэффициента на 100 является необязательным шагом для получения процента, а не десятичной дроби.
В символах: CV = (SD/x̄) * 100. Умножение коэффициента на 100 является необязательным шагом для получения процента, а не десятичной дроби.
Постоянен ли коэффициент трения?
Кинетическое трение имеет постоянное значение, равное , равное μ*Нормальной силе на объекте, где μ является коэффициентом кинетического трения.
Связанные
Что такое коэффициент трения скольжения?
Коэффициент трения скольжения — это число, которое указывает, насколько велико трение скольжения между двумя объектами при заданной нормальной силе, толкающей их вместе .
Связанные
Какое уравнение для силы трения?
Уравнение силы трения.
 Формула, позволяющая рассчитать силу трения, очень проста: F = µ * N. где: F — сила трения, измеряемая в ньютонах; μ — безразмерный коэффициент трения, а. N — нормальная сила (перпендикулярная поверхности земли), выраженная в ньютонах.
Формула, позволяющая рассчитать силу трения, очень проста: F = µ * N. где: F — сила трения, измеряемая в ньютонах; μ — безразмерный коэффициент трения, а. N — нормальная сила (перпендикулярная поверхности земли), выраженная в ньютонах.
Родственные
Что такое коэффициент трения в физике?
Коэффициент трения — это значение , которое показывает взаимосвязь между силой трения между двумя объектами и нормальная реакция между вовлеченными объектами . Это значение иногда используется в физике для определения нормальной силы объекта или силы трения, когда другие методы недоступны.
Родственные
Какова формула коэффициента статического трения?
Запись данных рампы. Объединение физики трения с геометрией наклонной плоскости дает простую формулу для коэффициента статического трения: μ = tan (θ) , где μ — коэффициент трения, а θ — угол.

Родственные
Как рассчитать силу кинетического трения?
Рассчитайте силу трения по формуле: F = мкН. Где N — нормальная сила , а μ — коэффициент трения для ваших материалов и независимо от того, неподвижны они или движутся. нормальный сила равна весу объекта, так что это также можно записать: F = µmg. Где m — масса объекта, а g — ускорение свободного падения.
Родственные
Что такое коэффициент трения? Что такое коэффициент трения?
Коэффициент трения. Сила трения возникает между соприкасающимися поверхностями двух тел и препятствует относительному движению тел. Сила трения F пропорциональна нормальной силе N и коэффициенту трения µ : F < µs N. статическая (отсутствие проскальзывания) F = µs N. статическая, приближающееся скольжение.
статическая, приближающееся скольжение.
Родственный
Что такое коэффициент статического трения и трения скольжения стали?Что такое коэффициент статического трения и трения скольжения стали?
Материал-1 Материал-2 Коэффициент статического трения (мкс) Коэффициент трения скольжения (мкк) Материал тормоза Чугун (Fe) 0,40 Латунь Чугун (Fe) 0,3 Латунь Сталь 0,35 0,24 Латунь Стекло 0,2 59больше строк …
Связанные
Что такое пример статического трения?Какой пример статического трения?
Например, статическое трение может предотвратить скольжение объекта по наклонной поверхности. Коэффициент статического трения, обычно обозначаемый как мкс, обычно выше, чем коэффициент кинетического трения. …
Связанные
Что такое коэффициент трения для кожи? Что такое коэффициент трения для кожи?
Уравнение коэффициента трения и табличная диаграмма Материал относительно материала Статический коэффициент трения Статический коэффициент трения Свинец Чугун .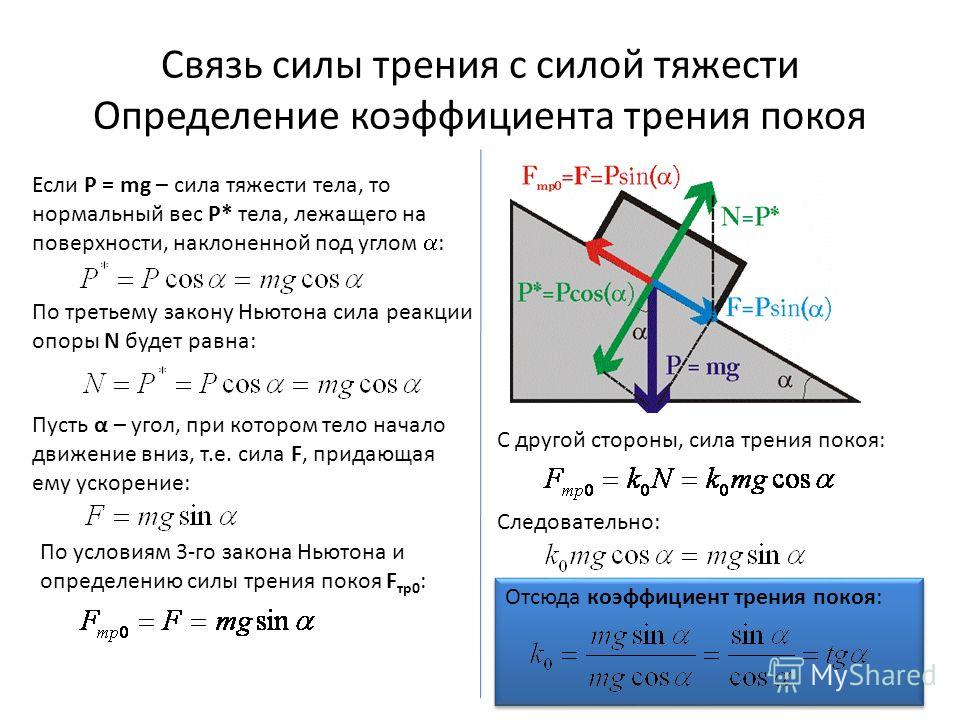


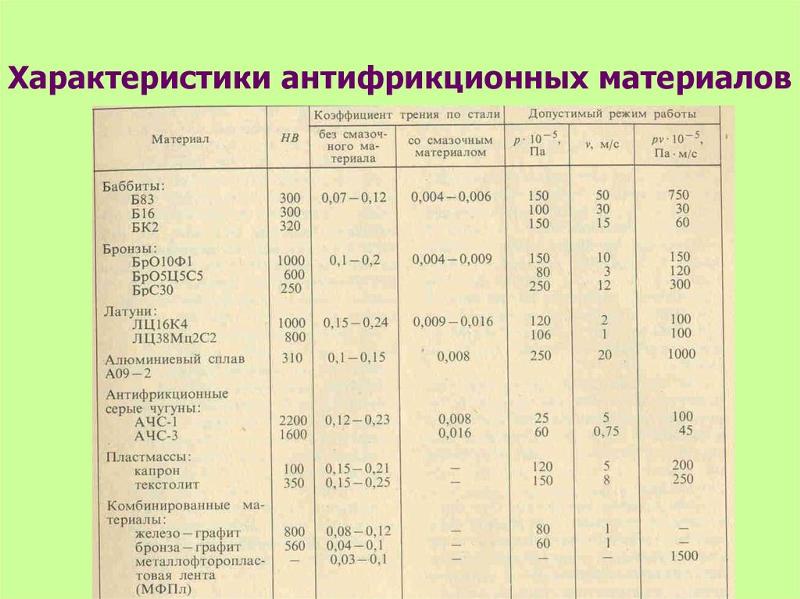 Выведенная Кулоном зависимость касается лишь силы трения покоя, которая действует между двумя контактирующими телами и препятствует возникновению относительного движения, то есть справедлива она только при условии, что колёса автомобиля неподвижны (отсутствует качение).
Выведенная Кулоном зависимость касается лишь силы трения покоя, которая действует между двумя контактирующими телами и препятствует возникновению относительного движения, то есть справедлива она только при условии, что колёса автомобиля неподвижны (отсутствует качение). А значит, и на автомобиль, который снижает скорость (тормозит), будут действовать другие силы.
А значит, и на автомобиль, который снижает скорость (тормозит), будут действовать другие силы.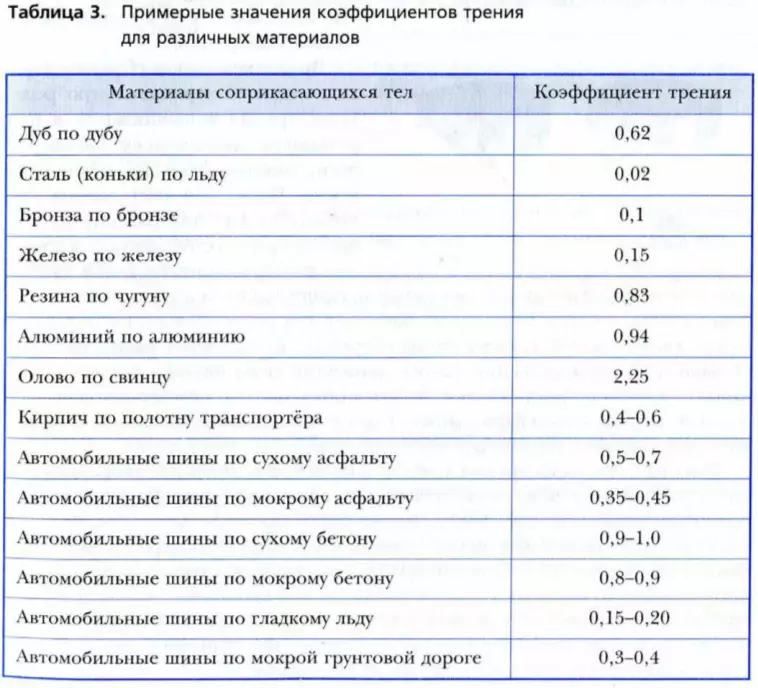 Да еще и присутствующее в этом процессе качение вносит свою лепту, непрерывно выводя из пятна контакта «отработавший» нагретый участок протектора и доставляя в него свежий — более холодный.
Да еще и присутствующее в этом процессе качение вносит свою лепту, непрерывно выводя из пятна контакта «отработавший» нагретый участок протектора и доставляя в него свежий — более холодный.
 Причем чем шире протектор, тем сцепные свойства лучше (конечно, если резиновая смесь не переохлаждена). Результаты наших шинных испытаний доказывают это. И, как вы уже поняли, не противоречат законам физики.
Причем чем шире протектор, тем сцепные свойства лучше (конечно, если резиновая смесь не переохлаждена). Результаты наших шинных испытаний доказывают это. И, как вы уже поняли, не противоречат законам физики. Звездочкой отмечены материалы, применяемые в тормозных и фрикционных устройствах.
Звездочкой отмечены материалы, применяемые в тормозных и фрикционных устройствах.
 груз)
груз) (Башелье, Париж, 1821 г.).
(Башелье, Париж, 1821 г.). Х. и Килгор, Б. Д. Непосредственное наблюдение фрикционных контактов: новое понимание свойств, зависящих от состояния. Чистое приложение Геофиз. 143, 283–30 (1994).
Х. и Килгор, Б. Д. Непосредственное наблюдение фрикционных контактов: новое понимание свойств, зависящих от состояния. Чистое приложение Геофиз. 143, 283–30 (1994).
 П. О динамике коэффициента трения. Носите 254, 852–858 (2003).
П. О динамике коэффициента трения. Носите 254, 852–858 (2003). Трение, зависящее от скорости и состояния, и устойчивость скольжения между упруго деформируемыми твердыми телами. Дж. `Мех. физ. Твердые тела 49, 1865–189 гг.8 (2001).
Трение, зависящее от скорости и состояния, и устойчивость скольжения между упруго деформируемыми твердыми телами. Дж. `Мех. физ. Твердые тела 49, 1865–189 гг.8 (2001).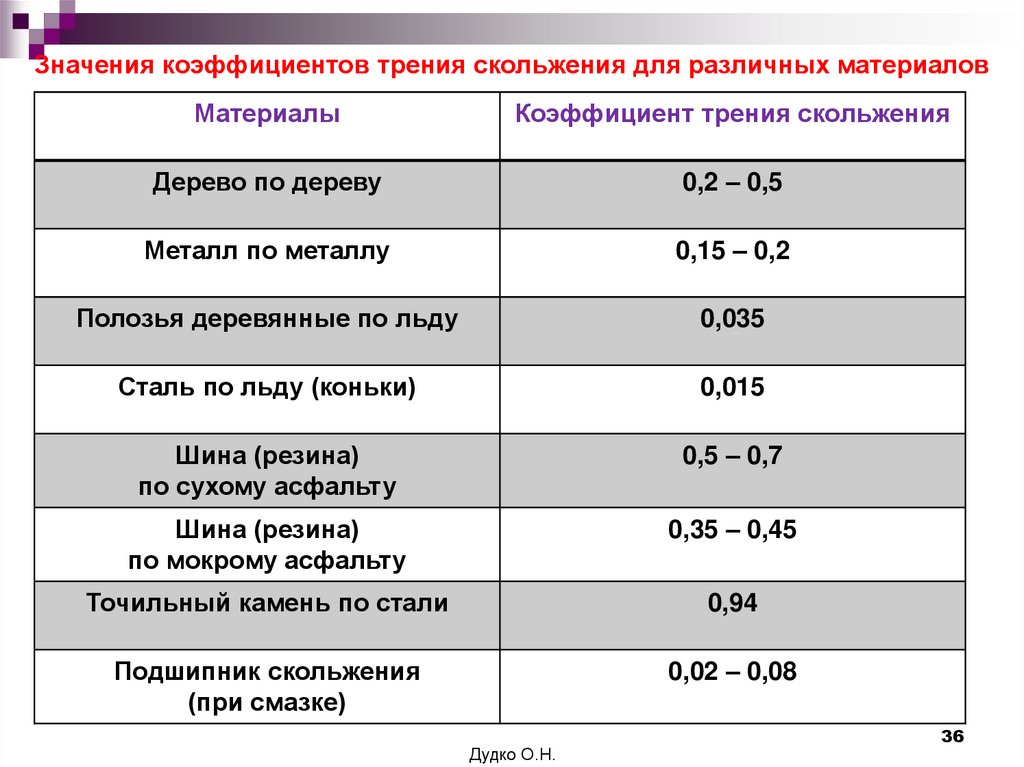 Адаптивная компенсация трения с частично известной динамической моделью трения. Междунар. Дж. Адаптировать. Процесс управляющих сигналов. 11, 65–80 (1997).
Адаптивная компенсация трения с частично известной динамической моделью трения. Междунар. Дж. Адаптировать. Процесс управляющих сигналов. 11, 65–80 (1997). Трибол. лат. 39, 25–30 (2010).
Трибол. лат. 39, 25–30 (2010).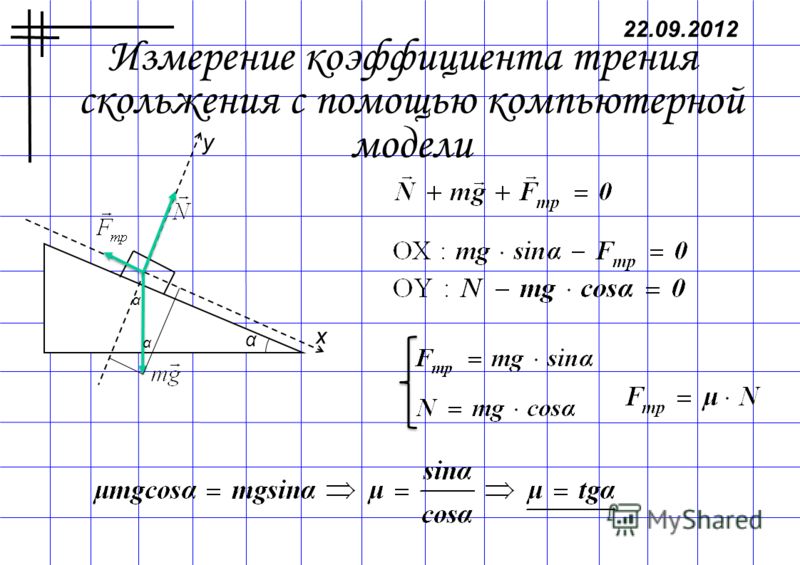 111, 034301 (2013).
111, 034301 (2013). (Springer-Verlag, Берлин, 2013 г.).
(Springer-Verlag, Берлин, 2013 г.).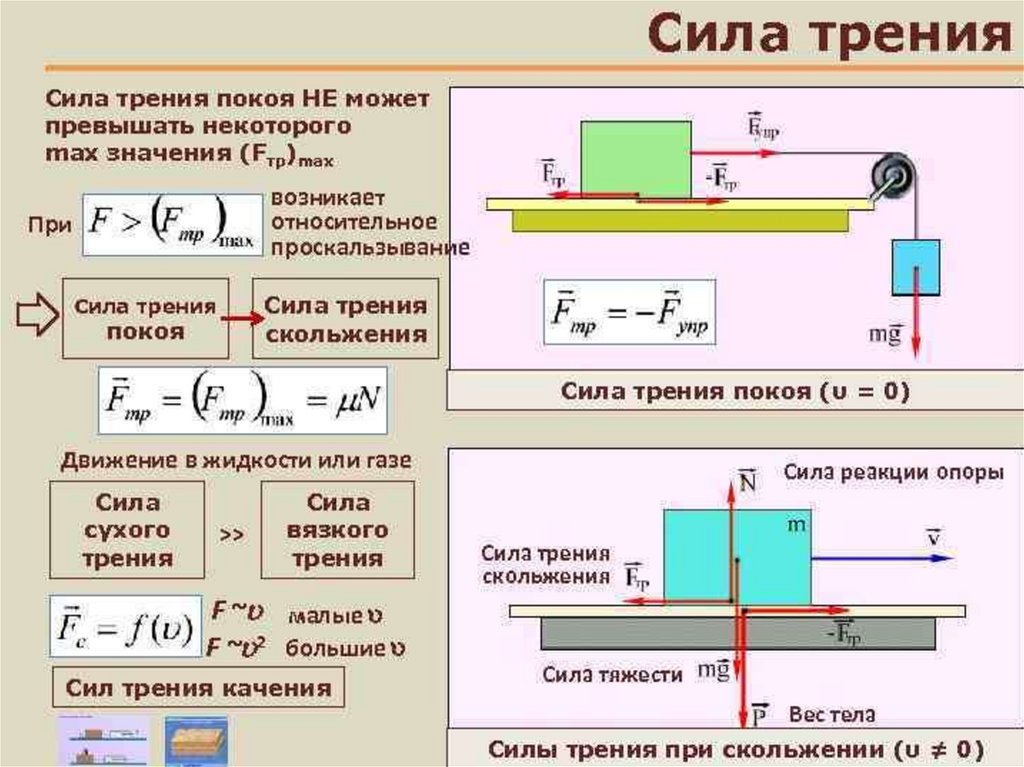 Носите 297, 811–817 (2013).
Носите 297, 811–817 (2013). Попов
Попов Псахье
Псахье Л. Попова
Л. Попова Формула, позволяющая рассчитать силу трения, очень проста: F = µ * N. где: F — сила трения, измеряемая в ньютонах; μ — безразмерный коэффициент трения, а. N — нормальная сила (перпендикулярная поверхности земли), выраженная в ньютонах.
Формула, позволяющая рассчитать силу трения, очень проста: F = µ * N. где: F — сила трения, измеряемая в ньютонах; μ — безразмерный коэффициент трения, а. N — нормальная сила (перпендикулярная поверхности земли), выраженная в ньютонах.