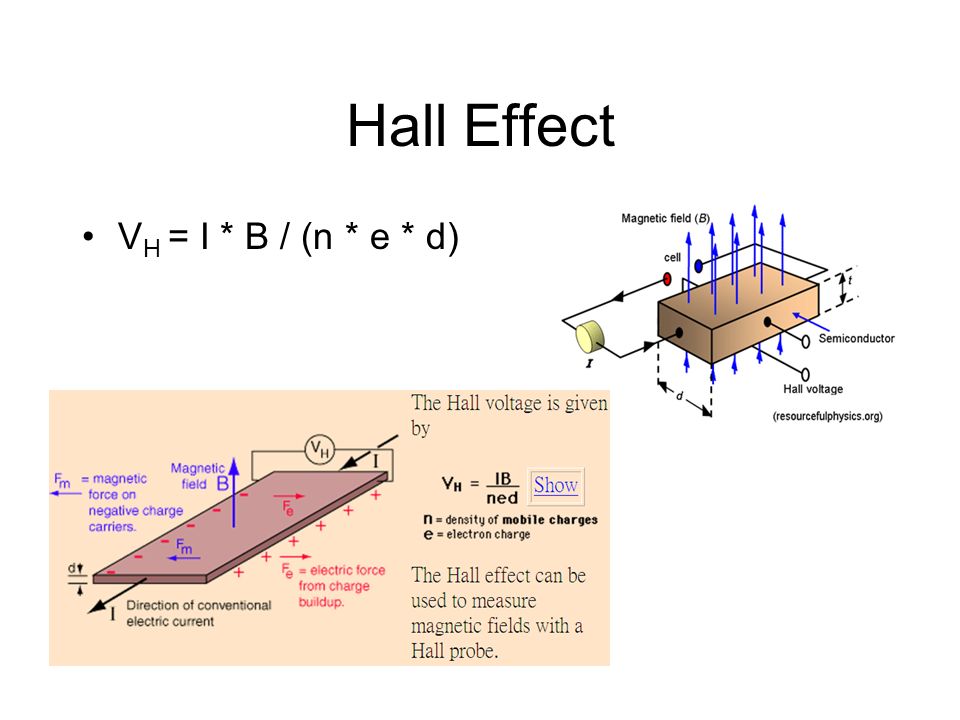
Температурная зависимость коэффициента Холла
Коэффициент Холла зависит от температуры, так как с ее изменением изменяется концентрация носителей. Измеряя ЭДС Холла и вычисляя коэффициент Холла в некотором диапазоне температур, можно получить экспериментальные данные температурной зависимости концентрации носителей заряда, по которым вычисляется энергия активации доноров или акцепторов.
Коэффициент Холла R (см. формулу (1.21)), как показывает расчет на основе кинетического уравнения, зависит сложным образом от магнитного поля. В области слабых магнитных полей для примесного полупроводника с носителями заряда одного типа коэффициент R уменьшается пропорционально В2, а для вырожденных — пропорционально μ2В2. В области сильных магнитных полей коэффициент R уменьшается пропорционально 1/В2.
Описание установки и методика измерений
Измерение эффекта
Холла в данной работе проводится по
методике постоянного тока и постоянного
магнитного поля.
Схема измерительной установки изображена на рис. 1.3.
Рис. 1.3. Схема установки для исследования эффекта Холла.
Ток, протекающий
через образцы, измеряется миллиамперметром
М2003, Величина тока задается регулятором
выходного напряжения источника питания
ЛИПС II-30.
Для изменения направления тока служит
переключатель П2. Образцы подключаются
к измерительной схеме поочередно
галетным переключателем П4. С помощью
переключателя П3 на вольтметр В7-27
подается либо ЭДС Холла, либо падение
напряжения на исследуемом кристалле.
Для определения истинной величины
ЭДС Холла (U
(1.26)
Для изменения
направления магнитного поля магнит
необходимо повернуть на 180° (поворачивать
плавно до упора по направлению стрелки).
Нагрев образцов производится минипечью, которая включается переключателем П5 (при включении печи на пульте управления загорается лампочка). Температура контролируется с помощью термопары хромель-алюмель и потенциометра КВП1-501.
Подготовка установки к работе
Внимание! При работе с магнитом снять часы. Не подносить к магниту металлические предметы
1. Включить в сеть измерительные приборы (вольтметр В7-27 и потенциометр КВП1-501) и источник питания ЛИПС II-30. Прогреть приборы в течение 5 минут. Тумблеры П7 («Ист.питания») и П5 («Печь») должны находиться в положении «Выкл.», переключатель П2 — в положении «+»
2. Проконтролировать напряжение (5В) на источнике питания ЛИПС II-30; при необходимости

В результате проведенных действий установка к работе готова.
Порядок выполнения работы
1. Измерение постоянной Холла и электропроводности образцов при комнатной температуре
1.1. Тумблер П3 поставить в положение Uобр. (измерение падения напряжения на образце),
1.2. Галетный переключатель П4 поставить в положение «1« (измерение образца №1) и включить ток тумблером П7 – в положение «Вкл»
1.3. Произвести измерение тока и падения напряжения на образце при двух направлении тока (переключатель П2 в положении «+», затем в положении «-»).
1.4. Тумблер П3 поставить в положение Uх (измерение ЭДС Холла), переключатель пределов измерений на вольтметре В7-27
1. 5. Произвести
измерение ЭДС Холла в исследуемом
образце в положениях магнита N и S и при направлении тока «+» и «-» (поворот магнита производить по
указанию стрелки).
5. Произвести
измерение ЭДС Холла в исследуемом
образце в положениях магнита N и S и при направлении тока «+» и «-» (поворот магнита производить по
указанию стрелки).
Результаты измерений занести в табл. 1.1
1.6. Переключатель П4 поставить в положение «2» (кристалл 2). Произвести измерение электропроводности и ЭДС Холла для исследуемого образца в той же последовательности, что и для образца №1.
Результаты измерений занести в таблицу 1.1
2.1. Переключатель П4 поставить в положение 3 (образец №3).
2.2. Произвести измерение ЭДС Холла при направление тока «+» (при комнатной температуре). Результаты измерений занести в табл. 1.2
2.3. Включить печь (тумблер П5 «Печь» в положение «Вкл», при этом загорится сигнальная лампочка)
2.4. Произвести измерения
ЭДС Холла при температурах 30°, 40°, 50°, 60°, 70° на
направлении тока «+». Сразу же после достижения температуры
Сразу же после достижения температуры
Результаты измерений занести в таблицу 1.2
Задание
Измерить постоянную Холла и электропроводность в образцах с электронной и дырочной проводимостью при комнатной температуре Ткомн.
По формуле
вычислить электропроводность образца для обоих направлений тока и среднее из двух измерений значение σ.
По формуле
вычислить величину и знак постоянной Холла.
Если образец
показывает дырочный тип проводимости,
то концентрация дырок определяется
по формуле (1.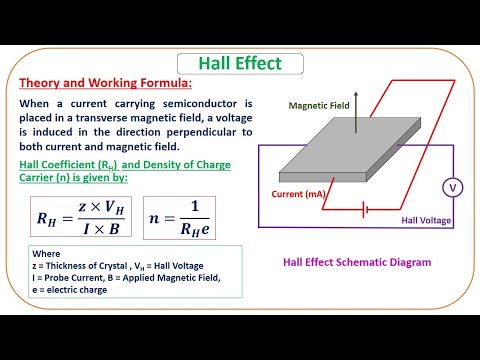 23) с
23) с
(1.27)
а подвижность — по формуле
Таблица 1.1
(мА) | Uобр (мВ) | UхN (мВ) | UхS (мВ) | Uх (мВ) | σ (Ом-1см-1) | Rх (см3/Кл) | (см-3) | μn(μp) (см2/В·с) | |
1 (+) | |||||||||
2 (-) | |||||||||
Среднее значение |
Произвести измерения падения напряжения и ЭДС Холла на образце № 2 при двух направлениях тока.

Вычислить электропроводность, определить тип проводимости и рассчитать концентрацию и подвижность носителей заряда в образце.
Измерить температурную зависимость постоянной Холла в собственном Ge.
Ап=1, Ар рассчитывается по формуле (1.27), b= μn/μp, μn и μp взять из табл.1.1.
Включить печь и произвести измерения ЭДС Холла при температурax 30, 40, 50,…70°С.
Вычислить Rx и ni для каждой температуры. Подвижность носителей заряда при температуре измерения рассчитывается по формулам
Температура
определяется в градусах Кельвина.
Таблица 1.2.
Т, оС | I (мА) | UхN (мВ) | UхS (мВ) | Uх (мВ) | Rх (см3/Кл) | μn (см2/В·с) | μp (см2/В·с) | Ар | ni (см-3) | Lg ni | 103/Т (К-1) |
Ткомн | |||||||||||
30 | |||||||||||
… |
Изучение эффекта Холла в германиевом проводнике n- и р-типа
Nach oben
Информация
- Контактное лицо
- Условия сотрудничества
- Декларация о конфиденциальности
- Вводные данные
Обслуживание
- Краткий обзор услуг
- Скачать
- Каталоги
- Вебинары и Видео
- Связаться со службой поддержки клиентов
Компания
- О нас
- Качественная политика
- Безопасность в классе
Please note
* Prices subject to VAT.
We only supply companies, institutions and educational facilities. No sales to private individuals.
Please note: To comply with EU regulation 1272/2008 CLP, PHYWE does not sell any chemicals to the general public. We only accept orders from resellers, professional users and research, study and educational institutions.
Пожалуйста, введите имя, под которым должна быть сохранена Ваша корзина.
Сохраненные корзины вы можете найти в разделе My Account.
Название корзины
Аномальный коэффициент Холла в системах с тяжелыми электронами | Успехи теоретической физики
Статья журнала
Косаку Ямада,
Косаку Ямада
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Хироши Контани,
Хироши Контани
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Хироши Коно,
Хироши Коно
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Сатору Инагаки
Сатору Инагаки
Ищите другие работы этого автора на:
Оксфордский академический
Google Scholar
Progress of Theoretical Physics , Volume 89, Issue 6, June 1993, Pages 1155–1166, https://doi.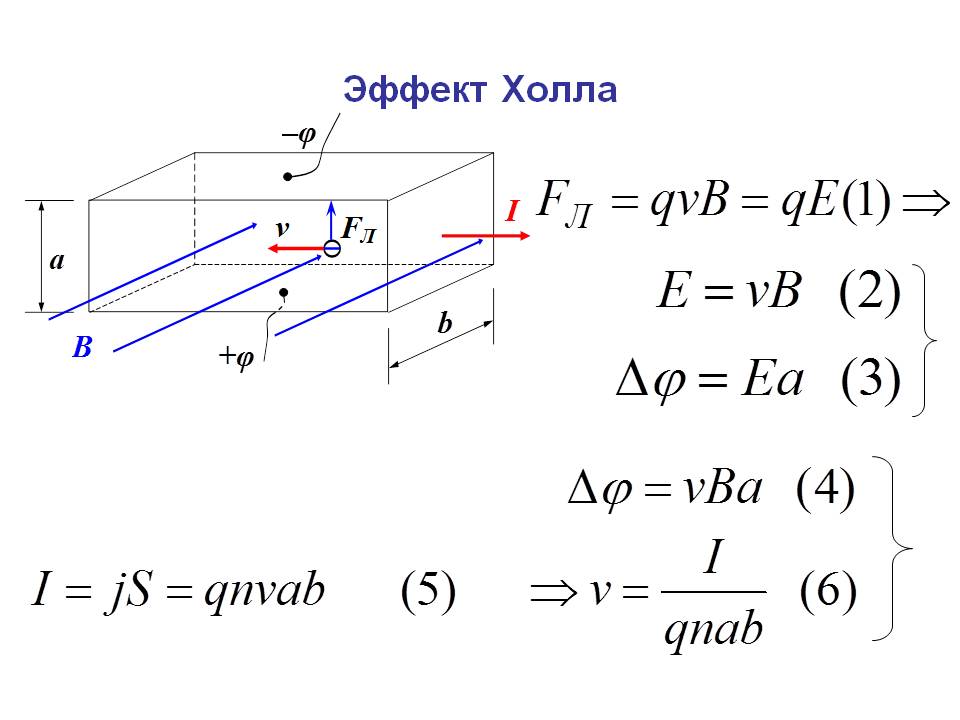 org/10.1143/ptp/89.6.1155
org/10.1143/ptp/89.6.1155
Опубликовано:
01 июня 1993 9043 История статьи
Получено:
02 февраля 1993 г.
Опубликовано:
01 июня 1993 г.
Фильтр поиска панели навигации Progress of Theoretical PhysicsЭтот выпускJPS JournalsPhysicsBooksJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Progress of Theoretical PhysicsЭтот выпускJPS JournalsPhysicsBooksJournalsOxford Academic Термин поиска на микросайте
Advanced Search
Abstract
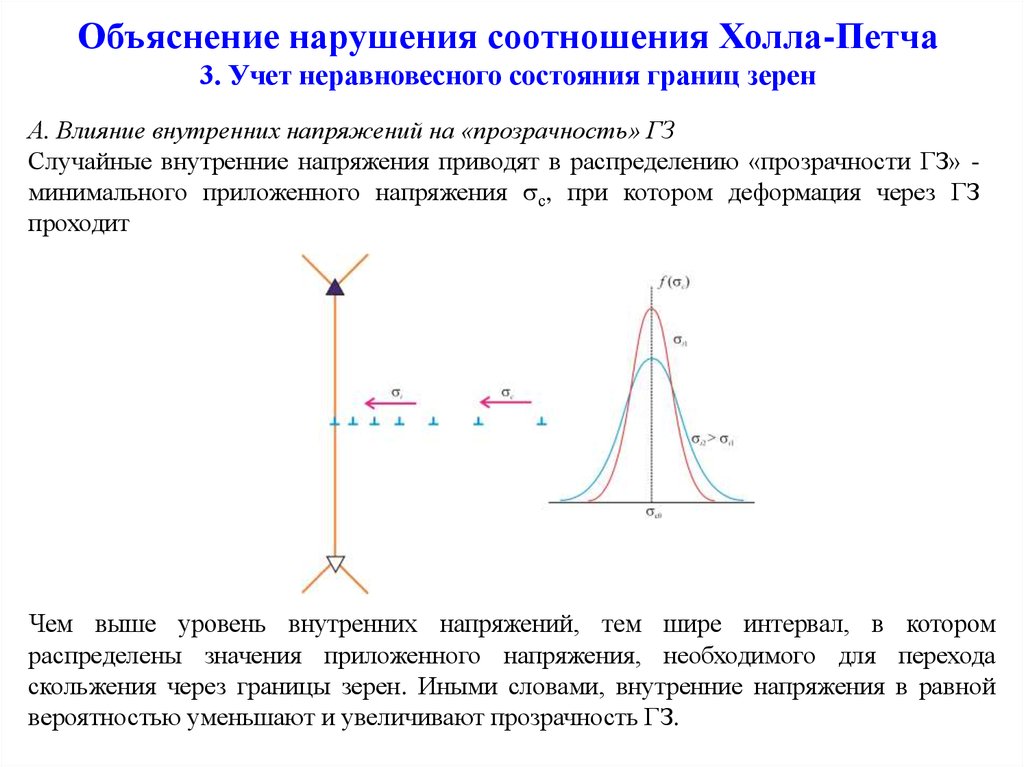
На основе периодического гамильтониана Андерсона с вырожденными орбиталями обсуждаются аномальные эффекты Холла при низких температурах в системе тяжелых электронов. Учтем косое рассеяние через спин-орбитальную связь f -орбитали. Следуя теории ферми-жидкости, получаем общее выражение для аномального коэффициента Холла в когерентном режиме. Из выражения видно, что аномальный коэффициент Холла, добавляемый к обычному коэффициенту Холла, пропорционален произведению восприимчивости на квадрат удельного сопротивления при низких температурах. Подтверждено, что такое поведение хорошо согласуется с экспериментальными результатами. Распространение этой теории на купратный высокотемпературный сверхпроводник также обсуждается в ближайшее время.
Учтем косое рассеяние через спин-орбитальную связь f -орбитали. Следуя теории ферми-жидкости, получаем общее выражение для аномального коэффициента Холла в когерентном режиме. Из выражения видно, что аномальный коэффициент Холла, добавляемый к обычному коэффициенту Холла, пропорционален произведению восприимчивости на квадрат удельного сопротивления при низких температурах. Подтверждено, что такое поведение хорошо согласуется с экспериментальными результатами. Распространение этой теории на купратный высокотемпературный сверхпроводник также обсуждается в ближайшее время.
References
1)
Ōnuki
Y.
,
Yamazaki
T.
,
Ukon
I.
,
Komatsubara
T.
,
Umezawa
A.
,
KWOK
W. K.
,
Crabtree
G. W.
,
Hinks
D. G.
. ,
J. Phys. соц. Япония.
,
1989
, том.
58
10.1143/JPSJ.58.2119
2)
Ōnuki
Y.
,
Yamazaki
T.
,
,
Ukon
I.
,
Кобори
А.
,
Комацубара
Т.
. ,
J. Phys. соц. Япония.
,
1989
, том.
58
10.1143/jpsj.58.2126
3)
KOHNO
H.
,
Yamada
K.
. ,
Прог. Теор. физ.
,
1988
, том.
80
10.1143/ptp.80.623
4)
Coleman
P.
,
Anderson
P. W.
,
Ramakrishnan
,
Ramakrishnan
,,
.0003
. ,
Физ. Преподобный Летт.
,
1985
, том.
55
10.1103/Physrevlett.55.41
5)
Fert
A.
,
Levy
P. M.
. ,
Физ.
,
1987
, том.
B36
10.1103/PhysRevB.36.1907
6)
Kohno
H.
,
Ямада
К.
. ,
Дж. Магн. Магн. Матер. & 91
,
1990
, том.
90
стр.
431
8)
Фукуяма
Х.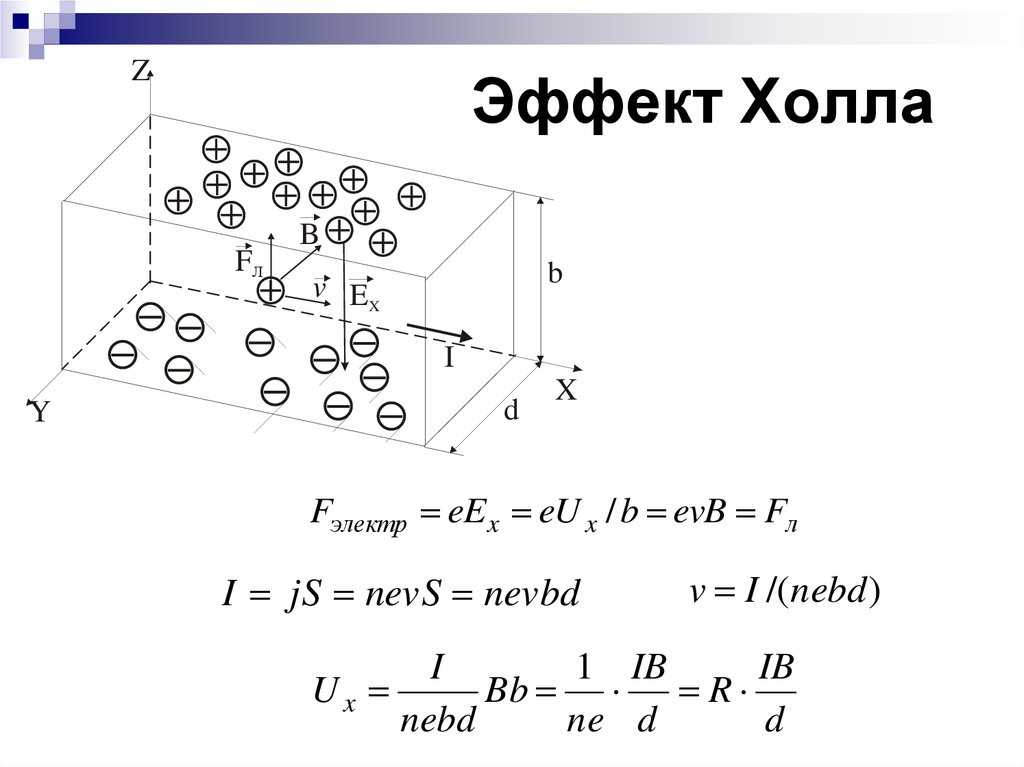
. ,
Прог. Теор. физ.
,
1986
, том.
42
стр.
621
10.1143/PTP.42.1281
9)
Ямада
К.
,
Йосида
К.
. ,
Прог. Теор. физ.
,
1986
, том.
76
10.1143/PTP.76.621
10)
Yamada
K.
,
Nakano
M.
,
Yosida
K.
,
Hanzawa
К.
,
Сакураи
А.
. ,
Прог. Теор. физ.
,
1989
, том.
82
10.1143/PTP.82.689
11)
Hanzawa
K.
,
Yosida
K.
,
Yamada
K.
. ,
Прог. Теор. физ.
,
1989
, том.
81
10.1143/PTP.81.960
13)
Yamada
K.
,
Okada
K.
,
Yosida
K.
,
Hanzawa
K.
. ,
Прог. Теор. физ.
,
1987
, том.
77
10.1143/PTP.77.1097
14)
Ямад
К.
,
3 Йосид0003К.
,
Ханзава
К.
. ,
Прог. Теор. физ.
,
1992
, том.
108
стр.
141
10.1143/PTPS.108.141
16)
Shimakawa
Y.
,
Kubo
Y.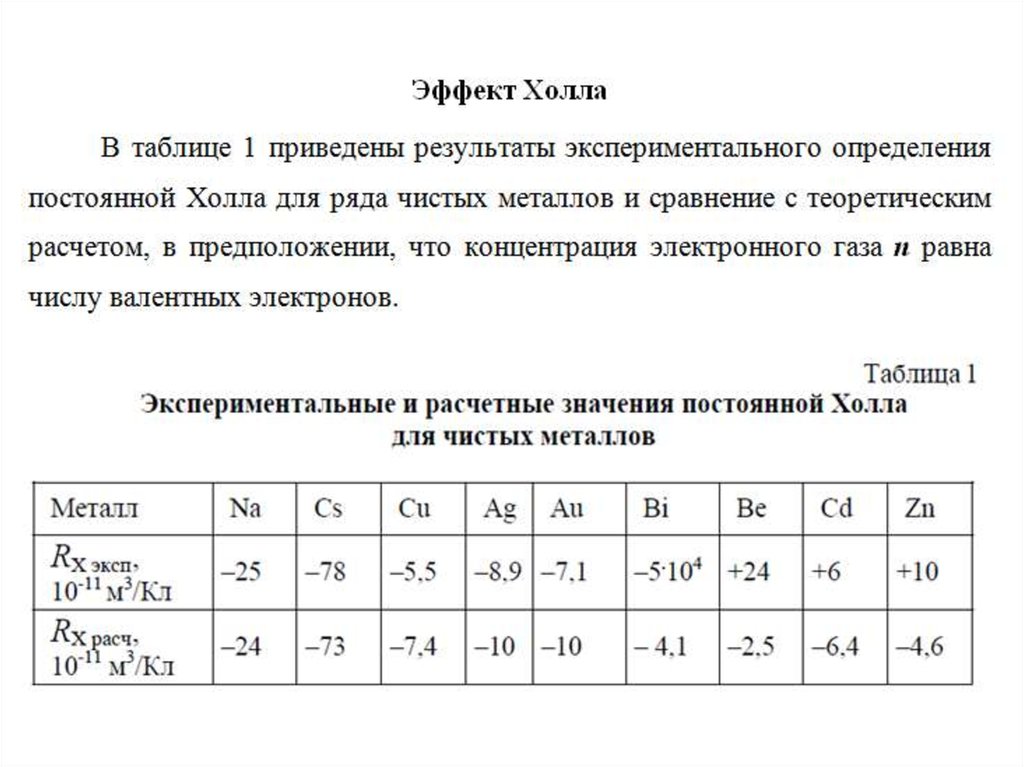
,
Manako
T.
,
Satch
Т.
,
Иидзима
С.
,
Ичихаси
Т.
,
Игараши
Х.
3 90. ,
Physica
,
1989
, том.
C157
стр.
279
Ссылка на статью(и):
Журнал Физического общества Японии 63 (1994) стр. 2627-2652
0352 Хироши Контани и Косаку Ямада
Журнал Физического общества Японии 66 (1997), стр. 2252-2255
Теория аномального эффекта Холла в системе тяжелых фермионов с сильным анизотропным кристаллическим полем Хироси Контани, Мороши Контани Миядзава и Косаку Ямада
Journal of the Physical Society of Japan 68 (1999) pp.
 1625-1631
1625-1631Аномальный эффект Холла в Sr 2
7 RuO 9 03514 40667 Morio Miyazawa, Hiroshi Kontani и Kosaku YamadaЖурнал физического общества Японии 70 (2001) с. 2999-3005
Необычная аномальная устойчивость к Cucr 9064 2 . Zn 0.5 Cr 2 Se 4 and Cr 3 Te 4 Keisuke Oda, Shunsuke Yoshii, Yukio Yasui, Masafumi Ito, Takahiko Ido, Youhei Ohno, Yoshiaki Kobayashi and Masatoshi Sato
Journal of the Physical Society of Japan 71 (2002) pp. 2792-2799
Magnetic Structure and the Hall Resistivity of Cu 1- x Zn x Cr 2 Se 4 Сатоши Икубо, Юкио Ясуи, Кейсуке Ода, Юхей Оно, Ёсиаки Кобаяши, Масатоси Сато и Казухиса Какураи
Журнал Физического общества Японии 76 (2007) 054708 (8 страниц)
2 90 Свойства транспортных средств CeCu 6 and CeCu 5. 9 Au 0.1 Takahiro Namiki, Hideyuki Sato, Hitoshi Sugawara, Yuji Aoki, Rikio Settai, and Yoshichika Ōnuki
9 Au 0.1 Takahiro Namiki, Hideyuki Sato, Hitoshi Sugawara, Yuji Aoki, Rikio Settai, and Yoshichika Ōnuki
© Copyright (c) 1993 Progress of Theoretical Physics 1993
Issue Section :
Артикул
Скачать все слайды
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Оповещение о теме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Ссылки на статьи по телефону
Последний
Самые читаемые
Самые цитируемые
Метод точного стационарного решения уравнения Вадати-Конно-Ичикавы-Симидзу (WKIS)
Гравитационные волны от частицы на круговых орбитах вокруг черной дыры Шварцшильда до 22-го постньютоновского порядка
Применение подхода фиксированного масштаба к статическим энергиям без кварков в закаленной и 2 + 1 вкусовой решетке КХД с улучшенным действием кварка Вильсона
Кварк-антикварковые потенциалы из амплитуд Намбу-Бете-Солпитера на решетке
Разделение кирального и деконфайнментного фазовых переходов в искривленном пространстве-времени
Реклама
Авианосец Тип
Как упоминалось на предыдущей странице, для простого металла и легированных полупроводников, в которых имеется только один тип носителей заряда (электроны или дырки), напряжение Холла V H определяется как
, где I — это ток по длине пластины, B — плотность магнитного потока, d — глубина пластины, e — заряд электрона, n — плотность носителей заряда.
Коэффициент Холла определяется как
, где j — плотность тока носителей. В единицах СИ это становится
.
В общем случае напряжение Холла не является линейной функцией магнитного поля, хотя его можно легко вычислить, если предположить, что все носители имеют одинаковую скорость дрейфа.
Этого можно добиться, выполнив одно из двух предположений:
- Все присутствующие носители относятся только к одному типу. Присутствует
- носителей обоих типов.
Один тип несущей
Это то же самое, что и общий случай, упомянутый выше, с коэффициентом Холла, равным
.
Когда преобладает один носитель, проводимость материала σ=eqμ, где μ — подвижность носителей заряда. Следовательно,
.
Это простое выражение для R позволяет определить как ширину запрещенной зоны, так и энергию донорного уровня путем изучения изменения R с температурой.
R H (T) зависит только от n(T), плотности носителей заряда. При низких температурах тепловой энергии достаточно только для возбуждения носителей с донорных уровней (Ed), близких к краю зоны проводимости, вверх в зону проводимости. Поэтому ожидается, что R H будет уменьшаться линейно с наклоном, пропорциональным -E d , прежде чем выйти на плато, как только все доноры будут ионизированы. При более высоких температурах теперь можно возбудить носители через запрещенную зону, и, таким образом, коэффициент Холла снова начнет уменьшаться, на этот раз с наклоном, пропорциональным E g .
При низких температурах тепловой энергии достаточно только для возбуждения носителей с донорных уровней (Ed), близких к краю зоны проводимости, вверх в зону проводимости. Поэтому ожидается, что R H будет уменьшаться линейно с наклоном, пропорциональным -E d , прежде чем выйти на плато, как только все доноры будут ионизированы. При более высоких температурах теперь можно возбудить носители через запрещенную зону, и, таким образом, коэффициент Холла снова начнет уменьшаться, на этот раз с наклоном, пропорциональным E g .
Два типа носителя
Этот подход полезен для собственных и слаболегированных полупроводников. Подвижности обоих типов носителей учитываются при расчете, и затем необходимо использовать средневзвешенное значение. Здесь,
.
, где μ h и μ e — подвижности дырок и электронов, а p, n — соответствующие плотности носителей.
Это уравнение получено, исходя из уравнений движения электронов и дырок в полупроводниковом кристалле [1]
, которые имеют стационарные решения:
, так что плотность тока j равна
.
Здесь принято принимать обычную геометрию, в которой ток течет по оси x, магнитное поле приложено по оси z, а поле Холла возникает по оси y. Граничные условия в этой геометрии требуют , но это не означает, что дырочный и электронный токи в этом направлении по отдельности равны нулю, просто они равны и противоположны.
Заметим, что y-компоненты скоростей носителей линейны по B и сохраняют только члены до первого порядка по B, тогда предыдущее уравнение принимает вид последняя строка.
Сокращение этих двух уравнений дает
.
Это из определения коэффициента Холла (в этой геометрии)
)
и, следовательно,
как раньше.
Это более сложное выражение, чем предыдущее выражение для R H . Энергия запрещенной зоны все еще может быть получена, но необходимо использовать другой метод. Этот метод более подробно описан на подстранице «Зависимость от температуры».
В общем случае μ h < μ e , поэтому, если p>n, то R может стать отрицательным.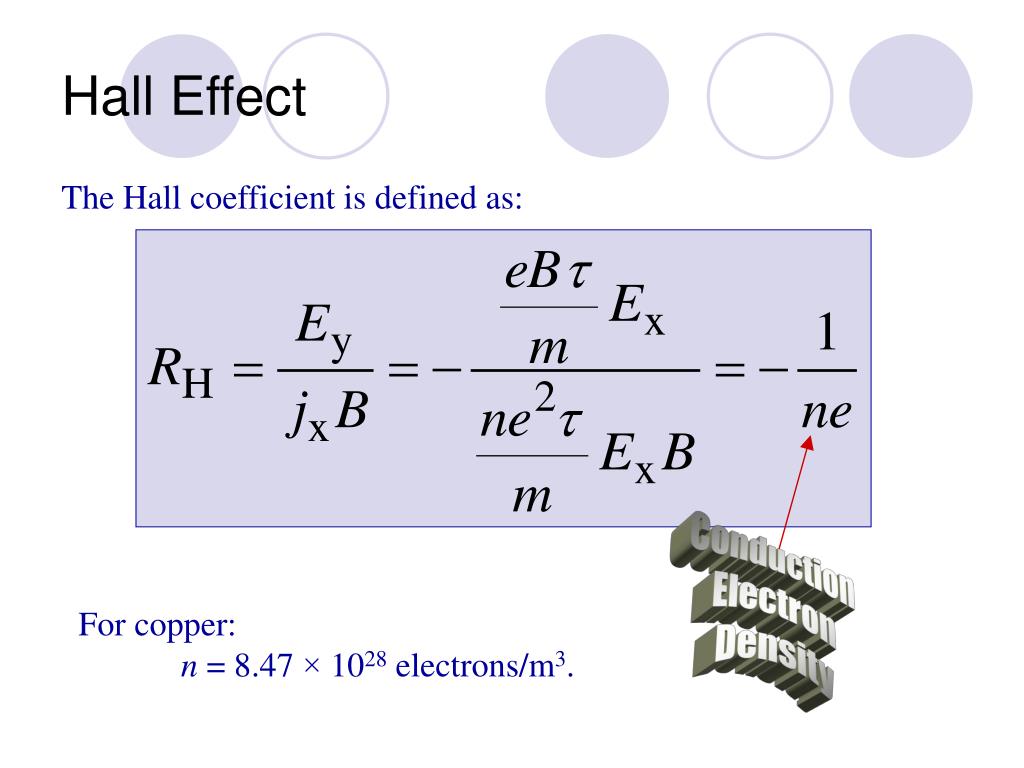



 org/10.1143/ptp/89.6.1155
org/10.1143/ptp/89.6.1155 1625-1631
1625-1631 9 Au 0.1 Takahiro Namiki, Hideyuki Sato, Hitoshi Sugawara, Yuji Aoki, Rikio Settai, and Yoshichika Ōnuki
9 Au 0.1 Takahiro Namiki, Hideyuki Sato, Hitoshi Sugawara, Yuji Aoki, Rikio Settai, and Yoshichika Ōnuki