Перевод из восьмеричной в двоичную систему счисления, калькулятор
Осуществить перевод числа из восьмеричной системы счисления в двоичную можно тремя способами.
Способ 1:
Перевести сначала в десятичную систему счисления, затем из нее в конечную.
Способ 2:
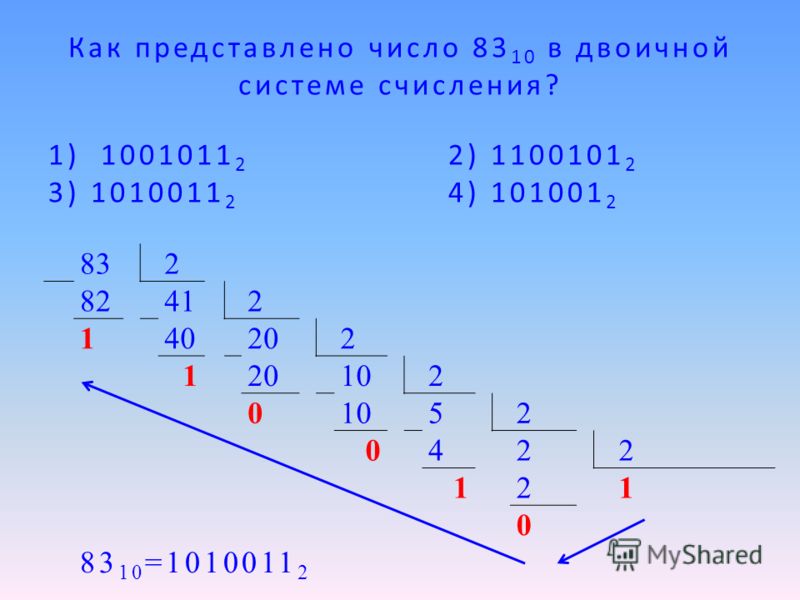
- Высший разряд восьмеричного числа делим на 2, записываем остаток и делим снова до тех пор, пока в результате не будет нуля. Каждый раз записываем остаток.
- Записываем полученные остатки в обратном порядке, получая двоичное число.
- Если полученное двоичное число имеет менее трех разрядов (то есть на если предыдущем шаге получили менее трех остатков), то дополняем нулями слева до трех разрядов.
- Повторяем предыдущие шаги для каждого следующего разряда восьмеричного числа, таким образом получаем несколько групп по 3 разряда двоичного числа.
- Записываем все вместе по порядку, отбрасываем нули слева при их наличии, получаем искомую двоичную запись числа.

- Делим высший разряд на 2, получаем остатки:
2 / 2 = 1, остаток 0
1 / 2 = 0, остаток 1
- Записываем остатки в обратном порядке: 10
- Дополняем до трех разрядом нулями слева: 010
- Повторяем для каждого следующего разряда:
5 / 2 = 2, остаток 1
2 / 2 = 1, остаток 0
1 / 2 = 0, остаток 1
Получаем 101
6 / 2 = 3, остаток 0
3 / 2 = 1, остаток 1
1 / 2 = 0, остаток 1
Получаем 110
- Записываем все вместе (010)(101)(110). Отбрасываем слева ноль, получаем двоичное число 10101110
Способ 3:
Используем таблицу триад:
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
|---|---|---|---|---|---|---|---|---|
| Триада | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
Каждую цифру исходного восьмеричного числа заменяется на соответствующие триады.
3518 = (011) (101) (001) = 0111010012 = 111010012
Смотрите также
- Перевод из двоичной в десятичную
- Перевод из двоичной в восьмеричную
- Перевод из двоичной в шестнадцатеричную
- Перевод из десятичной в двоичную
- Перевод из десятичной в восьмеричную
- Перевод из десятичной в шестнадцатеричную
- Перевод из восьмеричной в десятичную
- Перевод из шестнадцатеричной в двоичную
- Перевод из шестнадцатеричной в десятичную
Перевод из двоичной в восьмеричную систему счисления, калькулятор
Реклама
- CALCUS.RU org/ListItem»> Перевод систем счисления
- Перевод из двоичной в восьмеричную
Исходное число
Направление перевода
2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 2 (двоичная) 3 4 5 6 7 8 (восьмеричная) 9 10 (десятичная) 11 12 13 14 15 16 (шестнадцатеричная) 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36
Сообщить об ошибке
В избранное
Виджет
Вы можете сохранять ваши расчеты и они будут отображаться здесь.
Для сохранения расчета воспользуйтесь кнопкой под формой калькулятора.
Перевести число из двоичной системы в восьмеричную без калькулятора можно тремя способами.
Способ 1:
Перевести сначала в десятичную систему счисления, затем из нее в конечную.
Способ 2:
Для перевода в восьмеричную систему нужно разбить двоичное число на группы по 3 цифры справа налево. В последней (самой левой) группе вместо недостающих цифр поставить слева нули. Для каждой полученной группы произвести умножение каждого разряда на 2n, где n — номер разряда.
11012 = (001) (101) = (0*22 + 0*21 + 1*20) (1*22 + 0*21 + 1*20) = (0+0+1) (4+0+1) = (1) (5) = 158
Способ 3:
Так же как и в первом способе разбиваем число на группы. Но вместо преобразований в скобках просто заменим полученные группы (триады) на соответствующие цифры восьмеричной системы, используя таблицу триад:
| Триада | 000 | 001 | 010 | 011 | 100 | 101 | 110 | 111 |
|---|---|---|---|---|---|---|---|---|
| Цифра | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
101110102 = (010) (111) (010) = 2728
Смотрите также
- Перевод из двоичной в десятичную
- Перевод из двоичной в шестнадцатеричную
- Перевод из десятичной в двоичную
- Перевод из десятичной в восьмеричную
- Перевод из десятичной в шестнадцатеричную
- Перевод из восьмеричной в двоичную
- Перевод из восьмеричной в десятичную
- Перевод из шестнадцатеричной в двоичную
- Перевод из шестнадцатеричной в десятичную
Двоичный/десятичный/шестнадцатеричный/восьмеричный преобразователь
Двоичный/десятичный/шестнадцатеричный/восьмеричный преобразовательГлавная›Преобразование›Преобразование чисел›Преобразователь шестнадцатеричного/десятичного/восьмеричного/двоичного числа
Числовой формат NumberSigned 8-bitSigned 16-bitSigned 32-bitSigned 64-bit
Биты переключения
| 31 | 30 | 29 | 28 | 27 | 26 | 25 | 24 | 23 | 22 | 21 | 20 | 19 | 18 | 17 | 16 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
Двоичный
Десятичный
* Числа со знаком являются дополнением до 2.
ASCII, шестнадцатеричный, двоичный, десятичный преобразователь ►
Шестнадцатеричная/десятичная/восьмеричная/двоичная таблица преобразования
| Шестнадцатеричная | Десятичный | Окталь | Двоичный |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 1 | 1 | 1 | 1 |
| 2 | 2 | 2 | 10 |
| 3 | 3 | 3 | 11 |
| 4 | 4 | 4 | 100 |
| 5 | 5 | 5 | 101 |
| 6 | 6 | 6 | 110 |
| 7 | 7 | 7 | 111 |
| 8 | 8 | 10 | 1000 |
| 9 | 9 | 11 | 1001 |
| А | 10 | 12 | 1010 |
| Б | 11 | 13 | 1011 |
| С | 12 | 14 | 1100 |
| Д | 13 | 15 | 1101 |
| Е | 14 | 16 | 1110 |
| Ф | 15 | 17 | 1111 |
| 10 | 16 | 20 | 10000 |
| 20 | 32 | 40 | 100000 |
| 40 | 64 | 100 | 1000000 |
| 80 | 128 | 200 | 10000000 |
| 100 | 256 | 400 | 100000000 |
| 200 | 512 | 1000 | 1000000000 |
| 400 | 1024 | 2000 | 10000000000 |
Базовый преобразователь ►
См.
 также
также- Базовый преобразователь
- Базовый вычислитель
- Преобразователь десятичного числа в шестнадцатеричный
- Преобразователь шестнадцатеричного кода в двоичный
- Преобразователь двоичного кода в десятичный
- Восьмерично-десятичный преобразователь
- Как преобразовать шестнадцатеричный формат в десятичный
- Текст ASCII в шестнадцатеричный, двоичный, десятичный
- Преобразователь текста Hex в ASCII
- Преобразователь цвета Hex в RGB
- Системы счисления
- Преобразование номера
Напишите, как улучшить эту страницу
ПРЕОБРАЗОВАНИЕ ЧИСЕЛ
- ASCII, шестнадцатеричный, двоичный, десятичный преобразователь
- Текст ASCII в двоичный файл
- Текст ASCII в шестнадцатеричном формате
- Базовый преобразователь
- Двоичный преобразователь
- Двоичный код в текст ASCII
- Двоичный код в десятичный
- Двоичный код в шестнадцатеричный
- Дата римскими цифрами
- Десятичная дробь
- Десятичная до процентов
- Преобразование десятичного числа в двоичное
- Десятичный в восьмеричный
- Десятичный в шестнадцатеричный
- Градусы в градусы,минуты,секунды
- Градусы,минуты,секунды в градусы
- Градусов в радианы
- Дробь до десятичной дроби
- Дробь до процента
- Шестнадцатеричный/десятичный/восьмеричный/двоичный преобразователь
- Hex в текст ASCII
- Шестнадцатеричный код в двоичный
- Шестнадцатеричный в десятичный
- Восьмеричный в десятичный
- Проценты до десятичной дроби
- Проценты в дроби
- Проценты к ppm
- ppm в процентов
- частей на миллион до частей на миллиард
- частей на миллион до частей на миллион
- частей на миллиард до частей на миллион от
- до стр/мин Преобразователь
- частей на миллион
- радиан в градусов
- Римские цифры
- Научное обозначение
RAPID TABLES
- Рекомендовать сайт
- Отправить отзыв
- О
Octal to Binary Converter
Чтобы использовать этот инструмент для преобразования восьмеричного числа в двоичное , вы должны ввести восьмеричное значение, например 5432, в левое поле ниже и нажать кнопку «Преобразовать». Конвертер даст вам двоичный эквивалент данного восьмеричного числа.
Конвертер даст вам двоичный эквивалент данного восьмеричного числа.
Восьмеричное значение Прокладка
Двоичное значение Преобразование подкачки: Преобразователь двоичного кода в восьмеричный
Восьмеричное преобразование в двоичное приводит к базовым числам
Восьмеричная система счисления
Восьмеричная система счисления (или сокращенно октальная) использует число 8 в качестве основы (основания). В качестве системы счисления с основанием 8 она использует восемь символов: числа от 0 до 7, а именно 0, 1, 2, 3, 4, 5, 6 и 7. Хотя она использовалась некоторыми индейскими племенами до 20 века. , восьмеричная система стала популярной на заре вычислительной техники как язык компьютерного программирования. Это связано с тем, что восьмеричная система сокращает двоичную систему за счет упрощения длинных и сложных цепочек двоичных изображений, используемых компьютерами.
Восьмеричная система в основном используется для двоичного счета в группах по три: каждая восьмеричная цифра представляет три двоичных цифры. Поскольку 8 равно 2 в третьей степени (2 3 ), восьмеричная система стала идеальной аббревиатурой от двоичной для машин, которые используют размеры слов, кратные трем, то есть 6-битные, 12-битные, 24-битные или 36-битные. кусочек. В настоящее время большинство современных систем используют шестнадцатеричный формат, а не восьмеричный. Однако восьмеричные числа являются важной частью базовых знаний в области электроники.
Двоичная система
В двоичной системе счисления в качестве основания (основания) используется число 2. Как система счисления с основанием 2, она состоит только из двух чисел: 0 и 1.
Хотя она применялась в Древнем Египте, Китае и Индии для различных целей, двоичная система стала языком электроники и компьютеров в современный мир. Это наиболее эффективная система для обнаружения выключенного (0) и включенного (1) состояния электрического сигнала.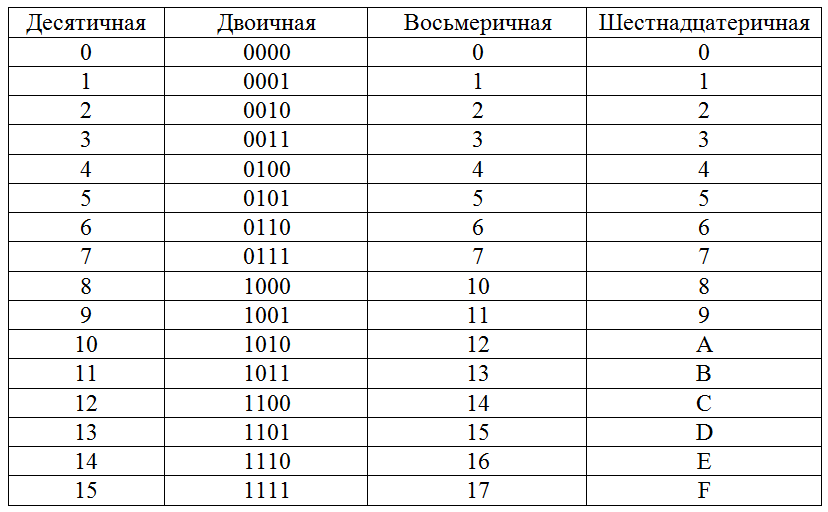 Это также основа для двоичного кода, который используется для составления данных в компьютерных машинах. Даже цифровой текст, который вы сейчас читаете, состоит из двоичных чисел.
Это также основа для двоичного кода, который используется для составления данных в компьютерных машинах. Даже цифровой текст, который вы сейчас читаете, состоит из двоичных чисел.
Чтение двоичного числа проще, чем кажется: это позиционная система; поэтому каждая цифра в двоичном числе возводится в степень 2, начиная с самой правой с 2 0 . В двоичной системе каждая двоичная цифра соответствует 1 биту.
Преобразование восьмеричного числа в двоичное
Преобразование восьмеричного числа в двоичное осуществляется очень просто, поскольку восьмеричные числа представляют собой укороченные версии двоичных строк. Помните, что каждая восьмеричная цифра представляет три двоичных цифры. Следовательно, одна восьмеричная цифра должна давать три двоичных цифры (бита). В то время как восьмеричное число может быть преобразовано в двоичное косвенно (сначала в десятичное, а затем в двоичное), прямой метод преобразования восьмеричного в двоичное с помощью шагов выглядит следующим образом:0003
- Шаг 1: Запишите восьмеричное число, разделяющее цифры.
 Каждая восьмеричная цифра представляет собой три двоичных разряда и, следовательно, равна степени числа 2. Самая правая цифра равна 2 0 (1), следующая равна 2 1 (2), а самая левая равна 2 . 2 (4). Запишите эти числа (4, 2 и 1) под восьмеричными цифрами.
Каждая восьмеричная цифра представляет собой три двоичных разряда и, следовательно, равна степени числа 2. Самая правая цифра равна 2 0 (1), следующая равна 2 1 (2), а самая левая равна 2 . 2 (4). Запишите эти числа (4, 2 и 1) под восьмеричными цифрами. - Шаг 2: Определите, какие степени двойки (4, 2 или 1) в сумме дают ваши восьмеричные цифры. Например, если одно из ваших восьмеричных чисел равно 6, это означает, что 4 и 2 в сумме дают 6 (и 1 не используется). Если ваше восьмеричное число равно 2, используется только 2; 4 и 1 нет.
- Шаг 3: Запишите 1 под используемыми цифрами 4, 2 и 1. Запишите 0 ниже тех, которые не используются.
- Шаг 4: Прочтите 1 и 0, которые вы только что написали, слева направо. Вы получите свое двоичное число.
Применим эти шаги к восьмеричному числу (456) 8
Шаг 1: 4 5 6 421 421 421 Шаг 2: 4 5 6 421 421 421 (Обратите внимание, что сумма цифр, выделенных жирным шрифтом, равна восьмеричному значению выше.Таким образом, цифры, выделенные жирным шрифтом, равны 1, а остальные — 0.) Шаг 3: 4 5 6 421 421 421 100 101 110 Шаг 4: (456) 8 = (1010011100) 2
Примеры преобразования восьмеричного числа в двоичное
Пример 1: (1234)8 = (001010011100)2 1 2 3 4 421 421 421 421 421 421 421 421 001 010 011 100
Пример 2: (75426)8 = (111101100010110)2 7 5 4 2 6 421 421 421 421 421 111 101 100 010 110
Пример 3: (6574,73)8 = (110101111100,111011)2 6 5 7 4. 7 3 421 421 421 421. 421 421 110 101 111 100. 111 011
Преобразователь двоичного кода в восьмеричный
Таблица преобразования восьмеричного кода в двоичный Таблица
| Восьмеричный | Двоичный |
|---|---|
| 1 | 00000001 |
| 2 | 00000010 |
| 3 | 00000011 |
| 4 | 00000100 |
| 5 | 00000101 |
| 6 | 00000110 |
| 7 | 00000111 |
| 10 | 00001000 |
| 11 | 00001001 |
| 12 | 00001010 |
| 13 | 00001011 |
| 14 | 00001100 |
| 15 | 00001101 |
| 16 | 00001110 |
| 17 | 00001111 |
| 20 | 00010000 |
| 21 | 00010001 |
| 22 | 00010010 |
| 22 | 00010010 |
| 0009 23 | 00010011 |
| 24 | 00010100 |
| 25 | 00010101 |
| 26 | 00010110 |
| 27 | 00010111 |
| 30 | 00011000 |
| 31 | 00011001 |
| 32 | 00011010 |
| 33 | 00011011 |
| 34 | 0001100 | 34 | 00011100 | 34 | 00011100 | 0073
| 35 | 00011101 |
| 36 | 00011110 |
| 37 | 00011111 |
| 40 | 00100000 |
| 41 | 00100001 |
| 42 | 00100010 |
| 43 | 00100011 |
| 44 | 00100100 |
| 45 | 00100101 |
| 46 | 9.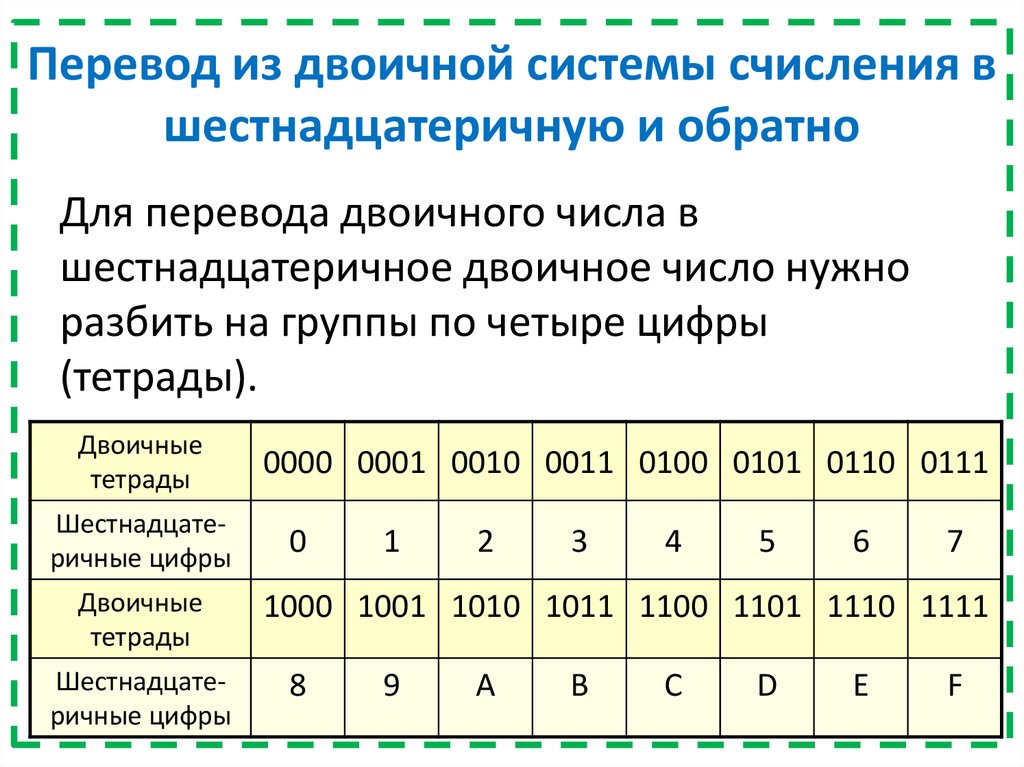 |



 Каждая восьмеричная цифра представляет собой три двоичных разряда и, следовательно, равна степени числа 2. Самая правая цифра равна 2 0 (1), следующая равна 2 1 (2), а самая левая равна 2 . 2 (4). Запишите эти числа (4, 2 и 1) под восьмеричными цифрами.
Каждая восьмеричная цифра представляет собой три двоичных разряда и, следовательно, равна степени числа 2. Самая правая цифра равна 2 0 (1), следующая равна 2 1 (2), а самая левая равна 2 . 2 (4). Запишите эти числа (4, 2 и 1) под восьмеричными цифрами. Таким образом, цифры, выделенные жирным шрифтом, равны 1, а остальные — 0.)
Шаг 3:
4 5 6
421 421 421
100 101 110
Шаг 4: (456) 8 = (1010011100) 2
Таким образом, цифры, выделенные жирным шрифтом, равны 1, а остальные — 0.)
Шаг 3:
4 5 6
421 421 421
100 101 110
Шаг 4: (456) 8 = (1010011100) 2