Калькулятор делителя напряжения [таблицы .ods, .xls]
Чтобы задать режим работы транзистора, стабилитрона или операционного усилителя, надо приготовить для них определённое напряжение. Чаще всего этим занимается делитель напряжения — простая схема из двух резисторов. Раньше мне всегда хватало калькуляторов на сайте joyta.ru. Но когда был нужен делитель с подстроечным резистором, приходилось вручную добавлять его сопротивление то к одному, то к другому плечу, чтобы узнать диапазон регулировки. Однажды мне это надоело, и я решил сделать удобный инструмент для расчётов любых делителей.Получились три таблички в форматах:
«Сложный» делитель (подбор сопротивления, расчёт напряжений)
На первый взгляд эта разновидность делителя кажется сложной, а формулы и вовсе отпугивают. Однако подстроечный резистор, включённый по схеме потенциометра, делает схему очень предсказуемой. Сопротивление R2 всегда постоянно, поэтому ток делителя не меняется, и высчитать диапазон регулировки напряжения очень просто.
Калькулятор построен так, что после расчётов можно распечатать его страницу со всеми результатами. Если вдруг понадобится пересчитать делитель — есть формулы на картинке. Справа висит таблица стандартных номиналов радиодеталей — чтобы вы не кошмарили магазины мифическими резисторами на 77 кОм.
Инструкция:1. Задать входное напряжение Uвх. 2. Установить R2max и R2.1 в нули. R2.2 обнулится автоматически. 3. Подобрать такие R1 и R3, чтобы Uвых среднее было близким к нужному. 4. Для точной регулировки укажите максимальное сопротивление подстроечного резистора R2max. 5. Калькулятор выдаст диапазон регулировки (Umin, Umax) и текущее значение Uвых. Последнее можно менять, увеличив сопротивление R2.1. 6. В реальную схему вместо потенциометра можно поставить постоянные R2.1 и R2.2 рассчитанных номиналов.
Ещё калькулятор умеет считать напряжение самого простого двухрезисторного делителя. Для этого надо указать значения R1 и R3 при R2max и R2.1 = 0.
Замечание вообще про любые делители напряжения:Ток делителя Iдел должен быть в 10 и более раз больше, чем ток нагрузки. Иначе её сопротивление войдёт в состав R3, R2.2 и собьёт настройку. Поэтому делители используются там, где токи небольшие — до нескольких десятков миллиампер. Если же вы надумали сделать автомобильную зарядку для телефона через делитель — вы погорячились. И резисторы ваши тоже очень быстро разгорячатся на десяти амперах. Не надо так.
Иначе её сопротивление войдёт в состав R3, R2.2 и собьёт настройку. Поэтому делители используются там, где токи небольшие — до нескольких десятков миллиампер. Если же вы надумали сделать автомобильную зарядку для телефона через делитель — вы погорячились. И резисторы ваши тоже очень быстро разгорячатся на десяти амперах. Не надо так.
Применение
Частотный разделитель ADSL — это фильтр нижних частот и три соединителя в корпусе
Конденсаторы часто используются в различных электрических и электронных устройствах и системах. Вероятно, вы не найдете ни одно электронное устройство, в котором не содержится хотя бы один конденсатор. Конденсаторы используются для хранения энергии, обеспечения импульсов энергии, для фильтрации питающего напряжения, для коррекции коэффициента мощности, для развязки по постоянному току, в электронных частотных фильтрах, для фильтрации шумов, для запуска электродвигателей, для хранения информации, для настройки колебательных контуров, в различных датчиках, в емкостных экранах мобильных телефонов… Этот список можно продолжать до бесконечности.
Резистивно-емкостные (RC) цепи обычно используются в качестве простых фильтров нижних и верхних частот, а также простейших интегрирующих и дифференцирующих цепей.
Делитель с подстройкой верхнего плеча (расчёт сопротивления, расчёт напряжений)
Здесь нижний вывод подстроечного резистора R2 соединён со средним выводом и выходом делителя, поэтому фактически R2 входит в состав R1 — верхнего плеча.
Этот калькулятор чуть удобнее — он рассчитывает R1 и R2 для заданного выходного напряжения и R3. Не придётся долго перебирать номиналы, чтобы попасть в нужный диапазон напряжений.
Инструкция:1. Задать входное и выходное напряжения Uвх, Uвых. 2. Установить R1, R2max и R2* в нули. 3. Выбрать R3 из таблицы стандартных номиналов и внести его в графу. Калькулятор выдаст расчётное значение суммы R1 и R2. 4. Задать стандартный номинал R1 — меньше, чем сумма R1+R2. 5. Указать максимальное сопротивление подстроечного резистора R2max. Итоговая сумма R1+R2max должна быть больше расчётного значения. Чем ближе R1 к сумме и чем меньше R2, тем уже диапазон регулировки Umin, Umax. 6. В графу R2* можно внести точное значение резистора, чтобы увидеть, какое при этом будет напряжение на выходе Uвых. И для реальной схемы дополнить R1 конкретно этим R2*.
Чем ближе R1 к сумме и чем меньше R2, тем уже диапазон регулировки Umin, Umax. 6. В графу R2* можно внести точное значение резистора, чтобы увидеть, какое при этом будет напряжение на выходе Uвых. И для реальной схемы дополнить R1 конкретно этим R2*.
Можно рассчитать и простой делитель на двух резисторах, если указать значения R1 и R3 при R2max и R2* = 0.
Параллельное соединение резисторов
При параллельном соединении общее сопротивление резисторов рассчитывается по формуле:
Параллельное соединение резисторов
Остались вопросы? Напишите комментарий. Мы ответим и поможем разобраться =)
0
Автор публикации
не в сети 1 год
Делитель с подстройкой нижнего плеча (расчёт сопротивления, расчёт напряжений)
Схема наоборот — здесь верхний вывод подстроечного резистора R2 соединён со средним выводом и выходом делителя, поэтому фактически R2 входит в состав R3 — нижнего плеча.
Этот калькулятор считает R1 по заданному выходному напряжению, R2 и R3.
Инструкция:1. Задать входное и выходное напряжения Uвх, Uвых. 2. Установить R1, R2max и R* в нули. 3. Выбрать R3 из таблицы стандартных номиналов и внести его в графу. Калькулятор выдаст расчётное значение R1. 4. Задать максимальное значение R2max и (опционально) R2*. Чем меньше R2max, тем уже будет диапазон регулировки Umin, Umax. 5. Задать стандартный номинал R1, близкий к рассчитанному. 6. Калькулятор рассчитает Uвых и диапазон регулировки Umin, Umax. 7. В графу R2* можно внести точное значение резистора, чтобы скорректировать Uвых. И для реальной схемы дополнить R3 конкретно этим R2*.
Как и раньше, делитель на двух резисторах можно рассчитать, указав значения R1 и R3 при R2max и R2* = 0.
Поделиться:
Емкостной делитель напряжения
Простейший емкостной делитель напряжения состоит из двух последовательно соединенных конденсаторов и используется для снижения величины U на отдельных элементах электрической цепи.
Делитель постоянного напряжения на конденсаторах чаще всего применяют многоуровневых инверторов напряжения, широко используемых как на электроподвижном составе, так и в других направлениях силовой электроники.
Главная сложность практического применения такой схемы (и всех подобных схем) заключается в невозможности обеспечения равномерного разряда конденсаторов, вследствие чего напряжения на них будет распределяться не поровну. Чем сильнее разряжен один конденсатор по сравнению с другим (иди с другими), тем большая разница в U будет на них, что наглядно отображает формула:
По этой причине подобные схемы крайне нестабильно работают и обязательно предусматривают узлов подзарядки конденсаторов с целью выравнивания напряжения на последних.
Емкостной делитель напряжения в цепи переменного тока
В радиоэлектронике в большей степени находят применение емкостные делители переменного напряжения.
Конденсатор, как и катушка индуктивности, относится к реактивному элементу, то есть потребляет реактивную мощность от источника переменного тока, в отличие от резистора, который является активным элементов и потребляет исключительно активную мощность.
Реактивный элемент
Здесь следует кратко пояснить разницу между активной и реактивной мощностями. Активная мощность выполняет полезную работу и реализуется только в том случае, когда ток и напряжение направлены в одном направлении и не отстают друг от друга, то есть находятся в одной фазе, что имеет место только на резисторе. На конденсаторе ток отстает от напряжения на угол φ = 90°. В результате чего ток напряжение находятся в противофазе, поэтому когда ток имеет максимальное значение напряжение равно нулю, а произведение этих двух величин дают мощность, которая в таком случае равна нулю, так как один из множителей равен нулю. Следовательно, мощность не потребляется.
Аналогичные процессы протекают и в цепи с катушкой индуктивности. Разница лишь в том, что на индуктивности i отстает от u на угол φ = 90°.
Реактивная мощность проявляется только в цепях переменного тока. Она составляет часть полной мощности и определяется по формуле:
Реактивная мощность в отличие от активной, не потребляется нагрузкой, а циркулирует между источником питания и нагрузкой.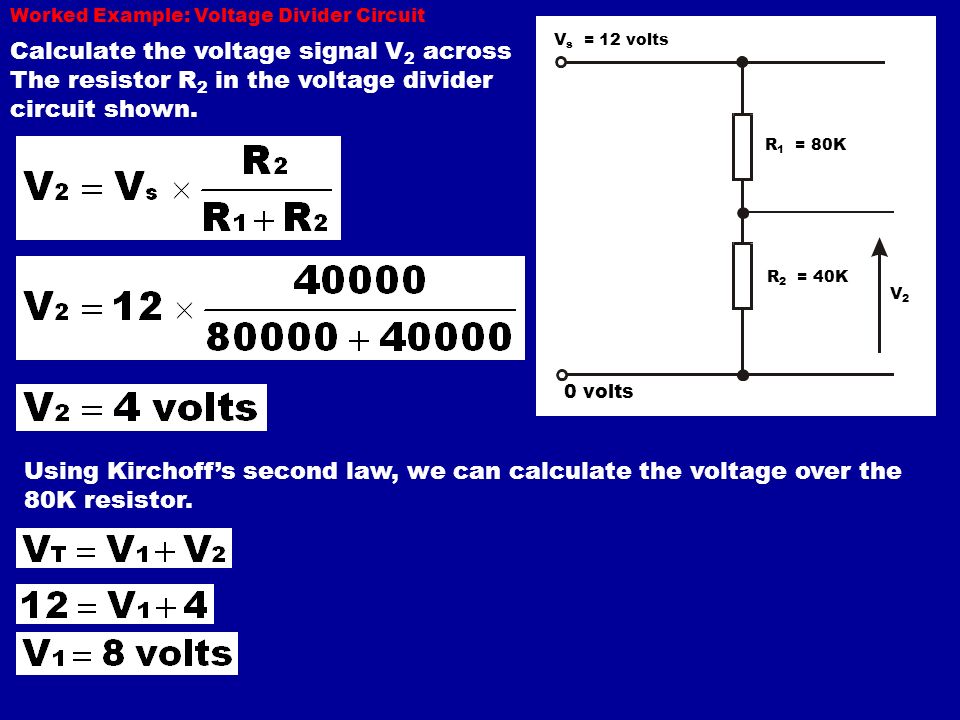 Поэтому конденсатора и катушка индуктивности являются реактивными элементами, не потребляющими активную мощность и по этой причине они практически не нагреваются.
Поэтому конденсатора и катушка индуктивности являются реактивными элементами, не потребляющими активную мощность и по этой причине они практически не нагреваются.
Расчет сопротивления делителя напряжения на конденсаторах заключается в определении необходимых значений сопротивлений.
Сопротивление конденсатора XC является величиной не постоянной и зависит от частоты переменного тока f и емкости C:
Как видно из формулы, сопротивление снижается с увеличением частоты и емкости. Для постоянного тока, частота которого равна нулю, сопротивление стремится к бесконечности, поэтому, рассматриваемая далее схема емкостного делителя напряжения не применяется постоянном токе.
Для снижения величины uвых, например в два раза, емкости C1 и C2 должны быть равны. Универсальные формулами для определения выходных uвых1 и uвых2 в зависимости от входного и емкостей C1 и C2 имеют вид, аналогичный для резисторных делителей:
Поскольку частота переменного тока для всех конденсаторов одинакова, то формулу можно упростить:
Индуктивный делитель напряжения
В качестве делителей переменного напряжения также, но гораздо реже, применяют катушки индуктивности, которые относятся к реактивным элементам. Однако, в отличие от конденсаторов, которые являются накопителями электрического поля, катушки индуктивности накапливают магнитное поле.
Однако, в отличие от конденсаторов, которые являются накопителями электрического поля, катушки индуктивности накапливают магнитное поле.
Индуктивное сопротивление зависит от индуктивности L и частоты переменного тока f. С ростом этих параметров сопротивление катушки переменному току возрастает.
XL = 2πfL.
Упрощенный вариант формулы:
Как вы наверняка уже заметили, чтобы рассчитать емкостной делитель напряжения достаточно знать емкости конденсаторов, а индуктивный делитель – индуктивности.
Еще статьи по данной теме
- Делитель напряжения на резисторах
- Инвертор напряжения
- Умножитель напряжения
- Замена электролитического конденсатора
Как «поделить» АЦП правильно / Хабр
Довольно часто в устройствах применяются активные датчики (терморезисторы, тензорезисторы, фоторезисторы, времярезисторы, счастьерезисторы и прочее).
Чтобы измерять соответствующую величину, датчик включают в цепь делителя в одно из его плеч.
Так рекомендуют поступать практически везде, особенно там, где точность не так важна как стоимость. В интернете множество уроков для ардуинщиков о считывании температуры именно при помощи терморезистора. Так поступают и в более серьезных приложениях.
Для примера ниже я представил часть схемы из драйвера VESC 4.2, который измеряет температуру ключей.
О величине резистора во втором плече все высказываются по-разному. Кто-то связывает величину только с ограничением тока на нагрев термистора.
Где-то существуют прикидки и советы.
Но я не нашел конкретных указаний по типу: «Сделай так, потому что так-то и так-то».
Интерес подогрел спор с коллегой. Что же, вызов принят.
Сразу скажу, что расчет выполнялся в программе SMath Studio. Прикладываю исходник. Вы можете использовать его в своих расчетах.
Постановка задачи
Необходимо ввести только диапазон изменения сопротивления, а формула должна возвратить оптимальное сопротивление второго плеча. Критерий оптимальности – максимальный размах напряжения на выходе.
Решение
Вариантов схем включения может быть две: либо изменяющееся сопротивление находится в лапах АЦП, либо наоборот.
С точки зрения оптимальности выбора значения не имеет, куда поставить резистор с изменяющимся сопротивлением, так как важно общее изменение сопротивления в цепи и как следствие тока, и как следствие падения напряжение, и не важно на каком плече.
Напряжение на входе АЦП зависит от сопротивления постоянного резистора и пределов изменения переменного:
где – сопротивление постоянного резистора;
– самое большое сопротивление изменяющегося резистора;
– самое маленькое сопротивление изменяющегося резистора;
– напряжение питания.
Если построить график зависимости этого напряжения от сопротивления постоянного резистора, то можно увидеть ярко выраженный пик, а это именно то, что нам нужно (график построен для случая питающего напряжения в 1 В при использовании NTC термистора в широком диапазоне температур).
Если надо найти максимум функции, то мы берем производную. (Входное напряжение я намеренно приравнял к нулю, так как здесь важны соотношения сопротивлений).
Корни нам подскажет либо листок бумаги, либо компьютерная алгебра (благодарность GarryC за пинок в сторону символьных вычислений):
Естественно, нам больше подойдет сопротивление больше нуля. Так как сроки поставки резисторов с отрицательным сопротивлением слишком большие.
Бывает, что считать числа сложно, но хочется покачать свое мышление навскидку. Бывает, люди навскидку считают децибелы, а все диву даются их уму. На самом деле они знают несколько секретов того как это делать.
Выделим и мы несколько правил для умничанья в дальнейшем. По графику такие прикидки делать легче. Как раз ниже он и представлен (но он лишь демонстрирует зависимость, описанную ранее).
По графику такие прикидки делать легче. Как раз ниже он и представлен (но он лишь демонстрирует зависимость, описанную ранее).
1 правило: Если изменение сопротивление незначительно, то постоянное сопротивление должно быть примерно равным среднему изменяющемуся. Но и изменение напряжения будет ничтожно. Используй лучше мостовую схему.
2 правило: Если сопротивление изменяется в разы, то постоянное сопротивление должно быть меньше максимально возможного у изменяемого.
3 правило: Чем больше изменяется сопротивление в изменяемом резисторе, тем меньше должно быть сопротивление постоянного относительно максимума изменяемого.
Например, при разнице между граничными заключениями сопротивления изменяемого резистора в 10 раз рекомендуемое сопротивление постоянного должно быть примерно в три раза меньше максимального, а в случае изменения в 50 раз постоянный резистор уже должен составлять 0,14 от максимального в диапазоне изменения переменного резистора.
Если кто-то выделил дополнительные правила или не согласен с имеющимся, делитесь, и мы сделаем наш мир более грамотным.
Если совсем не охота вникать, но хочется поставить в свой arduino проект «осознанный» делитель, то можно воспользоваться готовым ответом.
Какой резистор ставить в паре с NTC термистором на 10 кОм с В = 3950.
Ниже я представил таблицу, в которой показаны различные диапазоны измеряемых температур и соответственное сопротивление второго плеча.
| Диапазон изменения сопротивления, градусов целься | Применение | Рекомендуемое сопротивление второго плеча, кОм | Процент использования динамического диапазона АЦП, % |
|---|---|---|---|
| 0..+125 | Мониторинг температуры внутри устройств в помещении | 3,3 | 81 |
| -50…+125 | Максималка для данного термистора | 18 | 96 |
-20.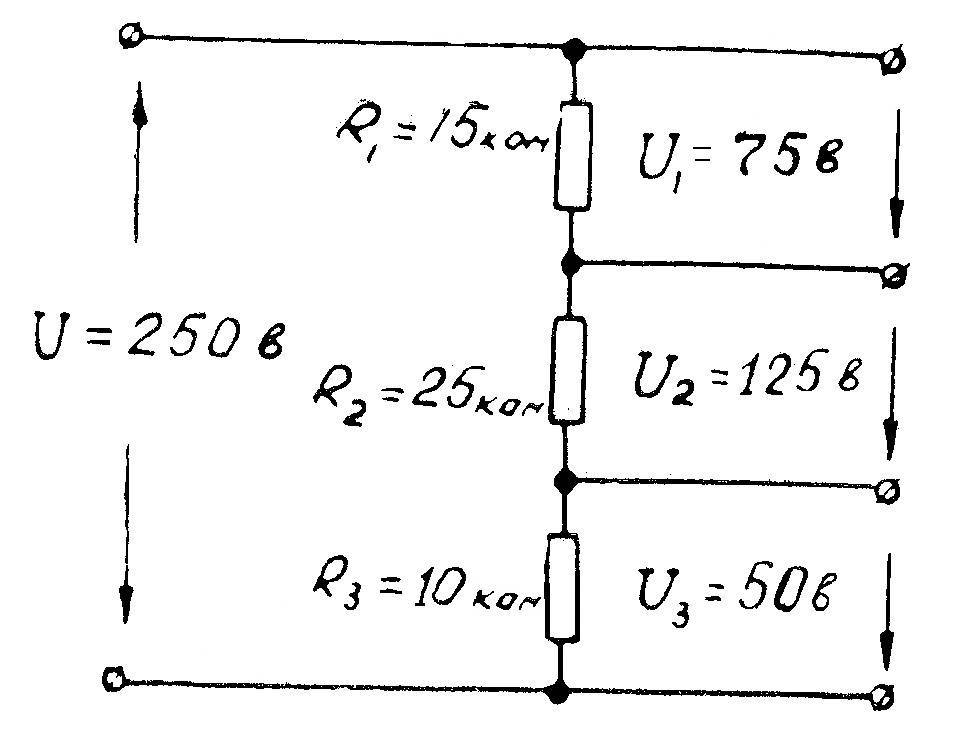 .+50 .+50 |
Температура на улице | 20 | 68 |
Если есть еще распространенные применения, то пишите, добавлю еще.
Надеюсь, теперь вы сможете оценить правильность используемого вами делителя. Конечно, все советы по выбору значения этого резистора, которые я упоминал ранее, верны. Но здорово осознавать то, что ты сделал все оптимально.
Калькулятор делителя напряжения
Потенциометр ALPS RK50
Делитель напряжения обычно состоит из двух резисторов, на которых общее напряжение Uges делится на два парциальных напряжения.
Базовой формой является ненагруженный делитель напряжения, который соответствует последовательному соединению двух резисторов. При подключении к потребителю ненагруженного делителя напряжения распределение напряжения в делителе напряжения меняется. Нагруженный делитель напряжения состоит из последовательно соединенных резисторов R 1 и R 2 . Кроме того, один из двух резисторов
нагружается потребителем, в данном случае резистором R
| ||||||
© mh-Audio.nl — Отказ от ответственности
Потрясающе точный калькулятор делителя напряжения — попробуйте
Делитель напряжения — это простая, но основная схема, которая очень часто используется в электронике. Его принцип работы прост: более высокое входное напряжение подается на вход, а затем преобразуется в более низкое выходное напряжение с помощью пары резисторов. Формула для расчета выходного напряжения основана на законе Ома и приведена ниже.
Формула для расчета выходного напряжения основана на законе Ома и приведена ниже.
В приведенном ниже калькуляторе введите любые три известных значения входного напряжения V в , требуемого выходного напряжения V из и сопротивления R 1 и нажмите « Рассчитать », чтобы найти значение сопротивления R 2 .
Входное напряжение В в (вольт): Требуемое выходное напряжение В из (вольт): Сопротивление R 1 (Ом): Сопротивление R 2 (Ом): Рассеиваемая мощность R 1 (Вт): Рассеиваемая мощность R 2 (Вт):
Силовая цепь делителя напряжения:
Формула делителя напряжения
Формула делителя напряжения: V out = V in * R 2 / (R 1 + Р 2 ), где V в — входное напряжение, а R 1 и R 2 — два последовательных резистора. Эта формула используется для расчета выходного напряжения на R 2 , когда напряжение приложено к последовательной комбинации R 1 и R 2 . Регулируя значения R 1 и R 2 , можно получить различные выходные напряжения.
Эта формула используется для расчета выходного напряжения на R 2 , когда напряжение приложено к последовательной комбинации R 1 и R 2 . Регулируя значения R 1 и R 2 , можно получить различные выходные напряжения.
Формула для расчета R 2 с использованием формулы делителя напряжения: R 2 = (V out * R 1 ) / (V in – V out ).
Пример
Предположим, у нас есть схема с входным напряжением 12 В и двумя последовательно соединенными резисторами R 1 и R 2 . Стоимость R 1 составляет 1 кОм, и мы хотим рассчитать значение R 2 , которое приведет к выходному напряжению 5 В на нем.
Используя формулу делителя напряжения, мы можем рассчитать R 2 следующим образом:
R 2 = (В из * R 1 ) / (В из – В 90 019 из ) = ( 5 * 1000) / (12 – 5) = 714,29 Ом
Следовательно, в этом примере значение R 2 , необходимое для достижения выходного напряжения 5 В, составляет примерно 714,29Ом.
Упрощения
При использовании делителей напряжения следует учитывать несколько общих моментов. Это упрощения, облегчающие оценку схемы делителя напряжения.
- Когда R 2 и R 1 равны, выходное напряжение составляет половину входного напряжения. Это верно независимо от номиналов резисторов. Итак, если R 1 = R 2 , мы получаем следующее уравнение: V out = V in * R 1 / (R 1 + R 1 ) = V в * R 1 / (2R 1 ) = V в / 2
- Если r 2 на порядок больше, чем r 1 , выходное напряжение v OUT будет очень близко к V в , то есть V в ≈ V OUT . И на R 1 будет очень мало напряжения. Итак, если R 2 >> R 1 , мы получаем следующее уравнение: V out ≈ (V в * R 2 ) / R 2 ≈ V в .



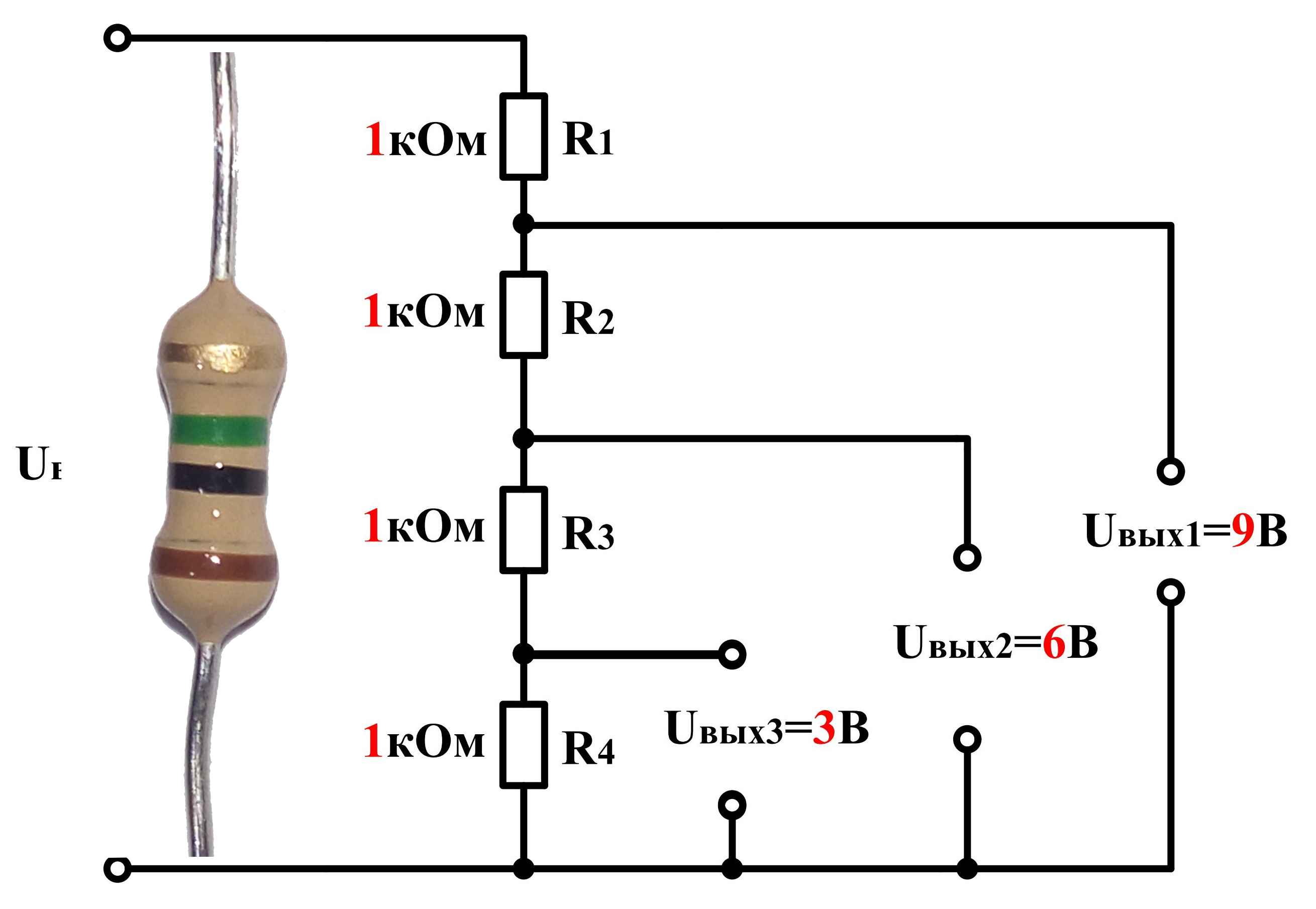
 Тогда можно пренебречь падением напряжения из-за нагрузки на делитель напряжения.
Этого можно добиться только с помощью нагрузочного резистора с большим сопротивлением.
Тогда можно пренебречь падением напряжения из-за нагрузки на делитель напряжения.
Этого можно добиться только с помощью нагрузочного резистора с большим сопротивлением.