Проекция силы на ось | ПроСопромат.ру
Часто геометрическое сложение векторов сил требует сложных и громоздких построений. В таких случаях прибегают к другому методу, где геометрическое построение заменено вычислениями скалярных величин. Достигается это проектированием заданных сил на оси прямоугольной системы координат.
Как известнее из математики, осью называют неограниченную прямую линию, которой приписано определенное направление. Проекция вектора на ось является скалярной величиной, которая определяется отрезком оси, отсекаемым перпендикулярами, опущенными из начала и конца вектора на ось.
Проекция вектора считается положительной (+), если направление от начала проекции к ее концу совпадает с положительным направлением оси.
Рассмотрим ряд случаев проектирования сил на ось.
- Дана сила Р (рис.а), она лежит в одной плоскости с осью х. Вектор силы составляет с положительным направлением оси острый угол α.
Чтобы найти величину проекции, из начала и конца вектора силы опускаем перпендикуляры на ось х, получаем
Проекция вектора в данном случае положительна.
2. Дана сила Q (рис. б), которая лежит в одной плоскости с осью х, но ее вектор составляет с положительным направлением оси тупой угол α.
Проекция силы Q на ось х
Qх = ab = Q cos α,
но
cos a = — cos β.
Так как
Qх = — Q cos β
В этом случае проекция силы отрицательна.
Итак, проекция силы на ось координат равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси.
При определении проекции вектора силы на ось пользуются обычно косинусом острого угла, независимо от того, с каким направлением оси — положительным или отрицательным — он образован.
Силу, расположенную на плоскости хОу, можно спроектировать на две координатные оси Ох и Оу. Рассмотрим рисунок.
На нем изображена сила Р и ее проекции Рх и Ру. Ввиду того что проекции образуют между собой
Этими формулами можно пользоваться для определения величины и направления силы, когда известны ее проекции на координатные оси. Эти же формулы могут применяться для определения величины и направления любого вектора через его проекции.
7) Проекция силы на ось и на плоскость
Проекция
силы на ось –
алгебраическая величина, равная
произведению модуля силы на косинус
угла между силой и положительным
направлением оси.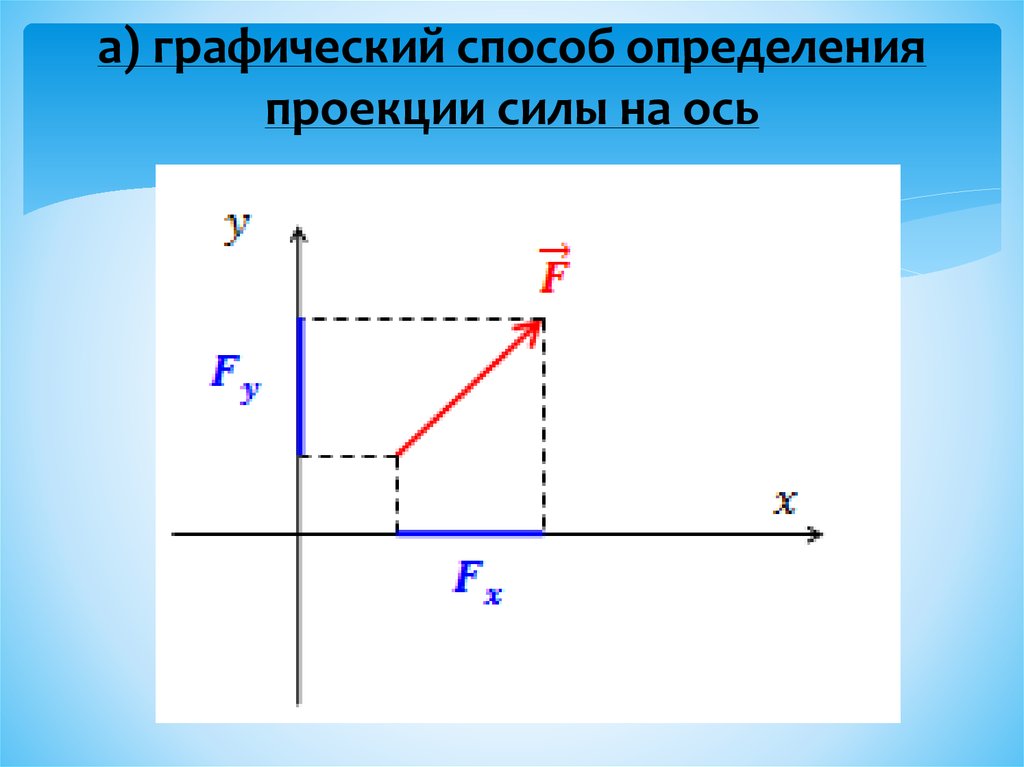
Проекция F
Проекция силы на плоскость Оху – вектор , заключенный между проекциями начала и конца силы на эту плоскость. Т.е. проекция силы на плоскость величина векторная, характеризуется не только числовым значением, но и направлением в плоскости Оху.
Тогда модуль проекции на плоскость Оху будет равен:
Fxy = F cosa, где a — угол между направлением силы и ее проекцией .
Если сила и ось координат не лежат в одной плоскости, то проекция силы на ось проводится методом двойного проецирования.
Например,
чтобы определить проекцию силы на
ось х,
надо спроецировать ее на плоскость Оху,
а затем разложить проекцию силы на
составляющие по осям координат Fxи Fy.
X= Fxy cosj = F cosa cosj; Fy = Fxy sinj = F cosa sinj; Fz = F sina.
8) Проекция силы относительно точки
Моментом
силы относительно
точки O называют
величину, равную векторному произведению
радиус-вектора
Этот вектор приложен в точке O и направлен перпендикулярно плоскости, содержащей векторы и в ту сторону, откуда вращение тела, вызываемое силой вокруг точки O, представляется происходящим против часовой стрелки.
Модуль
момента ,
где –
плечо силы относительно
точки O,
равное расстоянию от этой точки до линии
действия силы .
Из формулы следует, что ,
если h =
0, т.
Обозначим через x, y, z координаты точки приложения силы, – проекции силы на координатные оси. Тогда момент силы можно представить следующим образом
, откуда следует, что проекции момента силы на координатные оси равны
.
9) Теорема Вариньона о моменте равнодействующей
Эта теорема связана с моментом равнодействующей пространственной сходящейся системы сил относительно произвольной точки.
Теорема гласит следующим образом:
Момент равнодействующей пространственной системы сходящихся сил относительно произвольной точки равен векторной сумме моментов всех слагаемых сил относительно этой же точки.
Действительно, если совокупность всех сил, действующих на абсолютно твердое тело сходится в некоторой точке О, то ее равнодействующая находится как геометрическая сумма этих сил, т.е.:
= =
и
приложена в той же точке О.
|
Возьмем произвольную точку А и обозначим через вектор-радиус точки О относительно точки А. Тогда по определению момента равнодействующей находим:
=( х )+( х )+…+( х ) =
= ( )+ ( )+…+ ( )=
Подчеркнем, что теорема Вариньона верна только для сходящейся системы сил и для совокупности сил с параллельными друг другу линиями действия.
Если все силы лежат на некоторой плоскости и составляют плоскую систему сходящихся сил, то вместо геометрической суммы моментов берется алгебраическая сумма моментов этих сил, т.е.
M0( )=
сил — Разница между проекцией и компонентом вектора в произведении?
спросил
Изменено 2 года, 11 месяцев назад
Просмотрено 2к раз
$\begingroup$
Если я хочу переместить блок и приложу силу, параллельную перемещению, блок сдвинется и будет выполнена некоторая работа. Таким образом, в формуле будет $W= F\cdot S$, здесь мы будем вычислять не силу mg блока, а силу, которую мы приложили (параллельную силу).
Таким образом, в формуле будет $W= F\cdot S$, здесь мы будем вычислять не силу mg блока, а силу, которую мы приложили (параллельную силу).
Теперь допустим, что сила не параллельна и находится под некоторым углом к горизонтали
Значит, в этом случае выполненная работа будет проекцией силы $F_1$ на ось $x$, потому что именно так точка продукты определены (как прогнозы). Но нельзя ли сказать, что блок сдвинулся благодаря своей горизонтальной составляющей $F_1\cos(\theta)$ и ответ был бы таким же. И, очевидно, мы не будем считать $F_1\sin(\theta)$, поскольку она не делает работу.
Так почему же мы говорим проекция, а не компонент в скалярном или векторном произведении?
- силы
- векторы
- векторные поля
$\endgroup$
1
$\begingroup$
Как было сказано, проекция и компонент на самом деле относятся к одному и тому же.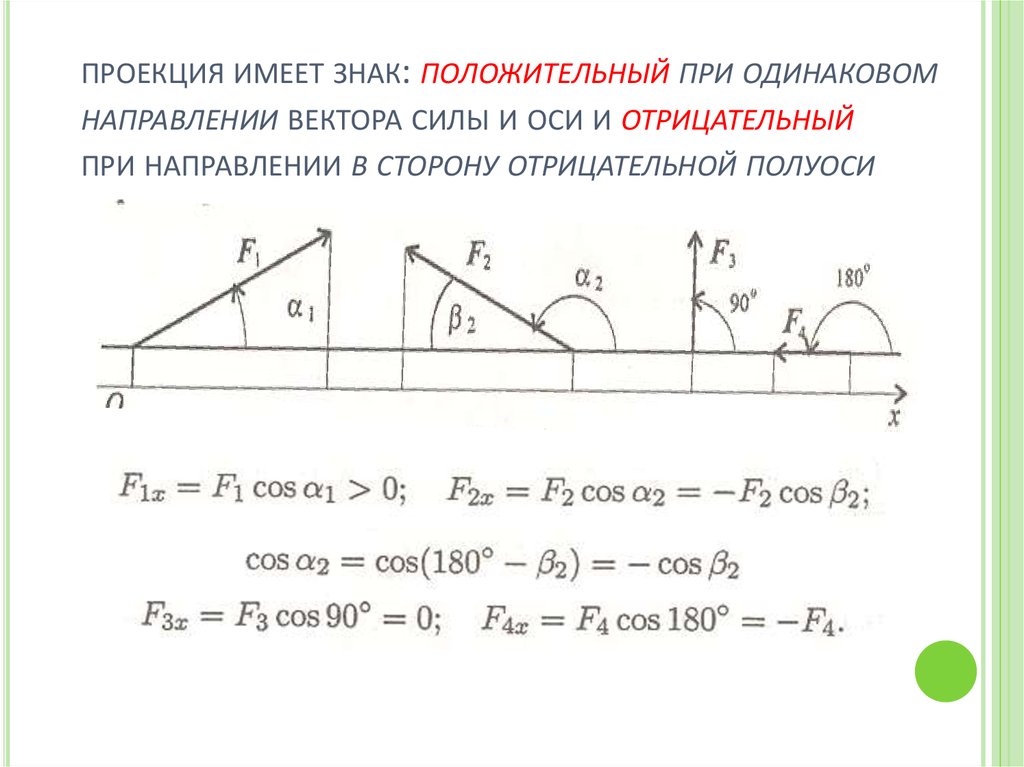 Для решения такой задачи полезно ввести систему координат, как вы сами упомянули, вы проецируете на ось x. Как только вы вводите систему координат, вы можете говорить о $\textit{компонентах}$ некоторого вектора. Например, $\vec{F} = F_1 \cos(\theta)\hat{x} + F_1 \sin(\theta) \hat{y}$ и $\vec{S} = S_1 \hat{x}$, если поле в вашем примере ограничено перемещением по горизонтали. Здесь компоненты векторов — это $\textit{проекции}$ векторов на координатную ось. С помощью этой конструкции скалярный продукт вычисляется как $W = \vec{F} \cdot\vec{S} = F_1\cos(\theta) S_1$.
Для решения такой задачи полезно ввести систему координат, как вы сами упомянули, вы проецируете на ось x. Как только вы вводите систему координат, вы можете говорить о $\textit{компонентах}$ некоторого вектора. Например, $\vec{F} = F_1 \cos(\theta)\hat{x} + F_1 \sin(\theta) \hat{y}$ и $\vec{S} = S_1 \hat{x}$, если поле в вашем примере ограничено перемещением по горизонтали. Здесь компоненты векторов — это $\textit{проекции}$ векторов на координатную ось. С помощью этой конструкции скалярный продукт вычисляется как $W = \vec{F} \cdot\vec{S} = F_1\cos(\theta) S_1$.
Однако нет необходимости вводить систему координат и записывать векторы по их компонентам, а затем применять правила скалярного произведения. Скалярный продукт определяется независимым от координат способом как проекция. Так что ваш вопрос — это просто вопрос терминологии. $\textit{компонента}$ вектора вдоль некоторой оси есть $\textit{проекция}$ вектора вдоль этой оси, и в этом смысле проекция является более фундаментальной вещью.
$\endgroup$
0
$\begingroup$
Выступ и компонент в данном контексте означают одно и то же.
Замечу, однако, что сила является частью физической реальности, существующей в мире (по крайней мере, для целей механики), тогда как проекция является математическим объектом/конструктом. С этой точки зрения работа совершается силой (или ее составляющей), а не проекцией.
$\endgroup$
Зарегистрируйтесь или войдите в систему
Зарегистрируйтесь с помощью Google
Зарегистрироваться через Facebook
Зарегистрируйтесь, используя электронную почту и пароль
Опубликовать как гость
Электронная почта
Требуется, но никогда не отображается
Опубликовать как гость
Электронная почта
Требуется, но не отображается
Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie
. Калькулятор векторной проекции
Калькулятор векторной проекцииСоздано Мирославом Йерковичем, доктором философии
Отредактировано Bogna Szyk и Jack Bowater
Последнее обновление: 02 февраля 2023 г.
Содержание:- Что такое формула векторной проекции?
- Как вывести формулу векторной проекции?
- Как пользоваться калькулятором векторных проекций
- Векторные проекции в физике — игра с силами
- Каковы применения векторных проекций в науке о данных?
- Часто задаваемые вопросы
Этот калькулятор векторной проекции находит ортогональную проекцию одного вектора на другой . Начнем с двух векторов, a и b , которые не лежат на одной прямой. Представьте себе источник света над векторами. Теперь подумайте о проекции вектора a на b как о тени , которую вектор a проецирует в направлении вектора b .
Вот почему этот тип вектора известен как ортогональная проекция вектор (отмечен как proj на изображении):
Представление векторной проекции в виде тени идет в том же направлении, что и вектор b ?Давайте теперь перейдем к деталям и обсудим формулу векторной проекции.
Что такое формула векторной проекции?
Вот формула ортогональной проекции вы можете использовать, чтобы найти проекцию вектора a на вектор b :
proj = (a·b / b·b) × b
В формуле используется скалярное произведение вектора, a ·b , также называемое скалярным произведением. Вы можете посетить калькулятор скалярного произведения, чтобы узнать больше об этой векторной операции.
Но откуда взялась эта формула векторной проекции?
На изображении выше есть скрытый вектор. Это вектор , ортогональный в вектор b, иногда также называемый вектором отклонения . Вот пошаговая процедура получения формулы векторной проекции: Разложить вектор Экспресс проект как Кроме того, поскольку proj параллелен b, мы можем записать его как Теперь у нас есть Вычислите скалярное произведение обеих частей этого уравнения с вектором b: Поскольку вектор или ортогонален вектору b, их скалярное произведение равно нулю, и мы имеем Наконец, мы имеем Когда вы вставите это выражение для C в Поскольку в этой формуле используется скалярное произведение, которое может быть определено для векторов любой целочисленной размерности, эта формула охватывает векторы любой размерности . Также имейте в виду, что эту формулу иногда называют формулой ортогональной проекции . Если бы мы следовали этой терминологии, нам пришлось бы называть наш калькулятор калькулятором ортогональной проекции . Нет большой разницы. В любом случае, это будет работать так же :)! Пусть a и b равны Используйте калькулятор проекции вектора, чтобы найти проекцию вектора Если вы хотите рассчитать проекцию вручную, используйте формулу векторной проекции Вычислить скалярное произведение векторов a и b: Вычислить скалярное произведение вектора b на самого себя: Вставьте эти два скалярных произведения в формулу векторной проекции, чтобы получить Этот результат, выраженный в десятичном виде, равен результату, полученному этим калькулятором. Возможно, вы задавались вопросом что происходит, когда a ортогонален b ; как выглядит проекция proj ? В этом случае тень вектора a, перпендикулярного b, должна отсутствовать, поэтому мы должны получить нулевой вектор. Это отражено в формуле векторной проекции: если a и b ортогональны, их скалярное произведение равно нулю: Изучение этого особого случая показано в следующем примере: Не удивляйтесь, когда выскочит Одно из самых простых и, возможно, самых интересных применений формулы векторной проекции связано с физикой сил и их разложением. Представьте себе тележку , катящуюся по склону холма. Какую силу нужно приложить, чтобы уравновесить силу тележки? Конечно, эта противодействующая сила зависит от веса тележки: чем массивнее тележка, тем сложнее будет остановить . Также играет роль наклон самого холма — чем круче холм, тем больше силы вам понадобится , чтобы остановить тележку. Вот изображение ситуации: Здесь α — угол наклона холма относительно земли, а F — сила тяжести между телегой и Землей. Обратите внимание, что вектор F перпендикулярен земле, а не самому склону холма. Обратите внимание, что вы можете найти уклон, используя математику, например, в калькуляторе уклона. Чтобы найти силу, необходимую для уравновешивания действия силы тяжести на тележку, мы должны вычислить проекцию вектора силы F вдоль направления холма. Допустим, что Вопрос в том, как найти вектор вдоль направления склона холма , на который проецируется вектор силы F? Мы можем использовать любой вектор, который имеет то же направление, что и склон холма, поэтому наиболее удобным будет единичный вектор Используйте калькулятор векторной проекции и выберите работу с векторами в двух измерениях, так как мы имеем дело с двумерной задачей . Итак, вектор а будет равен вектору силы F; и вектор b получен из вектора u, используя калькулятор тригонометрических функций, чтобы найти значения для Работая с этими числами, получаем вектор проекции: Так как мы хотим знать величину уравновешивающей силы , мы можем использовать калькулятор векторной величины, чтобы найти величину proj . Оно равно Если немного поиграть с наклоном холма, т.е. с углом α, то вы увидите, что чем менее узкий холм, тем меньшая сила вам потребуется, а в случае большего α – более крутого холма – вы потребуется большая требуемая реактивная сила. Помимо физики и проблемы нахождения составляющей силы в заданном направлении, векторная проекция широко распространена в одном из самых модных реальных приложений науки, а именно в науке о данных. Векторная проекция используется в важной статистической задаче линейной регрессии , а также в анализе главных компонентов , одном из наиболее часто используемых методов в наука о данных . Здесь возникает задача представить множество, возможно, многомерных точек данных в пространстве меньшей размерности таким образом, чтобы потери информации были минимальными. Чтобы определить проекцию вектора Вы можете найти длину проекции вектора 
a на сумму векторов проекции и отклонения: a = proj + ort проект = а-орт proj = C × b , где C — некоторый неизвестный фактор, который мы хотим определить C × b = a - ort C × b·b = a·b - ort·b С × b·b = a·b C = a·b / b·b . proj = C × b , вы получите формулу: proj = (a·b / b·b) × b ! Его практическое применение для 2-D и Трехмерные векторы , поэтому наш калькулятор предназначен для векторов с двумя или тремя компонентами.
Его практическое применение для 2-D и Трехмерные векторы , поэтому наш калькулятор предназначен для векторов с двумя или тремя компонентами. Как пользоваться калькулятором векторной проекции
а = 2i -3j + 5k и b = 3i + 6j - 4k . С этого момента мы будем записывать эти трехмерные векторы в их компонентной форме a = [2, -3, 5] и b = [3, 6, -4] . a на вектор b . В результате мы получаем: proj = [-1,5738, -3,1475, 2,0984] p = (a·b / b·b) × b и выполните следующую пошаговую процедуру: a·b = 2×3 + (-3)×6 + 5×(-4) = -32 b·b = 3×3 + 6×6 + (-4)×(-4) = 61 proj = (-32/61) × [3, 6, -4] = [-96/61, -192/61, 128/61] .
a·b = 0 . Теперь у нас есть: proj = (0 / b·b) × b = 0 × b = 0 . a = [2, 6, -3] и b = [6, 4, 12] . [0, 0, 0] , так как это правильный результат! Векторная проекция в физике – игра с силами

F = 400 Н (что соответствует телеге массой около м = 40 кг ) и что уклон холма равен α = 45° .
u = [cos 45°, sin 45°] , отмеченный синим вектором на изображении выше. Воспользуйтесь калькулятором единичных векторов, чтобы найти дополнительную информацию об объектах такого типа. Также в качестве вектора силы F возьмем F = [0, -400] . Знак минус здесь означает, что сила F направлена вниз. a = [0, -400] , sin 45° и cos 45° : b = [0,70710678, 0,70710678] .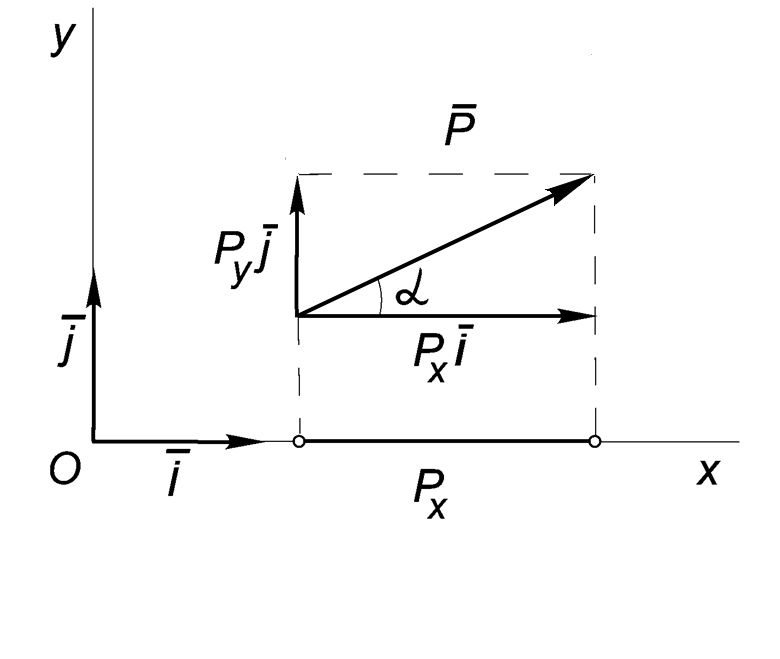
proj = [-200, -200] . 282,84 Н . Каковы применения векторных проекций в науке о данных?

Часто задаваемые вопросы
Как рассчитать проекцию вектора a на b?
a на вектор b : a·b . b·b . Это то же самое, что квадрат нормы b . a·b / b·b . b , на который мы проецируем: proj = (a·b / b·b) × b . Какова длина проекции вектора?
a на вектор b по формуле a·b / |b| , где a·b — скалярное произведение, а |b| — это длина вектора b (того, на который мы проецируем).

