7 — Логика и компьютер
1. Отметьте все фразы, которые являются высказываниями. | |
| Прошлогодний снег. | |
| Сегодня пасмурно. | |
| В N-ской воинской части обед. | |
| В Санкт-Петербурге 4 миллиона жителей. | |
| Почему я водовоз? | |
2. Какой ученый разработал основы алгебры логики? | |
| Аристотель | |
| Дж. Буль | |
| Б. Паскаль | |
| К. Шеннон | |
| И. Ньютон | |
3. Как называется правило преобразования входных логических значений в логическое значение-результат? | |
| логическая функция | |
| логическое выражение | |
| логическое правило | |
| логическая задача | |
| логическое высказывание | |
4. | |
| И | |
| ИЛИ | |
| НЕ | |
5. Какую логическую операцию иллюстрирует этот рисунок? | |
| И | |
| ИЛИ | |
| НЕ | |
6. Какой логической операции соответствует эта таблица истинности? | |
| И | |
| ИЛИ | |
| НЕ | |
7. Какой логической операции соответствует эта таблица истинности? | |
| И | |
| ИЛИ | |
| НЕ | |
8. Какая операция называется «конъюнкцией»? | |
| НЕ | |
| И | |
| ИЛИ | |
9. | |
| НЕ | |
| И | |
| ИЛИ | |
10. Какие из этих логических выражений ложны независимо от логического значения A? | |
| A или A | |
| A и 0 | |
| A или A | |
| (не A) и 0 | |
| (не A) или 1 | |
11. Какие из этих логических выражений истинны независимо от логического значения A? | |
| A или 1 | |
| A и 1 | |
| (не A) или 1 | |
| (не A) или A | |
| 1 или (0 и A) | |
12. Сколько существует различных логических операций с двумя логическими значениями? |
| Ответ: |
13. Какие операции обратимы, то есть, применив ту же самую операцию дважды можно восстановить исходное значение? | |
| НЕ | |
| И | |
| ИЛИ | |
14. | |
| На улице нет ни снега, ни ветра. | |
| На улице или нет снега, или безветрие. | |
| На улице нет снега и ветрено. | |
| На улице идет снег и нет ветра. | |
| На улице идет снег или дует ветер. | |
4
Рассмотрим более подробно некоторые логические связки, позволяющие конструировать из простых высказываний сложные. В математической логике такие связки называются логическими операциями.
2.3.1. Операция отрицания
Самой простой логической операцией,
применяемой только к одному высказыванию, является операция отрицания, которая в русском языке соответствует частице
«не». Отрицание высказывания А обозначается ØА или . Символ читается «не А» или «не верно, что А». Например, если высказывание А – «подсудимый виновен», то — «подсудимый не
виновен».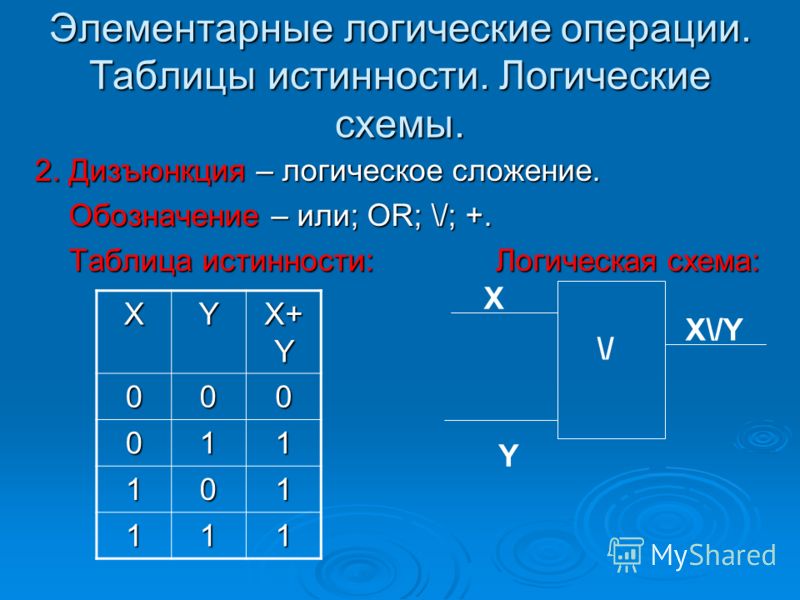
По смыслу,
отрицание высказывания – высказывание, противоположное данному. То есть, если
высказывание А – истинное, то
высказывание — ложное, и наоборот,
если А – ложное, то
|
А |
|
|
1 0 |
0 1 |
Подобная таблица называется таблицей
истинности[1].
Именно эту таблицу берут за определение операции отрицания. Высказывание 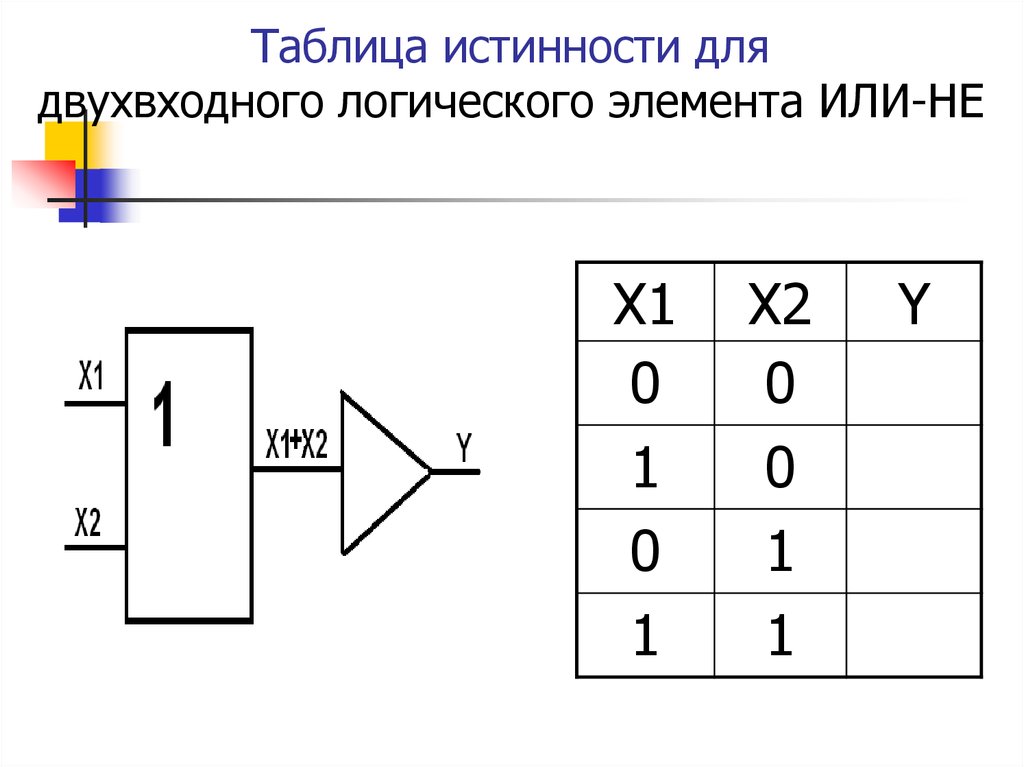
2.3.2. Дизъюнкция высказываний
Операция дизъюнкция применяется к двум высказываниям А и В и соответствует соединению их с помощью союза «или». Дизъюнкция обозначается с помощью знака Ú, который ставится между высказываниями: АÚВ, что читается «А или В» или «или А, или В». Например, «Грабеж может быть совершен с применением физического
Рассмотрим
значение составленного сложного высказывания АÚВ. Если одно из высказываний истинно, а
другое ложно, то дизъюнкция
будет истинной. Если оба простых высказывания А и В ложны, то и
дизъюнкция будет ложной. А вот если оба высказывания А и В истинны, то
существует два случая. Это связано с тем, что в русском языке союз «или» имеет два значения. Одно из них неисключающее
«или», а другое – исключающее.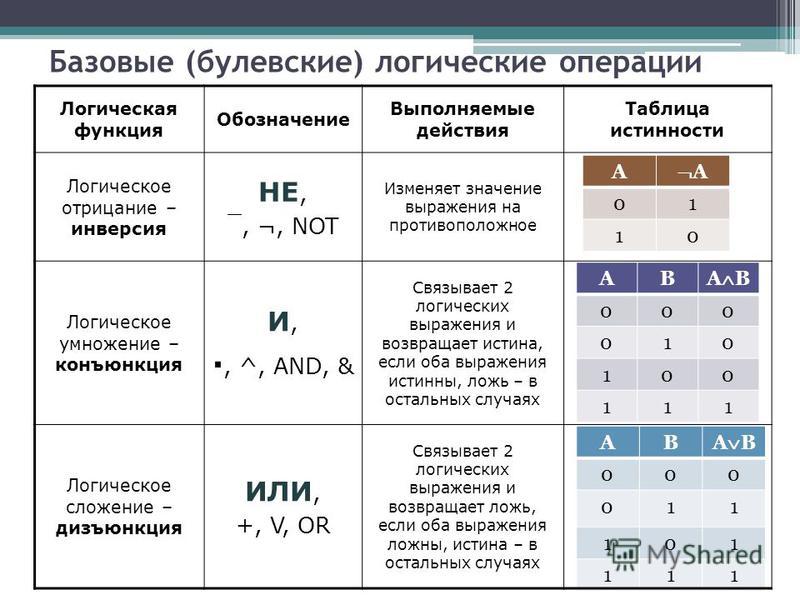
В логике высказываний дизъюнкция соответствует неисключающему «или». Можно дать следующее определение этой логической операции. Дизъюнкция АÚВ – сложное высказывание, которое ложно тогда и только тогда, когда оба высказывания А
|
А |
В |
AÚB |
|
1 |
1 |
1 |
|
1 |
0 |
1 |
|
0 |
1 |
1 |
|
0 |
0 |
0 |
Значения операции АÚВ (кроме первой строчки), как видно из таблицы, получаются
простым алгебраическим сложением значений А
и В.
2.3.3. Конъюнкция высказываний
Операция конъюнкция применяется также к двум высказываниям А и В и соответствует соединению их с помощью союза «и». Она обозначается с помощью знака Ù или &, который ставится между высказываниями: АÙВ, что читается «А и В» или «и А, и В». Например, «Юрист должен знать и теорию государства и права, и
Рассмотрим
значение конъюнкции, исходя из смысла союза «и». Если оба высказывания А и В
будут истинными, то и конъюнкция АÙВ будет истинной. Если же хотя бы одно из
них (или оба) будут ложными, то и конъюнкция также будет ложной. Например,
высказывание «3 – нечетное число и 3
делится на 2» будет ложным. Исходя из этого, можно дать следующее определение
операции конъюнкция.
Если же хотя бы одно из
них (или оба) будут ложными, то и конъюнкция также будет ложной. Например,
высказывание «3 – нечетное число и 3
делится на 2» будет ложным. Исходя из этого, можно дать следующее определение
операции конъюнкция.
Конъюнкция АÙВ – сложное высказывание, которое истинно тогда и только тогда, когда оба высказывания А и В одновременно истинны. Таблица истинности операции конъюнкция такова:
|
А |
В |
АÙВ |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
0 |
Проанализировав приведенную таблицу,
можно заметить, что значения операции АÙВ получаются простым алгебраическим
умножением значений А и В.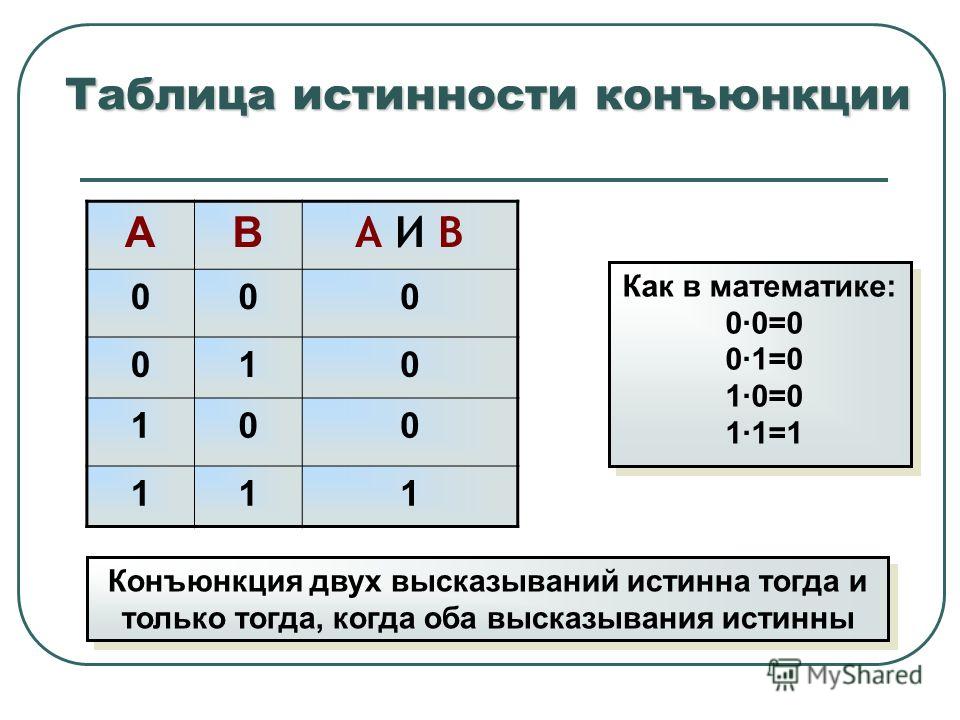 Поэтому конъюнкцию также называют
логическим умножением и обозначают, также как и в алгебре, знаком «×», который, также как и в алгебре, может опускаться.
Поэтому конъюнкцию также называют
логическим умножением и обозначают, также как и в алгебре, знаком «×», который, также как и в алгебре, может опускаться.
Рассмотренные операции отрицания, дизъюнкции и конъюнкции называют булевыми операциями. Они играют важную роль в применениях математической логики в электронике, автоматике, теории вычислительных устройств.
2.3.4. Импликация высказываний
Одной из важнейших логических
операций является операция импликация. Она соответствует объединению двух
высказываний с помощью союза «если …, то
…». Импликация обозначается с
помощью знака ®, ставящегося
между высказываниями: А®В,
что читается «А имплицирует В» или «если А, то В». В научной литературе по
логике высказываний также приводятся другие варианты прочтения этой операции: «А влечет
В», «из А следует В», «В только
если А».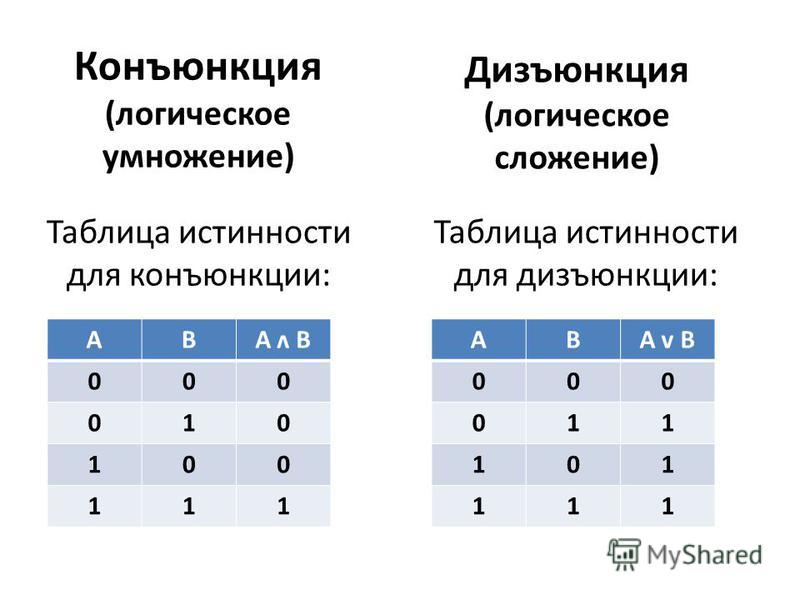
Примеры. Гражданский кодекс РФ: «Если банк отказывает в принятии документов …, то он обязан незамедлительно проинформировать об этом получателя средств». «Если новый уголовный закон смягчает наказание за деяние, которое отбывается лицом, то это наказание подлежит сокращению в пределах, предусмотренных новым уголовным законом. Статья 10 УК РФ». «Если осужденный после отбытия наказания вел себя безупречно, то по его ходатайству суд может снять с него судимость до истечения срока погашения судимости. Статья 86 УК РФ». «Если 2*2=4, то 3+2=6».
Операция импликации определяется следующим образом.
Импликация высказываний А и В (А®В) – сложное высказывание, которое истинно всегда, кроме случая когда А – истинно, а В – ложно. Таким образом, таблица истинности импликации такова:
|
А |
В |
A ® B |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
1 |
|
0 |
0 |
1 |
Проанализируем соответствие
определения импликации с общепринятым значением сложноподчиненного предложения
с использованием союза «если . .., то …». Рассмотрим
следующее сложное высказывание: «Если
гражданин Иванов совершил кражу, то
он может быть наказан лишением свободы на срок до двух лет». Если оба
простые высказывания «гражданин Иванов совершил кражу» и «он
может быть наказан лишением свободы на срок до двух лет» истинны, то
истинность сложного высказывания не вызывает сомнения. При истинности
совершения кражи невозможность применения наказания в виде лишения свободы на
срок до двух лет должно быть оценено нами как ложное высказывание, так как такое
наказание предусмотрено статьей 158 Уголовного кодекса РФ. При ложном первом
высказывании «гражданин Иванов совершил кражу» применение данного
вида наказания к Иванову все же может быть осуществимо, если он, например,
обвиняется по статье 127 УК РФ («Незаконное лишение свободы») или по
статье 139 часть 2 УК РФ («Нарушение неприкосновенности жилища»).
Поэтому оценивание сложного высказывания как истинного соответствует истинности
импликации при данных значениях простых высказываниях в этих конкретных условиях.
.., то …». Рассмотрим
следующее сложное высказывание: «Если
гражданин Иванов совершил кражу, то
он может быть наказан лишением свободы на срок до двух лет». Если оба
простые высказывания «гражданин Иванов совершил кражу» и «он
может быть наказан лишением свободы на срок до двух лет» истинны, то
истинность сложного высказывания не вызывает сомнения. При истинности
совершения кражи невозможность применения наказания в виде лишения свободы на
срок до двух лет должно быть оценено нами как ложное высказывание, так как такое
наказание предусмотрено статьей 158 Уголовного кодекса РФ. При ложном первом
высказывании «гражданин Иванов совершил кражу» применение данного
вида наказания к Иванову все же может быть осуществимо, если он, например,
обвиняется по статье 127 УК РФ («Незаконное лишение свободы») или по
статье 139 часть 2 УК РФ («Нарушение неприкосновенности жилища»).
Поэтому оценивание сложного высказывания как истинного соответствует истинности
импликации при данных значениях простых высказываниях в этих конкретных условиях. И, наконец, при ложности простых высказываний, т.е. истинности противоположных:
«гражданин Иванов не совершил кражу» и «он не может быть наказан
лишением свободы на срок до двух лет», рассмотренная причинно-следственная
связь является истинной.
И, наконец, при ложности простых высказываний, т.е. истинности противоположных:
«гражданин Иванов не совершил кражу» и «он не может быть наказан
лишением свободы на срок до двух лет», рассмотренная причинно-следственная
связь является истинной.
Рассмотрим следующие высказывания:
· «Волга впадает в Каспийское море» — истинное высказывание;
· «Дон впадает в Каспийское море» — ложное высказывание;
· «Дважды два – четыре» — истинное высказывание;
· «Дважды два – пять » — ложное высказывание.
Составим из этих простых высказываний сложные с помощью союза «если …, то …» и, интерпретируя использованный союз как импликацию, оценим значения полученных высказываний.
· «Если Волга впадает в Каспийское море, то дважды два – четыре» — истинное высказывание;
· «Если Волга впадает в Каспийское море, то дважды два – пять» — ложное высказывание;
· «Если Дон впадает в Каспийское море, то дважды два – четыре» — истинное высказывание;
·
«Если Дон впадает в Каспийское море, то дважды
два – пять» — истинное высказывание.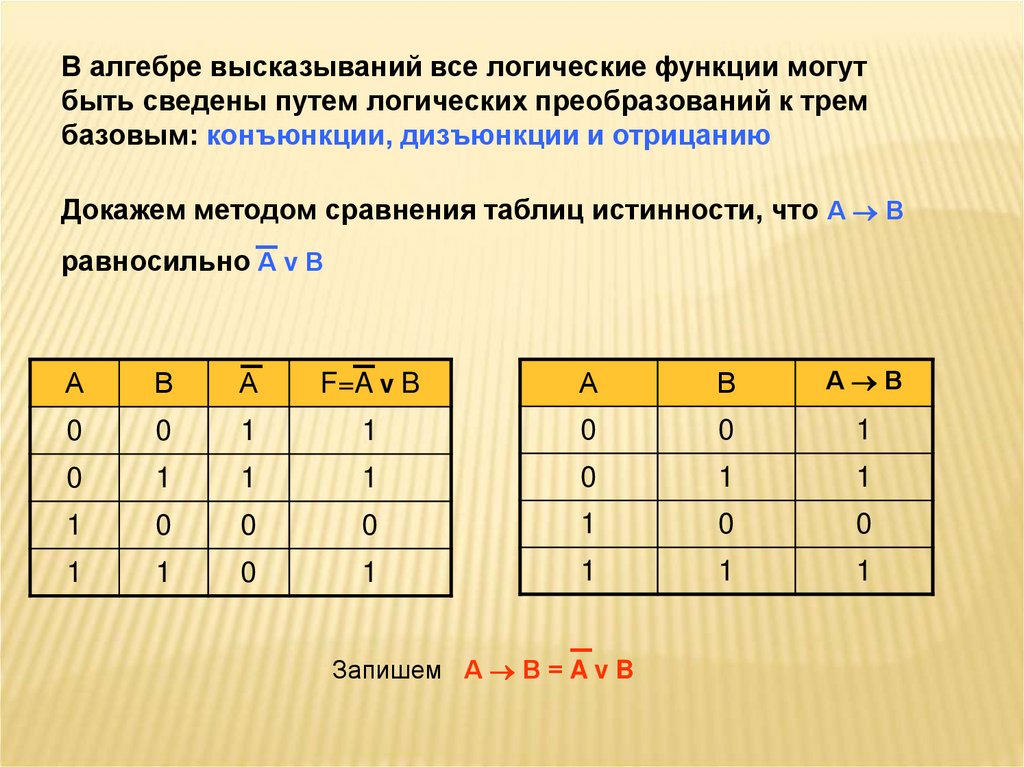
Эти утверждения не соответствуют привычному для естественного языка употреблению союза «если …, то …». Поэтому импликация лишь до некоторой степени соответствует этому союзу. И математически корректнее операцию А®В читать не «если А, то В», а «А имплицирует В». Операция импликации А®В хорошо описывается союзом «если …, то …» в случаях:
· описания причинно-следственной связи между А и В. Например, «Если долго мучиться, то что-нибудь получится»;
· выражения логического следования В из А. Например, «Если все люди смертны и Сократ – человек, то Сократ смертен».
В этих
высказываниях существует связь между содержанием высказываний А и В,
объединенных союзом. В логике высказываний рассматриваются только значения
истинности высказываний, а не их содержание. Тем самым логические операции не
выражают связь между содержанием высказываний. Логические операции, образующие
из простых высказываний сложные, определяют только соотношения между значениями
истинности этих высказываний.
Тем самым логические операции не
выражают связь между содержанием высказываний. Логические операции, образующие
из простых высказываний сложные, определяют только соотношения между значениями
истинности этих высказываний.
2.3.5. Эквивалентность высказываний
Последней введем операцию эквивалентности. Эта операция обозначается символом «, либо ~. Сложное высказывание А«В читается: «А эквивалентно В«, либо «А равносильно В«, либо «А тогда и только тогда, когда В«, либо «В, если и только если А«. Эквивалентность примерно соответствует употреблению выражения «тогда и только тогда, когда», хотя, как и в случае с импликацией, такое соответствие далеко не полное.
Приведем примеры использования операции
эквивалентности. «Два треугольника равны
тогда и только тогда, когда
три стороны одного треугольника равны соответствующим сторонам другого
треугольника».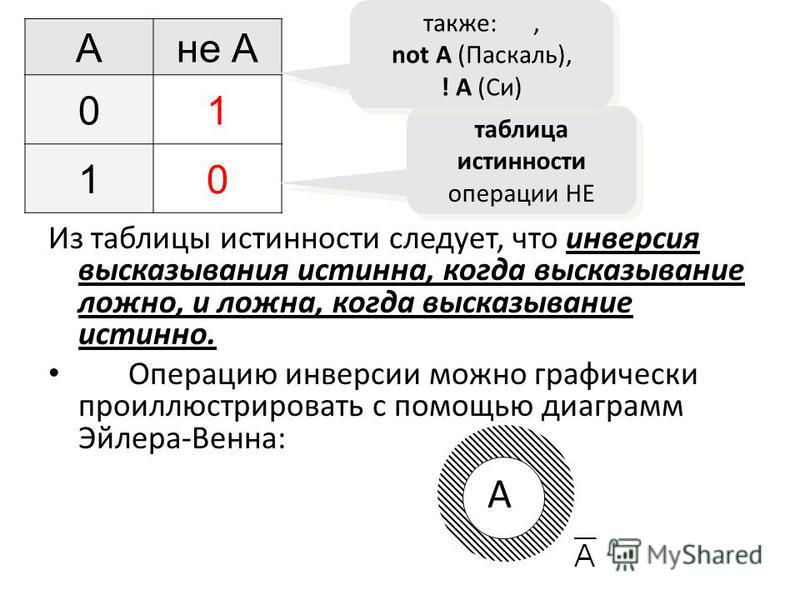 «Деяние кража равносильно тайному
хищению чужого имущества». «Распространение заведомо ложных сведений является
клеветой, если и только если эти
сведения порочат честь и достоинство другого лица или подрывают его репутацию».
«Деяние кража равносильно тайному
хищению чужого имущества». «Распространение заведомо ложных сведений является
клеветой, если и только если эти
сведения порочат честь и достоинство другого лица или подрывают его репутацию».
Эквивалентность высказываний А и В (А«В) – сложное высказывание, которое истинно, когда А и В одновременно либо истинны, либо ложны и ложно во всех других случаях. Эквивалентность определяется следующей таблицей истинности:
|
А |
В |
А«В |
|
1 |
1 |
1 |
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
0 |
0 |
1 |
Эквивалентность соответствует двум
операциям импликации, соединенных конъюнкцией. А«В равносильно (A ® B)Ù(A ® B) , т.е. имеет
такую же таблицу истинности (рассмотрим это позднее). Поэтому эквивалентность
также называют двойной импликацией.
А«В равносильно (A ® B)Ù(A ® B) , т.е. имеет
такую же таблицу истинности (рассмотрим это позднее). Поэтому эквивалентность
также называют двойной импликацией.
Таблицы истинности в логике :: CIS 301 Учебник
Теперь, когда мы увидели четыре основных логических элемента и таблицы истинности, мы можем объединить их, чтобы построить большие таблицы истинности для более длинных логических формул.
Приоритет оператора
Логические операторы имеют определенный приоритет (порядок операций), как и арифметические операторы. В арифметике наивысший приоритет имеют круглые скобки, за ними следуют показатели степени, затем умножение и деление и, наконец, сложение и вычитание.
Вот приоритет логических операторов, от самого важного (сделать первым) до наименее важного (сделать последним):
- Скобки
- Не оператор,
¬ - И оператор,
∧ - Или оператор,
∨ - Подразумевается оператор,
→
Например, в операторе (p ∨ q) ∧ ¬p мы будем оценивать операторы в следующем порядке:
- Скобки (которые разрешают
(p ∨ q)выражение) - Нет,
¬ - И,
∧
Иногда у нас есть несколько одинаковых операторов в одном выражении.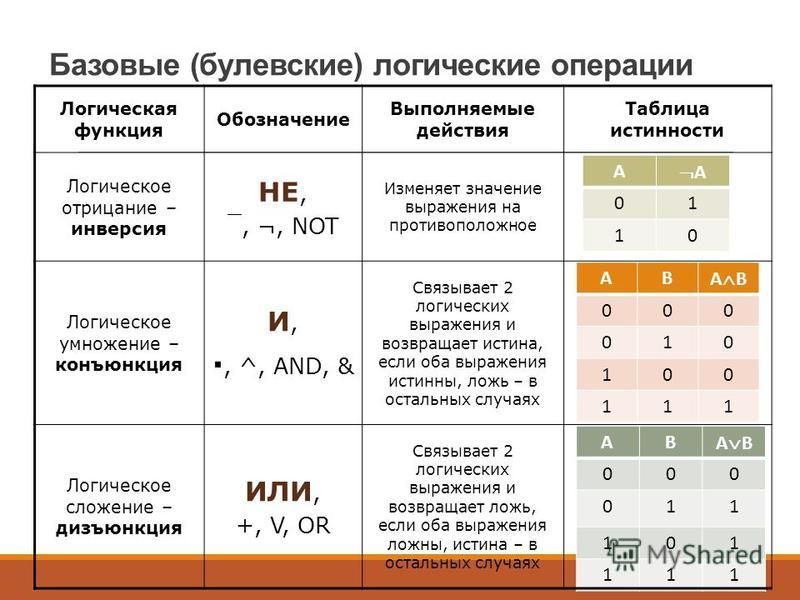 Например:
Например: p ∨ q ∨ r . Разные операторы имеют разные правила для разрешения множественных вхождений:
- Несколько круглых скобок — сначала разрешаются самые внутренние круглые скобки, работая изнутри наружу.
- Множественные операторы not (
¬) – самые правые¬разрешается первым, работая справа налево. Например,¬¬pэквивалентно¬(¬p). - Множественные операторы и (
∧) – самый левый∧разрешается первым, работая слева направо. Например,p ∧ q ∧ rэквивалентно(p ∧ q) ∧ r. - Множественные или (
∨) операторы – самый левый∨разрешается первым, работая слева направо. Например,p ∨ q ∨ rэквивалентно(p ∨ q) ∨ r. - Множественные подразумевают (
→) операторы – самый правый→разрешается первым, работая справа налево. Например,
Например, p → q → rэквивалентноp → (q → r).
Оператор высшего уровня
В логическом операторе оператор верхнего уровня является оператором, который применяется последним (после соблюдения приведенных выше правил приоритета).
Например, в заявлении:
p ∨ q → ¬p ∧ r
Сначала мы оцениваем ¬ , затем ∧ , затем ∨ и, наконец, ∨ . Таким образом, → является оператором верхнего уровня.
Классификация таблиц истинности
При изучении логики будет удобно характеризовать логические формулы описанием их таблиц истинности. Мы будем классифицировать каждую логическую формулу одним из трех способов:
- Тавтология — когда все назначения истинности для логической формулы верны
- Противоречие — когда все назначения истинности для логической формулы ложны
- Контингент — когда некоторые назначения истинности для логической формулы истинны, а некоторые ложны.

Например, p ∨ ¬ p является тавтологией . Является ли p истинным или ложным, p ∨ ¬ p всегда истинно.
С другой стороны, p ∧ ¬ p — это , противоречащее . Является ли p истинным или ложным, p ∧ ¬ p всегда ложно.
Наконец, что-то вроде p ∨ q является контингентом . Когда p и q оба ложны, тогда p ∨ q ложно. Однако p ∨ q верно во всех остальных случаях.
Если все присваивания истинности для логической формулы истинны, говорят, что формула является тавтологией.
Синтаксис логики
С этого момента курс предполагает, что вы будете использовать таблицы истинности в формате Logika. Таблица истинности логики для формулы ¬(p ∧ q) :
* ------------------ р д | ¬(р ∧ д) ------------------ Т Т | Ф Т Т Т Т Ф | Т Т Ф Ф Ф Т | Т Ф Ф Т Ф Ф | Т Ф Ф Ф ------------------ Контингент - Т: [Т Ф] [Ф Т] [Ф Ф] - Ф: [Т Т]
Таблицы истинности Логики имеют стандартный формат (синтаксис) и смысловое значение.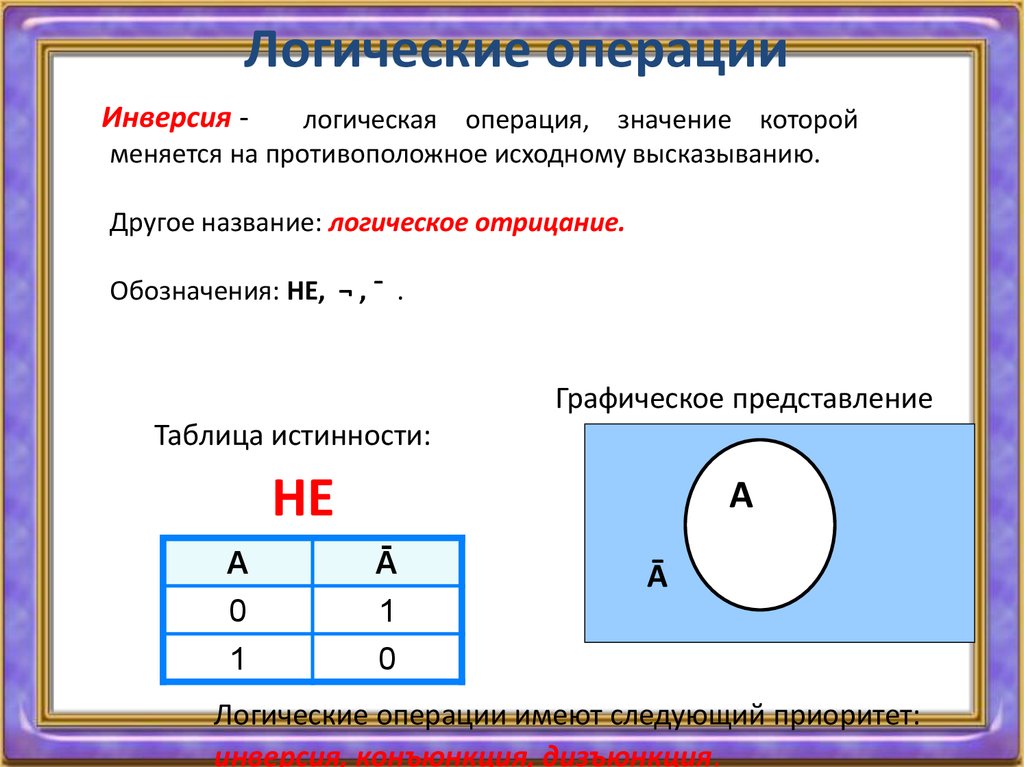 Все элементы таблицы истинности должны быть включены, чтобы считаться правильным.
Все элементы таблицы истинности должны быть включены, чтобы считаться правильным.
В первой строке над оператором верхнего уровня в формуле должна стоять одна звездочка (*).
Далее следует строка из — (знак минус) символов, длина которой должна быть не меньше длины третьей строки, чтобы избежать ошибок.
Третья строка содержит
переменных | формула. Поскольку в Logika некоторые заглавные буквы используются в качестве зарезервированных слов, вы должны использовать строчные буквы в качестве имен переменных. Кроме того, переменные должны быть перечислены в алфавитном порядке.Четвертая строка представляет собой еще одну строку из -, которая имеет ту же длину, что и вторая строка.
Далее идут задания на правду. Под переменными перечислите все возможные комбинации T и F. Начните со всех T и продвигайтесь линейно ко всем F. (T и F должны быть написаны с большой буквы).
 После заданий Правды идет еще один ряд -. Используя каждое присваивание истинности, заполните присваивания истинности (T или F) под каждым оператором в формуле в порядке старшинства (оператор верхнего уровня применяется последним). При желании вы можете заполнить значения для каждой переменной под форумой (как в примере выше). Однако требуется только, чтобы вы выполнили задания на истинность под каждым оператором. Будьте осторожны, выстраивая назначения истинности НЕПОСРЕДСТВЕННО под каждым оператором, так как Logika отклонит таблицы истинности, которые не выровнены тщательно.
После заданий Правды идет еще один ряд -. Используя каждое присваивание истинности, заполните присваивания истинности (T или F) под каждым оператором в формуле в порядке старшинства (оператор верхнего уровня применяется последним). При желании вы можете заполнить значения для каждой переменной под форумой (как в примере выше). Однако требуется только, чтобы вы выполнили задания на истинность под каждым оператором. Будьте осторожны, выстраивая назначения истинности НЕПОСРЕДСТВЕННО под каждым оператором, так как Logika отклонит таблицы истинности, которые не выровнены тщательно.Под заданиями истинности поставьте еще одну строку из — (знак минус) символов, длина которой должна быть такой же, как и во второй строке.
Наконец, классифицируйте формулу как либо
Тавтология(если все, что находится под оператором верхнего уровня, равно T),Противоречие,(если все, что находится под оператором верхнего уровня, является F), либоУсловное(если есть смесь T и F под оператором верхнего уровня). Если формула является условной, вы также должны перечислить, какие присваивания истинности сделали формулу истинной (т. е. какие присваивания истинности сделали оператор верхнего уровня T) и какие присваивания истинности сделали формулу ложной. Следуйте изображению выше, чтобы узнать синтаксис того, как перечислить назначения истинности для условных примеров.
Если формула является условной, вы также должны перечислить, какие присваивания истинности сделали формулу истинной (т. е. какие присваивания истинности сделали оператор верхнего уровня T) и какие присваивания истинности сделали формулу ложной. Следуйте изображению выше, чтобы узнать синтаксис того, как перечислить назначения истинности для условных примеров.
Альтернативные логические операторы
Для ввода каждого традиционного логического оператора в Логике необходимо вставить специальный символ Unicode. Вы можете сделать это, набрав: Shift-Command-Ctrl-точка с запятой , а затем букву, соответствующую определенному символу. Вот как вставить каждый оператор:
- НЕ,
¬.Shift-Command-Ctrl-точка с запятой-N - ИЛИ,
∨.Shift-Command-Ctrl-точка с запятой-V - И,
∧,Shift-Command-Ctrl-точка с запятой-∧ - ПОДРАЗУМЕВАЕТ,
→,Shift Command Ctrl -(последний символ — тире, -)
Это может быть утомительно. Пока вы можете создать
сочетания клавиш в IntelliJ для определенных нажатий клавиш, вместо этого проще использовать одну из доступных замен ASCII. Вот альтернативы для каждого оператора:
Пока вы можете создать
сочетания клавиш в IntelliJ для определенных нажатий клавиш, вместо этого проще использовать одну из доступных замен ASCII. Вот альтернативы для каждого оператора:
- НЕ:
!,~,не - ИЛИ:
V(заглавная V),|,или - И:
∧,и,и - ПОДРАЗУМЕВАЕТ:
→,подразумевает
В оставшейся части этой книги я буду часто использовать эти символы замены ASCII, потому что их легче набирать.
Пример
Предположим, мы хотим написать таблицу истинности Logika для:
(p ∧ q) → ¬r
Во-первых, мы убеждаемся, что у нас есть новый файл в Sireum с .логика расширение. Затем мы строим эту оболочку таблицы истинности:
* ---------------------- р кв р | (p ∧ q) → ¬r ---------------------- Т Т Т | Т Т Ф | Т Ф Т | Т Ф Ф | Ф Т Т | Ф Т Ф | Ф Ф Т | Ф Ф Ф | ----------------------
В приведенной выше таблице мы заметили, что оператор → был оператором верхнего уровня в соответствии с нашими правилами приоритета операторов.
Затем мы заполняем вывод для соответствующего присвоения истинности для каждого оператора, от самого высокого приоритета до самого низкого приоритета. Сначала мы оцениваем круглые скобки, которые имеют наивысший приоритет. Например, мы ставим T под ∧ в первой строке, так как p и q оба являются T в этой строке, а T ∧ T равно T :
* ---------------------- р кв р | (p ∧ q) → ¬r ---------------------- Т Т Т | Т Т Т Ф | Т Т Ф Т | Ф Т Ф Ф | Ф Ф Т Т | Ф Ф Т Ф | Ф Ф Ф Т | Ф Ф Ф Ф | Ф ----------------------
В этом примере мы заполняем данные только под каждым оператором (вместо того, чтобы также расшифровывать каждое значение переменной), но любой подход приемлем.
Затем мы заполняем под оператором ¬, который имеет следующий по старшинству:
* ---------------------- р кв р | (p ∧ q) → ¬r ---------------------- Т Т Т | Т Ф Т Т Ф | Т Т Т Ф Т | Ф Ф Т Ф Ф | Ф Т Ф Т Т | Ф Ф Ф Т Ф | Ф Т Ф Ф Т | Ф Ф Ф Ф Ф | Ф Т ----------------------
Затем мы заполняем под нашим оператором верхнего уровня → . Обратите внимание, что мы должны выстроить
Обратите внимание, что мы должны выстроить T/F значений под - в символе → . Например, мы помещаем F под → в первой строке, так как (p ∧ q) там T и ¬r есть F , и мы знаем, что T→F — это F , потому что он описывает нарушенное обещание.
* ---------------------- р кв р | (p ∧ q) → ¬r ---------------------- Т Т Т | Т Ф Ф Т Т Ф | Т Т Т Т Ф Т | Ф Т Ф Т Ф Ф | Ф Т Т Ф Т Т | Ф Т Ф Ф Т Ф | Ф Т Т Ф Ф Т | Ф Т Ф Ф Ф Ф | Ф Т Т ----------------------
Наконец, мы просматриваем список выходов под оператором верхнего уровня. Мы видим, что некоторые присваивания истинности сделали формулу истинной, а другие (одно) сделали формулу ложной. Таким образом, формула является условной. Мы помечаем ее как таковую и перечисляем, какие присваивания истинности сделали формулу истинной, а какие — ложной:
.* ---------------------- р кв р | (p ∧ q) → ¬r ---------------------- Т Т Т | Т Ф Ф Т Т Ф | Т Т Т Т Ф Т | Ф Т Ф Т Ф Ф | Ф Т Т Ф Т Т | Ф Т Ф Ф Т Ф | Ф Т Т Ф Ф Т | Ф Т Ф Ф Ф Ф | Ф Т Т ---------------------- Контингент - T: [T T F] [T F T] [T F F] [F T T] [F T F] [F F T] [F F F] - Ф: [Т Т Т]
Если вы все набрали правильно, вы должны увидеть всплывающее окно в Sireum logika с надписью «Logika Verified» с фиолетовой галочкой:
Если вместо этого вы видите красные метки ошибок, наведите на них курсор и прочитайте пояснения — это означает, что в вашей таблице истинности есть ошибки.
Если вы не видите ошибок и фиолетовой галочки, вам нужно будет запустить Logika вручную. Щелкните правой кнопкой мыши в текстовой области, содержащей вашу таблицу истинности, и выберите «Проверка логики».
2.1: Операторы и логические операторы
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 7039
- Тед Сандстром
- Государственный университет Гранд-Вэлли через ScholarWorks @Grand Valley State University
ПРЕДВАРИТЕЛЬНАЯ ЗАДАНИЕ \(\PageIndex{1}\): составные операторы
Математики часто разрабатывают способы создания новых математических объектов из существующих математических объектов. Можно сформировать новые утверждения из существующих утверждений, соединив утверждения такими словами, как «и» и «или», или отрицая утверждение. Логический оператор (или связка ) над математическими утверждениями — это слово или комбинация слов, которая объединяет одно или несколько математических утверждений для создания нового математического утверждения. А 9Составной оператор 0406 — это оператор, содержащий один или несколько операторов. Поскольку некоторые операторы так часто используются в логике и математике, мы даем им имена и используем специальные символы для их представления.
Можно сформировать новые утверждения из существующих утверждений, соединив утверждения такими словами, как «и» и «или», или отрицая утверждение. Логический оператор (или связка ) над математическими утверждениями — это слово или комбинация слов, которая объединяет одно или несколько математических утверждений для создания нового математического утверждения. А 9Составной оператор 0406 — это оператор, содержащий один или несколько операторов. Поскольку некоторые операторы так часто используются в логике и математике, мы даем им имена и используем специальные символы для их представления.
- Конъюнкцией утверждений \(P\) и \(Q\) является высказывание «\(P\) и \(Q\)» и обозначается через \(P \клин Q\). Утверждение \(P \клин Q\) истинно только тогда, когда оба \(P\) и \(Q\) верны.
- Дизъюнкция операторов \(P\) и \(Q\) является оператором «\(P\) или \(Q\)» и обозначается через \(P \vee Q\).
 Утверждение \(P \vee Q\) истинно только тогда, когда хотя бы одно из \(P\) или \(Q\) истинно.
Утверждение \(P \vee Q\) истинно только тогда, когда хотя бы одно из \(P\) или \(Q\) истинно. - Отрицание ( утверждения ) утверждения \(P\) является утверждением « не \(P\)» и обозначается \(\urcorner P\). Отрицание \(P\) истинно только тогда, когда \(P\) ложно, а \(\urcorner P\) ложно только тогда, когда \(P\) истинно.
- Импликация или условное является утверждением « Если \(P\) , то \(Q\)» и обозначается \(P \to Q\). Утверждение \(P \to Q\) часто читается как «\(P\) подразумевает \(Q\), и мы видели в разделе 1.1, что \(P \to Q\) ложно только тогда, когда \ (P\) истинно, а \(Q\) ложно.
Некоторые комментарии о дизъюнкции.
Важно понимать использование оператора «или». В математике мы используем « включительно или », если не указано иное. Это означает, что \(P \vee Q\) истинно, когда оба \(P\) и \(Q\) истинны, а также когда только одно из них истинно. То есть \(P \vee Q\) истинно, когда хотя бы одно из \(P\) или \(Q\) истинно, или \(P \vee Q\) ложно только тогда, когда оба \(P\ ) и \(Q\) ложны.
То есть \(P \vee Q\) истинно, когда хотя бы одно из \(P\) или \(Q\) истинно, или \(P \vee Q\) ложно только тогда, когда оба \(P\ ) и \(Q\) ложны.
Другое использование слова «или» — « эксклюзивное или ». Для исключающего или результирующее утверждение ложно, когда оба утверждения истинны. То есть «\(P\) исключающее или \(Q\)» истинно только тогда, когда истинно одно из \(P\) или \(Q\). В повседневной жизни мы часто используем исключающее или. Когда кто-то говорит: «На перекрестке поверните налево или идите прямо», этот человек использует исключающее или.
Некоторые комментарии к отрицанию . Хотя утверждение \(\urcorner P\) можно прочитать как «Это не так, что \(P\)», часто есть лучшие способы сказать или написать это на английском языке. Например, мы обычно говорим (или пишем):
- Отрицание утверждения «391 — простое число» равносильно «391 — не простое число».
- Отрицание утверждения «\(12 < 9\)» равно «\(12 \ge 9\)».

- Для заявлений
\(P\): 15 нечетно \(Q\): 15 просто
запишите каждое из следующих утверждений в виде предложений на английском языке и определите, истинны они или ложны.
(а) \(P \клин Q\). (б) \(P \vee Q\). (c) \(P \клин \urcorner Q\). (d) \(\urcorner P \vee \urcorner Q\). - Для заявлений
P : 15 нечетно R: 15 < 17
запишите каждое из следующих утверждений в символической форме, используя операторы \(\wedge\), \(\vee\) и \(\urcorner\)
(a) 15 \(\ge\) 17. (b) 15 нечетно или 15 \(\ge\) 17.
(c) 15 четно или 15 <17. (г) 15 нечетно и 15 \(\ge\) 17,
ПРЕДВАРИТЕЛЬНАЯ АКТИВНОСТЬ\(\PageIndex{2}\): истинностные значения утверждений
Мы будем использовать следующие два утверждения во всех этих предварительных действиях:
- \(P\) — это утверждение «Идет дождь».
- \(Q\) — это утверждение «Дейзи играет в гольф».
В каждой из следующих четырех частей истинностное значение будет присвоено утверждениям \(P\) и \(Q\). Например, в вопросе (1) мы будем предполагать, что каждое утверждение верно. В вопросе (2) мы будем предполагать, что \(P\) истинно, а \(Q\) ложно. В каждой части определите истинность каждого из следующих утверждений:
Например, в вопросе (1) мы будем предполагать, что каждое утверждение верно. В вопросе (2) мы будем предполагать, что \(P\) истинно, а \(Q\) ложно. В каждой части определите истинность каждого из следующих утверждений:
(a) (\(P \wedge Q\)) Идет дождь, а Дейзи играет в гольф.
(b) (\(P \vee Q\)) Идет дождь или Дейзи играет в гольф.
(c) (\(P \to Q\)) Если идет дождь, то Дейзи играет в гольф.
(d) (\(\urcorner P\)) Дождя нет.
Какие из четырех утверждений [(a)–(d)] верны, а какие нет в каждой из следующих четырех ситуаций?
1. Когда \(P\) верно (идет дождь) и \(Q\) верно (Дейзи играет в гольф).
2. Когда \(P\) истинно (идет дождь), а \(Q\) ложно (Дейзи не играет в гольф).
3. Когда \(P\) ложно (дождя нет) и \(Q\) истинно (Дейзи играет в гольф).
4. Когда \(P\) ложно (дождя нет) и \(Q\) ложно (Дейзи не играет в гольф).
В предварительных заданиях для этого раздела мы узнали о составных утверждениях и их значениях истинности. Эту информацию можно обобщить с помощью таблиц истинности, как показано ниже.
Эту информацию можно обобщить с помощью таблиц истинности, как показано ниже.
| \(П\) | \(\ур угол П\) |
|---|---|
| Т | Ф |
| Ф | Т |
| \(П\) | \(Q\) | \(П \клин Q\) |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Ф |
| Ф | Ф | Ф |
| \(П\) | \(Q\) | \(P \vee Q\) |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Т |
| Ф | Т | Т |
| Ф | Ф | Ф |
| \(П\) | \(Q\) | \(П\к Q\) |
|---|---|---|
| Т | Т | Т |
| Т | Ф | Ф |
| Ф | Т | Т |
| Ф | Ф | Т |
Вместо того, чтобы запоминать таблицы истинности, многим людям легче запомнить правила, обобщенные в Таблице 2. 1.
1.
| Оператор | Символическая форма | Сводка значений истинности |
|---|---|---|
| Соединение | \(П \клин Q\) | Истина, только если оба \(P\) и \(Q\) истинны |
| Разъединение | \(P \vee Q\) | Ложь, только если и \(P\), и \(Q\) ложны |
| Отрицание | \(\угол П\) | Значение истинности, противоположное \(P\) |
| Условный | \(П\к Q\) | Ложь, только если \(P\) истинно, а \(Q\) ложно |
Другие формы условных операторов
Условные операторы чрезвычайно важны в математике, потому что почти все математические теоремы формулируются (или могут быть сформулированы) в форме условного оператора в следующей форме:
Если «соблюдаются определенные условия», то «что-то происходит».
Крайне важно, чтобы все учащиеся, изучающие математику, полностью понимали значение условного утверждения и таблицу истинности условного утверждения.
Мы также должны знать, что в английском языке есть другие способы выражения условного оператора \(P \to Q\), кроме «If \(P\), then \(Q\)». Ниже приведены некоторые распространенные способы выражения условного оператора \(P \to Q\) в английском языке:
Проверка выполнения 2.1: заявление «Только если»
Напомним, что четырехугольник — это четырехугольник. Пусть \(S\) представляет собой следующее верное условное утверждение:
Если четырехугольник является квадратом, то он является прямоугольником.
Напишите это условное выражение на английском языке, используя
- слово «когда бы ни»
- фраза «только если»
- фраза «необходимо для»
- фраза «достаточно для»
- Ответить
Добавьте сюда текст.
 Не удаляйте этот текст первым.
Не удаляйте этот текст первым.
Построение таблиц истинности
Таблицы истинности для составных утверждений могут быть построены с использованием таблиц истинности для основных связок. Чтобы проиллюстрировать это, мы построим таблицу истинности для. \((P \клин \urcorner Q) \к R\). Первым шагом является определение необходимого количества рядов.
- Для таблицы истинности с двумя разными простыми утверждениями необходимы четыре строки, поскольку существует четыре различных комбинации значений истинности для двух утверждений. Мы должны быть последовательны в том, как мы настраиваем ряды. В этом тексте мы будем делать это следующим образом: пометим строки для первого утверждения (T, T, F, F), а строки для второго утверждения — (T, F, T, F). Все таблицы истинности в тексте имеют эту схему.
- Для таблицы истинности с тремя различными простыми утверждениями требуется восемь строк, поскольку существует восемь различных комбинаций значений истинности для трех утверждений.
 Наша стандартная схема для этого типа таблицы истинности показана в Таблице 2.2 .
Наша стандартная схема для этого типа таблицы истинности показана в Таблице 2.2 .
Следующим шагом является определение используемых столбцов. Один из способов сделать это — работать в обратном направлении от формы данного утверждения. Для \((P \wedge \urcorner Q) \to R\) последним шагом является работа с условным оператором \((\to)\). Для этого нам нужно знать истинностные значения \((P \клин \urcorner Q)\) и \(R\). Чтобы определить истинностные значения для \((P \клин \urcorner Q)\), нам нужно применить правила для оператора конъюнкции \((\клин)\) и нам нужно знать истинностные значения для \(P\ ) и \(\urcorner Q\).
Таблица 2.2 представляет собой заполненную таблицу истинности для \((P \клин \urcorner Q) \to R\) с номерами шагов, указанными внизу каждого столбца. Номера шагов соответствуют порядку заполнения столбцов.
| \(П\) | \(Q\) | \(R\) | \(\угол Q\) | \((P \клин\угол Q)\) | \((П\клин \уругол Q)\к R\) |
|---|---|---|---|---|---|
| Т | Т | Т | Ф | Ф | Т |
| Т | Т | Ф | Ф | Ф | Т |
| Т | Ф | Т | Т | Т | Т |
| Т | Ф | Ф | Т | Т | Ф |
| Ф | Т | Т | Ф | Ф | Т |
| Ф | Т | Ф | Ф | Ф | Т |
| Ф | Ф | Т | Т | Ф | Т |
| Ф | Ф | Ф | Т | Ф | Т |
| 1 | 1 | 1 | 2 | 3 | 4 |
- Заполняя столбец для \(P \клин \urcorner Q\), помните, что конъюнкция истинна только тогда, когда оба \(P\) и \(\urcorner Q\) истинны.

- Заполняя столбец для \((P \клин \urcorner Q) \to R\), помните, что условный оператор ложен только тогда, когда гипотеза \((P \клин \urcorner Q)\) верна и заключение \(R\) ложно.
Последний введенный столбец представляет собой таблицу истинности для утверждения \((P \wedge \urcorner Q) \to R\) с использованием настройки в первых трех столбцах.
Проверка выполнения 2.2: построение таблиц истинности
Построить таблицу истинности для каждого из следующих утверждений:
- \(P \клин \urcorner Q\)
- \(\угол(P\клин Q)\)
- \(\угол P \клин \urугол Q\)
- \(\urcorner P \vee \urcorner Q\)
Есть ли среди этих утверждений одинаковая таблица истинности?
- Ответить
Добавьте сюда текст. Не удаляйте этот текст первым.
Биусловное утверждение
Некоторые математические результаты формулируются в форме «\(P\) тогда и только тогда, когда \(Q\)» или «\(P\) необходимо и достаточно для \(Q\)». Примером может быть: «Треугольник равносторонний тогда и только тогда, когда три его внутренних угла конгруэнтны». Символическая форма биусловного утверждения «\(P\) тогда и только тогда, когда \(Q\)» — это \(P \leftrightarrow Q\). Чтобы определить таблицу истинности для биусловного утверждения, полезно внимательно посмотреть на форму фразы «\(P\) тогда и только тогда, когда \(Q\)». Слово «и» предполагает, что это высказывание является союзом. На самом деле это конъюнкция утверждений «\(P\), если \(Q\)» и «\(P\), только если \(Q\)». Символическая форма этого соединения: \([(Q \to P) \wedge (P \to Q]\).
Примером может быть: «Треугольник равносторонний тогда и только тогда, когда три его внутренних угла конгруэнтны». Символическая форма биусловного утверждения «\(P\) тогда и только тогда, когда \(Q\)» — это \(P \leftrightarrow Q\). Чтобы определить таблицу истинности для биусловного утверждения, полезно внимательно посмотреть на форму фразы «\(P\) тогда и только тогда, когда \(Q\)». Слово «и» предполагает, что это высказывание является союзом. На самом деле это конъюнкция утверждений «\(P\), если \(Q\)» и «\(P\), только если \(Q\)». Символическая форма этого соединения: \([(Q \to P) \wedge (P \to Q]\).
Проверка выполнения 2.3: Таблица истинности для биусловного утверждения
Заполните таблицу истинности для \([(Q \to P) \wedge (P \to Q]\). Используйте следующие столбцы: \(P\) , \(Q\), \(Q \к P\), \(P \к Q\) и \([(Q \к P) \клин (P \к Q]\). Последний столбец эта таблица будет истинной для \(P \leftrightarrow Q\).
Добавьте сюда текст. Не удаляйте этот текст первым.
Другие формы биусловного оператора
Как и в случае с условным оператором, существует несколько распространенных способов выражения биусловного оператора \(P \leftrightarrow Q\) в английском языке.
Пример
- \(P\) есть и только если \(Q\).
- \(P\) необходимо и достаточно для \(Q\).
- \(P\) подразумевает \(Q\), а \(Q\) подразумевает \(P\).
Тавтологии и противоречия
Определение: тавтология
тавтология — это составное утверждение S, истинное для всех возможных комбинаций значений истинности составных утверждений, являющихся частью \(S\). А противоречие является составным утверждением, которое ложно для всех возможных комбинаций значений истинности составных утверждений, входящих в \(S\).
То есть тавтология обязательно верна при любых обстоятельствах, а противоречие обязательно ложно при всех обстоятельствах.
Проверка прогресса 2.4 (тавтологии и противоречия)
Для утверждений \(P\) и \(Q\):
- Используйте таблицу истинности, чтобы показать, что \((P \vee \urcorner P)\) является тавтология.
- Используйте таблицу истинности, чтобы показать, что \((P \клин \urcorner P)\) является противоречием.
- Используйте таблицу истинности, чтобы определить, является ли \(P \to (P \vee P)\) тавтологией, противоречием или ни тем, ни другим.
- Ответить
Добавьте сюда текст. Не удаляйте этот текст первым.
Упражнения к разделу 2.1
- Предположим, что Дейзи говорит: «Если не будет дождя, я буду играть в гольф». Позже в тот же день вы узнаете, что шел дождь, но Дейзи все еще играла в гольф. Было ли утверждение Дейзи правдой или ложью? Поддержите свой вывод.
- Предположим, что \(P\) и \(Q\) являются высказываниями, для которых истинно \(P \to Q\) и для которых \(\urcorner Q\) истинно.
 Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?
Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?(a) \(P\)
(b) \(P \клин Q\)
(c) \(P \vee Q\) - Предположим, что \(P\) и \(Q\) являются высказываниями, для которых \(P \to Q\) ложно. Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?
(a) \(\угол P \to Q\)
(b) \(Q \to P\)
(c) \(P \ vee Q\) - Предположим, что \(P\) и \(Q\) являются высказываниями, для которых \(Q\) ложно, а \(\угол P\to Q\) истинен (и неизвестно, если \(R\) истинно или ложно). Какой вывод (если вообще есть) можно сделать об истинности каждого из следующих утверждений?
(а) \(\угол Q \к П\)
(б) \(Р\)
(в) \(Р \клин R\)
(г) \(R \к \уругол Р\) - Постройте таблицу истинности для каждого из следующих утверждений:
(a) \(P \to Q\)
(b) \(Q \to P\)
(c) \(\urcorner P \to \urcorner Q\)
(d) \(\urcorner Q \ в \urcorner P\)Имеют ли какие-либо из этих утверждений одинаковую таблицу истинности?
- Постройте таблицу истинности для каждого из следующих утверждений:
(a) \(P \vee \urcorner Q\)
(b) \(\urcorner (P \vee Q)\)
(c) \(\urcorner P \vee \urcorner Q\)
(d) \(\urcorner P \wedge \urcorner Q\)Имеют ли какие-либо из этих утверждений одинаковую таблицу истинности?
- Построить таблицу истинности для \(P \клин (Q \клин R)\) и \((P \клин Q) \ви (P \клин R)\).
 Что вы наблюдаете.
Что вы наблюдаете. - Предположим, что каждое из следующих утверждений верно.
- Лаура учится в седьмом классе.
- ��Лора получила пятёрку за тест по математике или Сара получила пятёрку за тест по математике.
- ��Если Сара получила пятёрку за контрольную по математике, значит Лора не учится в седьмом классе.
Если возможно, определите истинность каждого из следующих утверждений. Внимательно объясните свои рассуждения. 92\) четно». Выразите условное утверждение \(P \to Q\) на английском языке, используя
(a) Форма условного оператора «if then»
(b) Слово «подразумевает»
(c) Форма «только если» условного оператора условное утверждение
(d) Фраза «необходимо для»
(e) Фраза «достаточно для» - Повторите упражнение (9) для условного оператора \(Q \to P\).
- Для утверждений \(P\) и \(Q\) используйте таблицы истинности, чтобы определить, является ли каждое из следующих утверждений тавтологией, противоречием или ни тем, ни другим.

(a) \(\urcorner Q \vee (P \to Q)\).
(b) \(Q \клин (P \клин \urcorner Q)\).
(c) \((Q \клин P) \клин (P \к \углу Q)\).
(г) \(\угол Q\к (Р\клин \угол Р)\). - Для утверждений \(P\), \(Q\) и \(R\):
(a) Покажите, что \([(P \to Q) \клин P] \to Q\) является тавтологией. Примечание : В символической логике это важная форма логического аргумента, называемая modus ponens .
(b) Покажите, что \([(P \to Q) \клин (Q \to R)] \to (P \to R)\) является атавтологией. Примечание : В символической логике это важная форма логического аргумента, называемая силлогизмом .Разведка и деятельность
- Работа с условными операторами. Заполните следующую таблицу:
Английская форма Гипотеза Заключение Символическая форма Если \(P\), то \(Q\) \(П\) \(К\) \(П\к Q\) \(Q\) только если \(P\) \(К\) \(П\) \(К\к П\) \(P\) необходимо для \(Q\) \(P\) достаточно для \(Q\) \(Q\) необходимо для \(P\) \(P\) подразумевает \(Q\) \(P\) только если \(Q\) \(P\) если \(Q\) если \(Q\), то \(P\) если \(\urcorner Q\), то \(\urcorner P\) если \(Q\), то \(Q \клин R\) если \(P \vee Q\), то \(R\) - Работа с истинностными значениями утверждений.
 Предположим, что \(P\) и \(Q\) являются истинными утверждениями, что \(U\) и \(V\) являются ложными утверждениями, и что \(W\) является утверждением, и неизвестно, \(W\) истинно или ложно.
Предположим, что \(P\) и \(Q\) являются истинными утверждениями, что \(U\) и \(V\) являются ложными утверждениями, и что \(W\) является утверждением, и неизвестно, \(W\) истинно или ложно.Какие из следующих утверждений верны, какие ложны, и для каких утверждений невозможно определить, истинно оно или ложно? Обоснуйте свои выводы.
(a) \((P \vee Q) \vee (U \клин W)\) (f) \((\urcorner P \vee \urcorner U) \клин (Q \vee \urcorner V)\)
(b) \(P \клин (Q\to W)\) (g) \((P \клин \urcorner Q) \клин (U \vee W)\)
(c) \(P \клин ( W \к Q)\) (h) \((P \vee \urcorner Q) \to (U \клин W)\)
(d) \(W \to (P \клин U)\) (i) \((P \vee W) \to (U \клин W)\)
(e) \(W \к (P \клин \уругол U)\) (j) \((U \клин \urугол V) \к (P \клин W)\)
- Ответить
Добавьте сюда текст. Не удаляйте этот текст первым.
Эта страница под названием 2.1: Операторы и логические операторы распространяется в соответствии с лицензией CC BY-NC-SA 3. 0 и была создана, изменена и/или курирована Тедом Сандстромом (ScholarWorks @Grand Valley State University) посредством исходного содержимого, которое было отредактировано. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
0 и была создана, изменена и/или курирована Тедом Сандстромом (ScholarWorks @Grand Valley State University) посредством исходного содержимого, которое было отредактировано. к стилю и стандартам платформы LibreTexts; подробная история редактирования доступна по запросу.
- Наверх
- Была ли эта статья полезной?
- Тип изделия
- Раздел или страница
- Автор
- Тед Сандстром
- Лицензия
- CC BY-NC-SA
- Версия лицензии
- 3,0
- Показать страницу Содержание
- нет
- Теги
- Биусловный оператор
- составные операторы
- источник@https://scholarworks.



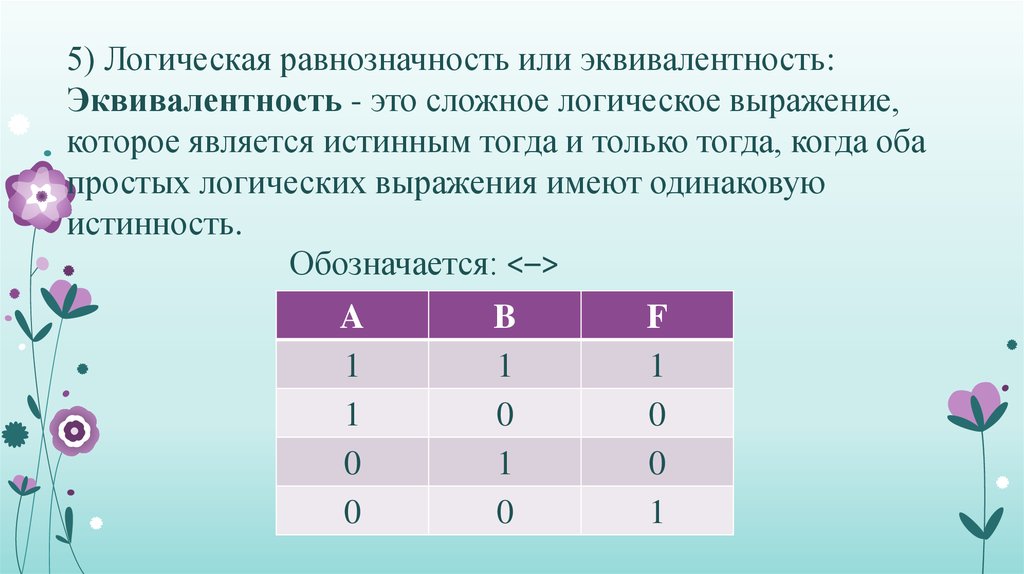 Какая операция называется «дизъюнкцией»?
Какая операция называется «дизъюнкцией»? Какая фраза является отрицанием утверждения «На улице идет снег и ветрено»?
Какая фраза является отрицанием утверждения «На улице идет снег и ветрено»? Например,
Например, 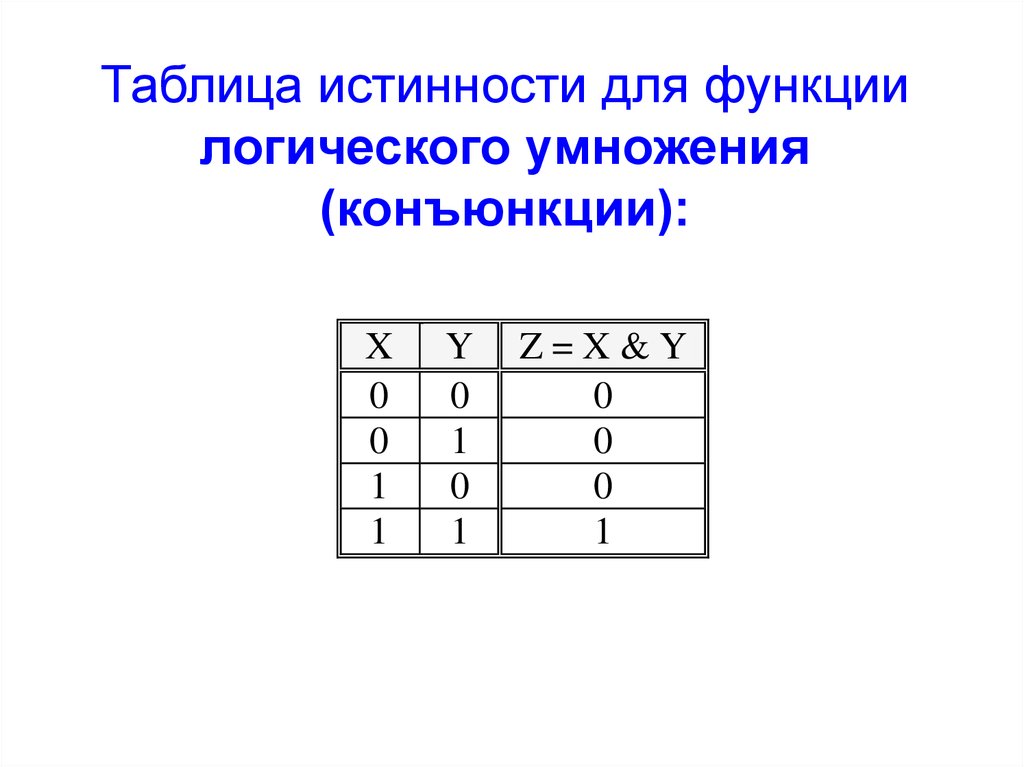
 После заданий Правды идет еще один ряд -. Используя каждое присваивание истинности, заполните присваивания истинности (T или F) под каждым оператором в формуле в порядке старшинства (оператор верхнего уровня применяется последним). При желании вы можете заполнить значения для каждой переменной под форумой (как в примере выше). Однако требуется только, чтобы вы выполнили задания на истинность под каждым оператором. Будьте осторожны, выстраивая назначения истинности НЕПОСРЕДСТВЕННО под каждым оператором, так как Logika отклонит таблицы истинности, которые не выровнены тщательно.
После заданий Правды идет еще один ряд -. Используя каждое присваивание истинности, заполните присваивания истинности (T или F) под каждым оператором в формуле в порядке старшинства (оператор верхнего уровня применяется последним). При желании вы можете заполнить значения для каждой переменной под форумой (как в примере выше). Однако требуется только, чтобы вы выполнили задания на истинность под каждым оператором. Будьте осторожны, выстраивая назначения истинности НЕПОСРЕДСТВЕННО под каждым оператором, так как Logika отклонит таблицы истинности, которые не выровнены тщательно. Если формула является условной, вы также должны перечислить, какие присваивания истинности сделали формулу истинной (т. е. какие присваивания истинности сделали оператор верхнего уровня T) и какие присваивания истинности сделали формулу ложной. Следуйте изображению выше, чтобы узнать синтаксис того, как перечислить назначения истинности для условных примеров.
Если формула является условной, вы также должны перечислить, какие присваивания истинности сделали формулу истинной (т. е. какие присваивания истинности сделали оператор верхнего уровня T) и какие присваивания истинности сделали формулу ложной. Следуйте изображению выше, чтобы узнать синтаксис того, как перечислить назначения истинности для условных примеров.