Конденсатор какой электроемкости следует подключить к катушке

Урок физики в 11 классеТема: Формула Томсона Учитель физики Тетерина Н.В. МОУ « Красногорская СОШ №1» 2010 год

Академик Мандельштам отмечал: “Теория колебаний объединяет, обобщает различные области физики. Каждая из областей физики — оптика, механика, акустика — говорит на своем “национальном” языке. Но есть “интернациональный” язык, и это — язык теории колебаний. Изучая одну область, вы получаете тем самым интуицию и знания совсем в другой области”.

Ключевые слова ПериодЕмкостьИндуктивностьЗависимостьЭлектромагнитный контур

Виртуальная лаборатория(видео эксперимент)

Виртуальная лаборатория(интерактивная модель)

Период свободных колебаний в контуре:

ТОМСОН Уильям(Thomson William) Лорд Кельвин (1824-1907), английский физик Заложил основы теории электромагнитных колебаний и в 1853 вывел формулу зависимости периода собственных колебаний контура от его емкости и индуктивности (формула Томсона).

Король викторианской физики получил образование в университетах Глазго и Кембриджа . с 1846 до 1899 г. был профессором натуральной философии в университете Глазго . посвящен в рыцари в 1866 г получил звание пэра и титул лорда Кельвина в 1892 г

Чему равен период собственных колебаний в контуре, если его индуктивность 2,5 Гн, а емкость 1,5 мкФ?

Задачи: Подставьте в формулу Томсона следующие значения:L = 0,5 Гн С = 0,5 мкФВычислите период, а затем частоту.Ответ: Т = 0,0031 с√ = 320 Гц

Задачи: Конденсатор какой электроемкости следует подключить к катушке индуктивности L= 20 мГн, чтобы в контуре возникли колебания с периодом Т=1 мс?Ответ: С= 1,27 мкФ

Задачи: Как изменится циклическая частота, если в колебательном контуре заменят конденсатор на другой меньшей в 36 раз емкостью? Ответ: частота увеличится в 6 раз

Задачи: Как изменится период свободных колебаний в электрическом контуре при увеличении электроемкости конденсатора в 2 раза?Ответ: увеличится в 1,4 раза

ПОДВЕДЕНИЕ ИТОГОВ «Счастливая случайность выпадает лишь на долю подготовленного ума» Л.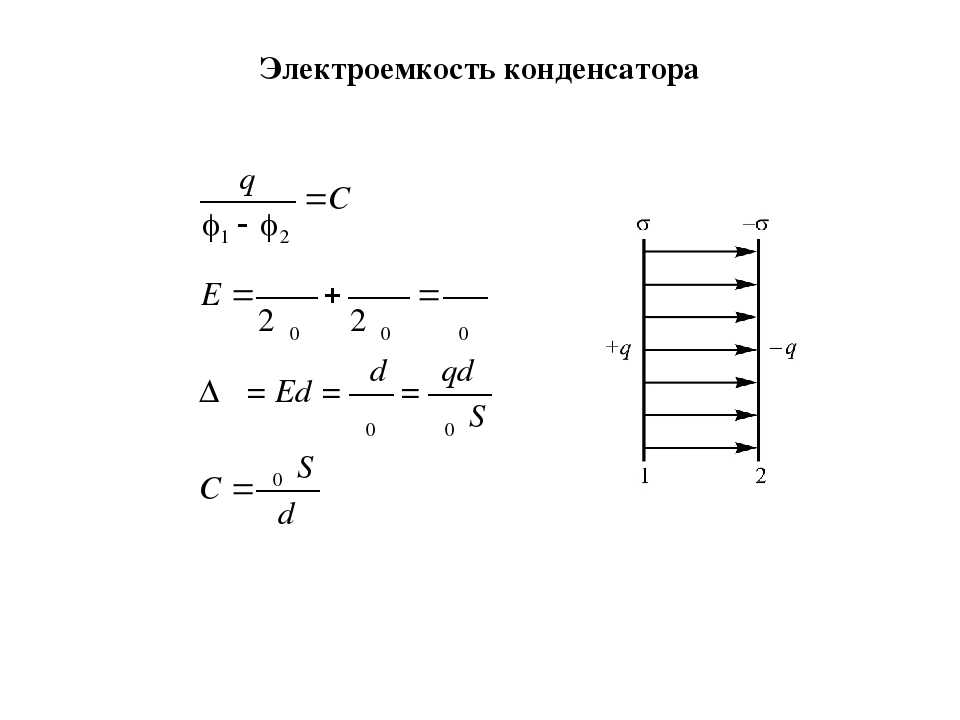 Пастер

Идёт приём заявок

Подать заявку

Для учеников 1-11 классов и дошкольников

Описание презентации по отдельным слайдам:

Колебательный контур 1.Автомобиль массой 1 тонна, движется прямолинейно со скоростью 20 м/с. Импульс автомобиля равен… 1) 0,5·103кг·м/с 2) 1·104 кг·м/с 3) 2·104 кг·м/с 4) 20кг·м/с 5) 50 кг·м/с

2. Грузик, колеблющийся на пружине, за 8 с совершил 32 колебания. Найдите период и частоту колебаний.

Определить направление силы Ампера: N S FA

Определить положение полюсов магнита, создающего магнитное поле. а) слева – северный полюс, б) слева – южный полюс.

Проверка усвоения знаний Какое устройство называют конденсатором? Какое свойство конденсатора характеризует электрическая ёмкость? Что называют электрической ёмкостью конденсатора? Какова единица электрической ёмкости? От чего и как зависит ёмкость плоского конденсатора?

Проверка усвоения знаний Расстояние между пластинами плоского конденсатора увеличили в 4 раза. Как изменилась ёмкость конденсатора? Площадь пластин плоского конденсатора увеличили в 3 раза. Как изменилась ёмкость конденсатора? Между пластинами конденсатора поместили пластину из эбонита. Как изменилась его ёмкость?

Колебательный контур. Получение электромагнитных колебаний.

Изучение нового материала Колебательной системой, в которой можно создать электромагнитные колебания, является колебательный контур. Колебательным контуром называют электрическую цепь, состоящую из конденсатора и катушки индуктивности.

Возникновение электромагнитных колебаний Соединим конденсатор с источником тока, поставив переключатель в положение 1. Конденсатор зарядится, на его пластинах появится электрический заряд: на одной +, на другой — . Переведём переключатель в положение 2, отключив тем самым конденсатор от источника тока.

Процесс разрядки конденсатора а) д) г) в) б) t=0 t=1/4T t=T/2 t=3/4T t=T + + — — qm i=0 q=0 Im ↓ i=0 qm — + + q=0 Im↑ + + — — i=0 qm Изучить процесс разрядки конденсатора

Электромагнитные колебания Периодические изменения электрического заряда, силы тока, электрического и магнитного полей, происходящие в колебательном контуре, называют электромагнитными колебаниями.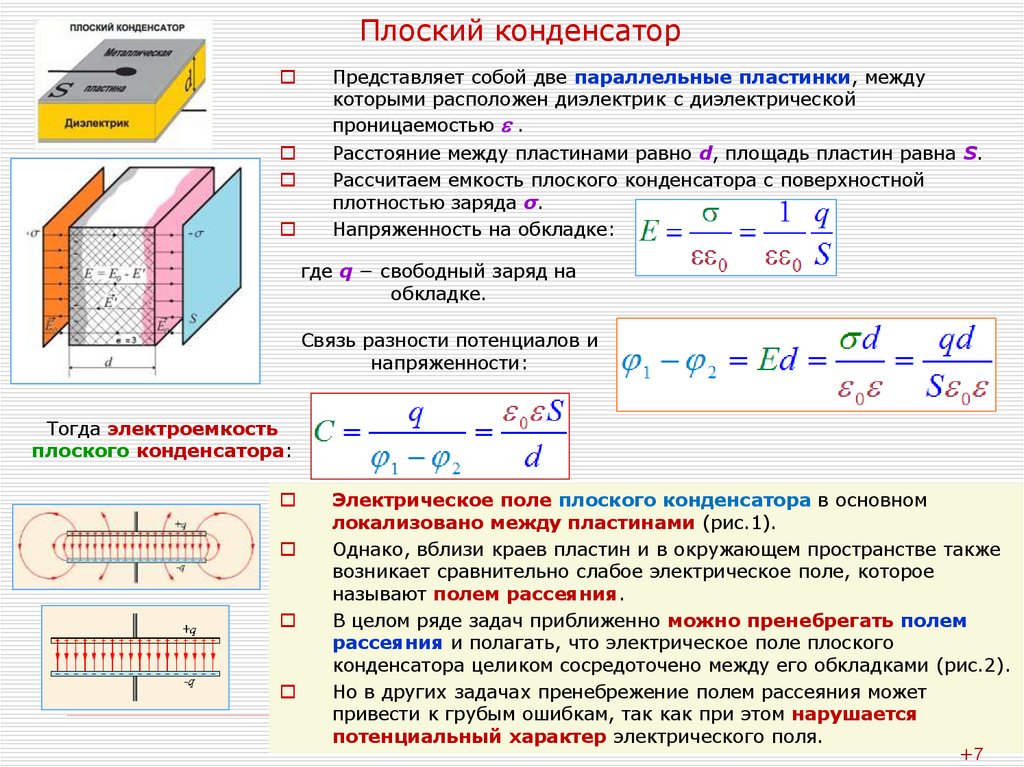 свободные вынужденные затухающие незатухающие

Электромагнитные колебания Свободные колебания — это колебания в системе, которые возникают после выведения её из положения равновесия. Система выводится из равновесия при сообщении конденсатору заряда. Вынужденные колебания — колебания в цепи под действием внешней периодической электродвижущей силы. Вынужденные э/м колебания происходят с частотой равной частоте изменения напряжения источника тока.

Период электромагнитных колебаний

Чему равен период собственных колебаний в контуре, если его индуктивность 2,5 Гн, а емкость 1,5 мкФ? Т = 12,16 * 10-3с = 12,16мс Дано: L = 2.5 Гн С = 1,5 мкФ = =1,5*10-6 Ф Т – ?

Задачи: Как изменится период свободных колебаний в электрическом контуре при увеличении электроемкости конденсатора в 2 раза? Ответ: увеличится в 1,4 раза

Задачи: Конденсатор какой электроемкости следует подключить к катушке индуктивности L= 20 мГн, чтобы в контуре возникли колебания с периодом Т=1 мс? Ответ: С= 1,27 мкФ

Домашнее задание Конспект, интернет ресурсы

• Митрофанова Юлия АлександровнаНаписать 879 23. 09.2016

Номер материала: ДБ-208936

23.09.2016 678

23.09.2016 3560

23.09.2016 517

23.09.2016 359

23.09.2016 996

23.09.2016 427

23.09.2016 802

Не нашли то что искали?

Вам будут интересны эти курсы:

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение редакции может не совпадать с точкой зрения авторов.

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако редакция сайта готова оказать всяческую поддержку в решении любых вопросов связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Как заколебать ток. Конденсаторы и катушки

Автор:
Опубликовано 01.01.1970

Начинаем с первого и самого главного блока — ГВЧ (Генератор Высокой частоты).

Как вы помните, генератор обязан преобразовать постоянный ток батарейки в переменный ток ВЧ. Для этого обычно используют транзистор и еще две детали, с которыми мы пока что не знакомы: конденсатор и катушку индуктивности.

Конденсатор — это элемент, способный накапливать в себе электрическую энергию. Конденсатор состоит из двух металлических пластин, изолированных между собой непроводящим материалом (диэлектриком). Эти пластины называют обкладками конденсатора.

Обозначение конденсатора на схеме полностью объясняет его конструкцию:

Конденсатор можно сравнить с батарейкой. Вот только, в нем нет той силы, которая перекидывает заряд в обратную сторону.
Если вспомнить нашу научно-экспериментальную установку с бутылками, то сначала (пока мы не стали вычерпывать воду из в одной бутылки в другую) ее можно было сравнить именно с конденсатором. То есть: наливаем воду в одну бутылку, вторая пуста. Пускаем воду по шлангу. Вторая бутылка — заполняется, первая — опустошается. Это происходит до тех пор, пока уровни в двух бутылках не сравняются, и ток не прекратится.

Так же и в конденсаторе. Когда он заряжен — на одной обкладке электронов больше, чем на другой. То есть, у них разные заряды, а значит — есть разность потенциалов (напряжение). Если к заряженному конденсатору подключить нагрузку, скажем, резистор — потечет ток, и через определенное время заряды двух обкладок сравняются, ток прекратится. То есть — конденсатор разрядится. Чтобы ток пошел снова, нужно опять создать разность потенциалов — то есть, зарядить конденсатор.

Вот так, в общем, все несложно.

Катушка индуктивности — это такая обычная катушка из металлической проволоки.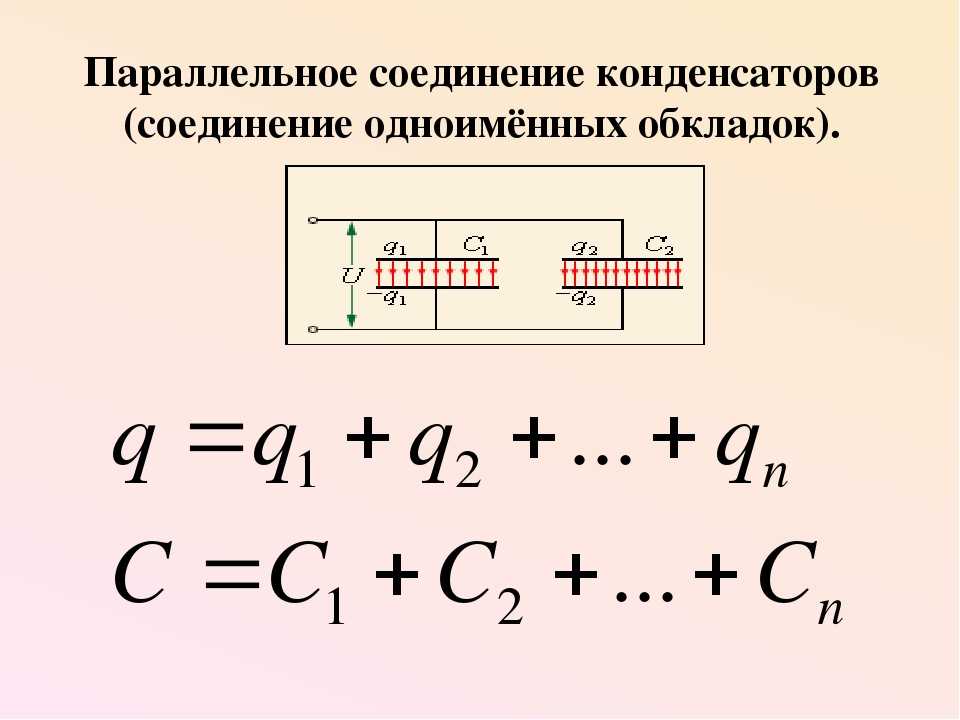

Можно на что угодно намотать кусок проволоки — это уже будет катушка индуктивности.
На схеме она изображается так:

Катушка обладает некоторыми полезными электрическими свойствами. Какими? Сейчас разберемся.

Итак, коль уж вспомнилась нам лабораторная установка из бутылок — давайте ее апгрейдить.

На сей раз нам понадобится водяная турбина. Честно говоря, я не пробовал ее делать, поэтому — не скажу рецепт приготовления =). Однако, если кто-то решится, и у него получится — можете поделиться с народом своим счастьем… и технологией.
Водяная турбина состоит из лопастей, сидящих на оси. Все это находится внутри герметичного кожуха, но ось выводится наружу. При протекании воды, лопасти начинают вращаться. Такие турбины используют, например, на гидроэлектростанциях. На их оси сидят электрогенераторы.

У нас же все проще и меньше. И на ось мы посадим не мощный генератор, а просто какое-нибудь тяжелое круглое колесико, чтобы воде было трудно его вращать.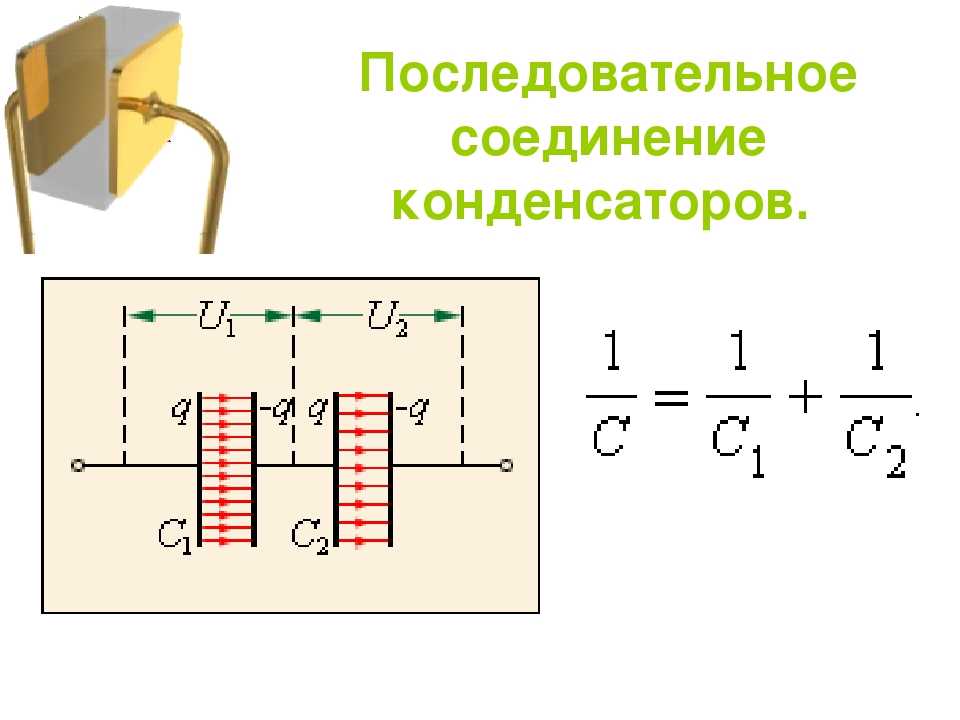

Кстати! Протекающая вода вращает турбину. Но возможно и обратное: вращающаяся турбина может вызывать ток воды. Помним об этом…

Ну, в общем, всобачим эту турбину между двумя бутылками, и нальем в левую бутылку воды. Смотрим, что происходит.
А вот что происходит. Поскольку есть разность потенциалов (то есть, давлений) — вода хочет течь из левой бутылки в правую. Но на пути — турбина! Ничего не остается, как ее крутить. Хочешь жить — умей вертеться. =)

Однако, турбина начинает крутиться не сразу, а постепенно, потому что на ее оси — тяжелое колесо, которое создает инерцию. Поэтому, сначала вода течет медленно, и постепенно, своим током разгоняет турбину. Чем быстрее крутится турбина — тем быстрее перетекает вода в правую бутылку. Перетекает, перетекает… И вот — уровни сравнялись! Казалось бы, пора остановиться. Куда там! Турбина раскрутилась до таких оборотов, что и не думает остановиться, и продолжает по инерции гнать воду из левой бутылки в правую. Однако, постепенно ее скорость снижается, и через некоторое время, она, все же, останавливается.

Но теперь уже в правой бутылке воды больше, чем в левой. И она хочет течь обратно. Турбина начинает крутиться в обратную сторону. Сначала — нехотя, потом — все быстрее и быстрее. В момент, когда уровни равны, турбина опять несется на полных оборотах, и продолжает гнать. Останавливается она, когда в левой бутылке уровень снова больше, чем в правой. Все повторяется заново.

То, что мы видим, называется простым и знакомым нам словом — «колебания».

В идеальных условиях (отсутствие трения и т.п.), этот колебательный процесс длится бесконечно. В реальности — через несколько циклов (периодов), он затухнет. То есть, уровни таки сравняются. Но не в этом суть. Главное, что мы только что познакомились с принципом работы самого распространенной в радиотехнике схемы — колебательного контура. На водяной его модели. =)

Так вот, турбина в нашей научно-экспериментальной мегаустановке — это и есть катушка индуктивности.

У катушки индуктивности, надо сказать, весьма скверный характер. Она, по русски выражаясь, «тормозит». То есть, когда ток, текущий через нее начинает увеличиваться — она всячески препятствует его увеличению. А когда ток уменьшается — она наоборот, «подгоняет» его, не давая уменьшаться. Ну чем не турбина?!

Однако, в счастливом союзе с конденсатором, катушка образует тот самый колебательный контур, без которого не смог бы работать ни один радиоприемник и передатчик.

Вот как выглядит колебательный контур:

Если зарядить конденсатор, а потом подключить к нему катушку — ток в катушке начнет мотаться туда-сюда точно так же, как вода — в турбине.

Как вы, может быть, уже догадались — именно колебательный контур мы будем использовать для преобразования постоянного тока в переменный в нашем генераторе. Однако, прежде чем преступить к преобразованию, познакомимся еще с одним элементом. Без него ничего не получится.

Как изменяется электроемкость плоского конденсатора при увеличении расстояния между пластинами

Как изменяется электроемкость плоского конденсатора.

Что такое электроемкость конденсатора? Электрическая емкость цилиндрического конденсатора

Одним их важнейших параметров, при помощи которого характеризуют конденсатор, является его электроёмкость (C). Физическая величина C, равная:

называется емкостью конденсатора. Где q — величина заряда одной из обкладок конденсатора, а — разность потенциалов между его обкладками. Электроемкость конденсатора — это величина, которая зависит то размеров и устройства конденсатора.

Для конденсаторов с одинаковым устройством и при равных зарядах на его обкладках разность потенциалов воздушного конденсатора будет в раз меньше, чем разность потенциалов между обкладками конденсатора, пространство которого между обкладками заполнено диэлектриком с диэлектрической проницаемостью . Значит емкость конденсатора с диэлектриком (C) в раз больше, чем электроемкость воздушного конденсатора ():

где — диэлектрическая проницаемость диэлектрика.

Единицей емкости конденсатора считают емкость такого конденсатора, который единичным зарядом (1 Кл) заряжается до разности потенциалов, равной одному вольту (в СИ). Единицей емкости конденсатора (как и любой эклектической емкости) в международной системе единиц (СИ) является фарад (Ф).

Электроемкость плоского конденсатора

Поле между обкладками плоского конденсатора в большинстве случаев считают однородным. Однородность нарушается только около краев. При расчете емкости плоского конденсатора данными краевыми эффектами обычно пренебрегают. Это возможно, если расстояние между пластинами мало в сравнении с их линейными размерами. В таком случае емкость плоского конденсатора вычисляют как:

где — электрическая постоянная; S — площадь каждой (или наименьшей) пластины; d — расстояние между пластинами.

Электрическая емкость плоского конденсатора, который содержит N слоев диэлектрика толщина каждого , соответствующая диэлектрическая проницаемость i-го слоя , равна:

Электрическая емкость цилиндрического конденсатора

Конструкция цилиндрического конденсатора включает две соосных (коаксиальных) цилиндрические проводящие поверхности, разного радиуса, пространство между которыми заполняет диэлектрик. Электрическая емкость такого конденсатора находят как:

где l — высота цилиндров; — радиус внешней обкладки; — радиус внутренней обкладки.

Емкости сферического конденсатора

Сферическим конденсатором называют конденсатор, обкладками которого являются две концентрические сферические проводящие поверхности, пространство между ними заполнено диэлектриком. Емкость такого конденсатора находят как:

где — радиусы обкладок конденсатора.

Примеры решения задач

В задаче при изменении расстояния между пластинами конденсатора заряд на его обкладках не изменяется, изменяются емкость и разность потенциалов на обкладках. Емкость плоского воздушного конденсатора равна:

где . Емкость этого же конденсатора можно определить как:

где U — разность потенциалов на обкладках конденсатора. Для конденсатора в первом случае имеем:

Для того же конденсатора, но после того как пластины раздвинули, имеем:

Используя формулу (1. 3) и применяя соотношение:

выразим разность потенциалов

Следовательно, для конденсатора во втором состоянии получим:

Найдем изменение разности потенциалов:

Рассмотрим два заряженных проводника. Предположим, что все силовые линии, начинающиеся на одном из них, заканчиваются на другом. Для этого, разумеется, они должны иметь равные и противоположные по знаку заряды. Такая система двух проводящих тел называется конденсатором.

Примеры конденсаторов. Примерами конденсаторов могут служить две концентрические проводящие сферы (сферический, или шаровой, конденсатор), две параллельные плоские проводящие пластины при условии, что расстояние между ними мало по сравнению с размерами пластин (плоский конденсатор), два коаксиальных проводящих цилиндра при условии, что их длина велика по сравнению с зазором между цилиндрами (цилиндрический конденсатор).

Два проводника, образующие конденсатор, называются его обкладками.

Рис. 41. Электрическое поле в сферическом, плоском и цилиндрическом конденсаторах

Во всех таких системах при сообщении обкладкам равных по модулю и противоположных по знаку зарядов электрическое поле практически целиком заключено в пространстве между обкладками (рис. 41). Внешний вид некоторых используемых в технике конденсаторов показан на рис. 42.

Основная характеристика конденсатора — электроемкость или просто емкость С, определяемая как отношение заряда одной из

обкладок к разности потенциалов т. е. к напряжению, между ними:

Распределение зарядов на обкладках будет одинаковым независимо от того, большой или малый заряд им сообщен. Это значит, что напряженность поля, а следовательно, и разность потенциалов между обкладками, пропорциональны сообщенному конденсатору заряду. Поэтому емкость конденсатора не зависит от его заряда.

Рис. 42. Устройство, внешний вид и условные обозначения на электрических схемах некоторых конденсаторов

В вакууме емкость определяется исключительно геометрическими характеристиками конденсатора, т. е. формой, размерами и взаимным расположением обкладок.

Единицы емкости. В СИ за единицу электроемкости принят фарад Емкостью 1 Ф обладает конденсатор, между обкладками которого устанавливается напряжение 1 В при сообщении заряда 1 Кл:

В абсолютной электростатической системе единиц СГСЭ электроемкость имеет размерность длины и измеряется в сантиметрах:

На практике обычно приходится иметь дело с конденсаторами, емкость которых значительно меньше 1 Ф. Поэтому используются доли этой единицы — микрофарад (мкФ) и пикофарад . Соотношение между фарадом и сантиметром легко установить, учитывая, что

Электроемкость и геометрия конденсатора. Зависимость емкости конденсатора от его геометрических характеристик легко проиллюстрировать простыми опытами. Воспользуемся для этого электрометром, подключенным к двум плоским пластинам, расстояние между которыми можно изменять (рис. 43). Чтобы заряды пластин были одинаковы и все поле было сосредоточено только между ними, следует заземлить вторую пластину и корпус электрометра. Отклонение стрелки электрометра пропорционально напряжению между обкладками. Если сдвигать или раздвигать пластины конденсатора, то при неизменном заряде напряжение будет соответственно уменьшаться или увеличиваться: емкость тем больше, чем меньше расстояние между пластинами. Аналогично можно убедиться в том, что емкость конденсатора тем больше, чем больше площадь его пластин. Для этого можно просто сдвигать пластины при неизменном зазоре между ними.

Рис. 43. Емкость конденсатора зависит от расстояния между пластинами

Емкость плоского конденсатора. Получим формулу для емкости плоского конденсатора. Поле между его обкладками однородно за исключением небольшой области вблизи краев пластин. Поэтому напряжение между обкладками равно произведению напряженности поля Е на расстоянии между ними: Для нахождения напряженности поля Е можно воспользоваться формулой (1) § 6, которая связывает Е вблизи поверхности проводника с поверхностной плотностью зарядов с: Выразим а через заряд конденсатора и площадь пластины, считая распределение заряда равномерным, что согласуется с используемым предположением об однородности поля: Подставляя приведенные соотношения в общее определение емкости (1), находим

В СИ, где емкость плоского конденсатора имеет вид

В системе единиц СГСЭ k = 1 и

Емкость сферического конденсатора. Совершенно аналогично можно вывести формулу для емкости сферического конденсатора, рассматривая электрическое поле в промежутке между двумя заряженными концентрическими сферами радиусов Напряженность поля там такая же, как в случае уединенного заряженного шара радиуса Поэтому для напряжения между обкладками радиусов справедливо

Выражение для емкости получаем, подставляя в формулу (1):

Емкость уединенного проводника.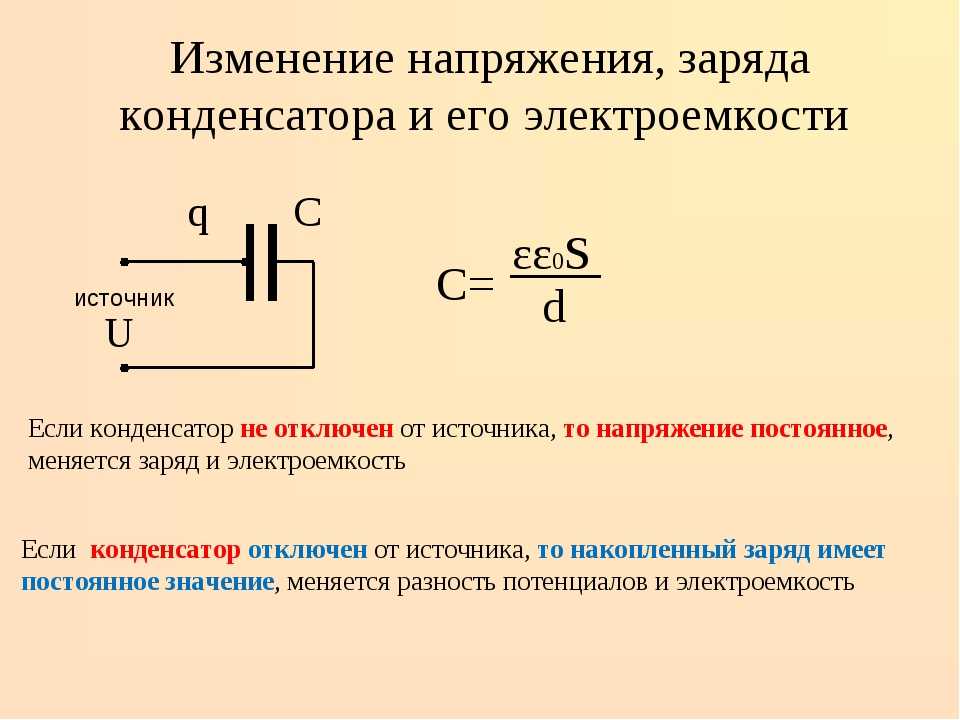 Иногда вводят понятие емкости уединенного проводника, рассматривая предельный случай конденсатора, одна из обкладок которого удалена на бесконечность. В частности, емкость уединенного проводящего шара получается из (5) в результате предельного перехода что соответствует неограниченному увеличению радиуса внешней обкладки при неизменном радиусе внутренней

В системе единиц СГСЭ, где емкость уединенного шара равна его радиусу. Если проводник имеет несферическую форму, его емкость по порядку величины равна характерному линейному размеру, хотя, конечно же, зависит и от его формы. В отличие от уединенного проводника, емкость конденсатора гораздо больше его линейных размеров. Например, у плоского конденсатора характерный линейный размер равен причем Как видно из формулы (4), при этом

Конденсатор с диэлектриком. В рассмотренных выше примерах конденсаторов пространство между обкладками считалось пустым. Тем не менее полученные выражения для емкости справедливы и тогда, когда это пространство заполнено воздухом, как это было в описанных простых опытах. Если пространство между обкладками заполнить каким-либо диэлектриком, емкость конденсатора увеличивается. В этом легко убедиться на опыте, вдвигая диэлектрическую пластину в промежуток между обкладками заряженного конденсатора, подключенного к электрометру (рис. 43). При неизменном заряде конденсатора напряжение между обкладками уменьшается, что свидетельствует о возрастании емкости.

Уменьшение разности потенциалов между обкладками при внесении туда диэлектрической пластины свидетельствует о том, что напряженность электрического поля в зазоре становится меньше. Это уменьшение зависит от того, какой именно диэлектрик используется в опыте.

Диэлектрическая проницаемость. Для характеристики электрических свойств диэлектрика вводят физическую величину, называемую диэлектрической проницаемостью. Диэлектрическая проницаемость — это безразмерная величина, показывающая, во сколько раз напряженность электрического поля в заполненном диэлектриком конденсаторе (или напряжение между его обкладками) меньше, чем в отсутствие диэлектрика при том же заряде конденсатора.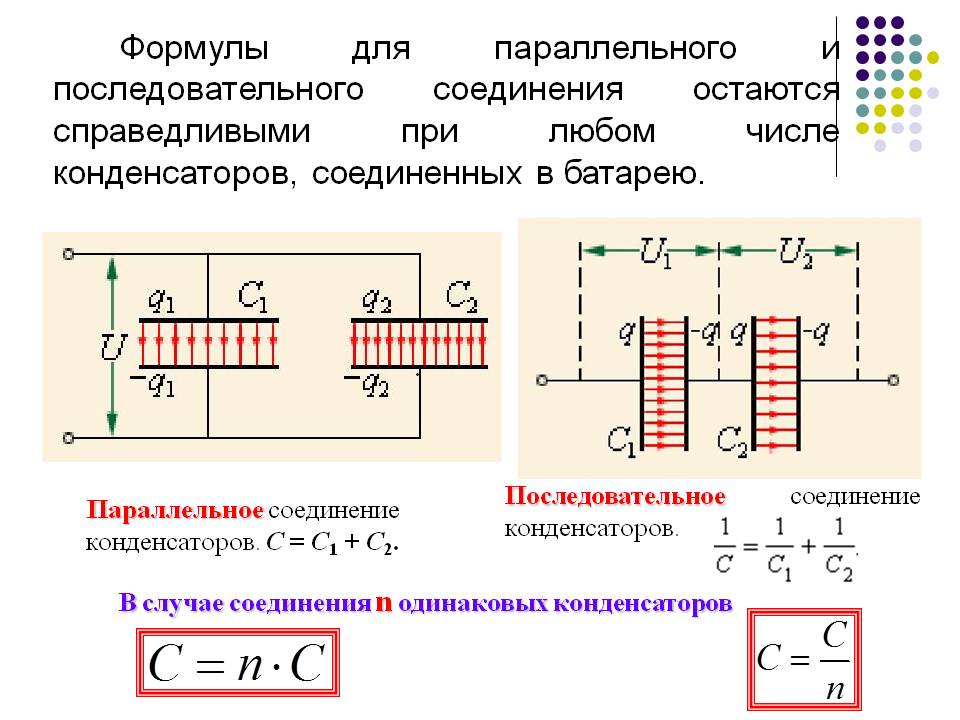 Другими словами, диэлектрическая проницаемость показывает, во сколько раз увеличивается емкость конденсатора при заполнении его диэлектриком. Например, емкость плоского конденсатора, заполненного диэлектриком с проницаемостью равна

Приведенное здесь определение диэлектрической проницаемости соответствует феноменологическому подходу, при котором рассматриваются только макроскопические свойства вещества в электрическом поле. Микроскопический подход, основанный на рассмотрении поляризации атомов или молекул, из которых состоит вещество, предполагает исследование какой-либо конкретной модели и позволяет не только подробно описывать электрические и магнитные поля внутри вещества, но и понять, как протекают макроскопические электрические и магнитные явления в веществе. На этом этапе мы ограничиваемся только феноменологическим подходом.

Рис. 44. Параллельное соединение конденсаторов

У твердых диэлектриков значение лежит в пределах от 4 до 7, а у жидких — от 2 до 81. Такой аномально большой диэлектрической проницаемостью обладает обыкновенная чистая вода. Кроме воздушного конденсатора переменной емкости (см. рис. 42), используемого для настройки радиоприемников, все другие применяемые в технике конденсаторы заполнены диэлектриком.

Батареи конденсаторов. При использовании конденсаторов их иногда соединяют в батареи. При параллельном соединении (рис. 44) напряжения на конденсаторах одинаковы, а полный заряд батареи равен сумме зарядов конденсаторов для каждого из которых, очевидно, справедливо Рассматривая батарею как один

С другой стороны,

Сравнивая (8) и (9), получаем, что емкость батареи параллельно соединенных конденсаторов равна сумме их емкостей:

Рис. 45. Последовательное соединение конденсаторов

При последовательном соединении предварительно незаряженных конденсаторов (рис. 45) заряды на всех конденсаторах одинаковы, а полное напряжение равно сумме напряжений на отдельных конденсаторах:

С другой стороны, рассматривая батарею как один конденсатор, имеем

Сравнивая (11) и (12), видим, что при последовательном соединении конденсаторов складываются обратные емкостям величины:

При последовательном соединении емкость батареи меньше самой малой из емкостей соединенных конденсаторов.

В каком случае два проводящих тела образуют конденсатор?

Что называется зарядом конденсатора?

Как установить связь между единицами емкости СИ и СГСЭ?

Объясните качественно, почему емкость конденсатора увеличивается при уменьшении зазора между обкладками.

Получите формулу для емкости плоского конденсатора, рассматривая электрическое поле в нем как суперпозицию полей, создаваемых двумя плоскостями, заряженными разноименно.

Получите формулу для емкости плоского конденсатора, рассматривая его как предельный случай сферического конденсатора, у которого стремятся к бесконечности так, что разность остается постоянной.

Почему нельзя говорить о емкости уединенной бесконечной плоской пластины или отдельного бесконечно длинного цилиндра?

Охарактеризуйте кратко различие между феноменологическим и микроскопическим подходами при исследовании свойств вещества в электрическом поле.

Каков смысл диэлектрической проницаемости вещества?

Почему при расчете емкости батареи последовательно соединенных конденсаторов оговаривалось условие, чтобы они предварительно не были заряжены?

В чем смысл последовательного соединения конденсаторов, если оно приводит лишь к уменьшению емкости?

Поле внутри и вне конденсатора. Чтобы подчеркнуть различие между тем, что называют зарядом конденсатора, и полным зарядом обкладок, рассмотрим следующий пример. Пусть наружная обкладка сферического конденсатора заземлена, а внутренней сообщен заряд д. Весь этот заряд равномерно распределится по внешней поверхности внутренней обкладки. Тогда на внутренней поверхности наружной сферы индуцируется заряд , следовательно, заряд конденсатора равен . А что будет на внешней поверхности наружной сферы? Это зависит от того, что окружает конденсатор. Пусть, например, на расстоянии от поверхности внешней сферы находится точечный заряд (рис. 46). Этот заряд никак не повлияет на электрическое состояние внутреннего пространства конденсатора, т. е. на поле между его обкладками. В самом деле, внутреннее и внешнее пространства разделены толщей металла наружной обкладки, в которой электрическое поле равно нулю.

Рис. 46. Сферический конденсатор во внешнем электрическом поле

Заряд на внешней поверхности обкладки. Но характер поля во внешнем пространстве и заряд, индуцированный на наружной поверхности внешней сферы, зависят от величины и положения заряда Это поле будет точно таким же, как и в случае, коща заряд находится на расстоянии от поверхности сплошного заземленного металлического шара, радиус которого равен радиусу внешней сферы конденсатора (рис. 47). Таким же будет и индуцированный заряд.

Для нахождения величины индуцированного заряда будем рассуждать следующим образом. Электрическое поле в любой точке пространства создается зарядом и зарядом, индуцированным

на поверхности шара, который распределен там, разумеется, неравномерно — как раз так, чтобы обратилась в нуль результирующая напряженность поля внутри шара. Согласно принципу суперпозиции потенциал в любой точке можно искать в виде суммы потенциалов полей, создаваемых точечным зарядом и точечными зарядами, на которые можно разбить распределенный по поверхности шара индуцированный заряд. Поскольку все элементарные заряды на которые разбит индуцированный на поверхности шара заряд находятся на одинаковом расстоянии от центра шара, то потенциал создаваемого им поля в центре шара будет равен

Рис. 47. Поле точечного заряда вблизи заземленного проводящего шара

Тогда полный потенциал в центре заземленного шара равен

Знак минус отражает тот факт, что индуцированный заряд всегда противоположного знака.

Итак, мы видим, что заряд на наружной поверхности внешней сферы конденсатора определяется тем окружением, в котором находится конденсатор, и не имеет никакого отношения к заряду конденсатора д. Полный заряд внешней обкладки конденсатора, разумеется, равен сумме зарядов ее внешней и внутренней поверхностей, однако заряд конденсатора определяется только зарядом внутренней поверхности этой обкладки, который связан силовыми линиями поля с зарядом внутренней обкладки.

В разобранном примере независимость электрического поля в пространстве между обкладками конденсатора и, следовательно, его емкости от внешних тел (как заряженных, так и незаряженных) обусловлена электростатической защитой, т. е. толщей металла внешней обкладки. К чему может привести отсутствие такой защиты, можно увидеть на следующем примере.

Плоский конденсатор с экраном. Рассмотрим плоский конденсатор в виде двух параллельных металлических пластин, электрическое поле которого практически целиком сосредоточено в пространстве между пластинами. Заключим конденсатор в незаряженную плоскую металлическую коробку, как показано на рис. 48. На первый взгляд может показаться, что картина поля между обкладками конденсатора не изменится, так как все поле сосредоточено между пластинами, а краевым эффектом мы пренебрегаем. Однако легко видеть, что это не так. Снаружи конденсатора напряженность поля равна нулю, поэтому во всех точках слева от конденсатора потенциал одинаков и совпадает с потенциалом левой пластины. Точно так же потенциал любой точки справа от конденсатора совпадает с потенциалом правой пластины (рис. 49). Поэтому, заключая конденсатор в металлическую коробку, мы соединяем проводником точки, имеющие разный потенциал.

В результате в металлической коробке будет происходить перераспределение зарядов до тех пор, пока не выравняются потенциалы всех ее точек. На внутренней поверхности коробки индуцируются заряды, и появится электрическое поле внутри коробки, т. е. снаружи конденсатора (рис. 50).

Рис. 48. Конденсатор в металлической коробке

Рис. 49. Электрическое поле заряженного плоского конденсатора

Рис. 50. Электрическое поле заряженного конденсатора, помещенного в металлическую коробку

Но это означает, что на внешних поверхностях пластин конденсатора тоже появятся заряды. Так как при этом полный заряд изолированной пластины не меняется, то заряд на ее внешней поверхности может возникнуть только за счет перетекания заряда с внутренней поверхности. Но при изменении заряда на внутренних поверхностях обкладок изменится напряженность поля между пластинами конденсатора.

Таким образом, заключение рассмотренного конденсатора в металлическую коробку приводит к изменению электрического состояния внутреннего пространства.

Изменение зарядов пластин и электрического поля в этом примере может быть легко рассчитано. Обозначим заряд изолированного конденсатора через Заряд, перетекающий на наружные поверхности пластин при надевании коробки, обозначим через Такой же заряд противоположного знака будет индуцирован на внутренних поверхностях коробки.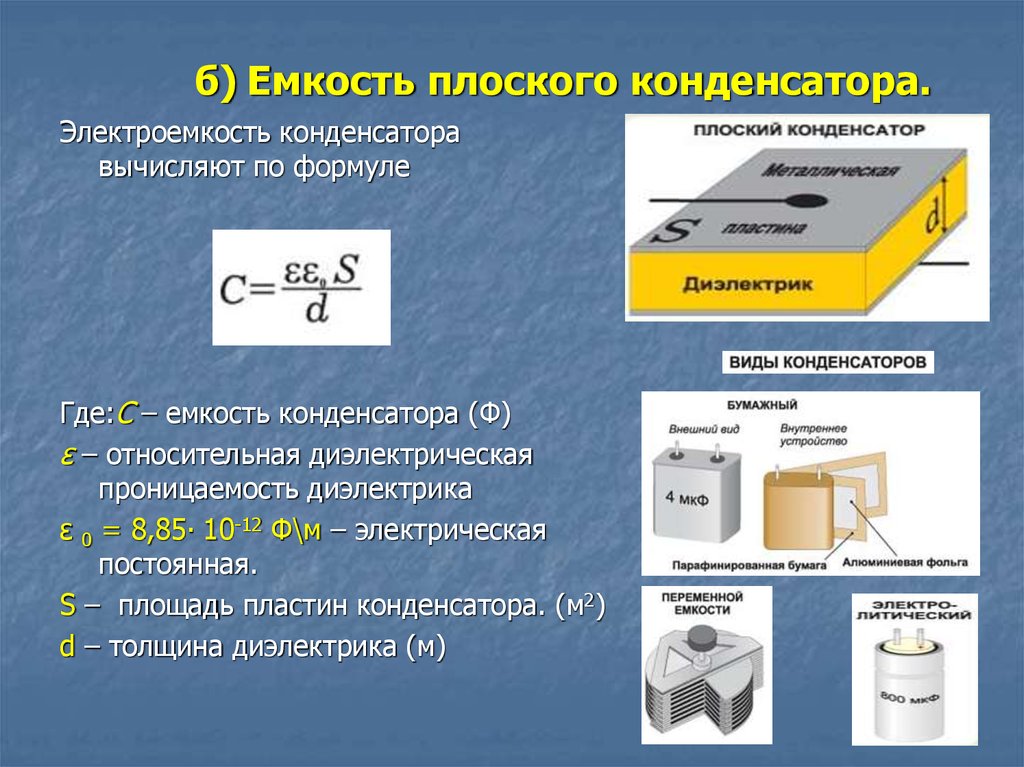 На внутренних поверхностях пластин конденсатора останется заряд Тогда в пространстве между пластинами напряженность однородного поля будет равна в единицах СИ, а вне конденсатора поле направлено в противоположную сторону и его напряженность равна где — площадь пластины. Требуя, чтобы разность потенциалов между противоположными стенками металлической коробки была равна нулю, и считая для простоты расстояния между всеми пластинами одинаковыми и равными то

Этот результат легко понять, если учесть, что после надевания коробки поле существует во всех трех промежутках между пластинами, т. е. фактически имеются три одинаковых конденсатора, эквивалентная схема включения которых показана на рис. 51. Вычисляя емкость получившейся системы конденсаторов, получаем .

Надетая на конденсатор металлическая коробка осуществляет электростатическую защиту системы. Теперь мы можем подносить снаружи к коробке любые заряженные или незаряженные тела и при этом электрическое поле внутри коробки не изменится. Значит, не изменится и емкость системы.

Обратим внимание на то, что в разобранном примере, выяснив все, что нас интересовало, мы тем не менее обошли стороной вопрос о том, какие же силы осуществили перераспределение зарядов. Какое электрическое поле вызвало движение электронов в материале проводящей коробки?

Очевидно, что это может быть только то неоднородное поле, которое выходит за пределы конденсатора вблизи краев пластины (см. рис. 39). Хотя напряженность этого поля мала и не принимается во внимание при расчете изменения емкости, именно она определяет суть рассматриваемого явления — перемещает заряды и этим вызывает изменение напряженности электрического поля внутри коробки.

Почему под зарядом конденсатора следует понимать не полный заряд обкладки, а только ту его часть, что находится на ее внутренней стороне. обращенной к другой обкладке?

В чем проявляется роль краевых эффектов при рассмотрении электростатических явлений в конденсаторе?

Как изменится емкость батареи конденсаторов, если замкнуть между собой обкладки одного из них?

Формула электроемкости следующая.

Измеряется эта величина в фарадах. Как правило, емкость элемента очень мала и измеряется в пикофарадах.

В задачах часто спрашивается, как изменится электроемкость конденсатора, если увеличить заряд или напряжение. Это вопрос с подвохом. Проведем другую аналогию.

Представьте, что речь идет про обычную банку, а не конденсатор. Например, у вас она трехлитровая. Аналогичный вопрос: что произойдет со вместимостью банки, если туда налить 4 литра воды? Разумеется, вода просто выльется, но при этом размеры банки никак не изменятся.

То же самое с конденсаторами. Заряд и напряжение никак не влияют на емкость. Этот параметр зависит только от реальных физических размеров.

Формула будет следующей

Только эти параметры влияют на реальную электроемкость конденсатора.

На любом конденсаторе есть маркировка с техническими параметрами.

Разобраться несложно. Достаточно минимальных знаний по электричеству.

Соединение конденсаторов

Конденсаторы, так же как и сопротивления, можно подключать последовательно и параллельно. Кроме этого, в схемах бывают и смешанные соединения.

Как видите, электроемкость конденсатора в обоих случаях считается по-разному. Это также относится к напряжению и заряду. По формулам видно, что электроемкость конденсатора, вернее, их совокупности в схеме, будет наибольшей при параллельном соединении. При последовательном общая емкость значительно уменьшается.

При подключении последовательно заряд размещается равномерно. Он будет везде одинаков — как суммарный, так и на каждом конденсаторе. А когда соединение параллельное, суммарный заряд складывается. Это важно помнить при решении задач.

Напряжение считается наоборот. При последовательном соединении складываем, а при параллельном оно равно везде.

Здесь приходится выбирать: если вам нужно больше напряжения, тогда жертвуем емкостью. Если емкость, то огромного напряжения не будет.

Виды конденсаторов

Существует огромное количество конденсаторов. Они отличаются как по размеру, так и по форме.

Разумеется, емкость вычисляется у всех по-разному.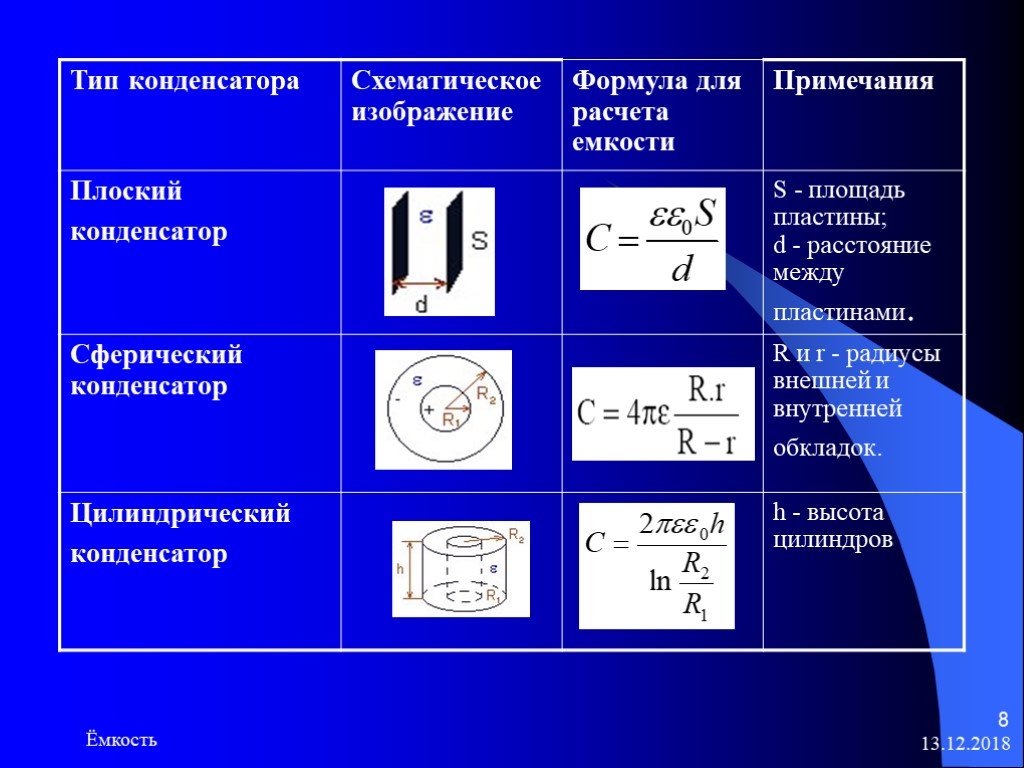

Электроемкость плоского конденсатора

Электроемкость плоского конденсатора определяется проще всего. Эту формулу в основном все и помнят, в отличии от других.

Здесь всё зависит от физических параметров и среды между пластинами.

Здесь также большое значение имеет, какой диэлектрик или материал помещен внутрь. Так как деталь имеет размер сферы, ее емкость зависит от радиуса.

В случае с цилиндрической формой, кроме среды внутри, значение имеют радиусы и длина цилиндра.

Подумайте, как изменится электроемкость плоского конденсатора, если на нем будут повреждения? Существуют различные сбои, которые могут повлиять на работоспособность конденсаторов.

Например, они рассыхаются или вздуваются. После этого они становятся непригодными для нормальной работы устройства, куда установлены.

Рассмотрим примеры повреждений и выхода из строя конденсаторов. Вздуться могут все сразу.

Иногда из строя выходят только несколько. Такое бывает, когда конденсаторы разных параметров или качества.

Наглядный пример порчи (вздутие, разрыв и выход наружу содержимого).

Если вы увидите вот такие ленты, это крайняя степень повреждения. Хуже и быть не может.

Если вы заметите на устройстве (например на видеокарте в компьютере) такие вздутые конденсаторы, это повод задуматься о замене детали.

Подобные проблемы можно устранить только заменой на аналогичную деталь. У вас должны совпадать все параметры один в один. Иначе работа может быть некорректной или очень кратковременной.

Менять конденсаторы нужно аккуратно, не повредив платы. Выпаивать нужно быстро, не допуская перегрева. Если вы не умеете этого делать, лучше отнесите деталь в ремонт.

Основной причиной разрушения является перегрев, который возникает в случае старения или большого сопротивления в цепи.

Рекомендуется не затягивать с ремонтом. Поскольку у поврежденных конденсаторов изменяется емкость, устройство, где они расположены, будет работать с отклонением от нормы. И со временем это может стать причиной выхода из строя.

Если у вас на видеокарте вздулись конденсаторы, то их своевременная замена может исправить ситуацию. В противном случае может сгореть микросхема или что-то еще. В таком случае ремонт будет стоить очень дорого или вовсе окажется невозможным.

Меры предосторожности

Выше был приведен пример с банкой воды. Там говорилось, что если воды налить больше, то воды выльется. А теперь подумайте, куда могут «вылиться» электроны в конденсаторе? Ведь он запечатан полностью!

Если вы подадите в цепи больше тока, чем тот, на который рассчитан конденсатор, то как только он зарядится, его излишек попытается выйти куда-то. А пространства свободного нет. Результатом будет взрыв. В случае незначительного превышения заряда хлопок будет небольшой. Но если подать колоссальное количество электронов на конденсатор, его просто разорвет, и диэлектрик вытечет.

Плоским конденсатором обычно называ-ют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Про-стота конструкции такого конденсатора по-зволяет сравнительно просто рассчитывать его электроемкость и получать значения, совпадающие с результатами эксперимента.

Укрепим две металлические пластины на изоляционных подставках и соединим с электрометром так, что одна из пластин будет присоединена к стержню электромет-ра, а вторая — к его металлическому кор-пусу (рис. 4.71). При таком соединении электрометр будет измерять разность по-тенциалов между пластинами, которые об-разуют плоский конденсатор из двух пла-стин. Проводя исследования, необходимо пом-нить, что

при постоянном значении заряда пластин уменьшение разности потенциалов свидетельствует об увеличении электроем-кости конденсатора, и наоборот.

Сообщим пластинам разноименные заря-ды и отметим отклонение стрелки электро-метра. Приближая пластины друг к другу (уменьшая расстояние между ними), заме-тим уменьшение разности потенциалов. Та-ким образом, при уменьшении расстояния между пластинами конденсатора его элект-роемкость увеличивается. При увеличении расстояния показания стрелки электрометра увеличиваются, что является свидетельст-вом уменьшения электроемкости.

об-ратно пропорциональна расстоянию между его обкладками.

где d — расстояние между обкладками.

Эту зависимость можно изобразить гра-фиком обратной пропорциональной зависи-мости (рис. 4.72).

Будем смещать пластины одну относи-тельно другой в параллельных плоскостях, не изменяя расстояния между ними.

При этом площадь перекрытия пластин будет уменьшаться (рис. 4.73). Увеличение разности потенциалов, отмеченное электрометром, будет свидетельствовать об умень-шении электроемкости.

Увеличение площади перекрытия пластан приведет к увеличению емкости.

Электроемкость плоского конденсатора про-порциональна площади пластин, которые пере-крываются.

где S — площадь пластин.

Эту зависимость можно представить гра-фиком прямой пропорциональной зависи-мости (рис. 4.74).

Возвратив пластины в начальное поло-жение, внесем в пространство между ними плоский диэлектрик. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увели-чении электроемкости конденсатора. Если между пластинами поместить другой диэлек-трик, то изменение электроемкости будет иным.

Электроемкость плоского конденсатора за-висит от диэлектрической проницаемости ди-электрика.

где ε — диэлектрическая проницаемость ди-электрика. Материал с сайта

Такая зависимость показана на графике рис. 4.75.

Результаты опытов можно обобщить в ви-де формулы ёмкости плоского конденсатора :

C = εε 0 S / d,

где S — площадь пластины; d — расстояние между ними; ε — диэлектрическая прони-цаемость диэлектрика; ε 0 — электрическая постоянная.

Конденсаторы, которые состоят из двух пластин, в практике применяются очень редко. Как правило, конденсаторы имеют много пластин, соединенных между собой по определенной схеме.

Задачи на тему Электроемкость конденсатора.

Энергия заряженного конденсатора, электрического поля

Задачи по Электродинамике ( ЭЛЕКТРИЧЕСКОЕ ПОЛЕ ), на тему
Электроемкость конденсатора. Энергия заряженного конденсатора. Энергия электрического поля
Из пособия: ГДЗ к задачнику Рымкевич для 10-11 классов по физике, 10-е издание, 2006 г.

Площадь каждой пластины плоского конденсатора 401 см2. Заряд пластин 1,42 мкКл. Найти напряженность поля между пластинами
РЕШЕНИЕ

Найти поверхностную плотность заряда на пластинах плоского конденсатора, разделенных слоем стекла толщиной 4 мм, если на конденсатор подано напряжение 3,8 кВ
РЕШЕНИЕ

Емкость первого конденсатора 0,5 мкФ, а второго — 5000 пФ. Сравнить напряжения, которые надо подавать на эти конденсаторы, чтобы накопить одинаковые заряды
РЕШЕНИЕ

Емкость одного конденсатора 200 пФ, а другого — 1 мкФ. Сравнить заряды, накопленные на этих конденсаторах при их подключении к полюсам одного и того же источника постоянного напряжения
РЕШЕНИЕ

Какова емкость конденсатора, если при его зарядке до напряжения 1,4 кВ он получает заряд 28 нКл
РЕШЕНИЕ

Наибольшая емкость школьного конденсатора 58 мкФ. Какой заряд он накопит при его подключении к полюсам источника постоянного напряжения 50 В
РЕШЕНИЕ

На конденсаторе написано: 100 пФ; 300 В. Можно ли использовать этот конденсатор для накопления заряда 50 нКл
РЕШЕНИЕ

Во сколько раз изменится емкость конденсатора при уменьшении рабочей площади пластин в 2 раза и уменьшении расстояния между ними в 3 раза
РЕШЕНИЕ

Во сколько раз изменится емкость конденсатора, если в качестве прокладки между пластинами вместо бумаги, пропитанной парафином, использовать листовую слюду такой же толщины

РЕШЕНИЕ

При введении в пространство между пластинами воздушного конденсатора твердого диэлектрика напряжение на конденсаторе уменьшилось с 400 до 50 В. Какова диэлектрическая проницаемость диэлектрика
РЕШЕНИЕ

Одна из пластин школьного плоского конденсатора соединена со стержнем электрометра, а другая с заземленным корпусом. Какими способами можно показания электрометра уменьшить? увеличить
РЕШЕНИЕ

Найти емкость плоского конденсатора, состоящего из двух круглых пластин диаметром 20 см, разделенных парафиновой прослойкой толщиной 1 мм
РЕШЕНИЕ

Площадь каждой пластины плоского конденсатора равна 520 см2.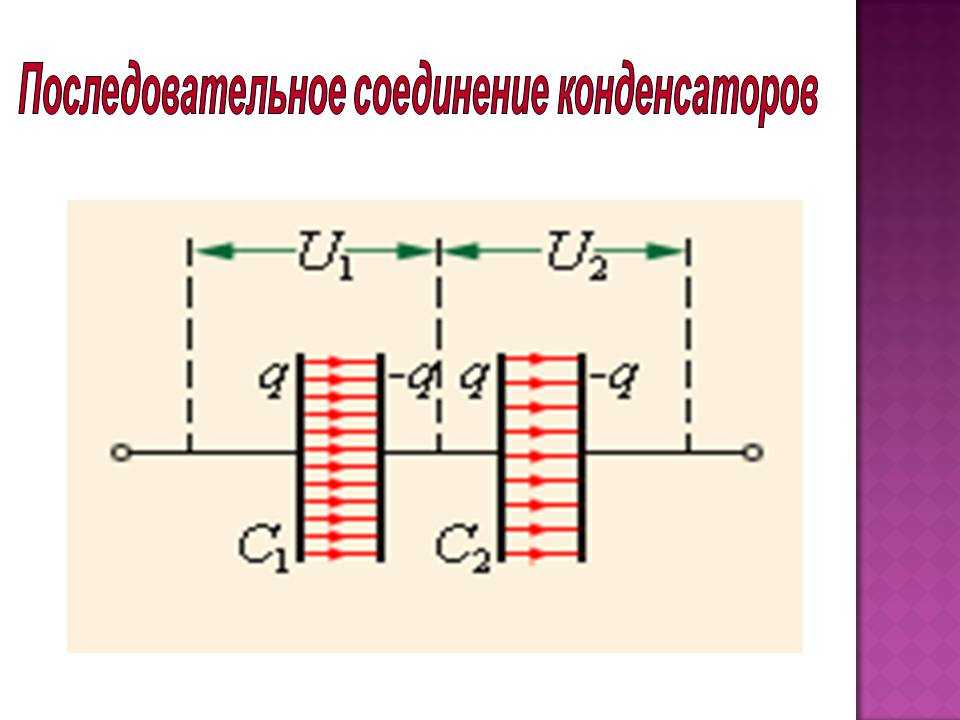

На каком расстоянии друг от друга надо расположить пластины в воздухе, чтобы емкость конденсатора была равна 46 пФ
РЕШЕНИЕ

Плоский конденсатор состоит из двух пластин площадью 50 см2 каждая. Между пластинами находится слой стекла. Какой наибольший заряд можно накопить на этом конденсаторе, если при напряженности поля 10 МВ/м в стекле происходит пробой конденсатора
РЕШЕНИЕ

Расстояние между пластинами плоского конденсатора увеличили в 3 раза. Во сколько раз изменился заряд, напряжение между пластинами и напряженность поля, если конденсатор: а) отключен от источника напряжения; б) остается подключенным к источнику постоянного напряжения

РЕШЕНИЕ

ПЛОСКИЙ конденсатор состоит из двух круглых пластин радиусом 10 см. Между пластинами находится слой диэлектрика толщиной 1 мм с диэлектрической проницаемостью 2,1. Заряжен конденсатор до напряжения 2,4 кВ. Найти емкость конденсатора, заряд на пластинах, энергию и плотность энергии электрического поля
РЕШЕНИЕ

В импульсной фотовспышке лампа питается от конденсатора емкостью 800 мкФ, заряженного до напряжения 300 В.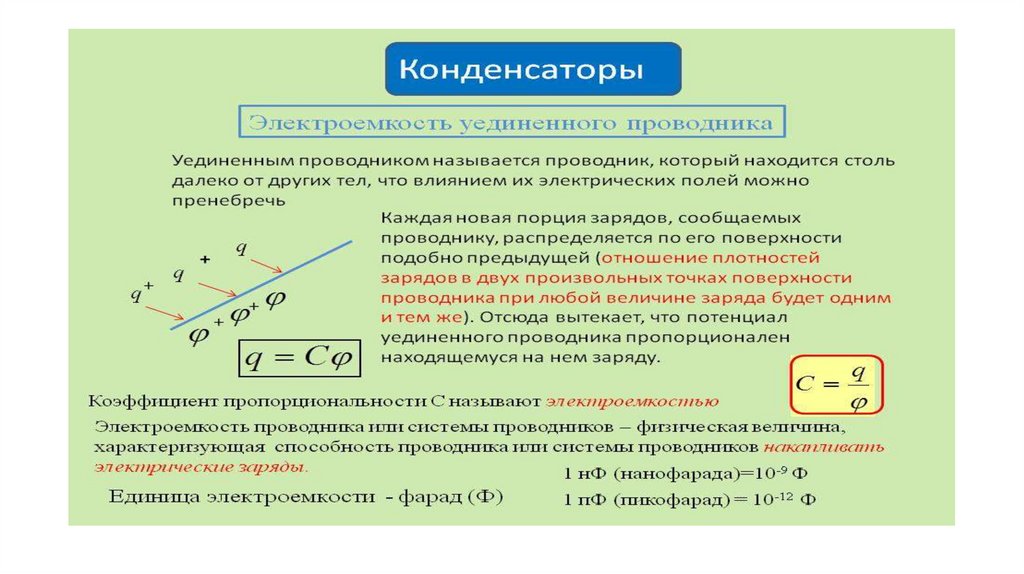 Найти энергию вспышки и среднюю мощность, если продолжительность разрядки 2,4 мс

РЕШЕНИЕ

Во сколько раз изменится энергия конденсатора при увеличении напряжения на нем в 4 раза
РЕШЕНИЕ

Емкость одного конденсатора в 9 раз больше емкости другого. На какой из этих конденсаторов надо подать большее напряжение, чтобы их энергия была одинаковой? во сколько раз большее
РЕШЕНИЕ

Конденсатору емкостью 10 мкФ сообщили заряд 4 мкКл. Какова энергия заряженного конденсатора
РЕШЕНИЕ

Площадь каждой из пластин плоского конденсатора 200 см2, а расстояние между ними 1 см. Какова энергия поля, если напряженность поля 500 кВ/м
РЕШЕНИЕ

Расстояние между пластинами плоского конденсатора с диэлектриком из бумаги, пропитанной парафином, равно 2 мм, а напряжение между пластинами 200 В. Найти плотность энергии поля

РЕШЕНИЕ

Во сколько раз изменится энергия поля заряженного конденсатора, если пространство между пластинами конденсатора заполнить маслом? Рассмотреть случаи: а) конденсатор отключен от источника напряжения; б) конденсатор остается присоединенным к источнику постоянного напряжения. Ответ объяснить, пользуясь законом сохранения энергии
РЕШЕНИЕ

Расстояние между пластинами заряженного плоского конденсатора уменьшили в 2 раза. Во сколько раз изменилась энергия и плотность энергии поля? Рассмотреть два случая: а) конденсатор отключили от источника напряжения; б) конденсатор остался присоединенным к источнику постоянного напряжения

РЕШЕНИЕ

При увеличении напряжения, поданного на конденсатор емкостью 20 мкФ, в 2 раза энергия поля возросла на 0,3 Дж. Найти начальные значения напряжения и энергии поля
РЕШЕНИЕ

База решений задач FIZMATBANK.RU — задачи по физике, страница 389

44149. Катушка перемещается в магнитном поле, индукция которого 2 Тл, со скоростью 0,6 м/с. ЭДС индукции равна 24 В. Найти активную длину проволоки в катушке, если активные части ее перемещаются перпендикулярно линиям индукции.

44150. Прямолинейный проводник длиной 0,5 м движется в магнитном поле со скоростью 6 м/с под углом 30° к вектору магнитной индукции. Определите магнитную индукцию, если в проводнике возникает ЭДС электромагнитной индукции 3 В.

44151. Каково направление индукционного тока в случаях, изображенных на рисунке, если направление движения каждого проводника показано стрелкой, а магнитное поле создано постоянными магнитами?

44152. Между полюсами подковообразного магнита вращается алюминиевый диск в направлении, указанном стрелкой. Каково направление индукционного тока: к центру или от центра диска?

44153. Прямолинейный проводник длиной 1,2 м с помощью гибких проводников присоединен к источнику тока с ЭДС 24 В и сопротивлением 0,5 Ом. Этот проводник помещают в однородном магнитном поле с индукцией 0,8 Тл, которое направлено на читателя. Сопротивление всей внешней цепи равно 2,5 Ом. Определить силу тока в проводнике в тот момент, когда он движется перпендикулярно к силовым линиям со скоростью 12,5 м/с. Во сколько раз изменится сила тока, когда проводник остановится?

44154. (-3) Вб. Число витков в катушке 120. Как изменится энергия поля, если сила тока изменится вдвое?

44157. Магнитное поле катушки с индуктивностью 95 мГн обладает энергией 0,19 Дж. Чему равна сила тока в катушке?

44158. Какой заряд пройдет через поперечное сечение витка, сопротивление которого 0,03 Ом, при уменьшении магнитного потока внутри витка на 12 мВб?

44159. Какова скорость изменения силы тока в обмотке реле с индуктивностью 3,5 Гн, если в ней возбуждается ЭДС самоиндукции 105 В?

44160. Катушку с ничтожно малым сопротивлением и индуктивностью 3 Гн присоединяют к источнику тока с ЭДС 15 В и ничтожно малым внутренним сопротивлением. Через какой промежуток времени сила тока в катушке достигнет 50 А?

44161. В каком направлении пойдет ток через амперметр в момент размыкания цепи ключом К?

44162. Колебательный контур состоит из катушки индуктивности L = 0,2 Гн и конденсатора емкостью С = 20 мкФ. Конденсатор зарядим до напряжения 4 В в начальный момент времени. Какими будут ток, напряжение и заряд в моменты времени, когда отношения энергии электрического и магнитного поля равны 0?

44163. Заряд на пластинах конденсатора колебательного контура изменяется с течением времени t в соответствии с уравнением q = 50 cos 100 nt. Найти период и частоту колебаний в контуре, циклическую частоту, амплитуду колебаний заряда и амплитуду колебаний силы тока. Записать уравнение i = i(t), выражающее зависимость силы тока от времени.

44164. Емкость конденсатора колебательного контура 0,4 мкФ, частота собственных колебаний 5 кГц; амплитуда заряда 8 мк Кл. Написать уравнение q = q(t), и = u(t), i = i(t). Найти амплитуду напряжения, амплитуду силы тока и индуктивность катушки.

44165. В колебательном контуре емкость конденсатора 3 мкФ, а максимальное напряжение на нем 4 В.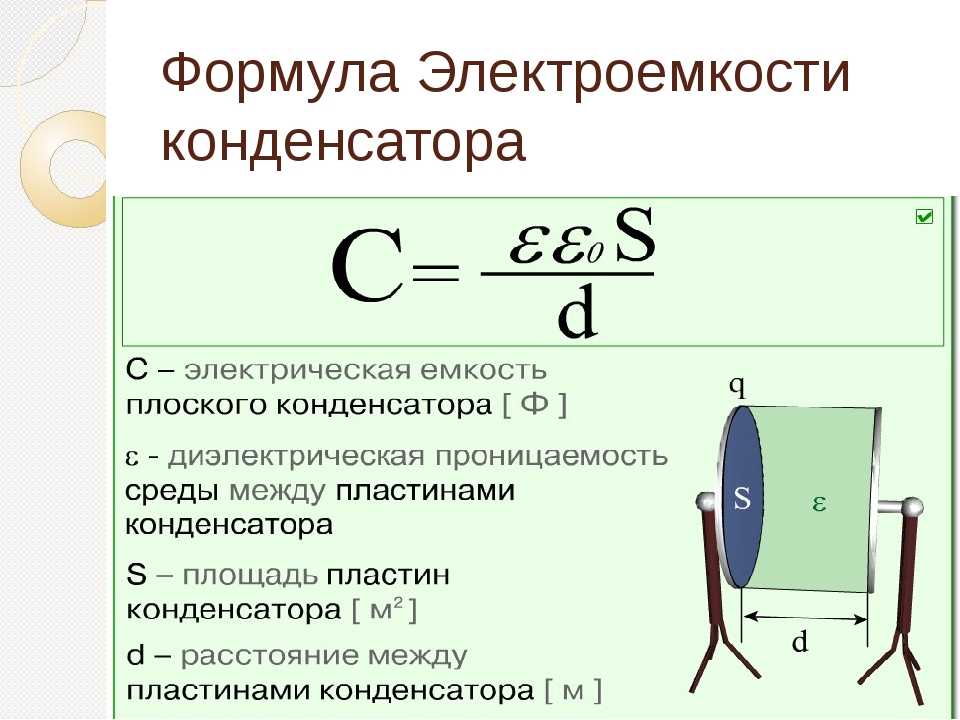 Найдите максимальную энергию магнитного поля катушки. Активное сопротивление принять равным нулю.

44166. Колебательный контур состоит из конденсатора емкостью 10 мкФ и катушки индуктивностью 100 мГн. Найти амплитуду колебаний напряжения, если амплитуда колебаний силы тока 0,1 А.

44167. В колебательном контуре индуктивность катушки равна 0,1 Гн, а амплитуда колебаний силы тока 20 мА. Найти энергию электрического поля конденсатора и магнитного поля катушки в тот момент, когда мгновенное значение силы тока в 2 раза меньше амплитудного значения.

44168. Индуктивность и емкость колебательного контура соответственно равны 70 Гн и 70 мкФ. Определите период колебаний в контуре. Можно ли эти колебания назвать высокочастотными?

44169. Индуктивность катушки колебательного контура 0,5 мГн. Требуется настроить этот контур на частоту 1 МГц. Какова должна быть емкость конденсатора в этом контуре?

44170. 2. Ось вращения рамки лежит в ее плоскости и перпендикулярна вектору индукции поля. Найти максимальный магнитный поток сквозь плоскость рамки и ЭДС индукции, возникающей в рамке при ее вращении. Написать уравнение е = e(t).

44175. Напряжение на концах участка цепи, по которому течет переменный ток, изменяется с течением времени по закону u = Um*sin (wt+n/6)|. В момент времени t = T/12 мгновенное напряжение равно 10 В. Определить амплитуду напряжения.

44176. Электродвижущая сила в цепи переменного тока выражается формулой е = 120*sin 628t, где t выражено в секундах, а ЭДС в вольтах. Определить действующее значение ЭДС и период ее изменения.

44177. Значение силы тока, измеренное в амперах, задано уравнением i = 8,5*sin (314t + 0,651). Определить действующее значение тока, его начальную фазу и частоту. Найти ток в цепи при t1 = 0,08 с.

44178. Амплитуда ЭДС переменного тока с частотой 50 Гц равна 100 В. Каковы значения ЭДС через 0,0025 с и 0,005, считая от начала периода?

44179. Мгновенное значение силы переменного тока частотой 50 Гц равно 2 А для фазы n/4 рад. Какова амплитуда силы тока, если при t = 0 i = 0?

44180. По графику, изображенному на рисунке, определим амплитуду напряжения, период и значение напряжения для фазы n/3 рад.

44181. По графику, изобра- женному на рисунке, определите амплитуду ЭДС, период и частоту тока. Напишите уравнение ЭДС.

44182. В цепь переменного тока с действующим значением напряжения 220 В включено активное сопротивление 50 Ом. Найдите действующее и амплитудное значение силы тока.

44183. Каково индуктивное сопротивление проводника с индуктивностью 0,05 Гн в цепи переменного тока частотой 50 Гц?

44184. Определите период переменного тока, для которого конденсатор емкостью 2 мкФ представляет сопротивление 8 Ом. 3 пФ соеди нен с катушкой индуктивности 32 мк Гн сопротивлени ем 2 Ом. Определите резонансную частоту контура.

44189. Конденсатор и катушка соединены последовательно. Индуктивность катушки 0,01 Гн. При какой емкости конденсатора ток частотой 1 кГц будет максимальным?

44190. Конденсатор и катушка соединены последовательно. Емкостное сопротивление 5000 Ом. Какой должна быть индуктивность катушки, чтобы резонанс напряжений наступил при частоте тока 20 кГц?

44191. В одном ящике находится реостат, в другом — конденсатор, в третьем — катушка индуктивности. Выводы подключены к наружным зажимам. Как, не открывая ящиков, узнать, что находится в каждом из них? (Даются источники постоянного и переменного напряжения одинаковой величины и лампочка, рассчитанная на это напряжение.)

44192. Трансформатор повышает напряжение с 220 В до 660 В и содержит в первичной обмотке 850 витков. Определите коэффициент трансформации и число витков во вторичной обмотке. В какой обмотке сила тока больше?

44193. Напряжение на зажимах вторичной обмотки понижающего трансформатора 60 В, сила тока во вторичной цепи 40 А. Первичная обмотка включена в цепь с напряжением 240 В. Найдите силу тока в первичной обмотке трансформатора.

44194. Трансформатор имеет коэффициент трансформации 20. Напряжение на первичной обмотке 120 В. Определите напряжение на вторичной обмотке и число витков в ней, если первичная обмотка имеет 200 витков.

44195. Сила тока в первичной обмотке трансформатора 0,5 А, напряжение на ее концах 220 В. Сила тока во вторичной обмотке 11 А, напряжение на ее концах 9,5 В. Определить КПД трансформатора.

44196. Мощность, потребляемая трансформатором, 90 Вт. Какой ток получили во вторичной обмотке при напряжении 12 В, если КПД трансформатора 75%?

44197. (-6) с.

44203. Емкость переменного конденсатора контура приемника изменяется в пределах от С1 до С2 = 9С1. Определить диапазон волн контура приемника, если емкости С1 конденсатора соответствует длина волны, равная 3 м.

44204. Диапазон каких радиоволн может принимать радиоприемник, если емкость конденсатора его колебательного контура изменяется от 30 до 300 пФ, а индуктивность катушки — от 40 до 100 мкГн?

44205. Электроемкость конденсатора переменной емкости в контуре радиоприемника может изменяться от 50 до 450 пФ. Индуктивность катушки остается при этом неизменной и равной 0,6 мГн. На каких длинах волн работает радиоприемник?

44206. Определите электроемкость конденсатора, включенного в колебательный контур, индуктивность которого 1,5 мГн, если он излучает электромагнитные волны длиной 500 м.

44207. На каком расстоянии от радиолокатора находится самолет, если отраженный от него сигнал принят через 0,2 мс после момента посылки этого сигнала?

44208. 5 nt. Найти длину излучаемой волны.

44209. В некоторой системе отсчета покоится заряд. Какое поле существует вокруг этого заряда с точки зрения неподвижного наблюдателя относительно заряда? С точки зрения движущегося наблюдателя?

44210. Магнит покоится на земле. Какое поле существует вокруг него?

44211. Почему в радиолокации применяют сверхвысокочастотные колебания (СВЧ)?

44212. Почему для радиосвязи применяют элект-рические колебания высоких частот?

44213. Почему радиоприемник в автомашине плохо работает, когда она проезжает под мостом или в тоннеле?

44214. Почему радиолокационная установка должна посылать радиосигналы в виде коротких импульсов, следующих друг за другом не непрерывно?

44215. Почему дальность действия передающей телевизионной станции ограничена линией горизонта? Почему башни телецентров строят очень высокими?

44216. Иногда изображение на экране телевизора двоится. Что заставляет электронный луч писать второе изображение?

44217. Предмет находится от плоского зеркала на расстоянии 20 см. На каком расстоянии от предмета окажется его изображение, если предмет отодвинуть на 10 см от зеркала?

44218. Плоское зеркало АВ может вращаться вокруг горизонтальной оси О. Луч света падает на зеркало под углом 10°. На какой угол повернется отраженный луч, если зеркало повернется на угол 16°?

44219. Луч света, направленный горизонтально, падает на вертикально стоящий экран. Если по пути луча положить плоское зеркало, то световое пятно на экране смещается вверх на 3,5 см. Определить угол падения луча на зеркало, если расстояние от зеркала до экрана 50 см.

44220. На стеклянную пластинку, показатель преломления которой 1,5, падает луч света. Найти угол падения луча, если угол между отраженным и преломленным лучами 90°.

44221. Абсолютные показатели преломления алмаза и стекла соответственно равны 2,42 и 1,5. Каково отношение толщин этих веществ, если время распространения света в них одинаково?

44222. Определите предельный угол падения луча на границу раздела стекла и воды.

44223. Лучи света выходят из скипидара в воздух. Предельный угол для этих лучей 42°53′. Определить скорость распространения света в скипидаре.

44224. На дне ручья лежит камешек. Мальчик хочет толкнуть его палкой. Прицеливаясь, мальчик держит палку под углом 45°. На каком расстоянии от камешка воткнется палка в дно ручья, если его глубина 50 см?

44225. Начертите ход лучей, которые падают на границу вода-воздух под углом 30° и 60°.

44226. Длина волны фиолетовых лучей света в воздухе 400 нм. Какова длина волны этих лучей в воде?

44227. Определить скорость света в воде красных лучей.

44228. На каком расстоянии от дифракционной решетки нужно поставить экран, чтобы расстояние между нулевым максимумом и спектром четвертого порядка было равно 50 мм для света с длиной волны 500 км? Период решетки 0,02 мм.

44229. Найти наибольший порядок спектра красной линии лития с длиной волны 671 нм, если период дифракционной решетки 0,01 мм.

44230. При помощи дифракционной решетки с периодом 0,02 мм получено первое дифракционное изображение на расстоянии 3,6 см от центрального и на расстоянии 1,8 м от решетки. Найти длину световой волны.

44231. При осуществлении интерференции света были получены световые пучки, в состав которых, наряду с когерентным светом, входил и некогерентный. Что при этом наблюдалось?

44232. Вода освещена красным светом. Какой свет видит человек, открывший глаза под водой?

44233. На расположенной вертикально проволочной рамке получим мыльную пленку. В каком месте пленки, в какой последовательности и почему появляются первые радужные полосы? Почему с течением времени интерференционные полосы перемещаются вниз, при этом верхняя часть пленки окрашивается в черный цвет и вслед за этим пленка рвется?

44234. Почему для запрещающих сигналов на транспорте принят красный цвет?

44235. Лента, имеющая при дневном свете свет-ло-синий цвет, кажется при свете свечи зеленой. По-чему?

44236. Какую скорость должно иметь тело, чтобы его продольные размеры уменьшались для наблюдателя в 3 раза? До этого тело покоилось относительно данного наблюдателя.

44237. Ракета движется относительно неподвижного наблюдателя со скоростью равной 0,6 скорости света в вакууме. Какое время пройдет по часам неподвижного наблюдателя, если по часам, движущимся вместе с ракетой, прошло 6 лет?

44238. Какой промежуток времени пройдет на звездолете, движущемся относительно Земли со скоростью, равной 0,4 скорости света, за 25 земных лет?

44239. При какой скорости масса движущегося электрона вчетверо больше массы покоящегося?

44240. Электрон движется со скоростью 0,8 скорости света. Определить: массу электрона, энергию покоя электрона (в джоулях и электрон-вольтах), полную энергию электрона, кинетическую энергию электрона.

44241. Дзе ракеты движутся навстречу друг другу со скоростями 3/4с относительно неподвижного наблюдателя. Определить скорость сближения ракет.

44242. Определите энергию, массу и импульс фотона видимого света с длиной волны L = 500 нм

44243. 6 м/с и ускоренного разностью потенциалов 4 В. Найти длину волны фотона.

44248. Определить наибольшую длину волны света, при которой может происходить фотоэффект для платины.

Электроемкость конденсатора: сущность и основные характеристики

Главная > Электродвигатели > Электроемкость конденсатора: сущность и основные характеристики

Электроемкость тела, как и его потен-циал, трудно определить однозначно. Для этого необходимо создать условия, при ко-торых полностью исключалось бы влияние окружающих тел. В реальных условиях ок-ружающие тела влияют на исследуемое те-ло, изменяя его потенциал и емкость.

Укрепим на стержне заземленного элект-рометра металлический шар и сообщим ему определенный заряд. Стрелка электрометра отклонится от положения равновесия и по-кажет значение потенциала шара относи-тельно земли. Поднесем к шару металли-ческую пластину, соединенную проволокой с землей (рис. 4.63). Показания электрометра уменьшатся. Поскольку заряд шара не из-менился, то уменьшение потенциала свиде-тельствует об увеличении электроемкости шара. Изменения потенциала и соответственно емкости будут наблюдаться в случае изменения расстояния между шаром и пла-стиной.

Таким образом, определяя емкость отдель-ного тела, необходимо учитывать размеще-ние всех окружающих тел.

Поскольку практически этого сделать не-возможно, то используют устройство, кото-рое называется конденсатором . Простейшей для изучения и расчетов является система из двух проводящих пластин, разделенных диэлектриком.

Конденсатор — это система из двух про-водников, разделенных диэлектриком.

Размеры этих пластин (длина и ширина) намного больше расстояния между ними. Электрические свойства такой системы про-водников не зависят от размещения окружа-ющих тел. Если пластинам сообщить разно-именные заряды, то они разместятся на внутренних поверхностях пластин вследст-вие взаимного притяжения.

Соответственно и поле заряженных пла-стин будет сосредоточено в пространстве между пластинами. Это можно объяснить на основе принципа суперпозиции полей .

На рис. 4.64 показана структура элект-рического поля пластины, заряженной поло-жительным зарядом. Силовые линии парал-лельные и направлены в противоположные от пластины направления.

На рис. 4.65 — подобная структура элект-рического поля отрицательно заряженной пластины. Силовые линии параллельные, а направление — противоположное предшест-вующему (рис. 4.64).

Если пластины разместить на расстоянии d, намного меньшем, чем линейные разме-ры пластин, то в пространстве между ними силовые линии обеих пластин будут иметь одинаковое направление (рис. 4.66), а потому напряженность электрического поля бу-дет равна сумме напряженностей обоих полей:

E’ = Е 1 + E 2 .

Вне пластин линии напряженности име-ют противоположное направление, а потому

E’ = E 1 — E 2 .

Поскольку E 1 = E 2 , то E’ = 0 (рис. 4.67). Материал с сайта

Конденсатор может накапливать значи-тельный заряд даже при небольшой раз-ности потенциалов между пластинами. В случае отдельного тела большой заряд со-здает большой потенциал, который приво-дит к автоэлектронной эмиссии или «стеканию зарядов».

Емкость конденсатора в отличие от ем-кости отдельного тела определяется разно-стью потенциалов между обкладками.

C = Q / (φ 1 — φ 2) = Q / Δφ .

где Q — заряд одной из пластин; (φ 1 — φ 2) — разность потенциалов между пластинами.

Для измерения емкости конденсатора ис-пользуется 1 фарад:

1Ф = 1 Кл/ 1 В.

На этой странице материал по темам:

• Кратко о конденсаторе (физика)

• Конденсатор физическое явление

• Почему емкость конденсатора не зависит от влияния окружающих тел

• Почему емкость конденсатора не зависит от окружающих тел

• Сообщение по физике применение конденсатора

Вопросы по этому материалу:

Электроемкость – количественная мера способности проводника удерживать заряд.

Простейшие способы разделение разноименных электрических зарядов – электризация и электростатическая индукция – позволяют получить на поверхности тел не большое количество свободных электрических зарядов. Для накопления значительных количеств разноименных электрических зарядов применяются конденсаторы .

Конденсатор – это система из двух проводников (обкладок), разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Так, например, две плоские металлические пластины, расположенные параллельно и разделенные слоем диэлектрика, образуют плоский конденсатор.

Если пластинам плоского конденсатора сообщить равные по модулю заряды противоположного знака, то напряженность электрического поля между пластинами будет в два раза больше, чем напряженность поля у одной пластины. Вне пластин напряженность электрического поля равна нулю, т. к. равные заряды разного знака на двух пластинах создают вне пластин электрические поля, напряженности которых равны по модулю, но противоположны по направлению.

Электроемкостью конденсатора называется физическая величина, определяемая отношением заряда одной из пластин к напряжению между обкладками конденсатора:

При неизменном положении пластин электроемкость конденсатора является постоянной величиной при любом заряде на пластинах.

За единицу электроемкости в системе СИ принимают Фарад. 1 Ф – электроемкость такого конденсатора, напряжение между обкладками которого равно 1 В при сообщении обкладкам разноименных зарядов по 1 Кл.

Электроемкость плоского конденсатора можно вычислить по формуле:

S – площадь обкладок конденсатора

d – расстояние между обкладками

– диэлектрическая проницаемость диэлектрика

Электроемкость шара можно вычислить по формуле:

Энергия заряженного конденсатора.

Если внутри конденсатора напряженность поля E, тогда напряженность поля, созданного зарядом одной из пластин E/2. В однородном поле одной пластины находится заряд, распределенный по поверхности другой пластины. Согласно формуле для потенциальной энергии заряда в однородном поле энергия конденсатора равна:

Используя формулу электроемкости конденсатора :

Конденсаторы.

Если изолированному проводнику сообщить заряд Dq, то его потенциал увеличиться на Dj, причем отношение Dq/Dj остается постоянным: Dq/Dj=С, где С – электрическая емкость проводника , т.е. величина, численно равная заряду, который надо сообщить проводнику, чтобы повысить его потенциал на единицу (на 1В). Электрическая емкость проводников зависит от их размеров, формы, диэлектрических свойств среды в которую они помещены, и расположения окружающих тел, но не зависит от материала проводника. В СИ за единицу электрической емкости 1 фарад (Ф): [C]=1A=1кл/1В=1А 2 *с 4 /кг*м 2 . Емкость равная 1Ф, очень велика, поэтому на практике чаще пользуются единицами микрофарад (1мкФ=10 -6 Ф) или пикофарад (1мкФ=10 -12 Ф). Конденсатор представляет собой систему двух проводников (обкладок) не соединенных друг с другом. Часто между обкладками помещают диэлектрик. При сообщении этим проводникам одинаковым по величине и разноименных зарядов, поле, создаваемое этими проводниками, практически полностью локализовано в пространстве между ними. Конденсаторы являются накопителями электрических зарядов. Отношение заряда на обкладке конденсатора к разности потенциалов между ними – постоянная величина: q/(j 1 -j 2)=C.

Плоский конденсатор состоит из двух пластин площадью S, расположенных на небольшом расстоянии d друг от друга, заряды на пластинах +q и –q. В общем случае, если пространство между пластинами заполнено диэлектриком с диэлектрической проницаемостью e, то напряженность электростатического поля между пластинами равна сумме напряженности полей создаваемых каждой из пластин.

Е=s/e 0 e. Емкость плоского конденсатора равна С=e 0 eS/d.

Параллельное и последовательное соединение конденсаторов . На практике конденсаторы часто соединяют различными способами. Найти эквивалентную емкость – это значит найти конденсатор такой емкости, который при тот же разности потенциалов будет накапливать тот же заряд q, что и батарея конденсаторов. При последовательном соединении N конденсаторов заряд на обкладках одинаков, напряжение на всей батарее конденсаторов равно сумме напряжений на каждом конденсаторе в отдельности: U общ =U 1 +U 2 +U 3 +…+U N , а общая емкость N конденсаторов 1/С общ =1/С 1 +1/С 2 +1/С 3 +…+1/С N . При параллельном соединении конденсаторов напряжение U на всех конденсаторах одинаково и общая емкость С общ батареи равна сумме емкостей отдельных конденсаторов, С общ =С 1 +С 2 +С 3 +…+С N .

Большой электроемкостью обладают системы из двух проводников, называемые конденсаторами. Конденсатор представляет собой два проводника, разделенные слоем диэлектрика, толщина которого мала по сравнению с размерами проводников. Проводники в этом случае называют обкладками конденсатора.

Простейший плоский конденсатор состоит из двух одинаковых параллельных пластин, находящихся на малом расстоянии друг от друга (рис. 134). Если заряды пластин одинаковы по модулю и противоположны по знаку, то силовые линии электрического поля начинаются на положительно заряженной обкладке конденсатора и оканчиваются на отрицательно заряженной. Поэтому почти все электрическое поле сосредоточено внутри конденсатора.

У сферического конденсатора, состоящего из двух концентрических сфер, все поле сосредоточено между ними.

Для зарядки конденсатора нужно присоединить его обкладки к полюсам источника напряжения, например к полюсам батареи аккумуляторов Можно также соединить одну обкладку с полюсом батареи, другой полюс которой заземлен, а вторую заземлить. Тогда на заземленной обкладке останется заряд, противоположный по знаку и равный по модулю заряду другой обкладки. Такой же по модулю заряд уйдет в землю.

Под зарядом конденсатора понимают — абсолютное значение заряда одной из обкладок.

Электроемкость конденсатора определяется формулой (8.29).

Электрические поля окружающих тел почти не проникают внутрь конденсатора и не влияют на разность потенциалов между его обкладками. Поэтому электроемкость конденсатора практически не зависит от наличия вблизи него каких-либо тел.

Первый конденсатор, названный лейденской банкой, был создан в середине XVIII в. Было обнаружено, что гвоздь, вставленный в стеклянную банку с ртутью, накапливает большой электрический заряд. В таком конденсаторе ртуть служила одной обкладкой, а ладони экспериментатора, державшего банку, — другой. Впоследствии обе обкладки стали делать из тонкой латуни или станиоля.

Электроемкость плоского конденсатора. Вычислим емкость плоского конденсатора. Обозначим площадь каждой его пластины а расстояние между пластинами Для вычисления емкости по формуле (8.29) надо выразить разность потенциалов через заряд Эта разность потенциалов определяется напряженностью Е поля, которая зависит от зарядов обкладок конденсатора.

Напряженность поля, созданного одной из пластин, вычисляется по формуле (8.16) Напряженности поля положительно и отрицательно заряженных пластин равны по модулю и направлены внутри конденсатора в одну и ту же сторону. Поэтому модуль Е результирующей напряженности равен сумме модулей напряженностей поля двух пластин:

Формула для емкости запишется более компактно, если вместо коэффициента использовать его выражение в виде (8. 6): Тогда, учитывая, что поверхностная плотность заряда

Получим:

Следовательно,

Подставляя это выражение в (8.29) и сокращая на получим формулу для электроемкости плоского конденсатора:

Мы видим, что электроемкость конденсатора зависит от геометрических факторов: площади пластин и расстояния между ними, а также от электрических свойств среды. Она не зависит от материала проводников: обкладки конденсатора могут быть железными, медными, алюминиевыми и т. д.

Проверим на опыте формулу (8.30), полученную теоретически. Для этого возьмем конденсатор, расстояние между пластинами которого можно изменять, и электрометр с заземленным корпусом (рис. 135). Соединим корпус и стержень электрометра с пластинами конденсатора проводниками и зарядим конденсатор. Для этого нужно коснуться наэлектризованной палочкой пластины конденсатора, соединенной со стержнем. Электрометр покажет разность потенциалов между пластинами.

Раздвинув пластины, мы обнаружим увеличение разности потенциалов. Согласно определению электроемкости (8.29) это указывает на ее уменьшение. В соответствии с формулой (8.30) электроемкость действительно должна уменьшаться с увеличением расстояния между пластинами.

Вставив между обкладками конденсатора пластину из диэлектрика, например из органического стекла, мы обнаружим уменьшение разности потенциалов. Следовательно, электроемкость конденсатора увеличивается.

Расстояние между пластинами может быть очень малым, а площадь и диэлектрическая проницаемость — достаточно большими Поэтому при небольших размерах конденсатор может иметь большую электроемкость. Впрочем, плоский конденсатор электроемкостью в 1 Ф должен был бы иметь площадь пластин при расстоянии между пластинами мм.

Измерение диэлектрической проницаемости. Зависимость

емкости конденсатора от электрических свойств веще стна между его обкладками используется для измерения диэлектрической проницаемости вещества. Для этого нужно экспериментально определить отношение емкостей конденсатора с диэлектрической пластиной между обкладками и без нее . Как следует из формулы (8.30), диэлектрическая проницаемость

Различные типы конденсаторов. В зависимости от назначения конденсаторы имеют различное устройство. Обычный технический бумажный конденсатор состоит из двух полосок алюминиевой фольги, изолированных друг от друга и от металлического корпуса бумажными лентами, пропитанными парафином. Полоски и ленты туго свернуты в пакет небольшого размера.

В радиотехнике широко применяют конденсаторы переменной электроемкости (рис. 136) Такой конденсатор состоит из двух систем металлических пластин, которые при вращении рукоятки могут входить одна в другую. При этом меняется площадь перекрывающейся части пластин и, следовательно, их электроемкость. Диэлектриком в таких конденсаторах служит воздух.

Значительного увеличения электроемкости за счет уменьшения расстояния между обкладками достигают в так называемых электролитических конденсаторах (рис. 137) Диэлектриком в них служит очень тонкая пленка оксидов, покрывающих одну из обкладок (полосу фольги).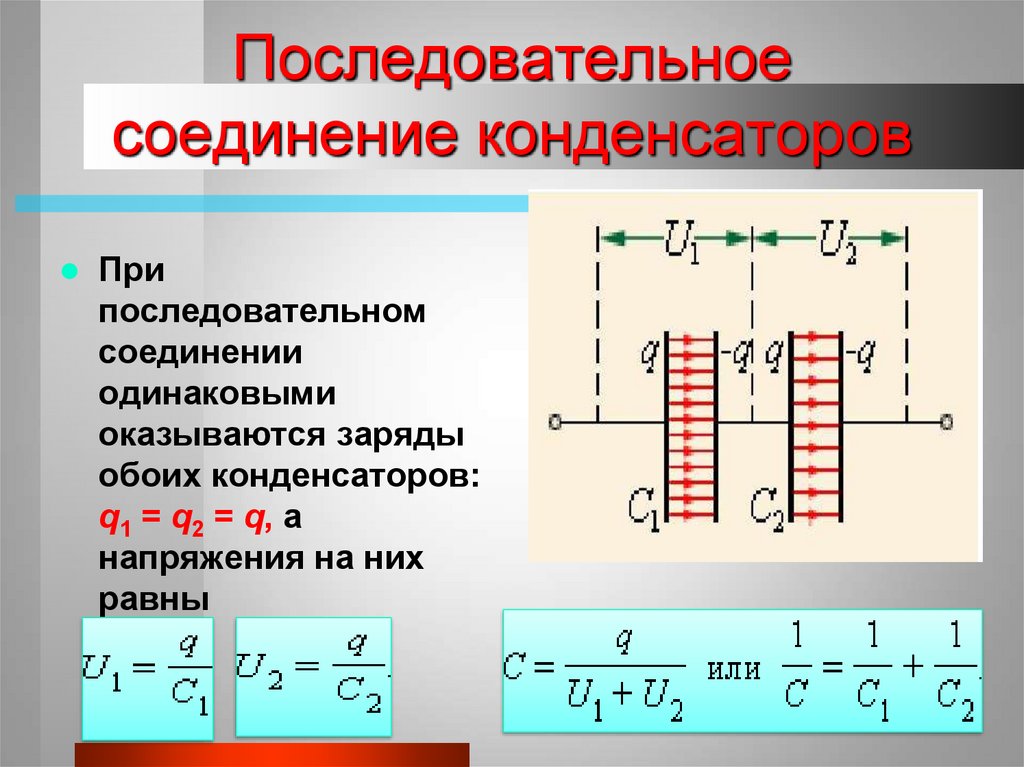 Второй обкладкой служит бумага, пропитанная раствором специального вещества (электролита).

Электроемкость конденсатора – физическая величина, характеризующая процесс заряда проводников, разделенных слоем диэлектрика. Используется многочисленными математическими расчетами, маркируется на корпусе изделия.

Формулы

Электроемкость конденсатора принято выражать через запасаемый заряд q при приложенном напряжении U следующим образом:

Что касается происхождения формулы, одна загадка. Известно только: из теоремы Гаусса по напряженности электрического поля найдем электроемкость конденсатора. Кто провел расчет, нигде не говорится. Физическая величина фарад изначально в системе СГС отсутствовала, в 1861 году ввела специальная комиссия, сформированная физиками.

По некоторым сведениям, впервые электроемкость конденсатора определил введший термины в обиход. Подразумеваем Алессандро Вольту. Поздние 70-е (XVIII века), ученый много уделил исследованиям вопроса, установил: электроемкость можно выразить через накапливаемый заряд, приложенное к электродам напряжение.

Помимо этого можно часто встретить формулу электроемкости плоского конденсатора:

Авторы избегают судить, кто занимался расчетами выражения. Рассуждая логически, то едва кого интересовала электроемкость плоского конденсатора до появления на свет изобретения Полака. Лейденские банки по-другому распределяют заряд. Рассуждения приводят к началу XX века. Быть может, вопросом занимались Тесла, Герц. С меньшей вероятностью – Попов.

Фамилии названы по критериям заинтересованности переменным током. Тесла изучал вопросы безопасности электричества, передачи на расстояние, конструировал двигатели. Герц и Попов исследовали антенны, заведомо настраиваются на некую длину волны, которую проще получить, применяя колебательный контур. Следовательно, ученые обязаны иметь представление об электроемкости конденсатора, катушках индуктивности.

Джеймс Максвелл, лорд Кельвин, Вильгельм Вебер много внимания уделяли совершенствованию единых систем измерения физических величин Существует некоторая вероятность, кто-то мог приложить руку к исследованию конденсаторов.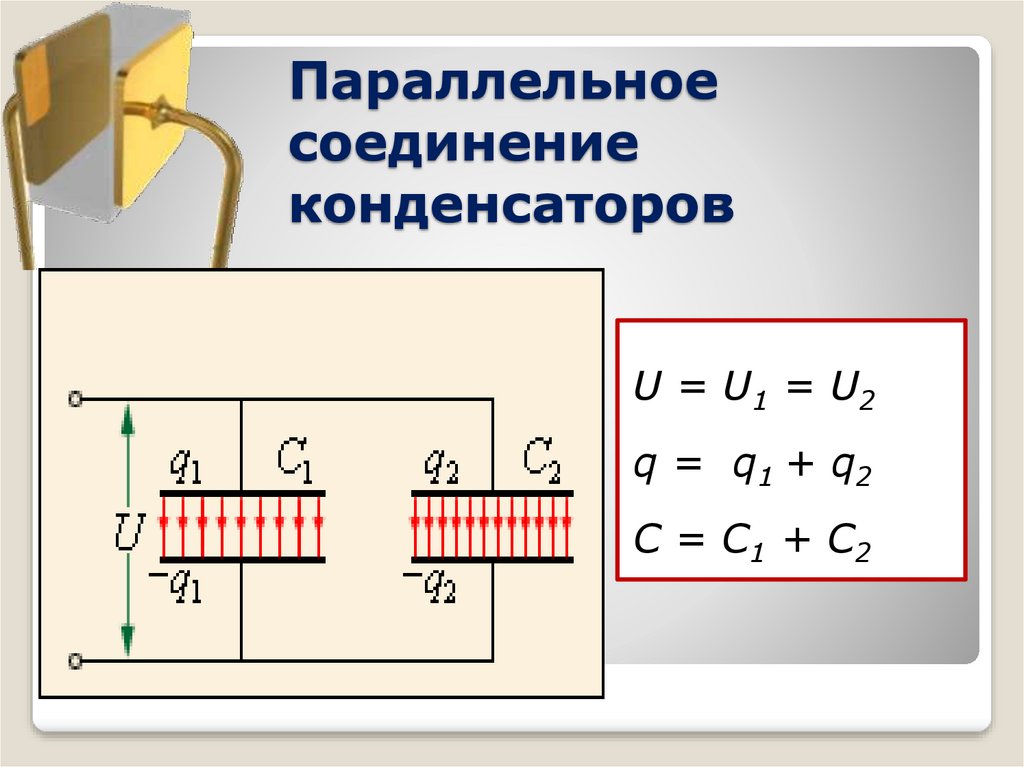 Ясно одно – в мировой истории естественных наук много белых пятен, когда дело касается русскоязычных источников. Портал ВашТехник одним из первых будет публиковать новейшие исследования в области правильного понимания произошедших событий.

История

Нетерпеливым читателям сразу же докладываем: Алессандро Вольта ввел собственно термин емкости. Неизвестно точно, употреблял ли кто раньше, но в своей работе итальянский ученый, называя, электрофорус конденсатором, одновременно применяет к нему термин емкости. Как сосуду, куда можно «налить» заряд из емкости. Конденсатором зовет за схожесть процесса с осаждением паров: понемногу наберем произвольное количество электричества. И по большому счету это верно.

Термин конденсатор

Исторически первым конденсатором следует считать лейденскую банку. Поныне ходят споры, кто изобрел прибор, поскольку оба ученых, увлеченных событиями, избегали ведения аккуратных записей, бесспорно одно – электроемкость прибора измерить было нельзя, отсутствовало соответствующее понятие «электроемкость конденсатора».

Скрин печатного варианта трактата Вольты, 1782 год

Придумавший термин бессилен произнести слово раньше, нежели Алессандро Вольта в 1782 году, докладывая Королевскому Научному обществу изыскания в области электростатики. Чтобы понять, откуда берется электричество. Известно, в течение следующих пяти лет Луиджи Гальвани откроет «животное электричество», приведшее Вольту прямиком к созданию первого элемента питания. Докладывая обществу, молодой ученый лишен упомянутых знаний, светило пытается понять, откуда появляется заряд. Рассуждает примерно так: «К настоящему времени много свидетельств существования атмосферного электричества. Люди бессильны найти следы присутствия. Может означать: имеющиеся электроскопы слишком слабы, неспособны уловить столь тонкую материю. Следовательно, нужно найти способ забрать из воздуха флюиды».

Осуществляя практически сказанное, Алессандро Вольта предлагает приспособление, называемое электрофорусом (не путать с ). Прибор захватывает флюиды атмосферного проводника (воздуха). Принцип служения Вольте напоминает процесс конденсации: собирает электричество.

Электрофорус

Запад электрофорус называет генератором емкостного типа. Указанное выше позволяет полагать: подобное определение прилепилось благодаря написанному Английскому Королевскому обществу Вольтой. Устройство придумано другим человеком – шведским физиком Джоном Кларком Вилке. Случилось двумя десятилетиями ранее – 1762 год.

Ныне считается, популярность прибору придал Вольта, называя любимца вечным генератором электричества. Тоже по сути правильно, тереть резину можно тысячелетиями. Больше «конденсатор» напоминает (см. рис.) здоровенную печать. Сверху, помимо основной центральной ручки, стоит боковая – снятия отрицательного потенциала. Видим три слоя:

1. Подложка необязательна, на нее наклеивается резина.
2. Тонкий слой резины служит телом электризации трением.
3. Сверху – тонкий лист металла, снабженный двумя рукоятками, одна (центральная) изолирована.

Внешний вид электрофоруса

Начав работы, нужно убрать «печать», натереть резину шерстью. Затем гладкий диск ставится обратно. Площадь соприкосновения с резиной невелика из-за присутствующих шероховатостей, положительный заряд приобретается нескоро. Нужно выждать. Оператор на короткий миг заземляет крышку боковой ручкой, снимая отрицательный заряд, снизу остается положительный. Прикасаясь одной рукой к металлу, можно слышать хорошо различимый треск. Резина после поднятия крышки несет избыток электронов, позволяющий повторить опыт несколько раз (верится с трудом, некоторые источники говорят о сотне повторений).

Разнимая тела, резким движением потянув изолирующую рукоятку, оператор получает статическое электричество. Изобретение достаточно революционное, примечательно, появилось в считаные годы после отмены закона охоты на ведьм. По заявлению Вольты, круг резины должен быть по возможности тонким, порядка 50-й доли дюйма. Удается получить наилучший результат. Лист металла фактически также является пластиной. В противном случае долго нужно ждать наполнения объема проводника. В простонародье «конденсатор» называют резиновым пирогом. Пирогом, покрытым металлической начинкой.

Действительно ли электрофорус является неисчерпаемым источником энергии? В идеальных условиях, хотя верится с трудом. Отрицательный заряд резины поляризует металлическую пластину, создавая некий потенциал. Вытесненные на внешнюю поверхность электроны снимаются прикосновением заземлителя. Остается разнять составные части электрофоруса. Уничтожив положительный заряд прикосновением, услышав звук проскочившей искры, можно заново начинать опыт.

Электрофорус действительно напоминает конденсатор. После снятия лишнего отрицательного заряда превращается фактически в упомянутый прибор. Долго храниться конденсатор не может, поскольку электроны с резины понемногу будут стекать на металл. Устройство разрядится. Фактически резина, металл отделены друг от друга воздухом, служащим диэлектриком. Вместо резины используем различные полимеры, например, Тефлон.

Осталось заметить: во времена Вольты не знали методов избавления резины от статического заряда. «Обкладка» конденсатора могла долгое время хранить груз электронов. Вольта предлагает для разрядки поместить образец под солнечные лучи, либо поводить рядом горящей свечой. Через ионизированное пламя электроны покидают конденсатор. Сегодня понятно, достаточно вымыть резину, чтобы следов не осталось статического напряжения. Для работы нужно будет вновь высушить.

Лейденская банка

Считается, именно Феликс Савари обнаружил колебания резонансного контура. Разряжая лейденскую банку через витую нить меди, наблюдал беспорядочное снование стрелки компаса. 1826 год, когда Англия, Франция, Германия, частично Италия лихорадочно исследовали новое явление, привнесенное в научный мир Эрстедом.

Историю создания можно прочитать в соответствующем обзоре. Следует сказать, никто не пытался толком понять, какова электроемкость конденсатора. Не нужно по очевидным соображениям: лейденскую банку преимущественно использовали научные круги, решая специфические задачи. Опыт Феликса Савари надолго остался без внимания…

В 1842 году колебательным контуром, электроемкостью конденсатора занялся наш старый знакомый, сэр Джозеф Генри, изобретатель , любитель телеграфа.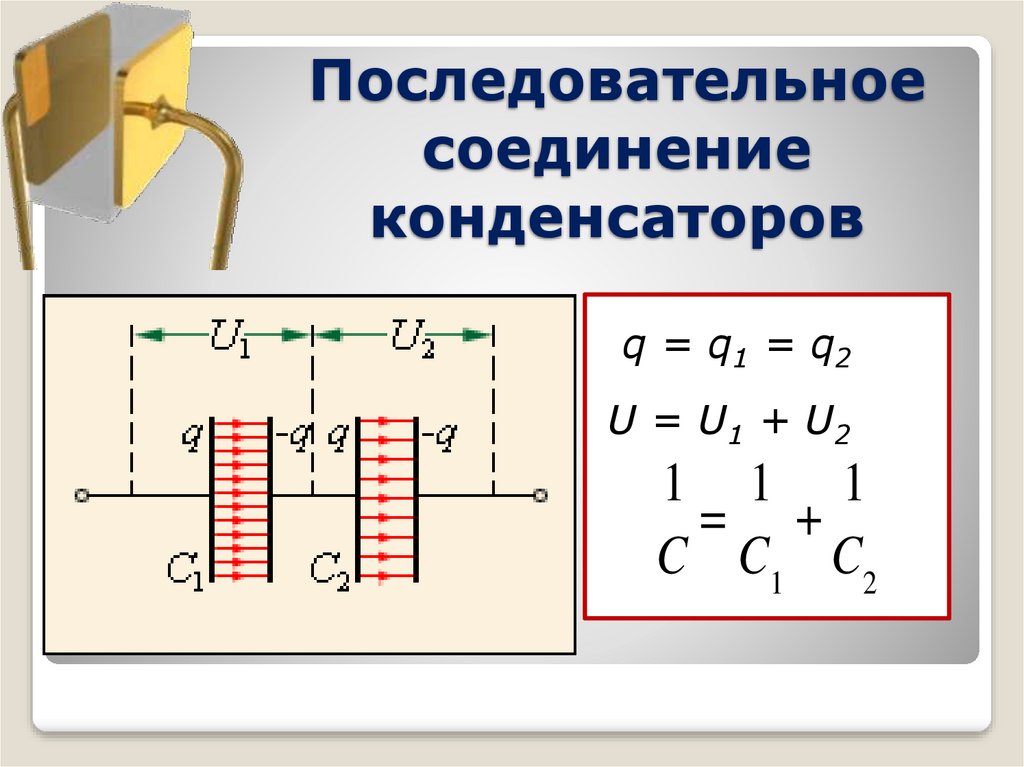 Изложил письменно после опробования заметок Савари практикой:

«Аномалия, остающаяся столь долго без объяснения, которая на первый взгляд представляется существующей наперекор нашей теории электричества и магнетизма, после тщательного изучения мною отнесена к доселе неизведанным явлениям. Разряд происходит странно (вразрез теории Франклина), ощущение, что, выходя из банки, флюид начинает странствовать взад-вперед. Увиденное принуждает признать: процесс начинается нормальным образом, затем происходит несколько смен направлений, каждый раз амплитуда становится меньше, пока движения затухнут вовсе. Судя по всему, феномен сегодня не может быть объяснен, физики встречались с ним (Савари), но оказались бессильны».

Очевидно, ученого совершенно не интересует электроемкость конденсатора – мысли поглощены аномалией, которую хотелось бы разведать. Пятью годами позже, ознакомившийся с отчетом Генри физик Гельмгольц на встрече Физического общества Берлина, говорит:

«Проводя электролиз, заметил необычные колебания. Такое ощущение, процесс колебаний продолжается, пока само vis viva не исчезнет навсегда, поглощенное суммарным сопротивлением цепи. Создается впечатление, по контуру текут два тока противоположных направлений, верх берет то один, то другой».

Конец спорам положил знаменитый Вильям Томсон, нареченный лорд Кельвин. Математически исследовав процесс, заявил: в цепи, очевидно существуют такие вещи, как электроемкость конденсатора и индуктивность свернутой медной проволоки. Работа On Transient Electric Currents стала классической. Хотя лорд Томсон зовет индуктивность электродинамической емкостью, смысл формулы однозначный. Ученый первым заявил: энергия передается меж конденсатором и катушкой индуктивности, постепенно затухая на активном сопротивлении цепи.

Формула, приведенная на рисунке, дана в современных величинах, обозначения стандартные. С – электроемкость конденсатора, L – индуктивность катушки, q – величина заряда, I – ток цепи. Прочие символы относятся к операциям дифференцирования.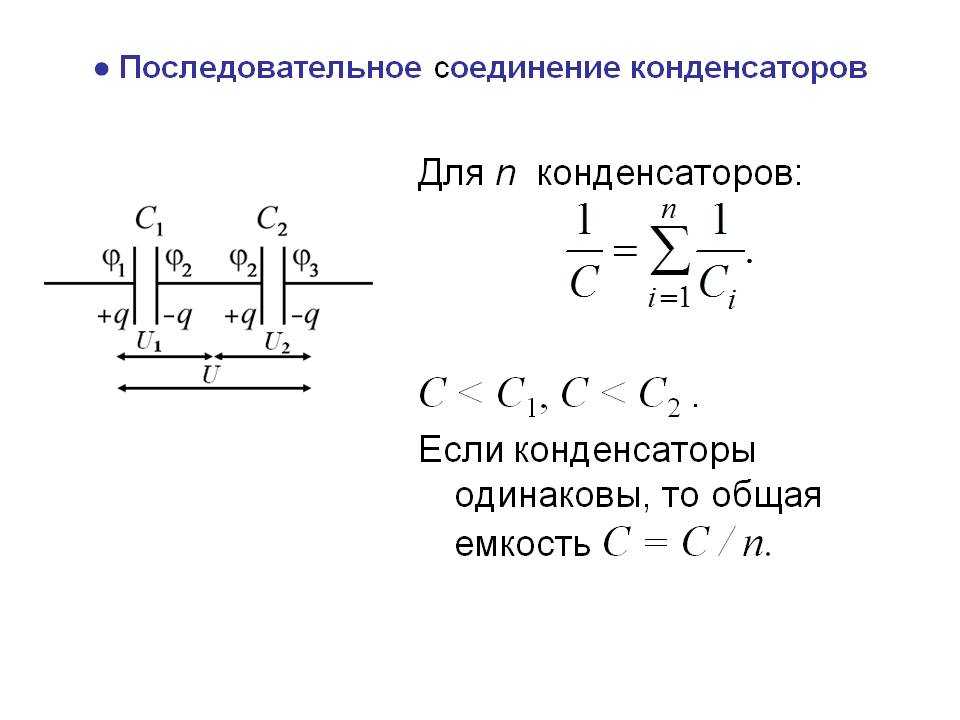 Термин индуктивность введен намного позже – в 1886 году Оливером Хэвисайдом. Формула резонансной частоты, зависящей от электроемкости конденсатора и индуктивности катушки, выведена Джеймсом Максвеллом в 1868 году.

Будем рассматривать уединенный проводник , т. е. проводник, значительно удаленный от других проводников, тел и зарядов. Его потенциал, как известно, прямо пропорционален заряду проводника. Из опыта известно, что разные проводники, будучи при этом одинаково заряженными, имеют различные потенциалы. Поэтому для уединенного проводника можно записать Величину (1) называют электроемкостью (или просто емкостью ) уединенного проводника. Емкость уединенного проводника задается зарядом, сообщение которого проводнику изменяет его потенциал на единицу. Емкость уединенного проводника зависит от его размеров и формы, но не зависит от материала, формы и размеров полостей внутри проводника, а также его агрегатного состояния. Причиной этому есть то, что избыточные заряды распределяются на внешней поверхности проводника. Емкость также не зависит ни от заряда проводника, ни от его потенциала. Единица электроемкости — фарад (Ф): 1 Ф — емкость такого уединенного проводника, у которого потенциал изменяется на 1 В при сообщении ему заряда 1 Кл. Согласно формуле потенциала точечного заряда, потенциал уединенного шара радиуса R, который находится в однородной среде с диэлектрической проницаемостью ε, равен Применяя формулу (1), получим, что емкость шара (2) Из этого следует, что емкостью 1 Ф обладал бы уединенный шар, находящийся в вакууме и имеющий радиус R=C/(4πε 0)≈9 10 6 км, что примерно в 1400 раз больше радиуса Земли (электроемкость Земли С≈0,7 мФ). Следовательно, фарад — довольно большая величина, поэтому на практике применяются дольные единицы — миллифарад (мФ), микрофарад (мкФ), нанофарад (нФ), пикофарад (пФ). Из формулы (2) следует также, что единица электрической постоянной ε 0 — фарад на метр (Ф/м) (см. (78.3)).

37. Конденсаторы. Электроемкость плоского конденсатора (вывод). Соединение конденсаторов.

Как нам известно из формулы емкости уединенного проводника, для того чтобы проводник имел большую емкость, он должен иметь довольно большие размеры. На практике необходимы устройства, обладающие способностью при малых размерах и небольших относительно окружающих тел потенциалах накапливать большие по величине заряды, иными словами, обладать большой емкостью. Эти устройства получили название конденсаторов . Если к заряженному проводнику перемещать другие тела, то на них возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды, при этом наиболее близкими к наводящему заряду Q будут заряды противоположного знака. Эти заряды, очевидно, ослабляют поле, которое создается зарядом Q, т. е. уменьшают потенциал проводника, что приводит, следуя из формулы зависимости емкости от потенциала С=Q/φ к повышению его электроемкости. Конденсатор состоит из двух проводников (обкладок), которые разделены диэлектриком. На емкость конденсатора не должны влиять окружающие тела, поэтому проводникам придают такую форму, чтобы поле, которое создавается накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют: 1) две плоские пластины; 2) две концентрические сферы; 3) два коаксиальных цилиндра. Поэтому в зависимости от формы обкладок конденсаторы делятся на плоские, сферические и цилиндрические . Так как поле сосредоточено внутри конденсатора, то линии напряженности начинаются на одной обкладке и кончаются на другой, поэтому свободные заряды, которые возникают на разных обкладках, равны по модулю и противоположны по знаку. Под емкостью конденсатора понимается физическая величина, равная отношению заряда Q, накопленного в конденсаторе, к разности потенциалов (φ 1 — φ 2) между его обкладками: (1) Найдем емкость плоского конденсатора, который состоит из двух параллельных металлических пластин площадью S каждая, расположенных на расстоянии d друг от друга и имеющих заряды +Q и –Q. Если считать, что расстояние между пластинами мало по сравнению с их линейными размерами, то краевыми эффектами на пластинах можно пренебречь и поле между обкладками считать однородным. Его можно найти используя формулу потенциала поля двух бесконечных параллельных разноименно заряженных плоскостей φ 1 -φ 2 =σd/ε 0 . Учитывая наличие диэлектрика между обкладками: (2) где ε — диэлектрическая проницаемость. Тогда из формулы (1), заменяя Q=σS, с учетом (2) найдем выражение для емкости плоского конденсатора: (3) Для определения емкости цилиндрического конденсатора, который состоит из двух полых коаксиальных цилиндров с радиусами r 1 и r 2 (r 2 > r 1), один вставлен в другой, опять пренебрегая краевыми эффектами, считаем поле радиально-симметричным и действующим только между цилиндрическими обкладками. Разность потенциалов между обкладками считаем по формуле для разности потенциалов поля равномерно заряженного бесконечного цилиндра с линейной плотностью τ =Q/l (l -длина обкладок). При наличии диэлектрика между обкладками разность потенциалов (4) Подставив (4) в (1), найдем выражение для емкости цилиндрического конденсатора: (5) Чтобы найти емкость сферического конденсатора, который состоит из двух концентрических обкладок, разделенных сферическим слоем диэлектрика, используем формулу для разности потенциалов между двумя точками, лежащими на расстояниях r 1 и r 2 (r 2 > r 1) от центра заряженной сферической поверхности. При наличии диэлектрика между обкладками разность потенциалов (6) Подставив (6) в (1), получим Если d=r 2 -r 1 пробивным напряжением — разностью потенциалов между обкладками конденсатора, при которой происходит пробой — электрический разряд через слой диэлектрика в конденсаторе. Пробивное напряжение также зависит от формы обкладок, свойств диэлектрика и его толщины. Для увеличения емкости и изменения ее возможных значений конденсаторы соединяют в батареи, при этом применяется их параллельное и последовательное соединения. 1. Параллельное соединение конденсаторов (рис. 1). У параллельно соединенных конденсаторов разность потенциалов на обкладках конденсаторов одинакова и равна φ A – φ B . Если емкости отдельных конденсаторов С 1 , С 2 , …, С n , то, как видно из (1), их заряды есть ………….. а заряд батареи конденсаторов Полная емкость батареи т. е. при параллельном соединении конденсаторов полная емкость равна сумме емкостей отдельных конденсаторов.

Рис. 1

2. Последовательное соединение конденсаторов (рис. 2). У последовательно соединенных конденсаторов заряды всех обкладок равны по модулю, а разность потенциалов на зажимах батареи где для любого из рассматриваемых конденсаторов Δφ i = Q/С i . С другой стороны, откуда т. е. при последовательном соединении конденсаторов суммируются величины, которые обратны емкостям. Значит, при последовательном соединении конденсаторов результирующая емкость С всегда меньше наименьшей емкости, которая используется в батарее.

Методическая разработка заняия по теме «Электрическая емкость. Конденсаторы» | Методическая разработка по физике (10 класс):

Тема: Электрическая емкость. Конденсаторы.

Ход учебного занятия:

1. Организационный момент

Здравствуйте, садитесь! Давайте проверим присутствующих. Староста, пожалуйста.

Тема сегодняшнего занятия: «Электрическая емкость. Конденсаторы». Запишите в тетрадях число и тему занятия. Сегодня нам необходимо изучить  одно из  важных понятий  в электротехнике  – электрическая емкость. А также познакомиться с техническим устройством, главной ценностью которого является накопление электрического заряда и энергии электрического поля.

Цель занятия: изучить, систематизировать и закрепить полученные знания об электрической емкости и конденсаторах (их значение в природе и технике, исследовать закономерности).

2. Фронтальный опрос

Для повторения пройденного материала, предлагаю вам разделиться на группы по 5 человек. Каждая группа получит задание, а потом вы проверите друг друга.

Групповые карточки-задания:

Карточка №1: продолжите предложения, чтобы получились верные утверждения:

1. Передача телу электрического заряда называется …(электризация)
2. Вещество, не имеющее свободных носителей заряда, называется …(диэлектрик)
3. Физическая величина, определяющая способность частиц или тел вступать в электромагнитные силовые взаимодействия, – это …(электрический заряд)
4. Явление перераспределения электрических зарядов в проводнике во внешнем электрическом поле – это …(электростатическая индукция)
5. Поверхности, в каждой точке которых потенциал электрического поля, имеет одно и то же значение, называются …. (эквипотенциальными)

Карточка №2: продолжите предложения, чтобы получились верные утверждения:

1. Наэлектризовать тело можно следующими способами: …(трением, соприкосновением, через влияние)
2. Вещество, имеющее свободные носители заряда, способные перемещаться под действием электрического поля, называется …(проводником)
3. Физическая величина, определяемая отношением работы,совершаемой электрическим полем при перемещении единичного положительного заряда из данной точки в бесконечность, – это …(электрический потенциал)
4. Смещение зарядов или преимущественная ориентация диполей под действием внешнего электрического поля – это …(поляризация)
5. Физическая величина, определяемая как сила, действующая на единичный положительный заряд, помещенный в данную точку поля, называется ….(напряженность)

Теперь проверим выполненные задания друг друга. За каждый правильный ответ – 1 балл. Молодцы. Хорошо потрудились.

3. Изучение нового материала

3. 1. Введение понятия «электрическая емкость»

Что нужно сделать, чтобы наэлектризовать тело? Правильно, сообщить ему электрический заряд. Уединенный проводник – это проводник, размеры которого много меньше расстояния до окружающих тел.

Возьмем электроскоп и будем передавать ему электрический заряд. Мы видим, что с ростом заряда, растет потенциал этого проводника:

Q = C·φ

Электроемкость –  скалярная физическая величина, численно равная отношению заряда, сообщенного проводнику,  к потенциалу, который этот заряд создает на поверхности проводника.

C = 

[С] = 1 Ф (фарада)

Электрическая ёмкость характеризует способность проводника накапливать электрические заряды.

Емкостью 1Ф обладает такой проводник, у которого потенциал возрастает на 1 В при сообщении ему заряда в 1 Кл.

Нам нужно вспомнить, от чего же зависит электроемкость. Самое главное – емкость не нужно сравнивать с вместимостью! Емкость не зависит от заряда проводника, его потенциала, материала из которого он изготовлен. Емкость показывает зависимость между зарядом и потенциалом! Электроемкость проводника зависит от его размеров, формы и среды.

А теперь попробуем свои силы. Давайте посостязаемся. Работаем командами, решаем задачи.

1 команда: Определить потенциал металлического шарика емкостью 4,54 пФ, получившего заряд 1,8·10-7 Кл.	2 команда: При электризации емкость проводника стала равна 150 мкФ, а потенциал 200 В. Какой заряд был сообщен проводнику?
3 команда: Определить емкость металлического шарика, если при сообщении ему  заряда 3·10-8 Кл его потенциал стал равным 6000 В.	4 команда: Какой заряд был сообщен проводнику, если его емкость стала равна 9 пФ, а потенциал 800 В?

Электризация при соприкосновении или электростатическая индукция позволяют получить на поверхности тел лишь сравнительно небольшой электрический заряд. Способность уединенных проводников накапливать электрические заряды ограничена. Чтобы проводник обладал большой емкостью, он должен иметь очень большие размеры. Емкость шара: С = 4πεε0R

3.2. Электрическая емкость системы проводников

Выясним важные для практики вопросы:

• при каком условии можно накопить на проводнике большой электрический заряд?
• Влияет ли на распределение зарядов в проводнике наличие рядом другого проводника?

На практике требуются устройства, способные накапливать значительные заряды. В основы конструкции таких устройств положен тот факт, что электроемкость проводника в окружении других тел возрастает.

Объясняется это тем, что под действием электрического поля заряженного проводника, на поднесенных к нему телах, если это проводники, возникают индуцированные заряды, а если диэлектрики – поляризационные.

Эти заряды будут ослаблять поле проводника. Они понижают его потенциал и повышают его электрическую емкость. Проводники с равными по модулю зарядами будут иметь большую емкость.

Электрическая емкость системы из двух проводников определяется как отношение заряда одного из них к разности потенциалов между ними:

Из формулы видно, что по сравнению с емкостью уединенного проводника, знаменатель дроби уменьшился, а значит емкость увеличилась.

3.3 Введение понятия конденсатор

Конденсатор – это система из двух разноименно заряженных проводников (обкладок), разделенных слоем диэлектрика.

        Электроемкость конденсатора равна отношению заряда одной из пластин Q к напряжению между ними U:

C =

Конденсатор служит для накопления и сохранения  заряда и энергии электрического поля.

Емкость конденсатора зависит от:

•  размеров обкладок,
•  формы обкладок,
•  расположения обкладок,
• диэлектрической проницаемости диэлектрика.

Примерами естественных природных конденсаторов являются облака и земля, линии электропередач, две жилы кабеля. К тому же вы должны помнить, что емкостью обладают не только конденсаторы, но и другие элементы электрических цепей, на которых может накапливаться электрический заряд (провода электрических линий, электроды электронных ламп и пр. ). Чаще мы этой емкостью пренебрегаем.

ЗАДАНИЕ: Изобразите электрическое поле внутри и вне двух параллельных пластин. Пожалуйста, изобразите на доске полученный результат. Обсудим:

Вне пластин векторы Е+ и Е- направлены в разные стороны, и поэтому E = 0. Внутри конденсатора векторы Е+ и Е- сонаправлены; поэтому модуль напряженности суммарного поля равен

Электростатическое поле будет сосредоточено внутри конденсатора между обкладками!

Линии напряженности электрического поля начинаются на положительной обкладке, заканчиваются на отрицательной. Поле практически не рассеивается в окружающем пространстве. На емкость конденсатора не должны оказывать влияния окружающие тела, поэтому проводникам придают такую форму, чтобы поле, создаваемое накапливаемыми зарядами, было сосредоточено в узком зазоре между обкладками конденсатора. Этому условию удовлетворяют:

1) две плоские пластины;

2) два коаксиальных цилиндра;

3) две концентрические сферы.

Поэтому в зависимости от формы обкладок конденсаторы делятся наплоские, цилиндрические и сферические. По типу диэлектрика, помещенного между обкладками, конденсаторы бывают: электролитические (на постоянном токе), бумажные, слюдяные, воздушные.

Сообщение конденсатору заряда называют зарядкой. Под зарядом конденсатора понимают абсолютное значение заряда одной из его обкладок. Чтобы зарядить конденсатор, достаточно сообщить заряд одной из его обкладок, а другую заземлить: при этом на другой обкладке появится заряд, равный по величине и противоположный по знаку заряду первой обкладки из-за явления электростатической индукции. Эффективнее зарядка конденсатора происходит при подключении его обкладок к разноименным клеммам источника постоянного тока.

А теперь нам предстоит определить, от чего зависит емкость конденсатора. Будем первооткрывателями. Исследуем зависимость электроемкости от расстояния между пластинами (1 студент) и от диэлектрической проницаемости диэлектрика (2 студент).

Вывод: При увеличении расстояния между пластинами, напряжение увеличивается, а электроемкость конденсатора уменьшается.

Если между обкладками конденсатора поместить диэлектрик с большей диэлектрической проницаемостью, то напряжение уменьшится, а электроемкость — увеличится.

Физкультминутка: сядьте прямо, руки отведите за спину и сомкните. Представьте, что вы едете в автобусе. Вдруг автобус резко тормозит, что с вами произойдет? А теперь разгоняемся, резко поворачиваем влево, едем прямо, опять поворот направо, стоп. Приехали. Продолжим.

3.4 Энергия заряженного конденсатора

Если обкладки заряженного конденсатора замкнуть металлическим проводником, то по цепи пойдет электрический ток (можно проверить с помощью лампочки),  и ток в цепи будет, пока конденсатор не разрядится. Значит, заряженный конденсатор содержит запас энергии.

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Источник напряжения, поставляя заряды на обкладки конденсатора, производит работу

A = F·d = Eq·d = Wp

Для одной обкладки:

Wp= =

Используя известные вам соотношения, получим формулы для расчета  энергии заряженного конденсатора:

Как сказал английский физик, один из создателей квантовой физики, лауреат Нобелевской премии (1933) Поль Андриен Морис Дирак: «Всякая физическая теория должна быть математически красивой». Формулы получились замечательные! А в каких единицах измеряется энергия?

Электрическую энергию Wр следует рассматривать именно как потенциальную энергию, запасенную в заряженном конденсаторе. По современным представлениям, электрическая энергия конденсатора локализована в пространстве между обкладками конденсатора, то есть в электрическом поле. Поэтому ее называют энергией электрического поля.

Давайте немного порассуждаем, чтобы закрепить полученные знания. Опять поработаем в командах.

Задание 1,3 команде: Как изменятся емкость, заряд, напряженность и энергия поля при удалении диэлектрика с ε? Если конденсатор не отключен от источника напряжения, то U = const!

Емкость		уменьшилась
Заряд		уменьшился
Напряженность		Не изменилась
Энергия электрического поля		уменьшилась

Задание 2,4 команде: Если расстояние между пластинами уменьшили в 2 раза, как изменились емкость, напряжение, напряженность, энергия поля?Если конденсатор отключен от источника напряжения, то q = const!

Емкость		Увеличилась
Напряжение		уменьшилось
Напряженность		Не изменилась
Энергия электрического поля		Уменьшилась

И опять любимые задачи. Работаем в командах.

1 команда: Определить емкость и заряд плоского конденсатора, обкладки которого имеют площадь 10 см2, толщина миканита между ними (ε = 5,2) равна 0,52 мм, а напряжение равно 100 В.	2 команда: Определить емкость и заряд плоского конденсатора, обкладки которого имеют площадь 5 см2, толщина миканита между ними (ε = 5,2) равна 0,885 мм, а напряжение равно 100 В.
3 команда: Определить емкость и заряд плоского конденсатора, обкладки которого имеют площадь 10 см2, толщина миканита между ними (ε = 5,2) равна 0,26 мм, а напряжение равно 100 В.	4 команда: Определить емкость и заряд плоского конденсатора, обкладки которого имеют площадь 10 см2, толщина миканита между ними (ε = 5,2) равна 0,885 мм, а напряжение равно 100 В.

Конденсатор –важное электротехническое устройство. Благодаря своим замечательным свойствам, конденсаторы нашли широкое применение в технике. Конденсаторы применяются, когда нужно:

• Накапливать на короткое время заряд или энергию для быстрого изменения потенциала. Конденсатор способен хранить электрические заряды тем больше, чем больше его емкость. Если необходимо получить электрический ток большой мощности, то выгодно иметь большую силу тока. Конденсатор большой емкости при разрядке дает большую мощность. Пример: фотовспышка
• В клавиатуре компьютера.
• конденсатор как измеритель времени: при зарядке и разрядке конденсатора время этих процессов зависит от емкости конденсатора. Это свойство можно использовать для отсчета времени. Например: часы, реле времени.
• Конденсатор в цепях переменного тока периодически перезаряжается, поэтому по подводящим к нему проводникам постоянно проходит ток, а в цепи постоянного тока конденсатор, зарядившись, ток не пропускает. Поэтому конденсатор можно использовать как фильтр. Пример: выпрямители.
• В зависимости от частоты переменного тока конденсатор быстро или медленно перезаряжается, при этом оказывая разное сопротивление переменному току. Это используют в частотных фильтрах переменного тока. Например: приемный контур радиоприемника, телевизора, генераторы переменных сигналов.

3.5 Соединение конденсаторов в батареи

Во многих случаях для получения нужной емкости конденсаторы приходится соединять в группу, которая называется батареей. Различают два основных типа соединения: последовательное и параллельное. Мы с вами сейчас рассмотрим особенности этих двух видов соединений. Для рациональной работы я попрошу вас подготовить таблицу, которую мы будем заполнять по ходу объяснения материала. Эта таблица поможет вам в подготовке к практической работе, которая будет на следующем занятии:

	Последовательное	Параллельное
схема
Электрический заряд	q = q1 = q2 = q3	q = q1 + q2 + q3
Эквивалентная емкость	=  +  +	С = С1 + С2 + С3

1) При параллельном соединении конденсаторов соединяются их одноименно заряженные обкладки:

Напряжения на конденсаторах одинаковы     U1 = U2 = U (т. к. они подключены к одним и тем же точкам цепи),  заряды равны:

q1 = С1U и    q2 = С2U.

Такую систему можно рассматривать как единый конденсатор электроемкости C, заряженный зарядом q = q1 + q2 при напряжении между обкладками равном U. Отсюда следует:

или С = С1 + С2

Таким образом, при параллельном соединении электроемкости складываются (увеличивается площадь обкладок – растет общая емкость). Такое соединение применяется для увеличения емкости батареи.

 2) При последовательном соединении конденсаторов соединяют разноименно заряженные обкладки:

Заряды обоих конденсаторов одинаковы    q1 = q2 = q (т.к. непосредственно от источника заряжаются только крайние обкладки, а соседние – через влияние),  напряжения на них равны  и 

Такую систему можно рассматривать как единый конденсатор, заряженный зарядом q при напряжении между обкладками U = U1 + U2.

Следовательно,   или  

При последовательном соединении конденсаторов складываются обратные величины емкостей. Последовательное соединение конденсаторов применяется тогда, когда во избежание пробоя большую разность потенциалов требуется распределить между несколькими конденсаторами.

Формулы для параллельного и последовательного соединения остаются справедливыми при любом числе конденсаторов, соединенных в батарею.

Т.е. в случае n конденсаторов одинаковой емкости С емкость батареи

при параллельном соединении Собщ = nС

при последовательном соединении Собщ = С/n

3) методика расчета эквивалентной емкости при смешанном соединении конденсаторов (метод свертывания):

— найти участки с простым соединением конденсаторов;

— по соответствующим формулам, вычислить эквивалентные емкости этих участков;

— перечертить схему, заменив соединения конденсаторов их эквивалентными емкостями;

— повторить алгоритм с начала, пока не останется цепь с одним конденсатором.

Рассмотрим на примере: дан участок цепи со смешанным соединением конденсаторов:

1. Определяют эквивалентную емкость участка с параллельным соединением конденсаторов:

2. Рассчитывают эквивалентную емкость двух последовательно соединенных конденсаторов с емкостями С1 и С2-3:

4 Подведение итогов  и рефлексия

Сегодня мы с вами хорошо поработали. Результаты следующие (выставить и прокомментировать оценки). А еще ответьте на вопросы:

1. Что нового узнали? Чему научились?

2. Пригодятся ли эти знания в вашей профессиональной деятельности?

5 Домашнее задание

1. Приготовить  сообщение (презентацию) по одной из предложенных тем:

— виды конденсаторов;

— применение конденсаторов;

— конденсаторы в электромеханическом оборудовании.

2. Решить задачу: При сообщении конденсатору заряда 5·10-6 Кл его энергия оказалась равной 0,01 Дж. Определить напряжение на обкладках конденсатора.

Хочу закончить это занятие следующим высказыванием: «Хитрые люди презирают знание, простаки удивляются ему, мудрые пользуются им» (Т. Маколей). Всем спасибо. До свидания.

Под новизной понимается отличие полученных (ожидаемых) результатов, рассматриваемых в методической разработке инновационного опыта, от имеющихся и отраженных в научной литературе.

Различают три степени новизны:

1. Методическая разработка уточняет и конкретизирует какие-либо теоретические положения или практические рекомендации.

2.Методическая разработка дополняет, развивает, вносит новые элементы в какие-либо теоретические положения или практические рекомендации.

3.Методическая разработка отражает принципиально новые идеи, концепции, подходы, рекомендации и отличается наиболее высокой степенью новизны.

Рекомендуемый объем — до 2 страниц машинописного текста.

Мозговые «разрушители» — Емкость и т. д.

Мозговые «разрушители» — Емкость и т. д. «Но люди воображают, что знают о природе вещей,
, когда о них не знают, и, не придя в
понимая сначала, потому что думают, что знают, они заканчиваются,
, как и следовало ожидать, в противоречии друг другу и самим себе».
Платон (429-347 до н.э.)
греческий философ,
в Федр (ок. 360 г. до н.э.).

Попробуйте эти «бастеры», чтобы размять свой мозг. .. они должны помочь вам понять концепции, лежащие в основе емкости и т. д. Чтобы получить максимальный эффект, вы должны попытаться ответить на них , прежде чем , глядя на ответы!

---

[1] Конденсатор состоит из двух параллельных пластин, отстоящих друг от друга на d. Верхняя пластина имеет заряд +Q, нижняя пластина имеет заряд -Q. Металлическая пластина толщиной l (d) вставлена ​​между пластинами, но не соединена ни с одной из них. Что произойдет с разностью потенциалов между двумя пластинами, когда пластина вставлена?

Отвечать

---

[2] Конденсатор с плоскими пластинами заряжается от батареи. Затем аккумулятор отключается, но заряд остается на пластинах. Объясните, увеличивается ли, уменьшается или остается неизменным каждое из следующих явлений по мере увеличения расстояния между пластинами:

• емкость конденсатора,
• разность потенциалов между пластинами,
• электрическое поле между пластинами,
• электрическая потенциальная энергия, запасенная конденсатором.

Отвечать

---

[3] Между обкладками конденсатора и система заряжается от аккумулятора. Если батарея отключена и диэлектрик удален, что происходит с энергией, запасенной в конденсаторе?

Отвечать

---

[4] Конденсатор с плоскими пластинами подключен к батарее, поддерживающей постоянную разность потенциалов между пластинами. Пока батарея все еще подключена, вставляется стеклянная пластина, чтобы просто заполнить пространство между пластинами. Что происходит с накопленной энергией?

Отвечать

---

[5] У вас есть четыре одинаковых конденсатора емкостью C каждый. Вам нужно соединить все четыре конденсатора вместе так, чтобы их эквивалентная емкость была равна C. Сколько способов вы можете найти для этого?

Отвечать

---

[6] Два одинаковых плоскопараллельных конденсатора X и Y подключены к аккумулятору, как показано ниже.

Если лист бумаги вставить между пластинами конденсатора Y, как заряд, разность потенциалов и накопленная энергия Y теперь соотносятся с X? То есть эти количества увеличиваются, остаются неизменными или уменьшаются?

Отвечать

---

[7] Представьте, что у вас есть конденсатор с расстоянием между пластинами a, как показано ниже, с пластиной из металла толщиной b между пластинами, которая может перемещаться между пластинами вертикально.

Объясните, что происходит с емкостью системы, когда пластина движется вниз от контакта с верхней пластиной к контакту с нижней пластиной.

Отвечать

---

[8] В этих четырех контурах есть что-то необычное — возможно, забавное или удивительное. Вы можете понять, что это такое?

Отвечать

---

[9] Конденсатор состоит из N параллельных пластин площадью A каждая, расположенных на расстоянии d друг от друга. Второй набор из N одинаковых пластин располагается посередине между первым набором, как показано ниже. Какова общая емкость всей системы?

Отвечать

---

[10] Мы определили, что энергия, запасенная в заряженном конденсаторе, равна

U = (1/2)QV = (1/2)CV ² = (1/2)Q ² /C

Как или каким образом хранится эта энергия . ?

Отвечать

---

[11] На рисунке ниже показан конденсатор с параллельными пластинами, в котором пластины претерпели боковой сдвиг, так что они лишь частично «перекрываются».

Можете ли вы выяснить, какова приблизительная емкость?

Отвечать

---

[12] (Этот мозговой «разрушитель» имеет дело со сравнением «настоящей» батареи с конденсатором в качестве источника энергии.) энергоемкость 3Вт.ч (ватт.час) в новом состоянии.Какую емкость должен иметь конденсатор,чтобы запасать сравнимое количество энергии при 1,5В?Прежде чем начинать пытаться решить задачу…как думаете будет большая или маленькая емкость?

Отвечать

---

[13] Вы и ваш друг стоите как можно ближе друг к другу, фактически не касаясь друг друга.

Если вы оба держите проводник в одной руке, сможете ли вы вычислить его приблизительную емкость?

Отвечать

---

[14] Четыре конденсатора емкостью С расположены, как показано ниже.

Какова эквивалентная емкость между A-B?

Если другой конденсатор емкостью C подключен через X-Y, какова «новая» эквивалентная емкость?

Отвечать

---

Идею «разрушителей мозгов» мне подсказала мисс Лилиан Джордан из муниципального колледжа Палм-Бич. Задачи были собраны из ряда источников на протяжении многих лет, включая меня (!) и вдохновлены идеями из таких текстов, как «Концептуальная физика», Пола Хьюитта, «Работа с коллегами», Эрика Мазура, «Физика». для ученых и инженеров» Пол Типлер, «Университетская физика» Хью Янга и Роджера Фридмана, «Физика» Джона Катнелла и Кеннета Джонсона и «Летающий цирк физики» Джерла Уокера. Я адаптировал их для своих курсов.

18.5 Конденсаторы и диэлектрики | Техасский шлюз

Учебные задачиКонденсаторыУчебные задачиДиэлектрикиУчебные задачиПроверьте свое понимание

Учебные задачи

К концу этого раздела вы сможете делать следующее:

• Вычислять энергию, запасенную в заряженном конденсаторе, и емкость конденсатора
• Объясните свойства конденсаторов и диэлектриков

Основные термины раздела

конденсатор

диэлектрик

Конденсаторы

Снова рассмотрим рентгеновскую трубку, рассмотренную в предыдущем примере задачи. Как создать однородное электрическое поле? Один положительный заряд создает электрическое поле, направленное от него, как показано на рис. 18.18. Это поле неоднородно, так как расстояние между линиями увеличивается по мере удаления от заряда. Однако, если мы объединим положительный и отрицательный заряды, мы получим электрическое поле, показанное на рис. 18.20 (а). Обратите внимание, что между зарядами силовые линии электрического поля расположены более равномерно.

Что произойдет, если мы поместим, скажем, пять положительных зарядов в линию напротив пяти отрицательных зарядов, как показано на рис. 18.29? Теперь область между линиями заряда содержит довольно однородное электрическое поле.

Рис. 18.29. Красные точки — положительные заряды, синие — отрицательные. Направление электрического поля показано красными стрелками. Обратите внимание, что электрическое поле между положительными и отрицательными точками довольно однородно.

Мы можем распространить эту идею еще дальше и на два измерения, поместив две металлические пластины лицом к лицу и зарядив одну положительным зарядом, а другую равной по величине отрицательной зарядкой. Это можно сделать, подключив одну пластину к положительной клемме батареи, а другую пластину к отрицательной клемме, как показано на рис. 18.30. Электрическое поле между этими заряженными пластинами будет чрезвычайно однородным.

Рис. 18.30. Две параллельные металлические пластины заряжаются противоположным зарядом при подключении пластин к противоположным клеммам батареи. Величина заряда на каждой пластине одинакова.

Давайте подумаем о работе, необходимой для зарядки этих пластин. До того, как пластины подключены к батарее, они нейтральны, то есть имеют нулевой суммарный заряд. Размещение первого положительного заряда на левой пластине и первого отрицательного заряда на правой пластине требует очень мало работы, потому что пластины нейтральны, поэтому противоположные заряды отсутствуют. Теперь рассмотрите возможность размещения второго положительного заряда на левой пластине и второго отрицательного заряда на правой пластине. Поскольку первые два заряда отталкивают вновь прибывших, к двум новым зарядам нужно приложить силу на расстоянии, чтобы они оказались на пластинах. Это определение работы, которое означает, что по сравнению с первой парой требуется больше работы, чтобы положить вторую пару зарядов на пластины. Чтобы разместить третий положительный и отрицательный заряды на пластинах, требуется еще больше работы, и так далее. Откуда эта работа? Батарея! Его химическая потенциальная энергия преобразуется в работу, необходимую для разделения положительных и отрицательных зарядов.

Несмотря на то, что батарея работает, эта работа остается в рамках системы аккумуляторной пластины. Следовательно, закон сохранения энергии говорит нам, что если потенциальная энергия батареи уменьшится до отдельных зарядов, энергия другой части системы должна увеличиться на ту же величину. По сути, энергия батареи запасается в электрическом поле между пластинами. Эта идея аналогична рассмотрению того, что потенциальная энергия поднятого молота хранится в гравитационном поле Земли. Если бы гравитационное поле исчезло, у молота не было бы потенциальной энергии. Точно так же, если бы между пластинами не существовало электрического поля, между ними не накапливалась бы энергия.

Если мы сейчас отсоединим пластины от батареи, они будут удерживать энергию. Мы могли бы, например, подключить пластины к лампочке, и лампочка будет гореть до тех пор, пока эта энергия не будет израсходована. Таким образом, эти пластины обладают способностью накапливать энергию. По этой причине устройство, подобное этому, называется конденсатором. Конденсатор — это совокупность объектов, которые в силу своей геометрии могут накапливать энергию электрического поля.

Различные реальные конденсаторы показаны на рис. 18.31. Обычно они изготавливаются из проводящих пластин или листов, разделенных изоляционным материалом. Они могут быть плоскими или свернутыми или иметь другую геометрию.

Рисунок 18.31 Некоторые типовые конденсаторы. (кредит: Уинделл Оскей)

Емкость конденсатора определяется его емкостью C , которая определяется как

18.35 К=КВ,К=КВ,

, где Q — величина заряда на каждой пластине конденсатора, а В — разность потенциалов при переходе от отрицательной пластины к положительной. Это означает, что и Q , и V всегда положительны, поэтому емкость всегда положительна. Из уравнения для емкости видно, что единицами измерения емкости являются C/V, которые называются фарадами (F) в честь английского физика девятнадцатого века Майкла Фарадея.

Уравнение C=Q/VC=Q/V имеет смысл: конденсатор с плоскими пластинами (подобный показанному на рис. 18.30) размером с футбольное поле может удерживать большой заряд, не требуя слишком большой работы на единицу заряда для втолкнуть заряд в конденсатор. Таким образом, Q будет большим, а V будет маленьким, поэтому емкость C будет очень большой. Вдавливание того же заряда в конденсатор размером с ноготь потребовало бы гораздо больше работы, поэтому V было бы очень большим, а емкость была бы намного меньше.

Хотя из уравнения C=Q/VC=Q/V кажется, что емкость зависит от напряжения, на самом деле это не так. Для данного конденсатора отношение запасенного в конденсаторе заряда к разности напряжений между обкладками конденсатора всегда остается одним и тем же. Емкость определяется геометрией конденсатора и материалами, из которых он изготовлен. Для плоского конденсатора, между пластинами которого ничего нет, емкость равна

.

18,36 C0=ε0Ad,C0=ε0Ad,

где А площадь пластин конденсатора и d их расстояние между собой. Мы используем C0C0 вместо C , потому что между пластинами конденсатора ничего нет (в следующем разделе мы увидим, что происходит, когда это не так). Константа ε0,ε0, равная эпсилон ноль , называется диэлектрической проницаемостью свободного пространства, и ее значение равно

.

18,37ε0=8,85  ×  10−12 Ф/мε0=8,85  ×  10−12 Ф/м

Возвращаясь к энергии, запасенной в конденсаторе, мы можем спросить, сколько именно энергии хранит конденсатор. Если конденсатор зарядить, поставив напряжение В через него, например, подключив его к батарее с напряжением В — электрическая потенциальная энергия, запасенная в конденсаторе, равна

18,38 UE=12CV2.UE=12CV2.

Обратите внимание, что форма этого уравнения аналогична форме для кинетической энергии, K=12mv2K=12mv2.

Физика часов

Откуда берется емкость?

В этом видео показано, как определяется емкость и почему она зависит только от геометрических свойств конденсатора, а не от напряжения или накопленного заряда. При этом он дает хороший обзор понятий работы и электрического потенциала.

Щелкните для просмотра содержимого

Проверка захвата

Если увеличить расстояние между пластинами конденсатора, как изменится его емкость?

1. Удвоение расстояния между пластинами конденсатора уменьшит емкость в четыре раза.
2. Удвоение расстояния между пластинами конденсатора уменьшит емкость в два раза.
3. Удвоение расстояния между пластинами конденсатора увеличивает емкость в два раза.
4. Удвоение расстояния между пластинами конденсатора увеличит емкость в четыре раза.

Виртуальная физика

Зарядите конденсатор

Рисунок 18.32 Щелкните здесь, чтобы перейти к моделированию в лаборатории конденсаторов.

Для этой симуляции выберите вкладку Введение в левом верхнем углу экрана. Вам представлен конденсатор с плоскими пластинами, подключенный к батарее переменного напряжения. Аккумулятор изначально находится при нулевом напряжении, поэтому конденсатор не заряжен. Сдвиньте ползунок батареи вверх и вниз, чтобы изменить напряжение батареи, и наблюдайте за зарядами, которые накапливаются на пластинах. Отображение емкости, заряда верхней пластины и накопленной энергии при изменении напряжения батареи. Вы также можете отобразить линии электрического поля в конденсаторе. Наконец, проверьте напряжение между различными точками этой цепи с помощью вольтметра и исследуйте электрическое поле в конденсаторе с помощью детектора электрического поля.

Проверка захвата

Правда или ложь — в конденсаторе накопленная энергия всегда положительна, независимо от того, заряжена ли верхняя пластина отрицательным или положительным зарядом.

1. ложный
2. правда

Рабочий пример

Емкость и заряд, накопленный в конденсаторе с параллельными пластинами

(a) Какова емкость конденсатора с плоскими пластинами, каждая из которых имеет площадь 1,00 м ² , разделенные расстоянием 0,0010 м? б) Какой заряд сохраняется в этом конденсаторе, если напряжение 3,00·10 ³ В на него подается?

СТРАТЕГИЯ ДЛЯ (A)

Используйте уравнение C0=ε0AdC0=ε0Ad.

Решение для (a)

Ввод данных значений в это уравнение для емкости плоского конденсатора дает × 10−9 F=8,9 нФ. C=ε0Ad=(8,85  ×  10-12 Ф/м)1,00 м20,0010 м=8,9 × 10-9 Ф=8,9 нФ.

Обсуждение для (a)

Это маленькое значение емкости указывает на то, насколько сложно сделать устройство с большой емкостью. Помогают специальные методы, такие как использование тонкой фольги очень большой площади, расположенной близко друг к другу, или использование диэлектрика (будет обсуждаться ниже).

СТРАТЕГИЯ ДЛЯ (B)

Зная C , найдите накопленный заряд, решив уравнение C=Q/VC=Q/V для заряда Q .

Решение для (b)

Заряд Q на конденсаторе равен

18,40Q=CV=(8,9×10-9 Ф)(3,00×103 В)=2,7×10-5 C.Q=CV=( 8,9×10−9 F)(3,00×103 В)=2,7×10−5 C

Обсуждение для (b)

Этот заряд лишь немного превышает типичный заряд статического электричества. Больше заряда можно сохранить, используя диэлектрик между обкладками конденсатора.

Рабочий пример

Какая батарея нужна для зарядки конденсатора?

Ваш друг дает вам конденсатор емкостью 10 мкФ10 мкФ. Чтобы хранить 120 мкКл120 мкКл на этом конденсаторе, аккумулятор какого напряжения нужно купить?

СТРАТЕГИЯ

Используйте уравнение C=Q/VC=Q/V, чтобы найти напряжение, необходимое для зарядки конденсатора.

Решение

Решение C=Q/VC=Q/V для напряжения дает V=Q/CV=Q/C. Вставка C=10 мкФ=10×10−6 FC=10 мкФ=10×10−6 F и Q=120 мкC=120×10−6 CQ=120 мкC=120×10−6 C дает

18.41V=QC=120×10−6 C10×10−6 F=12 VV=QC=120×10−6 C10×10−6 F=12 V

Обсуждение

добыть. Остается вопрос, содержит ли аккумулятор достаточно энергии для обеспечения нужного заряда. Уравнение UE=12CV2UE=12CV2 позволяет рассчитать требуемую энергию.

18,42UE=12CV2=12(10×10−6 F)(12 В)2=72 мJUE=12CV2=12(10×10−6 F)(12 В)2=72 мДж

Типичная промышленная батарея может легко обеспечить столько энергии.

Практические задачи

Какое напряжение на 35 мкФ при заряде 25 нКл?

1. 8,75 × 10 ⁻¹³ В
2. 0,71 × 10 ⁻³ В
3. 1,4 × 10 ⁻³ В
4. 1,4 × 10 ³ В

Какое напряжение находится на конденсаторе емкостью 100 мкФ, хранящем 10 Дж энергии?

1. −4,5 × 10 ² В
2. 4,5 × 10 ² В
3. ±4,5 × 10 ² В
4. ±9× 10 ² В

Диэлектрики

Прежде чем работать с некоторыми примерами задач, давайте посмотрим, что произойдет, если мы поместим изоляционный материал между пластинами заряженного конденсатора, а затем отсоединим его от заряжаемой батареи, как показано на рис. 18.33. Поскольку материал является изолирующим, заряд не может через него переходить с одной пластины на другую, поэтому заряд Q на конденсаторе не меняется. Между пластинами заряженного конденсатора существует электрическое поле, поэтому изолирующий материал поляризуется, как показано в нижней части рисунка. Электроизоляционный материал, который поляризуется в электрическом поле, называется диэлектриком.

На рис. 18.33 показано, что отрицательный заряд молекул материала смещается влево, в сторону положительного заряда конденсатора. Этот сдвиг происходит из-за электрического поля, которое действует слева на электроны в молекулах диэлектрика. Правые стороны молекул теперь лишены небольшого количества отрицательного заряда, поэтому их суммарный заряд положительный.

Рисунок 18.33 Верхний и нижний конденсаторы несут одинаковый заряд Q . Верхний конденсатор не имеет диэлектрика между пластинами. Нижний конденсатор имеет диэлектрик между пластинами. Молекулы в диэлектрике поляризуются электрическим полем конденсатора.

Все электроизоляционные материалы являются диэлектриками, но некоторые являются лучшими диэлектриками, чем другие. Хорошим диэлектриком является тот, молекулы которого позволяют своим электронам сильно смещаться в электрическом поле. Другими словами, электрическое поле немного оттягивает их электроны от их атома, но они не убегают полностью от своего атома (именно поэтому они являются изоляторами).

На рис. 18.34 показано макроскопическое изображение диэлектрика в заряженном конденсаторе. Обратите внимание, что линии электрического поля в конденсаторе с диэлектриком разнесены дальше, чем линии электрического поля в конденсаторе без диэлектрика. Это означает, что электрическое поле в диэлектрике слабее, поэтому оно хранит меньше электрической потенциальной энергии, чем электрическое поле в конденсаторе без диэлектрика.

Куда делась эта энергия? На самом деле молекулы в диэлектрике действуют как крошечные пружинки, и энергия электрического поля идет на то, чтобы растянуть эти пружинки. При ослаблении электрического поля разница напряжений между двумя сторонами конденсатора меньше, поэтому становится легче зарядить конденсатор. Таким образом, помещение диэлектрика в конденсатор перед его зарядкой позволяет накопить в конденсаторе больше заряда и потенциальной энергии. Параллельная пластина с диэлектриком имеет емкость

18.43 C=κε0Ad=κC0,C=κε0Ad=κC0,

, где κκ ( каппа ) — безразмерная постоянная, называемая диэлектрической проницаемостью . Поскольку κκ больше 1 для диэлектриков, емкость увеличивается, когда диэлектрик помещается между пластинами конденсатора. Диэлектрическая проницаемость некоторых материалов показана в таблице 18.1.

Under the header “Material” are the following names of materials: “Vacuum”, “Air”, “Fused quartz”, “Neoprene rubber”, “Nylon”, “Paper”, “Polystyrene”, “Pyrex glass”, “Silicon oil”, “Strontium titanate”, “Teflon”, and “Water”. Under the header “Dielectric constant” are the following values: “1.00000”, “1.00059”, “3.78”, “6.7”, “3.4”, “3.7”, “2.56”, “5.6”, “2.5”, “233”, “2.1”, and “80”.»>

Материал	Диэлектрическая проницаемость (κκ)
Вакуум	1.00000
Воздух	1.00059
Плавленый кварц	3,78
Неопреновый каучук	6,7
Нейлон	3,4
Бумага	3,7
Полистирол	2,56
Стекло пирекс	5,6
Силиконовое масло	2,5
Титанат стронция	233
Тефлон	2,1
Вода	80

Таблица 18. 1 Диэлектрическая проницаемость различных материалов при 20 °C

Рис. 18.34. Верхний и нижний конденсаторы несут одинаковый заряд Q. Между пластинами верхнего конденсатора нет диэлектрика. Нижний конденсатор имеет диэлектрик между пластинами. Поскольку некоторые линии электрического поля заканчиваются и начинаются на поляризационных зарядах в диэлектрике, электрическое поле в конденсаторе менее сильное. Таким образом, при том же заряде конденсатор запасает меньше энергии, если он содержит диэлектрик.

Рабочий пример

Конденсатор для фотовспышки

Типичная вспышка для компактной фотокамеры использует конденсатор емкостью около 200 мкФ200 мкФ. (а) Если разность потенциалов между обкладками конденсатора составляет 100 В, то есть 100 В подается «через конденсатор», сколько энергии хранится в конденсаторе? б) Если бы диэлектриком, используемым в конденсаторе, был лист нейлона толщиной 0,010 мм, какова была бы площадь поверхности пластин конденсатора?

СТРАТЕГИЯ ДЛЯ (A)

Учитывая, что V=100 VV=100 В и C=200×10−6 FC=200×10−6 F, мы можем использовать уравнение UE=12CV2UE=12CV2, чтобы найти электрическую потенциальную энергию, запасенную в конденсаторе.

Вставка данных величин в UE=12CV2UE=12CV2 дает

18,44UE=12CV2=12(200×10−6 F)(100 V)2=1,0J.UE=12CV2=12(200×10−6 F )(100 В)2=1,0Дж.

Обсуждение для (a)

Этой энергии достаточно, чтобы поднять 1-килограммовый мяч примерно на 1 м над землей. Вспышка длится около 0,001 с, поэтому мощность, отдаваемая конденсатором за это короткое время, составляет P=UEt=1,0 J0,001 с=1 kWP=UEt=1,0 J0,001 с=1 кВт. Учитывая, что автомобильный двигатель выдает около 100 кВт мощности, для маленького конденсатора это неплохо!

СТРАТЕГИЯ ДЛЯ (B)

Поскольку пластины конденсатора находятся в контакте с диэлектриком, мы знаем, что расстояние между пластинами конденсатора составляет d=0,010 мм=1,0×10−5 md=0,010 мм=1,0×10−5 м. Из предыдущей таблицы диэлектрическая проницаемость нейлона составляет κ = 3,4 κ = 3,4. Теперь мы можем использовать уравнение C=κε0AdC=κε0Ad, чтобы найти площадь A конденсатора.

Решение (b)

Решение уравнения площади A и подстановка известных величин дает

18,45C=κε0AdA=Cdκε0=(200×10−6 F)(1,0×10−5 м)(3,4)(8,85  ×  10−12 F/м)=66 м2. C=κε0AdA=Cdκε0=(200 ×10−6 Ф)(1,0×10−5 м)(3,4)(8,85  ×  10−12Ф/м)=66 м2.

Обсуждение для (b)

Это слишком большая площадь, чтобы свернуть ее в конденсатор, достаточно маленький, чтобы поместиться в переносную камеру. Вот почему в этих конденсаторах используются не простые диэлектрики, а более продвинутая технология для получения высокой емкости.

Практические задания

При напряжении 12 В на конденсаторе он принимает заряд 10 мКл. Какова его емкость?

1. 0,83 мк F
2. 83 μ F
3. 120 мк F
4. 830 мк F

Плоский конденсатор имеет площадь 10 см ² и расстояние между пластинами 100 мк м . Какова его емкость, если между пластинами конденсатора находится бумага?

1. 3,3 × 10 ⁻¹⁰ F
2. 3,3 × 10 ⁻⁸ F
3. 3,3 × 10 ⁻⁶ F
4. 3,3 × 10 ⁻⁴ F

Проверьте свое понимание

Упражнение 13

Если площадь плоского конденсатора удвоится, как изменится его емкость?

1. Емкость останется прежней.
2. Емкость удвоится.
3. Емкость увеличится в четыре раза.
4. Емкость увеличится в восемь раз.

Упражнение 14

Если удвоить площадь пластинчатого конденсатора и уменьшить расстояние между пластинами в четыре раза, как изменится емкость?

1. Увеличится в два раза.
2. Увеличится в четыре раза.
3. Увеличится в шесть раз.
4. Увеличится в восемь раз.

• Печать
• Поделиться

Энергия, хранящаяся в конденсаторах | Физика

Цели обучения

К концу этого раздела вы сможете:

• Перечислить некоторые области применения конденсаторов.
• Выразите в виде уравнения энергию, запасенную в конденсаторе.
• Объясните работу дефибриллятора.

Большинство из нас видели инсценировки, в которых медицинский персонал использует дефибриллятор для пропускания электрического тока через сердце пациента, чтобы заставить его нормально биться. (Рассмотрите рисунок 1.) Часто реалистично в деталях, человек, применяющий разряд, приказывает другому человеку «сделать на этот раз 400 джоулей». Энергия, подаваемая дефибриллятором, сохраняется в конденсаторе и может регулироваться в зависимости от ситуации. Часто используются единицы СИ – джоули. Менее драматично использование конденсаторов в микроэлектронике, например, в некоторых карманных калькуляторах, для подачи энергии при зарядке аккумуляторов. (См. рис. 1.) Конденсаторы также используются для питания ламп-вспышек на камерах.

Рисунок 1. Энергия, запасенная в большом конденсаторе, используется для сохранения памяти электронного калькулятора, когда его батареи заряжаются. (кредит: Kucharek, Wikimedia Commons)

Энергия, хранящаяся в конденсаторе, представляет собой электрическую потенциальную энергию и, таким образом, связана с зарядом Q и напряжением V на конденсаторе. Мы должны быть осторожны, применяя уравнение для электрической потенциальной энергии ΔPE = q Δ В к конденсатору. Помните, что ΔPE — это потенциальная энергия заряда q прохождение напряжения Δ В . Но конденсатор начинает с нулевого напряжения и постепенно достигает своего полного напряжения по мере зарядки. Первый заряд, помещенный на конденсатор, испытывает изменение напряжения Δ В  = 0, поскольку в незаряженном состоянии конденсатор имеет нулевое напряжение. Окончательный заряд, помещенный на конденсатор, испытывает Δ В  =  В , так как на конденсаторе теперь есть полное напряжение В . Среднее напряжение на конденсаторе в процессе зарядки равно [latex]\frac{V}{2}\\[/latex], поэтому среднее напряжение при полной зарядке q — это [латекс]\frac{V}{2}\\[/латекс]. Таким образом, энергия, запасенная в конденсаторе E _cap , равна [latex]E_{\text{cap}}=\frac{QV}{2}\\[/latex], где Q  — заряд. на конденсатор с напряжением В подается . (Обратите внимание, что энергия равна не QV , а [латекс]\frac{QV}{2}\\[/латекс].) Заряд и напряжение связаны с емкостью C конденсатора как Q = CV , поэтому выражение для 92}{2C}\\[/latex],

, где Q — заряд, V — напряжение, а C — емкость конденсатора. Энергия в джоулях для заряда в кулонах, напряжения в вольтах и ​​емкости в фарадах.

В дефибрилляторе доставка большого заряда коротким импульсом к набору пластин на груди человека может спасти жизнь. Сердечный приступ у человека мог возникнуть в результате быстрого, нерегулярного сокращения сердца — сердечной или желудочковой фибрилляции. Применение сильного разряда электрической энергии может остановить аритмию и позволить кардиостимулятору вернуться к нормальной работе. Сегодня в машинах скорой помощи обычно есть дефибриллятор, который также использует электрокардиограмму для анализа характера сердцебиения пациента. Автоматические наружные дефибрилляторы (АНД) можно найти во многих общественных местах (рис. 2). Они предназначены для использования мирянами. Устройство автоматически диагностирует состояние сердца пациента, а затем применяет разряд с соответствующей энергией и формой волны. СЛР рекомендуется во многих случаях перед использованием AED.

Рис. 2. Автоматические наружные дефибрилляторы можно найти во многих общественных местах. Эти портативные устройства дают словесные инструкции по использованию в первые несколько важных минут для человека, страдающего сердечным приступом. (кредит: Owain Davies, Wikimedia Commons)

Пример 1. Емкость дефибриллятора сердца

Дефибриллятор сердца вырабатывает 4,00 × 10 ² Дж энергии, разряжая конденсатор первоначально при 1,00 × 10 ⁴ Что такое V. его емкость?

9{-6}\text{ F}\\\text{ }&=&8. {2}}{2C}\\[/latex], где  Q — заряд, V — напряжение, C — емкость конденсатора. Энергия выражается в джоулях, если заряд – в кулонах, напряжение – в вольтах, а емкость – в фарадах.

Концептуальные вопросы

1. Как изменяется энергия, содержащаяся в заряженном конденсаторе, когда в него вставлен диэлектрик, если предположить, что конденсатор изолирован и его заряд постоянен? Означает ли это, что работа была сделана?
2. Что происходит с энергией, запасенной в конденсаторе, подключенном к батарее, когда в него вставлен диэлектрик? Была ли работа выполнена в процессе?

Задачи и упражнения

1. (a) Какая энергия хранится в конденсаторе 10,0 мкФ сердечного дефибриллятора, заряженного до
   9,00 × 10 ³ В? б) Найдите количество накопленного заряда.
2. При операции на открытом сердце для дефибрилляции сердца требуется гораздо меньшее количество энергии. а) Какое напряжение приложено к конденсатору 8,00 мкФ сердечного дефибриллятора, хранящего 40,0 Дж энергии? б) Найдите количество накопленного заряда.
3. Конденсатор емкостью 165 мкФ используется вместе с двигателем. Сколько энергии хранится в нем, когда 119V применяется?
4. Предположим, у вас есть батарея на 9,00 В, конденсатор на 2,00 мкФ и конденсатор на 7,40 мкФ. а) Найдите запасенный заряд и энергию, если конденсаторы соединены с батареей последовательно. (b) Сделайте то же самое для параллельного соединения.
5. Нервный физик опасается, что две металлические полки его книжного шкафа с деревянной рамой могут получить высокое напряжение, если они будут заряжены статическим электричеством, возможно, вызванным трением. а) Какова вместимость пустых полок, если их площадь 1,00 × 10 ² м ² и находятся на расстоянии 0,200 м друг от друга? б) Чему равно напряжение между ними, если на них поместить противоположные заряды величиной 2,00 нКл? (c) Чтобы показать, что это напряжение представляет небольшую опасность, рассчитайте накопленную энергию.
6. Покажите, что для данного диэлектрического материала максимальная энергия, которую может хранить конденсатор с плоскими пластинами, прямо пропорциональна объему диэлектрика (объем = A  · d ). Обратите внимание, что приложенное напряжение ограничено диэлектрической прочностью.
7. Создайте свою собственную задачу.  Рассмотрите дефибриллятор сердца, подобный описанному в примере 1. Постройте задачу, в которой вы исследуете заряд, хранящийся в конденсаторе дефибриллятора, как функцию накопленной энергии. Среди вещей, которые необходимо учитывать, — приложенное напряжение и должно ли оно меняться в зависимости от подаваемой энергии, диапазон вовлеченных энергий и емкость дефибриллятора. Вы также можете рассмотреть гораздо меньшую энергию, необходимую для дефибрилляции во время операции на открытом сердце, как вариант этой проблемы.
8. Необоснованные результаты. (a) В определенный день для запуска двигателя грузовика требуется 9,60 × 10 ³ Дж электроэнергии. Вычислите емкость конденсатора, способного хранить такое количество энергии при напряжении 12,0 В. (b) Что неразумного в этом результате? (c) Какие предположения ответственны?

Глоссарий

дефибриллятор:  устройство, используемое для подачи электрического разряда в сердце жертвы сердечного приступа с целью восстановления нормального ритма сердца

Избранные решения задач и упражнений

1. (a) 405 Дж; (б) 90,0 мКл

2. (а) 3,16 кВ; (б) 25,3 мКл

4. (а) 1,42×10 ^–5 Кл, 6,38×10 ^–5 Дж; (б) 8,46×10 ⁻⁵ С, 3,81×10 ⁻⁴ Дж

5. (а) 4,43×10 ^–12 F; (б) 452 В; (в) 4,52 × 10 ^–7 Дж

8. (а) 133 F; (b) Такой конденсатор будет слишком большим, чтобы его можно было перевозить на грузовике. Размер конденсатора был бы огромным; (c) Неразумно предполагать, что конденсатор может хранить необходимое количество энергии.

Capacitor Energy — AP Physics 2

Все ресурсы AP Physics 2

6 Диагностические тесты 149 практических тестов Вопрос дня Карточки Learn by Concept

AP Physics 2 Справка » Электричество и магнетизм » Схемы » Компоненты схемы » Энергия конденсатора

Рассмотрим схему:

Если падение напряжения на C2 равно 5 В, какова общая энергия, накопленная в C2 и C3?

Возможные ответы:

Правильный ответ:

Пояснение:

В параллельных ветвях цепи падения напряжения одинаковы. Следовательно, мы знаем, что падение напряжения на C3 также равно 5В.

Затем мы можем использовать следующее уравнение для расчета общей накопленной энергии:

Поскольку напряжение обоих конденсаторов одинаково, мы можем просто сложить две емкости, чтобы выполнить одно вычисление энергии:

Сообщить об ошибке

Конденсатор подключен к аккумулятору. Когда конденсатор полностью заряжен, сколько энергии запасается?

Возможные ответы:

Ни один из других ответов не является правильным

Правильный Ответ:

19

30. Объяснение:

Чтобы найти количество энергии, запасенной в конденсаторе, мы используем уравнение

.

Нам известны емкость () и напряжение (), поэтому воспользуемся третьим уравнением.

Сообщить об ошибке

У вас есть 4 конденсатора, , , , и , , расположенные, как показано на схеме ниже.

Их емкости следующие:

Если к цепи подключена батарея на 6 В, какова общая энергия, хранящаяся в конденсаторах?

Возможные ответы:

Правильный ответ:

Объяснение:

Уравнение для энергии, хранящейся в конденсаторе, выглядит так:

При добавлении конденсаторов помните, как добавлять последовательно и параллельно.

Конденсаторы  и  соединены последовательно,  и  соединены параллельно, и  и  соединены параллельно.

Теперь, когда у нас есть полная емкость, мы можем использовать предыдущее уравнение, чтобы найти энергию.

Суммарная накопленная энергия составляет 121,5 Дж.

Сообщить об ошибке

Если , и , сколько энергии хранится в ?

Возможные ответы:

Правильный ответ:

Объяснение:

В этой цепи источник напряжения,  и , и  параллельны, то есть имеют одинаковое напряжение.

Чтобы найти энергию, мы можем использовать формулу

, где – энергия, – емкость, а – падение напряжения на этом конденсаторе.

Чтобы использовать формулу, нам нужно напряжение на .

Еще одна подсказка, которую мы можем использовать, заключается в том, что  и  имеют одинаковый заряд, поскольку они соединены последовательно. Сначала найдем эквивалентную емкость:

Теперь мы можем использовать формулу

для расчета заряда конденсатора.

Теперь, когда мы знаем, что в обоих конденсаторах имеется заряд , мы можем снова использовать формулу, чтобы найти напряжение только в .

Наконец, мы подставляем это в первое уравнение для расчета энергии.

Сообщить об ошибке

Представьте конденсатор с величиной заряда Q на каждой пластине. Этот конденсатор имеет площадь A, разделительное расстояние D и не подключен к батарее. Если какое-то внешнее воздействие разорвет конденсатор так, что D удвоится, увеличится, уменьшится или останется неизменной внутренняя энергия U, хранящаяся в конденсаторе?

Возможные ответы:

Остается постоянным

Увеличивается

Необходимо знать диэлектрическую проницаемость

Уменьшается

Правильный ответ:

109

Увеличивается

1 Объяснение:

Требуемые уравнения:

 

Из первого уравнения видно, что при удвоении D C уменьшится вдвое (поскольку  и  постоянны). Из третьего уравнения мы исходим из того, что при уменьшении C вдвое потенциальная энергия U удвоится.

Сообщить об ошибке

Представьте конденсатор с величиной заряда Q на каждой пластине. Этот конденсатор имеет площадь A, разделительное расстояние D и подключен к батарее с напряжением V. Если какое-то внешнее воздействие разъединит конденсатор, так что D удвоится, внутренняя энергия U, запасенная в конденсаторе, увеличится, уменьшится или останется на прежнем уровне? такой же?

Возможные ответы:

Увеличивается

Остается постоянным

Уменьшается

Увеличивается ровно в 2 9 раз0021

Правильный ответ:

Уменьшение

Объяснение:

Соответствующие уравнения:

 

В этой задаче мы должны отметить, что напряжение V поддерживается батареей постоянным. Глядя на второе уравнение, если C изменяется (за счет изменения D), то Q должен измениться, когда V поддерживается постоянным. Это означает, что наша формула для U должна быть изменена. Как мы можем делать заявления относительно U, если Q и C изменяются? Нам нужна постоянная переменная в уравнении для U, чтобы мы могли установить прямую связь между D и U. Если мы подставим второе уравнение в третье, мы получим:

Теперь мы знаем, что V поддерживается батареей постоянным, поэтому, когда C уменьшается (поскольку D удваивается), мы видим, что здесь U действительно уменьшается. Поэтому имеет значение, подключен ли конденсатор к батарее.

Сообщить об ошибке

Уведомление об авторских правах

Все ресурсы AP Physics 2

6 Диагностические тесты 149 практических тестов Вопрос дня Карточки Learn by Concept

Электрическое сопротивление

Ом. Как протекает ток в цепи с конденсатором?

Спросил 1 год, 3 месяца назад

Изменено 1 год, 3 месяца назад

Просмотрено 10 тысяч раз

$\begingroup$

Когда конденсатор подключен к батарее, в цепи начинает течь ток, который заряжает конденсатор до тех пор, пока напряжение между обкладками не станет равным напряжению батареи.

Так как между обкладками конденсатора находится изолятор/диэлектрик, как возможно, что в цепи с конденсатором протекает ток, ведь по закону Ома ток обратно пропорционален сопротивлению, а изолятор по определению имеет большое сопротивление, так что у нас в основном разомкнутая цепь?

• электрические цепи
• электрическое сопротивление
• напряжение
• емкость
• диэлектрик

$\endgroup$

$\begingroup$

Так как это физика q и a, объяснение физики в порядке.

Есть два вида тока.

Ток проводимости представляет собой чистый поток зарядов. Это то, о чем люди обычно думают, когда используют слово «ток».

Ток смещения — еще одна форма тока, впервые обнаруженная Максвеллом. Ток смещения играет существенную роль в уравнениях Максвелла. Плотность тока смещения пропорциональна производной по времени от изменения плотности электрического потока.

Когда ток электронов течет в одну сторону конденсатора, электроны накапливаются, так как им некуда деваться. По мере накопления электронов плотность электрического потока изменяется. Это вызывает или, возможно, «является» током смещения.

На противоположной обкладке конденсатора происходит аналогичный процесс, но с противоположной электрической полярностью.

Ток смещения течет от одной пластины к другой через диэлектрик всякий раз, когда ток втекает или выходит из пластин конденсатора, и имеет точно такую ​​же величину, что и ток, протекающий через клеммы конденсатора.

Можно предположить, что этот ток смещения не имеет никакого реального эффекта, кроме «сохранения» тока. Однако ток смещения создает магнитные поля так же, как и ток проводимости.

Этот ответ, возможно, больше, чем хотелось бы знать, но это часть истории электричества, которую стоит рассказать.

$\endgroup$

1

$\begingroup$

как возможно, что ток течет в цепи с конденсатором так как по закону Ома сила тока обратно пропорциональна сопротивление, а изолятор по определению имеет большое сопротивление, поэтому мы в основном есть разомкнутая цепь?

Короткий ответ заключается в том, что электроны могут течь к конденсатору и от него без необходимости прохождения электронов через изоляцию между пластинами. Предлагается следующее качественное объяснение:

Если предположить, что конденсатор изначально не заряжен, то перед его подключением к батарее каждая металлическая пластина имеет равное количество протонов (положительный заряд) и высокоподвижных электронов (отрицательный заряд), так что каждая пластина электрически нейтральна и между пластинами нет напряжения (разности потенциалов).

Когда конденсатор подключен к батарее, положительная клемма батареи притягивает электроны от пластины, соединенной с ним, перемещая их к положительной клемме батареи. Это оставляет дефицит электронов на этой пластине, что делает ее положительно заряженной.

В то же время отрицательный полюс батареи подает равное количество электронов на подсоединенную к нему пластину, создавая избыток электронов, делая пластину отрицательно заряженной.

Это перемещение электронов с одной пластины на положительную клемму батареи и с отрицательной клеммы батареи на другую пластину представляет собой ток конденсатора. Обратите внимание, что электроны не проходят через изоляционный материал (диэлектрик) между пластинами.

Вы можете представить себе это примерно как электроны, «стягиваемые» с одной пластины и «выталкиваемые» на другую силой электрического поля, создаваемого батареей, но заряды «застревают» на пластине. пластины, потому что они не могут пройти через изолирующий диэлектрик.

В конце концов, как вы, кажется, уже знаете, батарея перестает перемещать электроны между пластинами, когда разность потенциалов между пластинами становится равной разности потенциалов батареи.

Надеюсь, это поможет.

$\endgroup$

9

$\begingroup$

Удаление электронов с обкладки конденсатора, подключенной к клемме +, представляет собой ток. Поскольку эти электроны удаляются для этой пластины, происходит накопление электронов на другой пластине. Это движение электронов составляет ток.

Ток прекращается, когда потенциалы обкладок конденсатора становятся равными потенциалам соответствующих клемм батареи. Это не происходит мгновенно, а скорее зависит от времени, потому что транспорт электронов из конденсатора и в него требует времени, а потенциалы зависят от дисбаланса заряда пластин.

$\endgroup$

$\begingroup$

Наличие плоского конденсатора означает, что в части цепи (лишь малая часть; конденсаторы редко имеют такой большой зазор как один миллиметр) нет движения электронов, только накопление поля (в сопровождении электронов, если конденсатор не вакуумный тип). Это проблематично, потому что есть простой способ обнаружения ток, который заключается в наблюдении за магнитным полем, создаваемым током, и ЧАСТЬ цепи больше не имеет тока.

Дело в том, что «поправка» на магнитное поле не существует. Соответствующее уравнение Максвелла для тока, создающего магнетизм имеет член, добавленный к текущему току смещения, который представляет собой скорость изменения электрическое поле (например, поле внутри диэлектрика конденсатора). Это дополнение к уравнению необходимо не только для цепей, у него есть дополнительный побочный эффект, заключающийся в том, что изменяющееся электрическое поле создает магнитное поле даже при отсутствии движущихся заряженных частиц.

Этот член уравнения объясняет, почему электромагнитные волны (свет) путешествует в вакууме. И, почему зарядка конденсатора (по-нашему измерений) неотличимы от непрерывного течения тока в цепь.

Буквально мы можем видеть, как светит солнце, потому что в цепи есть разрыв конденсатора. не отличим от непрерывного тока в цепи.

$\endgroup$

2

$\begingroup$

Конденсатор действительно блокирует постоянный ток (DC). Однако значительный переменный ток (AC) может протекать, когда период колебаний меньше времени зарядки конденсатора.

$\endgroup$

3

$\begingroup$

Накачка электронов в одну пластину конденсатора приводит к тому, что свободные электроны на другой пластине отталкиваются, когда они «видят» входящие другие электроны. другая пластина. Для больших тарелок этот короткий импульс длинный, а для маленьких тарелок короткий импульс.

Это означает, что короткие импульсы переменного тока могут легко протекать через конденсатор, в то время как установившийся постоянный ток полностью блокируется.

$\endgroup$

$\begingroup$

Емкость (конденсатор) может первоначально заряжаться при кратковременном накоплении заряда на конденсаторе при замыкании цепи. Обычно:

$𝑡 = 𝑅.𝐶$

С:

$R$: Сопротивление цепи.

$C$: значение емкости.

На самом деле это и есть механизм способности емкости пропускать переменную во времени составляющую сигнала (ток, индуцированный изменением заряда на стенках емкости), блокируя при этом постоянную его компонент.

$\endgroup$

Твой ответ

Зарегистрируйтесь или войдите в систему

Зарегистрируйтесь с помощью Google

Зарегистрироваться через Facebook

Зарегистрируйтесь, используя электронную почту и пароль

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Опубликовать как гость

Электронная почта

Требуется, но не отображается

Нажимая «Опубликовать свой ответ», вы соглашаетесь с нашими условиями обслуживания, политикой конфиденциальности и политикой использования файлов cookie

.

Энергия, хранящаяся в конденсаторах | Физика |

Цели обучения

К концу этого раздела вы сможете:

• Перечислить некоторые области применения конденсаторов.
• Выразите в виде уравнения энергию, запасенную в конденсаторе.
• Объясните работу дефибриллятора.

Большинство из нас видели инсценировки, в которых медицинский персонал использует дефибриллятор для пропускания электрического тока через сердце пациента, чтобы заставить его нормально биться. (Рассмотрите рисунок 1.) Часто реалистично в деталях, человек, применяющий разряд, приказывает другому человеку «сделать на этот раз 400 джоулей». Энергия, подаваемая дефибриллятором, сохраняется в конденсаторе и может регулироваться в зависимости от ситуации. Часто используются единицы СИ – джоули. Менее драматично использование конденсаторов в микроэлектронике, например, в некоторых карманных калькуляторах, для подачи энергии при зарядке аккумуляторов. (См. рис. 1.) Конденсаторы также используются для питания ламп-вспышек на камерах.

Рисунок 1. Энергия, запасенная в большом конденсаторе, используется для сохранения памяти электронного калькулятора, когда его батареи заряжаются. (кредит: Kucharek, Wikimedia Commons)

Энергия, хранящаяся в конденсаторе, представляет собой электрическую потенциальную энергию и, таким образом, связана с зарядом Q и напряжением V на конденсаторе. Мы должны быть осторожны, применяя уравнение для электрической потенциальной энергии ΔPE = q Δ В к конденсатору. Помните, что ΔPE — это потенциальная энергия заряда q прохождение напряжения Δ В . Но конденсатор начинает с нулевого напряжения и постепенно достигает своего полного напряжения по мере зарядки. Первый заряд, помещенный на конденсатор, испытывает изменение напряжения Δ В  = 0, поскольку в незаряженном состоянии конденсатор имеет нулевое напряжение. Окончательный заряд, помещенный на конденсатор, испытывает Δ В  =  В , так как на конденсаторе теперь есть полное напряжение В . Среднее напряжение на конденсаторе в процессе заряда 9 В.0021

V2\frac{V}{2}\\2V​

, поэтому среднее напряжение при полной зарядке q равно

V2\frac{V}{2}\\2V​

. Таким образом, энергия, запасенная в конденсаторе, E _cap , равна

Ecap=QV2E _{\text{cap}}=\frac{QV}{2}\\Ecap=2QV​

, где Q — заряд конденсатора при напряжении В . (Обратите внимание, что энергия равна не QV , а

QV2\frac{QV}{2}\\2QV​ 92}{2C}\\Ecap=2QV=2CV2=2CQ2

, где Ом — заряд, В — напряжение, С — емкость конденсатора. Энергия в джоулях для заряда в кулонах, напряжения в вольтах и ​​емкости в фарадах.

В дефибрилляторе доставка большого заряда короткой очередью к набору пластин на груди человека может спасти жизнь. Сердечный приступ у человека мог возникнуть в результате быстрого, нерегулярного сокращения сердца — сердечной или желудочковой фибрилляции. Применение сильного разряда электрической энергии может остановить аритмию и позволить кардиостимулятору вернуться к нормальной работе. Сегодня в машинах скорой помощи обычно есть дефибриллятор, который также использует электрокардиограмму для анализа характера сердцебиения пациента. Автоматические наружные дефибрилляторы (АНД) можно найти во многих общественных местах (рис. 2). Они предназначены для использования мирянами. Устройство автоматически диагностирует состояние сердца пациента, а затем применяет разряд с соответствующей энергией и формой волны. СЛР рекомендуется во многих случаях перед использованием AED.

Рис. 2. Автоматические наружные дефибрилляторы можно найти во многих общественных местах. Эти портативные устройства дают словесные инструкции по использованию в первые несколько важных минут для человека, страдающего сердечным приступом. (кредит: Оуайн Дэвис, Wikimedia Commons)

Пример 1. Емкость дефибриллятора сердца

Сердечный дефибриллятор выдает 4,00 × 10 ² Дж энергии, разряжая конденсатор первоначально при 1,00 × 10 ⁴ В. Какова его емкость? 9{-6}\text{ F}\\\text{ }&=&8.00\mu\text{F}\end{массив}\\C ​==​V22Ecap​​=(1.00×104 В)22 (4,00×102 Дж)​=8,00×10−6 F8,00 мкФ​

Обсуждение

Это довольно большая, но управляемая емкость при 1,00 × 10 ⁴  В.

Резюме раздела

• Конденсаторы используются в различных устройствах, включая дефибрилляторы, микроэлектронику, такую ​​как калькуляторы, и лампы-вспышки, для подачи энергии. .
• Энергия, запасенная в конденсаторе, может быть выражена тремя способами:  9{2}}{2C}\\Ecap=2QV=2CV2=2CQ2
  , где Q  – заряд, V  – напряжение, а C  – емкость конденсатора. Энергия выражается в джоулях, если заряд – в кулонах, напряжение – в вольтах, а емкость – в фарадах.

Концептуальные вопросы

1. Как изменяется энергия, содержащаяся в заряженном конденсаторе, когда в него вставлен диэлектрик, если предположить, что конденсатор изолирован и его заряд постоянен? Означает ли это, что работа была сделана?
2. Что происходит с энергией, запасенной в конденсаторе, подключенном к батарее, когда в него вставлен диэлектрик? Была ли работа выполнена в процессе?

Задачи и упражнения

1. (a) Какая энергия хранится в конденсаторе 10,0 мкФ сердечного дефибриллятора, заряженного до

   9,00 × 10 ³ В? б) Найдите количество накопленного заряда.

2. При операции на открытом сердце для дефибрилляции сердца требуется гораздо меньшее количество энергии. а) Какое напряжение приложено к конденсатору 8,00 мкФ сердечного дефибриллятора, хранящего 40,0 Дж энергии? б) Найдите количество накопленного заряда.
3. Конденсатор емкостью 165 мкФ используется вместе с двигателем. Сколько энергии запасается в нем при подаче 119 В?
4. Предположим, у вас есть батарея на 9,00 В, конденсатор на 2,00 мкФ и конденсатор на 7,40 мкФ. а) Найдите запасенный заряд и энергию, если конденсаторы соединены с батареей последовательно. (b) Сделайте то же самое для параллельного соединения.
5. Нервный физик опасается, что две металлические полки его книжного шкафа с деревянной рамой могут получить высокое напряжение, если они будут заряжены статическим электричеством, возможно, вызванным трением. а) Какова вместимость пустых полок, если их площадь 1,00 × 10 ² м ² и находятся на расстоянии 0,200 м друг от друга? б) Чему равно напряжение между ними, если на них поместить противоположные заряды величиной 2,00 нКл? (c) Чтобы показать, что это напряжение представляет небольшую опасность, рассчитайте накопленную энергию.
6. Покажите, что для данного диэлектрического материала максимальная энергия, которую может хранить конденсатор с плоскими пластинами, прямо пропорциональна объему диэлектрика (объем = A  · d ). Обратите внимание, что приложенное напряжение ограничено диэлектрической прочностью.
7. Создайте свою собственную задачу.  Рассмотрите дефибриллятор сердца, подобный описанному в примере 1. Постройте задачу, в которой вы исследуете заряд, хранящийся в конденсаторе дефибриллятора, как функцию накопленной энергии. Среди вещей, которые необходимо учитывать, — приложенное напряжение и должно ли оно меняться в зависимости от подаваемой энергии, диапазон вовлеченных энергий и емкость дефибриллятора. Вы также можете рассмотреть гораздо меньшую энергию, необходимую для дефибрилляции во время операции на открытом сердце, как вариант этой проблемы.
8. Необоснованные результаты. (a) В определенный день для запуска двигателя грузовика требуется 9,60 × 10 ³ Дж электроэнергии. Вычислите емкость конденсатора, способного хранить такое количество энергии при напряжении 12,0 В. (b) Что неразумного в этом результате? (c) Какие предположения ответственны?

Глоссарий

дефибриллятор:  устройство, используемое для подачи электрического разряда в сердце жертвы сердечного приступа с целью восстановления нормального ритма сердца

Избранные решения задач и упражнений

1.